Introduction

Seagrasses are bottom-attached, flowering plants adapted to exist fully submersed in salty and brackish coastal water. They support numerous fish species as their feeding ground and shelter (Block et al. 2016; Green & Short 2003; Short et al. 2007). Seagrasses impact the water column's physical and chemical composition by controlling the amount of dissolved oxygen, nutrients, and chlorophyll (Nixon & Oviatt 1972; Short & Short 1984). They are also a vital part of the blue carbon ecosystems, coastal ocean ecosystems that store a significant amount of CO2. Seagrasses capture CO2 at an average rate of 586–681 g m−2 year−1(Duarte et al. 2010), which is approximately 35 times faster than a tropical forest for a unit area (Mcleod et al. 2011).

Seagrasses exhibit complex growth behavior to environmental variables. Their habitats are partly driven by sexual productive systems that depend on local environmental factors (Phillips & Backman 1983; Robertson & Mann 1984). The interplay of depth (Duarte 1991) and light penetration (Drew 1979), the impact of temperature (Pérez and Romero 1992), sediment nutrients (F. T. Short 1987), and oxygen production (Bulthuis 1983) exhibit nonlinear relationships for seagrass presence. Understanding factors that promote and hinder seagrass growth is vital for conservation planning and mitigation strategies. Predictive models of species' habitats have been instrumental in predicting ecosystems' future health at varying time scales ranging from short-term impacts of anthropogenic activities (Hughes et al. 2003) to long-term impacts of climate change (Halpern et al. 2008). Specific species can serve as an indicator for their ecosystem's overall health (Carignan and Villard 2002), thus placing quantitative habitat models in the center of ecosystem preservation and planning workflows ( Guisan and Thuiller 2005). Despite their importance for our planet, seagrass habitats do not have global protection (Orth et al. 2006). Modeling studies are performed to understand the conditions that support seagrass habitats and aid in conserving this vital species under stress (Evans et al. 2018; Thayer et al. 1975; Jayathilake and Costello 2018; Downie et al. 2013; Krause-Jensen and Duarte 2014).

An empirical model between seagrass presence and environmental variables is proposed to explicitly model conditions that favor seagrass growth (Fong et al. 1997). Relationships between temperature, salinity, light, phosphorus concentration, and sediment concentration were used to predict seagrass species' productivity (Fong et al. 1997). Short and Neckles (1999) provide a survey of methods to characterize seagrass habitats as they pertain to modeling the impact of global climate change on seagrass habitats. A challenge in modeling seagrass habitats is defining salient relationships between environmental factors and habitat formation that cover a wide range of values. General-purpose species distribution models (SDMs) are utilized to model habitat suitability from the presence and absence of seagrass species at survey locations via regression analysis (Guisan & Zimmermann 2000). A frequently used regression model is the generalized linear model (Nelder and Wedderburn 1972), particularly logistic regression (Cox 1958; Hosmer and Lemeshow 1989). The presence and absence of a target species are encoded with a binary variable, and its relationships to environmental variables are modeled via a linear model (Green et al. 1990; Manel et al. 2001; Osborne and Tigar 1992; Pearce and Ferrier 2000). Support-vector machine is another frequently-used technique due to its ability to capture nonlinear relationships and fit a model with multicollinear predictors (Lek et al. 1996; Manel et al. 1999). Lastly, tree-based methods are used in capturing complex relationships in ecological predictors and the presence-absence of a species (Cutler et al. 2007b). The random forest (RF) has shown promising results for exploring drivers underlying habitats and defining predictive SDMs (Cutler et al. 2007a).

Logistic regression suffers from multicollinearity when predictor variables with strong linear relationships exist. This shortcoming is limiting for environmental drivers such as temperature and dissolved nutrients where linear relationships are significant. Thus, SDMs that rely on generalized linear regression models are limited in their application to include not linearly independent variables. A popular nonlinear method, support vector machines (SVMs), suffers from overfitting to training data and doesn't have intuitive model outputs that explain drivers behind habitat formation. Presence-absence data is often unbalanced, with the majority of measurements consisting of presence labels. Under such training data, SVMs are prone to overestimate presence and underestimate absence. Classification and regressions trees (CARTs) are prone to overfitting to the data and require regularization. Random forest methodology is introduced to avoid overfitting to data with minimal hyper-parameter optimization. However, during random subsampling of training data to define decision trees, the minority category is often underrepresented in defining CARTs. Some CARTs in a random forest model may not receive any absences samples in cases where absence observations are sparse, a common aspect for presence-absence data. In ecological studies, presence is often the dominating label that generally makes up more than 90% of observations (Fielding and Bell 1997), making RF unsuitable for such unbalanced data.

Despite its sparseness, absence data contains vital information on conditions that do not favor a species' growth and sustenance. We propose a balanced random forest model that takes advantage of the random forest methodology and samples presences and absences via stratified sampling. We discuss the significance of modeling absence conditions for conservation planning and focus our study on the Australian coast's seagrass biome that stretches for 32,000 km, containing the most spatially extensive (approximately 50,000 km2) and diverse seagrass habitat (Butler and Jernakoff 1999). Scenarios that involve changes to environmental conditions or anthropological drivers require effective modeling of conditions that hinder a species growth. We use two independent datasets to quantify the balanced random forest methodology's predictive power for our study.

Materials and methods

Overall workflow

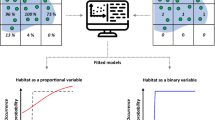
The overall workflow for making predictions of seagrass habitats along the Australian coast is summarized in Fig. 1.

Fig. 1
figure 1

Overall workflow for the seagrass presence-absence absence model of Australian coast. Orange indicates raw data, green indicates processed data, blue are modeling steps, and yellow symbolizes predictions of seagrass presence-absence

Full size image

In this paper, the predictive model is trained on presence and absence data from the Australian Centre for Ecological Analysis and Synthesis (ACEAS) that is enriched with environmental variables from the Ecological Marine Units (EMU) dataset (Sayre et al. 2017), and the nearest distance to a major port. Port locations are obtained from the World Port Index. The data is spatially and tabularly wrangled to remove inconsistent data points. Coincident data points, points with the same latitude and longitude, in the ACEAS dataset are removed. The resulting seagrass presence and absence locations are geoenriched by extracting the values of the ocean conditions at these locations and computing the nearest distance to a major port. The resulting spatial data frame is the training dataset for the balanced random forest and random forest models. Predictions from both models are compared to assess the value in target label (presence-absence) balancing. In this paper, we perform internal validation by assessing the performance of both predictive models on the training dataset from ACEAS. External validation for presence-absence prediction accuracy is assessed using the test dataset from ACEAS. Lastly, seagrass habitat (presence) prediction accuracy is assessed externally with the CAMRIS dataset by mapping the predicted seagrass habitats from models trained on the ACEAS presence-absence dataset on observed seagrass habitats from CAMRIS.

Data sources

Training dataset: ACEAS presence-absence dataset

We train random forest models on presence-absence data compiled by the Australian Centre for Ecological Analysis and Synthesis (ACEAS) along the Australian coast and assess the quality of the results on occurrence polygons defined in the Coastal and Marine Resources Information System (CAMRIS) dataset.

The Australian Centre produced a seagrass habitat map for Ecological Analysis and Synthesis (ACEAS) as part of its seagrass habitat risk modeling effort. Areas of seagrass presence delineated in this dataset are based on the National Intertidal-Subtidal Benthic (NISB) habitat map and UNEP WCMC seagrass map of 2005.

The ACEAS seagrass presence-absence dataset used in this study is merged for the entire Australian coast from the original data source that divides the data into five distinct geographic areas: Northern Territory (NSW) (Canto et al. 2014a); Queensland (QLD) (Canto et al. 2014b); South Australia (SA) (Canto et al. 2014c); Tasmania (TAS) (Canto et al. 2014d); and Western Australia (WA) (Canto et al. 2014e). Seagrass presence-absence observations for the Australian coast are depicted in Fig. 2.

Fig. 2
figure 2

Seagrass presence-absence for Australian coast. Green indicate seagrass presence and red indicates seagrass absence. Basemap courtesy of Esri Ocean Basemap and its partners

Full size image

Figure 2 displays the spatial heterogeneity of seagrass presence and absence. The ACEAS dataset does not contain data for the Joseph Bonaparte Gulf (JBG). However, it contains detailed presence-absence data for the rest of the Australian coast. Dense observations of seagrass absence near Montebello Saddle makes up more than 90% of the absence data.

In this study, ACEAS seagrass presence-absence data displayed in Fig. 2 is used as training data for (balanced) random forest models. ACEAS dataset consists of 1737 distinct locations where seagrass presence-absence was recorded. Seagrass absence was recorded at 42 locations or 2.4% of the observations, making this dataset highly imbalanced for classifying presence-absence.

Validation dataset for seagrass biome: CAMRIS seagrass occurrence polygons

Our approach to validating the results of the proposed SDM is performed with an independent seagrass presence dataset. Seagrass presence polygons of the Coastal and Marine Resources Information System (CAMRIS) (Neil et al. 1994) are used to assess random forest and balanced random forest performance for seagrass prediction at the Australian coast. A depiction of the CAMRIS seagrass dataset is presented in Fig. 3.

Fig. 3
figure 3

CAMRIS Seagrass Presence Polygons for Australian Coast. Basemap courtesy of Esri Ocean Basemap and its partners

Full size image

The CAMRIS dataset contains small-scale national maritime spatial analysis system outputs from several research divisions of the CSIRO (Neil et al. 1994). In particular, seagrass polygons displayed in Fig. 3 are mapped by the CSIRO Division of Fisheries.

The CAMRIS dataset is used to assess the accuracy of balanced random forest and serve as ground truth for evaluating the impact of balancing in modeling with random forest. In Fig. 3, note the break in CAMRIS data for the coast of the Timor Sea. Generalizability assessments of balanced random forest and random forest will be conducted in portions of the Australian coast where presence data is present as a part of the CAMRIS dataset.

Environmental predictors: Ecological Marine Units (EMU) dataset

Baseline physicochemical conditions are obtained from the neritic portion of the globally-extensive Ecological Marine Units (EMU) dataset (Sayre et al. 2017). The EMU dataset is a compilation of:

  • World Oceans Atlas (WOA) dataset version 2 (Locarnini et al. 2013; Zweng et al. 2013; Garcia et al.  2014a, 2014b)

  • 13 year average of chlorophyll-a levels from NASA Aqua-MODIS (Savtchenko et al. 2004)

  • Seafloor depths and geomorphology from SRTM30 (Farr et al. 2007 and Harris et al. 2014)

  • Additional derived outputs of marine ecosystems (Sayre et al. 2017).

The WOA dataset version 2 is compiled from various ocean research and monitoring programs dating back to the 1960s. The EMU dataset involves spatial discretization over 52 million points up to a maximum depth of 5,500 m.

Components of the WOA dataset consist of temperature (Locarnini et al. 2013), salinity (Zweng et al. 2013), dissolved oxygen (Garcia et al. 2014b), and nutrient data (phosphate, nitrate, and silicate) (Garcia et al. 2014a) are corrected for the effect of pressure at different depths (Sayre et al. 2017). Data from the WOA have a horizontal spatial resolution of ¼° × ¼° for temperature and salinity (~ 27 × 27 km at the equator), and 1° × 1° for oxygen, nitrate, phosphate, and silicate. The EMU dataset downscales 1° × 1° variables onto a ¼° × ¼° grid for consistency in the spatial scale of each variable (see Sayre et al. (2017) for the downscaling procedure). Vertical resolution is adaptive, starting with 5-m increments near the surface to 100-m increments at depth. The maximum depth for this study is 100 m, which is reported as the light penetration limit in the literature (Dennison 1987b; Pérez and Romero 1992; Bulthuis 1983). The following parameters from the EMU dataset are used in the predictive model for seagrass occurrence-absence in the coast of Australia: temperature (oC), salinity [PSU], nitrate (µmol/l), silicate (µmol/l), phosphate (µmol/l), apparent oxygen (µmol/l), oxygen saturation (µmol/l), dissolved oxygen (µmol/l), srtm30 (m), 13-year average Chlorophyll-a (mg/m3). Note that redundancy and multicollinearity in the dataset are expected, as solubility depends on temperature and three predictors on oxygen content exist.

Anthropologic explanatory variables: ship traffic & distance to coast

We include distance-to-main-harbors and coastlines as additional predictors for seagrass habitats. The aim is to capture the impact of anthropological impacts of ship traffic and human activity on seagrass presence-absence. We acknowledge that human impact on seagrasses is multi-faceted, and these variables are intended to serve as a precursor in modeling studies for seagrass habitats.

Scars in seagrass beds form due to mechanical impact caused by ship propellers at shallow depths (Zieman 1976). Scarring can permanently damage an area if a contiguous portion of seagrasses is uprooted due to heavy ship traffic (Dawes et al. 1997; Bell et al. 2002; Uhrin and Holmquist 2003). The harbors are used as a proxy for ship traffic, and a subset of the World Port Index (WPI) dataset (National Geospatial-Intelligence Agency 2009) is utilized. The WPI dataset contains information on approximately 3700 ports throughout the world with harbor classifications such as very small (V), small (S), medium (M), and large (L) based on such factors as area, facilities, and wharf space. A subset of the WPI dataset contains 143 large (L) harbors and seven on the Australian coast. A depiction of the WPI for large harbors at the Australian coasts used in this study is given in Fig. 4.

Fig. 4
figure 4

Major harbors in Australia from WPU dataset. Basemap courtesy of Esri Ocean Basemap and its partners

Full size image

Distance-to-shore is incorporated as another distance variable to model the impact of variations to coast on seagrass occurrence. Shoreline data used in this study are from a 10-m-resolution multi-line shoreline dataset (Kelso and Patterson 2009).

Methods

Balanced random forest model for sparse seagrass absence data

We propose defining a random forest model with balanced CARTs to effectively represent the impact of sparse absence data for learning patterns between seagrass presence/absence and explanatory variables (environmental and anthropological). In random forest models, each tree is created by sampling the training dataset with replacement using approximately two-thirds of the training data (Breiman 1996, 2001). Under sparse data conditions, data randomly sampled data available to a CART may not contain the sparse category, resulting in CARTs that cannot distinguish two categories. Balanced sampling constrains the number of samples for each decision tree with respect to the minority-label sample size. In the context of balancing for the minority category, we employ a down-sampling scheme dictated by the minority category sample size (Chen et al. 2004).

The balanced sample obtained from the data is then randomly sampled to build decision trees. The balanced sampling scheme employed is summarized pictorially in Fig. 5.

Note in Fig. 5 middle step for stratified sampling exists to obtain a balanced sample from the original (unbalanced) dataset. Stratified sampling is repeated for the majority label (in black) before randomly sub-sampled to build decision trees. Balancing scheme produces samples balanced decision tree receives is a subsample of the stratified sample. In a species distribution model, the balancing allows a similar number of absence and presence conditions in every decision tree.

Fig. 5
figure 5

Random (A) and Balanced (B) sampling for decision trees. Balanced sampling scheme for unbalanced training data. T denotes trees making up the random forest

Full size image

Random sampling does not guarantee sampling of the minority label in the process of creating decision trees. Thus, decision trees will be prone to predict the majority category, and the one that receives a small number of (or none) minority categories will be shallow (one level). Thus, they cannot learn patterns in physicochemical variables and distance features from seagrass presence and absence.

One disadvantage of balancing is the restriction on sample size. Figure 5 illustrates that the number of samples received by every tree is dictated by the minority label's (absence) sample size. For the ACEAS dataset that contains 42 locations with seagrass absence, every tree will have 84 data points after stratification, and on average, every tree will receive roughly 67% of these 84 data points. Thus, a higher number of decision trees need to be built than the random forest model without balancing to ensure all the available data is used in building decision trees for the random forest.

This study uses the ArcGIS Pro (Law and Collins 2020) implementation of random forest algorithm (Forest-Based Classification and Regression, FBCR) with the balancing scheme implemented as proposed in this section. The random forest model implemented for FBCR has full parity with the randomForest package in R.

Accuracy metrics for seagrass habitat prediction

We test the efficiency and accuracy of balancing in the context of habitat modeling for the following metrics:

  1. 1.

    Sensitivity, Presence Prediction Accuracy (PPA)

  2. 2.

    Specificity, Absence Prediction Accuracy (APA)

  3. 3.

    True Skill Statistic (TSS) (Omri et al. 2006)

  4. 4.

    Matthew's Correlation Coefficient (MCC) (Matthews 1975)

Some of the metrics above, such as TSS and MCC, quantify the effective overall accuracy of a classifier in the presence of rare categories. They are sensitive to recall rate for minority category and effectively quantify a classifier's accuracy in the presence of rare categories. In the context of presence-absence modeling, these metrics quantify the overall accuracy of predicted absence and presence. Secondly, we include APP and PPP to quantify retrieval characteristics of presence and absence separately. For effective conservation modeling, understanding conditions that result in the absence of seagrass is vital. Thus, we use these metrics to evaluate the usefulness of BRF for informing conservation.

We adopt terminology specific to presence-absence modeling and denote confusion matrix rates related to habitat modeling in Table 1.

Table 1 Confusion Matrix Rates for Presence Absence Modelling
Full size table

Comparison metrics are defined in terms of the confusion rates in Table 1 as follows:

$$PPA= \frac{TP}{TP+FP}$$
(1)
$$APA= \frac{TA}{TA+FA}$$
(2)
$$TSS= \frac{TA}{TA+FA}+\frac{TP}{TP+FP}-1$$
(3)
$$MCC=\frac{TA.TP-FA.FP}{\sqrt{\left(TA+FA\right)\left(TA+FP\right)\left(TP+FA\right)\left(TP+FP\right)}}$$
(4)

Results

The predictive performance of BRF and RF do not improve after 1,000,000 trees. Thus, we report our accuracy metrics for BRF and RF models with 1,000,000 trees with no level limitation on decision trees. We train models on 90% of the presence/absence data from ACEAS and cross-validate against the remaining 10%. We use stratified sampling to ensure the presence/absence ratio in both datasets are the same. We present accuracy metrics in Fig. 6.

Fig. 6
figure 6

Comparison of Accuracy Metrics for Balanced Random Forest and Random Forest for forest models with 1,000,000 trees with unlimited forest depth

Full size image

BRF predicts absence data with an accuracy of 80% from the test sample compared to RF, which predicts absence with 58% as per APA distribution (Fig. 6). PPA results indicate an overall 20% improvement in absence prediction for BRF. PPA comparison shows, on average, BRF underestimates presence by 5% when compared to RF. As per the TSS metric, the BRF model's average accuracy is 72%, compared to the RF model's average accuracy of 60%. Lastly, MCC shows considerably low accuracy for the BRF model (42%) compared to RF (76%), conflicting with the one suggested by TSS. We discuss this in further detail in the discussion section.

Impact of forest depth and size on model accuracy

We evaluate performance metrics as a function of the number of trees and tree depth. The rule of thumb for the number of trees in a random forest creates as many as computationally feasible. As per tree depth, a measure of model complexity, the desirable level is the smallest one with high model accuracy, as per Occam's Razor. Thus, understanding changes to model accuracy concerning the number of trees informs convergence behavior in the SDM context. Furthermore, limiting maximum tree depth (level) is common in forest-based models to avoid over-fitting. Thus, a forest-based model that can achieve high accuracy with low maximum tree depth is preferred in practice.

We compare the MCC for BRF and RF for models with different numbers of trees and maximum tree depth. MCC surfaces for forest-based models with changing maximum tree depth and number of trees are depicted in Fig. 7.

Fig. 7
figure 7

Response surface for MCC with respect to maximum tree depth and number of trees

Full size image

BRF model outperforms RF, with the highest MCC for RF being at 0.5 and 0.75 for BRF (Fig. 7). We note that both methods are sensitive to maximum tree depth. For deep forest-based models (Max. Tree Depth > 5), where it is allowed to learn complex relationships between explanatory variables and presence/absence, BRF is sensitive to the forest number. Shallow models show higher accuracy for the BRF model. The RF model does not predict absence for any forest-based model shallower than seven levels, indicating that absence information cannot be captured with RF with simple CARTs.

Next, we evaluate the True Skill Statistics for both models. As per our results on forest-based models with an unlimited depth of trees, TSS shows a considerable performance disparity between BRF and RF.

Note that for deeper forest-based models, BRF is more sensitive to the number of trees. Thus, if a balancing scheme is utilized for sparse absence data, we observe that rule of thumb for the number of trees holds. The average TSS for BRF with 106 trees is at 95%, whereas the RF's maximum accuracy is 25% (Fig. 8). Lastly, we compare the method's accuracy for their retrieval characteristics for presence and absence (Fig. 9).

Fig. 8
figure 8

Response surface for TSS with respect to maximum tree depth and number of trees

Full size image
Fig. 9
figure 9

Response surfaces for Presence Prediction Accuracy and Absence Prediction Accuracy with respect to maximum tree depth and number of trees

Full size image

APA comparison shows a stark difference between BRF and RF, with BRF predicting absence at an average rate of 99% for experiments where maximum tree depth is more than eight. For the same experiments, RF predicts absence with an average accuracy of 21%. RF predicts presence with an average of 99% in all experiments, whereas BRF predicts 80%. The RF model can capture patterns behind seagrass presence with simpler (smaller maximum tree depth) forest models than BRF. BRF's presence prediction accuracy increases drastically for complex forest models where the maximum tree depth is eight or more.

Variable importance for predicting seagrass presence/absence

Variable importance is a critical metric for understanding each explanatory variables' impact on ecological prediction results (Cutler et al. 2007a). We performed 1000 permutations to address this challenge. The distribution of variable importance for 1000 balanced random forest model is depicted with a violin plot in Fig. 10.

Fig. 10
figure 10

Balanced random forest variable importance on EMU variables’ and distance features’ impact on seagrass occurrence

Full size image

Variable significance defined by BRF possesses a strong modality for every predictor. Thus, the importance of physicochemical variables and distance features are stable between different runs, with the average importance for a predictor is most frequently observed. This behavior is an indicator of model stability, showing that the model does not suffer from the randomness of data even in the presence of unbalanced absence labels. The same analysis is conducted for the random forest, and the violin plot for variable importance is displayed in Fig. 11.

Fig. 11
figure 11

Random forest variable importance on EMU variables’ and distance features’ impact on seagrass occurrence

Full size image

Note that the variable importance for most predictors in the RF model does not display strong modality. Phosphate, silicate, and distance to coast exhibit quasi-uniform distributions of model importance between different runs. Lack of modality implies variable importance varies vastly due to the randomness of the training data's subsamples. Similar to BRF, distance to the coast has the highest average variable importance. However, it is difficult to discern the second most important variable. Percent oxygen saturation, phosphate, and temperature have similar medians with a quasi-uniform distribution. Thus the second most important variable will vary vastly due to random sampling of training data. Variable importance rank for the two models is compared in Table 2.

Table 2 Variable importance rank for balanced random forest and random forest
Full size table

Note that random forest (without balancing) cannot capture the relationship between chlorophyll-a content and seagrass presence-absence. Similarly, SRTM 30, a proxy for light penetration, is an uninfluential predictor for the random forest, and it is the most important variable for the balanced random forest.

Comparison of prediction performance of BRF and RF at the Australian coast

We assess the accuracy of balanced random forest in areas where seagrass-absence is predicted and juxtapose it against the CAMRIS dataset. We acknowledge the time lag between the two datasets and that we are investigating areas where absence is predicted where the CAMRIS dataset indicates seagrass presence. In all of the results below, we train BRF and RF on the entire ACEAS dataset. We compared our predictions against CAMRIS for all study areas except Joseph Bonaparte Gulf that falls outside of the CAMRIS dataset's coverage.

Hervey BAY and Fraser Island

We first focus on Hervey Bay and Fraser Island, where strong spatial variability of seagrass habitats exist. The disparity in seagrass habitat suitability between Hervey Bay and Fraser Island has been reported (Lee Long et al. 1993). Accurate prediction of seagrass presence-absence in such areas indicates that a balanced random forest does capture spatial variability in seagrass occurrence. BRF and RF predictions from the ACEAS dataset are overlain on CAMRIS seagrass polygons in Fig. 12.

Fig. 12
figure 12

Seagrass presence-absence predicted using balanced random forest (above) and random forest (below) between Hervey Bay and Fraser Island. Basemap courtesy of Esri Ocean Basemap and its partners

Full size image

Locations where seagrass presence-absence is predicted from the ACEAS dataset using BRF, does not contradict seagrass polygons given by CAMRIS. BRF models the absence of seagrass at higher depths, where RF predicts the presence of seagrass indiscriminately. Note that random forest predicted the entire area as seagrass presence, including the shore of Fraser Island. Absence prediction is in 95% agreement with the CAMRIS data, with only a single location inside CAMRIS presence polygon predicted as an absence.

Coast of Far North Queensland

Seagrasses in North Queensland's shores are reported to exist at shallow depths, highest biomass existing at depths 2–6 m (Coles et al. 1987). BRF trained on ACEAS data is utilized to predict seagrass presence-absence in this area, and the result is mapped in Fig. 13.

Fig. 13
figure 13

Seagrass presence-absence predicted using balanced random forest (above) and random forest (below) between Princess Charlotte Bay and Cooktown. Basemap courtesy of Esri Ocean Basemap and its partners

Full size image

BRF model predicts the absence of seagrass at depths exceeding 20 m, supporting the findings from a previous study conducted in the area (Rasheed et al. 2016) (Fig. 13). Note that SRTM 30 was the most important variable for BRF. Thus the impact of depth on seagrass absence was readily captured at this location. Random forest predicted only seagrass occurrence for the data, violating the previous observations reported in the literature (Rasheed et al. 2016). CAMRIS presence polygons are patchy for this study area, and only two localized spots are identified with the presence of seagrass near Cooktown. A similar trend is observed in BRF, with the absence locations predicted in high numbers in the southern section of the study area near Cooktown.

Joseph Bonaparte Gulf (JGB)

Lastly, we compare seagrass-presence absence from Joseph Bonaparte Gulf (JBG). CAMRIS data does not contain seagrass occurrence polygons for this area. JBG is an example of the importance of accurate SDMs because neither ACEAS nor CAMRIS contains data in this region. Delineating seagrass species is crucial for preservation due to oil and gas exploration and production proposals in this area.

An updated report of seagrass beds for this area (Przeslawski et al. 2011) will be used to investigate discrepancies between balanced random forest and random forest outputs. Seagrass presence-absence predictions from both methods are depicted in Fig. 14.

Fig. 14
figure 14

Seagrass presence-absence predicted using balanced random forest (above) and random forest (below) for eastern Joseph Bonaparte Gulf (JBG). Basemap courtesy of Esri Ocean Basemap and its partners

Full size image

Seagrass patches in the Eastern JBG coast are reported in the following areas: King Shoals, Medusa Banks, Howland Shoals, Emu Reefs (Przeslawski et al. 2011; RPS 2009). King Shoal is identified with seagrass presence with both models. Medusa Banks, Howland Shoals, and Emu Reefs are modeled as seagrass absence by RF, but it is modeled as a presence by BRF. Predictions of the balanced random forest also follow empirical evidence regarding the optimal depths for seagrass presence. Note that balanced random forest defines suitable habitats for seagrass near the shore, whereas random forest predicts absence at these locations.

Torres Strait

Torres Strait is characterized by high spatial heterogeneity of seagrass occurrence reflected by heterogeneity in the sea surface's depth (Harris 1988) and dynamics of sediments making up the seafloor (Hemer et al. 2004). We predict the presence and absence of seagrass with BRF and RF models trained on the ACEAS dataset. The resulting predictions are juxtaposed against the CAMRIS presence polygons in Fig. 15.

Fig. 15
figure 15

Seagrass presence-absence predicted using balanced random forest (above) and random forest (below) for the Torres Strait. Basemap courtesy of Esri Ocean Basemap and its partners

Full size image

RF model did not define the absence of seagrasses in the study area whereas (Fig. 15). Compared to presence polygons given in the CAMRIS dataset, BRF has an absence prediction accuracy of 92%, whereas RF is 0%. RF shows a 100% presence prediction accuracy because it only predicts presence, and BRF has a presence prediction accuracy of 85%.

Due to the availability of high spatial heterogeneity between presence and absence points, we demonstrate the differences in environmental and anthropological drivers' seagrass presence and absence as defined by the BRF model.

Significant disparities in environmental variables between areas where seagrass are observed vs. absent exist (Fig. 16). We note that dissolved oxygen content is one of the most distinguishing variables. This finding does not contradict common understanding about these species. Seagrasses produce oxygen as a part of photosynthesis, resulting in high oxygen content in areas where they are found. Areas where seagrasses are modeled to be absent, and confirmed by the CAMRIS dataset, are the ones that have high salinity and low nutrient content.

Fig. 16
figure 16

Comparison of Distribution of Explanatory Variables at the Torres Strait between modelled locations with and without seagrass

Full size image

Impact of absence data for conservation planning: Gulf of Carpenteria

Our study's focus is representing sparse absence data for presence/absence modeling of the seagrass biome at the Australian Coast. This section demonstrates the impact of incorporating absence data for seagrass habitat prediction and its consequences for conservation planning.

Two new ports are proposed for the Gulf of Carpenteria. The first port is proposed to be built in Karumba Point was expected to open up the area for international trade (Taylor et al. 2008). Port of Karumba will be connected to Mt Isa with a 450 km rail line, allowing a direct connection to the mines. The port has since come online for shipping traffic, and its vicinity is being monitored for seagrass populations (Taylor et al. 2008). However, it has not been operational at the time of data collection. Thus its impact is not reflected in the training data.

The second proposed port is near the Roper River's outlet, and the initial stage proposed is a barge landing to support mining operations (Fitzgerald 2018). The proposed port is located at the north-western corner of the gulf. We will refer to this port as the Roper Port.

We use presence/absence models trained on ACEAS datasets to delineate areas that two new ports might impact. We model the impact of new ports as distance features and predict seagrass presence/absence using BRF and RF. We numerically represent the extent of dredging due to ship traffic with a distance feature to proposed ports. We demonstrate the value of effectively utilizing sparse absence data via balancing for conservation planning. We train a BRF and RF model on the entire ACEAS dataset and predict seagrass presence/absence on the scenario that contains two new ports in the Gulf of Carpentaria. The resulting maps are displayed in Fig. 17.

Fig. 17
figure 17

Maps displaying predicted seagrass presence absence with addition of two proposed ports in the Gulf of Carpentaria. BRF (Above) and RF (below). Basemap courtesy of Esri Ocean Basemap and its partners

Full size image

BRF predicts seagrass habitat loss in an area east of the Wellesley Islands. ACEAS dataset contains areas similar to this area that are shallow and proximal to a port to exhibit seagrasses' absence. Note that the SDM forecast indicates potential seagrass loss that can be more spatially extensive than the predicted area. Nevertheless, the BRF model captures patterns observed in training data that resulted in seagrass absence. RF model did not capture any spatial variation in seagrass habitat due to the abundance of seagrass presence samples in the training dataset. We investigate differences in environmental conditions between areas modeled to experience seagrass loss due to proposed ports vs. others.

We observe differences in environmental variables between areas modeled to lose seagrasses compared and areas not modeled to be impacted by proposed harbors (Fig. 18). We note that areas around Wellesley Islands are lower in dissolved oxygen compared to the coast of the Gulf of Carpenteria. Our model indicates that added stress from ship traffic can result in seagrass habitat loss in these areas. Similarly, areas prone to seagrass loss due to proposed ports are characterized by low nitrate, phosphate, and high silicate levels. BRF finds patterns in presence/absence data that correspond to seagrass absence in areas close to major ports with low nutrient levels, high silicate levels, and high oxygen content. Note that BRF does not indicate causation for seagrass loss. Rather it finds similarities between the training dataset, ACEAS, and the scenario that contains two new proposed ports in the Gulf of Carpenteria (Fig. 18).

Fig. 18
figure 18

Juxtaposition of environmental variables between areas where seagrass is modelled as present vs absent

Full size image

Discussion

The discrepancy between TSS and MCC

BRF predictions result in a high TSS and a low MCC, two metrics with contradicting outcomes about the proposed approach's performance (Fig. 6). Firstly, we observe that the multiplicative false recall rates \(FA.FP\) in Eq. 4 can underestimate the overall error rate in cases where a method, such as RF, predicts presence at all prediction locations, \(FP=0\). We further observe that TSS serves as a more stable metric as FA and FP's impact are represented as additive terms in the denominator in Eq. 4. The limit behavior of MCC in the context of absence prediction is as follows:

$${lim}_{\left(TA+FA\right)\to 0}MCC\to 1$$
(5)

Thus, for cases where RF does not predict absence for any sample, a high MCC value is observed. In our experiments, we observe that for cases where both methods correctly identify at least one absence location, MCC results in informative metrics. Our randomized experiments contain cases where RF does not predict absence in the study area, resulting in a misleadingly high MCC.

Differences in required model complexity & performance

Our results indicate that BRF requires a deeper, higher number of trees to reach the same accuracy for presence (Fig. 9). BRF describes conditions that result in the absence accurately with moderately deep trees (more than four levels) and requires a high number of trees for stability. This result is due to stratified sampling that reduces the sample size available for every tree to \(2{n}_{abs}\) with \({n}_{abs}\) the number of absence labels in the training data. Thus, under stratification, more trees are required to learn patterns of presence/absence. Our results support this behavior due to a considerable increase in APA, PPA, and TSS for large maximum tree depth (Figs. 7, 8, 9).

Our results show that BRF provides a method for accurately modeling conditions that result in the presence and absence of seagrass jointly for large maximum tree depth. From a practical perspective, BRF allows defining a flexible SDM that can be improved with a high number of trees. In contrast, our experiments show that RF cannot learn sparse absence category, even with a high number of decision trees and unlimited depth. Thus, RF has limitations on its ability to learn sparse absence even when trained with a high number of deep decision trees.

Lastly, the BRF model suffers from its predictive abilities for the presence category. The stratified sampling scheme inadvertently censors the prevalence presence labels. BRF exceeds RF in overall predictive capabilities by at least 20% improvement on TSS (Fig. 8). However, the PPA for BRF is consistently lower compared to RF (Fig. 9). This effect is due to restricting the amount of presence data a decision tree can use, thus limiting presence patterns.

Data-driven drivers behind seagrass presence/absence

Our results indicate that the BRF model captures environmental drivers' impact on seagrass presence-absence that supports biological studies on seagrasses. In particular, the niche identified by the BRF model shows that seagrasses in the Australian coast are most sensitive to the distance to coast, SRTM30, and temperature (Fig. 10). The first two variables are proxies for the depth of the water column. Various authors study the impact of water depth on seagrass growth, and depth is an important driver as it controls light penetration (Drew 1979; Dennison 1987a; Duarte et al. 2007). The temperature's impact is significant on net photosynthesis rate and dark respiration (Pérez and Romero 1992). The RF model defines the distance to coast as the most important predictor, while the importance of SRTM30 and temperature are lowered (Fig. 11). Unbalanced presence/absence labels used in training CARTs in RF can mask the impact of important drivers such as temperature and SRTM30, since the variability of the target variable (presence indicator) is lower per tree.

As per nutrients used in this study, phosphate is the most important nutrient as per BRF results (Fig. 10). Seagrasses in tropical environments growing in carbonate sediments are reported to experience phosphorus limitation (F. T. Short 1987). Thus, changes to phosphorus in the water column are expected to a distinguishing factor for where seagrasses are present. Phosphate is also an important variable in the RF model(Fig. 11). However, permutation tests show that its importance varies significantly (Fig. 11). Lastly, chlorophyll's importance for modeling the presence and absence of seagrass varies greatly between BRF (Fig. 10) and RF (Fig. 11). BRF model assigns high importance to chlorophyll, whereas RF is the variable with the least average importance (Fig. 11). The importance of chlorophyll level for defining whether a location has seagrass or not is intuitive and also reported in the literature (F. T. Short and Neckles 1999).

Impact of absence data for conservation planning

We juxtaposed BRF and RF models trained on the ACEAS presence-absence dataset with the presence polygons of the CAMRIS dataset. ACEAS dataset consisted of 99% seagrass occurrence and only 1% seagrass absence, a commonly observed ratio for presence-absence datasets. The BRF captures spatial heterogeneity in seagrass distribution under unbalanced presence-absence data. We demonstrated the difference between balanced and random forest on three distinct locations: Fraser Island, Coast of Far North Queensland, and Joseph Bonaparte Gulf (JGF). Both Fraser Island and Coast of Far North Queensland predictions for presence-absence were compared against CAMRIS seagrass polygons and literature reporting seagrass at these locations. Lastly, JGF, an area where neither ACEAS nor CAMRIS has data on seagrass, is used to demonstrate the predictive power of balanced random forest compared to surveys conducted in the area. JGF is also used as an example of the need for robust SDMs. It is an area of active oil and gas exploration, and mapping seagrasses accurately from existing data is extremely important.

Torres Straits, an area with high spatial heterogeneity of seagrass presence-absence, showed some counter-intuitive results. 84% of the absence points defined by BRF fall outside of the CAMRIS seagrass presence polygons, showing that BRF can capture presence-absence patterns effectively here. However, SRTM30, temperature, and the distance to coast conditions are not distinguishable between presence and absence at the Torres Straits (Fig. 16). For the entire Australian coast, these parameters were among the most important for BRF. However, in this location, distributions of these variables at presence and absence locations are quite similar. This result might indicate low variability of these conditions than the entire Australian coast or other drivers that show more variability. Oxygen levels (dissolved, apparent, and saturation) are among variables that show the highest distribution dissimilarity between presence and absence locations at the Torres Straits. For the entire coast, these variables were of low importance.

Lastly, we applied BRF to a model risk associated with building two new ports in the Bay of Carpenteria. Our results showed that BRF successfully models an area (Wellesley Islands) losing its seagrass habitat due to new ports. In contrast, the RF model could not capture any seagrass absence under current conditions in the area. We acknowledge that habitat loss can be spatially more extensive than modeled by BRF. However, our model delineated an area that was susceptible to seagrass loss due to human impact. Our case study shows the value of absence data in conservation studies and the importance of incorporating such data in numerical SDMs for conservation planning.

Conclusions

Environmental and human-driven conditions at the absence locations of a sessile species contain important information pertinent to factors that inhibit growth and development. Findings in this paper suggest that sparse absence data can significantly impact understanding conditions that favor and inhibit a species growth if it is modeled explicitly. The proposed model's impact on understanding stressors for seagrass habitats at the Australian coast is demonstrated on ACEAS and CAMRIS datasets. Both in-sample and out-of-sample quality metrics point to an improved forecast accuracy for seagrass absence compared to the random forest (RF). Lastly, the impact of understanding absence conditions for conservation planning is demonstrated by assessing the impact of two proposed ports in the Bay of Carpenteria on seagrass habitats. The proposed model defined areas of absence, areas where the seagrass is expected to disappear due to extensive ship traffic and associated scarring. Although the proposed model effectively models absence and presence, it requires deterministic and time-insensitive labels. Future work should investigate the modeling fuzzy presence-absence labels that change over time.