Approximation of multistage stochastic programming problems by smoothed quantization

Abstract

We present an approximation technique for solving multistage stochastic programming problems with an underlying Markov stochastic process. This process is approximated by a discrete skeleton process, which is consequently smoothed down by means of the original unconditional distribution. Approximated in this way, the problem is solvable by means of Markov Stochastic Dual Dynamic Programming. We state an upper bound for the nested distance between the exact process and its approximation and discuss its convergence in the one-dimensional case. We further propose an adjustment of the approximation, which guarantees that the approximate problem is bounded. Finally, we apply our technique to a real-life production-emission trading problem and demonstrate the performance of its approximation given the “true” distribution of the random parameters.

1 Introduction

Stochastic programming evolved from its deterministic counterpart by the realization that the parameters influencing the objective function and constraints are usually uncertain, coming from the real world around us. Real world applications range from economy to biology or logistics and engineering. Developments in this field led to multistage stochastic programming, which allows for resolving multiple stages of the decision-making and data processes. Such models capture the dynamics of the underlying random process, and we are able to adjust our decisions based on the random parameters observed so far. Our decisions cannot depend on the parameters which are still uncertain and will be resolved in future stages; in other words, the decisions fulfill the notion of nonanticipativity. Even though we can describe this generalization in a straightforward manner, it brings substantial issues with theoretical properties, random process models and tractability. The applicability of such models often depends on the structure of the problem we are trying to solve. Multistage stochastic models have provided us with valuable improvements over the two-stage models in certain particular cases, usually involving a complex time-dependent structure. Such examples can be found, for instance, in finance (e.g. Pflug 2001), energy management (e.g. Pereira and Pinto 1991) or transportation (e.g. Cavagnini et al. 2022).

There are two usual ways to describe uncertainty in the stochastic programming models. The first approach is to collect some historical values or experts’ opinions and produce a discrete distribution that consists of scenarios with assigned probabilities. The second approach is to assume that the random inputs follow a certain continuous distribution and estimate its parameters from the data or use the experts’ opinions to choose those parameters. When a continuous distribution is selected, sampling methods are commonly used to convert it to the discrete version in order to obtain a numerically tractable approximation; see, for example, Pflug and Pichler (2014). For large-scale problems, we are unable to compute precise solutions even for such discrete approximations.

Most of the stochastic programming models optimize the expected outcome of the random costs or returns. The resulting decisions are optimal on average, but possible risks are neglected. In many cases, this goal need not necessarily be appropriate because such decisions could produce a very unsatisfactory performance or, under the worst-case scenarios, even lead to bankruptcy. First developments in modeling risk aversion by using utility functions can be found in Bernoulli (1954), or a more formal and precise description in Von Neumann and Morgenstern (1944). Other significant ways to produce more robust solutions include mean-risk models. These bi-criterial models aim to find an efficient solution with respect to maximization of the mean return and minimization of the risk which is linked to the future uncertainty. Basics of the mean-risk concept using variance and semivariance as a measure of the risk were published in the article (Markowitz 1952) and book (Markowitz 1959) by Harry Markowitz back in the 1950 s. In recent years, risk-averse stochastic optimization based on various risk measures has been receiving significant attention. The properties required of coherent risk measures, introduced in Artzner et al. (1999), are now widely accepted for time-static risk-averse optimization. One of the most popular risk measures, Conditional Value at Risk (CVaR, see Rockafellar and Uryasev 2002), is known to satisfy these properties; for an overview of many others see, for instance, Krokhmal et al. (2011). A number of proposals have been put forward to extend the concept of coherent risk measures to handle multistage stochastic optimization.

Due to the complexity of stochastic programs, discussed, for example, in Shapiro and Nemirovski (2005), approximations are often employed. Monte Carlo sampling and scenario approximations had been used even before they were given the name of Sample Average Approximation in the article by Kleywegt et al. (2001). Approximate solutions depend on the particular set of sampled scenarios and are therefore random in general. Such approximate solutions require statistical validation, which is usually based on performing multiple replications and examining the stability of solutions and objective values, see Bayraksan and Morton (2011) for a summary of available methods. Scenario-based stochastic programs can often be reformulated as one large-scale standard optimization program, and such a program can be directly solved by solvers like CPLEX, Gurobi or COIN-OR. The reformulated programs are usually very large and require long solving times or are not solvable at all. This aspect led to the development of algorithms which exploit the special structure of stochastic programs and take advantage of particular properties, such as convexity. Optimization problems containing integer variables are known to be very hard to solve in general, and they are, of course, even more demanding in the stochastic setting. Most of the recent algorithms employ a technique of building so-called cuts on the feasible space or objective function. These cuts are used to eliminate infeasible or suboptimal decisions, or to approximate the objective function. The basic algorithm–Benders’ decomposition, sometimes called the L-shaped method, was developed by Benders (1962), see also Van Slyke and Wets (1969). Many improvements of this basic algorithm have been proposed, especially the multicut method by Birge and Louveaux (1988), regularized decomposition by Ruszczyński (1986), and stochastic decomposition by Higle and Sen (1991). These decomposition algorithms usually provide an approximate solution and control its quality by computing lower and upper bounds on the true optimal objective value.

The structure of recourse functions in the multistage stochastic programs is particularly difficult from the algorithmic perspective. If we transform a multistage stochastic program into a dynamic programming recursion, the last-stage program can be solved by the algorithms mentioned above. For the preceding stages, we need to realize that the precise form of the recourse function cannot be obtained, and we need to rely on its approximation, provided by the cuts. Therefore we are recursively accumulating approximation error, which leads to slower convergence and requires further validation of correctness. The basic multistage decomposition algorithm, Nested Benders’ decomposition (Birge 1985), applied to a multistage stochastic program, requires computational effort that grows exponentially in the number of stages. Other important algorithms designed to solve multistage stochastic programs include extensions of stochastic decomposition to the multistage case (Higle et al. 2010; Sen and Zhou 2014), progressive hedging (Rockafellar and Wets 1991), and stochastic Dual Dynamic Programming (SDDP) (Pereira and Pinto 1991). SDDP will be used as the main solution technique for multistage stochastic programs in this article.

SDDP originated in the work of Pereira and Pinto (1991), and inspired a number of related algorithms (Chen and Powell 1999; Donohue and Birge 2006; Linowsky and Philpott 2005; Philpott and Guan 2008), which aim to improve its efficiency. SDDP-style algorithms have computational effort per iteration that grows linearly in the number of stages. To achieve this, SDDP algorithms rely on the assumption of stage-wise independence, which is rarely fulfilled in practice, especially in financial applications. The requirement of time-independence can sometimes be circumvented by a suitable reformulation of the decision problem – see, e.g., Kozmík and Morton (2015) working with (independent) returns rather than (time-dependent) prices or (Löhndorf and Shapiro 2019) using artificial decision variables; however, in the majority of real-life applications, nothing similar is at our disposal. A relatively recent modification of the SDDP (Philpott et al. 2013), which we call Markov SDDP, permits the underlying process to be conditioned by a finite Markov chain, which allows us to approximate a time-dependent underlying process by a hidden Markov model. However, as the Markov chain has to be sparse for computational reasons, the original process is approximated only roughly, which may result in serious errors. When CVaR is used as a risk measure, the discretized version may completely fail to approximate the original problem because the tails of the distribution are approximated at most by several atoms, or even a single one; this feature causes CVaR to degenerate into the worst-case risk measure: instead of a risk-averse problem, we would thus solve a minimax one.

In this paper, we overcome the latter problem by proposing a novel approximation technique, which we call smoothed quantization, consisting of two steps at each stage t. In the first step, the exact (conditional) t-th stage distribution is approximated by its quantization, i.e., an atomic distribution with the probabilities equal to the exact (conditional) probabilities of pre-chosen regions surrounding its atoms (see Löhndorf and Shapiro 2019, Kreitmeier 2011 or Pflug 2001). In the second step, the quantization is smoothed down by means of the exact unconditional distribution, restricted to those regions. In result, the shape of the approximation resembles that of the original distribution with the first-stage approximation being equal to the original distribution. This approximating process remains dependent on the past only through a finite number of possible values, which allows us to use the Markov SDDP to solve optimization problems with time-dependent underlying processes (approximated by our technique).

To measure the accuracy of our approximation, we use nested distance, denoted by $\textbf{d}$, which has been specifically designed for multistage stochastic programs (see Pflug and Pichler 2012 or Pflug and Pichler 2014). Under certain conditions mentioned in Pflug and Pichler (2014), Theorem 6.1:

$$\begin{aligned} |v(\xi )-v(\varsigma )|\le K\textbf{d}(\xi ,\varsigma ) \end{aligned}$$

(1)

holds true where ${\xi }$ and ${\varsigma }$ stand for the exact process and its approximation, respectively, K is a constant, and $v(\bullet )$ is the corresponding value function. This could help us keep the approximation error (the l.h.s. of (1)) under control, but the above-mentioned “certain conditions” are rarely fulfilled in practice. Even though we might expect for (1) to hold locally, we demonstrate later that the left-hand side of (1) is infinite for some approximations $\varsigma$. Nevertheless, in our opinion, the nested distance is still the most suitable metric for measuring approximations of random parameters in multistage stochastic programming (see e.g. Pflug and Pichler 2016 for relevant arguments).

The computation of the nested distance for general $\varsigma$ is intractable and even determining the optimal skeleton (in a certain particular sense of optimality as described in Löhndorf and Shapiro (2019)) leads to non-trivial non-convex optimization problems. Hence we give up on finding the optimal approximation. Instead, we state an upper bound of the nested distance between the exact process and its smoothed quantization and, in the one-dimensional case, we show that this distance converges. Further, we discuss settings of the approximation’s parameters so that the distance is kept small, and propose a refinement of the approximation guaranteeing that the approximated problem is bounded. Finally, we apply our approximation technique to a real-life optimal production and emission trading multistage problem and test the performance of the approximate solution w.r.t. the exact distribution of the underlying process.

The paper is organized as follows. After the introduction of the risk-averse multistage problem (Sect. 2) and the discussion of the nested distance (Sect. 3), we introduce the smoothed quantization (Sect. 4) and we discuss the choice of its parameters and its refinement (Sect. 5). The practical illustration is then presented (Sect. 6) and the paper is concluded (Sect. 7). Auxiliary results are provided in the Appendix.

2 Risk averse multistage problem

In line with (Kozmík and Morton 2015), we consider the risk-averse T-stage linear stochastic programming problem:

$$\begin{aligned} \inf \quad&\rho (c'_{0}x_{0},\dots ,c'_{T}x_{T})\nonumber \\ \text {s.t.}\quad&x_{0}\in {\mathbb {R}}_{+}^{d_{0}},\quad A_{0}x_{0}=b_{0},\nonumber \\&x_{t}\in {\mathbb {R}}_{+}^{d_{t}},\quad x_{t}\in {\mathcal {F}}_{t},\quad A_{t} \left[ \begin{array}{c} x_{t-1}\\ x_{t} \end{array}\right] =b_{t},\quad 1\le t\le T. \end{aligned}$$

(2)

Here, $b_{0}\in {\mathbb {R}}^{j_{0}},c_{0}\in {\mathbb {R}}^{d_{0}}$ are deterministic vectors, $A_{0}\in {\mathbb {R}}^{j_{0}\times d_{0}}$ is a deterministic matrix. Further, for each $1 \le t\le T$, $b_{t}\in {\mathbb {R}}^{j_{t}}$ and $c_{t}\in {\mathbb {R}}^{d_{t}}$ are (possibly random) vectors and $A_{t}\in {\mathbb {R}}^{j_{t}\times (d_{t-1} + d_t)}$ is a (possibly random) matrix. Symbol $'$ denotes transposition. The dimensions, $d_{0},\dots ,d_{T}$ and $j_{0},\dots ,j_{T}$ are deterministic. Finally, $({\mathcal {F}}_{t})_{t=0,\dots ,T}$ is the filtration generated by process $(A_{t},b_{t},c_{t})_{0\le t\le T}$, and $\rho$ is a nested risk measure defined as

$$\begin{aligned} \rho (z_{0},\dots ,z_{T})=z_{0}+\sigma _{1}(z_{1}+\sigma _{2}(z_{2}\dots +\sigma _{T}(z_{T}))),\qquad z_{t}\in {\mathcal {F}}_{t},\quad 0\le t\le T, \end{aligned}$$

where, for each $1\le t\le T$, $\sigma _{t}$ is a conditional risk mapping, i.e., a convex, monotone and translation invariant function from the space of integrable ${\mathcal {F}}_{t}$-measurable real functions into the space of integrable ${\mathcal {F}}_{t-1}$-measurable real functions (see Ruszczyński and Shapiro 2006, Definition 2.1).

One of the most frequent choices for $\sigma _{\bullet }$ is the mean-CVaR risk mapping, defined as

$$\begin{aligned} \sigma _{t}(z)=(1-\lambda ){\mathbb {E}}(z|{\mathcal {F}}_{t-1})+\lambda \textrm{CVaR}_{\alpha }(z|{\mathcal {F}}_{t-1}),\qquad 1\le t\le T, \end{aligned}$$

where $0\le \lambda \le 1$ is a risk-aversion parameter and $\alpha \in [0,1)$ is the CVaR level (see e.g. Rockafellar and Uryasev 2002 for the discussion of CVaR and its evaluation within stochastic programs).

Without loss of generality,¹ we assume that

$$\begin{aligned} A_{t}=\Xi _{t}(\xi _{t},\eta _{t}),\qquad b_{t}=\phi _{t}(\xi _{t},\eta _{t}),\qquad c_{t}=\psi _{t}(\xi _{t},\eta _{t}),\qquad 0\le t\le T, \end{aligned}$$

(3)

where $\xi$ is a Markov process taking values in ${\mathbb {R}}^{p}$ with deterministic $\xi _{0}$, $\eta$ is a time-independent stochastic process taking values in ${\mathbb {R}}^{q}$ with deterministic $\eta _{0}$, independent of $\xi$, and, for each $0\le t\le T$, $\Xi _{t}:{\mathbb {R}}^{p+q}\rightarrow {\mathbb {R}}^{j_{t}\times (d_{t-1}+d_{t}) },$ $\phi _{t}:{\mathbb {R}}^{p+q}\rightarrow {\mathbb {R}}^{j_{t}}$ and $\psi _{t}:{\mathbb {R}}^{p+q}\rightarrow {\mathbb {R}}^{d_{t}}$ are measurable mappings.

As it has already been mentioned, the computationally easiest situation occurs when the random parameter of the problem is time-independent, i.e., $\xi \equiv 0$. A problem with a time dependence may sometimes be reformulated as a problem dependent only on an i.i.d. underlying process. If, for instance,

$$\begin{aligned} b_{t}=B_{t}\xi _{t}+\delta _{t}(\eta _{t}),\qquad 1\le t\le T, \end{aligned}$$

(4)

where $B_{t}$ is a deterministic matrix, $\delta _{t}:{\mathbb {R}}^q \rightarrow {\mathbb {R}}^{j_t}$ is a mapping, and $\xi _{t}=C+D\xi _{t-1}+\epsilon _{t}$, $0<t\le T$, for some time-independent vector process $\epsilon$ and deterministic matrices C, D, then $b_{t}$ may be made dependent only on an i.i.d. random process by adding a vector of artificial variables $y_{t}$ and constraints $b_{t}=B_{t}y_{t}+\delta _{t}(\eta _{t})$, $y_{t}=C+Dy_{t-1}+\epsilon _{t}$ for each $1\le t\le T$. If, alternatively, $\xi _{t}=C\xi _{t-1}\epsilon _{t}$ is true for a certain matrix C, then the second constraint would be $y_{t}=C\epsilon _{t}y_{t-1}$. Unfortunately, a similar transformation cannot be done for $A_{t}$ or for $c_{t}$, since for both of them this would bring multiplication of decision variables into the optimization problem, destroying its convex structure. That said, many cases of inter-stage dependence cannot be circumvented by reformulations.

3 Nested distance

In this Section, we discuss the notion of nested distance, introduced in Pflug and Pichler (2012) and further elaborated in Pflug and Pichler (2014). Contrary to Pflug and Pichler (2014), we do not proceed in full generality; instead, we restrict ourselves to distributions of vector-valued stochastic processes, and we take the $l_{1}$ norm as the only distance function. The main reason for choosing $l_{1}$ is the fact that it can be expressed as a sum of its one-dimensional counterparts, see below or Šmíd (2009) for detailed explanation.

Nested distance is defined by means of conditional probabilities. Before proceeding, let us recall that, having two measurable spaces $(A,{\mathcal {A}})$ and $(B,{\mathcal {B}})$, the conditional distribution of a random element $\alpha \in A$ given a random element $\beta \in B$ may be understood either as a collection of random variables $({\mathbb {P}}[\alpha \in S|\sigma (B)],S \in {\mathcal {A}})$, or as a random measure, i.e., a mapping $\mu (\bullet |\blacktriangle ):{\mathcal {A}}\times B\rightarrow [0,1]$ such that, for fixed $b\in B$, $\mu (\bullet |b)$ is a probability distribution and, for fixed $S\in {\mathcal {A}}$, $\mu (S|\blacktriangle )$ is measurable (see Kallenberg 2002, Chap. 1.). In the present paper, we understand conditional probabilities in the latter sense. Moreover, once $\mu (\bullet |\blacktriangle )$ is the (random-measure version of a) conditional distribution of $\alpha$ given $\beta$, we put ${\mathbb {P}}[\alpha \in \bullet |\beta =\blacktriangle ]{\mathop {=}\limits ^{\text {def}}}\mu (\bullet |\blacktriangle )$, ${\mathbb {P}}[\alpha \in \bullet |\beta ]{\mathop {=}\limits ^{\text {def}}}\mu (\bullet |\beta )$ and, by writing $\mu (\blacktriangle )$, we mean the mapping from B into the space of probability distributions on ${\mathcal {A}}$ defined by $\mu$.

Until the end of this Section, let $p\in {\mathbb {N}}\setminus \{0\}$ and let $\xi$ and $\varsigma$ be processes defined on $\{0,\dots T\}$ taking values in ${\mathbb {R}}^{p}$ with deterministic $\xi _{0}=\varsigma _{0}$ and with finite first moments. Further, for any collection $(x_{0},\dots ,x_{t})$ where $x_\tau \in {\mathbb {R}}^p$, $0\le \tau \le t$, put $\overline{x}_{t}{\mathop {=}\limits ^{\text {def}}}(x_{1},\dots ,x_{t})$, and put $\bar{p}_{T}{\mathop {=}\limits ^{\text {def}}}Tp$.

Definition 1

Let ${\mathcal {B}}^{p}{\mathop {=}\limits ^{\text {def}}}{\mathcal {B}}({\mathbb {R}}^{p})$ be the Borel sigma-field on ${\mathbb {R}}^{p}$. Let P and Q be probability distributions, both defined on $({\mathbb {R}}^{p},{\mathcal {B}}^{p})$. A probability measure $\pi$ on $({\mathbb {R}}^{p}\times {\mathbb {R}}^{p},{\mathcal {B}}^{p}\otimes {\mathcal {B}}^{p})$ is called transportation from P into Q if P and Q are its marginal distributions, i.e.,

$$\begin{aligned} \pi [A\times {\mathbb {R}}^{p}]=P(A) \end{aligned}$$

(5)

for each $A\in {\mathcal {B}}^{p}$ and

$$\begin{aligned} \pi [{\mathbb {R}}^{p}\times B]=Q(B) \end{aligned}$$

(6)

for each $B\in {\mathcal {B}}^{p}$.

Definition 2

Let ${\mathcal {L}}(X)$ denote a distribution of random element X. A probability measure $\pi$ on $({\mathbb {R}}^{2\bar{p}_{T}},{\mathcal {B}}({\mathbb {R}}^{2\bar{p}_{T}}))$ is called nested transportation from ${\mathcal {L}}(\xi )$ to ${\mathcal {L}}(\varsigma )$ (or, briefly, from $\xi$ to $\varsigma$) if, for each $1\le t\le T$, $\pi (\xi _{t},\varsigma _{t}\in \bullet |\overline{\xi }_{t-1},\overline{\varsigma }_{t-1})$² is a transportation from ${\mathbb {P}}[\xi _{t}\in \bullet |\overline{\xi }_{t-1}]$ into ${\mathbb {P}}[\varsigma _{t}\in \bullet |\overline{\varsigma }_{t-1}]$.

Definition 3

The nested distance between $\xi$ and $\varsigma$ is defined as

$$\begin{aligned} \textbf{d}(\xi ,\varsigma )=\inf _{\pi }&\int _{{\mathbb {R}}^{2\bar{p}_{T}}}\Vert x-y\Vert \pi (dx,dy)\\ s.t.&\,\pi \text { is a nested transportation from} \,\xi \ \text {to }\varsigma , \end{aligned}$$

where $\Vert x\Vert =\sum _{i=1}^{n}|x^{i}|$ for any $x = (x^1,\dots ,x^n)'\in {\mathbb {R}}^n$.

Remark 1

For $T=1$, $\textbf{d}$ coincides with the Wasserstein distance, which we later denote by $\textrm{d}$ (see Pflug and Pichler (2014) or Villani (2003) for the definition and the properties of the Wasserstein distance).

Remark 2

Our definition of nested distance is equivalent to that from (Pflug and Pichler 2012). In particular, our Definition 2 is equivalent to Definition 1 from (Pflug and Pichler 2012) with $\Omega =\Upsilon ={\mathbb {R}}^{\bar{p}_{T}}$, ${\mathcal {F}}_{t}={\mathcal {G}}_{t}={\mathcal {B}}^{\bar{p}_{t}}\otimes \{\emptyset ,{\mathbb {R}}\}^{\bar{p}_{T}-\bar{p}_{t}}$ therein.³

Proof

See Appendix B.1. $\square$

The following Proposition, similar to Pflug and Pichler (2014), Proposition 4.26, provides an upper bound of the nested distance between two Markov processes. Recall that the process $\xi$ is Markov if, for any $t=1,\dots ,T$, the conditional distribution of $\xi _t$ given $\overline{\xi }_{t-1}$ depends only on $\xi _{t-1}$ (below, we call such conditional distributions Markov).

Proposition 1

Let $\xi$ and $\varsigma$ be Markov processes. Denote $\mu _{1},\dots ,\mu _{T}$, and $\nu _{t},\dots ,\nu _{T}$ the probability distributions ruling $\xi ,\varsigma ,$ respectively. Let

$$\begin{aligned} \textrm{d}(\mu _{t}(x),\mu _{t}(s))\le K_{t}\Vert x-s\Vert ,\qquad x,s\in {\mathbb {R}}^{p},\qquad 1\le t\le T, \end{aligned}$$

(7)

for some constants $K_{1},\dots ,K_{T}\ge 0$. Then, for any $1\le t\le T$,

$$\begin{aligned} \textbf{d}(\overline{\xi }_{t},\overline{\varsigma }_{t})\le & {} (1+K_{t})\textbf{d}(\overline{\xi }_{t-1}, \overline{\varsigma }_{t-1})+{\mathbb {E}}\textrm{d}(\mu _{t}(\varsigma _{t-1}),\nu _{t}(\varsigma _{t-1}))\nonumber \\\le & {} \sum _{\tau =1}^{t}\left( \prod _{i=\tau +1}^{t}(1+K_{i})\right) {\mathbb {E}}d(\mu _{\tau }(\varsigma _{{\tau }-1}),\nu _{\tau }(\varsigma _{\tau -1})) \end{aligned}$$

(8)

where $\prod _{i=t+1}^{t}(1+K_{i}) = 1$ by definition.

Proof

See Appendix B.2$\square$

4 Smoothed quantization

As stated in the Introduction, our motivation is to construct a continuous approximation for a time-dependent stochastic process which will depend on the past information only through a finite set of possible values. The present Section introduces a technique leading to such an approximation, which we call smoothed quantization, and discusses some of its properties.

Definition 4

A collection ${\mathcal {C}}=(\{C_{1},\dots ,C_{k}\},\{e_{1},\dots ,e_{k}\})$ is a covering of ${\mathbb {R}}^{p}$ (with representatives) if $C_{1},\dots ,C_{k}\subseteq {\mathbb {R}}^{p}$ are disjoint measurable such that ${\mathbb {R}}^{p}=\bigcup _{i}C_{i}$ and $e_{i}\in C_{i},1\le i\le k$.

The covering is rectangular if

$$\begin{aligned}{} & {} \{C_{1},\dots ,C_{k}\}=\{[c_{i_{1}-1}^{1},c_{i_{1}}^{1}) \times \dots \times [c_{i_{p}-1}^{p},c_{i_{p}}^{p}):1\le i_{1}\le k_{1},\dots ,1\le i_{p}\le k_{p}\}, \\{} & {} \{e_{1},\dots ,e_{k}\}=\{(e_{i_{1}}^{1},\dots ,e_{i_{p}}^{p}):1\le i_{1}\le k_{1},\dots ,1\le i_{p}\le k_{p}\}, \end{aligned}$$

for some $k_{1},\dots ,k_{p}\in {\mathbb {N}}$, where $-\infty =c_{0}^{j}<e_{1}^{j}<c_{1}^{j}\le e_{2}^{j}<\dots \le e_{k_{j}}^{j}<c_{k_{j}}^{j}=\infty$, $1\le j\le p$. Here, by writing $[-\infty ,c)$, we understand $(-\infty ,c)$ for any $c\in {\mathbb {R}}$.

Definition 5

Let $\mu$ be a probability measure on ${\mathbb {R}}^{p}$ and let

$$\begin{aligned} {\mathcal {C}}=(\{C_{1},\dots ,C_{k}\},\{e_{1},\dots ,e_{k}\}) \end{aligned}$$

be a covering of ${\mathbb {R}}^{p}$ with representatives. A probability measure $\theta$ on ${\mathbb {R}}^{p}$ is called quantization of $\mu$ defined by ${\mathcal {C}}$ if

$$\begin{aligned} \theta \{e_{i}\}=\mu (C_{i}),\qquad 1\le i\le k. \end{aligned}$$

The following Proposition discusses computation of the Wasserstein distance between $\mu$ and $\theta$ when ${\mathcal {C}}$ is rectangular:

Proposition 2

Let $\zeta$ be a p-dimensional real random vector with distribution $\mu$ having finite first moments of its components, let ${\mathcal {C}}=(\{C_{1},\dots ,C_{k}\},\{e_{1},\dots ,e_{k}\})$ be a rectangular covering of ${\mathbb {R}}^{p}$ and let $\theta$ be a quantization of $\mu$ defined by ${\mathcal {C}}$. Then

$$\begin{aligned} \textrm{d}(\mu ,\theta )=\sum _{i=1}^{p}\textrm{d}(\mu ^{i},\theta ^{i})={\mathbb {E}}\Vert \zeta -\epsilon (\zeta )\Vert =\sum _{i=1}^{p}{\mathbb {E}}|\zeta ^{i}-\epsilon ^{i}(\zeta ^{i})|, \end{aligned}$$

(9)

where $\epsilon (\bullet )=\sum _{j=1}^{k}e_{j}^{k}\textbf{1}_{C_{j}}(\bullet )$ and, for any $1\le i \le p$, $\mu ^{i}$ and $\theta ^{i}$ are the i-th marginal distributions of $\mu$, $\theta ,$ respectively, $\zeta ^{i}$ is the i-th component of $\zeta$, and $\epsilon ^{i}(\bullet )=\sum _{j=1}^{k_{i}}e_{j}^{i}\textbf{1}_{[c_{j-1}^{i},c_{j}^{i})}(\bullet )$. Here, $\textbf{1}_S(\bullet )$ is an indicator function of a set S.

Proof

See (Šmíd 2009), Definition 4, Lemma 4 and its proof. $\square$

Coming to the topic of the present Section, let $\xi$ be a Markov process on $\{0,\dots ,T\}$ taking values in ${\mathbb {R}}^{p}$ with deterministic $\xi _{0}$ and with $\xi _1,\dots ,\xi _T$ ruled by the set of (Markov) probability distributions $\mu _{1},\dots ,\mu _{T}$, respectively. Assume ${\mathbb {E}}\Vert \xi _{1}\Vert<\infty ,\dots ,{\mathbb {E}}\Vert \xi _{T}\Vert <\infty$. We approximate $\xi$ in two steps: first, we define a discrete “skeleton” process $\varepsilon$, and then we “smooth” the skeleton in order to get the final approximation $\varsigma$.

Strictly speaking, we choose a suitable collection of rectangular coverings of ${\mathbb {R}}^{p}$ with representatives:

$$\begin{aligned} \mathfrak {C}{\mathop {=}\limits ^{\text {def}}}({\mathcal {C}}_{0},{\mathcal {C}}_{1},\dots ,{\mathcal {C}}_{T}),\qquad {\mathcal {C}}_{0}=(\{\xi _{0}\},\{{\mathbb {R}}^{p}\}),\\ {\mathcal {C}}_{t}=(\{C_{t,1},\dots ,C_{t,k_{t}}\},\{e_{t,1},\dots ,e_{t,k_{t}}\}),\quad 1\le t\le T, \end{aligned}$$

next we put

$$\begin{aligned} \varepsilon _{0}=\xi _{0},\qquad \varsigma _{0}=\xi _{0}, \end{aligned}$$

and, finally, for any $1\le t\le T$, we define (the conditional distributions of) $\varepsilon _t$ and $\varsigma _t$ as

$${\mathbb{P}}\left[ {\varepsilon _{t} = \bullet |\bar{\varsigma }_{{t - 1}} ,\bar{\varepsilon }_{{t - 1}} } \right] = \theta _{t} ( \bullet |\varepsilon _{{t - 1}} ),$$

(10)

$$\begin{aligned}{} & {} {\mathbb {P}}[\varsigma _{t}=\bullet |\overline{\varsigma }_{t-1},\overline{\varepsilon }_{t}] =\omega _{t,i_{t}(\varepsilon _{t})}(\bullet ),\qquad i_{t}(\bullet ){\mathop {=}\limits ^{\text {def}}}\sum _{i=1}^ {k_{t}}i\textbf{1}_{C_{t,i}}(\bullet ), \end{aligned}$$

(11)

where, for each $1\le t\le T$ and any representative e of ${\mathcal {C}}_{t-1}$, $\theta _{t}(e)$ is the quantization of $\mu _{t}(e)$ defined by ${\mathcal {C}}_{t}$ and

$$\begin{aligned} \omega _{t,i}(\bullet )=\frac{\tilde{\mu }_{t}(\bullet \cap C_{t,i})}{\tilde{\mu }_{t}(C_{t,i})},\qquad \tilde{\mu }_{t}{\mathop {=}\limits ^{\text {def}}}{\mathcal {L}}(\xi _{t}), \end{aligned}$$

with $\frac{0}{0}=0$, is the smoothing distribution. Note that, for each i and t, $|\omega _{t,i}|\le 1$ and $\textrm{support}(\omega _{t,i})\subseteq C_{t,i}$.

Definition 6

We call $\varsigma$ smoothed quantization of $\xi$ defined by $\mathfrak {C}.$

Let us describe our technique informally. As $\varsigma _{0}=\xi _0=\epsilon _0$ are deterministic, $\tilde{\mu }=\mu (\epsilon _0)$ holds true, so the approximation of $\xi _1$ by $\varsigma _1$ is perfect. The best approximation of the conditional distribution of $\xi _2$ given a past value x of $\xi$ would certainly be $\mu _2(x)$; however, as we want to have only a few values the future can depend on, we use the “second best” choice to condition $\mu _2$: a representative e of a region in which x lies. So we quantize $\mu _2(e)$, and we consequently obtain (conditional) probabilities of $e_{2,1},\dots ,e_{2,k_2}$. We could now smooth the approximating distribution by means of $\mu _2(e)$ to get the exact approximation of the conditional distribution, yet with a different condition. However, the smoothed distribution would then depend on both $\epsilon _1$ (determining the shape of the distribution) and $\epsilon _2$ (determining the region we truncate it to), which would mean $k_1 \times k_2$ different distributions at $t=2$ hence $k_1 \times k_2$ sets of cuts in the SDDP algorithm (see below). By using the same smoothing distribution regardless of the condition (the truncated unconditional one), the number of possible distributions, hence of the cut sets, will be equal only to $k_2$ at $t=2$.

Next, we summarize some basic properties of the smoothed quantization.

Fig. 1

Smoothed quantization–illustration. Realizations of $\epsilon$: circles, realizations of $\varsigma$: squares, quantized (conditional) distributions: blue, (conditional) distributions of $\varsigma$: orange. Succession of simulation: green arrows

Proposition 3

• (i) $\varepsilon$ is uniquely defined by $\varsigma$. In particular, for each $1\le t\le T$,

  $$\begin{aligned} \varepsilon _{t}=\epsilon _{t}(\varsigma _{t}),\qquad \epsilon _{t}(s) {\mathop {=}\limits ^{\text {def}}}\sum _{i=1}^{k_{t}}e_{t,i}\textbf{1}_{C_{t,i}}(s), \end{aligned}$$

• (ii) $\varsigma$ is Markov, ruled by distributions

  $$\begin{aligned} \nu _{t}(\bullet |s)=\sum _{i=1}^{k_{t}}\omega _{t,i}(\bullet )\mu _{t}(C_{t,i}|\epsilon _{t-1}(s)),\qquad s\in {\mathbb {R}}^p,\qquad 1\le t\le T, \end{aligned}$$

• (iii) for each $1\le t\le T$, $\nu _{t}(\bullet )$ is constant on any $C_{t-1,i}$, $1\le i\le k_{t-1}$; in particular, $\nu _{t}(\varsigma _{t-1})=\nu _{t}(\varepsilon _{t-1})$,

• (iv) $\xi _{1}{\mathop {=}\limits ^{d}}\varsigma _{1}$ (meaning that the distributions of the left-hand side and the right-hand side agree),

• (v) ${\mathcal {L}}(\varsigma )$ does not depend on $e_{T,1},\dots ,e_{T,k_T}$.

Proof

• (i) is clear.

• (ii) Denote $\iota _{t}{\mathop {=}\limits ^{\text {def}}}i_{t}(\varepsilon _{t})$, $0\le t\le T.$ We have

  $$\begin{aligned} {\mathbb {P}}[\varsigma _{t}\in \bullet |\overline{\varsigma }_{t-1}]{\mathop {=}\limits ^{(i)}} {\mathbb {P}}[\varsigma _{t}\in \bullet |\overline{\varsigma }_{t-1},\overline{\varepsilon }_{t-1}]= {\mathbb {E}}({\mathbb {P}}[\varsigma _{t}\in \bullet |\overline{\varsigma }_{t-1}, \overline{\varepsilon }_{t}]|\overline{\varsigma }_{t-1},\overline{\varepsilon }_{t-1}) \\ {\mathop {=}\limits ^{(11)}}{\mathbb {E}}(\omega _{t,\iota _{t}}(\bullet )|\overline{\varsigma }_{t-1},\overline{\varepsilon }_{t-1}) =\sum _{i=1}^{k_{t}}\omega _{t,i}(\bullet ){\mathbb {P}}[\iota _{t}=i| \overline{\varsigma }_{t-1},\overline{\varepsilon }_{t-1}]\\ {\mathop {=}\limits ^{(10)}} \sum _{i=1}^{k_{t}}\omega _{t,i}(\bullet )\mu (C_{t,i}|\varepsilon _{t-1}) {\mathop {=}\limits ^{(i)}}\nu _{t}(\bullet |\varsigma _{t-1}). \end{aligned}$$

• (iii) follows from the definition of $\nu _t$ and from (i).

• (iv) follows by substituting.

• (v) is clear from (ii).

$\square$

Equations (10) and (11) give us instructions how to simulate the process $\varsigma$: at the t-th time step, a value of $\epsilon _t$ is drawn from $\theta (\bullet |\epsilon _{t-1})$ first and, consequently, $\varsigma _t$ is drawn from $\omega _{t,i_t(\epsilon _t)}$. Alternatively, as the distribution of $\varsigma _t$ depends on the past only through $\epsilon _t$, we can generate the skeleton process first and smooth it afterwards. For better understanding, we graphically illustrate our construction using an example with $T=2$, $k_1=2$, and $k_2=3$ in Fig. 1.

Before determining an upper bound of the approximation error, measured by $\textbf{d}(\xi ,\varsigma )$, we assume, without loss of generality, that

$$\begin{aligned} \xi _{t}=g_{t}(\xi _{t-1},U_{t}),\qquad 1\le t\le T, \end{aligned}$$

(12)

where $U_{1},\dots ,U_{T}$ are i.i.d. and $g_{1},\dots g_{T}$ measurable (see (Kallenberg 2002) Proposition 8.6 for the proof that such a representation always exists).

Theorem 1

Let there exist a measurable function $h_{t}$ with ${\mathbb {E}}h_{t}(U_{t})<\infty$ for any $1\le t\le T$ such that

$$\begin{aligned} \Vert g_{t}(x,u)-g_{t}(y,u)\Vert \le h_{t}(u)\Vert x-y\Vert ,\qquad x,y\in {\mathbb {R}}^{p},\quad u\in \textrm{support}(U_{t}). \end{aligned}$$

(13)

Then, for any $1\le t\le T,$

$$\begin{aligned} \textbf{d}(\overline{\xi }_{t},\overline{\varsigma }_{t})\le & {} (1+K_{t})\textbf{d}(\overline{\xi }_{t-1},\overline{\varsigma }_{t-1})+K_{t}{\mathbb {E}}\Vert \varsigma _{t-1}-\varepsilon _{t-1}\Vert \nonumber \\{} & {} \qquad \qquad +{\mathbb {E}}\textrm{d}(\mu _{t}(\varepsilon _{t-1}),\nu _{t}(\varepsilon _{t-1})) \end{aligned}$$

(14)

$$\begin{aligned}\le & {} \sum _{\tau =1}^{t-1}\kappa _{\tau }\sum _{i=1}^{p}\sum _{j=1}^{k_{\tau }}\int |x-e_{\tau ,j}^{i}|q_{\tau ,j}\omega ^i_{\tau ,j}(dx) \nonumber \\{} & {} \qquad \qquad +\sum _{\tau =2}^{t}\lambda _{\tau }\sum _{i=1}^{k_{\tau -1}}q_{\tau -1,i} \textrm{d}(\mu _{\tau }(e_{{\tau }-1,i}),\nu _{\tau }(e_{\tau -1,i})), \end{aligned}$$

(15)

where

$$\begin{aligned}{} & {} K_{\tau }={\mathbb {E}}h_\tau (U_{\tau }),\qquad 1\le \tau \le T, \\{} & {} \kappa _{\tau }=K_{\tau +1}\prod _{i=\tau +2}^{t}(1+K_{i}),\qquad 1\le \tau \le t-1, \\{} & {} \lambda _{\tau }=\prod _{i=\tau +1}^{t}(1+K_{i}),\qquad 2\le \tau \le t, \end{aligned}$$

with $\prod _{i=s+1}^{s}x_{i}{\mathop {=}\limits ^{\text {def}}}1;$ here, for any $1\le \tau \le t,$ $1\le k\le k_{\tau },$ $q_{\tau ,k}={\mathbb {P}}[\varepsilon _{\tau }=e_{\tau ,k}],$ and, for any $1\le i\le p$, $\omega _{\tau ,k}^{i}$ is the i-th marginal distribution of $\omega _{\tau ,k}$.

Remark 3

(13) holds if

• (i) $\xi _{t}=C+D\xi _{t-1}+U_{t}$ (with $h_{t}(u)\equiv \Vert D\Vert$).

• (ii) $\xi _{t}=U_{t}\xi {}_{t-1}$ and ${\mathbb {E}}\Vert U_t \Vert < \infty$ (with $h_{t}(u)\equiv \Vert u\Vert$).

Proof

As, by Lemma 2 in Appendix and (13),

$$\begin{aligned}{} & {} \textrm{d}(\mu _{t}(x),\mu _{t}(y))\le \int \Vert g(x,u)-g(y,u)\Vert {\mathcal {L}}(U_{t})(du) \nonumber \\{} & {} \quad \le \Vert x-y\Vert \int h_{t}(u){\mathcal {L}}(U_{t})(du) =K_t \Vert x-y\Vert ,\qquad x,y\in {\mathbb {R}}^{p}, \end{aligned}$$

(16)

(7) holds true. Consequently, by Proposition 1,

$$\begin{aligned} \textbf{d}(\overline{\xi }_{t},\overline{\varsigma }_{t})\le (1+K_{t})\textbf{d}(\overline{\xi }_{t-1},\overline{\varsigma }_{t-1}) +{\mathbb {E}}\textrm{d}(\mu _{t}(\varsigma _{t-1}),\nu _{t}(\varsigma _{t-1})). \end{aligned}$$

(17)

Using the triangular inequality, Proposition 3 (iii), and (16), we have

$$\begin{aligned}{} & {} \textrm{d}(\mu _{t}(\varsigma _{t-1}),\nu _{t}(\varsigma _{t-1}))\le \textrm{d}(\mu _{t}(\varsigma _{t-1}),\mu _{t}(\varepsilon _{t-1})) +\textrm{d}(\mu _{t}(\varepsilon _{t-1}),\nu _{t}(\varepsilon {}_{t-1})) \\{} & {} \quad \le K_t {\mathbb {E}}\Vert \varsigma _{t-1}-\varepsilon _{t-1}\Vert +\textrm{d} (\mu _{t}(\varepsilon _{t-1}),\nu _{t}(\varepsilon {}_{t-1})). \end{aligned}$$

Combined with (17) we get (14).

Further, by induction, using the facts that $\xi _{0}=\varepsilon _{0}$ and $\textbf{d}(\overline{\xi }_{1},\overline{\varsigma }_{1})=0$ (by Proposition 3 (iv)), we get

$$\begin{aligned} \textbf{d}(\overline{\xi }_{t},\overline{\varsigma }_{t})\le \sum _{\tau =1}^{t-1}\kappa _{\tau }{\mathbb {E}}\Vert \varsigma _{\tau } -\varepsilon _{\tau }\Vert +\sum _{\tau =2}^{t}\lambda _{\tau }{\mathbb {E}}\textrm{d}(\mu _{\tau }(\varepsilon _ {{\tau }-1}),\nu _{\tau }(\varepsilon _{\tau -1})) \end{aligned}$$

which proves (15) since

$$\begin{aligned} {\mathbb {E}}\textrm{d}(\mu _{\tau }(\varepsilon _{{\tau }-1}),\nu _{\tau }(\varepsilon _{\tau -1})) =\sum _{i=1}^{k_{\tau -1}}q_{\tau -1,i}\textrm{d}(\mu _{\tau }(e_{{\tau }-1,\text {i}}),\nu _{\tau }(\varvec{e}_{\tau -1,i})) \end{aligned}$$

and

$$\begin{aligned} {\mathbb {E}}\Vert \varsigma _{\tau }-\varepsilon _{\tau }\Vert {\mathop {=}\limits ^{\text {Prop. }3 \text {(i)}}}{\mathbb {E}}\Vert \varsigma _{\tau }-\epsilon _{\tau }(\varsigma _{\tau })\Vert ={\mathbb {E}}({\mathbb {E}}(\Vert \varsigma _{\tau }-\epsilon _{\tau }(\varsigma _{\tau })\Vert |\varsigma _{\tau -1}))\\ {\mathop {=}\limits ^{\text {Prop. }3 \text {(ii)}}}{\mathbb {E}}(\int \Vert s-\epsilon _{\tau }(s)\Vert \nu _{\tau }(ds|\varsigma _{\tau -1})){\mathop {=}\limits ^{\text {Prop.} 3 (iii)}}{\mathbb {E}}(\int \Vert s-\epsilon _{\tau }(s)\Vert \nu _{\tau }(ds|\varepsilon _{\tau -1}))\\ =\sum _{k=1}^{k_{\tau -1}}q_{\tau -1,i}\sum _{j=1}^{k_{\tau }}\mu _{\tau }(C_{\tau ,j} |e_{\tau -1,k})\int \Vert s-e_{\tau ,j}\Vert \omega _{\tau ,j}(ds)\\ {\mathop {=}\limits ^{q_{\tau ,j}=\sum _{k}q_{\tau -1,k}\mu _{\tau }(C_{\tau ,j}|e_{\tau -1,k})}} \sum _{j=1}^{k_{\tau }}q_{\tau ,j}\int \Vert s-e_{\tau ,j}\Vert \omega _{\tau ,j}(ds)\\ =\sum _{j=1}^{k_{\tau }}q_{\tau ,j}\sum _{i=1}^{p}\int |s-e_{\tau ,j}^{i}|\omega _{\tau ,j}^ {i}(ds)=\sum _{i=1}^{p}\sum _{j=1}^{k_{\tau }}\int |s-e_{\tau ,j}^{i}|\left( q_{\tau ,j}\omega _{\tau ,j}^{i}\right) (ds) \end{aligned}$$

$\square$

The next Theorem provides conditions for convergence of the smoothed quantization in the one-dimensional case.

Theorem 2

Let $p=1$. Assume (13) and let the unconditional distributions $\tilde{\mu }_{1},\dots ,\tilde{\mu }_{t}$ be absolutely continuous such that their tails

$$T_\tau (x) {\mathop {=}\limits ^{\text {def}}}\max (\tilde{\mu }_\tau (-\infty ,-x],\tilde{\mu }_\tau (x,\infty ))$$

are $O(x^{-a})$, $\tau =1,\dots ,t$, for some $a>1$. For each $1\le t\le T$ and for each covering with representatives ${\mathcal {C}}=((C_{1},\dots ,C_{k}),(e_{1},\dots ,e_{k}))$, denote

$$\begin{aligned}{} & {} D_{t}^{{\mathcal {C}}}(\bullet ){\mathop {=}\limits ^{\text {def}}}\textrm{d}(\mu _{t}(\bullet ), \theta _{t}(\bullet )), \end{aligned}$$

(18)

$$\begin{aligned}{} & {} E_{t}^{{\mathcal {C}}}(\bullet ){\mathop {=}\limits ^{\text {def}}}\sum _{i=2}^{k_{t}-1} \mu _{t}(C_{i}|\bullet )\int |x-e_{t,i}|\omega _{t,i}(dx), \end{aligned}$$

(19)

$$\begin{aligned} F_{t}^{{\mathcal {C}}}(v){\mathop {=}\limits ^{\text {def}}}\mu _{t}(C_{1}|\bullet ),\qquad{} & {} G_{t}^{{\mathcal {C}}}(\bullet ){\mathop {=}\limits ^{\text {def}}}\mu _{t}(C_{k}|\bullet ), \end{aligned}$$

(20)

and assume that $D^{{\mathcal {C}}}$, $E^{{\mathcal {C}}}$, $F^{{\mathcal {C}}}$, and $G^{{\mathcal {C}}}$ are Lipschitz (their Lipschitz constants may depend on ${\mathcal {C}}$). Then there exists a sequence $\mathfrak {C}_{1},\mathfrak {C}_{2},\dots$ of collections of coverings such that $\textbf{d}(\overline{\xi }_{T},\overline{\varsigma }_{,T}^{\varvec{\mathfrak {C}_{i}}})\rightarrow 0$, where, for any covering collection $\mathfrak {C}$, $\varsigma ^{\mathfrak {C}}$ is the smoothed quantization of $\overline{\xi }_{T}$ defined by $\mathfrak {C}$.

Proof

Let $\mathfrak {C}=({\mathcal {C}}_{0},\dots ,{\mathcal {C}}_{T})$ be a collection of coverings. For any $1\le t\le T$, let $R_{t}^{{\mathcal {C}}_{t}}$ and $T_{t}^{{\mathcal {C}}_{t}}$ be the Lipschitz constants of $D_{t}^{{\mathcal {C}}_{t}}$, $E_{t}^{{\mathcal {C}}_{t}}$, respectively and let $S_{t}^{{\mathcal {C}}_{t}}$ be the common Lipschitz constant of $F_{t}^{{\mathcal {C}}_{t}}$ and $G_{t}^{{\mathcal {C}}_{t}}$. First we show that, for any $1\le t\le T$, it holds that

$$\begin{aligned} \textbf{d}(\overline{\xi }_{t},\overline{\varsigma }_{t}^{\mathfrak {C}})\le 2\textrm{d}(\xi _{t},\epsilon _{t}(\xi _{t})) +(1+2K_{t})\textbf{d}(\overline{\xi }_{t-1},\overline{\varsigma }_{t-1}^{\mathfrak {C}})\nonumber \\ +(R_{t}^{{\mathcal {C}}_{t}}+S_{t}^{{\mathcal {C}}_{t}}(\Phi _{t}^{{\mathcal {C}}_{t}}+\Psi _{t}^{{\mathcal {C}}_{t}})+T_{t}^{{\mathcal {C}}_{t}} +K_{t})\textbf{d}(\overline{\xi }_{t-1},\overline{\varepsilon }_{t-1}^{\mathfrak {C}}) \end{aligned}$$

(21)

where $\Phi _{t}^{{\mathcal {C}}_{t}}=\frac{\int _{-\infty }^{c_{t,1}} \tilde{\mu }_{t}(-\infty ,x]dx}{\tilde{\mu }_{t}(-\infty ,c_{t,1}]}$, $\Psi _{t}^{{\mathcal {C}}_{t}}=\frac{\int _{c_{t,k_{t}-1}}^{\infty } \tilde{\mu }_{t}(x,\infty )dx}{\tilde{\mu }_{t}(c_{t,k_{t}-1},\infty )}$, and it holds that

$$\begin{aligned} \textbf{d}(\overline{\xi }_{t},\overline{\varepsilon }_{t}^{\mathfrak {C}})\le \textrm{d}(\xi _{t},\epsilon _{t} (\xi _{t}))+(K_{t}+R_{t}^{{\mathcal {C}}_{t}}+1)\textbf{d}(\overline{\xi }_{t-1},\overline{\varepsilon }_{t-1}^{\mathfrak {C}}), \end{aligned}$$

(22)

where $\varepsilon ^{\mathfrak {C}}$ the skeleton process defined by $\mathfrak {C}$. To this end, fix $\mathfrak {C}$ and agree to omit the superscripts indicating the coverings. We prove (21) and (22) simultaneously by induction.

Clearly, (21) and (22) hold for $t=1$ (by Proposition 3 (iv)).

Let $t>1$ and assume (21) and (22) to hold for $t-1$. By the Lipchitz property of $D_t$, Proposition 2 and Kantorovich-Rubinstein Theorem (implying that ${\mathbb {E}}\Vert x-y\Vert \le \textrm{d}(x,y)$ for any x, y with ${\mathbb {E}}\Vert x\Vert +{\mathbb {E}}\Vert y\Vert <\infty$, by Pflug and Pichler (2014) Theorem 2.29),

$$\begin{aligned}{} & {} {\mathbb {E}}D_{t}(\varepsilon _{t-1}) \le \underbrace{{\mathbb {E}}D_{t}(\xi _{t-1})}_ {\begin{array}{c} ={\mathbb {E}}\textrm{d}(\mu _t(\xi _{t-1}),\theta _t(\xi _{t-1})) \\ = {\mathbb {E}}({\mathbb {E}}\Vert \xi _{t}-\epsilon _t(\xi _{t})\Vert |\xi _{t-1})) \\ {={\mathbb {E}}\Vert \xi _{t}-\epsilon _t(\xi _{t})\Vert = \textrm{d}(\xi _t,\epsilon _t(\xi _t))} \end{array}} + R_t {\mathbb {E}}\Vert \xi _{t-1}-\varepsilon _{t-1}\Vert \nonumber \\{} & {} \quad \le \textrm{d}(\xi _t,\epsilon _t(\xi _t))+R_{t}\textrm{d}(\xi _{t-1},\varepsilon _{t-1}). \end{aligned}$$

(23)

Further, by Proposition 2 (note that $\theta _{t}(\varepsilon _{t-1})$ is the quantization of $\nu _{t}(\varepsilon _{t-1})$), the Lipschitz properties and the K-R Theorem again, we get

$$\begin{aligned}{} & {} {\mathbb {E}}(\textrm{d}(\nu _{t}(\varepsilon _{t-1}),\theta _{t}(\varepsilon _{t-1}))) {\mathop {=}\limits ^{\text {Prop. }2}}{\mathbb {E}}(\sum _{i=1}^{k_{t}}\mu _{t}(C_{t,i}|\varepsilon _{t-1})\int |x-e_{t,i}|\omega _{t,i}(dx))\nonumber \\{} & {} \quad =\Phi _{t}{\mathbb {E}}F_{t}(\varepsilon _{t-1})+{\mathbb {E}}E_{t}(\varepsilon _{t-1})+\Psi _{t}{\mathbb {E}}G_{t}(\varepsilon _{t-1}) \nonumber \\{} & {} \le \underbrace{\Phi _{t}{\mathbb {E}}F_{t}(\xi _{t-1})+{\mathbb {E}}E_{t}(\xi _{t-1})+\Psi _{t}{\mathbb {E}}G_{t}(\xi _{t-1})}_{=\textrm{d}(\xi _{t},\epsilon _{t}(\xi _{t}))}+U_{t}\textrm{d}(\xi _{t-1},\varepsilon _{t-1}),\nonumber \\{} & {} \quad U_{t}=S_{t}(\Phi _{t}+\Psi _{t})+T_{t}. \end{aligned}$$

(24)

Thus,

$$\begin{aligned}{} & {} \textbf{d}(\overline{\xi }_{t},\overline{\varsigma }_{t}) {\mathop {\le }\limits ^{{(14),\text { Prop.}2}}}(1+K_{t})\textbf{d}(\overline{\xi }_{t-1},\overline{\varsigma }_{t-1})+K_{t}\textrm{d}(\varsigma _{t-1},\varepsilon _{t-1}) +{\mathbb {E}}\textrm{d}(\mu _{t}(\varepsilon _{t-1}),\nu _{t}(\varepsilon _{t-1}))\\{} & {} {\mathop {\le }\limits ^{\text {triang. ineq.}}}(1+K_{t})\textbf{d}(\overline{\xi }_{t-1},\overline{\varsigma }_{t-1})+K_{t}(\textrm{d}(\xi _{t-1},\varsigma _{t-1})+\textrm{d}(\xi _{t-1},\varepsilon _{t-1}))\\{} & {} + \underbrace{{\mathbb {E}}\textrm{d}(\mu _{t}(\varepsilon _{t-1}),\theta _{t}(\varepsilon _{t-1}))} _{\qquad \qquad {\mathop {\le }\limits ^{(23)}}\textrm{d}(\xi _t,\epsilon _t(\xi _t))+ R_{t}\textrm{d}(\xi _{t-1},\varepsilon _{t-1})} + \underbrace{{\mathbb {E}}\textrm{d}(\nu _{t}(\varepsilon _{t-1}),\theta _{t}(\varepsilon _{t-1})))} _ {\qquad \qquad {\mathop {\le }\limits ^{(24)}}\textrm{d}(\xi _t,\epsilon _t(\xi _t))+ U_{t}\textrm{d}(\xi _{t-1},\varepsilon _{t-1})}, \end{aligned}$$

giving (21) by Lemma 3 in Appendix.

The proof of (22) is simpler, based on the fact that

$$\begin{aligned} \textbf{d}(\overline{\xi }_{t-1},\overline{\varepsilon }_{t-1})\le (1+K_{t})\textbf{d}(\overline{\xi }_{t-1},\overline{\varepsilon }_{t-1}) +{\mathbb {E}}\textrm{d}(\mu _{t}(\varepsilon _{t-1}),\theta _{t}(\varvec{\varepsilon }_{t-1})), \end{aligned}$$

which may be proved analogously to (14) of Theorem 1 and implies (22) by (23) and Lemma 3 in Appendix.

Therefore, both (21) and (22) have been proved.

Next we show that, for each $1\le t\le T$, there exist a series of covering collections $\mathfrak {C}_{1},\mathfrak {C}_{2},\dots$ such that

$$\begin{aligned} \textbf{d}(\overline{\xi }_{t},\overline{\varsigma }_{t}^{\mathfrak {C}_{n}})\rightarrow 0,\qquad \textbf{d}(\overline{\xi }_{t},\overline{\varepsilon }_{t}^{\mathfrak {C}_{n}})\rightarrow 0. \end{aligned}$$

(25)

Clearly, (25) with $t=T$ proves the Theorem. We shall proceed by induction while for $t=0$, (25) holds trivially.

Let $t>0$ and assume (25) to hold for $t-1$, i.e., that there exists a sequence $\mathfrak {D}_{1},\mathfrak {D}_{2},\dots$ of covering collections such that (25) holds for $t-1$ and $\mathfrak {D_{\bullet }}$ instead of t and $\mathfrak {C_{\bullet }}$.

First, let ${\mathcal {C}}_{i}=(\{C_{1}^{i},\dots ,C_{k_{i}}^{i}\},\{e_{1}^{i},\dots ,e_{k_{i}}^{i}\}),$ $i\in {\mathbb {N}}$, be coverings such that $\lim _{i}\textrm{d}(\xi _{t},\epsilon _{i,t}(\xi _{t}))\rightarrow 0$ where $\epsilon _{i,t}(\bullet )=\sum _{j}e_{j}^{i}\textbf{1}_{C_{j}^{i}}(\bullet )$: their existence is guaranteed by Šmíd (2009), Theorem 1. For each $n\in {\mathbb {N}}$, let i(n) be such that $\textrm{d}(\xi _{t},\epsilon _{i(n),t}(\xi _{t}))\le \frac{1}{4n}$.

Next, for any $n\in {\mathbb {N}}$ and any covering ${\mathcal {C}}$, put

$$\begin{aligned} \delta _{n}^{{\mathcal {C}}}=(1+2K_{t})\textrm{d}(\overline{\xi }_{t-1},\overline{\varsigma }_{t-1}^{\mathfrak {D}_{n}}) +(K_{t}+R_{t}^{{\mathcal {C}}}+\max (1,S_{t}^{{\mathcal {C}}}(\Phi _{t}^{{\mathcal {C}}}+\Psi _{t}^{{\mathcal {C}}})+T_{t}^{{\mathcal {C}}})) \textrm{d}(\overline{\xi }_{t-1},\overline{\varepsilon }_{t-1}^{\mathfrak {D}_{n}}) \end{aligned}$$

(26)

and note that $\delta _{n}^{{\mathcal {C}}}\rightarrow 0$ by the induction hypothesis. For each $i,n\in {\mathbb {N}}$, let j(i, n) be such that $\delta _{j(i,n)}^{{\mathcal {C}}_{i}}\le \frac{1}{2n}$.

Finally, for any n, put $\mathfrak {C}_{n}=(\mathfrak {D}_{j(i(n),n)},{\mathcal {C}}_{i(n)})$. By substituting into (21), we get

$$\begin{aligned} \textbf{d}(\overline{\xi }_{t},\overline{\varsigma }_{t}^{\mathfrak {C}_{n}})\le 2\textrm{d}(\xi _{t},\epsilon _{i(n),t} (\xi _{t}))+\delta _{j(i(n),n)}^{{\mathcal {C}}_{i(n)}}\le \frac{1}{n}. \end{aligned}$$

(27)

Similarly we get, using (22), that $\textbf{d}(\overline{\xi }_{t},\overline{\varepsilon }_{t}^{\mathfrak {C}_{n}})\le \frac{1}{n}$, which, together with (27), proves (25). $\square$

The next Proposition states sufficient conditions for (18)–(20).

Proposition 4

Let $p=1$ and, for each $1\le t\le T$, let

$$\begin{aligned} G_{t}(x|y){\mathop {=}\limits ^{\text {def}}}\mu _{t}((-\infty ,x]|y) \end{aligned}$$

be differentiable in both x and y such that, for each x and y,

$$\begin{aligned} \left| \frac{\partial }{\partial y}G_{t}(x|y)\right| \le h(x,y) \end{aligned}$$

for some unimodal $h(\bullet ,y)$ with $\int h(x,\bullet )dx$ and $\max _{x}h(x,\bullet )$ uniformly bounded. Let

$$\begin{aligned} \frac{\partial }{\partial y}\int _{-\infty }^{c}G_{t}(x|y)dx=\int _{-\infty }^{c}\frac{\partial }{\partial y}G_{t}(x|y)dx \end{aligned}$$

and

$$\begin{aligned} \frac{\partial }{\partial y}\int _{c}^{\infty }[1-G_{t}(x|y)]dx=-\int _{c}^{\infty }\frac{\partial }{\partial y}G_{t}(x|y)dx \end{aligned}$$

for any $c\in {\mathbb {R}}$. Then the Lipschitz properties of (18)–(20) hold true.

Proof

Fix $1\le t\le T$ and a covering ${\mathcal {C}}$ and agree to omit corresponding indexes. Let $y\in {\mathbb {R}}.$ By Vallander (1973) (or perhaps (Pflug 2001)), we have

$$\begin{aligned} D(y)=I_{0}(y)+\dots +I_{k}(y), \end{aligned}$$

where

$$\begin{aligned}{} & {} I_{0}(y)=\int _{-\infty }^{e_{1}}G(x|y)dx,\qquad I_{k}(y)=\int _{e_{k}}^{\infty }[1-G(x|y)]dx, \\{} & {} I_{i}(y)=\int _{e_{i}}^{c_{i}}[G(c_{i}|y)-G(x|y)]dx+\int _{c_{i}}^{e_{i+1}}[G(x|y)-G(c_{i}|y)]dx, \qquad 1\le i\le k-1. \end{aligned}$$

Denoting $g(\bullet |y)=\frac{\partial }{\partial y}G(\bullet |y)$, we get

$$\begin{aligned}{} & {} I'_{0}(y)=\int _{-\infty }^{e_{1}}g(x|y)dx,\qquad I'_{k}(y)=-\int _{e_{k}}^{\infty }g(x|y)dx, \\{} & {} \quad I_{i}'(y)=-\int _{e_{i}}^{c_{i}}g(x|y)dx\\{} & {} \qquad +\int _{c_{i}}^{e_{i+1}}g(x|y)dx+[(c_{i}-e_{i})-(e_{i+1}-c_{i})]g(c_{i}|y),\\ \qquad 1\le i\le k-1, \end{aligned}$$

so

$$\begin{aligned}{} & {} \left| \frac{\partial }{\partial y}D(y)\right| \le {\int _{-\infty }^\infty |g(x|y)|dx+ \sum _{i=1}^{k-1}((c_{i}-e_{i})+(e_{i+1}-c_{i}))}|g(c_{i}|y)|\nonumber \\{} & {} \quad \le \int h(x,y)dx+2\sum _{i=1}^{k-1}|e_{i+1}-e_{i}||h(c_{i},y)|\le \int h(x,y)dx+2\int h^{*}(x,y)dx,\nonumber \\{} & {} \quad h^{*}(x,y)={\left\{ \begin{array}{ll} h(x+\hat{e},y) &{} x<m-\hat{e}\\ \max h(\bullet ,y) &{} m-\hat{e}\le x\le m+\hat{e}\\ h(x-\hat{e},y) &{} x>m+\hat{e} \end{array}\right. } \end{aligned}$$

(28)

where m is the mode of $h(\bullet ,y)$ and $\hat{e} = \max _{i=1,\dots ,k-1} |e_{i+1}-e_i|$ (we have used the fact that $h(\bullet ,y)$ is non-decreasing up to m and non-increasing from m). Clearly, $\int h^{\star }(x,y)dx\le \int h(x,y)dx+2\hat{e}\max h(\bullet ,y)$ which, together with (28), proves (18) as both $\int h(x,y)dx$ and $\max h(\bullet ,y)$ are uniformly bounded, hence the derivative is uniformly bounded and the Lipschitz property of D holds.

As for (19), we have

$$\begin{aligned}{} & {} E(y)=G(c_{1}|y)\int _{e_{1}}^{c_{1}}(x-e_{1})\omega _{1}(dx) +\sum _{i=2}^{k-1}(G(c_{i}|y)-G(c_{i-1}|y))\int _{c_{i-1}}^ {c_{i}}|x-e_{i}|\omega _{i}(dx)\\{} & {} \quad +(1-G(c_{k}|y))\int _{c_{k-1}}^{e_{k}}(e_{k}-x)\omega _{k}(dx) \end{aligned}$$

so

$$\begin{aligned}{} & {} \left| \frac{\partial }{\partial y}E(y)\right| \le h(c_{1},y)\int _{e_{1}}^{c_{1}}(c_{1}-e_{1})F_{1}(dx) +\sum _{i=2}^{k-1}(h(c_{i},y)+h(c_{i-1},y))\int _{c_{i-1}}^ {c_{i}}(c_{i}-c_{i-1})\omega _{i}(dx)\\{} & {} \qquad +h(c_{k-1},y)\int _{c_{k-1}}^{e_{k}}(e_{k}-c_{k-1})\omega _{k}(dx)\\{} & {} \quad \le h(c_{1},y)(c_{1}-e_{1})+\sum _{i=2}^{k-1}(h(c_{i},y) +h(c_{i-1},y))(c{}_{i}-c_{i-1})+h(c_{k-1},y)(e_{k}-c_{k-1}) \end{aligned}$$

which implies the Lipschitz property of (19) by applying a similar trick as in the case of D to the middle term.

Finally, as h is uniformly bounded, so is the derivative of G and the Lipschitz property of (20) holds. $\square$

Example 1

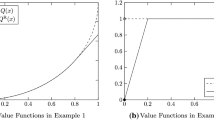
Let $p=1$ and let $\xi _{t}$ be AR(1), i.e., $\xi _{t}=a\xi _{t-1}+\epsilon _{t}$, $1\le t\le T,$ where the c.d.f. F of ${\epsilon _{t}}$ is differentiable with $F'=f$ unimodal. Then

$$\begin{aligned} G_{t}(x|y)=F(x-ay),\qquad \frac{\partial }{\partial y}G_{t}(x|y)=-af(x-ay), \end{aligned}$$

so we may choose $h(x,y)=|a|f(x-ay)$, giving $\int h(x,y)=a$, $\max h=|a|\max f$.⁴ Thus, by Proposition 4, the Lipschitz properties of (18)–(20) hold and, consequently, Theorem 2 holds once the tails of each $\sum _{\tau =1}^{t}a^{t-\tau }\epsilon _{t}$, $1\le t\le T,$ are $O(x^{-\alpha })$ for some $\alpha >1$, which is true in most cases because the converse would imply infinite second moments.

Example 2

If $\xi _{t}=\xi _{t-1}\epsilon _{t}$ then $G_{t}(x|y)={\mathbb {P}}[\epsilon _{t}\le \frac{x}{y}]=F(\frac{x}{y})$ where F is the c.d.f. of $\epsilon _{t}$. Here, unfortunately, Proposition 4 cannot be used because $\int \frac{\partial }{\partial y}G_{t}(x|y)dx=-\frac{1}{y^{2}}\int F'(\frac{x}{y})dx=-\frac{1}{y}$ is unbounded. We can, of course, assume $\xi _{t}$ to be a random walk and modify the mappings $\phi _{t},\psi _{t}$ and $\Xi _{t}$ in (3) (i.e., use $\phi _{t}(e^{x},u)$ instead of $\phi _{t}(x,u)$ etc.); however it is not guaranteed that the nested distance of the exponentials would converge, too.

Remark 4

A version of Theorem 2 for $p>1$ can be formulated for the price of more complex notation; however, a counterpart of (19) seems impossible to be verified even for the auto-regression as the probabilities $q_{\bullet }$ are involved.

Finally, we prove that the nested distance does not increase when we consider the i.i.d. part of the underlying process, which is not approximated.

Proposition 5

Let $\eta$ be a process taking values in ${\mathbb {R}}^{q}$ with deterministic $\eta _{0}$, such that $\xi {\perp \hspace{-2mm}\perp }\eta$ and $\varsigma {\perp \hspace{-2mm}\perp }\eta$, where ${\perp \hspace{-2mm}\perp }$ means independence. Then $\textbf{d}((\xi ,\eta ),(\varsigma ,\eta ))\le \textbf{d}(\xi ,\varsigma )$.

Proof

See Lemma 4 in Appendix. $\square$

5 Approximation of the multistage problem

The question we deal with in the present Section is the choice of a (rectangular) covering collection $\mathfrak {C}=({\mathcal {C}}_{1},\dots ,{\mathcal {C}}_{T})$ so that the smoothed quantization $\varsigma$ of $\xi ,$ defined by $\mathfrak {C}$ is suitable and as exact as possible.

The first thing to be taken into account is computability. Within the plain SDDP, $T-1$ collections of cuts, approximating the cost-to-go functions, are maintained, and each of these collections is updated during each backward pass, while, in our implementation of Markov SDDP, the number of the cut collections equals $\kappa =\sum _{t=1}^{T}k_{t}=\sum _{t=1}^{T}\prod _{i=1}^{p}k_{t,i}$ (the total number of the skeleton processes atoms) and, during each backward pass, only one collection per stage is updated. Therefore, it could be expected that the time complexity of the solution will be roughly linear in $\kappa$. Taking into account that a solution of a single problem by the plain SDDP could take tens of minutes on a regular PC (with processor Intel Core 5 and 16 GB RAM), it is clear that the numbers $k_{t,i}$ cannot be large, especially given multidimensional $\xi _{t}$, and even in the one-dimensional it would be very time consuming to exploit the asymptotic properties we proved. In any case, the number of the atoms is limited by our computational resources.

Having determined the numbers of the atoms we can computationally afford, the next step is to choose the frontiers of the covering sets and their representatives. As we have already premised, we find it reasonable to choose these parameters so that $\textbf{d}(\xi ,\varsigma )$ (hence $\textbf{d}((\xi ,\eta ),(\varsigma ,\eta ))$ by Proposition 5) is minimized. Unfortunately, such minimization is a very complex task, even if we resort to the minimization of the upper bound (15). That said, finding the optimal representatives with respect to (15) with the frontiers known is a complex, possibly non-convex problem: the second part of (15) and the dependence between the stages being due. However, if we believe that the distributions $\omega _{t,i}(\bullet |e)$ approximate the normalized versions of $\mu _{t}(\bullet \cap C_{t,i}|e)$ well, then we can regard the second part of (15) less critical and concentrate on the first part; contrary to the whole expression, finding the optimal representatives (with the frontiers known) is easy here as we minimize a sum of terms

$$\begin{aligned} \sum _{j=1}^{k_{\tau }}\int |x-e_{\tau ,j}^{i}|q_{\tau ,j}\omega ^i_{\tau ,j}(dx) = \sum _{k=1}^{k_{\tau ,i}} \int |x-e_{\tau ,i,k}| \left( \sum _{j:e^i_{\tau ,j}=e_{\tau ,i,k}} q_{\tau ,i,k} \right) \omega ^i_{\tau ,k} (dx) \end{aligned}$$

where $e_{\tau ,i,1},\dots e_{\tau ,i,k_{\tau ,i}}$ are the possible values of $e^i_{\tau ,\bullet }$. It is well known that (each term on the) right-hand side is minimized by $e_{t,i}^{i}=\textrm{median}(\omega ^i_{t,j})$.

Unfortunately, as we have premised, not all $\varsigma$’s with a reasonable value of the nested distance are suitable for the approximation of Problem (2). In particular, it may happen that, unlike the original problem, the approximate version is unbounded. To illustrate this possibility, consider a (hypothetical) asset-liability problem in which it is necessary to satisfy a random liability, no greater than some constant b, at the time T by means of buying an asset at the times $0,\dots ,T-1$. Say that the decision criterion is a nested mean-CVaR and that, in line with Efficient Market Hypothesis (see Cuthbertson (1997)), the asset prices form a martingale (see Kallenberg (2002), Chapter 7). Given these assumptions, there is no reason to buy more assets than b, because buying more than b assets up to $T-1$ and selling them at T would (possibly) increase risk (CVaR in our case) without increasing the mean value. However, as our approximation uses an “incorrect” conditioning value, it can happen that, despite the true price process being a martingale, the approximated one is a sub-martingale, i.e., the prices increase on average (to see it, recall that ${\mathbb {E}}(\varsigma _{t+1}|\varsigma _t=\bullet )$ is a piece-wise constant by Proposition 15 (iii), so ${\mathbb {E}}(\varsigma _{t+1}|\varsigma _{t})\ne \varsigma _{t}$ almost surely once $\omega$’s are absolutely continuous). If this (false) increase is high enough and/or the risk aversion is small enough, then, within the approximating problem, it could be “reasonable” to buy unlimited amounts of the asset to sell it at T. In result, these (false) arbitrage opportunities can completely overshadow the asset-liability management since the profits from the “speculation” would be unlimited. Clearly, to avoid this problem, the approximation has to be modified.

Proceeding generally, we start by giving a simple criterion, which, if fulfilled, guarantees boundedness of $\rho$ in Problem (2) from below, which, among other things, precludes arbitrage.

Proposition 6

Let there exist integrable random functions $f_{t}:{\mathbb {R}}^{d_{t}}\rightarrow {\mathbb {R}}$, $f_t \in {\mathcal {F}}_t$, $0\le t<T$, and a constant $\gamma$ such that, for each feasible policy x,

$$\begin{aligned}{} & {} \sigma _T(c'{}_{T}x_{T})\ge f_{T-1}(x_{T-1}) \end{aligned}$$

(29)

$$\begin{aligned}{} & {} \sigma _t(c'{}_{t}x_{t}+f_{t}(x_{t}))\ge f_{t-1}(x_{t-1}),\qquad 1\le t< T, \end{aligned}$$

(30)

$$\begin{aligned}{} & {} c'_{0}x_{0}+f_{0}(x_{0})\ge \gamma . \end{aligned}$$

(31)

Then the optimal value of (2) is bounded from below by $\gamma$.

Proof

Follows easily by gradual application of (29)– (31) to the criterion of Problem (2). $\square$

Corollary 1

Let $\sigma _{t}(z|{\mathcal {F}}_{t-1})\ge {\mathbb {E}}(z|{\mathcal {F}}_{t-1})$ for any ${\mathcal {F}}_t$-measurable random variable z and any $1\le t\le T$ and let (29)–(31) hold with ${\mathbb {E}}(\bullet |{\mathcal {F}}_{t-1})$ in place of $\sigma _t(\bullet )$ for any t. Then the optimal value of (2) is bounded from below by $\gamma$.

Proof

Follows from the fact that

$$\begin{aligned}{} & {} \rho (c'_{0}x_{0},\dots ,c'_{T}x_{T}) \\{} & {} \ge c'_{0}x_{0}+{\mathbb {E}}(\dots {\mathbb {E}}(c'_{T-2}x_{T-2}+{\mathbb {E}}(c_{T-1}x_{T-1}+{\mathbb {E}}(c'_{T}x_{T}|{\mathcal {F}}_{T-1})|{\mathcal {F}}_{T-2})|{\mathcal {F}}_{T-3})\dots ). \end{aligned}$$

$\square$

Remark 5

The mean-CVaR risk mapping fulfills the assumptions of Corollary 1. Indeed, as CVaR is the mean of the right tail distribution (see (Rockafellar and Uryasev 2002)), which is easy to show to first-order stochastically dominate the one from which it is computed, we have $\textrm{CVaR}(z|{\mathcal {F}}) \ge {\mathbb {E}}(z|{\mathcal {F}})$ and, consequently, $\text {mean-CVaR}(z|{\mathcal {F}})\ge {\mathbb {E}}(z|{\mathcal {F}})$ for any z and ${\mathcal {F}}$.

The way of finding an approximation $\varsigma$ such that the boundedness criterion is met clearly depends on the structure of the approximated problem. As we will see in the next Section, one of the conditions guaranteeing the boundedness of the Problem (2) with $p=1$ could be

$$\begin{aligned} \varrho {\mathbb {E}}(\xi _{t}|\xi _{t-1})\le \xi _{t-1},\qquad 1\le t\le T, \end{aligned}$$

(32)

where $\varrho$ is a discount factor. Now say that we have a smoothed quantization $\varsigma$ for which (32) does not hold and we look for a refined Markov approximation $\chi$ fulfilling (32) which is “similar” to $\varsigma$ in the sense that it is ruled by conditional probabilities $\varpi _{1},\dots ,\varpi _{T}$ such that, for any $1\le t \le T$ and $1\le i \le k_{t-1}$,

• (i) $\varpi _{t}(\bullet )$ is constant on $C_{t-1,i}$,

• (ii) $\varpi _{t}(\bullet |e_{t-1,i})=\sum _{j}\pi _{t,i,j}\omega '_{t,j}(\bullet )$ for some discrete distribution $\pi _{t,i,\bullet }$,

where, for any j, $\omega '_{t,j}$ is a distribution with $\textrm{support}(\omega '_{t,j})\subseteq C_{t,j}$. It may be easily seen that such a process fulfills (32) if

$$\begin{aligned} \varrho \sum _{j}\pi _{t,i,j}{\mathbb {E}}\omega '_{t,j}\le d_{t-1,i-1},\qquad 1\le i\le k_{t-1},1<t<T, \end{aligned}$$

(33)

where, for any $\tau$, $d_{\tau ,0}=\inf (\textrm{support}(\omega '_{\tau ,1}))$ and $d_{\tau ,j}=c_{\tau ,j},1<j\le k_{\tau }.$

One way to guarantee that such $\chi$ is close to $\varsigma$, for each $2\le t \le T$ and $1\le i \le k_{t-1}$, is to find $\pi _{t.i,1},\dots ,\pi _{t,i,k_{t}}$ so that $\textrm{d}(\theta _{t}(e_{t-1,i}),\vartheta _{t,i})$ is minimal, where $\vartheta _{t,i}$ is the distribution with atoms $e_{t,1},\dots ,e_{t,k_{t}}$ and corresponding probabilities $\pi _{t,i,1},\dots ,\pi _{t,i,k_{t}}$, i.e., for each i and t, to solve the transportation problem

$$\begin{aligned} \min _{\pi _{j}\ge 0,r_{j,k}\ge 0,1\le j,k\le k_{t}}&\sum _{j=1}^{k_{t}}\sum _{k=1}^{k_{t}}|e_{t,j}-e_{t,k}|r_{j,k} \end{aligned}$$

(34)

$$\begin{aligned} \text {s.t.}&\sum _{j=1}^{k_{t}}r_{j,k}=\mu _{t}(C_{t,k}^{k}|e_{t-1,i}),\qquad 1\le k\le k_{t}\nonumber \\&d_{t-1,i-1}\ge \varrho \sum _{j=1}^{k_{t}}\pi _{j}{\mathbb {E}}\omega '_{t,i},\qquad \pi _{j}=\sum _{k=1}^{k_{t}}r_{j,k},\qquad 1\le j\le k_{t} \end{aligned}$$

(35)

and set $\pi _{t,i,j}=\hat{\pi }_j$, $1\le j \le k_t$, where $\hat{\pi }_1,\dots , \hat{\pi }_{k_t}$ is the optimal solution of Problem (34). Note that this does not have to be done for $t=1$ as the approximation is perfect here. For all the Problems (34) to be feasible, it should hold

$$\begin{aligned} d_{t-1,0}\ge \varrho {\mathbb {E}}\omega '_{t,1},\qquad 2\le t\le T \end{aligned}$$

(36)

because otherwise no combination of $\pi _{1},\dots ,\pi _{k_{t}}$ would exist satisfying (35). To guarantee (36), we may set

$$\begin{aligned} \omega '{}_{t,1}=\delta _{e_{t,1}},\qquad \omega '{}_{t,i}=\omega _{t.i},\qquad 1<i\le k_{t},\quad 1\le t<T, \end{aligned}$$

(37)

which implies (36) given that

$$\begin{aligned} e_{0,1}\ge \varrho e_{1,1}\ge \dots \ge \varrho ^{T}e_{1,T}. \end{aligned}$$

(38)

In order to have $\chi$ as similar as possible to $\varsigma ,$ we may set $c_{t,1}$ so that ${\mathbb {P}}[\xi _{t}\le c_{t,1}]$ is negligible for each $1\le t\le T$.

Finally, we summarize our approximation algorithm:

Algorithm 1

1.	Determine suitable rectangular sets $(C_{t,i})_{1\le i\le k_{t}1\le ,t\le T}$
2.	For each $t=1$ to $T-1$
3.	For each $i=1$ to p
4.	For each $j=1$ to $k_{t,i}$
5.	Put $e_{t,i}^{j}=\textrm{median}({\omega }^i_{t,j})$
6.	End For
7.	End For
8.	End For
9.	Construct the smoothed quantization $\varsigma$ of $\xi$ defined by $C_\bullet$ and $e_\bullet$.
10.	If $\varsigma$ is suitable
11.	Solve Problem (2) with $\varsigma$ instead of $\xi$
12.	Else
13.	Refine $\varsigma$ to get a suitable approximation $\chi$
14.	Solve Problem (2) with $\chi$ instead of $\xi$
15.	End If

When $p=1$, a procedure constructing $\chi$ fulfilling the suitability condition (32) with $\varrho <1$ may be as follows

Algorithm 2

1.	Let c be such that ${\mathbb {P}}[\xi _t\le c]$ is small for each $1\le t\le T$
2.	Let e be slightly smaller than c
3.	For each $t=1$ to T
4.	Add c to the collection $c_{t,\bullet }$
5.	Add e to the collection $e_{t,\bullet }$
6.	Determine $\omega '_{t,\bullet }$ according to (37)
7.	Put $p_{t,i,j}=\mu _t(C_{t,j}|e_{t-1,i})$, $1\le j\le k_t$, $1\le i\le k_{t-1}$
8.	End For
9.	For each $t=2$ to T
10.	For each $i=1$ to $k_{t-1}$
11.	If $\varrho \int x \varpi _{t}(dx|e_{t-1,i})> e_{t-1,i}$
12.	Assign $p_{t,i,\bullet }$ the optimal solution of Problem (34)
13.	End If
14.	End For
15.	End For

Remark 6

“Suitable rectangular sets” may be determined according to (proofs of) Theorem 1 or Lemma 5, both from Šmíd (2009).

Remark 7

If $p=1$, then $\tilde{\omega }_{t,1,j}=q_{t,j}\omega _{t,j}$, $1\le j\le k_{t}$, $1\le t\le T-1$, so $\textrm{median}(\tilde{\omega }_{t,1,j})=\textrm{median}(\omega _{t,j})$, depending neither on $q_{t,\bullet }$ nor on t.

6 Application

In the present Section, we illustrate our approximation technique by a simplified version of a production-planning emission-trading problem of a steel company, published in Zapletal et al. (2019). The company produces four products made out of five raw products, and buys necessary carbon allowances on a secondary market. The subject of their decision is the production and the timing of the allowances purchase. The decision problem is as follows:

$$\begin{aligned} \inf&\rho (-z_{0},\dots ,-\varrho ^{T}z_{T})\nonumber \\ \text {s.t.}&\quad z_{0}\in {\mathbb {R}},\quad z_{0}=-P_{0}s_{0},\nonumber \\&\quad z_{t}\in {\mathbb {R}},\quad z_{t}=M'_{t}x_{t-1}-P_{t}s_{t},\quad 0<t\le T, \nonumber \\&\quad x_{t}\in {\mathbb {R}}_{+}^{4},\quad x_{t}\le D_{t},\quad 0\le t<T,\nonumber \\&\quad y_{t}\in {\mathbb {R}}_{+}^{5},\quad y_{t}=rx_{t},\quad y_{t}\le w,\quad 0\le t<T,\nonumber \\&\quad u_{0}\in {\mathbb {R}}_{+},\quad u_{0}=s_{0},\nonumber \\&\quad u_{t}\in {\mathbb {R}}_{+},\quad u_{t}=u_{t-1}+s_{t}-h'y_{t-1},\quad 0<t\le T,\nonumber \\&\quad s_{t}\in {\mathbb {R}},\quad 0\le t \le T,\nonumber \\&\quad \text {Any variable indexed by }t\text { is }{\mathcal {F}}_t-\text {measurable,}\qquad 0\le t\le T. \end{aligned}$$

(39)

Here, $\rho$ is the nested mean-CVaR risk measure. The decision variables include: $z_t$ – the monetary income of the company, $x_t$ – the final production, $y_t$ – the raw production, $u_t$ and $s_t$ – the numbers of the allowances held and purchased, respectively.

The constants include: $r \in {\mathbb {R}}^{5 \times 4}$ – the production matrix, $w\in {\mathbb {R}}^5$ – the raw production limits, $h \in {\mathbb {R}}^5$ – the vector of unit emissions, $\varrho \in {\mathbb {R}}$ – the discount factor.

As for the random parameters,

$$\begin{aligned} P_t \in {\mathbb {R}},\qquad P_t = P_{t-1}\exp \left\{ -\frac{\upsilon ^2}{2} + \upsilon V_t \right\} , \qquad 1\le t \le T, \end{aligned}$$

is the process of the allowance prices, where $V_1,\dots ,V_T$ are i.i.d. standard normal random variables and $\upsilon > 0$ is a parameter. Note that $P_t$ is, in fact, a discretized martingale Geometrical Brownian motion with a volatility of $\upsilon$.

Further,

$$\begin{aligned} M_{t}\in {\mathbb {R}}^4,\qquad M_{t}=[1+ \omega U_{t}]_{+}\mu ,\qquad 1\le t\le T, \end{aligned}$$

is the random profit from production where $\mu \in {\mathbb {R}}^{4}$ is a constant vector (equal to the mean prices) and $U_1,\dots ,U_T$ are i.i.d. standard normal, $t=1,\dots ,T$ (note that $M_t$ are i.i.d.).

Finally,

$$\begin{aligned} D_{t}\in {\mathbb {R}}^4,\qquad D_{0}=d,\qquad D_{t}=0.5D_{t-1}+0.5(d\text {+}E_{t}),\quad 1\le t<T, \end{aligned}$$

is the process of demand with d being a constant vector and $E_{t}$ is binomial symmetric with its atoms set so that the unconditional variance matrix equals $\frac{1}{4^2}$ of the demand process from Zapletal et al. (2019), Sect. 3. For the values of the constants and for more details, see (Zapletal et al. 2019).

In the present Section, we deal with the instance of Problem (39) with $T=2$, $\rho$ being the nested Mean-CVaR risk measure (with $\lambda =0.5$ and $\alpha =0.2)$, $\varrho =0.96$, $\omega = 0.0325$, $\nu =0.439$ and $P_{0}=24.29$ EUR (the price valid in November 2019). All these values have been estimated from real-world data (see (Zapletal et al. 2019)).

The simplifications we made in comparison with the original problem from (Zapletal et al. 2019) in order to be more illustrative are as follows: our problem is one stage less, we do not allow derivatives, no allowances are granted for free here, and the distributions of the random parameters are rescaled (in order to accommodate the allowance price increases in comparison with the time of (Zapletal et al. 2019)). Moreover, to be able to estimate the criterion better, we set the $\textrm{CVaR}$ level to 0.2 rather than 0.05.

As the random parameter $D_{t}$ lies on the right-hand side of the constraints, it may be expressed by means of an artificial decision vector $d_{t}$. After doing this and some substitutions, the decision problem is transformed to:

$$\begin{aligned} \inf&\rho (P_{0}u_{0},-\varrho z_{1},\dots ,-\varrho ^{T}z_{T})\\ \text {s.t.}&\quad z_{t}\in {\mathbb {R}},\quad z_{t}=M'_{t}x_{t-1}-P_{t}(u_t-u_{t-1}+h'rx_{t-1}),\quad 0<t\le T,\\&\quad x_{t}\in {\mathbb {R}}_{+}^{4},\quad x_{t}\le d_{t},\quad rx_{t}\le w,\quad 0\le t<T,\\&\quad u_{t}\in {\mathbb {R}}_{+},\quad 0<t<T,\\&\quad u_{T}=0,\\&\quad d_{t}=0.5d_{t-1}+0.5(d+E_{t}),\quad 0<t<T,\\&\quad d_{0}=d,\\&\quad \text {Any variable indexed by }t\text { is }{\mathcal {F}}_t\text {-measurable,}\qquad 0\le t\le T. \end{aligned}$$

In the language of Sect. 2, we have $\eta _{t}=(M_{t},E_{t})$ and $\xi _{t}=P_{t}$, $0\le t\le T$ with $M_{0}\equiv 0$, $E_{0}\equiv 0$. Note that $u_T=0$, i.e., no allowances are kept for future use at the time horizon.

The following Proposition shows that (32) is a sufficient condition for the boundedness of the Problem.

Proposition 7

If

$$\begin{aligned} P_{t}\ge \varrho {\mathbb {E}}(P_{t+1}|P_{t}),\qquad 0\le t<T, \end{aligned}$$

(40)

then the optimal value in (39) is bounded from below.

Proof

Put

$$\begin{aligned} f_{t}(e)=-\varrho ^{t+1}{\mathbb {E}}(P_{t+1}|P_{t})e-\nu \sum \nolimits _{\tau =t+1}^{T} \varrho ^\tau ,\qquad 0<t<T, \end{aligned}$$

where $\nu =\max _{x\ge 0,rx\le w}\mu 'x$. As ${\mathbb {E}}(P_t|{\mathcal {F}}_{t-1})={\mathbb {E}}(P_t|P_{t-1})$ and ${\mathbb {E}}(M_t|{\mathcal {F}}_{t-1})=\mu$ for any $1\le t \le T$, we have

$$\begin{aligned}{} & {} {\mathbb {E}}(-\varrho ^{T}z_{T}|{\mathcal {F}}_{T-1})\\{} & {} \quad =\varrho ^{T}(\underbrace{-\mu 'x_{T-1}}_{\ge -\nu }+\underbrace{{\mathbb {E}}(P_{T}|P_{T-1})h'rx_{T-1}}_{\ge 0}-{\mathbb {E}}(P_{T}|P_{T-1})e_{T-1}) \ge f_{T-1}(e_{T-1}), \end{aligned}$$

and

$$\begin{aligned} {\mathbb {E}}(-\varrho ^{t}z_{t}+f_{t}(e_{t})|{\mathcal {F}}_{t-1})\\ =\varrho ^{t}{\mathbb {E}}(\underbrace{-M'_{t}x_{t-1}}_{\ge -\nu }+\underbrace{(P_{t}-\varrho {\mathbb {E}}(P_{t+1}|P_{t}))}_{\ge 0}e_t-P_te_{t-1}+\underbrace{P_th'rx_{t-1}}_{\ge 0} |{\mathcal {F}}_{t-1})-\nu \sum \nolimits _{\tau =t+1}^{T} \varrho ^\tau \\ \ge f_{t-1}(e_{t-1}) \end{aligned}$$

for any $0<t<T$, and

$$\begin{aligned} P_{0}e_{0}+f_{t}(e_0) \ge -\nu \sum \nolimits _{\tau =1}^{T} \varrho ^\tau , \end{aligned}$$

which together guarantee the boundedness by Corollary 1. $\square$

Remark 8

Proposition 7 holds not only for geometrically Brownian prices $P_t$, but also for any P general Markov with finite first moments.

To investigate the impact of the accuracy of the approximation on the quality of the solution, we solved Problem (39) for 22 different combinations of $k_{1}$ and $k_{2}$. For each pair, we proceeded using Algorithms 1 and 2. In particular, we put $c_{1,1}=$0.5, $e_{1,1}=0.45,$ $c_{2,1}=0.3$, $e_{2,1}=0.27$ (note that ${\mathbb {P}}[\xi _{t}\le c_{t,1}],t=1,2,$ are negligible); the rest of the frontiers we set, according to Šmíd (2009), to

$$\begin{aligned} c_{t,i}=F_{t}^{-1}\left( \frac{i-1}{k_{t}-1}\right) ,\quad 1<i<k_{t},\qquad t=1,2, \end{aligned}$$

where $F_{t}$ is the unconditional c.d.f. of $P_{t}$. The representatives have been set to

$$\begin{aligned} e_{1,i}=\textrm{median}(\omega _{1.i}),\quad 1<i\le k_{1} \end{aligned}$$

(see Remark 7).

As the boundedness criterion (40) coincides with (32), we might set $\omega '_{\bullet }$ according to (37) and use Problem (34) to compute conditional probabilities defining $\chi$. Note that (38) is fulfilled whenever $k_{2}\ge k_{1}$).

Next, we solved the problem with $\chi$ instead of $\xi$ by the Markov SDDP algorithm, implemented in $\texttt {C++}$ with $\texttt {CPlex}$ serving as the linear programming solver.

To evaluate the resulting optimal policy, we have tested it given the true (Geometrical Brownian) distribution of P; in particular, we have estimated $\rho$ given the “true” distribution using the policy stemming from the approximation. We have proceeded by simulation; namely, we have computed 20 estimators of $\rho$, each by means of 10, 000 scenarios $S{\mathop {=}\limits ^{\text {def}}}(P_{1},\eta _{1},P_{2},\eta _{2})$ drawn from the “true” distribution. To be able to estimate the inner $\textrm{CVaR}$’s, we have drawn the sample using conditional sampling, i.e., 100 observations are drawn from ${\mathcal {L}}(P_1)\circ {\mathcal {L}}(\eta _1)$ and, for each value $(p,\eta )$ obtained this way, 100 observations are drawn from ${\mathcal {L}}(P_2|P_1=p)\otimes {\mathcal {L}}(\eta _2)$. For each scenario S, we compute the corresponding “Markov” scenario $M{\mathop {=}\limits ^{\text {def}}}(\epsilon _{1}(P_{1}),P_{1},\eta _{1},\epsilon _{2}(P_{2}),P_{2},\eta _{2})$,⁵ and subsitute it into the approximate policy to get the corresponding incomes $Z=(Z_1,Z_2){\mathop {=}\limits ^{\text {def}}}(\varrho z_1, \varrho ^2 z_2)$. As a result of this procedure, we have a sample of 100 values of $Z_1$ and 100 values of $Z_2$ for each $Z_1$. The mean part of the criterion has been estimated by the sample means of Z, each $\textrm{CVaR}(Z_2|Z_1=z)$ as a mean of the 20 highest values of $Z_2$ with $Z_1=z$, and the outer $\textrm{CVaR}$ as the average of the highest 20 inner CVaRs. Finally, we estimate $\rho$ by the average of our 20 estimators, denoting it by $\tilde{v}(=\tilde{v}_{k_1,k_2})$.

The results of solutions for individual pairs $k_1,k_2$ are summarized in Table 1 and depicted in Fig. 2. Though the estimations of the objective value are noised, an increasing trend is visible at the first look. By linear regression

$$\begin{aligned} \tilde{v}_{k_1,k_2}\sim a+b\kappa ,\qquad \kappa =k_{1}+k_{2} \end{aligned}$$

we get $b=0.019(0.002)$, where there is the standard error in brackets, which means that, by adding one node to the optimization, the value of the criterion increases by roughly EUR 19,000. Figure 3 shows the dependence of the computational times on $\kappa$; even though the trend comes out quadratic, it is close to the linear one as we supposed.

Table 1 Evaluation of optimal policies given various $k_1$, $k_2$. $\tilde{v}_{k_{1},k_{2}}$: average value of $-\rho$ (in millions of EUR) with standard deviation (within the 20 estimates), t: average solution time in minutes (over the 20 estimates), “no opt”: objective value without optimization of emission trading (allowances are not pre-purchased)

Fig. 2

Evaluation of optimal policies. Points: average value of $-\rho$, bars: standard deviations, line: trend $a+b\kappa$. The horizontal axis – labels: $k_1$ and $k_2$, positions: $k_1+k_2$

Fig. 3

Computational times in dependence on $\kappa$. Vertical axis: time in minutes

Clearly, once the true optimal value v is finite, the trend of the criterion improvement cannot be linear in $\kappa$ as the series should converge to v from below. Unfortunately, the noise of the estimation prevented us from fitting more complex trends. However, when we rerun the same analysis with all the processes except for deterministic P, the noisiness of the criterion estimation decreased enough for the non-linear regression

$$\begin{aligned} v-\tilde{v}_{k_1,k_2}\sim a\exp \{b\kappa \} \end{aligned}$$

to be significant, giving $v=63.46(0.06)$, $a=2.40(0.11)$, $b=-0.092(0.009)$, see also Fig. 4. This suggests that the convergence rate of the approximation error as $\kappa \rightarrow \infty$ is exponential (a similar model with $v-\tilde{v}=O(\kappa ^{b})$ came out insignificant).

Fig. 4

Evaluation of optimal policy with deterministic $\eta$

Finally, as an experiment, we run several optimizations with discrete approximations and tried to evaluate them the same way as the smoothed quantization. In particular, we have used the skeleton process $\varepsilon$ calibrated to be a martingale as an approximation instead of $\varsigma$. The resulting optimal policies, however, have proved to be useless because they recommended arbitrage as a reaction to a significant portion of scenarios; needless to say, such recommendations mostly lead to huge losses “in reality”, as the true discounted price process is a supermartingale. This clearly speaks in favor of the smoothed quantization. However, it should be said in defense of discrete approximations that, when the decision period is long, a new optimization could (and should) be done at each stage rather than using the policy from the previous optimization; this new optimization can clearly be calibrated not to produce arbitrage in its first stage. If, on the other hand, the decision period is short, as in high-frequency trading for instance, then having a policy not producing arbitrage at hand is more than necessary.

7 Conclusions

We have proposed an approximation technique suitable for multistage problems with Markov random parameters and illustrated its usefulness on a realistic problem. Our technique is especially suitable for financial applications as it does not neglect the distribution tails and it can cope with arbitrage potentially arising in approximated problems.

In the present paper, the approximation is designed to minimize the nested distance; however, its parameters may be set to meet other criteria, e.g., to keep the first two moments of the exact process (the moments of $\varsigma$ may be easily evaluated by the Law of Iterated Expectation and the Law of Iterated Variance). Inspired by Kozmík and Morton (2015), one may also think of finer approximation of the tails in order to fit tail measures more accurately.

Regarding future research, three ideas come to mind. First, looking at Fig. 1, it suggests itself to set ${\mathbb {P}}[\varepsilon _{t}=\bullet |\varepsilon _{t-1}=e]$ so that $\textbf{d}(\nu _{t}(e),\mu _t(e))$ is minimized rather than determine the probabilities by (10). It should, however, be noted that such minimization could be difficult and, moreover, some of our theoretical results may no longer hold. Second, our “anti-arbitrage protection” could be built into the initial construction of $\varsigma$. We did not do this in the present paper as the “anti-arbitrage” condition is problem-dependent; however, maybe it is possible to find more general conditions precluding arbitrage and build them into the initial construction of the approximation. Third, condition

$$\begin{aligned} P_t \ge \varrho \sigma _{t+1}(P_{t+1}) \end{aligned}$$

(41)

would probably suffice for boundedness of Problem (39) (as well as of similar ones); as this condition is less strict than (40), it would lead to smaller distortions of the original approximations. However, proving this, e.g., for Problem (44) would require dealing with estimation of $\sigma _t(cM_t+dP_t)$ from below for some constants c, d, which would require either uniform boundedness of $M_t$, which is not the case in our example, or a general estimate of risk mappings of independent sums from below which we, however, are not aware of. But nothing prevents anyone from using approximations restricted only by (41) given that they do not produce arbitrage in practice.

Clearly, our technique might be improved in many ways; however, even in the present form, it may be useful for a wide area of problems, including portfolio selection, derivative replication or asset-liability management.

Appendices

A. Auxiliary results

Lemma 1

Let $1<t\le T$ and let $\xi ,\varsigma$ be processes on $\{1,\dots ,t\}$ taking values in ${\mathbb {R}}^p$. Denote $P={\mathcal {L}}$($\overline{\xi }_{t}$), $Q={\mathcal {L}}(\overline{\varsigma }_{t})$. Let $\pi$ be a nested transportation from P into Q. Then, for each $x,s\in {\mathbb {R}}^{\bar{p}_{t-1}}$, an optimal transportation $\varpi _{t}(\bullet |x,s)$ from $P[\xi _{t}\in \bullet |\overline{\xi }_{t-1}=x]$ into $Q[\varsigma _{t}\in \bullet |\overline{\varsigma }_{t-1}=s]$ (w.r.t. $\textrm{d}$) exists (being a well defined conditional probability).

Proof

By Villani (2003), Theorem 1.3. $\varpi _{t}(\bullet |x,s)$ exists (and is a probability measure) for each x, s. To prove that $\varpi _{t}$ is a conditional probability, it remains to show that

$$\begin{aligned} {\varpi _{t}(A|\bullet ) \text{ is measurable for each } A\in {\mathcal {B}}^{p}\otimes {\mathcal {B}}^{p}.} \end{aligned}$$

(42)

Certainly, (42) holds if

$$\begin{aligned} A\in {\mathcal {C}}, \qquad {\mathcal {C}}=\{B\times C:B,C\in {\mathcal {B}}^{p},\text{ at least one of } B \text{ and } C\text{ is }{\mathbb {R}}^p\} \end{aligned}$$

(because $\varpi _{t}(A|\bullet )={\mathbb {P}}[B|\xi _{t-1}=\bullet _{1}]$ which is measurable by definition, similarly for the second coordinate). Clearly, ${\mathcal {C}}$ is a $\pi$ system with $\sigma ({\mathcal {C}})={\mathcal {B}}^{p}\otimes {\mathcal {B}}^{p}$. Put $\mathcal {D=}\{A\in {\mathcal {B}}^{p}\otimes {\mathcal {B}}^{p}:A\text { fulfils }(42)\}.$ Trivially, ${\mathbb {R}}^{p}\times {\mathbb {R}}^{p}\in {\mathcal {D}}$. Further, once $A,B\in {\mathcal {D}}$ and $B\subset A$, we have $\varpi _{t}(A{\setminus } B|\bullet )=\varpi _{t}(A|\bullet )-\varpi _{t}(B|\bullet )$ (by the elementary properties of probability measures), so $A{\setminus } B\in {\mathcal {D}}$ by Kallenberg (2002), Lemma 1.12. Finally, once for $A_{1}\subset A_{2}\subset \dots$, $A_{i}\in {\mathcal {D}}$, $i\in {\mathbb {N}}$, we have $\lim _{i}A_{i}\in {\mathcal {D}}$ by Kallenberg (2002), Lemmas 1.14 and 1.10 (ii). Thus, ${\mathcal {D}}$ is a $\lambda$-system containing ${\mathcal {C}}$, and, by the Monotone Class Argument ((Kallenberg 2002), Theorem 1.1), ${\mathcal {B}}^{p}\times {\mathcal {B}}^{p}\in {\mathcal {D}}$, i.e., (42) holds true. $\square$

Lemma 2

Let $\mu$ be a conditional distribution on $({\mathbb {R}}^{p},{\mathcal {B}}^{p})$ given values from a measurable space $(S,{\mathcal {S}})$. Let $U\in {\mathbb {R}}^{s}$ be a random vector and let $g:S\times {\mathbb {R}}^{s}\rightarrow {\mathbb {R}}^{p}$ be a measurable mapping such that

$$\begin{aligned} \mu (\bullet |x)={\mathbb {P}}[g(x,U)\in \bullet ]. \end{aligned}$$

(43)

Then

$$\begin{aligned} \textrm{d}(\mu (x),\mu (y))\le \int \Vert g(x,u)-g(y,u)\Vert {\mathcal {L}}(U)(du). \end{aligned}$$

Proof

Fix $x,y\in S$. Put

$$\begin{aligned} X=\zeta (U),\qquad \zeta :({\mathbb {R}}^{s},{\mathcal {B}}^{s})\rightarrow (S\times S,{\mathcal {S}}\otimes {\mathcal {S}}),\qquad \zeta (u)=(g(x,u),g(y,u)), \end{aligned}$$

and denote $\pi ={\mathcal {L}}(X)$. As

$$\begin{aligned} \pi (\bullet \times S)={\mathbb {P}}[\zeta (U)\in \bullet \times S]={\mathbb {P}}[g(x,U)\in \bullet ]=\mu (\bullet |x) \end{aligned}$$

and, similarly, $\pi (S\times \bullet )=\mu (\bullet |y)$, $\pi$ is a transportation from $\mu (x)$ to $\mu (y)$. Moreover, by calculus,

$$\begin{aligned} \int \Vert r-s\Vert \pi (dr,ds)=\int \Vert g(x,u)-g(y,u)\Vert {\mathcal {L}}(U)(du) \end{aligned}$$

which proves the Lemma because the l.h.s. majorizes the Wasserstein distance. $\square$

Lemma 3

For any processes $\xi ,\varsigma$ in ${\mathbb {R}}^{p}$ and any $1\le t,$

$$\begin{aligned} \textrm{d}(\xi _{t},\varsigma _{t})\le \textrm{d}(\overline{\xi }_{t},\overline{\varsigma }_{t})\le \textbf{d}(\overline{\xi }_{t},\overline{\varsigma }_{t}) \end{aligned}$$

Proof

Let $\pi$ be the optimal transportation from $\overline{\xi }_{t}$ to $\overline{\varsigma }_{t}$. Then $\pi _{t}(X,S){\mathop {=}\limits ^{\text {def}}}\pi ({\mathbb {R}}^{(t-1)p}\times X,{\mathbb {R}}^{(t-1)p}\times S)$ is a transportation from $\xi _{t}$ to $\varsigma _{t}$ which proves the first inequality. For the second one, see (Pflug and Pichler 2014), Lemma 2.37. $\square$

Lemma 4

Let $\xi$ and $\varsigma$ be processes in ${\mathbb {R}}^p$ on $\{0,\dots ,T\}$ with deterministic $\xi _0$ and $\varsigma _0$. Let $q\in {\mathbb {N}}$ and let $\eta ,\eta '$ be processes on ${0,\dots ,T}$ with $\eta _{t},\eta '_{t}\in$ ${\mathbb {R}}^{q}$, $0\le t\le T$, having the same distribution, with deterministic $\eta _{0}=\eta '_{0}$, such that $\eta {\perp \hspace{-2mm}\perp }\xi$, $\eta '{\perp \hspace{-2mm}\perp }\varsigma$. Then $\textbf{d}((\xi ,\eta ),(\varsigma ,\eta '))\le \textbf{d}(\xi ,\varsigma )$.

Proof

Let $\rho$ be a nested transportation, $\epsilon$-optimal with respect to $\textbf{d}(\xi ,\varsigma )$. For any $1\le t\le T$, denote $\rho _t$ the transportation from $\xi _t|\overline{\xi }_{t-1}$ to $\varsigma _t|\overline{\varsigma }_{t-1}$ (its existence is assured by the definition of the nested transportation).

Further, for each t and $\overline{u},\overline{v}\in {\mathbb {R}}^{\bar{q}_{t-1}},$ $\bar{q}_{t-1}=(t-1)q$, let $\sigma _{t}(v|\overline{u},\overline{v})$ the optimal transportation from ${\mathcal {L}}(\eta _{t}|\overline{\eta }_{t-1}=\overline{u})$ into ${\mathcal {L}}(\eta _{t}|\overline{\eta }_{t-1}=\overline{v})$. By Lemma 1, $\sigma _{t}$ is a well-defined conditional probability. As $\textrm{d}$ is a metric, we have $0=\textrm{d}(\eta _{t}|\overline{u},\eta '_{t}|\overline{u})=\int \Vert u-v\Vert \sigma {}_{t}(du,dv|\overline{u},\overline{u})$, so we can choose $\sigma _{t}$ so that $\sigma _{t}(\bullet |\overline{u},\overline{u})$ is concentrated on $\{(u,u):u\in {\mathbb {R}}^{q}\}$.

For any $1\le t\le T$, denote $\theta =(\xi ,\eta ),$ $\theta '=(\varsigma ,\eta ')$ and consider the conditional distribution $\pi _t$ defined as

$$\begin{aligned}{} & {} \pi _{t}(\xi _{t}\in A,\eta _{t}\in B,\varsigma _{t}\in C,\eta '_{t}\in D|\overline{\theta }_{t-1},\overline{\theta '}_{t-1}) \\{} & {} \quad =\sigma _{t}(B\times D|\overline{\eta }_{t-1},\overline{\eta '}_{t-1})\otimes \rho _{t}(A\times C|\overline{\xi }_{t-1},\overline{\varsigma }_{t-1}). \end{aligned}$$

It could be easily proved by the Monotone Class Argument (see the proof of Remark 2 in Appendix B.1) that $\pi _{t}$ is a transportation from $\theta _{t}|\overline{\theta }_{t-1}$ into $\theta '_{t}|\overline{\theta '}_{t-1}$. Consequently, the distribution $\pi$ defined by the composition of $\pi _{1},\dots ,\pi _{T}$ is a nested transportation, so we have

$$\begin{aligned} \textbf{d}(\theta ,\theta ')\le & {} \int \Vert \overline{y}_{T}-\overline{z}_{T}\Vert \pi (d\overline{y}_{T},d\overline{z}_{T})\\= & {} \int \dots \int (\Vert \overline{x}_{T}-\overline{s}_{T}\Vert +\Vert \overline{u}_{T}-\overline{v}_{T}\Vert )\sigma _{T} (du_{T},dv_{T}|\overline{u}_{T-1},\overline{v}_{T-1})\rho _{T}(dx_{T},ds_{T}|\overline{x}_{T-1},\overline{s}_{T-1})\dots \sigma _{1}(u_{1},v_{1})\rho _{t}(x_{1},s_{1})\\= & {} \int \Vert \overline{u}_{T}-\overline{v}_{T}\Vert \sigma _{T}(du_{T},dv_{T} |\overline{u}_{T-1},\overline{v}_{T-1})\dots \sigma _{1}(u_{1},v_{1}) \\{} & {} \quad +\int \Vert \overline{x}_{T}-\overline{s}_{T}\Vert \rho _{T}(dx_{T},ds_{T}| \overline{x}_{T-1},\overline{s}_{T-1})\dots \rho _{t}(x_{1},s_{1})\\= & {} 0+\int \Vert \overline{x}_{T}-\overline{s}_{T}\Vert \rho _{T}(d\overline{x}_{T},d\overline{s}_{T})\le \textbf{d}(\xi ,\varsigma )+\epsilon . \end{aligned}$$

The Lemma now follows by limit transition. $\square$

B Proofs

1.1 B.1 Proof of Remark 2

By the Tower Property ((Pflug and Pichler 2012), Lemma 10), $\pi$ is a nested transportation in the sense of (Pflug and Pichler 2012) if and only if, for each $1\le t\le T$,

$$\begin{aligned}{} & {} \pi ((\overline{\xi }_{t},\overline{\varsigma }_{t})\in A\times {\mathbb {R}}^{\bar{p}_{t}}|\overline{\xi }_{t-1},\overline{\varsigma }_{t-1})=P[\overline{\xi }_{t}\in A|\overline{\xi }_{t-1}],\qquad A\in {\mathcal {B}}^{\bar{p}_{t}}, \end{aligned}$$

(44)

$$\begin{aligned}{} & {} \pi ((\overline{\xi }_{t},\overline{\varsigma }_{t})\in {\mathbb {R}}^{\bar{p}_{t}}\times B|\overline{\xi }_{t-1},\overline{\varsigma }_{t-1})=Q[\overline{\varsigma }_{t}\in B|\overline{\varsigma }_{t-1}],\qquad B\in {\mathcal {B}}^{\bar{p}_{t}}. \end{aligned}$$

(45)

Applying (44) to sets $A=A_{t}\times {\mathbb {R}}^{\overline{p}_{t-1}}$, $A_{t}\in {\mathcal {B}}^{p}$, we see that (44) implies (5). To prove the reverse implication, note first that (5) implies (44) for any $A\in {\mathcal {C}}{\mathop {=}\limits ^{\text {def}}}\{B\times C:B\in {\mathcal {B}}^{p}$, $C\in {\mathcal {B}}^{\bar{p}_{t-1}}\}$; indeed,

$$\begin{aligned} P\left[ \overline{\xi }_{t}\in A|\overline{\xi }_{t-1}\right]= & {} {\mathbb {E}}_{P}\left( \textbf{1}_{B}\left( \xi _{t}\right) \textbf{1}_{C}\left( \overline{\xi }_{t-1}\right) |\overline{\xi }_{t-1}\right) \\= & {} \textbf{1}_{C}\left( \overline{\xi }_{t-1}\right) P\left[ \xi _{t}\in B|\overline{\xi }_{t-1}\right] =\textbf{1}_{C}\left( \overline{\xi }_{t-1}\right) \pi \left[ (\xi _{t},\varsigma _{t})\in B\times {\mathbb {R}}^{p}|\overline{\xi }_{t-1},\overline{\varsigma }_{t-1}\right] \\= & {} \textbf{1}_{C}\left( \overline{\xi }_{t-1}\right) {\mathbb {E}}_{\pi }\left( \textbf{1}_{B}\left( \xi _{t}\right) |\overline{\xi }_{t-1},\overline{\varsigma }_{t-1}\right) ={\mathbb {E}}_{\pi }\left( \textbf{1}_{C}\left( \overline{\xi }_{t-1}\right) \textbf{1}_{B}\left( \xi _{t}\right) |\overline{\xi }_{t-1},\overline{\varsigma }_{t-1}\right) \\= & {} \pi \left[ \left( \overline{\xi }_{t},\overline{\varsigma }_{t}\right) \in A\times {\mathbb {R}}^{\bar{p}_{t}}|\overline{\xi }_{t},\overline{\varsigma }_{t}\right] \end{aligned}$$

(we used the pull-out property of conditional expectations (Kallenberg 2002, Theorem 6.1 (v) twice). As, by the definition of the product sigma fields, ${\mathcal {C}}$ is a generator of ${\mathcal {B}}^{\bar{p}_{t}}$, closed under finite intersections, and as the system of sets A fulfilling (44) contains ${\mathbb {R}}^{\bar{p}_{t}}$ and is closed under proper differences and increasing limits (by the properties of probability measures⁶), (5) follows by the Monotone Class Argument (Kallenberg 2002, Theorem 1.1.). The proof of the equivalence of (45) and (6) is symmetric.

1.2 B.2 Proof of proposition 1

Let $\pi _{t-1}$ be an $\epsilon$-optimal (w.r.t. $\textbf{d}(\overline{\xi }_{t-1},\overline{\varsigma }_{t-1})$) nested transportation from $\overline{\xi }_{t-1}$ to $\overline{\varsigma }_{t-1}$. Let, for each $x,s\in {\mathbb {R}}^{p}$, $\varpi _{t}(\bullet |x,s)$ be the optimal transportation from $\mu (x)$ into $\nu (s)$; by Lemma 1 (Appendix), $\varpi _{t}$ is a well-defined probability distribution.

Put

$$\begin{aligned} \pi _{t}(d\overline{x}_{t},d\overline{s}_{t})=\varpi _{t}(dx_{t},ds_{t}|x_{t-1},s_{t-1}) \pi _{t-1}(d\overline{x}_{t-1},d\overline{s}_{t-1}). \end{aligned}$$

As, by the Markov property, $\mu _{t}(\xi _{t-1})={\mathcal {L}}(\xi _{t}|\overline{\xi }_{t-1})$, $\nu _{t}(\varsigma _{t-1})={\mathcal {L}}(\varsigma _{t}|\overline{\varsigma }_{t-1})$, and as, by definition, $\varpi _{t}$ is a conditional distribution of the last 2p components of $\pi _{t}$, we have, by Definition 2, that $\pi _{t}$ is a nested transportation from $\overline{\xi }_{t}$ to $\overline{\varsigma }_{t}$. Thus

$$\begin{aligned} \textbf{d}(\overline{\xi }_{t},\overline{\varsigma }_{t})\le & {} \int \Vert \overline{x}_{t}-\overline{s}_{t}\Vert \pi _{t}(d\overline{x}_{t},d\overline{s}_{t})\nonumber \\= & {} \int \int [\Vert \overline{x}_{t-1}-\overline{s}_{t-1}\Vert +\Vert x_{t}-s_{t}\Vert ] \varpi _{t}(dx_{t},ds_{t}|x_{t-1},s_{t-1})\pi _{t-1}(d\overline{x}_{t-1},d\overline{s}_{t-1})\nonumber \\\le & {} \textbf{d}(\overline{\xi }_{t-1},\overline{\varsigma }_{t-1})+\epsilon +B_{t}, \end{aligned}$$

(46)

where

$$\begin{aligned} B_{t}= & {} \int \left( \int \Vert x{}_{t}-s_{t}\Vert \varpi _{t}(dx_{t},ds_{t}|x_{t-1},s_{t-1})\right) \pi _{t-1}(d\overline{x}_{t-1},d\overline{s}_{t-1})\\= & {} \mathrm {\int d}(\mu _{t}(x_{t-1}),\nu _{t}(s_{t-1})) \pi _{t-1}(d\overline{x}_{t-1},d\overline{s}_{t-1})\\\le & {} \int \textrm{d}(\mu _{t}(x_{t-1}),\mu _{t}(s_{t-1})) \pi _{t-1}(d\overline{x}_{t-1},d\overline{s}_{t-1})\\{} & {} \quad +\int \textrm{d}(\mu _t(s_{t-1}),\nu _{t}(s_{t-1})) \pi _{t-1}(d\overline{x}_{t-1},d\overline{s}_{t-1})\\\le & {} K_{t}\int \Vert x_{t-1}-s_{t-1}\Vert \pi _{t-1}(d\overline{x}_{t-1},d \overline{s}_{t-1})+{\mathbb {E}}d(\mu _{\tau }(\varsigma _{\tau }\text {-1}), \nu _{\tau }(\varvec{\varsigma }_{\tau -1}))\\\le & {} K_{t}(\mathrm {\textbf{d}}(\overline{\xi }_{t-1},\overline{\varsigma }_{t-1})+\epsilon ) +{\mathbb {E}}d(\mu _{\tau }(\varsigma _{\tau }\text {-1}),\nu _{\tau }(\varvec{\varsigma }_{\tau -1})) \end{aligned}$$

(we have used the triangular inequality for $\textrm{d}$). The Proposition now follows by substituting this into (46) and by a limit transition.