Introduction

Lattice structures have attracted extensive attention in various fields, such as protection systems, aerospace, and biomedical areas, due to the specific characteristics of lightweight and high energy absorption.1,2,3,4,5 These phenomena are associated with the geometric characteristic of lattice structures formed by duplicating unit cells in two- or three-dimensional scale, resulting in reducing the use of materials and being lightweight compared to solid structures. The 2D re-entrant unit cell and the Kelvin cell as representative models have been widely employed for patterning lattice structures due to their specific properties, i.e., re-entrant auxetic structure possessing a negative Poisson’s ratio, which makes it have indentation resistance,6,7 high energy absorption,8 and fracture toughness,6,7,9,10 while Kevin cells consisted of eight hexagonal honeycombs and six quadrilaterals with high energy absorption capacity. Historically, Evans et al.11 first proposed an orthotropic 3D re-entrant lattice structure extended through a 2D re-entrant, while the Kelvin cell was initially studied in the form of foam.12,13,14,15,16 Later, a large number of lattice structures in terms of geometry were developed based on the two conventional unit cell fundamentals to study their compressive behaviors. For instance, Yang et al.17 and Wang et al.18 conducted their experimental and simulation work on the 3D re-entrant lattice structure to draw a similar conclusion to Evans et al.,11 where the structure displayed a negative Poisson’s ratio in three directions under compression. Meanwhile, they also found that the strut thickness and the re-entrant angle have a greater effect on the mechanical properties than the ratio of the vertical strut length over the oblique strut. Alomarah et al.19 proposed a 3D re-entrant chiral auxetic structure by connecting solid cubes with struts, and found that the plastic bending and bulking were the main deformation mechanics of the lattice, and that the structure also displayed excellent energy absorption under uniaxial compression. Ozdemir et al.20 experimentally studied the energy absorption and failure modes of lattice structures patterned by diamond, cubic, and re-entrant unit cells. Simone and Gibson21 discussed the influence of the solid distribution and relative density on the mechanical properties by finite element (FE) models of 2D honeycomb and 3D Kelvin cell foam. Fischer et al.22 predicted the mechanical properties of the Kelvin cell model through the distribution of cell size. Grenestedt and Tanaka23 theoretically and numerically found that the cell wall thickness and cell shape had significant effects on the stiffness of the Kelvin cell model. The 3D re-entrant lattice structure and the Kelvin cell lattice have been commonly used to study the mechanical behavior of cellular structures, as they are lightweight materials. Jiang et al.24 concluded that auxetic structures have demonstrated a superior performance compared to conventional structures, such as honeycomb and Kelvin cell, in various aspects, like stiffness, hardness, and energy absorption, during compressive loading scenarios, including impacts and cyclic loading. Wang et al.25 found that an auxetic-BCC structure outperformed the Kelvin cell lattice, displaying earlier peak acoustic resistance and reactance. However, it is worth mentioning that the research has historically placed a relatively lesser emphasis on studying the tensile behavior of lattice structures compared to their compressive behavior. This disparity can be attributed to the inherent challenges associated with experimental designs for tensile testing of lattice structures. However, there is still a paucity of studies focusing on the tensile behavior of lattice structures. Zhang et al.26 conducted quasi-static tensile tests by fabricating small fixtures to pin-join two ends of a 2D auxetic structure to investigate the tension post-yield behavior of re-entrant structures made of polymer and stainless steel under two principles of loading directions. They found that the tensile stress–strain curves of auxetic structures have the same linear, plateau, and densification stages as the compressive characteristics of conventional cellular structures. Further, Zhang and Lu27 continued to study the tension behavior of re-entrant honeycomb under dynamic tests, and classified three deformation modes, the quasi-static mode, localized mode, and transitional mode, under dynamic loading. Subramani et al.28 employed polyester filaments and epoxy resin to tie the structures to conduct tensile tests for studying the tensile properties and Poisson’s ratio of 2D auxetic structures. Tserpes and Labeas29 adopted numerical methods to explore the failure modes of 2D triangular, hexagonal, and Kagome planar lattices. It is widely known that the tensile behavior of 2D structures is incapable of explaining the mechanical behavior of 3D structures. To the authors’ best knowledge, despite there being a paucity of studies on 3D lattice structures under tensile conditions, Alsalla et al.30 fabricated solid end plate joined struts of lattice structure to conduct tensile tests on a gyroid lattice, and concluded that the end constraint affected the deformation of the cellular solid. Geng et al.31 performed tensile tests on three types of lattice structures, namely, the rhombic dodecahedron and two types of BCC cellular lattice structures, by gluing two sides of the lattice structures to the grips of tensile jaws and found that the fracture mode of the lattice structure was determined by the type of unit cell. However, there have still been limited studies on investigating and comparing the tensile mechanical behaviors of the 3D printed re-entrant lattice and the Kelvin cell lattice. Therefore, in this current work, it is essential and imperative to delve into understanding their performance under tensile loading, which will provide valuable insights into various engineering applications and help advance the design and implementation of lattice structures for enhanced performance in different load-bearing scenarios.

In this paper, the two common, typical lattice structures, namely, 3D re-entrant and Kelvin cell lattice structures, were employed to investigate their mechanical responses. First, the numerical model of the re-entrant lattice structure was established and validated against the uniaxial tensile test. Second, the deformation modes, stress–strain curves, energy absorption, and Poisson’s ratio of the two conventional lattice structures under tensile loading were numerically studied and compared.

Materials and Methods

Structure Design and Fabrication

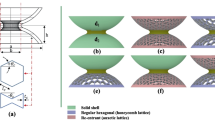
The relative density, representing the ratio of lattice specimen density to that of the parent solid material, plays a critical role in determining the mechanical properties of structures.32 In order to thoroughly investigate and compare the mechanical response and energy absorption of lattice structures, it is imperative to ensure that the structures maintain the same relative density. The re-entrant lattice was constructed by the re-entrant unit cell of \(6\times 7\times 6\) in the X, Y, and Z directions with dimensions of \(92 \mathrm{mm}\times 96 \mathrm{mm}\times 92\mathrm{ mm}\), while the Kelvin cell lattice structure was patterned by a Kelvin cell unit of \(6\times 6\times 6\) in the corresponding directions with similar dimensions of \(90 \mathrm{mm}\times 90 \mathrm{mm}\times 90 \mathrm{mm}\). Therefore, a relative density of the re-entrant and Kelvin cell lattice configurations used for consistent analysis was 15%. The unit cell and the representative volume element of the re-entrant and Kelvin cell lattice structures are shown in Fig. 1. The specifications of the 2D re-entrant auxetic were: the length of the vertical structs \(h=16 \mathrm{mm}\), the length of the oblique struts \(l=8.06 \mathrm{mm}\), re-entrant angle \(\theta =30^\circ ,\) and the width or depth of the vertical struts and oblique struts \(t=1.7 \mathrm{mm}\), while those of the Kevin cell were: the cell wall thickness \(n=0.7 \mathrm{mm}\), the cell size \(m=14.99 \mathrm{mm}\) and \(k=15.9 \mathrm{mm}\). The 3D re-entrant lattice structure was printed using FS 1092A-TPU powder via selective laser sintering (SLS), shown in Fig. 2 to conduct the tensile test for validating with the FE result, and its physical properties are shown in Table I, as per the manufacturer’s specification.

Fig. 1
figure 1

Geometry of the lattice structures: (a) 3D re-entrant auxetic lattice and (b) Kelvin lattice.

Full size image
Fig. 2
figure 2

Printed prototypes of 3D re-entrant auxetic using TPU powder via SLS.

Full size image
Table I Physical properties of FS 1092A-TPU powder, provided by the manufacturer
Full size table

Mechanical Testing

All the quasi-static uniaxial tensile tests in the work were conducted on an MTS Criterion model 43 equipped with a 10-kN load cell and an optical extensometer at the loading rate of 2 mm/min. Firstly, three type-IV dumbbell-shaped samples were examined based on ASTM D638 to characterize the mechanical behavior of the parent solid material, FS 1092A-TPU. Secondly, two nominally identical re-entrant lattice structures were employed to conduct the tensile tests to validate the accuracy of the FE models. Each test was terminated when fracture occurred. It is worth mentioning that it is very challenging to fix lattice structures with multiple short struts on tension wedge grips. Therefore, the struts of the top and bottom ends of the lattice structures were bonded onto the surfaces of the two steel planes using a high-strength epoxy (Araldite 420 A/B) which was mixed at 2.5A:1B. It should be noted that this bonding method has been verified to ensure there was no damage to the boundaries under tensile tests.

The engineering stress–strain curve was obtained by converting the force–displacement curves recorded on the testing machine based on the measured dimensions of the specimens, i.e., the stress was acquired by the ratio of the instantaneous load and the initial cross-section area (3.4 mm × 6 mm) of the tensile sample. The strain was obtained by the ratio of the instantaneous change in displacement and the initial gauge length (25 mm). Figure 3 plots the stress–strain curves from the three dumbbell-shaped samples made of TPU powder under uniaxial tension. Notably, it can be seen that all the curves exhibit a similar trend, indicating a non-linear behavior during the tensile process until reaching failure at an approximate yield stress of 2.5 MPa. The level of variation among the curves was small. However, there are slight discrepancies in the failure strains due to experimental defects present in some of the samples. The experimental data as material property were input into the FE model.

Fig. 3
figure 3

Stress versus strain curves of dumbbell-shaped structure made of TPU powder under tensile test.

Full size image

Finite Element Simulations

As a cost-efficient means, the Abaqus/explicit package v.2021 (Dassault Systèmes, Vélizy-Villacoublay, France) was employed to predict the failure locations and failure stress, as well as the progression of failure of the lattice structures under uniaxial quasi-static tension. To minimize the boundary effect during tensile loading and to overcome the challenge of real tensile experiments on structures with many struts on the top and bottom ends, the first step was to validate the FE model by replicating all the boundaries and geometries of each lattice, as the tension experiment detailed in Sect. "Mechanical Testing", against the experimental results in terms of stress–strain curves and deformation mode. After validation, a series of simulated tensile tests of re-entrant and Kelvin cell structures were performed by applying displacement-controlled load in the Y direction, allowing the other two free to reduce boundary effects. The FE models of the re-entrant and Kelvin cell lattice structure under tensile loading are shown in Fig. 4a and b, respectively. A 4-node linear tetrahedron (C3D4) was employed to assign the lattice structures, while the top and bottom plates were represented by discrete rigid bodies which were discretized using 4-node 3D bilinear rigid quadrilateral elements (type R3D4). A proper mesh size of 0.5 mm × 0.5 mm was chosen after a mesh convergence analysis to capture the stresses and deformations with reasonable accuracy. Interaction for all the solid–solid contacts was applied to ALL WITH SELF with a friction coefficient of 0.2.33 Tie contact was applied between the top and bottom surfaces of the struts of the structure and the rigid plates. The FE models and specific mesh characteristics are depicted in Fig. 4.

Fig. 4
figure 4

FE models of (a) 3D re-entrant lattice, (b) Kelvin cell lattice under tensile loading.

Full size image

The TPU material property was taken from the tensile stress–strain curves (Fig. 3). It is widely known that hyperelastic models such as Mooney–Rivlin,34 Polynomial,35 Arruda–Boyce.36 and Ogden37 in Abaqus are good methods to deal with a non-linear relationship of the material. Through the curve fitting with the experimental data, the coefficients of hyperelastic constitutive models were evaluated with Abaqus and are given in Table II. It is clear from Fig. 5 that the Ogden (n = 2) model was the most suitable and stable for predicting the behavior of the TPU powder due to its fitting curve agreeing well with the experimental data. Therefore, the coefficients of Ogden (n = 2) were imputed into the FE method to define the material property of the TPU powder (Table III). Meanwhile, the TPU powder as a polymer material often has a high ductility and good stress–strain recovery under both tension and compression. Therefore, the ductile failure criterion was usually used to predict the onset failure of the TPU powder in Abaqus/Explicit.38 The damage model used was the one that has equivalent plastic strain at the beginning of the damage (\({\overline{\varepsilon }}_{D}^{pl}\)), which is a function of stress triaxiality and strain rate:

$${\overline{\varepsilon }}_{D}^{pl}(\eta ,{\dot{\overline{\varepsilon }}}^{pl})$$
(1)
$$\eta =-\frac{p}{ql}=\frac{\frac{1}{3}\cdot trace \left(T\right)}{{\sigma }_{mises}}=\frac{\frac{1}{3}\cdot ({\sigma }_{xx}+{\sigma }_{yy}+{\sigma }_{zz})}{{\sigma }_{mises}}$$
(2)

where p is the pressure stress, \(\eta \) is the stress triaxiality, \({\dot{\overline{\varepsilon }}}^{pl}\) is the equivalent plastic strain rate, and q is the Mises equivalent stress. Based on the results from Fig. 3 (axial tension standard tests), these ductile parameters are easily obtained, as shown in III.

Table II Material coefficients and stability checks for hyperelastic constitutive models
Full size table
Fig. 5
figure 5

Fitted and experimental stress–strain curves of hyperelastic Ogden (n = 2) model.

Full size image
Table III Ductile damage model parameters for TPU in Abaqus
Full size table

Results and Discussion

Validation of the FE Model

As mentioned before, the uniaxial tensile experimental data of the re-entrant lattice structure described in Sect. "Structure Design and Fabrication" were chosen to validate the accuracy of the FE model. Figure 6 displays the stress–strain curve of the 3D re-entrant lattice structure from the experimental and numerical results. It can be seen that the numerical result was well coincident with the experimental result in regard to the stress–strain tendency and the stress magnitudes, in which the stress from the numerical result non-linearly increased with the strain but the post-yield curves were different, i.e., the numerical stress had a dramatic reduction after the structure arrived at its yield stress, but the experimental stress slowly decreased with strain. This is due to the fact that element deletion control was used in Abaqus, and, when arriving at the yield stress, the failure element was ultimately deleted, resulting in the failure of the entire structure with a sudden drop. In addition, the comparison in the deformation mode between the simulation and the experiment is shown in Fig. 7. It is clear that the deformation mode of the simulated result agreed well with that of the experiment, in which the middle part of the structure displayed expansion behavior and the vertical struts became horizontal when the stretch strain arrived at the strain of 0.21, while the top and bottom parts narrowed due to the struts of the top and bottom ends bonded to the platen limiting their expansion. Therefore, the FE model could be used with sufficient accuracy to further numerically compare the mechanical responses of the re-entrant and Kelvin cell lattice structures.

Fig. 6
figure 6

Comparison of stress–strain curves of the re-entrant lattice structure from the experimental and numerical results under constrained boundary conditions.

Full size image
Fig. 7
figure 7

Comparison of deformation patterns of re-entrant lattice from experimental and numerical results at the strain of 0.21.

Full size image

Mechanical Responses

In order to eliminate the boundary effect of the lattice structures under tensile loading mentioned in Sect. "Finite Element Simulations", the FE method was employed to observe their tensile deformation under a specific boundary condition that applied loading to nodes of the top ends in the Y direction and constrained all the nodes on the bottom ends in Y direction, keeping the other directions free. As seen in Fig. 8, the stress–strain curves of the re-entrant and Kelvin cell lattice structures displayed similar features, where the stress non-linearly increased with the stretching strain until, arriving at the yield stress, the stress dramatically dropped with a small strain, which had similar characteristics to the parent solid material TPU (Fig. 3). Meanwhile, it is worth mentioning that the fracture stress and strain were smaller than those of the parent solid material, i.e., at the strain of 0.28, the stress for the re-entrant lattice structure reached 1.85 MPa and the stress of the Kelvin cell lattice reached only 0.96 MPa at the strain of 0.23, while the yield stress of the parent solid was 2.50 MPa at the strain of 0.38, indicating that the ductility of the lattice structures was inferior to that of the parent solid material This could likely be due to the imperfection of the fabricating lattice process and the widely accepted paradox that a bar has a lower ductility than a beam in tension.39 Meanwhile, the re-entrant lattice had larger stress and fracture strain than those of the Kelvin cell lattice. This phenomenon may be explained by the deformation of the two lattice structures.

Fig. 8
figure 8

The simulated stress–strain curves of the re-entrant lattice structure and the Kelvin cell lattice under unconstrained boundary conditions.

Full size image

The deformation processes of the re-entrant and Kelvin cell lattice structures with instantaneous strain are shown in Fig. 9. It can be seen from Fig. 9a that the re-entrant lattice expanded with the stretching strain until the original inclined struts became horizontal. The concentrated force focused on the joints of the struts. The horizontal displacement increased from the original displacement of 28 mm to 30.1 mm at the strain of 0.15, indicating that the re-entrant lattice structure had auxetic behavior with a negative Poisson’s ratio. In contrast, the horizontal displacement of the Kelvin cell lattice decreased from the original displacement of 28 mm to 27 mm during the same strain period, displaying shrinking deformation with a positive Poisson’s ratio like traditional materials, and the concentrated force occurred the inclined wall, different from the re-entrant lattice. This phenomenon indicates that the mechanical behaviors of the two lattice structures may be associated with the unit cell geometry. The re-entrant lattice structure was extended through a 2D re-entrant structure with auxetic behavior, while the Kelvin cell lattice structure was patterned by a honeycomb-like tetrakaidecahedron. Meanwhile, it is well known that Poisson’s ratio is a critical parameter of the material, which is obtained by the negative ratio of the lateral extension over the longitudinal extension. Therefore, a series of fixed nodes in the FE models were tracked to record their lateral and longitudinal displacements for calculating the Poisson’s ratio. Figure 10 depicts the evolution of Poisson’s ratio for the two lattice structures up to a strain of 0.32. The re-entrant lattice had a negative Poisson ratio and increased with stretching strain, while the Kelvin cell lattice displayed a positive Poisson ratio and kept almost constant at around 2.1 during the whole stretching process. These mechanical behaviors agree well with the deformation process observed in Fig. 9.

Fig. 9
figure 9

The deformations of (a) the re-entrant lattice structure and (b) the Kelvin cell lattice under different strains.

Full size image
Fig. 10
figure 10

The Poisson’s ratio strain curves of the re-entrant lattice structure and the Kelvin cell lattice.

Full size image

The energy absorption capacity of structures usually provides a comprehensive insight into choosing an ideal energy absorber under compressive impact.40,41 The evaluating indices are often energy absorption and specific energy absorption. To evaluate the energy absorption of structures under tension, the same indices were adopted. The energy absorption is calculated and the area under the tensile stress–strain curve before the point of structure fracture,39 while the specific energy absorption is the ratio of the energy absorption and the mass of the structure. The energy absorption results are set out in Table IV, and it can be seen that the re-entrant lattice had a better energy absorption than the Kelvin cell lattice. The energy absorption of the re-entrant lattice was 7770.67 mJ, almost 3 times that of the Kelvin cell lattice (2595.18 mJ). Similarly, the specific energy absorption of the re-entrant lattice was 110.07 mJ/g, around 1.63 times that of the Kelvin cell lattice.

Table IV Energy absorption of the re-entrant and Kelvin cell lattice structures under tensile load
Full size table

Conclusion

The 3D re-entrant lattice structure as a typical lattice was printed using TPU powder via SLS technology and validated against the FE model under tensile test. The FE results coincided well with the experimental results in terms of tensile stress–strain curves and deformation. Then, the tensile mechanical responses of the 3D re-entrant structure and Kelvin cell lattice were numerically compared and explored. It was observed that the two stretching-dominated lattice structures displayed similar mechanical behaviors as the parent solid structure, in which stress non-linearly increased until arriving at the yield stress when a brittle break occurred. However, the failure stress and strain of the two lattice structures were smaller than those of the parent solid. This could be the imperfection of the fabricating process results in lower ductility and a well-known paradox that the ductility of a bar is inferior to that of a beam. In addition, the re-entrant lattice structure had better energy absorption capacity than the Kelvin cell lattice, i.e., the energy absorption and specific energy absorption of the re-entrant lattice were 3 times and 1.6 times, respectively, those of the Kelvin cell lattice. Additionally, the Poisson’s ratio of the re-entrant lattice was negative and increased with the strain during the whole stretching process, while the Kelvin cell had a relatively constant positive Poisson’s ratio, similar to those of conventional materials. These results could provide insights into the extensive applications of lattice structures under tension.