Introduction

Throughout recent years, multiple aspects, for example, the growth in power usage and sustainability and environmental concerns, have increased the progress from conventional fuels to environmentally friendly power sources and the improvement of energy capacity frameworks of enormous scope.1 In 2019, renewable sources delivered 19.7% of the energy consumed in the European Union (EU), just 0.3% shy of the 2020 objective of 20%. Currently, the EU is still attempting to expand the portion of renewables to arrive at the objective of 32% by 2030.2 Nonetheless, one of the fundamental difficulties that sustainable power sources present is their irregularity because, compared to conventional sources, for example, the amount of energy from the sun or wind varies contingent upon the natural circumstances. Subsequently, the examination of enormous energy stockpiling frameworks has attracted broad consideration recently as they present the possibility to facilitate the coordination of renewables in the ongoing energy foundation by supplementing their shortcomings and providing more adaptable activity.3,4,5

According to the World Energy Council, up to 250 GW of energy storage could be installed by 2030.6 In this structure, the redox flow battery (RFB) innovation has been extensively explored because of the potential benefits that it offers because of the ability to freely size both the power and energy.7,8 Specifically, vanadium redox flow batteries (VRFB), proposed in 1985 by Skyllas-Kazacos et al.,9,10 are the most well-known arrangement in light of its better exhibition compared with other redox sciences regarding power and energy density and, as a result of the utilization of a solitary component, vanadium, in both negative and positive electrolytes. The last option is of utmost significance for long haul application as it permits electrolyte remixing methodologies to lengthen battery lifetime. The principal parts of a VRFB cell are the electrolytes, which characterize the energy of the battery, the carbon felt (CF) electrodes, which are the site where the electrochemical reactions to happen, and a ion exchange membrane to guarantee that the anode and cathode side are secluded while allowing the ion movement to keep the electroneutrality among arrangements.11 The electrolytes are stored in two isolated tanks and redirected with mechanical pumps through the stack, which characterizes the power of the battery and is where electrodes and membranes are located.

To enhance reaction kinetics, much research has been done on the compression of the electrode. Recent experimental research has concentrated on how the performance of a VRFB is affected by the compression of the electrodes. Three distinct compression ratios (CR), 23.1%, 38.5% and 53.8%, were studied by Hsieh et al.12 This study claims that a compression of the graphite felts above 50% caused a drop in the CE. The ideal energy efficiency (EE) was demonstrated by a CR of 38.5% and an operational current density of 80 mA cm−2, with a value of 73%. The coulombic efficiency (CE) increased from 89% to 98% when Monteiro et al.13 examined CR values in the 8–33% range when compression was raised from 8% to 17%. In addition, the voltage efficiency (VE) remained stable up to a compression ratio (CR) of 25%, and a minor decline in cell performance was seen above that level. The most notable EE value, 84%, was obtained at 25% compression and 40 mA cm−2 current density. In their study of the effects of various electrode design parameters, Rao and Jayanti14 examined the effects of CR values of 17%, 35% and 50% at low temperatures. They concluded that a thinner electrode and higher compression improve VRFB performance under the low temperature conditions investigated. A charge and discharge experiment was recently carried out by Tai et al.15 under various CR values and electrolyte flow rates. They discovered that the battery discharge capacity is significantly influenced by both variables. The effects of decreasing electrode thickness for both serpentine and interdigitated flow fields were compared by Messaggi et al.16 They highlighted the greater punishment for serpentine with thinner walls close to the cell outflow. The primary findings of various investigations in this area were compiled in the point-of-view work of Gundlapalli,17 which points to an ideal compression rate for big cells between 35% and 50%. Lower permeability values and a larger concentration overpotential are the results of further compression.

Recent studies at the nexus of vanadium redox flow batteries and nanomaterials have yielded promising insights for energy storage applications. Nanoengineering has enabled a closer examination of material properties, leading to groundbreaking developments.18,19,20,21 These studies not only deepen our understanding of nanomaterials but also offer potential avenues for enhancing redox flow batteries' efficiency and stability. This synergy between nanomaterial advancements and battery technology paves the way for more effective and sustainable energy storage solutions.

However, due to the high cost of extensive experimental facilities, research is typically conducted in small cells or short stacks with active regions no greater than 25 cm2. Furthermore, they make it impossible to quantify several factors that affect how a flow battery operates. To develop and optimize VRFB systems under various load states, distribution routes, flow rates or material qualities, the development of computational fluid dynamic (CFD) simulations as a substitute tool has occurred in these situations.22 With the creation of a 1D model, Vivona et al.23 dissected the limiting processes in kinetics and mass transport. Three fundamental mechanisms, namely diffusion, convection and migration, were considered in the two-dimensional numerical model that Knehr et al.24 devised to characterize the transport of active species. You et al.25 examined the performance of the cell when the electrode thickness ratio was reduced and also supplied a two-dimensional CFD stationary model for a qualitative investigation. To evaluate the vanadium distribution at various profiles of the electrodes and the membrane, Ozgoli et al.26 used a two-dimensional model to examine the hydrodynamic and electrochemical performance. The effect of electrode penetration into the flow channel was researched by Kumar et al.27 To that goal, numerical simulations were run while considering that some of the electrode protruded into the flow channel because of compression. Using CFD approaches, the consequences of electrode compression were also investigated. According to the model created by Oh et al.,28 highly compressed, thinner electrodes had a more equal distribution of species throughout the electrode. Emmel et al.’s recent work29 concentrated on the electrochemically active region and examined the electrolyte flow through the electrode to identify the hot areas and favored pathways where the highest velocity values were recorded.

Over the years, other traditional flow channel designs have also been examined to determine which one is most suited for an effective VRFB. According to Wang et al.,30 analyzing of the effects of various CR values for a serpentine flow field, a compression ratio of 55.7% offers the best performance. Compared to a serpentine flow field design, an interdigitated flow field design generates more constant reaction rates, according to the study of Messaggi et al.31 The concentration overpotential rose in the low flow speed zone, as demonstrated by the two-dimensional CFD model of Ishitobi et al.,27 which underlined the need to create electrodes with high permeability.

The purpose of this work is to evaluate various electrode compression and flow rate conditions to visualize the flow field, concentration species and current and potential distribution in a positive half-cell. To that end, the performance of GFD 4.6 EA is evaluated by means of a 2D numerical model. The article is structured as follows: Section “Numerical model” describes the numerical model in detail, while the results obtained under different operating conditions are discussed in Section “Results”; our conclusions are given in Section “Conclusions”.

Numerical Model

Model Characteristics and Assumptions

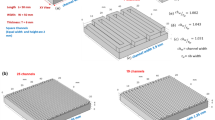
In this part, the model of a 2D VRFB is fully described. The Canzi model serves as the foundation for this32 and represents a positive half-cell. COMSOL Multiphysics®,33 a commercial program often used for electrochemical applications, was used to model the positive half-cell. As illustrated in Fig. 1, the computational domain of the half-cell is divided into three subdomains: the cathode ion exchange membrane and flow channel. The evaluated electrode is a commercial Sigracell GFD 4.6 EA (nominal thickness of 4.6 mm, compressed at 20%). A Nafion membrane was used to allow the transport of protons. The main dimensions of the half-cell are listed in Table I. With a refinement close to those interfaces where greater gradients are anticipated, a structured mesh made up of 22,050 quadrilateral pieces was developed; see Fig. 2.

Fig. 1
figure 1

Scheme of the bidimensional computational domain.

Full size image
Table I Dimensions of the 2D computational domain
Full size table
Fig. 2
figure 2

Mesh configuration of the 2D VRFB.

Full size image

The following presumptions were considered for the simulation model:

  • Steady state model.

  • Dilute solution approximation.

  • The cell is considered isothermal.

  • Parasitic reactions are disregarded.

  • The properties of the membrane and electrode are isotropic.

  • Incompressibility of the fluid is considered.

  • Ideal membrane selectivity only allows H+ crossover.

  • Complete wettability of the membrane.

  • Electroneutrality across all the computational domain.

As shown in Eq. 1, the electrochemical reaction occurring on the surface of the positive electrode is:

$${\mathrm{VO}}_{2}^{+}+2{\mathrm{H}}^{+}+{\mathrm{e}}^{-}\rightleftharpoons {\mathrm{VO}}^{2+}+{\mathrm{H}}_{2}\mathrm{O}$$
(1)

Dissociation of sulfuric acid is also present with these reactions; see Eqs. 2 and 3:

$${\mathrm{H}}_{2}{\mathrm{SO}}_{4}\rightleftharpoons {\mathrm{HSO}}_{4}^{-}+{\mathrm{H}}^{+}$$
(2)
$${\mathrm{HSO}}_{4}^{-}\rightleftharpoons {\mathrm{SO}}_{4}^{2-}+{\mathrm{H}}^{+}$$
(3)

In this model, the first reaction (Eq. 2) is neglected, according to Knehr et al.,24 as products are favorited, and the presence of H2SO4 will be negligible. The second reaction (Eq. 3) is modeled as an additional source of H+, as shown in Eq. 4.

$${R}_{d}={k}_{d}\left(\frac{{c}_{{\mathrm{H}}^{+}}-{c}_{{\mathrm{HSO}}_{4}^{-}}}{{c}_{{\mathrm{H}}^{+}}+{c}_{{\mathrm{HSO}}_{4}^{-}}}-\beta \right)$$
(4)

where kd is a rate parameter, ci is the concentration of each species, and β refers to the degree of dissociation.

Species Balance and Charge Conservation

The species balance is addressed by solving the conservation equation below for the various species present in the electrolyte mixture; see Eq. 5:

$${\nabla \mathbf{N}}_{i}={S}_{i}$$
(5)

The left-hand side term is the molar flux of the specie i, described by the Nernst-Planck-equation considering the diffusive, migrative and convective transport mechanisms as shown in Eq. 6.

$${\mathbf{N}}_{i}=-{D}_{i}^{\mathrm{eff}}\nabla {c}_{i}-{z}_{i}{u}_{i}{c}_{i}F\nabla {\varphi }_{l}+\mathbf{u}{c}_{i}$$
(6)

The first term (diffusion term) considers the transport of species due to concentration gradients. The diffusivity Di is an intrinsic characteristic of the electrolyte typically measured by a rotating disk electrode. Nevertheless, to considering the effect of the porous media in the diffusive transport, the effective diffusivity Dieff is estimated by means of the Bruggeman correlation; see Eq. 7.

$${D}_{i}^{\mathrm{eff}}={\epsilon }^{3/2}{D}_{i}$$
(7)

The second term (migrative term) accounts for the electrophoretic force acting on ions under the influence of an electric field. The mobility of each specie ui is calculated using the Nernst–Einstein expression; see Eq. 8.

$${u}_{i}=\frac{{D}_{i}^{\mathrm{eff}}}{RT}$$
(8)

The third and last term of Eq. 6 (convective term) represents the species transport caused by the electrolyte recirculation imposed by the mechanical pumps. The estimation of the electrolyte mixture’s velocity field u differentiates among the two flow domains, flow-channel and porous electrode. The Navier–Stokes equations are used to calculate the former under the assumption of a laminar flow, and the Brinkman equations, which extend Darcy’s law to compute the dissipation of kinetic energy by viscous shear and resemble the Navier–Stokes equations, are used to solve the latter.

The Nernst–Plank equation has not been solved for one of the species as a result of the electroneutrality principle; see Eq. 9.

$$\sum_{i}{z}_{i}{c}_{i}=0$$
(9)

Coming back to Eq. 6, in the right-hand side the species’ molar source term is found, which accounts for the amount of moles produced/consumed for each specie because of the electrochemical reactions given at the electrolyte-electrode interface and the dissociation process of the HSO4. Notice that the source terms related to the species involved in the generation of the faradaic current are only applicable in the porous domain, while the source terms of the species involved in the dissociation process are also applied in the flow channel; see Eqs. 10, 11, 12, 13, and 14.

$${S}_{{\mathrm{V}}^{5+}}=\frac{{i}_{R}}{F}$$
(10)
$${S}_{{\mathrm{V}}^{4+}}=-\frac{{i}_{R}}{F}$$
(11)
$${S}_{{\mathrm{H}}^{+}}=-\frac{2 {i}_{R}}{F-{R}_{d}}$$
(12)
$${S}_{{\mathrm{HSO}}_{4}^{-}}= {R}_{d}$$
(13)
$${S}_{{\mathrm{SO}}_{4}^{2-}}= {-R}_{d}$$
(14)

Then, to couple the balance of species with the electrochemical reactions and the actual current flowing through the electrode during charge/discharge operations, the charge conservation equation is solved in the porous domain. As shown in Eqs. 15, 16, and 17, the charges exiting the electrolyte il are balanced by the charges entering the electrode is, and these are equal to the electrochemical reaction rate iR.

$${\nabla \cdot \mathbf{i}}_{l}={-\nabla \cdot \mathbf{i}}_{s}={i}_{\mathrm{R}}$$
(15)
$${\mathbf{i}}_{l}=F\sum_{i}{z}_{i}{\mathbf{N}}_{i}$$
(16)
$${\mathbf{i}}_{s}={-\sigma }_{s}^{eff}\nabla {\mathrm{\varphi }}_{s}$$
(17)

The effective conductivity of the porous electrode σseff is estimated based on the intrinsic conductivity of the electrode material σs by means of Eq. 18:

$${\sigma }_{s}^{\mathrm{eff}}={\left(1-\varepsilon \right)}^\frac{3}{2}{\sigma }_{s}$$
(18)

Besides, the electrochemical reaction rate iR is estimated by Butler–Volmer’s kinetic model shown in Eq. 19:

$$ i_{R} = k_{0} aF\left( {c_{{V^{{4 + }} }}^{s} \cdot e^{{\frac{{\alpha F\eta ^{*} }}{{RT}}}} - c_{{V^{{5 + }} }}^{s} \cdot e^{{\frac{{\alpha F\eta ^{*} }}{{RT}}}} } \right) $$
(19)

where k0 is the reaction rate constant, a is the specific surface area, α is the charge transfer coefficient, T is the temperature, the \({c}_{i}^{s}\) terms are the concentrations of vanadium IV and V on the surface of the electrode, and η* = ϕs − ϕl − E0+ is the potential difference between the solid electrode and bulk electrolyte. The open circuit voltage of the positive half-cell E0 is calculated using the Nernst equation given as Eq. 20:

$${E}_{0}^{+}={E}_{0}^{{\prime}+}+\frac{RT}{F}\mathrm{ln}\left(\frac{{c}_{\mathrm{V}}{c}_{{\mathrm{H}}^{+}}}{{c}_{IV}}\right)$$
(20)

where \({E}_{0}^{{\prime}+}\) is the standard reduction potential for the positive electrode.

Additionally, for the estimation of the overpotential η*, a tertiary current density distribution model is used in this work, considering ohmic drops, sluggish reaction kinetics and mass-transport limitations.

Boundary Conditions

The computational domain is divided into three subdomains, as shown in Fig. 1, and the borders between them must be carefully modeled, especially for the electrochemical component. Table II reports the boundary conditions that were applied.

Table II Description of the electrochemical boundary conditions
Full size table

See Table III for the boundary conditions for the fluid dynamic modeling, which include a laminar flow at the flow channel's input and atmospheric pressure at the output. The geometrical features of the flow channel and each volumetric flow rate analyzed are used to compute the velocity at the inlet.

Table III Description of the fluid-dynamic boundary conditions
Full size table

Table IV summarizes the key physical characteristics of the electrode and electrolyte used in the current investigation. Electrode porosity refers to the void fraction regarding the total volume of the electrode material.

Table IV Parameters used to define the numerical model
Full size table

Results

In this section, the results obtained from the simulations are analyzed. Different ranges for electrode compression and flow rate have been tested to study the impact on the cell performance. For this purpose, velocity profiles, vanadium concentrations, reaction rate and overpotentials were evaluated. Operating parameters for all cases are listed in Table V.

Table V Operating parameters used in the simulation
Full size table

Electrode GFD 4.6 EA

Polarization curves are utilized to examine the operational behavior of the VRFB. The validation curves for the model are displayed in Fig. 3a–d. The four situations presented share the same operational parameters shown in Table V. Four different state-of-charge (SOC) values were tested to confirm the good predictive capability of the model across the whole operation range of the battery. The curves plotted in Fig. 3a, b, and c show a good correlation between experimental and numerical results. At SOC close to 50%, Fig. 3c and d, ohmic resistance is the main contributor to the cell overvoltage, and good correlation is observed between experimental and numerical results. There are additional contributions to the overpotential at larger current densities via mass transport. This phenomenon is more clearly observed at low SOC (Fig. 3a), leading to a higher deviation of numerical results at high discharge currents.

Fig. 3
figure 3

Experimental validation of polarization curves for a flow rate of 20 mL/min. (a) SOC at 15%. (b) SOC at 75%. (c) SOC at 45%. (d) SOC at 97%.

Full size image

The fluctuation in power density at various SOCs is depicted in Fig. 4. The status of charge has a significant impact on the VRFB power supply, as would be predicted. Higher values for the power density are attained as the SOC rises. When Fig. 4a and d are compared, the latter’s maximum power output is up to six times greater than that of the former.

Fig. 4
figure 4

Polarization and power density curves for a flow rate of 20 mL/min. (a) SOC at 15%. (b) SOC at 75%. (c) SOC at 45%. (d) SOC at 97%.

Full size image

Another factor that needs to be examined is the electrolyte flow rate because of how crucial it is to the battery’s electrochemical performance. The experimental and numerical polarization curves presented in Fig. 5 for low flow rates (Q = 10 mL/min) and SOC = 0.15 provide proof of the model’s robustness to this parameter. Even in cases where transportation phenomena predominate, the model nevertheless provides a high level of accuracy. The same operational factors apply as in the earlier situations, which are stated in Table V.

Fig. 5
figure 5

Experimental validation for flow rate at 10 mL/min.

Full size image

Effects of Varying Compression

Effects of different compressions have been examined to analyze battery behavior. The following operating criteria have been established: With a flow rate of 20 mL/min, a SOC of 0.75 and an input voltage of 0.7 V, the battery is in a discharge mode. At compressions of 20%, 30%, 40%, and 50%, the electrode has been tested. At y = H_cell/2, every variable is examined along a horizontal line. First, Fig. 6 displays velocity profiles. Velocity does appear to be significantly influenced by compression, as the higher the compression, the faster the velocity. The natural correlation between flow rate and inlet area is what causes the increase in flow velocity.

Fig. 6
figure 6

Velocity profiles for GFD 4.6 EA at y = H_cell/2.

Full size image

To facilitate the graphical comprehension when altering compression, variables are studied per unit of electrode length. The x-axis is used to represent the thickness of the electrode. The boundary between the electrode and the membrane is marked as 0 on the x-axis, and the interface between the channel and the electrode is marked as 1. The values of the variables are assigned based on their position along the x-axis. Specifically, the value corresponding to a particular point is determined by dividing the x-coordinate of that point by the total thickness of the electrode. By focusing on this unit length analysis, a clearer understanding of the effects of compression variations on the system can be achieved.

Reaction rate seems to vary proportionally with compression; see Fig. 7. Peak values are obtained near the interface between electrode and channel for higher compressions, while in the membrane there is a significant decrease. In the particular case of 20% compression, peak reaction rate is identified close to both interfaces, while for higher compression rates, the reaction proceeds clearly faster close to the membrane.

Fig. 7
figure 7

Reaction rate trends for GFD 4.6 EA at y = H_cell/2.

Full size image

Reaction rates and concentration gradients are correlated parameters. It can be observed that lower reaction rates at the membrane boundary are in good agreement with lower V(V) concentration and therefore can be ascribed to mass limitations. Moreover, reaction rate remains stable across the electrode in the x-axis direction, which is the primary factor responsible for the observed smooth concentration trends in Fig. 8.

Fig. 8
figure 8

V(IV) and V(V) concentration trends for GFD 4.6 EA at y = H_cell/2.

Full size image

Concentration trends of V(IV) and V(V) are not particularly affected by the change in compression. The values obtained are very similar and evenly distributed along the x-axis of the electrode; see Fig. 8. The concentration gradients of V(IV) and V(V) are in good agreement with the consumption of oxidized form during the discharge stage to generate V(IV); thus, Fig. 8a and b are symmetric. This gradient is more pronounced close to the electrode-membrane boundary, while in the electrode-channel interface vanadium reduction and electrolyte renewal have opposing effects. Overpotential is noticeably impacted, with a linear behavior along the x-axis direction; see Fig. 9.

Fig. 9
figure 9

Overpotential trends for GFD 4.6 EA at y = H_cell/2.

Full size image

Effects of Varying Flow Rate

Another crucial operating parameter to consider is the flow rate. The same analysis as before was performed, fixing SOC = 0.75, input voltage = 0.7 V and compression at 20%. Four flow rate values were tested, 10 mL/min, 20 mL/min, 30 mL/min, and 40 mL/min. Figure 10 shows that velocity and flow rate exhibit a proportional relationship. As the flow rate increases, so does the velocity of the electrolyte. This finding is noteworthy when compared to the observations from Fig. 6. In the latter figure, the impact of flow rate on electrolyte velocity was explored, but the relationship was not as pronounced as in Fig. 10. Dotted lines indicate the membrane-electrode and channel-electrode interfaces.

Fig. 10
figure 10

Velocity profiles for GFD 4.6 EA at y = H_cell/2.

Full size image

The reaction rate exhibits dependence on changes in the flow rate, as evidenced by the observations presented in Fig. 11. Specifically, when the flow rate is set at 10 mL/min, the peak value of the reaction rate occurs at the membrane-electrode boundary. This suggests that the reaction kinetics are particularly active in this region under the given flow conditions.

Fig. 11
figure 11

Reaction rate trends for GFD 4.6 EA at y = H_cell/2.

Full size image

However, as the flow rate is increased to 20 mL/min, a distinct change in the distribution of the reaction rate is observed, also depicted in Fig. 7. In this case, the maximum values of the reaction rate are achieved at both the membrane-electrode boundary and the channel-electrode interface. The higher flow rate appears to enhance the transport of reactants towards both interfaces, thereby promoting more intensive electrochemical reactions in these regions.

Interestingly, with further increments in the flow rate beyond 20 mL/min, a noticeable shift in the location of the maximum reaction rate is observed. It moves closer to the channel-electrode interface, suggesting a stronger concentration of reactants in this region due to the increased convective transport induced by higher flow velocities.

The flow rate exerts a significant influence on the concentration gradients, as depicted in Fig. 12. Lower flow rates result in higher concentration gradients due to the longer residence time of the electrolyte within the cell. A distinct disparity is observed with a flow rate of 10 mL/min, where the highest concentration of V(IV) is attained. This phenomenon can be attributed to the reduction in flow velocity caused by the low flow rate, allowing for a more even distribution of the electrolyte. Notably, while the concentration gradients exhibit rapid variations at the electrode-membrane and electrode-channel boundaries for all flow rates, a linear behavior is observed throughout the remainder of the cell.

Fig. 12
figure 12

V(IV) and V(V) concentration trends for GFD 4.6 EA at y = H_cell/2.

Full size image

It is crucial to carefully balance the benefits of increased residence time and concentration gradients against the potential drawbacks of elevated overpotentials, as observed in Fig. 13. Achieving an optimal flow rate is crucial to ensuring efficient and controlled electrochemical processes, as low flow rates tend to result in higher overpotentials in Fig 13.

Fig. 13
figure 13

Overpotential trends for GFD 4.6 EA at y = H_cell/2.

Full size image

Conclusion

The current work presents a two-dimensional computational model of a half-cell of a vanadium redox flow battery. Cell performance has been tested under different electrode compressions and flow rate conditions. Main conclusions are set out below:

  • Changes in compression have a significant effect on velocity profiles and reaction rates. The GFD 4.6 EA caused high velocity variations when altering compression. This increase in velocity came along with higher reactions rates. However, an increase in overpotential values was also observed, highlighting the importance of finding a proper balance between the benefits of concentration gradients and the potential drawbacks of elevated overpotentials.

  • The electrolyte flow rate influences concentration gradients and reaction rates. It was found that a lower flow rate results in more pronounced concentration gradients due to increased residence time of the electrolyte in the cell. Furthermore, reaction rates were observed to be faster near the electrode-channel interface at lower flow rates, while they remain more uniform throughout the electrode at higher flow rates. However, it is important to note that lower flow rates can also lead to significant overpotentials.