Abstract
Nanoindentation, laser ablation inductively coupled plasma mass spectroscopy and weighing ion-spiked organic matrix standards revealed structure-property relations in the microscopic jaw structures of a cosmopolitan bristle worm, Platynereis dumerilii. Hardness and elasticity values in the jaws’ tip region, exceeding those in the center region, can be traced back to more metal and halogen ions built into the structural protein matrix. Still, structure size appears as an even more relevant factor governing the hardness values measured on bristle worm jaws across the genera Platynereis, Glycera and Nereis. The square of the hardness scales with the inverse of the indentation depth, indicating a Nix-Gao size effect as known for crystalline metals. The limit hardness for the indentation depth going to infinity, amounting to 0.53 GPa, appears to be an invariant material property of the ion-spiked structural proteins likely used by all types of bristle worms. Such a metal-like biogenic material is a major source of bio-inspiration.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Bristle worms (Polychaeta) are a highly successful group of invertebrate worms with a broad geographic distribution, in particular across the entire marine benthos. While they are generally soft-bodied, they also synthesize specific classes of hard structures such as segmented bristles (chaetae) and jaw apparatuses.1,2 These typically lack the mineralized calcium composition found in vertebrate bones, instead employing alternative biogenic materials, such as polysaccharide chitin (in the bristles) or secreted proteins enriched with glycine and histidine (in the jaws).3,4,5,6,7,8 These structures fulfill important mechanical functionalities thanks to their specific chemical composition. Their chemical resistance allowed them to be preserved in the fossil record,9 with jaws forming their own characteristic type of microfossils, scolecodonts.10 The abundance of scolecodonts in the Ordovician (490–440 million years ago) and their additional presence in late Cambrian rocks11 are consistent with the notion that the evolution of jaws marked an early step in Polychaeta phylogeny. In turn, the evolutionary innovation that enabled the production of jaws and bristles likely contributed to the subsequent success and diversification of Polychaeta. This has spurred interest in the material scientific investigation of jaws, primarily in larger species of the Nereis and Glycera genus.4,5,6,7 Whereas these species offer the advantage of large jaw apparatuses, measuring several millimeters in length, they are currently not available as standard laboratory cultures.
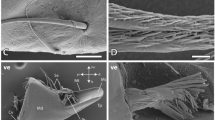
Over the past decades, the marine bristle worm Platynereis dumerilii has emerged as a highly accessible model system for Polychaeta research. Namely, Platynereis cultures can be bred in the laboratory under controlled conditions, providing a constant supply of larvae that exhibit stereotypical development.12 Thanks to a variety of molecular tools,13,14,15Platynereis dumerilii has become an important invertebrate reference model system for developmental, evolutionary, reproductive, neuro- and chronobiology.16 As part of the larger Nereidid family of Polychaeta, Platynereis possesses fang-like jaws reminiscent of the jaws of its larger Nereis relatives. Jaw development has been described by Fischer et al.12: A pair of jaws starts forming during the mid-nectochaetae development stage, i.e., 3 to 4 days post-fertilization at 18 °C water temperature. At this point in time, the primary tooth of each jaw becomes visible, which will later define the anterior end of the jaw. The jaws continue to grow in the subsequent development stages, with additional teeth being continuously added. The final number of one primary and nine secondary teeth, see Fig. 1a and b, is reached in the tubiculous juvenile stage, with the jaws eventually measuring 800 µm in length. They are then used during a remaining life span of typically 6–18 months, before the worm normally dies after the relatively short (only a few hours long) nuptial dance.
Despite the insight into the timing and morphology of jaw biogenesis, other features of Platynereis dumerilii jaws have remained unexplored. We therefore set out to characterize the chemical and mechanical properties of Platynereis dumerilii jaws. As outlined above, mineral phases are virtually absent in the chewing instruments of Polychaeta. Instead, as in other invertebrate groups, such hard mouth parts typically rely on a protein matrix. This protein matrix may be reinforced by chitin fibers, as was shown for beaks of the jumbo squid Dosidicus gigas,17 and it may incorporate metal or halogen ions, such as zinc, chloride or magnesium, as was shown for the mandibles of six species from four families of Isoptera.18 Intensive studies have been devoted to the deciphering of the relation between hardness properties and the presence of metal and halogen ions in the jaws of several bristle worm species. Lichtenegger and co-workers, in their studies of jaws from the genera Glycera5 and Nereis,6 showed that nanoindentation-derived elastic and hardness properties are positively correlated with concentrations of metal ions. In this context, zinc concentrations were quantified through x-ray absorption and fluorescence imaging of Nereis jaws, and electron micro-probe experiments on Glycera jaws provided access to copper concentrations. Later on, partial peptide mapping and molecular cloning of a partial cDNA from a jaw pulp library4 allowed for identification of \(Nvjp-1\) as the key protein making up the organic matrix of Nereis jaws. The latter matrix hosted not only zinc ions, but also halogen ions, such as chloride, bromide and iodine. Corresponding ionic concentrations were quantified through energy dispersive x-ray spectroscopy (EDS).19,20,21 In the case of Glycera jaws,7,22 EDS evidenced copper and chloride as the key ions were incorporated into the structural protein matrix.
The present article extends these studies toward the significantly smaller species Platynereis dumerilii, introducing unprecedented miniaturization steps to the nano-indentation protocol, including a refined polishing procedure; in this context, we do not only invest into the identification of metal and halogen ions as drivers of the mechanical properties, but we complement the current state of the art in bristle worm mechanics by the key topic of size effects—elucidating astonishing similarities between the nanoindenter-probed hardness of crystalline metals23 and those of ion-enriched protein complexes making up Polychaeta jaws.
Materials and Methods
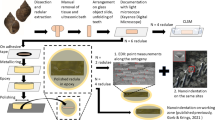
Sample Selection and Preparation
Jaws were harvested from adult Platynereis dumerilii worms by mild dissociation. Briefly, worm trunks were lysed in a buffer containing 0.2% (w/v) sodium dodecyl sulfate (SDS), 50 mM tris-(hydroxymethyl)-aminomethan-hydrochloride (Tris, pH8) and 0.5 M sodium chloride (NaCl) for 5–6 days with frequent agitation. Jaws and other sedimented material were washed twice in 50 mL lysis buffer. Jaws were isolated from cellular debris by manual elutriation. Isolated jaws were washed twice more in 50 mL lysis buffer and subsequently in 0.5 M NaCl to remove residual detergent. Finally, jaws were stored in 0.5 M NaCl supplemented with 0.05% sodium azide until testing. To check the integrity and intactness of the jaws, they were then observed by light microscopy, being mounted into a Zeiss Axio Imager Z1m (Carl Zeiss, Germany), with images taken by a Zeiss AxioCam MRc5 camera, as seen in Fig. 1b. Afterwards, 90 jaws were embedded in a two-component EpoFix resin (Struers, Denmark), ten each in 5-ml Eppendorf microtubes (Eppendorf, Germany). Air pockets within the resin were removed using a desiccator and a pump. Next, a micro-tomography device (\(\mu \)CT 100, Scanco, Switzerland) was employed at a resolution of 1.2 \(\mu \)m to identify the orientation of the jaw planes orthogonal to the dorsal-ventral axis with respect to the tube axis. A single intact jaw, the dorsal ventral axis of which was lying perfectly parallel to the tube axis (within the precision provided by the micro-tomography device), was further analyzed: Therefore, the jaw, together with a surrounding 3-mm-thick slice with faces orthogonal to the tube axis, was cut out of the tube using an Isomet low-speed saw (Buehler, USA); see Fig. 2a. This slice was attached with resin to a glass microscope slide. The latter was mounted onto a Logitech PM5 circular polishing system (Logitech, Scotland); see Fig. 2b. There, it was polished with a Microtex 300-mm polishing disc in a suspension of agglomerated polycrystals made of alpha aluminum oxide (Struers, Denmark). The individual polycrystalline agglomerates initially exhibited a particle size of 1 \(\mu \)m, diminishing during the polishing process. The latter process was terminated once the slice thickness had been reduced to 2 mm; see Fig. 2c. At this stage, a surface roughness of 15 nm, as measured in a Triboindenter TI 900 device in scanning probe microscopy (SPM) mode, was reached. In more detail, raster scanning of the polished surface with the Berkovich diamond tip yields topographical images like the one seen in Fig. 2e; it is made up of pixels of 78 nm size. Such images also allow computing the root-mean-squared average (RMS) of the topography of the surface, \(R_q\), according to Miller et al.:24
where P is the number of scanned pixels from the image obtained by scanning probe microscopy, and \(z_{mn}\) is the height difference between the pixels and the mean scanned plane.24,25
Sample preparation steps and outcome: (a) cutting resin-embedded jaws out of the microtube, (b) circular polishing of the indentation surface, (c) sample preparation completed with (d) indentation areas “middle” and “tip” indicated in a light micrograph taken by a nanoindenter-inbuilt microscope and with (e) scanning probe-microscopic topography quantification of the polished surface portion measuring 400 \(\mu \hbox {m}^2\)and lying within the middle region; the pixel-wise heights are given in nanometers.
Nanoindentation of Platynereis dumerilii Jaw
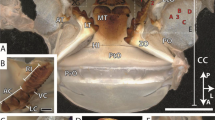
The polished surface, with its outward normal pointing in the ventral direction, was indented by a Berkovich tip attached to a Hysitron Triboindenter TI900, according the following protocol for load control: At a rate of 0.01 mN/s, the load was increased up to 100 \(\mu \)N maximum load; the latter was held for 5 s before unloading took place, again at a rate of 0.01 mN/s. This indentation process was repeated 156 times to realize two grids of 6 \(\times \) 6 and one grid of 6 \(\times \) 5 indents in the middle region of the jaw, depicted as a red area in Fig. 2d, and one grid of 6 \(\times \) 9 indents in the tip region of the jaw, depicted as the green area in Fig. 2d. Thereby, the spacing between the indents always amounted to 5 \(\mu \)m. The corresponding maximum indentation depths \(h_\mathrm{max}\) ranged from 80 nm to 120 nm; hence, they were at least 2.5 to 5 times larger than the roughness of 15 nm, as is required for the experimental realization of an elasto-plastic half-space.24,26 Oliver and Pharr27 computed the maximum indentation depth \(h_\mathrm{max}\) as follows:
where \(h_\mathrm{c}\) is the contact indentation depth and \(h_\mathrm{s}\) is the displacement of the surface at the perimeter of the contact. For such a half-space, the recorded load-displacement curves were evaluated according to the method of Oliver and Pharr:27 The reduced modulus E and the hardness H were computed from the unloading stiffness S and the contact area \(A_\mathrm{c}\) according to:
Chemical Analysis of Platynereis dumerilii Jaw
To quantify the spatial concentration distributions of halogen and metal ions in the Platynereis dumerilii jaw, the polished jaw surface was further analyzed after the nanoindentation campaign. More precisely, it was scanned, in line mode, by a laser ablation inductively coupled plasma mass spectrometer (LA-ICP-MS). This device analyzed the uppermost 12 µm below the surface, while keeping the rest of the jaw sample virtually unaltered. The LA-ICP-MS set-up consisted of a New Wave 213 laser ablation system (Elemental Scientific Inc., USA) with a frequency quintupled neodymium-doped yttrium aluminum garnet laser operating at a wavelength of 213 nm, coupled, through polytetrafluoroethylene tubing, to a quadropole iCAPQ-induced coupled plasma mass spectrometer (ICP-MS; ThermoFisher Scientific, USA). The laser spot size was set to 10 \(\mu \)m, and the scan speed was chosen as 10 \(\mu \)m/s. Helium was used as the ablation gas, and argon was admixed as make-up gas before entering the ICP-MS. The measurements of the LA-ICP-MS provided intensities I of the isotopes of bromide, copper, iodine, iron and zinc in counts per second. These counts needed to be related to the ionic “concentrations,” which were approached here via weight fractions in matrix-matched standards.28
In more detail, a Mettler Toledo precision balance PGH403-S (Mettler-Toledo International Inc., Switzerland) was employed to define the amounts of selected salts in terms of well defined weight, namely: ammonium bromide, copper(II) chloride, iron(II) chloride, potassium iodide and zinc chloride. Then, a certain weight-defined amount of the fluid organic compound N-methyl-2-pyrrolidon (Merck KGaA, Germany) was put into 15-ml polycarbonate test tubes together with the aforementioned salt portions. These components were then well mixed, in the sense that crystal formations could no longer be discerned by the naked eye. Thereafter, we added, again at a well-defined weight, the same two-compound resin acid which we had already used for the embedding of the worm jaws. The resulting fluid was then stirred by a vibrating mixer for 10 min and by a centrifuge for another 10 min. The weight fractions of the metal ions with respect to the weight of the overall mixture are given in the upper part of Table I. Thereafter, our mixing products were cured, for 2 days, in the Duran Borosilicate Glass 3.3 Complete Vacuum Desiccator. Subsequently, all standards, the four spiked ones as well as the blank one, were cut by an Isomet low-speed saw (Buehler, USA) into 3-mm-thick circular slices and then attached, using resin, to a glass slide. The free surfaces of these slices underwent a polishing protocol as described in:29 They were machined using a Leica SM2500 heavy-duty sectioning system and the Leica SP2600 ultramiller (Leica Biosystems GmbH, Germany), equipped with a diamond cutting edge rotating at 1000 rpm, at a feeding speed (i.e., a speed orthogonal to the surface) of 2 nm/polishing cycle and an advancing speed (i.e., a speed within the plane of the surface) of 1.5 mm/s, until a roughness measure \(R_q\) according to Eq. 1, of around 15 nm was reached. Precautions were taken to avoid cross-contamination during the polishing process. Therefore, whenever a sufficiently fine surface was realized, the diamond blade was cleaned twice, 15 min in an ultrasonic bath containing 99% ethanol followed by a rinse with distilled water.
The polished surfaces of the four spiked and one blank standard then underwent the same LA-ICP-MS protocol as the Platynereis dumerilii jaw, yielding the intensities \(I^s\) given in the middle part of Table I. The ionic intensities and ionic weight fractions turned out to be almost perfectly proportional to each other, so the weight fractions could be expressed as a linear function, through the origin, of the intensities. Mathematically, this reads as
with ion-specific slope values \(\beta _i\) assembled in the lower portion of Table I, representing the slopes seen in Fig. 3. These slope factors \(\beta \) were then used to convert the ionic intensity distributions measured on the jaws into corresponding weight fraction distributions, employed here as “concentration quantities.”
Size Effect-Related Re-evaluation of Nanoindentation Tests on Jaws of Nereis and Glycera
Nanoindentation-tested hardness may not only depend on the chemical composition and the microstructure of the investigated material, but also on the indentation depths and the correspondingly tested three-dimensional domain below the indenting tip. Considering that the strength of the tested material is governed, according to Taylor,30 by the amount of dislocations in the aforementioned three-dimensional domain, Nix and Gao23 derived the following relation between tested hardness and the contact indentation depths \(h_\mathrm{c}\) (see, e.g., Figure 2 of Nix and Gao23)
with a size-independent hardness value \(H_0\) associated with infinitely large indentation depths and a characteristic length \(h^*\) depending on indenter shape and material properties. Relation (6) was experimentally validated through tests on polycrystalline copper31 and silver.32
Herein, we check whether relation (6) may also hold for the material making up Polychaeta jaws. In this context, hardness values have been reported for Glycera and Nereis genera by Broomell et al.,21 Pontin et al.,22 Moses et al.7 and Lichtenegger et al.6 These authors do not directly provide the indentation depths \(h_\mathrm{c}\); however, they still give sufficient information from which the latter can be assessed. Namely, in case of a Berkovich indenter considered by Oliver and Pharr,27 the indentation depth \(h_\mathrm{c}\) is related to the maximum indentation force \(F_\mathrm{max}\) via
and the maximum indentation forces applied to jaws of Glycera and Nereis have been reported in;7,21,22 see Fig. 7a. Lichtenegger et al.6 do not provide explicit information on the maximum indentation force; however, the indenter contact area \(A_\mathrm{c}\) can be assessed from Fig. 6a given in,6 and also this area gives access to the indentation depth \(h_\mathrm{c}\), via,27
Results
Mechanical and Chemical Property Distributions in Platynereis dumerilii Jaw
The nanoindentation-probed hardness values according to Eq. 4 are only weakly correlated with the corresponding maximum indentation depths \(h_\mathrm{max}\); see Fig. 4a. This holds true for the total set of all measurements, as it does for the subsets “middle” and “tip” according to Fig. 2d. This is even more the case for the reduced elastic modulus values according to Eq. 3, where hardly any correlation can be observed in Fig. 4b. Moreover, no significant correlation between reduced modulus and hardness values can be found; see Fig. 4c. It is instructive to evaluate these nanoindentation-derived values in a statistical way, first by means of computing mean values and standard deviations and of plotting histograms according to Scott’s rule:33 It turns out that the the mean value over all 156 reduced elastic modulus values, 11.7 GPa, see Fig. 5a, is slightly higher than the characteristic value of the most frequently inhabited histogram bin, amounting to 10.5 GPa; see Fig. 5b. The situation for the hardness values is different, where the mean value of 0.9 GPa lies within the interval of the most inhabited histogram bin; see Fig. 5c.
Once we distinguish between the middle and the tip indentation regions, a slightly different picture emerges: As for the tip region, the mean value of the reduced modulus data, 12.7 GPa, see Fig. 5a, lies within the most populated histogram bin, see Fig. 5d, while the mean value of the hardness data, 1.08 GPa, is slightly larger than the characteristic value of the most frequently inhabited histogram bin, amounting to 0.9 GPa; see Fig. 5e. As for the middle region, the mean values of both hardness and modulus data, 0.81 GPa and 11.2 GPa, see Fig. 5a, are slightly larger than the characteristic values of the most frequently populated histogram bins, which are 0.7 GPa and 10.5 GPa; see Fig. 5d and e.
Statistical evaluation of 156 nanoindentation experiments, 54 in the tip region and 102 in the middle region: (a) mean values and standard deviations of reduced elastic modulus data and hardness data, (b) histogram over 156 reduced modulus values, (c) histogram over 156 hardness data values, (d) tip- and middle-related histograms of reduced modulus values and (e) tip- and middle-related histograms of hardness values.
Deeper statistical analysis realized through software package IBM SPSS Statistics34 concerns the question whether the data collected from the tip region may be significantly different from those collected in the middle region: Parametric tests, i.e., analysis of variance (ANOVA), cannot be applied because of the non-normal distribution nature of the data. Graphical interpretations of the data such as histograms are extremely helpful when judging normality. However, Mishra et al.35 recommend the combination of graphical interpretations with a more rigorous numerical statistical test to conclude on the normal distribution of data. Thus, the normality of E and H were further tested by means of the Kolmogorov-Smirnov and Shapiro-Wilk tests,36,37 with the latter one being regarded as the most powerful normality test.38 However, both tests provided similar outcomes when applied to the indentation data recollected from both the tip and the middle regions of the investigated jaw: The data sets turned out to be not normally distributed. Hence, non-parametric approaches were needed to determine whether or not the data arising from the tip and middle indentation regions are similar. Accordingly, we resorted to the Mann-Whitney U and the Kruskal-Wallis H tests, which are non-parametric equivalents of parametric tests such as Student’s t-test and ANOVA.39,40,41,42,43 Our correspondingly tested null hypothesis was that there is no statistically significant difference between the indentation results obtained at the tip region and the middle region. However, examining the E and H results from both regions with the Mann-Whitney U and Kruskal-Wallis H tests showed that they both rejected our null hypothesis.
With these local differences in mind, it is instructive to study the ion distributions across the polished surface layer determined according to Sect. 2.3: Among all tested ions, zinc and iodine are much more concentrated in the jaw tip region than they are in the middle region, with maximum local weight fractions of up to almost 5% in the case of zinc and up to more than 10% in the case of iodine; see Fig. 6d and e. Hence, the higher modulus and hardness values in the tip region compared to the middle region may well stem from the correspondingly higher concentrations of iodine and zinc. The situation is different when it comes to bromide, iron and copper ions: Bromide ions are fairly uniformly distributed across the jaw and locally reach very high weight fractions of > 20%, see Fig. 6a; copper ions are hardly present at all in the investigated Platynereis dumerilii jaw, see Fig. 6b. Iron ions, at weight fractions reaching almost 9%, are more frequently present in the middle region than they are in the tip region; see Fig. 6c.
Trans-species Size Effect Law for Hardness of Jaws Across Different Polychaeta
The species-specifically averaged hardness values reported by Lichtenegger et al.6 for Nereis limbata, by Broomell et al.21 for Nereis virens, by Pontin et al.22 and by Moses et al.7 for Glycera dibranchiata, as well as by us, in Fig. 5a, for Platynereis dumerilii virtually perfectly follow Nix-Gao’s size effect law (Eq. 6); see Fig. 7b. This is underlined by an impressively large coefficient of determination amounting to \(R^2 = 99.7\%\). The size-independent hardness and indentation quantities amount to \(H_0=0.53\) GPa and \(h^*=0.13~\mu \hbox {m}\). The limiting hardness \(H_0\) is very close to that of crystalline copper (0.58 GPa).23
The potential validity of Nix-Gao’s size effect cannot be checked from a series of nanoindentation tests characterized by only one maximum indentation force. This is shown by Eq. 7: Within such a test series, the hardness square would scale with (1/\(h_\mathrm{c}^4\)), and not with (1/\(h_\mathrm{c}\)). Hence, for checking the relevance of the Nix-Gao relation, results associated with different maximum indentation forces need to compared. In this sense, given the available data, our analysis was naturally restricted to the mean values associated with one and same indentation force each. To further elucidate this issue, and to show the high quality of the mean values used for confirming the relevance of Eq. 6, we complemented our analysis by the 95% confidence intervals for the mean values of the hardness and indentation depth data; see Fig. 7b. These intervals were computed as the mean values \(\pm 1.96\) times the standard error (SE),44 the latter being the standard deviation divided by the square root of the number of tests; see the table labeled in Fig. 7a. Corresponding hardness data are assembled in Appendix A, Supplementary Material.
Nix-Gao size effect law across different species of Polychaeta: (a) tabular representation of experimental sources used for the determination of hardness and indentation depth \(h_\mathrm{c}\); (b) graphical representation. The bars represent the 95% confidence interval for the mean values of hardness and contact indentation depth data; (c) sketch of histidine enriched proteins with metal coordinated bonds.
Discussion
To the best knowledge of the authors, this is the first systematic experimental study on the chemical and mechanical properties, namely nanoindentation-probed hardness and reduced modulus as well as LA-ICP-MS- and calibration standard-derived ionic concentration distributions, across a jaw harvested from a bristle worm of species Platynereis dumerilii, a key model organism in marine biology.
The novel experimental results may be evaluated and discussed in terms of three major traditions found in the nanoindentation and applied material mechanics literature:
-
1.
histogram representations
-
2.
chemo-mechanical couplings
-
3.
size effect laws for metals
With respect to histogram representations,45 distributions with only one peak were observed, see Fig. 5, indicating that only one material phase was present at the observation scale tested by the nanoindentation device, which is about one half to one third of the indentation depth,25 i.e., around 33 to 50 nm.
With respect to chemo-mechanical couplings, larger zinc and iodine concentrations found in the tip region of the jaw are correlated with slightly but still statistically significantly larger hardness and elasticity properties in the tip region; an effect which has been extensively discussed in the literature on other bristle worm jaws.5,6,7,19,20,21,22
However, the probably most remarkable original insight comes from setting our novel data in context with existing data that were obtained from larger bristle worm species tested at larger indentation depths \(h_\mathrm{c}\). The differences between the hardness tested herein, and the hardness values reported earlier, exceed the variations reported as results of local ionic concentration variations. As shown in Fig. 7b, these observed differences likely do not result from significant species-to-species differences in the jaw material itself, but can be well explained as consequences of the different indentation depths \(h_\mathrm{c}\) used in the different studies. More precisely, the square of the hardness being proportional to the inverse of the indentation depth indicates variations in the dislocation density of the investigated material domain, as explained by Nix and Gao23 in the context of crystalline metals. An important biological implication of this finding is that the matter that forms the jaws of diverse species within the large Polychaeta class may be less variable than commonly assumed. Rather, our data suggest that ion-spiked structural proteins likely represent an early innovation in Polychaeta phylogeny and allowed the formation of a basic architectural building block with “universal,” i.e., species-invariant, hardness properties. The latter exhibit unexpected parallels with crystalline metals, with respect to both magnitude and Nix-Gao-type size effect features which are characteristic for ductile materials. However, metals are produced at high temperatures with high energy consumption, while the ion-spiked high performance structural proteins are products of regular biological synthesis. Of note, the biosynthesis of Polychaeta jaws appears to be markedly different from the situation in vertebrates. There, two main types of building blocks, structural proteins (such as collagen) and metal ion forming minerals (such as calcium being part of hydroxyapatite), are combined into nano-composites governing the mechanical properties of tissues such as bone.46 Thereby, the minerals with size effect properties47 far off the Nix-Gao law are markedly more brittle than ion-spiked proteins present in Polychaeta jaws. The latter therefore provide novel, unprecedented opportunities in the wide field of bioengineering.
This motivates a re-discussion of our results from a mechano-chemical perspective: The interesting “universal” feature integrating largely differing species- and testing protocol-specific hardness values is their obedience of the Nix-Gao size effect law. This means that the Platynereis jaw tested herein is not necessarily harder than the previously tested Nereis and Glycera jaws; it rather means that the mechanical properties of all these different jaw materials are actually fairly similar. At the same time, the validity of the Nix-Gao size effect law indicates an important qualitative feature shared by all of these materials: the occurrence of dislocation-type dissipative processes within their nanostructures—such dislocations are the very fundament based on which Nix and Gao have mathematically derived their size effect law. Classically, dislocations are considered the atomic scale origin of metal plasticity,48 i.e., of ductile material behavior. Interestingly, the idea of dislocations can be reconciled with the knowledge on metal coordination bonds occurring in all of the tested and discussed jaws.49,50 After mechanical rupture of somewhat aligned metal coordination bonds, see Fig. 7c, these bonds can quickly re-form under a new geometrical configuration associated with a corresponding “dislocation” emerging along the re-bonded line of metal ions. Such reformation processes along “dislocation-like lines” are beautifully consistent with the overall plastic or ductile behavior, as reflected by the Nix-Gao size effect law. In this context, the essential feature is the existence of the rupturing and re-forming metal coordination bonds rather than the actually used metal ions or organic ligands. The latter vary largely between species. In Platynereis, the dominant ions are bromide, iron, iodine and zinc; copper is the dominant ion in Glycera, and in Nereis, bromide, iodine and zinc dominate. Again, while the actually used ions and ligands are only of secondary importance, their local chemical concentrations have a remarkable impact on the locally prevailing stiffness and hardness values. In this sense, Nereis jaw material hardens with increasing zinc concentration;6,20Glycera jaw material hardens with copper concentration,7,22 an effect which is further enhanced by crystalline atacamite fibers. Platynereis jaw material hardens with increasing zinc and iodine concentrations, as was shown in the present study.
References
H. Hausen, Chaetae and Chaetogenesis in Polychaetes (Annelida) (Springer, 2005a)
R.A. Merz and S.A. Woodin, Integr. Comp. Biol. 46(4), 481 (2006)
H. Hausen, Chaetae and chaetogenesis in polychaetes (Annelida), in chapter Morphology, Molecules, Evolution and Phylogeny in Polychaeta and Related Taxa, vol. 179, ed. by T. Bartolomaeus, G. Purschke, (Springer, 2005b), pp. 37–52
C.C. Broomell, S.F. Chase, T. Laue, and J.H. Waite, Biomacromolecules 9(6), 1669 (2008)
H.C. Lichtenegger, T. Schöberl, M.H. Bartl, H. Waite, and G.D. Stucky, Science 298(5592), 389 (2002)
H.C. Lichtenegger, T. Schöberl, J.T. Ruokolainen, J.O. Cross, S.M. Heald, J.H. Birkedal, H. Waite, and G.D. Stucky, Proc. Natl. Acad. Sci. 100(16), 9144 (2003)
D.N. Moses, M.A. Mattoni, N.L. Slack, J.H. Waite, and F.W. Zok, Acta biomaterialia 2(5), 521 (2006)
G.W. Bryan, and P.E. Gibbs, J. Mar. Biol. Assoc. UK 59(4), 969 (1979)
D.E.G. Briggs and A.J. Kear, Paleobiology 19(1), 107 (1993)
Z. Kielan-Jaworowska, Lethaia 1(1), 39 (1968)
O. Hints and M.E. Eriksson, Palaeogeogr. Palaeoclimatol. Palaeoecol. 245(1–2), 95 (2007)
A.H.L. Fischer, T. Henrich, and D. Arendt, Front. Zool. 7(1), 31 (2010)
B. Backfisch, V.B.V. Rajan, R.M. Fischer, C. Lohs, E. Arboleda, K. Tessmar-Raible, and F. Raible, Proc. Natl. Acad. Sci. 110(1), 193 (2013)
S. Bannister, O. Antonova, A. Polo, C. Lohs, N. Hallay, A. Valinciute, F. Raible, and K. Tessmar-Raible, Genetics 197(1), 77 (2014)
L.A. Bezares-Calderón, J. Berger, S. Jasek, C. Verasztó, S. Mendes, M. Gühmann, R. Almeda, R. Shahidi, and G. Jékely, eLife 7 (2018)
F. Raible and K. Tessmar-Raible, Curr. Biol. 24(15), R676 (2014)
A. Miserez, J.Y. Li, H. Waite, and F. Zok, Acta Biomaterialia 3(1), 139 (2007)
B.W. Cribb, A. Stewart, H. Huang, R.Truss, B. Noller, R. Rasch, and M.P. Zalucki, Naturwissenschaften 95(1), 17 (2008)
H. Birkedal, R.K. Khan, N. Slack, C. Broomell, H.C. Lichtenegger, F. Zok, G.D. Stucky, and J.H. Waite, ChemBioChem 7(9), 1392 (2006)
C.C. Broomell, M.A. Mattoni, F.W. Zok, and J.H. Waite, J. Exp. Biol. 209(16), 3219 (2006)
C.C. Broomell, F.W. Zok, and J.H. Waite, Acta Biomaterialia 4(6), 2045 (2008)
M.G. Pontin, D.N. Moses, J.H. Waite, and F.W. Zok, Proc. Natl. Acad. Sci. 104(34), 13559 (2007)
W.D. Nix and H. Gao, J. Mech. Phys. Solids 46(3), 411 (1998)
M. Miller, C. Bobko, M. Vandamme, and F.-J. Ulm, Cement Concrete Res. 38(4), 467 (2008)
V. Jagsch, P. Kuttke, O. Lahayne, L. Zelaya-Lainez, S. Scheiner, and C. Hellmich, Constr. Build. Mater. 238, 117768 (2020)
E. Donnelly, S.P. Baker, A.L. Boskey, M.C.H. van der Meulen, J. Biomed. Mater. Res. Part A 77A(2), 426 (2006)
W.C. Oliver and G.M.Pharr, J. Mater. Res. 7, 1564 (1992)
M. Bonta, H. Lohninger, V. Laszlo, B. Hegedus, and A. Limbeck, J. Anal. At. Spectrom. 29(11), 2159 (2014)
L. Zelaya-Lainez, H. Kariem, W. Nischkauer, A. Limbeck, and C. Hellmich, Mater. Sci. Eng. C 117, 111234 (2020)
G.I. Taylor, Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Charact. 145(855), 362 (1934)
K.W. McElhaney, J.J. Vlassak, and W.D. Nix, J. Mater. Res. 13(5), 1300 (1998)
Q. Ma and D.R. Clarke, J. Mater. Res. 10(4), 853 (1995)
D.W. Scott, Wiley Interdiscip. Rev. Comput. Stat. 2(4), 497 (2010)
IBM Corp. IBM SPSS Statistics for Windows, Version 26.0, 2019. Released 2019
P. Mishra, C.M. Pandey, U. Singh, A. Gupta, C. Sahu, and A. Keshri, Ann. Cardiac Anaesthesia 22(1), 67 (2019)
S.S. Shapiro and M.B. Wilk, Biometrika 52(3–4), 591 (1965)
M.A. Stephens, J. Am. Stat. Assoc. 69(347), 730 (1974)
S.S. Shapiro, M.B. Wilk, and H.J. Chen, J. Am. Stat. Assoc. 63(324), 1343 (1968)
G.W. Corder and D.I. Foreman, Nonparametric Statistics for Non-Statisticians: A Step-By-Step Approach (Wiley, London, 2009)
M.P. Fay and M.A. Proschan, Stat. Surv. 4, 1 (2010)
W.H. Kruskal and W.A. Wallis, J. Am. Stat. Assoc. 47(260), 583 (1952)
H.B. Mann and D.R. Whitney, Ann. Math. Stat. 18(1), 50 (1947)
R.R. Sokal and F.J. Rohlf, Biometry: The Principles and Practice of Statistics in Biological Research (W. H. Freeman, San Francisco, 1981)
R.A. Fisher, Statistical Methods for Research Workers (Oliver and Boyd, 1954)
G. Constantinides, F.J. Ulm, and K. Van Vliet, Mater. Struct. 36(3), 191 (2003)
A. Fritsch and C. Hellmich, J. Theor. Biol. 244(4), 597 (2007)
R. Khanna, K.S. Katti, and D.R. Katti, J. Eng. Mech. 135(5), 468 (2009)
D.J. Bacon and V. Vitek, Metall. Mater. Trans. A 33(3), 721 (2002)
E. Khare, N. Holten-Andersen, and M.J. Buehler, Nat. Rev. Mater. (2021)
E. Degtyar, M.J. Harrington, Y. Politi, and P. Fratzl, Angew. Chem. Int. Ed. 53(45), 12026 (2014)
Acknowledgements
This project was financially supported by the Austrian Academy of Sciences (OEAW), through the project Bio3DPrint.
Funding
Open access funding provided by TU Wien (TUW).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zelaya-Lainez, L., Balduzzi, G., Lahayne, O. et al. Jaws of Platynereis dumerilii: Miniature Biogenic Structures with Hardness Properties Similar to Those of Crystalline Metals. JOM 73, 2390–2402 (2021). https://doi.org/10.1007/s11837-021-04702-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11837-021-04702-1