Abstract
The grain boundary network of WC in WC-Co is important, as cracks often travel intergranularly. This motivates the present work, where we experimentally measure the fracture energy of Σ2 twist grain boundaries between WC crystals using a double cantilever beam opened with a wedge under displacement control in a WC-10wt%Co sample. The fracture energy of this boundary type was compared with cleaving {\(10\overline{1}0\)} prismatic planes in a WC single crystal. Fracture energies of 7.04 ± 0.36 Jm−2 and 3.57 ± 0.28 Jm−2 were measured for {\(10\overline{1}0\)} plane and Σ2 twist boundaries, respectively.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Cemented carbide (WC-Co) cutting tools are essential for modern manufacturing, as they are used in drilling, mining, and cutting tool inserts.1 These WC-Co composites consist of tungsten carbide and cobalt that act as hard particle and binder, respectively.2 WC-Co has a higher toughness relative to other hardmaterials, such as polycrystalline diamond with KIC in the range of 8–26 MPam1/2 .3 Yet, WC-Co tools are limited in performance and lifetime owing to wear and fracture. Hence, crack propagation and fracture in WC-Co has been extensively studied.4,5,6
In WC-Co, cracks can propagate near the WC/Co interface, along WC/WC boundaries and transgranular in the carbide.4 Formation of a multiligament zone during WC/Co failure is the main source of toughening in WC-Co.7 However, typically, a smaller fraction of the crack path is along WC/Co phase boundaries at lower binder fractions.4,6 Currently, we lack detailed knowledge of WC/WC boundary properties despite a large fraction of the fracture path being along it. This motivates us to study WC/WC boundary fracture, to provide an opportunity to enhance understanding of the life span of hardmetal-based machining parts.
Tungsten Carbide Crystal Structure and Σ2 Boundaries
WC has a simple hexagonal crystal with one carbon and a tungsten atom per primitive unit cell. Its c/a ratio is close to unity as the lattice parameters, a and c, are 0.2906 nm and 0.2837 nm, respectively.8 Alternating layers of W and C planes are present along the 〈\(10\overline{1}0\)〉 and 〈0001〉 of a WC crystal. While WC grains adopt either an equilibrium triangular prism shape or a truncated trigonal prism, as shown in Fig. 1a.9
(a) The hcp unit cell of WC as well as possible growth of the grains into either the equilibrium triangular prism or truncated trigonal prism shapes. (b) Type I and type II prismatic planes as seen from the [\(0001\)] direction. Potential ways of cleaving a prismatic plane are also shown in the illustration by dashed lines.
The high toughness hardmetal microstructure is formed during processing. The cobalt metal binder melts and wets the carbide particles with a dihedral angle of zero during liquid phase sintering.10,11 Anisotropy in the WC/Co interface energy means that the presence of cobalt during sintering promotes the growth of three of the prismatic planes compared to the other three in a WC grain, as corresponding pairs of prismatic planes (e.g., (\(10\overline{1}0\)) and (\(\overline{1}010\))) are not equivalent because the WC crystal structure is non-centrosymmetric.12
The two types of prismatic planes are illustrated in Fig. 1b. The difference between the prismatic plane types can be inferred from the number of dangling bonds for a given atom at the terminating layer. If each of the terminating W or C atoms have 4 dangling bonds, the prismatic plane is of type I. On the other hand, the prismatic plane is type II if there are 2 dangling bonds per terminating surface atom. The interplanar spacing is also different between the two types of prismatic planes. Interplanar spacing between type I W and C planes is 0.084 nm in comparison to 0.168 nm for type II W and C planes.13 Density functional theory (DFT) studies have been conducted to determine {\(10\overline{1}0\)} surface energies. A summary of such DFT data is given in Table I.
There are two ways to cleave prismatic planes as shown in Fig. 1b. The crystal can be cleaved between either a type I W and C terminated planes, or a type II W and C terminated planes. The cleavage energies (defined as twice the surface energy) in these two scenarios have been determined to be 13.85–14.09 Jm−2 and 7.25–7.33 Jm−2, respectively, in the literature.14,15,16 Four W–C bonds are broken per unit surface in the former compared to two in the latter. This explains the difference in energy by a factor of 2. The anisotropic plane energies explain the faceted morphology of WC grains due to preferential growth of {\(0001\)} and type II {\(10\overline{1}0\)} low-energy planes. Hence, WC-Co is likely to contain straight WC/WC boundaries and, for a (near) random crystallographic texture, some of these will be perpendicular to the surface. This makes WC/WC boundaries suitable for fracture analysis using a DCB test.
WC’s c/a ratio being close to unity results in several coincidence site lattice (CSL) boundaries.8 Σ2 boundaries with a misorientation of 90°/[\(10\overline{1}0\)] are the most frequently encountered CSL WC/WC boundaries in WC-Co.17 Σ2 twist in particular which has {\(10\overline{1}0\)}/{\(10\overline{1}0\)} boundary habit planes are most often found owing to lower energy relative to the tilt counterpart.18,19,20 It is important to study the most frequent boundaries to understand the macroscopic performance of the WC-Co tools. Our study can inform grain boundary engineering (GBE) approaches to control microstructure, and ultimately lead to an increase in WC-Co tool performance.
Micromechanical Fracture Testing
Study of brittle fracture has advanced significantly owing to Griffith’s work.21 Here, we return to his premise that the energy required for fracture is directly related to energy needed to create two new surfaces. To provide a mechanistic understanding of the toughness of ceramics at a microscopic scale, micromechanical testing can be applied where individual microstructural features are tested to reveal physical properties, such as fracture energy.
Four microscale fracture testing techniques are used for determining fracture properties: pillar splitting,22 single cantilever bending,23,24 clamped beam bending,25,26 and DCB compression.27 These are prone to limitations in sample fabrication and testing, with issues concerning ion implantation at the crack tip28 and unstable crack growth, respectively. These issues can lead to erroneous fracture energy measurements.
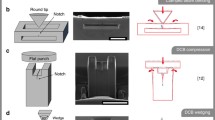
To address these challenges, a new displacement-controlled DCB geometry loaded by a wedge tip was introduced in the work of Sernicola et al.29 The wedge-loaded DCB geometry allows for a stable crack growth. A stable crack growth in turn facilitates the measurement of fracture energy values further away from notch tip which are more accurate. This technique was designed to use the in situ SEM observation of the crack length as well as physical measurement of each beam flexure to measure the critical energy release rate while the DCB cracks. This was inspired by the macroscopic wedge-loaded DCB test fixture of Obreimoff’s in mica.30
Sernicola et al. fabricated a DCB vertically using a focused ion beam (FIB), with a ‘slot’ to accept a wedge indenter. The DCB is deformed using direct displacement control, using a piezo-driven diamond wedge indenter, inside a scanning electron microscope (SEM). This geometry is stable, as the continued movement of the wedge downwards opens up the crack, but more displacement is required for the crack to progress further. Therefore, the strain energy release rate of the crack grown within the DCB can be measured.31 Load cell information is not used, and the energy is calculated from the statics of the loaded double cantilever system.
In the present work, we apply the method of Sernicola et al.29 to determine the fracture properties of WC-Co, which include the fracture energy of WC/WC Σ2 twist boundaries and the [\(10\overline{1}0\)] prismatic plane. The grain boundaries were found using electron backscatter diffraction (EBSD) and analysis with MTEX.32
Σ2 twist boundary strength has been determined in the literature using single cantilever bending tests.33 However, the fracture energy of carbide boundaries has never been experimentally reported. Thus, we have used a wedge loaded DCB geometry to measure the fracture energy of Σ2 twist boundaries. We have also measured the surface energy of type II {\(10\overline{1}0\)} prismatic planes and compared it to values obtained from the literature.
Methods
Materials
The WC single crystal used in the study was provided by the National Physical Laboratory (NPL). It was grown in a furnace at Sandvik Hard Materials (Coventry, UK).
The multigrain sample used for Σ2 boundary analysis was prepared using conventional powder metallurgy routes. Pure WC and Co powders were mixed by milling in ethanol-10%H2O, using extra-coarse WC from Wolfram Bergbau FSSS (Fisher Sub Sive grainsize) of 15 µm, cobalt from Freeport and Polyethylengylcol as a pressing agent to make a WC-10wt%Co sample. To achieve as large WC grains as possible, the samples were only milled for 4 h in a WC-lined 0.25L rotating mill. Thereafter, the powder was pan dried at 40°C in gaseous N2 and finally uniaxially pressed into rectilinear (SNUN) geometry. Followed by de-binding in gaseous H2 to 450°C and sintered at 1500°C in controlled vacuum. The cemented carbide sample was cut into a 15 × 5 × 5 mm piece using an IsoMet 1000 precision cutter equipped with a diamond cut-off wheel.
The single-crystal and the cemented carbide samples were mounted on a disc grinder and a resin mount, respectively, for grinding, and then they were polished with polycrystalline diamond suspensions with particle sizes of 3 μm, 1 μm, and 0.25 μm. Finally, the cemented carbide sample was broad argon ion beam-polished in a PECS II system at 6 kV for 6 h with the ion beam glancing over the sample surface at an incidence angle of 0°.
Micromechanical Testing Theory
A DCB as illustrated in Fig. 2 is essentially two cantilever arms clamped at one of the ends, the crack tip. As a wedge is driven into the central trough of a DCB, the cantilever arms are point loaded at the arm–wedge contact. Elastic strain energy stored in the cantilever arms is then released and used for crack initiation and propagation.
The elastic strain energy, \(U_{M}\) (Jm−1), stored in each of the arms is given by the Euler–Bernoulli beam theory (EBT) in Eq. 1.34 The elastic strain energy release rate, \(G\) (Jm−2), in accordance with the Griffith criterion for this case is as in Eq. 2.
where \(E\), \(d\), \(\delta\), and \(a\) are the elastic modulus, cantilever arm width, arm lateral displacement, and crack length, respectively. \(G\) will give values of surface energy provided that the energy expended in bending the arms is the same as the energy stored in them. During initial crack growth, the EBT assumption of a << d is not valid. Hence, the Timoshenko beam theory (TBT) model for analyzing the behavior of short thick beams must be used.35 TBT accounts for the effects of transverse shear deformation during loading. G for each beam during early crack propagation is given as:
where \(\nu\) is the Poisson’s ratio. Equation 3 reduces to Eq. 2 as the crack evolves and a >> d. Rotation at the crack tip (clamped end) is corrected for by the solution developed by Williams.36 This involves replacing \(a\) in Eqs. 2 or 3 with \(a + \chi h\). Factors \(\chi\) and \(\Gamma\) in turn are given in Eqs. 4 and 5, respectively.
The value of \(\chi\) was approximated to be 0.67 by Williams, with the assumption of the arm being isotropic, as is necessary for applying any beam theory. \(\chi\) was also shown to be insensitive to \(\nu\). The validity of the correction was verified in the work of Aldegaither et al.37
EBSD Data Collection and Analysis
EBSD data were acquired using a Bruker e-FlashHD EBSD detector in a FEI Quanta 650 FEG-ESEM. The mapping area for acquisition was marked with four fiducial crosses to form a square grid of 400 × 400 μm area. Data were recorded with a step size of 0.4 μm. Once acquired, it was loaded into MTEX 5.1.1 in MATLAB. A custom script in MATLAB was then used for data analysis to identify Σ2 twist boundaries for mechanical testing, i.e., those with grain boundary planes perpendicular to the cut sample surface.
Σ2 boundaries were identified in MTEX based on the following criteria: grains sharing a Σ2 boundary will have {\(10\overline{1}0\)}||{\(10\overline{1}0\)} and {\(0001\)}||{\(11\overline{2}0\)} relationships. In polycrystalline WC, the Σ2 twist and tilt boundary types have a different habit plane. The twist has two {\(10\overline{1}0\)} planes terminating the crystals at the interface. The tilt has {\(0001\)} and a {\(11\overline{2}0\)} terminating each crystal. In this work, only the Σ2 twist boundary is of interest.
To find the boundaries of interest, the two habit planes were transformed from the crystal frame of reference into the sample frame, using the transformation in equations 6 and 7.
where g is the rotation matrix for each grain, while a and b are adjacent grains sharing a boundary. Six vectors are produced for each grain as there are six prismatic planes. The parallel planes are determined using a dot product test of the (unit) plane normal vector. For the planes pairing that is parallel, a second dot product test is used to compare this vector with the surface normal, i.e., if the shared plane is perpendicular to the surface normal. This identifies a subset of boundaries within the region of interest in which DCBs can be cut.
DCB Manufacture
The micromechanical test specimens were machined from specific sites using a FEI Helios NanoLab 600 DualBeam SEM. A custom script written in the Nano-Builder software was used for automated fabrication of DCBs following the method outlined by Sernicola et al.29
Micromechanical Testing Procedure
Single-crystal DCB fracture tests were performed on a [\(0001\)] oriented grain, cleaving {\(10\overline{1}0\)} prismatic planes apart. DCB tests were also conducted on the WC-10wt%Co sample to measure the fracture energy of the Σ2 twist boundary.
Micromechanical testing was conducted in situ within a FEI Quanta 650 FEG-ESEM microscope. This afforded continuous high spatial resolution imaging of the test process. Thus, alignment of the DCB with the indenter tip and tracking crack propagation was possible. Images were captured using an Everhart-Thornley detector in secondary electron mode at 5 kV and a working distance of ~10 mm.
An Alemnis nanoindenter was used for DCB testing. DCBs were loaded with a 50° cone angle and 10-μm-long, diamond wedge tip (Synton) in direct displacement control. Images were acquired at ~500-ms intervals during testing. Lateral arm displacement, arm width, and crack length were extracted from these images with the aid of custom MATLAB scripts. Linearly-fitted lateral displacement of the beams and linearly-fitted crack length data were utilized for fracture energy determination. This was done with the intention of reducing noise/scatter in the measurements. Further details regarding the test procedure can be found in the work by Sernicola et al.29
Results
Figure 3a shows one of the regions selected for EBSD analysis marked with FIB-milled fiducial crosses. The locations of the fiducial crosses had FIB damage and were not indexed during EBSD acquisition, as seen in Fig. 3b. A large pore located at the top region of interest (ROI) is also seen in the image. The microstructure of the sample shows WC grains and Co binder ligaments as relatively bright and dark areas, respectively, in Fig. 3a. Figure 3b shows a schematic of grain boundaries with Σ2 boundaries indicated in red. The twist and tilt variants were not distinguished at this point. Employing the method detailed in the section, EBSD data analysis, Σ2 twist boundaries were identified.
EBSD analysis of a Σ2 twist boundary site from the ROI is shown in Fig. 4. Both the image quality map and forescattered electron micrograph from Fig. 4b and c around one such site indicate the presence of a boundary at the expected location. The habit planes at this boundary being prismatic (\(10\overline{1}0\)) and perpendicular to the surface are conveyed via EBSD IPF map overlaid with equilibrium WC crystal shapes in Fig. 4c.
First, the WC single crystal was split, and micrographs from a representative in situ test are shown in Fig. 5a. The single crystal was oriented with [\(0001\)] plane normal along the displacement direction of the wedge indenter and that {\(10\overline{1}0\)} plane was cleaved. Then, DCB tests were performed at Σ2 twist boundaries sites. Fig. 5b shows a successful DCB test at a Σ2 twist boundary.
Fractures energies presented in Fig. 6a were evaluated with cantilever arm displacement, arm width, and crack length as measured from test images and the elastic modulus determined using elastic constants taken from Landolt-Börnstein38 in accordance with Hearmon’s work.39 In the case of the [\(0001\)]-oriented single crystal, an elastic modulus of 825.6 GPa was used. For the Σ2 twist boundaries, elastic moduli were calculated depending on grain orientation. Orientation and elastic moduli of Σ2 boundary grains is provided in Table II.
Discussion
DCB tests have been performed on a WC single crystal cleaving {\(10\overline{1}0\)} planes and compared with tests that measure the Σ2 twist boundary. There, the fracture energy of the {\(10\overline{1}0\)} plane was measured as 7.04 ± 0.36 Jm−2, agreeing with the DFT data (~7.33 Jm−2) if it is assumed that the low-energy plane is fractured.
Fracture energy determined from DCB wedge testing of Σ2 twist boundaries was 3.57 ± 0.28 Jm−2. This lower fracture energy is lower than for the {\(10\overline{1}0\)} planes, suggesting that the twist boundaries are more susceptible for crack propagation than the carbide grains, as expected. A comparison of the fracture energies from each of the DCB test are given in Fig. 6b.
Fracture energies of boundaries Σ2B1 and Σ2B3 increase near the end of their respective crack paths. The increase in energy is a consequence of that the cracks are deviating from a straight path and onto the sides of the DCBs. Bending of a crack results in the thickness of the cantilever arms (which is assumed to be constant) not being well defined, and the equation for calculating fracture energy is thus no longer valid. In the case of the DCBs at the grain boundaries, it must be noted that milling DCBs with the boundary sitting at the exact middle of a DCB geometry is challenging. Thus, a DCB notch is unlikely to be at the exact location of a boundary. Hence, it is likely that the crack initiates away from the boundary locale. However, it will eventually jump onto the low energy fracture path-, i.e., the boundary.
In contrast, cracks do not have a clear preferred path for propagation in a WC single crystal. This is because surface energies of some of the WC planes are similar. For example, type II {\(10\overline{1}0\)} and {\(0001\)} plane energies are similar. Thus, a crack will eventually deviate from the intended straight path (along type II {\(10\overline{1}0\)}) in a WC single crystal. Consequently, straight cracks in WC single-crystal DCBs are shorter compared to the boundary DCBs. There is also variability in the fracture energy for any given DCB test, as illustrated in Fig. 6a. This is potentially the result of the crack not propagating exactly straight.
Conclusion
DCB wedging tests have been performed on a WC single-crystal sample cleaving {\(10\overline{1}0\)} planes. Measured fracture energy values (7.04 ± 0.36 Jm−2) are similar to the cleavage energy values in the literature, determined from DFT calculations. We have devised a method to identify CSL boundaries within a microstructure, perpendicular to the surface from EBSD data analysis. Σ2 twist boundaries were identified via this process on a WC-10wt%Co sample. Fracture tests were conducted on such boundary features, producing precise measurements of Σ2 twist boundary energy (3.57 ± 0.28 Jm−2). This information is useful when controlling WC-Co microstructure via GBE.
References
R.E. Krebs, The History and use of our Earth’s Chemical Elements: A Reference Guide, 2nd edn. (Greenwood, Westport, 2006), p 154.
M. Srinivasan, and W. Rafaniello, Carbide, Nitride and Boride Materials Synthesis and Processing, 1st edn. (Chapman & Hall, London, 1997), pp 10–12.
K. Ravichandran, Acta Metall. Mater. 42, 143. (1994).
L.S. Sigl, and H.F. Fischmeister, Acta Metall. 36, 887. (1988).
L. Llanes, Y. Torres, and M. Anglada, Acta Mater. 50, 2381. (2002).
K.P. Mingard, H.G. Jones, M.G. Gee, B. Roebuck, and J.W. Nunn, Int. J. Refract. Met. Hard Mater. 36, 136. (2013).
A. G. Evans, A. H. Heuer, D. L. Porter and D. M. R. Taplin, Proceedings of the 4th International Conference on Fracture, (New York: Pergamon, 1977), pp. 529-556.
S. Hagege, J. Vicens, G. Nouet, and P. Delavignette, Phys. Status Solidi A 61, 675. (1980).
H. Exner, Int. Met. Rev. 24, 149. (1979).
J. Gurland, and J.T. Norton, JOM 4, 1051. (1952).
L. Ramqvist, Int. J. Powder Metall. 1, 2. (1965).
F. Vahldiek, Anisotropy in Single-Crystal Refractory Compounds, 1st edn. (Springer, New York, 1968), pp 55–66.
S. Lay, P. Donnadieu, and M. Loubradou, Micron 41, 472. (2010).
M.V. Petisme, S.A. Johansson, and G. Wahnström, Modell. Simul. Mater. Sci. Eng. 23, 045001. (2015).
Y. Zhong, H. Zhu, L.L. Shaw, and R. Ramprasad, Acta Mater. 59, 3748. (2011).
B. Yoon, B. Lee, and S.L. Kang, Acta Mater. 53, 4677. (2005).
S. Hagége, G. Nouet, and P. Delavignette, Phys. Status Solidi A 62, 97. (1980).
M. Christensen, and G. Wahnström, Acta Mater. 52, 2199. (2004).
K. Mannesson, M. Elfwing, A. Kusoffsky, S. Norgren, and J. Ågren, Int. J. Refract. Met. Hard Mater. 26, 449. (2008).
X. Yuan, G.S. Rohrer, X. Song, H. Chien, J. Li, and C. Wei, Int. J. Refract. Met. Hard Mater. 47, 38. (2014).
A.A. Griffith, Philos. Trans. R. Soc. A 221, 163. (1921).
M. Sebastiani, K. Johanns, E.G. Herbert, F. Carassiti, and G.M. Pharr, Philos. Mag. 95, 1928. (2015).
D. Di Maio, and S. Roberts, J. Mater. Res. 20, 299. (2005).
T. Halford, K. Takashima, Y. Higo, and P. Bowen, Fatigue Fract. Eng. Mater. Struct. 28, 695. (2005).
V. Srikar, and S.M. Spearing, Exp. Mech. 43, 238. (2003).
N. Jaya, B.V. Jayaram, and S.K. Biswas, Philos. Mag. 92, 3326. (2012).
S. Liu, J. Wheeler, P. Howie, X. Zeng, J. Michler, and W. Clegg, Appl. Phys. Lett. 102, 171907. (2013).
J.P. Best, J. Zechner, I. Shorubalko, J.V. Oboňa, J. Wehrs, M. Morstein, and J. Michler, Scr. Mater. 112, 71. (2016).
G. Sernicola, T. Giovannini, P. Patel, J.R. Kermode, D.S. Balint, T.B. Britton, and F. Giuliani, Nat. Commun. 8, 1. (2017).
J. Obreimoff, Proc. R. Soc. Lond. Ser. A 127, 290. (1930).
B. Lawn, and T. Wilshaw, Fracture of Brittle Solids, 2nd edn. (Cambridge University Press, Cambridge, 1993), p 37.
R. Heilscher., MTEX Toolbox, (2021), https://mtex-toolbox.github.io/. Accessed 13 Dec 2020.
M.R. Elizalde, I. Ocaña, J. Alkorta, and J.M. Sánchez-Moreno, Int. J. Refract. Met. Hard Mater. 72, 39. (2018).
C. Wang, J.N. Reddy, and K. Lee, Shear Deformable Beams and Plates: Relationships with Classical Solutions, 1st edn. (Elsevier, Amsterdam, 2000), p 11.
E. Esmailzadeh, D. Younesian, and H. Askari, Analytical Methods in Nonlinear Oscillations: Approaches and Applications, 1st edn. (Springer, Dordrecht, 2018), p 272.
J.G. Williams, Compos. Sci. Technol. 35, 367. (1989).
N. Aldegaither, G. Sernicola, A. Mesgarnejad, A. Karma, D. Balint, J. Wang, E. Saiz, S.J. Shefelbine, A.E. Porter, and F. Giuliani, Acta Biomater. 121, 475. (2021).
H. Landolt, A. Hellwege, M. Choy, K. Hellwege, and R. Boernstein, Elastische, Piezoelektrische, Pyroelektrische, Piezooptische, Elektrooptische Konstanten Und Nichtlineare Dielektrische Suszeptibilitaeten (Springer, Berlin, 1979).
R. Hearmon, Acta Crystallogr. 10, 121. (1957).
Acknowledgements
The authors would like to thank Seco Tools AB and MAPP (EPSRC EP/ N509486/1) for funding this project. We also would like to thank Gary Sweetman from Sandvik Hard Materials (Coventry, UK) and Helen Jones from NPL for the supply of WC single crystals used in this study. We would also like to thank Ida Borgh from Sandvik Mining (Stockholm, Sweden) for discussions regarding polishing of WC-Co. Finally, we gratefully acknowledge Prof. Luc Vandeperre’s (Imperial College London) help with calculating WC elastic moduli as well as fruitful discussions.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Emmanuel, M., Gavalda-Diaz, O., Sernicola, G. et al. Fracture Energy Measurement of Prismatic Plane and Σ2 Boundary in Cemented Carbide. JOM 73, 1589–1596 (2021). https://doi.org/10.1007/s11837-021-04638-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11837-021-04638-6