Introduction

Hydrogen embrittlement (HE) has been an ongoing interest and concern of the materials science community and industries over the past several decades. The oil and gas industries, which have to deal with harsh environments such as sour gas and seawater, suffer substantially from component failures due to HE.1,2 Additionally, current developments in alternative energy sources and energy storage are promoting more intensive research into HE. Therefore, while industry is interested in developing more resistant materials and alloys for application, the science community has a particular focus on revealing the underlying deformation and failure mechanisms.

In the last years different atomistic models for HE have been proposed.3 The most commonly known are the hydrogen-enhanced decohesion (HEDE),4,5 hydrogen-enhanced localized plasticity (HELP)6,7,8,–9 and adsorption-induced dislocation-emission (AIDE)3,10,11 models. In the HEDE model a weakening of the cohesive bonds between atoms was the mechanism used to explain the microscopically cleavage-like fracture surfaces in environments with high local hydrogen concentrations. It was first proposed by Oriani4 and later also mentioned by Troiano.5 The HELP mechanism proposes an enhanced localized plasticity and has been supported by TEM investigations.6 Solute hydrogen shields the elastic stress field of dislocations, alters interactions and facilitates planar slip.7 Due to the local higher relaxation, dislocations can cluster and therefore can lead to higher hardening. Enhanced local plasticity contrasts with the macroscopic brittle behaviour reported in body-centred cubic iron.8 The simulation work of Song and Curtin9 even suggests reduced dislocation mobility by hydrogen acting as Cottrell atmospheres. A mechanism that somehow combines elements of both, HEDE and HELP, is the AIDE mechanism proposed by Lynch.3,10,11 He explains the adsorbed hydrogen responsible for the hydrogen-assisted cracking. His model describes the adsorption of hydrogen at the crack tip, which reduces the dislocation formation energy resulting in an easier dislocation emission. Characteristic for the AIDE mechanism is the occurrence of micro-voids on cleavage-like or intergranular fracture surfaces ahead of the crack tip.

It seems that none of the above-mentioned mechanisms is able to provide a complete picture of HE at a macroscopic as well as microscopic scale. Despite some contradictions, overlaps are possible.11,12 Therefore, it is important to find new promising techniques, both experimentally and simulated, to investigate and understand the acting mechanisms in further detail. A promising experimental approach, which was first proposed by Barnoush and Vehoff13 in 2006, is electrochemical nanoindentation (ECNI). Since nanoindentation is a very localized testing method with a high depth resolution, material response can be tested directly in small volumes, where the hydrogen mechanisms take place. First experiments were dedicated to the analysis of pop-in loads.14,15,16,–17 This sudden displacement burst in the recorded load–displacement curve can be correlated to a homogeneous dislocation nucleation (HDN). However, this only applies for coarse-grained materials with a low intrinsic dislocation density. The volume below the indenter tip must be quasi-dislocation free to nucleate the first dislocation at the transition from elastic to elastic–plastic deformation behaviour.18 Barnoush et al.17 proposed a decrease of pop-in load with hydrogen by decreasing the necessary activation energy for HDN according to the classical dislocation theory. They suggested a combined HEDE and HELP mechanism by weakening of the interatomic bonds, which they either explain by a reduction of the shear modulus or the stacking fault energy.

Later investigations also focused on the hardness evolution during the ECNI.19,20,21,22,–23 The measured hardness increase supports their hypotheses of a decreasing dislocation mobility due to hydrogen. Further explanations are an increase in lattice friction20,21 as well as a classical solid solution strengthening contribution by hydrogen.16,22,23 Overall, a variety of ECNI experiments have been performed, first on fundamental materials such as iron or technically clean nickel,15,24 while more recent investigations have tried to meet the demands of industry by testing technically relevant engineering alloys.19,20,25

For reliable ECNI experiments the hydrogen diffusion behaviour has to be taken into account. After charging the sample ex situ with hydrogen in an electrolyte by applying a cathodic potential to the specimen, the problem of prompt outgassing during sample transfer from the charging environment to the nanoindenter has to be considered. Samples must be cooled with liquid nitrogen to prevent outgassing, and testing must be performed as soon as possible. All of these uncertainties can be avoided by using an in situ charging setup.

Most of the previous ECNI studies were performed using simple load-controlled indentation. Therefore, only mechanical properties of the specific selected indentation depth can be obtained. The G200 nanoindenter, which is used in this work, has an advanced dynamic testing method called continuous stiffness measurement (CSM),26,27 where a sinusoidal load signal is superimposed during loading. This method allows a continuous measurement of Young’s modulus and hardness over the whole indentation depth and can give further information on possible external influences, such as frame stiffness or depth-dependent properties. The newly developed in situ ECNI setup in combination with the CSM technique is used to investigate the nanomechanical response of a technically relevant nickel-based alloy under the influence of hydrogen.

Experimental

Material, Preparation and Microstructural Investigations

A trial melt of nickel-based alloy 725 was melted using a vacuum induction furnace and forged to a 130 mm bar. After forging and before the investigation, the alloy was heat treated in two conditions. For the solution-annealed (SA) condition, the material was held at 1040°C for 2 h and subsequently water quenched. For the second condition, aging was done at 740°C and 620°C for 8 h each after solution annealing. This aging cycle is in accordance with a standard of the American Petroleum Institute (API); therefore, it will be referred to the abbreviation API for the aged sample. Cylindrical samples with 12 mm diameter were produced via wire erosion. Before testing, all samples were cold embedded with Struers Durocit and cut into dimensions of 18 mm3 × 18 mm3 × 3 mm3 to fit into the electrochemical cell. The embedded samples were ground by using 320 and 800 grid SiC paper followed by polishing with 9 µm, 3 µm and 1 µm diamond paste, respectively. Struers OP-S solution was used as a last mechanic-chemical polishing step. To remove the remaining deformation layer, electropolishing with a methanolic H2SO4 solution was carried out in the Struers Lectropol applying 22 V for 40 s.19 The microstructure was analysed using a laser confocal microscope LEXT OLS4100 (Olympus, Tokyo, Japan) for topography images, which were post-processed with Gwyddion software. Scanning electron microscope (SEM) images and electron backscatter diffraction (EBSD) were carried out on a FEI 3D DualBeam workstation (Thermo Fisher Scientific, Waltham, MA, USA) with an EDAX Hikari XP EBSD camera (EDAX Inc., Mahwah, NJ, USA). In addition to grain orientation, also misorientation maps were created with TLS OIM Analysis 7 software (EDAX Inc.).

Electrochemical Setup and Calibration

An in situ electrochemical nanoindentation setup was implemented in a nanoindentation G200 platform (KLA, Milpitas, CA, USA). This indentation system is known for an overall high frame stiffness as well as for a well-developed dynamic measurement technique known as CSM. The high frame stiffness originates from a rigid frame with a movable table, which is fixed in z-height and leads to a consistent stability to measured mechanical properties. The electrochemical charging cell was designed to benefit from those unique features. A lifting table, consisting of a mini lab jack (Thorlabs Inc., Newton, NJ, USA) and a self-built control unit, was installed to mount the cell and allow precise indentation experiments in a liquid environment.28 Therefore, an additional fluid tip with an elongated stainless steel shaft was utilized to overcome the resultant difference in height. The electrochemical cell itself was designed in a sandwich-like manner as shown in Fig. 1a with an aluminium base plate to provide further stiffness and a top cover made out of Teflon (PTFE), which accommodates the electrolyte compartment as well as all necessary electrodes and also provides good chemical resistance.

Fig. 1
figure 1

Electrochemical nanoindentation setup for the G200 platform: (a) schematic drawing and (b) appropriate front view

Full size image

Electrochemical Measurements

All electrochemical measurements were conducted with a Gamry 1010B potentiostat in a glycerine-based electrolyte with phosphoric acid in a mixing ratio of 2:1.19 To promote the absorption of hydrogen, 1 g/L CH4N2S (Thiourea) was added as recombination poison. All reported potentials were measured against an Ag/AgCl reference electrode from ALS Japan with a platinum wire as counter electrode. Beforehand, an example polarization curve was recorded for the material in SA condition to allow for an appropriate choice of charging conditions. The polarization curve was recorded from − 1700 mV up to 1500 mV with a scanning rate of 3 mV/s.

Nanoindentation Parameters

All nanoindentation experiments were performed on a KLA G200 nanoindenter utilizing the mentioned electrochemical cell described above and a CSM technique superimposing a harmonic displacement of 2 nm with a frequency of 45 Hz to continuously measure the contact stiffness and thus hardness and Young’s modulus over indentation depth. A conical diamond tip with a specified radius of 2 µm and an elongated steel shaft with an additional protective epoxy coating (Synthon-MDP, Nidau, Switzerland) was used. Since the lifting table lowers the overall stiffness of the system, it is not suitable for a reliable tip calibration. To overcome this issue, tip shape calibrations were conducted with a standard fused silica calibration sample within a rigid brass holder. This allows performing reliable Young’s modulus and hardness measurements with a minimum of stiffness correction up to 1000 nm indentation depth.

All nanoindentation experiments were evaluated according to the Oliver and Pharr method29 using a Poisson ratio of 0.31 for nickel to convert the reduced modulus from the indentation experiment to a comparable Young’s modulus. Indentations were performed in a constant strain-rate mode (0.005 s−1) up to a maximum indentation depth of 150 nm. All hardness and Young’s moduli were averaged between 100 nm and 130 nm. For reliable nanomechanical data the lack of self-similarity of spherical tips has to be taken into account when performing a strain rate controlled experiment.30 Therefore, a simplified strain rate definition published by Feldner et al.31 was used for controlling the loading segment. The unloading rate was set to 50 nm/s.

In Situ ECNI

All ECNI experiments consist of four main parts. To describe the initial, pre-charging state of the materials, indentations were performed in air. For detecting any possible influences due to the electrolyte, the next set of indentations was made during the measurement of the open circuit potential (OCP) to represent an uncharged state in electrolyte contact. The charging part itself is divided into pre-charging and in situ charging. Pre-charging was conducted for 2.5 h at a relatively high cathodic current density of − 500 µA/cm2 on a total exposed area of 1.33 cm2. During the actual in situ nanoindentation tests the current density was lowered to − 10 µA/cm2 to reduce hydrogen bubble formation for fewer disturbances during indentation. The last part consists of an outgassing step, which was obtained by outgassing in air for 18 h for the SA sample. The hydrogen of the API specimen was withdrawn by applying an anodic potential of 0 mV for 3 h. A minimum of 12 indentations for each condition was performed to obtain reliable mean values with standard deviation error bars.

Results

Microstructure

Grain boundaries react preferentially during electropolishing, and thus the microstructure is visible in the light-optical microscope as well as in the SEM. Figure 2 sums up the initial microstructure, exemplarily shown for the SA sample in Fig. 2a, and correspondingly the orientations of the indented grains on both samples are shown in (b). Average grain size was 140 µm with no texture present. The orientations of the grains are marked with dots in the inverse pole figure (IPF) triangle in Fig. 2b. For the SA sample the orientation chosen for indentation had a (0 6 1) orientation, corresponding to a near (0 0 1) orientation. In comparison, the grain on the API sample was more in the (1 1 1) direction with Miller indices of (18 11 13). The unit cells are shown as inserts in Fig. 2b.

Fig. 2
figure 2

(a) Microstructure and grain size of an SA condition: SE image (top) and EBSD (bottom); (b) IPF map of indented grain for the SA (top) and API sample (bottom)

Full size image

Electrochemical Measurements

Figure 3a represents the polarization curve obtained. Starting in the cathodic regime, where hydrogen is produced on the sample surface, the current density decreases from a potential of − 1700 mV until the OCP is reached at a potential of − 310 mV. The anodic part reaches from the OCP till 1500 mV and includes an anodic nose followed from a passive region before the breakdown potential is reached at around 1000 mV. By taking the polarization curve characteristics into account, a cathodic charging current of − 500 µA/cm2 was chosen to ensure hydrogen absorption. For anodic discharging and promoting hydrogen outgassing, a potential in the beginning of the passive region of 0 mV was selected. All chosen states are marked with dashed lines in Fig. 3a. Figure 3b shows the electrochemical data received for the chosen potentials, which were applied according the procedure described in Sect. 2.5

Fig. 3
figure 3

(a) Representative polarization curve with applied current density and potentials for the SA sample; (b) resulting data from the potentiostat for charging and discharging of the API sample

Full size image

Surface Steps After Hydrogen Charging

Before and after in situ ECNI the sample surfaces were examined with a laser confocal microscope to exclude surface irregularities as well as corrosion effects. A reference position of the SA sample is depicted in Fig. 4. Before testing the root-mean-square roughness, Rq, averaged for three horizontal 15 µm line profiles for each grain in the examined section was 0.71 ± 0.05 nm. After charging, surface steps are present on the entire sample surface, which leads to an increase of Rq to 1.12 ± 0.3 nm in the selected region.

Fig. 4
figure 4

Representative laser confocal microscope height images of the SA sample (a) before and (b) after the hydrogen charging experiment

Full size image

When characterizing the slip steps with different techniques, e.g., compare Fig. 4a and b, it is obvious that the intensity and occurrence of slip steps vary between different grains depending on their orientation. The activated slip system corresponds to those with the maximum Schmid factor (see insert in Fig. 5a).32 Additionally, in the vicinity of some grain boundaries it can be observed that the slip lines disappear as soon as they approach the grain boundary. For example, such an area is marked in Fig. 5a with a red dashed circle. The green area in the orientation deviation map in Fig. 5c indicates an increasing misorientation of the fading slip lines. Moreover, the yellow dotted misorientation line profile verifies an increase of point-to-origin misorientation of around 0.4°.

Fig. 5
figure 5

Characterization of slip line formation on an SA sample with different techniques: (a) laser confocal microscope intensity image with marked area of interest; (b) IPF image with overlaid image quality (IQ); (c) orientation deviation map with overlaid IQ and yellow dotted line for the misorientation profile shown in (d)

Full size image

Nanomechanical Properties During ECNI

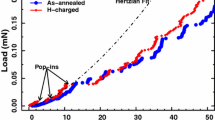
In addition to standard mechanical properties such as Young’s modulus and hardness, also the so-called pop-in load can be measured for the SA sample. This sudden displacement burst marks the transition from fully elastic to elastic–plastic deformation behaviour and is an indicator for a HDN in coarse-grained materials with low dislocation density.17,33

Figure 6 sums up the in situ ECNI results for the SA sample, (a) including exemplary load–displacement curves Young’s modulus and hardness (b). Large data points represent the average value for each condition, and small grey points symbolize a single indentation experiment. The pop-in load stays constant for indentations in air as well as with electrolyte at around 1.05 mN ± 0.05 mN. After charging, the mean value is slightly lower around 0.99 mN, but the standard deviation increases dramatically to 0.23 mN. This can be described by the results of single indentations, which include a few lower values but also pop-in loads near the mean value for air and even above. During outgassing, no recovery of the pop-in load is visible; only a slight decrease in the standard deviation takes place. As verification for the initial pop-in, the Hertzian fit for a tip radius of 1.5 µm is included in the load–displacement curve in Fig. 6b. More significant changes can be noticed in the hardness data. The first minor increase in hardness is visible from the air to electrolyte from 5.26 ± 0.11 GPa to 5.44 ± 0.12 GPa, which still lies within the uncertainty of the measurements and the corresponding error bars. Hydrogen charging leads to an obvious increase to 6.28 GPa ± 0.13 GPa, which corresponds to an increase of 15% compared with the hardness in the electrolyte. CSM data in Fig. 6b confirm the hardness increase over the entire indentation depth. The observed continuous decrease in hardness with increasing indentation depth for all conditions originates from the so-called indentation size effect, which is usually explained by the Nix–Gao model,34 but will not be discussed in further detail here (for details, see35,36). The Young’s modulus shows a slight increase there as well, but still in a negligibly regime. Especially when taking a closer look at the Young’s modulus in Fig. 6b, an overlap is clearly visible for all conditions.

Fig. 6
figure 6

(a) Averaged nanomechanical properties for SA sample during in situ ECNI including Young’s modulus, hardness and pop-in load; (b) examplary load-displacement curves as well as hardness and Young’s modulus over indentation depth for all four steps of ECNI (see text)

Full size image

The results for the API sample are presented in Fig. 7 in the same manner. The pop-in load was not evaluated because of the influence of precipitates, which can act as favourable sites for the dislocation nucleation by lowering the necessary activation energy. Therefore, these nucleation events are no longer representative for a homogeneous dislocation nucleation. In air, a hardness of 8.03 GPa ± 0.11 GPa is reached. The hardness reference value for the uncharged sample in the electrolyte is 7.88 GPa ± 0.16 GPa. After cathodic charging the hardness increases about 5.5% to 8.31 GPa ± 0.26 GPa. Outgassing by anodic discharging for 2 h leads to a decrease down to 8.01 GPa ± 0.44 GPa. At the same time the Young’s modulus stays more or less constant over the whole experiment with just a slight decrease within the standard deviation for the charging section. Exemplary nanoindentation data shown in Fig. 7b confirm the hardness increase, particularly also visible in the higher maximum load in the load–displacement curve. A perfect overlap of Young’s modulus curves is received over the total indentation depth for all four conditions. Pop-in events are still present for some indents, confirming a sufficient sample preparation exhibiting a low surface roughness and a low dislocation density.

Fig. 7
figure 7

(a) Averaged nanomechanical properties of the API sample during in situ ECNI including Young’s modulus and hardness; (b) examplary load–displacement curves as well as hardness and Young’s modulus over indentation depth for all four steps of ECNI (see text)

Full size image

Discussion

Surface preparation plays an important role in obtaining reliable nanoindentation data, especially when using the pop-in load as an evaluation criterion. Therefore, we first want to consider possible surface effects during ECNI experiments. Regarding our testing procedure surface changes can occur in different segments of the experiments. First, a deformation layer can remain from the mechanical preparation. By using OP-S polishing as the last mechanical-chemical preparation step, a mild ablation is achieved. A final electropolishing procedure removes the surface layer, which may contain dislocations. A good indicator of an adequate surface preparation is the occurrence of the initial pop-in.33 For indentations in a coarse-grained material with overall low dislocation density, the pop-in corresponds to the first dislocation nucleation and can also be associated with the theoretical strength of a material.18,37 Assuming a quasi-dislocation free volume under the indenter tip, the initial pop-in load can be directly correlated to the maximum shear stress \( \tau_{\hbox{max} } \) necessary for homogenous dislocation nucleation:

$$ \tau_{\hbox{max} } = 0.31\left( {\frac{{6E_{\text{r}}^{2} }}{{\pi^{3} R^{2} }}P_{\text{Pop-in}} } \right)^{1/3} $$
(1)

where \( P_{\text{Pop-in}} \) is the pop-in load, \( E_{\text{r}} \) the reduced modulus and \( R \) the tip radius of the indenter tip, as proposed in Eq. 1. Since the SA and API samples show an initial pop-in behaviour, a sufficient surface preparation can be assumed. When calculating the theoretical strength according to Eq. 1 for the SA sample, a maximum shear stress \( \tau_{\hbox{max} } \) of approximately 5 GPa is obtained. This value lies a bit below the literature value for nickel with 8 GPa.38 For the API sample, calculations including pop-in loads are not reasonable, since precipitations promote heterogeneous dislocation nucleation and therefore lower the pop-in loads. Generally, the pop-in load is influenced by the indentation spacing itself, which was set to a sufficient distance in this work.39 Additionally, the dynamic CSM testing method might affect the resultant pop-in load as well, but this behaviour is not completely clarified at the moment. Since only consistent CSM methods were used, the pop-in data are comparable.

The electrochemical charging procedure might lead to a surface modification. For these experiments corrosion should not appear during normal contact of the electrolyte and the sample surface for both the cathodic or anodic potential. One possible method to exclude surface changes during the charging procedure is to ensure a stable charging current or potential. Figure 3b shows a smooth development of each part of the electrochemical measurement, which again ensures a proper surface condition. Another indicator is the pattern quality of the EBSD after testing, which also indicates the presence of a good quality surface (Fig. 2b).

Slip steps only occurred on the electropolished surface of the SA sample after hydrogen charging; this might influence the measured mechanical properties. The sample surface is a fundamental requirement for the pop-in analysis as mentioned above. All possible irregularities, which differ from the perfect crystal lattice, can lead to a reduction in pop-in load by lowering the activation energy for dislocation nucleation. Such irregularities for example can be pre-existing dislocations, precipitations as well as enhanced surface roughness by slip steps. The slip steps can act as sites with higher stress concentration and therefore are facilitating the dislocation emission.18 Immediately after applying a current density of − 500 µA/cm2, the standard deviation of the pop-in load increases and does not drop anymore as shown in Fig. 6a. The occuring slip steps are a possible explanation for the high scatter in pop-in data. When the indenter tip hits near a surface step, it is a more favourable site for dislocation nucleation than the defect-free crystal underneath.40 Since the steps are not reversible, as seen by the laser confocal microscope image in Fig. 4b, and the surface roughness is increased, also after outgassing no recovery of the pop-in load scattering is observed.

By analysing the orientation deviation map in Fig. 5c, it is obvious that an irreversible plastic deformation takes place, which is depicted by the green area with higher misorientation near the grain boundary. In these areas, however, the dislocations have less possibility to exit the material, because the grain boundary inhibits the free motion of dislocations. When comparing the calculated slip systems with maximum Schmid factors for loading in the z-direction from the EBSD data,32 a correlation can be seen with the slip lines visible in the laser confocal microscope image. All these findings lead to the assumption that the present residual stresses are sufficient to induce irreversible slip traces. When looking for possible explanations for this induced deformation, different explanations can be found in the literature. First, Barnoush and Zamanzade41 reported such hydrogen-induced surface steps in an austenite phase of a super duplex steel. They interpreted the residual stresses from quench annealing responsible for the occurrence of slip steps, since the hydrogen lowers the required stress to activate these pre-existing dislocations. Similar observations were made by Wang et al.21 during ECNI of a high entropy alloy. For higher cathodic potentials, they detected irreversible slip steps originating from the hydrogen-induced internal stresses as well as the promotion of dislocation nucleation by lowering the dislocation formation energy. Consequently, the corresponding pop-in loads and also their Young’s modulus, calculated from the Hertzian fit, are permanently lowered by the higher surface roughness.

After discussing the influence of surface steps on the pop-in load, we interpret the changes in hardness for both heat treatment conditions. The SA sample shows an obvious increase of 15% from the reference hardness caused by the cathodic hydrogen charging. By measuring the outgassed condition, it is evident that the hardness is fully recovered compared with the pop-in load. Therefore, the hardness is not influenced by the higher surface roughness caused by the surface steps and the generated dislocations. This observation can be explained by the fact that the plastic deformation induced by hydrogen charging is very small compared with the indentation-induced plastic deformation. Furthermore, the hardness is determined from the CSM signal between 100 nm and 130 nm and hence is obtained at a greater depth of the material. By modelling the elastoplastic part of load–displacement curves with the Tabor relation based on the Nix-Gao model and taking into account the underlying lattice friction, Wang et al.21 proposed an increase in lattice friction by the dissolved hydrogen. This increase can be linked with hydrogen acting as a Cottrell atmosphere9 and retarding the dislocation motion, which leads to an measureable increased hardness in ECNI experiments.

As the Young’s modulus calculated also shows a slight increase, possible influences that might originate from artificial phenomena such as a pile-up formation42 should be taken into account. Therefore, a pile-up correction according to Joslin and Oliver43 can be used to reduce the dominant influence of surface roughness or pile up-formation. By applying their correction model and assuming a constant Young’s modulus from the literature, a corrected hardness of 5.79 GPa ± 0.06 GPa can be calculated for the charged SA specimen. This correction reduces the overall hardness increase compared with the electrolyte to 6.0%, but still lies above the electrolyte reference value and hence can be directly contributed to the dissolved hydrogen in the sample.

Compared with the SA sample, the API specimen shows no hydrogen-induced surface steps and no changes in Young’s modulus. Therefore, no corrections of Young’s modulus or hardness are necessary. The influence of the dissolved hydrogen on the hardness increase amounts to 5.5%. Figure 8 summarizes the Young’s modulus and hardness data for both heat treatments. The SA sample shows a more pronounced hardness increase when the uncorrected data are used. The effect of hydrogen as a Cottrell atmosphere seems to be less pronounced in the API sample, since precipitations can act as favourable sites for higher hydrogen concentrations. Therefore, less hydrogen can accumulate at the mobile dislocation to inhibit their motion. When comparing the absolute hardness increase of the corrected SA sample with the API sample, it is almost equal with approximately 0.5 GPa. By comparing the Young’s moduli for both samples, a difference of around 30 GPa is recorded. This can be attributed to the different indented orientations. Nickel shows a higher Young’s modulus in the (1 1 1) direction than in the (1 0 0) direction, which corresponds quantitatively to the orientations of the indented grains.44

Fig. 8
figure 8

Comparison of SA and API data regarding Young’s modulus and hardness (see text)

Full size image

Summary

The main findings and the outcome of the presented work can be summarized as follows.

  • An electrochemical hydrogen charging setup for a nanoindentation platform was designed and established.

  • Electrochemical measurements were performed to ensure appropriate surface integrity without corrosion.

  • The nickel-based alloy 725 was tested in two different heat treatments, and changes in nanomechanical properties were investigated. The solution-annealed sample showed a somewhat larger hardness increase around 15%, which can be contributed to the effect of hydrogen acting as Cottrell atmosphere. For the precipitation-hardened sample, more hydrogen can be stored at the precipitations and therefore inhibition of dislocation as well as the hardness increase is less pronounced with a hardness increase of 5%.

  • No reliable analysis of pop-in loads was possible on solution-annealed sample due to the hydrogen-induced surface steps. These steps led to an irreversible plastic deformation as revealed by EBSD misorientation maps. Therefore, the reduced pop-in load is more likely a consequence of the generated dislocations and surface steps than of the dissolved hydrogen.