Introduction

Quantitative local viscoelastic measurements in heterogeneous materials at the sub-100 nm scale are of great interest for next generation materials research and development. Such measurements allow determination of structure–property relationships of microphases where confinement effects alter structure, intermolecular interactions, and mechanical properties. Similarly, the symmetry break at interfaces leads to local structural changes and formation of interphases with different properties.1,2,–3 From a practical standpoint, both microphases and interphases determine bulk properties in nanostructured materials. As these structures and their properties only exist locally, a direct local measurement is needed to probe them.

Atomic force microscopy can provide nanomechanical measurements at high spatial resolution. Nanomechanical measurements are probably the most common AFM application aside from topography. Multiple non-resonant and resonant AFM-based methods exist for determining contact stiffness in the tip-sample junction.4,5,6,–7 These methods, together with the use of suitable tips, calibration, and contact mechanics models such as Derjaguin–Muller–Toporov (DMT) or Johnson–Kendall–Roberts (JKR)8 permit extraction of sample moduli. While instrumented nanoindenters provide advantages for quantifying moduli, hardness, and other properties with high accuracy, the combination of tip radii down to 1 nm and force detection levels in the low piconewton range give AFM the unique capability of mapping topography and stiffness with sub-nanometer spatial resolution.9

Common AFM Approaches to Nanomechanics

Most AFM nanomechanics approaches to date have been focused on imaging with important implications for nanomechanical property measurements. Nondestructive AFM imaging requires lifting the tip out of surface contact before lateral motion. Acquiring an AFM image at reasonable resolution and throughput, e.g., 250 k pixels in less than 10 min, limits the possible surface contact time per pixel to a millisecond or less. This can be sufficient when working within the approximation of purely elastic, frequency-independent properties. For example, PeakForce Quantitative Nanomechanical Mapping (PFQNM) mode provides Young’s modulus images at kHz pixel rates, while benefitting from the high information content of complete force-distance curves and directly measured load and adhesion for quantification.

Going beyond the elastic approximation necessitates consideration of frequency and temperature dependence. Here a sub-millisecond contact time is simply too short to measure mechanical properties at the frequencies employed in bulk dynamic mechanical analysis, 0.1-100 Hz. Moreover, while tip actuation during imaging may happen at a well-defined frequency, the establishment and breaking of tip-sample contact during each cycle makes the measurement nonlinear. This exposes the sample to higher harmonics of the actuation frequency,10 thus severely complicating frequency dependent modulus measurements.11 Since multiple frequencies are present, direct correlation to DMA measurements (which occur at a single frequency) is not possible. Further limitations come into play in resonant AFM modes, such as those based on contact resonance, tapping phase, multiple eigenmodes, or higher harmonics. In these kinds of measurements, actuation frequencies are limited to a sparse set of discrete eigenmodes that are typically all higher than 100 kHz, observables are limited, and load and adhesion are typically not measured directly.12 As a result, none of the imaging-centric AFM modes are suitable for quantifying moduli of viscoelastic materials at well-defined rheological frequencies, and a different approach is needed.

Dynamic Mechanical Analysis with AFM: Operating Principles

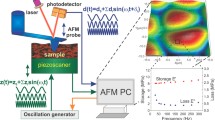
AFM-nDMA is an AFM based approach to dynamic mechanical analysis (DMA) suitable for quantitative measurements of polymer viscoelasticity at the nanoscale. To avoid tip contamination and sample damage during imaging and tip positioning, the rheological measurement is embedded in the contact portion of a force-distance curve, with any XY positioning done prior to bringing the tip into contact with the surface (Fig. 1 segment A). To enable a measurement within the range of linear material response, AFM-nDMA executes a force modulation while the AFM tip is in continuous contact (Fig. 1 segment B), using a modulation force much smaller than the average force (or preload)13,14 and with appropriate tip radius and force levels.15 A non-resonant measurement is chosen to allow continuous frequency coverage in the rheologically relevant 0.1 Hz to 100 Hz frequency range.

Fig. 1
figure 1

Deflection versus time plots of single frequency AFM-nDMA measurements. Two typical AFM-nDMA force curves from a force volume map. In segment A, the tip is brought into contact and a preload of about 15nN is applied. In segment B, the Z piezo is modulated and amplitude and phase of the response are recorded for later analysis. In segment C, the tip is retracted from the surface and the pull-off is observed. The red curve has smaller amplitude in segment B, indicating a softer area while the blue curve is from a stiffer area (Color figure online)

Full size image

By executing a sequence of segments at different frequencies, this approach can be used to acquire an entire frequency spectrum at a single location, within a single force curve. The total time needed is then dominated by the lowest frequency, typically a minute or more when including frequencies below 1 Hz. Alternatively, the measurement can be embedded into the force curve-based imaging mode known as fast force-volume (FFV) for imaging purposes. While the low frequency nature of the measurement precludes high imaging speed, imaging is realistic at moderately high but still rheologically relevant frequencies, e.g., a 64 × 64 pixel image will take about 20 min at a modulation frequency of 100 Hz.

As always with an indentation-based measurement, the conversion of measured contact stiffness into moduli depends on the contact radius. Here embedding the force modulation measurement into a force-distance curve has the added advantage of providing an adhesion measurement during pull-off (Fig. 1 segment C), which can be used to calculate the contact radius during the retract. However, the contact radius will not be constant during the preceding modulation segments. Executing what is effectively a force-step followed by a long force-hold leads to significant material creep in the tip sample junction, gradually changing contact radius for most tip geometries. This effect is a consequence of the very viscoelasticity of interest in the measurement and will be especially pronounced during the long hold time required for acquiring an entire frequency spectrum. Three strategies learned from the nanoindentation community were used to mitigate this effect and recover a quantitative modulus measurement. First, a relaxation segment is added at the start of the force-hold to eliminate most of the creep. Second, further changes in the contact radius are tracked through repeated measurements at the same reference frequency. These reference segments are described in more detail below. Third, randomizing the frequency order avoids any remaining artifacts in the frequency dependence.

Analysis of AFM-nDMA Data

AFM-nDMA operates through application of sinusoidal motion to a Z piezo and measurement of resulting low-amplitude oscillating motion of the tip in contact with the sample. Viscoelastic properties are determined through the resulting amplitude and phase shift of the cantilever oscillation. The Z piezo motion as a function of time is described by

$$ z\left( t \right) = Z_{1} \sin \left( {\omega t + \psi } \right) $$
(1)

Where Z1 is the amplitude of Z motion, ω is the measurement frequency, and ψ is its phase. Likewise, the cantilever deflection as a function of time is described by

$$ d\left( t \right) = D_{1} \sin \left( {\omega t + \varphi } \right) $$
(2)

Where D1 is the cantilever deflection amplitude, and φ is the deflection phase. The amplitude ratio (D1/Z1) and phase shift (φ − ψ) are extracted to yield the complex “dynamic stiffness”, S*13,16:

$$ S^{*} = S^{\prime } + iS^{\prime \prime } = \frac{\hbox{force}}{\hbox{deformation}} = \frac{{K_{{\rm c}} D_{1} e^{i\varphi } }}{{\left( {Z_{1} e^{i\psi } - D_{1} e^{i\varphi } } \right)}} $$
(3)

Where Kc is the cantilever spring constant. The real and imaginary parts of S* can then be separated into storage stiffness (S′) and loss stiffness (S″) respectively, while the loss tangent (also known as tan δ) is simply the ratio of the two:

$$ S^{\prime } = \frac{{K_{\text{c}} D_{1} }}{{Z_{1} }} \frac{{\cos \left( {\varphi - \psi } \right) - D_{1} /Z_{1} }}{{\left( {\cos \left( {\varphi - \psi } \right) - D_{1} /Z_{1} } \right)^{2} + \left( {\sin \left( {\varphi - \psi } \right)} \right)^{2} }} $$
(4)
$$ S^{\prime \prime } = \frac{{K_{\text{c}} D_{1} }}{{Z_{1} }} \frac{{\sin \left( {\varphi - \psi } \right)}}{{\left( {\cos \left( {\varphi - \psi } \right) - D_{1} /Z_{1} } \right)^{2} + \left( {\sin \left( {\varphi - \psi } \right)} \right)^{2} }} $$
(5)
$$ \tan \delta = S^{\prime \prime } /S^{\prime } = \frac{{\sin \left( {\varphi - \psi } \right)}}{{\cos \left( {\varphi - \psi } \right) - (D_{1} /Z_{1} )}} $$
(6)

The derivative of the force (F) with deformation (δ) of the appropriate contact mechanics model establishes the relationship between the storage and loss moduli and the dynamic stiffness. For a “flat punch” contact or Hertzian (DMT) mechanics the same relationship is obtained:

$$ S^{*} = \frac{\partial F}{\partial \delta } = 2a_{\text{c}} E^{*} $$
(7)

where ac is the contact radius and E* is the (complex) reduced modulus. For JKR, the stiffness would be slightly lower than that of the punch. However, the viscoelastic effect resists peeling of the contacting surfaces in the adhesion ‘crack tip’ zone surrounding the contact and contact size remains essentially constant at its average value during modulation. Consequently, the dynamic stiffness for JKR also follows that of a flat punch for all but the lowest frequencies.17 The real and imaginary parts of the complex modulus therefore give us the reduced storage modulus (E′) and reduced loss modulus (E″) respectively:

$$ E^{\prime } = \frac{{S^{\prime } }}{{2a_{\text{c}} }};\quad {\text{and}}\quad E^{\prime \prime } = \frac{{S^{\prime \prime } }}{{2a_{\text{c}} }} $$
(8)

The contact radius at the end of the measurement is determined from the final step in each FFV ramp or ramp script (Fig. 1, segment C) where the tip is pulled away from the sample. This segment is fit with an adhesive contact mechanics model such as DMT or JKR to obtain the contact radius at the beginning of the retract. For ramp scripts, the surface hold duration may be several minutes to allow for low frequency measurements. In this case, the contact radius can increase significantly during the measurement as the sample relaxes and the tip sinks into the surface. To compensate for these changes in contact radius, multiple “reference segments” with the same frequency (fref, typically around 100 Hz to minimize the required acquisition time) are collected among the other frequencies in the ramp script. The final reference segment is measured just before the retract segment. Using the storage stiffness from this reference segment, S′(fref), along with the contact radius from the retract fit, and Eq. 8 allows determination of the storage modulus at the reference frequency, E′(fref). By assuming that E′(fref) does not change during the ramp script and using the measured S′(fref) for each of the other reference segments, Eq. 8 allows calculation of the contact radii for the rest of them. One can then interpolate between the reference segments to estimate the contact radius at the non-reference segments and thus allow calculation of E′ and E″ for all the other frequencies.

Calibration and Probes

One of the challenges in quantitative AFM nanomechanical measurements has been the calibrations associated with the measurement: the tip shape, cantilever spring constant, and detector sensitivity. The tip geometry and size figures prominently into contact mechanics used to model the tip-sample interactions and so inaccuracies can significantly affect the results.

To maximize the accuracy of the measurements, pre-calibrated probes with rounded, well-defined tips were used.18 The tips were approximately parabolic with radii of curvature of either 30 nm or 125 nm as individually measured with SEM (Bruker, Inc.). This provides a controlled contact area for various indentations up to 100 or 500 nm respectively (for deeper indentations, the tip shape is no longer well-defined). This consistent geometry is important especially for measurements on heterogeneous samples where a constant load will result in different indentations on the different components based on the sample’s material properties. Using this well-defined geometry, it is possible to calculate the contact radius for a wide range of indentation depth.19 Additionally, using probes with rounded tips further helps to improve accuracy by avoiding non-linear deformation mechanisms that are not included in the elastic models such as plastic deformation.15 The benefits of using tips with larger diameters involve a trade-off in resolution. The contact radius increases approximately as the cube root of the tip radius (using the DMT model with constant force), so we expect the resolution to decrease slightly for the larger radii. For example, initial measurements (not shown) with 125 nm tips had resolution of better than 50 nm, while 30 nm tips were better than 25 nm, approximately as the cube root relationship would predict.

The spring constant of these probes is individually pre-calibrated with a laser Doppler vibrometer (LDV) providing significantly improved accuracy over AFM-based thermal tuning. The probes are available in a wide range of spring constants from 0.25 N/m to 200 N/m, allowing measurement accuracy to be optimized over a range of sample storage modulus of about 100 kPa to 20 GPa. For the results reported here, probes with spring constants of 5 N/m and 40 N/m were sufficient to cover all of the samples. The photodiode deflection sensitivity was calibrated by conducting force curves on a stiff sapphire sample.

Finally, the phase and amplitude of the Z position must be calibrated. For bulk DMA, the phase and amplitude are independent of sample loading (for a given clamp set) and it is only necessary to recalibrate about once a month. In AFM-nDMA, the phase can depend on the probe and probe mounting. Therefore, it is necessary to calibrate when the probe is changed. If an external actuator is used, the amplitude and phase depend on sample mounting as well. In this case, it is best to calibrate whenever a new sample is mounted on the actuator. The calibration is done by running the same script (with the same probe) on a sapphire substrate as will be used for the sample measurements. For low frequencies (below 300 Hz) where the AFM scanner is used for modulation, the amplitude can be obtained from the Z sensor within the scanner and only the phase difference between the Z sensor and deflection must be calibrated. For high frequency measurements using an external actuator, the amplitude is calibrated along with the phase by running the same script (and the same probe) on a sapphire substrate mounted to the actuator. The sample is mounted on this sapphire substrate adjacent to the calibration location for convenience and to maximize the accuracy of the calibration.

Results and Discussion

Since AFM-nDMA was developed to allow accurate measurement of viscoelastic properties, it is important to validate its performance by comparison to the industry standard for such measurements: DMA. Polydimethylsiloxane (PDMS) was chosen for comparison due to its well-known stability and relative ease of preparation. The PDMS (NuSil R21-2615, 2-part elastomer) was mixed 3:1 part A to B, and cured 24 h at 50 °C before cutting into pieces for distribution and measurement. Figure 2 compares the storage modulus (E′) and loss modulus (E″) of PDMS as measured by three methods: (1) bulk tensile strain modulation DMA (green line—TA Instruments Q800) (2) an instrumented nanoindenter (light blue ‘×’ - Hysitron TI980) and (3) AFM-nDMA in Santa Barbara lab (dark blue ‘○’) and (4) AFM-nDMA in a collaborator’s lab (orange ‘∆’). The collaborator did their experiment with a different AFM system, different operator and different probe than that used in Santa Barbara. Both AFM systems were independently calibrated as described above (using RTESPA-150-125 probes with 125 nm radius tips). There is excellent agreement among all these methods for both E′ and E″. For example, the RMS deviation in E′ between the Santa Barbara result and the bulk DMA was about 5% for E′ and about 25% for E″. Both the DMA and indenter methods span a more limited frequency range with an upper limit at approximately 200 Hz. The AFM-nDMA method additionally allows access to higher frequencies up to 20,000 Hz by using a small piece of sample mounted on an external high frequency actuator.

Fig. 2
figure 2

Storage and loss modulus spectra for PDMS as measured by various instruments. The top plots are storage modulus (E′), while the bottom plots are loss modulus (E″). The green lines were measured with bulk DMA, light blue ‘×’ were from an instrumented nanoindenter, the dark blue ‘○’ used AFM-nDMA in the Santa Barbara lab, and the orange ‘∆’ were collected by AFM-nDMA in a collaborator’s lab (Color figure online)

Full size image

A second important capability of AFM-nDMA is to enable generation of master curves through time–temperature superposition (TTS).20 To demonstrate this capability, a series of measurements on fluorinated ethylene propylene (FEP) were acquired as a function of frequency and temperature. Figure 3 shows the resulting series of curves for storage modulus (blue) and loss tangent or tan δ (orange) at frequencies ranging from 0.1 Hz to 100 Hz sweeping through a temperature range of 25°C through 130°C. The storage modulus exhibits the expected softening with increased temperature21 while the loss tangent has a peak at around 90°C associated with the material’s glass transition temperature (Tg). Additionally, as expected the softening occurs at lower temperatures for measurements acquired at lower frequencies.

Fig. 3
figure 3

Storage modulus (left axis) and loss tangent (right axis) of FEP from AFM-nDMA at different frequencies as a function of temperature. The blue squares are storage modulus at 0.1 Hz, 1 Hz, 10 Hz, 100 Hz (darkest to lightest blue respectively), while the brown circles are the loss tangent at 0.1 Hz, 1 Hz, 10 Hz, 100 Hz (darkest to lightest brown) (Color figure online)

Full size image

The AFM-nDMA data from Fig. 3 was used to generate the master curve of loss tangent for FEP. For both bulk DMA and AFM-nDMA data, we followed the industry standard operating procedure for time temperature superposition (TA Instruments, Rheology Advantage Data Analysis). A reference temperature and associated reference spectrum was selected, and the other spectra (collected at other temperatures) were shifted using initial shift factors estimated from the Williams–Landel–Ferry (WLF) equation.20 The shifts of each spectrum (except for reference spectrum) were further adjusted manually to optimize the overlap. Finally, master curves were generated along with plots of log-shift factors (aT) versus 1/T. In Fig. 4, the resulting AFM-nDMA master curve (blue ‘○’) is compared with the master curve from bulk DMA (green ‘×’). The AFM-nDMA result compares favorably with the bulk master curve including the size and shape of the peak at the glass transition. The most important function of the master curve is to describe the behavior of the material across a wide range of time or temperature. In this case, the master curve covers a range of over twenty decades of frequency. Arrhenius analysis of the shift factors (shown in the inset) provides a value for the activation energy from the AFM-nDMA measurements (490 kJ/mol) that matches very well with the bulk measurement (489 kJ/mol).

Fig. 4
figure 4

Time-temperature superposition analysis of AFM-nDMA results compared to those from bulk DMA. Main plot shows Loss tangent of FEP versus frequency and inset shows TTS shift factor versus 1/T plot for Arrhenius activation energy analysis. Green ‘×’ show results from TTS of bulk DMA data and blue ‘○’ are from AFM-nDMA. Arrhenius fits give activation energies from bulk DMA and AFM-nDMA of 489 kJ/mol and 490 kJ/mol respectively (Color figure online)

Full size image

Finally, and perhaps most importantly, AFM-nDMA allows the measurement of the viscoelastic properties of nanometer sized domains within polymer blends, composites and other heterogeneous materials. One example of this is shown in Fig. 5. The sample is a blend of polypropylene (PP) and cyclic olefin copolymer (COC). The COC forms a domain of approximately 1 µm diameter in a matrix of PP (scale bar represents 500 nm). The AFM-nDMA storage modulus (E′) and loss tangent maps were collected at 100 Hz over a temperature range of 25–175°C. There is little difference in E′ between the two materials at room temperature, while the loss tangent of the COC is lower than that of the PP. As the temperature increases, the E′ of the two materials quickly diverge as the PP modulus decreases more quickly than the COC, corresponding to a softening of the PP as it approaches its melting point at 164°C, after which it is a featureless viscoelastic melt. The loss tangent of the two materials is similar until 170°C, at which point the loss tangent of the COC inverts and becomes higher than the loss tangent of the PP. E′ and tan δ values were calculated from their respective domains in the image and plotted as a function of temperature in the corresponding graphs below. Measuring these viscoelastic moduli as a function of temperature are useful for pinpointing thermal and structural transitions. This type of contrast inversion also illustrates the importance of knowing the frequency and temperature at which the measurement is done, otherwise even qualitative maps of modulus can be misleading.

Fig. 5
figure 5

Storage modulus and loss tangent of PP-COC blend as a function of temperature. Top row: maps of storage modulus at 100 Hz with increasing temperature (500 nm scale bar). Middle row: maps of loss tangent with increasing temperature. Bottom row: storage modulus and loss modulus plots at 10 Hz versus temperature. Blue circles were measured within the COC domain and red triangles were measured on the PP matrix (Color figure online)

Full size image

A final example highlighting the power of AFM-nDMA in examining microscopic structures within polymer blends is shown in Fig. 6 with a 1.5 µm × 1.5 µm 100 Hz AFM-nDMA image of an impact copolymer comprising of a thermoplastic matrix and a rubber domain with inclusions. As reported by Ueda et al.,22 such inclusions can have properties distinct from corresponding bulk phases. The height map is shown on the bottom left with single force curves collected on the matrix, rubber, and inclusions within the rubber domain (shown on the top) clearly revealing different behavior on the various components. The AFM-nDMA storage modulus map is shown on the bottom center revealing a stiff thermoplastic surrounding a softer rubber, where the inclusions are slightly stiffer than the rubber. Some of the rubbery domains and inclusions within them are < 100 nm in diameter. The corresponding loss tangent image on the bottom right shows an expectedly much higher loss tangent in the rubber domain than the thermoplastic. Interestingly, the loss tangent of the inclusions is similar to that of the thermoplastic. Additionally, a region within about 50 nm of the interface between the larger domains and the thermoplastic matrix has a storage modulus between that of the rubber and the matrix and a loss tangent that is even higher than the rubber. While, at first glance, this may suggest the presence of an interphase mediating load transfer from domain to matrix, the tip radius of 29 nm and variation in topography in this region are sufficient to cause an artifact of this scale (where the side of the tip is interacting with the edge of the matrix). Additional work is planned to investigate this further.

Fig. 6
figure 6

The 100 Hz storage modulus and loss tangent maps of impact copolymer. Top row: typical force curves extracted from force volume dataset: (1) blue is from the PP matrix, (2) light green is from an inclusion within a rubbery domain, (3) dark green is from the soft part of a rubbery domain. Bottom row, left to right: topographic image with 300 nm scale bar, storage modulus map with colored circles corresponding to the force curves above, loss tangent map (Color figure online)

Full size image

Conclusion

Here we introduced AFM-nDMA, a new AFM mode for performing AFM-based viscoelastic measurements on heterogeneous polymer materials. Unlike conventional, imaging focused AFM modes that expose the sample to ill-defined and high (> 1 kHz) frequencies, AFM-nDMA addresses the frequency and temperature dependence and works directly in the rheologically relevant frequency range. As seen in the test case of PDMS, resulting E′ and E″ values compare well with bulk DMA over the entire frequency range (root mean square deviations of 5% and 25% respectively). Using an external actuator, the frequency range of the measurements was extended over that of DMA, allowing direct measurement of viscoelastic properties from 0.1 Hz to 20,000 Hz. A full TTS analysis for measurements of FEP at a range of temperatures and frequencies yields the correct activation energy. To achieve this, AFM-nDMA combines force-curve embedded, small-amplitude, low load measurements in the linear regime with calibrated probes and algorithms for mitigating changes in contact radius. Results on a binary COC-PP blend show the abilty to generate AFM-nDMA images on heterogeneous samples, and the importance of frequency and temperature for even qualitative image contrast. An AFM-nDMA image of an impact copolymer demonstrates the capability of measuring heterogeneous samples with a features under 100 nm in diameter, demonstrating the ability of AFM-nDMA to provide viscoelastic information where it was not previously available.