1 Introduction

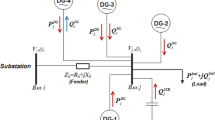
The nature of traditional distribution networks (TDNs) is radial configuration or alternatively named as open ring main units [1, 2]. Typically, such types of TDNs consist of distribution transformers, underground power cables and/or distribution overhead lines, switchgears including relays and so on [1]. Nowadays, the integration of renewable power sources including energy storage facilities plus electric vehicles and charging stations to the TDNs are in action in many countries [3,4,5,6,7,8]. The later mentioned make the topologies of the TDNs are very sophisticated and requires lot of control strategies and energy management frameworks [9, 10]. This previously mentioned justifies the need of such TDNs to be smarter which shall be called smart distribution networks (SDNs) [11,12,13]. Among the key challenges, to operate such SDNs in an optimum operation manner with high efficiency which achieve the resiliency for both customers and utilities as well [9, 14]. SDNs are intended to reduce the overall system losses and \({\mathrm{CO}}_{2}\) emissions plus achieving the operation’s resiliency along good protection integrity [15,16,17]. It may be mentioned that the average annual energy losses in European Union countries could reach up to 8% of total generated energy [18]. For example, in Poland 11.8%, Romania 13.5%, Turkey 19% and Sweden 2.3% [18]. However, in developing countries, the figure may reach up to 20% average [19] which varies from country to another. The two categories of network losses which are technical and non-technical [18]. Non-technical losses are due to thefts, unbilled accounts, and metering errors and this type requires regulations/laws to judge and smart meters [20,21,22]. On the other hand, the technical losses arises due to the resistances in transformer windings, conductors of transmission systems, contact resistances, etc. [23]. Using the calculations in Eqs. (1) and (2), the resistive and reactive power losses in branch i-j (as depicted in Fig. 1) are calculated:

Fig. 1
figure 1

Portion of a SDN of i-j nodes

Full size image
$${P}_{ij}^{loss}={R}_{ij}.\frac{{P}_{eff,j}^{2}+{Q}_{eff,j}^{2}}{{\left|{V}_{j}\right|}^{2}}$$
(1)
$${Q}_{ij}^{loss}={X}_{ij}.\frac{{P}_{eff,j}^{2}+{Q}_{eff,j}^{2}}{{\left|{V}_{j}\right|}^{2}}$$
(2)

Equations (3) and (4) determine the effective real and imaginary powers fed into receiving end-bus j, respectively.

$${P}_{eff,j}=\frac{\left|{V}_{i}\right|\left|{V}_{j}\right|}{\left|{Z}_{ij}\right|}cos\left({\theta }_{ij}-{\delta }_{i}+{\delta }_{j}\right)-\frac{{\left|{V}_{j}\right|}^{2}}{\left|{Z}_{ij}\right|}cos{\theta }_{ij}$$
(3)
$${Q}_{eff,j}=\frac{\left|{V}_{i}\right|\left|{V}_{j}\right|}{\left|{Z}_{ij}\right|}sin\left({\theta }_{ij}-{\delta }_{i}+{\delta }_{j}\right)-\frac{{\left|{V}_{j}\right|}^{2}}{\left|{Z}_{ij}\right|}sin{\theta }_{ij}$$
(4)

It may be useful stating that the technical losses comprise two types of losses namely fixed and variable. The constant/fixed type of losses or alternatively called type 2 losses includes hysteresis, and eddy losses in electric machines, stray losses, sheath losses, etc. and generally these kinds of losses are neglected in studying power networks. On the contrary, the other variable type of losses which depend on the square of absolute of current flow; should be treated carefully and to be minimized [24]. There are many strategies can be used for loss reductions along the SDNs which include but not limited to: (i) Selection and conductor sizing [25,26,27], (ii) Reactive power compensations (RPCs) [28, 29], (iii) Network reconfigurations (NRs) [23, 30,31,32], (iv) Distributed generations (DGs) allocations [19, 33, 34], (v) Higher voltage levels [35, 36], (vi) Solid-state transformers [37, 38], (vii) balancing current in phases [39,40,41,42,43], and (viii) Mixture of previous solutions. Among these hybrid simultaneous solutions are NRs with DGs [44,45,46], NRs with RPCs [47], DGs and RPCs [48, 49], DGs, RPCs and NRs [46], phase balancing and NR [50], phase balancing and DGs [51] and so on.

The concept of losses reductions as well as other goals using NRs along SDNs are covered in this review paper. Different traditional and contemporary methods (including heuristic-based and machine learning) used to achieve these goals are discussed. Various objective function (OF) formulations are announced. There are strategies for achieving system radiality. The LF for SDNs is also reviewed and condensed. For both classic and modern frameworks, the difficulties and potential insights are highlighted.

2 Common Formulation of NR Problem

The NR is typically formulated as optimization problem using single- and/or multiple-objective representations (SORs and/or MORs) subject to set of operating and design constraints. Once again, NR refers to the process of altering an SDNs’ topology by opening and closing switches in order to enhance the system’s performance. The goal of NR is to reduce total system power losses plus other many defined goals in case of many objectives representations, while keeping all loads powered within the system’s capacity and operating constraints.

2.1 Single-Objective Representation

The optimization issue of NR with a SOR is non-linear, non-convex, and combinatorial. Because the power losses (as a common objective in this case) are a non-linear function of the line currents, it is a non-linear problem. The OF is non-convex due to the binary nature (0–1) of the decision variables, hence the problem is non-convex. Because there are so many different switch configurations, it is a combinatorial challenge. It can be said that the adaption of the NR is mixed-integer 0–1 non-linear OF. The Power loss can be formulated in several possible forms as follows.

$$OF=\mathrm{Minimize}\left({\mathrm{P}}_{\mathrm{loss}}\right)$$
(5)
$${\mathrm{P}}_{\mathrm{loss}}=\sum_{\mathrm{i}=1}^{\mathrm{n}}\sum_{\mathrm{j}=1}^{\mathrm{n}}3.{\left|{\mathrm{I}}_{\mathrm{ij}}\right|}^{2}.{\mathrm{R}}_{\mathrm{ij}}, \forall \mathrm{ i}\ne \mathrm{j}$$
(6)
$${\mathrm{P}}_{\mathrm{loss}}=\sum_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{P}}_{\mathrm{Gi}}-\sum_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{P}}_{\mathrm{Dj}}$$
(7)
$${\mathrm{P}}_{\mathrm{Loss}}=\sum_{\mathrm{i}=1}^{\mathrm{n}}\sum_{\mathrm{j}=1}^{\mathrm{n}}\left\{\frac{{\mathrm{R}}_{\mathrm{ij}}\mathrm{cos}\left({\updelta }_{\mathrm{i}}-{\updelta }_{\mathrm{j}}\right)}{\lceil{\mathrm{V}}_{\mathrm{i}}\rceil\left|{\mathrm{V}}_{\mathrm{j}}\right|}.\left({\mathrm{P}}_{\mathrm{i}}{\mathrm{P}}_{\mathrm{j}}+{\mathrm{Q}}_{\mathrm{i}}{\mathrm{Q}}_{\mathrm{j}}\right)+\frac{{\mathrm{R}}_{\mathrm{ij}}\mathrm{sin}\left({\updelta }_{\mathrm{i}}-{\updelta }_{\mathrm{j}}\right)}{\lceil{\mathrm{V}}_{\mathrm{i}}\rceil\left|{\mathrm{V}}_{\mathrm{j}}\right|}\left({\mathrm{Q}}_{\mathrm{i}}{\mathrm{P}}_{\mathrm{j}}-{\mathrm{P}}_{\mathrm{i}}{\mathrm{Q}}_{\mathrm{j}}\right)\right\},\mathrm{ i}\ne \mathrm{j}$$
(8)
$${\mathrm{P}}_{\mathrm{Loss}}=\sum_{\mathrm{i}=1}^{\mathrm{n}}\sum_{\begin{array}{c}j=1\\ i\ne j\end{array}}^{\mathrm{n}}{\mathrm{R}}_{\mathrm{ij}}.\frac{{\left|{\mathrm{V}}_{\mathrm{i}}\right|}^{2}+{\left|{\mathrm{V}}_{\mathrm{j}}\right|}^{2}-2\left|{\mathrm{V}}_{\mathrm{i}}\right|\left|{\mathrm{V}}_{\mathrm{j}}\right|\mathrm{cos}{\updelta }_{\mathrm{ij}}}{{\left|{\mathrm{Z}}_{\mathrm{ij}}\right|}^{2}}$$
(9)

The fact that Eqs. (8, 9) are precise and frequently utilized in transmission networks may be relevant to mention. However, as the impact of shunt stray capacitance is disregarded, the simpler expressions of Eqs. (6, 7) are commonly utilized in distribution systems. The represented OF in Eq. (5) is subject to the restrictions listed in subsect. 2.3.

2.2 Multiple-Objective Representation

The NR problem can be formulated to achieve multiple objectives to be optimized simultaneously and this can be expressed as pareto front set or by using weighted single objective formulations with many goals. Weights are decided by the user needs.

The following are only a few of the most typical goals that have been extensively utilized in the literature. Among these common objectives are:

2.2.1 Active Power Loss Minimization

$${OF}_{1}=Minimize\left({P}_{loss}\right)$$
(10)

2.2.2 Minimization of Total Node Voltage Deviations

$${OF}_{2}=Minimize\left(\sum_{i=1}^{n}\left|\left|{V}_{ref}\right|-\left|{V}_{i}\right|\right|\right)$$
(11)

2.2.3 Maximization of Total Voltage Stability Index (VSI)

$${OF}_{3}=maximize\left(\sum_{j=2}^{n}VSI\left(j\right)\right)$$

where

$$VSI\left(j\right)={\left|{V}_{i}\right|}^{4}-4.\left({P}_{eff,j}.{R}_{ij}+{Q}_{eff,j}.{X}_{ij}\right).{\left|{V}_{i}\right|}^{2}-4.{\left({P}_{eff,j}.{X}_{ij}-{Q}_{eff,j}.{R}_{ij}\right)}^{2}$$
(12)

The following is an example of how many objectives can be optimized simultaneously.

$$OF=\left(\genfrac{}{}{0pt}{}{{OF}_{1}}{\begin{array}{c}{OF}_{2}\\ {OF}_{3}\\ \dots \\ {OF}_{k}\end{array}}\right), \forall k\in {N}_{oj}$$
(13)

The single-weighted OF can be represented as

$$OF=\sum_{k=1}^{{N}_{oj}}{\omega }_{k}.{OF}_{k}$$

where

$$\sum_{k=1}^{{N}_{oj}}{\omega }_{k}=1$$
(14)

The fuzzy membership functions of each objective are extracted independently so that the best compromise solution can be determined. The fuzzy solution can then be calculated, and the best compromise solution is that having the least value [52, 53].

2.3 Equality and Inequality Constraints

The following is a list of the equality and inequality boundaries:

Power balance:

$$\left.\begin{array}{c}{P}_{i}-{P}_{D,i}=\left|{V}_{i}\right| \sum_{j=1}^{n}\left|{V}_{j}\right|\left|{Y}_{ij}\right|cos\left({\theta }_{ij}+{\delta }_{j}-{\delta }_{i}\right)\\ {Q}_{i}-{Q}_{D,i}=\left|{V}_{i}\right| \sum_{j=1}^{n}\left|{V}_{j}\right|\left|{Y}_{ij}\right|sin\left({\theta }_{ij}+{\delta }_{j}-{\delta }_{i}\right)\end{array}\right\} i\forall n, i\ne j$$
(15)

Bus voltage bounds:

$$\left|{V}^{Min}\right|\le \left|{V}_{i}\right|\le \left|{V}^{Max}\right|, i\forall n$$
(16)

Line flow limits:

$$\left|{I}_{i}\right|\le \left|{I}_{i}^{rated}\right| , i \forall nbr$$
(17)

System radiality:

See Sect. 3.

3 System Radiality

Maintaining radiality of the while performing the NRs is essential to avoid the complications of protection schemes [13, 54]. Radiality in TDNs necessitates careful planning and design, taking into account network architecture, DG integration, load increase, outages, and cost concerns. The most common ways to ensure the validity of radiality are [55]: (i) Graphical theory using incidence matrix (IM) [30, 56], (ii), and (iii) Least spanning tree (LST) [57].

3.1 Graphical Theory Using Incidence Matrix

The IM is a rectangular matrix with entries indicating whether or not the two things are connected to one another (i.e. branch-to-node). The IM, called \(\mathrm{A}\), has a size of \(\left(n \times m\right)\) matrix of \({a}_{ij}\) entries as depicted in (18) [56, 58], the SDN is a graph of n-nodes linked by m-lines. Then, after forming the matrix \(\mathrm{A}\), radiality could be checked as described in (19). The distinct measures to confirm radiality of the suggested NR of switch combinations are illustrated in Fig. 2 [30].

Fig. 2
figure 2

Procedures of Radiality’s Checking using the IM

Full size image
$${{\text{a}}_{{\text{ij}}}} = \left\{ {\begin{array}{*{20}{l}} { + 1\,{\text{if}}\,{\text{branch}}\,{\text{starts}}\,{\text{at}}\,{\text{node}}\,i} \\ { - 1\,{\text{if}}\,{\text{branch}}\,{\text{starts}}\,{\text{at}}\,{\text{node}}\,j} \\ {0\,{\text{otherwise}}} \end{array}} \right.,\forall {\text{i}} \in {\text{n}}\,{\text{and}}\,{\text{j}} \in {\text{m}}$$
(18)
$$det\left(A\right)=\left\{\begin{array}{c}\pm 1\to \text{Radiality achieved}\\ {\text{otherwise}}\to \text{No radiality}\end{array}\right.$$
(19)

3.2 Least Spanning Tree

A tree that connects a group of network nodes while minimizing the overall weight or cost of the edges used to connect them is known as a LST for radiality. In the context of radiality, the nodes often represent places on a map or in a specific geographic area, while the edges indicate potential routes, like highways or power lines, that could connect those places [59, 60]. Nodes and lines, which are the electrical equivalent of a graph’s vertices and edges in graph theory, make up electrical SDNs [61]. As a result, A G graph with V vertices (or nodes) and E edges (or lines) can be used to illustrate SDN. If every node is radially connected, a spanning tree will be plainly seen. Edge weights in the SDN can represent the active power loss on the line. The edge weight changes when the network scheme changes because real power loss is proportional to the square of phase current. When calculating the LST, the edge weight is assumed to be constant, in contrast to the normal graph [61].

Numerous approaches, including Prim’s and Kruskal’s algorithms, can be used to find the LST for a DNs [62]. The node with the minimum weight is chosen by Prim’s method. Dijkstra’s approach, however, selects the node with the shortest path weight to the source node. Generally speaking, these algorithms begin by choosing an initial node, which in the case of a SDN is typically the Slack node, and then iteratively add edges to the tree while ensuring that no cycles occur and that the overall weight or cost of the tree is reduced [57, 63].

4 Methods of Achieving NRs Along SDNs

Many procedures are reported by scholars/researchers to realize the best combinations of open/close switches of tie-feeder to achieve the best solution for NRs of the SDNs under study [23, 64, 65]. Generally speaking, there are four generations of procedures are proposed which may be categories as follows: (i) Mathematical procedures, (ii) Modern heuristic-based procedures, and (iii) Machine learning (ML)-based procedures. Figure 3 describes the motivation and various categories of reported solutions. Further detailed survey in this regard are addressed in the subsequent subsections as follows.

Fig. 3
figure 3

Various methods for solving NRs problem in SDNs

Full size image

4.1 Mathematical Methods

Graph theory is a mathematical framework that can be used to model and analyze network topologies. Graph theory can be used to solve problems related to network connectivity, flow, and optimization [66, 67]. For example, graph theory can be used to find the shortest path between two nodes in a network or to identify critical nodes that are essential for network connectivity [68, 69]. Among the mathematical models used to tackle the NRs problem are object-oriented analysis [70], pivot curve analytical tool [71], mathematical representation [72], and switch opening and exchange sequentially method [73, 74]. The numerical/iterative method is proposed by scholars to overcome the drawbacks of analytical method [31]. Extended fast decoupled power flow was reported by [75]. In the same context, A quick and easy approach is suggested that is built using the node–node adjacency matrix and just requires topological network data, not an optimization or LF program [76]. This method of selecting initial solutions is quick, straightforward, and its computation is independent of the network dimension, making it appealing in practice. In [77], in the power flow solution of a multiphase network, a switch exchange compensation technique is proposed. This technique has been tested on IEEE 123-bus feeder.

OPF using Benders decomposition is used to achieve NRs along RDNs [78]. The study was applied on large scale RDN which has 1128-branch, and 129-switch, real-world distribution system. On the other hand, extended fast decoupled power flow is used to attain the same [75].

Classical optimization strategies have been utilized in the early stages of NR formulations to tackle this issue. Among them, mixed-integer programming model [79,80,81], mixed-integer linear programming model [82, 83], mixed-integer quadratic programming [84], mixed-integer nonlinear optimization problem [85, 86], mixed-integer second-order cone programming [87,88,89,90], and approximate dynamic programming approach [91]. In a common practice, all later mentioned methods are used to deal with mono-objective problems and limited constraints. In addition to that, the solution quality and burden depend on the likely choice of the initial point. Furthermore, their performances for large systems are inaccurate, time-consuming and might be fail in finding final answers.

4.2 Modern Heuristic-Based Procedures

At last decade, the heuristic-based optimizers are extensively employed to solve NRs problem with SORs and MORs as well [14, 65, 92]. Number of scholars use the same techniques to solve mixed problems such as NR and DG placement, NR and RPCs, NR and load balancing (LB), etc. Hybrid procedures of using two or more techniques for boosting the performance of the proposed methodology are reported. All such methodologies based on heuristic algorithm(s) are organized in Table 1.

Table 1 Some of various heuristic-based procedure techniques used for NRs
Full size table

4.3 ML Procedures

In few past years, there are a number of attempts of utilizing ML techniques in solving NR problems in SDNs. Historically, NRs in power systems has been accomplished through the use of heuristic-based algorithms as extensively indicated in Table 1 in subsection 4.2. These procedures, however, are frequently time-consuming and may not necessarily give the greatest outcomes in some cases. ML is a subfield of AI that involves creating statistical models and algorithms that let computers automatically learn from data and enhance their performance on a given task without having to be explicitly programmed [160]. A computer system is trained on a huge amount of relevant data in ML, and it uses this data to uncover patterns and relationships that allow it to make predictions or decisions on fresh data [161].

The issue of NRs in SDNs is being addressed more and more with the use of ML techniques. To improve system performance, NR involves altering the SDN’s topology by opening or closing switches. ML algorithms come in many different varieties, such as supervised learning, unsupervised learning, RL, and DRL. Each type of algorithm has its own strengths and weaknesses and is suited to different types of applications. Table 2 summarizes various types ML procedures used to solve NRs problem in the literature.

Table 2 Some of various types of ML techniques used for NRs
Full size table

5 Distribution load flow (DLF) and load models

There are several well-known methodologies for addressing LF in transmission power systems, including: (i) Gauss–Seidel, (ii) Newton–Raphson (N-R), and (iii) Decoupled and Fast Decoupled LF solution methods. In most circumstances, the N-R technique is successful and viable for transmission power networks. However, due to the high R/X of SDNs (alternatively, the system goes into ill-condition), the latter approaches had trouble convergent for DLF [74]. As a result, alternative approaches are tried in order to tackle the DLF challenges [176]. Among these DLF solution methods are network-topology-based/graph-theory-based DLF [177,178,179], backward/forward sweep (BFS) LF method [176, 180,181,182,183], conic programming [184], direct LF method [185], and load current injection based improved LF [186]. Some of recent reported DLF considering the various load models/voltage dependent loads [187, 188], an efficient DLF method [189], and others consider probabilistic LF [190] were published.

In general, backward sweep (BS) is used to compute the current across each load or bus, with the assumption that the voltages at each bus are equal to \(1\mathrm{\angle }0^\circ\) PU (for the first iteration) using KCL and then updated by the forward sweep (FS) approach. The FS method, in the same context, is the approach used to determine the magnitude of voltage at each node of the circuit using KVL. Complete procedures of BFS are described in Fig. 4.

Fig. 4
figure 4

BFS procedures for DLF

Full size image

It is vital to consider load models in LF solutions to ensure proper study investigations for panning and operational aspects [191]. Static/voltage-dependent and dynamic/frequency-dependent load models are the two different types of load models. For steady-state research, static load models are crucial [192, 193].

To examine the effects of various load models on DGs planning and NRs investigations, static load models are utilized to categorize customer classes. Particularly when conducting studies on voltage stability, it is imperative to take into account various voltage-dependent load variations. The residential, industrial, and commercial voltage dependent load models described in [194] are used for research were used. The load models can be stated quantitatively as given in Eqs. (20, 21).

$${P}_{k}={P}_{k0}{\left(\frac{{V}_{k}}{{V}_{k0}}\right)}^{\alpha }$$
(20)
$${Q}_{k}={Q}_{k0}{\left(\frac{{V}_{k}}{{V}_{k0}}\right)}^{\beta }$$
(21)

The values of the real and reactive power exponents used in typical practice for industrial, residential, and commercial loads are shown in Table 3 [194,195,196].

Table 3 Load types and exponent values
Full size table

6 Benchmark Test Cases

A closer look to Tables arranged in Sect. 4, the common test cases are used to evaluate the performance of NRs along SDNs complete with defined scenarios that can be utilized are: (i) 33-node RDN: This is a popular small-scale test case with 33-nodes (12.66 kV bus voltage), 37-branches, 5-tie switches, 3- lateral sections and having a total load of (3.73 + j2.30) MVA constant power. The SLD of this RDN is illustrated in Fig. 5 (ties are shown in dotted line), and the reader can find the complete data of this test case in [74, 139, 197], (ii) 69-node RDN: There are 69-nodes, 73-branches and 5 tie-switches in this test case, The SLD of this 69-bus RDN is illustrated in Fig. 6 (ties are shown in dotted line), and the reader can find the complete data of this test case in [139, 198], (iii) 118-node RDN: This is a more complex test case with 118-nodes (Operating voltage of 11 kV), 132-branches, 13-lateral sections, 14-tie switches and having a total load of (22.709 + j17.042) MVA constant power. Its SLD is illustrated in Fig. 7 (ties are shown in dotted line) and the reader can find the complete data of this test case in [139, 197, 199], (iv) 136-node RDN: This is a more complex test case with 136-nodes (Operating voltage of 13.8 kV), 135-branches and 21-tie switches between nodes 8–74, 10–25, 16–84, 39–136, 26–52, 51–97, 56–99, 63–121, 67–80, 80–132, 85–136, 92–105, 91–130, 91–104, 93–105, 93–133, 97–121, 111–48, 127–77, 129–78, and 136–99 and having a total load of (22.709 + j17.041) MVA. Figure 8 shows the SLD of this RDN and the reader can find the complete data of this 1136-node RDN test case in [197, 200], and (v) Real-world power systems: Real-world RDNs, in addition to synthetic test cases, can be used to evaluate the performance of network reconfiguration methods. Examples for these real test RDNs are the Taiwan Power Company’s actual network that has 83 sectionalizing switches, 13 tie-switches, and is operated at 11.4 kV with demand of 28.35 + j20.70 MVA [201], Tokyo Electric Power Company [202, 203] that has 432-bus, 468 switches with 300 A capacity and 6.6 kV operating voltage, the Iraqi power utilities [204], and many more [205,206,207,208,209].

Fig. 5
figure 5

SLD of the 33-node RDN comprising proposed ties

Full size image
Fig. 6
figure 6

SLD of the 69-node RDN comprising initial ties

Full size image
Fig. 7
figure 7

SLD of the 118-node RDN comprising initial ties

Full size image
Fig. 8
figure 8

SLD of the 136-node RDN (Ties are not shown—See above text)

Full size image

7 Conclusions

The electrical SDNs are always changing, so it is crucial to carry out a recurring update survey on this subject. This article offers a thorough overview of the most cutting-edge methods for addressing the problem of distribution network loss through NRs. It examines the widely utilized approaches for distribution NRs and provides a thorough analysis of the pertinent history, the state of the art, and practical demands. It is based on several published research publications that comprehensively and continuously describe the study done on this subject over the past 20 years. The more than 200 citations supplied in this article serve as a representative sample of the technical assessments now available about the improvement of SDN’s performance by achieving loss minimization and voltage profile rise. Numerous approaches have been tried in this survey to tackle the NRs problem as formulations of single and multi-objective with different restrictions. A future trend in the era of NRs including machine-learning procedures is being driven by several approaches for minimizing SDM’s loss that have been described in the literature. It can be announced that simultaneous procedures appear to be the most effective strategy for improving system performance among those methods that are described in the literature. In the near future, researchers in this discipline as well as SDNs will pay greater attention to utilize many other approaches concerning the AI and machine learning and considering the various load models.