Abstract
Fluid–structure interaction simulations can be performed in a partitioned way, by coupling a flow solver with a structural solver. However, Gauss–Seidel iterations between these solvers without additional stabilization efforts will converge slowly or not at all under common conditions such as an incompressible fluid and a high added mass. Quasi-Newton methods can then stabilize and accelerate the coupling iterations, while still using the solvers as black boxes and only accessing data at the fluid–structure interface. In this review, the IQN-ILS, IQN-MVJ, IBQN-LS, MVQN, IQN-IMVLS and IQN-ILSM methods are reformulated in the generalized Broyden framework to illustrate their similarities and differences. Also related coupling techniques are reviewed and a performance comparison is provided where available.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Fluid–Structure Interaction (FSI) is the interaction of a fluid with a moving or deforming structure and occurs in many different branches of engineering. In mechanical engineering, the blades of a wind turbine deform due to their interaction with the wind [1, 2]. Also Flow-Induced Vibration (FIV) can occur, for example in tube bundles with external flow, leading to leakage or even rupture of the tubes [3]. In civil engineering, there are interactions between wind flow and bridges [4], silos [5], tents [6] and many other structures. In the biomedical field, heart valves and arteries are flexible structures that interact with the blood flow [7, 8].
As fluid–structure interaction is a multi-physics problem, complex phenomena can occur and numerical simulations are frequently used for the analysis. These numerical simulations of FSI can be performed in a monolithic or partitioned way. Monolithic codes solve the equations for the fluid and for the structure simultaneously, for example with a Newton–Raphson procedure [9] or multigrid method [10]. In this review, the focus is on the partitioned approach, as it allows to reuse mature and optimized codes to solve the subproblems.
Among the partitioned approaches, one can distinguish between the weakly and strongly coupled techniques. Weakly coupled techniques (also called explicit or loose coupling) solve the flow equations and the structure equations only once per time step [11, 12]. Consequently, the equilibrium between the fluid and the structure is not satisfied exactly. In this context, the term equilibrium refers to the equality of velocities and forces on the fluid–structure interface. These weakly coupled techniques are typically suitable for aeroelastic simulations with light and compressible fluids [13], but specific schemes can also be applied with dense and incompressible fluids [14].
By contrast, strongly coupled techniques (or implicit coupling) use coupling iterations between the flow solver and structure solver to enforce the equilibrium at the fluid–structure interface up to a convergence tolerance in a steady simulation or in each time step of an unsteady one [15,16,17]. As a result, the flow problem and structure problem are solved multiple times per (time) step. Obviously, these coupling iterations increase the computational cost, but the cost per coupling iteration normally decreases during the iterations within a (time) step as the change per iteration decreases. In the remainder of the paper an unsteady simulation will be assumed; a steady simulation is then a special case with one large time step.
An important parameter for the choice between weakly and strongly coupled techniques, but also for the stability of the coupling iterations in several strongly coupled techniques, is the ratio of the added mass to the mass of the structure [18]. The added mass is the apparent increase in mass of the structure due to the fluid that is displaced by the motion of this structure. Physically, it is influenced by the shape of the fluid domain and the density of the fluid. Numerically, also the time step size determines its effect, but this effect depends on whether the fluid is compressible or not. FSI problems with a compressible fluid can always be stabilized as long as the time step is sufficiently small, regardless of the ratio of the apparent added mass to the structural mass. However, for an incompressible fluid, stability cannot be obtained by decreasing the time step size [13, 15]. On the contrary, for incompressible flows in combination with flexible structures, decreasing the time step size may even increase the instability [15, 19,20,21]. For example, for the simulation of an elastic panel clamped at both ends and adjacent to a semi-infinite fluid domain, the added mass effect of a compressible fluid is proportional to the time step size, while for incompressible fluids it approaches a constant as the time step size decreases [13].
Especially for an incompressible fluid, many cases have a high added mass, e.g., blood flow in a vascular system [22], vibrations of tube bundles in lead-bismuth eutectic [23] or flutter of a slender cylinder in axial flow [24]. For these cases, the straightforward iteration between flow and structure solver within a time step will typically converge very slowly, or not at all, if no additional stabilization efforts are implemented. In this work, the focus is on techniques which consider the solvers as black boxes, as this is typically the case in a partitioned approach. Then, stabilization methods that alter one of the solvers, e.g., including an approximate added mass operator in the structural solver as in [25], are not possible. To stabilize and accelerate the convergence of coupling iterations with black box solvers, quasi-Newton methods have been developed in the fluid–structure interaction community. These methods will be reviewed in this work using the generalized Broyden framework.
The remainder of this review paper is structured as follows. First the FSI problem is posed and the necessary notation is introduced in Sect. 2. Then, the most basic solution approach is discussed in Sect. 3, with focus on its shortcomings in terms of stability and convergence speed, and how they can be overcome by introducing Jacobian information. In Sect. 4, a general method to obtain these Jacobians is discussed, called generalized Broyden. Thereafter, in Sect. 5, different quasi-Newton techniques are discussed in detail, including the Interface Quasi-Newton technique with an approximation for the Inverse of the Jacobian from a Least-Squares model (IQN-ILS), the Interface Quasi-Newton technique with Multi-Vector Jacobian (IQN-MVJ), the Interface Block Quasi-Newton technique with approximations from Least-Squares models (IBQN-LS), the Multi-Vector update Quasi-Newton technique (MVQN), the Interface Quasi-Newton Implicit Multi-Vector Least-Squares (IQN-IMVLS) and the Interface Quasi-Newton algorithm with an approximation for the Inverse of the Jacobian from a Least-Squares model and additional Surrogate Model (IQN-ILSM). This section ends with further notes and extensions on these methods. Finally, some numerical results to compare the different techniques are provided in Sect. 6, followed by the conclusions in Sect. 7.
2 Formulation of the FSI Problem
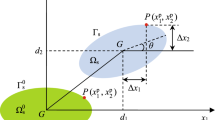
An abstract fluid–structure interaction problem, as shown in Fig. 1, consists of the subdomains \(\Omega _f\) and \(\Omega _s\), with the subscripts f and s denoting fluid and structure, respectively. The boundaries of the subdomains are denoted as \(\Gamma _f=\partial \Omega _f\) and \(\Gamma _s=\partial \Omega _s\) and the fluid–structure interface \(\Gamma _i=\Gamma _f\cap \Gamma _s\) is their common boundary.
Besides having to satisfy the flow and structure equations in the respective subdomains while taking into account the appropriate boundary conditions on \(\Gamma _f\setminus \Gamma _i\) and on \(\Gamma _s\setminus \Gamma _i\), the solution of the FSI problem is also required to fulfill the equilibrium conditions on the fluid–structure interface \(\Gamma _i\). The equilibrium conditions on a no-slip fluid–structure interface are twofold. First, the equality of fluid and solid velocity on \(\Gamma _i\) is needed (kinematic condition)
where \(\vec {v}\) is the velocity vector in the fluid domain and \(\vec {u}\) the displacement vector in the structure domain. Remark that this equality also implies equal accelerations on the interface. Second, equal magnitude but opposite sense of traction on \(\Gamma _i\) is required (dynamic condition)
where \(\bar{\sigma }_{f,s}\) is the stress tensor in \(\Omega _{f,s}\) and \(\vec {n}_{f,s}\) the unit normal vector that points outwards from the corresponding subdomain.
As this work discusses coupling techniques that consider the solvers as black boxes, only the variables on the fluid–structure interface \(\Gamma _i\) are of interest. However, the discretization of this interface is often different in the flow and structure subdomains. Given the focus of this review on coupling techniques, it is assumed that an interpolation layer is wrapped around or included in one (or both) of the solvers, invisible to the implementation of the coupling technique. As a consequence, the discretized displacement on either side of the fluid–structure interface can be represented as a column array \(\varvec{\lowercase {x}}\in \mathbb {R}^{n_x\times 1}\) containing all components of the displacement vector \(\vec {u}\) in each of the \(n_p\) grid points on the interface.
with the first subscript referring to the grid point (1 to \(n_p\)) and the second one to the component (1 to d, with d the dimension).
Similarly, the pressure p and all components of the viscous traction vector \(\vec {t}\) in each load point (1 to \(n_l\)) on either side of the fluid–structure interface are grouped in a column array \(\varvec{\lowercase {y}}\in \mathbb {R}^{n_y\times 1}\)
also called load vector, with the same meaning of the subscripts as above. Note that the \(n_l\) load points do not need to coincide with the discretization of the displacement. It is important that the pressure load \(p\cdot \vec {n}\) and viscous traction \(\vec {t}\) are not added, but included individually into \(\varvec{\lowercase {y}}\), because the pressure is typically dominant and has to stay perpendicular to the surface, also when interpolation is performed. If pressure and viscous traction were added, the resulting interpolated vector would have a pressure contribution that is not necessarily perpendicular to the surface after interpolation, resulting in an artificial shear component that can be much larger than the physical shear component.
With the typical Dirichlet–Neumann decomposition of the FSI problem, the displacement (linked to the velocity through the time discretization in time-dependent problems) is imposed at the interface in the flow solver and a pressure and viscous traction distribution is applied on the interface in the structure solver. A flow solver with a deforming grid using the Arbitrary Lagrangian–Eulerian (ALE) frame of reference will be assumed for the explanation, but this can be replaced by other techniques, for example the combination of the ALE approach and the Chimera technique [26] to handle large body motions or non-conforming alternatives, such as Immersed Boundary Methods (IBM) [27] and Embedded Boundary Methods (EBM) [28], which can handle large deformations and even topology changes. The flow calculation in a coupling iteration within a time step can be written as
This notation concisely represents several operations and hides the dependence on previous time steps and the variables in the fluid domain next to the interface, while emphasizing the dependence on the discretized displacement \(\varvec{\lowercase {x}}\) of the fluid–structure interface. It represents the following actions. First, the discretized displacement is given to the flow solver and the fluid domain adjacent to the interface is adapted accordingly. Then, the flow equations are solved in the entire fluid domain, resulting in a new load distribution \(\varvec{\lowercase {y}}\) on the interface.
Similarly, the calculation of the structure is represented by the function
As before, this expression hides the dependence on both the previous time steps and the variables in the structure domain next to the interface. It indicates that the fluid pressure and viscous traction distribution on the interface \(\varvec{\lowercase {y}}\) is given to the structure code. Subsequently, that code calculates the displacement of the entire structure and thus also the new displacement \(\varvec{\lowercase {x}}\) of the fluid–structure interface.
With these notations, the FSI problem is formulated as the system
that has to be solved for \(\varvec{\lowercase {x}}\) and \(\varvec{\lowercase {y}}\). This problem can be rewritten as the root-finding problem
with unknowns \(\varvec{\lowercase {x}}\) and \(\varvec{\lowercase {y}}\).
Moreover, the system in Eq. (7) can be reduced by substituting one equation in the other. Commonly, the first line is substituted in the second, but the other way around is equally possible. In this way, the FSI problem is simplified to a smaller system of equations
which has to be solved for \(\varvec{\lowercase {x}}\). The notation \(\circ\) refers to function composition, so \(\varvec{\mathcal {S}}\,\circ\, \varvec{\mathcal {F}}(\varvec{\lowercase {x}})\) is equivalent with \(\varvec{\mathcal {S}}(\varvec{\mathcal {F}}(\varvec{\lowercase {x}}))\). This looks like a fixed-point equation for \(\varvec{\lowercase {x}}\), but can also be written as a root-finding problem with unknown \(\varvec{\lowercase {x}}\)
To write this more compactly, the residual operator \({\varvec{\mathcal {R}}}(\cdot )\) is defined as
with output \(\varvec{\lowercase {r}}={\varvec{\mathcal {R}}}(\varvec{\lowercase {x}})\). The FSI problem thus reduces to finding the \(\varvec{\lowercase {x}}\) that fulfills
In this section, we have presented two formulations of the FSI problem. The first is the complete system Eq. (7) with \(n_x+n_y\) unknowns. The second is the reduced system Eq. (9), which has the benefit of having only \(n_x\) unknowns. This system has been written more compactly using the residual operator \({\varvec{\mathcal {R}}}\) resulting in Eq. (12). In the next sections, several methods are discussed to solve the FSI problem presented here, in one of both formulations.
Both the solver operators as well as the residual operator are typically nonlinear. Therefore, the FSI problem exhibits similarities with nonlinear root-finding problems. The main difference is that an FSI problem usually involves time stepping (except for steady cases), which means that a nonlinear system has to be solved in each time step. Therefore, within each time step, coupling iterations are performed until the solution is reached. The nonlinear systems in subsequent time steps are somehow related to each other, because the solver operators change only gradually in time. As the solution is typically continuous, the initial guess for \(\varvec{\lowercase {x}}\) at the start of each time step can be obtained by extrapolating the solution from previous time steps [29].
3 Solving the FSI Problem
3.1 Gauss–Seidel Scheme
In order to solve the FSI problem, Eq. (8) has to be solved in each time step. One of the basic methods to solve such a system of nonlinear equations is the block Gauss–Seidel scheme. In this block-iterate scheme, each of the nonlinear equations is solved for one of the unknowns consecutively, and each unknown is updated to its new value as soon as it becomes available.
Because, further on, it will become necessary to make a distinction between the output of one solver and the input of the next, a tilde symbol is introduced to indicate the output of a solver:
Using the superscript \(k+1\) to indicate the current iteration, the block Gauss–Seidel scheme takes the following form
The lastly calculated displacement vector \(\tilde{\varvec{\lowercase {x}}}{}^k\) is used as \(\varvec{\lowercase {x}}^{k+1}\), the input of the flow solver in the following iteration. Subsequently, this vector is used to calculate a new load vector \(\tilde{\varvec{\lowercase {y}}}{}^{k+1}\) which is thereafter used as input of the structure solver \(\varvec{\lowercase {y}}^{k+1}\), to calculate a new displacement vector \(\tilde{\varvec{\lowercase {x}}}{}^{k+1}\). This iteration scheme, in which the output of the flow and structure solver is passed unchanged to the structure and flow solver, respectively, is the most basic way to find an equilibrium and is also called Gauss–Seidel scheme or fixed point iteration scheme.
The final solution of the FSI problem Eq. (7) has to fulfill the kinematic Eq. (1) and dynamic equilibrium condition Eq. (2) up to a certain tolerance. This means that \(\tilde{\varvec{\lowercase {x}}}{}\) and \(\tilde{\varvec{\lowercase {y}}}{}\) have to approach \(\varvec{\lowercase {x}}\) and \(\varvec{\lowercase {y}}\), respectively, which is expressed by the convergence conditions
Because the output of each of the solvers is passed unchanged to the other, this can also be written as
which relates to the fixed point formulation in Eq. (9).
By eliminating the occurrence of the load vector \(\varvec{\lowercase {y}}\), the procedure can be simplified to
Furthermore, with the use of the residual operator introduced in Eq. (11), the iteration scheme becomes
which is considered converged once
3.2 Motivation for Using Quasi-Newton Methods
Unfortunately, the Gauss–Seidel scheme explained above is not unconditionally stable due to among others the added mass effect.
Many researchers have investigated the stability of Gauss–Seidel iterations. For example, its convergence behaviour has been studied based on a simple model problem with a single degree of freedom on the interface [30]. Some investigated the added-mass effect [31]. Many others have explored the case of blood flow through a simplified artery [15, 32, 33]. They observed that, besides an apparent fluid mass of the similar order of magnitude as the actual structural mass, also a decrease in the stiffness of the structure or increase in domain length has a destabilizing effect. A first attempt to mathematically analyze the stability was done through the determination of the maximum relaxation factor to obtain convergence [15, 25].
Instead of looking at a single number, the stability of a Gauss–Seidel scheme for a simplified flexible tube model with Dirichlet–Neumann decomposition can be examined by splitting the error on the interface into Fourier modes [34]. The mentioned error is the difference between the correct interface displacement and the one in a Gauss–Seidel iteration, based on linearized equations and without taking the boundary conditions into account. In this way, the authors were able to identify which frequency components become unstable. The analysis was first performed for a tube wall without inertia [34] and thereafter repeated including inertia [35], which proved to stabilize the convergence behaviour.
From this analysis it can be deduced that only a limited number of modes of the interface displacement are unstable and that the lowest wave numbers have the highest amplification factor and are hence the most unstable ones. This observation is true for different combinations of parameter values. In other words, the divergence or slow convergence of Gauss–Seidel iterations are caused by a limited number of unstable and slowly converging modes corresponding to the lowest wave numbers.
The physical explanation for this observation is shown in Fig. 2. The figure shows an axisymmetric tube, the wall of which is perturbed with two different wave numbers, while on the in- and outlet a zero pressure boundary condition is imposed. Initially, its cross section is constant and the incompressible fluid is at rest. In the upper part of Fig. 2, a low wave number perturbation is applied and, because the fluid is incompressible, it is accelerated globally resulting in large pressure variations. In the lower part, a higher wave number perturbation is applied and the fluid acceleration is confined to more local regions. As a consequence, the pressure variations are much smaller for higher wave numbers. The pressure variations in the lower part of Fig. 2 are even barely visible, because the same scale is used for both cases.
The pressure contours (in Pa) in an axisymmetric tube due to two displacements of the tube’s wall with the same amplitude but a different wave number. Initially, the fluid is at rest and the tube has a constant cross-section and zero pressure at both ends. A displacement of the tube’s wall with a low wave number (top) creates much larger pressure variations than a displacement with a high wave number (bottom). Only the difference between the two calculations and not the values as such are important [36]
Although the above analysis was performed on a flexible tube, the results are more widely applicable to incompressible fluids with a fluid–structure density ratio around one. For example, [37] arrived at the same conclusions by examining the stability of Gauss–Seidel iterations for a semi-infinite open fluid domain bounded by a string or a beam.
In summary, Gauss–Seidel iterations are not suitable for incompressible fluid cases with high added mass, because there is a limited number of error modes that are unstable. In order to obtain a solution for these cases, the unstable modes have to be removed by another technique to (efficiently) achieve convergence. Based on the results from the Fourier decomposition, it follows that only the low wave number modes have to be stabilized, while the others can still be treated using Gauss–Seidel iteration. The next section explains that the stabilization of these modes is achieved by including derivative information, which is the basic principle behind quasi-Newton techniques.
3.3 Quasi-Newton Schemes
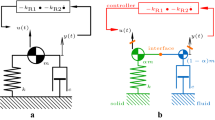
In order to overcome this limitation of the Gauss–Seidel iterations for problems with high added mass and an incompressible fluid, the quasi-Newton iteration scheme is adopted. To improve stability, one or both of the vectors \(\tilde{\varvec{\lowercase {x}}}{}\) and \(\tilde{\varvec{\lowercase {y}}}{}\) are modified before passing them to the other solver. If only one solver output is adapted, it is usually the output of the structural solver \(\varvec{\mathcal {S}}\) as in Fig. 3b, but the opposite is equally possible. Figure 3c shows a schematic representation of adapting both solver outputs.
In the remainder of this section we will first introduce the adaptation of one output where we will use the modification of the structural output as example. This scheme will be referred to as the residual formulation scheme. Thereafter, the adaptation of both solver outputs will be introduced. The corresponding scheme is called the block iteration scheme.
3.3.1 Residual Formulation Quasi-Newton Scheme
In this scheme, the output \(\tilde{\varvec{\lowercase {x}}}{}^k\) of the structural solver is modified to \(\varvec{\lowercase {x}}^{k+1}\) which is subsequently used as input for the flow solver. The output \(\tilde{\varvec{\lowercase {y}}}{}^k\) of the flow solver is passed unchanged to the structural solver. Therefore, the load vector \(\varvec{\lowercase {y}}\) can be left out altogether, as was the case for Gauss–Seidel iterations. With the use of the residual operator, defined in Eq. (11), the residual \(\varvec{\lowercase {r}}^{k+1}\) in iteration \(k+1\) is written as
and as before convergence is reached when Eq. (19) is satisfied. The difference with the Gauss–Seidel scheme is that \(\varvec{\lowercase {x}}^{k+1}\) is no longer equal to \(\tilde{\varvec{\lowercase {x}}}^{k}\). The adaption of the displacement vector follows from the use of a Newton–Raphson approach to solve the root-finding problem Eq. (12). This method uses the Jacobian of the nonlinear equation, which is denoted here by \({\varvec{\mathcal {R}}}'\), to estimate the input \(\varvec{\lowercase {x}}^{k+1}\) that will direct the residual to \(\varvec{\lowercase {0}}\) by solving
for \(\varvec{\lowercase {x}}^{k+1}\). Note that Gauss–Seidel iteration Eq. (18) is retrieved if \({\varvec{\mathcal {R}}}'(\varvec{\lowercase {x}}^k)=-\varvec{\uppercase {I}}\). Likewise, relaxed Gauss–Seidel iteration is obtained if the Jacobian is \(-\omega \varvec{\uppercase {I}}\).
Because both the flow and structure solvers are considered black box solvers, the Jacobians of \(\varvec{\mathcal {F}}\) and \(\varvec{\mathcal {S}}\) are not accessible and hence, neither is \({\varvec{\mathcal {R}}}'\). Therefore, the Jacobian of the residual operator is approximated, resulting in a quasi-Newton method
where \({\varvec{\widehat{{{{{\mathcal {R}}}}}'}}}(\varvec{\lowercase {x}}^k)\) is the approximated Jacobian.
As explained in the previous section, the instability of Gauss–Seidel iterations is caused by a limited set of modes, i.e., for the vectors \(\varvec{\lowercase {x}}\) in a small subspace of \(\mathbb {R}^{n_x\times 1}\). Consequently, an approximation of the complete Jacobian of the residual operator \({\varvec{\mathcal {R}}}\) is not required. An approximated Jacobian which takes care of these unstable modes and leaves the other modes unchanged is sufficient. Leaving some modes unchanged means that the quasi-Newton method will actually perform Gauss–Seidel iterations for those modes.
Solving the linear system in the equation above can be avoided by approximating the inverse of the Jacobian directly and calculating the update of the displacement vector as
To conclude this section, a new short-hand notation is introduced for the approximate (inverse) Jacobians. For a nonlinear function \(\varvec{\lowercase {r}}= {\varvec{\mathcal {R}}}(\varvec{\lowercase {x}})\), the approximate Jacobian and inverse Jacobian are written as
3.3.2 Block Iteration Quasi-Newton Scheme
Instead of only adapting the output of one solver, it is also possible to adapt the output of both the flow and structure solver. Now both \(\varvec{\lowercase {x}}^{k+1}\) and \(\varvec{\lowercase {y}}^{k+1}\) are different from \(\tilde{\varvec{\lowercase {x}}}^{k}\) and \(\tilde{\varvec{\lowercase {y}}}^{k+1}\), and, because the load vector is no longer passed unchanged, it is not possible to use the residual operator. The convergence conditions are again given by Eq. (15).
The modification of the output of the solvers is determined by applying block Newton–Raphson iterations to the root-finding problem Eq. (8) with unknowns \(\varvec{\lowercase {x}}\) and \(\varvec{\lowercase {y}}\)
where \(\Delta \varvec{\lowercase {x}}\) and \(\Delta \varvec{\lowercase {y}}\) are the updates for the input \(\varvec{\lowercase {x}}\) and \(\varvec{\lowercase {y}}\) of the flow and structure solvers, respectively. Further, \(\varvec{\uppercase {I}}\) is the identity matrix and \(\varvec{\mathcal {F}}'\) and \(\varvec{\mathcal {S}}'\) are the Jacobians of the flow and structure equations. Note that the two identity matrices will have different dimensions if the size of \(\varvec{\lowercase {x}}\) and \(\varvec{\lowercase {y}}\) differ.
Starting from the displacement \(\varvec{\lowercase {x}}^k\) that was given as input to the flow solver in the previous coupling iteration, the displacement \(\varvec{\lowercase {x}}^{k+1}=\varvec{\lowercase {x}}^k+\Delta \varvec{\lowercase {x}}^k\) is calculated by solving the system
for \(\Delta \varvec{\lowercase {x}}^k\).
Using the updated value \(\varvec{\lowercase {x}}^{k+1}\) and after calling the flow solver to determine \(\tilde{\varvec{\lowercase {y}}}^{k+1}=\varvec{\mathcal {F}}(\varvec{\lowercase {x}}^{k+1})\), the pressure and viscous traction distribution \(\varvec{\lowercase {y}}^{k+1}=\varvec{\lowercase {y}}^k+\Delta \varvec{\lowercase {y}}^k\) is calculated by solving the analogous system
for \(\Delta \varvec{\lowercase {y}}^k\). Subsequently, the structure solver is called to determine \(\tilde{\varvec{\lowercase {x}}}^{k+1}=\varvec{\mathcal {S}}(\varvec{\lowercase {y}}^{k+1})\).
Similar to the previous section, the Jacobians are not accessible, because the solvers are considered black boxes. Therefore, approximations denoted by \({\widehat{\varvec{{\mathcal {F}}}'}}\) and \({\widehat{\varvec{{\mathcal {S}}}'}}\) are used instead. Note that here two normal Jacobians are required, one for each solver, whereas in the previous section only one inverse Jacobian was required, namely the inverse Jacobian of the residual operator.
Adopting the same short-hand for the approximated Jacobians as in the previous section results in the following notations
4 Approximating Jacobians
The previous section introduced quasi-Newton approaches to stabilize and at the same time accelerate the convergence of coupling iterations. These schemes adapt either one or both of the solver outputs before passing them on, resulting in respectively, a quasi-Newton system for the residual formulation of the FSI problem, or a block iteration quasi-Newton system. These systems each contain one or more approximate Jacobians. The residual formulation scheme requires an approximation for the inverse of the Jacobian \({\varvec{\mathcal {R}}}'(\varvec{\lowercase {x}}^k)\), which is denoted as \(\partial ^{k}_{\varvec{\lowercase {r}}} \varvec{\lowercase {x}}\). The block iteration quasi-Newton scheme requires approximations for the Jacobians of the flow solver and structure solver, so \(\partial ^{k}_{\varvec{\lowercase {x}}} \tilde{\varvec{\lowercase {y}}}\) approximates \(\varvec{\mathcal {F}}'(\varvec{\lowercase {x}}^k)\) and \(\partial ^{k}_{\varvec{\lowercase {y}}} \tilde{\varvec{\lowercase {x}}}\) approximates \(\varvec{\mathcal {S}}'(\varvec{\lowercase {y}}^k)\). In these notations the superscript k refers to the iteration in which the Jacobian has been approximated.
All of these approximate Jacobians can be created using the generalized Broyden method. In this section, we will explain this method for the construction of an approximate Jacobian of an arbitrary nonlinear function \(\varvec{\lowercase {b}}= \varvec{\mathcal {B}}(\varvec{\lowercase {a}})\). For now, we leave out the added complexity of FSI problems, for which an approximate Jacobian has to be constructed in each time step. This will be explained in the next section. Here, we just have an iterative method, where in each iteration k the Jacobian \(\varvec{\mathcal {B}}'(\varvec{\lowercase {a}}^k)\) is approximated by \(\partial ^{k}_{\varvec{\lowercase {a}}} \varvec{\lowercase {b}}\). The same technique can also be used to approximate the inverse Jacobian \({\varvec{\mathcal {B}}'(\varvec{\lowercase {a}}^k)}^{-1}\) by \(\partial ^{k}_{\varvec{\lowercase {b}}} \varvec{\lowercase {a}}\).
Instead of immediately presenting the rather complex generalized Broyden equation, it is introduced step by step, in a way that better fits the quasi-Newton FSI explanations found in literature.
4.1 Satisfying the Secant Conditions
The core idea of any quasi-Newton Jacobian approximation is to use the nonlinear function input–output information from previous iterations. Indeed, an input \(\varvec{\lowercase {a}}^i\) resulting in a certain output \(\varvec{\lowercase {b}}^i\) is a piece of valuable information about the behavior of the black box function \(\varvec{\mathcal {B}}\), which can be used to approximate the Jacobian \(\varvec{\mathcal {B}}' (\varvec{\lowercase {a}}^k)\) by \(\partial ^{k}_{\varvec{\lowercase {a}}} \varvec{\lowercase {b}}\). In the current iteration \(k+1\), the inputs of all previous iterations
are available, as well as the corresponding outputs
The input–output info is stored and used in the form of differences between consecutive iterations, defined as
for \(0 \le i \le k-1\). The \(\delta\) notation refers to the difference between previous iterations, in contrast to the \(\Delta\) notation, which refers to the desired change or update that needs to be performed.
Each pair \((\delta \varvec{\lowercase {a}}^i, \delta \varvec{\lowercase {b}}^i)\) is called the secant information at iterations i and is related to a secant line to the nonlinear function \(\varvec{\mathcal {B}}\). Therefore, it can be interpreted as a finite difference approximation for the Jacobian in the direction \(\delta \varvec{\lowercase {a}}^i\).
Furthermore, each secant information pair has a corresponding secant equation:
If the approximated Jacobian \(\partial ^{k}_{\varvec{\lowercase {a}}} \varvec{\lowercase {b}}\) meets this secant condition, it uses a finite difference approximation for the actual Jacobian in the direction of \(\delta \varvec{\lowercase {a}}^i\), with the input–output information of iterations i and \(i+1\). This secant information is relevant only if the Jacobian stays more or less the same during the k iterations, which means that \(\varvec{\mathcal {B}}(\varvec{\lowercase {a}})\) has to behave close to linearly in the neighbourhood of \(\varvec{\lowercase {a}}^k\).
The idea is to construct \(\partial ^{k}_{\varvec{\lowercase {a}}} \varvec{\lowercase {b}}\), so that it fulfills all the k secant equations. To write this compactly, the differences defined previously in Eq. (31) are stored in the matrices \(\varvec{\uppercase {A}}^k\) and \(\varvec{\uppercase {B}}^k\) as follows
Now, the k secant conditions can be collected in the matrix equation
With \(n_a\) and \(n_b\) being the length of the input and output vectors, this is a system of \(n_b k\) scalar equations for \(n_b n_a\) unknowns (the elements of the matrix \(\partial ^{k}_{\varvec{\lowercase {b}}} \varvec{\lowercase {a}}\)). The system is thus typically underdetermined (\(k<n_a\)). In order to find a unique solution, the least-norm solution is sought, which is in this case defined as the smallest matrix in the Frobenius norm that satisfies all secant conditions. The solution is given as
where \({\varvec{\uppercase {A}}^k}^+\) is the pseudo-inverseFootnote 1 (or Moore–Penrose inverse) of the rectangular matrix \(\varvec{\uppercase {A}}^k\), defined as
To calculate the pseudo-inverse, it is necessary that the columns of \(\varvec{\uppercase {A}}^k\) are linearly independent. For now, we will assume this is always the case and the issue of linear dependence of the secant information is addressed in detail in the discussion on filtering in Sect. 5.1.
The expression for the approximate Jacobian presented above is elegant and short, but not very intuitive. Therefore, a different approach to obtain the same expression is given below.
The purpose of the approximate Jacobian is to determine an estimated change in output \(\Delta \varvec{\lowercase {b}}\) that corresponds to an arbitrary change in input \(\Delta \varvec{\lowercase {a}}\), by evaluating
For this purpose, the secant information from the previous iterations is utilised in the following approach.
First, the arbitrary vector \(\Delta \varvec{\lowercase {a}}\) is approximated as a linear combination of vectors \(\delta \varvec{\lowercase {a}}^i\), i.e.
with \(\varvec{\lowercase {c}} \in \mathbb {R}^{k \times 1}\) a coefficient vector.
It follows from the secant information that an input difference \(\delta \varvec{\lowercase {a}}^i\) corresponds to an output difference \(\delta \varvec{\lowercase {b}}^i\), for \(0 \le i \le k-1\). Therefore, and under the assumption that the linear behavior of \(\varvec{\mathcal {B}}\) is locally dominant, it can be stated that a linear combination of vectors \(\delta \varvec{\lowercase {a}}^i\) will correspond to the same linear combination of vectors \(\delta \varvec{\lowercase {b}}^i\). This principle allows to determine \(\Delta \varvec{\lowercase {b}}\) as
Finally, it remains to determine the coefficients \(\varvec{\lowercase {c}}\). The system in Eq. (38) is typically overdetermined. Hence, the least-squares solution for \(\varvec{\lowercase {c}}\) will be used, which can be obtained by solving the square system of normal equations
Therefore, the coefficient vector is given as
Using this to calculate \(\Delta \varvec{\lowercase {b}}\) results in
Comparison with Eq. (37) reveals the same Jacobian as determined before in Eq. (35).
Matrix-free implementation Some of the algorithms explained in Sect. 5 require the explicit construction of the Jacobian matrix, while for others only its product with a vector, e.g., \(\partial ^{k}_{\varvec{\lowercase {a}}} \varvec{\lowercase {b}} \ \Delta \varvec{\lowercase {a}}\), is required. This last set of algorithms allows matrix-free implementation, for which the Jacobian matrix Eq. (35) never has to be calculated explicitly in practice, nor is the explicit calculation of the pseudo-inverse defined in Eq. (36) needed. How this is achieved is explained here.
Equations (40) and (41) show that the product of the pseudo-inverse with a vector is in fact the solution of the normal equations, but solving the normal equations Eq. (40) becomes unstable if the number of columns in the matrix \(\varvec{\uppercase {A}}^k\) is rather high. A more robust method to calculate the pseudo-inverse uses the reduced or economy-size QR decomposition [38] of \(\varvec{\uppercase {A}}^k\)
where \(\varvec{\uppercase {Q}}_A^k \in \mathbb {R}^{n_a \times k}\) is a matrix with orthonormal columns and \(\varvec{\uppercase {R}}_A^k \in \mathbb {R}^{k \times k}\) is an upper triangular matrix.Footnote 2 Applying this to the normal equations Eq. (40) and using the fact that the inverse of \(\varvec{\uppercase {R}}_A^k\) exists because the columns of \(\varvec{\uppercase {A}}^k\) are linearly independent, results in
Symbolically, this means that the pseudo-inverse can be written as \({\varvec{\uppercase {R}}_A^k}^{-1}{\varvec{\uppercase {Q}}_A^k}^\textrm{T}\), but it should never be constructed or stored. Instead, the product of the pseudo-inverse with a vector can be calculated by first evaluating the right hand side of Eq. (44) and subsequently solving the system using back-substitution, as \(\varvec{\uppercase {R}}_A^k\) is an upper triangular matrix. The complete procedure to efficiently determine \(\Delta \varvec{\lowercase {b}}\) given \(\Delta \varvec{\lowercase {a}}\) is summarized in Algorithm 1.
In the following, the notation with the pseudo-inverse will still be used. Nonetheless, it should be kept in mind that the actual calculation has to be done using QR decomposition and back-substitution, avoiding the calculation of the inverse of matrices as well as the construction of large dense square matrices.

4.2 Adding an Initial Estimate for the Jacobian
Assuming the columns \(\varvec{\uppercase {A}}^k\) are linearly independent, the above obtained approximated Jacobian \(\varvec{\uppercase {B}}^k {\varvec{\uppercase {A}}^k}^+\) is of rank k. For the current discussion, it is assumed that \(k \ll n_a\). Therefore, the matrix is a low-rank Jacobian approximation, and has an image or range of dimension k and a nullspace of dimension \(n_a-k\). As a result, with regard to its product with an arbitrary \(\Delta \varvec{\lowercase {a}}\), only the part of \(\Delta \varvec{\lowercase {a}}\in \text {range}(\varvec{\uppercase {A}}^k)\) will have a non-zero result. This becomes clear from the definition of the pseudo inverse in Eq. (36). The part of \(\Delta \varvec{\lowercase {a}}\perp \text {range}(\varvec{\uppercase {A}}^k)\) falls in the nullspace of the approximated Jacobian and the product of this part with the Jacobian is therefore zero. In other words, the approximated Jacobian is zero in every direction that is not a linear combination of the directions \(\delta \varvec{\lowercase {a}}^i\), for \(0 \le i \le k-1\), encountered in the previous iterations.
Nonetheless, a full rank approximation of the Jacobian may be required, e.g., when it is used in a quasi-Newton method according to the residual formulation scheme. If this is the case, the current Jacobian approximation, using the approximation based on secant conditions for the part of \(\Delta \varvec{\lowercase {a}}\in \text {range}(\varvec{\uppercase {A}}^k)\), can be expanded with an initial estimate of the approximate Jacobian \(\partial ^{0}_{\varvec{\lowercase {a}}} \varvec{\lowercase {b}}\) for the remaining part \(\Delta \varvec{\lowercase {a}}\perp \text {range}(\varvec{\uppercase {A}}^k)\).
The splitting of \(\Delta \varvec{\lowercase {a}}\) in these two parts is based on orthogonal projection and visualized in Fig. 4. The orthogonal projection of a vector \(\Delta \varvec{\lowercase {a}}\) onto the range of \(\text {range}(\varvec{\uppercase {A}}^k)\) is given by
This is the part of \(\Delta \varvec{\lowercase {a}}\in \text {range}(\varvec{\uppercase {A}}^k)\). Using the complementary projector or just calculating the difference of \(\Delta \varvec{\lowercase {a}}\) and its orthogonal projection
gives the part of \(\Delta \varvec{\lowercase {a}}\perp \text {range}(\varvec{\uppercase {A}}^k)\). Refer to [39] for a more complete discussion of projectors. Moreover, note that, using the QR decomposition these two parts are given by \(\varvec{\uppercase {Q}}_A^k {\varvec{\uppercase {Q}}_A^k}^\textrm{T}\Delta \varvec{\lowercase {a}}\) and \((\varvec{\uppercase {I}} - \varvec{\uppercase {Q}}_A^k {\varvec{\uppercase {Q}}_A^k}^\textrm{T}) \Delta \varvec{\lowercase {a}}\).
Now, the Jacobian approximation based on secant information can be extended with an initial Jacobian \(\partial ^{0}_{\varvec{\lowercase {a}}} \varvec{\lowercase {b}}\):
The questions why and how an initial Jacobian can be added have been answered. What remains is the choice of its value. Often, the identity matrix is used, scaled with a factor, typically \(-1\) or \(-\omega\), which corresponds to (relaxed) Gauss–Seidel iteration, as explained below Eq. (21). This is the simplest approach to obtaining a full rank Jacobian approximation and will also be used in Sect. 5. In the case a low rank approximation suffices, e.g., the Jacobians for block iteration quasi-Newton, \(\partial ^{0}_{\varvec{\lowercase {a}}} \varvec{\lowercase {b}} = \varvec{\uppercase {0}}\) can be used, which means the second term disappears completely. In still other situations, a physics-based surrogate may be available to use as initial Jacobian. This approach may accelerate convergence, but is application-specific and will be discussed further in Sect. 5.6.
4.3 Generalized Broyden Method
Up to now, the approximation of the Jacobian \(\partial ^{k}_{\varvec{\lowercase {a}}} \varvec{\lowercase {b}}\) was determined such that it met all secant conditions. However, this is not the only way to use the secant information. Another often used method (although not in FSI) is to only require the approximated Jacobian to fulfill the latest secant equation. Therefore, the matrices \(\varvec{\uppercase {A}}^k\) and \(\varvec{\uppercase {B}}^k\) only contain the latest piece of secant information:
For all vectors \(\Delta \varvec{\lowercase {a}}\perp \text {range}(\varvec{\uppercase {A}}^k)\) (i.e., \(\Delta \varvec{\lowercase {a}}\perp \delta \varvec{\lowercase {a}}^{k-1}\)), we want to use the previous Jacobian \(\partial ^{k-1}_{\varvec{\lowercase {a}}} \varvec{\lowercase {b}}\). In other words, the effect of the approximated Jacobian remains unchanged in all directions orthogonal to \(\delta \varvec{\lowercase {a}}^{k-1}\). This is called the no-change condition, which can be written formally as
To obtain a Jacobian approximation with these specifications, \(\partial ^{0}_{\varvec{\lowercase {a}}} \varvec{\lowercase {b}}\) is replaced by \(\partial ^{k-1}_{\varvec{\lowercase {a}}} \varvec{\lowercase {b}}\):
where \(\varvec{\uppercase {A}}^k\) and \(\varvec{\uppercase {B}}^k\) now contain only one column. This is a recursive expression for the approximated Jacobian. In fact, this is Broyden’s original method,Footnote 3 to construct the approximate Jacobian [40]. It was developed in the sixties, to solve systems of nonlinear equations.
Furthermore, Broyden’s method can be generalized. Instead of using only one secant condition and the approximate Jacobian from the previous iteration, m secant conditions can be used in combination with the approximate Jacobian from m iterations ago. This gives rise to the generalized Broyden method
with
This equation for the approximate Jacobian in generalized Broyden, however, can also be obtained in a more formal way, namely as the unique matrix that satisfies a number of conditions. Two equivalent ways are described in [41].
First, the approximated Jacobian can be obtained as the only matrix that simultaneously satisfies the m secant conditions in Eq. (34) and the \(n_a - m\) no-change conditions
Secondly, it can be obtained as the unique matrix that satisfies the m secant conditions Eq. (34) and minimizes the difference with the approximate Jacobian from m iterations ago, i.e.
where the subscript F denotes the Frobenius norm.
Furthermore, previously discussed methods are retrieved by choosing certain values for the parameter m in the generalized Broyden method. For \(m=1\), Broyden’s original method is recovered, while for \(m = k\) the pure secant method from Sects. 4.1 and 4.2 is obtained.
The generalized Broyden method was established much later than Broyden’s original method. The first extension to the original one in the eighties led to a rather complex modified Broyden method [42, 43]. In the nineties, Eyert [44] simplified this method by removing some nonessential parameters, resulting in the generalized Broyden method presented here.
Around that same time, the connection between the generalized Broyden method and Anderson acceleration (or Anderson mixing) was discovered. Anderson acceleration [45] was introduced in the sixties to accelerate fixed-point iterations. Based on the work by Van Leuken [46], Eyert showed that Anderson acceleration is mathematically equivalent to generalized Broyden with \(m = k\), i.e., the pure secant method introduced in Sects. 4.1 and 4.2. This is not immediately apparent due to the very different ideas on which Anderson and Broyden originally based their methods.
In partitioned FSI simulations, several variants of the generalized Broyden method are used to approximate Jacobians in quasi-Newton iterations. These techniques were developed independently from the older methods (Anderson, Broyden and generalized Broyden) and the correspondence to those methods was only discovered recently [47, 48].
Because a nonlinear system of equations has to be solved in every time step of an FSI simulation, there are some particularities with respect to Jacobian approximation, such as the reuse of secant information from previous time steps, as well as the removal of old and irrelevant secant information. These topics are discussed in the next section.
Computational complexity and storage This section ends with a first look into the computational complexity to obtain and use these approximate Jacobians. For simplicity, it is assumed that \(\varvec{\lowercase {a}}\) and \(\varvec{\lowercase {b}}\) are both vectors of length \(n_a\). This is usually not true for the block methods, but \(n_b\) is typically proportional to \(n_a\). Further, it is assumed that \(n_a\gg k\), i.e., the length of the vectors are much larger than the number of secant pairs available. More details will be provided later on for the different FSI methods. No details about the number of operations will be given, only the complexity of the leading-order term will be discussed.
At the basis of the generalized Broyden method is the economy-size QR decomposition of \(\varvec{\uppercase {A}}^k\), which is used for determination of the pseudo-inverse of \(\varvec{\uppercase {A}}^k\). This QR decomposition is typically done with Householder transformations, resulting in a complexity of \(\mathcal {O}(n_a m^2)\), which is also the total complexity of the evaluation of the product of this pseudo-inverse with a vector. Already, it can be noted that, in the case that \(m = k\), the computational cost quickly rises relative to a low fixed value for m.
If the approximate Jacobian is only needed to calculate its product with a vector, its explicit construction can be avoided. In some algorithms of the next section, however, the approximate Jacobian is used explicitly. Then, the construction of this \(n_a \times n_a\) matrix has a complexity of \(\mathcal {O}(n_a^2 m)\). In addition, the \(n_a \times n_a\) matrix requires a storage capacity \(\mathcal {O}(n_a^2)\), which is a strong disadvantage of these select algorithms.
In other algorithms, it is possible to avoid this expensive construction and use a matrix-free method to multiply the approximate Jacobian with a vector, i.e., without large dense square matrices. In practice, this is done by evaluating the product using Eq. (47) and multiplying the factors within each term from right to left. Then the complexity of this evaluation is only \(\mathcal {O}(n_a m^2)\), which is the complexity of performing the QR decomposition needed to evaluate the product of the pseudo-inverse of \(\varvec{\uppercase {A}}^k\) with a vector. Because only the secant information has to be stored, the storage requirements \(\mathcal {O}(n_a m)\) are lower as well.
4.4 Difference Between the Anderson and Broyden Approach
The previous part formulated the generalized Broyden method, in which the parameter m determines how the secant information from previous iterations is included. Setting \(m=k\) corresponds to the Anderson method, in which the approximated Jacobian is determined by imposing all secant equations directly. For \(m=1\), Broyden’s original method is retrieved, here simply referred to as the Broyden method, in which the approximated Jacobian only fulfills the latest secant equation and the secant information from the previous iterations is included indirectly by imposing no-change conditions. In this section, the difference in behaviour between these two extreme versions of the generalized Broyden method will be clarified.
Consider for example the approximation of the Jacobian \(\varvec{\mathcal {B}}' \! (\varvec{\lowercase {a}}^k)\) by \(\partial ^{k}_{\varvec{\lowercase {a}}} \varvec{\lowercase {b}}\), when previously three iterations have been performed (\(k=2\)). The matrices containing the differences between consecutive iterations are
Without loss of generality, it is stated that
where \(\varvec{\lowercase {p}}\) and \(\varvec{\lowercase {q}}\) are orthonormal vectors, and x and y real scalars.
In the Anderson approach (\(m=k\)), the approximated Jacobian is
The QR decomposition of \(\varvec{\uppercase {A}}^2\) is given by
With this decomposition, the pseudo-inverse is calculated
Finally, the approximate Jacobian is given by
In the Broyden approach (\(m=1\)), the approximated Jacobian is
Note that the pseudo-inverse of a single column equals its transpose divided by its norm squared, such that
The resulting approximated Jacobian is given by
Comparing Eq. (61) with Eq. (64), it is clear that the Jacobian approximations are different. Their inequality is analyzed in Table 1 by looking at their product with particular vectors \(\Delta \varvec{\lowercase {a}}\).
For a vector \(\Delta \varvec{\lowercase {a}}\) equal to the lastly added difference \(\delta \varvec{\lowercase {a}}^{1}\), both approaches return the corresponding difference \(\delta \varvec{\lowercase {b}}^{1}\), as expected. If the one before last vector \(\delta \varvec{\lowercase {a}}^{0}\) is supplied, the results are different. The Anderson method simply returns \(\delta \varvec{\lowercase {b}}^{0}\), as this method attempts to approximate \(\Delta \varvec{\lowercase {a}}\) as closely as possible using the already available differences. In contrast, the Broyden method does not and returns a linear combination of \(\delta \varvec{\lowercase {b}}^{1}\) and \(\delta \varvec{\lowercase {b}}^{0}\). This approach gives priority to the lastly determined difference \(\delta \varvec{\lowercase {a}}^{1}\) and uses the corresponding \(\delta \varvec{\lowercase {b}}^{1}\) for the orthogonal projection of \(\Delta \varvec{\lowercase {a}}\) on that difference \(\delta \varvec{\lowercase {a}}^{1}\). For a result of the Broyden approach that lies along \(\delta \varvec{\lowercase {b}}^{0}\), a difference orthogonal to the last difference \(\delta \varvec{\lowercase {a}}^{1}\) needs to be supplied. Finally, the result for a general vector is given, where u, v and w are arbitrary scalars and \(\varvec{\lowercase {s}}\) a unit vector orthogonal to \(\varvec{\lowercase {p}}\) and \(\varvec{\lowercase {q}}\).
Both methods decompose \(\Delta \varvec{\lowercase {a}}\) in components along the previously determined vectors \(\delta \varvec{\lowercase {a}}^i\), \(0< i < k-1\), and multiply the respective components with the corresponding vectors \(\delta \varvec{\lowercase {b}}^i\). This is shown graphically in Fig. 5.
The vector \(\Delta \varvec{\lowercase {a}}\) is decomposed along the directions of the previously determined differences. The decomposition is different for the Anderson and Broyden approach. The green line is the direction of the lastly determined difference vector \(\delta \varvec{\lowercase {a}}^1\), the red line corresponds to the one before last \(\delta \varvec{\lowercase {a}}^0\). The red dotted vector is the remaining part after decomposition. The addition of the parts along \(\delta \varvec{\lowercase {a}}^1\) and \(\delta \varvec{\lowercase {a}}^0\) and the remaining part gives the original \(\Delta \varvec{\lowercase {a}}\). (Color figure online)
The Anderson method projects \(\Delta \varvec{\lowercase {a}}\) on all previously determined differences. Therefore, the remaining part
is orthogonal to these differences. The Broyden method projects \(\Delta \varvec{\lowercase {a}}\) first on the lastly obtained difference, and the leftover part on the one before last, and so on. Therefore, the remaining part
is not necessarily orthogonal to these differences. It will, however, always be orthogonal to the last difference onto which the projection was made, i.e., the oldest difference.
The difference between the two methods is essential to how nonlinearities in the secant information are dealt with. In general \(\varvec{\mathcal {B}}(\varvec{\lowercase {a}}^k)\) is nonlinear and its Jacobian is not constant, therefore the secant information will also contain nonlinear effects, especially when the step \(\delta \varvec{\lowercase {a}}^i\) is large. Because the Broyden method prioritizes more recent secant information, it effectively ignores these nonlinearities, while the Anderson method does not, as it wants to approximate \(\Delta \varvec{\lowercase {a}}\) as closely as possible using all available differences. This can lead to instabilities in the Anderson method. However, the Broyden method will also neglect small linear information, slowing down the convergence speed. More details and a method to remove nonlinearities from the secant information to stabilize Anderson are found in [49].
In the FSI community, the Anderson method is referred to as the least-squares approach and the Broyden method can be linked to the multi-vector approach. However, in FSI, fulfilling only the most recent secant equation as in the original Broyden method is typically not done and the multi-vector algorithms fulfill the secant equations in the most recent time step, using no-change conditions for older time steps. So in fact, the multi-vector approach is a generalized Broyden method, as will be explained in the following section.
5 Quasi-Newton Methods for FSI
In Sect. 3, different quasi-Newton schemes have been introduced. They required approximate Jacobians, which could be determined in different ways using information from previous iterations, as explained in Sect. 4. Up to this point, the focus was on solving the nonlinear equations in each time step separately. From here on, the distinction between different time steps will be necessary. Therefore, the superscript \(n+1\) will be used to indicate the values from the current time step, meaning that these are the values that are currently calculated. This notation is similar to the superscript \(k+1\), which indicates the current iteration.
In this section, the IQN-ILS, IBQN-LS, IQN-MVJ, MVQN, IQN-IMVLS and IQN-ILSM techniques will be derived and analyzed in the generalized Broyden framework. These techniques for partitioned FSI simulation have several differences, as summarized in Table 2.
The first difference is whether they use only the interface displacement as variables (IQN-ILS, IQN-MVJ, IQN-IMVLS, IQN-ILSM) or whether they are block iteration quasi-Newton methods using both interface displacement and load (IBQN-LS, MVQN). In the former case, they solve Eq. (12), in the latter they use Eq. (8), as explained in Sect. 3.
The second difference is related to how time stepping is handled, as most FSI simulations are time-dependent to capture a vibration or other dynamic behaviour. Assuming the inputs and outputs of the q previous time steps are stored, one can either impose the secant conditions from all time steps (IQN-ILS, IBQN-LS) or only for the latest time step, combined with no-change conditions for previous time steps (IQN-MVJ, MVQN, IQN-IMVLS, IQN-ILSM). This second difference is thus related to the choice of the parameter m of generalized Broyden, as explained in Sect. 4. On the one hand, m can be set to \(\infty\) (actually limited to q time steps), so all the info from q previous time steps is used together, without an old Jacobian, but only with an initial one to start the procedure. In fact, this corresponds with the Anderson approach and is typically termed least-squares approach in FSI. On the other hand, only the secant info from the current time step can be used, with an old approximate Jacobian that is the final one from the previous time step. This corresponds to \(m=k\), called multi-vector, and is really generalized Broyden, and not one of the limiting cases (Anderson or Broyden).
The third difference is the amount of memory required for the storage of the approximate Jacobian(s) and the computational time required for the calculations related to the quasi-Newton steps. This will be explained more in detail for each method below and will be summarized in Table 3.
5.1 IQN-ILS
IQN-ILS is the abbreviation for Interface Quasi-Newton technique with an approximation for the Inverse of the Jacobian from a Least-Squares model [50]. The IQN-ILS technique performs an update of the input for the flow solver in each coupling iteration, using an approximation for the inverse of the Jacobian of the residual operator, so
and \(\Delta \varvec{\lowercase {r}}^k=\varvec{\lowercase {0}}-\varvec{\lowercase {r}}^k\). The approximation for the inverse Jacobian \({\widehat{{\varvec{{\mathcal {R}}}}'^{-\hbox {1}}}}(\varvec{\lowercase {x}}^k)\equiv \partial ^{k}_{\varvec{\lowercase {r}}} \varvec{\lowercase {x}}\) can be obtained directly by following the method explained in Sect. 4.3 for \(\partial ^{k}_{\varvec{\lowercase {a}}} \varvec{\lowercase {b}}\), with \(\varvec{\lowercase {a}}=\varvec{\lowercase {r}}\) and \(\varvec{\lowercase {b}}=\varvec{\lowercase {x}}\). Because the approximation needs to be full rank for a working quasi-Newton method, an initial Jacobian \(\partial ^{k-m}_{\varvec{\lowercase {r}}} \varvec{\lowercase {x}}=-\varvec{\uppercase {I}}\) is used, which is the Jacobian of Gauss–Seidel iteration, as explained below Eq. (21). In the literature, however, the approximation for the inverse of the Jacobian \({\widehat{{\varvec{{\mathcal {R}}}}'^{-\hbox {1}}}}(\varvec{\lowercase {x}}^k)\) is usually rewritten using the identity \(\varvec{\lowercase {r}}=\tilde{\varvec{\lowercase {x}}}-\varvec{\lowercase {x}}\), giving
where the operator \(\partial _{\varvec{\lowercase {r}}}^k\tilde{\varvec{\lowercase {x}}}\) is constructed as explained in Sect. 4.3, with \(\varvec{\lowercase {a}}=\varvec{\lowercase {r}}\) and \(\varvec{\lowercase {b}}=\tilde{\varvec{\lowercase {x}}}\). In this way of explaining, no initial Jacobian is used, so \(\partial ^{k-m}_{\varvec{\lowercase {r}}} \tilde{\varvec{\lowercase {x}}}=\varvec{\uppercase {0}}\). It is worth mentioning that if instead of the inverse, the Jacobian \({\varvec{\mathcal {R}}}'(\varvec{\lowercase {x}}^k)\) is approximated, the Interface Quasi-Newton Least-Squares method (IQN-LS) is retrieved [51].
For an FSI simulation with a single step (e.g., a steady simulation), the generalized Broyden formula in Eq. (52) is used with \(m=k\) and without initial guess \(\partial ^{0}_{\varvec{\lowercase {r}}} \tilde{\varvec{\lowercase {x}}}=\varvec{\uppercase {0}}\), so
with
Note that \(\partial ^{k}_{\varvec{\lowercase {r}}} \tilde{\varvec{\lowercase {x}}}\) has at most rank k, while \({\widehat{{\varvec{{\mathcal {R}}}}'^{-\hbox {1}}}}(\varvec{\lowercase {x}}^k)\equiv \partial ^{k}_{\varvec{\lowercase {r}}} \varvec{\lowercase {x}}\) is full-rank.Footnote 4
In a time-dependent simulation, the secant information from the q previous time steps can be reused. As notation, the previous time steps are indicated with n, \(n-1\), \(\ldots\), \(n+1-q\), for the time step that is being calculated the superscript \(n+1\) is omitted and only the superscript k is used. The matrices \(\varvec{\uppercase {R}}^{\![\!k\!]\!}\) and \(\widetilde{\varvec{\uppercase {X}}}^{\![\!k\!]\!}\) are a concatenation of the matrices from the different time steps, giving
In this way, the information from each time step is treated equally, except when linear dependencies occur, because these are then removed by filtering, as will be explained below. The method thus satisfies all available secant conditions, i.e., from time step \(n+1\) and the q previous time steps. Consequently, m is equal to the number of columns in \(\varvec{\uppercase {R}}^{\![\!k\!]\!}\) and \(\widetilde{\varvec{\uppercase {X}}}^{\![\!k\!]\!}\), which is
if no filtering is applied. As no initial Jacobian \(\partial ^{k-m}_{\varvec{\lowercase {r}}} \tilde{\varvec{\lowercase {x}}}\) is used, the information from earlier time steps \(n < n+1-q\) is not considered. It is important to remark that the difference between the first \(\varvec{\lowercase {r}}\) or \(\tilde{\varvec{\lowercase {x}}}\) of a time step and the last one from the previous time step is not used. Only differences between vectors of the same time steps are taken into account. This approach ensures that the secant information matches with the meaning of the Jacobian that is being approximated, which is the derivative within a time step, and not between them.
The reuse parameter q has to be defined by the user. Reuse typically improves the performance, but too old data is no longer helping the convergence, and therefore an optimal value exists. In the literature, the existence of this parameter is often cited as a drawback of IQN-ILS, because the performance of the method would be sensitive to this parameter. However, by using filtering, the performance of the method is rendered rather insensitive to this parameter around the optimum, as is shown by numerical tests in Sect. 6 and in other work [52, 53]. Moreover, the parameter q allows the user to control how many time steps can be considered relevant, which is important in cases with rapid changes from one time step to the next, e.g., with multi-phase flows [54].
Matrix-free implementation Equation (69) is a symbolic notation to write IQN-ILS in the generalized Broyden framework, but this matrix should never be constructed or stored in the computer’s memory. One of the main benefits of IQN-ILS is its so-called matrix-free character, which means that no large square matrices need to be constructed or stored. The product of the approximation of the inverse of the Jacobian with \(\Delta \varvec{\lowercase {r}}^k=-\varvec{\lowercase {r}}^k\) in Eq. (67) is symbolically calculated as
In practice, the product \(\varvec{\lowercase {c}}^k={\varvec{\uppercase {R}}^{\![\!k\!]\!}}^+ \ \Delta \varvec{\lowercase {r}}^k\) of the pseudo-inverse of \(\varvec{\uppercase {R}}^{\![\!k\!]\!}\) with \(\Delta \varvec{\lowercase {r}}^k\) is calculated using the economy-size QR decomposition and back-substitution, resulting in
as explained in Algorithm 1. The vector \(\Delta \varvec{\lowercase {r}}^k\) is thus written as a linear combination of the \(\delta \varvec{\lowercase {r}}^i\), resulting in coefficients \(\varvec{\lowercase {c}}^k\). As each \(\delta \varvec{\lowercase {r}}^i\) has a corresponding \(\delta \tilde{\varvec{\lowercase {x}}}^i\), the change in \(\tilde{\varvec{\lowercase {x}}}\) corresponding with \(\Delta \varvec{\lowercase {r}}^k\) can be obtained by calculating \(\widetilde{\varvec{\uppercase {X}}}^{\![\!k\!]\!}\varvec{\lowercase {c}}^k\).
The complete procedure can be found in Algorithm 2, with a relaxation step with factor \(\omega\) on line 7, for the case in which \(\varvec{\uppercase {R}}^{\![\!k\!]\!}\) and \(\widetilde{\varvec{\uppercase {X}}}^{\![\!k\!]\!}\) do not have any columns, e.g., at the beginning of the simulation.
Using \(\varvec{\uppercase {R}}^{\![\!k\!]\!}=\widetilde{\varvec{\uppercase {X}}}^{\![\!k\!]\!}-\varvec{\uppercase {X}}^{\![\!k\!]\!}\), where \(\varvec{\uppercase {X}}^{\![\!k\!]\!}\) is defined analogous to Eq. (71), Eq. (73) can be rewritten as
This shows that \(\Delta \varvec{\lowercase {r}}^k\) is split into a part \(\varvec{\uppercase {R}}^{\![\!k\!]\!}{\varvec{\uppercase {R}}^{\![\!k\!]\!}}^+\Delta \varvec{\lowercase {r}}^k\) in the column span of \(\varvec{\uppercase {R}}^{\![\!k\!]\!}\) and a part \((\varvec{\uppercase {I}}-\varvec{\uppercase {R}}^{\![\!k\!]\!}{\varvec{\uppercase {R}}^{\![\!k\!]\!}}^+)\Delta \varvec{\lowercase {r}}^k\) perpendicular to it. The secant-based approximate Jacobian \(\varvec{\uppercase {X}}^{\![\!k\!]\!}{\varvec{\uppercase {R}}^{\![\!k\!]\!}}^+\) is applied to the former, while Gauss–Seidel iteration with Jacobian \(-\varvec{\uppercase {I}}\) is used for the latter.
Filtering When columns of \(\varvec{\uppercase {R}}^{\![\!k\!]\!}\) are linearly dependent up to a tolerance \(\epsilon _f\), the diagonal elements of \(\varvec{\uppercase {R}}_R^{\![\!k\!]\!}\) in Eq. (74) become small and this system can no longer be solved accurately. Hence, an essential component of IQN-ILS is filtering, especially when data from previous time steps is reused [50]. Columns of \(\varvec{\uppercase {R}}^{\![\!k\!]\!}\) that are linearly dependent up to the tolerance \(\epsilon _f\) need to be removed together with the matching columns in \(\widetilde{\varvec{\uppercase {X}}}^{\![\!k\!]\!}\). As the newest information is stored on the left-hand side in \(\varvec{\uppercase {R}}^{\![\!k\!]\!}\), a \(\delta \varvec{\lowercase {r}}^i\) that is a linear combination of newer \(\delta \varvec{\lowercase {r}}^j\) (j > i) is removed. Columns can be removed if \(\left|R^{\![\!k\!]\!}_{R,ii}\right|<\epsilon _f\) (QR0) or \(\left|R^{\![\!k\!]\!}_{R,ii}\right|<\epsilon _f\left\Vert \varvec{\uppercase {R}}^{\![\!k\!]\!}_R\right\Vert _2\) (QR1), with \(R^{\![\!k\!]\!}_{R,ii}\) referring to a diagonal element of \(\varvec{\uppercase {R}}^{\![\!k\!]\!}_R\) [55]. The advantage of the first approach is that the tolerance \(\epsilon _f\) can be set by perturbing \(\varvec{\lowercase {x}}\) with smaller and smaller changes until the change in \(\tilde{\varvec{\lowercase {x}}}\) is no longer smooth, but numerical noise. In this case, the tolerance \(\epsilon _f\) can be considered as a measure of how accurate the flow solver and structural solver are calculating their solution. This filtering procedure is shown step by step in Algorithm 3. Obviously, it will be difficult to obtain convergence of the coupling iterations to a level that is lower than \(\epsilon _f\).
Alternative filtering approaches are algebraic QR filtering and POD filtering [55]. In the algebraic filtering method (QR2), a column is removed if the diagonal element \(\left|R^{\![\!k\!]\!}_{R,ii}\right|<\epsilon _f\left\Vert \varvec{\uppercase {R}}^{\![\!k\!]\!}_{R,i}\right\Vert _2\), with \(\varvec{\uppercase {R}}^{\![\!k\!]\!}_{R,i}\) referring to column i of matrix \(\varvec{\uppercase {R}}^{\![\!k\!]\!}_R\). In the POD filtering, the eigenvalues of the autocorrelation matrix of \(\varvec{\uppercase {R}}^{\![\!k\!]\!}\) are used to truncate old data. The numerical tests in [55] showed that algebraic QR filtering worked better than POD filtering or filtering using \(\left|R^{\![\!k\!]\!}_{R,ii}\right|<\epsilon _f\left\Vert \varvec{\uppercase {R}}^{\![\!k\!]\!}_R\right\Vert _2\). However, the comparison with \(\left|R^{\![\!k\!]\!}_{R,ii}\right|<\epsilon _f\) was not performed and remains as an interesting future work. Because the latter is directly related to the solver tolerances themselves, as explained above, it has been chosen for this work.
Another reason to do filtering is to limit the number of secant conditions in cases with few degrees of freedom on the interface. Typically, \(m \ll n_x\), but with only few degrees of freedom on the interface, the oldest columns of \(\varvec{\uppercase {R}}^{\![\!k\!]\!}\) and \(\widetilde{\varvec{\uppercase {X}}}^{\![\!k\!]\!}\) need to be removed such that there are at most \(n_x\) columns, to avoid an overdetermined Jacobian.
Computational complexity and storage The additional storage required for the IQN-ILS method is the matrices \(\varvec{\uppercase {R}}^{\![\!k\!]\!}\) and \(\widetilde{\varvec{\uppercase {X}}}^{\![\!k\!]\!}\), both \(\in \mathbb {R}^{n_x\times m}\). Temporary storage is necessary for \(\varvec{\uppercase {Q}}_R^{\![\!k\!]\!}\in \mathbb {R}^{n_x\times m}\) and \(\varvec{\uppercase {R}}^{\![\!k\!]\!}_R\in \mathbb {R}^{m\times m}\), and the small vector \(\varvec{\lowercase {c}}^k\in \mathbb {R}^{m}\). The storage thus scales linearly with the number of degrees of freedom in the interface’s discretization. Furthermore, m can be reduced compared to Eq. (72) due to filtering. A rule of thumb is that it is typically not beneficial to include more than 50 columns.
The economy-size QR decomposition of \(\varvec{\uppercase {R}}^{\![\!k\!]\!}\) has at most a complexity of \(\mathcal {O}(n_x m^2)\) if the fast Givens method or the Householder method is used [38]. The matrix–vector product in the right-hand side of Eq. (74) has a computational complexity of \(\mathcal {O}(n_x m)\) and solving the triangular system a complexity of \(\mathcal {O}(m^2)\). Consequently, also the computational complexity scales linearly with \(n_x\) and is limited. In numerical tests, the IQN-ILS algorithm normally accounts for less than 1% of the total CPU time.


5.2 IBQN-LS
IBQN-LS stands for Interface Block Quasi-Newton method with approximation of the Jacobians using Least-Squares models (initially called reduced-order models) [21]. It uses the formulation in Eq. (25) and solves Eq. (26) and Eq. (27) in turn for \(\Delta \varvec{\lowercase {x}}^k\) and \(\Delta \varvec{\lowercase {y}}^k\). Low-rank approximations for \(\varvec{\mathcal {F}}'(\varvec{\lowercase {x}}^k)\) and \(\varvec{\mathcal {S}}'(\varvec{\lowercase {y}}^k)\) are constructed using the generalized Broyden method with m as in Eq. (72) and without initial value for the Jacobian, so like in IQN-ILS. The reuse of previous time steps and the filtering are also applied in the same way as explained above. Consequently, this technique enforces all secant conditions from the current and q previous time steps, for both the flow solver and the structural solver.
For the approximate Jacobian of the flow solver \({\widehat{\varvec{{\mathcal {F}}}'}}(\varvec{\lowercase {x}}^k)\), the generalized Broyden framework is applied using \(\varvec{\lowercase {a}}=\varvec{\lowercase {x}}\) and \(\varvec{\lowercase {b}}=\tilde{\varvec{\lowercase {y}}}\). For m as in Eq. (72) and without initial value for the Jacobian this can be written symbolically as
with
where the secant information from the q previous time steps is combined with that from the current time step
A symbolic formulation of the approximation \({\widehat{\varvec{{\mathcal {S}}}'}}\) in the generalized Broyden framework can be obtained in a similar way, using \(\varvec{\lowercase {a}}=\varvec{\lowercase {y}}\) and \(\varvec{\lowercase {b}}=\tilde{\varvec{\lowercase {x}}}\).
A disadvantage of this technique is that two linear systems need to be solved in each coupling iteration. In the original version, the \(n_x\times n_x\) and \(n_y\times n_y\) matrices corresponding with these systems were explicitly constructed using the symbolic notations as in Eq. (76) and they were solved with a direct linear solver [21]. However, by adopting an iterative linear solver like GMRES, only a procedure to calculate the product of the approximate Jacobians with a vector is required [56]. In practice, the number of iterations for the iterative solver is close to the number of columns used for the approximate Jacobians. Alternatively, the Woodbury matrix identity can be used to obtain a closed expression for the update [57].
Matrix-free implementation This matrix-free procedure will be explained here for the flow solver. When the product of \({\widehat{\varvec{{\mathcal {F}}}'}}(\varvec{\lowercase {x}}^k)\equiv \partial ^{k}_{\varvec{\lowercase {x}}} \varvec{\lowercase {y}}\) with a vector \(\Delta \varvec{\lowercase {x}}^k\) needs to be calculated during the iterative solution of Eqs. (26) or (27), this can symbolically be written as
For the practical implementation, Algorithm 1 is followed and this computation is split in two parts by the introduction of a coefficient vector \(\varvec{\lowercase {c}}^k\), giving
with \(\varvec{\lowercase {c}}^k\) the solution of
The last part is the least-squares solution to an overdetermined system that can be solved efficiently by calculating the economy-size QR decomposition, followed by using back-substitution.
To summarize this procedure, the \(\Delta \varvec{\lowercase {x}}^k\) is decomposed as a linear combination of the columns in \(\varvec{\uppercase {X}}^{\![\!k\!]\!}\), then the observation is made that columns in \(\varvec{\uppercase {X}}^{\![\!k\!]\!}\) and \(\widetilde{\varvec{\uppercase {Y}}}^{\![\!k\!]\!}\) with the same index form a secant pair, such that the result can be approximated as the same linear combination of the columns in \(\widetilde{\varvec{\uppercase {Y}}}^{\![\!k\!]\!}\), as shown in Eq. (80). The complete procedure can be found in Algorithm 4.
Computational complexity and storage Compared to IQN-ILS, IBQN-LS requires approximately twice the memory, as the data for two approximate Jacobians needs to be stored. Furthermore, even though the matrix-free procedure with the iterative linear solver is faster than explicit matrix construction and direct linear solver, the computing time is higher than for IQN-ILS, where none of this is required. Nevertheless, the time required for the coupling algorithm scales linearly with \(n_x\) and \(n_y\) and thus remains small compared to that of the actual solvers. The solution of the linear systems could be avoided by writing the solution to Eqs. (26) and (27) symbolically, using matrix inverses and applying the Woodbury matrix identity as in [57]. In this way, the size of the matrices that have to be inverted is reduced from \(n_x\) and \(n_y\) to m.

5.3 MVQN
MVQN is the abbreviation for Multi-Vector update Quasi-Newton [58]. This method is based on the IBQN-LS method and is even identical to it in the first time step. However, the differences appear when data from previous time steps is included. MVQN considers the current Jacobian as the sum of the Jacobian from the previous time step plus a rank-k update. This update is then determined by enforcing the secant conditions from the current time step and minimizing the Frobenius norm of the update. This coincides with the generalized Broyden method with \(m=k^{n+1}\) and the initial Jacobian equal to the one from the previous time step.
Considering again the approximate Jacobian of the flow solver \({\widehat{\varvec{{\mathcal {F}}}'}}\), the generalized Broyden framework is applied using \(\varvec{\lowercase {a}}=\varvec{\lowercase {x}}\) and \(\varvec{\lowercase {b}}=\tilde{\varvec{\lowercase {y}}}\). The value m is now \(k=k^{n+1}\) and the initial value for the Jacobian is the one for the previous time step, giving
Using the definition of the pseudo-inverse in Eq. (36), this can be reformulated as
which corresponds with the original formulation in [58]. However, analyzing this method is most straightforward when considering Eq. (81). If this approximate Jacobian is multiplied with a vector \(\Delta \varvec{\lowercase {x}}\), then the secant information from the most recent time step is used for the part for which it is available, i.e., within the column span of the matrix \(\varvec{\uppercase {X}}^{k}\). The previous approximate Jacobian is only multiplied with the leftover part of \(\Delta \varvec{\lowercase {x}}\), i.e., the part orthogonal to the column span of \(\varvec{\uppercase {X}}^{k}\). So, even if secant information from previous time steps is available for the first part of \(\Delta \varvec{\lowercase {x}}\), it will not be used. This relates to the difference between the least-squares and multi-vector approach explained in Sect. 4.4. The matrix \({\widehat{\varvec{{\mathcal {S}}}'}}\) is constructed in a similar way
Computational complexity and storage The main benefits of this method are that no parameter q is required and that filtering with a tolerance \(\epsilon _f\) is typically less essential as only a relatively small number of secant conditions from the most recent time step are considered. However, this comes at a significant cost, as the matrices \({\widehat{\varvec{{\mathcal {F}}}'}}\) and \({\widehat{\varvec{{\mathcal {S}}}'}}\) are constructed and stored in memory, such that the algorithm scales with \(n_x^2\) and \(n_y^2\), both in terms of memory use as in computational complexity. Combined with the linear systems that have to be solved in each coupling iteration, this becomes expensive compared to the actual solver for a reasonably large number of degrees of freedom on the interface (e.g., more than \(10^4\)). A linearly scaling adaptation is the RandomiZed Multi-Vector Quasi-Newton method (MVQN-RZ) [57], which will be explained in more detail with the other linearly scaling multi-vector methods at the end of Sect. 5.4.

5.4 IQN-MVJ
The IQN-MVJ method is an acronym for Interface Quasi-Newton with Multi-Vector Jacobian [59]. This method adopts the idea for reuse from previous time steps proposed in MVQN and transfers it from the block iteration to the residual formulation quasi-Newton scheme, i.e., with only the interface displacement as variable. It is thus a generalized Broyden method which satisfies the secant conditions from the current time step while using the Jacobian from the previous time step as initial value. IQN-MVJ is linked with IQN-ILS in the same way as MVQN is linked with IBQN-LS. Except for the explicit construction of the approximate Jacobian, this method is identical to IQN-ILS in the first time step.
In IQN-MVJ, the approximation for the inverse of the JacobianFootnote 5 is thus constructed as
with
Using the definition of the pseudo-inverse in Eq. (36), this can be reformulated as
which corresponds with the original formulation in [59].
Computational complexity and storage The main drawback of IQN-MVJ is that the square matrix with the approximation for the inverse of the Jacobian is constructed and stored in memory, such that computational cost and memory requirement scale with \(n_x^2\). Consequently, like MVQN, this approach becomes expensive compared to the solvers for a reasonably large number of degrees of freedom on the interface (e.g., more than \(10^4\)).
To avoid this scaling and achieve linear complexity in \(n_x\) and at the same time attempt to avoid a reuse parameter q, a matrix-free version of IQN-MVJ has been developed, named IQN-MVJ-RS-SVD [60]. Thereto, the approximation in Eq. (86) is reformulated as
with
To avoid storage of a square matrix, this can be written using a recursive formula
starting from \(\partial ^{0}_{\varvec{\lowercase {r}}} \tilde{\varvec{\lowercase {x}}}{}=\varvec{\uppercase {0}}\) at time 0. Obviously, this requires storage of matrices \(\bar{\widetilde{\varvec{\uppercase {X}}}{}}\) and \(\varvec{\uppercase {R}}\) for each time step, which is beneficial as long as the total number of columns is significantly smaller than \(n_x\). However, after a high number of time steps, this becomes prohibitively expensive and therefore three strategies are proposed in which the simulation is split into so-called chunks consisting of \(q'\) time steps after which a restart is performed [60]. The authors concluded that the IQN-MVJ-RS-SVD algorithm with a Singular Value Decomposition (SVD) restart strategy is the most promising. The approximate inverse Jacobian at the end of a chunk is then truncated by performing an SVD and truncating the singular values below a tolerance \(\epsilon _f'\). This truncated SVD is then the initial Jacobian for the following chunk. Furthermore, the SVD is efficiently updated at the end of each chunk. As opposed to the original IQN-MVJ, the IQN-MVJ-RS-SVD method has linear complexity in \(n_x\), but the implementation is more elaborate than for IQN-MVJ. Compared to IQN-ILS, which has a reuse parameter q and QR filter tolerance \(\epsilon _f\) and also has linear scaling in \(n_x\), this method now requires a chunk size parameter \(q'\) and SVD filter tolerance \(\epsilon _f'\), but with the claim that the performance is less sensitive to these parameters.
Another multi-vector method that achieves linear scaling memory requirements is the algorithm MVQN-RZ [57], which employs the randomized SVD not only to avoid the explicit construction of large square matrices, but also to circumvent the recursive reconstruction of the interface Jacobian. This algorithm has been applied to both block iteration quasi-Newton techniques and residual formulation quasi-Newton techniques. In every coupling iteration, the complexity of MVQN-RZ is \(\mathcal {O}(z^2 n_x + k^2 n_x)\), where z is the number of decomposition modes. This compares to IQN-MVJ-RS-SVD with a complexity of \(\mathcal {O}(z^2 n_x + k^2 n_x + M k n_x + k^4)\) in every coupling iteration, with z referring to the number of eigenvalues left after truncation and M the simulation chunk size. Additionally, this method requires an SVD update after every M steps, which has a complexity of \(\mathcal {O}(M z^2 n_x)\). In providing these complexities, it is assumed that \(n_x \gg k,z,M\).

5.5 IQN-IMVLS
To mitigate the quadratic scaling in \(n_x\) of IQN-MVJ, the IQN-IMVLS (Interface Quasi-Newton Implicit Multi-Vector Least-Squares) method has been developed with linear complexity in \(n_x\) [53]. The first observation is that the factor \(\widetilde{\varvec{\uppercase {X}}}{}^{k}-\partial ^{n}_{\varvec{\lowercase {r}}} \tilde{\varvec{\lowercase {x}}}{} \ \varvec{\uppercase {R}}^{k}\) in Eq. (86) can be updated by adding one additional column in each coupling iteration, instead of recomputing it entirely
so only the product \(\partial ^{n}_{\varvec{\lowercase {r}}} \tilde{\varvec{\lowercase {x}}}{} \ \delta \varvec{\lowercase {r}}^{k-1}\) needs to be evaluated.
Determining the product of \(\partial ^{n}_{\varvec{\lowercase {r}}} \tilde{\varvec{\lowercase {x}}}{}\) with a vector requires a procedure to calculate a matrix–vector product. It is proven in [53] that \(\partial ^{n}_{\varvec{\lowercase {r}}} \tilde{\varvec{\lowercase {x}}}{}\) in Eq. (86) can be reformulated as
if the initial Jacobian is assumed to be zero. This recursive formulation can be truncated after q terms, giving
In IQN-IMVLS the reuse parameter q typically does not exhibit an optimum in terms of performance. Instead, both performance and computational cost grow with increasing values of q as the method converges towards the IQN-MVJ approach.
Computational complexity and storage As can be observed in Eq. (92), this procedure requires the storage of \({\varvec{\uppercase {R}}^j}^+=\left( {\varvec{\uppercase {R}}^j}^\textrm{T}\varvec{\uppercase {R}}^j\right) ^{-1} {\varvec{\uppercase {R}}^j}^\textrm{T}\) for the q previous time steps. If the inverse of \({\varvec{\uppercase {R}}^j}^\textrm{T}\varvec{\uppercase {R}}^j\) is calculated via the LU decomposition using partial pivoting with row interchanges [38], then this scales with \(n_x\), but has slightly less robustness to bad conditioning than the Householder QR approach. As a result, the complete procedure has linear complexity in \(n_x\), like IQN-ILS. In addition, the QR decomposition is only applied on the secant information from the most recent time step, as opposed to the matrix with the secant information from all time steps in IQN-ILS. As not all secant information is combined into one matrix, the sensitivity to (almost) linear dependencies is smaller. Furthermore, no restart is required, but the implementation is a bit more involved than IQN-ILS or IQN-MVJ. It was also observed in [53] that including the secant information from the previous time step in \(\widetilde{\varvec{\uppercase {X}}}{}\) and \(\varvec{\uppercase {R}}\) as well can accelerate the convergence, especially at the beginning of a time step. The complete procedure can be found in Algorithm 7.

5.6 IQN-ILSM
All techniques mentioned above use the flow solver and structural solver as black boxes, while sometimes the user has additional insight into the behaviour of the problem. This additional information can be incorporated to accelerate the convergence of the coupling iterations using the Interface Quasi-Newton algorithm with an approximation for the Inverse of the Jacobian from a Least-Squares model and additional Surrogate Model method (IQN-ILSM) [61]. In this technique, the secant information is combined with a so-called surrogate model, which behaves similarly to the actual solvers but is significantly faster. The origins of this technique can be found in the FreQ-LeSS algorithm for free-surface calculation, where secant conditions from previous flow solver iterations was combined with an analytical model of the problem [62, 63].
The surrogate model is denoted as \({\varvec{\mathcal {R}}}_s\) and the subscript s will be used to denote quantities related to the surrogate model. The inverse Jacobian of \({\varvec{\mathcal {R}}}_s\) with respect to \(\tilde{\varvec{\lowercase {x}}}{}\) is referred to as the surrogate Jacobian, which is assumed to stay the same during the entire time step. A procedure to calculate the product of this matrix with a vector is sufficient, without requiring construction and storage. To emphasize this matrix-free aspect, the surrogate Jacobian is represented by a function \(\partial ^{}_{\varvec{\lowercase {r}}} \tilde{\varvec{\lowercase {x}}}{}_s(\cdot )\). Furthermore, this surrogate Jacobian can be either full-rank or only a low-rank approximation, with column space \(\varvec{\uppercase {R}}_s\). At the end of each time step, the surrogate model is synchronized with the original model by interpolating the solution from the latter to the former. This approach avoids large discrepancies between the original model and the surrogate model after some time steps.
To gain insight in the IQN-ILSM technique, Eq. (75b) should first be revisited. This equation shows how IQN-ILS splits \(\Delta \varvec{\lowercase {r}}^k\) in a part \(\varvec{\uppercase {R}}^k{\varvec{\uppercase {R}}^k}^+\Delta \varvec{\lowercase {r}}^k\) in the column span of \(\varvec{\uppercase {R}}^k\) and a part \((\varvec{\uppercase {I}}-\varvec{\uppercase {R}}^k{\varvec{\uppercase {R}}^k}^+)\Delta \varvec{\lowercase {r}}^k\) orthogonal to it, using secant conditions for the former and Gauss–Seidel iteration for the latter. The term \((\varvec{\uppercase {I}}-\varvec{\uppercase {R}}^k{\varvec{\uppercase {R}}^k}^+)\Delta \varvec{\lowercase {r}}^k\) for which no secant information is known can now be split once more into a part \(\varvec{\uppercase {R}}_s{\varvec{\uppercase {R}}_s}^+\left( \varvec{\uppercase {I}}-\varvec{\uppercase {R}}^k{\varvec{\uppercase {R}}^k}^+\right) \Delta \varvec{\lowercase {r}}^k\) for which the surrogate model has information and the remainder \(\left( \varvec{\uppercase {I}}-\varvec{\uppercase {R}}_s{\varvec{\uppercase {R}}_s}^+\right) \left( \varvec{\uppercase {I}}-\varvec{\uppercase {R}}^k{\varvec{\uppercase {R}}^k}^+\right) \Delta \varvec{\lowercase {r}}^k\) for which Gauss–Seidel iteration is the best option. Obviously, the latter is zero if the surrogate Jacobian is full-rank. The split of \(\Delta \varvec{\lowercase {r}}^k\) and the approximate Jacobian used for each part can be written as
Note that this equation is written in terms of \(\varvec{\uppercase {X}}^k\) rather than \(\widetilde{\varvec{\uppercase {X}}}{}^k\) and that \(\partial ^{}_{\varvec{\lowercase {r}}} \varvec{\lowercase {x}}_s(\cdot )\) is used rather than \(\partial ^{}_{\varvec{\lowercase {r}}} \tilde{\varvec{\lowercase {x}}}{}_s(\cdot )\). Here \(\partial ^{}_{\varvec{\lowercase {r}}} \varvec{\lowercase {x}}_s\) refers to \(\partial ^{}_{\varvec{\lowercase {r}}} \tilde{\varvec{\lowercase {x}}}{}_s-\varvec{\uppercase {R}}_s{\varvec{\uppercase {R}}_s}^+\) and not to the full-rank Jacobian \(\partial ^{}_{\varvec{\lowercase {r}}} \tilde{\varvec{\lowercase {x}}}{}_s-\varvec{\uppercase {I}}\) as was the case in Eq. (68). Equation (93) shows that the secant conditions have the highest priority, followed by the surrogate Jacobian and then Gauss–Seidel iteration. In the first coupling iteration, there are no secant conditions yet, so the surrogate Jacobian plays an important role. The contribution of the secant conditions will then become more significant during the coupling iterations as the column span of \(\varvec{\uppercase {R}}^k\) gradually increases. The expression in Eq. (93) can be simplified by using Jacobians with respect to \(\tilde{\varvec{\lowercase {x}}}{}\) instead, giving
These expressions can be expanded by including multiple surrogate models in a similar way.
Several types of surrogate models can be considered. A first type is a coarse grid version of the original problem, using the same solvers. When using such a surrogate model, it is important to note that the secant information obtained on the original grid and on the coarse grid is not combined. The surrogate Jacobian thus also uses the coarse grid and interpolation is performed when it needs to be multiplied with a vector from the original grid. A second option is to use solvers with simplified physics, such as solvers neglecting viscosity or nonlinearity. If the simplified physics solvers have a known Jacobian, e.g., because they are analytical functions, then the surrogate Jacobian will typically be constructed and stored but it will be full-rank and only a relatively small matrix.
Another option for the surrogate is reuse from previous time steps in a time-dependent simulation. As opposed to the previously mentioned surrogate types, this surrogate model does not require the solution of a separate problem and no synchronization at the end of each time step, so it is essentially free. The reuse of q previous time steps corresponds to q nested surrogate models, with decreasing importance when for older time steps, giving
with \(\widetilde{\varvec{\uppercase {X}}}{}^i\) and \(\varvec{\uppercase {R}}^i\) containing the secant information from time step i. This equation can be condensed to
When calculating the product \(\prod _{i+1}^{n+1}(\varvec{\uppercase {I}}-\varvec{\uppercase {R}}^j{\varvec{\uppercase {R}}^j}^+)\Delta \varvec{\lowercase {r}}^k\) for each of the terms in the summation, the value in the previous term is stored and updated with one factor for the next term. Therefore the summation is in fact done in reverse order (\(n+1 \xrightarrow {} n+1-q\)). The IQN-ILSM algorithm can be found in Algorithm 8 and an efficient calculation of \(\Delta \varvec{\lowercase {x}}_s=\partial ^{}_{\varvec{\lowercase {r}}} \tilde{\varvec{\lowercase {x}}}{}_s(\cdot )\) in the case of reuse from previous time steps in Algorithm 9.
Computational complexity and storage While in IQN-ILS the QR decomposition is applied on the secant information from all time steps combined in each coupling iteration, IQN-ILSM with reuse as surrogate only applies the QR decomposition on the data from the current time step during the coupling iterations. The QR decomposition of the data from previous time steps is stored and does not need to be updated. This difference is reflected in the computational cost, which scales as \({\mathcal {O}}(n_x(q\bar{k})^2)\) for IQN-ILS and \({\mathcal {O}}(n_x\bar{k}^2)\) for IQN-ILSM, with \(\bar{k}\) the number of coupling iterations averaged over the time steps. Moreover, as IQN-ILSM does not combine the secant conditions from all time steps in a single matrix, it typically does not require filtering, as opposed to IQN-ILS.
By comparing Eq. (96) with Eq. (92), it can be observed that the IQN-ILSM method with reuse as surrogate is identical to the IQN-IMVLS method, except for some implementation aspects mentioned in Sect. 5.5. IQN-ILSM can thus be considered as a generalization of IQN-IMVLS such that not only reuse of secant information from previous time steps, but also physics-based surrogate models can be used, although it was not developed as such. Furthermore, the IQN-ILSM method can be interpreted as part of a larger class of methods which combine data-driven relations with physics-based knowledge [64].
In addition to providing a surrogate Jacobian to accelerate the convergence of the coupling iterations, the surrogate can also provide an initial guess for the coupling iterations. This prediction can be found in line 5 of Algorithm 8. When reuse from previous time steps is the surrogate model, this corresponds to linear extrapolation.


5.7 Other Algorithms
Besides the already mentioned techniques, there are many other variants, a selection of which is touched upon below.Footnote 6 This section ends with an outlook to the application of quasi-Newton coupling techniques outside of the field of fluid–structure interaction.
Jacobi iteration and high-performance computing The algorithms mentioned above are all using a sequential solution of the flow problem and structural problem. So, they can be considered related to Gauss–Seidel iteration, as opposed to Jacobi iteration which is characterized by simultaneous solution of both problems. For several of the quasi-Newton coupling techniques mentioned in this review, similar techniques are available based on Jacobi iteration [65]. For linear systems, Gauss–Seidel iteration inherently converge faster than Jacobi iteration, and this typically also holds for nonlinear systems, such as the FSI problem [66]. However, the higher number of iterations in a Jacobi-based method may be compensated by its better parallel scalability, although this is not guaranteed. Therefore, the difference in parallel scalability between both iterations types will be explained in the following lines. For Gauss–Seidel iteration, the flow and structure solvers are run sequentially, so both solvers can use all available CPU cores. However, the work load and the parallel efficiency of both solvers is typically very different, and often much higher for the flow solver. If the structure solver does not scale up well to a large number of cores, this leads to a low parallel efficiency, or analogously a number of idle cores. This problem is overcome by Jacobi iteration where the flow and structure solvers are calculating simultaneously. The cores are distributed over the two solvers such that both solvers require the same amount of calculation time, i.e., they are perfectly balanced, but this load balancing may not be trivial. Furthermore, specific variants of quasi-Newton methods have been developed for High-Performance Computing (HPC) such as the Compact Interface Quasi-Newton method (CIQN) [67], which is a parallel adaptation of IQN-ILS focused on efficiently combining partitions to realize a scalable implementation.
Multi-solver variants Also Multi-Solver (MS) versions of both IQN-ILS and IBQN-LS have been developed [68]. Once an FSI simulation can no longer be accelerated by increasing the number of cores per solver, the multi-solver algorithms can be applied for an additional speed-up. These multi-solver algorithms reduce the calculation time by running multiple instances of the flow solver and structural solver, while keeping the number of cores per solver constant and running each instance on one or more cluster nodes. One instance of the flow solver and of the structural solver perform coupling iterations like in the normal IQN-ILS or IBQN-LS algorithm. However, data from previous time steps is not reused directly as explained in Sect. 5.1, because the relation between the columns of \(\varvec{\uppercase {R}}^n\) and \(\widetilde{\varvec{\uppercase {X}}}{}^n\) is only approximate at \(t^{n+1}\). The additional instances of the flow solver and structural solver first recalculate the data from the previous time steps at the current time level, before including that data in a least-squares model. The columns of the matrix \(\varvec{\uppercase {X}}^n\) contain specific combinations of the degrees of freedom on the interface that accelerated the convergence of the coupling iterations in the previous time step. Hence, it is expected that knowing the difference of the output at \(t^{n+1}\) due to the same difference of the input as used at time level \(t^n\) will improve the least-squares model for the approximate Jacobian.
Multi-level variants Furthermore, there exist Multi-Level (ML) versions of IQN-ILS and IBQN-LS [69]. Those could be considered similar to IQN-ILSM with a coarse grid surrogate model. However, the multi-level algorithms have important disadvantages compared to IQN-ILSM and therefore the IQN-ILSM algorithm is recommended. First, the multi-level algorithms combine the secant conditions obtained on all grids, which gives them all the same priority. By contrast, IQN-ILSM gives the highest priority to the finest grid, with a diminishing contribution from the coarser grid(s) as the coupling iterations on the finest grid converge. Furthermore, the multi-level algorithms interpolate the secant conditions obtained on the coarser grid(s) to the finest grid level and store it at the highest resolution, while IQN-ILSM stores the secant conditions with the resolution at which they have been calculated.
Aitken relaxation In addition to the quasi-Newton algorithms, Aitken relaxation [70,71,72] is frequently used for partitioned FSI simulations. This technique uses a dynamically varying scalar relaxation factor \(\omega ^k\) for the Gauss–Seidel iterations within a time step. It can thus also be interpreted as an interface quasi-Newton technique: if the inverse of the Jacobian in Eq. (23) is approximated by \(-\omega ^k\varvec{\uppercase {I}}\), the Aitken relaxation method is retrieved.
The next input for \({\varvec{\mathcal {R}}}\) is thus a linear combination of the last output and the previous input. Therefore, the update of the interface’s displacement is in the direction of the residual vector, as opposed to the update of the IQN-ILS method in Eq. (73). The value of \(\omega ^k\) is calculated recursively as
which can be interpreted as the secant method for scalars directly applied to vectors and projected on \(\varvec{\lowercase {r}}^k-\varvec{\lowercase {r}}^{k-1}\) [70]. By combining Eqs. (97) and (98), it can be seen that the update of the interface’s displacement is given by
for \(k>0\), which is similar to Eq. (73). If the Jacobian were created explicitly in the IQN-ILS algorithm and if the matrices \(\varvec{\uppercase {R}}^k\) and \(\widetilde{\varvec{\uppercase {X}}}{}^k\) were limited to their newest column, Eq. (73) would yield
Note the different location of the transpose sign in Eqs. (99) and Eq. (100). They are thus not identical because the coefficient of \(-\varvec{\lowercase {r}}^k\) is a scalar in the first equation and a matrix in the second one. Consequently, Aitken relaxation is different from IQN-ILS, even when the latter is restricted to one column in the matrices \(\varvec{\uppercase {R}}^k\) and \(\widetilde{\varvec{\uppercase {X}}}{}^k\). While Aitken relaxation uses a single relaxation factor for all interface degrees of freedom, IQN-ILS assigns a different value to each one based on a combination of the previously determined modes, i.e., the columns of \(\varvec{\uppercase {R}}^k\) and \(\widetilde{\varvec{\uppercase {X}}}{}^k\).
Prediction In all the quasi-Newton algorithms, the coupling iterations begin from \(\varvec{\lowercase {x}}^0\), which is an extrapolation or prediction. This can be a constant, linear or quadratic extrapolation based on \(\varvec{\lowercase {x}}^n, \varvec{\lowercase {x}}^{n-1}, \ldots\). While there is an effect of the order of this prediction on the convergence of the coupling iterations, it is case dependent and it is thus difficult to state whether higher order is always faster [29]. In the IQN-ILSM algorithm, the surrogate model can also be used for a prediction, but this is also not always faster than a linear extrapolation [61].
Quasi-Newton methods with Robin–Neumann decomposition Instead of the typical Dirichlet–Neumann decomposition of the FSI problem, a Robin–Neumann decomposition can be used as well. This decomposition modifies the boundary condition in the flow solver to also include the pressure and traction forces. The effect is the introduction of Interface Artificial Compressibility (IAC), which allows to solve FSI problems with enclosed incompressible fluids. To combine the idea of IAC with quasi-Newton methods a pressure correction has to be introduced to obtain corresponding inputs and outputs for the quasi-Newton technique [73]. However, by switching the order of the solvers and performing the quasi-Newton update on the pressure and traction forces instead of the displacements, this pressure correction can be avoided [74].
Applications in other fields Finally, it should be remarked that the quasi-Newton coupling techniques can also be used for coupled problems other than FSI. The main requirement for good results is significant interaction between both subproblems such that an approximate Jacobian stabilizes and accelerates the convergence compared to Gauss–Seidel iterations. The interaction should however not be so strong that an exact Jacobian satisfying all possible secant conditions is required to achieve convergence.
An example of a suitable problem is Conjugate Heat Transfer (CHT), where the partitioned spatial regions are each modelled by independent heat transfer codes and linked by temperature and flux matching conditions at the common boundaries [75]. A furnace radiation model can be coupled with a melt crystal growth model to investigate growth processes [76]. Another example is soil–structure interaction problems. The effect of excavations on the frame of a building can be studied by coupling a model of the soil’s behaviour with a code for nonlinear structural dynamics [77]. In this case, the interaction between the models occurs at a relatively small number of points. Finally, they can even be used to calculate the combustion in a fluidized bed reactor under pressure [78]. The calculation of the carbon and oxygen concentrations is performed separately from the calculation of the temperature field. In this last example, there is only one domain and data are exchanged throughout the domain, as opposed to the other examples, where the domains do not overlap and data are only exchanged at the common boundary of the subdomains. Therefore, the cost of the coupling is no longer negligible compared to the solution of the subproblems, which necessitates coupling techniques with low computational complexity and low memory requirements.
6 Numerical Tests
Several comparisons of quasi-Newton techniques can be found in the literature [52, 56, 59]. This section aims at providing an idea about the relative performance of the described techniques using a test case that can be reproduced in a straightforward way, but without claim of general applicability. It focuses on the scaling with increasing number of degrees of freedom on the interface.
6.1 Test Case
The six quasi-Newton techniques presented in Sect. 5 are now evaluated on a one-dimensional (1D) flexible tube, through which an incompressible fluid flows. This test case runs quickly and still features the destabilizing added mass phenomenon [35].
The straight tube has a length \(\ell\), a circular cross-section with nominal inner diameter \(r_0\) and wall thickness h. Its geometry is sketched in Fig. 6.
The ratio of the fluid density \(\rho _f\) to the structure density \(\rho _s\) is close to one, resulting in a large added mass. The structure has a modulus of elasticity E and a Poisson’s ratio \(\nu\). The values of these parameters are reported in Table 4.
On the inlet, a pressure pulse of 1333.2 Pa is applied for a duration of 0.003 s. Due to the flexible tube wall, the pulse travels at a finite velocity, despite the incompressible fluid. The pressure at the outlet of the tube is atmospheric pressure, i.e., 0 Pa. The total simulation time is 0.01 s, divided in 100 time steps.
The flow solver solves the nonlinear continuity and momentum equation in which viscosity and gravity are neglected. The deformation of the tube wall is calculated by the structure solver, which only considers radial displacements, so the length of the tube stays constant. The tube is discretized in \(n_p\) equal intervals. For the details regarding the governing equations and applied discretizations, the reader is referred to [35].
The FSI problem is solved with the open-source code CoCoNuT. This code allows to couple different software packages, which are treated as black boxes. It has the advantage of being modular and flexible in combining interpolators, solvers and coupling algorithms. Moreover, due to its comprehensive structure and implementation in Python, the code can be adapted to the user’s own requirements, if needed. The most recent code can be found on GitHub in the repository https://github.com/pyfsi/coconut/. The version used in this paper as well as scripts and result data are available for download on the Zenodo platform [79]. Both a flow and structure solver were written for the 1D flexible tube case described above and this code is equally available online.
6.2 Results
As the solvers are typically very expensive in FSI calculations, the focus is on the number of solver executions per time step. The term iteration will be used to denote a subsequent flow and structure solver call. Table 5 shows the number of iterations for the different quasi-Newton methods discussed above, as well as for a fixed relaxation factor and Aitken relaxation. Time data is included for completeness. A relative convergence tolerance is used, so that a time step is considered converged when \(\left\Vert \varvec{\lowercase {r}}^k\right\Vert _2<10^{-6}\left\Vert \varvec{\lowercase {r}}^0\right\Vert _2\), with \(\varvec{\lowercase {r}}^0\) the residual at the start of the time step.
Dynamic Aitken relaxation improves the convergence greatly compared to simple relaxation, but does not perform as well as the quasi-Newton methods. The block iteration and residual formulation methods perform similarly, whereas the least-squares techniques turn out to be somewhat more efficient compared to the multi-vector techniques for this test case. IQN-ILS (q = 0) corresponds to the method without reuse from previous time steps, but the IQN-ILS method performs best for q equal to 10. This shows the importance of reusing information from previous time steps. Note that the average number of coupling iterations per time step is not so sensitive to the value of q around the optimum. The indications (reuse) and (coarse) for the IQN-ILSM algorithm, refer respectively to the use of the previous time steps, and the use of an identical problem with half as many discretization intervals (without reuse) as surrogate model.
Next, Fig. 7 shows the memory requirements, for different number of discretization intervals \(n_p\). The data depict the peak memory usage as determined using the Python module guppy3.Footnote 7 The reported values are the total memory use minus that of the solvers. The results clearly show quadratically scaling memory requirements for the multi-vector techniques with explicit Jacobian construction, in contrast to the linear scaling for the methods with matrix-free implementation. Starting from \(10^4\) degrees of freedom, the memory requirements of MVQN and IQN-MVJ become much higher than those of the other coupling techniques. Furthermore, the block iteration methods require more memory compared to their corresponding residual formulation techniques, as two Jacobian matrices are approximated. Finally, IQN-IMVLS and IQN-ILSM (reuse) require more memory compared to the other matrix-free methods, because they retain information form every time step (\(q=100\)), instead of only from the last few (\(q=10\)). However, this could be reduced by applying a truncation after q time steps in the recursive formulas.
Lastly, Fig. 8 reports the coupling time, for different number of discretization intervals \(n_p\). The coupling time is calculated as the run time, excluding initialization, minus the time spent in both solvers and the interpolation routine. It is important to note that the code generating these results is not optimized for speed, such that care has to be taken when interpreting the results. Nonetheless, some relevant conclusions can be made. For example, remark that the quadratically scaling methods IQN-MVJ and MVQN require considerably more time than their linearly scaling counterparts. The same can be concluded for the block iterations methods, which are implemented here with an iterative procedure to obtain the quasi-Newton updates. Using the Woodbury matrix identity instead is expected to reduce the computational cost, but not to the extent that they will become cheaper than residual formulation techniques. Finally, the coupling time for the linearly scaling residual formulation techniques are in the order of 10 s for the investigated range of discretization intervals. These values remain low compared to the typical cost of solving the subproblems. Therefore, the difference in computational cost of the coupling for these methods is only moderately important.
7 Conclusion
The IQN-ILS, IBQN-LS, MVQN, IQN-MVJ, IQN-IMVLS and IQN-ILSM can all be reformulated as quasi-Newton techniques using generalized Broyden techniques for the approximate (inverse of the) Jacobian. In a time-dependent simulation with reuse from previous time steps, IQN-ILS and IBQN-LS enforce the secant conditions from all time steps in the same way, while MVQN, IQN-MVJ, IQN-IMVLS and IQN-ILSM only enforce the secant conditions from the latest time step directly. The block iteration quasi-Newton techniques like IBQN-LS and MVQN achieve similar performance in terms of number of coupling iterations per time step compared to the equivalent residual formulation quasi-Newton techniques IQN-ILS and IQN-MVJ, but the block iteration quasi-Newton techniques require more memory, more computational time for the coupling and a longer source code, entailing more involved implementation. Hence, it can be stated that, in general terms, it is better to use a residual formulation quasi-Newton method instead of the block iteration quasi-Newton techniques. For real-scale applications with a reasonable number of degrees of freedom on the interface, linear scaling of the coupling technique is essential, so MVQN and IQN-MVJ can only be used for smaller problems. The IQN-ILS technique has a short implementation and linear scaling thanks to the matrix-free procedure, but it requires filtering when reusing secant conditions from previous time steps. Finally, IQN-ILSM can be seen as a generalization of IQN-IMVLS, such that not only reuse from previous time steps can be applied but also other prior knowledge can be included to accelerate the convergence.
Notes
Note that for \(\varvec{\uppercase {A}}^k \in \mathbb {R}^{n_a \times k}\) with \(n_a > k\), \({\varvec{\uppercase {A}}^k}^+ \varvec{\uppercase {A}}^k\) is the identity matrix of size \(k \times k\), while \(\varvec{\uppercase {A}}^k {\varvec{\uppercase {A}}^k}^+\) is a \(n_a \times n_a\) matrix of rank k if the columns of \(\varvec{\uppercase {A}}^k\) are linearly independent.
Note that \(\varvec{\uppercase {Q}}_A^k {\varvec{\uppercase {Q}}_A^k}^\textrm{T}= \varvec{\uppercase {A}}^k {\varvec{\uppercase {A}}^k}^+ \ne \varvec{\uppercase {I}}\) and that \({\varvec{\uppercase {Q}}_A^k}^\textrm{T}\varvec{\uppercase {Q}}_A^k = {\varvec{\uppercase {A}}^k}^+ \varvec{\uppercase {A}}^k = \varvec{\uppercase {I}}\) equals the identity matrix of size \(k \times k\).
Approximating the Jacobian, respectively the inverse Jacobian, results in the good Broyden’s method respectively the bad Broyden’s method.
The term Jacobian is used for both \(\partial ^{k}_{\varvec{\lowercase {r}}} \varvec{\lowercase {x}}\) and \(\partial ^{k}_{\varvec{\lowercase {r}}} \tilde{\varvec{\lowercase {x}}}\), depending on which is relevant in the section.
Some authors rewrite the update \(\varvec{\lowercase {x}}^{k+1} = \varvec{\lowercase {x}}^k - {\widehat{{\varvec{{\mathcal {R}}}}'^{-\hbox {1}}}}(\varvec{\lowercase {x}}^k) \ \varvec{\lowercase {r}}^k\) as \(\varvec{\lowercase {x}}^{k+1} = \tilde{\varvec{\lowercase {x}}}^k - \partial ^{k}_{\varvec{\lowercase {r}}} \tilde{\varvec{\lowercase {x}}}\ \varvec{\lowercase {r}}^k\), since \({\widehat{{\varvec{{\mathcal {R}}}}'^{-\hbox {1}}}}(\varvec{\lowercase {x}}^k)\equiv \partial ^{k}_{\varvec{\lowercase {r}}} \tilde{\varvec{\lowercase {x}}}-\varvec{\uppercase {I}}\), and then \(\partial ^{k}_{\varvec{\lowercase {r}}} \tilde{\varvec{\lowercase {x}}}\) is called the approximation of the inverse Jacobian, but this notation is not used here to avoid confusion.
See GitHub repository https://github.com/zhuyifei1999/guppy3/.
References
Bazilevs Y, Hsu MC, Kiendl J, Wuechner R, Bletzinger KU (2010) 3D simulation of wind turbine rotors at full scale. Part II: fluid–structure interaction modeling with composite blades. Int J Numer Methods Fluids 65(1–3):236–253. https://doi.org/10.1002/fld.2454
Santo G, Peeters M, Van Paepegem W, Degroote J (2019) Dynamic load and stress analysis of a large horizontal axis wind turbine using full scale fluid–structure interaction simulation. Renew Energy 140:212–226. https://doi.org/10.1016/j.renene.2019.03.053
Paidoussis M (2016) Fluid–structure interactions: volume 2 slender structures and axial flow, 2nd edn. Elsevier, Amsterdam
Billah KY, Scanlan RH (1991) Resonance, Tacoma narrows bridge failure, and undergraduate physics textbooks. Am J Phys 59(2):118–124. https://doi.org/10.1119/1.16590
Hillewaere J, Degroote J, Lombaert G, Vierendeels J, Degrande G (2015) Wind–structure interaction simulations of ovalling vibrations in silo groups. J Fluids Struct 59:328–350. https://doi.org/10.1016/j.jfluidstructs.2015.09.013
Narayanan NK, Wüchner R, Degroote J (2019) Coupling of structural solver and volume-conserving solver for form-finding of membrane structures subjected to ponding. In: 8th international conference on computational methods for coupled problems in science and engineering, Sitges. pp 1–12. http://hdl.handle.net/1854/LU-8639251
Kamensky D, Hsu MC, Schillinger D, Evans JA, Aggarwal A, Bazilevs Y, Sacks MS, Hughes TJR (2015) An immersogeometric variational framework for fluid–structure interaction: application to bioprosthetic heart valves. Comput Methods Appl Mech Eng 284:1005–1053. https://doi.org/10.1016/j.cma.2014.10.040
Peskin CS, McQueen DM (1989) A three-dimensional computational method for blood flow in the heart I. Immersed elastic fibers in a viscous incompressible fluid. J Comput Phys 81(2):372–405. https://doi.org/10.1016/0021-9991(89)90213-1
Schott B, Ager C, Wall WA (2019) A monolithic approach to fluid–structure interaction based on a hybrid Eulerian-ALE fluid domain decomposition involving cut elements. Int J Numer Methods Eng 119(3):208–237. https://doi.org/10.1002/nme.6047
Ryzhakov PB, Marti J, Dialami N (2022) A unified arbitrary Lagrangian–Eulerian model for fluid–structure interaction problems involving flows in flexible channels. J Sci Comput. https://doi.org/10.1007/s10915-021-01748-w
Farhat C, van der Zee KG, Geuzaine P (2006) Provably second-order time-accurate loosely-coupled solution algorithms for transient nonlinear computational aeroelasticity. Comput Methods Appl Mech Eng 195(17–18):1973–2001. https://doi.org/10.1016/j.cma.2004.11.031
Lesoinne M, Farhat C (1998) A higher-order subiteration free staggered algorithm for non-linear transient aeroelastic problems. Am Inst Aeronaut Astronaut J 36(9):1754–1756. https://doi.org/10.2514/3.14041
van Brummelen EH (2009) Added mass effects of compressible and incompressible flows in fluid–structure interaction. J Appl Mech 76(2):021206. https://doi.org/10.1115/1.3059565
Boilevin-Kayl L, Fernandez MA, Gerbeau JF (2019) A loosely coupled scheme for fictitious domain approximations of fluid–structure interaction problems with immersed thin-walled structures. SIAM J Sci Comput 41(2):351–374. https://doi.org/10.1137/18m1192779
Causin P, Gerbeau JF, Nobile F (2005) Added-mass effect in the design of partitioned algorithms for fluid–structure problems. Comput Methods Appl Mech Eng 194(42–44):4506–4527. https://doi.org/10.1016/j.cma.2004.12.005
Förster C, Wall WA, Ramm E (2007) Artificial added mass instabilities in sequential staggered coupling of nonlinear structures and incompressible viscous flows. Comput Methods Appl Mech Eng 196(7):1278–1293. https://doi.org/10.1016/j.cma.2006.09.002
Le Tallec P, Mouro J (2001) Fluid structure interaction with large structural displacements. Comput Methods Appl Mech Eng 190(24–25):3039–3067. https://doi.org/10.1016/s0045-7825(00)00381-9
Gerbeau JF, Vidrascu M, Frey P (2005) Fluid–structure interaction in blood flows on geometries based on medical imaging. Comput Struct 83(2–3):155–165. https://doi.org/10.1016/j.compstruc.2004.03.083
Förster C, Wall WA, Ramm E (2006) The artificial added mass effect in sequential staggered fluid–structure interaction algorithms. In: Wesseling P, Oñate E, Périaux J (eds) 4th European conference on computational fluid dynamics, Egmond aan Zee. pp 1–20. http://resolver.tudelft.nl/uuid:f6316ca6-b02a-4a6f-b5ad-4e2f6744c7de
Riemslagh K, Vierendeels J, Dick E (2000) An efficient coupling procedure for flexible wall fluid–structure interaction. In: 3th European congress on computational methods in applied sciences and engineering, Barcelona. pp 1–13. http://hdl.handle.net/1854/LU-128926
Vierendeels J, Lanoye L, Degroote J, Verdonck PR (2007) Implicit coupling of partitioned fluid–structure interaction problems with reduced order models. Comput Struct 85(11–14):970–976. https://doi.org/10.1016/j.compstruc.2006.11.006
Taelman L, Bols J, Degroote J, Muthurangu V, Panzer J, Vierendeels J, Segers P (2015) Differential impact of local stiffening and narrowing on hemodynamics in repaired aortic coarctation: an FSI study. Med Biol Eng Comput 54(2–3):497–510. https://doi.org/10.1007/s11517-015-1336-1
Dolfen H, De Ridder J, Brockmeyer L, Merzari E, Kennedy G, Van Tichelen K, Degroote J (2022) A multi-stage approach of simulating turbulence-induced vibrations in a wire-wrapped tube bundle for fretting wear prediction. J Fluids Struct 109:103460. https://doi.org/10.1016/j.jfluidstructs.2021.103460
Delcour L, Bral A, Van Langenhove L, Degroote J (2022) Investigating the influence of compressibility on the second mode flutter instability of a clamped-free cylinder in axial flow using fluid–structure interaction simulations with the Chimera technique. J Fluids Struct 109:103469. https://doi.org/10.1016/j.jfluidstructs.2021.103469
Badia S, Nobile F, Vergara C (2008) Fluid–structure partitioned procedures based on Robin transmission conditions. J Comput Phys 227(14):7027–7051. https://doi.org/10.1016/j.jcp.2008.04.006
Deuse M, Sandberg RD (2020) Implementation of a stable high-order overset grid method for high-fidelity simulations. Comput Fluids 211:104449. https://doi.org/10.1016/j.compfluid.2020.104449
Zhang ZQ, Liu GR, Khoo BC (2012) A three dimensional immersed smoothed finite element method (3D IS-FEM) for fluid–structure interaction problems. Comput Mech 51(2):129–150. https://doi.org/10.1007/s00466-012-0710-1
Zorrilla R, Rossi R, Wüchner R, Oñate E (2020) An embedded finite element framework for the resolution of strongly coupled fluid–structure interaction problems. Application to volumetric and membrane-like structures. Comput Methods Appl Mech Eng 368:113179. https://doi.org/10.1016/j.cma.2020.113179
Erbts P, Düster A (2012) Accelerated staggered coupling schemes for problems of thermoelasticity at finite strains. Comput Math Appl 64(8):2408–2430. https://doi.org/10.1016/j.camwa.2012.05.010
Joosten MM, Dettmer WG, Perić D (2009) Analysis of the block Gauss–Seidel solution procedure for a strongly coupled model problem with reference to fluid–structure interaction. Int J Numer Methods Eng 78(7):757–778. https://doi.org/10.1002/nme.2503
Idelsohn SR, Del Pin F, Rossi R, Oñate E (2009) Fluid–structure interaction problems with strong added-mass effect. Int J Numer Methods Eng 80(10):1261–1294. https://doi.org/10.1002/nme.2659
Formaggia L, Gerbeau JF, Nobile F, Quarteroni A (2001) On the coupling of 3D and 1D Navier–Stokes equations for flow problems in compliant vessels. Comput Methods Appl Mech Eng 191(6–7):561–582. https://doi.org/10.1016/s0045-7825(01)00302-4
Vierendeels J, Dumont K, Dick E, Verdonck PR (2005) Analysis and stabilization of fluid–structure interaction algorithm for rigid-body motion. Am Inst Aeronaut Astronaut J 43(12):2549–2557. https://doi.org/10.2514/1.3660
Degroote J, Bruggeman P, Haelterman R, Vierendeels J (2008) Stability of a coupling technique for partitioned solvers in FSI applications. Comput Struct 86(23–24):2224–2234. https://doi.org/10.1016/j.compstruc.2008.05.005
Degroote J, Annerel S, Vierendeels J (2010) Stability analysis of Gauss–Seidel iterations in a partitioned simulation of fluid–structure interaction. Comput Struct 88(5–6):263–271. https://doi.org/10.1016/j.compstruc.2009.09.003
Degroote J (2013) Partitioned simulation of fluid–structure interaction: coupling black-box solvers with quasi-Newton techniques. Arch Comput Methods Eng 20(3):185–238. https://doi.org/10.1007/s11831-013-9085-5
van Brummelen EH (2010) Partitioned iterative solution methods for fluid–structure interaction. Int J Numer Methods Fluids 65(1–3):3–27. https://doi.org/10.1002/fld.2465
Golub GH, Van Loan CF (1996) Matrix computations, 3rd edn. Johns Hopkins University Press, Baltimore https://doi.org/10.56021/9781421407944
Trefethen LN, Bau DI (1997) Numerical linear algebra. Cambridge. https://doi.org/10.1137/1.9780898719574
Broyden CG (1965) A class of methods for solving nonlinear simultaneous equations. Math Comput 19(92):577–593. https://doi.org/10.1090/s0025-5718-1965-0198670-6
Fang HR, Saad Y (2009) Two classes of multisecant methods for nonlinear acceleration. Numer Linear Algebr Appl 16(3):197–221. https://doi.org/10.1002/nla.617
Johnson DD (1988) Modified Broyden’s method for accelerating convergence in self-consistent calculations. Phys Rev B 38(18):12807–12813. https://doi.org/10.1103/physrevb.38.12807
Vanderbilt D, Louie SG (1984) Total energies of diamond (111) surface reconstructions by a linear combination of atomic orbitals method. Phys Rev B 30(10):6118–6130. https://doi.org/10.1103/physrevb.30.6118
Eyert V (1996) A comparative study on methods for convergence acceleration of iterative vector sequences. J Comput Phys 124(2):271–285. https://doi.org/10.1006/jcph.1996.0059
Anderson DG (1965) Iterative procedures for nonlinear integral equations. J ACM 12(4):547–560. https://doi.org/10.1145/321296.321305
van Leuken H (1991) Electronic structure of metallic multilayers. PhD thesis, University of Amsterdam
Scheufele K (2015) Robust quasi-Newton methods for partitioned fluid–structure simulations. Master’s thesis, University of Stuttgart. https://doi.org/10.13140/RG.2.2.28442.08648
Uekermann BW (2016) Partitioned fluid–structure interaction on massively parallel systems. PhD thesis, Technische Universität München. https://doi.org/10.14459/2016md1320661
Demeester T, Delaissé N, van Brummelen EH, Haelterman R, Degroote J (2022) On the effect of nonlinearity and Jacobian initialization on the convergence of the generalized Broyden quasi-Newton method. Int J Numer Methods Eng 123(17):4054–4072. https://doi.org/10.1002/nme.6998
Degroote J, Bathe KJ, Vierendeels J (2009) Performance of a new partitioned procedure versus a monolithic procedure in fluid–structure interaction. Comput Struct 87(11–12):793–801. https://doi.org/10.1016/j.compstruc.2008.11.013
Haelterman R, Degroote J, Van Heule D, Vierendeels J (2009) The quasi-Newton least squares method: a new and fast secant method analyzed for linear systems. SIAM J Numer Anal 47(3):2347–2368. https://doi.org/10.1137/070710469
Gallinger T, Bletzinger KU (2010) Comparison of algorithms for strongly coupled partitioned fluid–structure interaction—efficiency versus simplicity. In: Pereira JCF, Sequeira A (eds) 5th European conference on computational fluid dynamics, Lisbon. pp 1–20
Spenke T, Hosters N, Behr M (2020) A multi-vector interface quasi-Newton method with linear complexity for partitioned fluid–structure interaction. Comput Methods Appl Mech Eng 361:112810. https://doi.org/10.1016/j.cma.2019.112810
Degroote J, Souto-Iglesias A, Van Paepegem W, Annerel S, Bruggeman P, Vierendeels J (2010) Partitioned simulation of the interaction between an elastic structure and free surface flow. Comput Methods Appl Mech Eng 199(33–36):2085–2098. https://doi.org/10.1016/j.cma.2010.02.019
Haelterman R, Bogaers AEJ, Scheufele K, Uekermann B, Mehl M (2016) Improving the performance of the partitioned QN-ILS procedure for fluid–structure interaction problems: filtering. Comput Struct 171:9–17. https://doi.org/10.1016/j.compstruc.2016.04.001
Degroote J, Haelterman R, Annerel S, Bruggeman P, Vierendeels J (2010) Performance of partitioned procedures in fluid–structure interaction. Comput Struct 88(7–8):446–457. https://doi.org/10.1016/j.compstruc.2009.12.006
Zorrilla R, Rossi R (2023) A memory-efficient multivector quasi-Newton method for black-box fluid–structure interaction coupling. Comput Struct 275:106934. https://doi.org/10.1016/j.compstruc.2022.106934
Bogaers AEJ, Kok S, Reddy BD, Franz T (2014) Quasi-Newton methods for implicit black-box FSI coupling. Comput Methods Appl Mech Eng 279:113–132. https://doi.org/10.1016/j.cma.2014.06.033
Lindner F, Mehl M, Scheufele K, Uekermann B (2015) A comparison of various quasi-Newton schemes for partitioned fluid–structure interaction. In: Schrefler B, Oñate E, Papadrakakis M (eds) 6th international conference on computational methods for coupled problems in science and engineering. pp 477–488. http://hdl.handle.net/2117/191193
Scheufele K, Mehl M (2017) Robust multisecant quasi-Newton variants for parallel fluid–structure simulations and other multiphysics applications. SIAM J Sci Comput 39(5):404–433. https://doi.org/10.1137/16m1082020
Delaissé N, Demeester T, Fauconnier D, Degroote J (2022) Surrogate-based acceleration of quasi-Newton techniques for fluid–structure interaction simulations. Comput Struct 260:106720. https://doi.org/10.1016/j.compstruc.2021.106720
Demeester T, Brummelen EH, Degroote J (2020) An efficient quasi-Newton method for two-dimensional steady free surface flow. Int J Numer Methods Fluids 92(7):785–801. https://doi.org/10.1002/fld.4806
Demeester T, van Brummelen EH, Degroote J (2021) An efficient quasi-Newton method for three-dimensional steady free surface flow. Int J Numer Methods Fluids 93(8):2581–2610. https://doi.org/10.1002/fld.4989
De Groote W, Kikken E, Hostens E, Van Hoecke S, Crevecoeur G (2022) Neural network augmented physics models for systems with partially unknown dynamics: application to slider-crank mechanism. IEEE/ASME Trans Mechatron 27(1):1–11. https://doi.org/10.1109/tmech.2021.3058536
Mehl M, Uekermann B, Bijl H, Blom D, Gatzhammer B, van Zuijlen AH (2016) Parallel coupling numerics for partitioned fluid–structure interaction simulations. Comput Math Appl 71(4):869–891. https://doi.org/10.1016/j.camwa.2015.12.025
Cervera M, Codina R, Galindo M (1996) On the computational efficiency and implementation of block-iterative algorithms for nonlinear coupled problems. Eng Comput 13(6):4–30. https://doi.org/10.1108/02644409610128382
Santiago A, Zavala-Aké M, Borrell R, Houzeaux G, Vázquez M (2020) HPC compact quasi-Newton algorithm for interface problems. J Fluids Struct 96:103009. https://doi.org/10.1016/j.jfluidstructs.2020.103009
Degroote J, Vierendeels J (2011) Multi-solver algorithms for the partitioned simulation of fluid–structure interaction. Comput Methods Appl Mech Eng 200(25–28):2195–2210. https://doi.org/10.1016/j.cma.2011.03.015
Degroote J, Vierendeels J (2012) Multi-level quasi-Newton coupling algorithms for the partitioned simulation of fluid–structure interaction. Comput Methods Appl Mech Eng 225–228:14–27. https://doi.org/10.1016/j.cma.2012.03.010
Küttler U, Wall WA (2008) Fixed-point fluid–structure interaction solvers with dynamic relaxation. Comput Mech 43(1):61–72. https://doi.org/10.1007/s00466-008-0255-5
Mok DP, Wall WA (2001) Partitioned analysis schemes for the transient interaction of incompressible flows and nonlinear flexible structures. In: Schweizerhof K, Wall WA, Bletzinger KU (eds) Trends in computational structural mechanics, Barcelona. pp 688–698
Mok DP, Wall WA, Ramm E (2001) Accelerated iterative substructuring schemes for instationary fluid–structure interaction. In: Bathe KJ (ed) Computational fluid and solid mechanics. Elsevier, Amsterdam, pp 1325–1328. https://doi.org/10.1016/b978-008043944-0/50907-0
Bogaers AEJ, Kok S, Reddy BD, Franz T (2015) Extending the robustness and efficiency of artificial compressibility for partitioned fluid–structure interactions. Comput Methods Appl Mech Eng 283:1278–1295. https://doi.org/10.1016/j.cma.2014.08.021
Spenke T, Make M, Hosters N (2022) A Robin–Neumann scheme with quasi-Newton acceleration for partitioned fluid–structure interaction. Int J Numer Methods Eng 124(4):979–997. https://doi.org/10.1002/nme.7151
Rüth B, Uekermann B, Mehl M, Birken P, Monge A, Bungartz HJ (2020) Quasi-Newton waveform iteration for partitioned surface-coupled multiphysics applications. Int J Numer Methods Eng 122(19):5236–5257. https://doi.org/10.1002/nme.6443
Yeckel A, Lun L, Derby JJ (2009) An approximate block Newton method for coupled iterations of nonlinear solvers: theory and conjugate heat transfer applications. J Comput Phys 228(23):8566–8588. https://doi.org/10.1016/j.jcp.2009.08.003
Jahromi HZ, Izzuddin BA, Zdravkovic L (2009) A domain decomposition approach for coupled modelling of nonlinear soil–structure interaction. Comput Methods Appl Mech Eng 198(33–36):2738–2749. https://doi.org/10.1016/j.cma.2009.03.018
Artlich S, Mackens W (1995) Newton-coupling of fixed point iterations. In: Hackbusch W, Wittum G (eds) 11th GAMM-seminar: numerical treatment of coupled systems. Notes on numerical fluid mechanics, vol 51. Vieweg, Braunschweig, Kiel, pp 1–10. https://doi.org/10.1007/978-3-322-86859-6_1
Delaissé N, Demeester T, Haelterman R, Degroote J (2023) Quasi-Newton methods for partitioned simulation of fluid–structure interaction reviewed in the generalized Broyden framework: code and data. https://doi.org/10.5281/zenodo.7565680
Boutet N, Haelterman R, Degroote J (2021) Secant update generalized version of PSB: a new approach. Comput Optim Appl 78(3):953–982. https://doi.org/10.1007/s10589-020-00256-1
Matthies HG, Niekamp R, Steindorf J (2006) Algorithms for strong coupling procedures. Comput Methods Appl Mech Eng 195(17–18):2028–2049. https://doi.org/10.1016/j.cma.2004.11.032
Acknowledgements
The authors humbly acknowledge the contribution of Jan Vierendeels (1968–2018) to the field of partitioned simulation of fluid–structure interaction.
Funding
N. Delaissé gratefully acknowledges the funding received from the Research Foundation–Flanders (FWO) as part of the SBO CONTACTLUB project (S006519N).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Delaissé, N., Demeester, T., Haelterman, R. et al. Quasi-Newton Methods for Partitioned Simulation of Fluid–Structure Interaction Reviewed in the Generalized Broyden Framework. Arch Computat Methods Eng 30, 3271–3300 (2023). https://doi.org/10.1007/s11831-023-09907-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11831-023-09907-y