1 Introduction

Bearing is a vital element used in modern high-speed industrial machinery. In high-precision rotating machinery [1], mainly supports multi-directionally applied loads and minimizes friction between the moving surfaces resulting in reduced noise and vibration [2]. Journal or radial bearings are used to support radial loads. This rotor-bearing system consists of two eccentric cylinders separated by a continuous lubricant film. The outer cylinder (bearing) is commonly held stationary, while the inner cylinder (journal) is made to rotate about its axis [3]. Hydrodynamic pressure generation results in the relative motion between the two conformal surfaces and the viscous drag. This helps the bearing to carry the radial load.

Experimental and theoretical investigations by Tower, Petroff and Reynolds [4] performed between 1800 and 1886 provided a deep understanding of the phenomenon of hydrodynamic flow. They observed that two sliding surfaces could be separated by the hydrodynamic pressure of a viscous liquid, and friction can be reduced between the surfaces. In 1886, Reynold derived a mathematical model for hydrodynamic lubrication. Modified forms of the Reynolds equation have been used in several theoretical studies.

Many theoretical, experimental, and computational works have been carried out in the last 50 years to relate journal bearing performance, bearing profiles to friction and wear. Researchers have analyzed the flow phenomenon in a journal bearing using analytical as well as numerical methods viz. finite element method (FE), finite difference methods (FDM), and finite volume method (FVM). The computational domain is discretized into small segments in all these numerical methods. The governing equations are then discretized and solved iteratively.

ANSYS Fluent, CFX, or any CFD software tool uses FVM to solve the governing equations for numerical solutions. Development in computer technologies helped researchers work on journal bearing using CFD and FSI techniques. Chen and Hahn [5] observed that CFD software was more proficient in handling hydrodynamic cases for different bearings, including journal bearing operating in constant unidirectional loading conditions. The author used commercially available CFD software to solve the full Navier–Stokes equation.

Fluid–structure interaction is a coupling of laws that describes the dynamics of fluid and structural mechanics. FSI plays an essential part in the area of hydrodynamic lubrication research. Pressure develops in the oil film due to hydrodynamic action in journal bearings. The amount of pressure developed in the oil film depends on several factors viz shape of the bearing, operating conditions, geometry and material properties of the structural components and environment in which fluid is moving, etc. Deformation of bearing and journal surface, in turn, depends on the forces exerted by the lubricant on the structure. These deformations in the structure may lead to failures and also changes fluid properties (velocity, pressure, etc.) Hence a study of the fluid–structure interaction (FSI) is also significant in fluid film bearing.

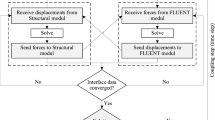
There are two approaches for solving FSI related numerical analysis namely monolithic and partitioned and schematic representation is shown in Fig. 1. In a monolithic solver or approach, both flow and structural related equations are solved together in a single solver (or single monolithic matrix) (with Newton–Raphson iterations) such that the physical changes took place in both flow and structures were taken into account [6]. However in the partitioned approach [7,8,9,10], two solvers have been utilized in which one solves the governing equations related to fluid and another solver is for the equation related to the displacement of the structure.

Fig. 1
figure 1

Pictorial representation of two approaches of FSI solver (a) Monolithic (b) Partitioned

Full size image

Since the early 1990s many researchers in the field of tribology made efforts to include the cavitation and its repercussions on the bearing performance. Developments in computing technology enabled tribologists to incorporate phenomena like cavitation, temperature, turbulence, structural deformation, and many others in their study. This literature review focuses on theoretical, numerical, and experimental work carried out in the area of performance evaluation of journal bearings using CFD and FSI techniques. Influence of cavitation and thermal effects on bearing performance as well as challenges involved in the implementation of FSI analysis of journal bearing are also summarized.

2 Fluid Film Bearing Performance Neglecting the Cavitation and Thermal Effects

Various numerical studies carried out to evaluate bearing performance by neglecting the effect of cavitation and temperature are highlighted in this section.

Gertzos et al. [11] used and validated [12, 13] CFD model to investigate the performance characteristics of a journal bearing lubricated with a smart fluid (Bingham fluid) for different L/D ratios. Performance characteristics such as coefficient of friction, attitude angle (ɸ), pressure variations, oil flow, and the location of maximum pressure in bearing were obtained by neglecting cavitation and thermal effects. From the analysis, it was observed that the use of Bingham fluids as lubricant showed improved bearing performance than those with Newtonian fluid. Also, CFD techniques can be used in the design of journal bearing with smart lubricants like magnetorheological (MR) or Electrorheological (ER) fluids.

Similarly, CFD tools adopted by Bompos and Nikolakopoulos [14] for the analysis of a journal bearing lubricated with magnetorheological fluids and having different L/D ratios as well as current intensity, provided good validation [11, 15]. Based on the CFD results they concluded that MR fluids as a lubricant can improve the load-carrying capacity and friction coefficient when the intensity of current varies from 0 to 28A. However, an increase in friction coefficient leads to enhancement in energy consumptions which is not a favorable result for a rotor-bearing system. Holmberg and Erdemir [16] reported that out of 23% (119 EJ) of the world’s consumption of energy, 20% is utilized to get rid of friction, and the remaining is used for the rework of damaged parts due to friction. These frictional losses can be reduced by using smart journal-bearing systems. Hence, it is important to note that CFD techniques can be used to visualize the flow phenomenon in bearings that utilize smart fluids like ER and MR fluids as lubricants [14, 17,18,19,20].

Yiping et al. [9] and Shenoy et al. [10] studied the hydrodynamic behavior of 360° journal bearing using the FSI technique in ANSYS/FLOTRAN. The fluid–structure interaction effect on the hard elastohydrodynamic lubrication (EHL) system was investigated with the help of ANSYS software. A partitioned approach is adopted to create a new form of 3D FSI model wherein multigrid method was used to find initial film thickness. Compared to other FSI models, it is concluded that the new form of the FSI model shows a better hydrodynamic performance of side leakage and stresses inside the structure.

Shenoy et al. [10] initially carried out a CFD analysis to obtain the fluid pressure values in the laminar region with various L/D ratios and eccentricity ratio (ε) followed by a structural analysis to obtain stresses and deformation in the bearing liner. All the negative pressure generated in the fluid region was equated to zero by writing APDL code. The methodology and results were validated with the existing experimental findings [21]. They observed that under isothermal conditions, the eccentricity ratio has a significant effect on the fluid film pressure compared to L/D ratios and as ε increases, structural deformation increases.

Bhat et al. [21] performed a one-way FSI analysis on 60° adjustable partial arc bearing having upward and downward tilt adjustments and various operating conditions. APDL was used for setting cavitation conditions. Based on the one-way FSI analysis, it was concluded that hydrodynamic pressure and stresses developed in the bearing are much higher when the partial arc bearing was given a radial adjustment in an upward direction. This is mainly because of a reduction in the clearance between the journal and bearing.

CFD and monolithic FSI analysis on rotor-bearing systems for different bearing materials (such as nylon, steel, and babbitt) operating under steady and dynamic loading as well as half-Sommerfeld and phase change boundary conditions was discussed by Liu et al. [22]. Based on the outcomes, the phase change boundary condition was adopted for further analysis. It was observed that, for both static and dynamic loading conditions, bearing with lower Young’s modulus experienced more displacement which in turn lowered the fluid film pressure, load-carrying capacity, and other performance parameters.

Nonlinear transient response of long and short plain journal bearing under the application of large dynamic loads (including the deflection due to oil whirl) was studied by Meruane and Pascual [7]. CFD simulation was performed in ADINA 8.1 considering no-slip boundary condition, incompressible laminar flow, and Full Sommerfeld neglecting cavitation effects. Numerical results were validated with the experimental work. It was concluded that for the bearing stability analysis, it is essential to take into account nonlinear parameters like stiffness and damping coefficient, especially during oil whirl. These nonlinear terms have a major influence on the journal response. The results of structural deformation and stresses were not taken into account.

Liu et al. [23] carried out CFD studies on three journal bearings models namely pure fluid bearing model, FSI squeeze-film model, and bearing-rotor FSI model. Sommerfeld and Gumbel boundary conditions were adopted for the study and later results were compared with Reynolds equation-based analytical solution. ADINA 8.4.4 numerical tool was used for the CFD simulation under laminar conditions. Results showed that load-carrying capacity differs between 1.10% and 0.33% when compared with the analytical results.

Turbulence in fluid film bearing was caused mainly because of the increase in operating speeds. Bearing performance under laminar and turbulent flow regimes are not identical and it is important to study the bearing performance under these conditions. Analytically, bearing performance under turbulent conditions can be calculated using several turbulence models such as Ng and Pan [24, 25], Elord and Ng [26], Ng-Pan-Elrod model [27, 28], simple zero equation models of Constantinescu [27, 29] etc. Also, the performance of the bearing was predicted using various numerical methods considering different turbulence models [2, 30,31,32]. It was reported [2, 32, 33] that an increase in Reynolds number due to turbulence, enhances the shear stress between the fluid layers, and this, in turn, results in increased load carrying capacity, frictional coefficient, and side leakage (or oil flow). The influence of turbulence on the load-carrying capacity of a single pad externally adjustable pad bearing was numerically analyzed by Shenoy and Pai [33] for various tilt and radial adjustments. They observed that turbulence has a greater influence on the load capacity, oil flow, and friction variable when compared to laminar flows.

The influence of fluid inertia and turbulence in a water-lubricated four pad bearing at high Reynold’s number was studied by Armentrout et al. [33]. They used both analytical and numerical methods (CFD). All negative pressure was set to zero and the variation of viscosity was allowed during the analysis by applying the k-ω turbulence model in ANSYS CFX. The influence of convective inertia (density) on the load-carrying capacity of the bearing was observed to be low in laminar and also in turbulent conditions. However, the conventional method (based on the Reynolds equation) yields a lower load-carrying capacity (almost 29%) compared to the CFD solution (based on full Navier–Stokes equation) when both fluid inertia and turbulence conditions were considered. Hence, for better comparison, Armentrout et al. suggested mesh and turbulent model refinements in the Reynolds-based conventional method.

Manshoor et al. [30] compared the various turbulence models used in a three-dimensional CFD study on journal bearing lubricated with oil. Results of a standard k-ε model, the Realizable k-ε model, and Reynolds Stress Model (RSM) were analyzed. In comparison, all three turbulence models showed identical results in the form of load-carrying capacity, fluid pressure, and wall shear stress. However, a standard k-ε model was identified to be one of the simplest and faster models compared to others.

All these investigators carried out CFD/FSI analysis of journal bearing under uniform vertical load, steady-state, isoviscous flow, incompressible flow, and no-slip condition neglecting cavitation effect.

3 Fluid Film Bearing Performance Considering the Cavitation Effect

Cavitation is an undesirable phenomenon in fluid film bearing. It affects the static and dynamic performance parameters of a bearing such as load-carrying capacity and stability [30]. Cavitation is the formation of vapor molecules (or bubbles) when the pressure of a liquid falls below the saturated vapor pressure, at constant temperature [34, 35]. The development of bubbles due to the rupturing of liquid at constant temperature is called cavitation and it begins with the microscopic nuclei. These microscopic bubble jets increase with the decreasing pressure and later microscopic cavities are produced [36, 37]. Bubble formation in the divergent region of fluid film lubrication will deteriorate the hydrodynamic effect and reduction load-carrying capacity [2] due to the transfer of momentum phenomenon on the interface between lubricant and bubbles. The intensity of these bubble formations increases as viscosity and shaft rotational speed (ω) increase [2]. However, the rotational speed is a dominating factor compared to viscosity [38]. Several investigators highlighted the importance of the cavitation effect in journal bearing using the CFD technique and is discussed in this section.

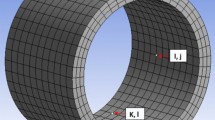
Active and cavitation region in the journal bearing is shown in Fig. 2 with vertical load W’ acting on the shaft whose center of rotation is ‘Jc’ at a distance ‘e’ (eccentricity) from the bearing center (Bc).

Fig. 2
figure 2

Journal bearing with active and cavitation region

Full size image

Formation of cavitation in journal bearing is broadly classified into two categories namely gaseous and vapor cavitation. Gaseous cavitation arises when the gas pressure goes below the saturation pressure. Vapor cavitation takes place when the liquid pressure drops below the vapor pressure and hence formation of vapor bubbles takes place [34, 39]. Vapor cavitation is commonly found in pumps, pipes, etc. which leads to fatigue failure in the machine components [40, 41]. Also, the formation of vapor cavitation directly depends on rotational speed and load acting on the bearing shaft. As the load and the rotational speed increase the risk of vapor formation also increases. Hence cavitation effects cannot be neglected especially in fluid machinery components.

Braun and Hannon [34] reviewed the importance of different cavitation models and the formation of cavitation in fluid film bearing. They have compared the various cavitation models like the Sommerfeld model [42], Gumbel [9, 11, 14, 22, 23, 43, 44] Swift-Stieber model [45, 46], JFO model [47,48,49], Elrod algorithm [50], Vijayaraghavan and Keith model [51], Booker [52], Kumar et al. model [53], and Boedo et al. model [54] are summarized as follows.

  • In the lubricant, large tensile forces (negative pressure) are generated mainly due to divergent regions and sudden unloading in the bearing.

  • JFO model and Elrod cavitation model were the best-suited models when compared to the Sommerfeld model, Gumbel, and Swift-Stieber model, as it considers mass continuity. The Elrod’s cavitation model was further modified by Vijayaraghavan and Keith made modifications to the Elrod's cavitation model in order to increase computational efficiency.

  • When physical and propagation characteristics are considered, the formation of cavitation in fluid film bearing has similarities with the crack formation and propagation in solids.

Many researchers have tried to capture the inception of cavitation, bubble formation, and its growth using several images capturing techniques (flash photography [51], ultrasound technology [55], slow-motion photography [56], oil film photography [57], laser light sheet illumination techniques [58], neutron radiography [59]). However, due to limitations of experimental methods, lack of evaluation standards [57], and need for high precision equipment, researchers started focusing on numerical tools like CFD cavitation models to understand the cavitation phenomenon in an effective way. Table 1 shows the most commonly used cavitation model in the numerical investigation.

Table 1 List of cavitation model adopted for the numerical study on Journal bearing
Full size table

The cavitation models like the half-Sommerfeld boundary condition are implemented not only in journal bearing but also in turbocharger bearing [72] by setting all the negative pressures created in the fluid region to zero [10].

Singhal et al. [73] developed a full cavitation model (known as the Singhal model) considering the effect of turbulence, rate of phase change, and bubble dynamics. A modified Rayleigh Plesset equation was used to include bubble dynamics into the model. The authors have implemented the model into CFD code and validated the model by comparing the results obtained from experimental results of hydrofoil and submerged cylindrical objects. This model can be used in automobile thermostatic valves, gear pumps, rocket turbomachinery, and others. The limitation of the current model is that it cannot be used if the properties of the fluid vary with temperature.

Gao et al. [64, 67] used the CFD tool to perform the analysis on water-lubricated plain journal bearing considering the Zwart-Gerber-Belamri cavitation model which can be used for both mixture and multiphase models. Based on the numerical results obtained, a design reference chart was generated for 0.6 and 0.7 eccentricity ratios using the numerical fitting method. The reason for the selection of 0.6 and 0.7 eccentricity ratios was mainly due to poor hydrodynamic performance obtained at lower and higher eccentricity ratios [64]. This chart can be used for the selection of the initial diameter of the journal (between 10 and 100 mm with an interval of 10 mm) with a speed that varies from 100 to 5000 rpm. Later, a reference chart was validated with the experimental work under specified conditions.

Gao et al. [67] studied the correlation between variables like eccentricity ratio and Sommerfeld number and a later design reference chart for the selection of water-lubricated bearing was generated. Additionally, the effect of cavitation is analyzed by comparing three boundary conditions namely Sommerfeld, Half-Sommerfeld, and Reynold with the Zwart-Gerber-Belamri Cavitation model. Results indicated that the Zwart-Gerber-Belamri cavitation model captured the more realistic pressure values compared to the results of the other three boundary conditions.

CFD analysis on water lubricated journal bearing was carried out by Zhang et al. [68] and found the influence of L/D ratios and eccentricity ratios on the stiffness coefficient. Cavitation effects were considered by adopting the Zwart-Gerber-Belamri model available in ANSYS. Results obtained from CFD as well as the method adopted for calculating the stiffness coefficient were validated [74,75,76]. However, an error is observed in pressure values at minimum film thickness till the load line. This might be due to the consideration of the cavitation model during the analysis by Zhang et al. [68]. It was also found that the stiffness coefficient increases with the increase in external load but it is not true for lower eccentricity ratios. Hence, the stiffness coefficient is quite an important parameter to keep in mind while selecting the dimensions of water-lubricated bearing.

Wang et al. [62] adopted the Rayleigh-Plesset cavitation model for the FSI analysis of Polytetrafluoroethylene (PTFE) based water lubricated journal bearing. Due to Young's modulus, deformation in PTFE cannot be ignored, and hence the effect of Young's modulus and Poisson’s ratio on the load capacity of water-lubricated bearing was studied further. Numerical results indicated that with the increase in Young’s modulus and Poisson’s ratio of the material, elastic deformation reduces, and hence the load-carrying capacity of the bearing is increased. The method adopted for CFD analysis was compared with the Gao et al. [64] and the results are in good agreement. Later, a design reference chart was developed for the selection of water-lubricated composite journal bearing for different load and shaft speeds. This chart was developed by considering the effect of cavitation and elastic deformation. Results indicated that by considering elastic deformation, load carrying capacity has been decreased with the increase in rotational speed. Furthermore, the author has proposed that if the elastic deformation is greater than 15% of the minimum film thickness of water lubricant, then elastic deformation must be considered.

Similarly, Wodtke et al. [63] investigated water-lubricated journal bearing (case 1) and oil-lubricated single tilting pad thrust bearing (case 2) using the FSI technique. Experimental work was also carried out for single tilting pad thrust bearing under the laminar and turbulence regime. Rayleigh-Plesset based cavitation equation was activated and an SST turbulence model was used for the numerical study. Results indicated that the influence of turbulence is significant at higher shaft speeds. In case 2, the thermal deformation of pads can alter the film thickness due to temperature effects.

Dhande and Pande [65] used CFD coupled fluid–structure interaction (FSI) technique to study the journal bearing performance considering the cavitation. The numerical method was validated [43] and design optimization techniques i.e. multi-objective genetic algorithm (MOGA) was employed to optimize attitude angle as well as eccentricity, at different loads and shaft speeds. Results showed that use of Zwart-Gerber-Belamri cavitation model reduces the hydrodynamic fluid pressure and in turn the performance of the bearing.

Similarly, Dhande and Pande [66] performed a two-way FSI study of hydrodynamic journal bearing considering the Zwart-Gerber-Belamri cavitation model. It was concluded that hydrodynamic fluid pressure built up in elastohydrodynamic bearing reduces when it was compared with rigid bearing. This is mainly due to the deformation of bearing which increases the clearance space and hence this space acts as a reservoir for the lubricant.

Misalignment of bearing is one of the important factors which can disrupt the hydrodynamic bearing performance. Conditions like non-central loading, elastic deformation of the shaft, thermal distortion of the shaft, and manufacturing errors may lead to misalignment of bearing. It can also occur in different types of machinery because of assembly defects and deflection of the rotor due to its weight. This leads to changes in the shape of the fluid domain continuously with respect to time. Hence capturing this phenomenon of the fluid domain in a numerical study is quite challenging and there has been a limited amount of research was undertaken considering transient analysis.

Transient flow analysis of double groove journal bearing has been studied by Li et al. [71] using the FSI technique. The Mesh movement method was employed as it was recommended for better transient analysis. The cavitation effect was captured by using the full cavitation model available in Software Fluent. This model captures the effects of bubble dynamics, phase change, and pressure fluctuation that occur in the fluid domain. Experimental results of double-groove journal bearing were compared with the numerical results and it was concluded that the full cavitation model and dynamic mesh technique can be used for the nonlinear behavior of the rotor-bearing system. But results of deformation and stresses in the bearing material were not discussed in this study.

Li et al. [70] studied the effects of misalignment in two axial grooved journal bearings. CFD-FSI along with the mesh movement method has been employed to analyze the transient flow field of a misaligned grooved journal bearing. The effect of cavitation was considered by including the Full cavitation model (or Singhal model) for the analysis. Initially, the CFD method was validated by comparing static and dynamic performance results with Guo et al. [43]. Results indicate that the values of maximum film pressure increased significantly when the degree of misalignment increased. However, other parameters such as oil film force and attitude angle did not vary significantly with the misalignment.

A CFD and monolithic FSI study on journal bearing by Liu et al. [22] highlighted the effect of different bearing materials. The influence of different bearing materials like steel, nylon, Babbit was considered for numerical analysis under steady and unbalanced loading conditions. Cavitation-based CFD Analysis was carried out considering both half-Sommerfeld and phase change boundary conditions. The general comments drawn were that under both static and dynamic load, larger displacement of the rotor was observed for bearing with lower young’s modulus (soft bearing material i.e. nylon bearing). Due to this, a reduction in hydrodynamic pressure generation takes place and in turn, it lowers the load-carrying capacity of the rotor-bearing system. Therefore, it can be concluded that deformations in the bearing greatly influence the performance of the rotor-bearing system.

4 Fluid Film Bearing Performance Considering the Thermal Effects

It is a widely known fact that the viscosity of the lubricant is significantly impacted by the surrounding temperature. Liquid lubricant viscosity decreases with the temperature rise and consequently load-carrying capacity of the bearing will reduce with a decrease in viscosity of the lubricant. Hence the effect of temperature on lubricant film holds a crucial part in the evaluation of static and dynamic characteristics (like dynamic stability, stiffness) of journal bearing. In 1958, Hughes and Osterle studied the effect of temperature in a hydrodynamic lubrication system and found the relationship between viscosity, temperature, and pressure [77]. In most of the literature, for the simplicity of numerical methods, material properties of journal and bearing were assumed to be temperature independent. Also, the energy conservation equation was solved if the effect of temperature is considered during numerical analysis.

The relation between viscosity, temperature, and pressure are listed in Table 2 and it is incorporated by the researchers in the study of journal bearing [35]. These relations are represented in the form of equations Eqs. (1) to (7)

Table 2 List of equations/models define lubricant viscosity–temperature–pressure characteristics
Full size table

The relation between lubricant viscosity and temperature is explained by the temperature effect model, Vogel’s equation, and Walther’s equation [78] represented by Eqs. (1), (2), and (3) respectively. The equations are written in the form:

$$\eta ={\eta }_{0}{e}^{-\beta (T-{T}_{in})}$$
(1)
$$\eta =A{e}^{\frac{B}{T-C}}$$
(2)
$$\mathrm{loglog}\left[\frac{\eta }{\rho }+0.6\right]=C1-C2\left(\mathrm{log }T\right)$$
(3)

The relation between fluid pressure and temperature is explained by Barus Equation [78] and is given by Eq. (4):

$$\eta ={\eta }_{0}{e}^{\alpha p}$$
(4)

where p is the fluid pressure and pressure-viscosity coefficient α is:

$$\alpha =1.81+0.0073(400-T)$$
(5)

The effect of temperature and pressure on lubricant viscosity is captured by Khonsari and Wang [79] named Pressure–Temperature effect model and Knezevic and Savic Equation [80] represented by Eqs. (6) and (7) respectively:

$$\eta ={\eta }_{0}{e}^{-\beta \left(T-{T}_{in}\right)+\alpha p}$$
(6)
$$\eta \left(\rho ,T\right)=A{e}^{\frac{B}{(T+273.15)-C}}{ e}^{\frac{p}{{A}_{1}+{A}_{2}T}}$$
(7)

From Table 2, it can be seen that many researchers considered laminar and isothermal conditions for the numerical study so that analysis becomes simple and easy to implement during the analysis. However, when the numerical results were compared by incorporating turbulence and temperature effects, it showed that these effects cannot be ignored. In turbulent conditions, fluid pressure developed in the bearing is higher than that of the laminar. Hence the study of temperature and turbulent effect on bearing performance is also crucial for high-speed machinery as these decide the bearing performance parameters.

The influence of oil entrance temperature and eccentricity ratio (or effect of external load) on the frictional torque in the case of a turbocharger journal bearing was studied by Deligant et al. [72] using the finite volume method. Temperature effects were adopted in the analysis using Vogel’s Equation [78]. CFD analysis is carried out at a different rotational speed of the shaft and results were validated with experimental work carried out at the CNAM lab. The general comment drawn is the variation in the eccentricity ratio doesn’t have a significant influence on frictional torque. This torque, however, decreases with an increase in oil entrance (Toil-in) temperature and rotational speed. The reason behind this to happen is due to viscous heating.

In continuation, thermohydrodynamic analysis was carried out on a journal bearing considering viscosity variation using the CFD technique by Singla et al. [81]. The pressure–temperature effect model [81] has been used for defining the relation between viscosity, pressure, and temperature. Performance parameters of the bearing were calculated under constant and varying viscosity of lubricant using ANSYS Fluent software. Authors highlighted that by considering the effect of temperature, lubricant viscosity decreases, and hence load carrying capacity will reduce.

Static and dynamic characteristics of journal bearing, hydrostatic bearing, hybrid bearing, and squeeze film bearing were numerically studied by Guo et al. [43] using the CFD technique. CFX-TASCflow numerical tool with the k-ε turbulence model was validated against the standard lubrication solution and they are in good agreement. Also, results obtained from this software were compared with the other CFD codes like VT-FAST, DyRoBeS-BePerf, and VT-EXPRESS with and without consideration of temperature into account. Similarly, the same group of researchers [44] calculated the dynamic forces acting on labyrinth seals of a steam turbine and compressor eye seals by the CFD technique. Forces obtained from CFX-TASCflow were matched with already available computer program results of bulk flow analysis.

Thermal elastohydrodynamic (TEHD) i.e. the influence of thermal effect, thermal expansion of bearing and shaft, and mechanical effects (like deformation and stresses) on a highly loaded plain journal bearing working in extreme conditions were studied by Bouyer and Fillon [8]. The FDM is used to solve Reynolds, energy, and Laplace equations by an iterative process. Walther’s equation [78] was used to define the relationship between oil viscosity and temperature but the influence of cavitation was neglected. Fluid pressure, dissipated power, and minimum film thickness results of the TEHD model and thermal (THD) model were compared with the isothermal model. Comparing the results of the isothermal model with the THD model, dissipated power is decreased by 44%, film thickness by 65%, and fluid pressure is greatly increased by more than 41% when the THD model is considered. The increase in the fluid pressure was due to the reduction in viscosity and hence eccentricity increases. Further, comparing results of the THD and TEHD model, dissipated power is reduced by 7.3%, fluid pressure is reduced (48.5%) remarkably due to the consideration of thermal and mechanical effect (TEHD model). It was also found that due to mechanical deformation, lubricant reservoirs (called ‘pockets’) were created, and hence because of these pockets, fluid pressure and temperature value reduces.

Wang et al. [82] carried out stability analysis of both herringbone groove gas journal bearing (HGGJB) and plain gas journal bearing (PGJB) using the two-way FSI Technique. The influence of temperature, rotational speed, and bearing load on the stability of both the bearing was analyzed. Initially numerical results (stiffness and damping coefficients) were validated by comparing it with the results of the perturbation method and were in good agreement. Later, along with the FSI technique, the stability of the bearing is determined by calculating direct and cross-coupled damping and stiffness coefficients. Results showed that the PGJB and the HGGJB may lose their stability as the ambient temperature and rotational speed increase, and their stabilities were enhanced as the bearing capacity (or load on the bearing) increases. Also, the stiffness values for PGJB are sensitive to temperature, and the HGGJB is sensitive to the bearing capacity. Generally, the author has concluded that HGGJB is more stable than PGJB.

Based on thermal effects, the following major conclusions can be drawn from the literature.

  • An increase in the eccentricity ratio will vary the temperature of the lubricant. With the increase in oil film thickness (or decrease in eccentricity ratio) between journal and bearing, it is obvious that the oil temperature decreases.

  • The temperature of the lubricant rises as the rotational speed of the journal bearing increases. This is because of the increase in shear stress and velocity gradient between the oil films. Also, rotational speed has a major impact on the structural deformation and stresses developed in fluid film bearing.

  • Temperature rise takes place with the increase in the load on the shaft (it is nothing but an increase in eccentricity ratio)

  • Temperature rise can be reduced by having more oil grooves. The behavior of reduction in the oil temperature with respect to groove numbers is almost linear [60, 83].

  • To reduce the oil temperature rise in high-speed bearings, it is recommended to supply the lubricant at high pressure.

5 Fluid Film Bearing Performance Considering both the Cavitation and Thermal Effects

From Sects. 3 and 4, it is observed that the influence of cavitation and thermal effect is extremely important for predicting the performance of fluid film bearing. In this regard, recent articles have focused on the influence of cavitation and thermal effects on bearing performance.

Concli [69] numerically studied the influence of eccentricity ratio and the shaft rotational speed on the performance of the journal bearing by incorporating the cavitation model. Cavitation models namely Schnerr–Saurer (S–S) and Kunz model (K) were compared with a non-cavitation model like Sommerfeld and half-Sommerfeld models. The influence of temperature was also studied by incorporating Eq. (8). Specific gravity of oil at any temperature (TO) is:

$${\rho }_{t}={\rho }_{15}-0.00063({T}_{O}-15)$$
(8)

Initially, numerical code was written using OpenFOAM, and code was validated with the results for long journal bearing with eccentricity ratio (ε) = 0.6 [64]. CFD analysis was carried out with different cavitation models at different eccentricity ratios and the shaft rotational speed. Numerical studies reveal that eccentricity ratio and rotational speed have a direct relationship with the fluid film pressure. Also, results obtained from both the cavitation model (S–S model and K model) were almost similar except at the lower eccentricity ratio. Due to bubble formation in the divergent region, a reduction in fluid film pressure values was observed, and hence the load-carrying capacity of the bearing will reduce. Therefore, the effect of cavitation and temperature cannot be underrated in finding the performance of the journal bearing. Underestimation of cavitation in journal bearing leads to under design of bearing elements, which may result in component failure.

Similarly, multiple effects (cavitation, temperature, turbulence, and inertia) on the performance of water-lubricated spiral groove thrust bearing (SGTB) were studied and CFD analysis was performed by Lin et al. [2]. Temperature effects were adopted in the analysis as per the temperature effect Model [78]. Static characteristics like load carrying capacity, frictional torque, and frictional coefficient of the bearing were investigated at higher shaft speed. Initially, the theoretical model with consideration of multiple effects is validated with the experimental results [84] and found agreeable occurrence (˂ 4%). Numerical results indicated that static characteristics like load carrying capacity and frictional torque decrease with the consideration of inertia and cavitation. These static characteristics reduce with the increase in rotational speed. This is mainly due to the formation of bubbles in the water lubricant which in turn weakens the hydrodynamic effect. It is also observed that oil film temperature increases with the inertia but on the other hand it reduces by the occurrence of cavitation in bearing. However, the effect of inertia was more than cavitation, especially in high-speed applications. Hence it was concluded that the effect of inertia and cavitation effect can’t be neglected for SGTB. The authors have limited their study to CFD analysis.

FSI analysis on a special type of journal bearing called tilting pad bearing considering multiphase flow has been studied by Geller et al. [61]. This multiphase flow was integrated with vapor cavitation by using the Rayleigh-Plesset equation along with thermal effect (Knezevic and Savic equation [80]) is used. The advantage of using this cavitation-based model is it describes the effect of condensation (i.e. collapse of a bubble) and vaporization (i.e. bubble formation). This model was fully integrated into the ANSYS CFX for the FSI simulation. Numerical study indicates that consideration of the cavitation effect, plays a significant role in the FSI analysis and this FSI technique can be utilized to explain the behavior of lubricants in a journal bearing.

In CFD coupled FSI analysis by Chen et al. [83] the effect of the number of oil grooves and its location on journal bearing surface was carried out in the high-speed application. Simulations were conducted for a different number of grooves located at equal intervals on the bearing surface as shown in Fig. 3. Thermal effects (as per Khonsari and Wang’s [79] pressure–temperature effect model), and cavitation in the form of a multiphase flow model (or simulation model) were taken into account for the analysis. Initially, CFD results of simple journal bearing were validated with the experimental work of Kasolang et al. [85] and results were in good agreement. CFD results indicate that by increasing the number of oil grooves, load-carrying capacity was decreased which is mainly due to low fluid film pressure generation in the bearing. However, elastic deformation and stresses in the bearing significantly reduce with the increase in the oil groove. Therefore, parameters like cavitation, the number of grooves, and their location play a key role in changing the elastohydrodynamic lubrication (EHL) characteristics of journal bearing.

Fig. 3
figure 3

Rotor bearing geometry with (a) four and (b) two grooves around the bearing circumference [83]

Full size image

In continuation, a similar study on the effect of a number of oil groove locations on the bearing surface was analyzed numerically by Lin et al. [60] using the FSI technique. FSI method was validated with the results of experimental studied conducted by San Andres et al. [85] and Childs and Hale [85] on five groove journal bearing considering thermal effects at different loading conditions and results were in an agreeable range. Considering both cavitation and thermal effects, transient analysis was carried out on a rotor-bearing system with two, three, four (Fig. 3), and five numbers groove around the bearing surface. It was observed that for constant 400 N external load when the journal speed increased from 5000 rpm to 50,000 rpm, cavitation volume fraction and maximum temperature were increased by 28.3% and 350% (i.e. from 2.7 to 12.4 °C) respectively. The rise in the temperature is mainly due to the shear rate across the film thickness. However, Lin et al. observed that as the number of oil grooves increases, more amount of lubricant will be flowing in and hence there is a reduction in cavitation volume fraction and improved cooling ability.

Li et al. [71] carried out the transient flow of oil lubricant in double groove journal bearing using CFD-FSI techniques. The dynamics of the oil lubricant are calculated using the dynamic mesh technique of commercially available software Fluent. The Mesh movement method was employed in the study as it was highly recommended when the transient analysis is carried out. The movement of the journal is described by Fluent user-defined function (UDF) using C-language. For the FSI analysis, the coupling method of Fluent and MATLAB was done with the transient flow. The cavitation effect was considered using the full cavitation model available in software Fluent. The phase-change rate expression is deduced from the reduced Rayleigh-Plesset equation in this cavitation model, which accounts for all first-order effects (i.e., phase change, bubble dynamics, turbulent pressure fluctuations, and noncondensable gases). Experimental results of double-groove journal bearing were compared with the above-said model and it was concluded that the full cavitation model and dynamic mesh technique can be used for the nonlinear behavior of the rotor-bearing system. Deformation or stresses in the bearing material were not presented in the study.

6 Conclusion

In the past few decades, CFD and FSI technique has become a more convenient tool to evaluate the performance of fluid film bearings due to the development in the field of computational resources.

The results presented in this review study provide useful information for enhancing the bearing performance by adopting real-time boundary conditions. The conclusions drawn from the present review are as follows:

  • Journal bearing lubricated with Bingham fluid yielded better bearing performance characteristics compared to Newtonian fluid [11]. Hence FSI study on smart fluids such as MR and ER fluids as a lubricant incorporating cavitation and the thermal effect is needed for the moment.

  • The effect of considering the thermal models on bearing performance parameters in the CFD analysis of journal bearing has been witnessed. With the increase in temperature, load-carrying capacity has greatly reduced which is mainly due to a reduction in lubricant viscosity [2, 8, 46, 48, 58, 74, 77].

  • Eccentricity ratio (or bearing load) and shaft rotational speeds are the influencing parameters for increasing oil film temperature and cavitation [85].

  • Even though bearing deformation due to oil film pressure is fairly small, it can’t be underrated. Rotational speed has a major influence on the deformation and stresses in the bearing. The deformed bearing elements act like a lubricant reservoir (famously known as pockets) and reduce the bearing performance by reducing the fluid pressure. Also, over a prolonged period, the life of the bearing components will reduce [86].

  • Correlation between oil viscosity, pressure, and temperature are well explained and are listed in Table 2. Many researchers conducted and analyzed the importance of thermal effects on the journal bearing performance.

  • CFD and FSI study of fluid film bearing was carried out based on the assumptions such as uniform load is acting on the bearing, laminar lubricant flow, perfectly aligned bearing, isothermal conditions, and iso-viscous fluid property. Numerical analysis can be undertaken considering real-time boundary conditions for more precise results.

  • Due to cavitation, a reduction in the bearing performance parameters are observed which is mainly due to decrease in hydrodynamic fluid pressure [65].

  • During the cavitation phenomenon, high-intensity microjets are formed due to the bubble burst. These microjets damage the bearing material and over the period, bearing may fail by fatigue [87]. The influence of cavitation on the bearing performance can’t be underrated.

Non-availability of experimental data for the validation of FSI models leads to the consideration of realistic boundary conditions for numerical simulations. Further, the authors foresee various challenges involved in carrying out experimental and numerical work, viz. the accuracy level of measuring devices, alignment of the bearing for a longer period, the feasibility of considering real-time boundary conditions for the numerical analysis, computational time used during CFD and FSI analysis (especially for complex geometry), discretization (or meshing) of numerical model and coupling technique used for FSI study.