1 Introduction

Depletion of fossil fuels and their environmental impacts have pushed the development of renewable energy sources (RESs) as valuable alternatives. RESs either have no inherent inertia such as photovoltaic (PV)sources, or their inertia is decoupled from frequency variations such as variable speed wind turbines (VSWTs) i.e., type 3 and 4 wind turbines (WTs). Therefore, increased integration of RESs in the electric power systems may lead to problems with frequency control and stability. Modern grid codes, such as the UK code [1], encourage the participation of offshore WTs which are larger than 50 MW in frequency regulation.

It is very important to continuously maintain the frequency of electrical power systems. Any frequency deviation (\(\Delta F\)) from nominal value is an indication of unbalance between demand and generation. For example, if load demand is increased or an outage of any generating units occurs, the grid frequency will be decreased and vice versa [2]. When electrical power systems based on conventional synchronous generators (CSGs) are subjected to any abrupt load changes, the stored kinetic energy (KE) in the rotating rotors will tolerate these load changes until primary and secondary frequency control operates [3, 4]. Nowadays, the new trend for generating electricity is based on RESs due to the depletion problem of fossil fuel and some environmental issues such as global warming [5, 6]. Unfortunately, RESs are usually operated at maximum power point (MPP) unlike some of CSGs which usually contain spinning reserve which is used to overcome \(\Delta F\) and steady state errors, which means that the frequency stability of power systems with increased penetration of RESs has become worrying [3, 7], specially, with the encountered increase in the rate of change of frequency (RoCoF). So, it is very important to develop new methods for frequency control to overcome the frequency stability problem [8].

Frequency regulation depends on the stored energy due the inertia of CSGs. Various studies have been devoted to increasing system inertia via virtual inertia sources. For example, the authors in [9] introduce and optimize controllers to enhance frequency stability of doubly-fed induction generator (DFIG) wind farm. While in [10], the authors have discussed frequency regulation through controlling the rotor current of DFIG. In [11], the authors have demonstrated the role of using derivative controlled virtual inertia of energy storage systems (ESSs) and PV systems in enhancing frequency stability. Also, frequency control with RESs under load shedding is performed in [8]. In [12, 13], fuzzy logic controller is designed to determine the appropriate percentage of de-loading of wind farm (WF) in order to regulate system frequency. In [14], the authors studied the effect of the de-loading method of PV generation on power system frequency. Frequency regulation by centralized droop controller is performed for de-loaded permanent magnet synchronous generator (PMSG) offshore WF in [15]. Frequency control for PV system in microgrid using direct current (DC) link voltage and the de-loading method is introduced in [16].

ESSs with rapid response, high efficiency and large power density are suitable for frequency regulation of electric grids. A brief overview on ESSs is given in [17]. In [18], the authors have discussed the effect of hybrid energy storge (HES) on frequency stability of a microgrid. Enhancing frequency stability for an isolated system using an ultracapacitor is found in [19]. In [20], the authors illustrate the difference between proportional integral derivative (PID) and factional order PID (FOPID) controller on \(\Delta F\) for hybrid fractional order power generation and ESSs. Frequency regulation with increased penetration of PV systems using EESs is studied in [4]. Battery energy storage (BES) for frequency control with increased penetration of wind energy is demonstrated in [5].

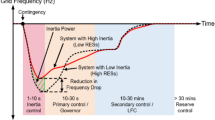
Frequency can be regulated through the inverters of RESs. This is achieved by adding a supplementary control signal that depends on either \(\Delta F\) or RoCof. For example, frequency control for a microgrid with PV power plant using PV inverter is introduced in [21]. While smart PV inverter for frequency control of smart grids is justified in [22]. In addition to this, modern load management strategies and control techniques are tested for frequency control. For example, frequency control for a microgrid using the stored energy in electric vehicles (EVs) is studied in [23, 24]. Some researchers have discussed various algorithms and controllers, for example, frequency control of PV connected microgrids using fuzzy logic controllers [25], and frequency control for power systems with high penetration of RESs using a stochastic fractal optimizer [3]. Figure 1 summarizes the various methods discussed in literature for frequency regulation in the presence of RESs.

Fig. 1
figure 1

Summary of the methods of frequency support with RESs

Full size image

The importance of integration of RESs with electrical grids and their effects on frequency regulation has attracted many researchers, therefore, an extensive published work has been found in the literature.

This paper aims to introduce a comprehensive review of the effect of high penetration of RESs on frequency regulation of electrical power systems and to compare, evaluate and classify methods of mitigation. This work may be a guide for future grid codes regulation regarding the participation of RESs in frequency control.

This paper is organized as follows: Sect. 2 discusses the incentives towards 100% RESs power systems and its effect on power system inertia and frequency. Modelling of RESs which include PV and wind energy is illustrated in Sect. 3. Section 4 discusses the effective frequency regulation methods for power systems with high penetration of RESs. Section 5 summarizes and concludes the paper outcomes.

2 Increased Penetration of RESs in Power Systems

Many countries around the world are now moving towards complete dependence on RESs and have set their future plans to achieve this goal. Therefore, flow of research is found in literature to study the effect of high penetration of RESs in electric grids on different aspects such as their operation and control. This section provides a summary for global rush towards replacing conventional energy sources by RESs, and a comprehensive review of their effect on power system frequency stability.

2.1 Toward Power Systems with 100% RESs

Extensive research has been done to discuss the problems of fossil fuel resources which are running out and a source of global warming [26]. The depletion of these resources is expected to occur nearly by 2050 to 2060 [27]. Emissions from these resources are mainly due to fuel burning during the electric power generation process, while emissions from renewable power plants especially wind and solar power plants are mainly due to the fabricating process of power plant equipment (see Fig. 2) [27]. For these reasons, many conferences (like Paris agreement) have been organized to reduce these emissions and solve the problem of global warming [28]. Moreover, the climate action conference which was held in New York in 2019 by the United Nations put goals to achieve. These goals are to decrease the greenhouse emissions to 55% before 2029 and to reach zero emissions before 2050 [29]. A model which discusses the increase in fossil fuel price with depletion while using only fossil fuels and fossil fuels integrated with RESs is demonstrated in [30]. In [31], the authors investigate a method to calculate carbon dioxide emissions in Tokyo and its relation to wind speed.

Fig. 2
figure 2

Maximum carbon dioxide emissions (g/kWh) by different energy source

Full size image

Increased penetration of RESs in electric power systems will reduce both the carbon dioxide emissions and cost of electric power generation [32]. In [33], the authors discuss carbon concentration, its tax cost and vulnerability of climate change, particularly their effects on the extensive use of RESs. In [34], the authors conclude (for Egyptian grid) that the total cost reduction (fuel and environmental cost) can be 220,000$, 1,500,000$ and 2,200,000$ if the RESs are 2%, 16% and 22% of the total generation capacity respectively.

In 2016, the global electricity generations were 1096, 487, 303, 112 and 13.5 GW from hydroelectric, wind, PV, biomass and geothermal, respectively [35]. While in 2019, these values were 1310.3, 622.7, 580.16, 123.8 and 13.93 GW respectively [36]. Furthermore, it is planned for global electricity generation from RESs to reach nearly 35% before 2030 [35]. There was a significant increase in the use of RESs in the European electrical power sector from 14.3% (in 2004) to 30.8% (in 2017) [37]. Portugal is one of many countries that plan to reach 100% RESs in the electric power sector [38]. Its electric grid has a high rank in using RESs compared to other European countries, it reached 57% RESs in 2016 [39]. Also, it is expected for Kazakhstan to reach 100% RESs before 2050 [40]. A statistical for global wind and PV increased penetration is illustrated in Fig. 3 [36, 41, 42].

Fig. 3
figure 3

Increased penetration of global wind and PV generation

Full size image

2.2 Power System Inertia and Frequency Stability

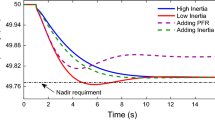
Frequency stability of power systems is known as the behavior of power systems against any disturbances which tend to reduce frequency of power systems below their nominal value [43]. Inertia is known as the time duration of a generator in which the generator provides its rated power from its stored KE to the power system during disturbances as given by Eq. (1) [4, 44]. Solar PV systems do not have rotating masses, hence no stored KE, while wind generators have rotating masses but decoupled from power systems through power electronic devices and MPP techniques. So, the more the RESs penetration in power systems, the more the rated MVA of power systems with constant KE and the less the inertia of power systems as described by Eq. (2). Increasing RESs, especially solar PV and wind energy, has a negative effect on power system inertia [45]. Equation (3) shows that lower inertia power systems have faster RoCoF and higher frequency nadir (\({F}_{nadir}\)) as demonstrated in Fig. 4 [6, 44]. Figure 4 describes the \(\Delta F\) characteristics extracted from MATLAB/SIMULINK for a primary controlled synchronous generator with governor speed droop 5%, governor time constant 0.2 s, turbine time constant 0.5 s and is subjected to 0.1 pu power imbalance assuming zero load damping factor. Load shedding, nuisance tripping of power plants and grid blackout may occur at higher \({F}_{nadir}\) and RoCoF [46, 47], which are consequences of low inertia systems.

$$H=\frac{J{{\omega }_{n}}^{2}}{2{S}_{n}}$$
(1)
$${H}_{sys}=\frac{\sum KE}{{S}_{sys}}$$
(2)
$$\frac{d\Delta f}{dt}=\frac{1}{2{H}_{sys}}\left(\Delta {P}_{m}-\Delta {P}_{l}-D\Delta f\right)$$
(3)

where \(H\) is the generator inertia, \(J\) is the generator moment of inertia, \({\omega }_{n}\) is the generator rated speed, \({S}_{n}\) is the rated MVA of the generator, \({H}_{sys}\) is the power system inertia, \({S}_{sys}\) is the rated MVA of the power system, \(\sum KE\) is the summation of stored KE (in MW.s) in all synchronous generators, \({\Delta P}_{m}\) is the change in generator mechanical power, \({\Delta P}_{l}\) is the change in electrical frequency independent demand and \(D\) is the load damping factor.

Fig. 4
figure 4

Frequency deviation characteristics with different values of inertia constant

Full size image

Many studies have been conducted to investigate how increasing RESs affects power systems. In [48, 49], the authors discuss the effect of increasing RESs on power system reliability. The authors in [50, 51], shed light on the effect of renewable distributed generators on the settings of protective devices. The effect of increased penetration of RESs on power system frequency stability is illustrated in [52,53,54,55]. While [56] discusses the effect of increasing the VSWTs and other factors on the RoCoF of the Croatian power system in case of islanding operation. Furthermore, a comparison between the frequency response of CSGs and WF is demonstrated in [57].

Therefore, the philosophy of participation of RESs in frequency has been changed. Recently, new grid codes state that RESs must participate in frequency regulation which will be discussed in detail in Sect. 4. In Germany, for example, if the power system frequency increased to 50.2 Hz, the RESs must decrease their output by a rate of 40% of their capacity per Hz [58]. On the other hand, some papers have been conducted to determine the allowable penetration level of RESs especially wind energy such as [59, 60]. The flow chart in Fig. 5 describes a criterion for calculating the acceptable level of RESs while achieving the standard \({F}_{nadir}\) for the Korean power system [61]. If the minimum frequency (\({F}_{min}\)) is larger than \({F}_{nadir}\), the power system can accept more RESs instead of CSGs, otherwise the limit of RESs can be calculated from the previous loop.

Fig. 5
figure 5

Algorithm of determining the acceptable level of RESs for achieving frequency stability

Full size image

3 Modelling of RESs for Frequency Control

Studying the performance of power systems with high penetration of RESs requires mathematical modelling of these RESs [62]. So, the appropriate model of RESs for frequency control studies has been discussed in literature. This section discusses a literature survey into modelling of PV systems and WFs especially VSWTs.

3.1 Modeling of PV

PV systems convert solar energy into electrical energy. The efficiency of conversion is less than or equal 18%. Usually bulk PV stations are equipped with maximum power point tracking (MPPT) techniques [63]. A comprehensive survey of MPPT techniques for PV is introduced in [64, 65], and PV mathematical modelling are surveyed in [66, 67]. In [68], the authors demonstrate the equivalent linearized dynamic model of a high penetration of PV energy integrated with multi-machine power system. There are different formulas in literature that describe the output power of the PV panels. These formulas are summarized in Table 1. A dynamic model of frequency droop controller of PV which is validated by [69] for PV rating larger than 10 MW is shown in Fig. 6 with the enabling of governor response, where \({\mathrm{Freq}}_{\mathrm{ref}}\) is the reference frequency, \(\mathrm{Freq}\) is the actual frequency, \({\mathrm{P}}_{\mathrm{branch}\_\mathrm{ref}}\) is the branch reference power, \({\mathrm{P}}_{\mathrm{branch}}\) is the branch power, \({\mathrm{P}}_{\mathrm{command}}\) is the power command of the controller, \({\mathrm{D}}_{\mathrm{dn}}\) is the down regulation droop, \({\mathrm{D}}_{\mathrm{up}}\) is the up regulation droop, \({\mathrm{K}}_{\mathrm{i}}\) is the integral gain of the droop controller, \({\mathrm{K}}_{\mathrm{p}}\) is the proportional gain of the droop controller, \({\mathrm{T}}_{\mathrm{p}}\) is the time constant of the active power filter, \({\mathrm{T}}_{\mathrm{lag}}\) is the time constant of plant controller, \({\mathrm{Pe}}_{max}\), \({\mathrm{Pe}}_{\mathrm{min}}\) are the maximum and minimum power error in the droop controller respectively and \({\mathrm{P}}_{\mathrm{max}}\), \({\mathrm{P}}_{\mathrm{min}}\) are the maximum and minimum power command respectively. Also; the schematic diagram of frequency regulation using overvoltage de-loaded PV based on \(\Delta \mathrm{F}\) is shown in Fig. 7 [70], where \({I}_{t}\) is the solar irradiance, \({T}_{c}\) is the actual PV panel temperature, \({V}_{dc-del-ref}\) is the reference de-loading DC voltage, \({V}_{dc-meas}\) is the measured DC voltage, \({P}_{FFR}\) is the fast frequency response power signal which is an emulation of droop signal of CSGs and \({I}_{d-ref}\) is the reference direct axis current which control active power through PV converter.

Table 1 Summary of various PV solar energy models
Full size table
Fig. 6
figure 6

Illustration of frequency control through PV active power control

Full size image
Fig. 7
figure 7

Dynamic modelling of frequency regulation using de-loaded PV

Full size image
Fig. 8
figure 8

Configuration diagram of type 3 WT

Full size image
Fig. 9
figure 9

Configuration diagram of type 4 WT

Full size image

3.2 Modeling of Wind Energy

WFs can be categorized into fixed speed wind turbines (FSWTs) and VSWTs. DFIGs are the most common generators for VSWTs as they have higher efficiency than FSWTs [71, 72]. In DFIGs (type 3 WT), MPP is achieved by controlling the rotor speed through controlling rotor current by rotor side converter (RSC) [73]. A comparison between type 3 and type 4 WT is illustrated in Table 2 [74,75,76,77]. In [71], the authors discuss the various MPPT techniques for WTs.

Table 2 Comparison between type 3 and type 4 WTs
Full size table

A comprehensive survey of various modelling categories of WT generators is demonstrated in [78]. In [66, 67], a review of mathematical modeling of wind power is illustrated. The mechanical power of WT (\({P}_{wt}\)) is shown by equations in Table 3. In addition to this, [79] discusses the relation between WF output power and wind speed including spatial effect. While the equivalent model of single and multi-machine WF is illustrated in [72] including the model of wind speed, WT, RSC, grid side converter (GSC) and DFIG. Moreover, the equivalent model of DFIG WT is discussed in [73].The transient stability linearized model of VSWT is illustrated in [74]. In [80], the authors illustrate the transfer function (TF) of a WF which has 16 WTs. This TF relates the output active and reactive power to WF terminal voltage and wind speed. While in [81], the authors shed light on a standard model (AGC30) for RESs which is used in MATLAB/SIMULINK to study both economic dispatch and frequency regulation. The dynamic modelling of VSWT and its pitch angle and droop controllers are shown in Figs. 10, 11, 12 respectively [3], where \({P}_{e}\) is the WT output electrical power, \({\mathrm{H}}_{\mathrm{wt}}\) is the VSWT inertia constant, \({\omega }_{ref}\) is the ref VSWT speed at MPP, \({T}_{com}\) is the command torque, \({P}_{com}\) is the command power, \({\beta }_{ref}\) is the pitch angle at rated rotor speed, \({\beta }_{a}\) is the additional pitch angle which regulate \(\Delta F\) during disturbances and \(\tau \) is the time constant of the pitch angle controller.

Table 3 Formulas for output power of WTs
Full size table
Fig. 10
figure 10

Block diagram of VSWT

Full size image
Fig. 11
figure 11

Block diagram of VSWT pitch angle controller

Full size image
Fig. 12
figure 12

Block diagram of VSWT droop controller

Full size image

Extensive work in literature has shed light on modelling of type 3 WT since it is the most effective and has active power regulation. Equations (4–11) describe the dynamic model of DFIG while Figs. 13 and 14 describe the modelling of rotor side controller of RSC which controls the output active and reactive power of DFIG and grid side controller of GSC which controls the voltage of the dc bus and reactive power flowing between grid and rotor respectively [72], where \({v}_{gd}\),\({v}_{gq}\),\({i}_{gd}\),\({i}_{gq}\) are d, q axis voltages and currents of the GSC respectively; \({v}_{d}\), \({v}_{q}\) are d, q axis voltages of the grid respectively; \({i}_{rd}\), \({i}_{rq}\) are d, q axis currents of the RSC respectively; \({{v}_{d}}^{,}\), \({{v}_{q}}^{,}\) are d, q axis voltages of the rotor respectively; and \(\sigma =1-\frac{{{L}_{m}}^{2}}{{L}_{s}{L}_{r}}\).

Fig. 13
figure 13

Block diagram of GSC controller of type 3WT

Full size image
Fig. 14
figure 14

Block diagram of RSC controller of type 3WT

Full size image

WTs can be modeled in detail or simplified [74]. Detailed models, especially for the driven generators, are important to show the electromagnetic transients, however, for frequency studies simplified models can be satisfactory. For example in [73], with step variation of wind speed from 8 to 14 and back to 8 by 2 m/s steps, the results of the simplified model are accurate for both steady state and transient response (pitch angle, generator angular speed and power) with a time delay between both models less than 3% of the H constant of type 3 WT. While in [90], for wind speed 8 m/s and 0.1 pu load increasing, the results of the simplified model are accurate with small deviation in rotor speed and \({F}_{nadir}\) compared with the exact model. In addition to this, the simplified model is used in [91] to test a large network which has more than 30,000 buses, 2000 SGs, a WF has 468 MW (130 × 3.6 MW WTs). The simulation results show that the simplified model is accurate for transient stability studies. From the authors’ point of view, the simplified WT model is accurate, so it is recommended for frequency control studies.

$${v}_{ds}={R}_{s}{i}_{ds}+\frac{d{\psi }_{ds}}{dt}-{\psi }_{qs}{\omega }_{e}$$
(4)
$${v}_{qs}={R}_{s}{i}_{qs}+\frac{d{\psi }_{qs}}{dt}+{\psi }_{ds}{\omega }_{e}$$
(5)
$${v}_{dr}={R}_{r}{i}_{dr}+\frac{d{\psi }_{dr}}{dt}-{\psi }_{qr}{\omega }_{s}$$
(6)
$${v}_{qr}={R}_{r}{i}_{qr}+\frac{d{\psi }_{qr}}{dt}+{\psi }_{dr}{\omega }_{s}$$
(7)
$${\psi }_{ds}={L}_{s}{i}_{ds}+{L}_{m}{i}_{dr}$$
(8)
$${\psi }_{qs}={L}_{s}{i}_{qs}+{L}_{m}{i}_{qr}$$
(9)
$${\psi }_{dr}={L}_{r}{i}_{dr}+{L}_{m}{i}_{ds}$$
(10)
$${\psi }_{qr}={L}_{r}{i}_{qr}+{L}_{m}{i}_{qs}$$
(11)

where \({v}_{ds}\), \({v}_{qs}\), \({v}_{dr}\), \({v}_{qr}\) are d, q axis stator and rotor voltages (V) respectively; \({i}_{ds}\), \({i}_{qs}\), \({i}_{dr}\), \({i}_{qr}\) are d, q axis stator and rotor currents (KA) respectively; \({\psi }_{ds}\), \({\psi }_{qs}\), \({\psi }_{dr}\), \({\psi }_{qr}\) are d, q axis stator and rotor magnetic fluxes (Wb) respectively; \({R}_{s}\), \({R}_{r}\) are stator and rotor resistances (\(\Omega \)) respectively; \({L}_{s}\), \({L}_{r}\) are stator and rotor self inductances (mH) respectively; \({L}_{m}\) is the mutual inductance between rotor and stator (mH), \({\omega }_{e}\) and \({\omega }_{s}\) are the rotational and slip speeds (rad/s) respectively.

4 Efficient Frequency Regulation Techniques

In this section, the common methods for frequency regulation in literature are introduced. These methods depend on adding a virtual inertia via energy storage device, de-loading the RESs to have a spinning power reserve for frequency manipulation, using the load demand response for interchanging power with smart distribution networks and inertial response to support power systems with temporary active power. These.

four principles are widely discussed as follows:

4.1 Energy Storage Systems

ESSs are considered a good solution to mitigate the problem of RESs intermittency by satisfying equilibrium between load and generation while operating RESs under MPPT condition [97,98,99]. Their techniques can be classified as follows [97]:

  • Electrical such as super capacitor energy storage (SCES) and superconducting magnetic energy storage (SMES).

  • Electrochemical such as BES and fuel cell energy storage (FCES).

  • Mechanical such as flywheel energy storage (FWES), pumped hydro energy storage (PHES) and compressed air energy storage (CAES).

  • Chemical such as hydrogen energy storage (H2ES).

A review of various ESSs techniques and their efficiency, life time, charging rate, discharging rate and capacity is illustrated in [100]. While [99] discusses a survey about HES mainly BES integrated with SCES. A comparison between various aspects of different ESSs techniques is demonstrated in Table 4 [17, 101,102,103,104,105,106]. The authors in [17] shed light on various ESSs techniques which are used to smooth output power of WF. While the authors in [102] demonstrate the various control techniques which are used with BES to smooth the output power of WF. [103] illustrates the various techniques of mechanical ESSs which are used in PV and wind plants and their advantages and disadvantages. In addition to this, [107] investigates the optimal location (from power smoothing point of view) of 5 MJ SMES which integrates with renewable power systems. The authors in [108] categorize the target of ESSs into two classifications.

Table 4 Comparison between various aspects of different types of ESSs
Full size table

The power system operator must save a certain reserve active power to regulate the frequency of power systems during disturbances [104]. Using ESSs not only helps to smooth the output of RESs but also introduces frequency regulation for power systems during disturbances [109]. ESSs play an important role in regulating the frequency of power systems with high penetration of RESs as they can charge and discharge power into power systems [110]. In [111], the frequency regulation is achieved through active power control using SCES hybridized with BES for a microgrid consisting of a diesel generator and a WT. While the authors in [112] demonstrate the effect of BES location on power system frequency response due to load change at different locations. Moreover, energy control of type 3 WT integrated with FCES and SCES is illustrated in [113]. While the effect of fast response ESSs on frequency stability for Gotland island is illustrated in [114]. In addition to this, the authors in [98] investigate the effect of load increasing on frequency stability of two connected microgrids under different operating conditions of super capacitors. The authors in [115], illustrate the frequency stability of two-area power system subjected to a disturbance under three conditions. While in [116], the authors discuss the frequency regulation of a power system consisting of a diesel generator and a WT using BES under two different operating conditions. In [117], the authors investigate transient stability of an offshore WF connected to a marine current farm using a FWES based PID controller. Moreover, [118] investigates an optimization algorithm to optimize the parameters of SMES and PID which are used in secondary frequency control. A summary of some studies that have been conducted to enhance frequency stability using ESSs is given in Table 5. From the authors’ point of view based on the conclusion of Tables 4 and 5, the most effective recommendation for improving the power system stability especially frequency stability is to use BES.

Table 5 Some studies that have been performed to promote power system stability using ESSs
Full size table

4.2 De-loading of RESs

As mentioned earlier, RESs operate under MPPT condition which means that they do not have any reserve power to support frequency contingency event. One method of frequency regulation techniques is to de-load RESs which means to operate below MPPT to maintain a certain reserve power for frequency regulation [14]. The de-loading of PV systems is performed by controlling the output PV voltage either by under voltage or over voltage as shown in Fig. 15 [14, 70, 123]. Over voltage de-loading is preferred due to voltage stability wise. Figure 15 is extracted from MATLAB/SIMULINK for a PV model which has a 7.34 short circuit current and a 0.6 V open circuit voltage at standard conditions. More details for de-loading of PV is given in [124].

Fig. 15
figure 15

Demonstrates the de-loading of PV system by under voltage and over voltage

Full size image

Although de-loading of RESs below MPPT is not an efficient method for frequency regulation, it may be more effective than ESSs from cost point of view [125]. The efficient limits of PV de-loading are discussed in [125]. In [126], a cost analysis is carried out to show that the concept of de-loaded PV is economical when compared to BES for frequency control. So, many studies have been performed to illustrate frequency regulation by reserving a certain amount of active power using de-loading of RESs. Frequency regulation by active power control of PV system through inverter is investigated in [127]. [128] introduces a grid consisting of a PV system, a diesel generator and a WT and discusses the effect of using droop PV on frequency regulation while load is disturbed. While [129] discusses frequency regulation of an isolated microgrid through the de-loading of PV system, the percentage of de-loading is related to the \(\Delta F\) by a boost converter. Moreover, in [123] a microgrid that has 2688 KW of PV is simulated for frequency response due to 5% of load change while operating at MPP and de-loaded mode. The frequency response of northern Chile isolated grid is investigated in [70] for various PV levels and at different de-loading conditions which are MPP, 3% de-loading and 5% de-loading of PV. The results show that the level of PV slightly affects the frequency response unless the level is greater than 20% of the grid capacity. The authors in [126] combine the \(\Delta F\) with the MPP voltage in the de-loading criteria of PV. For the previous case study, the authors conclude that the de-loading is more cost-effective than ESSs.

On the other hand, WTs can be de-loaded through pitch angle control or rotor speed control (over speed or under speed), over speed control is recommended due to WT frequency stability issue at under speed operation [130,131,132]. Pitch angle control can be performed by operating the WT at a pitch angle close to the optimal value to reserve a certain amount of power to participate in frequency regulation [130]. [133] sheds light on the de-loading of VSWTs in order to satisfy power balance and then frequency regulation. The authors in [132] shed light on the acceptable range of rotor over speed de-loading and pitch angle de-loading based on wind speed. Figure 16 illustrates the de-loading technique of VSWTs by pitch angle control and rotor speed control [12, 130, 132]. Figure 16 is extracted from MATLAB for General Electric (GE) DIFG 3.6 MW with wind speed 16 m/s. More details are given in [134,135,136] for frequency regulation by de-loading of VSWTs either by rotor speed control or pitch angle control.

Fig. 16
figure 16

Demonstration of de-loading of VSWTs by pitch angle and rotor speed control

Full size image

The authors in [12] discuss the frequency regulation of a two-area power system penetrated with wind energy using de-loading technique based on adaptive PID controller. In addition to this, the authors in [137] compare the frequency response at various load disturbances while operating type 4 WT under MPPT condition and de-loading condition. While the authors in [138] compare the frequency regulation obtained from de-loading of WT while using fixed droop and wind speed adaptive droop. Moreover, the authors in [139, 140] investigate the frequency regulation introduced by traditional PID controller and adaptive PID controller which is based on artificial bee colony (ABC) algorithm. Also, the contribution of FOFPID de-loaded tidal plant on frequency regulation is discussed in [141] and compared with fixed droop, PID droop and fuzzy PID droop. Table 6 discusses the effect of de-loading of RESs on the frequency response of power systems. Based on the conclusion of various studies that have been done to improve the power system frequency, the authors prefer and recommend using ESSs rather than de-loading RESs from frequency improvement point of view although de-loading is more cost-effective than ESSs.

Table 6 Summarizes the effect of the de-loading operation of RESs
Full size table

4.3 Demand Response

Demand response is considered an effective frequency regulation solution at the load side which can be performed by under frequency load shedding (UFLS) or by the contribution of EVs [143]. UFLS is a process of removing a certain amount of power system load when an outage of large generating unit occurs. It is performed to keep balance between generated and demand power [8]. It is performed as a last solution if the power system reserve power is not sufficient for power balancing [8, 143, 144].

The authors in [144] introduce a criterion for UFLS for power systems which are penetrated with high RESs and integrated with ESSs. While the effect of UFLS on New England 39 bus frequency is illustrated in [145]. Moreover, in [146] the authors discuss UFLS for a two-area power system which has 500 MW of wind energy while considering the effect of inertial control of WT. In [144] the authors discuss the effect of UFLS on the frequency response of El Hierro power system while losing the largest generating unit and also discuss the contribution of VSWT in regulating the frequency as an alternative for UFLS. In addition to this, a criterion of UFLS is performed in [147] which depends on load flow and the convergence in errors, voltage violation and frequency violation. Also, this criterion is tested by Monte Carlo simulation.

The parameters of UFLS relay depend on the system \(\Delta F\) and RoCoF [143]. The role of datacenter in the optimization process of UFLS relay is illustrated in [148]. While the authors in [149] discuss the frequency response of a smart grid while using an adaptive UFLS relay which adapts its parameters each hour of the day.

Spread of EVs contributes to minimizing greenhouse gas emissions [150]. So, many researchers shed light on the impact of EVs. In [151], the authors discuss the effect of EVs on the emissions of carbon dioxide while integrating power systems with and without RESs. While [150] discusses the smart infrastructure which is required for smart EVs. In addition to this, a comprehensive detail about EVs, their ESSs and their energy consumption is discussed in [152]. Moreover, different EVs topologies with RESs based power systems are introduced in [153]. While various construction types of EVs are introduced in [154]. In addition to this, IEEE 33 bus system is studied in [155] as a case study to investigate the reduction in the cost of the system and minimizing the degradation of batteries while using EVs with RESs. Moreover, the authors in [156] optimize the integration of plug in EVs (PEVs) and RESs into power systems and verify the results on IEEE 9 bus power system.

EVs play an important role in frequency stability while minimizing UFLS at the same time [157]. [158] sheds light on the benefits of using both PV and EVs from power system stability and quality point of view. Modes of EVs which participate in frequency regulation can be classified to vehicle to grid (V2G), grid to vehicle (G2V) and EV aggregator [158]. Controlling the charging and discharging processes of EVs which are operated in G2V and V2G mode can participate in the frequency regulation of power systems while ensuring satisfaction for EV owner [158,159,160,161]. A comprehensive survey into V2G mode of EVs with RESs based power systems is introduced in [154]. V2G mode is more effective than plug in mode from frequency regulation point of view, but less effective than plug in mode from battery life time point of view [162]. EV aggregator is the communication ring between EV and power system operator which manages the charging process of EV and contributes to frequency regulation [163]. A Chinese two-area power system penetrated with wind energy is studied in [160] and discussed with the effect V2G EVs. While [164] discusses the effect of PEVs on the load frequency control (LFC) of a thermal power system based on two degrees of freedom PID. Moreover, a control methodology of EVs contribution in frequency regulation based on frequency disturbance and state of charge (SoC) is discussed in [165]. The authors in [166] illustrate a comprehensive survey about the different methods of EV charging and the effect of V2G from power system cost point of view. Usually, the droop charging control of EVs (only charging) is preferred as the discharging of EVs reduces battery life time [24]. So, the new trend of EVs is to use a secondary battery for frequency regulation [167].

The contribution of EVs in the primary frequency control of a power system integrated with RESs consisting of 38 generating units is studied in [168]. While the authors in [169] discuss intelligent energy management system for vehicle-to-vehicle (V2V) mode which is used to calculate the optimal energy supplied to grid to participate in frequency regulation. Moreover, the effect of EVs on the frequency regulation of Egyptian power system is illustrated in [170] at different levels of RESs and various load disturbances. In addition to this, [171] discusses the contribution of 1000 PEVs as an ESS for the frequency regulation of a PV grid. From the authors’ point of view, EVs are more effective than UFLS based on the summarization which is given in Table 7.

Table 7 Summarizes the effect of demand response
Full size table

4.4 Inertial Response

Inertial response is to temporarily support power systems with a certain amount of active power extracted from VSWTs based on the stored KE in the rotating masses of rotor and blades of WT. Inertia response is categorized into droop control, synthetic inertia and fast power reserve.

Droop control is an emulation of the CSGs’ governor which provides additional active power during frequency disturbance according to Eq. (12) [4, 57], where \(\Delta P\) is the additional active power released through the WT inverter, \({R}_{wt}\) is the droop coefficient of WT. However, the fixed droop gain is not feasible due to the intermittence of wind energy. So, [172] introduces a dynamic droop controller which control the RSC controller of type 3 WT.

Synthetic inertia is an emulation of the inertial response of CSGs (fast primary response) which is used with VSWTs to extract KE during frequency disturbances [173]. The reference power signal of synthetic inertia in [173] depends only on RoCoF, so the frequency could not be recovered to its nominal value. While the signal in [174] depends both on RoCoF and \(\Delta F\), so the frequency could be recovered to its nominal value.

Fast power reserve is to support the power systems with an additional KE from VSWTs by the overproduction of WT for a certain period [57]. The amount of temporary active power may reach 20% of the VSWT rating for 10 s or more [175]. The rotational speed of WT is reduced due to the overproduction process, so this KE is recovered back to the WT after the frequency disturbance is mitigated to sustain the stability of WT [57] as shown in Fig. 17. One of the fast power reserve challenges is that a secondary frequency dip (SFD) may occur during the recovering period. The SFD can be avoided through increasing the recovery period by controlling the accelerating power (\({P}_{acc}\)) [57]. SFD can also be avoided by adding an additional torque signal which depends on the deviation between WT rotating speed at the beginning and at the end of the overproduction period [176]. Table 8 provides a summarization of various inertial response techniques that have been conducted to enhance the power system frequency stability.

Fig. 17
figure 17

Illustration of fast power reserve inertia response criterion

Full size image
Table 8 Enhancing the power system frequency using various inertial response techniques
Full size table
$$\Delta P=-\frac{\Delta F}{{R}_{wt}}$$
(12)

4.5 Application of Metaheuristic Optimization on Frequency Control

Metaheuristic optimization algorithms differ from each other according to their constraints [50]. A summarization of some studies that have been conducted to enhance power system frequency based on various optimization algorithms for different frequency regulation techniques is given in Table 9.

Table 9 Promoting power system frequency stability based on optimization algorithms
Full size table

5 Conclusion

This paper discussed the motivative issues towards the 100% use of RESs power systems and its effect on power system inertia, \(\Delta F\) and RoCoF. Moreover, the dynamic modelling of PV and various WTs especially type 3 and 4 and their controllers which are used for frequency stability study were illustrated in this paper. Also, various frequency regulation methods, their advantages and disadvantages were discussed. In addition to this, some metaheuristic optimization algorithms were illustrated. Comprehensive comparisons between various frequency regulation methods have been made in this paper to help researchers and grid operators to select the most effective method to optimize the \(\Delta F\) and RoCoF. From the authors’ point of view based on various papers conclusion, ESSs especially BES are more effective than the de-loading of renewable energy sources from frequency regulation point of view. The authors recommend resorting the de-loading of renewable energy sources at very high penetrations while the spinning reserve of CSGs is not sufficient to support power system frequency disturbances. Demand response is considered a good solution to regulate frequency, but it requires an excellent communication infrastructure between generation and demand sectors. Various demand response techniques which are UFLS and EVs including their advantages and disadvantages were introduced in this paper. Inertia response is an excellent, cost-effective and fast frequency regulation solution and the most spreading technique, but it may cause a SFD during the power recovery period as it is a temporary technique. Prolongation of the recovery time can avoid the problem of SFD. For further studies, the authors recommend studying the effect of the prolongation of the recovery time on a wider scale and the effect of various electric vehicle topologies on frequency stability.