Small Strains in Soil Constitutive Modeling

Abstract

This paper reviews the state of the art of soil behavior in the range of small strains and its constitutive modeling, which is an important issue when predicting displacements under serviceability conditions. The factors that control nonlinear, hysteretic and dependent on recent history soil behavior are described. Likewise, concepts of soil constitutive modeling are explored in detail and two criteria are explained and used to classify the analyzed models: (1) a first criterion based on the concept of tensorial zones; and (2) a second criterion based on the elements that defines the hysteretic soil behavior, including reversal criteria, memory rules and the effects of reversals on soil degradation and on soil stiffness recovery. The fundamentals of the formulation of the analyzed models are provided, as well as their scope of application, advantages and disadvantages.

1 Introduction: The Kinematic Nature of Soil Stiffness

The stiffness of a body, understood as its resistance to deformation under applied forces, depends on its shape, its boundary conditions and the stiffness of its constitutive materials [1].

From the experiments carried out by Hardin and Drnevich [2], Simpson et al. [3], Jardine [4] and Smith et al. [5], Jardine [6] developed the idea previously stated by Skinner [7] and supported by a large number of researchers [8,9,10,11,12,13], to explain soil stiffness behavior depending on the range of stress and strain to which it is subjected, within the framework of the theories of Kinematic Yield Surfaces (KYS) and plasticity. Jardine [6] differentiated four zones around any point in stress space, which move and change their shape according to the stress paths followed. In each of these zones, Jardine identified a characteristic behavior of the soil, which was related to the nature of the strains that take place in them (Fig. 1).

Fig. 1

a Zones 1–4 (I-IV) in the stress space. b Axial plastic strains $\left( {\varepsilon_{p} } \right)$ normalized by the maximum axial total strain ($\varepsilon_{max }$) vs. total shear strain ($\varepsilon_{s,max }$). From [6]

Zone I:

Externally limited by ${\text{Y}}_{1}$ (Fig. 1a), soil behavior in this area is linear reversible [6, 14,15,16,17,18,19,20,21]. Some researchers indicate that a purely linear elastic behavior does not occur in any strain range, although it is a sufficient approximation from a practical point of view [1]. Likewise, Hueckel and Nova [22] affirm that irreversible deformations occur in all primary loading processes. Zone I of Jardine can be very small [23,24,25], especially in uncemented and normally consolidated soils [26, 27].

Zone II:

Internally limited by ${\text{Y}}_{1}$ and externally by ${\text{Y}}_{2}$ (Fig. 1a), soil behavior in this zone is nonlinear reversible, hysteretic and dependent on recent history [3, 4, 6, 15, 16, 20, 22, 28,29,30,31,32,33,34].

Zone III:

Internally limited by ${\text{Y}}_{2}$ and externally by ${\text{Y}}_{3}$ (Fig. 1a), soil behavior in this zone shows a first degree of irreversibility (plastic deformations), which depends on the $OCR$ [6, 35]. As can be seen in Fig. 1b, if $OCR > 1$, plastic strains in this zone tend to increase linearly with the strain, while if $OCR = 1$, they tend to do it in a nonlinear way.

Zone IV:

Internally limited by ${\text{Y}}_{3}$ (Fig. 1a), soil behavior in this zone shows a high degree of irreversibility [6, 35]. The plastic strains in this zone always increase in a nonlinear way with the strain (Fig. 1b).

The definition of these zones is useful to understand and to classify the soil response in the context of mechanical constitutive equations, and they will be used in this paper for this purpose.

2 The Range of Small Strains in Engineering Practice

The application of Soil Mechanics to the new problems faced by civil engineers at the beginning of the twentieth century was focused on the prevention of collapse, but this conception changed in the 70 s due, among other reasons, to: (1) a good knowledge of most soil failure mechanisms; (2) the need to build new structures in dense urban areas and to protect nearby existing structures; (3) the need to build especially sensitive structures, such as nuclear plants; and (4) the advances in numerical analysis tools and in computing power [1]. During the 70 s, it was observed how the soil stiffness obtained in conventional laboratory tests did not coincide with the stiffness obtained in dynamic field tests [8]. The dynamic field tests stiffness was usually an order of magnitude higher than the one of laboratory tests [36]. Later, researchers [15, 37, 38] realized that these differences were due to stiffness measurement at different strain levels, which allowed unifying the theories that tried to explain, until that moment, the value of the soil shear modulus. These facts suggested that conventional laboratory tests were not adequate to assess natural soil stiffness. In addition to that, it was shown that the low stiffness measured in conventional laboratory tests also came, among others, from deficiencies in the strain measurement techniques and from the disturbance of the samples during their extraction process [9]. During the subsequent years, measurements of soil displacements in various London works, new instrumentation techniques in laboratory tests and advances in numerical analysis methods, helped to improve the understanding of soil behavior in the range of small strains, in which stiffness plays a fundamental role [15, 36]. These findings promoted the development of new instrumentation techniques for field and laboratory tests, which Clayton [1], Elhakim [39] and Cudny [40] classify as follows:

• Dynamic field tests: Cross-hole [41], Down-hole [42,43,44], Spectral Analysis of Surface Wave SASW [45, 46], Continuous Surface Wave System CSWS [47], Suspension logger [48], Seismic cone CPTU [49] and Seismic dilatometer SDMT [50].

• Laboratory tests: Resonant column [2], Hollow cylinder [18, 51], triaxial devices with internal strain measurements [9, 20] or bender elements and compression and shear seismic wave measuring devices [52, 53] in oedometers [18, 54,55,56,57], in direct simple shear apparatus [55], in triaxial apparatus [55, 58, 59], in resonant column apparatus [60,61,62], in double simple shear apparatus [63] and in unconfined samples immediately after their extraction [64, 65].

There are numerous advanced constitutive models capable of simulating soil behavior in the whole range of strains (Zones I, II, III and IV of Jardine [6]), which is essential for a complete analysis of geotechnical problems, although the use of many of these models is reduced to an academic ambit and according to Tamagnini and Viggiani [66] this is due to: (1) its complex formalism; (2) the use of a large number of parameters which are difficult to obtain experimentally; (3) the use of a large number of state variables which are difficult to initialize; and (4) the difficulties associated with the formulation of precise, efficient and robust algorithms for the numerical implementation of equations (although there have been significant advances in recent years regarding this point). However, some of these advanced models have managed to extend to the professional practice, for example, the Hardening Soil Small model (HS-S) [67].

Figures 2, 3 and 4 show the need to consider soil behavior in the range of small strains in different geotechnical problems. It can be observed that models incorporating small strain stiffness improve the prediction of soil displacements with respect to the conventional elastoplastic models.

Fig. 2

Surface settlements during the construction of the St James’s Park tunnel in London. a Numerical simulations with a linear elastic model with perfect plasticity and two nonlinear isotropic models, L4 and J4, from [68]. b Numerical simulations with a linear elastic model with perfect plasticity and two nonlinear models, Brick and SRD-Brick, from [69]

Fig. 3

Soil displacements during an excavation between diaphragm walls in the Taipei Enterprise Center (TNEC), from [70]. a Numerical simulations with the MCC model. b Numerical simulations with the USC model

Fig. 4

Load–displacement curve under an experimental spread footing of 3 × 3 m on sand, conducted by the Texas A&M University National Geotechnical Experimentation Site (NGES), extracted from [67]. a Numerical simulation with the HS model ($OCR > 1$). b Numerical simulation with the HS-S[MC] ($OCR > 1$)

3 Soil Behavior in the Range of Small Strains

3.1 The Range of Small Strains

Jardine [6] identifies soil behavior in the range of small strains with Zones I and II. Zone I usually corresponds to strains less than $10^{ - 6}$ in sands and $10^{ - 5}$ in clays, while Zone II does so with strains within the interval $10^{ - 6}$ to $10^{ - 3}$ [40]. On the other hand, the range of intermediate and large strains is identified with Zones III and IV defined by Jardine. These zones usually correspond to strains greater than $10^{ - 3}$.

3.2 Considerations About Stiffness

3.2.1 Bulk Modulus

Regarding the drained bulk modulus, it is not usual to distinguish between values at small, intermediate or large strains, unlike what happens with the shear stiffness modulus. Duncan et al. [71] proposed the expression (1) to calculate the apparent bulk secant modulus (Fig. 5).

$$K_{s}^{\prime ap} = K_{b} p_{a} \left( {\frac{{\sigma_{3}^{\prime } }}{{p_{a} }}} \right)^{m}$$

(1)

Fig. 5

Dependence of the apparent secant bulk modulus ($B \equiv K_{s}^{\prime ap}$) on $\sigma_{3}^{\prime } /p_{a}$ in high plasticity clays from Barind, according to the expression (1), from [72]

The use of the confinement $\sigma_{3}^{{\prime}}$ as a variable in the expressions of the stiffness moduli is a common practice in many hypoelastic and quasi-hypoelastic models. This is because soil parameters of many models are usually adjusted to theoretical curves based on the results obtained in the deviatoric phase of triaxial tests, in which the confinement remains constant, which simplifies the fitting. However, the use of the $\sigma_{3}^{\prime }$ as a variable in these expressions makes it difficult to generalize these models to multiaxial loading states. The expression (2) for $K_{s}^{\prime ap}$ is considered more appropriate.

$$K_{s}^{\prime ap} = K_{s}^{\prime ap,ref} \left( {\frac{{p^{\prime } }}{{p_{ref}^{\prime } }}} \right)^{m}$$

(2)

Duncan et al. [71] proposed an expression analogous to (2) for the drained tangent elastic longitudinal modulus $E_{t,ur}^{\prime } \left( {p^{\prime } } \right)$, from which it is possible to calculate the drained tangent elastic bulk modulus $K_{t,ur}^{\prime } = E_{t,ur}^{\prime } /\left( {3\left( {1 - 2\nu_{ur}^{\prime } } \right)} \right)$.

Likewise, Roscoe and Schofield [73] and Roscoe and Burland [74] proposed the following expression for the elastic tangent bulk modulus in their critical state models (Fig. 6).

$$K_{t}^{\prime } = \frac{{\left( {1 + \text e} \right)}}{\kappa }p^{\prime }$$

(3)

Fig. 6

Tests in silty clays, from [75]. Isotropic compression, $\upsilon - 1 = \left( {1 + \text e_{0} } \right)\varepsilon_{v} .$

Lade and Abelev [76] analyze the hysteretic volumetric soil behavior through the study of the variation of volumetric stiffness during isotropic loading and unloading in sands due to the introduction of small loading cycles (Fig. 7). In the primary loading branch, they observed that the cycles led to a significant increase in volumetric stiffness, which did not happen during the cycles in the unloading branch, in which any differences in the value of such stiffness were hardly observed.

Fig. 7

Stiffening of the bulk modulus in sands of Nevada during small loading and unloading cycles in the primary loading branch and during the unloading branch [76], extracted from [67]

3.2.2 Shear Stiffness Modulus

Unlike the bulk modulus, shear stiffness modulus in soils is more difficult to specify and there are many studies about the parameters controlling it. The parameters considered most relevant are: shear strain ($\gamma$), mean stress ($p^{\prime }$), void ratio (e), plasticity index (PI), overconsolidation ratio (OCR, $R_{0}$), diagenesis, recent history, loading rate and anisotropy.

• Shear strain ($\gamma$): There are many evidences indicating that shear stiffness modulus $G$ degrades with shear strain. To generalize the concept of shear strain to a multiaxial state of stress and strain, it is usual to work with the octahedral shear strain. Figure 8 shows the results of diverse experimental tests involving the degradation of the apparent shear modulus with the total shear strain in clays and sands.

• Mean stress ($p^{\prime}$): Shear modulus depends on confinement. Authors such as Ohde [79], Hardin [80], Janbu [81], Hardin and Richart Jr. [82] or Hardin and Drnevich [2], based on experimental observations, proposed relations as $G_{0} \propto \left( {p^{\prime } } \right)^{m}$ between the value of maximum shear modulus $G_{0}$ and mean stress (Fig. 9). The introduction of the Hertzian contact theory in spherical particles for the calculation of $G_{0}$ results in $m = 0.33$ [86, 87]. Experiments in sands provide values of $m = 0.40 - 0.60$ [88,89,90], while in clayey soils, values of $m = 0.50 - 1.00$ are usually taken, being close to $0.50$ for low plasticity clays and to $1.00$ for high plasticity clays.

• Void ratio (${\text{e}}$): Hardin and Richart [82] observed the dependence of the maximum shear modulus $G_{0}$ on the void ratio from experiments with Ottawa sands, and proposed expressions like $G_{0} \propto \left( {\hat{B} - \text e} \right)^{2} /\left( {1 + \text e} \right)$. Authors such as Biarez and Hicher [91] or Lo Presti and Jamiolkowski [92] proposed expressions as $G_{0} \propto \text e^{ - \text x}$, and Bui [93] proposed expressions as $G_{0} \propto 1/\left( {1 + \text e} \right)^{3}$ (Fig. 10).

• Plasticity Index (PI): It is experimentally observed that higher values of the plasticity index in a soil result in a shift of the degradation curve of the apparent shear modulus towards higher shear strain values (Fig. 11). Vucetic and Dobry [94] proposed patterns for this dependence.

• Overconsolidation ratio (OCR, $R_{0}$): Hardin and Black [86] proposed correlations like $G_{0} \propto \left( {OCR} \right)^{{\hat{k}}}$, based on experimental observations between the maximum shear modulus $G_{0}$ and the overconsolidation ratio OCR. On the other hand, Houlsby and Wroth [95], based on the works of Hardin and Black [86] and Atkinson and Little [96], proposed correlations as $G_{0} \propto \left( {R_{0} } \right)^{{\hat{k}}}$ between the maximum shear modulus $G_{0}$ and the overconsolidation ratio $R_{o}$ (Fig. 12).

• Diagenesis: The diagenesis is the physicochemical process by which a sediment is transformed into a sedimentary rock. This process gradually alters the stiffness of the soil. Some of the main processes that alter soil stiffness are cementation [98] and aging [99,100,101,102,103,104], understood as the alteration of mechanical properties of the soil resulting from secondary compression under a constant external loading. Trhlíková et al. [105] proposed a relation between the maximum shear stiffness modulus $G_{0}$ and the structure as $G_{0} \propto \left( {s^{*} /s_{f}^{*} } \right)^{l}$. On the other hand, Anderson and Stokoe [106] proposed a relation between $G_{0}$ and the aging like $G_{0} \left( t \right) \propto G_{0} \left( {t_{p} } \right)\left( {1 + N_{G,1} log\left( {t/t_{p} } \right)} \right)$.

• Recent history: Atkinson et al. [30] defined the concept of recent history as that corresponding to recent stress or strain path in relation with the previous one, from which it is differentiated by a change in its direction (reversal) or by an extended period of rest. Soil behavior after a reversal and before a subsequent monotonous strain suggests a gradual adaptation of its internal state until it exclusively depends on $\varvec{\sigma ^{\prime}}$ and e [107]. In such state, that it is inside the SOM region [108], proportional strain paths lead to proportional stress paths. It is for the latter that the influence of the internal state of the soil over its behavior can only be revealed during small strains after reversals [107]. The studies of soil recent history require the use of tests with different stress or strain paths. Sayao [109] show these tests as indicated below:

  • Tests without rotation of the principal stresses ($\dot{\alpha }_{\sigma } = 0)$.

    • Axisymmetric triaxial tests (control over $\sigma_{1}^{{\prime}} \ge \sigma_{2}^{{\prime}} = \sigma_{3}^{{\prime}}$ in triaxial compression (Lode angle is equal to 0º) and over $\sigma_{1}^{{\prime}} = \sigma_{2}^{{\prime}} \ge \sigma_{3}^{{\prime}}$ in triaxial extension (Lode angle is equal to 30º).

    • Biaxial tests with plane strain ($\varepsilon_{2} = 0$ and control over $\sigma_{1}^{{\prime}}$ and $\sigma_{3}^{{\prime}}$).

    • True triaxial tests (control over $\sigma_{1}^{{\prime}}$, $\sigma_{2}^{{\prime}}$ and $\sigma_{3}^{{\prime}}$).

    • Triaxial hollow cylinder (control over $\sigma_{1}^{{\prime}}$, $\sigma_{2}^{{\prime}}$ and $\sigma_{3}^{{\prime}}$).

  • Tests with rotation of the principal stresses ($\dot{\alpha }_{\sigma } \ne 0)$

    • Axisymmetric triaxial tests with torsion (control over $\sigma_{1}^{{\prime}} \ge \sigma_{2}^{{\prime}} = \sigma_{3}^{{\prime}}$ or $\sigma_{1}^{{\prime}} = \sigma_{2}^{{\prime}} \ge \sigma_{3}^{{\prime}}$ and $sin^{2} \left( {\alpha_{\sigma } } \right) = \left( {\sigma_{2}^{{\prime}} - \sigma_{3}^{{\prime}} } \right)/\left( {\sigma_{1}^{{\prime}} - \sigma_{3}^{{\prime}} } \right)$).

    • Simple shear tests ($\varepsilon_{x} = \varepsilon_{y} = 0$, $\tau_{xy} = 0$ and control over $\sigma_{1}^{\prime } ,\sigma_{2}^{\prime }$ and $\sigma_{3}^{\prime }$).

    • Tests with directional shear cell ($\varepsilon_{2} = 0$ and control over $\sigma_{1}^{\prime } ,\sigma_{3}^{\prime }$, and $\alpha_{\sigma }$).

    • Hollow cylinder with torsion (control over $\sigma_{1}^{\prime } ,\sigma_{2}^{\prime } ,\sigma_{3}^{\prime }$ and $\alpha_{\sigma }$).

Fig. 8

a Degradation of the apparent shear modulus in clay tests with different plasticity index, from [77]. b Degradation of the apparent shear modulus in sand tests, from [78]

Fig. 9

a Influence of $p^{\prime }$ on the value of $G_{0}$ [83], extracted from [84]. b Influence of $p^{\prime}$ in the degradation of $G$, from [85]

Fig. 10

Results of experiments with resonant column on well graded sands and reconstituted clays, from [93]

Fig. 11

Degradation curve of the apparent shear modulus for different PI values, from [77]

Fig. 12

$G_{0} = G_{0} \left( {R_{0} } \right)$ in reconstituted samples of kaolinite clay, from [97]

Volumetric strain reflects the effect of isotropic loadings that tend to increase the value of the contact forces between particles, while deviatoric strain, usually generated by a deviatoric loading, modifies the direction of such forces and affects the stiffness of the soil. Some notable works in which soil recent history has been studied in relation to deviatoric loadings and deviatoric strains are those carried out in triaxial tests by Richardson [29], in hollow cylinder tests by Sayao [109], in biaxial tests by Topolnicki et al. [110] and in true triaxial tests by Sture et al. [111], Fig. 13. Nevertheless, there are few tests in which, in addition, suitable measurement methods have been implemented for the range of small strains, among which stand out the triaxial tests with local strain measurement [29] (despite the limitations they present in terms of the possible stress and strain paths), as well as the hollow cylinder tests [112, 113].

Fig. 13

a Triaxial test: stress paths in $q/p^{\prime } - \varepsilon_{s}$ space with different angles $\tan \left( {\theta_{{q/p^{\prime } }} } \right) = \Delta q/\Delta p^{\prime }$ in reconstituted London clay, with $OCR = 2$ and $p^{\prime } = 200\;{\text{kPa}}$, from [29]. b Hollow cylinder test: stress and strain paths in $R = \sigma_{1}^{\prime } /\sigma_{2}^{\prime } - \gamma_{max }$ space, where $\alpha = \alpha_{\sigma }$ is the rotation angle of the principal stress, in Ottawa sand with $p^{\prime } = 300\;{\text{kPa}}$ and $D_{R} = 36\%$, from [109]. c Biaxial test: stress and strain paths in the respective deviatoric planes in reconstituted Karlsruhe clay, from [110]. d True triaxial test: strain path in the deviatoric plane and deviatoric stress $\sqrt {s_{ij} s_{ij} }$ – deviatoric strain $\sqrt {\dot{e}_{ij} \dot{e}_{ij} }$ space in a Leighton Buzzard sand with $D_{R} = 72\%$, from [111]

The work of Atkinson et al. [30] shows the results of a set of triaxial tests on reconstituted overconsolidated samples ($OCR = 2$) with London clay (Fig. 14). All of them were initially brought to the same stress state (O in Fig. 14a) using different stress paths (PO and QO in Fig. 14a). After a rest period of 3 h, they were subjected to a deviatoric phase of $\Delta q = 90kPa$ with $\Delta p^{\prime } = 0$ (OA in Fig. 14a). As it can be seen in Fig. 14b, the stiffness of the soil during the OA path depends on the angle of such path with respect to the previous paths (PQ and QO). The wider the angle between paths, the higher is the value of the shear stiffness $G_{0}$ at the beginning of the new path.

Fig. 14

Undrained triaxial tests on reconstituted London clay, from [30]. a Paths followed in the tests. b Effect of stress recent history on soil stiffness

Clayton and Heymann [20] conducted tests on natural samples of London clay, applying the stress paths depicted in Fig. 15a. After completing the AB phase, they allowed the samples to rest for a period of 6–12 days before starting the triaxial extension (BE) and compression (BC) phases, thus allowing the soil yielding, which did not happen in the tests of Atkinson et al. [30], in which only a rest period of 3 h was left. Thus, Clayton and Heymann observed how plastic strains significantly reduced the effect of soil recent history on the $G_{0}$ value (Richardson [29] had observed a similar behavior in his experiments). Nevertheless, despite this attenuation of the path rotation effect on the $G_{0}$ value, Fig. 15b shows how, even allowing soil yielding, the stress history still has some effect on the shape of the degradation curve.

Fig. 15

Undrained triaxial tests on London clay with a rest period of 6–12 days after AB and before BC and BE, from [20]. a Stress paths followed. b Undrained longitudinal modulus $E_{u}$ in trajectories BC and BE

Gasparre [75] studied the effects of plastic deformations on the value of soil stiffness (through the control of resting times of the sample before applying new loads), as well as the effects of the loading magnitude prior to the rotation of stress paths, extending the research of Atkinson et al. [30] and Clayton and Heymann [20]. Gasparre et al. [34] conducted a set of tests on natural samples of London clay (Fig. 16), in which the following was observed:

• 1. When the stress state in recent history remains within the contour ${\mathrm{Y}}_{2}$ (Zone I or II according to Jardine),

  • If plastic deformations are allowed, the effect of stress path rotation on the shear stiffness of the soil is reduced, Fig. 16a (as observed by Clayton and Heymann [20]).

  • If plastic strains are not allowed, the same behavior observed by Atkinson et al. [30] is obtained, that is, a clear dependence of the ${G}_{0}$ value on the stress path rotation, Fig. 16b.

• 2. When the stress state in recent history tends to overcome and displace the contour ${\mathrm{Y}}_{2}$ (Zone III or IV according to Jardine [6]),

  • There is a clear dependence both on ${G}_{0}$ and on the shape of the degradation curve with the stress path rotation, regardless of whether plastic strains are allowed or not before starting the stress path after the rotation conducted, Fig. 16c.

Fig. 16

Degradation curves in undrained triaxial tests in London clay ($G_{eq,\tan } \equiv G_{t}^{ap} = \dot{q}/3\dot{\varepsilon }_{q}$), from [34]. a Within ${\text{Y}}_{2}$ (Zones I or II), allowing plastic strains. b Within ${\text{Y}}_{2}$ (Zones I or II) without allowing plastic strains. c Overcoming and displacing ${\text{Y}}_{2}$ (Zones III or IV), allowing or not plastic strains

Fig. 17

The effect of strain rate on stiffness during the deviatoric phase of an undrained triaxial test on an intact sample of London clay, from [116]

Fig. 18

Strain rate shear modulus parameter [118], extracted from [67]. a Dependence on strain rate and strain amplitude. b Dependence on the PI value

• Strain rate and inertia effects: There are numerous experimental tests on plastic soils that show the dependence of their stiffness on the strain rate [36], an effect attributed to their viscosity and plasticity. In sands, generally, this effect is very small or non-existent [114]. On the other hand, this effect is negligible in the range of small strains $\gamma < 0.001\%$ [115], and increases its relevance for larger strains $0.01\% < \gamma < 0.1\%$ [116], as it can be seen in Fig. 17. Yong and Japp [117] defined the strain rate shear modulus parameter (Fig. 18) as $\alpha_{G} = \Delta G/\Delta \left( {\log \left( {\dot{\gamma }} \right)} \right)$.

• Anisotropy: Multiple correlations have been proposed to calculate the soil maximum shear modulus value, several of which can be found in the work of Obrzud and Truty [119]. Below there are some expressions for the calculation of $G_{{0\left( {ij} \right)}}$ in a plane i according to direction j, based on the relations discussed above, which also introduce the effect of soil anisotropy:

Hardin and Black [89]:

$$G_{{0\left( {ij} \right)}} = \hat{A}f\left( \text{e} \right)\left( {OCR} \right)^{{\hat{k}}} \left( {p_{ref}^{\prime } } \right)^{{ - m_{ij} }} \left( {p^{\prime } } \right)^{{m_{ij} }}$$

(4)

Hardin and Blandford [14]:

$$G_{{0\left( {ij} \right)}} = S_{ij} f\left( \text{e} \right)\left( {OCR} \right)^{{\hat{k}}} \left( {p_{ref}^{\prime } } \right)^{{\left( {1 - n_{i} - n_{j} } \right)}} \left( {\sigma_{i}^{\prime } } \right)^{{n_{i} }} \left( {\sigma_{j}^{\prime } } \right)^{{n_{j} }}$$

(5)

Rampello et al. [120]:

$$G_{{0\left( {ij} \right)}} = S_{ij} f\left( \text{e} \right)\left( {OCR} \right)^{{\hat{k}}} p^{\prime } \overline{\beta }^{n/2}$$

(6)

Pennington [121]:

$$G_{{0\left( {ij} \right)}} = S_{ij} f\left( \text{e} \right)\left( {OCR} \right)^{{\hat{k}}} \left( {p^{\prime } } \right)^{{n_{ij} }} \left( {p_{ref}^{\prime } } \right)^{{\left( {1 - n_{ij} } \right)}} \overline{\beta }_{ij}^{{n_{ij} /2}}$$

(7)

Pennington [121]:

$$G_{{0\left( {ij} \right)}} = S_{ij} f\left( \text{e} \right)\left( {OCR} \right)^{{\hat{k}}} \left( {p_{ref}^{\prime } } \right)^{{\left( {1 - n_{i} - n_{j} - n_{k} } \right)}} \left( {\sigma_{i}^{\prime } } \right)^{{n_{i} }} \left( {\sigma_{j}^{\prime } } \right)^{{n_{j} }} \left( {\sigma_{k}^{\prime } } \right)^{{n_{k} }}$$

(8)

3.3 Considerations about the Hysteretic Behavior

A fundamental aspect of soil behavior in Zone II of Jardine [6], along with the nonlinearity and dependence on recent history, is the hysteresis (Fig. 19).

Fig. 19

a Loading cycles in triaxial tests in a loose Lubiatowo sand, from [122]. b Loading cycles in undrained triaxial tests in a Speswhite kaolinite clay with $p^{\prime } = 300\;{\text{kPa}}$, from [123]

Soils are formed by particles and, therefore, will experience energy dissipation during loading cycles, which will result in a hysteretic behavior [124]. Nevertheless, the micromechanical mechanism through which the soil dissipates energy during such cycles is not clear and Cudny [40] points out to two possible explanations: (1) the dissipated energy is the result of a process of local yield and friction in the contacts between particles, which are subjected to normal and shear forces, in which case, the energy absorbed by the soil would be a function of the deformation amplitude [125]; and (2) the dissipated energy is the result of a viscous behavior due to the presence of fluid in the soil pores [126].

As Hueckel and Nova [22] indicate in their fundamental work on hysteretic behavior in soils, hysteretic cycles are characterized by having different apparent stiffness after rotations in stress or strain paths. In addition to that, if a perfect hysteretic behavior is considered, the deformations would only be recoverable if the cycles starting from the same reversal point were closed. Nevertheless, according to Hueckel and Nova, there are no perfect hysteretic cycles, generally observing: (1) certain permanent strain after the closing of the cycles, which depends on the number of these; (2) viscous effects or cyclic hardening/softening; and (3) dependence of the stiffness in unloadings/reloadings on the magnitude of the accumulated plastic strain (elastoplastic coupling).

As Gudehus [107] points out, when reproducing the hysteretic soil behavior, the state of a representative soil element is not sufficiently characterized by the void ratio ${\text{e}}$ and the effective stress tensor ${\varvec{\sigma}}^{\prime }$. In these cases, it is necessary to define hidden state variables ${\varvec{\chi}}^{hist}$ that cannot be observed macroscopically and represent the spatial fluctuation of the chains of internal forces between soil particles (called force-roughness effect). It is also possible to attribute to these variables the nonlinearity and the soil behavior dependence on its recent history. As previously commented, soil behavior after a reversal and before a subsequent monotonous strain path suggests a gradual adaptation of its internal state (characterized by the mentioned hidden state variables) until it depends exclusively on the stress tensor and the void ratio, state in which proportional strain paths lead to proportional stress paths. It is for this last reason that the influence of the internal state of the soil on its behavior can only be revealed during small strains after reversals. Furthermore, the state variables ${\varvec{\chi}}^{hist}$, within the set of state variables ${\varvec{\chi}}$, are, in general, of two types: α (back stress) normally in elastoplastic or viscoelastoplastic models (these models tend to underestimate the hysteretic effects of the soil) and ${\varvec{\delta}}$ (internal strain) normally in hypoplastic or viscohypoplastic models (these models tend to overestimate the hysteretic effects of the soil) [107]. Although α and δ can be formally treated as strains and stresses respectively, they cannot be interpreted physically as such [107], which is due to the fact that the internal variables α and δ are obtained, respectively, from σ′ and ε (α is obtained from stress through the establishment of an elastic center ${\varvec{\alpha}} = {\varvec{\sigma}}^{\prime }$ when a reversal takes place, and $\dot{\varvec{\delta }}$ is proportional to $\dot{\varepsilon }$ and is calculated from it).

4 Constitutive Modeling

As proposed by Popper [127], theoretical models can capture part of reality if they are logically consistent and the hypotheses they use are not refuted by observations. Nowadays, there are several theoretical frameworks that try to explain distinct aspects of soil behavior. Within these theoretical frameworks, several constitutive soil models that consider the mechanical behavior of the soil in the range of small strains have been developed over the last decades.

The mechanical soil behavior must be explained by the interaction of the distinct phases that constitute the soil along with the internal and external actions on it. Despite the discontinuous nature of soil, most of the models used in the professional practice consider soil as a continuous medium. Although there has been important progress in models that considers soil as a discontinuous medium [128,129,130,131], the scope of this paper has been limited to continuous ones.

According to Tobita [132], any type of soil micromechanical behavior (slide, rotation, deformation or breakage of the particles or aggregates) leads to a nonlinear incremental type of macromechanical behavior, therefore, any constitutive model that considers soil as a continuous medium should be able to reproduce this behavior.

Mechanical constitutive modeling of soils can be framed in Continuum Mechanics problems, which involve a set of well-known general conservation and balance equations and a particular constitutive equation, which for simple materials [133], is expressed in (9).

$${\varvec{\sigma}}^{\prime } \left( t \right) = {\mathcal{F}}\left[ {{\varvec{F}}\left( \tau \right)} \right]\quad - \infty < \tau \le t$$

(9)

The consideration of a functional ${\mathcal{F}}$, and not a function, is due to the irreversible soil behavior that should be reproduced. In this type of behavior, knowing the state of deformation $\varepsilon \left( t \right)$ at a given instant t does not allow to know the stress state at that instant and vice versa [134]. Furthermore, not any functional ${\mathcal{F}}$ will represent a valid constitutive relation [133].

As Owen and Williams [135] show, in the case of non-viscous type materials, which are the kind of materials analyzed in this paper, it is common to resort to incremental type formulations in which the functional ${\mathcal{F}}$ is reduced to a tensorial function of the type $\dot{\varvec{\sigma }}^{\prime } = {\varvec{G}}\left( {\varepsilon ,{\varvec{\sigma}}^{\prime } ,{\varvec{\chi}},\dot{\varepsilon }} \right)$. Considering that the tensorial function G is homogeneous grade one in the term of $\dot{\varepsilon }$, allows expressing the constitutive equation as $\dot{\varvec{\sigma }}^{\prime } = {\varvec{E}}_{t}^{\prime } \left( {\varepsilon ,{\varvec{\sigma}}^{\prime } ,{\varvec{\chi}},{\varvec{\eta}}} \right):\dot{\varepsilon }$.

The dependence of the tensor ${\varvec{E}}_{t}^{\varvec{^{\prime}}}$ on ${\varvec{\eta}} = \dot{\varepsilon }/\left\| {\dot{\varepsilon }} \right\|$ leads to the tensorial zone concept defined by Darve [136, 137] and Darve and Labanieh [138], which will be very useful to classify the analyzed models. A tensorial zone Z is defined as the part of strain increments space in which the tensorial function G is linear with $\dot{\varepsilon }$. This will imply that in a certain tensorial zone Z, the tangent stiffness tensor will be independent from ${\varvec{\eta}}$, and the relation between $\dot{\varvec{\sigma }}^{\prime }$ and $\dot{\varepsilon }$ will be incrementally linear, that is, $\dot{\varvec{\sigma }}^{\prime } = {\varvec{E}}_{t}^{{\prime {\rm Z}}} \left( {\varepsilon ,{\varvec{\sigma}}^{\prime } ,{\varvec{\chi}}} \right):\dot{\varepsilon }$, where ${\varvec{E}}_{t}^{\prime } \left( {\varepsilon ,{\varvec{\sigma}}^{\prime } ,{\varvec{\chi}},{\varvec{\eta}}} \right) = {\varvec{E}}_{t}^{{\prime {\rm Z}}} \left( {\varepsilon ,{\varvec{\sigma}}^{\prime } ,{\varvec{\chi}}} \right)$,$\forall {\varvec{\eta}} \in {\rm Z}$. Different tensorial zones conform different adjacent hypercones with the vertex in common, and the condition of continuity does not allow the election of any tangent stiffness tensors in two adjacent tensorial zones.

4.1 Some Previous Considerations About Constitutive Modeling in the Range of Small Strain

To approximate soil behavior in Zone II, it is necessary to use nonlinear hysteretic models that consider the effect of recent history on stiffness. A common way to simulate this nonlinearity is by using nonlinear elastic stiffness moduli. Such moduli depend exclusively on the elastic strain $\varepsilon^{e}$ or, equivalently, on the effective stress ${\varvec{\sigma}}\boldsymbol{^{\prime}}$. However, the experimental measurement of soil stiffness is normally conducted in tests in which soil is subjected to primary loading processes. During such processes, it is usual to obtain stiffness values lower than those measured during unloading or reloading processes. According to Hueckel and Nova [22], this is due to the fact that irreversible strains occur in every process of primary loading. Based on this, it is possible to define the concept of apparent stiffness moduli of the soil, which are calculated using the total strain and not the elastic ones.

The apparent stiffness moduli usually depend on the total strain ε, the effective stress ${\varvec{\sigma}}^{\prime }$ and the state variables ${\varvec{\chi}}^{hist}$.

$$K_{s}^{\prime ap} = K_{s}^{\prime ap} \left( {\varepsilon ,{\varvec{\sigma}}^{\prime } ,{\varvec{\chi}}^{hist} } \right)\quad G_{s}^{ap} = G_{s}^{ap} \left( {\varepsilon ,{\varvec{\sigma}}^{\prime } ,{\varvec{\chi}}^{hist} } \right)$$

(10)

$$K_{t}^{\prime ap} = K_{t}^{\prime ap} \left( {\varepsilon ,{\varvec{\sigma}}^{\prime } ,{\varvec{\chi}}^{hist} } \right)\quad G_{t}^{ap} = G_{t}^{ap} \left( {\varepsilon ,{\varvec{\sigma}}^{\prime } ,{\varvec{\chi}}^{hist} } \right)$$

(11)

From a numerical point of view, using the apparent stiffness moduli instead of the elastic ones within an elastoplastic model significantly simplifies the calculation algorithms (Fig. 20), although it can lead to theoretical inconsistencies.

Fig. 20

Algorithms for obtaining the value of stress in elastoplastic models

Tensorial zones [136,137,138] can be bijectively related to the apparent stiffness of the soil and, therefore, to the aforementioned apparent stiffness moduli. In this way, for each tensor zone ${\rm Z}_{i}$ a value of $K_{i}^{\prime ap}$ and $G_{i}^{ap}$ will be obtained. Table 1 summarizes these correspondences.

Table 1 Tensor zones and values of $K_{i}^{\prime ap}$ and $G_{i}^{ap}$ for incrementally linear, multilinear and nonlinear models

In any model that uses elastic theory, it should be considered what is pointed out by Zytynski et al. [139] regarding to the choice of elastic moduli. They showed that considering constant values of drained Poisson’s ratio in a model implies that this model will not be conservative and the generation of energy in closed loading cycles will take place. In fact, several incrementally multilinear models that consider soil behavior in the range of small strains, such as those of Papadimitriou et al. [140], Wongsaroj [141], SSOM and HS-S [67] or HS-SS of Plaxis, use as elastic parameters the shear modulus G and a constant value of the drained Poisson’s ratio. Based on these parameters, such models internally calculate the value of drained bulk modulus $K^{\prime }$ using expression (12). Other incremental multilinear models that consider soil behavior in the range of small strains, such as those of Whittle [142], Al-Tabbaa and Wood [10], Yu [143], Gryczmanski et al. [144] or Gryczmanski and Uliniarz [145], use the drained bulk modulus $K^{\prime }$ and a constant value of the drained Poisson’s ratio as elastic parameters. Based on these parameters, such models internally calculate the value of the shear modulus G through expression (12).

$$K^{\prime } = \frac{{2G\left( {1 + \nu_{const}^{{\prime}} } \right)}}{{3\left( {1 - 2\nu_{const}^{{\prime}} } \right)}} \propto G\quad G = \frac{{3K^{\prime } \left( {1 - 2\nu_{const}^{{\prime}} } \right)}}{{2\left( {1 + \nu_{const}^{{\prime}} } \right)}} \propto K^{\prime }$$

(12)

From the previous expressions it follows that the fact of adopting a constant value of drained Poisson’s ratio implies the proportionality $K^{\prime } \propto G$, which generally does not respond to experimental observations in the range of small strains (Fig. 21). The expression of Poisson’s ratio as a function of $K^{\prime }$ and G is given by (13), as well as the elastic thermodynamic limitations and the condition $\nu^{\prime } > 0$ that must be satisfied in all soils, based on experimental observations. On the other hand, in the expression (14), $\dot{\nu }$ is deduced from expression (13).

$$0 < \nu^{\prime } = \frac{{3K^{\prime } -2G}}{{2\left( {3K^{\prime } + G} \right)}} < 0.50$$

(13)

$$\dot{\nu }^{\prime } = \frac{9}{2}\frac{{G\dot{K}^{\prime } - K^{\prime } \dot{G}}}{{\left( {3K^{\prime } + G} \right)^{2} }}$$

(14)

Fig. 21

(a) Variation of $\nu^{\prime }$ with $\gamma_{oct}$ in cohesive soils, from [146]. (b) Variation of $\nu^{\prime }$ with $\gamma_{oct}$ in sandy soils, from [146]. (c) Variation of $\nu^{\prime }$ with $\varepsilon_{oct}$ in different sandy soils, from [147]

Experimentally, it is observed how, in the range of small strains, the drained bulk modulus $K^{\prime}$ does tend to stiffen with the volumetric deformation, while the shear modulus G tends to degrade with the octahedral shear strain. Considering on the one hand $G = G\left( {\gamma_{oct} } \right)$ with $\dot{G}\dot{\gamma }_{oct} < 0$ (degradation of G with $\gamma_{oct}$), and on the other hand $K^{\prime } \left( {\varepsilon_{oct} } \right)$, with $\dot{K}^{\prime } \dot{\varepsilon }_{oct} > 0$ (stiffening of $K^{\prime }$ with $\varepsilon_{oct}$), leads to values $\dot{\nu }^{\prime } > 0$ if $\dot{G} < 0$ and $\dot{K}^{\prime } > 0$, and values $\dot{\nu }^{\prime } < 0$ if $\dot{G} > 0$ and $\dot{K}^{\prime } < 0$. For $\dot{\nu }^{\prime } = 0$ ($\nu^{\prime } = \nu_{const}^{\prime }$), according to the expression (14), $\dot{K}^{\prime } /K^{\prime } = \dot{G}/G$ must be complied, that is $K^{\prime } = \left( {K_{0}^{\prime } /G_{0} } \right)G \propto G$, which is equivalent to expression (12).

4.2 Classification of Models Using the Elements that Define the Hysteretic Behaviour

To reproduce the hysteretic soil behavior in a constitutive model it is necessary to define hidden state variables ${\varvec{\chi}}^{hist}$ [107], within the set of state variables ${\varvec{\chi}}$.

In addition to that, it is necessary to distinguish and define the following concepts in each model, which are directly related to the state variables ${\varvec{\chi}}^{hist}$ and define a specific classification criterion for constitutive models: (1) reversal criteria; (2) memory rules; (3) effect of reversals on the variables that control degradation; and (4) effect of reversals on maximum soil stiffness.

4.2.1 Reversal Criteria

The models that consider the hysteretic behavior of the soil use reversal criteria to identify points where changes of direction occur in the stress or strain paths, whose effect induces changes in soil stiffness. These criteria can be divided as follows:

Extrinsic Reversal Criteria One or more loading and unloading criteria are defined and added to the model equations. These criteria are usually formulated based on stress [143, 144], strain [67, 140, 142, 148, 149] or energy/power [150].

Intrinsic Reversal Criteria

The loading or unloading criteria arise naturally from the own equations of the constitutive model [3, 10,11,12, 22, 31, 123, 151,152,153,154,155,156].

4.2.2 Memory Rules

Memory rules are those that allow models to store information of a certain number of active reversal points, understanding as an active reversal point that which appears in $t_{0}$ and can influence the soil behavior for $t > t_{0}$. Depending on the number of active reversal points from which information is stored, all or part of the recent history of the soil will be considered. Furthermore, the models that store only part of this information may reproduce a certain finite number of symmetric loading cycles without transgressing the 1st Principle of Thermodynamics. It is possible to distinguish three types of models based on the number of reversal points from which information is stored.

Information storage from a single active reversal point

These models store information of the last active reversal point and, therefore, only consider the history between such reversal point and the current state, offering important limitations to reproduce hysteretic behavior but requiring little computational memory to store such information. Some models that belong to this group are the following: Simpson et al. [3]; Whittle [142]; Al-Tabbaa and Wood [10]; Bolton et al. [148]; Yu [143]; Puzrin and Burland [152]; Gryczmanski et al. [144]; Pestana and Whittle [149]; Papadimitriou et al. [140].

Information storage of several active reversal points

These models store information of a certain number of active reversal points, so they can better reproduce the hysteretic behavior with respect to the previous ones and, therefore, they will have a greater computational memory requirement. Likewise, these models use different typologies of state variables to store information, such as, for example, the situation of yield surfaces in multisurface or bubble models, or state variables in diverse elastoplastic and hypoplastic models. The effect of reversals on these variables depends on the rotation angle of reversal that takes place, and it may be the case that an important reversal erases the effect of previous active reversal points, although these are recent. Some models that belong to this group are the following: Prévost [11, 12]; Simpson [31]; Stallebrass and Taylor [123]; Niemunis and Herle [151]; Benz [67]; Cudny and Truty [155].

Information storage of all active reversal points

These models can store information of all the active reversal points, improving their capability to reproduce the hysteretic soil behavior, although they will generally require a high computational cost. Nevertheless, for practical purposes, this type of models ends up limiting the number of reversal points from which they store information. The maximum number of reversal points considered will depend on the number of expected loading cycles. Some models that belong to this group are the following: Hueckel and Nova [22]; Niemunis et al. [153]; Schädlich and Schweiger [154]; Castellón and Ledesma [156] and those that fulfill the Generalized Masing Rules [157, 158].

4.2.3 Effect of the Reversals on the Variables that Control Stiffness Degradation

The nonlinear models consider shear stiffness degradation with deformation. The mechanisms that control this degradation are identified here with the variables ${\Upsilon }_{i} \ge 0$, which can be considered as part of the variables ${\varvec{\chi}}^{hist}$. These models can be grouped in two categories:

The variables ${\Upsilon }_{i}$ that controls the degradation are always fully reinitialized after a reversal

These models consider that the variables ${\Upsilon }_{i}$ adopt a value of $0$ after a reversal (Fig. 22) (${\Upsilon }_{i} = {\Upsilon }_{i}^{R - } > 0$ before the reversal $R$ and ${\Upsilon }_{i} = {\Upsilon }_{i}^{R + } = 0{ }$ after the reversal $R$). This implies that in these models the maximum value of stiffness is reached after a reversal, which does not allow simulating the experimental soil behavior described in the work of Atkinson et al. [30] (Fig. 14), Clayton and Heymann [20] (Fig. 15), Gasparre [75] or Gasparre et al. [34] (Fig. 16). Some models that belong to this group are the following: Hueckel and Nova [22]; Simpson et al. [3]; Whittle [142]; Al-Tabbaa and Wood [10]; Bolton et al. [148]; Yu [143]; Stallebrass and Taylor [123]; Gryczmanski et al. [144]; Puzrin and Burland [152]; Pestana and Whittle [149]; Papadimitriou et al. [140]; Niemunis et al. [153] and those that fulfill the Generalized Masing Rules [157, 158].

Fig. 22

Effect of reversals on the variables that control degradation, drawn on the graphic of the shear modulus degradation of a London clay, extracted from the work of Atkinson et al. [30]

The variables ${\Upsilon }_{i}$ that controls the degradation are fully or partially reinitialized after a reversal depending on the reversal rotation angle

These models consider that the variables ${\Upsilon }_{i}$ reduce their value after a degradation process (Fig. 22) (${\Upsilon }_{i} = {\Upsilon }_{i}^{R - } > 0$ before the reversal R and ${\Upsilon }_{i} = {\Upsilon }_{i}^{R + } < {\Upsilon }_{i}^{R - }$ after the reversal R). Depending on the values ${\Upsilon }_{i}^{R + }$ different stiffness values are obtained after a reversal. This type of models allows partially simulating the experimental soil behavior described by Atkinson et al. [30] (Fig. 14), Clayton and Heymann [20] (Fig. 15), Gasparre [75] or Gasparre et al. [34] (Fig. 16) Some models that belong to this group are the following: Prévost [11, 12]; Simpson [31]; Niemunis and Herle [151]; Benz [67]; Schädlich and Schweiger [154]; Cudny and Truty [155]; Castellón and Ledesma [156].

4.2.4 Effect of the Reversals on Maximum Soil Stiffness

Experimentally, it is observed how the magnitude of shear stiffness recovery depends on the stress/strain reversal rotation angle, as shown in Fig. 23. Considering this aspect of soil behavior, it is possible to classify the models following two different criteria: (1) depending on whether the soil stiffness recovery is continuous or discontinuous with the rotation of stress/strain recent path; and (2) depending on whether such recovery is always total after a reversal or can be partial or total after it. Introducing the second criterion within the first, the models can be classified as follows:

Fig. 23

Effect of reversals on maximum stiffness according to the two defined criteria, drawn on the London clay degradation graph extracted from the work of Atkinson et al. [30]. a Continuous or discontinuous recovery according to the rotation angle of the recent path of stress/strain. b Total or partial/total recovery of stiffness

Discontinuous recovery of stiffness with the rotation angle of stress/strain recent path

This group integrates those models in which the recovery of soil stiffness occurs discontinuously (staggered) according to the rotation angle of the stress/strain recent path. This is because the variables ${\Upsilon }_{i}$, that control the degradation process of shear stiffness, experience finite jumps in their value for certain values of such rotation (Fig. 23a). These models will be, therefore, incrementally multilinear. In turn, the models that consider a total recovery after a reversal or a recovery that can be partial or total are distinguished in this group (Fig. 23b). Some models with a total recovery after a reversal are the following: Hueckel and Nova [22]; Simpson et al. [3]; Whittle [142]; Al-Tabbaa and Wood [10]; Bolton et al. [148]; Yu [143]; Stallebrass and Taylor [123]; Puzrin and Burland [152]; Gryczmanski et al. [144]; Pestana and Whittle [149]; Papadimitriou et al. [140]; Niemunis et al. [153] and those that fulfill the Generalized Masing Rules [157, 158]. Some models with a partial discontinuous recovery according to the rotation angle of the stress/strain after a reversal are the following: Prévost [11, 12]; Simpson [31]; Benz [67]; Cudny and Truty [155].

Continuous recovery of stiffness with the rotation angle of stress/strain recent path

This group integrates those models in which the recovery of soil stiffness occurs continuously according to the rotation angle of the stress/strain recent path. This is because the variables ${\Upsilon }_{i}$ that control the degradation process of the shear stiffness vary continuously with the values of such rotation (Fig. 23a). These models will therefore be incrementally nonlinear, and the recovery of stiffness is continuous with the rotation of the strain path. Some models that can be considered to have a partial continuous recovery according to the rotation angle of the stress/strain after a reversal are the following: Niemunis and Herle [151]; Schädlich and Schweiger [154]; Castellón and Ledesma [156].

4.3 Classification of the Models Using the Tensorial Zone Criterion

The tensorial zone criterion has been used to classify the models that consider soil behavior in the range of small strains (Zones I and II of Jardine [6]), as follows:

• (A) Incrementally linear models associated to one tensorial zone (Fig. 24a)

  Fig. 24

  

  Schematic representation of the tensorial zones for distinct types of models. a Incrementally linear models. b Incrementally multilinear models. c Incrementally nonlinear models

  • (A.1) Elastic models

    • (A.1.1) Linear elastic models

      • Anisotropic

      • Isotropic

    • (A.1.2) Nonlinear elastic models

      • Algebraic formulation (Cauchy elastic models and pseudoelastic models)

      • Integral formulation (hyperelastic models)

      • Differential formulation (hypoelastic models stricto sensu)

• (B) Incrementally multilinear models associated to several tensorial zones (Fig. 24b)

  • (B.1) Hysteretic models

    • (B.1.1) Paraelastic models

    • (B.1.2) Quasi-hypoelastic models

      • Generalized Masing rules

  • (B.2) Advanced models

    • (B.2.1) Classic elastoplastic models

    • (B.2.2) Multisurface models

    • (B.2.3) Brick models

    • (B.2.4) Bounding plasticity models

    • (B.2.5) Bubble models

    • (B.2.6) Multilaminated models

• (C) Incrementally nonlinear models associated to infinite tensorial zones (Fig. 24c)

  • (C.1) Hypoplastic models

  • (C.2) Hypoplastic hybrid models

The set of incrementally linear models include the elastic models, although both linear elastic models and nonlinear elastic models can also be formulated non-incrementally, that is, according to ${\varvec{\sigma}}^{\prime } = {\varvec{F}}\left( {\varepsilon^{e} } \right)$.

Finally, it should be noted that the fact of not having the numerical codes of most of analyzed models complicates and limits their study, idea shared by Gudehus [107].

(A) Incrementally linear models

The number of tensorial zones $\# Z$ considered in the incrementally linear models is reduced to one. These models can reproduce soil nonlinear behavior in Zone II, but not its hysteretic and dependent on recent history behavior.

(A.1) Elastic models

Elasticity constitutes one of the fundamental pillars of mechanics of deformable solids.

Two fundamental characteristics of these type of models are: (1) the proportionality between effective stress ${\varvec{\sigma}}^{\prime }$ and elastic strains $\varepsilon^{e}$; and (2) the possibility of determining the stress state ${\varvec{\sigma}}^{\prime } \left( {{\varvec{x}},t} \right)$ at any point of the continuous medium and at any instant, only from the state of elastic strains $\varepsilon^{e} \left( {{\varvec{x}},t} \right)$ in such point and instant, without the need to know the previous history.

Soil behavior in Zone I can be approximated by a linear elastic model. In addition to that, it is common to find inherent and induced anisotropy in most soils, although it is often complex to separate the influence of each of them on the test results. Several discrepancies in numerical simulations regarding experimental results come precisely from the fact that the effects of anisotropy are not considered. Piriyakul [159] demonstrates the need to consider inherent and induced anisotropy in the range of small strains, and Poulos [160], Simpson [6], Simpson et al. [161], Addenbrooke et al. [68], Zwanenburg [162], Kung et al. [163] and Whittle [36] point out the importance of considering soil anisotropy when elastic models are used. Nevertheless, the difficulty to obtain the parameters associated with anisotropic linear elastic models leads, on multiple occasions, to the use of isotropic linear elastic models.

The elastic stiffness moduli in the range of strains characteristic of Zone I correspond to the dynamic elastic stiffness type that are $G = G_{0}$ and $K^{\prime } = K_{0}^{\prime }$ when considering isotropy. These can be calculated from the soil density $\rho_{soil}$ and the speed at which the shear waves S ($v_{s}$) and compression waves P ($v_{p}$) are transmitted through its skeleton, according to the following expressions:

$$G_{0} = \rho_{soil} v_{s}^{2}$$

(15)

$$K_{0}^{\prime } = \rho_{soil} \left( {v_{p}^{2} - \frac{4}{3}v_{s}^{2} } \right)$$

(16)

(A.1.1) Linear elastic model

Linear elastic models use a linear tensorial function ${\varvec{F}}\left( \cdot \right)$ for the total constitutive equation.

$${\varvec{\sigma}}^{\prime } = {\varvec{F}}(\varepsilon^{e} ) = {\varvec{E}}^{\prime } :\varepsilon^{e}$$

(17)

Since the elastic stiffness tensor ${\varvec{E}}^{\prime }$ is constant ($\dot{\varvec{E}}^{\prime } = 0)$, the incremental constitutive equation can be expressed as follows:

$$\dot{\varvec{\sigma }}^{\prime } = \dot{\varvec{F}}\left( {\varepsilon^{e} } \right) = {\varvec{E}}^{\prime } :\dot{\varepsilon }^{e}$$

(18)

Considering the symmetry of ${\varvec{\sigma}}^{\prime }$ and $\varepsilon^{e}$, and some elastic thermodynamic considerations, the components of ${\varvec{E}}^{\prime }$ can be reduced from 81 to 21.

Anisotropic linear elastic model

The most general expression of ${\varvec{E}}^{\prime }$ for a general anisotropic linear elastic material has 21 independent components. In anisotropic materials, it is common to use $E_{ij}^{{\prime}}$, $\nu_{ij}^{{\prime}}$ o $G_{ij}$ as elastic parameters. In case the material properties present three planes of symmetry, the material is said to be orthotropic, and the independent components are reduced from 21 to 9. And if the properties of the material have an axis of symmetry, it is said that it has transversal isotropy and the independent components are reduced from 21 to 5. Orthotropic elastic models are rarely used. In contrast, elastic or hypoplastic models that consider soil transversal anisotropy have been used in professional practice to reproduce soil behavior in the range of small strains [14, 154, 159, 164].

Isotropic linear elastic model

In case the material properties present three symmetry axes, the material is said to be isotropic and the independent components are reduced from 21 to 2. The constitutive equation of an isotropic linear elastic model can be expressed as follows:

$${\varvec{\sigma}}^{\prime } = {\varvec{E}}^{\prime } :\varepsilon^{e} = \left( {\left( {K^{\prime } - \frac{2}{3}G} \right)\varvec{1} \otimes \varvec{1} + 2G{\mathbb{I}}} \right):\varepsilon^{e} = 3K^{\prime } \varepsilon_{oct}^{e} \varvec{1} + 2G{\varvec{e}}^{e}$$

(19)

On the other hand, considering ${\varvec{s}} = {\varvec{\sigma}}^{\prime } - \sigma_{oct}^{\prime } \varvec{1}$ with $\sigma_{oct}^{\prime } = p^{\prime } = 1/3\sigma_{ii}^{\prime }$ and the invariants $\tau_{oct} = \sqrt {1/3} \left\| {\varvec{s}} \right\|$ and $\gamma_{oct}^{e} = \sqrt {4/3} \left\|{\varvec{e}}^{e} \right\|$, it is possible to uncouple the volumetric and deviatoric behavior of the soil in the expression (19), obtaining the expressions $\sigma_{oct}^{\prime } = 3K^{\prime } \varepsilon_{oct}^{e}$ and $\tau_{oct} = G\gamma_{oct}^{e}$.

Linear elastic models:

• Are linear models.

• Do not distinguish between stiffness in loading and unloading/reloading and, therefore, cannot reproduce the hysteretic behavior of the soil.

• Do not consider the effect of recent history on soil stiffness.

• Constitute the theoretical base of nonlinear elastic models and other advanced models.

• Constitute very simple formulations from a conceptual and mathematical point of view.

• The parameters of the models are, in general, easy to obtain from simple tests.

• In closed stress/strain cycles, they conserve the values of stress and strain, $\oint\limits_{{\varepsilon^{e} }} {{\varvec{E}}^{\prime } :\dot{\varepsilon }^{e} = 0}$ and $\oint\limits_{{{\varvec{\sigma}}^{\prime } }} {\left( {{\varvec{E}}^{\prime } } \right)^{ - 1} :\dot{\varvec{\sigma }}^{\prime } = 0}$.

• Do not generate energy in closed stress or strain cycles, $\oint\limits_{{\varepsilon^{e} }} {{\varvec{\sigma}}^{\prime } :\dot{\varepsilon }^{e} = 0}$.

(A.1.2) Nonlinear elastic models

The classification proposed by William [165], based on the structure of the tensorial function ${\varvec{F}}\left( \cdot \right)$ that relates stress to elastic strain, is used to define the nonlinear elastic models.

The hypoelastic models stricto sensu are not elastic models per se. As previously commented, one of the fundamental properties of the elastic models is the possibility to determine ${\varvec{\sigma}}^{\prime } \left( {{\varvec{x}},t} \right)$ only knowing $\varepsilon^{e} \left( {{\varvec{x}},t} \right)$, without the need of knowing the previous history. On the contrary, in hypoelastic models, the stress state at a given point and instant does depend on such previous history. Despite this, the hypoelastic models have been traditionally considered within the framework of elastic materials, therefore, such classification has been respected in this work.

Algebraic formulation (Cauchy elastic models and pseudoelastic models)

Cauchy elastic models

Cauchy elastic models use a nonlinear tensorial function ${\varvec{F}}\left( \cdot \right)$ for the constitutive equation of the material.

$${\varvec{\sigma}}^{\prime } = {\varvec{F}}\left( {\varepsilon^{e} } \right) = \phi_{1} \left( {\varepsilon^{e} } \right) \varvec{1} + \phi_{2} \left( {\varepsilon^{e} } \right)\varepsilon^{e} + \phi_{3} \left( {\varepsilon^{e} } \right)\left(\varepsilon^{e}\right)^2$$

(20)

A priori, and given the arbitrariness in the functions $\phi_{i}$, this type of models can generate energy during the application of cyclic loading, thus transgressing the thermodynamic principles.

The linearized constitutive incremental equation is expressed as follows:

$$\dot{\varvec{\sigma }}^{\prime } = \dot{\varvec{F}}\left( {\varepsilon^{e} } \right) = \mathop \sum \limits_{i = 1}^{3} {\left( {\frac{{\partial \phi_{i} \left( {\varepsilon^{e} } \right)}}{{\partial \varepsilon^{e} }}:\dot{\varepsilon }^{e} } \right)\left(\varepsilon^{e}\right)^{i-1} } + \phi_{2} \left( {\varepsilon^{e} } \right)\dot{\varepsilon }^{e} + 2\phi_{3} \left( {\varepsilon^{e} } \right)\varepsilon^{e} \cdot \dot{\varepsilon }^{e}$$

(21)

Pseudoelastic models

Pseudoelastic models are a particular case of Cauchy elastic models. In this case, the nonlinearity in ${\varvec{F}}\left( \cdot \right)$ is incorporated through the secant elastic stiffness tensor. As with linear elastic models, if an isotropic material is considered, the secant elastic stiffness tensor ${\varvec{E}}_{s}^{{\prime}}$ depends on two parameters, being able to be expressed according to the drained secant elastic bulk modulus $K_{s}^{\prime }$ and to the secant elastic shear modulus $G_{s}$, which leads to the known $K - G$ nonlinear models formulation.

$${\varvec{\sigma}}^{\prime } = {\varvec{F}}\left( {\varepsilon^{e} } \right) = {\varvec{E}}_{s}^{\prime } :\varepsilon^{e} = \left( {\left( {K_{s}^{\prime } - \frac{2}{3}G_{s} } \right){\varvec{1}} \otimes {\varvec{1}} + 2G_{s} {\mathbb{I}}} \right):\varepsilon^{e} = 3K_{s}^{\prime } \varepsilon_{oct}^{e} \varvec{1} + 2G_{s} {\varvec{e}}^{e}$$

(22)

In the same way it was deduced for the constitutive equation of an isotropic linear elastic material, it is also possible in this case to uncouple the volumetric and deviatoric behavior from expression (22), provided that $G_{s} = G_{s} \left( {\gamma_{oct}^{e} } \right)$ and $K_{s}^{\prime } = K_{s}^{\prime } \left( {\varepsilon_{oct}^{e} } \right)$, leaving the expressions $\sigma_{oct}^{\prime } = 3K_{s}^{\prime } \left( {\varepsilon_{oct}^{e} } \right)\varepsilon_{oct}^{e}$ and $\tau_{oct} = G_{s} \left( {\gamma_{oct}^{e} } \right)\gamma_{oct}^{e}$. In case of considering transversal anisotropy, it is necessary to introduce the secant coupling modulus $J_{s}$ into the previous formulation, resulting $\sigma_{oct}^{\prime } = 3K_{s}^{\prime } \varepsilon_{oct}^{e} + J_{s} \gamma_{oct}^{e}$ and $\tau_{oct} = J_{s} \varepsilon_{oct}^{e} + G_{s} \gamma_{oct}^{e}$.

The linearized constitutive incremental equation of the pseudoelastic models is the following:

$$\dot{\varvec{\sigma }}^{\prime } = {\varvec{E}}_{s}^{\prime } :\dot{\varepsilon }^{e} + \dot{\varvec{E}}_{s}^{\prime } :\varepsilon^{e} = {\varvec{E}}_{s}^{\prime } :\dot{\varepsilon }^{e} + \left( {\frac{{\partial {\varvec{E}}_{s}^{\prime } }}{{\partial K_{s}^{\prime } }}\frac{{\partial K_{s}^{\prime } }}{{\partial \varepsilon_{oct}^{e} }}\dot{\varepsilon }_{oct}^{e} + \frac{{\partial {\varvec{E}}_{s}^{\prime } }}{{\partial G_{s} }}\frac{{\partial G_{s} }}{{\partial \gamma_{oct}^{e} }}\dot{\gamma }_{oct}^{e} } \right):\varepsilon^{e}$$

(23)

The above expression can be rewritten as $\dot{\varvec{\sigma }}^{\prime } = {\varvec{E}}_{t}^{\prime } :\dot{\varepsilon }^{e}$, where ${\varvec{E}}_{t}^{{\prime}}$ can be written as follows:

$${\varvec{E}}_{t}^{\prime } = {\varvec{E}}_{s}^{\prime } + \left( {K_{t}^{\prime } - K_{s}^{\prime } } \right)\varvec{1} \otimes \varvec{1} + \frac{8}{3}\frac{{\left( {G_{t} - G_{s} } \right)}}{\left( {\gamma_{oct}^{e} }\right)^2 }{\varvec{e}}^{e} \otimes {\varvec{e}}^{e}$$

(24)

In the previous expression $K_{t}^{{\prime}}$ and $G_{t}$ are the tangent moduli which, considering $G_{s} = G_{s} \left( {\gamma_{oct}^{e} } \right)$ and $K_{s}^{\prime } = K_{s}^{\prime } \left( {\varepsilon_{oct}^{e} } \right)$, can be expressed as:

$$K_{t}^{\prime } = \frac{1}{3}\frac{{d\sigma_{oct}^{\prime } }}{{d\varepsilon_{oct}^{e} }} = K_{s}^{\prime } + \varepsilon_{oct}^{e} \frac{{dK_{s}^{\prime } }}{{d\varepsilon_{oct}^{e} }}$$

(25)

$$G_{t} = \frac{{d\tau_{oct} }}{{d\gamma_{oct}^{e} }} = G_{s} + \gamma_{oct}^{e} \frac{{dG_{s} }}{{d\gamma_{oct}^{e} }}$$

(26)

Based on the above and considering that ${\varvec{e}}^{e} :\dot{\varvec{e}}^{e} = 3/4\gamma_{oct}^{e} \dot{\gamma }_{oct}^{e}$, the constitutive incremental Eq. (23) becomes expression (27), which is possible to express uncoupled as $\dot{\sigma }_{oct}^{\prime } = 3K_{t}^{\prime } \left( {\varepsilon_{oct}^{e} } \right)\dot{\varepsilon }_{oct}^{e}$ and $\dot{\tau }_{oct} = G_{t} \left( {\gamma_{oct}^{e} } \right)\dot{\gamma }_{oct}^{e}$.

$$\dot{\varvec{\sigma }}^{\prime } = 3K_{t}^{\prime } \dot{\varepsilon }_{oct}^{e} \varvec{1} + 2G_{s} \dot{\varvec{e}}^{e} + 2\frac{{\left( {G_{t} - G_{s} } \right)}}{{\gamma_{oct}^{e} }}\dot{\gamma }_{oct}^{e} {\varvec{e}}^{e}$$

(27)

Cauchy elastic models and pseudoelastic models:

• Are nonlinear models.

• Do not distinguish between stiffness in loading and unloading/reloading and, therefore, cannot reproduce the hysteretic behavior of the soil.

• Do not consider the effect of recent history on soil stiffness.

• Constitute simple formulations from a conceptual and mathematical point of view.

• The parameters of the models are, in general, easy to obtain from simple tests.

• In stress/strain closed cycles, they conserve stress and strain, $\oint\limits_{{\varepsilon^{e} }} {{\varvec{E}}_{t}^{\prime } :\dot{\varepsilon }^{e} = 0}$ and $\oint\limits_{{\sigma^{\prime } }} {\left( {{\varvec{E}}_{t}^{\prime } } \right)^{ - 1} :\dot{\varvec{\sigma }}^{\prime } = 0}$.

• Depending on the selection of soil parameters, they can generate energy in stress/strain closed cycles, thus transgressing the thermodynamic principles, $\oint\limits_{{\varepsilon^{e} }} {{\varvec{\sigma}}^{\prime } :\dot{\varepsilon }^{e} \ne 0}$. If a Cauchy elastic model or a $K - G$ pseudoelastic model comply with $G = G\left( {\gamma_{oct}^{e} } \right)$ or $G = G^{*} \left( {\tau_{oct} } \right)$ and $K^{\prime } = K^{\prime } \left( {\varepsilon_{oct}^{e} } \right)$ or $K^{\prime } = K^{\prime *} \left( {\sigma_{oct}^{\prime } } \right)$ it will be conservative, since, under these conditions, the elastic energy ${{W}}_{{{{el}}}}$ is independent from the followed path, complying with ${{W}}_{{{{el}}}} = 0$ in a closed cycle, where $W_{el} = \oint\limits_{{\gamma_{oct}^{e} }} {\left( {3/2G_{s} \left( {\gamma_{oct}^{e} } \right)\gamma_{oct}^{e} } \right)\dot{\gamma }_{oct}^{e} } + \oint\limits_{{\varepsilon_{oct}^{e} }} {\left( {9K_{s}^{\prime } \left( {\varepsilon_{oct}^{e} } \right)\varepsilon_{oct}^{e} } \right)\dot{\varepsilon }_{oct}^{e} }.$

Integral formulation (hyperelastic models)

The hyperelastic models define an energy potential from which the expression of ${\varvec{F}}\left( \cdot \right)$ is derived. This potential is called elastic strain energy $\Psi = \Psi \left( {\varepsilon^{e} } \right)$. In the case of isotropic materials, $\Psi \left( {\varepsilon^{e} } \right)$ depends on the invariants of ${\varvec{\sigma}}^{\prime }$ and $\varepsilon^{e}$.

$${\varvec{\sigma}}^{\prime } = {\varvec{F}}\left( {\varepsilon^{e} } \right) = \frac{{\partial \Psi \left( {\varepsilon^{e} } \right)}}{{\partial \varepsilon^{e} }}$$

(28)

From expression (28), it is verified that this type of models complies with the 1st Principle of Thermodynamics, thus not allowing energy to be generated in stress/strain closed cycles (expression 29).

$$\oint {{\varvec{\sigma}}^{\prime } :\dot{\varepsilon }^{e} } = \oint {\frac{{\partial {\Psi }\left( {\varepsilon^{e} } \right)}}{{\partial \varepsilon^{e} }}:\dot{\varepsilon }^{e} } = \oint {{\dot{\Psi }}\left( {\varepsilon^{e} } \right) = 0}$$

(29)

Hereunder, the most general expression of ${\varvec{F}}\left( \cdot \right)$ for isotropic materials is derived. For that purpose, the strain tensor invariant moments $\hat{I}_{i}^{{\varepsilon^{e} }} = \left( {1/i} \right)tr\left( \left({\varepsilon^{e} }\right)^i \right)$ are defined. Using the chain rule and the notation $\Psi_{i} \left( {\varepsilon^{e} } \right) = \partial \Psi \left( {\varepsilon^{e} } \right)/\partial \hat{I}_{i}^{{\varepsilon^{e} }}$, the expression (30) is obtained:

$$\varvec{\sigma^{\prime }} = \Psi_{1} \left( {\varepsilon^{e} } \right){\varvec{1}} + \Psi_{2} \left( {\varepsilon^{e} } \right)\varepsilon^{e} + \Psi_{3} \left( {\varepsilon^{e} } \right)\left( \varepsilon^{e}\right)^2$$

(30)

As it can be seen, expression (30) has the same form as expression (20). Nevertheless, the coefficients $\Psi_{i} \left( {\varepsilon^{e} } \right)$, unlike $\phi_{i} \left( {\varepsilon^{e} } \right)$, satisfy the theorem of Schwartz, which implies the integrability conditions $\partial^{2} \Psi \left( {\varepsilon^{e} } \right)/\partial \hat{I}_{i}^{{\varepsilon^{e} }} \partial \hat{I}_{j}^{{\varepsilon^{e} }} = \partial^{2} \Psi \left( {\varepsilon^{e} } \right)/\hat{I}_{j}^{{\varepsilon^{e} }} \partial \hat{I}_{i}^{{\varepsilon^{e} }}$, from which it follows that the tangent elastic stiffness and compliance tensors have greater symmetry in hyperelastic models and it can be shown that this is a necessary condition to satisfy the 1^st Principle of Thermodynamics. These conditions do not have to be complied in the Cauchy elastic models or in pseudoelastic models.

The constitutive incremental equation in the hyperelastic models is expressed as follows:

$$\dot{\varvec{\sigma }}^{\prime } = {\varvec{E}}_{t}^{\prime } :\dot{\varepsilon }^{e} = \frac{{\partial^{2} {\Psi }\left( {\varepsilon^{e} } \right)}}{{\partial \varepsilon^{e} \otimes \partial \varepsilon^{e} }}:\dot{\varepsilon }^{e}$$

(31)

Several authors developed hyperelastic models that consider the relation $G = G\left( {p^{\prime } } \right)$ [166,167,168,169,170,171]. Such models, in the case of isotropic materials, adopt the following uncoupled form $\dot{\sigma }_{oct}^{\prime } = 3K_{t}^{\prime } \dot{\varepsilon }_{oct}^{e} + J_{t} \dot{\gamma }_{oct}^{e}$ and $\dot{\tau }_{oct} = G_{t} \dot{\gamma }_{oct}^{e} + J_{t} \dot{\varepsilon }_{oct}^{e}$.

Hyperelastic models:

• Are nonlinear models.

• Do not distinguish between stiffness in loading and unloading/reloading and, therefore, cannot reproduce the hysteretic behavior of the soil.

• Do not consider the effect of recent history on soil stiffness.

• Introduce a great number of parameters, which are often difficult to obtain from simple tests.

• In stress/strain closed cycles, they conserve stress and strain,$\oint\limits_{{\varepsilon^{e} }} {\varvec{E}_{t}^{\prime } :\dot{\varepsilon }^{e} = 0}$ and $\oint\limits_{{\sigma^{\prime } }} {\left( {{\varvec{E}}_{t}^{\prime } } \right)^{ - 1} :\dot{\varvec{\sigma }}^{\prime } = 0}$.

• Satisfy the theoretical requirements of continuity, stability, uniqueness and the 1^st Principle of Thermodynamics, $\oint\limits_{{\varepsilon^{e} }} {{\varvec{\sigma}}^{\prime } :\dot{\varepsilon }^{e} = 0}$.

The hyperelasticity framework has allowed the subsequent development of hyperelastic-plastic models. This is the case of the model of Likitlersuang and Houlsby [172], from which it is possible to deduce multisurface models with kinematic hardening, or the model of Zhang et al. [173], that is able to consider, among others, soil cementation, stress-induced anisotropy, cyclic shear behaviour or shear modulus degradation under small strain conditions due to the fact that energy dissipations and irreversible strains are allowed within all strain ranges.

Differential formulation (hypoelastic models stricto sensu)

Incrementally linear hypoelastic models stricto sensu consider the existence of tensorial functions that relate the stress increments with total strains, total stresses and strain increments. Such models do not directly define the tensorial function ${\varvec{F}}\left( \cdot \right)$, but this results from integrating the incremental constitutive Eq. (32), leading to expression (33).

$$\dot{\varvec{\sigma }}^{\prime } = {\varvec{E}}_{t}^{\prime } \left( {{\varvec{\sigma}}^{\prime } } \right):\dot{\varepsilon }^{e}$$

(32)

$${\varvec{\sigma}}^{\prime } = \smallint {\varvec{E}}_{t}^{\prime } \left( {{\varvec{\sigma}}^{\prime } } \right):\dot{\varepsilon }^{e} dt$$

(33)

where ${\varvec{E}}_{t}^{\prime } \left( {{\varvec{\sigma}}^{\prime } } \right)$, in its most general form, depends on 12 functions $C_{i}^{*}$, which in turn depend on the three invariants of ${\varvec{\sigma}}{^{\prime}}$, as $\begin{aligned} \varvec{E}_{t}^{\prime } \left( { \varvec{\sigma}^{\prime } } \right) = C_{1}^{*} \varvec{1} \otimes \varvec{1} + C_{2}^{*} \varvec{\sigma}^{\prime } \otimes \varvec{1} + C_{3}^{*} \varvec{\sigma}^{\prime 2} \otimes \varvec{1} + C_{4}^{*} \varvec{1} \otimes \varvec{\sigma}^{\prime } + C_{5}^{*} \varvec{\sigma}^{\prime } \otimes \varvec{\sigma}^{\prime } + C_{6}^{*} \varvec{\sigma}^{\prime 2} \otimes \varvec{\sigma}^{\prime } + C_{7}^{*} \varvec{1} \otimes \varvec{\sigma}^{\prime 2} + C_{8}^{*} \varvec{\sigma}^{\prime } \otimes \varvec{\sigma}^{\prime 2} + C_{9}^{*} \varvec{\sigma}^{\prime 2} \otimes \varvec{\sigma}^{\prime 2} + C_{10}^{*} \left( {\varvec{1}\overline{ \otimes }\varvec{1} + \varvec{1}\underline { \otimes } \varvec{1}} \right) + C_{11}^{*} \left( {\varvec{\sigma}^{\prime } \overline{ \otimes }\varvec{1} + \varvec{1}\underline { \otimes } \varvec{\sigma}^{\prime } } \right) + C_{12}^{*} \left( {\varvec{\sigma}^{\prime 2} \overline{ \otimes }\varvec{1} + \varvec{1}\underline { \otimes } \varvec{\sigma}^{\prime 2} } \right) \\ \end{aligned}$Unlike what happens with the algebraic formulation and the integral formulation exposed in the previous sections, the recent history in the constitutive law of the material is considered in the hypoelastic formulation. This is why hypoelastic models stricto sensu are not elastic models per se.

Incrementally linear hypoelastic models stricto sensu:

• Are nonlinear models.

• Do not distinguish between stiffness in loading and unloading/reloading and, therefore, cannot reproduce the hysteretic behavior of the soil.

• The extension of these models led to the appearance of quasi-hypoelastic models, framed within the incrementally multilinear models (see Sect. B.1.2). Quasi-hypoelastic models do allow the hysteretic behavior of the soil to be reproduced, since they introduce different stiffness depending on whether the processes are of loading or unloading type, and define the reversal criteria, the memory rules and the effect that reversals have on the variables which control the degradation of stiffness and on the maximum soil stiffness.

• Consider the effect of recent history on soil stiffness.

• Constitute simple formulations from a conceptual and mathematical point of view.

• The parameters of the models are, in general, easy to obtain from simple tests.

• In stress/strain closed cycles, they do not conserve the values of stress and strain, $\oint\limits_{{\varepsilon^{e} }} {{\varvec{E}}_{t}^{\prime } :\dot{\varepsilon }^{e} \ne 0}$ and $\oint\limits_{{{\varvec{\sigma}}^{\prime } }} {\left( {{\varvec{E}}_{t}^{\prime } } \right)^{ - 1} :\dot{\varvec{\sigma }}^{\prime } \ne 0}$.

• Depending on the selection of soil parameters, they can generate energy in stress/strain closed cycles, thus transgressing the thermodynamic principles, $\oint\limits_{{\varepsilon^{e} }} {{\varvec{\sigma}}^{\prime } :\dot{\varepsilon }^{e} \ne 0}$.

• Simulations with these types of models should be limited to the stress and strain paths corresponding to the tests with which their parameters were obtained.

(B) Incrementally multilinear models

The number of tensorial zones $\# Z$ considered in the incrementally multilinear models is a finite number greater than one. These models can reproduce nonlinear, hysteretic and dependent on recent history soil behavior, characteristic of Zone II.

(B.1) Hysteretic models

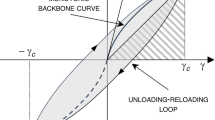
Hysteretic models emerged with the aim of simulating hysteretic soil behavior in the range of small strains originally in dynamic problems. Assuming that the hysteretic behavior of the soil was perfect, deformations would be recoverable only if the stress/strain cycles that started from the same reversal point were closed. This behavior differs from the reversible behavior of elastic models and from the irreversible behavior of elastoplastic models, as can be seen in Fig. 25.

Fig. 25

Schematic representation of soil behavior in different types of models. a Nonlinear elastic. b Hysteretic. c Elastoplastic

Nevertheless, reality does not show a perfect hysteretic soil behavior. Indeed, Hueckel and Nova [22] point to the elements described in Sect. 3.3 that separate the real soil behavior from such idealization (Fig. 26).

Fig. 26

a Loading cycle according to the model of Hueckel and Nova. b Real loading cycle with jump in the strain between a and d when reaching the same level of stress. From [22]

(B.1.1) Paraelastic models

A particular type of hysteresis is the so-called paraelastic hysteresis or paraelasticity, a theory that was developed by Hueckel and Nova [22], being one of the fundamentals in this field.

The term paraelastic refers precisely to the fact that strains reversibility is conditioned to the closure of the cycles (Fig. 27). The paraelastic models consider that soil stiffness degrades as a function of variables that depend on the paraelastic strains $\varepsilon^{pe} = \varepsilon^{e} + \varepsilon^{mp}$, sum of the elastic strains $\varepsilon^{e}$ and the microplastic strains $\varepsilon^{mp}$, the latter reversible only under the condition of the corresponding stress/strain cycle closure. The cycles of this kind of models can overlap one another using simple memory rules with two information levels, 1st for the constitutive equation and 2nd for recent history.

Fig. 27

Idealization of the hysteretic behavior of paraelastic models, from [22]. a One simple cycle. b One minor cycle overlapped to a major cycle. c Closure of minor overlapped cycles

Table 2 analyzes the stiffness formulation, the treatment of hysteretic behavior and general aspects of some paraelastic hysteretic models.

Table 2 Paraelastic hysteretic models

The clear, robust and intuitive way in which the paraelastic theory defines the hysteretic behavior of the soil, in addition to its versatility to be combined with other theoretical frameworks, endows it with a high potential. So far, interesting models have been developed using concepts from paraelastic theory combined with elastoplastic, bounding plasticity, multilaminate or hypoplastic models [140, 153, 154, 156, 174,175,176,177].

(B.1.2) Quasi-hypoelastic hysteretic models

Among the incrementally multilinear models stand out the ones here called quasi-hypoelastic hysteretic models, which have been normally used to simulate soil behavior in the range of small strains. A widespread methodology to build quasi-hypoelastic hysteretic models is to incorporate the elements that allow reproducing the hysteretic behavior of the soil into quasi-hypoelastic models, for example, through the Generalized Masing Rules [157, 158]. Quasi-hypoelastic models simulate soil behavior during monotonous loadings and resemble hypoelastic models, although instead of elastic stiffness moduli they use apparent stiffness moduli which act on total strains (and no just on the elastic ones). Following the classification by Sellers [124], quasi-hypoelastic models can be classified into two types depending on how their parameters are defined:

• Variable parameter models [178,179,180] are those that propose a relation between stress and strain based on nonlinear functions (hyperbolic, elliptical, logarithmic, spline, etc.). Variable parameter models can generally be reformulated as variable moduli models.

• Variable moduli models [181,182,183,184] are those that propose nonlinear functions to describe apparent volumetric and shear stiffness moduli in a constitutive equation with an algebraic structure equal to that of an elastic model.

The general constitutive equation of the variable moduli models usually adopts the following expression:

$$\varvec{\sigma}^{\prime } = 3K_{s}^{\prime ap} \left( {p^{\prime } ,\varepsilon_{oct} ,\varvec{\chi}^{hist} } \right)\varepsilon_{oct} \varvec{1} + 2G_{s}^{ap} \left( {p^{\prime } ,\gamma_{oct} ,\varvec{\chi}^{hist} } \right)\varvec{e}$$

(34)

$$\dot{\varvec{\sigma }}^{\prime } = 3K_{t}^{\prime ap} \left( {p^{\prime } ,\varepsilon_{oct} ,{\varvec{\chi}}^{hist} } \right)\dot{\varepsilon }_{oct} \varvec{1} + 2G_{t}^{ap} \left( {p^{\prime } ,\gamma_{oct} ,{\varvec{\chi}}^{hist} } \right)\dot{\varvec{e}}$$

(35)

The following decomposition of secant stiffness modulus is usually considered based on experimental observations [66]: $K_{s}^{\prime ap} \left( {\sigma_{oct}^{\prime } ,\varepsilon_{oct} ,{\varvec{\chi}}^{hist} } \right) = K_{s,0}^{\prime ap} \left( {p^{\prime } } \right)f_{{K_{s}^{\prime ap} }} \left( {\varepsilon_{oct} ,{\varvec{\chi}}^{hist} } \right)$ and $G_{s}^{ap} \left( {\sigma_{oct}^{\prime } ,\gamma_{oct} ,{\varvec{\chi}}^{hist} } \right) = G_{s,0}^{ap} \left( {p^{\prime } } \right)f_{{G_{s}^{ap} }} \left( {\gamma_{oct} ,{\varvec{\chi}}^{hist} } \right).$ The popularity of quasi-hypoelastic hysteretic models come from its relative simplicity and easy incorporation into finite element numerical codes for solving practical engineering problems [66], as can be seen in the work of Jardine and Potts [185] and St. John et al. [186]. Some disadvantages in relation to the quasi-hypoelastic hysteretic models are pointed out [66, 182, 187]:

• Lack of continuity during neutral loading processes.

• Functions $f_{{K_{s}^{\prime ap} }} \left( {\varepsilon_{oct} ,{\varvec{\chi}}^{hist} } \right)$ and $f_{{G_{s}^{ap} }} \left( {\gamma_{oct} ,{\varvec{\chi}}^{hist} } \right)$ are calibrated from tests with specific stress or strain paths that can be very different from paths followed by the soil in practical applications.

• The constitutive equation implies that stress and strain increases are coaxial, which does not always correspond to experimental observations [188]. Nevertheless, it should be considered that in the tests used to calibrate these models this coaxiality will generally be complied.

• To reproduce the hysteretic behavior of the soil, loading/unloading criteria that can lead to numerical instabilities are introduced.

• The dependence of $G_{s,0}^{ap} \left( {p^{\prime } } \right)$ implies that the shear modulus depends on the volumetric strain $G = G\left( {\gamma_{oct} ,\varepsilon_{oct} ,{\varvec{\chi}}^{hist} } \right)$ which, in case of not considering the coupling modulus $J_{t}$, may not be thermodynamically consistent.

Generalized Masing rules

A common and widespread way to build hysteretic models from models that simulate the nonlinear behavior of soil during monotonous loading is through the application of the original and extended Masing Rules [157, 158], jointly denominated as Generalized Masing Rules, to which the corresponding loading/unloading criteria must be added. Such rules are formulated in a one-dimensional stress or strain context, although the extension to multiaxial states can be made with an appropriate change in the variables. For the one-dimensional case, the Generalized Masing Rules consider that the state variables ${\varvec{\chi}}^{hist}$ are identified with the total strain ε. However, despite these variables ${\varvec{\chi}}^{hist}$ can be formally treated as strains, they cannot be physically interpreted as such (see Sect. 3.3). The original Masing rules Nr. 1 and Nr. 2 [157] for symmetric loading, along with the extended Masing rules Nr. 3 and Nr. 4 [158] are the following:

• 1. Rule Nr. 1: For the primary loading, the constitutive law adopts the expression $\sigma^{\prime } = F\left( \varepsilon \right)$. In general, this relation considers the total strain $\varepsilon$. This is because in the tests used to calibrate the nonlinear function $F\left( \cdot \right)$, the reversible and irreversible strain components are not separated.

• 2. Rule Nr. 2: In loading or unloading, after a reversal point R, the constitutive law considers a two-scale factor, as compared to the constitutive law for primary loading, taking as reference the local origin given by the reversal point $\left( {\sigma^{\prime R} ,\varepsilon^{R} } \right)$, as $\sigma^{\prime } - \sigma^{\prime R} = 2F\left( {\left( {\varepsilon - \varepsilon^{R} } \right)/2} \right)$. In general, this relation also considers the total strain $\varepsilon$, although in elastoplastic models, this will coincide with the elastic strain, as this law is activated within elastic domain. Rule Nr. 2 can also be applied through different strategies [158, 189].

• 3. Rule Nr. 3: If the unloading or reloading curves intersect the initial loading curve, they resume such curve.

• 4. Rule Nr. 4: If the unloading or reloading curves intersect a previous unloading or reloading curve, they resume such curve.

Some quasi-hypoelastic hysteretic models

Some models that are classified as quasi-hypoelastic hysteretic models are described and analyzed hereafter. They all are variable parameter models, except for the SSOM model [67] and the HQH model [156, 175], which are variable moduli models. Nevertheless, practically all of them can be reformulated as variable moduli models, which allows obtaining the equivalent apparent stiffness moduli in each case. In this type of models, the state variables that control the value of the stiffness moduli are identified with those proposed by Gudehus [107] to describe the hysteretic behavior of the soil.

In all the models studied in this section, excluding the SSOM and HQH models, it is necessary to define ad hoc components that allow reproducing hysteretic soil behavior for example, through the Generalized Masing Rules.

Tables 3 and 4 analyze the small strain stiffness formulation and general aspects of some quasi-hypoelastic hysteretic models.

Table 3 Quasi-hypoelastic models (1/2)

Table 4 Quasi-hypoelastic models (2/2)

The SSOM [67] and HQH [156] models have great potential to be used in professional practice, given their ability to integrate multiple aspects of the soil in the range of small strains, in addition to their capacity to be combined with plastic models which let extend its applicability to the range of medium and large strains.

Both models: (1) are based on the apparent secant shear modulus $G_{s}^{ap}$ degradation curve provided by the Dos Santos and Correia model [231], which is limited by a minimum value of the tangent shear modulus $G_{ur}$; (2) consider the recent history of deviatoric strains; (3) use history tensors that act as Simpson block models [31]; (4) consider similar thermodynamic-type corrections; and (5) can be combined with multiple plastic models leading to advanced elastoplastic models.

When both models are used by themselves, they use the Hashiguchi [189] criterion to differentiate primary load from unloadings/reloadings, but when they are combined with an elastoplastic model, they consider, on the one hand, a factor $\xi = 2$ in the expression of the apparent secant shear modulus $G_{s}^{ap}$ and, on the other hand, a factor $h_{i}$ that modifies the hardening laws to avoid overlapping the mechanisms of these models and the plastic models with which they are combined, that try to explain the reduction of soil stiffness during the primary loading.

The SSOM model describes the elastic part of the well-known HS-SS model, implemented in Plaxis and based on the HS-S model [67] (see Sect. B.2.1). However, despite its great advantages, the SSOM model presents some limitations that the HQH model solves, with the following considerations: (1) the use of an intrinsic reversal criterion (and not an extrinsic one like in the SSOM model); (2) the ability to recover the stiffness continuously with the rotation angle of strain recent paths, through the use of a history tensor inspired by the intergranular strain tensor of the Niemunis and Herle model [151] (and not discontinuously like the SSOM model); (3) the consideration of infinite degradation curves of the shear modulus, which provides the model with versatility and great adaptability to experimental results (and not just a single degradation curve like the SSOM model); (4) the consideration of a variable Poisson's ratio $\nu^{\prime} \ge \nu_{min}^{{\prime}}$ that does not limit the values of the bulk modulus (and not of a constant Poisson’s ratio $\nu^{\prime } = \nu_{const}^{\prime }$ like the SSOM model, that forces the proportionality ${{K}} \propto G$); (5) the consideration of multiple state variables that define different short and long-term memory levels in a similar way to how the Hueckel and Nova model [22] does, which endows the HQH model with robustness to reproduce the hysteretic behavior of the soil; (6) the consideration of the strain-induced anisotropy; or (7) a higher level of compliance with the Generalized Masing Rules, especially with Rule No. 4, thanks to the greater amount of information that the HQH model stores at the reversal points. In summary, the HQH model unifies different concepts with great potential from several proven models.

Both models (SSOM and HQH) require the same or equivalent few and simple parameters, except for an additional parameter required by the HQH model, which is the maximum shear modulus after a reversal of the deviatoric strains of 90º ($G_{s,0}^{ap,90,H,ref}$). This parameter must be obtained from biaxial, true triaxial or hollow cylinder with torsion tests with internal strain measures, or it can be estimated from $G_{s,0}^{ap,180,H,ref}$ throughout the relation $G_{s,0}^{ap,90,H,ref} = {\Lambda }G_{s,0}^{ap,180,H,ref}$, taking ${\Lambda }$ values of $0.40 - 0.58$ for sands and of $0.50$ for clays [156] (${\Lambda } \approx m_{T} /m_{R}$, where $m_{T}$ and $m_{R}$ are the parameters that control stiffness in the Niemunis and Herle model [151]).

(B.2) Advanced models

The advanced models are those incrementally multilinear models that are capable of reproducing soil behavior in the entire strain range (Zones I, II, III and IV of Jardine [6]).

(B.2.1) Classic elastoplastic models

Classic elastoplastic models that consider soil behavior in the range of small strains add, to the elastic regime of the classic elastoplastic formulation, the nonlinear, hysteretic and dependent on history behavior of the soil through the incorporation of new state variables ${\varvec{\chi}}^{el,hist}$ to the constitutive equation within yield surfaces $\dot{\varvec{\sigma }}^{\prime } = {\varvec{G}}\left( {\varepsilon ,{\varvec{\sigma}}^{\prime } ,{\varvec{\chi}}^{el,hist} ,\dot{\varepsilon }} \right)$. This is normally attained by adopting the structure of a quasi-hypoelastic hysteretic model to describe the elastic formulation of the elastoplastic model. In this case, to calculate the stress, the apparent stiffness moduli are operated with the elastic strains and not with the total ones. According to Jardine [6] and Jardine et al. [8], this semiempirical methodology allows attaining very precise predictions thanks to the wide range of strains considered, although its use entails a loss of generality and a lack of consistency of the theoretical framework on which it is based. Among others, these assumptions lead to the following: (1) it is not correct to apply the elastic relations to the apparent stiffness moduli; and (2) the mechanisms of the quasi-hypoelastic hysteretic models and the elastoplastic models that try to explain the reduction of soil stiffness during the primary loading processes, in comparison with the stiffness in unloading or reloading processes, are being overlapped. The basic equations used in classic elastoplastic models, generalized to the case of $k = 1 \ldots q$ yield surfaces are widely known.

The number of tensorial zones $\# Z$ that present these models will depend on the number of yield surfaces and their intersections. In general, it will be complied that $\# Z = 2$ in models with a single yield surface and $\# Z > 2$ in models with multiple yield surfaces.

Table 5 analyzes small strain stiffness formulation, hysteretic behavior treatment and general aspects of some elastoplastic models that consider soil behavior in the range of small strains.

Table 5 Elastoplastic models that consider soil behavior in the range of small strains

The widespread use of the elastoplastic formulation and its balance between complexity and usability, gives the models that are based on it the greatest potential to be used in the practical applications, among all those analyzed in this paper, of which stand out the HS-SS model (based on the HS-S model [67]), and the EPHYSS model [156]. The incorporation of formulations that can reproduce soil behavior in the range of small strains within models used in professional practice (as it was achieved with the HS-SS model in Plaxis), would allow professional engineers to familiarize themselves with the characteristics and complexity of non-linear, hysteretic and dependent on recent history soil behavior in the range of small strains. Once this first goal has been achieved, introducing more complex models into commercial software could be less traumatic.

The HS-SS model is one of the few models widely used in professional practice that considers soil behavior in the range of small strains and it uses known and relatively easy to obtain/estimate parameters. The HS-SS model is based on the HS-S model which adds, to the elastic formulation of the SSOM, the plastic formulation of the HS model [233] with two modifications: (1) it replaces the dilatancy criterion of Rowe [238] with that of Li and Dafalias [239] to describe the contractive behavior of the soil; and (2) modifies the hardening laws and introduces the factor $h_{i} = \left( {G_{m} } \right)^{{1 + E_{t,ur}^{{\prime}} /E_{{{ }i}}^{{\prime}} }}$. The HS-S model significantly improves the approach to soil behavior provided by the HS model, although it has certain limitations [67]. Some applications can be found in [240,241,242].

The HS-SS model presents some small differences with respect to the HS-S model on which it is based. These differences appear in the expressions both models use to calculate the dilatancy angle and in the expression of the Cap-surface hardening law, where the increase of the state variable depends on the confinement in the HS-S model and on the state variable itself in the HS-SS model.

Despite its great advantages, some aspects of the HS-SS model could be improved, and some inconsistencies whose effects can have a considerable influence on the numerical simulations of boundary value problems, as these are cumulative, should be corrected [156, 175, 243,244,245]. This is achieved with the EPHYSS model.

The EPHYSS model adds to the elastic formulation of the HQH model, the plastic formulation of the HS_MOD model [156], which is the same as that used in the HS-S model and, like this one, also uses known and relatively easy to obtain/estimate parameters. EPHYSS model improves the approach to the soil behavior in the range of small strains with respect to the HS-SS model (see Sect. B.1.2) and corrects the numerical inconsistencies detected in it. Simulations with EPHYSS model of different element tests and several boundary value problems can be found in Castellón [175].

Although unsaturated soil models are not analyzed in this paper, it should be pointed out that recently some advanced elastoplastic models for unsaturated soils capable of reproducing soil behavior in the range of small strains have been proposed, such as, for example, the model of Ng et al. [246].

(B.2.2) Multisurface models

The multisurface models with kinematic hardening were initially developed by Iwan [247] and Mróz [13], based on previous works, as those of Duwez [248] and Besseling [249]. Subsequently, Prévost [11, 12] extended these models and applied them to Soil Mechanics. These models consider various nested yield surfaces ($f^{{\left( {m^{\prime \prime } } \right)}} = 0,\; m^{\prime \prime } \ge 2$), generally in the stress space (Fig. 28a). Each of these surfaces is activated at the moment when the stress state reaches its boundary, leading to a finite decrement in the global plastic hardening modulus, which, at the same time, generates greater plastic strains (Fig. 28b).

Fig. 28

a Schematic representation of a multisurface model. b Experimental curve $q - \varepsilon_{1}$ (left) and curve $q - \varepsilon_{1}$ resulting from multisurface model (right). From [250]

Multisurface models can reproduce a discontinuous variation of elastoplastic stiffness. When $j$ nested yield surfaces are activated, and depending on the followed stress path, they are displaced keeping them tangent at the contact points. The number, form, size and situation of the nested surfaces constitute the state variables ${\varvec{\chi}}^{hist}$. The approximation to the soil behavior that these models provide depends on the number of nested yield surfaces considered, since a greater number of surfaces implies a softer variation in stiffness. However, if this number is high, using these models can be computationally expensive. Based on this limitation, bounding surface plasticity models and bubble models were created.

The multisurface models have two tensorial zones $\#Z$ [66].

Table 6 analyzes small strain stiffness formulation, hysteretic behavior treatment and general aspects of some multisurface models.

Table 6 Multisurface models

Puzrin and Burland [152], after studying and evaluating the models of Kondner [195], Hardin and Drnevich [2], Griffiths and Prévost [253], Tatsuoka and Shibuya [115] and Jardine et al. [203], and based on the works of Puzrin and Burland [254], developed a model based on the theoretical framework of Jardine [6], distinguishing, in the stress space, three zones where the soil has different behaviors around any local origin constituted by a point of the stress path. Addenbrooke et al. [68] proposed the generalization of the model of Puzrin and Burland to the multiaxial case and Puzrin et al. [255] extended the original model, introducing the plastic behavior in a thermodynamically consistent formulation. However, Puzrin and Burland [152] model requires unusual parameters in the professional practice, which may be a handicap for its use. On the other hand, this model has certain limitations to reproduce the hysteretic behavior of the soil, since: (1) it only stores information of the last reversion point; (2) after a reversion the state variables that control degradation can only be fully reinitialized; and (3) stiffness recovery is discontinuous with the rotation of the recent path.

The approach proposed by Seyedan and Solowski [252] seems more promising for future practical applications, due to its ability to introduce soil behavior in the range of small strains in classical models. Seyedan and Solowski developed a methodology to introduce shear stiffness nonlinearity to classic elastoplastic models that have a constant elastic shear modulus. A new Small Strain Yield Surface is defined to reproduce the small strain shear stiffness nonlinearity following the expression from Dos Santos and Correia [231]. This methodology increases the total number of parameters of the original model by only two, and does not affect its original plastic formulation. Seyedan and Solowski apply this methodology to the MCC and MC models. State variable $\alpha_{q}$ replaces $\varepsilon_{q}^{p}$ in the calculation of the hardening law to include errors caused by $G_{MCC}^{e}$. Once $G$ reduces its value to $G_{MCC}^{e}$, it is maintained within an elastic behavior until stress state reaches MCC Yield Surface or a reversal occurs. The movement of the Small Strain Yield Surface does not produce any volumetric plastic strain and, therefore, does not affect the MCC Yield Surface, but the deviatoric plastic strain of the MCC Yield Surface does affect the Small Strain Yield Surface. In Seyedan and Solowski [256] it is showed how $F_{ss}$ is well defined within an hyperplastic framework. Despite the remarkable potential of this methodology, the resulting models are not capable of reproducing soil hysteretic behavior, for which it would be necessary to define new state variables. Future research lines should focus on this aspect.

(B.2.3) Brick models

Most of the elastoplastic models for soils are formulated in the stress space, although some have been formulated in the strain space [31, 67, 257, 258]. Yoder and Iwan [259] and Iwan and Chelvakumar [260] highlight some of the advantages of the models that are formulated in the strain space. Many of them have not prospered, but the brick model of Simpson [31] has led to a theoretical framework that has subsequently been successfully applied to various models. Among them are the model of Clarke [69], the model of Ellison [261] or the HS-Brick Model [155].

To explain how the brick models work, Simpson [31] uses an analogy in which he considers that soil behavior in the range of small strains resembles a man pulling a set of bricks attached to him by inextensible strings. The movement of the man represents the imposed strains path and the movement of the bricks represents the plastic strains. When any of the strings is not tensioned, the part of the plastic strain corresponding to such string is not generated. But when such string is tensioned, as the man is at a distance equal to that of the length of the string and in its direction of stretching, the respective plastic strains are activated, with the consequent decrease in the elastoplastic stiffness of the soil (Fig. 29). The number and situation of the bricks constitute the state variables ${\varvec{\chi}}^{hist}$.

Fig. 29

Brick model of Simpson, from [31]. a Scheme of the analogy of man pulling bricks attached to him by inextensible strings. b Degradation curve of the model

To explain the advantages of working in the strain space, Ellison et al. [262] state that, despite the connection between stress and strain, the changes in soil behavior are determined by micromechanical changes in its fabric, which is reflected at the macroscopic level as an accumulation of strains. Furthermore, they affirm that anisotropy due to the orientation of soil particles changes when large strains occur, even if the stress is the same at the beginning and at the end of these strains. Finally, they remember the well-known statement of Burland (1967) cited by Simpson [31]: "stress is a philosophical concept—deformation is the physical reality". Ellison et al. conclude that the models formulated in the strain space are more suitable to explain the mechanisms that govern soil behavior. This approach allows explaining, in a relatively simple way, the observations made by Atkinson et al. [30], Clayton and Heymann [20], Gasparre [75] and Gasparre et al. [34]. From a practical point of view, the models formulated in the strain space can be easily implemented in numerical models without the need to isolate, in each calculation step, the strain as an independent variable [260], just as the models formulated in the stress space should do. In addition, as Yoder and Iwan [259] demonstrate, the models formulated in the strain space do not have the problem of surface intersection, nor some of the instability problems that the models formulated in the stress space do.

Brick models consider as many tensorial zones as possible combinations of active and non-active bricks exist. If $n$ bricks are considered, the maximum number of tensorial zones can be calculated as the sum of the possible combinations with repetition of $1 \ldots n^{\prime \prime }$ bricks, plus the case in which no brick is active, that is, $\# Z = \mathop \sum \limits_{k = 0}^{{n^{\prime \prime } }} n^{\prime \prime } !/\left(k!\left( {n^{\prime \prime } - k} \right)!\right)$.

Table 7 analyzes stiffness formulation, hysteretic behavior treatment and general aspects of some brick models.

Table 7 Brick models

The original model of Simpson [31] is formulated in the strain space, considering a plane strain state. A finite number of bricks is required to define the degradation curve. This model introduces the effect of soil overconsolidation through the parameter $\beta_{mod}$. A higher proportion of volumetric and shear elastic strains is assumed for higher mean stress. It reproduces well the undrained trajectories, and worse the drained ones, unless the effect of dilatancy is introduced. It does not reproduce the critical state, therefore it should be used in stiff clays or its formulation should be extended.

The Simpson model [31] formulation that reproduce the behavior of the soil in the range of small strains can be used with relative ease in classic or advanced models (for example, in the HS-Brick Model [155], which improves the HS-SS model). The ability of Simpson model to be combined with other models provides it with great potential. Moreover, the Simpson model establishes a theoretical framework that allows to easily understand part of the formulation of other models, as happens with the history tensors of the advanced elastoplastic models HS-SS and EPHYSS (see Sect. B.2.1).

(B.2.4) Bounding surface plasticity models

Bounding surface plasticity models were initially developed by Dafalias [263], Krieg [264], Dafalias and Popov [265] and Dafalias and Herrmann [266] with the aim of attaining a continuous evolution of the elastoplastic stiffness, which is extended to the interior of the yield surface in the range of small strains in these models, and of reducing, therefore, the computational cost of the multisurface models. Bounding surface plasticity models generally use two surfaces: an exterior surface, named bounding surface, and an interior surface, called current loading surface (Fig. 30). Between both surfaces, unlike the multisurface models, which consider $m^{\prime\prime}$ surfaces that give place to a discrete variation in stiffness, bounding surface plasticity models consider continuous functions to represent the plastic hardening modulus, obtaining continuous variations of stiffness (which is equivalent to consider $m^{\prime\prime} \to \infty$ in multisurface models). The form, situation and orientation of both surfaces, along with other information stored at the last reversal point, constitute the state variables ${\varvec{\chi}}^{hist}$.

Fig. 30

Schematic representation of surfaces of a bounding surface plasticity model, from [84]

The formulation of these models is based on that of the classic elastoplastic models, although unlike the latter, the bounding surface plasticity models consider plastic strains also during loading processes within the bounding surface ($OCR > 1)$. Such plastic strains are made to depend on the distance between the current stress state, located on the current loading surface, and the denominated image point, located on the bounding surface plasticity, according to the mapping rules.

The number of tensorial zones $\# Z$ of these models is reduced to two when there is only one bounding surface and more than two in case there is a greater number of bounding surfaces [66] (similar to the case of classic elastoplastic models with yield surfaces).

Table 8 analyzes small strain stiffness formulation, hysteretic behavior treatment and general aspects of some bounding surface plasticity models.

Table 8 Bounding surface plasticity models

Although these models can reproduce different aspects of the soil in a wide range of strains, including also small strains, they require parameters difficult to obtain experimentally and with which geotechnical engineers are not familiar. During the coming years it is very possible that these models will remain limited to an academic use.

(B.2.5) Bubble models

Bubble models were developed to solve some of the limitations posed by the bounding surface plasticity models. The latter allow reproducing the nonlinear plastic isotropic hardening or softening behavior of the soil during loading processes and assume that part of the deformations corresponding to these loading processes are plastic, even in the range of small strains. Conversely, they consider that soil behavior is elastic during unloading processes, which restricts the degree of coupling between volumetric and deviatoric behavior [84] and limits their ability to reproduce the hysteretic soil behavior in the range of small strains. Bubble models are based on the concepts of bounding surface plasticity models and multisurface models and include one or more surfaces, called bubbles (Fig. 31), with kinematic hardening, in addition to the isotropic hardening within the bounding plasticity surface. The number, shape, size and situation of the bubbles constitute the state variables ${\varvec{\chi}}^{hist}$. Likewise, bubble models must include, apart from the mapping rules that control the plastic hardening modulus as the bubbles move, translation rules that control the movement of such bubbles.

Fig. 31

a Bounding surface and bubble of a bubble model. b Conceptual scheme of the bubble movement of a bubble model. From [84]

The number of tensorial zones $\# Z$ of these models, as in multisurface models, is two.

Table 9 analyzes small strain stiffness formulation, hysteretic behavior treatment and general aspects of some bubble models. Other bubble models have introduced the effect of soil destructuration [294, 295], soil anisotropy [296] and some improvements to the Three Surface Kinematic Hardening model (3-SKH) [297].

Table 9 Bubble models

The ability of bubble models to reproduce the hysteretic behavior of the soil is potentially greater than that of bounding surface models. However, bubble models use has been very limited in practical applications, and present a great sensitivity to the exponent that appears in the expressions of the plastic modulus, which has a significant effect on the stress–strain curves [298].

(B.2.6) Multilaminated models

The concept of multilaminated model was initially formulated by Batdorf and Budiansky [299]. Zienkiewicz and Pande [300] extended the concept to the analysis of joints in rocks. Subsequently, Pande and Sharma [301] and Sadrnejad and Pande [302] extended these models to Soil Mechanics. Multilaminated models are based on the concept that the three-dimensional stress or strain state at a point of the continuous medium (global state) can be obtained as the sum of the two-dimensional stress or strain state on different $i$ planes with different orientations that pass through such point (local state). For that purpose, a set of fundamental equations are established in each plane: $\dot{\varvec{\sigma }}_{i}^{\prime } = \left( {{\varvec{T}}_{i} } \right)^{T} \cdot\dot{\varvec{\sigma }},\dot{\varepsilon }_{i}^{e} = {\varvec{C}}_{i} \cdot\dot{\varvec{\sigma }}_{i}^{\prime } ,\dot{\varepsilon }_{i} = \dot{\varepsilon }_{i}^{e} + \dot{\varepsilon }_{i}^{p}$ $\dot{\varepsilon }_{i}^{p} = \dot{\lambda }_{i} \partial g_{i} /\partial {\varvec{\sigma}}_{i}^{\prime }$. The number of planes considered in multilaminated models is reduced to a finite number and, through the formulation adopted in the model, they are able to represent all orientations in space, grouped by sectors. Bazant and Oh [303] and Ehret et al. [304] demonstrate that using 33 planes in the calculation of $\dot{{\varvec{\epsilon}}}$ offers acceptable results and an acceptable computational cost. Global strain increments, which correspond to an increment in global stress, are calculated from the integration of local strains into the planes. For the deduction of the expression that relates these magnitudes, the principle of virtual works is used $\delta W_{macro} = \left( {4/3} \right)V\dot{\varvec\sigma }^{\prime } :\dot{\varepsilon } = \int\limits_{\partial V} {\delta W_{micro} dS^{\prime } } = \int\limits_{\partial V} {\dot{\varvec\sigma }_{i}^{\prime } :\dot{\varepsilon }_{i} dS}$ and assuming $dS^{\prime } \approx \Delta S^{\prime } = \left( {\sin \tilde{\alpha }} \right)\left( {\sin \tilde{\beta }} \right)\Delta \tilde{\alpha }\Delta \tilde{\beta }$ where $\Delta \tilde{\alpha }$ and $\Delta \tilde{\beta }$ are finite spherical sectors, $\dot{\varepsilon } = 3\mathop \sum \limits_{i} \left( {{\varvec{T}}_{i} \cdot \dot{\varepsilon }_{i} } \right)w_{i}$ and $w_{i} = \left( {sin\tilde{\alpha }} \right)\Delta \tilde{\alpha }\Delta \tilde{\beta }/\left( {4V} \right)$ are satisfied. In this type of models, the state variables that control the value of stiffness modulus in each plane, the number of considered planes and variables that store information of reversion points are identified with the state variables ${\varvec{\chi}}^{hist}$.

The number of tensorial zones $\# Z$ in multilaminated models will depend on the amount of planes considered. Nevertheless, this number is generally high; therefore, despite not being incrementally nonlinear models, for practical purposes, it can be considered that the stiffness of this type of models does depend continuously on the increments in the total strain tensor $\dot{\varepsilon }$.

Table 10 analyzes small strain stiffness formulation, hysteretic behavior treatment and general aspects of Schädlich and Schweiger [154] multilaminated model that considers soil behavior in the range of small strains.

Table 10 Multilaminated models that consider soil behavior in the range of small strains

Schädlich and Schweiger model considers the elastoplastic behavior of the soil using a Cap-Cone type model (based on the model of Wiltafsky [305] and Wiltafsky et al. [306]), which allows describing plastic behavior in each plane. It also considers the following concepts to describe the nonlinear, hysteretic and history dependent behavior of the soil within yield surfaces: (1) inherent and strain-induced cross-anisotropy (using the spectral decomposition of the global elastic compliance matrix [307]); (2) dependence on stiffness with stress; (3) degradation of elastic stiffness with the strain $\varepsilon_{deg}$; and (4) dependence on strains history satisfying the Generalized Masing Rules. Schädlich and Schweiger model is based on the model of Scharinger et al. [308], but it introduces some differences: (1) it uses a linearization for the degradation curve of the shear modulus in each plane instead of the expression proposed by Soga et al. [309]; and (2) it reproduces the effect of loading history using an approach similar to that of Simpson's brick model [31] instead of the linear approximation of the experimental results from Richardson [29].

Multilaminate models can reproduce multiple soil characteristics, including its complex behavior in the range of small strains. To do this, these models use parameters known in professional practice and a clear and not contrived formulation, which places them in an advantageous position compared to other incrementally multilinear models. Even so, its use has been very limited in practical applications, although some commercial software, such as ZSoil, already incorporate basic multilaminate models in their libraries.

(C) Incrementally nonlinear models

Incrementally nonlinear models emerged from the generalization of the hypoelastic theory of Truesdell [310] and from the theoretical framework of elastoplasticity [66]. The most important characteristics of incrementally nonlinear models are: (1) the absence of explicit decomposition of strain increments in reversible and irreversible parts; and (2) the continuous nonlinear dependence of the tangent stiffness tensor on the direction of the increment strain tensor. The most general constitutive equation of this type of models is expression (36) [136, 311] and it is composed of a linear part $\varvec{L}\left( {\varvec{\sigma}^{\prime } ,\varvec{\chi} } \right):\varvec{d}$ and a nonlinear part $\left\|\varvec{d}^{ - 1}\right\| \varvec{Q}\left( {\varvec{\sigma}^{\prime } ,\varvec{\chi} } \right)::\left[ {\varvec{d} \otimes \varvec{d}} \right].$

$$\dot{\varvec{\sigma }}^{\prime } = {\varvec{L}}\left( {{\varvec{\sigma}}^{\prime } ,{\varvec{\chi}} } \right):{\varvec{d}} + {\left\|\varvec{d}^{ - 1}\right\|} {\varvec{Q}}\left( {{\varvec{\sigma}}^{\prime } ,{\varvec{\chi}} } \right)::\left[ {{\varvec{d}} \otimes {\varvec{d}}} \right]$$

(36)

It is considered that incrementally nonlinear models have an infinite number of tensorial zones $\# Z \to \infty$. In some cases, nevertheless, as in hypoplastic models with intergranular strain ${\varvec{\delta}}$, the incremental nonlinearity in the range of small strains is linked to the sign $\hat{\varvec{\delta }}:{\varvec{d}}$, not appearing the strain rate tensor d in the resulting tangent stiffness formulation for $\hat{\varvec{\delta }}:{\varvec{d}} > 0$ nor for $\hat{\varvec{\delta }}:{\varvec{d}} \le 0$. Therefore, for practical purposes, such models can be considered conceptually closer to multilinear models than to incrementally nonlinear models when describing soil behavior in the range of small strains.

These models can reproduce nonlinear, hysteretic and dependent on recent history soil behavior, characteristic of Zone II.

(C.1) Hypoplastic models

Hypoplastic models represent a particular case of incrementally nonlinear models. Specifically, hypoplastic theory was initially developed by Kolymbas [312]. Subsequently, two hypoplastic formulations were distinguished: K-hypoplasticity [313] and CLoE hypoplasticity [314, 315]. Afterward, these formulations were extended by Gudehus [316], Bauer [317], Wolffersdorff [318], Niemunis and Herle [151] and Herle and Kolymbas [319], among others. The first generation of hypoplastic models considered ${\varvec{L}}\left( {{\varvec{\sigma}}^{\prime } ,{\varvec{\chi}} } \right) = {\varvec{L}}\left( {{\varvec{\sigma}}^{\prime } } \right)$ and ${\varvec{Q}}\left( {{\varvec{\sigma}}^{\prime } ,{\varvec{\chi}}} \right) = \varvec{ N}\left( {{\varvec{\sigma}}^{\prime } } \right) \otimes {\mathbb{I}}$, that is, $\dot{\varvec{\sigma }}^{\prime } = {\varvec{L}}\left( {{\varvec{\sigma}}^{\prime } } \right):{\varvec{d}} + {\varvec{N}}\left( {{\varvec{\sigma}}^{\prime } } \right)\|{\varvec{d}}\|.$ Using the envelopes of Gudehus in the Rendulic space, it is possible to decompose the effect of the linear and nonlinear part of the previous constitutive equation (Fig. 32).

Fig. 32

Graphical interpretation of the hypoplastic constitutive equation, from [66] a Unitary circle in strain space. b Effect of the linear part of equation. c Effect of the nonlinear part of equation

Hypoplasticity offers a theoretical framework for describing the nonlinear mechanical behavior of granular materials, which is capable of reproducing soil strains by reordering their solid skeleton. Furthermore, unlike elastoplastic theory, in hypoplastic theory it is not necessary to neither define yield surfaces nor flow rules, since these can be derived from expression (36).

Nevertheless, classic hypoplastic models have some limitations. Among them, the requirement of a large number of parameters that limit their practical use, as well as the fact that they are not able to reproduce correctly soil behavior in the range of small strains during cyclic loadings due to ratcheting effect. Classic hypoplastic models must incorporate new state variables to describe the hysteretic and dependent on recent history soil behavior [107]. To solve this problem, diverse strategies have been proposed, some of them exposed by Tamagnini and Viggiani [66]:

• Include the void ratio as a state variable to obtain a unified formulation for soils with different densities and to incorporate the concept of critical state. In this case, ${\varvec{L}}\left( {{\varvec{\sigma}}^{\prime } ,{\varvec{\chi}} } \right) = {\varvec{L}}\left( {{\varvec{\sigma}}^{\prime } ,{\text{e}}} \right)$ and ${\varvec{Q}}\left( {{\varvec{\sigma}}^{\prime } ,{\varvec{\chi}} } \right) = \varvec{ N}\left( {{\varvec{\sigma}}^{\prime } ,{\text{e}}} \right) \otimes {\mathbb{I}}$ are considered. An expression of the tensors ${\varvec{L}}\left( {{\varvec{\sigma}}^{\prime } ,{\text{e}}} \right)$ and ${\varvec{N}}\left( {{\varvec{\sigma}}^{\prime } ,{\text{e}}} \right)$ appears in the work of Wolffersdorff [318] or Gudehus [316], including the barotropy and picnotropy factors.

• Introduce a structure tensor to consider the inherent soil anisotropy.

• Introduce an internal variable dependent on strains for modelling the cyclic soil behavior.

• Combine a hypoplastic model with a paraelastic one (hypoplastic hybrid models).

Table 11 analyzes small strain stiffness formulation, hysteretic behavior treatment and general aspects of the hypoplastic model with intergranular strain of Niemunis and Herle [151] that considers soil behavior in the range of small strains.

Table 11 Hypoplastic models that consider soil behavior in the range of small strains

According to Niemunis and Herle [151], the strain in a granular material is composed of the granular interface strain, which should be understood as a macroscopic measure of the microdeformations of the interface between particles, and the strain caused by the reordering of the grains that constitute the solid skeleton. The intergranular strain tensor ${\varvec{\delta}}$, which aims to characterize the strain of the granular interface in the range of small strains, is defined and partially solves the effect of excessive stress or strain accumulation during cycles. Other remarkable aspect is that this model allows considering different degradation curves based on the rotation of the strain path which provides versatility to the model and adaptability to experimental results. However, it requires parameters that are unusual in the engineering practice. Soil model parameters for different sands can be found in Mohammadi-Haji and Ardakani [320]. Mašín [321] proposed some modifications in this model to solve the effect of $\eta = q/p^{\prime}$ on $G_{0}$ and the effect that the axis $p^{\prime} = 0$ has on the degradation curve when it is crossed by a stress path. Wong and Mašín [322] introduced the behavior of unsaturated soil to the Niemunis and Herle model, and recent applications can be found in Mohyla et al. [323].

Hypoplastic models have historically been barely used in professional practice due to their formulation and parameters away from the elastoplastic “standard”. However, considerable efforts are being made to incorporate these models into commercial software. In the case of the Niemunis and Herle model, it is considered especially useful, beyond its ability to reproduce certain aspects of soil behavior, the mathematical definition of the concept of intergranular strain by means of the state variable ${\varvec{\delta}}$ that takes the role of internal strain in the sense given by Gudehus [107]. The mathematical structure of ${\varvec{\delta}}$ allows extending its use to elastoplastic models [324], taking advantage of its great potential, as is the case of the EPHYSS model [156].

(C.2) Hypoplastic hybrid models

Some recent advanced hypoplastic models combine different concepts from previous theoretical frameworks. This section briefly shows the specific case of the combination between hypoplasticity and paraelasticity, proposed by Niemunis and Prada-Sarmiento [176].

Table 12 analyzes small strain stiffness formulation, hysteretic behavior treatment and general aspects of Niemunis and Prada-Sarmiento hypoplastic hybrid model that considers soil behavior in the range of small strains.

Table 12 Hybrid models that consider soil behavior in the range of small strains

The Niemunis and Prada-Sarmiento model improves the hypoplastic model with integranular strain, providing it with greater robustness to reproduce soil hysteretic behavior, however, as an hybrid model, it not only inherits the strengths of the base models, but also the weaknesses, such as the unusual parameters and the lack of familiarity with these theoretical frameworks in the professional practice.

5 Conclusions

Soil behavior in the range of small strains should be considered in the analysis of geotechnical problems, especially when it is necessary to build new structures in dense urban areas and to protect nearby existing structures, or when sensitive constructions are built or affected.

Several circumstances during the 70 s of the twentieth century motivated the development of new theoretical frameworks and constitutive models that tried to explain the soil behavior in the range of small strains, characterized by being nonlinear reversible, hysteretic and dependent on recent history.

The theoretical framework of Jardine [6], based on the theories of KYS and plasticity, allows describing the behavior of soil stiffness according to the range of stress and strain to which it is subjected, giving place to four differentiated zones (Zones I to IV). This theoretical framework has been very useful to identify the strategies to reproduce soil behavior in the range of small strains used in the different constitutive models that have been analyzed.

Furthermore, in order to classify these constitutive models, the concept of tensorial zone [136, 137] has been used, grouping: (1) within the incrementally linear models with a single tensorial zone, the linear and the nonlinear elastic models (Cauchy elastic models, pseudoelastic models, hyperelastic models and hypoelastic models stricto sensu); (2) within the incrementally multilinear models with several tensorial zones, the hysteretic models (paraelastic and quasi-hypoelastic models) and the advanced models (classic elastoplastic models, multisurface models, brick models, bounding surface plasticity models, bubble models and multilaminated models); and (3) within the incrementally nonlinear models with infinite tensorial zones, the hypoplastic and the hypoplastic hybrid models.

In addition to that, there have been established four elements considered fundamental for the characterization of soil hysteretic behavior and which have led to a specific model classification criterion. These elements are: (1) reversal criterion, which can be extrinsic or intrinsic; (2) memory rules, which allow storing information of one, several or all active reversal points; (3) the effect of reversals on the variables that control the degradation, which can be fully or partially reinitialized after a reversal; and (4) the effect of reversals on maximum soil stiffness, where the stiffness recovery can occur continuously or discontinuously with the rotation angle of the recent stress/strain path, being total or partial.

Using the previous classification criteria, a total of 54 constitutive models that consider soil behavior in the range of small strains have been analyzed and classified. The study of these models has focused on describing and explaining the constitutive relations that allow the reproduction of nonlinear reversible, hysteretic and dependent on recent history behavior of the soil, as well as their applications, advantages and disadvantages. It should be noted that the fact of not having the numerical codes of most of these models complicates and limits their study, idea shared by Gudehus [107].

The most relevant aspects of the formulation of those models have been presented. All of them are capable of reproducing, to a greater or lesser extent, the behavior of the soil in the range of small strains. Some features that should be highlighted follow:

• i. The robust, clear and intuitive formulation of paraelastic models, based on the Hueckel and Nova model [22], to reproduce soil hysteretic behavior, in addition to its versatility to be combined with other theoretical frameworks. So far, interesting models have been developed using concepts from paraelastic theory combined with elastoplastic, bounding plasticity, multilaminate or hypoplastic models [140, 153, 154, 156, 174,175,176,177].

• ii. The ability of quasi-hypoelastic hysteretic models [67, 156] to integrate multiple aspects of the soil in the range of small strains, in addition to their flexibility to be combined with plastic models, give them a great potential to be used in practical applications. However, these models also present some disadvantages [66, 182, 187].

• iii. The balance between complexity and usability of elastoplastic models that gives them the greatest potential to be used in professional practice. Among all those analyzed in this paper, the Plaxis HS-SS model (based on the HS-S model [67]) and the EPHYSS model [156] stand out. The latter improves the HS-SS model and resolves some inconsistencies whose effects can have considerable influence on the numerical simulations of boundary value problems, as they are cumulative [156, 175, 243,244,245].

• iv. The potential use of brick models, based on the Simpson model [31], in the development of future constitutive models. This is due to their ability to be easily combined with classic or advanced models (such as the HS-Brick Model [155], which improves the HS-SS model), in addition to its clear theoretical framework that allows to easily understand part of the formulation of other models, as happens with the history tensors of the advanced elastoplastic models HS-SS and EPHYSS.

• v. The ability of multilaminate models, such as the Schädlich and Schweiger [154] model, to reproduce multiple soil characteristics, including its complex behavior in the range of small strains, using parameters known in professional practice and a clear and no contrived formulation. This place them in an advantageous position compared to other incrementally multilinear models, and although their use has been limited in practical applications, some commercial software, such as ZSoil, already incorporate basic multilaminate models in their libraries.

• vi. The advantages of hypoplastic models with intergranular strain, based on the Niemunis and Herle model [151], to define the soil behavior in the range of small strains through the state variable ${\varvec{\delta}}$ (intergranular strain), whose mathematical structure allows its use to be extended to elastoplastic models [324], such as the EPHYSS model [156]. However, hypoplastic models have historically been barely used in professional practice due to their formulation and parameters away from the elastoplastic “standard”.

In addition to these considerations, and regarding the behavior of the soil in the range of small strains, it is considered that the multisurface, bounding plasticity, bubbles or hypoplastic hybrid models that have been analyzed in this paper do not present great potential for their use in practical applications, due to: (1) their complex formulations; (2) the requirement of numerous unusual parameters in professional practice; (3) the lack of description of the hysteretic and dependent on recent history soil behavior in some cases; or (4) their limited use in solving boundary value problems. Future improvements of these models, especially in the case of multisurface models [252], might allow them to be considered in practical applications. It should be mentioned, however, that these models can correctly reproduce other soil characteristics, such as irreversible strains, plastic anisotropy, plastic hardening, contractive/dilatant behavior, critical state in clays and the effect of the soil fabric.

Finally, the incorporation of formulations that can reproduce soil behavior in the range of small strains within well-known models used in professional practice, would allow professional engineers to familiarize themselves with the characteristics and complexity of non-linear, hysteretic and dependent on recent history soil behavior in the range of small strains. Once this first goal has been achieved, introducing more complex models into commercial software could be less traumatic.

6 List of symbols

a :

Parameter whose value is $a = 0.385$ according to Dos Santos and Correia [231]

$a^{\prime }$ :

Soil parameter in the model of Hansen [197]

$a^{\prime \prime }$ :

æ Drnevich [2]

$\tilde{a}$ :

Soil parameter in the model of Kondner and Zelasco [194]

$\hat{a}^{\prime }$ :

Soil parameter in the model of Darendeli [229]

$a^{*}$ :

Soil parameter in the NAHOS model [144]

$\hat{a}^{*}$ :

Soil parameter in the SC1SS model [236]

$a_{LER}$ :

$= n^{\prime } J_{LER}^{u}$

$a_{SSR}$ :

$= n^{\prime } J_{SSR}^{u}$

$a_{1}$ :

Soil parameter in the model of Papadimitriou et al. [140]

$\overline{a}_{1}$ :

$= 1 + x_{v} - x_{e}$

$\overline{a}_{2}$ :

$= 1 + x_{D} - x_{e}$

$\tilde{a}$ :

$= 1/E_{i}^{\prime }$

A :

Soil parameter in the expression of Viggiani [290] used for the calculation of $G_{t}$ in the 3-SKH model [123]

$\overline{A}$ :

Soil parameter in the model of Jardine et al. [207]

$\hat{A}$ :

Soil parameter in the expressions that relate $G_{0}$ with e, OCR and $p^{\prime}$

$A_{i}$ :

Functions of soil parameters $C_{1} \left( {X = 0} \right)$, $C_{1} \left( {X \to \infty } \right), C_{2} \left( {X = 0} \right)$, $C_{2} \left( {X \to \infty } \right)$ in the model of Tatsuoka and Shibuya [115]

$A_{G}$ :

Soil parameter in the SDMCC model [148]

$A_{1}$ :

$= \left( {1/\overline{a}_{1} } \right) \left( {\left( {x_{v} - x_{e} } \right)R^{\prime } \left( {\ln \overline{a}_{1} } \right)^{{R^{\prime } - 1}} } \right) + \left( {\ln \overline{a}_{1} } \right)^{{R^{\prime } }}$

$A_{2}$ :

$= \left( {1/\overline{a}_{2} } \right) \left( {\left( {x_{D} - x_{e} } \right)R^{\prime}\left( {{\text{ln}}\overline{a}_{2} } \right)^{{R^{\prime} - 1}} } \right) + \left( {{\text{ln}}\overline{a}_{2} } \right)^{{R^{\prime}}}$

b :

$= G_{SSR} /G_{LER} = K_{SSR}^{{\prime}} /K_{LER}^{{\prime}}$

$b^{\prime }$ :

Soil parameter in the model of Hansen [197]

$b^{\prime \prime }$ :

Soil parameter in the model of Hardin and Drnevich [2]

$\hat{b}$ :

$= \frac{1}{{\hat{R}p_{c}^{\prime } /2}}\left( {\left( {p^{\prime } - p_{\alpha }^{\prime } } \right)\left( {\frac{{ {p^{\prime } - p_{\alpha }^{\prime } } }}{{\hat{R}}} - \left( {p^{\prime } - \frac{{p_{c}^{\prime } }}{2}} \right)} \right) + {\frac{{J - J_{\alpha } }}{{M_{J}^{2} }}}\left( {\frac{{ {J - J_{\alpha } } }}{{\hat{R}}} - J} \right)} \right)$

$\tilde{b}$ :

$= 1/q_{ult}$ soil parameter in the model of Kondner and Zelasco [198]

$\hat{b}_{max }$ :

$= \left( {1 - \hat{R}} \right)p_{c}^{{\prime}}$

$\hat{b}_{1}$ :

$= {\frac{1}{{\hat{T}p_{c}^{\prime } }}} \left( { {\frac{{ {p^{\prime } - p_{b}^{\prime } } }}{{\hat{S}}}} \left( {\frac{{ {p^{\prime } - p_{b}^{\prime } } }}{{\hat{T}\hat{S}}} - \left( {\frac{{ {p^{\prime } - p_{b}^{\prime } } }}{{\hat{S}}} + p_{a}^{\prime } - p_{c}^{\prime } } \right)} \right) + {\frac{{ {q - q_{b} } }}{{\hat{S}M^{2} }}} \left( { {\frac{{ {q - q_{b} } }}{{\hat{T}\hat{S}}}} - \left( {\frac{{ {q - q_{b} } }}{{\hat{S}}} + q_{a} } \right)} \right)} \right)$

$\hat{b}_{2}$ :

$= \frac{1}{{\hat{T}\hat{S}p_{c}^{\prime } }}\left( {\left( {p^{\prime } - p_{b}^{\prime } } \right)\left( {\frac{{ {p^{\prime } - p_{b}^{\prime } }}}{{\hat{S}}} - \left( {p^{\prime } - p_{a}^{\prime } } \right)} \right) + \left( {\frac{{ {q - q_{b} } }}{{M^{2} }}} \right)\left( {\frac{{ {q - q_{b} } }}{{\hat{S}}} - \left( {q - q_{a} } \right)} \right)} \right)$

$\hat{b}_{1max }$ :

$2\left( {1 - \hat{T}} \right)p_{c}^{\prime }$

$\hat{b}_{2max }$ :

$2\hat{T}\left( {1 - \hat{S}} \right)p_{c}^{\prime }$

${\check{b}}_{i}$ :

Soil parameters in the SDMCC model [148] that control stiffness strain dependency, for $i = 2,4$

$\hat{b}^{*}$ :

Soil parameter in the SC1SS model [236]

B :

Soil parameter in the expression of Hardin [287] for the calculation of $G_{0}$ used in the model of Papadimitriou et al. [140]

$\overline{B}$ :

Soil parameter in the model of Jardine et al. [203]

$\hat{B}$ :

Soil parameter in the expressions of Hardin and Richart [82] that relates $G_{0}$ with e

$B_{i}$ :

Functions of soil parameters $C_{1} \left( {X = 0} \right),C_{1} \left( {X \to \infty } \right), C_{2} \left( {X = 0} \right),C_{2} \left( {X \to \infty } \right)$ in the model of Tatsuoka and Shibuya [115]

$B_{G}$ :

Soil parameter in the SDMCC model [148]

$c^{\prime }$ :

Effective cohesion

$c_{u}$ :

Undrained shear stregth

C :

Soil parameter in the MIT-E3 model [142]

$C^{*}$ :

Soil parameter in the NAHOS model [144]

$\overline{C}$ :

Soil parameter in the model of Jardine et al. [203]

$C_{b}$ :

Soil parameter in the MIT-S1 model [149] related to soil compressibility after a reversal

$C_{i}$ :

$i = 1 \ldots 6$, soil parameters in the model of Jardine et al. [8]

$C_{i}^{*}$ :

Functions that depend on ${\varvec{\sigma}}^{\prime }$ invariants in the expression of ${\varvec{E^{\prime}}}_{t}$

$C_{i} \left( X \right)$ :

$i = 1,2$ soil parameters in the model of Tatsuoka and Shibuya [115]

$C_{K}$ :

Soil parameter in the SDMCC model [148]

$C_{\alpha }$ :

Secondary consolidation coefficient

${\varvec{C}}\left( {\chi^{hist,L} } \right)$ :

$= {\varvec{C}}_{0} \cdot\left( {\varvec{\mathit 1} + \chi^{hist,L} {{\varvec{\Omega}}}} \right)$

${\varvec{C}}_{i}$ :

Constitutive elastic flexibility tensor in the i-th plane that relates $\dot{\varvec{\sigma }}_{i}^{\prime }$ and $\dot{\varepsilon }_{i}^{e}$ in multilaminated models

${\varvec{C}}_{0}$ :

Maximum flexibility tensor in the model of Hueckel and Nova [22]

$d_{i}$ :

$i = 1,2$ soil parameters in the model of Tatsuoka and Shibuya [115]

$d_{L}$ :

Soil parameter in the model of Niemunis and Prada-Sarmiento [176]

$d_{0}$ :

Soil parameter in the model of Niemunis and Prada-Sarmiento [176]

$d^{b}$ :

$= \check{{s}} \left( {M^{b} - \eta } \right)$

$d_{ref}^{b}$ :

$= M_{c}^{b} + M_{e}^{b} - 2\check{m}$

D :

Soil parameter that controls nonlinearity during an unloading in the MIT-S1 model [149]

$D_{K}$ :

Soil parameter in the SDMCC model [148]

$D_{R}$ :

$= \left( {\text e_{max } - \text e} \right)/\left( {\text e_{max } - \text e_{min } } \right)$ is the relative density of the soil

d :

Strain rate tensor ($\dot{\varepsilon } \approx {\varvec{d}}$)

e:

Void ratio

$\text e_{max }$ :

Maximum void ratio

$\text e_{min }$ :

Minimum void ratio

${\text{e}}_{0}$ :

Initial void ratio

$\left( {{\text{e}}_{CS} } \right)_{a}$ :

Void ratio on the critical state line for $p^{\prime } = p_{a}$

e :

$= \varepsilon - \varepsilon_{oct} {\varvec{1}}$

${\varvec{e}}_{rev}$ :

Value of e in the last reversal point in the MIT-S1 model [149]

${\varvec{e}}^{e}$ :

$= \varepsilon^{e} - \varepsilon_{oct}^{e} {\varvec{1}}$

${\varvec{e}}^{p}$ :

$= \varepsilon^{p} - \varepsilon_{oct}^{p} {\varvec{1}}$

${\varvec{e}}^{R}$ :

State variable that stores the total deviatoric strain tensor value at the last reversal point R that conforms the endpoint of the active strain cycle in the HQH and EPHYSS models [156, 175]

${\varvec{e}}^{\Delta R}$ :

$= {\varvec{e}} - {\varvec{e}}^{R}$

${}_{{}}^{AR1} {\varvec{e}}$ :

$= \varepsilon^{pe} -^{R1} \varepsilon^{pe}$

$E_{u}$ :

Undrained elastic modulus

$E_{s,u}^{ap}$ :

Apparent undrained secant elastic modulus

$E_{s}^{^{\prime{ap}}}$ :

Apparent drained secant elastic modulus

$E_{i}^{\prime }$ :

Initial drained modulus (Janbu [81] proposed an expression for $E_{i}^{{\prime}}$)

$E_{max }^{\prime }$ :

Maximum stiffness modulus

$E_{t,ur}^{{\prime}}$ :

Drained tangent stiffness modulus during unloadings and reloadings

$E_{t}^{^{\prime{ap}}}$ :

Drained apparent tangent elastic modulus

E :

Transformed variable $E_{i} = \left( {\varvec{E}} \right)_{i} = {\Pi }_{i} \left( \varepsilon \right)$ in the MIT-E3 model [142]

${\varvec{E}}^{\prime }$ :

Elastic stiffness tensor

${\varvec{E}}_{m}^{\prime }$ :

Eigenvector of the spectral decomposition of ${\varvec{\sigma}}^{\prime }$

${\varvec{E}}_{max }^{\prime }$ :

$= \overline{\lambda }{\varvec{1}} \otimes {\varvec{1}} + 2\overline{\mu }{\mathbb{I}}$

${\varvec{E}}_{rev}$ :

Value of $E_{i} = \left( {\varvec{E}} \right)_{i} = {\Pi }_{i} \left( \varepsilon \right)$ in the last reversal point in the MIT-E3 model [142]

${\varvec{E}}_{max }^{\prime }$ :

Maximum stiffness tensor

${\varvec{E}}_{t}^{{{\prime}}}$ :

Tangent stiffness tensor

${\varvec{E}}_{t}^{{\prime {\rm Z}_{i} }}$ :

Tangent stiffness tensor corresponding to the tensorial zone ${\rm Z}_{i}$

f :

Soil parameter in the model of Fahey and Carter [219]

$f\left( {\text{e}} \right)$ :

Function that represents the dependence of $G_{0}$ on e

$f\left( {\alpha_{q} } \right)$ :

$= \frac{{\left( { - 1 + G_{0} /G_{MCC}^{e} + f_{2} \left( {\alpha_{q} } \right) - \sqrt {\left( {1 - G_{0} /G_{MCC}^{e} - f_{2} \left( {\alpha_{q} } \right) } \right)^{2} + 4f_{2} \left( {\alpha_{q} } \right) } } \right)}}{{2\left( {a/\varepsilon_{qr} } \right)}}$

$f_{2} \left( {\alpha_{q} } \right)$ :

$= \left( {a/\varepsilon_{qr} } \right)\alpha_{q}$

$f^{\prime }$ :

$= 0$ equation that defines the bounding plasticity surface in the model of Al-Tabbaa and Wood [10] and in the 3-SKH model [123]

$\overline{f}$ :

Soil parameter in the model of Niemunis et al. [153, 174]

$\hat{f}$ :

Soil parameter in the model of Lee and Salgado [225]

$\hat{f}^{\prime }$ :

$= 1/2\left( {a^{*} + sign\left( {n_{p} } \right)\left| {n_{p} } \right|^{1/w} } \right)$

$f_{{K_{s}^{\prime ap} }}$ :

Function that considers the hardening of $K_{s}^{\prime ap}$

$f_{{G_{s}^{ap} }}$ :

Function that considers the degradation of $G_{s}^{ap}$

$f_{k}$ :

K-th yield surface

f ₁ :

= 0 equation that defines the bubble within which an elastic soil behavior is considered in the model of Al-Tabbaa and Wood [10] and a dependent behavior on recent history is considered in the 3-SKH model [123]

f ₂ :

$= 0$ equation that defines the bubble within which an elastic soil behavior is considered in the 3-SKH model [123]

$f^{{\left( {m^{\prime\prime}} \right)}}$ :

Yield surfaces in multisurface models

F :

$= F_{0} \left( {p_{0}^{\prime } /p_{a} } \right)^{ - X\prime } \langle \psi_{0} \rangle$

$F_{LER}$ :

Linear Elastic Region of the Puzrin and Burland [152] model

$F_{ss}$ :

Small strain yield surface function of the Seyedan and Solowski [252] model

$F_{SSR}$ :

Small Strain Region of the Puzrin and Burland [152] model

$F_{0}$ :

Soil parameter in the model of Papadimitriou et al. [140]

g :

Soil parameter in the model of Fahey and Carter [219]

$\hat{g}$ :

Soil parameter in the model of Lee and Salgado [225]

$g_{i}$ :

Plastic potential associated to the i-th plane

G :

Shear modulus

$G_{\left( 0 \right)ij}$ :

Maximum drained elastic shear modulus according to the i-th plane and the j-th direction

$G_{m}$ :

$= G_{t,min ,\xi = 1}^{ap} /G_{t,ur}$

$G_{s}$ :

Secant elastic shear modulus

$G_{SSR}$ :

Shear modulus on the SSR

$G_{t}$ :

Tangent elastic shear modulus

$G_{t,ur}$ :

Minimum value of the tangent elastic shear modulus

$G_{0}$ :

Maximum shear modulus

$G_{0}^{ref}$ :

Maximum apparent shear modulus for $p^{\prime} = p_{ref}^{{\prime}}$

$G^{ap}$ :

Apparent shear modulus

$G_{i}^{ap}$ :

Apparent shear modulus associated to the tensorial zone $Z_{i}$

$G_{MCC}^{e}$ :

Elastic shear modulus used in the MCC model

$G_{LER}^{ref}$ :

Value of $G_{LER}$ when $p^{\prime } = p_{ref}^{{\prime}}$

$G_{MCC}^{e}$ :

Constant elastic shear modulus of the MCC model

$G_{s}^{ap}$ :

Secant apparent shear modulus

$G_{s,0}^{ap}$ :

Maximum value of $G_{s}^{ap}$ which depends on $p^{\prime }$

$G_{s,0}^{ap,\alpha ,H,ref}$ :

State variable that stores the maximum value of the secant apparent shear stiffness modulus for the active degradation curve $\alpha$ for $p^{\prime } = p_{ref,2}^{\prime }$ in the HQH and EPHYSS models [156, 175]

$G_{t,min ,\xi = 1}^{ap}$ :

Minimum apparent tangent shear modulus for primary loading ($\xi = 1$)

$G_{t}^{ap}$ :

Tangent apparent shear modulus

$G_{t,ur}^{ref}$ :

Value of $G_{t,ur}$ for $\sigma_{3}^{\prime } = p_{ref}^{\prime }$ in the SSOM and HS-S models [67] and in the HS-SS model implemented in Plaxis, and $p^{\prime } = p_{ref,2}^{\prime }$ in the HQH and EPHYSS models [156, 175]

G :

Tensorial function that relates $\dot{\varvec {\sigma} }^{\prime }$ with $\varepsilon ,\varvec{\sigma}^{\prime } ,\varvec{\chi}$ and $\dot{\varepsilon }$

h :

Soil parameter in the CASM-c model [143]

$h_{b}$ :

$= h_{0}^{\prime } \left| {d^{b} } \right|/\langle d_{ref}^{b} - \left| {d^{b} } \right|\rangle$

$h_{f}$ :

$= \left( {1 + F\langle\smallint \dot{\varepsilon }_{oct}^{p} \left( \% \right)^{2} }\rangle \right)/\left( {1 - F\mathop \smallint \limits_{R - 1}^{R} \langle- \dot{\varepsilon }_{oct}^{p} \left( \% \right)}\rangle \right)$factor that consider the macroscopic effect of soil fabric during deviatoric stress path in the model of Papadimitriou et al. [140]

$h_{i}$ :

Factor that modifies hardening laws in the models HS-S [67], HS-SS and EPHYSS [156, 175]

$h_{0}^{{\prime}}$ :

Soil parameter in the model of Papadimitriou et al. [140]

h :

State variable that stores recent total deviatoric strain history tensor in the HQH and EPHYSS models [156, 175]

$\left( {\hat{\varvec{h}}:\widehat{{\dot{\varvec{e}}}}} \right)^{\varvec{*}}$ :

Cosine of the rotation angle in the recent total deviatoric strain path from which reversals appear in the HQH and EPHYSS models [156, 175]

H _R :

Soil parameter in the CASM-c model [143]

$H_{U}$ :

Soil parameter in the CASM-c model [143]

$H^{{\left( {m\prime \prime } \right)}}$ :

Hardening modulus of the yield surface $f^{{\left( {m^{\prime\prime}} \right)}}$

H :

State variable that stores recent total deviatoric strains history tensors in the SSOM and HS-S models [67] and in the HS-SS model implemented in Plaxis

H′ :

Stiffness tensor in the model of Niemunis et al. [153, 174] and in the model of Niemunis and Prada-Sarmiento [176]

J :

$= \sqrt {1/2} \left\|{\varvec{s}}\right\|$

$\overline{J}$ :

$= J/J_{SSR}$

$J_{max }$ :

Maximum value of J

$J_{s}$ :

Secant coupling modulus

$J_{t}$ :

Tangent coupling modulus

$J_{SSR}$ :

Projection of the deviatoric stress on the SSR

$J_{0}$ :

Initial value of J

$J_{\alpha }$ :

Value of J in the center of the bubble $f_{1}$ in the model of Al-Tabbaa and Wood [10]

$J_{LER}^{u}$ :

Deviatoric stress in the LER boundary obtained from triaxial tests

$J_{SSR}^{u}$ :

Deviatoric stress in the SSR boundary obtained from triaxial tests

$\hat{k}$ :

Soil parameter that relate $G_{0}$ with OCR or $R_{0}$

$k^{*}$ :

Soil parameter in the CASM-c model [143]

$k_{c}^{d}$ :

Soil parameter in the model of Papadimitriou et al. [140]

$k_{e}^{d}$ :

Soil parameter in the model of Papadimitriou et al. [140]

$K^{\prime }$ :

Drained elastic bulk modulus

$K\left( {\gamma ,PI} \right)$ :

$= 0.5\left( {1 + \tanh \left( {\ln \left( {\left( {0.000102 + n\left( {PI} \right)} \right)/\gamma } \right)} \right)^{0.492} } \right)$

$K_{b}$ :

Parameter with the value of $K_{s}^{\prime ap}$ for $\sigma_{3}^{\prime } = p_{a}$ in the expression proposed by Duncan et al. [71]

$K_{s}^{\prime }$ :

Drained secant elastic bulk modulus

$K_{SSR}^{\prime }$ :

Drained bulk modulus on SSR

$K_{t}^{{\prime}}$ :

Drained tangent elastic bulk modulus

$K_{t,ur}^{{\prime}}$ :

Drained linear elastic bulk modulus in unloadings or reloadings

$K_{0}$ :

Coefficient of lateral earth stress

$K_{0}^{\prime }$ :

Maximum drained elastic bulk modulus

$K^{\prime ap}$ :

Drained apparent bulk modulus

$K_{i}^{\prime ap}$ :

Apparent bulk modulus associated to the tensorial zone $Z_{i}$

$K_{LER}^{\prime ref}$ :

Value of $K_{LER}^{\prime }$ when $p^{\prime } = p_{ref}^{\prime }$

$K_{s}^{\prime ap}$ :

Drained secant apparent bulk modulus

$K_{s}^{\prime ap,ref}$ :

Value of $K_{s}^{\prime ap}$ for $p^{\prime } = p_{ref}^{\prime }$

$K_{s}^{\prime ref}$ :

Value of $K_{s}^{\prime }$ for $p^{\prime } = p_{ref,1}^{\prime }$

$K_{s,0}^{\prime ap}$ :

Maximum value of $K_{s}^{\prime ap}$ which depends on $p^{\prime }$

$K_{t}^{\prime ap}$ :

Drained tangent apparent bulk modulus

$\overline{K}_{P}$ :

$= \left( {\left( {4/3} \right)M^{4} \left( {p_{j}^{\prime } - \left( {1/\overline{R}} \right)p_{c}^{\prime } } \right)^{2} + 6\left( {\overline{R} - 1} \right)^{4} q_{j}^{2} } \right)^{ - 1} \left(v/\left( {\lambda - \kappa } \right)\right)\left( {4/\overline{R}} \right)M^{4} p_{c}^{\prime } \left( {p_{j}^{\prime } + \left( {\overline{R} - 2} \right)p_{c}^{\prime } } \right)\left( {p_{j}^{\prime } - \left( {1/\overline{R}} \right)p_{c}^{\prime } } \right)$

l :

Soil parameter in the expression that relates $G_{0}$ with $s^{*}$ [105]

${\varvec{L}}\left( {{\varvec{\sigma}}^{\prime } } \right)$ :

Fourth-order linear tensor in the first generation of hypoplastic models

${\varvec{L}}\left( {{\varvec{\sigma}}^{\prime }, \text e} \right)$ :

Fourth-order linear tensor in an hypoplastic model that introduces void ratio as a state variable [316, 318]

${\varvec{L}}\left( {{\varvec{\sigma}}^{\prime } ,{\varvec{\chi}} } \right)$ :

Fourth-order linear tensor in hypoplastic models

m :

Soil parameter that controls stiffness dependence on stress in many models

$m^{\prime}$ :

Soil parameter in the model of Prévost and Keane [204] that must comply $m^{\prime } \ge 4y_{max } - 1$

$m^{\prime \prime }$ :

Number of surfaces in multisurface models

$m^{*}$ :

Soil parameter in the CASM-c model [143]

$\overline{m}$ :

Soil parameter in the model of Mayne [220]

$\overline{m}^{\prime }$ :

Soil parameter in the model of Shibuya et al. [221]

$\tilde{m}^{\prime }$ :

Soil parameter in the expression of Viggiani [290] used for the calculation of $G_{t}$ in the 3-SKH model [123]

$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{m}$ :

Soil parameter that controls the opening of the yield surface in the model of Papadimitriou et al. [140]

$\tilde{m}\left( {\gamma ,PI} \right)$ :

$= 0.272\left( {1 - \tanh \left( {\ln \left( {0.000556/\gamma } \right)} \right)^{0.4} } \right)e^{{ - 0.0145PI^{1.3} }}$

$m_{ij}$ :

Soil parameter that controls the dependence of $G_{{0\left( {ij} \right)}}$ on $p^{\prime } /p_{ref}^{\prime }$ in the expression of Hardin and Black [89]

$m_{R}$ :

Soil parameter that controls stiffness value before a rotation of the total strain path of 180º in the model of Niemunis and Herle [151]

$m_{T}$ :

Soil parameter that controls stiffness value before a rotation of the total strain path of 90º in the model of Niemunis and Herle [151]

m ₁ :

Soil parameter that controls the dependence of $K_{s}^{{\prime}}$ on $p^{\prime }$ in the HQH and EPHYSS models [156, 175]

m ₂ :

Soil parameter that controls the dependence of $G_{s}^{ap}$ and $G_{t,ur}$ on $p^{\prime }$ in the HQH and EPHYSS models [156, 175]

${\check{m}}_{i}$ :

Soil parameters in the SDMCC model [148] that control stiffness dependency with OCR, for $i = 1 \ldots 4$

M :

Slope of the critical state line in the plane $q - p^{\prime }$

$M_{J}$ :

Slope of the critical state line in the plane $J - p^{\prime }$

$M^{b}$ :

$= \check{s}\left( {M_{c}^{c} \left\langle \check{s} \right\rangle + M_{e}^{c} \left\langle -\check{s} \right\rangle } \right)$

$M_{c}^{b}$ :

$= M_{c}^{c} + k_{c}^{d} \left\langle -\psi \right\rangle$

$M_{c}^{c}$ :

Soil parameter in the model of Papadimitriou et al. [140]

$M_{e}^{b}$ :

$= M_{e}^{c} + k_{e}^{d} \left\langle -\psi \right\rangle$

$M_{e}^{c}$ :

Soil parameter in the model of Papadimitriou et al. [140]

M :

Tangent stiffness tensor in the hypoplastic model with intergranular strain of Niemunis and Herle [151]

n :

Soil parameter that relate $G_{0}$ with $\eta$

n(PI):

$= \left\{ {\begin{array}{*{20}l} 0 \hfill & {{\text{if}}\quad PI = 0} \hfill \\ {3.37\cdot10^{ - 6} PI^{1.404} } \hfill & {{\text{if}}\quad 0 < PI \le 15} \hfill \\ {7.00\cdot10^{ - 7} PI^{1.976} } \hfill & {{\text{if}}\quad 15 < PI \le 70} \hfill \\ {2.70\cdot10^{ - 5} PI^{1.115} } \hfill & {{\text{if}}\quad PI > 70} \hfill \\ \end{array} } \right.$

$n^{\prime }$ :

$= \sqrt {K_{LER}^{{\prime}} /G_{LER} }$

$n^{*}$ :

Soil parameter in the MIT-E3 model [142]

$\hat{n}$ :

Soil parameter in the model of Lehane and Cosgrove [147]

$\overline{n}^{\prime }$ :

Soil parameter in the model of Shibuya et al. [221]

$\tilde{n}^{\prime }$ :

Soil parameter in the expression of Viggiani [290] used for the calculation of $G_{t}$ in the 3-SKH model [123]

$n_{g}$ :

Soil parameter in the model of Lee and Salgado [225]

$n_{i}$ :

Soil parameter that relates $G_{0}$ with $\sigma_{i}^{{\prime}} /p_{ref}^{{\prime}}$ and $p_{ref}^{{\prime}}$

$n_{ij}$ :

Soil parameter that relates $G_{0}$ with $p^{\prime}/p_{ref}^{{\prime}}$, $p_{ref}^{{\prime}}$ and $\overline{\beta }_{ij}$

$n_{p}$ :

Factor of NAHOS model [144] which varies from $n_{p} = 1$ $\left(q/p^{\prime } = 0\right)$ on the wet side, $n_{p} = 0$ $\left(q/p^{\prime } = M\right)$ and $n_{p} = 0$ $\left(q/p^{\prime } = 0\right)$ on the dry side

${\check{n}}_{i}$ :

Soil parameters in the SDMCC model [148] that control stress stiffness dependency, for $i = 1 \ldots 4$

$N_{b}$ :

Number of Bricks in the HS-Brick Model [155]

$N_{G,1}$ :

Factor related to the secondary consolidation coefficient ${ }C_{\alpha }$ $(N_{G,1} = \sqrt {C_{\alpha } }$ according to Lo Presti et al. [325])

${\varvec{N}}\left( {{\varvec{\sigma}}^{\prime } } \right)$ :

Second-order tensor in the first generation of hypoplastic models

${\varvec{N}}\left( {{\varvec{\sigma}}^{\prime } ,{\text{e}}} \right)$ :

Second-order tensor in an hypoplastic model that introduces void ratio as a state variable [316, 318]

${}_{{}}^{R1} {\varvec{N}}$ :

Normal exterior to the loading circle from the last reversal point $R1$

OCR :

$= \sigma_{v,max }^{\prime } /\sigma_{v}^{\prime }$

$p^{\prime }$ :

$= \sigma_{oct}^{\prime } = 1/3\sigma_{ii}^{\prime }$

$\overline{p}^{\prime }$ :

$= p^{\prime } /p_{SSR}^{\prime }$

$p_{a}$ :

Atmospheric pressure

$p_{w}$ :

Water pressure

$p_{a}^{\prime }$ :

Value of $p^{\prime }$ in the center of the $f_{1}$ of the 3-SKH model [123]

$p_{b}^{{\prime}}$ :

Value of $p^{\prime }$ in the center of the bubble $f_{2}$ of the 3-SKH model [123]

$p_{c}^{\prime }$ :

Size of the major axis of the bounding plasticity surface (consolidation stress) in the NAHOS model [144] and bubble models of Al-Tabbaa and Wood [10] and Stallebrass and Taylor [123]

$p_{j}^{\prime }$ :

Mean stress in the image point on the bounding plasticity surface in the models CASM-c [143] and NAHOS [144]

$p_{ref}^{\prime }$ :

Reference confinement stress

$p_{ref,1}^{{\prime}}$ :

Reference mean stress in the expression of $K_{s}^{{\prime}}$ in the HQH and EPHYSS models [156, 175]

$p_{ref,2}^{\prime }$ :

Reference mean stress in the expressions of $G_{s}^{ap}$ and $G_{t,ur}$ in the HQH and EPHYSS models [156, 175]

$p_{rev}^{\prime }$ :

Transformed variable $p^{\prime } = {\Pi }_{0,p} \left( {{\varvec{\sigma}}^{\prime } } \right)$ on the last reversal point in the models MIT-E3 [142] and MIT-S1 [149]

$p_{SSR}^{\prime }$ :

Projection of the mean stress on the SSR

$p_{\alpha }^{\prime }$ :

Values of $p^{\prime }$ in the center of the bubble $f_{1}$ in the model of Al-Tabbaa and Wood [10]

$p_{0}^{\prime } { }$ :

Mean stress that fulfills $G_{0} \left( {p^{\prime } = p_{0}^{\prime } } \right) = G_{0}^{ref}$

$P^{{\prime \prime \left( {m\prime \prime } \right)}}$ :

Projection of ${\varvec{P}}^{{\left( {m\prime \prime } \right)}} = \partial g^{{\left( {m\prime \prime } \right)}} /\partial {\varvec{\sigma}}$ on the hydrostatic axis

${\varvec{P}}^{{\prime \left( {m\prime \prime } \right)}}$ :

Projection of ${\varvec{P}}^{{\left( {m\prime \prime } \right)}} = \partial g^{{\left( {m\prime \prime } \right)}} /\partial {\varvec{\sigma}}$ on the deviatoric plane

P I :

Plasticity index

q :

$= \sigma_{1}^{{\prime}} - \sigma_{3}^{{\prime}}$

$q_{a}$ :

Value of q in the center of the bubble $f_{1}$ of the 3-SKH model [123]

$q_{b}$ :

Value of q in the center of the bubble $f_{2}$ of the 3-SKH model [123]

$q_{f}$ :

Deviatoric soil strength (it can be estimated with the Mohr–Coulomb criterion)

$q_{j}$ :

Deviatoric stress in the image point on the bounding plasticity surface in the models CASCM-c [143] and NAHOS [144]

$\dot{q}_{max }$ :

Maximum value of the deviatoric stress increment in triaxial compression

$q_{ult}$ :

Maximum deviatoric stress

$Q^{{\prime \prime }{\left( {m^{\prime \prime } } \right)}}$ :

Projection of ${\varvec{Q}}^{{\left( {m^{\prime\prime}} \right)}} = \partial f^{{\left( {m^{\prime\prime}} \right)}} /\partial {\varvec{\sigma}}$ on the hydrostatic axis

$Q_{e}^{R}$ :

$= \sqrt {3/2} \left\| {{\varvec{e}} - {\varvec{e}}^{R} } \right\|$

${\varvec{Q}}\left( {{\varvec{\sigma}}^{\prime } ,{\varvec{\chi}} } \right)$ :

Sixth order tensor in hypoplastic models

${\varvec{Q}}^{{\prime }{\left( {m^{\prime \prime } } \right)}}$ :

Projection of ${\varvec{Q}}^{{\left( {m^{\prime \prime } } \right)}} = \partial f^{{\left( {m^{\prime \prime } } \right)}} /\partial {\varvec{\sigma}}$ on the deviatoric plane

$r^{\prime }$ :

Soil parameter in the model of Atkinson [32]

$\overline{r}$ :

Soil parameter in the CASM-c model [143]

$\hat{r}$ :

Soil parameter in the model of Ramberg and Osgood [194]

$\tilde{r}$ :

Soil parameter that controls nonlinearity during an unloading in the MIT-S1 model [149]

$\hat{r}^{\prime }$ :

$= \left\| {\overline{\varvec{\sigma }}^{\prime } - {\varvec{\sigma}}^{\prime } } \right\|$

$\hat{r}_{0}^{{\prime}}$ :

$= \left\| {\overline{\varvec{\sigma }}^{\prime } - {\varvec{\sigma}}_{{\varvec{S}}}^{\prime } } \right\|$

$R^{\prime }$ :

$= \left( {\left( {1 - x_{e} } \right)/\left( {x_{u} - x_{e} } \right) - b} \right)\left( {\left( {1 + x_{u} - x_{e} } \right)ln\left( {1 + x_{u} - x_{e} } \right)/\left( {x_{u} - 1} \right)} \right)$

$\overline{R}$ :

Soil parameter in the NAHOS model [144]

$\hat{R}$ :

Ratio between the sizes of the bubble $f_{1}$ and the bounding plasticity surface $f^{\prime }$ in the model of Al-Tabbaa and Wood [10]

$\tilde{R}$ :

Parameter with the maximum value of $\left\| {\varvec{\delta}} \right\|$ in the model of Niemunis and Herle [151]

$R_{f}$ :

$= q_{f} /q_{ult}$ (this factor takes values between 0.75 and 1.0)

$R_{o}$ :

$= p_{max }^{\prime } /p^{\prime }$

$s^{\prime }$ :

$= \left( {\sigma_{1}^{\prime } + \sigma_{2}^{\prime } } \right)/2$

$\hat{s}$ :

Soil parameter in the model of Matasovic and Vucetic [210]

$\check{{s}}$ :

Soil parameter in the model of Papadimitriou et al. [140] which adopts values $\check{{s}} = + 1$ if $\eta - \check{{\alpha}} \ge 0$ and $\check{{s}} = - 1$ if $\eta - \check{{\alpha}} < 0$

$s^{*}$ :

Parameter that represents the soil structure

$s_{0}^{\prime }$ :

Initial value of $s^{\prime }$

$s_{f}^{*}$ :

Reference value of $s^{*}$ for reconstituted soil

${s}^{b}$ :

Soil parameter of the HS-Brick model [155] that represents the string length of b-th brick

s :

$= {\varvec{\sigma}}^{\prime } - \sigma_{oct}^{\prime } \varvec{1}$

${\varvec{s}}^{\prime }$ :

Transformed variable $s_{i} = \left( {\varvec{s}} \right)_{i} = {\Pi }_{i} \left( {{\varvec{\sigma}}^{\prime } } \right)$

${\varvec{s}}_{rev}^{\prime }$ :

Value of ${\varvec{s}}^{\prime }$ in the last reversal point in MIT-E3 model [142] and value of ${\varvec{s}}$ in the last reversal point in MIT-S1 model [149]

${\varvec{s}}^{R}$ :

Deviatoric stress tensor in the reversal point R

$S^{\prime }$ :

Surface of V

$\hat{S}$ :

Ratio between the sizes of the bubbles $f_{2}$ and $f_{1}$ in the 3-SKH model [123]

$S_{ij}$ :

Dimensionless soil parameters in the expressions that relate $G_{{0\left( {ij} \right)}}$ with ${\text{e}}$, $OCR$ and $\sigma_{i}^{{\prime}}$

t:

Time

$t^{\prime }$ :

$= \left( {\sigma_{1}^{\prime } + \sigma_{2}^{\prime } } \right)/2$

$t_{p}$ :

Time required to finalize primary consolidation

$t_{0}$ :

Time in which a reversal appears

$\hat{T}$ :

Ratio between the size of the bubble $f_{1}$ and the bounding plasticity surface $f^{\prime }$ in the 3-SKH model [123]

${\varvec{T}}_{i}$ :

Transformation matrix that relates the plane direction with the global reference system in multilaminated models

$TOL_{{\varepsilon_{abs}^{e} }}$ :

Absolute error tolerance $\varepsilon_{abs}^{{e,\left( {n + 1} \right)}}$ considered for the convergence of $\Delta \varepsilon_{{\left[ {i + 1} \right]}}^{{e,\left( {n + 1} \right)}}$

$TOL_{{\varepsilon_{rel}^{e} }}$ :

Relative error tolerance $\varepsilon_{rel}^{{e,\left( {n + 1} \right)}}$ considered for the convergence of $\Delta \varepsilon_{{\left[ {i + 1} \right]}}^{{e,\left( {n + 1} \right)}}$

$u^{\prime }$ :

$= 0.50\varepsilon_{q,SSR}^{u} J_{SSR}^{u}$ is a measure of the strain incremental energy

$v_{p}$ :

Compression waves speed

$v_{s}$ :

Shear waves speed

V :

Representative volume

w :

Soil parameter in the NAHOS model [144]

$W_{el}$ :

Elastic energy

$W_{macro}$ :

Global power in a sphere of volume V

$W_{micro}$ :

Local power in the considered planes

x :

Soil parameter in the expressions that relate $G_{0}$ with e

$x_{D}$ :

$= \left| {\varepsilon_{q} } \right|G_{LER} /J_{SSR}$

$x_{e}$ :

$= a_{LER} /a_{SSR}$

$x_{u}$ :

$= 2K_{LER}^{\prime } u^{\prime } /a_{SSR}^{2}$

$x_{v}$ :

$= \left| {\varepsilon_{v} } \right|K_{LER}^{\prime } /p_{SSR}^{\prime }$

${\varvec{x}}$ :

$= \varphi \left( {{\varvec{X}},t} \right)$ position of point ${\varvec{X}} \in {\Omega }$ in the current configuration

$X$ :

$= \gamma^{p} /\gamma_{ref}$

$X^{\prime}$ :

Soil parameter in the model of Papadimitriou et al. [140]

X:

${\varvec{X}} \in {\Omega }$ point of the initial configuration

$y_{max }$ :

$= \tau_{max } /G_{0} \gamma_{max }$

$y_{1}$ :

$= \left( {y_{max } - 1/2 + \sqrt {1/4 - y_{max } /\left( {m^{\prime } + 1} \right)} } \right)/\left( {m^{\prime } \left( {m^{\prime } + 1} \right) - \gamma_{max } } \right)$

Y :

$= \left( {\tau /p^{\prime } } \right)/\left( {\tau /p^{\prime } } \right)_{max }$

$\alpha$ :

Soil parameter in the model of Ramberg and Osgood [190]

$\overline{\alpha }$ :

Soil parameter in the model of Jardine et al. [203]

$\hat{\alpha }$ :

$= \left( {x_{u} - 1} \right)/\left( {\left( {x_{u} - x_{e} } \right)\left( {\ln \left( {1 + x_{u} - x_{e} } \right)} \right)^{R\prime } } \right)$

$\check{{\alpha}}$ :

State variable in the model of Papadimitriou et al. [140] that controls kinematic hardening

$\tilde{\alpha }$ :

Angular coordinate in multilaminated models

$\hat{\alpha }^{*}$ :

$= arccos\left( {\hat{\varvec{h}}:\widehat{{\dot{\varvec{e}}}}} \right)^{\varvec{*}}$ is the rotation angle in the recent total deviatoric strain path from which reversals appear in the HQH and EPHYSS models [156, 175]

$\overline{\alpha }^{{\prime}}$ :

Soil parameter in the model of Bolton and Whittle [222]

$\alpha_{q}$ :

Internal variable of the Seyedan and Solowski [252] model that replaces $\varepsilon_{q}^{p}$ in the calculation of hardening law to include errors caused by constant $G_{MCC}^{e}$

$\alpha_{\sigma }$ :

Rotation angle of principal stresses

$\beta$ :

Soil parameter in the model of Simpson [31]

$\beta^{{^{\prime \prime } }}$ :

Soil parameter in the model of Matasovic and Vucetic [210]

$\overline{\beta }$ :

$= {1 + \eta /3 - 2\eta^{2} /9}$

$\hat{\beta }$ :

Soil parameter in the model of Puzrin and Burland [152]

$\tilde{\beta }$ :

Angular coordinate in multilaminated models

$\overline{\beta }^{\prime }$ :

Soil parameter in the model of Bolton and Whittle [222]

$\beta_{mod}$ :

$= 1 + \beta \left( {\varepsilon_{v} - \varepsilon_{v,0} - \lambda^{*} \ln \left( {s^{\prime } /s_{0}^{\prime } } \right)} \right)$

$\beta_{R}$ :

Soil parameter in the model of Niemunis and Prada-Sarmiento [176]

$\beta_{R}^{\prime }$ :

Soil parameter in the model of Niemunis and Herle [151]

$\overline{\beta }_{ii}$ :

$= \left( {1 - \eta /3} \right)^{2}$

$\overline{\beta }_{ij}$ :

$= \overline{\beta }_{ji} = {1 + \eta /3 - 2\eta^{2} /9}$

$\gamma$ :

Total shear strain

$\gamma^{*}$ :

$= p^{\prime } /p_{j}^{\prime }$

$\overline{\gamma }$ :

Soil parameter in the model of Jardine et al. [203]

$\hat{\gamma }$ :

Soil parameter in the model of Puzrin and Burland [152]

$\gamma_{c}$ :

$= \xi \gamma_{0,7} /a\left( {\sqrt {G_{0}^{ref} /G_{t,ur}^{ref} } - 1} \right)$

$\gamma_{HIST}$ :

History variable that controls the degradation of $G_{s}^{ap}$ in the SSOM and HS-S models [67] and in the HS-SS model implemented in Plaxis

$\gamma_{max }$ :

Maximum or reference shear strain

$\gamma_{oct}$ :

$= \sqrt {4/3} \left\| {\varvec{e}} \right\|$

$\gamma_{r}$ :

Shear strain that complies $\tau_{f} = G_{0} \gamma_{r}$

$\gamma_{ref}$ :

$= \left( {\tau /p^{\prime } } \right)_{max } /\left( {G_{0} /p_{0}^{\prime } } \right)$

$\gamma_{s}$ :

Total shear strain in the ${\varvec{s}}$ direction of the considered plane

$\gamma_{s,centre}$ :

Value of $\gamma_{s}$ in the last reversal point

$\gamma_{t}$ :

Total shear strain in the t direction of the considered plane

$\gamma_{t,centre}$ :

Value of $\gamma_{t}$ in the last reversal point

$\gamma_{0.7}$ :

Shear strain value in the model of Dos Santos and Correia [231] for which $G_{s}^{ap} \left( {\gamma_{0.7} } \right) = 0.722G_{0}$

$\gamma_{1}$ :

Threshold shear strain in the model of Papadimitriou et al. [140] from which $G_{t} = G_{0} /\left( {1 + 2\left( {1/a_{1} - 1} \right)} \right)$ (minimum value of $G_{t}$) is considered

$\gamma_{R}$ :

Shear strain at the last reversal point in the model of Pyke [158]

$\hat{\gamma }_{r}$ :

Shear strain in the model of Darendeli [229] which complies $G_{s}^{ap} \left( {\hat{\gamma }_{r} } \right) = 0.50G_{0}$

${\upgamma }^{b}$ :

Shear strain invariant of actual relative strain distance between the man (following Simpson’s analogy) and b-th brick in the HS-Brick model [155]

$\gamma^{p}$ :

Plastic shear strain

$\gamma_{oct}^{e}$ :

$= \sqrt {4/3} \left\| {{\varvec{e}}^{e} } \right\|$

$\gamma_{oct}^{H}$ :

$= \sqrt {4/3} \left\| {\varvec{h}} \right\|$ is a history variable that controls the degradation of $G_{s}^{ap}$ in the HQH and EPHYSS models [156, 175]

$\gamma_{oct}^{R}$ :

$= \sqrt {4/3} \left\| {{\varvec{e}}^{R} } \right\|$

$\gamma_{ur}^{\alpha }$ :

$= \xi \gamma_{0,7} /a\left( {\sqrt {G_{s,0}^{ap,\alpha ,H,ref} /G_{t,ur}^{ref} } - 1} \right)$

$\gamma_{oct}^{\Delta R}$ :

$= \gamma_{oct} - \gamma_{oct}^{R}$

$\overline{\delta }$ :

Soil parameter in the model of Jardine et al. [8]

${\varvec{\delta}}$ :

Intergranular strain tensor in the model of Niemunis and Herle [151]

$\varepsilon$ :

Total strain in 1D

$\varepsilon_{deg}$ :

$= \sqrt {\left( {\varepsilon_{n,dev} - \varepsilon_{n,dev,centre} } \right)^{2} + \left( {\gamma_{s} - \gamma_{s,centre} } \right)^{2} + \left( {\gamma_{t} - \gamma_{t,centre} } \right)^{2} }$

$\varepsilon_{f}$ :

Axial strain at failure

$\varepsilon_{i}$ :

I-th principal strain, $i = 1,2,3$

$\varepsilon_{n,dev}$ :

Total deviatoric strain due to the normal stress to the considered plane

$\varepsilon_{n,dev,centre}$ :

Value of $\varepsilon_{n,dev}$ in the last reversal point

$\varepsilon_{oct}$ :

$= 1/3\varepsilon_{ii}$

$\varepsilon_{q}$ :

Deviatoric strain

$\varepsilon_{qr}$ :

Reference deviatoric shear strain equal to deviatoric shear strain in which sear modulus reduces to 70% of its maximum value

$\varepsilon_{r}$ :

Reference strain equivalent to $E^{\prime } /E^{\prime }_{max} = 0.50$

$\varepsilon_{s}$ :

$= 2/3\left( {\varepsilon_{1} - \varepsilon_{3} } \right)$

$\varepsilon_{th}$ :

Total threshold strain that separates linear from nonlinear behavior

$\varepsilon_{v}$ :

$= \varepsilon_{oct} = 1/3\varepsilon_{ii}$

$\varepsilon_{v,0}$ :

Initial value of $\varepsilon_{v}$

$\varepsilon_{v,rev}$ :

Value of $\varepsilon_{v}$ in the last reversal point in the models MIT-E3 [142] and MIT-S1 [149]

$\varepsilon^{R}$ :

Total strain in reversal point R

$\varepsilon_{q}^{Error}$ :

Variable of the model of Seyedan and Solowski [252] that stands for the error caused by a constant elastic shear modulus $G_{MCC}^{e}$ in the MCC model

$\varepsilon_{oct}^{e}$ :

$= 1/3\varepsilon_{ii}^{e}$

$\varepsilon_{oct}^{p}$ :

$= 1/3\varepsilon_{ii}^{p}$

$\varepsilon_{q}^{p}$ :

Plastic shear strain

$\varepsilon_{q,SSR}^{u}$ :

Shear strain value on the SSR surface

ε :

Total strain tensor

$\varepsilon_{i}$ :

Total strain tensor of the i-th plane

$\varepsilon^{e}$ :

Elastic strain tensor

$\varepsilon^{mp}$ :

Microplastic strain tensor in the model of Hueckel and Nova [22]

$\varepsilon^{p}$ :

Plastic strain tensor

$\varepsilon^{pe}$ :

$= \varepsilon^{e} + \varepsilon^{mp}$ is the paraelastic strain tensor in the model of Hueckel and Nova [22]

$\varepsilon^{peL}$ :

Paraelastic strain $\varepsilon^{pe}$ in the reversal point L

$^{AR1} \varepsilon^{pe}$ :

$= \varepsilon^{pe} -^{R1} \varepsilon^{pe}$

$^{R1} \varepsilon$ :

Strain tensor in the last reversal point in the model of Niemunis and Prada-Sarmiento [176]

$^{\Delta L} \varepsilon^{pe}$ :

$= \varepsilon^{pe} - \varepsilon^{peL}$

$\dot{\varepsilon }_{brick - i}^{p}$ :

Plastic strain tensor corresponding to i-th brick in the model of Simpson [31]

$\varepsilon_{i}^{e}$ :

Elastic strain tensor on i-th plane

$\varepsilon_{i}^{p}$ :

Plastic strain tensor on i-th plane

$\eta$ :

$= q/p^{\prime }$

$\overline{\eta }$ :

Soil parameter in the model of Jardine et al. [8]

$\eta_{1}$ :

$= \left( {G_{0}^{ref} /p_{0}^{\prime } } \right)\gamma_{1}$

${\varvec{\eta}}$ :

$= \dot{\varepsilon }/\left\| {\dot{\varepsilon }} \right\|$

${\varvec{\eta}}^{\prime }$ :

$= {\varvec{s}}^{\prime } /p^{\prime }$ in the MIT-E3 [142] model

$\overline{\varvec{\eta }}$ :

$= {\varvec{s}}/p^{\prime }$ in the MIT-S1 model [149]

${\varvec{\eta}}_{rev}^{\prime }$ :

$= {\varvec{s}}_{rev}^{\prime } /p_{rev}^{\prime }$ in the MIT-E3 [142] model

$\overline{\varvec{\eta }}_{rev}$ :

$= {\varvec{s}}_{rev}^{\prime } /p_{rev}^{\prime }$ in the MIT-S1 model [149]

$\kappa$ :

Slope of the swelling line in the plane $\upsilon - \ln \left( {p^{\prime } } \right)$

$\kappa^{*}$ :

Slope of the swelling line in the plane $\ln \left( \text e \right) - \ln \left( {p^{\prime } } \right)$

$\kappa_{0}$ :

Maximum slope of the swelling line in the plane $\upsilon - \ln \left( {p^{\prime } } \right)$

$\lambda$ :

Slope of the primary consolidation line in the plane $\ln \left( \text e \right) - \ln \left( {p^{\prime } } \right)$

$\overline{\lambda }$ :

Lambda coefficient of Lamé

$\lambda^{*}$ :

Slope of the primary consolidation line in the plane $\upsilon - \ln \left( {p^{\prime } } \right)$

$\dot{\lambda }_{i}$ :

Plastic multiplier associated to $g_{i}$

$\lambda_{m}$ :

Eigenvalue of the spectral decomposition of ${\varvec{\sigma}}^{\prime }$

$\lambda_{Si}$ :

I-th eigenvalue of e in the SSOM and HS-S models [67] and in the HS-SS model implemented in Plaxis

$\Lambda$ :

Soil parameter in the EPHYSS model [156]

$\overline{\mu }$ :

Mu coefficient of Lamé

$\mu^{*}$ :

Soil parameter in the NAHOS model [144]

$\nu^{\prime }$ :

Drained Poisson’s ratio

$\nu_{const}^{\prime }$ :

Drained Poisson’s ratio of constant value

$\nu_{u}$ :

Undrained Poisson’s ratio

$\nu_{ij}^{\prime }$ :

Drained Poisson’s ratio according to the i-th plane and the j-th direction

$\nu_{min }^{\prime }$ :

Minimum value of drained Poisson’s ratio

$\nu_{t}^{\prime }$ :

Tangent drained Poisson’s ratio

$\nu_{ur}^{\prime }$ :

Drained Poisson’s ratio in reversible unloading/reloading processes

$\nu_{0}^{{\prime}}$ :

Drained Poisson’s ratio for small strain

$\xi$ :

Scale factor that controls the shape of the degradation curve of $G_{s}^{ap}$. A value of $\xi = 1$ is considered for the calculation of $G_{s}^{ap}$ during primary loading and $\xi = 2$ for the calculation of $G_{s}^{ap}$ during unloading/reloading

$\xi^{\prime }$ :

Variable that measures the mean stress with respect to the last reversal point in the MIT-S1 model [149]

$\xi_{s}^{\prime }$ :

Variable that measures the deviatoric stress with respect to the last reversal point in the MIT-S1 model [149]

$\Pi_{i}$ :

Functions to calculate the transformed variables, $\Pi_{0} \left( \varvec{\phi} \right) = \sum\nolimits_{i = 1}^{3} {\phi_{i} }$, $\Pi_{1} \left( \varvec{\phi} \right) = \left( {2\phi_{2} - \phi_{1} - \phi_{3} } \right)/\sqrt 6$, $\Pi_{2} \left( \varvec{\phi} \right) = \left( {2\phi_{3} - \phi_{1} } \right)/\sqrt 2$, $\Pi_{3} \left( \varvec{\phi} \right) = \sqrt 2 \phi_{12}$, $\Pi_{4} \left( \varvec{\phi} \right) = \sqrt 2 \phi_{23}$, $\Pi_{5} \left( \varvec{\phi} \right) = \sqrt 2 \phi_{31}$ in the MIT-E3 [142] model

$\Pi_{0,p} \left( {\varvec{\phi}_{p} } \right)$ :

$= 1/3\sum\nolimits_{i = 1}^{3} {\left( {\varvec{\phi}_{p} } \right)_{i} }$

$\rho$ :

$= \left\| {\varvec{\delta}} \right\|/\tilde{R}$

$\sigma_{i}^{{\prime}}$ :

Effective i-th principal stress, $i = 1,2,3$

$\sigma_{oct}^{\prime }$ :

$= 1/3\sigma_{ii}^{\prime }$

$\sigma_{v}^{\prime }$ :

Effective vertical stress

$\sigma_{v,max }^{\prime }$ :

Maximum historic effective vertical stress

$\sigma_{0}^{\prime }$ :

$= \sigma_{v}^{\prime } (1 + 2K_{0} )/3$

$\sigma^{\prime R}$ :

Effective stress in the reversal point R

${\varvec{\sigma}}$ :

Total stress tensor

${\varvec{\sigma}}^{\prime }$ :

$= {\varvec{\sigma}} - p_{w} \varvec{1}$ is the effective stress tensor

$\overline{\varvec{\sigma }}^{\prime }$ :

Effective stress tensor of the image point on the bounding plasticity surface in the NAHOS model [144]

${\varvec{\sigma}}_{i}^{\prime }$ :

Effective stress tensor on the i-th plane in the multilaminated models

${\varvec{\sigma}}_{S}^{\prime }$ :

Elastic centre in the NAHOS model [144]

${\varvec{\sigma}}^{\prime L}$ :

Effective stress tensor in the reversal point L

$^{\Delta L} {\varvec{\sigma}}^{\prime }$ :

$= {\varvec{\sigma}}^{\prime } - {\varvec{\sigma}}^{\prime L}$

$\tau$ :

Shear stress

$\tau_{f}$ :

$= G_{0} \gamma_{r}$

$\tau_{max }$ :

Maximum shear stress

$\tau_{oct}$ :

$= \sqrt {1/3} \left\| {\varvec{s}} \right\|$

$\tau_{1}$ :

$= y_{1} G_{0} /\gamma_{max }$

$\upsilon$ :

$= 1 + \text e$

$\vartheta_{i}^{\prime }$ :

$i = 1,2$ soil parameters in the model of Tatsuoka and Shibuya [115]

$\varphi^{\prime }$ :

Maximum effective friction angle

$\varphi \left( {{\varvec{X}},t} \right)$ :

Position of material point ${\varvec{X}} \in {\Omega }$ at time t

$\chi$ :

Parameter of the model of Niemunis and Herle [151]

$\chi^{\prime }$ :

$= \sqrt {9\left( {\varepsilon_{v} - \varepsilon_{v,rev} } \right)^{2} + \left( {{\varvec{E}} - {\varvec{E}}_{rev} } \right):\left( {{\varvec{E}} - {\varvec{E}}_{rev} } \right)}$

$\dot{\chi }^{\prime \prime } \chi^{\prime \prime }$ :

$= \left\{ {\begin{array}{*{20}l} {\left( {\varepsilon_{v} - \varepsilon_{v,rev} } \right)\dot{\varepsilon }_{v} } \hfill & {{\text{for}}\quad \dot{\varepsilon }_{v} \ne 0} \hfill \\ {\left( {{\varvec{e}} - {\varvec{e}}_{rev} } \right):\dot{\varvec{e}}} \hfill & {{\text{for}}\quad \dot{\varepsilon }_{v} = 0} \hfill \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}l} { \ge 0} \hfill & { \to {\text{load}}} \hfill \\ { < 0} \hfill & { \to {\text{unload}}} \hfill \\ \end{array} } \right\}$

$\overline{\chi }$ :

Soil parameter in the model of Niemunis et al. [153, 174]

${\varvec{\chi}}$ :

State variables

${\varvec{\chi}}^{hist}$ :

State variables responsible for describing nonlinear, hysteretic and dependent on recent history behavior of the soil

${\varvec{\chi}}^{el,hist}$ :

State variable ${\varvec{\chi}}^{hist}$ in elastoplastic models

$\psi$ :

$= \text e - \left( {\text e_{CS} } \right)_{a} + \lambda \ln \left( {p^{\prime } /p_{a} } \right)$

$\hat{\psi }$ :

Soil parameter in the model of Al-Tabbaa and Wood [10] and in the 3-SKH model [123]

$\psi_{0}$ :

$= {\text{e}}_{0} - \left( {{\text{e}}_{CS} } \right)_{a} + \lambda ln\left( {p_{0}^{{\prime}} /p_{a} } \right)$

${\Psi }$ :

Hyperelastic energy potential

$\omega$ :

Soil parameter in the models MIT-E3 [142] and MIT-S1 [149]

$\omega_{s}$ :

Soil parameter that controls nonlinearity during the application of shear stress in the MIT-S1 model [149]

${\Omega }$ :

Domain on which the problem to be solved is defined

${{\varvec{\Omega}}}$ :

Second order symmetric tensor of constant coefficients that complies that ${\mathbf{C}}_{0} \cdot{{\varvec{\Omega}}}$ is semi-defined positive [22]

#Z:

Number of tensorial zones

1 :

$\left( \varvec{1} \right)_{ij} = \delta_{ij}$

${\mathbb{I}}$ :

$\left( {\mathbb{I}} \right)_{ijkl} = 1/2\left( {\delta_{ik} \delta_{jl} + \delta_{il} \delta_{jk} } \right)$

$\left\| {\varvec{A}} \right\|$ :

$= \sqrt {A_{ij} A_{ij} }$

$\left| a \right|$ :

$\left| a \right| = a$ if $a > 0$ and $\left| a \right| = - a$ if $a < 0,a \in {\mathbb{R}}$

$sign\left( a \right)$ :

$sign\left( a \right) = + 1$ if $a > 0$ and $sign\left( a \right) = - 1$ if $a < 0,a \in {\mathbb{R}}$

$a^{\left( n \right)}$ :

The superscript (n) indicates that a is evaluated at the end of the calculation step $\left( n \right) \to \left( {n + 1} \right)$

$a_{\left[ i \right]}$ :

The subscript [i] indicates that a is evaluated in the i-th iteration

$\left\langle a \right\rangle$ :

Parenthesis of Macauley, where $\left\langle a \right\rangle = a$ if $a \ge 0$ and $\left\langle a \right\rangle = 0$ if $a < 0$

$A_{ij \ldots k}$ :

$ij \ldots k - th$ component of A

$\dot{\varvec{A}}$ :

Infinitesimal rate of A

$\Delta {\varvec{A}}$ :

Finite rate of A

$\widehat{{\varvec{A}}}$ :

$\widehat{{\varvec{A}}} = {\varvec{A}}/\left\| {\varvec{A}} \right\|$ if $\left\| {\varvec{A}} \right\| \ne 0$ and $\widehat{{\varvec{A}}} = 0$ if $\left\| {\varvec{A}} \right\| = 0$

${\varvec{A}}^{T}$ :

Transposed of A

${\varvec{A}}^{ - 1}$ :

Inverse of A

${\varvec{A}} \otimes {\varvec{B}}$ :

$\left( {{\varvec{A}} \otimes {\varvec{B}}} \right)_{ijkl} = A_{ij} B_{kl}$

${\varvec{A}}\overline{ \otimes }{\varvec{B}}$ :

$\left( {{\varvec{A}}\overline{ \otimes }{\varvec{B}}} \right)_{ijkl} = A_{ik} B_{jl}$

${\varvec{A}}\underline { \otimes } {\varvec{B}}$ :

$\left( {{\varvec{A}}\underline { \otimes } {\varvec{B}}} \right)_{ijkl} = A_{il} B_{jk}$

${\varvec{A}}:{\varvec{B}}$ :

$= A_{ij} B_{ij}$

7 Abbreviations

ARCS:

Axis Rotation and Cubic Spline [202]

CASM-c:

Clay and Sand Model – c [143]

EPHYSS:

Elastoplastic Hysteretic Small Strain model [156, 175]

FC+MCC:

Fahey Carter Modified Cam Clay model [145]

HQH:

Hysteretic Quasi-Hypoelastic model [156, 175]

HS:

Hardening Soil model [233]

HS-Brick:

Hardening Soil Brick Model [155]

HS_MOD:

Modified Hardening Soil model [156, 175] (based on plastic part of HS-S)

HS-S:

Hardening Soil Small model [67]

HS-S[MC]:

Hardening Soil Small model with Mohr-Coulomb limit surface [67]

HS-SS:

Hardening Soil with Small Strain Stiffness model of Plaxis (based on the HS-S and recently implemented in other software)

KYS:

Kinematic Yield Surfaces

LER:

Linear Elastic Region in the model of Puzrin and Burland [152]

MC:

Mohr-Coulomb model

MCC:

Modified Cam Clay model [74]

MIT-E3:

MIT-E3 model [142]

MIT-S1:

MIT-S1 model [149]

NAHOS:

Elastoplastic NAHOS model [144]

OCR:

Overconsolidation Ratio

RU+MCC:

Reloading-Unloading Modified Clam Clay model [234]

S-CLAY1:

Anisotropic Clay model [237]

SDMCC:

Strain Dependent Modified Cam Clay model [148]

SOM:

Swept Out Memory region [108]

SSOM:

Small Strain Overlay Model [67]

SSR:

Small Strain Region in the model of Puzrin and Burland [152]

USC:

Undrained Soft Clay model [326]

3-SKH:

Three Surface Kinematic Hardening model [123]