Abstract
This review/research paper deals with the reduction of nonlinear partial differential equations governing the dynamic behavior of structural mechanical members with emphasis put on theoretical aspects of the applied methods and signal processing. Owing to the rapid development of technology, materials science and in particular micro/nano mechanical systems, there is a need not only to revise approaches to mathematical modeling of structural nonlinear vibrations, but also to choose/propose novel (extended) theoretically based methods and hence, motivating development of numerical algorithms, to get the authentic, reliable, validated and accurate solutions to complex mathematical models derived (nonlinear PDEs). The review introduces the reader to traditional approaches with a broad spectrum of the Fourier-type methods, Galerkin-type methods, Kantorovich–Vlasov methods, variational methods, variational iteration methods, as well as the methods of Vaindiner and Agranovskii–Baglai–Smirnov. While some of them are well known and applied by computational and engineering-oriented community, attention is paid to important (from our point of view) but not widely known and used classical approaches. In addition, the considerations are supported by the most popular and frequently employed algorithms and direct numerical schemes based on the finite element method (FEM) and finite difference method (FDM) to validate results obtained. In spite of a general aspect of the review paper, the traditional theoretical methods mentioned so far are quantified and compared with respect to applications to the novel branch of mechanics, i.e. vibrational behavior of nanostructures, which includes results of our own research presented throughout the paper. Namely, considerable effort has been devoted to investigate dynamic features of the Germain–Lagrange nanoplate (including physical nonlinearity and inhomogeneity of materials). Modified Germain–Lagrange equations are obtained using Kirchhoff’s hypothesis and relations based on the modified couple stress theory as well as Hamilton’s principle. A comparative analysis is carried out to identify the most effective methods for solving equations of mathematical physics taking as an example the modified Germain–Lagrange equation for a nanoplate. In numerical experiments with reducing the problem of PDEs to ODEs based on Fourier’s ideas (separation of variables), the Bubnov–Galerkin method of static problems and Faedo–Galerkin method of dynamic problems are employed and quantified. An exact solution governing the behavior of nanoplates served to quantify the efficiency of various reduction methods, including the Bubnov–Galerkin method, Kantorovich–Vlasov method, variational iterations and Vaindiner’s method (the last three methods include theorems regarding their numerical convergence). The numerical solutions have been compared with the solutions obtained by various combinations of the mentioned methods and with solutions obtained by FDM of the second order of accuracy and FEM for triangular and quadrangular finite elements. The studied methods of reduction to ordinary differential equations show high accuracy and feasibility to solve numerous problems of mathematical physics and mechanical systems with emphasis put on signal processing.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this review, we consider numerous computational approaches derived from mathematical physics and more widely used over the years to find nonlinear PDE solutions that govern the dynamic behavior of structural members. This section will include the description of advantages (sometimes disadvantages) of the classical and extended theoretical variants of methods developed by Fourier and Galerkin, variational methods, as well as the variational iteration and Kantorovich–Vlasov methods, and others.
1.1 Fourier Methods (FM)
A number of computational methods aimed at solving a wide variety of problems in mathematical physics and technology were based on the ideas of the great French scientist J. Fourier including the method of separation of variables or the method of eigenfunctions [1]. He formulated the methods which later gave impetus to the use of the variable separation procedure when creating new approaches to solving equations for functions of several variables. William Thomson (Lord Kelvin) called this work “The Great Mathematical Poem”.
The advantage of the Fourier method is that it creates a simple way to obtain an explicit solution. This method allows us to present a series of very wide class of functions, since it requires that one smoothness condition is satisfied inside the area, and others on the boundary. Employment of the apparatus of asymptotic analysis to obtain estimates of the Fourier coefficients improved the convergence and highlighted the features of the series. There are many other benefits while using Fourier’s method, which are specific to each particular problem. For example, it includes the clear physical meaning of Fourier coefficients in vibrations problems and heat dissipation problems.
Nowadays the Fourier-based methods have found various applications while analyzing linear and nonlinear PDEs. Propagation processes governed by PDEs can be solved using the so-called split-step Fourier method. It requires a simple numerical implementation and can cause phenomena which are not detected by other numerical methods. This approach is widely used in the numerical analysis of nonlinear optical fiber channels [2]. The algorithm is a combination of reducing the step-size for the integration along a chosen variable, and then by utilizing a discrete-time representation of the propagating signals to get back and forth between time and frequency domains using FFT (Fast Fourier Transform).
Though the direct Fourier method and the split-step Fourier method are faster than most commercial programs, in general they are computationally time-consuming, and often the finite-difference methods are used instead [3].
When analyzing mechanical systems, machines and mechanisms, the signal processing is based on the time-frequency resolution of Fourier methods and wavelets. The Fourier methods belong to the oldest and have been used to solve static and dynamic problems of structural members, including rods, beams, plates and shells, and the solutions can be obtained either in the form of stresses or displacement functions. Numerous problems of nonlinear discrete and continuum mechanics are solved with a help of the Fourier methods. In the former case the system of governing ODEs is solved using either single (periodicity) or double (quasi-periodicity) Fourier series, while in the latter case usually the governing PDEs are solved using the Galerkin and Bubnov–Galerkin methods, as well as the separation of variable method matched with the Fourier series. The Fourier methods and the associated harmonic analysis are always involved either explicitly or implicitly in solving a variety of problems of mathematical physics including the Navier-Stokes equations, Litllewood–Paley decompositions, Besov spaces, etc.
Fourier series representation includes both real and complex sinusoids. In the case of signals (noise) often measured in engineering problems, the Fourier representation has a direct physical interpretation. Various waveforms have Fourier series representations, and therefore the Fourier-based analysis is inherently involved in any engineering action. Any periodic/quasi-periodic signal with the given period/periods can be approximated by 1D/2D Fourier series. The Fourier series can approximate odd and even square waves/signals. In addition, regular pulse trains, triangle waveform as well as saw tooth waveforms have their Fourier expressions.
As it has already been mentioned, in engineering Fourier methods serve as a paradigm for solving majority of problems dealing with signal processing, including the Fourier transform, discrete-time Fourier transform, discrete Fourier transform, short-time Fourier transform and different wavelets. Though FFT does not belong strictly to the Fourier methods, it can be understood also as the Fourier idea matched with a computational technique for evaluating the discrete Fourier transforms. It should be noticed that the short-time Fourier transform makes it also possible to trace time evolution of the frequency components, although usually wavelet transforms are used for this purpose.
From the engineering point of view the Fourier methods represent the strength of a signal measured by its amplitudes versus its frequencies, i.e. an arbitrary signal can be presented as a sum of sinusoids (harmonics) of different frequencies. This allows us to carry out the spectral analysis and detect numerous important frequencies, including those occurring in periodic, quasi-periodic and chaotic signals. The discrete-time/discrete Fourier transforms, and the short Fourier transform use the discrete-time complex sinusoids, whereas the Fourier transform employs signals as weighted combinations of continuous-time complex-valued sinusoids.
In mathematical modeling of mechanical/mechatronic systems mainly differential equations are studied. ODEs describe lumped mass mechanical systems and refer to displacements (positions), velocity and accelerations, whereas PDEs describe the behavior (statics and dynamics) of continuously distributed mass systems and enable the prediction of vibrations, sound, fluid flow, waves, etc.
A property of the Fourier series, i.e. differentiation of a sum of harmonics of different frequencies yields a sum of harmonics of the same frequencies corresponds to the behavior met in real world processes, physics and engineering. It is well known that the engineering approaches based on measuring and control of the mechanical, electric and mechatronic systems involve time delay. This is well fitted by the Fourier series, since a delay of the sum of harmonics of different frequencies results in the sum of harmonics of the same frequencies.
The Fourier methods are well suited to study signal-system interactions. In the case of linear time-invariant systems, the so-called “eigenfunction” property holds, i.e. an input described as an arbitrary sum of complex harmonics of different frequencies yields an output given by the sum of complex harmonics of the same frequencies. The FMs allow also for employing filters to separate certain frequency components of the input signal. In addition, they give efficient computational results of the FFT algorithms based on the properties of complex harmonics. The Fourier methods are extensively described in numerous books [4,5,6]. Fornberg [7] employed the Fourier method based on FFT to approximate space derivatives for hyperbolic PDEs with emphasis put on its stability and accuracy.
Kreiss and Oliger [8] developed a stability theory for the Fourier pseudo-spectral method with the application to the linear hyperbolic/parabolic PDEs with variable coefficients.
Majda et al. [9] employed the Fourier method to general linear hyperbolic Cauchy problems with nonsmooth initial data. It was proven that the appropriate smoothing techniques give stability, whereas smoothing combined with smoothing of the initial data yielded infinite order accuracy of the obtained results.
Kosloff et al. [10] used the Fourier method to construct a 2D forward modeling algorithm. The solution included discretization in both space and time. Temporal derivatives were approximated by the second order differencing, whereas spatial derivatives were estimated via FFT. The algorithm was validated using the analytic solutions for 2D Lamb problem.
Peyret [11] employed the Fourier method to solve the problems of spatial periodicity in one/two directions matched with the Chebyshev polynomials.
1.2 Galerkin Method (GM)
The Galerkin method can be thought as an extension of the method of Ritz [12] who considered the problem \(\alpha u=f\) (\(\alpha\)stands for a differential operator acting in a Banach space). The approximating solution is \(u(x)={{U}_{N}}(x)=\sum \nolimits _{i=1}^{N}{{{\alpha }_{i}}{{w}_{i}}(x)},\) where N is the natural number and \({{w}_{i}}\in {{X}_{N}}\subset X\) forms a linearly independent system. It is expected that \({{\alpha }_{i}}\) (weights) can be defined using the condition that the residual (i) \(r=\alpha u-f\rightarrow \min .\) However, a question arises how to define coordinate functions and test functions to find a suitable form of the residual to satisfy the requirement that \({{u}_{N}}\) tends to u, where u is the exact solution. Galerkin proposed a general method and pointed out that the residual should be orthogonal to a system of test functions (linearly independent) where the orthogonality refers to the integral sense [13]. (Nowadays, it is recognized that Galerkin employed not widely known, brilliant idea published by Bubnov (an engineer and marine officer) who applied his method to ship building problems. This is why in many cases the method is referred to as the Bubnov–Galerkin method, while some researchers distinguish the Galerkin and the Bubnov–Galerkin methods).
Therefore, after modifications, the general Galerkin-based idea is to find weight coefficients \({{\alpha }_{i}}\) using the orthogonality relation of the form (ii) \(\langle \alpha {{u}_{N}}-f,\) \({{\eta }_{k}} \rangle =0\) for all \({{\eta }_{k}}\in {{Y}_{M}},\) where \({{u}_{N}}\) is given by (i), and \({{Y}_{M}}\subset {{Y}^{/}}\) is the set of independent test functions in the space conjugate to Y; duality pairing of Y and \({{Y}^{/}}\) is defined by \(\left\langle \cdot ,\cdot \right\rangle .\) The latter general formulation includes various special cases: (a) the Bubnov–Galerkin method when X and Y are Hilbert spaces and spaces \({{X}_{N}}\) and \({{Y}_{N}}\) coincide (see [14]); (b) the Ritz–Galerkin method when (ii) is generated by a quadratic equation and comes from the Euler equation ([15], chapter 4; [16]); (c) the Petrov-Galerkin method where the problem was applied to fit the eigenvalues ([17,18,19]); (d) the Taylor–Galerkin method where emphasis is laid on the finite element method applied to PDEs [20]; the Faedo–Galerkin method where dynamic properties are concerned [21].
Nowadays the Galerkin methods play a fundamental role in numerical solutions of PDEs including elliptic, parabolic and hyperbolic equations [22].
The method is widely used by the classical and extended discretization algorithms employed explicitly and/or implicitly in the finite element methods (FEMs), finite difference methods (FDMs), and spectral element methods (SEMs).
Nodal (Lagrangian interpolants/polynomials) and modal Fourier basis and Legendre polynomials may serve as basis functions in 1D, and they can be extended to higher space dimensions by using SEM and a concept of tensor products. It should be emphasized that the global modes can be formulated in a mathematical, physical and/or empirical way.
A particular role in finding solutions to a PDE plays the modified FEM known as the Galerkin FEM. In this case the Lagrange and Hermite elements are used as trial functions and this approach can be formulated in both global and local way.
More recently the classical FEM includes extension to fit the discontinuous problems based on completely discontinuous basis functions instead of the piece-wise polynomials [23]. The review paper [23] addressed the problems of the discontinuous Galerkin methods for solving high-order time-dependent PDEs with emphasis put on the consideration of numerical flux, stability, time discretizations, accuracy of the solution and error estimates.
As already mentioned, Galerkin-type approaches have found great application in both mathematical physics [24,25,26,27,28] and mechanical engineering as well as signal processing [29] (due to the page limit of our review, we have omitted here numerous articles dealing with these issues).
Importance of the Galerkin methods, its sound application and possible further extension can be found in the editorial written by Repin [30].
1.3 Kantorovich–Vlasov Methods (KVM)
Among variety of the numerical methods devoted to the solution of static and dynamic problems of structural members, a key role is played by the methods introduced by Kantorovich [31] and Vlasov [32], further known as the Kantorovich–Vlasov method (KVM). It has the following advantages:
-
(i)
solution to a nonlinear PDE(s) considered in the Cartesian coordinates is represented by a single series of infinite terms as a combination of functions with separable variables where all components of the approximation are unknown. For example, in the case of uniformly loaded Kirchhoff–Love rectangular plate deflection, w(x, y) is represented as \(w(x,y)=\sum \nolimits _{n=1}^{\infty }{f(x){{g}_{n}}(y)};\)
-
(ii)
the original 2D (3D) problem is reduced to a system of two (three) coupled 1D problems;
-
(iii)
the iterative procedure of KVM is efficient for computations, since it converges rapidly (usually, it takes a few iterations with a few terms in the approximating function to achieve the validated and stable solution);
-
(iv)
KVM is useful and shows advantages over other traditional methods of reduction of PDEs to ODEs while dealing with vibrations of beams, plates and shells.
In the beginning, the reduction of PDEs dimension occurring in mathematical physics and mechanics to that of the counterpart 1D problem was carried out by Grigorenko and his disciples [33,34,35,36] as well as by Krysko and his co-workers [37,38,39]. Then, Bespalova successfully employed this method to various problems of nonlinear structural mechanics [40,41,42].
More recently, Bespalova and Urusova [43] used the advanced Kantorovich–Vlasov approach to reduce the 3D problem of torsion of an anisotropic prism to three corresponding 1D problems. In addition, they reported new results regarding warping of the cross-section and deformation of the prism axis for different types of anisotropy.
Bespalova [44] proposed also to match the inverse-iteration method of successive approximations and the advanced KVM to calculate natural frequencies of an elastic parallelepiped with different boundary conditions. The dependence of lower frequencies of a 3D cantilever beam was reported.
Surianinov and Chaban [45] used the KVM to reduce the 2D problem of calculating the anisotropic plate based on the proposed analytical-numerical method. This approach yielded the solution of a basis differential equation of bending an anisotropic plate with any boundary conditions and without any restrictions given to the external load.
Nwoji et al. [46] applied the KVM to the flexural investigation of simply supported Kirchhoff plates subjected to transverse uniformly distributed load. The Vlasov approach was applied to construct coordinate functions in the x direction, whereas the Kantorovich method was used to consider the displacement field. They reported that the obtained solutions were rapidly convergent for both deflection and bending moments. The results obtained were validated by the Levi-Nadai solutions.
Then, Kerr [47] extended the Kantorovich method to get the exact solution in both directions by using the iterative procedure. Kapuria and Kumari [48] applied KVM to study a 3D problem of elasticity solution of laminated composite structures in cylindrical bending. Aghdam et al. [49] used successfully the Kantorovich method in the static analysis of moderately thick, functionally graded sector plates. Wu et al. [50] found the Kantorovich-based solution when studying a simply supported beam under linearly distributed loads. The multi-term extended KVM was applied to find analytical solution for the bending problem of moderately thick composite annular sector plates with general boundary conditions and loadings [51].
The free vibration analysis based on KVM of symmetrically laminated fully clamped skew plates and of moderately thick, functionally graded plates was carried out in the works [52, 53]. Vibrations of laminated plates with various boundary conditions based on the extended Kantorovich method were analyzed [54].
Kapuria et al. [55] studied the 3D elasticity solution of laminated plates with a help of multi-term extended Kantorovich method, whereas Kumari et al. [56] used the 3D extended Kantorovich solution for Levy-type rectangular laminated plates with edge effects.
Huang et al. [57] used KVM to estimate local stresses in composite laminates upon polynomial stress function.
Kumari and Behera [58] obtained a closed form 3D solution for a rectangular laminated plate with Levy type support based on the extended Kantorovich method. Natural frequencies were estimated for composite and sandwich laminates. In addition, the effect of the span to thickness ratio and in-plane modulus ratio on the natural frequencies was also investigated. Ike and Mama [59] carried out the flexural analysis of Kirchhoff–Love plates using the variational Kantorovich method.
1.4 Variational Methods (VM)
The variational methods belong to the fundamental tools for solving variety of linear/nonlinear problems not only in mechanics but in mathematical physics due to the rigorous mathematical bases. In the classical mechanics it concerns the mechanics of solids and fluids, materials modeling and properties (creeps, plasticity and smart materials fabrication, materials with memories, etc.), the statics and dynamics of structural members dealing with real engineering constructions, heat transfer, and others. It allows us to model complex behavior of both discrete systems and continuum.
Theoretical achievements, counted from the 18th century, introduced by seminal works of Euler, Lagrange, Bubnov, Galerkin, Kantorovich, Nowacki, Vlasov, Vaindiner, Reissner and Ritz along with Hamilton’s principle have recently attracted great interest of the researches, and have brought back the classical approaches based on the variational methods and energy principles. This is motivated by growing attractiveness of numerical/computational methods in applied sciences, and in particular in engineering including the final element method, finite difference method, Ritz method, weighted-residual methods, and more.
The variational methods require good mathematical background, as it is shown by the authors of the outstanding monographs [60,61,62,63,64,65], but it seems that the pressure of rapidly developing technology and engineering approaches shifted and somehow shallowed the fundamental achievements of variational classical theories to engineering and applied sciences with direct application to the finite element methods.
However, the classical variational approaches can be extended to mathematical branches of science (geometry, topology, analysis), mathematical physics, optimization problems and mathematical modeling and analysis of nonlinear behavior in biology, medicine, and economics.
There are numerous publications devoted to the theory and application of variational methods. Since the latter have been closely matched with the computational methods, it is almost impossible and perhaps useless to cite all or majority of them. Therefore, only few of them will be mentioned.
Courant [66] pointed out importance of the calculus of variations and its equivalence with the boundary value problems of PDEs. He considered variational problems with reference to quadratic functionals, rigid and natural boundary conditions, the Rayleigh–Ritz method, the method of finite differences, and the method of gradients.
The rigorous treatment and extension of the classical variational methods is offered by Marsden et al. [67] who proposed a variational and multisymplectic formulation of compressible/incompressible models of continuum mechanics on general Riemannian manifolds. An interplay of compressible/incompressible continuum mechanics, constrained multisymplectic field theories, symmetries, momentum maps and Noether’s theorem was offered.
Direct applications of variational methods for engineers can be found in the book [68]. It gives friendly written basic material devoted to variational methods for algebraic equations, and to differential equations, the treatment of Hilbert and functional spaces feasible for engineers, as well as functionals and calculus of variations.
Finally, it should be emphasized that the classical variational methods still attract interest of the scientists which is documented by the original treatment and extension to the thematic issues presented in the monographs/books [69,70,71,72,73,74].
1.5 Variational Iteration Method (VIM)
The next method is the variational iteration method (VIM), which relieves a researcher from the need to construct a system of approximating functions like in the Galerkin method. Arbitrarily defined functions (satisfying only the smoothness conditions) are taken and then they are refined in the process of calculation by VIM based on the solutions of the original system of differential equations.
This method was first proposed and applied in 1933 by Shunk [75] to calculate the bending of cylindrical panels. But the work went unnoticed and the method was rediscovered again in 1964 by Zhukov [76], who used it to calculate a thin rectangular plate. Further, VIM was widely used by many researchers to solve the problems of shell and plate theory [37]. The substantiation of this method for the class of equations described by positive definite operators was given in [38].
It is worth noting here that in the literature there is a large number of different names for the method of variational iterations. This method is often called by Kerr [77,78,79] the extended Kantorovich method and it was published 38 years after Shunk and 5 years after Zhukov. Given this, we can say that the method has been rediscovered.
The variational iteration method or extended Kantorovich method has been used over the past half century to solve the problems of statics, stability, natural frequencies and dynamics.
The VIM was extended by Ji-Huan He [80, 81] who used the old concept of Lagrange multiplier method, with emphasis put on analytical solutions. The approach proposed by He found many followers and his modification to the classical VIM was employed in a wide range of issues of mathematical physics dealing with ODEs and PDEs. On the other hand, the convergence of VIM was discussed in many papers, including [82,83,84,85,86].
Solodov and Svaiter [87] proposed a novel projection algorithm to solve variational inequality. First, an appropriate hyperplane separating the current iterate from the solution was employed. It required a single projection onto the feasible set and application of the Amijo-type line search along a feasible direction. The next iteration was a projection of the current iterate onto the intersection of the feasible set with the halfspace including the solution.
Matinfar et al. [88] developed a so called modified variational iteration method (MVIM) by merging the classical VIM with He’s polynomials and applied it to solve heat transfer problems governed by PDEs with variable coefficients. The proposed algorithms matched the variational iterations with the homotopy, perturbation methods and exhibited all advantages of the coupled technique. The authors showed that MVIM was employed without any discretization procedures and strong assumptions and was free from errors.
Noor and Mohyud-Din [89] developed an analytical version of VIM called the variational decomposition method based on the example of the eighth-order boundary value problem. Analytical solutions were found as the conventional technique confirmed the reliability, validity and high accuracy of the proposed method.
Ji-Huan He [90] again considered VIM with emphasis laid on recent results and new interpretations. Procedures illustrating the solution were based on nonlinear oscillators governed by ODEs. Then, He and Wu [91] discussed the application of VIM to nonlinear wave equations and nonlinear fractional differential equations occurring in various engineering problems. They noticed that VIM may serve as a candidate to solve problems of strongly nonlinear equations which cannot be attacked by the classical approximate methods.
Barari et al. [92] combined the homotopy perturbation method and VIM to solve nonlinear ODEs with an oscillating solution. They stressed that the method did not require either linearization or small perturbation which is needed in the classical approaches.
Saadatmandi and Dehghan [93] employed He’s variational method to solve the generalized pantograph equation. They demonstrated that only a few iterations were sufficient to guarantee a highly accurate solution, and it was not affected by computation round of errors.
Abbasbandy and Shivanian [94] used VIM successfully to solve nonlinear Volterra’s integro-differential PDEs. They observed that VIM yielded more accurate results as compared to the homotopy perturbation method and the Adomian decomposition method.
Salehoor and Jafari [95] employed the VIM extended by He to find a solution to nonlinear gas dynamics equation and Stefan equation. The method involved the Lagrange multipliers to identify the optimal values of parameters in a functional.
Heydari et al. [96] combined the spectral method and VIM for heat transfer problems with high order of nonlinearity. The method was implemented to solve an unsteady nonlinear convective-radiative equation with two small independent parameters.
Wazwaz [97] applied VIM for solving linear/nonlinear ODEs with variable coefficients. He tested a variety of models including the hybrid selection model, Thomas-Fermi equations, as well as the Kidder and Ricatti equations.
Zhang et al. [98] used a new scheme while adopting VIM to solve the problem of infrared radiative transfer in a scattered medium. Both upward and downward intensities were calculated separately by VIM and it was found that VIM was more accurate comparing to the discrete-ordinates method.
Narayanamoorthy and Mathankumar [99] used VIM to solve problems governed by the linear Volterra fuzzy integro-differential equations. Two test problems were considered and the approximate versus exact solutions were validated.
El-Sayed and El-Mongy [100] employed the modified VIM to solve the free vibration problem of a tapered Euler-Bernoulli beams mounted on 2DoF mass-spring-damper subsystem. Natural frequencies and mode shapes for uniform/tapered beam were studied. It was demonstrated how highly accurate results were obtained by adjusting only a few iterations of VIM.
1.6 Vaindiner’s Method (VaM)
This method, while rigorous and powerful, did not attract, however, special attention particularly among the western-oriented researchers. The method can be viewed as an extension and modification of the Kantorovich and Bubnov–Galerkin methods. An approximate solution to a problem governed by PDEs was searched in the form of the sum of products of the coordinate and sought functions with applications to the Fourier general polynomials and series [101, 102]. In the first product, a given function depends on x, whereas in the second product it depends on y. The approach was then further extended and developed by studying many problems of the convergence of the methods used, the decreasing order of the studied systems, interpolation of functions with many variables, lattice collocation, boundary value problems and singular integral equations of elasticity in 3D [101,102,103,104,105,106,107].
Vaindiner’s method was widely used to study stationary geometrically nonlinear problems of the shell theory [108]. The system of nonlinear ordinary differential equations was reduced to a nonlinear system of algebraic equations by the finite difference method. And then, the problem was solved by the general iteration method. A solution for square plates with three types of boundary conditions was obtained including the analysis of a simple support, sliding clamping of the contour, a simple support on two opposite edges and sliding clamping on the other two. More recently, Vaindiner’s method was used to study the static bending of plates taking into account physical nonlinearity and different moduli of material [109, 110], and also to consider the problems of one-sided corrosion of shells [111].
A brief review of the literature reveals that there is no available comparative analysis of the methods so far described and schematically shown in Fig. 1 (description of the Agranovskii–Baglai–Smirnov method (ABSM) is omitted here, because it is presented in Sect. 3.3). Many of the above methods have not been applied to problems in the theory of plates and shells. This is why we have employed and quantified the effectiveness of the methods based on the example of the Germain–Lagrange PDE.
1.7 Closing Remarks
It is well recognized that in solving multidimensional problems of mathematical physics, the reduction of dimension plays a crucial role, and next an attempt to achieve a solution in a compact way is highly required. In this respect, an original multidimensional problem is substituted by its counterpart sequence of one-dimensional problems. This makes it possible to obtain solutions without time-consuming numerical computations, which is important for engineering applications. Since in most cases it is impossible to obtain an exact match between the original multidimensional problem and the sequence of one-dimensional problems, appropriate functionals are proposed and used to solve the problem in an approximate way.
Nonlinear dynamics of the one-dimensional macro-structural-mechanical issues has been recently deeply revisited with regard to chaotic and bifurcational features (see books [112,113,114] and review paper [115]). Thus, with the appropriate methodology suitable from the engineering point of view and reliable and accurate approaches to the transition from nonlinear multidimensional problems to a set of nonlinear but one-dimensional problems, progress can be made in the computational aspects of modern mechanics, aeronautics and civil engineering.
Worth noting is the interest of engineering community in the so called reduced order models (ROMs), where the transition from multidimensional infinite problems governed by nonlinear PDEs is reduced to a set of nonlinear ODEs, where the problem is highly truncated to the single-mode approximation. Although this approach allows us to find a relationship between the dynamics of structural members with infinite degrees of freedom and the dynamics of lumped massed systems with one degree of freedom governed by the second order ODE, in many cases it does not allow us to obtain reliable results. Therefore, recognizing several advantages of this engineering-oriented approach, such as direct fit to the well-known classical 1 DoFs oscillators, including Duffing, Duffing-Helmholtz and van der Pol archetypal systems, and capturing the basic dynamic phenomena of structural members under study, we prefer to highlight more rigorous mathematically and reliable methods to be used by engineering community, which is why ROMs are not covered by our review article.
The rest of the paper is organized in the following way. Problem statement is given in Sect. 2, whereas solutions based on the methods described in Sect. 1 are reported in Sect. 3. Section 4 presents solutions of the problem using FEM and FDM, and concluding remarks are given in Sect. 6.
2 Problem Statement
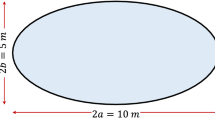
To construct a mathematical model of a Germain–Lagrange nanoplate based on the modified couple stress theory, an elastic isotropic rectangular plate is considered. The rectangular coordinate system associated with the nanoplate is introduced in the following way: \(\varOmega =\{ x,y,z\text { }/\text { }( x,y,z\text { })\in [ 0,a ]\times [ 0,b ]\times\) \(\text { }[ -{h}/{2}\;,\,\,{-h}/{2}\;]\}\). The nanoplate has dimensions a, b, h along axes x, y, z, respectively. Its middle surface at \(z=0\) is denoted by \(B=\{ x,y\text { }/( x,y\text { })\in [ 0,a ]\) \(\times [ 0,b ]\}\) (see Fig. 2).
The displacements along the x, y axes refer to \(u,\,\,v,\) respectively. Deflection (normal plate movement) along the z axis is denoted by \(w=\,w(x,\,y)\). In order to construct the mathematical model, we introduce the following assumptions and hypotheses: (i) Kirchhoff hypothesis holds; (ii) rotation inertia of the plate elements are not taken into account; (iii) plate material is homogeneous and isotropic, i.e. it is assumed that for the same stress the same deformations occur in all points and elastic properties in each point of the plate are the same in all directions; (iv) all displacement components are considered to be significantly smaller than the characteristic size of the considered rectangular plate; (v) the deformations of middle surface \({{\varepsilon }_{xx}},\,\,{{\varepsilon }_{yy}},\,\,{{\varepsilon }_{xy}}\) are assumed to be negligible compared to unity (this does not mean that the relationship between movements and deformations must be linear).
Owing to the modified couple stress theory [116], the accumulated energy of deformation U of the plate, taking its size-dependent behavior into account, is governed by the following formula
where \({{\sigma }_{xx}},{{\sigma }_{yy}},{{\sigma }_{xy}}\),\({{\varepsilon }_{xx}},{{\varepsilon }_{yy}},{{\varepsilon }_{xy}}\),\(m_{xx}^{{}},m_{yy}^{{}},m_{xy}^{{}}\),\(\chi _{xx}^{{}},\chi _{yy}^{{}},\chi _{xy}^{{}}\) denote the components of the symmetric part of stress tensor \(\text { }\!\!\sigma \!\!\text { }\), components of deformation tensor \(\varepsilon\), components of the deviatory part of the symmetric tensor of the higher order m, and the components of the symmetric part of curvature tensor \(\chi\).
Linear deformations and displacements are coupled via the following relations
The following relation for the non-zeroth component of the symmetric curvature tensor part holds
For non-zero components of the symmetric part of stress tensor \(\sigma\) and for the deviatory part of the tensor of the higher order m, the following relations take place [116]:
where: \(\lambda \left( x,y,z,{{e}_{i}} \right) =\frac{E\nu }{(1+\nu )(1-2\,\nu )},\,\,\mu \left( x,y,z,{{e}_{i}} \right) =\frac{E}{2(1+\nu )}\) are the Lamé parameters; \({{e}_{i}}=\frac{\sqrt{2}}{3}\sqrt{{{\left( \varepsilon _{xx}^{{}}-\varepsilon _{yy}^{{}} \right) }^{2}}+\varepsilon _{yy}^{2}+\varepsilon _{xx}^{2}+\frac{3}{2}\varepsilon _{xy}^{2}}\) describes the intensity of deformation; E - Young modulus; \(\nu\) - Poisson’s coefficient; \({{l}_{{}}}\) - material length parameter associated with the symmetric tensor of the relation gradient.
According to the method of variable parameters of elasticity [117], \(E\left( x,y,z,{{e}_{i}} \right)\) and \(\nu \left( x,y,z,{{e}_{i}} \right)\) are not constant but they depend on the coordinates and intensity of deformations.
Equations (2), (3) and (4) are used to derive deformation energy U of the nanoplate, i.e. we have
We introduce the following notation: \(\int \limits _{-\frac{h}{2}}^{\frac{h}{2}}{\left( \lambda +2\mu \right) {{z}^{2}}\,dz}={{\alpha }_{1}}\),\(\int \limits _{-\frac{h}{2}}^{\frac{h}{2}}{\mu {{z}^{2}}\,dz}={{\alpha }_{2}}\), \(\int \limits _{-\frac{h}{2}}^{\frac{h}{2}}{\mu \,dz}={{\alpha }_{3}}\). Then, \({{\alpha }_{i}}={{\alpha }_{i}}\left( x,y,{{e}_{i}} \right)\) are the functions of coordinates and intensity of deformations. Equation (5) takes the following form
where the underlined members include higher order terms.
External work related to the distributed forces takes the following form
Kinetic plate energy is as follows
The associated variations of U, W, K are as follows
where: \(I=\int \limits _{-\frac{h}{2}}^{\frac{h}{2}}{\rho dz}\).
Employing Hamilton’s principle, we get
and we obtain the following equation of dynamics of the nanoplate based on the modified couple stress theory with variable elastic parameters
The corresponding choice of the boundary conditions is given with regard to the plate edge [0; b]:
For the case, when elasticity parameters are independent of both coordinates and time, the modified couple stress theory, the Germain–Lagrange equations of the following form can be used
where \(D=\frac{E{{h}^{3}}}{12\left( 1-{{\nu }^{2}} \right) }+\frac{Eh{{l}^{2}}}{2\left( 1+\nu \right) }\), and it will be further referred to as the modified Germain–Lagrange equation.
In the future, we will use two types of boundary conditions and their combinations:
where n stands for a normal to the plate boundary.
For the numerical study, we use the non-dimensional form of Eq. (14). We introduce the following non-dimensional variables
Then Eq. (14) can be rewritten as follows (bars over the dimensionless parameters are omitted)
where: \(D=\frac{1}{12\left( 1-{{\nu }^{2}} \right) }+\frac{{{\gamma }^{2}}}{2\left( 1+\nu \right) }\), \(\gamma\) - non-dimensional material length parameter equal to 0 for the classical mechanics case, and it is in the interval (0; 0.5] for higher order mechanics.
Boundary conditions (15), (16) should be attached to Eq. (18) in the same dimensionless form. The derived PDEs will be solved both analytically and numerically by several methods: the Kantorovich–Vlasov method, variational iteration method, Vaindiner’s method, Bubnov–Galerkin method, by the use of double trigonometric series, the finite element method and the finite difference method. In order to keep accuracy of the solution, the Agranovskii–Baglai–Smirnov method will be used [118, 119].
Equation (18) can be presented in its counterpart operator form
where L is the operator (in general nonlinear) acting in a Hilbert space H. Boundary conditions (14) and (15) have the following operator representations
Remark 1
It should be noted that Eq. (12) with the corresponding boundary conditions stands for the generalization of the modified Germain–Lagrange equation (MGLE). It allows one to take into account the heterogeneous structure of the nanoplates. The properties of nanoplates can be heterogeneous prior to deformation and can be changed during loading. This theory is based on the deformation theory of plasticity and makes it possible to recalculate elastic moduli and Poisson’s ratios, depending on the deformation diagram and the loading process.
Remark 2
Equation (12) is used to consider physical nonlinearity for nanostructures using the iterative scheme of the method of variable elastic parameters. The method of variable parameters of elasticity [117], used to solve a physically nonlinear problem, employs the fact that \({{E}_{i}}(x,\,y,\,z,\,e_{i}^{{}})\), \({{v}_{i}}(x,\,y,\,z,\,e_{i}^{{}})\) are not constant. They depend on the deformed state at a structure point and are defined by the following formulas
Here we consider that volumetric deformation \(K_{1i} = const\). In the deformation theory of plasticity [120], the shear modulus is defined in the following form:
where \(\sigma _{i}^{{}}\), \(e_{i}^{{}}\) stand for the plate stress intensity and plate deformations, respectively. The relationship \(\sigma _{i}^{{}}(e_{i}^{{}})\) is determined experimentally for a given nanomaterial.
3 Analytical and Numerical Methods for Solving MGLE
3.1 Exact Solution of MGLE Based on Navier’s Double Trigonometric Series
We consider first a possibility to get analytical solution to Eq. (18) with boundary conditions (15). External transverse load q(x, y) is taken into account in the following form
where
Deflection function w(x, y) is taken in the form of the double trigonometric series
and each term of solution (23) satisfies all boundary conditions (15).
Equations (21), (23) and (18) allow us to derive the following algebraic equation
Taking into account the linear independence of the terms in Eq. (24), we obtain
Then the counterpart solution in a general form can be written as follows
For uniformly distributed constant load \(q={{q}_{0}},\) coefficients \({{B}_{mn}}\) take the following form
Therefore, we obtain
where
For Eq. (18), convergence of the solution is studied depending on the number of terms of series N in (28), for the following fixed values \(\gamma =0,\,\,\gamma =0.3,\,\gamma =\,0.5\) (see Table 1).
Analysis of the results given in Table 1 shows that for \(\gamma =0\), five members of the series should be considered, whereas for \(\gamma \ne 0\) three members of the series are sufficient to get a reliable solution. In what follows, we will consider this as an exact solution and compare it with the solutions obtained numerically using other methods.
3.2 Bubnov–Galerkin Method
Further, we will formulate an application scheme of the Bubnov–Galerkin method using the example of operator equation (19) and taking into account boundary conditions (20).
Let an algebraic base \(\{{{\phi }_{j}}\}\subset D(L)\) be chosen in H (Hilbert space) and approximate solution (19) be sought in the following form
where: \({{a}_{j}}\) are the unknown numerical coefficients, \({{\phi }_{j}}(x,y)\) are the known analytical functions (approximation), and \({{w}_{0}}(x,y)\) is the function satisfying boundary conditions (20).
Substitution of (30) into (19) yields the following residual
In order to determine unknown coefficients \({{a}_{j,}}j=1,\ldots ,N,\) according to the Bubnov–Galerkin method [121, 122], we require that the basis functions \(\{{{\phi }_{j}}\}_{k=1}^{N}\) were also orthogonal to residual (31), i.e. so that the following condition
is satisfied.
For the Bubnov–Galerkin method the unknown coefficients \({{a}_{j}}\) included in (31) must be determined from the solution of the following system of linear algebraic equations
where R is the residual equation (19), and \({{\phi }_{k}}\) are the same analytic functions (weights) that appear in (30). Since the linear problem is considered in (19), Eq. (33) can be written in its counterpart matrix form
Solving the system of algebraic equations by any method aimed at estimating \({{a}_{j}},\) and substituting the obtained solution into (31), we obtain an approximate solution w.
Applying the Bubnov–Galerkin method when choosing weights \({{\phi }_{k}}(x,y)\) and approximating functions \({{\phi }_{j}}(x,\,y)\), the following conditions are hypothesized:
-
1.
\({{\phi }_{j}}(x,y)\in H\), \({{\phi }_{k}}(x,y)\in H\) where H is the Hilbert space;
-
2.
\(\forall \,j,k\) function \({{\phi }_{j}}(x,y)\), \({{\phi }_{k}}(x,y)\) are linearly independent and continuous in space \(\varOmega\);
-
3.
\({{\phi }_{j}}(x,y)\), \({{\phi }_{k}}(x,y)\) satisfy rigorously the main boundary conditions (and arbitrary initial conditions);
-
4.
\({{\phi }_{j}}(x,y)\) and \({{\phi }_{k}}(x,y)\) should represent the first N elements of the complete system of functions;
-
5.
\({{\phi }_{j}}(x,y)\) and \({{\phi }_{k}}(x,y)\) satisfy a completeness property in H.
Now, let us illustrate the advantages of BGM. We illustrate the process of finding solutions of the modified Germain–Lagrange equation for boundary conditions (15).
Displacements w can be expanded by using the following series:
After applying the Bubnov–Galerkin method for \(q(x,y)=q=const,\) we find
Table 2 presents solutions of the deflection in the center of the plate \({{w}_{m}}(0.5;0.5)\) depending on the number of terms in the series (36) for three values of \(\gamma\) and fixed parameters \(q = 7\), \(\lambda =1\).
Solutions, which coincide completely with the solution obtained by Navier, are highlighted in Table 2. The given example illustrates the fact that inclusion of \(\gamma\) in the modified Germain–Lagrange equation improves the convergence of the Bubnov–Galerkin method.
3.3 Agranovskii–Baglai–Smirnov Method (ABSM)
The idea is to construct an iterative procedure for solving the original equation (19) with the right-hand side as a residual from the solution at the previous step [118, 119]. We consider the algorithm for applying the Agranovskii–Baglai–Smirnov method (ABSM) using an example of the operator equation (19).
A new differential equation is constructed in the following way
where we changed the right-hand side in Eq. (19); now it plays the role of the residual of the solution to the original equation. This process is repeated n times. Finally, the following series is used as the input solution
The proof of the convergence of the ABSM method was given in references [118, 119]. In the following sections, the method of combinations of the Kantorovich–Vlasov method, the variational iteration method, and the Vaindiner method will be considered.
3.4 Solving MGLE by Kantorovich–Vlasov Method
Owing to the Kantorovich–Vlasov method (KVM) [31, 32], a solution to Eq. (19) can be searched in the following form
Weight functions \({{X}_{j}}(x)\) satisfy boundary conditions (15) and (16). Functions \({{Y}_{j}}(y)\) are the searched functions defined by the following system of projected equations (we substitute (39) into (19) and employ the BGM with respect to co-ordinate x):
Procedure (40) reduces the problem of PDEs to ODEs by employing the Bubnov–Galerkin method regarding one of the coordinates. Solving the system of ODEs with the corresponding boundary conditions, we obtain a set of functions \({{Y}_{j}}(y)\), and next substituting them into (39), we obtain the desired solution.
3.5 Proof of the Convergence of KVM for Some Class of Problems
In this section we will prove that the KVM method for a certain class of problems (including geometrically nonlinear problems of the theory of plates and shells [39]) coincides with the projection methods. A distinctive feature of the method relies on the way of constructing an extremely dense system of subspaces [123].
Let G be a bounded space \({{R}^{2}}\) with boundary \(\varGamma\). Consider the first boundary problem for a quasi-linear elliptic equation type of order 2m of the following form
where: \(\alpha =({{\alpha }_{1}}+{{\alpha }_{2}})\) - integer multi-index of differentiation; \(\left| \alpha \right| ={{\alpha }_{1}}+{{\alpha }_{2}}\); \({{D}^{\alpha }}=D_{1}^{{{\alpha }_{1}}}D_{2}^{{{\alpha }_{2}}}\); \({{D}_{i}}={\partial }/{\partial {{x}_{i}}}\;\); the same holds for \(\gamma \text { and }\omega\). Function \({{A}_{\alpha }}(x,{{\xi }_{\gamma }})\) where \({{\xi }_{\gamma }}=({{\xi }_{\gamma 1}},{{\xi }_{\gamma 2}})\) is nonlinear and depends on all possible indices \(\gamma\) at \(\left| \gamma \right| \le m\), \(x=({{x}_{1}}.{{x}_{2}})\). Finally, let \(h(x)\in {{L}_{2}}(G)\). Function u(x) is called the generalized solution of problem (31) and (32), if \(u(x)\in \overset{\circ }{\mathop {W_{2}^{m}}}\,(G)\) and if for any function \(v(x)\in \overset{\circ }{\mathop {W_{2}^{m}}}\,(G)\) the following integral identity holds
We introduce a few assumptions, which will be implemented in the next steps of the article.
-
1.
The problem of solving Eq. (41) under condition (42) is equivalent to solving the operator equation
$$\begin{aligned} u=Tu,\quad T:\overset{\circ }{\mathop {W_{2}^{m}}}\,(G)\rightarrow \overset{\circ }{\mathop {W_{2}^{m}}}\,(G), \end{aligned}$$(44) -
2.
Area \(G={{E}_{1}}\times {{E}_{2}}\), where \({{E}_{1}}\) and \({{E}_{2}}\) are the bounded sets of space\({{R}^{1}}\).
-
3.
Each element of the complete system of functions \(\left\{ {{\theta }_{i}}(x) \right\}\) of space \(\overset{\circ }{\mathop {W_{2}^{m}}}\,({{E}_{1}}\times {{E}_{2}})\) takes the form
$$\begin{aligned} {{\theta }_{i}}({{x}_{1}},{{x}_{2}})={{\phi }_{i}}({{x}_{1}}){{\psi }_{i}}({{x}_{2}}),\quad {{x}_{1}}\in {{E}_{1}},\quad {{x}_{2}}\in {{E}_{2}}, \end{aligned}$$(45)
and moreover, the system of functions \(\left\{ {{\psi }_{i}}({{x}_{2}}) \right\}\) is complete in space \(\overset{\circ }{\mathop {W_{2}^{m}}}\,({{E}_{2}})\), and \(\left\{ {{\phi }_{i}}({{x}_{1}}) \right\}\) in \(\overset{\circ }{\mathop {W_{2}^{m}}}\,({{E}_{1}})\). (In the future, we will employ the following lemma).
Lemma 1
If sequence \(\left\{ {{v}_{n}}({{x}_{1}},{{x}_{2}}) \right\}\) of the elements of space \(\overset{\circ }{\mathop {W_{2}^{m}}}\,(G)\) converges in norm to a certain element \({{v}^{*}}\in \overset{\circ }{\mathop {W_{2}^{m}}}\,(G)\), i.e.
and for \(\forall n\), function \({{v}_{n}}\) can be taken as
where \({{g}_{i}}({{x}_{2}})\) are the given elements of the complete system of functions \(\left\{ {{\phi }_{i}}({{x}_{2}}) \right\}\), and N is the fixed number, then function \({{v}^{*}}({{x}_{1}},{{x}_{2}})\) can also be represented in a similar way, i.e.
In order to prove the Lemma, it suffices to consider only one term in expression (47). Indeed, \(\int \limits _{{{E}_{1}}\times {{E}_{2}}}{{{\left| {{v}_{n}}-{{v}^{*}} \right| }^{2}}d{{x}_{1}}d{{x}_{2}}}\rightarrow 0,\text { }n\rightarrow \infty ,\) or, according to Fubini’s theorem, we have
where \(0\le {{F}^{n}}({{x}_{1}})=\int \limits _{{{E}_{2}}}{{{\left| {{v}_{n}}-{{v}^{*}} \right| }^{2}}d{{x}_{2}}}\).
It follows from (48) that there is a sequence \(\left\{ {{F}^{{{n}_{k}}}}({{x}_{1}}) \right\}\) such that
for almost all \({{x}_{1}}\).
Formula (49) shows that a certain sequence of elements from a finite-dimensional subspace of dimension N (which linearly spans N given elements \({{g}_{j}}({{x}_{2}})\in \overset{\circ }{\mathop {W_{2}^{m}}}\,({{E}_{2}})\)) converges for almost all \({{x}_{1}}\) to the element \({{v}^{*}}({{x}_{1}},{{x}_{2}})\). Since every finite-dimensional subspace is closed, it is obvious that \({{v}^{*}}({{x}_{1}},{{x}_{2}})\) has the representation (47). The Lemma is proved. \(\blacksquare\)
Now let us pay attention to the proof of convergence of the Kantorovich–Vlasov method.
Definition 1
We will say that an approximate solution to problem (41) and (42) is sought by the Kantorovich–Vlasov method, if the following assumptions hold:
-
(1)
the solution to problem (41) and (42) is sought in the form
$$\begin{aligned} {{u}_{N}}({{x}_{1}},{{x}_{2}})=\sum \limits _{j=1}^{N}{{{\omega }_{j}}({{x}_{1}}){{g}_{j}}({{x}_{2}})}, \end{aligned}$$(50)where: \(\forall j\text { }{{\omega }_{j}}({{x}_{1}})\in \overset{\circ }{\mathop {W_{2}^{m}}}\,({{E}_{1}}),\text { }{{g}_{j}}({{x}_{2}})\) N - known elements from the complete system of functions \(\left\{ {{\psi }_{i}}({{x}_{2}}) \right\}\), N - fixed number;
-
(2)
N unknown functions \({{\omega }_{j}}({{x}_{1}})\) are estimated from the following system of equations:
$$\begin{aligned} \begin{aligned}&\sum \limits _{\left| \alpha \right| \le m}{\int \limits _{{{E}_{1}}} {\left[ \int \limits _{{{E}_{2}}}{F({{x}_{1}},\,{{x}_{2}}) \,D_{2}^{{{\alpha }_{2}}}{{g}_{l}}({{x}_{2}})d{{x}_{2}}} \right] }\, D_{1}^{{{\alpha }_{1}}}\phi ({{x}_{1}})d{{x}_{1}}}=0, \\&F({{x}_{1}},\,{{x}_{2}})={{A}_{\alpha }}\left( x,{{D}^{\gamma }} \sum \limits _{j=1}^{N}{{{\omega }_{j}}({{x}_{1}}){{g}_{j}}({{x}_{2}})} \right) -h({{x}_{1}},{{x}_{2}}), \\&\forall \phi ({{x}_{1}})\in \overset{\circ }{\mathop {W_{2}^{m}}}\, ({{E}_{1}}),\text { }l=1,\ldots ,N. \\ \end{aligned} \end{aligned}$$(51)The formulated method with the defined assumptions satisfies the following convergence theorem.
Theorem 1
Let T be a completely continuous operator on a certain non-empty open set \(\varOmega \subset \overset{\circ }{\mathop {W_{2}^{m}}}\,({{E}_{1}}\times {{E}_{2}})\), and let Eq. (44) have an isolated solution \({{u}_{0}}\in \varOmega\) with non-zero index, then there is \({{N}_{0}}\) and \({{\delta }_{0}}\) such that when \(N\ge {{N}_{0}}\), the system of equations (51) has in the area \({{\left\| u-{{u}_{0}} \right\| }_{\overset{\circ }{\mathop {W_{2}^{m}}}\,}}\le {{\delta }_{0}}\) at least one solution \({{u}_{N}}\) and all solutions \({{u}_{N}}\) when \(N\rightarrow \infty\) tend to \({{u}_{0}}\) by the norm.
Indeed, we see that the system of equations (51) is equivalent to the system obtained from projection of Eq. (44) onto the set
where: \({{g}_{j}}({{x}_{2}})\) N - fixed elements from the system \(\left\{ {{\psi }_{i}}({{x}_{2}}) \right\}\); \(\forall j\text { }{{\omega }_{j}}({{x}_{1}})\) go over the whole space \(\overset{\circ }{\mathop {W_{2}^{m}}}\,({{E}_{1}})\), and N is the given number.
It is enough to observe that we can substitute \(v\rightarrow \phi ({{x}_{1}}){{g}_{l}}({{x}_{2}})\) to identity (43), where \(\phi ({{x}_{1}})\) is the arbitrary function from \(\overset{\circ }{\mathop {W_{2}^{m}}}\,({{E}_{1}})\). Obviously, set \({{M}_{N}}\) is linear and, as follows from the Lemma, it is a closed set. Thus, \({{M}_{N}}\) is the subspace of space \(\overset{\circ }{\mathop {W_{2}^{m}}}\,({{E}_{1}}\times {{E}_{2}})\) (in general, of infinite dimension). Taking into account the latter statement and (51), we see that Eq. (44) is projected onto subspace \({{M}_{N}}\) orthogonally, and therefore projection operator \({{P}_{N}}\) is bounded. Further, from the representation of the elements of the basic system \(\left\{ {{\theta }_{i}}({{x}_{1}},{{x}_{2}}) \right\}\) of space \(\overset{\circ }{\mathop {W_{2}^{m}}}\,({{E}_{1}}\times {{E}_{2}})\) in the form (45) it follows that the sequence of subspaces \({{M}_{N}}\) is extremely dense in \(\overset{\circ }{\mathop {W_{2}^{m}}}\,({{E}_{1}}\times {{E}_{2}})\), i.e. \(\forall y\in \overset{\circ }{\mathop {W_{2}^{m}}}\,{{\left\| {{P}_{N}}y-y \right\| }_{\overset{\circ }{\mathop {W_{2}^{m}}}\,}}\rightarrow 0,\,N\rightarrow \infty\).
The theorem is proved. This proof of the theorem is similar to the proof of the convergence of the Galerkin method for nonlinear problems (see [119]).
Comment The obtained results can be easily extended to fit the nanoplate behavior, and the authors refer to the modified Germain–Lagrange equation.
3.5.1 Analytical Solution of MGLE by KVM in the First Approximation
The approximate solution \(w\,\,(x,y)\) can be written in the form
As an initial approximation for boundary conditions (15), we take function \({{X}_{0}}(x)=\sin (\pi x)\) and use notation \(Q=\frac{q}{D}\). Substituting (53) into (18), we obtain
where \({{X}_{0}}^{(4)}=\frac{{{d}^{4}}{{X}_{0}}(x)}{d{{x}^{4}}}\).
Using the Bubnov–Galerkin method, we get
and we obtain the following differential equation:
where
The following function is used to solve Eq. (56):
where
Finally, substituting (58) into (53) we find the desired solution
Equation (56) can be solved numerically, for example, by the finite difference method (FDM) with approximation \(O({{h}^{2}})\). A very important point plays a number of partitions of variable y. Results of the study on convergence of the solution depending on the number of partitions n, are reported in Table 3 for \(\gamma =0\).
On the other hand, Table 4 shows the results achieved using the Kantorovich–Vlasov method (KVM) in the first approximation, obtained analytically (54) and numerically (\({{w}_{Ag}}\)) applying the Agranovskii–Baglai–Smirnov method (ABSM). The analytical solution of MGLE by the Kantorovich–Vlasov method in the first approximation taking into account the Agranovskii–Baglai–Smirnov approach is difficult to find. The numerical solution obtained by matching KVM + ABSM is presented in Table 4.
Let us consider the solution of Eq. (18) found via the Kantorovich–Vlasov method in the first approximation for the clamped boundary conditions (16).
As an initial approximation, we take function \({{X}_{1}}(x)={{\sin }^{2}}(\pi x)\). Similarly, for the boundary condition (15) we obtain the following solution to the original equation:
where
Coefficients \({{c}_{1}},{{c}_{2}},{{c}_{3}},{{c}_{4}}\) are determined from the boundary conditions as the solution of the following system of algebraic equations
The equations are solved using the finite difference method. Table 5 shows the deflection values depending on the number of partitions for \(\gamma =0\). The results reported in Table 5 show that \(n=55\) partitions are required to achieve convergence of the results. However, for boundary condition (15) \(n = 15\) partitions are sufficient. The increase in the number of partitions is directly related to the edge effect caused by boundary condition (16).
Table 6 gives analytical results obtained by the KVM method in the first approximation and numerical results for (\({{w}_{Ag}}\)) taking into account the ABSM method for boundary condition (16).
3.5.2 Analytical Solution of MGLE by KVM in the Second Approximation
Now, we consider a similar approach but for the second approximation of the KVM. Deflection function is represented by \(w(x,y)=\sin (\pi x){{Y}_{1}}(y)+\sin (3\pi x){{Y}_{2}}(y)\). After applying the Bubnov–Galerkin method, the following system of differential equations is obtained
or equivalently
where coefficients \({{A}_{1}}\,,\,{{C}_{1}},\,{{B}_{1}}\,,\,{{D}_{1}},{{A}_{2}}\,,\,{{C}_{2}}, \,{{B}_{2}}\,,\,{{D}_{2}}\) are defined in the following way:
Solving the system of equations (64) we get
where
Table 7 shows the results obtained using the Kantorovich–Vlasov method in the second approximation \({{w}_{2m}}\) for boundary conditions (15), while \({{w}_{1m}}\) is used in the first approximation.
Analysis of the results given in Table 7 leads to the conclusion that the analytical solution of the first approximation according to the Kantorovich–Vlasov method gives results close to those obtained by Navier, the difference is 0.9% for \(\gamma =0\), and 1.3% for \(\gamma =0.3\) and \(\gamma =\,0.5\). Obtaining an analytical solution using the Agranovskii–Baglai–Smirnov method matched with the Kantorovich–Vlasov method is problematic due to the large amount of calculations. Comparison with the results obtained by the above combinations of methods in comparison with the Navier method gives the same result, and the comparison of results obtained by the Kantorovich–Vlasov method in the second approximation with the Navier results yields the following errors: 0.3% for \(\gamma =0\), and 0.7% for \(\gamma =0.3\) and \(\gamma =0.5\). Though the Kantorovich–Vlasov method in the second approximation slightly improves the solution, it does not coincide with the exact one. Apparently, the reason for this lies in the idea of separating variables.
3.6 Variational Iteration Method (VIM)
This method presents a modification of the Kantorovich–Vlasov method (KVM). Owing to VIM, an n term trial solution for a two-dimensional problem is taken to have the following form
Here, \(\,X_{j}^{(0)}(x)\) is a priori specified, and in general may not satisfy the given boundary conditions \(\,{{Y}_{j}}^{(1)}(y)\). We employ the Bubnov–Galerkin method with regard to coordinate x and we get a set of n ordinary differential equations (ODEs) with regard to coordinate y. Its solution with an account of the boundary conditions yields the system of functions where \(\,{{Y}_{j}}^{(1)}(y)\) is substituted into (67):
Therefore, the solutions by the Kantorovich–Vlasov method coincides exactly with the first iteration in the VIM. Further, we use \(\,{{Y}_{j}}^{(1)}(y)\) obtained through KVM as the test functions \({{X}_{j}}\left( x \right)\) are unknown to be re-determined after applying the Bubnov–Galerkin method and with regard to y we obtain a set of n ordinary differential equations (ODEs) with the respect to x. They yield a set of functions \(\,{{X}_{j}}^{(1)}\), which allows us to present the solution in the following form
The so far described procedure can be repeated m-times until the result converges to a desired degree:
This method eventually removes all assumptions on both sets of \(~{{X}_{j}}\left( x \right)\) and \({{Y}_{j}}\left( y \right)\), but the accuracy of the obtained approximate solution depends on the number of trial solution terms.
3.7 Proof of the Convergence of VIM While Solving the Operator Equation
Let us present a proof of the convergence of the variational iteration method (VIM) for the operator equation reported in [38].
The scheme of VIM can be formally described in the following way. It is necessary to find a solution to the equation
where \(L\left[ w \right]\) is the operator defined on the manifold D(L) of the Hilbert space \({{L}_{2}}(\varOmega )\); \(q(x,\,\,y)\) stands for a given function of two variables x and y; \(w\,\,(x,\,\,y)\) is the searched function of the same variables; and \(\varOmega (x,\,\,y)\) is the space associated with variations of x and y.
If \(\varOmega (x,\,\,y)=T\times P\) (T - a certain bounded set of variables x, P bounded set of y), then the solution of Eq. (71) takes the form
where functions \({{X}_{i}}(x)\) and \({{Y}_{i}}(y)\) are defined by the system of equations
in the following way. A certain system composed of N functions with respect to one of the variables, for instance, \(\text { }\!\!~\!\!\text { }X_{1}^{0}\left( x \right) ,\,\,X_{2}^{0}\left( x \right) ,\ldots ,\,\,X_{N}^{0}\left( x \right)\) is given. Then, the first N equations of system (73) is determined by the system of N functions \(\text { }\!\!~\!\!\text { }Y_{1}^{1}\left( x \right) ,\,\,Y_{2}^{1}\left( x \right) ,\ldots ,\,\,Y_{N}^{1}\left( x \right)\). Next, the obtained functions are employed to create a new set of functions x, i.e. \(X_{1}^{2}\left( x \right) ,\,\,X_{2}^{2}\left( x \right) ,\ldots ,\,\,X_{N}^{2}\left( x \right)\), which is further used to construct a set of new functions with respect to variable y, i.e. \(Y_{1}^{3}\left( x \right) ,\,\,Y_{2}^{3}\left( x \right) ,\ldots ,\,\,Y_{N}^{3}\left( x \right)\), and so on.
Definition 2
The process of calculating a given system of functions by another one will be called the VIM step. The number of steps taken to determine any set of functions corresponds to the superscript (number) of functions from the set under consideration.
Breaking the process of finding functions \({{X}_{i}}\left( x \right)\) and \({{Y}_{i}}\left( y \right)\) on the k-th step (which, for example, corresponds to getting a set of functions \(\text { }\!\!~\!\!\text { }( Y_{1}^{k}( y ),\,\,Y_{2}^{k}( y ),\) \(\ldots ,\,\,Y_{N}^{k}( y ))\), allows us to construct function \(w_{N}^{k}=\underset{i=1}{\overset{N}{\mathop \sum }}\,X_{i}^{k-1}\left( x \right) Y_{i}^{k}\left( y \right) ,\) which is taken as an approximate solution to Eq. (71) obtained by the VIM.
Remark 1
Here and further on, by operator \(L\left[ w \right]\) we mean a certain differential operator, which is defined on set D(L) of Hilbert space \({{L}_{2}}\left( \varOmega \right)\). Thus, at each step, system (73) will disintegrate into the corresponding system of ordinary differential equations, with resolved the solvability problem.
Remark 2
Function \({{w}_{N}}\left( x,\,y \right)\) is called the N-th approximation of the solution for Eq. (71), if the number of terms of the series in representation (70) is equal to N.
Consider the case of the first approximation, i.e. the solution of Eq. (73) will be sought in the form \(\text { }\!\!~\!\!\text { }{{w}_{1}}\left( x,y \right) =X\left( x \right) Y\left( y \right) ,\) where functions \(X\left( x \right)\) and \(Y\left( y \right)\) are determined in the above described way from the system of equations
Let operator L in (71) be positive definite. Let us introduce the notation: \({{H}_{L}}\left( T\times P \right)\) is the energy space of operator L [123], \(\left[ \bullet ,\,\bullet \right]\) is the scalar product of elements in \({{H}_{L}};\) and \({{w}_{0}}\) is the exact solution to Eq. (71).
Theorem 2
If L is a positive definite operator with its action space \(~D\left( L \right) \subset {{H}_{L}}\),then the sequence of elements of \({{\alpha }_{k}}=w_{1}^{k}\left( x,\,y \right) -{{w}_{0}}_{{{H}_{L}}}\) is monotonically decreasing, that is, for arbitrary i and j and if \(~i\ge j\), the following inequality holds
Proof of Theorem 2
Consider subset \(M_{1}^{1}\) of space \({{H}_{L}}\), which takes the form
Obviously, set \(M_{1}^{1}\) is the subspace of space \({{H}_{L}}\left( T\times P \right)\) (in the general case the problem has infinite dimension). Accordingly, it is possible to define the projection of element \({{w}_{0}}\) onto space \(M_{1}^{1}\). It is known that to satisfy the condition for element \({{X}^{0}}\left( x \right) {{Y}^{*}}\left( y \right) \in M_{1}^{1}\) as the projection of \({{w}_{0}}\) onto \(M_{1}^{1}\) it is required that
for arbitrary elements \(\text { }\!\!~\!\!\text { }{{X}_{0}}\left( x \right) Y\left( y \right) \in M_{1}^{1}\). Hence, if \(\text { }\!\!~\!\!\text { }{{X}^{0}}\left( x \right) {{Y}^{*}}\left( y \right) \in M_{1}^{1}\), then Eq. (76) coincides with the first equation of system (64).
Consequently, element \({{X}^{0}}\left( x \right) {{Y}^{1}}\left( y \right)\), which is a result of the first step of the variational iteration method, stands as the projection of element \({{\omega }_{0}}\) onto subspace \(M_{1}^{1}\). Therefore, the inequality
for elements \(\text { }\!\!~\!\!\text { }{{X}^{0}}( x )Y( y )\in M_{1}^{1}\), holds. By a similar construction, we obtain the inequality for subspace \(M_{2}^{1}=\{ w( x,y )|w( x,y)={{X}^{0}}( x ){{Y}^{1}}( y); X( x )\in\) \({{H}_{L}}( T ),\,\,{{Y}^{1}}( y )\in {{H}_{L}}( P )\}\) which corresponds to the second step of the VIM, i.e.
for arbitrary elements \(X\left( x \right) {{Y}^{1}}\left( y \right) \in M_{2}^{1}\). From (77) and (79) it follows that \(||{{X}^{2}}\left( x \right) {{Y}^{1}}\left( y \right) -{{w}_{0}}||_{{{H}_{T}}}\le ||{{X}^{0}}\left( x \right) {{Y}^{1}}\left( y \right) -{{w}_{0}}||_{{{H}_{L}}}\). Arguments similar to those given above are valid for the functions obtained at the k-step of the VIM. Finally, the mathematical induction method proves the theorem and at the same time inequality (75). \(\square\)
Proof of the Theorem (the case of higher approximations)
The result of Theorem 1 is extended to the case of higher approximations. Namely, inequality (75) takes the following form
Further investigation requires proof of the following lemma. \(\square\)
Lemma 2
Let each element of the basis system of the space \({{H}_{L}}\) satisfy the following conditions
If the components of some basis function \(\text { }\!\!~\!\!\text { }{{\theta }_{i}}\) serve as the initial approximation of VIM, i.e. \({{X}^{0}}\left( x \right) \equiv {{\phi }_{i}}\left( x \right)\), then for any number k of steps taken by VIM, the following inequality holds \(w_{1}^{k}\left( x,y \right) -{{w}_{0}}_{{{H}_{L}}}\le \,\,\,\,c{{\phi }_{i}}\left( x \right) {{\psi }_{i}}\left( y \right) -{{w}_{0}}_{{{H}_{L}}}\), where c is the arbitrary real number.
Proof of the Lemma
Since \(\text { }\!\!~\!\!\text { }{{X}^{0}}\left( x \right) {{Y}^{1}}\left( y \right) \equiv {{\phi }_{i}}\left( x \right) {{Y}^{1}}\left( y \right)\), then by Theorem 2 we have
On the basis of the above Lemma, one criterion for VIM convergence is formulated. First, we identify the space \({{H}_{L}}\) with the space \(\overset{0}{\mathop {W_{2}^{m}}}\,\left( \varOmega \right)\), which is obtained by enclosing the norm
of the set of infinitely differentiable functions \(\overset{0}{\mathop {C_{{}}^{\infty }}}\,\left( \varOmega \right)\) with compact carrier in \(\varOmega\). \(\square\)
Theorem 3
Let each element of the basis system of the space \(\overset{0}{\mathop {W_{2}^{m}}}\,\left( T\times P \right)\) take the following form
where \(\left\{ {{\phi }_{i}}\left( x \right) \right\}\) is the basis system in space \(\overset{0}{\mathop {W_{2}^{m}}}\,\left( T \right)\), similarly \(\left\{ {{\psi }_{i}}\left( y \right) \right\}\) in space \(\overset{0}{\mathop {W_{2}^{m}}}\,\left( P \right)\) and to obtain an arbitrary N-th approximation by VIM, the base elements of the system are taken \(\left\{ {{\theta }_{i}}\left( x,y \right) \right\}\) as the first approximation. Then, for a large value of N, VIM gives a unique approximate solution \({{\omega }_{N}}\) and the sequence \(\left\{ {{w}_{N}} \right\}\) converges by the norm of the space \(\overset{0}{\mathop {W_{2}^{m}}}\,\left( T\times P \right)\) to the exact solution \({{w}_{0}}\) regardless of the number of steps k, which can be performed for every N-th approximation, i.e.
Proof of Theorem 3
If the theorem is proved for the approximations obtained in the first step of VIM, then based on the results of the Lemma it will be valid for any chosen k-th step. Therefore, we consider the N-th approximation of the solution to problem (71), which was obtained in the first step. Similarly to the statement used in Theorem 2, it can be shown that each \(w_{N}^{1}\) is the projection of the element \({{w}_{0}}\) into the subspace
where \(X_{i}^{0}\left( x \right)\) consists of N fixed elements from the system \(\left\{ {{\phi }_{i}}\left( x \right) \right\}\) for arbitrary i, \({{Y}_{i}}\left( y \right)\) takes all values from space \(\overset{0}{\mathop {W_{2}^{m}}}\,\left( P \right)\). Thus \(w_{N}^{1}={{\varPi }_{N}}{{w}_{0}}\), where \({{\varPi }_{N}}\) is the operator of an orthogonal projection on the subspace \(M_{N}^{1}\), which is bounded. Since the elements of the basis system \({{\theta }_{i}}\left( x,y \right)\) have the form (73), it is extremely dense in \(\overset{0}{\mathop {W_{2}^{m}}}\,\left( T\times P \right)\) [123]. The proof can be completed similarly to the proof of Theorem 16.2 [123]. \(\square\)
Remark 3
The results of Theorem 1 and the Lemma show that using VIM, one can obtain an approximate solution to Eq. (71) not worse than using the Ritz method in the corresponding subspace.
VIM can be extended to cover more variables. For example, if the desired solution to Eq. (71) is a function of three variables \(x,\,\,y,\,\,z\), then an approximate solution by VIM will be searched for in the form \(Q\left( x,y,z \right) =X\left( x \right) Y\left( y \right) Z(z)\), and the VIM procedure can be applied to each variable.
Remark 4
When implementing VIM, it is not necessary to construct an initial approximation that satisfies the boundary conditions of the problem. Suppose that operator \(L\left[ w \right]\) defines a boundary problem. As an initial approximation we take any function from the domain of definition of the differential operator of this problem. Then, in the first step, we obtain a system of functions satisfying the boundary conditions in one of the variables, and in the second step - in both variables.
Remark 5
These results can be extended to the equations of the nanoplate, which the authors called the modified Germain–Lagrange equation.
3.8 Variational Iteration Method for Solving MGLE
Our goal is to apply the variational iteration method to solve the modified Germain–Lagrange equation with boundary conditions (15).
The Kantorovich–Vlasov method in the first approximation yielded the solution \({{Y}_{1}}(y)={{c}_{1}}{{e}^{{{S}_{1}}y}}+{{c}_{2}}y{{e}^{{{S}_{1}}y}} +{{c}_{3}}{{e}^{-{{S}_{1}}y}}+{{c}_{4}}y{{e}^{-{{S}_{1}}y}}+{{k}_{1}}\) to Eq. (56).
As mentioned above, further the approximate solution can serve as an initial approximation to obtain the solution with respect to x. The obtained \({{Y}_{1}}(y)\) as the specified functions and \({{X}_{2}}\left( x \right)\) as unknown are to be re-determined after applying the Bubnov–Galerkin method. For this, we follow a similar procedure and, as a result, we find the function
Then, using the variational iteration procedure, we find functions \({{X}_{i}},\,{{Y}_{i}}\) that allow us to obtain a solution with a given accuracy \(\varepsilon\). The solution takes the following form:
where
Next, the Agranovskii–Baglai–Smirnov procedure is used in combination with the variational iteration method in the first term approximation. It should be mentioned that the analytical solution of the problem is not an easy task. This is why in this case, we use finite difference method of the second-order accuracy to solve the obtained ODEs. The convergence of the solution is investigated as a function of the number of partition points along the appropriate coordinate. It was found that the optimal partitioning in spatial coordinates for a hinged support is 15 points, and for clamping it is 55 points. The same partition is equal for all values of the dimensionless parameter length of material \(\gamma\).
Table 8 shows results of the analytical procedure using the variational iteration method with respect to the first term approximation for boundary conditions (15), and numerical results for \({{w}_{Ag}}\) using the Agranovskii–Baglai–Smirnov method versus the exact solution.
The solution for boundary conditions (16) will be the same as for boundary conditions (15). Following the above reasoning, we obtain function \({{Y}_{i}},\ \ {{X}_{i}}\) in the following form:
where
Table 9 shows the values of displacement w obtained analytically and displacement \({{w}_{Ag}}\) obtained using the Agranovskii–Baglai–Smirnov method, for boundary conditions (16).
A few comments on the application of the variational iteration method in the analytical and numerical solution using the Agranovskii–Baglai–Smirnov method in the first approximation are given below. The numerical results obtained by the Kantorovich–Vlasov method in the first and second term approximations, by the Kantorovich–Vlasov method using the variational iteration method and by the Agranovskii–Baglai–Smirnov method give practically the same results. The use of the variational iteration method offers the following advantage: the system of approximating functions does not need to be known, while in the Bubnov–Galerkin method two coordinates should be defined, whereas in the Kantorovich–Vlasov method it is required to know one coordinate. The system of approximating functions is obtained from the solutions of ODEs. The variational iteration procedure converges even when the set of approximating functions does not satisfy boundary conditions of the problem.
3.9 Vaindiner’s Method
Vaindiner’s method (VaM) can be considered as an extension of the Kantorovich–Vlasov method. The proof of the convergence of this method is given in [103] for a linear inhomogeneous second order equation with variable coefficients.
Consider the application of this method to the operator equation (19). This equation can be both linear and non-linear and up to the eighth order. In our case, operator equation (19) is an inhomogeneous fourth-order equation, i.e. the modified Germain–Lagrange equation. An n term trial solution is assumed in the following form
where weight functions \({{Y}_{1j}}(y)\) and \({{X}_{2j}}(x)\), and functions \({{X}_{1j}}(x)\) and \({{Y}_{2j}}(y)\) are unknown. They are determined using the Bubnov–Galerkin procedure, i.e. we have
In other words, a system of 2N ordinary differential equations is obtained. This allows us to find the \(\left\{ {{X}_{1j}}(x) \right\} _{N}^{{}}\) and \({{\left\{ {{Y}_{2j}}(y) \right\} }_{N}}\) functions, and then substituting them in (85) we get a trial solution of the problem.
3.9.1 Analytical Solution of MGLE by Vaindiner’s Method
To solve (18) with boundary conditions (15) using VaM, a trial solution takes the form \(w(x,y)=\sin (\pi x){{Y}_{11}}(y)+{{X}_{12}}(x)\sin (\pi y)\). Applying the Bubnov–Galerkin procedure, the following system of differential equations is obtained
where coefficients \({{A}_{11}}\,,\,\,{{B}_{11}}\,,{{C}_{11}},\,{{D}_{11}},{{A}_{12}}\,, \,\,{{B}_{12}}\,,{{C}_{12}},\,{{D}_{12}}\) are as follows
Solving the system of equations (87), we get
where
By substituting functions \({{Y}_{11}}(y)\) and \({{X}_{12}}(x)\) into the expression for displacement w(x, y), we obtain the desired solution. This iterative procedure can be repeated.
If function \({{Y}_{11}}(y),\,\,{{X}_{12}}(x)\) is known, we can find function \({{X}_{12}}(x),\,{{Y}_{22}}(y)\). Then
We obtain the functions
As a result, we have the following displacement function
In order to solve the modified Germain–Lagrange equation, we will use combined Vaindiner’s and the Agranovskii–Baglai–Smirnov methods (VaM+ABSM). In this case each ordinary differential equation is solved by the finite difference method with the error \(O\left( {{h}^{2}} \right)\). The convergence of the solution of ordinary differential equations depending on the number of partitions along the spatial coordinate is investigated. As a result of a numerical experiment, it is found that the required number of partitions in the finite difference method is 9 points for boundary condition (15) and 55 points for boundary condition (16).
Table 10 gives displacement \({{w}_{m}}\left( 0.5;0.5 \right)\) obtained by the analytical Vaindiner’s method and displacement \({{w}_{}}\left( 0.5;0.5 \right)\) obtained by Vaindiner’s method combined with the Agranovskii–Baglai–Smirnov method and exact Navier’s solution.
Solution for boundary conditions (16) is obtained like that for boundary conditions (15). In this case, a trial function of displacement \(w\,\,(x,y)\) takes the following form
Next, we obtain the system of equations
where
Solving the system of equations (94), we obtain
where
Substituting the obtained values into the form for the displacement, we obtain the following solution to the original equation
where
Formula (97) forms a classical solution obtained by Vaindiner’s method. However, this solution can be refined. Since we know functions \({{Y}_{11}}(y),\,\,{{X}_{12}}(x),\) we can find functions \({{X}_{12}}(x),\,{{Y}_{22}}(y)\). To do this, the iterative procedure can be repeated, and hence
As a result, we have the following displacement function
Table 11 shows the displacement obtained analytically by Vaindiner’s method for boundary conditions (16), and the numerical solution obtained by the combined methods of Vaindiner and Agranovskii–Baglai–Smirnov.
The following conclusions can be formulated. The accuracy of the solution for two types of boundary conditions obtained by the Vaindiner method is comparable to the accuracy of the solution obtained by the Kantorovich–Vlasov method and variational iteration method. It is worth noting that the solution by Vaindiner’s method and the Kantorovich–Vlasov method depends on a correct choice of the initial approximation. This limitation can be removed by using the procedure of the variational iteration method in each equation of the system obtained by the Vaindiner method (100). Like in the case of the variational iteration method, this will allow us to use any smooth function for the initial approximation.
4 Numerical Solution of MGLE by FDM and FEM
We will use the well-known methods to obtain numerical solutions for numerous PDEs of mathematical physics. This is the finite difference method (FDM) with approximation \(O\left( {{h}^{2}} \right)\) and the finite element method (FEM). Recently, these methods have been widely used in various fields of continuum mechanics. It seems interesting to compare the solutions obtained by the methods of reducing partial differential equations to ordinary differential equations with the solutions obtained by the above methods. Next, we compare the numerical solutions of the modified Germain–Lagrange equation obtained by the methods of reducing partial differential equations to ordinary differential equations with the solutions attained by the finite difference method and finite element method for some types of boundary conditions.
4.1 Finite Difference Method
Let us apply the second-order finite difference method to equation (18). We get
We obtain a system of linear equations \({{n}^{2}}\) for each grid node, where n is the number of grid nodes, each on the x and y axes. We solve this system by the Gauss method. In order to determine the values of the extreme grid nodes, we use the following boundary conditions.
For boundary conditions (15), we have
For boundary conditions (16), we have
Tables 12 and 13 show the results obtained for boundary conditions (102) and (103), using the finite difference method for a square plate under the action of a constant transverse load.
Analysis of the results shows that the material length parameter \(\gamma\) can significantly influence the results obtained. The solution for the material length parameter \(\gamma =0.3;\,\gamma =\,0.5\) coincides with Navier’s exact solution. The convergence of the solution obtained by the finite difference method depends essentially on the type of boundary conditions. Namely, for boundary conditions (103) three times more partition points are required than in the case of boundary condition (102).
4.2 Finite Element Method
In this case we will use linear triangular and quadrangular elements while employing FEM. According to the algorithm for solving the problem, the area is automatically divided into a given number of elements. The solution is obtained by the system of linear algebraic equations using the Gauss method. A convergence study is provided depending on the number of the used elements.
Table 14 shows the results of the study on convergence for the finite element method when solving the modified Germain–Lagrange equation for boundary conditions (15) at a constant transverse load \(q=7\) and for boundary conditions (16) for fixed \(q=21\), and \(\gamma =0\).
Thus, the best convergence is achieved for 11 triangular finite elements, both for boundary conditions (15) and (16).
Table 14 presents the analysis of results of the study on the convergence of the solution of the modified Germain–Lagrange equation by the finite element method. Thus, the best convergence is achieved for 11 triangular finite elements, for both boundary conditions studied. For quadrangular finite elements for both types of boundary conditions, convergence is achieved for 21 finite elements. To reduce the number of elements when solving the problem, it is possible to use symmetry of the solution and reduce the number of elements by 4 times, but in this case it was not done.
5 Comparison of Results Obtained by the Methods of Reducing PDEs to ODEs and by Numerical Methods
Previously, the equation governing bending of a nanoplate taking into account the modified couple stress theory and the method of variable parameters of elasticity has been derived. Now, it is solved by some of the already mentioned methods: the Kantorovich–Vlasov method with various modifications; variational iteration method, Vaindiner’s method, the Agranovskii–Baglai–Smirnov method, Bubnov–Galerkin method, the method of double trigonometric series approximation, the finite element method and the finite difference method.
Table 15 presents the values of the maximum displacement calculated by various methods for solving the equation of bending of a nanoplate under the action of a uniformly distributed load (\(q=7\)) for boundary conditions (15).
The analysis of the numerical results and final data reported in Table 15 shows that the solutions obtained by various numerical methods including the finite element method, finite differences method, Kantorovich–Vlasov method in N terms and the variational iteration method combined with the Agranovskii–Baglai–Smirnov method are very close to the exact solution.
The maximum difference between the exact solution and solutions obtained by other methods does not exceed 1.2%, so these methods are competitive. Methods for reducing PDEs to ODEs allow us to obtain an analytical solution with extremely high accuracy. The most important conclusion based on the obtained results is as follows. The cost of computer time when using these methods is several times cheaper than when using the numerical methods based on FEM and FDM.
In addition, Table 16 presents the values of the maximum nanoplate displacement calculated by various methods for solving the equation of bending of a nanoplate under the action of uniformly distributed load (\(q=21\)) for boundary conditions (16).
In this case, the comparative analysis of the numerical results based on the data reported in Table 16 for boundary condition (16) for square nanoplate leads to the conclusion that if \(\gamma =0.3,\,\,\,\gamma =0.5\) the results of all methods are quite close. The largest differences in the solutions arise when \(\gamma =0\). It should be emphasized that the values of solutions by the mentioned methods devoted to the reduction of PDEs to ODEs are close to each other and their difference is 0.6%.
In addition, we have compared the number of algebraic equations while employing the Kantorovich–Vlasov method, variational iteration method, Vaindiner’s method, FEM and FDM. Table 17 shows a comparison of the number of equations required to solve Eq. (18) at \(\gamma =0\) for boundary conditions (15). The following notation is used: n is the number of equations, N - is the number of iterations (if necessary), \(n*N\) is the total number of equations to obtain a solution.
Table 17 presents the results of analysis for different number of equations for \(\gamma =0\), and for various methods.
The same is done in Table 18 but for \(\gamma =0.5\).
We have also analyzed the same problem regarding equation (14) for \(\gamma =0\) for boundary conditions (16) (see Table 19).
The same analysis has been extended for the case when \(\gamma =0.5\) (see Table 20).
Based on the analysis of Tables 17, 18, 19 and 20, it can be concluded that in terms of computer time the most expensive are the finite difference and finite element methods.
The analysis of the numerical results given in Tables 17, 18, 19 and 20 leads to the conclusion that in terms of computer time the most expensive are the finite difference and finite element methods. The methods that reduce the original problem for a partial differential equation to solving an ordinary differential equation use a one-dimensional grid. This leads to a decrease in the number of algebraic equations and an increase in the speed of obtaining a solution.
6 Concluding Remarks
This article presents a comprehensive review of the literature on methods of reducing nonlinear partial differential equations to a set of nonlinear differential equations with emphasis put on their reliability, validity, accuracy and computational efficiency. Since the nonlinear PDEs govern dynamic and static behavior of numerous systems in mechanics, aeronautics and civil engineering, a proper choice of the feasible computational method to study mass distributed mechanical systems based on the signal processing plays an important role in the system modeling, identification, monitoring and control.
The classical methods aimed at solving the problem have their origin in mathematical physics. However, the problem has not yet been fully resolved and, as our review has shown, it requires revision and more attention to the known methods of finite elements and finite differences widely used in engineering community but not well recognized as competitive approaches. The methodology is well known: a given multidimensional problem should be substituted by its counterpart sequence of one-dimensional problems. However, the obtained results strongly depend on the used methods, which answer numerous questions and require checking of the authenticity, reliability, validity, stability of results, etc.
The following methods have been reviewed and examined due to their state-of-the art levels of performance and computational advantages: the Fourier methods, the Galerkin-type methods, the variational methods, the variational iterations, the Kantorovich–Vlasov methods, Vaindiner’s method, the Agranov- skii-Baglai-Smirnov method with respect to the archetypal finite element and finite difference methods.
The quantification and comparison of the tested (above mentioned) methods was carried out on the basis of the modified Germain–Lagrange PDE governing the dynamics of a nanoplate and with comparison to the exact results obtained on the basis of Navier’s method.
Although the paper has a review character, it includes also our original results. The whole work can be briefly summarized based on the following major conclusions.
-
A mathematical model of Germain–Lagrange nanoplates, taking into account the physical nonlinearity and inhomogeneity of the material, has been derived.
-
The comparative analysis of numerous methods, including the Kantorovich–Vlasov method, the variational iteration method, and Vaindiner’s method aiming at the reduction of PDEs to ODEs was carried out for the first time.
-
For each method described above, theorems have been both formulated and proved and thus their mathematical justification has been given.
-
The proven convergence theorems for solutions obtained by the Kantorovich–Vlasov methods and variational iteration method can be applied to solve the modified Germain–Lagrange equations.
-
The solutions obtained by the mentioned methods of reducing the equations of mathematical physics to ordinary differential equations have been compared with the exact Navier solution obtained by the authors for the modified Germain–Lagrange equation.
-
These methods appeared to be effective. The computation time for obtaining a solution by these methods is much shorter than the computation with the use of either the finite difference or finite element methods.
-
A numerical experiment has shown that the investigated methods of reducing partial differential equations to ordinary differential equations are highly accurate. They provide a solution with an error of less than 1 percent.
-
The convergence to the exact solution for the investigated methods has been significantly improved for nanostructures.
-
For the first time, we have proposed to use the procedure for refining solutions based on the Agranovskii–Baglai–Smirnov method while reducing PDEs to ODEs for problems in the theory of nanoplates.
-
When solving ODEs numerically, it has been found that the accuracy of solution depends on the type of boundary conditions and the number of partition intervals.
-
Analysis of the methods for reducing elliptic PDEs of mathematical physics to ODEs allows drawing conclusions about their effectiveness in solving problems of the theory of plates, taking into account physical nonlinearity and material heterogeneity.
-
The presented review and analysis of the methods imply that they can be applied to hyperbolic equations of mathematical physics, including construction of an iterative procedure within the algorithms of the Faedo–Galerkin method.
References
Fourier J (1822) Théorie Analytique de la Chaleur. Firmin Didot Pére et Fils, Paris
Secondini M (2020) Information capacity of optical channels. Opt Fibre Telecommun VI I:867–920
Agrawal G (2013) Nonlinear fiber optics. Academic Press, Oxford
Bloomfield P (2001) Fourier analysis of time series: an introduction, 2nd edn. Wiley, New York
Proakis JG, Manolakis DK (2014) Digital signal processing, 4th edn. Pearson Education Limited, Edinburg
Chatfield Ch (2003) The analysis of time series: an introduction, 6th edn. Chapman and Hall, Boca Raton
Fornberg B (1975) On a Fourier method for the integration of hyperbolic equations. SIAM J.Numer Anal 12(4):509–528
Kreiss H-O, Oliger J (1977) Stability of the Fourier method. Stanford University, Stanford
Majda A, McDonough J, Osher S (1978) The Fourier method for nonsmooth initial data. Math Comput 32(144):1041–1081
Kosloff D, Reshef M, Loewenthal D (1984) Elastic wave calculations by the Fourier method. Bull Seismol Soc Am 74(3):875–891
Peyret R (2002) Spectral methods for incompressible viscous flow. Springer, New York
Ritz W (1909) Über eine neue Methode zur Lösung gewisser Variations Problem der Mathematischen Physik. J Reine Angew Math 135:1–61
Galerkin BG (1915) Beams and plates. Series in some questions of elastic equilibrium of beams and plates. Vest Inger 19:897–908 (in Russian)
Mikhlin SG (1964) Variational methods in mathematical physics. Pergamon, Oxford
Axelsson O, Barker VA (1984) Finite element solution of boundary value problems. Theory and computation. Academic Press, New York
Rashedi K, Adibi H, Dehghan M (2013) Application of the Ritz–Galerkin method for recovering the spacewise-coefficients in the wave equation. Comput Math Appl 65(12):1990–2008
Gomes S, Cortina E (1997) Fourier analysis of Petrov–Galerkin methods based on biorthogonal multiresolution analysis. In: D’Attellis CE, Fernandez-Berdaguer EM (eds) Wavelets theory and harmonic analysis in applied sciences. Birkhauser, Boston, pp 119–140
Schoombie SW (1982) Spline Petrov–Galerkin methods for the numerical solution of the Kortveg-de Vries equation. IMA J Numer Anal 2:95–109
Villegas JG, Castano JB (2012) Wavelet-Petrov–Galerkin method for the numerical solution of the KdV equation. Appl Math Sci 6(69):3411–3423
Chiavassa G, Liandrat JA (2001) A fully adaptive wavelet algorithm for parabolic partial differential equations. Appl Numer Math 36:333–358
Gawinecki JA (1987) The Faedo–Galerkin method in thermal stresses theory. Comment Math 27(1):83–107
Zeidler E (1990) Nonlinear functional analysis and its applications. II/A: linear monotone operators. Springer, New York
Xu Y, Shu Ch-W (2010) Local discontinuous Galerkin methods for high-order time-dependent partial differential equations. Commun Comput Phys 7:1–46
Noack BR, Eckelmann H (1994) A low-dimensional Galerkin method for the three-dimensional flow around a circular cylinder. Phys Fluids 6:124–129
Feng X, Wu H (2011) hp-discontinuous Galerkin methods for the Helmholtz equation with large wave number. Math Comput 80:1997–2024
Mu L, Wang J, Ye X, Zhang S (2015) A weak Galerkin finite element method for the Maxwell equations. J Sci Comput 65:363–386
Du Y, Zhu L (2016) Preasymptotic error analysis of high order interior penalty discontinuous Galerkin methods for the Helmholtz equation with high wave number. J Sci Comput 67:130–152
Zhai Q, Zhang R, Mu L (2016) A new weak Galerkin finite element scheme for the Brinkman model. Commun Comput Phys 19:1409–1434
Musa AES (2017) Galerkin method for bending analysis of beams on non-homogeneous foundation. J Appl Math Comput Mech 16(3):61–72
Repin S (2017) One hundred years of the Galerkin method. Comput Methods Appl Math 17(3):351–357
Kantorovich LV, Krylov VI (1958) Approximate methods of higher analysis. Inter Science Publishers, New York
Vlasov VZ (1932) A new practical method to design folded-plate structures and shells. Stroit Promyshlen 11:33–38
Grigorenko Ya M, Vasilenko AT (1981) Theory of shells of variable rigidity, vol 4. Naukova Dumka, Kyiv (in Russian)
Grigorenko Ya M, Bespalova EI, Kitaigorodskii AB, Shinkar AI (1986) Free vibrations of elements of shell structures. Naukova Dumka, Kyiv (in Russian)
Grigorenko Ya M, Vasilenko AT, Golub GP (1987) Statics of anisotropic shells with finite shear stiffness. Naukova Dumka, Kyiv (in Russian)
Grigorenko Ya M (2007) Nonconventional approaches to static problems for noncircular cylindrical shells in different formulations. Int Appl Mech 43(1):35–53
Krysko VA (1976) Nonlinear statics and dynamics of nonhomogeneous shells. Saratov University Press, Saratov
Kirichenko VF, Krysko VA (1981) The variational iteration method in the theory of plates and shells and its justification. Appl Mech XVI(4):71–76
Kirichenko VF, Krysko VA (1980) On the question of the solving of nonlinear boundary value problems by the Kantorovich-Vlasov method. Differ Equ 16(12):2186–2189
Bespalova EI (1989) Solving problems of elasticity by methods of complete systems. Zh Vych Mat Mat Fiz 29(9):1346–1353
Bespalova EI (2007) Vibrations of polygonal plates with various boundary conditions. Int Appl Mech 43(5):526–533
Bespalova EI (2008) Solving stationary problems for shallow shells by a generalized Kantorovich–Vlasov method. Int Appl Mech 44(11):1283–1293
Bespalova EI, Urusova GP (2010) Solving the torsion problem for an anisotropic prism by the advanced Kantorovich-Vlasov method. Int Appl Mech 46(11):149–158
Bespalova EI (2011) Determining the natural frequencies of an elastic parallelepiped by the advanced Kantorovich–Vlasov method. Int Appl Mech 47(4):410
Surianinov M, Chaban V (2015) About the use of numerical, analytical boundary element method to calculate anisotropic plate. Eng Mech 22(2):103–108
Nwoji CU, Mama BO, Onah HN, Ike CC (2017) Kantorovich–Vlasov method for simply supported rectangular plates under uniformly distributed transverse loads. Int J Civ Mech Energy Sci 3(2):69–77
Kerr AD (1968) An extension of the Kantorovich method. Q Appl Math 4:219–229
Kapuria S, Kumari P (2011) Extended Kantorovich method for three-dimensional elasticity solution of laminated composite structures in cylindrical bending. J Appl Mech Trans ASME 78:061004
Aghdam MM, Shahmansouri N, Mohammadi M (2012) Extended Kantorovich method for static analysis of moderately thick functionally graded sector plates. Math Comput Simul 86:118–130
Wu X, Huang C, Sun J (2013) Kantorovich solution for bimodulous simply supported beam under linear distributed loads. J Cent South Univ 44(5):2082–2087
Tahani M, Mousavi SM (2013) Analytical solution for bending problem of moderately thick composite annular sector plates with general boundary conditions and loadings using multi-term extended Kantorovich method. Arch Appl Mech 83(6):969–985
Fallah A, Kargarnovin MH, Aghdam MM (2011) Free vibration analysis of symmetrically laminated fully clamped skew plates using extended Kantorovich method. Key Eng Mat 471–472:739–744
Fallah A, Aghdam MM, Kargarnovin MH (2013) Free vibration analysis of moderately thick functionally graded plates on elastic foundation using the extended Kantorovich method. Arch Appl Mech 83(2):177–191
Singhatanadgid P, Wetchayanon T (2014) Vibration analysis of laminated plates with various boundary conditions using extended Kantorovich method. Struct Eng Mech 52(1):115–136
Kapuria S, Kumari P (2012) Multiterm extended Kantorovich method for three-dimensional elasticity solution of laminated plates. J Appl Mech Trans ASME 79(6):061018
Kumari P, Kapuria S, Rajapakse RKND (2013) Three-dimensional extended Kantorovich solution for Levy-type rectangular laminated plates with edge effects. Compos Struct 107:167–176
Huang B, Wang J, Du J, Guo Y, Ma T, Yi L (2016) Extended Kantorovich method for local stress in composite laminates upon polynomial stress functions. Acta Mech Sin 32(5):854–865
Kumari P, Behera S (2017) Three-dimensional free vibration analysis of Levy-type laminated plates using multi-term extended Kantorovich method. Compos Part B 116:224–238
Ike ChCh, Mama BO (2018) Kantorovich variational method for the flexural analysis of CSCS Kirchhoff–Love plates. Math Mod Eng 4(1):29–41
Courant R, Hilbert D (1953) Methods of mathematical physics. Wiley, New York
Weinstock R (1974) Calculus of variations with applications to physics and engineering. Dover Publications, New York
Hildebrand FR (1992) Methods of applied mathematics. Dover Publications, New York
Wan FYM (1995) Introduction to the calculus of variations and its applications. Chapman and Hall, London
Gelfand IM, Fomin SV (2000) Calculus of variations. Dover Publications, New York
Masterton-Gibbons M (2009) A primer on the calculus of variations and optimal control theory. American Mathematical Soc, Providence
Courant R (1943) Variational methods for the solution of problems of equilibrium and vibrations. Bull Am Math Soc 49(1):1–23
Marsden JE, Pekarsky S, Shkoller S, West M (2001) Variational methods, multisymplectic geometry and continuum mechanics. J Geom Phys 38(3–4):253–284
Souza de Cursi E (2015) Variational methods for engineers with Matlab. Wiley, New York
Mura T, Koya T (1992) Variational methods in mechanics. Oxford University Press, New York
Reddy JN (2002) Energy principles and variational methods in applied mechanics. Wiley, New York
Basdevant JL (2007) Variational principles in physics. Springer, Berlin
Tabarrok C (2010) Variational methods and complementary formulations in dynamics. Springer, Berlin
Mordukhovich BS (2018) Variational analysis and applications. Springer, Berlin
Kravvaritis DC, Yannacopoulos AN (2020) Variational methods in nonlinear analysis with applications in optimization and partial differential equations. De Gruyter, Berlin
Schunk TE (1933) Zur Knienfestigkeit schwach gekrummter zylindrischer Schalen. Ing Arch IV:394–414
Zhukov EE (1964) Variational technique of successive approximations as applied to the calculation of thin rectangular plates. In: Rzhanitsin AR (ed) Calculation of thin-walled spatial structures. Stroizdat, Moscow, pp 27–35
Kerr AD (1968) An extension of the Kantorovich method. Q Appl Math 26:219–229
Kerr AD, Alexander H (1968) An application of the extended Kantorovich method to the stress analysis of a clamped rectangular plate. Acta Mech 6:180–196
Kerr AD (1969) An extended Kantorovich method for the solution of eigenvalue problems. Int J Solids Struct 5:559–572
He JH (1997) A new approach to nonlinear partial differential equations. Commun Nonlinear Sci Numer Simul 2:230–235
He JH (1999) Variational iteration method: a kind of nonlinear analytical technique: some examples. Int J Nonlinear Mech 34:699–708
Tatari M, Dehghan M (2007) On the convergence of He’s variational iteration method. J Comput Appl Math 207:121–128
Salkuyeh DK (2008) Convergence of the variational iteration method for solving linear systems of ODE with constant coefficients. Comput Math Appl 56:2027–2033
Torvattanabun M, Koonprasert S (2009) Convergence of the variational iteration method/solving a first-order linear system of PDEs with constant coefficients. Thai J Math 56:1–13
Odibat ZM (2010) A study on the convergence of variational iteration method. Math Comput Model 51:1181–1192
Salkuyeh DK, Tavakoli A (2015) Interpolated variational iteration method. J Comput Appl Math 207:121–128
Solodov MV, Svaiter BF (1999) A new projection method for variational inequality problems. SIAM J Control Optim 37(3):765–776
Matinfar M, Saeidy M, Raeisi Z (2011) Modified variational iteration method for heat equation using He’s polynomials. Bull Math Anal Appl 3(2):238–245
Noor MA, Mohyud-Din ST (2007) Variational iteration decomposition method for solving eighth-order boundary value problems. Differ Equ Nonlinear Mech 2007:19529
Ji-Huan He (2007) Variational iteration method-some recent results and new interpretations. J Comput Appl Math 207:3–17
He J-H, Wu X-H (2007) Variational iteration method: new development and applications. Comput Math Appl 54(7–8):881–894
Barari A, Omidvar M, Ghotbi AR, Ganji DD (2008) Application of homotopy perturbation method and variational iteration method to nonlinear oscillator differential equations. Acta Appl Math 104(2):161–171
Saadatmandi A, Dehghan M (2009) Variational iteration method for solving a generalized pantograph equation. Comput Math Appl 58(11–12):2190–2196
Abbasbandy S, Shivanian E (2009) Application of the variational iteration method for system of nonlinear Volterra’s integro-differential equations. Math Comput Appl 14(2):147–158
Salehpoor E, Jafari H (2011) Variational iteration method a tools for solving partial differential equations. J Math Comput Sci 2(2):388–393
Heydari M, Loghmani GB, Hosseini SM, Yildirim A (2013) A novel hybrid spectral-variational iteration method (HS-VIM) for solving nonlinear equations arising in heat transfer. Iran J Sci Technol Trans A Sci 37(4):501–512
Wazwaz A-M (2014) The variational iteration method for solving linear and nonlinear ODEs and scientific models with variable coefficients. Cent Eur J Eng 4(1):64–71
Zhang F, Shi Y, Li J, Wu K, Iwabuchi H (2017) Variational iteration method for infrared radiative transfer in a scattering medium. J Atmos Sci 74:419–430
Narayanamoorthy S, Mathankumar S (2018) Variational iterative method: an appropriate numerical scheme for solving system of linear Volterra fuzzy integro-differential equations. Adv Differ Equ 2018:394
Elsayed T, El-Mongy H (2018) Application of variational iteration method to free vibration analysis of a tapered beam mounted on two-degree of freedom subsystems. Appl Math Model 58:349–364
Vaindiner AI (1967) On a new form of Fourier series and the choice of best Fourier polynomials. USSR Comput Math Math Phys 7(1):240–251
Vaindiner AI (1969) On estimation of the remainder of a generalized Fourier series for differentiable functions of two variables. Dokl Akad Nauk SSSR 184(3):511–513
Vaindiner AI (1968) The convergence of a certain direct method. USSR Comput Math Math Phys 8(4):285–293
Vaindiner AI (1970) Approximation of continuous and differentiable functions of several variables by generalized polynomials (by finite linear superposition of functions of fewer variables). Dokl Akad Nauk SSSR 192(3):483–486
Vaindiner AI (1973) The interpolation of functions of many variables by generalized polynomials and lattice collocation method for solving equations of mathematical physics. USSR Comput Math Math Phys 13(4):326–328
Vaindiner AI (1973) Generalized polynomials, deviating least from zero, and effective direct methods for solving boundary-value problems. Dokl Akad Nauk SSSR 210(6):1265–1268
Vaindiner AI, Moskvitin VV (1976) Singular integral equations in three-dimensional problems of elasticity theory. Regularization, cubature formulas, differential properties, and approximate methods of solution. Dokl Akad Nauk SSSR 228(6):1310–1313
Mushtari ChM, Galimov KZ (1957) Nonlinear theory of elastic shells. Tatknigoizdat, Kazan
Krysko AV, Awrejcewicz J, Pavlov SP, Zhigalov MV, Krysko VA (2014) On the iterative methods of linearization, decrease of order and dimension of the Karman-type PDEs. Sci World J 2014:792829
Krysko AV, Awrejcewicz J, Zhigalov MV, Krysko VA (2016) On the contact interaction between two rectangular plates. Nonlinear Dyn 84(4):2729–2748
Awrejcewicz J, Krysko AV, Krylova EYu, Yaroshenko TY, Zhigalov MV, Krysko VA (2020) Analysis of flexible elastic–plastic plates/shells behavior under coupled mechanical/thermal fields and one-sided corrosion wear. Int J Nonlinear Mech 118:103302
Awrejcewicz J, Krysko VA, Papkova IV, Krysko AV (2016) Deterministic chaos in one-dimensional continuous systems. World Scientific, Singapore
Krysko VA, Awrejcewicz J, Zhigalov MV, Kirichenko VF, Krysko AV (2019) Mathematical models of higher orders. Springer, Berlin
Awrejcewicz J, Krysko VA (2020) Elastic and thermoelastic problems in nonlinear dynamics of structural members. Applications of the Bubnov–Galerkin and finite difference methods. Springer, Berlin
Rega G, Settimi V, Lenci S (2020) Chaos in one-dimensional structural mechanics. Nonlin Dyn. https://doi.org/10.1007/s11071-020-05849-3
Yang F, Chong ACM, Lam DCC, Tong P (2002) Couple stress based strain gradient theory for elasticity. Int J Solids Struct 39:2731–2743
Birger IA (1951) Some general solution methods for problems in plasticity theory. Appl Mat Mech 15(6):765–770 (in Russian)
Baglai RD, Smirnov KK (1975) To processing two-dimensional signals on a computer. Zh Vychisl Mat Mat Fiz 15(1):241–248 (in Russian)
Agranovskii ML, Baglai RD, Smirnov KK (1978) Identification of a class of nonlinear operators. Zh Vychisl Mat Mat Fiz 18(2):284–293 (in Russian)
Chakrabarty J (2006) Theory of plasticity, 3rd edn. Elsevier, Amsterdam
Timoshenko SP (1907) Longitudinal bending of rods in an elastic medium. Bull St Petersburg Polytech Inst 7(1):145–157 (in Russian)
Galerkin BG (1915) Rods and plates. Series in some questions of elastic equilibrium of rods and plates. Eng Bull I(19):897–908
Krasnoselskii MA, Vaynikko GM, Zabreyko PP, Rutitskii NB, Stetsenko V. Ya. (1969) Approximate solution of operator equations. Nauksa, Moscow (in Russian)
Acknowledgements
This work has been supported by the Polish National Science Centre under the Grant PRELUDIUM 16 No. 2018/31/N/ST8/00707 and OPUS 14 No. 2017/27/B/ ST8/01330.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Awrejcewicz, J., Krysko-Jr., V.A., Kalutsky, L.A. et al. Review of the Methods of Transition from Partial to Ordinary Differential Equations: From Macro- to Nano-structural Dynamics. Arch Computat Methods Eng 28, 4781–4813 (2021). https://doi.org/10.1007/s11831-021-09550-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11831-021-09550-5