Abstract
Metamodels aim to approximate characteristics of functions or systems from the knowledge extracted on only a finite number of samples. In recent years kriging has emerged as a widely applied metamodeling technique for resource-intensive computational experiments. However its prediction quality is highly dependent on the size and distribution of the given training points. Hence, in order to build proficient kriging models with as few samples as possible adaptive sampling strategies have gained considerable attention. These techniques aim to find pertinent points in an iterative manner based on information extracted from the current metamodel. A review of adaptive schemes for kriging proposed in the literature is presented in this article. The objective is to provide the reader with an overview of the main principles of adaptive techniques, and insightful details to pertinently employ available tools depending on the application at hand. In this context commonly applied strategies are compared with regards to their characteristics and approximation capabilities. In light of these experiments, it is found that the success of a scheme depends on the features of a specific problem and the goal of the analysis. In order to facilitate the entry into adaptive sampling a guide is provided. All experiments described herein are replicable using a provided open source toolbox.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Computational models play a more and more significant role for many applications in engineering, including computationally demanding studies such as optimization [87], sensitivity analysis [46], classification [31], reliability analysis [24] or fatigue [6]. Metamodels or surrogate models have appeared appealing to reduce intensive computational costs [27, 83, 113]. Common techniques such as support vector machines [35], kriging or Gaussian processes [89] and neural networks [99] have been extensively reviewed [2, 66, 84].
Metamodel scheme: samples lying in a parametric domain are evaluated from an expensive black box (experiment or simulator), then results are exploited to build a metamodel on the whole domain (inspired by Crombecq et al. [20])
A general metamodel process is schematized in Fig. 1. Samples are distributed in a user-defined parametric space. The relevant black-box function is thereafter evaluated at each sample point and results are exploited to fit the surrogate model over the whole parametric domain. Hence, the accuracy of the resulting metamodel is highly dependent on the samples. Moreover, because evaluating the black-box function may be computationally demanding for engineering applications, a further goal in the process is to reduce the number of samples as much as possible, while generating a proficient surrogate model.
Within this context, since the groundbreaking work of Sacks et al. [91], a large variety of adaptive sampling techniques have been proposed for kriging [13, 30, 37, 47, 54, 55, 71]. Kriging, originally developed by Krige [57] for use in geostatistics, has been expanded to computer experiments with both deterministic [91] and random [106] nature. Its interpolative and stochastic properties make it very attractive, and so it is referred to as the most intensively investigated metamodel in Jiang et al. [43].
To circumvent the limitation of one-shot sampling, sequential sampling techniques have been proposed since the 1950s [14, 90], including two families, space-filling and adaptive design, as illustrated in Fig. 2. Space-filling techniques aim to spread the samples evenly in an iterative manner, whereas using adaptive sampling techniques, new samples are designed based on information extracted during previous iterations in order to place them in locations of high interest. These approaches have received increasing attention in recent years, from the 1990s for neural networks [15, 36] and later for support vector machines [56, 85].
Existing reviews have offered an overview of existing adaptive sampling strategies, focusing either on space-filling techniques [48, 51, 88], or on adaptive design [72]. However, there is a lack of exhaustive comparisons between alternative adaptive techniques suggested in the literature. Oftentimes presented techniques are just compared to a small selection of other adaptive algorithms, or even compared only to one-shot or space-filling approaches. Furthermore comparisons are generally performed on a low number of reference functions, which restricts the scope of the analysis and does not allow to draw general conclusions about algorithms.
The goal of the comparative review proposed here is to provide a sound analysis of the state-of-the-art for adaptive design in kriging metamodeling, such that users can find orientation within the dense literature to choose the most pertinent method for the problem of interest. The scope is restricted to single-fidelity and single-selection adaptive sampling techniques. Space-filling techniques are mainly excluded, and deterministic regression-based simulations are assessed for both global metamodeling and optimization. Characterizing features of existing methods are exposed, such that they can be categorized. Furthermore, a comparative review is performed on a broad spectrum, including various reference functions and adaptive techniques based on different characteristics. For sound analysis and understanding, results can be replicated using a MATLAB [78] implementation of all investigated techniques as well as investigated benchmark tests, which is supplied on Github.
The review is organised as follows. In Sect. 2 an overview of ordinary kriging surrogate model is given. Then, in Sect. 3, goals and general features of adaptive schemes for ordinary kriging are introduced. Different exploitation strategies are exposed in Sect. 4, then exploration approaches are presented in Sect. 5. Adaptive schemes are generally based on a combination of both perspectives. Schemes proposed in the literature are reviewed in Sect. 6. Finally, in Sect. 7, existing methods are compared on various benchmark problems, including both analytical functions and mechanical problems, and a short guidance for users is offered in Sect. 8 with regards to choosing an adaptive technique for a given application.
2 Ordinary Kriging
Among kriging metamodeling, several families, such as simple kriging, ordinary kriging and universal kriging, may be distinguished depending on considered assumptions leading to different complexity levels (see [52]). Ordinary kriging is highlighted as the most commonly used technique, due to better accuracy compared to simple or universal kriging for many reference problems (see [53]). Thus, the focus herein is restricted to ordinary kriging though all the mentioned adaptive techniques are also applicable for simple as well as for universal kriging.
Ordinary kriging is briefly summarized here, the reader can refer to Santner et al. [92] for proof and further details. Consider a black-box function \({\mathcal{M}}: {\mathbb{X}} \rightarrow {\mathbb{Y}}\) between an input \(\varvec{x} \in {\mathbb{X}} \subset {\mathbb{R}}^{n}\) and a univariate output \(y \in {\mathbb{Y}} \subset {\mathbb{R}}\). Furthermore consider some existing samples \(\chi = \lbrace \varvec{x}^1, \ldots , \varvec{x}^m \rbrace \) corresponding with a set of training data
Using ordinary kriging the exact mapping \({\mathcal{M}}\) between input and output data is approximated as the mean of a stochastic process Y defined as follows,
i.e. a combination of a global mean contribution denoted \(\mu \) and a localized variation contribution in terms of a stationary Gaussian process denoted \(Z(\varvec{x})\). The element ij of the covariance matrix \(\varvec{Cov}\) relative to this stochastic process yields
with cov the covariance operator, \(\sigma \) the standard deviation of the stochastic process and \(\varvec{R}_{ij}(\varvec{\theta })\) the correlation between outputs corresponding with two samples \(\varvec{x}^{i}\) and \(\varvec{x}^{j}\), defined as the component of the autocorrelation matrix \(\varvec{R}\), also named correlation matrix. The correlation function R, which depends on unknown correlation parameters \(\varvec{\theta }\), is usually chosen by the user. Correlation parameters are estimated as solution of an optimization problem [5], and the elements of the correlation matrix read \(\varvec{R}_{ij}= R(\varvec{x}^{i},\varvec{x}^{j},\varvec{\theta })\).
Thus, the idea of kriging metamodeling is to obtain \(\widehat{{\mathcal{M}}}\) the most accurate approximation of \({\mathcal{M}}\) for any point \(\varvec{x}^0\) belonging to \({\mathbb{X}}\) as the mean of the realizations of the stochastic process defined by Eq. (2) at that point i.e.
The best linear unbiased predictor for any unobserved value \(y^{0}\) corresponding with \(\varvec{x}^{0} \in {\mathbb{X}}\) yields
with \(\varvec{1}\) the vector with m components equal to 1 and \(\varvec{y}\) the vector gathering the m observation outputs. The prior estimation of the global mean denoted \({\widehat{\mu }}\) is obtained through a generalized least-square estimate as
It can be seen that it depends on the choice of the autocorrelation structure. The vector \(\varvec{r}_{0}\) collects the crosscorrelations between \(\varvec{x}^{0}\) and every sample point as
Besides, information about the variance of the metamodel can be extracted for any point \(\varvec{x}^{0}\) as
with
and the prior estimation of the global variance which reads
Similarly to the prior estimation of the mean, prior estimation of the global variance depends also on the correlation matrix.
3 Goals and General Features of Adaptive Schemes
In this paper the state-of-the-art for selecting the best design of experiments \({\mathcal{X}} = \lbrace \varvec{x}^{i}, \, i=1, \, \ldots , \, m \rbrace \) for kriging metamodeling is explored. The best design of experiments means the set of tests, which should be employed in order to be the most informative with respect to the quality of the emulator \(\widehat{{\mathcal{M}}}\) in substituting \({\mathcal{M}}\) over the entire input space \({\mathbb{X}}\), or with respect to the accuracy of the surrogate estimation of any quantity of interest. By reducing the number of observations, computational or experimental cost and time effort, depending on the usage, could be reduced.
3.1 Reducing the Number of Observations
An efficient metamodel should be based on as few sample points m as possible. Indeed, a surrogate model is constructed to emulate and so to replace computationally expensive simulation models. Therefore, the strategy appears interesting and viable only if the cost for building the surrogate model and exploiting it for the purpose of interest (e.g. optimization, reliability analysis, parametric investigation) is significantly smaller comparing with the cost of the same analysis based on the exact simulator \({\mathcal{M}}\). On the contrary, if the number of experiments is relatively large, obtaining the metamodel \(\widehat{{\mathcal{M}}}\) may turn into an overwhelming computational task, even possibly an insoluble numerical problem, which would ruin the interest of the strategy [26].
Principle of adaptive kriging surrogate process [30]
The principle of adaptive schemes to define the best experiments for kriging metamodel is illustrated in Fig. 3. From an initial design of experiments, an exact simulator \({\mathcal{M}}\) is evaluated in designed points and so information is available and employed to build the metamodel. That metamodel is intrinsically uncertain in terms of epistemic uncertainty, i.e. uncertainty due to a lack of knowledge which can be reduced by gaining more information. Thus, the metamodel is analyzed to identify where further experiments should be performed to benefit the most from supplementary information to reduce the lack of knowledge. Incorporating this new sample, a further experiment based on the exact simulator \({\mathcal{M}}\) is performed and an updated metamodel is built, which remains epistemically uncertain, and so the lack of knowledge corresponding with the current metamodel can be further assessed, and a new sample can be chosen. This loop is repeated until a stopping criterion is reached.
Because detailed knowledge of the mapping \({\mathcal{M}}\) is a priori unavailable, gauging the size of the experimental design required to reach a certain accuracy is generally a challenge. Sequential design and more particularly adaptive sampling techniques are appealing to build the design of experiments through an iterative procedure, which allows to observe the behaviour evolution.
Adaptive sampling approaches can be classified with respect to the number of sample points which are added per iteration [72]. Design based on single-selection procedures adds only one point per iteration. On the contrary, batch-selection strategies refer to algorithms in which several sample points are added simultaneously at each iteration. This approach is generally preferred in case the surrogate model is constructed from parallelized estimations of sample outputs, for instance using several cores for numerical estimation. However, the usage of auxiliary optimization procedures for defining the new sample points is rather conducive to single selection, as used for most adaptive sampling strategies proposed in the literature [72]. Hence, only single-selection approaches will be thoroughly discussed here.
3.2 Steps of Adaptive Sampling Schemes
The general algorithm workflow of an adaptive sampling technique for global metamodeling is depicted in Fig. 4. Consider an initial design of experiments \(\chi = \lbrace \varvec{x}^1, \ldots , \varvec{x}^m \rbrace \) associated with a data set as defined in Eq. (1). The creation of the surrogate model begins by fitting \(\widehat{{\mathcal{M}}}\) from this data. Then, supplementary sample points are included to the dataset \({\mathcal{D}}\) through successive iterations until reaching a convergence or stopping criterion.
3.2.1 Initial Design of Experiments
For starting the adaptive sampling procedure, an initial data set is required for building the first metamodel. Either one-shot or sequential space-filling sampling procedures can be considered for that step. Latin Hypercube Design (LHD) is a very classical technique for defining the initial data set [52], because it is an efficient space-filling sampling technique, particularly for initial data sets including very few sample points [19].
Initial Sampling Algorithm
After building a hypercube denoted \(\left[ 0, m-1 \right] ^{n}\) on the input parametric space \({\mathbb{X}}\), n-dimensional LHD creates a set of m points of the form \(\varvec{x}^{i} \in \left[ 0, \, \ldots , \, m-1 \right] ^{n}\) \(\forall i \in \left[ 1,m\right] \), such that
which means distinction and space-filling distribution of sampling points are ensured separately for every dimension [38]. A space-filling character of the initial design appears particularly crucial when no a priori knowledge of the mapping behavior over the parametric domain is available, which suggests an equal scan of the entire input space \({\mathbb{X}}\) for building the initial metamodel. To enhance the space-filling character of LHD, it can be employed in combination with the maximin criterion, i.e. a constraint which maximizes the minimum distance between samples [108].
Besides, LHD appears interesting as a non-collapsing strategy [38]. A strategy is called collapsing when two or more points differ by only one or very few parametric dimensions. Therefore, outputs may be identical for these points, in case their corresponding inputs differ only with respect to dimensions with very low influence on the response (see e.g. [40]). For kriging, collapsing points lead to numerical issues through ill-conditioned matrices. As LHD enforces concomitant difference between sample points in terms of all dimensions, see Eq. (11), non-collapsing property is intrinsically ensured through the process. Thus, even if one or more parametric dimensions have insignificant influence on the output, the LHD data set would still be usable for building kriging metamodels.
3.2.1.1 Size of the Initial Design of Experiments
Decisions about the number of samples included in the initial design appear relatively arbitrary in the literature. However, globally, it can be sketched as a compromise between two perspectives. Small initial designs lead to starting metamodels associated with large lack of knowledge, which could mislead the first steps of the adaptive procedure [34, 50]. On the contrary, large initial designs may cause high computational cost due to numerous evaluations of the black-box, which might be avoided using a smaller initial dataset and supplementary points designed by adaptive sampling [18].
Thus, the size of initial dataset is generally chosen by the user in dependence on the application. Main features for decision are the dimension of the parametric space, space-filling quality of the initial sampling algorithm, computational cost due to the evaluation of the black-box function and a priori knowledge about the complexity of the mapping \({\mathcal{M}}\) over the parametric domain. Despite the potential influence of the initial sample size on the efficiency of the metamodel construction, there is a lack of goal-oriented and formal guidance for information-based decision about this criterion in the literature. A few empirical formulas or rules of thumb have been proposed for specific applications. An investigation on the influence of the initial sample size with respect to the dimensionality of the problem has been proposed in Liu et al. [69]. The rule \(m = 10 \, n\) has been suggested by Jones et al. [47] and investigated for Gaussian processes by Loeppky et al. [74], which conclude that it appears as an interesting and reasonable rule of thumb. Besides, these authors also suggest some complementary options to improve the decision for cases in which the simple rule is a posteriori evaluated as insufficient.
3.2.2 Alternative Stopping Criteria
Whatever the adaptive sampling technique employed for creating surrogate model, a stopping criterion is required to decide when to stop the adaptive process. Four alternative criteria are generally considered:
-
The adaptive scheme is stopped with respect to time constraints. Even if it can appear as a trivial approach, budgeted time, project deadline or real-time simulations are usual and crucial issues for most industrial applications.
-
The adaptive scheme is stopped with respect to computational or experimental facilities constraints. A maximum number of mapping evaluations is imposed depending on what the available resources offer (see, for instance [65, 76, 107]).
-
The adaptive scheme is stopped with respect to an accuracy goal. This strategy generally requires to benefit from a reference solution with respect to which errors are estimated. Among available error measures as listed in Table 1, the choice is generally based on the application of interest. The Normalized Mean Absolute Error (NMAE) or Normalized Root Mean-Squared Error (NRMSE) are global performance metrics [16], whereas the Normalized Mean Absolute Error At Minima (\(\mathrm{NMAE}_min\)) provides information about optimization capabilities at certain points of interest, e.g. local minima. The three indicators NRMSE, NMAE and NMaxAE are usual error measures, which means zero value indicates an exact estimation of the reference solution and the larger the error is, the more inaccurate the metamodel. On the contrary, the \(R^{2}\) score provides information about the fit accuracy, such that accurate metamodels are associated with a value of 1, while a value of 0 indicates a bad-quality prediction. Furthermore we define a relative improvement metric, called Relative Error Improvement, which tracks the improvement of an error measure E with regards to an initial value \(E_{0}\).
-
The adaptive scheme is stopped with respect to the relative correction between two successive iterations. If no significant improvement appears while adding a new experiment, it is judged as useless to pursue the enlargement of the experimental design. Various measures of the correction can be considered such as variation of the cross-validation error [27], jackknifing variance based on cross-validation [54], or variation in terms of the absolute relative error [50].
The stopping criterion is generally chosen with respect to application case and study goal.
3.3 General Features of Adaptive Sampling Schemes
Sample points are designed through adaptive sampling strategy by solving an optimization problem. Considering single-selection schemes, only one sample point \(\varvec{x}^{m+1}\) is added per iteration, which is defined as the point maximizing the refinement criterion denoted RC as follows
The superscript \(\star \) emphasizes the feasible solution of the optimization process.
3.3.1 Exploration and Exploitation
Generally, two strategies, namely local exploitation and global exploration, are offered for adaptive sampling algorithms.
Exploration aims at evenly scanning the whole input domain to gain a ‘general’ knowledge of the mapping. Thus, pure exploration strategy performs adaptive sampling while ignoring previously evaluated outcomes.
On the contrary, exploitation is based on the knowledge extracted from available observations. The goal is to place sampling points in subregions, which have been identified as demanding for accurate goal-oriented representation, i.e. subregions associated with large prediction error, or of peculiar interest such as zones with significant non-linear response, optimum, or discontinuity. For instance, if the aim of the analysis is to evaluate the global maximum of the black-box function, it is essential that the metamodel is an accurate emulator of the function in the zone in which that optimum lies. Therefore, samples should be added by preference nearby, even if this leads to rough estimation of the function in other areas. However, it can be highlighted that the true metamodel error is generally a priori unknown, the choice of most beneficial areas is then challenging.
Local exploitation and global exploration: two alternative perspectives for adaptive sampling (true function grey dashed line, initial samples represented as blue dots, supplementary samples as red diamond and red triangle markers, for exploitation and exploration respectively), generated metamodel from sample points in blue line, inspired by Crombecq et al. [20]. (Color figure online)
Thus, considering the example illustrated in Fig. 5, the initial metamodel based on a data set of seven samples as represented in Fig. 5a could lead to the assumption, that the function features a linear general behavior except for one subdomain. Exploration and exploitation are contemplated through an adaptive process stopped after adding seven new observations. Considering a local exploitation adaptive scheme, see Fig. 5b, the identified non-local behavior is further investigated by adding all supplementary samples near to the outstanding initial sample. The focus on the nonlinear area allows to obtain a precise description of that fluctuation, however the second local non-linearity of the true function is not detected. Furthermore, even though not apparent in this example, employing pure exploitation-based sampling strategy may also lead to high risk of sample clustering [44]. On the contrary considering global exploration, as shown in Fig. 5c, the six supplementary samples are designed to evenly explore the whole design space. This strategy allows to identify the other non-linear region, but does not provide a precise description of both non-linear local behaviors.
Some sampling methods proposed in the literature are based only on one characteristic, whereas more sophisticated techniques combine both perspectives.
3.3.2 Smart Strategies to Combine Exploration and Exploitation
Exploration and exploitation offer to all appearances opposing strategies to build adaptive dataset. However, instead of considering them as contradictory paths requiring a definitive choice between them and restricting the design ability to one scenario, it seems more appealing to append both of them in hybrid adaptive sampling approaches to benefit simultaneously from both features. Thus, advanced adaptive procedures are built by combining exploration and exploitation to yield the global refinement criterion as follows [72]
with \(w_{\text {local}}\) and \(w_{\text {global}}\) the weights for the local exploitation and global exploration, respectively, such that the summation of both weights equals to 1. The combined strategy is specifically defined through both functions \(local(\varvec{x})\) and \(global(\varvec{x})\). In general workflow, this combinatorial score leads to estimate the supplementary sample point as the optimal solution of an objective function as follows
Three general balance strategies between exploration and exploitation have been proposed in the literature, as illustrated in Fig. 6 (see [72]).
3.3.2.1 Decreasing Strategy
Using a decreasing strategy (see Fig. 6a) as proposed in Turner et al. [103] and Kim et al. [50], the global weight \(w_{\text {global}}\) equals 1 at the beginning of the metamodel construction leading to pure exploration of the parametric space during first adaptive steps, which look blindly for some regions of peculiar interest. Then, with iterations, the weight \(w_{\text {global}}\) decreases whereas the weight \(w_{\text {local}}\) increases until the local weight equals to 1 and the global weight vanishes at the end of the adaptive construction of the metamodel. Therefore, during last iterations of the adaptive algorithm, the sampling strategy is purely based on exploitation of specific regions of interest.
Greedy Strategy
Greedy strategies are based on a switch between pure exploitation-based and pure exploration-based adaptive steps along the iterations, as depicted in Fig. 6b. Initially an adaptive scheme with full exploration-character is used, here the adaptive metamodel is built by reducing the lack of knowledge equally on the entire parametric domain. Then, switching from an exploration-based to an exploitation-based strategy, the adaptive scheme aims at improving metamodel accuracy on some specific zones of interest. If these local improvements are considered sufficient, the scheme switches back to an exploration-based sampling procedure, this enhances the discovery of new regions of particular interest. Thus, switching between both strategies, a metamodel is built by combining exploration and exploitation iteratively, see for example Sasena [93] and Sasena et al. [94].
3.3.2.2 Switch Strategy
Switch strategies build upon dynamic switching between local and global weights, as illustrated in Fig. 6c. Weights are, for instance, estimated by exploiting information based on previous iterations in terms of the differences between successive prediction errors in Liu et al. [71]. This procedure has been evaluated as more efficient than decreasing or greedy strategies in Singh et al. [97].
Adaptive sampling approaches suggested in the literature can generally be analyzed with respect to the nature of their exploration and exploitation components. Assuming an initial or current experimental design comprising m observations, which provides a metamodel \(\widehat{{\mathcal{M}}}\), alternative exploitation and exploration approaches can be examined.
4 Techniques for Exploitation
Using exploitation, samples are placed in areas of specific interest. If the true function was known as assumed in Fig. 7\(\mathrm{a}_1\), it would be straightforward to evaluate the true error defined as
and represented in Fig. 7\(\mathrm{a}_2\), as well as the positions of highest interest for new observations. However, generally, the true function is unknown. The basic idea is then to substitute the exact error estimation by a sampling score, as suggested in Fig. 7\(\mathrm{b}_2\), c and \(\mathrm{d}_2\), hopefully able to inform about areas with the highest true error. Exploitation-based strategies may be globally classified in three main families depending on the method employed to evaluate the score function. It might either be done by comparing the current metamodel with auxiliary metamodels built by modifying the existing metamodel at low cost, using cross-validation (see Fig. 7\(\mathrm{b}_1\) and \(\mathrm{b}_2\)) or query by committee (see Fig. 7\(\mathrm{d}_1\) and \(\mathrm{d}_2\)), or in the analysis of the geometry of the response surface, for instance through its gradient information (see Fig. 7c).
4.1 Cross-Validation-Based Exploitation
Cross-validation-based adaptive sampling is a strategy based on the analysis of the metamodel accuracy with regard to unknown data [17, 79]. Different variants of cross-validation are proposed in the literature. Algorithms generally rest either on cross-validation error or on cross-validation variance.
4.1.1 k-Fold Cross-Validation
Considering the k-fold cross-validation as employed in Fushiki [32], the dataset \({\mathcal{D}}\) is divided in k mutually exclusive and collectively exhaustive subsets denoted \({\mathcal{D}}_{i}\), i.e.
Then, \(k-1\) subsets are chosen as training subset to establish a metamodel, whereas the remaining subset is employed for validation and estimation of a performance score. The process is repeated k times such that all the subsets are successively used for validation, and the cross-validation error is evaluated as the mean of the k results. However, this general tool is not commonly used for adaptive techniques, whereas the specific form called leave-one-out cross-validation has been frequently employed for exploitation purpose.
4.1.2 Leave-One-Out Cross-Validation (LOOCV)
The Leave-One-Out Cross-Validation (LOOCV) is a special case of the general k-fold cross-validation, with \(k=m\). Thus, for every \(i \in [1,m]\), an auxiliary surrogate model \(\widehat{{\mathcal{M}}}_{-i}\) is trained on \(m-1\) observations consisting of the reduced set \({\mathcal{D}}_{-i} = {\mathcal{D}} \setminus \left( \varvec{x}^{i}, y^{i} \right) \). An example of family of such auxiliary metamodels is shown in Fig. 7\(\mathrm{b}_1\) for a metamodel based on seven experiments. Then, the accuracy of the metamodel of interest \(\widehat{{\mathcal{M}}}\) is evaluated through the cross-validation error denoted \( e_{\text {LOOCV}}\) at point \(\varvec{x}^{i}\), as follows
As one auxiliary metamodel \(\lbrace \widehat{{\mathcal{M}}}_{-i} \rbrace _{i \in [1,m]}\) is built to evaluate local error for every available observation, correlation parameters \(\varvec{\theta }\) need to be reevaluated m times in the context of ordinary kriging, which may be a numerically demanding task [49]. In order to mitigate computational costs, correlation parameters can be fixed as constant (see [69]), and LOOCV error can then be efficiently approximated (see [71, 100]) as
where \(\varvec{H} = \varvec{1} (\varvec{1}^{T} \varvec{1})^{-1} \varvec{1}^{T}\), \(\varvec{d} = \varvec{y} - \varvec{1} {\widehat{\mu }}\) and the indices (i, : ), ( : , i) and ii designate the i-th row, the i-th column and the i-th diagonal element of the matrix, respectively.
A low value of \(e_{\text {LOOCV}}(\varvec{x}^{i})\) defined by Eq. (17) or its approximation provided by Eq. (18) means that a lack of observation \(\varvec{x}^{i}\) does not significantly perturb the metamodel, i.e. interpolation around \(\varvec{x}^{i}\) is robust and accurate, whereas a large value of the error \(e_{\text {LOOCV}}(\varvec{x}^{i})\) or \(e_{\text {LOOCV}}^{app}(\varvec{x}^{i})\) implies that available information around \(\varvec{x}^{i}\) is deficient. Therefore, adaptive algorithms can be based on the idea of sampling preferentially in areas with large local LOOCV error. However, the LOOCV error can not strictly be seen as a measure of the accuracy of the surrogate model particularly for not sampled subdomains, but rather as a measure of the metamodel sensitivity to loss of information [17]. Indeed, \(e_{\text {LOOCV}}(\varvec{x}^{i})\) as defined by Eq. (17) or approximated by Eq. (18) only yields discrete information about prediction error for all \(\lbrace \varvec{x}^{i} \rbrace _{i \in [1,m]}\), which are anyway already sampled positions. Therefore, it is guaranteed that true error vanishes at these points.
Two main approaches have been suggested to approximate LOOCV-based prediction error at any point \(\varvec{x}\) of the parametric space \({\mathbb{X}}\) from the discrete knowledge at sample points \(\varvec{x}^{i}\).
4.1.2.1 Continuous LOOCV Estimation
Continuous approaches consist in approximating the error as a continuous score function over the whole parametric domain as shown in Fig. 7\(\mathrm{b}_2\). For instance, an error at any point \(\varvec{x}\) can be approximated as the superposition of the relative errors between the current metamodel and the leave-one-out metamodels considering successively the lack of each sample [45], as follows
The method has also been adopted by Kim et al. [50] and extended as a weighted version in Jiang et al. [42].
It has been highlighted that this LOOCV error generally overestimates the true error, which may be a problem for a precise tuning of the metamodel accuracy [70]. However, a reduction of this overestimation has been observed while increasing the number of data points [111]. A weighted version has been proposed in Li et al. [65] based on the mean absolute difference. Similar continuous versions are found in Laurenceau and Sagaut [61], Liu et al. [71] and Garud et al. [33].
A different approach for continuous LOOCV estimation has been employed by Aute et al. [4] or Li et al. [65] based on fitting a kriging metamodel \({\widehat{e}}_{\text {LOOCV}}\) to the LOOCV error values.
Discontinuous LOOCV Estimation
Discontinuous strategies for estimating the cross-validation error rely on dividing the parametric space into discrete cells. Then, each cell is assigned a variant of \(e_{\text {LOOCV}}(\varvec{x}^{i})\) based on some proximity metrics, and the cell associated with highest error is branded as priority cell for further sampling. As a side effect, the division of the parametric space into cells leads to implicit exploration contribution [72], as detailed later in Sect. 5.1. Besides, this approximation generates discontinuity of the error estimate at bounds between neighbor cells.
Among discontinuous LOOCV approximations, Xu et al. [116] have proposed a decomposition of the parametric space by Voronoi tessellation and a simple assignment of the \(e_{\text {LOOCV}}(\varvec{x}^{i})\) value to the Voronoi cell associated with \(\varvec{x}^{i}\). Similar methods are used in Jiang et al. [43] and Jiang et al. [41].
A different approach has been suggested by Busby et al. [11] and later employed in Busby [10], in which cells are built through a gridding process. Then, each cell containing one or more sample points is associated with the highest \(e_{\text {LOOCV}}(\varvec{x}^{i})\) among included points, whereas an arbitrarily high error is assigned to cells which do not contain any sample.
4.2 Geometry-Based Exploitation
The fundamental postulate corresponding to geometry-based exploitation strategies is that the current metamodel may have a high prediction error near certain geometric features such as high gradient or local optimum. Among them, distance-based and gradient-based geometric exploitation strategies are distinguished.
4.2.1 Distance-Based Exploitation
The term ‘distance’ refers here to information distance, i.e. distance between outputs in the image of \(\widehat{{\mathcal{M}}}\). Thus, Jones et al. [47] proposed an adaptive technique, which is commonly utilized for optimization, in which samples are preferably added in subdomains associated with metamodel response very close to the global minimum observation. Variants have been developed in Sóbester et al. [98] and later in Xiao et al. [115].
Another distance-based exploitation strategy has been exposed in Lam [59], in which samples are added in regions where the metamodel response differs most significantly from the closest observation.
4.2.2 Gradient-Based Exploitation
Gradient-based techniques are built around the premise that an accurate metamodel requires less observations in subdomains corresponding with low gradient of the response surface than in subdomains with large gradient (see [8, 105]). In the context of kriging metamodeling, the gradient information is not directly available and so its numerical approximation represents the milestone of this approach.
Crombecq et al. [18] partition the input parametric space with Voronoi tessellation, and then approximate the gradient in each cell from some neighborhood information. Expansions of this approach can be found in Crombecq et al. [21] and van der Herten et al. [109]. Local non-linearities are evaluated in Lovison and Rigoni [75] from an approximation of the Lipschitz constant using neighbor points also defined from a Delaunay triangulation, the idea has been reused in Liu et al. [68]. In Mo et al. [82], the gradient is approximated using central difference method and nonlinearities are described by incorporating higher-order Taylor terms in the expansion.
As a side note, an extension to ordinary kriging including gradient information has been proposed in the literature and named gradient-enhanced kriging [73] or co-kriging [62]. A good overview of general gradient-enhanced metamodels which also includes gradient-enhanced kriging is given in Laurent et al. [63]. Adaptive sampling in the framework of gradient-enhanced kriging models has not yet been extensively researched. Paul-Dubois-Taine and Nadarajah [86] present an adaptive method designed for sensitivity analysis with co-kriging.
4.3 Query-by-Committee-Based Exploitation
When using Query by Committee (QBC) adaptive schemes, the new sample is selected from a set of randomly proposed candidate points, which are sorted using a committee of surrogate models [29, 95]. The supplementary point is selected as the candidate for which the “difference” between evaluations using alternative committee metamodels is the most significant. For instance, “difference” in terms of the metamodel variance can be examined [58].
In details, first a large set of candidate points is randomly selected within the parametric space considering uniform distribution. A committee of metamodels, which can a priori contain any kind of surrogate approach, is designed based on available information. In the framework of kriging, concurrent committee surrogates could be kriging metamodels based on different autocorrelation functions such as various Matérn and power exponential autocorrelation functions. Let a committee C consist of \(n_{C}\) members i.e. \(C = \lbrace \widehat{{\mathcal{M}}}^{C}_{i} \rbrace \) with \(i=1, \, \ldots , \, n_{C}\). Finally each candidate point is evaluated based on the fluctuation \(F_{\text {QBC}}\) of the predictions provided by alternative surrogate models defined as
where \(\overline{\widehat{{\mathcal{M}}}^{C}}(\varvec{x}) = \frac{1}{n_{C}} \sum _{i=1}^{n_{C}} \widehat{{\mathcal{M}}}^{C}_{i} (\varvec{x})\) is the average of the output estimation considering the different committee members. The candidate with highest fluctuation is selected as next sample point. The QBC-based algorithms appear very generic as they are intrinsically model-independent.
Examples of the QBC adaptive framework can be found in Kleijnen and Beers [54], Acar and Rais-Rohani [1], Mendes-Moreira et al. [81] and Eason and Cremaschi [28]. Although QBC appears rather proficient in reducing the approximation error of the metamodel along with the adaptive sampling steps [81], it has been highlighted that the committee members should exhibit some differences to be able to reduce the surrogate model error efficiently [80]. This might be problematic when utilizing a QBC approach based only one metamodel type.
Thus, three main exploitation-based families have been proposed to exploit knowledge from available observations to design the new experiment. In a complementary way, exploration sampling can be used to discover crucial behavior which has not been discovered yet.
5 Techniques for Exploration
Sample points can be spread over the whole parametric domain employing exploration strategy in order to unveil regions with high prediction error due to local non-linearity for instance. This feature is particularly important if the current design of experiments is very small. Another interest of exploration is preventing local clustering of points which leads to numerical instabilities in the kriging approach.
As illustrated in Fig. 8, there are conceptually two different tools to create an exploration component with kriging, i.e. distance-based and variance-based exploration.
5.1 Distance-Based Exploration
From the distance information between existing sample points, distance-based exploration either generates a criterion to sparsely sample regions or sets restrictions for new sample points. Continuous and discontinuous distance-based exploration can be distinguished or can sometimes be brought together in the same adaptive sampling method.
5.1.1 Continuous Distance Criterion
Continuous distance criteria appear in different contexts in the literature. Lovison and Rigoni [75] for example define the exploration component as the euclidean distance to the nearest sample point cf. Fig. 8a. Normalized versions of this approach have been chosen by Eason and Cremaschi [28] and Mo et al. [82]. A crowding distance metric denoted CDM is defined by Garud et al. [33] as
to impose that preferred points have a large cumulative distance from existing samples. Here the notation \(\Vert \bullet \Vert \) denotes the \({\mathcal{L}}_2\) norm operator.
Other approaches employ relative distances in order to constrain the solution domain of the general optimization problem of Eq. (12) by introducing a cluster threshold denoted S which should be exceeded, as follows
The challenge in this approach lies in the definition of the space-filling metric value S. Different techniques have been suggested. Li et al. [65] choose the cluster threshold to be proportional to the average minimum distance of all sample points. A similar approach designed by Jiang et al. [42] defines the cluster threshold \(S_{Jiang}\) as detailed in Box 1.
A slightly different approach has been chosen in Aute et al. [4] where the maximum of the minimum distances is used instead of their average as described in Box 2.
Cluster threshold SAute defined as a maximum of minimum distances [4]
A distance threshold is also utilized in Li et al. [64] and Garud et al. [33]. However, they do not specify a value and make it therefore dependent on the user experience.
5.1.2 Discontinuous Distance Criterion
Another option for distance criteria is dividing the input space \({\mathbb{X}}\) into a set \({\mathcal{L}}\) of \(n_{\omega }\) discontinuous cells as \({\mathcal{L}} = \lbrace \omega _i \rbrace _{i \in [1,n_{\omega }]}\) such that
where the cell sizes depend on the sample point positions. In this context, a division can be performed through Voronoi tessellation, Delaunay triangulation or gridding.
In Voronoi tessellation, as first shown in Crombecq et al. [20] for adaptive sampling exploration purposes, the input parametric space is divided into set of m cells \(\lbrace Z_{1}, \ldots , Z_{m} \rbrace \) around the existing m sample points [3]. Here, a point \(\varvec{x}\) belongs to the cell relative to \(\varvec{x}^{i}\) if it is at least as close to \(\varvec{x}^{i}\) as to any other sampled points \(\left\{ \varvec{x}^{j}\right\} _{\begin{array}{c} j\in \left[ 1,m\right] \\ j \ne i \end{array}}\), see Fig. 9. The method has been used by various authors such as van der Herten et al. [109], Liu et al. [68] or Jiang et al. [41].
The computation of the Voronoi tessellation is known to be computationally demanding, particularly for high-dimensional spaces. However the volume of each cell can be evaluated at low cost using Monte Carlo methods (see [18]).
Delaunay triangulation as employed by Lovison and Rigoni [75] or Jiang et al. [43] is an exploration tool which goes hand in hand with Voronoi tessellation. Indeed, as represented in Fig. 9, Delaunay triangles are commonly formed by connecting the central points of adjacent Voronoi cells [102].
A different approach was introduced by Busby et al. [11] and further in Busby [10] in which an adaptive gridding algorithm is proposed to divide any edge of the \(n \times 2^{n-1}\) edges of the parametric space into uniformly split pairwise disjoint subintervals. Subinterval size is defined for each dimension i through corresponding correlation length \(\theta _{i}\).
5.2 Variance-Based Exploration
Variance-based adaptive sampling relies on the idea that large errors on the metamodel approximation \(\widehat{{\mathcal{M}}}\) are probably localized in areas where the predicted variance is large. The variance being directly available as a byproduct of the kriging surrogate model, variance-based adaptive sampling appears very natural in the framework of kriging metamodel.
Thus, Jin et al. [45] propose to find a new sample point by solving
with \(\sigma _{{\widehat{Y}}}^{2}\) the variance operator as defined in Eq. (8). Because the variance is based on distance information combined with the autocorrelation kernel, there is a clear link between distance and variance, as plotted in Fig. 8a and b respectively. The approach is commonly referred to as the maximum mean-squared error [91], as it is a peculiar representation of the entropy approach initially suggested by Shannon [96] and then developed by Currin et al. [22] and further by Currin et al. [23] for cases in which only one point is designed per iteration. Other approaches include the integrated mean-squared error which is based on a weighted averaged mean-squared error estimation over the whole parametric space [91]. Then, the new sample point is defined as follows
where w denotes a user-defined probability density function. Variations of this exploration technique can be found in Jones et al. [47], Sóbester et al. [98], Lam [59], Xiao et al. [115] and Liu et al. [71].
From the alternative perspectives on exploitation and exploration offered in the literature, many advanced adaptive strategies can be built.
6 Commonly Applied Adaptive Sampling Techniques
The idea here is to review commonly used, state-of-the-art adaptive sampling techniques. An overview of the most common techniques, which are described here, is given in Table 2. For sake of clarity, they are classified with respect to:
-
Exploration component,
-
Exploitation component,
-
Combination of exploration and exploitation in refinement criterion,
-
Optimization scheme.
In details, exploration is either based on variance or on distance and, if existing, exploitation is based on cross-validation, query by committee or geometry. The computational costs of adaptive schemes is mainly due to the optimization scheme, which is either continuous or discrete. Exploration and exploitation may be combined in a fixed manner, a conventional non-fixed manner (i.e. decreasing strategy), or using a complex scheme.
6.1 Adaptive Methods Without Exploitation Contribution
In the literature many approaches based only on space-filling properties have been proposed. Reviews dedicated to space-filling techniques have been reported in Kleijnen [51], Pronzato and Müller [88] or Joseph [48]. However, as this idea is not the core of adaptive schemes, only one method is considered here to be analyzed as a reference pure-exploration strategy in order to make comparisons with adaptive schemes involving an exploitation character.
6.1.1 Monte Carlo-Intersite-proj-th (MIPT)
The Monte Carlo-intersite-proj-th (MIPT) method is based only on exploration [19]. Using MIPT, among a large set of possible candidates provided by Monte-Carlo sampling, the supplementary sampling point is chosen as the candidate point maximizing the distance to the sample points already included in the design of experiments. The distance metric considered for the optimization problem is the minimum distance between each candidate and the existing samples, i.e.
6.2 Adaptive Methods using Cross-Validation Based Exploitation
Several techniques have been developed based on continuous or discontinuous cross-validation error.
6.2.1 Space-Filling Cross-Validation Tradeoff (SFCVT)
The Space-Filling Cross-Validation Tradeoff (SFCVT) approach combines a leave-one-out cross-validation for exploration and a distance criterion to ensure an exploration character [4]. The authors define a normalized LOOCV error as
In order to interpolate the error over the parametric space, a kriging metamodel for the error \({\widehat{e}}_{\text {LOOCV}}^{norm}\) is built based on the dataset \({\mathcal{D}} = \lbrace (\varvec{x}^{i}, e_{\text {LOOCV}}^{norm}(\varvec{x}^{i})) \rbrace \). Then the supplementary sampling point is defined as the solution of the following constrained optimization problem
where the space-filling metric is estimated as detailed in Box 2. Thus, the distance condition ensures that the new point is created further than a certain euclidean distance to pre-existing points.
6.2.2 Accumulative Error (ACE)
In the ACcumulative Error (ACE) adaptive technique, a combination of cross-validation for exploitation and distance criterion for exploration is proposed [65]. First the authors use the common LOOCV error defined by Eq. (17). In order to make this error continuously available over the parametric space, a degree-of-influence function denoted DOI is introduced such that the error for any unobserved value \(\varvec{x} \in {\mathbb{X}}\) is estimated from the knowledge of the error \(e_{\text {LOOCV}}(\varvec{x}^{i})\) at the observation points, as
Here the degree of influence of any observation \(\varvec{x}^i\) on \(\varvec{x}\) is assumed to have an exponential decrease as
where the factor \(\alpha \) is used to adjust the decreasing rate of influence. A discussion on the influence of \(\alpha \) on the adaptive sampling process and some advise on its value are given in Li et al. [65].
A new sample point is thus defined as solution of the constrained optimization
where the space-filling metric is estimated by the algorithm given in Box 1.
Cross-Validation Voronoi (CVVor)
The Cross-Validation Voronoi (CVVor) scheme is also based on the combination of a cross-validation exploitation with a distance-based exploration [116]. Its algorithm is given in Box 3. From existing sample points, a Voronoi tessellation is employed to divide the whole input space into a set of Voronoi cells [3]. The cell with the largest cross-validation error is associated with the sensitive sample denoted \(\varvec{x}^{sens}\), and as the most sensitive cell, it is sampled with random points leading to a set \({\mathcal{C}}_{sens}\) of candidate points. Among them, the point that is the furthest away from \(\varvec{x}^{sens}\) is picked as the new sample, i.e.
Thus, CVVor reaches a compromise between proficient local exploitation and prevention from clustering of observation points.
6.2.3 Smart Sampling Algorithm (SSA)
Using the Smart Sampling Algorithm (SSA) proposed by Garud et al. [33], a new sample point is defined as the solution of a set of optimization problems based on a combination of cross-validation exploitation and distance-based exploration. As proposed by Zhang et al. [117], exploration is performed by maximizing the crowding distance metric CDM given by Eq. (21). Indeed, a point \(\varvec{x}\) corresponding with a large value of \(CDM(\varvec{x})\) would be localized relatively far away from the m samples already incorporated in the dataset. In order to incorporate an exploration component the authors compute \(CDM(\varvec{x}^{j}), \, \forall j \in [1,m]\). Afterwards the resulting values are sorted in descending order using ordering index \(p=1, \ldots m\).
By starting with \(p=1\) a new candidate sample is contemplated as the point maximizing both the crowding metric and the departure function as follows
Then, it is checked that the solution satisfies a non-clustering parameter \(\epsilon \) as a minimum distance to all existing samples. If the condition is fulfilled, the candidate point is accepted as new sample \(\varvec{x}_{\text {SSA}}^{m+1} = \varvec{x}_{\text {SSA}}^{cand}\), otherwise set \(p=p+1\) and the subsequent optimization problem defined by Eq. (33) is solved again until a candidate fulfills the non-clustering requirement. The SSA adaptive approach is summarized through its algorithm in Box 4.
6.2.4 Weighted Accumulative Error (WAE)
A sequential sampling strategy called Weighted Accumulative Error (WAE) has been proposed by Jiang et al. [42]. It employs cross-validation for exploitation and a distance criterion for exploration. The method is based on a weighted version of the LOOCV root-mean-squared error defined as
with the weights given by
A new sample point is then found by solving the constrained optimization problem
where the space-filling metric is defined as described in Box 1. The technique is summarized in Box 5.
6.2.5 Adaptive Maximum Entropy (AME) Algorithm
The Adaptive Maximum Entropy (AME) scheme combines variance-based exploration and cross-validation exploitation [69]. Sample clustering is prevented by introducing some adjustment factors defined as
where, for any unsampled point \(\varvec{x} \in {\mathbb{X}}\), \(e_{\text {LOOCV}}(\varvec{x})\) is approximated as equal to the LOOCV error at the closest sample point and \(e_{max}\) is the maximum LOOCV error, i.e.
The adjustment parameter \(\gamma \) is estimated through a pattern \(\gamma = \lbrace \gamma _{1} = \gamma (\Theta = 1), \ldots , \gamma _{N} \rbrace \) of length N designed by the authors in order to establish a tradeoff between exploration and exploitation. The pattern index is denoted \(\Theta \) and is updated to \(\Theta = \Theta +1\) each time a sample is added to the design of experiments. In case \(\Theta \) becomes equal to \(N+1\), the pattern is scanned again by setting \(\Theta =1\).
Given the auxiliary notation
with an adjusted correlation function \(R_{adj}(\bullet )\) the adjusted correlation matrix
can be defined. The new sample point maximizes the determinant of the correlation matrix through the following optimization problem
The overall adaptive AME algorithm is summarized in Box 6.
6.2.6 Maximizing Expected Prediction Error (MEPE)
The Maximizing Expected Prediction Error (MEPE) adaptive scheme, which was proposed by Liu et al. [71], utilizes cross-validation exploitation and variance-based exploration. Within a switch strategy, a balance factor \(\alpha \) is employed to adaptively balance exploitative and exploratory contributions. The authors use the fast approximation of the LOOCV error at each sample point as proposed by Sundararajan and Keerthi [100] and established in Eq. (18). The main interest is that it exempts building the leave-one-out auxiliary metamodels, as usually required, see Fig. 7. In order to make this value continuously available, it is assumed that the LOOCV error denoted \({\widehat{e}}^{approx}_{\text {LOOCV}}\) at an unobserved point \(\varvec{x} \in {\mathbb{X}}\) is equal to the error at the closest sample. The continuous refinement criterion denoted by \(RC_{\text {EPE}}\) is then defined as
where the balance factor \(\alpha \) is given by estimating the evolution of the lack of knowledge at sample point \(\varvec{x}^{m}\) during the previous step as
with \(m_0\) the number of samples added to the initial design by the adaptive scheme. The new sample point is consequently found by maximizing this quantity over the parametric space
The algorithm is presented in Box 7.
6.3 Adaptive Methods using Geometry-Based Exploitation
Among geometry-based exploitation components, distance-based and gradient-based methods are distinguished.
6.3.1 Distance-Based Methods
Several methods exploit the distance between outputs within the parametric domain.
6.3.1.1 Expected Improvement (EI)
The Expected Improvement (EI) uses geometry-based exploration and exploitation obtained by using the variance [47]. The goal of this adaptive scheme is mainly to predict accurately the global minimum value of the output over the whole parametric space. The authors define a refinement criterion denoted \(RC_{\text {EI}}\) which can be simplified to [7]
Here \(y_{min} \) represents the smallest observation output, and \(\varphi \) and \(\Phi \) denote the probability density function and the cumulative distribution function of a standard Gaussian random variable, respectively. Thus, EI uses a fixed balance between exploration and exploitation contributions. A new sample point can be obtained through a maximization, as follows
Here, the scheme is introduced for accurate estimation of the minimum of the response surface, it can be highlighted that a variant for evaluating the global maximum of the output could be straightforwardly designed.
6.3.1.2 Expected Improvement for Global Fit (EIGF)
As indicated by its name, Expected Improvement for Global Fit (EIGF) proposed by Lam [59] is a variant of EI, with the aim of providing an accurate estimation over the whole parametric domain. The method combines exploitation based on a geometric feature and a variance-based exploration component. The refinement criterion denoted \(RC_{EIGF}\) is defined as
where \(y(\varvec{x}^{\star })\) is the observed value at the closest neighbor to the point of interest \(\varvec{x}\). The first term gets larger when the difference between the surrogate estimation \(\widehat{{\mathcal{M}}}(\varvec{x})\) and the exact response at the nearest sample point increases. The second term, which offers the exploration sampling feature, is large in subdomains where the surrogate model has the largest intrinsic uncertainty. A new sample point is then obtained by solving
6.3.2 Gradient-Based Methods
Exploiting the variation of outputs over the parametric domain can also be done through gradient estimation.
6.3.2.1 Local Linear Approximation (LOLA)
Local Linear Approximation (LOLA)-Voronoi is a discontinuous adaptive sampling technique proposed by Crombecq et al. [18] based on an exploitation feature with gradient estimation and exploration given by the volume of Voronoi tessellation cells.
In details, for the exploration part of the adaptive scheme, Voronoi tessellation is employed to evaluate the density of points included in the current design of experiments through cell volume information. To avoid cumbersome procedures [3], an approximation of the volume of each cell V is done using a Monte Carlo approach [18].
Exploitation is based on the linear approximation of the gradient of each cell utilizing neighborhood information obtained by the tessellation. This measure is denoted E.
From a set of candidate points \({\mathcal{C}}\), n randomly distributed on the parametric domain, the LOLA sample point is found by solving a maximization problem involving a score combining the two previously introduced measures as
Lipschitz Sampling Lovison and Rigoni [75] propose an adaptive sampling technique, which is hereafter referred to as Lipschitz Sampling (LIP), using a distance criterion for exploration and an approximated local nonlinear character as an exploitation component. A set \({\mathcal{C}}\) of candidate points evenly spread in the parametric domain is built and a distance metric is defined and evaluated for each candidate point as the closest distance to a sample point, i.e.
Variation information is provided through the Lipschitz constant as
with \({\mathcal{X}}_{adj}\) the set of points adjacent to \(\varvec{x}^{i}\) and belonging to \({\mathcal{X}}\). Adjacent points are found by utilizing Delaunay triangulation on existing samples (see e.g. [114]). From the values evaluated at sample points, the Lipschitz constant for the Voronoi cell associated with sample \(\varvec{x}^{i}\) is given by the maximum value of the Lipschitz constant between \(\varvec{x}^{i}\) and all adjacent samples of the tessellation. A new sample point is defined as the optimal candidate point that maximizes a refinement criterion defined as follows
with \(L(\varvec{x}^{\star })\) the Lipschitz constant value of the Voronoi cell associated to candidate point \(\varvec{x}^{\star }\). The technique is summarized in Box 8.
6.3.2.2 Taylor-Expansion Based Adaptive Design (TEAD)
The Taylor-Expansion based Adaptive Design (TEAD) technique was proposed by Mo et al. [82] and combines gradient-based exploitation and distance-based exploration based on the metric previously defined by Eq. (50). A Taylor-expansion based scheme is used to obtain a local nonlinearity information. The authors approximate second- and higher-order Taylor expansion values around point \(\varvec{x}\) as
Here \(\widehat{{\mathcal{M}}}\) is the current metamodel and t denotes the first-order Taylor expansion of \(\widehat{{\mathcal{M}}}\), which includes an estimation of the local gradient based on central difference approximation. A new sample point is then found by solving a discontinuous optimization problem which consists of a weighted summation of exploration and exploitation components, as follows
It can be noticed that the exploitation term is weighted using a weight function \(w_{\text {TEAD}}(\varvec{x})\) given by
where \(L_{max}\) is the maximum distance between two sample points in the input space. The technique is summarized in Box 9.
6.4 Adaptive Methods using Query-by-Committee-Based Exploitation
Only one method based on query-by-committee is studied here because the essential process is similar in many techniques of this kind.
6.4.1 Mixed Adaptive Sampling Algorithm (MASA)
Mixed Adaptive Sampling Algorithm (MASA) has been proposed by Eason and Cremaschi [28] for neural networks. It combines a local exploitation contribution based on QBC fluctuation and a global exploration based on distance. The new sample point is found among a set of candidates points \({\mathcal{C}}\) randomly distributed over the parametric space by evaluating
where \(D_{min}(\varvec{x}^{\star })\) is the minimum distance between \(\varvec{x}^{\star }\) and the set of samples as previously defined by Eq. (50). To normalize the score, the maximum over all the minimum distances \(D^{max}_{min}\) corresponding with the different candidate points in \({\mathcal{C}}\) is evaluated. The term \(F_{\text {QBC}}\) denotes the fluctuation among committee member estimations as previously defined in Eq. (20), which is here normalized with respect to the maximum committee fluctuation evaluated over all candidate points. The MASA algorithm is summarized in Box 10.
7 Investigation of Main Adaptive Sampling Techniques in Ordinary Kriging
In order to expose a sound comparison between the presented sampling techniques various numerical tests of different complexity are investigated.
7.1 Numerical Perspectives on the Test Campaign
To provide fair parallel between examples and sampling approaches, similar numerical conditions are ensured for all the studies.
7.1.1 Initial Data Set Design
Translational Propagation Latin Hypercube Design (TPLHD) is employed for defining initial data sets. This variant of LHD proposed by Viana et al. [112] gives a LHD obtained by the translational propagation algorithm with a one-point seed. The idea is to build almost optimal Latin hypercube designs approximating the solution of the optimization problem without performing formal optimization. Thus, less computational effort is required and quick estimations are possible. It has been shown in Liao et al. [67] that the process provides a good approximation of the optimal solution in low dimensions, up to six-dimensional parametric space from their experience. On the contrary, for higher-dimensional cases, TPLHD estimation of the sample positions diverges from the optimal design. As here mainly relatively low-dimensional cases are considered, employing TPLHD appears satisfying for building initial designs from which adaptive schemes are compared.
If not specified differently, the size of initial dataset is defined for all benchmark tests by the simple rule of thumb \(m = 10 \, n\) as exposed in Sect. 3.2.1.
7.1.2 Autocorrelation Structure of the Random Process
In this study the influence of autocorrelation functions is out of the scope. Therefore, to yield comparable results for all problems and methods, a Matérn 3/2 autocorrelation function [77] has been chosen, defined as
in which \(x_{k}^{i}\) and \(x_{k}^{j}\) are the components in dimension k of the vectors \(\varvec{x}^{i}\) and \(\varvec{x}^{j}\) respectively, and \(\theta _k\) is the correlation parameter corresponding with dimension \(k \in [1;n]\) of the parametric domain.
Utilizing the maximum likelihood estimate, these correlation parameters can be evaluated by solving an auxiliary optimization problem [27], as follows
where \(\psi _{{\text {Mat}}acute{e}{\text {rn}} 3/2}\) is the reduced likelihood given, for ordinary kriging, by
with \(\det \) denoting the determinant operator. The optimization problem given by Eq. (58) is solved numerically by employing a hybridized particle swarm optimization similar to the strategy suggested by Toal et al. [101]. However in the software provided online, other alternatives possibly faster are also available, including an interior point-based method [12], simulated annealing [39], genetic algorithm-based optimization [25] as well as a multistart algorithm combined with the interior point technique see e.g. Ugray et al. [104].
7.1.3 Method-Specific Parameters
When method-specific parameters are involved, the values recommended in the original paper by the authors proposing the method have been employed, such as e.g. an adjustment parameter set of \(\gamma = \lbrace 0.0, 0.5, 1.0, 100 \rbrace \) for AME. Similarly, the LOLA technique is sped up based on authors suggestions by restricting the radius defining the local neighborhood. Specifically an initial radius of \(r=0.25 \, n\) has been chosen, and then it has been adaptively designed to ensure the number of points including in the neighborhood equals \(10 \, n\). For AME, as Matérn 3/2 autocorrelation function is herein utilized for kriging metamodel the entries of the covariance matrix are also adjusted using the same type of autocorrelation function. For the MASA approach, five committee members derived from different autocorrelation functions are considered, consisting of Matérn 3/2, Matérn 5/2, cubic spline, exponential and squared exponential autocorrelation functions. For SSA, a distance threshold of \(\epsilon =0.01\) has been arbitrarily chosen since the authors do not specify any reference value. All Monte-Carlo procedures are performed based on \(5000 \, n\) candidate points.
7.1.4 Reference Solution and Performance Analysis
Relative errors are evaluated with respect to reference solutions based on a set of \(5000 \cdot n\) observation points randomly placed in the parametric space using TPLHD.
One challenge to provide quantified comparison of adaptive techniques is the usage of optimization strategies based on populations of candidates to estimate hyperparameters and also for many methods to obtain the optimal new sample point. Using these Monte Carlo methods, numerical results vary for each realization of the process. In order to circumvent performance fluctuation and expose significant results, error values are given in terms of average performances over ten realizations for each adaptive sampling scheme.
As initial sampling positions are uniquely chosen with TPLHD, same initial design is considered for all the realizations. Plots illustrating set of experiments provided by adaptive processes correspond to one realization randomly chosen among the ten performed realizations. The later a sample point has been added to the dataset the brighter the color of the dot representing it is. Furthermore sample position highlighted in bright red indicate that the point is closer than 0.0005 in the normalized parametric space to an existing sample point, which could possibly result in numerical issues due to clustering behavior.
Alternative algorithms are investigated on a large variety of test cases.
7.2 Analysis of the Optimization Problems
All investigated adaptive sampling techniques rely on solving optimization problems in order to design a new sample point. The complexity of the cost function drives the choice of the solver and directly affects time and computational effort required to find the optimum. Thus, features of alternative objective functions are exposed here to lead to sound use of adaptive sampling methods.
Consider the one-dimensional problem setting as depicted in Fig. 10. The blue dotted line indicates the target function. The black dots symbolize the positions of the initial samples. It can be seen they are not evenly distributed due to the small size of initial data set. Furthermore, peculiar dataset including two leftmost samples lying quite close to each other has been chosen to analyze how cost functions deal with this feature. The metamodel built from this initial dataset is represented by the red line. From that set, alternative optimisation problems to be solved for designing the 11-th observation point are studied through the shape of their corresponding cost function over the whole parametric domain. To simplify the visualization, cost functions have been transformed and normalized into a score denoted \( {\overline{RC}}\) which lies between 0 and − 1, thus all corresponding optimization problems would be a minimization to look for the sample position corresponding to the global minimum, which equals − 1 if not submitted to any constraint.
7.2.1 Optimization Based on Continuous Cost Functions
Objective functions corresponding with adaptive schemes based on continuous optimizations can be observed on Fig. 11. AME, EI, EIGF, MEPE and SSA are schemes for which exploration and exploitation are combined in a unique refinement criterion, whereas ACE, SFCVT and WAE include the exploration character through a constraint in the optimization scheme. Constraints are represented by red-shaded areas. A dashed red line gives the optimal point for each case. It can be highlighted that its position depends significantly on the chosen scheme.
The optimization problem corresponding with ACE is illustrated in Fig. 11a. The unconstrained cost function shows spikes near to existing samples, whereas it is is roughly flat and close to zero further away from sample points. Indeed, the unconstrained global minimum is at the position of an existing sample point. However, a predominant part of the parametric space is rejected through the distance constraint of the scheme. Thus, this adaptive technique, at least for this test case, will simply lead to a randomly picked point as it can be seen through the optimum point found. Therefore the features of the ACE optimization problem requires a robust solver for optimization under constraint and a pertinent definition of the distance constraint.
The next investigated technique is AME as shown in Fig. 11b and c for different values of \(\gamma \). The authors specify that a \(\gamma \) close to zero leads to a technique with a high exploration character whereas as a higher \(\gamma \) value features a scheme with significant exploitation component. The objective function using \(\gamma =0\), as depicted in Fig. 11b, exhibits its maxima at the already sampled positions, which prevents clustering around the samples. However, the cost function being essentially flat further away from the samples, the new point is inherently picked at random by the optimization scheme. When the \(\gamma \) value is increased to 50 the cost function has a drastically different shape as seen in Fig. 11c. The optimum is now found close to the already clustered points, which does not appear attractive. Besides the objective function is basically flat for the main part of the parametric domain, worryingly also around existing samples which makes point clustering possible.
The EI cost function, given in Fig. 11d, vanishes at sample positions. However the function drops off rather fast quickly. Therefore the optimum is found very close to an existing sample point. Furthermore the optimum is not unique.
In Fig. 11e the optimization problem of EIGF is depicted. The cost function equals zero for existing sample points, but does not drop off as quickly as e.g. EI. It also shows several discontinuities with significant jumps. However, for the considered test case, the optimum is unique and the cost function is not very complex in comparison to other methods.
The shape of the objective function for MEPE is shown in Fig. 11f. The function is not zero at all sample points. Additionally discontinuous behavior can be observed, and the optimum is not unique. The smoothness of the function around sample point makes it easier to avoid clustering since the gradients are reliable.
Among continuous adaptive techniques, the unconstrained SFCVT cost function, as illustrated in Fig. 11g, is clearly the smoothest. Based on the same distance constraint as ACE, a large part of the parametric domain is alike rejected, and the choice of a reliable solver for constrained optimization is crucial. It can be noticed that the optimum position is similar to MEPE.
The shape of the objective function of SSA is presented in Fig. 11h. The function is maximal at the sample points. In contrast to the other techniques there is a clear global optimum in the neighborhood of the two initially close sample points. However, the user-chosen distance constraint reject a limited part of the parametric domain, so this point would be overshadowed by a larger distance constraint. The authors did not specify any value. Therefore this method capabilities are clearly dependent on the user understanding of the influence of this distance criterion.
The last continuous optimization scheme called WAE is shown in Fig. 11i. Here again, the solution space is constrained. The unconstrained cost function has its maximum near the two close sample points, whereas its global minimum is located exactly at the position of an existing sample point. Therefore the distance criterion needs to be accurately chosen to avoid clustering, and a solver able to reliably constrain the solution space is required.
7.2.2 Optimization Based on Discontinuous Cost Functions
Similarly cost functions for discontinuous optimization schemes based on ranking a large set of candidate points are given in Fig. 12. The objective function of CVVor is shown in Fig. 12a. It can be noticed that the value of the objective function is constant around each sample point, which results from the definition of the LOOCV error of this technique.
The cost function of the Lipschitz technique is depicted in Fig. 12b. It vanishes at all sample point positions, which avoids clustering behavior, and exhibits a clear and unique global minimum facilitating the optimization process.
The LOLA cost function as shown in Fig. 12c is also constant within the Voronoi cell surrounding each sample point, because it is based on an estimation of the largest gradient in each cell. In light of the true function plotted in Fig. 10, it can be observed that the minimum of the objective function does not fit with a parametric domain with true large gradients. Interestingly, on the opposite the cell associated with the largest value of the cost function around \(x=0\) is actually in the area with the largest gradients of the true function.
MIPT, as seen in Fig. 12d, is a technique purely based on distance exploration. Naturally the cost function is decreasing linearly with the distance to the nearest sample. Starting from a set of several samples multiple global minima can be observed. The next sample point is randomly picked among them based on Monte-Carlo sampling.
The objective function of MASA can be seen in Fig. 12e. Since the technique is based on the highest local difference between a committee of kriging-based metamodels, the global minimum is located in the unsampled region around \(x=0\) of the parametric space. Furthermore the cost function is zero at the position of existing samples and interestingly the function value is decreasing nearly linearly with the distance to the nearest sample.
The last discontinuous-based technique is TEAD which is depicted in Fig. 12f. The objective function seems very similar to the MASA function. Analyzing the cost function with regard to the true solution given in Fig. 10, this technique, which is gradient-based, appears to estimate properly the value of the highest gradient in the area near to 0.
Even from this simple one-dimensional study it can be noticed the large discrepancy in the prediction for the best next sample point. MASA, TEAD, Lipschitz and AME with \(\gamma =0.0\) orient towards a new sample point at \(x=0\), SSA and AME using \(\gamma =50\) around the position of the clustered initial samples at \(x \approx 0.08\) whereas MEPE, SFVCT, CVVor and LOLA provides the new point at \(x \approx 0.45\).
7.3 One-Dimensional Problems
First, four one-dimensional applications are considered.
7.3.1 Single Hump Function \({\mathcal{M}}_{SH,1D}\)
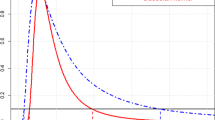
In order to comprehend the exploitation component of the investigated techniques, the first problem considered is the single-Hump function defined on \(x \in \left[ -1.5, 5 \right] \) as
This function, which is plotted onto a normalized space as blue dotted lined in Fig. 13a, is characterized by predominantly linear behavior and a hump containing the global and a local minima at the upper bound of the parametric space.
7.3.1.1 Initial Dataset
The positions of the six initial sample points are highlighted by black dots in Fig. 13a. Among them, five lie in the linear regime.
As pointed out before, the target function behaves linearly on the main part of the parametric domain. The initial metamodel is able to capture well that behavior and to detect the hump as well. So, the best-case adaptive sampling technique should exploit that knowledge and sample in and around the hump to describe it accurately.
7.3.1.2 Analysis of Different Sets with 25 Samples
For every sampling technique, the positions of the samples when reaching a size of 25 samples in the dataset and the corresponding metamodel are displayed on a normalized space in Fig. 13.
Two main failures of the investigated techniques can be highlighted. First, some methods feature an exploitation not sufficiently significant to describe properly the localized non-linearity, such as ACE (Fig. 13b), EIGF (Fig. 13f), LOLA (Fig. 13h), MIPT (Fig. 13j), SFVCT (Fig. 13l) and TEAD (Fig. 13n). The problem of ACE seems to be the definition of the distance constraint because the global minimum is not well captured even though the samples predominantly lie around the hump. MIPT being only based on exploration, most of samples are located within the linear domain. Similarly, a large number of sample points can be found in the linear regime of the target function for EIGF, TEAD, SFVCT, thus the exploration component is too dominant. This similar behavior is particularly interesting as the three of them rely on different concepts for exploitation.
The second issue is that the exploitation component of some techniques focus on insignificant characteristics, at least with respect to the problem of interest. This problem appears for EI (Fig. 13e) and WAE (Fig. 13o) whose samples concentrate in an area near to the lower bound. For EI this can be explained by the fact that the technique aims to sample around the point associated with the lowest output, which initially is the value at \(x=0\). However, as this point is not the true global minimum, EI is unable to capture the proper behavior of the function through this exploitation behavior. Nevertheless this behavior highly depends on the initial dataset. For instance, if the initial dataset included a point located in the hump trough, its output would have been smaller than all other sample outputs leading to a majority of EI sample points generated in the hump.
AME (Fig. 13c), MEPE (Fig. 13i) and SSA (Fig. 13m) capture the behavior of the target function rather well by balancing exploration and exploitation, even if they still include a lot of ineffective points in the linear part of the domain.
CVVor (Fig. 13d), Lipschitz (Fig. 13g) and MASA (Fig. 13k) sample the space ideally. A majority of points can be found at the hump whereas the linear domain is seldom sampled.
7.3.1.3 Analysis of the Error Evolution While Sampling
Variant performances can also be analyzed through the error evolution during adaptive process as given by Fig. 14. The mean normalized RMSE values of the various techniques, as defined in Table 1, are shown in Fig. 14a and b. CVVor, Lipschitz, MASA and MEPE yield the best performances for this global criterion. At the opposite, the worst metamodels are clearly obtained from EI, LOLA and WAE. The relative improvement in terms of NRMSE from the initial metamodel based on 6 samples and metamodels based on 9 and 19 samples is displayed in Fig. 16a. It can be observed that while adding 4 samples the majority of the techniques present similar improvement performances, except for LOLA, MIPT and WAE which even worsen performances while increasing the data. When reaching a dataset of 19 samples, a discrepancy of performances can be observed among alternative methods, where Lipschitz is clearly the best performing technique followed by MASA and MEPE.
In order to investigate the reliability of the adaptive schemes in terms of ease of optimization and reproducibility of results, the evolution of the variance of the NRMSE over the 10 realizations is depicted along the sampling process in Fig. 14c and d. It can be seen that CVVor, LOLA and AME show the biggest variations with CVVor peaking at around 0.2%. However, for almost all methods the optimization scheme is able to yield negligible variations. This quantity will not be represented for further one-dimensional cases, as no difference appears between one-dimensional performed tests.
The evolution of the mean normalized error at the global minimum over the sampling process is shown in Fig. 15a and b. Unsurprisingly more significant difference among alternative approaches can be observed for this local error measure. CVVor, Lipschitz and MASA remain high performers, whereas MEPE is not as good for local objective. The relative improvement in terms of \(NMAE_{min}\) from the initial set to datasets including 10 and 20 samples is depicted in Fig. 16b. The variation is here even more apparent. Only 4 methods are able to improve performances by adding the first 3 samples. Considering 19 samples, four methods still performs worst than initial dataset whereas MASA, CVVor and Lipschitz show the best performance.
7.3.2 Two-Hump Function \({\mathcal{M}}_{Hump,1D}\)
The second one-dimensional benchmark test is the two-hump function defined by
over \(x \in \left[ -0.5, 5 \right] \). This function is utilized to study the exploration component of the adaptive sampling techniques. The target function is plotted as blue dotted line over the normalized space in Fig. 17a. Similar to the previous benchmark this function is predominantly linear over the parametric domain, but here two non-linear peaks emerge.
7.3.2.1 Initial Dataset
The initial dataset, which is represented in Fig. 17a, comprises solely three samples chosen specifically to lie exclusively in one of the peaks. Therefore, the initial metamodel (see also Fig. 17a) only represents roughly the local behavior of this hump. Thus, an ideal adaptive technique should have here enough exploration to represent the linear part of the parametric domain well and also capture the second peak, which has not been sampled at all by the initial dataset.
7.3.2.2 Analysis of Different Sets with 40 Samples
Alternative positions of samples when a dataset of 40 observations is reached, are displayed in Fig. 17b–o, as well as the corresponding surrogate models. Three sampling problems can arise. Some techniques, such as ACE (Fig. 17b) and WAE (Fig. 17o), do not possess enough exploration character to generate any sample outside the initially identified hump. A second problematic case is when the exploration component is pronounced enough to sample other parts of the parametric domain but not sufficient to find the second hump. The sampling behavior of LOLA (Fig. 17h) can be categorized in this group. The last issue is when the overall domain is sampled enough to reveal the second hump but then the exploitation behavior of the technique is not proficient enough to describe accurately both humps. This category consists of AME (Fig. 17c), MIPT (Fig. 17j) and SFVCT (Fig. 17l). Similarly, EI (Fig. 17e), and SSA (Fig. 17m) are not able to describe the whole behavior because they focus on other characteristics. Finally, only CVVor (Fig. 17d), Lipschitz (Fig. 17g), MEPE (Fig. 17i), MASA (Fig. 17k) an TEAD (Fig. 17n) show a good sampling behavior for this test case.
7.3.2.3 Analysis of the Error Evolution While Sampling
The mean NRMSE error over the 10 performed realizations for the adaptive techniques over the whole process is shown in Fig. 18a and b. Initially, the best performing method is AME, which however basically stagnates for the next 20 sample points. As seen from the discussion about the sample point positions, the outliers are the bad performances of ACE as well WAE. It can be seen that Lipschitz, MASA, MEPE and EIGF yield the best adaptive process. The best technique is Lipschitz which reaches basically a perfect fit after around 30 samples.
7.3.3 Gramacy and Lee Function \({\mathcal{M}}_{Gr,1D}\)
The next one-dimensional problem is the Gramacy & Lee function defined for \(x \in \left[ -1.5 , 1.0 \right] \) as
From the initial dataset and corresponding metamodel represented in Fig. 19a it can be observed that the response function feature large gradient variation, and peculiarly the largest gradients do not lie in the area of the global minimum.
Alternative sample points obtained when the set of experiments reaches 30 samples are exposed in Fig. 19.
With regard to global metamodeling, it can be seen that the exploration component of some adaptive technique is too pronounced for that benchmark test, which has a complex behavior. This is particularly the case for EI (Fig. 19e) and WAE (Fig. 19o), and to a lesser extent also for ACE (Fig. 19b), AME (Fig. 19c), CVVor (Fig. 19d), Lipschitz (Fig. 19g) and LOLA (Fig. 19h). However schemes based only on exploration such as MIPT (Fig. 19j) is not sufficient to capture the numerous fluctuations of the true function. Therefore for functions with an irregular pattern, multiple local maxima and minima and large local gradients, adaptive techniques with high degree of exploration and a small but significant exploitation component should be preferred, such as EIGF (Fig. 19f), MEPE (Fig. 19i), MASA (Fig. 19k), SFCVT (Fig. 19l), SSA (Fig. 19m) and TEAD (Fig. 19n). This can also be observed from the global error measure NRMSE which is plotted over the sampling process in Fig. 20 where also the relative improvement of this value is depicted. The local error at the global minimum is displayed in Fig. 21.
Global error measure for the \(\widehat{{\mathcal{M}}}_{Gram,1D}\) metamodel, a, b Evolution of the mean NRMSE estimate over the adaptive process, c relative improvement of the NRMSE estimates from the 10 samples-based initial metamodel to the 20 samples- and 50 samples-based metamodels. (Color figure online)
7.3.4 Adjusted Gramacy and Lee Function
An adjusted variant of the Gramacy & Lee function defined for \(x \in \left[ -1.5 , 6.0 \right] \) as
with
is studied. This function as shown in Fig. 22a has more drastic fluctuations than the classical Gramacy & Lee function previously investigated and does not exhibit a regular pattern.
From the knowledge extracted from the initial metamodel illustrated in Fig. 22a based on 10 samples, alternative metamodels based on 50 samples are shown in Fig. 22. Alike previous examples, a few methods exhibit an exploitation component, which is not pertinent to fit the response surface globally, e.g. EI (Fig. 22e) creates a majority of the points around the lowest sample output and Lipschitz (Fig. 22g) samples majorly nearby the largest gradient. Besides sampling techniques with higher exploration contribution, such as EIGF (Fig. 22f), SSA (Fig. 22m), MEPE (Fig. 22i) or TEAD (Fig. 22n), perform overall better with regard to global metamodeling.
This can also be seen when studying the mean NRMSE value as given in Fig. 23. In contrast to previous examples, pure exploration behavior such as given by MIPT is insufficient to represent the target accurately. This can also be noticed through the evolution of the local error at the global minimum over the adaptive process, i.e. Fig. 24. Promising performances of the Lipschitz scheme and MEPE can be highlighted. Lipschitz performs well as the global minimum is close to the domain with largest gradient. It appears that the adaptive balance between exploration and exploitation offered by MEPE is crucial for accurate metamodel for such complex irregular functions.
7.3.5 Supplementary One-Dimensional Benchmark Tests
Three supplementary one-dimensional test cases (Problems P1, P2 and P3) are exposed in “Appendix 1.1”. These three functions are rather simple. It can be noticed that most adaptive techniques have good behavior for these simple functions with low gradient and low variation of the gradient, even strategies purely based on exploration such as MIPT can perform well, even better than some advanced strategies. It appears thus that the choice of the adaptive scheme is not of very high importance for such cases.
A distinction can thus be done with cases of more complex functions such as previous examples where balance between exploitation and exploration is required to reduce number of required samples, and a large discrepancy of performance occurs among the adaptive schemes.
7.4 Two-Dimensional Tests
To highlight further the differences in performance of the adaptive techniques an in-depth analysis of two two-dimensional benchmark tests as well as an engineering application are performed.
7.4.1 Michalewicz Function \({\mathcal{M}}_{Mi,2D}\)
The first two-dimensional problem is the Michalewicz function given by
where the parametric space is \((x_{1},x_{2}) \in \left[ 0.0 , \pi \right] ^2\). The target surface of the function over the normalized space is displaced in Fig. 25a. The function shows an irregular response behavior. The initial sample positions are depicted as black dots in Fig. 25b over the normalized absolute error of the initial metamodel. It can be seen that the initial surrogate model yields a large error in the upper right-hand corner of the parametric space as well as in the area around the steep valley of the response surface at \(y\approx 0.9\). Proficient adaptive sampling techniques should sample in these areas. The position of the global minimum of the function is symbolized by the grey dot.
From an initial dataset comprising 20 points, one realization of dataset with 45 samples for each adaptive technique is plotted over the initial error map in Fig. 27. As in previous one-dimensional tests it can be seen that WAE (Fig. 27n) fails to sample the parametric space pertinently. Besides, pure distance-based exploration approach as MIPT (Fig. 27i) is not efficient for the given problem setting. Overall the characteristics of the adaptive techniques observed for one-dimensional cases also appear for that problem. Thus, EI (Fig. 27d) predominantly clusters around the position of the minimum known value, which is undesirable for global metamodeling. SSA (Fig. 27l) generates a majority of samples close to the boundaries of the parametric space, which is observed in all investigated benchmark tests. It can be highlighted that all techniques design samples in regions where the error of the initial metamodel was already quite low. This is particularly noticeable for the Lipschitz technique (Fig. 27f) as well as LOLA (Fig. 27g).
The bad performances of Lipschitz and LOLA are also visible in Fig. 26, which depicts the evolution of the global NRMSE value over the sampling process. Except them most of the adaptive sampling techniques fall into similar error range. Since the initial error is predominantly high in areas with a low output, it can be noticed that EI yields comparably proficient results. Along with EI, MEPE (Fig. 27h), EIGF (Fig. 27e) and SSA (Fig. 27l) show the best approximation behavior with samples located in the areas with highest initial error.
7.4.2 Drop-Wave Function \({\mathcal{M}}_{DW,2D}\)
Next, a more complicated two-dimensional problem, the drop-wave function, is investigated, which is given by
on the parametric domain \((x_{1},x_{2}) \in \left[ -0.6 , 0.9 \right] ^2\). The response surface of the function over a normalized space is illustrated in Fig. 28a. It can be seen that the response surface is highly complex with high gradients and irregular shape.
7.4.2.1 Initial Dataset
The initial sample positions as well as the normalized maximum absolute error of the initial metamodel are depicted in Fig. 28b. The position of the global minimum is indicated by a grey dot. It can be noticed that the initial error is larger and its map more complex than for previous case \(M_{Mi,2D}\) due to the complexity of the true function. To obtain an accurate metamodel, adaptive sampling process should sample in each subdomain associated with large error. This task appears cumbersome as seven disconnected subdomains are to be targeted.
7.4.2.2 Analysis of Different Sets with 75 Samples
Realizations of sample positions when reaching 75 samples in the dataset are plotted over the error map of the respective metamodel in Fig. 29. For sake of comparison, the color scale is kept fixed for all schemes as the color scale of the initial error map (Fig. 28b).
WAE (Fig. 29n) and to a lesser degree SSA (Fig. 29l) show clustering behavior, due to the weak exploration component of these methods. As noted in previous examples, SSA samples are mainly located near to the boundaries of the parametric space, therefore SSA is able to properly estimate the function in the problematic area close to (0, 0). However the final error (Fig. 29l) in the central region of the parametric domain is still comparably high. ACE (Fig. 29a) and CVVor (Fig. 29c) fail to sample in the domain near to (0, 0).
It appears that for a target function with such a complexity none of the exploitation components of the investigated techniques are beneficial to the final metamodel. Indeed, the pure exploration-based approach of MIPT (Fig. 29i) shows the most promising result.
Sample point positions after reaching 75 samples in the dataset plotted over the absolute error of the final \(\widehat{{\mathcal{M}}}_{DW,2D}\) metamodel (colorscale as given in Fig. 28b for the initial error surface, red point indicates a sample very close to a neighbor point). (Color figure online)
7.4.2.3 Analysis of the Error Evolution While Sampling
MIPT appears also as best-performer through the evolution of the global NRMSE error while sampling, as exposed in Fig. 30a and b. However after 100 samples MEPE has a similar error as MIPT because of a fast error decrease after around 75 samples. In comparison to previous tests, more significant difference between method performances is observable. With more than 80 samples the NRMSE value of WAE is noisy which indicates a clustering effect. As all optimizations are done using identical solvers and solver-settings, this specific behavior suggests that WAE leads to a peculiarly complex optimization problem.
In order to study the complexity of the optimization process, the variances of the NRMSE value over the 10 realizations are compared Fig. 30c and d. The spread of NRMSE value substantiates the presented results because low variances indicate that the optimised solution is accurately found, whereas high variances highlight that the optimization solver is not adequate for a given problem. It can be seen that the variance of all investigated methods is significantly smaller (factor 1/100) in order of magnitude comparing with mean error values. Noisy RMSE value of WAE corresponds to an increase in variance which hints towards inaccurate solution of optimization problem for both hyperparameter identification and sample design.
7.4.3 Supplementary Two-Dimensional Benchmark Functions
Adaptive sampling behavior for eight supplementary two-dimensional benchmark tests with a large variety of features are available in “Appendix 1.2”. Surprisingly MIPT does not yield significantly worse results than other schemes on average. Techniques with high degree of exploration provide best results with regard to global metamodeling. This includes AME, EIGF, MASA, MEPE, MIPT, SFCVT and TEAD. Other methods show weaker performances in at least one of the studied cases.
7.4.4 Engineering Application
Finally, performances of the adaptive techniques are tested for an engineering application. Consider the two-dimensional contact problem as sketched in Fig. 31a. An elastically deformable block with Young modulus \(E= 10\) MPa and Poisson ratio \( \nu = 0.3\) is pushed over an infinitely extended rigid and flat surface. On the top of the body a displacement boundary \({\overline{u}} = 0.3 \, \text {mm}\) is applied and parameterized by an application angle \(\gamma \). The behavior of the contact between the block and the rigid surface is modelled using Coulomb model with friction coefficient denoted \(\mu \). The mechanical problem is solved with the finite element method, where the non-linear contact problem is approximated through the penalty method. The parametric space is defined by the friction coefficient \(\mu \in [0.35, 0.5]\) and the displacement angle \(\gamma \in [0.7,2.4]\). The quantity of interest is the maximum von Mises stress value among all considered Gauss points during the whole duration of the simulation. The resulting response surface over the normalized parameter space is shown in Fig. 31b. It can be seen that the surface is highly nonlinear but symmetric, so with only one line of turning points. This response surface might appear as rather complex in comparison to many quasi-static engineering applications, for which common quantities of interest oftentimes yield linear or slightly nonlinear response surface. For these cases, as shown before, exploration-based technique are generally proficient enough for accurate adaptive metamodeling.
Relative improvement of the NRMSE value between initial metamodel based on 10 samples and metamodels based on 15 and 35 samples is shown in Fig. 32. It can be seen that, even for this highly non-linear response surface, pure exploration strategy as proposed by MIPT is satisfactory. Nevertheless, techniques, which combine a high degree of exploration and some exploitation component, perform slightly better, such as AME, MASA, MEPE, SSA and TEAD.
7.5 Higher-Dimensional Tests
The question arises to test the ability of adaptive schemes to tackle higher-dimensional problems in order to determine if the established performance characteristics can straightforwardly be extended for higher dimensions. Indeed, due to the curse of dimensionality, training a kriging surrogate model in high dimensions can become more complex or even unmanageable [110]. Different strategies have been proposed to deal with metamodels for very high-dimensional parameter space see e.g. Bouhlel et al. [9] or Lataniotis et al. [60]. However this specific problem is out of the scope of this review, so here the dimension of benchmark tests is restricted to a maximum of six dimensions. Six benchmark functions have been tested. Among them, three are three-dimensional, two are four-dimensional and one is six-dimensional. Results are detailed in “Appendix 1.3”.
Overall the adaptive techniques behave rather similarly in higher dimensions as in low-dimensional cases. Main, difference to be highlights is the computational. Indeed, computational effort required for example by methods based on the LOOCV error such as CVVor or SFCVT is considerably higher, almost prohibitive, when dimensions increase.
8 A Guide to Adaptive Sampling for Kriging Metamodeling
To sum-up this exhaustive analysis, a guide is offered in Table 3 to offer an efficient orientation for the choice of adaptive techniques such that goal-oriented and information-based decisions can be made pertinently. Three main families of criteria are suggested to analyze the adaptive sampling performance, namely the goal of the study, the known characteristics of the function of interest and the properties of the design of experiments. Finally methods are also compared by some miscellaneous criteria. Naturally the \(+\) and − symbols indicate positive and negative results in a subcategory. A doubled sign (\(++\) or \(--\)) symbolizes especially promising or unfavorable behavior.
8.1 Regarding the Goal of the Study
Two major goals of study are contemplated, global metamodeling and optimization.
For global metamodeling the studies have shown that adaptive sampling techniques with higher exploration component yield more proficient metamodels, so MASA, MEPE and MIPT are recommended. WAE and EI lead to unpredictable and unfavorable performances for this application.
For optimization, MEPE and EI outperform other strategies. However EI is strongly dependent on the size of the initial sample. Performances are good for a large enough dataset, based on evenly spread samples. MIPT is not recommended for optimization, because it does not include any exploitation feature. WAE is also not dependable in this regard and a bad choice overall. The rest of the methods perform more or less similarly with regards to optimization.
8.2 Regarding a Priori Known Characteristics of the Response Surface
Detailed characteristics are a priori unknown before building a metamodel. However, general behavior is oftentimes known based on previously obtained expert knowledge and experience. Particularly, in most cases, it can be established or properly guessed if the target function exhibits regular and irregular pattern behavior. With the exception of EI and WAE, it must be acknowledged that most adaptive sampling methods perform well for regular pattern without crucial difference in terms of performances. In case of irregular patterns, adaptive methods with emphasis on exploration show superior approximation prowess. Therefore, MEPE and the pure exploration-based technique MIPT are more recommended. On the contrary, ACE should also be avoided due to clustering risk.
8.3 Regarding Properties of the Initial Design of Experiments
Crucial properties of the design of experiments are the size of the initial dataset, the parametric dimension of the problem and the risk of running into clustering issues.
Small initial design of experiments are a challenge for adaptive schemes. Higher emphasise on exploration provides better robustness regarding small initial design of experiments. So, MASA, MEPE, MIPT and SFCVT are favored in that scenario. On the other hand EI and ACE fail to cope well with small initial designs of experiments.
Adaptive techniques with low complexity are favorable to tackle high-dimensional parametric space, a crucial limiting factor being computational time and resources to design the new sample. Indeed, high-dimensional parametric dimensions usually require a large dataset-size and therefore more adaptive sampling steps. Hence, schemes based on leave-one-out cross-validation errors for exploitation require building m new metamodels in order to define the \(m+1\)-st sample. So, using LOOCV, the needed computational resources dramatically increase with parametric dimension. Hence, methods such as ACE, CVVor, SSA and WAE cannot be recommended in that case. Similarly query-by-committee methods such as MASA should be avoided as they are also based upon building various metamodels in order to compare the differences. Finally, LOLA also shows some problems in high dimension because the gradient estimation approach used gets increasingly complex and resource-heavy in high dimensions. Similar performance results as provided by these more complex approaches can be obtained in high dimension by less demanding methods such as MEPE, EIGF or even MIPT.
Risk of clustering is a major point in methods without strong exploratory feature such as EI and WAE. Furthermore, some adaptive techniques such as ACE, AME and SSA search for the next sample point by optimizing a highly complex cost function, which leads to clustering issues when it is not solved accurately.
8.4 Regarding Supplementary and Miscellaneous Criteria
It may be of high interest to employ methods which are versatile for different surrogate modelling approaches, such as kriging, neural network, support vector machines. Versatility leads to reduction of developing time if the target is included in a more general framework and goal. Among the investigated adaptive schemes, AME, EI, EIGF and MEPE, which are specifically based on kriging characteristics can not straightforwardly be included in other frameworks. All other schemes can be extended to other surrogate frameworks.
In low dimensions, computational costs are not of significant interests, as they are mainly negligible. However, the computational costs become notable for high-dimensional problems that require a larger number of adaptive samples. Therefore this criteria correlates perfectly with the previously discussed utilisation of the schemes for high dimensions, where cross-validation-based techniques such as WAE and ACE can be seen as unfavorable. The computational complexity of MASA highly depends on the number of chosen committee members. Due to the large number of neighborhood cases for higher dimensions LOLA is also judged as a resource-heavy scheme. EI and EIGF appear especially positive in this regard, because they just require the solution of a simple optimization problem built from the sum of a geometric feature and the local kriging variance.
The next evaluated criterion is the coding complexity of the respective techniques, i.e. how much development time is needed from the user. This feature is highly depending on the user’s previous experiences and skills. However, to picture a general scheme for a naive user, SFCVT is considered as the hardest from a programming perspective, because it approximates the LOOCV error by generating further kriging models and uses a constrained optimization problem. Besides, methods based on the tessellation of the input space into Voronoi cells such as CVVor and LOLA require also higher effort. On the contrary, EI, EIGF and MIPT are simply to implement when a kriging routine is already available.
Lastly the complexities of the optimization problems given by the cost functions that need to be minimized in order to obtain the new sample points are compared. This feature is oftentimes not mentioned or commented on in the literature. However, it appears as an important feature since a simple cost function helps to obtain reproducible and less volatile results and furthermore makes the utilization of simple and fast optimization tools possible. In this context, ACE, AME and WAE which are associated with highly complex cost functions usually require the usage of very precise optimization tools in order to avoid clustering problems. CVVor, EI, MEPE appear as problematic techniques because they do not have a maximum cost function value around existing sample points or sharp drop offs around these points. Finally, SFCVT, SSA, WAE require additional computational costs because the investigated solution space is constrained.
8.5 Overview
It can be highlighted that no perfect one-size-fits-all scheme can be extracted from the series of benchmark test and a compromise appears as the best practice. Over all the examined criteria, MEPE yields the most complete performance regarding all investigated test cases. This method is especially advised when no prior knowledge about function characteristics is available. In the authors opinion it is also the best candidate for a reference scheme to compare and analyze future innovative schemes with. In addition, EIGF and the purely exploration-based technique MIPT yield reliable results and require less development and user-knowledge.
9 Open Issues
From this comparative review it can be concluded that with regard to global metamodeling pure exploration-based approaches such as MIPT yield on average comparable results to other dedicated adaptive techniques. This is not only the case for specific target function characteristics such as sharp humbs or valley-shaped functions for which MIPT sampling converges slower.
The adaptive techniques proposed in the literature regularly try to obtain a one-fits-all approach for adaptive sampling, i.e. that a specific adaptive technique is supposed to work for all dimensions and function complexities. In this review it has been observed that some adaptive techniques perform better given some specific initial setting (a larger initial design of experiments) or for a specific response surface shape, e.g. a valley. For instance, large exploitation component is beneficial or detrimental depending on function characteristics. Therefore user knowledge about the unknown function is crucial when choosing the right adaptive tool. Hence, based on the shape and characteristic of the target function different adaptive solutions need to be proposed.
The results of this paper show that MEPE which employs a switching strategy between exploration and exploitation proves to be a promising approach that is able to cope with different function complexities and requirements. Efforts to investigate adaptive strategies that balance local exploitation and global exploration accordingly need to be increased. Additionally while proposing new adaptive techniques researchers need to look for the complexity of the presented optimization problem because this complexity is a limiting factor with regards to computational costs and resources required to utilize the respective technique and furthermore enhances reproducibility. Finally for easier accountability and in order to facilitate and speed up the development of new and better adaptive techniques we encourage researchers to make a running example of their algorithms publicly available.
10 Conclusion
This work offered a comprehensive overview of the state-of-the-art techniques for adaptive sampling for the kriging method. This specific metamodeling technique has proven to yield proficient regression results and is specifically useful for a low number of data samples. It has seen use in a wide range of engineering applications. For high-cost simulations or otherwise hard to obtain sampling procedures adaptive sampling techniques have been established and widely applied. In this work we tried to categorize existing methods found in the literature based on their main characteristics, specifically distinguishing between techniques used for exploration and exploitation of the parametric space. The applied exploration components can be divided into distance-based and variance-based techniques. The techniques to achieve exploitation behavior can be subdivided into cross-validation-based, geometry-based and query-by-committee-based methods. For each of the given subclasses multiple references have been collected.
In a next step 14 different techniques adaptive sampling techniques have been thoroughly reviewed in order to propose a clear overview of the current state-of-the-art. Due to a lack of thorough comparisons as well as distinctions between the methods found in the literature a comparative review of these 14 methods has been conducted. Here the methods have been studied on 27 different benchmark tests of various dimensions and complexities in order to highlight the respective strengths and weaknesses. In order to provide transparency the MATLAB code which has been used to obtain the presented results has been made publicly available. It includes all analysed adaptive techniques as well as investigated benchmark tests.
It has been found that on average adaptive techniques with a large degree of exploration are preferable for cases where the characteristics of the target function are unknown. Furthermore pure exploration-based techniques offer a cheap but acceptable option and seem to yield better performances than a majority of the investigated adaptive techniques. A user-guide has been developed in order to assist the interested user in the choice of an adaptive technique for a given problem setting. It can be used to rule out adaptive techniques for given problem settings. Open questions with regard to adaptive sampling techniques for the kriging method have been discussed and existing problems have been highlighted.
Availability of data and material
The data that supports the findings of this study can be directly reproduced by the provided code. However, if required, it is also available from the corresponding author under reasonable request.
References
Acar E, Rais-Rohani M (2009) Ensemble of metamodels with optimized weight factors. Struct Multidiscip Optim 37(3):279–294
Asher M, Croke B, Jakeman A, Peeters L (2015) A review of surrogate models and their application to groundwater modeling. Water Resources Res 51(8):5957–5973
Aurenhammer F (1991) Voronoi diagrams—a survey of a fundamental geometric data structure. ACM Comput Surv (CSUR) 23(3):345–405
Aute V, Saleh K, Abdelaziz O, Azarm S, Radermacher R (2013) Cross-validation based single response adaptive design of experiments for kriging metamodeling of deterministic computer simulations. Struct Multidiscip Optim 48(3):581–605
Bachoc F (2013) Cross validation and maximum likelihood estimations of hyper-parameters of Gaussian processes with model misspecification. Comput Stat Data Anal 66:55–69
Bhattacharyya M, Fau A, Nackenhorst U, Néron D, Ladevèze P (2018) A model reduction technique in space and time for fatigue simulation. In: Soric J, Wriggers P, Allix O (eds) Multiscale modeling of heterogeneous structures. Springer, Cham, pp 183–203
Bichon B (2010) Efficient surrogate modeling for reliability analysis and design. Ph.D. thesis, Vanderbilt University
Bouhlel M, Martins J (2019) Gradient-enhanced kriging for high-dimensional problems. Eng Comput 35(1):157–173
Bouhlel M, Bartoli N, Otsmane A, Morlier J (2016) Improving kriging surrogates of high-dimensional design models by partial least squares dimension reduction. Struct Multidiscip Optim 53(5):935–952
Busby D (2009) Hierarchical adaptive experimental design for Gaussian process emulators. Reliab Eng Syst Saf 94(7):1183–1193
Busby D, Farmer C, Iske A (2007) Hierarchical nonlinear approximation for experimental design and statistical data fitting. SIAM J Sci Comput 29(1):49–69
Byrd R, Gilbert J, Nocedal J (2000) A trust region method based on interior point techniques for nonlinear programming. Math Program 89(1):149–185
Chen Z, Qiu H, Gao L, Li X, Li P (2014) A local adaptive sampling method for reliability-based design optimization using kriging model. Struct Multidiscip Optim 49(3):401–416
Chernoff H (1959) Sequential design of experiments. Ann Math Stat 30(3):755–770
Cohn D, Atlas L, Ladner R (1994) Improving generalization with active learning. Mach Learn 15(2):201–221
Coulibaly P, Anctil F, Bobee B (2000) Daily reservoir inflow forecasting using artificial neural networks with stopped training approach. J Hydrol 230(3–4):244–257
Cressie N (1992) Statistics for spatial data. Terra Nova 4(5):613–617
Crombecq K, Gorissen D, Deschrijver D, Dhaene T (2011a) A novel hybrid sequential design strategy for global surrogate modeling of computer experiments. SIAM J Sci Comput 33(4):1948–1974
Crombecq K, Laermans E, Dhaene T (2011b) Efficient space-filling and non-collapsing sequential design strategies for simulation-based modeling. Eur J Oper Res 214(3):683–696
Crombecq K, Couckuyt I, Gorissen D, Dhaene T (2009) Space-filling sequential design strategies for adaptive surrogate modelling. In: The first international conference on soft computing technology in civil, structural and environmental engineering, vol 38
Crombecq K, Gorissen D, Deschrijver D, Dhaene T (2011) Adaptive sampling algorithm for macromodeling of parameterized S-parameter responses. IEEE Trans Microw Theory Tech 59:39–45
Currin C, Mitchell T, Morris M, Ylvisaker D (1988) A Bayesian approach to the design and analysis of computer experiments. Technical report, Oak Ridge National Lab., TN (USA)
Currin C, Mitchell T, Morris M, Ylvisaker D (1991) Bayesian prediction of deterministic functions, with applications to the design and analysis of computer experiments. J Am Stat Assoc 86(416):953–963
de Angelis M, Patelli E, Beer M (2015) Advanced line sampling for efficient robust reliability analysis. Struct Saf 52:170–182
Deb K (2000) An efficient constraint handling method for genetic algorithms. Comput Methods Appl Mech Eng 186(2–4):311–338
Dubourg V (2011) Adaptive surrogate models for reliability analysis and reliability-based design optimization. Ph.D. thesis, Université Blaise Pascal-Clermont-Ferrand II
Dubourg V, Sudret B, Deheeger F (2013) Metamodel-based importance sampling for structural reliability analysis. Probab Eng Mech 33:47–57
Eason J, Cremaschi S (2014) Adaptive sequential sampling for surrogate model generation with artificial neural networks. Comput Chem Eng 68:220–232
Freund Y, Seung H, Shamir E, Tishby N (1993) Information, prediction, and query by committee. In: Advances in neural information processing systems, pp 483–490
Fuhg JN, Fau A (2019a) An innovative adaptive kriging approach for efficient binary classification of mechanical problems. arXiv preprint arXiv:190701490
Fuhg JN, Fau A (2019b) Surrogate model approach for investigating the stability of a friction-induced oscillator of Duffing’s type. Nonlinear Dyn 98(3):1709–1729
Fushiki T (2011) Estimation of prediction error by using k-fold cross-validation. Stat Comput 21(2):137–146
Garud S, Karimi I, Kraft M (2017) Smart sampling algorithm for surrogate model development. Comput Chem Eng 96:103–114
Ghoreyshi M, Badcock K, Woodgate M (2009) Accelerating the numerical generation of aerodynamic models for flight simulation. J Aircr 46(3):972–980
Gunn S (1998) Support vector machines for classification and regression. ISIS Tech Rep 14(1):5–16
Hasenjäger M, Ritter H (2002) Active learning in neural networks. In: Jain LC, Kacprzyk J (eds) New learning paradigms in soft computing. Springer, Heidelberg, pp 137–169
Huang D, Allen TT, Notz WI, Miller RA (2006) Sequential kriging optimization using multiple-fidelity evaluations. Struct Multidiscip Optim 32(5):369–382
Husslage B, Rennen G, van Dam E, den Hertog D (2011) Space-filling Latin hypercube designs for computer experiments. Optim Eng 12(4):611–630
Ingber L (1993) Adaptive simulated annealing (asa). Global optimization C-code. Caltech Alumni Association, Pasadena, CA
Janssen H (2013) Monte-Carlo based uncertainty analysis: sampling efficiency and sampling convergence. Reliab Eng Syst Saf 109:123–132
Jiang C, Cai X, Qiu H, Gao L, Li P (2018) A two-stage support vector regression assisted sequential sampling approach for global metamodeling. Struct Multidiscip Optim 58:1–16
Jiang P, Shu L, Zhou Q, Zhou H, Shao X, Xu J (2015) A novel sequential exploration-exploitation sampling strategy for global metamodeling. IFAC-PapersOnLine 48(28):532–537
Jiang P, Zhang Y, Zhou Q, Shao X, Hu J, Shu L (2017) An adaptive sampling strategy for kriging metamodel based on Delaunay triangulation and TOPSIS. Appl Intell 48:1–13
Jin R, Chen W, Simpson T (2001) Comparative studies of metamodelling techniques under multiple modelling criteria. Struct Multidiscip Optim 23(1):1–13
Jin R, Chen W, Sudjianto A (2002) On sequential sampling for global metamodeling in engineering design. In: ASME 2002 international design engineering technical conferences and computers and information in engineering conference. American Society of Mechanical Engineers, pp 539–548
Jones A, Wilcox R (2008) Finite element analysis of the spine: towards a framework of verification, validation and sensitivity analysis. Med Eng Phys 30(10):1287–1304
Jones D, Schonlau M, Welch W (1998) Efficient global optimization of expensive black-box functions. J Glob Optim 13(4):455–492
Joseph R (2016) Space-filling designs for computer experiments: a review. Qual Eng 28(1):28–35
Joseph V, Hung Y, Sudjianto A (2008) Blind kriging: a new method for developing metamodels. J Mech Des 130(3):031102
Kim B, Lee Y, Choi D (2009) Construction of the radial basis function based on a sequential sampling approach using cross-validation. J Mech Sci Technol 23(12):3357–3365
Kleijnen J (2008) Design of experiments: overview. In: 2008 winter simulation conference. IEEE, pp 479–488
Kleijnen J (2009) Kriging metamodeling in simulation: a review. Eur J Oper Res 192(3):707–716
Kleijnen J (2017) Regression and kriging metamodels with their experimental designs in simulation: a review. Eur J Oper Res 256(1):1–16
Kleijnen J, Beers W (2004) Application-driven sequential designs for simulation experiments: kriging metamodelling. J Oper Res Soc 55(8):876–883
Kleijnen J, Van Beers W, Van Nieuwenhuyse I (2012) Expected improvement in efficient global optimization through bootstrapped kriging. J Global Optim 54(1):59–73
Kremer J, Steenstrup Pedersen K, Igel C (2014) Active learning with support vector machines. Wiley Interdiscip Rev: Data Min Knowl Discov 4(4):313–326
Krige D (1951) A statistical approach to some basic mine valuation problems on the Witwatersrand. J Southern Afr Inst Min Metall 52(6):119–139
Krogh A, Vedelsby J (1995) Neural network ensembles, cross validation, and active learning. In: Advances in neural information processing systems, pp 231–238
Lam C (2008) Sequential adaptive designs in computer experiments for response surface model fit. Ph.D. thesis, The Ohio State University
Lataniotis C, Marelli S, Sudret B (2020) Extending classical surrogate modelling to ultrahigh dimensional problems through supervised dimensionality reduction: a data-driven approach. Int J Uncertain Quant 10(1):1–38
Laurenceau J, Sagaut P (2008) Building efficient response surfaces of aerodynamic functions with kriging and cokriging. AIAA J 46(2):498–507
Laurent L, Boucard P, Soulier B (2013) Generation of a cokriging metamodel using a multiparametric strategy. Comput Mech 51(2):151–169
Laurent L, Le Riche R, Soulier B, Boucard P (2019) An overview of gradient-enhanced metamodels with applications. Arch Comput Methods Eng 26(1):61–106
Li B, Peng L, Ramadass B (2009) Accurate and efficient processor performance prediction via regression tree based modeling. J Syst Arch 55(10–12):457–467
Li G, Aute V, Azarm S (2010a) An accumulative error based adaptive design of experiments for offline metamodeling. Struct Multidiscip Optim 40(1–6):137
Li Y, Ng S, Xie M, Goh T (2010b) A systematic comparison of metamodeling techniques for simulation optimization in decision support systems. Appl Soft Comput 10(4):1257–1273
Liao X, Yan X, Xia W, Luo B (2010) A fast optimal Latin hypercube design for Gaussian process regression modeling. In: Third international workshop on advanced computational intelligence. IEEE, pp 474–479
Liu H, Xu S, Wang X, Wu J, Song Y (2015) A global optimization algorithm for simulation-based problems via the extended direct scheme. Eng Optim 47(11):1441–1458
Liu H, Xu S, Ma Y, Chen X, Wang X (2016a) An adaptive Bayesian sequential sampling approach for global metamodeling. J Mech Des 138(1):011404
Liu H, Xu S, Wang X, Meng J, Yang S (2016b) Optimal weighted pointwise ensemble of radial basis functions with different basis functions. AIAA J 54:3117–3133
Liu H, Cai J, Ong Y (2017) An adaptive sampling approach for kriging metamodeling by maximizing expected prediction error. Comput Chem Eng 106:171–182
Liu H, Ong Y, Cai J (2018) A survey of adaptive sampling for global metamodeling in support of simulation-based complex engineering design. Struct Multidiscip Optim 57(1):393–416
Liu W (2003) Development of gradient-enhanced kriging approximations for multidisciplinary design optimization. Ph.D. thesis, University of Notre-Dame, Indiana
Loeppky J, Sacks J, Welch W (2009) Choosing the sample size of a computer experiment: a practical guide. Technometrics 51(4):366–376
Lovison A, Rigoni E (2011) Adaptive sampling with a Lipschitz criterion for accurate metamodeling. Commun Appl Ind Math 1(2):110–126
Martin J, Simpson T (2002) Use of adaptive metamodeling for design optimization. In: 9th AIAA/ISSMO symposium on multidisciplinary analysis and optimization, p 5631
Matérn B (1960) Spatial variation: Meddelanden fran statens skogsforskningsinstitut. Lect Not Stat 36:21
MATLAB (2019) version 9.7.0.1190202 (r2019b)
Meckesheimer M, Booker A, Barton R, Simpson T (2002) Computationally inexpensive metamodel assessment strategies. AIAA J 40(10):2053–2060
Melville P, Mooney R (2004) Diverse ensembles for active learning. In: Proceedings of the twenty-first international conference on Machine learning. ACM, p 74
Mendes-Moreira J, Soares C, Jorge A, Sousa J (2012) Ensemble approaches for regression: a survey. ACM Comput Surv (CSUR) 45(1):10
Mo S, Lu D, Shi X, Zhang G, Ye M, Wu J, Wu J (2017) A Taylor expansion-based adaptive design strategy for global surrogate modeling with applications in groundwater modeling. Water Resources Res 53(12):10802–10823
Mukhopadhyay T, Dey T, Chowdhury R, Chakrabarti A (2015) Structural damage identification using response surface-based multi-objective optimization: a comparative study. Arab J Sci Eng 40(4):1027–1044
Østergård T, Jensen R, Maagaard S (2018) A comparison of six metamodeling techniques applied to building performance simulations. Appl Energy 211:89–103
Pasolli E, Melgani F, Bazi Y (2010) Support vector machine active learning through significance space construction. IEEE Geosci Remote Sens Lett 8(3):431–435
Paul-Dubois-Taine A, Nadarajah S (2013) Sensitivity-based sequential sampling of cokriging response surfaces for aerodynamic data. In: 31st AIAA applied aerodynamics conference, p 2652
Pellegrino G, Cupertino F (2010) FEA-based multi-objective optimization of IPM motor design including rotor losses. In: 2010 IEEE energy conversion congress and exposition. IEEE, pp 3659–3666
Pronzato L, Müller W (2012) Design of computer experiments: space filling and beyond. Stat Comput 22(3):681–701
Rasmussen C, Williams C (2006) Gaussian processes for machine learning, vol 38. The MIT Press, Cambridge, MA, pp 715–719
Robbins H (1952) Some aspects of the sequential design of experiments. Bull Am Math Soc 58(5):527–535
Sacks J, Welch W, Mitchell T, Wynn H (1989) Design and analysis of computer experiments. Stat Sci 4:409–423
Santner T, Williams B, Notz W (2013) The design and analysis of computer experiments. Springer, Berlin
Sasena M (2002) Flexibility and efficiency enhancements for constrained global design optimization with kriging approximations. Ph.D. thesis, University of Michigan
Sasena M, Parkinson M, Goovaerts P, Papalambros P, Reed M (2002) Adaptive experimental design applied to ergonomics testing procedure. In: ASME 2002 international design engineering technical conferences and computers and information in engineering conference. American Society of Mechanical Engineers, pp 529–537
Seung H, Opper M, Sompolinsky H (1992) Query by committee. In: Proceedings of the fifth annual workshop on computational learning theory. ACM, pp 287–294
Shannon C (1948) A mathematical theory of communication. Bell Syst Tech J 27(4):623–656
Singh P, Deschrijver D, Dhaene T (2013) A balanced sequential design strategy for global surrogate modeling. In: Simulation conference (WSC). Winter, IEEE, pp 2172–2179
Sóbester A, Leary S, Keane A (2005) On the design of optimization strategies based on global response surface approximation models. J Global Optim 33(1):31–59
Specht D (1991) A general regression neural network. IEEE Trans Neural Netw 2(6):568–576
Sundararajan S, Keerthi S (2000) Predictive approaches for choosing hyperparameters in Gaussian processes. In: Advances in neural information processing systems, pp 631–637
Toal D, Bressloff N, Keane A, Holden C (2011) The development of a hybridized particle swarm for kriging hyperparameter tuning. Eng Optim 43(6):675–699
Tuceryan M, Jain A (1990) Texture segmentation using Voronoi polygons. IEEE Trans Pattern Anal Mach Intell 12(2):211–216
Turner CJ, Crawford RH, Campbell MI (2007) Multidimensional sequential sampling for NURBs-based metamodel development. Eng Comput 23(3):155–174
Ugray Z, Lasdon L, Plummer J, Glover F, Kelly J, Martí R (2007) Scatter search and local NLP solvers: a multistart framework for global optimization. INFORMS J Comput 19(3):328–340
Ulaganathan S, Couckuyt I, Dhaene T, Degroote J, Laermans E (2016) High dimensional kriging metamodelling utilising gradient information. Appl Math Model 40(9–10):5256–5270
Van Beers W, Kleijnen J (2003) Kriging for interpolation in random simulation. J Oper Res Soc 54(3):255–262
Van Beers W, Kleijnen J (2008) Customized sequential designs for random simulation experiments: kriging metamodeling and bootstrapping. Eur J Oper Res 186(3):1099–1113
Van Dam E, Husslage B, Den Hertog D, Melissen H (2007) Maximin Latin hypercube designs in two dimensions. Oper Res 55(1):158–169
van der Herten J, Couckuyt I, Deschrijver D, Dhaene T (2015) A fuzzy hybrid sequential design strategy for global surrogate modeling of high-dimensional computer experiments. SIAM J Sci Comput 37(2):A1020–A1039
Verleysen M, François D (2005) The curse of dimensionality in data mining and time series prediction. In: International work-conference on artificial neural networks. Springer, pp 758–770
Viana F, Haftka R, Steffen V (2009) Multiple surrogates: how cross-validation errors can help us to obtain the best predictor. Struct Multidiscip Optim 39(4):439–457
Viana F, Venter G, Balabanov V (2010) An algorithm for fast optimal latin hypercube design of experiments. Int J Numer Methods Eng 82(2):135–156
Viana F, Simpson T, Balabanov V, Toropov V (2014) Special section on multidisciplinary design optimization: metamodeling in multidisciplinary design optimization: how far have we really come? AIAA J 52(4):670–690
Wood G, Zhang B (1996) Estimation of the Lipschitz constant of a function. J Global Optim 8(1):91–103
Xiao S, Rotaru M, Sykulski J (2012) Exploration versus exploitation using kriging surrogate modelling in electromagnetic design. COMPEL Int J Comput Math Electr Electron Eng 31(5):1541–1551
Xu S, Liu H, Wang X, Jiang X (2014) A robust error-pursuing sequential sampling approach for global metamodeling based on Voronoi diagram and cross validation. J Mech Des 136(7):071009
Zhang J, Chowdhury S, Messac A (2012) An adaptive hybrid surrogate model. Struct Multidiscip Optim 46(2):223–238
Acknowledgements
Open Access funding provided by Projekt DEAL.
Funding
The first author acknowledges the financial support from the Deutsche Forschungsgemeinschaft under Germanys’ Excellence Strategy within the Cluster of Excellence PhoenixD (EXC 2122, Project ID 390833453). Open Access funding provided by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
J.N.F. performed the numerical simulations and implemented the algorithms. Both J.N.F. and A.F. contributed significantly to the final version of the manuscript. All authors contributed to improve the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Code availability
The code can be found under https://github.com/FuhgJan/StateOfTheArtAdaptiveSampling.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Appendix 1.1: Simple One-Dimensional Benchmark Tests
Because many function of interest might have a rather simple behavior. Three supplementary tests are explored in this appendix to analyze the adaptive sampling methods for this scenario. Details about the three tests are given in Table 4. It can be noticed that \(\mathbf{P1} \) is a rather simple but common convex function exhibiting one global minimum. \(\mathbf{P2} \) and \(\mathbf{P3} \) also have one global minimum, \(\mathbf{P2} \) is a smooth function of class \({\mathcal{C}}^{\infty }\) whereas \(\mathbf{P3} \) is a \({\mathcal{C}}^{0}\) function.
Results corresponding to Problem \(\mathbf{P1} \) are shown in Fig. 33. In Fig. 33a it can be seen that with four initial samples the metamodel is able to roughly capture the global behavior and furthermore the global minimum rather accurately. The improvements of the global error measure NRMSE from the initial dataset to sets including seven or ten samples are given in Fig. 33b. It can be noticed that most methods have the same performances for both seven and ten samples-based metamodels. EI does not perform well with respect to the global criterion, as this sampling method is not designed for a global purpose but for accurately estimating the global minimum. WAE is also not able to provide a good metamodel for that case. MIPT does not perform well with 7 samples, but offers good performances after ten samples. These results are confirmed by the evolution of the error value during the sampling process as shown in Fig. 33c and d.
Results for Problem \(\mathbf{P2} \) are given in Fig. 34. Five initial samples as displayed in Fig. 34a allow to capture a part of the parametric domain well, but the global minimum is not fitted accurately. The evolution of the NRMSE error during the sampling process plotted in Fig. 34c and d shows that most methods perform very well, similarly to Problem \(\mathbf{P1} \). However, WAE is also not able to approximate the target function well, whereas EI performs rather better as the main challenge is sampling near to the global minimum. The same analysis can be extracted from the error improvement given in Fig. 34b.
Results corresponding to Problem \(\mathbf{P3} \) are summed up in Fig. 35. From initial an metamodel, which is rather poorly fitted (see Fig. 35a), improvements of the performance are detailed in Fig. 35b. From 5 initial samples to 10 samples, several adaptive techniques such as AME, EI, MEPE or WAE fail to majorly improve the predictions. However with 20 samples in the dataset, most methods perform well, CVVor, Lipschitz and WAE being the only ones not able to reach 80% improvement. It can be observed through the error evolution given in Fig. 35c and d, that Lipschitz bad performances are corrected once 21 samples are reached and the method is even a high performer after 25 samples in the dataset. Looking at the other convergence behaviors indicate that after 25 samples most methods perform well, but the error evolution depends significantly on the considered approach.
Problem P1: a plot of \({\mathcal{M}}_{Pe,1D}\), 4 initial samples and corresponding metamodel over normalized parameter space, b relative improvement of the NRMSE value from the 4 samples-based initial metamodel to the 6 samples- and 9 samples-based metamodels, c, d evolution of the NRMSE value over the sampling process. (Color figure online)
Problem P2: a plot of \({\mathcal{M}}_{DC,1D}\), 5 initial samples and corresponding metamodel over normalized parameter space, b relative improvement of the NRMSE value from the 5 samples-based initial metamodel to the 7 samples- and 20 samples-based metamodels, c, d Evolution of the NRMSE value over the sampling process. (Color figure online)
Problem P3: a plot of \({\mathcal{M}}_{Exploit,1D}\), 5 initial samples and corresponding metamodel over normalized parameter space, b relative improvements of the NRMSE value from the 5 samples-based initial metamodel to the 10 samples- and 20 samples-based metamodels, c, d evolution of the NRMSE value over the sampling process using various adaptive schemes. (Color figure online)
1.2 Appendix 1.2: Supplementary Two-Dimensional Benchmark Tests
Some supplementary two-dimensional benchmark tests referred to as Problems P4 to P11 are defined in Table 5. The complexity of the function varies, in order to explore a large scope of behaviors. Most of benchmark functions are \({\mathcal{C}}^{\infty }\), except for Problems P8 and P10 which are of class \({\mathcal{C}}^{0}\). Some functions highlight rather smooth behavior with low values of gradient and small variations of the gradients such as Problems P4 to P8, whereas Problems P9 to P11 have more fluctuations with a large number of turning points.
Results corresponding to Problem P4 are given in Fig. 36. Most methods show similar performances, except for EI and WAE which clearly fail to provide global fitting. EIGF, CVVor, Lipschitz, MASA, SFCVT, MEPE, SSA, MIPT and TEAD have similar convergence behavior. They outperform ACE, LOLA and CVVor.
Problem P5, displayed in Fig. 37 leads to similar difficulties for EI, WAE and in a restricted manner for ACE also. Other methods perform well. It can be noticed that Lipschitz, EIGF and MIPT show error fluctuation when the number of samples are less than 10 due to the restricted size of the dataset. Afterwards the convergence behavior is smooth.
For Problem P6 (Fig. 38), not only ACE, EI and WAE fail, but also Lipschitz. Besides, CVVor and LOLA have a slow converge rate. AME, EIGF, MASA, SFCVT, MEPE, SSA, MIPT and TEAD yield similarly promising results.
Only ACE and WAE fail to provide good metamodels for Problem P7 illustrated in Fig. 39. WAE diverges with the worst prediction results after finding 60 samples from an initial dataset with 10 samples. Other methods are able to provide proficient target approximations after 60 samples. However, SFCVT and SSA convergence poorly.
ACE, CVVor and and WAE have bad performances for Problem P8 (Fig. 40), with the WAE error index even increasing with the number of samples. AME, EI, EIGF, MASA, SFCVT, MEPE, SSA, MIPT and TEAD outperform LOLA and Lipschitz.
The Problem P9 with more fluctuations of the response surface leads to similarly unfavorable performances for EI, WAE and in a restricted manner also for ACE as shown in Fig. 41. Except AME, which shows error fluctuations, and furthermore CVVor, the remaining methods show similar approximation behavior.
Most methods are able to reduce the error with an increasing number of samples for Problem P10 (Fig. 42). Only WAE leads to a stagnating error. However, this problem induces fluctuations of the error for most methods. Only MEPE, MIPT and TEAD are able to converge smoothly, even if the convergence rate is low.
Finally, Problem P11 (Fig. 43) is a challenge for all methods. EI, SSA and WAE are not able to significantly decrease the error while enlarging the number of samples. Other methods lead to a regular but slow decrease of the error, except for AME, which decreases the error with many fluctuations.
Global error measure for the \(\widehat{{\mathcal{M}}}_{Booth,2D}\) metamodel (P4 Problem), a, b evolution of the mean NRMSE estimate over the adaptive process, c relative improvement of the NRMSE estimates from the 10 samples-based initial metamodel to the 12 samples- and 20 samples-based metamodels. (Color figure online)
Global error measure for the \(\widehat{{\mathcal{M}}}_{Boha,2D}\) metamodel (P5 Problem), a, b Evolution of the mean NRMSE estimate over the adaptive process, c relative improvement of the NRMSE estimates from the 10 samples-based initial metamodel to the 12 samples- and 20 samples-based metamodels. (Color figure online)
Global error measure for the \(\widehat{{\mathcal{M}}}_{Br,2D}\) metamodel (P6 Problem), a, b evolution of the mean NRMSE estimate over the adaptive process, c relative improvement of the NRMSE estimates from the 10 samples-based initial metamodel to the 15 samples- and 25 samples-based metamodels. (Color figure online)
Global error measure for the \(\widehat{{\mathcal{M}}}_{Fr,2D}\) metamodel (P7 Problem), a, b evolution of the mean NRMSE estimate over the adaptive process, c relative improvement of the NRMSE estimates from the 10 samples-based initial metamodel to the 20 samples- and 40 samples-based metamodels. (Color figure online)
Global error measure for the \(\widehat{{\mathcal{M}}}_{Ro,2D}\) metamodel (P8 Problem), a, b evolution of the mean NRMSE estimate over the adaptive process, c relative improvement of the NRMSE estimates from the 10 samples-based initial metamodel to the 30 samples- and 50 samples-based metamodels. (Color figure online)
Global error measure for the \(\widehat{{\mathcal{M}}}_{SH,2D}\) metamodel (P9 Problem), a, b evolution of the mean NRMSE estimate over the adaptive process, c relative improvement of the NRMSE estimates from the 10 samples-based initial metamodel to the 20 samples- and 30 samples-based metamodels. (Color figure online)
Global error measure for the \(\widehat{{\mathcal{M}}}_{Ra,2D}\) metamodel (P10 Problem), a, b evolution of the mean NRMSE estimate over the adaptive process, c relative improvement of the NRMSE estimates from the 10 samples-based initial metamodel to the 40 samples- and 80 samples-based metamodels. (Color figure online)
Global error measure for the \(\widehat{{\mathcal{M}}}_{Gr,2D}\) metamodel (P11 Problem), a, b evolution of the mean NRMSE estimate over the adaptive process, c relative improvement of the NRMSE estimates from the 10 samples-based initial metamodel to the 40 samples- and 70 samples-based metamodels. (Color figure online)
1.3 Appendix 1.3: Higher-Dimensional Benchmark Tests
Benchmark problems with dimension larger than two are summarized in Table 6. The goal of this study is to confirm that the results obtained for the lower-dimensional cases also hold for higher-dimensional problems.
Therefore the first considered function is the test case \(\mathbf{P12} \) which has a simple, symmetric bowl-shaped form in all dimensions. This benchmark problem is studied for three, four and five dimensions to see if the performances of the respective adaptive techniques change with a dimensional increase. The global error results are depicted in Figs. 44, 45 and 46 . It can be noticed that, similarly to the lower dimensional cases, most of the adaptive techniques show equal prediction prowess based on this global error measure for simple problems in higher dimensions. Equivalently to the lower dimensional benchmarks the negative outliers are ACE, EI and WAE.
The same phenomenon can also be seen in the valley-shaped four-dimensional problem \(\mathbf{P13} \) as seen in Fig. 47. For more complex shapes of the target function the different adaptive techniques show a wider divergence from each other. This is similar to the lower-dimensional cases and can for example be seen by looking at the results for the global error measure obtained for problems \(\mathbf{P14} \), \(\mathbf{P15} \) and \(\mathbf{P16} \). Results corresponding with Problem \(\mathbf{P14} \) are shown in Fig. 48. After around 90 samples five of the adaptive techniques (AME, MIPT, SFVCT, SSA, TEAD) show a good performance rating with an improvement to the initial error of around 80%. However MEPE and surprisingly MASA outperform the rest of the methods.
The error convergences for the test case \(\mathbf{P15} \) are illustrated in Fig. 49. It can be observed that similar to the small-dimensional cases most adaptive techniques perform in a similar range. However for high-dimensional cases MIPT does not seem to perform as well as exploitation-based adaptive techniques. WAE shows by far the worst performance again. Therefore, the usage of this method in that scenario is not recommended and it is not employed for the six-dimensional Problem \(\mathbf{P16} \) as given in Fig. 50. Here MEPE shows again the best performance behavior. Besides, it can also be observed by wide variance and jitter of the error convergence behavior of ACE, AME, EI, LOLA and SSA that the utilized optimization technique has issues with finding the global optimum of hyperparameters and the adaptive sampling problem.
Global error measure for the \(\widehat{{\mathcal{M}}}_{Sp,3D}\) metamodel (P12—\(d=3\) Problem), a, b evolution of the mean NRMSE estimate over the adaptive process, c relative improvement of the NRMSE estimates from the 10 samples-based initial metamodel to the 20 samples- and 40 samples-based metamodels. (Color figure online)
Global error measure for the \(\widehat{{\mathcal{M}}}_{Sp,4D}\) metamodel (P12—\(d=4\) Problem), a, b evolution of the mean NRMSE estimate over the adaptive process, c relative improvement of the NRMSE estimates from the 10 samples-based initial metamodel to the 30 samples- and 50 samples-based metamodels. (Color figure online)
Global error measure for the \(\widehat{{\mathcal{M}}}_{Sp,5D}\) metamodel (P12 \(d=5\) Problem), a, b evolution of the mean NRMSE estimate over the adaptive process, c relative improvement of the NRMSE estimates from the 10 samples-based initial metamodel to the 30 samples- and 50 samples-based metamodels. (Color figure online)
Global error measure for the \(\widehat{{\mathcal{M}}}_{DP,4D}\) metamodel (P13 Problem), a, b evolution of the mean NRMSE estimate over the adaptive process, c relative improvement of the NRMSE estimates from the 10 samples-based initial metamodel to the 30 samples- and 50 samples-based metamodels. (Color figure online)
Global error measure for the \(\widehat{{\mathcal{M}}}_{Ish,3D}\) metamodel (P14 Problem), a, b evolution of the mean NRMSE estimate over the adaptive process, c relative improvement of the NRMSE estimates from the 10 samples-based initial metamodel to the 50 samples- and 90 samples-based metamodels
Global error measure for the \(\widehat{{\mathcal{M}}}_{Ha,3D}\) metamodel (P15 Problem), a, b Evolution of the mean NRMSE estimate over the adaptive process, c relative improvement of the NRMSE estimates from the 10 samples-based initial metamodel to the 50 samples- and 90 samples-based metamodels. (Color figure online)
Global error measure for the \(\widehat{{\mathcal{M}}}_{Ha,6D}\) metamodel (P16 Problem), a, b evolution of the mean NRMSE estimate over the adaptive process, c relative improvement of the NRMSE estimates from the 10 samples-based initial metamodel to the 110 samples- and 160 samples-based metamodels. (Color figure online)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fuhg, J.N., Fau, A. & Nackenhorst, U. State-of-the-Art and Comparative Review of Adaptive Sampling Methods for Kriging. Arch Computat Methods Eng 28, 2689–2747 (2021). https://doi.org/10.1007/s11831-020-09474-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11831-020-09474-6