Abstract
Species knowledge is essential for protecting biodiversity. The identification of plants by conventional keys is complex, time consuming, and due to the use of specific botanical terms frustrating for non-experts. This creates a hard to overcome hurdle for novices interested in acquiring species knowledge. Today, there is an increasing interest in automating the process of species identification. The availability and ubiquity of relevant technologies, such as, digital cameras and mobile devices, the remote access to databases, new techniques in image processing and pattern recognition let the idea of automated species identification become reality. This paper is the first systematic literature review with the aim of a thorough analysis and comparison of primary studies on computer vision approaches for plant species identification. We identified 120 peer-reviewed studies, selected through a multi-stage process, published in the last 10 years (2005–2015). After a careful analysis of these studies, we describe the applied methods categorized according to the studied plant organ, and the studied features, i.e., shape, texture, color, margin, and vein structure. Furthermore, we compare methods based on classification accuracy achieved on publicly available datasets. Our results are relevant to researches in ecology as well as computer vision for their ongoing research. The systematic and concise overview will also be helpful for beginners in those research fields, as they can use the comparable analyses of applied methods as a guide in this complex activity.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Biodiversity is declining steadily throughout the world [113]. The current rate of extinction is largely the result of direct and indirect human activities [95]. Building accurate knowledge of the identity and the geographic distribution of plants is essential for future biodiversity conservation [69]. Therefore, rapid and accurate plant identification is essential for effective study and management of biodiversity.
In a manual identification process, botanist use different plant characteristics as identification keys, which are examined sequentially and adaptively to identify plant species. In essence, a user of an identification key is answering a series of questions about one or more attributes of an unknown plant (e.g., shape, color, number of petals, existence of thorns or hairs) continuously focusing on the most discriminating characteristics and narrowing down the set of candidate species. This series of answered questions leads eventually to the desired species. However, the determination of plant species from field observation requires a substantial botanical expertise, which puts it beyond the reach of most nature enthusiasts. Traditional plant species identification is almost impossible for the general public and challenging even for professionals that deal with botanical problems daily, such as, conservationists, farmers, foresters, and landscape architects. Even for botanists themselves species identification is often a difficult task. The situation is further exacerbated by the increasing shortage of skilled taxonomists [47]. The declining and partly nonexistent taxonomic knowledge within the general public has been termed “taxonomic crisis” [35].
The still existing, but rapidly declining high biodiversity and a limited number of taxonomists represents significant challenges to the future of biological study and conservation. Recently, taxonomists started searching for more efficient methods to meet species identification requirements, such as developing digital image processing and pattern recognition techniques [47]. The rich development and ubiquity of relevant information technologies, such as digital cameras and portable devices, has brought these ideas closer to reality. Digital image processing refers to the use of algorithms and procedures for operations such as image enhancement, image compression, image analysis, mapping, and geo-referencing. The influence and impact of digital images on the modern society is tremendous and is considered a critical component in a variety of application areas including pattern recognition, computer vision, industrial automation, and healthcare industries [131].
Image-based methods are considered a promising approach for species identification [47, 69, 133]. A user can take a picture of a plant in the field with the build-in camera of a mobile device and analyze it with an installed recognition application to identify the species or at least to receive a list of possible species if a single match is impossible. By using a computer-aided plant identification system also non-professionals can take part in this process. Therefore, it is not surprising that large numbers of research studies are devoted to automate the plant species identification process. For instance, ImageCLEF, one of the foremost visual image retrieval campaigns, is hosting a plant identification challenge since 2011. We hypothesize that the interest will further grow in the foreseeable future due to the constant availability of portable devices incorporating myriad precise sensors. These devices provide the basis for more sophisticated ways of guiding and assisting people in species identification. Furthermore, approaching trends and technologies such as augmented reality, data glasses, and 3D-scans give this research topic a long-term perspective.
An image classification process can generally be divided into the following steps (cp. Fig. 1):
-
Image acquisition—The purpose of this step is to obtain the image of a whole plant or its organs so that analysis towards classification can be performed.
-
Preprocessing—The aim of image preprocessing is enhancing image data so that undesired distortions are suppressed and image features that are relevant for further processing are emphasized. The preprocessing sub-process receives an image as input and generates a modified image as output, suitable for the next step, the feature extraction. Preprocessing typically includes operations like image denoising, image content enhancement, and segmentation. These can be applied in parallel or individually, and they may be performed several times until the quality of the image is satisfactory [51, 124].
-
Feature extraction and description—Feature extraction refers to taking measurements, geometric or otherwise, of possibly segmented, meaningful regions in the image. Features are described by a set of numbers that characterize some property of the plant or the plant’s organs captured in the images (aka descriptors) [124].
-
Classification—In the classification step, all extracted features are concatenated into a feature vector, which is then being classified.
The main objectives of this paper are (1) reviewing research done in the field of automated plant species identification using computer vision techniques, (2) to highlight challenges of research, and (3) to motivate greater efforts for solving a range of important, timely, and practical problems. More specifically, we focus on the Image Acquisition and the Feature Extraction and Description step of the discussed process since these are highly influenced by the object type to be classified, i.e., plant species. A detailed analysis of the Preprocessing and the Classification steps is beyond the possibilities of this review. Furthermore, the applied methods within these steps are more generic and mostly independent of the classified object type.
2 Methods
We followed the methodology of a systematic literature review (SLR) to analyze published research in the field of automated plant species identification. Performing a SLR refers to assessing all available research concerning a research subject of interest and to interpret aggregated results of this work. The whole process of the SLR is divided into three fundamental steps: (I) defining research questions, (II) conducting the search process for relevant publications, and (III) extracting necessary data from identified publications to answer the research questions [75, 109].
2.1 Research Questions
We defined the following five research questions:
RQ-1: Data demographics: How are time of publication, venue, and geographical author location distributed across primary studies?—The aim of this question is getting an quantitative overview of the studies and to get an overview about the research groups working on this topic.
RQ-2: Image Acquisition: How many images of how many species were analyzed per primary study, how were these images been acquired, and in which context have they been taken?—Given that the worldwide estimates of flowering plant species (aka angiosperms) vary between 220,000 [90, 125] and 420,000 [52], we would like to know how many species were considered in studies to gain an understanding of the generalizability of results. Furthermore, we are interested in information on where plant material was collected (e.g., fresh material or web images); and whether the whole plant was studied or selected organs.
RQ-3: Feature detection and extraction: Which features were extracted and which techniques were used for feature detection and description?—The aim of this question is categorizing, comparing, and discussing methods for detecting and describing features used in automated plant species classification.
RQ-4: Comparison of studies: Which methods yield the best classification accuracy?—To answer this question, we compare the results of selected primary studies that evaluate their methods on benchmark datasets. The aim of this question is giving an overview of utilized descriptor-classifier combinations and the achieved accuracies in the species identification task.
RQ-5: Prototypical implementation: Is a prototypical implementation of the approach such as a mobile app, a web service, or a desktop application available for evaluation and actual usage?—This question aims to analyzes how ready approaches are to be used by a larger audience, e.g., the general public.
2.2 Data Sources and Selection Strategy
We used a combined backward and forward snowballing strategy for the identification of primary studies (see Fig. 2). This search technique ensures to accumulate a relatively complete census of relevant literature not confined to one research methodology, one set of journals and conferences, or one geographic region. Snowballing requires a starting set of publications, which should either be published in leading journals of the research area or have been cited many times. We identified our starting set of five studies through a manual search on Google Scholar (see Table 1). Google Scholar is a good alternative to avoid bias in favor of a specific publisher in the initial set of the sampling procedure. We then checked whether the publications in the initial set were included in at least one of the following scientific repositories: (a) Thomson Reuters Web of ScienceTM, (b) IEEE Xplore®, (c) ACM Digital Library, and (d) Elsevier ScienceDirect®. Each publication identified in any of the following steps was also checked for being listed in at least one of these repositories to restrict our focus to high quality publications solely.
Backward snowball selection means that we recursively considered the referenced publications in each paper derived through manual search as candidates for our review. Forward snowballing analogously means that we, based on Google Scholar citations, identified additional candidate publications from all those studies that were citing an already included publication. For a candidate to be included in our study, we checked further criteria in addition to being listed in the four repositories. The criteria referred to the paper title, which had to comply to the following pattern:
S1 AND (S2 OR S3 OR S4 OR S5 OR S6) AND NOT (S7) where
-
S1: (plant* OR flower* OR leaf OR leaves OR botan*)
-
S2: (recognition OR recognize OR recognizing OR recognized)
-
S3: (identification OR identify OR identifying OR identified)
-
S4: (classification OR classify OR classifying OR classified)
-
S5: (retrieval OR retrieve OR retrieving OR retrieved)
-
S6: (“image processing” OR “computer vision”)
-
S7: (genetic OR disease* OR “remote sensing” OR gene OR DNA OR RNA).
Using this search string allowed us to handle the large amount of existing work and ensured to search for primary studies focusing mainly on plant identification using computer vision. The next step, was removing studies from the list that had already been examined in a previous backward or forward snowballing iteration. The third step, was removing all studies that were not listed in the four literature repositories listed before. The remaining studies became candidates for our survey and were used for further backward and forward snowballing. Once no new papers were found, neither through backward nor through forward snowballing, the search process was terminated. By this selection process we obtained a candidate list of 187 primary studies.
To consider only high quality peer reviewed papers, we eventually excluded all workshop and symposium papers as well as working notes and short papers with less than four pages. Review papers were also excluded as they constitute no primary studies. To get an overview of the more recent research in the research area, we restricted our focus to the last 10 years and accordingly only included papers published between 2005 and 2015. Eventually, the results presented in this SLR are based upon 120 primary studies complying to all our criteria.
2.3 Data Extraction
To answer RQ-1, corresponding information was extracted mostly from the meta-data of the primary studies. Table 2 shows that the data extracted for addressing RQ-2, RQ-3, RQ-4, and RQ-5 are related to the methodology proposed by a specific study. We carefully analyzed all primary studies and extracted necessary data. We designed a data extraction template used to collect the information in a structured manner (see Table 2). The first author of this review extracted the data and filled them into the template. The second author double-checked all extracted information. The checker discussed disagreements with the extractor. If they failed to reach a consensus, other researchers have been involved to discuss and resolve the disagreements.
2.4 Threats to Validity
The main threats to the validity of this review stem from the following two aspects: study selection bias and possible inaccuracy in data extraction and analysis. The selection of studies depends on the search strategy, the literature sources, the selection criteria, and the quality criteria. As suggested by [109], we used multiple databases for our literature search and provide a clear documentation of the applied search strategy enabling replication of the search at a later stage. Our search strategy included a filter on the publication title in an early step. We used a predefined search string, which ensures that we only search for primary studies that have the main focus on plant species identification using computer vision. Therefore, studies that propose novel computer vision methods in general and evaluating their approach on a plant species identification task as well as studies that used unusual terminology in the publication title may have been excluded by this filter. Furthermore, we have limited ourselves to English-language studies. These studies are only journal and conference papers with a minimum of four pages. However, this strategy excluded non-English papers in national journals and conferences. Furthermore, inclusion of grey literature such as PhD or master theses, technical reports, working notes, and white-papers also workshop and symposium papers might have led to more exhaustive results. Therefore, we may have missed relevant papers. However, the ample list of included studies indicates the width of our search. In addition, workshop papers as well as grey literature is usually finally published on conferences or in journals. Therefore excluding grey literature and workshop papers avoids duplicated primary studies within a literature review. To reduce the threat of inaccurate data extraction, we elaborated a specialized template for data extraction. In addition, all disagreements between extractor and checker of the data were carefully considered and resolved by discussion among the researchers.
3 Results
This section reports aggregated results per research question based on the data extracted from primary studies.
3.1 Data Demographics (RQ-1)
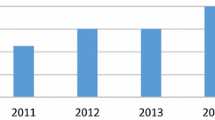
To study the relative interest in automating plant identification over time, we aggregated paper numbers by year of publication (see Fig. 3). The figure shows a continuously increasing interest in this research topic. Especially, the progressively rising numbers of published papers in recent years show that this research topic is considered highly relevant by researchers today.
To gain an overview of active research groups and their geographical distribution, we analyzed the first author’s affiliation. The results depict that the selected papers are written by researchers from 25 different countries. More than half of these papers are from Asian countries (73/120), followed by European countries (26/120), American countries (14/120), Australia (4/120), and African countries (3/120). 34 papers have a first author from China, followed by France (17), and India (13). 15 papers are authored by a group located in two or more different countries. 108 out of the 120 papers are written solely by researches with computer science or engineering background. Only one paper is solely written by an ecologist. Ten papers are written in interdisciplinary groups with researchers from both fields. One paper was written in an interdisciplinary group where the first author has an educational and the second author an engineering background.
3.2 Image Acquisition (RQ-2)
The purpose of this first step within the classification process is obtaining an image of the whole plant or its organs for later analysis towards plant classification.
3.2.1 Studied Plant Organs
Identifying species requires recognizing one or more characteristics of a plant and linking them with a name, either a common or so-called scientific name. Humans typically use one or more of the following characteristics: the plant as a whole (size, shape, etc.), its flowers (color, size, growing position, inflorescence, etc.), its stem (shape, node, outer character, bark pattern, etc.), its fruits (size, color, quality, etc.), and its leaves (shape, margin, pattern, texture, vein etc.) [114].
A majority of primary studies utilizes leaves for discrimination (106 studies). In botany, a leaf is defined as a usually green, flattened, lateral structure attached to a stem and functioning as a principal organ of photosynthesis and transpiration in most plants. It is one of the parts of a plant which collectively constitutes its foliage [44, 123]. Figure 4 shows the main characteristics of leaves with their corresponding botanical terms. Typically, a leaf consists of a blade (i.e., the flat part of a leaf) supported upon a petiole (i.e., the small stalk situated at the lower part of the leaf that joins the blade to the stem), which, continued through the blade as the midrib, gives off woody ribs and veins supporting the cellular texture. A leaf is termed “simple” if its blade is undivided, otherwise it is termed “compound” (i.e., divided into two or more leaflets). Leaflets may be arranged on either side of the rachis in pinnately compound leaves and centered around the base point (the point that joins the blade to the petiole) in palmately compound leaves [44]. Most studies use simple leaves for identification, while 29 studies considered compound leaves in their experiments. The internal shape of the blade is characterized by the presence of vascular tissue called veins, while the global shape can be divided into three main parts: (1) the leaf base, usually the lower 25% of the blade; the insertion point or base point, which is the point that joins the blade to the petiole, situated at its center. (2) The leaf tip, usually the upper 25% of the blade and centered by a sharp point called the apex. (3) The margin, which is the edge of the blade [44]. These local leaf characteristics are often used by botanists in the manual identification task and could also be utilized for an automated classification. However, the majority of existing leaf classification approaches rely on global leaf characteristics, thus ignoring these local information of leaf characteristics. Only eight primary studies consider local characteristics of leaves like the petiole, blade, base, and apex for their research [19, 85, 96, 97, 99, 119, 120, 158]. The characteristics of the leave margin is studied by six primary studies [18, 21, 31, 66, 85, 93].
In contrast to studies on leaves or plant foliage, a smaller number of 13 primary studies identify species solely based on flowers [3, 29, 30, 57, 60, 64, 104, 105, 112, 117, 128, 129, 149]. Some studies did not only focus on the flower region as a whole but also on parts of the flower. Hsu et al. [60] analyzed the color and shape not only of the whole flower region but also of the pistil area. Tan et al. [128] studied the shape of blooming flowers’ petals and [3] proposed analyzing the lip (labellum) region of orchid species. Nilsback and Zisserman [104, 105] propose features, which capture color, texture, and shape of petals as well as their arrangement.
Only one study proposes a multi-organ classification approach [68]. Contrary to other approaches that analyze a single organ captured in one image, their approach analyzes up to five different plant views capturing one or more organs of a plant. These different views are: full plant, flower, leaf (and leaf scan), fruit, and bark. This approach is the only one in this review dealing with multiple images exposing different views of a plant.
3.2.2 Images: Categories and Datasets
Utilized images in the studies fall into three categories: scans, pseudo-scans, and photos. While scan and pseudo-scan categories correspond respectively to plant images obtained through scanning and photography in front of a simple background, the photo category corresponds to plants photographed on natural background [49]. The majority of utilized images in the primary studies are scans and pseudo-scans thereby avoiding to deal with occlusions and overlaps (see Table 3). Only 25 studies used photos that were taken in a natural environment with cluttered backgrounds and reflecting a real-world scenario.
Existing datasets of leaf images were uses in 62 primary studies. The most important (by usage) and publicly available datasets are:
-
Swedish leaf dataset—The Swedish leaf dataset has been captured as part of a joined leaf classification project between the Linkoping University and the Swedish Museum of Natural History [127]. The dataset contains images of isolated leaf scans on plain background of 15 Swedish tree species, with 75 leaves per species (1125 images in total). This dataset is considered very challenging due to its high inter-species similarity [127]. The dataset can be downloaded here: http://www.cvl.isy.liu.se/en/research/datasets/swedish-leaf/.
-
Flavia dataset—This dataset contains 1907 leaf images of 32 different species and 50–77 images per species. Those leaves were sampled on the campus of the Nanjing University and the Sun Yat-Sen arboretum, Nanking, China. Most of them are common plants of the Yangtze Delta, China [144]. The leaf images were acquired by scanners or digital cameras on plain background. The isolated leaf images contain blades only, without petioles (http://flavia.sourceforge.net/).
-
ImageCLEF11 and ImageCLEF12 leaf dataset—This dataset contains 71 tree species of the French Mediterranean area captured in 2011 and further increased to 126 species in 2012. ImageCLEF11 contains 6436 pictures subdivided into three different groups of pictures: scans (48%), scan-like photos or pseudo-scans (14%), and natural photos (38%). The ImageCLEF12 dataset consists of 11,572 images subdivided into: scans (57%), scan-like photos (24%), and natural photos (19%). Both sets can be downloaded from ImageCLEF (2011) and ImageCLEF (2012): http://www.imageclef.org/.
-
Leafsnap dataset—The Leafsnap dataset contains leave images of 185 tree species from the Northeastern United States. The images are acquired from two sources and are accompanied by automatically-generated segmentation data. The first source are 23,147 high-quality lab images of pressed leaves from the Smithsonian collection. These images appear in controlled backlit and front-lit versions, with several samples per species. The second source are 7719 field images taken with mobile devices (mostly iPhones) in outdoor environments. These images vary considerably in sharpness, noise, illumination patterns, shadows, etc. The dataset can be downloaded at: http://leafsnap.com/dataset/.
-
ICL dataset—The ICL dataset contains isolated leaf images of 220 plant species with individual images per species ranging from 26 to 1078 (17,032 images in total). The leaves were collected at Hefei Botanical Garden in Hefei, the capital of the Chinese Anhui province by people from the local Intelligent Computing Laboratory (ICL) at the Institute of Intelligent Machines, China (http://www.intelengine.cn/English/dataset). All the leafstalks have been cut off before the leaves were scanned or photographed on a plain background.
-
Oxford Flower 17 and 102 datasets—Nilsback and Zisserman [104, 105] have created two flower datasets by gathering images from various websites, with some supplementary images taken from their own photographs. Images show species in their natural habitat. The Oxford Flower 17 dataset consists of 17 flower species represented by 80 images each. The dataset contains species that have a very unique visual appearance as well as species with very similar appearance. Images exhibit large variations in viewpoint, scale, and illumination. The flower categories are deliberately chosen to have some ambiguity on each aspect. For example, some classes cannot be distinguished by color alone, others cannot be distinguished by shape alone. The Oxford Flower 102 dataset is larger than the Oxford Flower 17 and consists of 8189 images divided into 102 flower classes. The species chosen consist of flowers commonly occurring in the United Kingdom. Each class consists of between 40 and 258 images. The images are rescaled so that the smallest dimension is 500 pixels. The Oxford Flower 17 dataset is not a full subset of the 102 dataset neither in images nor in species. Both datasets can be downloaded at: http://www.robots.ox.ac.uk/ ~vgg/data/flowers/.
Forty-eight authors use their own, not publicly available, leaf datasets. For these leave images, typically fresh material was collected and photographed or scanned in the lab on plain background. Due to the great effort in collecting material, such datasets are limited both in the number of species and in the number of images per species. Two studies used a combination of self-collected leaf images and images from web resources [74, 138]. Most plant classification approaches only focus on intact plant organs and are not applicable to degraded organs (e.g., deformed, partial, or overlapped) largely existing in nature. Only 21 studies proposed identification approaches that can also handle damaged leaves [24, 38, 46, 48, 56, 58, 74, 93, 102, 132, 141, 143] and overlapped leaves [18–20, 38, 46, 48, 74, 85, 102, 122, 130, 137, 138, 148].
Most utilized flower images were taken by the authors themselves or acquired from web resources [3, 29, 60, 104, 105, 112]. Only one study solely used self-taken photos for flower analysis [57]. Two studies analyzed the Oxford 17 and the Oxford 102 datasets (Table 4).
A majority of primary studies only evaluated their approach on datasets containing less than a hundred species (see Fig. 5) and at most a few thousand leaf images (see Fig. 6). Only two studies used a large dataset with more than 2000 species. Joly et al. [68] used a dataset with 2258 species and 44,810 images. In 2014 this was the plant identification study considering the largest number of species so far. In 2015 [143] published a study with 23,025 species represented by 1,000,000 images in total.
3.3 Feature Detection and Extraction (RQ-3)
Feature extraction is the basis of content-based image classification and typically follows the preprocessing step in the classification process. A digital image is merely a collection of pixels represented as large matrices of integers corresponding to the intensities of colors at different positions in the image [51]. The general purpose of feature extraction is reducing the dimensionality of this information by extracting characteristic patterns. These patterns can be found in colors, textures and shapes [51]. Table 5 shows the studied features, separated for studies analyzing leaves and those analyzing flowers, and highlights that shape plays the most important role among the primary studies. 87 studies used leaf shape and 13 studies used flower shape for plant species identification. The texture of leaves and flowers is analyzed by 24 and 5 studies respectively. Color is mainly considered along with flower analysis (9 studies), but a few studies also used color for leaf analysis (5 studies). In addition, organ-specific features, i.e., leaf vein structure (16 studies) and leaf margin (8 studies), were investigated.
Numerous methods exist in the literature for describing general and domain-specific features and new methods are being proposed regularly. Methods that were used for detecting and extracting features in the primary studies are highlighted in the subsequent sections. Because of perception subjectivity, there does not exist a single best presentation for a given feature. As we will see soon, for any given feature there exist multiple descriptions, which characterize the feature from different perspectives. Furthermore, different features or combinations of different features are often needed to distinguish different categories of plants. For example, whilst leaf shape may be sufficient to distinguish between some species, other species may have very similar leaf shapes to each other, but have different colored leaves or texture patterns. The same is also true for flowers. Flowers with the same color may differ in their shape or texture characteristics. Table 5 shows that 42 studies do not only consider one type of feature but use a combination of two or more feature types for describing leaves or flowers. No single feature may be sufficient to separate all the categories, making feature selection and description a challenging problem. Typically, this is the innovative part of the studies we reviewed. Segmentation and classification also allow for some flexibility, but much more limited. In the following sections, we will give an overview of the main features and their descriptors proposed for automated plant species classification (see also Fig. 7). First, we analyze the description of the general features starting with the most used feature shape, followed by texture, and color and later on we review the description of the organ-specific features leaf vein structure and leaf margin.
3.3.1 Shape
Shape is known as an important clue for humans when identifying real-world objects. A shape measure in general is a quantity, which relates to a particular shape characteristic of an object. An appropriate shape descriptor should be invariant to geometrical transformations, such as, rotation, reflection, scaling, and translation. A plethora of methods for shape representation can be found in the literature [151]. Shape descriptors are classified into two broad categories: contour-based and region-based. Contour-based shape descriptors extract shape features solely from the contour of a shape. In contrast, region-based shape descriptors obtain shape features from the whole region of a shape [72, 151]. In addition, there also exist some methods, which cannot be classified as either contour-based or region-based. In the following section, we restrict our discussion to those techniques that have been applied for plant species identification (see Table 6). We start our discussion with simple and morphological shape descriptors (SMSD) followed by a discussion of more sophisticated descriptors. Since the majority of studies focusses on plant identification via leaves, the discussed shape descriptors mostly apply to leaf shape classification. Techniques which were used for flower analysis will be emphasized.
3.3.2 Simple and Morphological Shape Descriptors
Across the studies we found six basic shape descriptors used for leaf analysis (see first six rows of Table 7). These refer to basic geometric properties of the leaf’s shape, i.e., diameter, major axis length, minor axis length, area, perimeter, centroid (see, e.g., [144]). On top of that, studies compute and utilize morphological descriptors based on these basic descriptors, e.g., aspect ratio, rectangularity measures, circularity measures, and the perimeter to area ratio (see Table 6). Table 6 shows that studies often employ ratios as shape descriptors. Ratios are simple to compute and naturally invariant to translation, rotation, and scaling; making them robust against different representations of the same object (aka leaf). In addition, several studies proposed more leaf-specific descriptors. For example, [58] introduce a leaf width factor (LWF), which is extracted from leaves by slicing across the major axis and parallel to the minor axis. Then, the LWF per strip is calculated as the ratio of the width of the strip to the length of the entire leaf (major axis length). Yanikoglu et al. [148] propose an area width factor (AWF) constituting a slight variation of the LWF. For AWF, the area of each strip normalized by the global area is computed. As another example, [116] used a porosity feature to explain cracks in the leaf image (Table 7).
However, while there typically exists high morphological variation across different species’ leaves, there is also often considerable variance among leaves of the same species. Studies’ results show that SMSD are too much simplified to discriminate leaves beyond those with large differences sufficiently. Therefore, they are usually combined with other descriptors, e.g., more complex shape analysis [1, 15, 40, 72, 73, 106, 110, 137, 146], leaf texture analysis [154], vein analysis [5, 144], color analysis [16, 116], or all of them together [43, 48]. SMSD are usually employed for high-level discrimination reducing the search space to a smaller set of species without losing relevant information and allowing to perform computationally more expensive operations at a later stage on a smaller search space [15].
Similarly, SMSD play an important role for flower analysis. Tan et al. [129] propose four flower shape descriptors, namely, area, perimeter of the flower, roundness of the flower, and aspect ratio. A simple scaling and normalization procedure has been employed to make the descriptors invariant to varying capture situations. The roundness measure and aspect ratio in combination with more complex shape analysis descriptors are used by [3] for analyzing flower shape.
In conclusion, the risk of SMSD is that any attempt to describe the shape of a leaf using only 5–10 descriptors may oversimplify matters to the extent that meaningful analysis becomes impossible, even if they seem sufficient to classify a small set of test images. Furthermore, many single-value descriptors are highly correlated with each other, making the task of choosing sufficiently independent features to distinguish categories of interest especially difficult [33].
3.3.3 Region-Based Shape Descriptors
Region-based techniques take all the pixels within a shape region into account to obtain the shape representation, rather than only using boundary information as the contour-based methods do. In this section, we discuss the most popular region-based descriptors for plant species identification: image moments and local feature techniques.
Image moments. Image moments are a widely applied category of descriptors in object classification. Image moments are statistical descriptors of a shape that are invariant to translation, rotation, and scale. Hu [61] proposes seven image moments, typically called geometric moments or Hu moments that attracted wide attention in computer vision research. Geometric moments are computationally simple, but highly sensitive to noise. Among our primary studies, geometric moments have been used for leaf analysis [22, 23, 40, 65, 72, 73, 102, 110, 137, 138, 154] as well as for flower analysis [3, 29]. Geometric moments as a standalone feature are only studied by [102]. Most studies combine geometric moments with the previously discussed SMSD [3, 23, 40, 72, 73, 110, 137, 154]. Also the more evolved Zernike moment invariant (ZMI) and Legendre moment invariant (LMI), based on an orthogonal polynomial basis, have been studied for leaf analysis [72, 138, 159]. These moments are also invariant to arbitrary rotation of the object, but in contrast to geometric moments they are not sensitive to image noise. However, their computational complexity is very high. Kadir et al. [72] found ZMI not to yield better classification accuracy than geometric moments. Zulkifli et al. [159] compare three moment invariant techniques, ZMI, LMI, and moments of discrete orthogonal basis (aka Tchebichef moment invariant (TMI)) to determine the most effective technique in extracting features from leaf images. In result, the authors identified TMI as the most effective descriptor. Also [106] report that TMI achieved the best results compared with geometric moments and ZMI and were therefore used as supplementary features with lower weight in their classification approach.
Local feature techniques. In general, the concept of local features refers to the selection of scale-invariant keypoints (aka interest points) in an image and their extraction into local descriptors per keypoint. These keypoints can then be compared with those obtained from another image. A high degree of matching keypoints among two images indicates similarity among them. The seminal Scale-invariant feature transform (SIFT) approach has been proposed by [86]. SIFT combines a feature detector and an extractor. Features detected and extracted using the SIFT algorithm are invariant to image scale, rotation, and are partially robust to changing viewpoints and changes in illumination. The invariance and robustness of the features extracted using this algorithm makes it also suitable for object recognition rather than image comparison.
SIFT has been proposed and studied for leaf analysis by [26, 27, 59, 81]. A challenge that arises for object classification rather than image comparison is the creation of a codebook with trained generic keypoints. The classification framework by [26] combines SIFT with the Bag of Words (BoW) model. The BoW model is used to reduce the high dimensionality of the data space. Hsiao et al. [59] used SIFT in combination with sparse representation (aka sparse coding) and compared their results to the BoW approach. The authors argue that in contrast to the BoW approach, their sparse coding approach has a major advantage as no re-training of the classifiers for newly added leaf image classes is necessary. In [81], SIFT is used to detect corners for classification. Wang et al. [139] propose to improve leaf image classification by utilizing shape context (see below) and SIFT descriptors in combination so that both global and local properties of a shape can be taken into account. Similarly, [74] combines SIFT with global shape descriptors (high curvature points on the contour after chain coding). The author found the SIFT method by itself not successful at all and its accuracy significantly lower compared to the results obtained by combining it with global shape features. The original SIFT approach as well as all so far discussed SIFT approaches solely operate on grayscale images. A major challenge in leaf analysis using SIFT is often a lack of characteristic keypoints due to the leaves’ rather uniform texture. Using colored SIFT (CSIFT) can address this problem and will be discussed later in the section about color descriptors.
Another substantially studied local feature approach is the histogram of oriented gradients (HOG) descriptor [41, 111, 145, 155]. The HOG descriptor, introduced by [86] is similar to SIFT, except that it uses an overlapping local contrast normalization across neighboring cells grouped into a block. Since HOG computes histograms of all image cells and there are even overlap cells between neighbor blocks, it contains much redundant information making dimensionality reduction inevitably for further extraction of discriminant features. Therefore, the main focus of studies using HOG lies on dimensionality reduction methods. Pham et al. [111], Xiao et al. [145] study the maximum margin criterion (MMC), [41] studies principle component analysis (PCA) with linear discriminant analysis (LDA), and [155] introduce attribute-reduction based on neighborhood rough sets. Pham et al. [111] compared HOG features with Hu moments and the obtained results show that HOG is more robust than Hu moments for species classification. Xiao et al. [145] found that HOG-MMC achieves a better accuracy than the inner-distance shape context (IDSC) (will be introduced in the section about contour based shape descriptors), when leaf petiole were cut off before analysis. A disadvantage of the HOG descriptor is its sensitivity to the leaf petiole orientation while the petiole’s shape actually carrying species characteristics. To address this issue, a pre-processing step can normalize petiole orientation of all images in a dataset making them accessible to HOG [41, 155].
Nguyen et al. [103] studied speeded up robust features (SURF) for leaf classification, which was first introduced by [9]. The SURF algorithm follows the same principles and procedure as SIFT. However, details per step are different. The standard version of SURF is several times faster than SIFT and claimed by its authors to be more robust against image transformations than SIFT [9]. To reduce dimensionality of extracted features, [103] apply the previously mentioned BoW model and compared their results with those of [111]. SURF was found to provide better classification results than HOG [111].
Ren et al. [121] propose a method for building leaf image descriptors by using multi-scale local binary patterns (LBP). Initially, a multi-scale pyramid is employed to improve leaf data utilization and each training image is divided into several overlapping blocks to extract LBP histograms in each scale. Then, the dimension of LBP features is reduced by a PCA. The authors found that the extracted multi-scale overlapped block LBP descriptor can provide a compact and discriminative leaf representation.
Local features have also been studied for flower analysis. Nilsback and Zisserman [104], Zawbaa et al. [149] used SIFT on a regular grid to describe shapes of flowers. Nilsback and Zisserman [105] proposed to sample HOG and SIFT on both, the foreground and its boundary. The authors found SIFT descriptors extracted from the foreground to perform best, followed by HOG, and finally SIFT extracted from the boundary of a flower shape. Combining foreground SIFT with boundary SIFT descriptors further improved the classification results.
Qi et al. [117] studied dense SIFT (DSIFT) features to describe flower shape. DSIFT is another SIFT-like feature descriptor. It densely selects points evenly in the image, on each pixel or on each n-pixels, rather than performing salient point detection, which make it strong in capturing all features in an image. But DSIFT is not scale-invariant, to make it adaptable to changes in scale, local features are sampled by different scale patches within an image [84]. Unlike the work of [104, 105], [117] take the full image as input instead of a segmented image, which means that extended background greenery may affect their classification performance to some extent. However, the results of [117] are comparable to the results of [104, 105]. When considering segmentation and complexity of descriptor as factors, the authors even claim that their method facilitates more accurate classification and performs more efficiently than the previous approaches.
3.3.4 Contour-Based Shape Descriptors
Contour-based descriptors solely consider the boundary of a shape and neglect the information contained in the shape interior. A contour-based descriptor for a shape is a sequence of values calculated at points taken around an object’s outline, beginning at some starting point and tracing the outline in either a clockwise or an anti-clockwise direction. In this section, we discuss popular contour-based descriptors namely shape signatures, shape context approaches, scale space, the Fourier descriptor, and fractal dimensions.
Shape signatures. Shape signatures are frequently used contour-based shape descriptors, which represent a shape by an one dimensional function derived from shape contour points. There exists a variety of shape signatures. We found the centroid contour distance (CCD) to be the most studied shape signature for leaf analysis [10, 28, 46, 130] and flower analysis [3, 57]. The CCD descriptor consists of a sequence of distances between the center of the shape and points on the contour of a shape. Other descriptors consist of a sequence of angles to represent the shape, e.g., the centroid-angle (AC) [10, 46] and the tangential angle (AT) [6]. A comparison between CCD and AC sequences performed by [46] demonstrated that CCD sequences are more informative than AC sequences. This observation is intuitive since the CCD distance includes both global information related to the leaf area and shape as well as local information related to contour details. Therefore, when combining CCD and AC, which is expected to further improve classification performance, the CCD should be emphasized by giving it a higher classification weight [46].
Mouine et al. [92] investigate two multi-scale triangular approaches for leaf shape description: the well-known triangle area representation (TAR) and the triangle side length representation (TSL). The TAR descriptor is computed based on the area of triangles formed by points on the shape contour. TAR provides information about shape properties, such as the convexity or concavity at each contour point of the shape, and provides high discrimination capability. Although TAR is affine-invariant and robust to noise and deformation, it has a high computational cost since all the contour points are used. Moreover, TAR has two major limitations: (a) the area is not informative about the type of the considered triangle (isosceles, equilateral, etc.), which may be crucial for a local description of the contour. (b) The area is not accurate enough to represent the shape of a triangle [94]. The TSL descriptor is computed based on the side lengths rather than the area of a triangle. TSL is invariant under scale, translation, rotation, and reflection around contour points. Studies found TSL to provide yield higher classification accuracy than TAR [92, 94]. The authors argue that this result may be due to the fact that using side lengths to represent a triangle is more accurate than using its area. In addition to the two multi-scale triangular approaches, [94] also proposed two representations that they denote triangle oriented angles (TOA) and triangle side lengths and angle representation (TSLA). TOA solely uses angle values to represent a triangle. Angle orientation provides information about local concavities and convexities. In fact, an obtuse angle means convex, an acute angle means concave. TOA is not invariant under reflection around the contour point: only similar triangles having equal angles will have equal TOA values. TSLA is a multi-scale triangular contour descriptor that describes the triangles by their lengths and angle. Like TSL, the TSLA descriptor is invariant under scale and reflection around the contour points. The authors found that the angular information provides a more precise description when being jointly used with triangle side lengths (i.e., TSL) [94].
A disadvantage of shape signatures for leaf and flower analysis is the high matching cost, which is too high for online retrieval. Furthermore, shape signatures are sensitive to noise and changes in the contour. Therefore, it is undesirable to directly describe a shape using a shape signature. On the other hand, further processing can increase its robustness and reduce the matching load. For example, a shape signature can be simplified by quantizing a contour into a contour histogram, which is then rotationally invariant [151]. For example, an angle code histogram (ACH) has been used instead of AC by [148]. However, the authors did not compare AC against ACH.
Shape context approaches. Beyond the CCD and AC descriptors discussed before, there are other alternative methods that intensively elaborate a shape’s contour to extract useful information. Belongie et al. [12] proposed a shape descriptor, called shape context (SC), that represent log-polar histograms of contour distribution. A contour is resampled to a fixed number of points. In each of these points, a histogram is computed such that each bin counts the number of sampled contour points that fall into its space. In other words, each contour point is described by a histogram in the context of the entire shape. Descriptors computed in similar points on similar shapes will provide close histograms. However, articulation (e.g., relative pose of the petiole or the position of the blade) results in significant variation of the calculated SC. In order to obtain articulation invariance, [83] replaced the Euclidean distance and relative angles by inner-distances and inner-angles. The resulting 2D histogram, called inner-distance shape context (IDSC), was reported to perform better than many other descriptors in leaf analysis [11]. It is robust to the orientation of the footstalk, but at the cost of being a shape descriptor that is extensive in size and expensive in computational cost. For example, [139] does not employ IDSC due to its expensive computational cost.
Hu et al. [62] propose a contour-based shape descriptor named multi-scale distance matrix (MDM) to capture the geometric structure of a shape, while being invariant to translation, rotation, scaling, and bilateral symmetry. The approach can use Euclidean distances as well as inner distances. MDM is considered a most effective method since it avoids the use of dynamic programming for building the point-wise correspondence. Compared to other contour-based approaches, such as SC and IDSC, MDM can achieve comparable recognition performance while being more computationally efficient [62]. Although MDM effectively describes the broad shape of a leaf, it fails in capturing details, such as leaf margin. Therefore, [73] proposed a method that combines contour (MDM), margin (average margin distance (AMD), margin statistics (MS)), SMSD and Hu moments and demonstrated higher classification accuracy than reached by using MDM and SMSD with Hu moments alone.
Zhao et al. [158] made two observations concerning shape context approaches. First, IDSC cannot model local details of leaf shapes sufficiently, because it is calculated based on all contour points in a hybrid way so that global information dominates the calculation. As a result, two different leaves with similar global shape but different local details tend to be misclassified as the same species. Second, the point matching framework of generic shape classification methods does not work well for compound leaves since their local details are hard to be matched in pairs. To solve this problem, [158] proposed an independent-IDSC (I-IDSC) feature. Instead of calculating global and local information in a hybrid way, I-IDSC calculates them independently so that different aspects of a leaf shape can be examined individually. The authors argue that compared to IDSC [11, 83] and MDM [62], the advantage of I-IDSC is threefold: (1) it discriminates leaves with similar overall shape but different margins and vice versa; (2) it accurately classifies both simple and compound leaves; and (3) it only keeps the most discriminative information and can thus be more efficiently computed [158].
Wang et al. [134, 135] developed a multi scale-arch-height descriptor (MARCH), which is constructed based on the concave and convex measures of arches of various levels. This method extracts hierarchical arch height features at different chord spans from each contour point to provide a compact, multi-scale shape descriptor. The authors claim that MARCH has the following properties: invariant to image scale and rotation, compactness, low computational complexity, and coarse-to-fine representation structure. The performance of the proposed method has been evaluated and demonstrated to be superior to IDSC and TAR [134, 135].
Scale space analysis. A rich representation of a shape’s contour is the curvature-scale space (CSS). It piles up curvature measures at each point of the contour over successive smoothing scales, summing up the information into a map where concavities and convexities clearly appear, as well as the relative scale up to which they persist [151]. Florindo et al. [45] propose an approach to leaf shape identification based on curvature complexity analysis (fractal dimension based on curvature). By using CSS, a curve describing the complexity of the shape can be computed and theoretically be used as descriptor. Studies found the technique to be superior to traditional shape analysis methods like FD, Zernike moments, and multi-scale fractal dimension [45]. However, while CSS is a powerful description it is too informative to be used as a descriptor. The implementation and matching of CSS is very complex. Curvature has also been used to detect dominant points (points of interest or characteristic points) on the contour, and provides a compact description of a contour by its curvature optima. Studies select this characteristic or the most prominent points based on the graph of curvature values of the contour as descriptor [15, 18]. Lavania and Matey [81] use mean projection transform (MPT) to extract corner candidates by selecting only candidates that have high curvature (contour-based edge detection). Kebapci et al. [74] extract high curvature points on the contour by analyzing direction changes in the chain code. They represent the contour as a chain code, which is a series of enumerated direction codes. These points (aka codes) are labeled as convex or concave depending on their position and direction (or curvature of the contour). Kumar et al. [76] suggest a leaf classification method using so-called histograms of curvature over scale (HoCS). HoCS are built from CSS by creating histograms of curvature values over different scales. One limitation of the HoCS method is that it is not articulation-invariant, i.e., that a change caused by the articulation either between the blade and petiole of a simple leaf, or among the leaflets of a compound leaf can cause significant changes to the calculated HoCS feature. Therefore, it needs special treatment of leaf petioles and the authors suggest to detect and remove the petiole before classification. Chen et al. [28] used a simplified curvature of the leaf contour, called velocity. The results showed that the velocity algorithms were faster at finding contour shape characteristics and more reasonable in their characteristic matching than CSS. Laga et al. [77] study the performance of the squared root velocity function (SRVF) representation of closed planar curves for the analysis of leaf shapes and compared it to IDSC, SC, and MDM. SRVF significantly outperformed the previous shape-based techniques. Among the lower performing techniques in this study, SC and MDM performed equally, IDCS achieved the lowest performance.
Fourier descriptors. Fourier descriptors (FD) are a classical method for shape recognition and have grown into a general method to encode various shape signatures. By applying a Fourier transform, a leaf shape can be analyzed in the frequency domain, rather than the spatial domain as done with shape signatures. A set number of Fourier harmonics are calculated for the outline of an object, each consisting of only four coefficients. These Fourier descriptors capture global shape features in the low frequency terms (low number of harmonics) and finer features of the shape in the higher frequency terms (higher numbers of harmonics). The advantages of this method are that it is easy to implement and that it is based on the well-known theory of Fourier analysis [33]. FD can easily be normalized to represent shapes independently of their orientation, size, and location; thus easing comparison between shapes. However, a disadvantage of FDs is that they do not provide local shape information since this information is distributed across all coefficients after the transformation [151]. A number of studies focused on FD, e.g., [147] use FD computed on distances of contour points from the centroid, which is advantageous for smaller datasets. Kadir et al. [72] propose a descriptor based on polar Fourier transform (PFT) to extract the shape of leaves and compared it with SMSD, Hu, and Zernike moments. Among those methods, PFT achieved the most prospective classification result. Aakif and Khan [1], Yanikoglu et al. [148] used FD in combination with SMSD. The authors obtained more accurate classification results by using FD than with SMSD alone. However, they achieved the best result by combining all descriptors. Novotny and Suk [106] used FD in combination with TMI and major axis length. Several studies that propose novel methods for leaf shape analysis benchmark their descriptor against FD in order to prove effectiveness [45, 62, 134, 147, 158].
Fractal dimension. The fractal dimension (FracDim) of an object is a real number used to represent how completely a shape fills the dimensional space to which it belongs. The FracDim descriptor can provide a useful measure of a leaf shape’s complexity. In theory, measuring the fractal dimension of leaves or flowers can quantitatively describe and classify even morphologically complex plants. Only a few studies used FracDim for leaf analysis [14, 65, 67] and flower analysis [3]. Bruno et al. [14] compare box-counting and multi-scale Minkowski estimates of fractal dimension. Although the box-counting method provided satisfactory results, Minkowski’s multi-scale approach proved superior in terms of characterizing plant species. Given the wide variety of leaf and flower shapes, characterizing their shape by a single value descriptor of complexity likely discards useful information, suggesting that the FracDim descriptors may only be useful in combination with other descriptors. For example, [65] demonstrated that leaf analysis with FracDim descriptors are effective and yield higher classification rates than Hu moments. When combining both, even better results were achieved. One step further, [14, 65, 67] proposed methods for combining the FD descriptor of a leaf’s shape with a FracDim descriptor computed on the venation of the leaf to rise classification performance (further details in the section about vein feature).
3.3.5 Color
Color is an important feature of images. Color properties are defined within a particular color space. A number of color spaces have been applied across the primary studies, such as red-green-blue (RGB), hue-saturation-value (HSV), hue-saturation-intensity (HSI), hue-max-min-diff (HMMD), LUV (aka CIELUV), and more recently Lab (aka CIELAB). Once a color space is specified, color properties can be extracted from images or regions. A number of general color descriptors have been proposed in the field of image recognition, e.g., color moments (CM), color histograms (CH), color coherence vector, and color correlogram [153]. CM are a rather simple descriptor, the common moments being mean, standard deviation, skewness, and kurtosis. CM are used for characterizing planar color patterns, irrespective of viewpoint or illumination conditions and without the need for object contour detection. CM is known for its low dimension and low computational complexity, thus, making it convenient for real-time applications. CH describes the color distribution of an image. It quantizes a color space into different bins and counts the frequency of pixels belonging to each color bin. This descriptor is robust to translation and rotation. However, CH does not encode spatial information about the color distribution. Therefore, visually different images can have similar CH. In addition, a histogram is usually of high dimensionality [153]. A major challenge for color analysis is light variations due to different intensity and color of the light falling from different angles. These changes in illumination can cause shadowing effects and intensity changes. For species classification the most studied descriptors are CM [16, 43, 48, 87, 116, 148] and CH [3, 16, 29, 57, 74, 87, 104, 105, 112, 148]. An overview of all primary studies that analyze color is shown in Table 8.
Leaf analysis. Only 8 of 106 studies applying leaf analysis also study color descriptors. We always found color descriptors being jointly studied together with leaf shape descriptors. Kebapci et al. [74] use three different color spaces to produce CH and color co-occurrence matrices (CCM) for assessing the similarity between two images; namely RGB, normalized RGB (nRGB), and HSI, where nRGB-CH facilitated the best results. Yanikoglu et al. [148] studied the effectiveness of color descriptors, specifically the RGB histogram and CM. The authors found CM to provide the most accurate results. However, the authors also found that color information did not contribute to the classification accuracy when combined with shape and texture descriptors. Caglayan et al. [16] defined different sets of color features. The first set consisted of mean and standard deviation of intensity values of the red, the green, and the blue channel and an average of these channels. The second set consisted of CH in red, green, and blue channels. The authors found the first four CM to be an efficient and effective way for representing color distribution of leaf images [43, 48, 116, 148]. Che Hussin et al. [27] proposed a grid-based CM as descriptor. Each image is divided into a 3x3 grid, then each cell is described by mean, standard deviation, and the third root of the skewness. In contrast, [87] evaluated the first three central moments, which they found to be not discriminative according their experimental results.
Flower analysis. Color plays a more important role for flower analysis than for leaf analysis. We found that 9 out of 13 studies on flower analysis use color descriptors. However, using color information solely, without considering flower shape features, cannot classify flowers effectively [104, 105]. Flowers are often transparent to some degree, i.e., that the perceived color of a flower differs depending on whether the light comes from behind or in front of the flower. Since flower images are taken under different environmental conditions, the variation in illumination is greatly affecting analysis results [126]. To deal with this problem, [3, 30, 57, 60] converted their images from the RGB color space into the HSV space and discarded the illumination (V) component. Apriyanti et al. [3] studied discrimination power of features for flower images and identified the following relation from the highest to the lowest: CCD (shape), HSV color, and geometric moments (shape). Hsu et al. [60] found that color features have more discriminating ability than the center distance sequence and the roundness shape features. Qi et al. [117] study a method where they select local keypoints with colored SIFT (CSIFT). CSIFT is a SIFT-like descriptor that builds on a color invariants. It employs the same strategy as SIFT for building descriptors. The local gradient-orientation histograms for the same-scale neighboring pixels of a keypoint are used as descriptor. All orientations are assigned relative to a dominant orientation of the keypoint. Thus, the built descriptor is invariant to the global object orientation and is stable to occlusion, partial appearance, and cluttered surroundings due to the local description of keypoints. As CSIFT uses color invariants for building the descriptor, it is robust to photometric changes [2]. Qi et al. [117] even found the performance of CSIFT to be superior over SIFT.
3.3.6 Texture
Texture is the term used to characterize the surface of a given object or phenomenon and is undoubtedly a main feature used in computer vision and pattern recognition [142, 153]. Generally, texture is associated to the feel of different materials to human touch. Texture image analysis is based on visual interpretation of this feeling. Compared to color, which is usually a pixel property, texture can only be assessed for a group of pixels [153]. Grayscale texture analysis methods are generally grouped into four categories: signal processing methods based on a spectral transform, such as, Fourier descriptors (FD) and Gabor filters (GF); statistical methods that explore the spatial distribution of pixels, e.g., co-occurrence matrices; structural methods that represent texture by primitives and rules; and model-based methods based on fractal and stochastic models. However, some recently proposed methods cannot be classified into these four categories. For instance, methods based on deterministic walks, fractal dimension, complex networks, and gravitational models [37]. An overview of all primary studies that analyze texture is shown in Table 9.
Leaf analysis. For leaf analysis, twelve studies analyzed texture solely and another twelve studies combined texture with other features, i.e., shape, color, and vein. The most frequently studied texture descriptors for leaf analysis are Gabor filter (GF) [17, 23, 32, 74, 132, 150], fractal dimensions (FracDim) [7, 8, 36, 37], and gray level co-occurrence matrix (GLCM) [23, 32, 43, 48].
GF are a group of wavelets, with each wavelet capturing energy at a specific frequency and in a specific direction. Expanding a signal provides a localized frequency description, thereby capturing the local features and energy of the signal. Texture features can then be extracted from this group of energy distributions. GF has been widely adopted to extract texture features from images and has been demonstrated to be very efficient in doing so [152]. Casanova et al. [17] applied GF on sample windows of leaf lamina without main venation and leaf margins. They observed a higher performance of GF than other traditional texture analysis methods such as FD and GLCM. Chaki et al. [23], Cope et al. [32] combined banks of GF and computed a series of GLCM based on individual results. The authors found the performance of their approach to be superior to standalone GF and GLCM. Yanikoglu et al. [148] used GF and HOG for texture analysis and found GF to have a higher discriminatory power. Venkatesh and Raghavendra [132] proposed a new feature extraction scheme termed local Gabor phase quantization (LGPQ), which can be viewed as the combination of GF with a local phase quantization scheme. In a comparative analysis the proposed method outperformed GF as well as the local binary pattern (LBP) descriptor.
Natural textures like leaf surfaces do not show detectable quasi-periodic structures but rather have random persistent patterns [63]. Therefore, several authors claim fractal theory to be better suited than statistical, spectral, and structural approaches for describing these natural textures. Authors found the volumetric fractal dimension (FracDim) to be very discriminative for the classification of leaf textures [8, 122]. Backes and Bruno [7] applied multi-scale volumetric FracDim for leaf texture analysis. de M Sa Junior et al. [36, 37] propose a method combining gravitational models with FracDim and lacunarity (counterpart to the FracDim that describes the texture of a fractal) and found it to outperform FD, GLCM, and GF.
Surface gradients and venation have also been exploited using the edge orientation histogram descriptor (EOH) [10, 10, 91, 148]. Here the orientations of edge gradients are used to analyze the macro-texture of the leaf. In order to exploit the venation structure, [25] propose the EAGLE descriptor for characterizing leaf edge patterns within a spatial context. EAGLE exploits the vascular structure of a leaf within a spatial context, where the edge patterns among neighboring regions characterize the overall venation structure and are represented in a histogram of angular relationships. In combination with SURF, the studied descriptors are able to characterize both local gradient and venation patterns formed by surrounding edges.
Elhariri et al. [43] studied first and second order statistical properties of texture. First order statistical properties are: average intensity, average contrast, smoothness, intensity histogram’s skewness, uniformity, and entropy of grayscale intensity histograms (GIH). Second order statistics (aka statistics from GLCM) are well known for texture analysis and are defined over an image to be the distribution of co-occurring values at a given offset [55]. The authors found that the use of first and second order statistical properties of texture improved classification accuracy compared to using first order statistical properties of texture alone. Ghasab et al. [48] derive statistics from GLCM, named contrast, correlation, energy, homogeneity, and entropy and combined them with shape, color, and vein features. Wang et al. [136] used dual-scale decomposition and local binary descriptors (DS-LBP). DS-LBP descriptors effectively combine texture and contour of a leaf and are invariant to translation and rotation.
Flower analysis. Texture analysis also plays an important role for flower analysis. Five of the 13 studies analyze the texture of flowers, whereby texture is always analyzed in combination with shape or color. Nilsback and Zisserman [104, 105] describe the texture of flowers by convolving the images with a Leung-Malik (MR) filter bank. The filter bank contains filters with multiple orientations. Zawbaa et al. [149] propose the segmentation-based fractal texture analysis (SFTA) to analyze the texture of flowers. SFTA breaks the input image into a set of binary images from which region boundaries’ FracDim are calculated and segmented texture patterns are extracted.
3.3.7 Leaf-Specific Features
Leaf venation. Veins provide leaves with structure and a transport mechanism for water, minerals, sugars, and other substances. Leaf veins can be, e.g., parallel, palmate, or pinnate. The vein structure of a leaf is unique to a species. Due to a high contrast compared to the rest of the leaf blade, veins are often clearly visible. Analyzing leaf vein structure, also referred to as leaf venation, has been proposed in 16 studies (see Table 10).
Only four studies solely analyzed venation as a feature discarding any other leaf features, like, shape, size, color, and texture [53, 78–80]. Larese et al. [78–80] introduced a framework for identifying three legumes species on the basis of leaf vein features. The authors computed 52 measures per leaf patch (e.g., the total number of edges, the total number of nodes, the total network length, median/min/max vein length, median/min/max vein width). Larese et al. [80] defines and discusses each measure. The author [80] performed an experiment using images that were cleared using a chemical process (enhancing high contrast leaf veins and higher orders of visible veins), which increased their accuracy from 84.1 to 88.4% compared to uncleared images at the expense of time and cost for clearing. Gu et al. [53] processed the vein structure using a series of wavelet transforms and Gaussian interpolation to extract a leaf skeleton that was then used to calculate a number of run-length features. A run-length feature is a set of consecutive pixels with the same gray level, collinear in a given direction, and constituting a gray level run. The run length is the number of pixels in the run and the run length value is the number of times such a run occurs in an image. The authors obtained a classification accuracy of 91.2% on a 20 species dataset.
Twelve studies analyzed venation in combination with the shape of leaves [4, 5, 14, 65, 67, 101, 107, 108, 139, 144] and two studies analyzed venation in combination with shape, texture, and color [43, 48]. Nam et al. [101], Park et al. [107, 108] extract structure features in order to categorize venation patterns. Park et al. [107, 108] propose a leaf image retrieval scheme, which analyzes the venation of a leaf sketch drawn by the user. Using the curvature scale scope corner detection method on the venation drawing they categorize the density of feature points (end points and branch points) by using non-parametric estimation density. By extracting and representing these venation types, they could improve the classification accuracy from 25 to 50%. Nam et al. [101] performed classification on graph representations of veins and combined it with modified minimum perimeter polygons as shape descriptor. The authors found their method to yield better results than CSS, CCD, and FD. Four groups of researchers [5, 43, 48, 144] studied the ratio of vein-area (number of pixels that represent venation) and leaf-area (\(A_{vein}/ A_{leaf}\)) after morphological opening. Elhariri et al. [43], Ghasab et al. [48] found that using a combination of all features (vein, shape, color, and texture) yielded the highest classification accuracy. Wang et al. [139] used SC and SIFT extracted from contour and vein sample points. They noticed that vein patterns are not always helpful for SC based classification. Since in their experiments, vein extraction based on simple Canny edge detection generated noisy outputs utilizing the resulting vein patterns in shape context led to unstable classification performance. The authors claim that this problem can be remedied with advanced vein extraction algorithms [139]. Bruno et al. [14], Ji-Xiang et al. [65] and Jobin et al. [67] studied FracDim extracted from the venation and the outline of leafs and obtained promising results. Bruno et al. [14] argues that the segmentation of a leaf venation system is a complex task, mainly due to low contrast between the venation and the rest of the leaf blade structure. The authors propose a methodology divided into two stages: (i) chemical leaf clarification, and (ii) segmentation by computer vision techniques. Initially, the fresh leaf collected in the herbarium, underwent a chemical process of clarification. The purpose was removing the genuine leaf pigmentation. Then, the fresh leaves were digitalized by a scanner. Ji-Xiang et al. [65], Jobin et al. [67] did not use any chemical or biological procedure to physically enhance the leaf veins. They obtained a classification accuracy of 87% on a 30 species dataset and 84% on a 50 species dataset, respectively.
Leaf margin. All leaves exhibit margins (leaf blade edges) that are either serrated or unserrated. Serrated leaves have teeth, while unserrated leaves have no teeth and are described as being smooth. These margin features are very useful for botanists when describing leaves, with typical descriptions including details such as the tooth spacing, number per centimeter, and qualitative descriptions of their flanks (e.g., convex or concave). Leaf margin has seen little use in automated species identification with 8 out of 106 studies focusing on it (see Table 10). Studies usually combine margin analysis with shape analyses [18, 20, 21, 73, 85, 93]. Two studies used margin as sole feature for analysis [31, 66].
Jin et al. [66] propose a method based on morphological measurements of leaf tooth, discarding leaf shape, venation, and texture. The studied morphological measurements are the total number of teeth, the ratio between the number of teeth and the length of the leaf margin expressed in pixels, leaf-sharpness, and leaf-obliqueness. Leaf-sharpness, is measured per tooth as an acute triangle obtained by connecting the top edge and two bottom edges of the leaf tooth. Thus, for a leaf image, many triangles corresponding to leaf teeth are obtained. In their method, the acute angle for each leaf tooth is exploited as a measure for plant identification. The proposed method achieves an average classification rate of around 76% for the eight studied species. Cope and Remagnino [31] extracts a margin signature based on the leaf’s insertion point and apex. A classification accuracy of 91% was achieved on a larger dataset containing 100 species. The authors argue that accurate identification of insertion point and apex may also be useful when considering other leaf features, e.g., venation. Two shape context based descriptors have been presented and combined for plant species identification by [93]. The first one gives a description of the leaf margin. The second one computes the spatial relations between the salient points and the leaf contour points. Results show that a combination of margin and shape improved classification performance in contrast to using them as separate features. Kalyoncu and Toygar [73] use margin statistics over margin peaks, i.e., average peak height, peak height variance, average peak distance, and peak distance variance, to describe leave margins and combined it with simple shape descriptors, i.e., Hu moments and MDM. In [18, 20], contour properties are investigated utilizing a CSS representation. Potential teeth are explicitly extracted and described and the margin is then classified into a set of inferred shape classes. These descriptors are combined base and apex shape descriptors. Cerutti et al. [21] introduces a sequence representation of leaf margins where teeth are viewed as symbols of a multivariate real valued alphabet. In all five studies [18, 20, 21, 73, 85] combining shape and margin features improved classification results in contrast to analyzing the features separately.
3.4 Comparison of Studies (RQ-4)
The discussion of studied features in the previous section illustrates the richness of approaches proposed by the primary studies. Different experimental designs among many studies in terms of studied species, studied features, studied descriptors, and studied classifiers make it very difficult to compare results and the proposed approaches themselves. For this section, we selected primary studies that utilize the same dataset and present a comparison of their results. We start the comparison with the Swedish leaf dataset (Table 11), followed by the ICL dataset (Table 12), and the Flavia dataset (Table 13). A comparison of the other introduced datasets, i.e., ImageCLEF and LeafSnap is not feasible since authors used varying subsets of these datasets for their evaluations making comparison of results impossible.
Classification accuracy as typically reported in studies is defined as follows:
3.4.1 Swedish Leaf Dataset
Classifiers. For the Swedish leaf dataset, nearly all authors apply a k-nearest neighbor (k-NN) classifier [62, 62, 83, 94, 136, 147], occasionally in the simple 1-NN form [134, 135, 145, 158], to perform classification and to evaluate their approaches (see Table 11). k-NN is a non-parametric classification algorithm that classifies unknown samples based to their k nearest neighbors among the training samples. The most frequent class among these k neighbors is chosen as the class for the sample to be classified. A challenge of k-NN is to select an appropriate value of k, typically based on error rates [16]. In order to improve robustness and discriminability of classification, a fuzzy k-nearest neighbors classifier was proposed [136]. Unlike the conventional k-NN, which only considers the congeneric number of k-nearest neighbors, fuzzy k-NN synthetically considers the congeneric number and the similarity between the k-nearest neighbors and the unknown sample. Only one study used support vector machines (SVM) as classifier on this dataset. A Radial basis function (RBF) kernel for the SVM was used [121], which can handle a high dimensional space of data points that are not linearly separable. SVM are known as classifiers with simple structure and comparatively fast training phase and are easy to implement.
Classification accuracies. Table 11 shows classification accuracies achieved on the Swedish leaf dataset with the different methods proposed in the primary studies. The four lowest classification rates are obtained with Gabor Filter (GF) (85.75%), Shape Context (SC) (88.12%), and Fourier descriptor (FD) (87.54 and 89.60%) classified using fuzzy-k-NN, k-NN, and 1-NN. As discussed in the feature section, [94] found TSLA to give better identification scores than TAR, TOA, and TSL. Xiao et al. [145] noticed that the IDSC descriptor performs better than HOG on the original Swedish leaf dataset. Ren et al. [121] used multi-scale overlapped block local binary pattern (LBP) with a SVM classifier and obtained the fourth best classification performance on this dataset. Zhao et al. [158] introduced I-IDSC and obtained with 97.07% the third best result. The multi-scale-arch-height descriptor (MARCH) method [135] achieved the second best classification rate (97.33%). The best result with 99.25% was obtained by [136]. They used dual-scale decomposition and local binary descriptors (DS-LPB). DS-LBP combines textures and contour information of a leaf and is invariant to translation and rotation.
Images of the Swedish leaf dataset contain leafstalks. The benefit of leafstalks is controversially debated by authors. On one hand, they can provide discriminant information for classification, but on the other hand length and orientation of leafstalks depends on the collection and imaging process and is therefore considered unreliable. Table 11 shows that for all with and without leafstalks studied descriptors the classifications accuracy dropped when removing leafstalks, e.g., the performance of IDSC decreased from 93.73 to 85.07%. This result indicates that leafstalks indeed provide useful information for recognition.
3.4.2 ICL Dataset
Table 12 shows classification accuracies on the ICL leaf dataset using the methods proposed in the primary studies. The upper part of the table shows results gained on the whole dataset containing 220 species. Several studies do not use the whole dataset, but merely evaluate their approaches on two subsets of the ICL leaf dataset (subset A and B). Subset A includes 50 species sharing the characteristic that the contained species’ shapes can be distinguished easily by humans. Subset B also includes 50 species with shapes that are very similar but still distinguishable [62, 121, 145, 158]. Furthermore, [147, 156, 157] also used a subset of the ICL dataset but without specifying the selected species. Their results are not considered for comparison here.
Classifier. The set of utilized classification methods (k-NN, 1-NN, fuzzy k-NN, and SVM) is the same as for the Swedish leaf dataset.
Classification accuracies. On the entire dataset, the lowest classification accuracies were obtained with FD, followed by TAR, and IDSC with a simple 1-NN classifier. Similar to the Swedish leaf dataset, the best results were obtained by combining texture and shape features. Wang et al. [140] combined entropy sequence (EnS) representing texture features and center distance sequence (CDS) representing shape features and utilized SVM with a RBF kernel for classification. They achieved the second best classification accuracy with 95.87%. As for the Swedish leaf dataset, the best results were also obtained by [136] using a dual-scale decomposition and local binary descriptors (DS-LPB) and a fuzzy k-NN classifier. Furthermore, classification accuracies of the same methods applied to the Swedish leaf and the ICL dataset show lower accuracies on the ICL dataset, suggesting that species and samples in the ICL leaf dataset represent a more complicated classification task. Wang et al. [136] argues that the ICL dataset contains many species with similar shapes. This characteristic can also explain a higher drop in classification accuracies for shape-based methods, such as HoCS, IDCS, and MDM, than for texture-based methods. A similar effect is visible for the subsets A and B containing 50 species. Subset B (accuracies in brackets) consistently yields lower accuracies than subset A. Especially, IDCS is found to be not a discriminative descriptor for distinguishing leaves with visually similar shapes, it obtains an accuracy of only 64% on subset B compared to 96% on subset A.
3.4.3 Flavia Dataset
The Flavia dataset is a benchmark used by researchers to compare and evaluate methods across studies and publications. The dataset contains leaf images of 32 different species. Table 13 shows a comparison of different methods applied by the primary studies on the Flavia dataset.
Classifier. Primary studies used a richer set of classification methods for their experiments on the Flavia dataset compared to the Swedish leaf dataset and the ICL dataset. In addition to the previously mentioned k-NN and SVM classifiers, also the following methods were used: Naive Bayes (NB) [16], decision tree (DT) [116], random forest (RF) [16], neuro fuzzy classifier (NFC) [23, 24], multi-layered perceptron (MLP) [23], Riemannian metrics [77], artificial neural network (ANN) with back-propagation (BPNN) [1], and probabilistic neural networks (PNN) [58, 144]. Bayesian classifiers are statistical models able to predict the probability for an unknown sample to belong to a specific class. They are a practical learning approach based on Bayes’ Theorem. A disadvantage of Bayesian classifiers is that conditional independence may decrease accuracy thereby imposing a constraint over attributes that may not be dependent. A Decision Tree is a classifier that uses a tree-like graph to represent decisions and their possible consequences. A decision tree consists of three types of nodes: decision nodes, which evaluate each feature at a time according their relevance; chance nodes, which choose between possible values of features; and end nodes, which represent the final decision, i.e., the wing label. The Random Forest classifier is based on the classification tree approach. It aggregates predictions of multiple classification trees for a dataset. Each tree in the forest is grown using bootstrap samples. At prediction time, classification results are taken from each tree in the forest. The class with the most votes among the separate trees is selected by the forest. Random forests are efficient on large datasets with high accuracy. Random forests also allow to estimate the importance of input variables (in their original dimensional space). However, they have constraints on memory and computing time. Finally, an artificial neural network (ANN) is an interconnected group of artificial neurons simulating the thinking process of the human brain. One can consider an ANN as a “magical” black box trained to achieve an expected intelligent process, against the input and output information stream [144].
Classification accuracies. The lowest classification rates with 25.30% were obtained with Hu moments [111] and Hu moments in combination with curvelet transform 41.6% [23]. The results demonstrate that the Hu descriptor is not robust when working with leaf shape and should be combined with other features like vein, margin, color, or texture [23, 111]. Prasad et al. [116] study shape and color information of leaves using SMSD and FD to represent the shape. Once the initial classification is calculated solely based on these shape descriptors using k-NN, the two classes with the highest probability are selected. Then, color is analyzed and a binary decision tree is used to decide between these two classes. Prasad et al. [116] found that color information of leaves increased accuracy from 84.45% (shape only) to 91.30% (shape + color). Arun Priya et al. [5] compared SVM with RBF kernel and k-NN classification based on shape and vein features and found that SVM with 94.5% outperformed k-NN with only 78%. Caglayan et al. [16] compared four classification algorithms: k-NN, SVM with linear kernel function, Naive Bayes, and Random Forest based on shape and color features. Across all their experiments, Random Forest yielded the best classification results. The lowest accuracy was achieved with SVM based on shape features. Combining shape and color increased classification accuracy significantly. The greatest increase was demonstrated with SVM using SMSD, color moments, and color histograms improving accuracy about 15% compared to a Naive Bayes classifier using the same features. Wang et al. [140] obtained the highest accuracy on the Flavia dataset with 97.80% by combining EnS representing texture features with CDS representing shape features and utilized SVM with RBF kernel for classification (see results of ICL dataset).
Four primary studies used neural network classifiers [1, 23, 58, 144]. Aakif and Khan [1] applied back-propagation neural networks (BPNN) and obtained a classification accuracy of 96.0%. Hossain and Amin [58] and Wu et al. [144] applied probabilistic neural networks (PNN) for classification of leaf shape features and obtained an accuracy of 90.31 and 91.40% respectively. The PNN learns rapidly compared to the traditional back-propagation, and guarantees to converge to a Bayes classifier if enough training examples are provided, it also enables faster incremental training and is robust to noisy training samples [58]. Chaki et al. [23] used two types of supervised feed-forward neural classifiers: a multi-layered perceptron using back propagation (MLP) and a neuro fuzzy classifier using a scaled conjugate gradient algorithm (NFC). The accuracies obtained by solely using texture-based descriptors are 81.6% with NFC and 87.1% with MLP, by only using shape-based descriptors a significantly lower accuracy of 50.16% using NFC and 41.6% using MLP were obtained. As for the Swedish leaf dataset and the ICL dataset, the combination of texture and shape obtained the best results. Chaki et al. [23] found that by combining texture and shape, classification accuracy rose to 97.6% with NFC and dropped to 85.6% with MLP. The former being the second highest accuracy achieved on the Flavia dataset.
3.5 Prototypical Implementation (RQ-5)
In addition to studying classification approaches, 13 studies provide an implementation of the proposed method as app for mobile devices [11, 20, 26, 76, 87, 100, 101, 103, 111, 112, 116, 134, 135], two studies as a web service [68, 110], and four studies as a desktop application [57, 58, 102, 158].
Mobile applications. A smartphone possesses everything required for the implementation of a mobile plant identification system, including a camera, a processor, a user interface, and an internet connection. These preconditions make smartphones highly suitable for field use by professionals and the general public. However, these devices still have less available memory, storage capacity, network bandwidth and computational power than desktop or server machines, which limits algorithmic choices. Due to these constraints, it can be tempting to offload some of the processing to a high performance server. This requires a reliable internet connection (Table 14). Using an online service can be attractive when dataset or algorithm are likely to be updated regularly or when they have large computational and memory requirements. However, in remote areas where plant identification applications are likely to be most useful, an internet connection may be unreliable or unavailable. The contrary approach is using efficient algorithms that run directly on the device without the need for a network connection or a support server but with potential limitations in their classification performance [134].
Belhumeur et al. [11] developed LeafView, a Tablet-PC based application for the automated identification of species in the field. Leaf images are captured on a plain background. A computer vision component finds the best set of matching species and results are presented in a zoomable user interface. Samples are matched with existing species or marked unknown for further study. LeafView was built with C#, MatLab, and Piccolo. Kumar et al. [76] designed Leafsnap, the so far most popular mobile app based on iOS for plant species identification. A user can take a photo of a leaf on plain background, transfer the image to the Leafsnap server for analysis, and eventually see information about the identified species. This application is restricted to tree species of the Northeastern United States and can perform the identification only with access to the internet. Cerutti et al. [20] provide an educational iOS application called FOLIA to help users recognizing a plant species in its natural environment. In order to perform this task, the application first lets the user take a picture of a unknown leaf with the smartphone camera. Then, it extracts high-level morphological features to predict a list of the most corresponding species.
Ma et al. [87] implemented an Android-based plant image retrieval system in JAVA. Here the user is supposed to place a single leaf taken on a light, untextured, and uniform background. Compared to [76], users can identify the species without internet and also use existing digital images as query image, i.e., for identifying a species. Also [134, 135] implemented an Android application in Java. Classification can alternatively be performed on the server for more computationally expensive algorithms or offline on the device. Even in online mode, only a feature vector is being sent to the server rather than the actual image. The feature extraction is performed on the device thereby drastically reducing bandwidth requirements for the server connection. The server returns a dynamic webpage, opened in the device’s browser, showing closest matches. Another Android application has been developed by [103]. Similar to Leafsnap, this system uses a client-server implementation. Initially, a user takes a leaf photo with the phone. This photo is then being sent to the server on which it is analyzed in order to identify the species. The server procedure contains of two main analyzes. First, a leaf/no-leaf classification aims at checking the validity of the uploaded photo. Second, for leaf containing photos the species identification is triggered, otherwise the system will ask for another photo. Upon a leaf identification, the client will display species information to the user. Chathura Priyankara and Withanage [26] developed an Android client application, which interacts with a leaf recognition algorithm running on the server through a SOAP-based web service. OpenCV is used for the actual image processing. Prasad et al. [116] developed an offline mobile application for Android using OpenCV. Leaf images are captured with the device’s camera and must exhibit a uniform background for simplifying the segmentation. The classification process is done on the mobile device.
Web services. Pauwels et al. [110] implemented a web service that allows users to upload a tree leaf image. The service is designed as a two-tier system. The front-end allows to upload query images and the back-end performs the matching. Eventually, a webpage is created showing the ten most similar exemplars along with the names of the species. Pham et al. [111] developed among others a graphical web tool of their approach. This version is developed in PHP and uses a mySQL database. Joly et al. [68] developed Pl@ntNet Identify, an interactive web service dedicated to the content-based identification of plants using general public contributed image data. It is composed of three main parts: an interactive web GUI for the client, a content-based visual search engine, and a multi-view fusion module on the server side. Pl@ntNet Identify was the first botanical identification system able to consider a combination of habit, leaf, flower, fruit, and bark images for classification. In the meantime, Pl@ntNet also provides a mobile version of their service on iOS and Android.
Desktop applications. Hossain and Amin [58] developed the Chloris desktop application for plant identification. The system was trained with 1200 images of simple leaves on plain background from 30 plant species. They also tested their system with partially damaged leaves and demonstrated that it was able to successfully identify the plants. However, no more information about the system is given. Hong and Choi [57] implemented a flower recognition system with Microsoft Visual Studio to evaluate the performance of their proposed recognition process. Based on a flower image, the system finds the contour of flowers using color and edge information and then extracts image features of flowers. The system compares these features with the features of images stored in the system. Eventually, the system determines species with the most similar features and presents the top three ranked species.
4 Discussion
This paper aimed at identifying, analyzing, and comparing research work in the field of plant species identification using computer vision techniques. A systematic review was conducted driven by research questions and using a well-defined process for data extraction and analysis. The following findings summarize principal results of this systematic review and provide directions for future research.
Finding-1: Most studies conducted by computer scientist
Automated plant species identification is a topic mostly driven by academics specialized in computer vision, machine learning, and multimedia information retrieval. Only a few studies are conducted by interdisciplinary groups of biologist and computer scientists. Increasingly, research is moving towards more interdisciplinary endeavors. Effective collaboration between people from different disciplines and backgrounds is necessary to gain the benefits of joined research activities and to develop widely accepted approaches [13]. This is also the case for automated plant species identification. Here biologist can learn from computer science methods and vice versa. For example, leaf shape is very important not only for species identification, but also in other studies, such as plant ecology and physiology. We therefore foresee an increasing interest in this trans-disciplinary challenge.
Finding-2: Only two approaches evaluated on large datasets
Since there exist more than 220,000 plant species around the world [52, 90, 125], it is important to develop plant identification methods capable of handling this high variability. Only two primary studies evaluated their approaches on large datasets with realistic numbers of species [68, 143]. Furthermore, considering that changes in illumination, background, and position of plants or their organs may create dramatically different images for the same plant, also larger datasets in this regard are required to yield high accuracy in plant identification under realistic conditions. Apart from the effort for acquiring the required images, further research is necessary to effectively store, handle, and analyze such large numbers of images [143].
Finding-3: Most studies used images with plain background avoiding segmentation
Most analyzed images in the studies were taken under simplified conditions (e.g., one mature leaf per image on plain background). If the object of interest is imaged against a plain background, the often necessary segmentation in order to distinguish foreground and background can be performed fully automated with high accuracy. Segmenting the leaf with natural background is particularly difficult when the background shows a significant amount of overlapping green elements. Towards real-life application, studies should utilize more realistic images containing multiple leafs, having a complex background, and been taken in different lighting conditions.
Finding-4: Main research focus on leaf analysis for plant identification
Except for one study [68], proposed approaches for plant identification are based on the analysis of only one of the plant’s organs. The most widely studied organs are leaf followed by flower. Reasons for focusing on leaves in plant identification are that leaves are available for examination throughout most of the year, that they are easy to find and to collect, and that they can easily be imaged compared to other plant morphological structures, such as flowers, barks, or fruits [33]. These characteristics simplify the data acquisition process. In contrast, traditional keys often utilize flowers or their parts to characterize species, but flowers are typically only available for a few weeks of the year during the blooming season. A smaller number of 13 primary studies proposed to identify species solely based on flowers. Researchers even argue [29] that machine learning based flower classification is one of the most difficult tasks in computer vision. If captured in their habitat, images of flowers greatly vary due to lighting conditions, time, date, and weather. Due to being a complex 3D object, there is also variation in viewpoint, occlusions, and scale of flower images compared to leaf images. All these problems make flower-based classification a challenging task. On the positive side, the segmentation of typically colored flowers in their natural habitat can be considered an easier task than the segmentation of leaves in the same setting.
Finding-5: Shape is the dominant feature for plant identification
Shape analysis of leaves has received by far the most attention among the primary studies. Leaf shape is considered more heritable and often favored over leaf geometry since this is largely influenced by a plant’s habitat. Although species’ leaves differ in detail, differences across species are often obvious to humans. Most text-based taxonomic keys involve leaf shape for discrimination. Additionally, leave shape is among the easiest aspect for automated extraction assuming that the leaf can easily be separated from a plain background. Shape analysis of flowers has also been considered for species identification. For example, the shape of individual petals, their configuration, and the overall shape of a flower can be used to distinguish between flowers and eventually species. However, the petals are often soft and flexible making them bend, curl, or twist; which lets the shape of the same flower appear very different. The difficulty of describing the shape of flowers is increased by natural deformations. Furthermore, a flower’s shape typically also changes with its age to the extent where petals even fall off [104].
Finding-6: Multi-feature fusion facilitates higher classification accuracy
Several primary studies showed the benefits of multi-feature fusion in terms of a gain in classification accuracy [10, 16, 23, 65, 116]. Although texture is often overshadowed by shape as the dominant or more discriminative feature for leaf and flower classification, it is nevertheless of high significance as it provides complementary information. This review revealed that texture is the feature that highly influenced the identification rate. In particular, texture captures leaf venation information as well as any eventual directional characteristics, and more generally allows describing fine nuances or micro-texture at the leaf or flower surface [148]. Color is not expected to be as discriminative as shape or texture for leaf analysis, since most leaves are colored in some shade of green that also vary greatly under different illumination [148]. In addition to the low inter-class variability in terms of color, there is also high intra-class variability, i.e., even the colors of leaves belonging to the same species or even plant can present a wide range of colors depending on the season and the plant’s overall condition (e.g., nutrient and water). For example, many dried leaves turn brown, so color is not usually a useful feature for leaf analysis. Regardless of the aforementioned complications, color can still contribute to plant identification, considering leaves that exhibit an extraordinary hue [148]. However, further investigation on leaf color is necessary. For flower analysis color plays a more important role. Color as feature is also known for its low dimensionality and low computational complexity thus making it convenient for real-time applications. Despite being a useful feature of leaves in traditional species identification, leaf margin has seen little use in automated species identification being studied by only 8 out of 106 studies. Reasons may be that teeth are not present for all plant species, that teeth can easily be damaged or get lost before and after specimen collection, and that it is difficult to acquire quantitative margin measurements automatically [34]. Also vein structure as a leaf-specific feature plays a subordinate role and should be explored more deeply in the future.
Finding-7: Contour-based shape description more popular than region-based description
Research on contour-based shape description is more active than that on region-based shape description. A possible explanation is that humans discriminate shapes mainly by their contour features. A major difficulty for contour-based methods is the problem of ’self-intersection’. This is where part of a leaf overlaps other parts of the same leaf and can result in errors when tracing the outline. Self-intersection occurs especially with lobed leaves, and may not even occur consistently for a particular species. Furthermore, the performance of contour-based approaches is often sensitive to the quality of the contour extracted in a segmentation process, which naturally complicates distinguishing between species with very similar shapes. However, region-based methods are more robust as they use the entire shape information. These methods can cope well with shape defection which arises due to missing shape part or occlusion.
Finding-8: Cross-comparing and evaluating proposed methods is very difficult
For the analysis of experimental results, researchers use different datasets, the size of samples is different per dataset as well as the reported evaluation metrics (e.g., rank-1 accuracy, rank-10 accuracy, precision). This makes it difficult to compare the performance of different approaches. Efficient evaluation criteria are necessary for plant recognition. Using the same evaluation criteria makes the evaluation of proposed methods more objectively.
Finding-9: LeafSnap, Pl@ntNet, and Folia only publicly available implementations
Some of the proposed approaches have been implemented as web, mobile, or desktop application and have initiated interactions between computer scientists and end-users, such as ecologists, botanists, educators, land managers, and the general public [71]. Mobile applications offering image-based identification services are particularly promising for setting-up massive ecological monitoring systems, involving many contributors at low cost. One of the first system in this domain was the LeafSnap application (iOS), supporting a few hundred tree species of North America. This was followed by other applications, such as Pl@ntNet (iOS, Android, and web) and Folia (iOS) dedicated to the European flora [70]. As promising as these applications are, their performances are still far from the requirements of a real-world social-based ecological surveillance scenario. Allowing the mass of citizens to produce accurate plant observations requires to equip them with much more accurate identification tools [50].
References
Aakif A, Khan MF (2015) Automatic classification of plants based on their leaves. Biosyst Eng 139:66–75. doi:10.1016/j.biosystemseng.2015.08.003
Abdel-Hakim AE, Farag AA (2006) Csift: a sift descriptor with color invariant characteristics. In: 2006 IEEE computer society conference on computer vision and pattern recognition (CVPR’06), vol 2. IEEE, pp 1978–1983. doi:10.1109/CVPR.2006.95
Apriyanti D, Arymurthy A, Handoko L (2013) Identification of orchid species using content-based flower image retrieval. In: 2013 International conference on computer, control, informatics and its applications (IC3INA), pp 53–57. doi:10.1109/IC3INA.2013.6819148
Aptoula E, Yanikoglu B (2013) Morphological features for leaf based plant recognition. In: 2013 20th IEEE international conference on image processing (ICIP), pp 1496–1499. doi:10.1109/ICIP.2013.6738307
Arun Priya C, Balasaravanan T, Thanamani A (2012) An efficient leaf recognition algorithm for plant classification using support vector machine. In: 2012 International conference on pattern recognition, informatics and medical engineering (PRIME), pp 428–432. doi:10.1109/ICPRIME.2012.6208384
Asrani K, Jain R (2013) Contour based retrieval for plant species. Int J Image Graph Signal Process 5(9):29–35. doi:10.5815/ijigsp.2013.09.05
Backes A, Bruno O (2009) Plant leaf identification using multi-scale fractal dimension. In: Foggia P, Sansone C, Vento M (eds) Image analysis and processing ICIAP 2009, lecture notes in computer science, vol 5716. Springer, Berlin, pp 143–150. doi:10.1007/978-3-642-04146-4_17
Backes AR, Casanova D, Bruno OM (2009) Plant leaf identification based on volumetric fractal dimension. Int J Pattern Recognit Artif Intell 23(06):1145–1160. doi:10.1142/S0218001409007508
Bay H, Tuytelaars T, Van Gool L (2006) Surf: speeded up robust features. In: European conference on computer vision. Springer, Berlin, pp 404–417. doi:10.1007/11744023_32
Beghin T, Cope J, Remagnino P, Barman S (2010) Shape and texture based plant leaf classification. In: Blanc-Talon J, Bone D, Philips W, Popescu D, Scheunders P (eds) Advanced concepts for intelligent vision systems, lecture notes in computer science, vol 6475. Springer, Berlin, pp 345–353. doi:10.1007/978-3-642-17691-3_32
Belhumeur PN, Chen D, Feiner S, Jacobs DW, Kress WJ, Ling H, Lopez I, Ramamoorthi R, Sheorey S, White S et al (2008) Searching the world’s herbaria: a system for visual identification of plant species. In: Computer Vision–ECCV 2008. Lecture notes in computer science, vol 5305. Springer, Berlin, pp 116–129. doi:10.1007/978-3-540-88693-8_9
Belongie S, Malik J, Puzicha J (2002) Shape matching and object recognition using shape contexts. IEEE Trans Pattern Anal Mach Intell 24(4):509–522. doi:10.1109/34.993558
Bridle H, Vrieling A, Cardillo M, Araya Y, Hinojosa L (2013) Preparing for an interdisciplinary future: a perspective from early-career researchers. Futures 53:22–32. doi:10.1016/j.futures.2013.09.003
Bruno OM, de Oliveira Plotze R, Falvo M, de Castro M (2008) Fractal dimension applied to plant identification. Information Sciences 178(12):2722–2733. doi:10.1016/j.ins.2008.01.023
Caballero C, Aranda MC (2010) Plant species identification using leaf image retrieval. In: Proceedings of the ACM international conference on image and video retrieval (CIVR’10). ACM, New York, NY, USA, pp 327–334. doi:10.1145/1816041.1816089
Caglayan A, Guclu O, Can A (2013) A plant recognition approach using shape and color features in leaf images. In: Petrosino A (ed) Image analysis and processing ICIAP 2013, lecture notes in computer science, vol 8157. Springer, Berlin, pp 161–170. doi:10.1007/978-3-642-41184-7_17
Casanova D, de Mesquita S, Junior JJ, Bruno OM (2009) Plant leaf identification using gabor wavelets. Int J Imaging Syst Technol 19(3):236–243. doi:10.1002/ima.20201
Cerutti G, Tougne L, Coquin D, Vacavant A et al (2013a) Curvature-scale-based contour understanding for leaf margin shape recognition and species identification. In: Proceedings of the international conference on computer vision theory and applications, vol 1, pp 277–284
Cerutti G, Tougne L, Mille J, Vacavant A, Coquin D (2013b) A model-based approach for compound leaves understanding and identification. In: 2013 20th IEEE international conference on image processing (ICIP), pp 1471–1475. doi:10.1109/ICIP.2013.6738302
Cerutti G, Tougne L, Mille J, Vacavant A, Coquin D (2013c) Understanding leaves in natural images? A model-based approach for tree species identification. Comput Vision Image Underst 117(10):1482–1501. doi:10.1016/j.cviu.2013.07.003
Cerutti G, Tougne L, Coquin D, Vacavant A (2014) Leaf margins as sequences: a structural approach to leaf identification. Pattern Recognit Lett 49:177–184. doi:10.1016/j.patrec.2014.07.016
Chaki J, Parekh R (2012) Designing an automated system for plant leaf recognition. Int J Adv Eng Technol 2(1):149–158
Chaki J, Parekh R, Bhattacharya S (2015a) Plant leaf recognition using texture and shape features with neural classifiers. Pattern Recognit Lett 58:61–68. doi:10.1016/j.patrec.2015.02.010
Chaki J, Parekh R, Bhattacharya S (2015b) Recognition of whole and deformed plant leaves using statistical shape features and neuro-fuzzy classifier. In: 2015 IEEE 2nd international conference on recent trends in information systems (ReTIS), pp 189–194. doi:10.1109/ReTIS.2015.7232876
Charters J, Wang Z, Chi Z, Tsoi AC, Feng D (2014) Eagle: a novel descriptor for identifying plant species using leaf lamina vascular features. In: 2014 IEEE international conference on multimedia and expo workshops (ICMEW), pp 1–6. doi:10.1109/ICMEW.2014.6890557
Chathura Priyankara H, Withanage D (2015) Computer assisted plant identification system for android. In: 2015 Moratuwa engineering research conference (MERCon), pp 148–153. doi:10.1109/MERCon.2015.7112336
Che Hussin N, Jamil N, Nordin S, Awang K (2013) Plant species identification by using scale invariant feature transform (sift) and grid based colour moment (gbcm). In: 2013 IEEE conference on open systems (ICOS), pp 226–230. doi:10.1109/ICOS.2013.6735079
Chen Y, Lin P, He Y (2011) Velocity representation method for description of contour shape and the classification of weed leaf images. Biosyst Eng 109(3):186–195. doi:10.1016/j.biosystemseng.2011.03.004
Cho SY (2012) Content-based structural recognition for flower image classification. In: 2012 7th IEEE conference on industrial electronics and applications (ICIEA), pp 541–546. doi:10.1109/ICIEA.2012.6360787
Cho SY, Lim PT (2006) A novel virus infection clustering for flower images identification. In: 18th International conference on pattern recognition, 2006 (ICPR 2006), vol 2, pp 1038–1041. doi:10.1109/ICPR.2006.144
Cope J, Remagnino P (2012) Classifying plant leaves from their margins using dynamic time warping. In: Blanc-Talon J, Philips W, Popescu D, Scheunders P, Zemc KP (eds) Advanced concepts for intelligent vision systems, lecture notes in computer science, vol 7517. Springer, Berlin pp 258–267. doi:10.1007/978-3-642-33140-4_23
Cope J, Remagnino P, Barman S, Wilkin P (2010) Plant texture classification using gabor co-occurrences. In: Bebis G, Boyle R, Parvin B, Koracin D, Chung R, Hammound R, Hussain M, Kar-Han T, Crawfis R, Thalmann D, Kao D, Avila L (eds) Advances in visual computing, lecture notes in computer science, vol 6454. Springer, Berlin pp 669–677. doi:10.1007/978-3-642-17274-8_65
Cope JS, Corney D, Clark JY, Remagnino P, Wilkin P (2012) Plant species identification using digital morphometrics: a review. Expert Syst Appl 39(8):7562–7573. doi:10.1016/j.eswa.2012.01.073
Corney DP, Tang HL, Clark JY, Hu Y, Jin J (2012) Automating digital leaf measurement: the tooth, the whole tooth, and nothing but the tooth. PLoS ONE 7(8):e42112. doi:10.1371/journal.pone.0042112
Dayrat B (2005) Towards integrative taxonomy. Biol J Linn Soc 85(3):407–415. doi:10.1111/j.1095-8312.2005.00503.x
de M Sa Junior J, Backes A, Cortez P (2013) Plant leaf classification using color on a gravitational approach. In: Wilson R, Hancock E, Bors A, Smith W (eds) Computer analysis of images and patterns, lecture notes in computer science, vol 8048. Springer, Berlin, pp 258–265. doi:10.1007/978-3-642-40246-3_32
de M Sa Junior J, Backes AR, Cortez P (2013) Gravitational based texture roughness for plant leaf identification. In: Wilson R, Hancock E, Bors A, Smith W (eds) Computer analysis of images and patterns, lecture notes in computer science, vol 8048. Springer, Berlin, pp 416–423. doi:10.1007/978-3-642-40246-3_52
Du JX, Wang XF, Gu X (2005) Shape matching and recognition base on genetic algorithm and application to plant species identification. In: Huang DS, Zhang XP, Huang GB (eds) Advances in intelligent computing, lecture notes in computer science, vol 3644. Springer, Berlin, pp 282–290. doi:10.1007/11538059_30
Du JX, Huang DS, Wang XF, Gu X (2006) Computer-aided plant species identification (capsi) based on leaf shape matching technique. Trans Inst Meas Control 28(3):275–285. doi:10.1191/0142331206tim176oa
Du JX, Wang XF, Zhang GJ (2007) Leaf shape based plant species recognition. Appl Math Comput 185(2):883–893. doi:10.1016/j.amc.2006.07.072
Du M, Wang X (2011) Linear discriminant analysis and its application in plant classification. In: 2011 Fourth international conference on information and computing (ICIC), pp 548–551. doi:10.1109/ICIC.2011.147
Du M, Zhang S, Wang H (2009) Supervised isomap for plant leaf image classification. In: Huang DS, Jo KH, Lee HH, Kang HJ, Bevilacqua V (eds) Emerging intelligent computing technology and applications. With aspects of artificial intelligence, lecture notes in computer science, vol 5755. Springer, Berlin pp 627–634. doi:10.1007/978-3-642-04020-7_67
Elhariri E, El-Bendary N, Hassanien A (2014) Plant classification system based on leaf features. In: 2014 9th International conference on computer engineering systems (ICCES), pp 271–276. doi:10.1109/ICCES.2014.7030971
Ellis B, Daly DC, Hickey LJ, Johnson KR, Mitchell JD, Wilf P, Wing SL (2009) Manual of leaf architecture. Cornell University Press, Ithaca. ISBN: 978-0-8014-7518-4
Florindo J, Backes A, Bruno O (2010) Leaves shape classification using curvature and fractal dimension. In: Elmoataz A, Lezoray O, Nouboud F, Mammass D, Meunier J (eds) Image and signal processing, lecture notes in computer science, vol 6134. Springer, Berlin pp 456–462. doi:10.1007/978-3-642-13681-8_53
Fotopoulou F, Laskaris N, Economou G, Fotopoulos S (2013) Advanced leaf image retrieval via multidimensional embedding sequence similarity (mess) method. Pattern Anal Appl 16(3):381–392. doi:10.1007/s10044-011-0254-6
Gaston KJ, O’Neill MA (2004) Automated species identification: why not? Philos Trans R Soc Lond B Biol Sci 359(1444):655–667. doi:10.1098/rstb.2003.1442
Ghasab MAJ, Khamis S, Mohammad F, Fariman HJ (2015) Feature decision-making ant colony optimization system for an automated recognition of plant species. Expert Syst Appl 42(5):2361–2370. doi:10.1016/j.eswa.2014.11.011
Goëau H, Joly A, Bonnet P, Bakic V, Barthélémy D, Boujemaa N, Molino JF (2013) The image CLEF 2013 plant identification task. In: Proceedings of the 2nd ACM international workshop on multimedia analysis for ecological data (MAED’13). ACM, New York, pp 23–28. doi:10.1145/2509896.2509902
Goëau H, Joly A, Bonnet P, Selmi S, Molino JF, Barthélémy D, Boujemaa N (2014) Lifeclef plant identification task 2014. In: Working notes for CLEF 2014 conference, Sheffield, UK, September 15–18, 2014, CEUR-WS, pp 598–615
Gonzalez RC, Woods RE (2007) Digital image processing, 3rd edn. Pearson Prentice-Hall Inc, NJ. ISBN: 978-0131687288
Govaerts R (2001) How many species of seed plants are there? Taxon 50(4):1085–1090. doi:10.2307/1224723
Gu X, Du JX, Wang XF (2005) Leaf recognition based on the combination of wavelet transform and Gaussian interpolation. In: Huang DS, Zhang XP, Huang GB (eds) Advances in intelligent computing, lecture notes in computer science, vol 3644. Springer, Berlin, pp 253–262. doi:10.1007/11538059_27
Gwo CY, Wei CH, Li Y (2013) Rotary matching of edge features for leaf recognition. Comput Electron Agric 91:124–134. doi:10.1016/j.compag.2012.12.005
Haralick RM (1979) Statistical and structural approaches to texture. Proc IEEE 67(5):786–804. doi:10.1109/PROC.1979.11328
Hearn DJ (2009) Shape analysis for the automated identification of plants from images of leaves. Taxon 58(3):934–954
Hong SW, Choi L (2012) Automatic recognition of flowers through color and edge based contour detection. In: 2012 3rd International conference on image processing theory, tools and applications (IPTA), pp 141–146. doi:10.1109/IPTA.2012.6469535
Hossain J, Amin M (2010) Leaf shape identification based plant biometrics. In: 2010 13th International conference on computer and information technology (ICCIT), pp 458–463. doi:10.1109/ICCITECHN.2010.5723901
Hsiao JK, Kang LW, Chang CL, Lin CY (2014) Comparative study of leaf image recognition with a novel learning-based approach. In: 2014 Science and information conference (SAI), pp 389–393. doi:10.1109/SAI.2014.6918216
Hsu TH, Lee CH, Chen LH (2011) An interactive flower image recognition system. Multimed Tools Appl 53(1):53–73. doi:10.1007/s11042-010-0490-6
Hu MK (1962) Visual pattern recognition by moment invariants. Inf Theory IRE Trans 8(2):179–187. doi:10.1109/TIT.1962.1057692
Hu R, Jia W, Ling H, Huang D (2012) Multiscale distance matrix for fast plant leaf recognition. Image Process IEEE Trans 21(11):4667–4672. doi:10.1109/TIP.2012.2207391
Huang P, Dai S, Lin P (2006) Texture image retrieval and image segmentation using composite sub-band gradient vectors. J Vis Commun Image Represent 17(5):947–957. doi:10.1016/j.jvcir.2005.08.005
Huang RG, Jin SH, Kim JH, Hong KS (2009) Flower image recognition using difference image entropy. In: Proceed the 7th international conference on advances in mobile computing and multimedia (MoMM’09). ACM, New York, pp 618–621. doi:10.1145/1821748.1821868
Ji-Xiang D, Zhai CM, Wang QP (2013) Recognition of plant leaf image based on fractal dimension features. Neurocomputing 116:150–156. doi:10.1016/j.neucom.2012.03.028
Jin T, Hou X, Li P, Zhou F (2015) A novel method of automatic plant species identification using sparse representation of leaf tooth features. PLoS ONE 10(10):e0139482. doi:10.1371/journal.pone.0139482
Jobin A, Nair MS, Tatavarti R (2012) Plant identification based on fractal refinement technique (FRT). Procedia Technol 6:171–179. doi:10.1016/j.protcy.2012.10.021
Joly A, Goëau H, Bonnet P, Bakić V, Barbe J, Selmi S, Yahiaoui I, Carré J, Mouysset E, Molino JF et al (2014a) Interactive plant identification based on social image data. Ecol Inform 23:22–34. doi:10.1016/j.ecoinf.2013.07.006
Joly A, Müller H, Goëau H, Glotin H, Spampinato C, Rauber A, Bonnet P, Vellinga WP, Fisher B (2014) LifeCLEF: multimedia life species identification. In: International workshop on environmental multimedia retrieval 2014, Glasgow
Joly A, Goëau H, Glotin H, Spampinato C, Bonnet P, Vellinga WP, Planqué R, Rauber A, Palazzo S, Fisher B et al (2015) Lifeclef 2015: multimedia life species identification challenges. In: Experimental IR meets multilinguality, multimodality, and interaction. Proceedings of the 6th international conference of the CLEF Association, CLEF'15, Toulouse, France, September 8–11, 2015. Lecture notes in computer science, vol 9283. Springer, Berlin, pp 462–483. doi:10.1007/978-3-319-24027-5
Joly A, Goëau H, Champ J, Dufour-Kowalski S, Müller H, Bonnet P (2016) Crowdsourcing biodiversity monitoring: how sharing your photo stream can sustain our planet. In: Proceedings of the 2016 ACM on Multimedia Conference (MM’16). ACM, New York, pp 958–967. doi:10.1145/2964284.2976762
Kadir A, Nugroho LE, Susanto A, Santosa PI (2011) A comparative experiment of several shape methods in recognizing plants. Int J Comput Sci Inform Technol 3(3). doi:10.5121/ijcsit.2011.3318
Kalyoncu C, Toygar Ö (2015) Geometric leaf classification. Comput Vis Image Underst 133:102–109. doi:10.1016/j.cviu.2014.11.001
Kebapci H, Yanikoglu B, Unal G (2010) Plant image retrieval using color, shape and texture features. Comput J 54:1475–1490. doi:10.1093/comjnl/bxq037
Kitchenham B (2004) Procedures for performing systematic reviews, Technical Report TR/SE-0401, vol 33. Keele University, Keele, pp 1–26. ISSN:1353-7776
Kumar N, Belhumeur P, Biswas A, Jacobs D, Kress W, Lopez I, Soares J (2012) Leafsnap: a computer vision system for automatic plant species identification. In: Fitzgibbon A, Lazebnik S, Perona P, Sato Y, Schmid C (eds) Computer vision–ECCV 2012. Lecture notes in computer science, vol 7573. Springer, Berlin, pp 502–516. doi:10.1007/978-3-642-33709-3_36
Laga H, Kurtek S, Srivastava A, Golzarian M, Miklavcic S (2012) A riemannian elastic metric for shape-based plant leaf classification. In: 2012 International conference on digital image computing techniques and applications (DICTA), pp 1–7. doi:10.1109/DICTA.2012.6411702
Larese M, Craviotto R, Arango M, Gallo C, Granitto P (2012) Legume identification by leaf vein images classification. In: Alvarez L, Mejail M, Gomez L, Jacobo J (eds) Progress in pattern recognition, image analysis, computer vision, and applications, lecture notes in computer science, vol 7441. Springer, Berlin, pp 447–454. doi:10.1007/978-3-642-33275-3_55
Larese MG, Bay AE, Craviotto RM, Arango MR, Gallo C, Granitto PM (2014a) Multiscale recognition of legume varieties based on leaf venation images. Expert Syst Appl 41(10):4638–4647. doi:10.1016/j.eswa.2014.01.029
Larese MG, NamÌas R, Craviotto RM, Arango MR, Gallo C, Granitto PM (2014b) Automatic classification of legumes using leaf vein image features. Pattern Recognit 47(1):158–168. doi:10.1016/j.patcog.2013.06.012
Lavania S, Matey PS (2014) Leaf recognition using contour based edge detection and sift algorithm. In: 2014 IEEE international conference on computational intelligence and computing research (ICCIC), pp 1–4. doi:10.1109/ICCIC.2014.7238345
Lee CL, Chen SY (2006) Classification of leaf images. Int J Imaging Syst Technol 16(1):15–23. doi:10.1002/ima.20063
Ling H, Jacobs DW (2007) Shape classification using the inner-distance. IEEE Trans Pattern Anal Mach Intell 29(2):286–299. doi:10.1109/TPAMI.2007.41
Liu C, Yuen J, Torralba A, Sivic J, Freeman WT (2008) Sift flow: dense correspondence across different scenes. In: European conference on computer vision, lecture notes in computer science, vol 5304. Springer, Berlin, pp 28–42. doi:10.1007/978-3-540-88690-7_3
Liu H, Coquin D, Valet L, Cerutti G (2014) Leaf species classification based on a botanical shape sub-classifier strategy. In: 2014 22nd International conference on pattern recognition (ICPR), pp 1496–1501. doi:10.1109/ICPR.2014.266
Lowe DG (2004) Distinctive image features from scale-invariant keypoints. Int J Comput Vis 60(2):91–110. doi:10.1023/B:VISI.0000029664.99615.94
Ma LH, Zhao ZQ, Wang J (2013) ApLeafis: an android-based plant leaf identification system. In: Huang DS, Bevilacqua V, Figueroa J, Premaratne P (eds) Intelligent computing theories, lecture notes in computer science, vol 7995. Springer, Berlin, pp 106–111. doi:10.1007/978-3-642-39479-9_13
MacLeod N, Benfield M, Culverhouse P (2010) Time to automate identification. Nature 467(7312):154–155. doi:10.1038/467154a
Mohanty P, Pradhan AK, Behera S, Pasayat AK (2015) A real time fast non-soft computing approach towards leaf identification. In: 2014 Proceedings of the 3rd international conference on frontiers of intelligent computing: theory and applications (FICTA). Advances in Intelligent Systems and Computing, vol 327. Springer, Berlin, pp 815–822. doi:10.1007/978-3-319-11933-5_92
Mora C, Tittensor DP, Adl S, Simpson AG, Worm B (2011) How many species are there on Earth and in the ocean? PLoS Biol 9(8):e1001127. doi:10.1371/journal.pbio.1001127
Mouine S, Yahiaoui I, Verroust-Blondet A (2012) Advanced shape context for plant species identification using leaf image retrieval. In: Proceedings of the 2nd ACM international conference on multimedia retrieval (ICMR’12), vol 49. ACM, New York, pp 1–49. doi:10.1145/2324796.2324853
Mouine S, Yahiaoui I, Verroust-Blondet A (2013a) Combining Leaf Salient Points and Leaf Contour Descriptions for Plant Species Recognition. In: Kamel M, Campilho A (eds) Image analysis and recognition, lecture notes in computer science, vol 7950. Springer, Berlin, pp 205–214. doi:10.1007/978-3-642-39094-4_24
Mouine S, Yahiaoui I, Verroust-Blondet A (2013b) Plant species recognition using spatial correlation between the leaf margin and the leaf salient points. In: 2013 20th IEEE international conference on image processing (ICIP), pp 1466–1470. doi:10.1109/ICIP.2013.6738301
Mouine S, Yahiaoui I, Verroust-Blondet A (2013c) A shape-based approach for leaf classification using multiscaletriangular representation. In: Proceedings of the 3rd ACM conference on international conference on multimedia retrieval (ICMR’13). ACM, New York, NY, USA, pp 127–134. doi:10.1145/2461466.2461489
Murphy GE, Romanuk TN (2014) A meta-analysis of declines in local species richness from human disturbances. Ecol Evol 4(1):91–103. doi:10.1002/ece3.909
Mzoughi O, Yahiaoui I, Boujemaa N (2012) Petiole shape detection for advanced leaf identification. In: 2012 19th IEEE international conference on image processing (ICIP), pp 1033–1036. doi:10.1109/ICIP.2012.6467039
Mzoughi O, Yahiaoui I, Boujemaa N, Zagrouba E (2013a) Advanced tree species identification using multiple leaf parts image queries. In: 2013 20th IEEE international conference on image processing (ICIP), pp 3967–3971. doi:10.1109/ICIP.2013.6738817
Mzoughi O, Yahiaoui I, Boujemaa N, Zagrouba E (2013b) Automated semantic leaf image categorization by geometric analysis. In: 2013 IEEE international conference on multimedia and expo (ICME), pp 1–6. doi:10.1109/ICME.2013.6607636
Mzoughi O, Yahiaoui I, Boujemaa N, Zagrouba E (2016) Semantic-based automatic structuring of leaf images for advanced plant species identification. Multimed Tools Appl. 75(3):1615–1646. doi:10.1007/s11042-015-2603-8
Nam Y, Hwang E (2005) A shape-based retrieval scheme for leaf images. In: Ho YS, Kim H (eds) Advances in multimedia information processing—(PCM 2005), lecture notes in computer science, vol 3767. Springer, Berlin, pp 876–887. doi:10.1007/11581772_77
Nam Y, Hwang E, Kim D (2005) CLOVER: a mobile content-based leaf image retrieval system. In: Fox E, Neuhold E, Premsmit P, Wuwongse V (eds) Digital libraries: implementing strategies and sharing experiences, lecture notes in computer science, vol 3815. Springer, Berlin, pp 139–148. doi:10.1007/11599517_16
Nesaratnam R J, Bala Murugan C (2015) Identifying leaf in a natural image using morphological characters. In: 2015 International conference on innovations in information, embedded and communication systems (ICIIECS), pp 1–5. doi:10.1109/ICIIECS.2015.7193115
Nguyen QK, Le TL, Pham NH (2013) Leaf based plant identification system for android using surf features in combination with bag of words model and supervised learning. In: 2013 International conference on advanced technologies for communications (ATC), pp 404–407. doi:10.1109/ATC.2013.6698145
Nilsback ME, Zisserman A (2006) A visual vocabulary for flower classification. In: 2006 IEEE computer society conference on computer vision and pattern recognition, vol 2, pp 1447–1454. doi:10.1109/CVPR.2006.42
Nilsback ME, Zisserman A (2008) Automated flower classification over a large number of classes. In: ICVGIP. IEEE, pp 722–729. doi:10.1109/ICVGIP.2008.47
Novotny P, Suk T (2013) Leaf recognition of woody species in central europe. Biosyst Eng 115(4):444–452. doi:10.1016/j.biosystemseng.2013.04.007
Park J, Hwang E, Nam Y (2008) Utilizing venation features for efficient leaf image retrieval. J Syst Softw 81(1):71–82. doi:10.1016/j.jss.2007.05.001
Park JK, Hwang E, Nam Y (2006) A venation-based leaf image classification scheme. In: Ng H, Leong MK, Kan MY, Ji D (eds) Information retrieval technology, lecture notes in computer science, vol 4182, Springer, Berlin, pp 416–428. doi:10.1007/11880592_32
Pautasso M (2013) Ten simple rules for writing a literature review. PLoS Comput Biol 9(7):e1003149. doi:10.1371/journal.pcbi.1003149
Pauwels EJ, de Zeeuw PM, Ranguelova EB (2009) Computer-assisted tree taxonomy by automated image recognition. Eng Appl Artif Intell 22(1):26–31. doi:10.1016/j.engappai.2008.04.017
Pham NH, Le TL, Grard P, Nguyen VN (2013) Computer aided plant identification system. In: 2013 International conference on computing, management and telecommunications (ComManTel), pp 134–139. doi:10.1109/ComManTel.2013.6482379
Phyu KH, Kutics A, Nakagawa A (2012) Self-adaptive feature extraction scheme for mobile image retrieval of flowers. In: 2012 Eighth international conference on signal image technology and internet based systems (SITIS), pp 366–373. doi:10.1109/SITIS.2012.60
Pimm SL, Jenkins CN, Abell R, Brooks TM, Gittleman JL, Joppa LN, Raven PH, Roberts CM, Sexton JO (2014) The biodiversity of species and their rates of extinction, distribution, and protection. Science 344(6187). doi:10.1126/science.1246752
Prasad S, Kudiri KM, Tripathi RC (2011) Relative sub-image based features for leaf recognition using support vector machine. In: Proceedings of the 2011 international conference on communication, computing & security, ACM, New York, NY, USA (ICCCS ’11), pp 343–346. doi:10.1145/1947940.1948012
Prasad S, Kumar P, Tripathi R (2011) Plant leaf species identification using curvelet transform. In: 2011 2nd international conference on computer and communication technology (ICCCT), pp 646–652. doi:10.1109/ICCCT.2011.6075212
Prasad S, Peddoju S, Ghosh D (2013) Mobile plant species classification: a low computational aproach. In: 2013 IEEE second international conference on image information processing (ICIIP), pp 405–409. doi:10.1109/ICIIP.2013.6707624
Qi W, Liu X, Zhao J (2012) Flower classification based on local and spatial visual cues. In: 2012 IEEE international conference on computer science and automation engineering (CSAE), vol 3, pp 670–674. doi:10.1109/CSAE.2012.6273040
Rashad M, el Desouky B, Khawasik MS (2011) Plants images classification based on textural features using combined classifier. Int J Comput Sci Inf Technol (IJCSIT) 3(4):93–100. doi:10.5121/ijcsit.2011.3407
Rejeb Sfar A, Boujemaa N, Geman D (2013) Identification of plants from multiple images and botanical idkeys. In: Proceedings of the 3rd ACM conference on international conference on multimedia retrieval, ACM, New York, NY, USA (ICMR’13), pp 191–198. doi:10.1145/2461466.2461499
Rejeb Sfar A, Boujemaa N, Geman D (2015) Confidence sets for fine-grained categorization and plant species identification. Int J Comput Vis 111(3):255–275. doi:10.1007/s11263-014-0743-3
Ren XM, Wang XF, Zhao Y (2012) An efficient multi-scale overlapped block LBP approach for leaf image recognition. In: Proceedings of the 8th international conference on intelligent computing theories and applications (ICIC’12). Springer, Berlin, pp 237–243. doi:10.1007/978-3-642-31576-3_31
Rossatto D, Casanova D, Kolb R, Bruno O (2011) Fractal analysis of leaf-texture properties as a tool for taxonomic and identification purposes: a case study with species from neotropical melastomataceae (miconieae tribe). Plant Syst Evol 291(1):103–116. doi:10.1007/s00606-010-0366-2
Rudall PJ (2007) Anatomy of flowering plants: an introduction to structure and development. Cambridge University Press, Cambridge. ISBN: 9780521692458
Santana FS, Costa AHR, Truzzi FS, Silva FL, Santos SL, Francoy TM, Saraiva AM (2014) A reference process for automating bee species identification based on wing images and digital image processing. Ecol Inf 24:248–260. doi:10.1016/j.ecoinf.2013.12.001
Scotland RW, Wortley AH (2003) How many species of seed plants are there? Taxon 52(1):101–104. doi:10.2307/3647306
Seeland M, Rzanny M, Alaqraa N, Thuille A, Boho D, Wäldchen J, Mäder P (2016) Description of flower colors for image based plant species classification. In: Proceedings of the 22nd German Color Workshop (FWS), Zentrum für Bild- und Signalverarbeitung e.V, Ilmenau, Germany, pp 145–154
Söderkvist O (2001) Computer vision classification of leaves from swedish trees. Master’s thesis, Department of Electrical Engineering, Computer Vision, Linköping University
Tan WN, Tan YF, Koo AC, Lim YP (2012) Petals shape descriptor for blooming flowers recognition. In: Fourth international conference on digital image processing (ICDIP 2012), international society for optics and photonics, pp 83,343K–83,343K. doi:10.1117/12.966367
Tan WN, Sem R, Tan YF (2014) Blooming flower recognition by using eigenvalues of shape features. In: Sixth International Conference on Digital Image Processing, International Society for Optics and Photonics, pp 91591R–91591R. doi:10.1117/12.2064504
Teng CH, Kuo YT, Chen YS (2009) Leaf segmentation, its 3D position estimation and leaf classification from a few images with very close viewpoints. In: Kamel M, Campilho A (eds) Image analysis and recognition, lecture notes in computer science, vol 5627. Springer, Berlin, pp 937–946. doi:10.1007/978-3-642-02611-9_92
Valliammal N, Geethalakshmi S (2011) Automatic recognition system using preferential image segmentation for leaf and flower images. Comput Sci Eng 1(4):13–25. doi:10.5121/cseij.2011.1402
Venkatesh S, Raghavendra R (2011) Local gabor phase quantization scheme for robust leaf classification. In: 2011 Third national conference on computer vision, pattern recognition, image processing and graphics (NCVPRIPG), pp 211–214. doi:10.1109/NCVPRIPG.2011.52
Wäldchen J, Thuille A, Seeland M, Rzanny M, Schulze ED, Boho D, Alaqraa N, Hofmann M, Mäder P (2016) Flora Incognita – Halbautomatische Bestimmung der Pflanzenarten Thüringens mit dem Smartphone. Landschaftspflege und Naturschutz in Thüringen 53(3):121–125
Wang B, Brown D, Gao Y, La Salle J (2013) Mobile plant leaf identification using smart-phones. In: 2013 20th IEEE international conference on image processing (ICIP), pp 4417–4421. doi:10.1109/ICIP.2013.6738910
Wang B, Brown D, Gao Y, Salle JL (2015) March: multiscale-arch-height description for mobile retrieval of leaf images. Inf Sci 302(0):132–148. doi:10.1016/j.ins.2014.07.028
Wang X, Liang J, Guo F (2014) Feature extraction algorithm based on dual-scale decomposition and local binary descriptors for plant leaf recognition. Digit Signal Process 34:101–107. doi:10.1016/j.dsp.2014.08.005
Wang XF, Du JX, Zhang GJ (2005) Recognition of leaf images based on shape features using a hypersphere classifier. In: Huang DS, Zhang XP, Huang GB (eds) Advances in intelligent computing, lecture notes in computer science, vol 3644. Springer, Berlin, pp 87–96. doi:10.1007/11538059_10
Wang XF, Huang DS, Du JX, Xu H, Heutte L (2008) Classification of plant leaf images with complicated background. Appl Math Comput 205(2):916–926. doi: 10.1016/j.amc.2008.05.108
Wang Z, Lu B, Chi Z, Feng D (2011) Leaf image classification with shape context and sift descriptors. In: 2011 International conference on digital image computing techniques and applications (DICTA), pp 650–654. doi:10.1109/DICTA.2011.115
Wang Z, Sun X, Ma Y, Zhang H, Ma Y, Xie W, Zhang Y (2014) Plant recognition based on intersecting cortical model. In: 2014 International joint conference on neural networks (IJCNN), pp 975–980. doi:10.1109/IJCNN.2014.6889656
Watcharabutsarakham S, Sinthupinyo W, Kiratiratanapruk K (2012) Leaf classification using structure features and support vector machines. In: 2012 6th International conference on new trends in information science and service science and data mining (ISSDM), pp 697–700
Wechsler H (1980) Texture analysis: a survey. Signal Proces 2(3):271–282. doi:10.1016/0165-1684(80)90024-9
Wu H, Wang L, Zhang F, Wen Z (2015) Automatic leaf recognition from a big hierarchical image database. Int J Intell Syst 30(8):871–886. doi:10.1002/int.21729
Wu S, Bao F, Xu E, Wang YX, Chang YF, Xiang QL (2007) A leaf recognition algorithm for plant classification using probabilistic neural network. In: 2007 IEEE international symposium on signal processing and information technology, pp 11–16. doi:10.1109/ISSPIT.2007.4458016
Xiao XY, Hu R, Zhang SW, Wang XF (2010) Hog-based approach for leaf classification. In: Proceedings of the advanced intelligent computing theories and applications, and 6th international conference on intelligent computing (ICIC’10). Springer, Berlin, pp 149–155. doi:10.1007/978-3-642-14932-0_19
Yahiaoui I, Mzoughi O, Boujemaa N (2012) Leaf shape descriptor for tree species identification. In: Proceedings of the 2012 IEEE International Conference on Multimedia and Expo, IEEE Computer Society, Washington, DC, USA (ICME ’12), pp 254–259, doi:10.1109/ICME.2012.130
Yang LW, Wang XF (2012) Leaf image recognition using fourier transform based on ordered sequence. In: Huang DS, Jiang C, Bevilacqua V, Figueroa J (eds) Intelligent computing technology, lecture notes in computer science, vol 7389. Springer, Berlin, pp 393–400. doi:10.1007/978-3-642-31588-6_51
Yanikoglu B, Aptoula E, Tirkaz C (2014) Automatic plant identification from photographs. Mach Vis Appl 25(6):1369–1383. doi:10.1007/s00138-014-0612-7
Zawbaa HM, Abbass M, Basha SH, Hazman M, Hassenian AE (2014) An automatic flower classification approach using machine learning algorithms. In: 2014 International conference on advances in computing, communications and informatics (ICACCI), IEEE, pp 895–901. doi:10.1109/ICACCI.2014.6968612
Zhai CM, xiang Du J (2008) Applying extreme learning machine to plant species identification. In: International conference on information and automation, 2008. ICIA 2008, pp 879–884. doi:10.1109/ICINFA.2008.4608123
Zhang D, Lu G (2004) Review of shape representation and description techniques. Pattern Recogn 37(1):1–19. doi:10.1016/j.patcog.2003.07.008
Zhang D, Wong A, Indrawan M, Lu G (2000) Content-based image retrieval using gabor texture features. IEEE Pacific-Rim conference on multimedia. University of Sydney, Australia, pp 392–395
Zhang D, Islam MM, Lu G (2012) A review on automatic image annotation techniques. Pattern Recognit 45(1):346–362. doi:10.1016/j.patcog.2011.05.013
Zhang L, Kong J, Zeng X, Ren J (2008) Plant species identification based on neural network. In: Fourth international conference on natural computation, 2008. ICNC ’08, vol 5, pp 90–94. doi:10.1109/ICNC.2008.253
Zhang S, Feng Y (2010) Plant leaf classification using plant leaves based on rough set. In: 2010 International conference on computer application and system modeling (ICCASM), vol 15, pp V15-521–V15-525. doi:10.1109/ICCASM.2010.5622528
Zhang S, Lei YK (2011) Modified locally linear discriminant embedding for plant leaf recognition. Neurocomput 74(14–15):2284–2290. doi:10.1016/j.neucom.2011.03.007
Zhang SW, Zhao MR, Wang XF (2012b) Plant classification based on multilinear independent component analysis. In: Proceedings of the 7th international conference on advanced intelligent computing theories and applications: with aspects of artificial intelligence (ICIC’11). Springer, Berlin, pp 484–490. doi:10.1007/978-3-642-25944-9_63
Zhao C, Chan SS, Cham WK, Chu L (2015) Plant identification using leaf shapes? A pattern counting approach. Pattern Recogn 48(10):3203–3215. doi:10.1016/j.patcog.2015.04.004
Zulkifli Z, Saad P, Mohtar I (2011) Plant leaf identification using moment invariants & general regression neural network. In: 2011 11th International conference on hybrid intelligent systems (HIS), pp 430–435. doi:10.1109/HIS.2011.6122144
Acknowledgements
Open access funding provided by Max Planck Society. We thank Markus Eisenbach, Tim Wengefeld, and Ronny Stricker from the Neuroinformatics and Cognitive Robotics Lab at the TU Ilmenau for their insightful comments on our manuscript. We are funded by the German Ministry of Education and Research (BMBF) Grants: 01LC1319A and 01LC1319B; the German Federal Ministry for the Environment, Nature Conservation, Building and Nuclear Safety (BMUB) Grant: 3514 685C19; and the Stiftung Naturschutz Thüringen (SNT) Grant: SNT-082-248-03/2014.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Wäldchen, J., Mäder, P. Plant Species Identification Using Computer Vision Techniques: A Systematic Literature Review. Arch Computat Methods Eng 25, 507–543 (2018). https://doi.org/10.1007/s11831-016-9206-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11831-016-9206-z