1 Introduction

Most studies on seakeeping have focused on developing theoretical and numerical models for investigating the complexity of fluid exerting hydrodynamic forces on the deformation of a structural component. This is because experiments are extremely costly and time-consuming, especially on the evaluation of individual ship designs. Numerical simulations coupled with enhanced computational power have thus become crucial for validating the theoretical predictions of hydrodynamics while providing useful insights for interpreting experimental results. Traditionally, linear and nonlinear strip theories (Kroukovsky and Jacobs, 1957) are widely employed in the assessment of potential hazards and risk factors that might harm a ship advancing in waves with an arbitrary forward speed and in the overall structural design in shipbuilding (Jensen et al., 2004).

In most linear cases, especially in low and moderately regular waves, linear methods adequately predict the vertical ship motion and wave-induced loads (Faltinsen et al., 1991), in which the problems of the boundary condition are generally solved through correction with the forward speed. This condition is commonly seen in the approach of the linear three-dimensional (3D) panel methods of Green’s function (Chapchap, 2015; Sun et al., 2018). Nevertheless, panel methods show limitations and drawbacks if they are used for analyzing the intricate geometrical estimation of the free surface, mitigation of extreme boundary-layer separation, and solving the free-surface Green’s theorem that often profoundly depends on multiplex equations (Cartwright et al., 2004). Likewise, ordinary linear strip theories, linear 3D methods, and potential flow are unsuitable for modeling large wave conditions where the ship motion would create breaking water on the surface. Thus, the fluid force must be nonlinearly treated (Lee et al., 2010).

For large wave conditions, methods coupling linear and nonlinear techniques have been used to resolve the nonlinearity in fluid force. For example, panel methods and time-domain strip theories have incorporated this coupling approach using Rankine sources to distribute particles over the hull surface (Lin et al., 2007) or Rankine panel methods to distribute particles across the keel and free surface (Huang et al., 1998). As a result, nonlinear effects are observed to be at low Froude numbers, with many discrepancies at high wave amplitudes (Fonseca and Guedes Soares, 2002). Such a limitation has been resolved via a combination of nonlinear and undirected methods comprising the Eulerian set procedure and Lagrangian trajectories for analyzing the fluid dynamics of a body, which has been shown to yield good projections for irregular ship motions and wave loads (Greco et al., 2013).

Nonlinear strip methods are mainly employed for estimating the navigation bearing of a ship advancing in waves with large amplitude motions that give rise to nonlinearities. Frequently, fully nonlinear methods presume that the wave flow is conservative with an independent line integral, continuous, and smooth with no interruption or smashing on the free surface (Chapchap, 2015). These nonlinear methods in seakeeping are generally analyzed via RANS codes. Incorporating viscous and rotational effects into RANS codes to analyze the flow and free surface waves makes it a popular nonlinear method (Tezdogen et al., 2015; Xie et al., 2019). However, nearly all these techniques are hinged on the boundary integral approach and inadequate in resolving the effect of massive water washing along with the deck, i.e., green water effect, fragmenting waves, or water spindrift. Therefore, this study used the meshfree technique of smoothed particle hydrodynamics (SPH) to address the Navier–Stokes problems for nonlinear wave structures (Cercos-Pita et al., 2015).

In this work, the Lagrangian method of SPH was implemented due to its meshless feature. The advantage of using this method is that the competitional domain is discretized into a set of interpolation points called particles, where each particle carries individual properties that evolve over time according to governing equations. This method can be adaptable and versatile with a simple algorithm for engineering applications (Tafuni, 2016; Leonardi et al., 2019). The two methods of applying incompressibility in SPH are enforcing true incompressibility and implementing small incompressibility, also known as weakly compressible SPH (WCSPH). The WCSPH is simple in concept and easy to implement in applications (Ramli et al., 2018; Dominguez et al., 2021). The application of SPH to water waves was started by Monaghan (1994) and then was further investigated by other researchers. The use of SPH has also been extended to study seakeeping analysis (Servan-Camas et al., 2016; Kawamura et al., 2016; Ma and Oka, 2019; Cheng et al., 2020). However, the analysis using SPH is still not common due to the high number of particles needed to capture details with good resolution. The method can be computationally costly, particularly in 3D applications. Therefore, a highly optimized open-source DualSPHysics code, which is based on the WCSPH that is run on a graphics processing unit (GPU), is widely used in many practical engineering problems (Altomare et al., 2020; O’Connor and Rogers, 2021; Pringgana et al., 2021). The GPU offers a high computing power in managing huge amounts of data with a significant reduction in the computation time.

The main objective of this work is to investigate an efficient approach in predicting the response amplitude operators (RAOs) of a floating structure over different wave conditions. Vertical displacements were examined using the WCSPH by DualSPHysics, where fluid and boundary domains were transformed into discrete, smoothed particles. Wave heights along the numerical wave tank (NWT) were verified before installing the floating structure, and damping zones were introduced to suppress the effect of reflective waves on the incident waves. Numerical results generated from this study were then compared with experimental data and numerical results from other studies. Consequently, this study showed that the motion responses from the WCSPH were analogous to the theoretical, experimental, and numerical results for various wave conditions along the structure.

2 Methodology of SPH

2.1 Interpolation of SPH

In SPH, numerical evaluations involve transforming the entire fluid domain in SPH into a finite set of discretely moving elements known as particles (Monaghan, 2006). These particles possess individual mass and various other properties, such as velocity, position, and pressure, which are computed through the interpolation process of neighboring particles (Dominguez et al., 2021). At any designated position vector, the estimated integral form of a function for a particle can be represented by Eq. (1):

$$\langle f({\varvec{x}})\rangle ={\int }_{\Omega }f\left({{\varvec{x}}}^{\boldsymbol{^{\prime}}}\right)\omega \left({\varvec{x}}-{{\varvec{x}}}^{\boldsymbol{^{\prime}}},h\right)\mathrm{d}{\varvec{x}}\boldsymbol{^{\prime}}$$
(1)

where \({\varvec{x}}\boldsymbol{^{\prime}}\) is another random position vector in the domain of integration Ω, \(\omega ({\varvec{x}}-{{\varvec{x}}}^{\boldsymbol{^{\prime}}},h)\) is a weighting function (Liu et al., 2014) with a smoothing length, and h represents the effective width of the kernel.

If \(f({{\varvec{x}}}^{^{\prime}})\) is known only for a discrete set of N points \({x}_{1},{x}_{2},\dots \dots {x}_{N}\), then \(f({{\varvec{x}}}^{\boldsymbol{^{\prime}}})\) can be estimated to give the particle approximation as follows:

$$\langle f({\varvec{x}})\rangle =\sum\nolimits_{j=1}^{N}\frac{{m}_{j}}{{\rho }_{j}}f({{\varvec{x}}}_{j})\omega ({\varvec{x}}-{{\varvec{x}}}_{j},h)$$
(2)

where the summation index \(x\) denotes a particle and \({{\varvec{x}}}_{j}\) is the position vector of particle \(j\) within the support domain of \(x\).

For particle \(i\), Eq. (2) can also be expressed as

$$\langle f({x}_{i})\rangle =\sum\nolimits_{j=1}^{N}\frac{{m}_{j}}{{\rho }_{j}}f({x}_{j}){\omega }_{ij}$$
(3)

where particle \(j\) carries a mass \({m}_{j}\) at position \({x}_{j}\) and a density \({\rho }_{j}\) within the support domain of particle \(i\), i.e., \({\omega }_{ij}=\omega ({x}_{i}-{x}_{j},h)\). The derivative of a function for particle \(i\) can be formulated as

$$\langle \nabla \bullet f({x}_{i})\rangle =\sum\nolimits_{j=1}^{N}\frac{{m}_{j}}{{\rho }_{j}}f({x}_{j}){\bullet {\nabla }_{i}\omega }_{ij}$$
(4)

where the equation obeys a similar integral representation and particle estimation.

$${\nabla }_{i}{\omega }_{ij}=\frac{{x}_{i}-{x}_{j}}{{r}_{ij}}\frac{\partial {\omega }_{ij}}{\partial {r}_{ij}}$$
(5)

where \({r}_{ij}\) is the distance between particles \(i\) and \(j\). Based on Eqs. (3) and (4), the continuity and momentum equation or particle \(i\) becomes

$$\frac{\mathrm{D}{\rho }_{i}}{\mathrm{D}t}={\rho }_{i}\sum\nolimits_{j=1}^{N}\frac{{m}_{j}}{{\rho }_{j}}{{\varvec{v}}}_{ij}\frac{\partial {\omega }_{ij}}{\partial {x}_{i}}$$
(6)
$$\frac{\mathrm{D}{{\varvec{v}}}_{i}}{\mathrm{D}t}=-\sum\nolimits_{j=1}^{N}{m}_{j}\left[\frac{{P}_{i}}{{\rho }_{i}^{2}}\right.+\left.\frac{{P}_{j}}{{\rho }_{j}^{2}}\right]\frac{\partial {\omega }_{ij}}{\partial {x}_{i}}+F$$
(7)

where the summation is over all particles j, P is the pressure, ρ is the density, and F is the body force (gravity). All interpolations of the WCSPH in this study employed a Wendland quantic kernel (Wendland, 1995; Ramli, 2018) with a length (radius) h = 1.3dx, which determines the resolution, where dx is the initial particle spacing. In DualSPHysics, boundary conditions are based on the dynamic boundary condition (DBC), fluid-driven objects, and modified DBC. In this work, the DBC is implemented, which treats boundary and fluid particles with the same equations. This boundary condition was tested in the work of Ramli (2018).

2.2 Characteristics of the Structure.

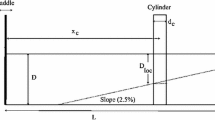
In this work, an appropriate structure was chosen according to the availability of experimental datasets used for the validation process. Given that the structure was analyzed as a rigid body for a numerical prediction (Lakshmynarayanana et al., 2015), in this study, the probing model of a flexible structure (Remy et al., 2016) was used for validating the WCSPH. Figure 1 shows the composition and setup of the segmented model used in their studies, with the structure consisting of 12 segregated caissons, each fastened to a steel rod set at 57 mm over the deck. The square-shaped cross section of the rod was 1 cm × 1 cm. The principal caisson was slightly altered to generate a beveled shape (Figure 2), while the remainder caissons comprised rectangular sections. Meanwhile, an NWT of 30 m × 16 m × 1 m was used, and Table 1 shows the properties of the structure and flexible pole. Depending on the modes of deformations, vertical, horizontal, and torsional bendings were permitted for the flexible structure model. The structure motion responses and deformations were evaluated in regular and irregular waves in head waves devoid of the forwarding speed, with tracking points placed at six different locations on the structure. Table 2 shows the six local reference positions for the structure, where x, y, and z are estimated from the stern, centerline, and hull of the structure, respectively (Figure 2). For the evaluation in regular waves, the structure motions were estimated for several wave periods. Additional details of the experiment are available in Remy et al. (2006).

Figure 1
figure 1

Experimental layout by Remy (2006)

Full size image
Figure 2
figure 2

Reference points for quantification (beveled shape of the bow)

Full size image
Table 1 Attributes of the structure
Full size table
Table 2 Measuring points from aft to forward of the structure
Full size table

2.3 Computational Setup

Similar to the approach used for describing 2D arrangements, the boundaries of structures in the 3D domain are also discretized into particles that directly interact with the fluid domain in the NWT. Each boundary particles hold the properties of the floating structure and interact with the fluid particles at each time step. The pressure between these boundary and fluid particles was then computed to determine the updated velocity and position at each time step, which were the motion responses of the floating structure. However, because the boundary was not a symmetrical rectangular form, discretizing a boundary domain into particles could be tedious. Therefore, the fill point technique was used in this study to transform a single point into discrete boundary particles and redistribute the points throughout the domain based on the shape of the boundary (Figure 3), in which all frames were discretized without disrupting the mesh refinement of the particle (Dominguez et al., 2021).

Figure 3
figure 3

Transformation from the solid to particle interface

Full size image

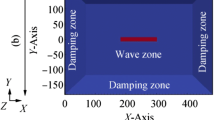
In the numerical setups for the NWT, a 3D platform was used with the x-axis along with the structure and the y-axis and z-axis in the athwartships and upright directions, respectively. Given that the symmetry boundary condition in the finite volume method was not an available option in DualSPHysics, modeling the structure and fluid domain in full dimension was essential. Thus, rendering it became computationally intensive because the dimensions of the fluid domain and side walls were dependent on the individual wavelengths (λ). Figure 4 shows that the structure was initially placed at 1.5 λ from the wavemaker on the left side with the damping beach located at the terminus of the NWT to restrain the approaching waves. Assuming that the longest wavelength produced in this test was 5 m, the damping beach was fixed to 1.5 times the structure length. Meanwhile, each of the side walls was fixed at 2.2 m from the structure’s centroid for all tests, with three probes placed around the structure for tracking the advancing waves and their reflections from the side walls. The movement in the x-direction was also riveted, capturing only the vertical wave motion and pitching.

Figure 4
figure 4

Top and side views of the computational structure

Full size image

For the simulation of a rigid body in head waves, the particle mesh was estimated on the true size of the structure and NWT. The NWT was sufficiently large for producing waves near the floating structure while completely restraining the wave at the far end of the damping zone. Apart from the overall dimension, the choice of the appropriate particle spacing for the fluid domain and rigid boundary also depended on the total number of particles generated, computational cost required, and numerical instability. Following the preliminary convergence test of another study (Ramli, 2018), three-particle spacings with consistently well-maintained wave profiles were used in this study: dx = 0.010 m, dx = 0.015 m, and dx = 0.020 m. Particle spacings within this range of numbers were generally deemed appropriate for the study. Given that 25 M particles were generated from dx = 0.010 m, i.e., larger than the utmost number that the current GPU could handle, dx = 0.020 m was used in all tests. The total number of particles was 4 M particles with 3.5 M fluid particles and 0.5 M boundary particles. Particle spacings, i.e., dx = 0.012 m and 0.015 m, were employed to examine motion responses with relatively lower frequencies in these convergence studies. Boundary particles were chosen for each wall to mimic the actual setups of the NWT. In each repetition, the movement of the piston wavemaker was controlled by a sinusoidal function. The rigid-body response of the structure in head regular waves under different test conditions was computed for five-wave periods (Table 3). These rigid-body responses were then compared with the findings of the 3D finite volume computational fluid dynamics (CFD) technique (Star-CCM +) proposed by Lakshmynarayanana et al. (2015) and 2D numerical (MARS) and empirical examination of Remy (2006).

Table 3 Selected numerical experimental setups
Full size table

3 Results and Discussion

3.1 Production of Waves via the Paddle Motion

Prior to the installation of the structure model, the wave profiles that the piston wavemaker produced were tested for two purposes: (i) to verify the wave heights of regular waves generated at various frequencies and (ii) to establish the position of the structure with a minimum reduction in the wave height while allowing a gap between the structure and wavemaker for periodic solutions without being corrupted by reflection. A similar experiment was conducted on the 2D case for the WCSPH with a satisfactory result (Ramli, 2018). However, wave reflections from the side walls were not assessed in these tests, which could influence the wave height (Lakshmynarayanana et al., 2015). In this study, six additional probes were incorporated into the analysis. Figure 5 shows all six tracking probes. The tracking points were fixed within 1.5λ from the wavemaker based on frequencies, and then wave heights were noted in each repetition. Experiments were performed in various conditions to optimize the results.

Figure 5
figure 5

Average wave height at each tracking probe (prior to installing the barge) at various frequencies

Full size image

In Figure 5, dotted lines representing findings from the WCSPH were compared with the analytical results of the 0.10 m wave height. The wave profiles and analytical solution were generally congruent, except for minor discrepancies at relatively low frequencies. The time record of the wave advancement for ω = 3.490 rad/s showed a minimum wave dissipation at each probe, with the largest reduction of 12% in the wave height throughout the test (Figure 6). Figure 7 shows the wave advancement at different time steps, and the visualization could be enhanced by depicting the particles onto the surface via IsoSurface.exe in DualSPHysics (Crespo et al., 2015).

Figure 6
figure 6

Time history of the wave elevation along the NWT without the structure. T = 1.8 s, λ = 5.058 m (≅ 0.7λ)

Full size image
Figure 7
figure 7

Wave advancements at various moments in the simulation at ω = 6.283 rad/s. Colors represent the swiftness of wave movements

Full size image

3.2 Rigid-Body Motion Responses in Head Waves.

Figure 8 presents the RAOs calculated from the WCSPH, in which the amplitudes from four to six wave periods were averaged to yield RAOs. The 2D linear potential flow yielded rigid-body motion responses via the strip theory, designated as MARS (Bishop and Price, 1979), and a finite element method using ABAQUS (version 6.14) denoted by STAR. In the absence of distortions, displacements comprising solely rigid-body motions of heaves and pitches were represented by MARS_Rigid and STAR_Rigid. A particle spacing dx of 0.020 m used for all simulations was denoted by the WCSPH. Altogether, MARS_Rigid qualitatively agreed well with STAR_Rigid in responses, except for minor discrepancies around points 7 and 9 with relatively low frequencies. Supplementary hydroelastic measurements from Remy et al. (2006) were graphed to chart the relation between motion responses and deformations. The results from the experimental data reflect the behavior of a flexible structure, providing insights on how it differs in comparison with motion responses from rigid structures.

Figure 8
figure 8

RAO values of vertical displacements along with the structure. In the analyses of the rigid and flexible bodies, point 12 was located near the stern and point 1 near the bow, as shown in Figure 2

Full size image

Overall, the behaviors of flexible and rigid structures differed in several ways. At comparatively high-frequency ranges of ω > 5.235 rad/s, the instantaneous wave contour around the body exerted 3D effects on the structure at points 1, 3, and 5, which was indicative of overestimation by the WCSPH (Figure 9). The 3D effects were largely the results of strong but localized nonlinear wave systems, and a 2D linear model of the potential flow theory would not project it appropriately. However, projections from the WCSPH were lower than that of STAR_Rigid, notably at ω = 5.283 rad/s with the largest difference of less than 30%. Lower WCSPH projections were probably due to the waves fragmenting on the free surface around the forward section. The repulsive character of the dynamic boundary particles could also cause fluctuations in pressure that affect the flow fields. Predictions from the WCSPH and STAR_Rigid agreed better with the experimental data at all points for the highest frequency. In this case, the impact of diffraction prevailed at the vicinity of waves approaching the bow, perturbing the free surface at the structure regardless of its flexible or rigid condition, thus yielding a minor change in the vertical motion.

Figure 9
figure 9

Development of the wave profile hitting the floating barge for ω = 6.981 rad/s

Full size image

When ω < 5.235 rad/s, most deviations from the potential theory were revealed. Overprediction occurred at points 1, 3, and 12 for the WCSPH, whereas at points 5, 7, and 9, the values underpredicted the potential theory. The rigid structure was most likely linked to the impact of a strong bow and stern waves because of the motion when moving in the pitch motion. Nevertheless, most projections were closely complemented with STAR_Rigid, except for points 7 and 9, probably because of their distant locations from the bow and stern. At positions near the bow (point 1) and stern (point 12), the flexible structure was deformed following the wave advancement, thus generating lower vertical responses than the potential theory.

For points 7 and 9, the attributes of the projection marginally varied from MARS_Rigid and STAR_Rigid, largely because these points were located at the amidships, where the fluid dynamic was primarily affected by the vertical motion of the barge. However, the added mass coefficient obtained from the WCSPH did not corroborate well with the theoretical and experimental data collected at low-frequency ranges. This discrepancy might be attributable to the fluctuations of pressure at the interface between the fluid and structure.

A thorough assessment between RAOs at various frequencies is given in Figures 10 and 11 with colors representing the velocity of the created waves. At ω = 3.926 rad/s, with \({\varvec{\lambda}}\ge 2.245\boldsymbol{ }\mathbf{m}\) (length of the structure), the bow reflected most of the waves arriving in succession. A higher wave velocity encircling the bow suggests a strong influence of slamming due to higher vertical displacement, thereby generating an uninterrupted and strong but localized wave contour along with the structure, notably at the amidship (points 7 to 9). This nonlinear pattern was not visible in the symmetry boundary approach in STAR-Rigid, which could explain the discrepancy around the amidship area. Figure 11 shows a similar nonlinear pattern for high frequencies, with the slamming effect occurring at the bow, which could differentiate the 3D motion from its 2D equivalent in the simulation. A high frequency appeared to produce short waves that traveled through the structure with minimal wave dissipation. Therefore, the vertical displacement around the amidship was less perturbed and maintained similar responses, as shown in Figure 8.

Figure 10
figure 10

Illustration of the instantaneous wave contour surrounding the rigid structure at 9.15 s and 9.85 s for ω = 3.926 rad/s

Full size image
Figure 11
figure 11

Instantaneous wave contours around the rigid structure at 13.95 s and 14.5 s for ω = 6.283 rad/s

Full size image

To better understand the relationship of particle spacing and the accuracy and capability of the WCSPH in predicting the RAOs for low-frequency ranges, particle numbers were increased for two cases of ω < 3.490 rad/s and ω < 3.926 rad/s. The simulations are expected to yield a better prediction as what has been observed in the case of propagating regular waves. The number of particles was carefully selected on the basis of keeping the balance between the acceptable accuracy of the simulation and a reasonable computational cost. Both cases shown in Figure 8 were denoted as WCSPH_0.012 and WCSPH_0.015 with 18 M and 9 M particles, respectively. However, both results did not show any significant improvements, particularly at the amidships.

4 Conclusions

The open-source code DualSPHysics has been used as a numerical tool to study the interaction of a beveled-shaped structure in head waves. This is a 3D hydrodynamic experiment to develop an efficient approach in predicting the motion response in comparison with other numerical techniques and experimental data. The beveled-shaped structure was modeled using a model similar to that of Lakshmynarayanana et al. (2015), which was, in turn, based on a hydroelastic test conducted by Remy et al. (2006). Some concluding observations from the investigation are given below:

  1. 1)

    Overall, the motion responses of the WCSPH agreed well with the theoretical and experimental findings, except for minor disparities at low frequencies at the amidship of the structure.

  2. 2)

    The disparities were largely the result of the vertical motion, which was presumably affected by a strong but localized wave along the structure and a regular long-crested wave.

  3. 3)

    The convergence test was conducted to examine the small discrepancies noted at relatively low frequencies. However, no apparent improvement was attained through the test.

  4. 4)

    The overprediction of motion responses from the WCSPH occurred at bow regions, and this finding was similar to that of STAR_Rigid at relatively higher frequencies.

  5. 5)

    The comparison with the experimental data provided useful insights into the differences in motion responses between the rigid and deformable structures.

  6. 6)

    The results of this study could be improved with a hydroelastic module to simulate deformable structures. Improvements might also be achieved via a double-precision technique for particle position or variable particle resolution near the structure.