1 Introduction

Accurate prediction of a ship’s speed loss due to encountering waves is essential for both ship design and efficient operations. When a ship operated at a specific power, the speed loss (involuntary speed reduction) ΔV due to encountered waves is usually defined as the difference between her sailing speed in still water (Vcalm) and the actual speed sailing in the waves (Vreal). The magnitude of ΔV depends on the added resistance due to wind and waves in comparison with the calm water resistance (Rcalm) in still water (Pérez Arribas 2007). The methods to estimate Rcalm and added resistance due to wind (RAA) are rather mature than added resistance in waves (RAW), which is hardly seized especially for arbitrary wave heading angles (Jiao et al. 2016; Tillig et al. 2018).

Several theoretical methods have been developed to estimate added resistance due to waves, such as the direct pressure integration method (Havelock 1942; Boese 1970), the momentum conservation method (Maruo 1957, 1960, 1963), the radiated energy method (Gerritsma and Beukelman 1972; Salvesen 1978), and the asymptotic calculation formula for wall-side ship hull in short waves (Faltinsen et al. 1980). These methods are normally based on the traditional slender-body theory or the 3D panel method. They often underestimate the added resistance in the short-wave region and overestimate the resistance in long waves. Alternatively, various semi-empirical models have been continuously developed based on the above theoretical models with parameters regressed using experimental results. For example, Strom-Tejsen et al. (1973) proposed to categorize the added resistance due to waves into two components, i.e., the reflection resistance caused by short waves and the ship motion–induced resistances by long waves. Jinkine and Ferdinande (1974) first proposed a simplified model to calculate added resistance due to ship motions in head waves. It was further developed in several joint industry projects lead by MARIN known as the STAwave-1 method (Boom et al. 2013). In parallel, formulas to estimate diffraction-dominated added resistance were proposed (Fujii and Takahashi 1975; Takahashi 1988) with further development using more experiment data as in Tsujimoto et al. (2008) (here referred to as the NMRI method). In the empirical STAwave-2 method (ITTC 2014), the added resistance models for both short waves based on Faltinsen et al. (1980) and long waves based on Jinkine and Ferdinande (1974) were further developed by using large amount of experiment test data. Lang and Mao (2020) proposed a semi-empirical model for added resistance due to head waves. This model tuned parameters in the NMRI formulas for short waves and further developed formulas based on Jinkine and Ferdinande (1974) for long waves to be better agreed with model test results.

Recently, some CFD methods and full-scale measurement–based methods have also been investigate for the speed loss prediction (Sasa et al. 2015; Mao et al. 2016; Kim et al. 2017; Zhang et al. 2019). The obvious drawback of these methods is the large amount of computation effort or measurement investment. For developing measures to aid a ship’s operation, such as ship voyage optimization and ship performance monitoring, reliable fast calculation models are often required to estimate a ship’s added resistance due to waves in arbitrary heading angles (from 0° to 180°). The empirical method proposed by Kwon (2008) as an extension to Townsin and Kwon (1982) is one of the most well-recognized methods. It has been widely used for the ship voyage optimization systems, e.g., Larsson et al. (2015), Lu et al. (2015), Wang et al. (2016), Simões et al. (2018), etc.

However, most of the semi-empirical methods were developed for added resistance in head sea to beam sea that is important for ship design. Furthermore, the parameters in the semi-empirical formulas are tuned or regressed based on large amount of seakeeping model test results. From the ship design purpose, these methods may give good average of speed loss for the large ship samples from long-term service perspectives. While for applications to guide a ship’s operation, it is essential to have a speed loss prediction model that can accurately describe the specific ship’s performance at individual sea state or along a voyage (Wang et al. 2020). To facilitate fast and accurate computation of a ship’s speed performance at sea that is essential for the development of ship operation–related measures, the semi-empirical model for head waves developed in Lang and Mao (2020) is first extended to estimate added resistance due to arbitrary wave headings. Furthermore, a nonlinear correction factor is proposed to consider the effect of large ship motion–induced increase of wave resistance and reduction of propulsion efficiency when sailing in large sea states.

The proposed semi-empirical model is described in detail in Section 2. Section 3 verifies the developed semi-empirical method using model test data. Full-scale measurements of three ship types are used to validate the proposed model in Section 4. The impact of implementing this proposed semi-empirical model in comparison with the simple Kwon’s method for a ship’s voyage optimization is investigated in Section 5. The paper is concluded in Section 6.

2 The Semi-empirical Model Proposed for Speed Loss Prediction

When a ship is operated in a seaway under a specific engine power, her Vreal is a consequence of an involuntary speed reduction (loss) due to encountering waves from the “imaginary” speed Vcalm. Here, the imaginary ship speed Vcalm is defined as a ship’s sailing speed in the ideal calm water conditions under a specific engine power setting, i.e., there is no wind and wave. The prediction of speed loss in waves is essential for ship design and operations. In this study, the iterative workflow for such a prediction is proposed as in Fig. 1. To estimate Vreal under a specific sea condition and engine power, Vcalm is set as the initial ship speed for the iteration process to get the Vreal. First, a small adjustment speed (Vadjustment) is chosen to update the speed prediction. The convergence of the iterative prediction of Vreal is achieved if the absolute difference between the real engine power (Psetting) and the calculated engine power (Pprediction) is less than 5% of Psetting. As shown in Fig. 1, the accuracy of a ship’s resistance and propulsion calculation is vital for the entire iterative process. First, a further improved semi-empirical model for added resistance due to head regular waves is presented. Then, extension formulas are proposed to consider effect of other wave headings. Finally, a correction factor is proposed in the component of added resistance to consider nonlinear effect of power consumption in large sea states.

Fig. 1
figure 1

Flowchart of the proposed model to predict a ship’s speed loss when sailing at sea

Full size image

2.1 The Semi-empirical Model for R aw in Head Waves

For a ship sailing in head waves with speed V and β = 0, the added resistance in regular waves of frequency ω can be evaluated by the sum of two components, i.e., added resistance due to wave reflection Rawr, and due to ship motions Rawm as (Strom-Tejsen et al. 1973):

$$ {R}_{aw}\left(\omega |V,0\right)={R}_{aw r}\left(\omega |V,0\right)+{R}_{aw m}\left(\omega |V,0\right) $$
(1)

For the semi-empirical models of added resistance in head waves, the corresponding improvement compared with other well-known methods has been investigated in Lang and Mao (2020). In this method, models to estimate Rawr is further developed based on the NMRI formulas (Fujii and Takahashi 1975), and Rawm is further developed based on Jinkine and Ferdinande (1974). The added resistance due to wave reflection is given by:

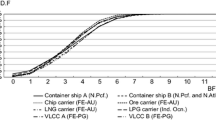
$$ {R}_{awr}=\frac{1}{2}\rho g{\zeta}_a^2B{B}_f{\alpha}_T\left(1+{\alpha}_U\right)\left(\frac{0.19}{C_B}\right){\left(\frac{\lambda }{L_{pp}}\right)}^{Fr-1.11} $$
(2)

where ρ is the fluid density, g the gravitational acceleration, B the ship width, Lpp the ship length between perpendicular, CB the block coefficient, Fr the Froude number, and λ the wave length. The bluntness coefficient (Bf) is simply determined by the average entrance angle (E):

$$ {B}_f=2.25{\sin}^2E $$
(3)

with E = arctan(B/2LE). The LE is defined as the length between the fore perpendicular, and the point reaches 99% ship width at the waterline surface. Whereas, the draft coefficient (αT) is related to the circular frequency (ω) and wave number (k) of regular waves viz:

$$ {\upalpha}_T=1-{e}^{-2{k}_eT} $$
(4)

where ke = k(1 + Ω cos β)2 and \( \varOmega =\frac{\omega V}{g} \). The advance coefficient (1 + αU) is written as:

$$ 1+{\alpha}_U=1+{C}_U Fr,\mathrm{where}\kern0.2em {C}_U=\max \left(-310{B}_f+68,10\right) $$
(5)

The added resistance due ship motions is calculated by:

$$ {R}_{awm}=4\rho g{\zeta}_a^2{B}^2/{L}_{pp}{\overline{\omega}}^{b_1}\exp \left[\frac{b_1}{d_1}\left(1-{\overline{\omega}}^{d_1}\right)\right]{a}_1{a}_2 $$
(6)

where the amplitude factor (a1), speed correction factor (a2), frequency factor (\( \overline{\omega} \)), and the slope adjustment factor b1, d1 are further developed by Lang and Mao (2020) as follow:

$$ {a}_1=60.3{C_B}^{1.34}{\left(\frac{1}{C_B}\right)}^{1+ Fr} $$
(7)
$$ {a}_2=\left\{\begin{array}{ll}0.0072+0.24 Fr& \mathrm{for}\ Fr<0.12\\ {}{Fr}^{-1.05{C}_B+2.3}\exp \left(\left(-2-\left\lceil \frac{k_{yy}}{0.25}\right\rceil -\left\lfloor \frac{k_{yy}}{0.25}\right\rfloor \right) Fr\right)&\ \mathrm{for}\ Fr\ge 0.12\end{array}\right. $$
(8)
$$ {b}_1=\left\{\begin{array}{c}\genfrac{}{}{0pt}{}{\left(19.77\frac{C_B}{k_{yy}}-36.39\right)/\left\lceil \frac{k_{yy}}{0.25}\right\rceil \kern2em \mathrm{for}\ \overline{\omega}<1,{C}_B<0.75\kern1em }{11/\left\lceil \frac{k_{yy}}{0.25}\right\rceil \kern9.5em \mathrm{for}\ \overline{\omega}<1,{C}_B\ge 0.75}\\ {}\genfrac{}{}{0pt}{}{-12.5/\left\lceil \frac{k_{yy}}{0.25}\right\rceil \kern8em \mathrm{for}\ \overline{\omega}\ge 1,{C}_B<0.75\ }{-5.5/\left\lceil \frac{k_{yy}}{0.25}\right\rceil \kern8.5em \mathrm{for}\ \overline{\omega}\ge 1,{C}_B\ge 0.75}\end{array}\right. $$
(9)
$$ {d}_1=\left\{\begin{array}{ll}14& \mathrm{for}\ \overline{\omega}<1,{C}_B<0.75\\ {}566{\left(\frac{L_{pp}}{B}\right)}^{-2.66}\cdotp 2&\ \mathrm{for}\ \overline{\omega}<1,{C}_B\ge 0.75\\ {}-566{\left(\frac{L_{pp}}{B}\right)}^{-2.66}\cdotp 6&\ \mathrm{elsewhere}\end{array}\right. $$
(10)
$$ \overline{\omega}=\left\{\begin{array}{cc}\frac{\sqrt{L_{pp}/g}\sqrt[{c}_1]{k_{yy}}{0.05}^{0.143}}{1.09+\left\lceil \frac{k_{yy}}{0.25}\right\rceil 0.08}\omega & \mathrm{for}\ Fr<0.05\\ {}\frac{\sqrt{L_{pp}/g}\sqrt[{c}_1]{k_{yy}}{Fr}^{0.143}}{1.09+\left\lceil \frac{k_{yy}}{0.25}\right\rceil 0.08}\omega & \mathrm{for}\ Fr\ge 0.05\end{array}\kern0.5em \mathrm{with}\ {c}_1=0.4567\frac{C_B}{k_{yy}}+1.689\right. $$
(11)

where kyy is the longitudinal radius of gyration. These semi-empirical formulas can accurately estimate added resistance in head waves for both the fine hull and full hull ships with different sailing speeds. An extension is proposed in the following subsection to consider added resistance in waves with arbitrary heading angles.

2.2 The Semi-empirical Model for R aw at Arbitrary Heading Angles

For a ship sailing in speed (V) with arbitrary heading angle (β), the added resistance due to wave reflection (Rawr(ω| V, β)), and due to ship motions (Rawm(ω| V, β)) in a regular wave of frequency (ω), are assumed to be uncoupled and estimated separately. The total added resistance under such a wave is computed by:

$$ {R}_{aw}\left(\omega |V,\beta \right)={R}_{aw r}\left(\omega |V,\beta \right)+{R}_{aw m}\left(\omega |V,\beta \right) $$
(12)

where Rawr(ω| V, β) and Rawm(ω| V, β) are calculated by the method proposed as follows.

The Rawr(ω| V, β) is mainly caused by the short waves (large values of ω) reflection on a ship waterline non-shaded area, which is presented by \( \frac{1}{2}\rho g{\zeta}_a^2B{B}_f{\alpha}_T \). According to the model test results in, e.g., Kadomatsu (1988), Moctar et al. (2012), Valanto and Hong (2015), etc., the magnitude of Rawr reduces as the β increase, i.e., from the head wave till the following sea. Negative values of Rawr are also observed for a few very short waves at 120 ° ≤ β ≤ 180°. Thus, a simplified modification factor cosβ is proposed to express the above experimental phenomenon. Based on the aforementioned model test results with high Froude numbers, the resistance force has shown obvious increase when β ≤ 90°, and the negative resistance becomes weaker when β > 90°. Therefore, the advance coefficient (1 + αU) is further modified by adding parameters to consider the influence of the Fr in different wave β. The modified formula for Rawr(ω| V, β) at arbitrary wave heading angles is written as:

$$ {R}_{awr}\left(\omega |V,\beta \right)=\left\{\begin{array}{ll}{R}_{awr}\left(\omega |V,0\right)\cdotp {Fr}^{\left(\left\lfloor \mathrm{zcos}\beta \right\rfloor -\left\lceil \cos \beta \right\rceil \right) Fr}\cos \beta & \mathrm{for}\ 0\le \beta \le \frac{\pi }{2}\\ {}{R}_{awr}\left(\omega |V,0\right)\cdotp {Fr}^{-1.5\left(\left\lfloor \cos \beta \right\rfloor +\left\lceil \cos \beta \right\rceil \right) Fr}\cos \beta &\ \mathrm{for}\kern0.5em \frac{\pi }{2}<\beta \le \pi \end{array}\right. $$
(13)

The ship motions induced added resistance Rawm(ω| V, β) is mainly caused by long waves (small values of ω). According to the experimental tests by e.g., Fujii and Takahashi (1975); Takahashi (1988); Journée (2001); Moctar et al. (2012); Valanto and Hong (2015), etc., the wave length λ leading to the peak value of Rawm moves horizontally from λ/Lpp = 1 to lower λ/Lpp region as β increases. It means that the encountered frequency ω decreases from the head wave till the following wave. According to linear potential theory, the pitch and heave motion transfer functions in the following sea should be of the same magnitude as that in the head sea but with very different encountered frequency. High motions should also contribute to high Rawm rather than values close to zero, and it should become more pronounced in high sea states. Thus, a novel encountered frequency correction factor \( {C}_{\overline{\omega}}\left(\beta \right) \) was proposed in this study viz:

$$ \overline{\omega_{\beta }}=\overline{\omega}\ast {C}_{\overline{\omega}}\left(\beta \right) $$
(14)

where the proposed values of \( {C}_{\overline{\omega}}\left(\beta \right) \) for various heading angles are listed in Table 1.

Table 1 Encountered frequency correction factor for various heading angles (other angles are interpolated)
Full size table

Furthermore, the peak values of Rawm(ω| V, β) decreases as the wave β increases. The roll motion dominates ship motions rather than heave and pitch when β close to 90° (Jiao et al. 2021). Thus, an amplitude adjustment factor \( {e}^{-{\left(\frac{\beta }{\pi}\right)}^{4\sqrt{Fr}}} \) and a compensation factor for the roll motion in terms of the ratio between wave length (λ) and ship width (B), Fr, relative wave angle (β), is proposed to be added in the formula of Rawm as:

$$ {R}_{awm}\left(\omega |V,\beta \right)={R}_{awm}\left(\omega |V,0\right)\cdotp {e}^{-{\left(\frac{\beta }{\pi}\right)}^{4\sqrt{Fr}}}+\rho g{\zeta}_a^2{B}^2/{L}_{pp}{\left[\frac{\lambda }{B}\cdotp \max \left(\cos \beta, 0.45\right)\right]}^{-6 Fr}\sin \beta $$
(15)

2.3 Added Resistance in Waves R AW Under Irregular Waves

An actual sea state is often described by a wave spectrum of predefined formats multiplied by a spreading function D(θ). In this study, the JONSWAP wave spectrum and a Consine-Squared spreading function D(θ), in terms of the significant wave height (Hs), wave peak period (Tp), peakedness factor (γ), and the wave spreading direction (θ), are applied to describe irregular waves of a ship’s actual sailing wave conditions (Hasselmann et al. 1973):

$$ S\left(\omega |{H}_s,{T}_p,\gamma \right)D\left(\theta \right)=\frac{320{H_s}^2}{{T_p}^4{\omega}^5}\exp \left(\frac{-1950}{{T_p}^4{\omega}^4}\right){\gamma}^{\exp \left[\frac{-{\left(\omega -{\omega}_p\right)}^2}{2{\sigma}^2{\omega}_p^2}\right]}D\left(\theta \right) $$
(16)
$$ D\left(\theta \right)=\left\{\begin{array}{c}\frac{2}{\pi}\mathrm{co}{\mathrm{s}}^2\left(\theta \right)\kern4em \mathrm{if}-\frac{\pi }{2}\le \theta \le \frac{\pi }{2}\\ {}0\kern9.75em \mathrm{otherwise}\end{array}\right. $$
(17)

where γ is set to the standard value 3.3, and the spectral width parameters σ = 0.07 for ω ≤ ωp, σ = 0.09 when ω > ωp. The added resistance in waves RAW under actual wave environments (irregular waves) is conventionally estimated by:

$$ {R}_{AW}\left(\omega |{H}_s,{T}_p,\gamma, V,\beta \right)=2{\int}_0^{\infty }{\int}_{-\frac{\pi }{2}}^{+\frac{\pi }{2}}S\left(\omega |{H}_s,{T}_p,\gamma \right)\frac{R_{aw}\left(\omega |V,\beta \right)}{\zeta_a{\left(\omega \right)}^2}D\left(\theta -\beta \right) d\theta d\omega $$
(18)

where ζa(ω) is amplitude of the regular wave to get the added resistance Raw(ω). The term \( {R}_{aw}/{\zeta}_a^2 \) is often referred as the transfer function (RAOs) of ship resistance.

2.4 A Correction Factor for Ship Resistance and Power Consumption

Let Pe denotes the effective power to push a vessel at a forward speed through water V with the total resistance (Rtotal). The effective propulsive power is transmitted from the engine brake power Pb (simply denoted as power P in this study) through her shaft and propulsion system with the overall propulsive efficiency ηD:

$$ P:= {P}_b=\frac{R_{\mathrm{total}}\times V}{\eta_D} $$
(19)

where the total resistance as indicated in Fig. 1 is often divided into three major components. However, there are large uncertainties in the calculation of added resistance due to waves. First, the integration of transfer function (RAOs) in Eq. (18) assumes that a ship’s response is assumed to be linear to waves (Lewis 1988; Mao 2014). But a ship’s response (motions, reflections) and their contributions to Raw is known to be nonlinear especially in high sea states with large Hs. Furthermore, large nonlinear motions in high sea environment can also reduce a ship’s propulsion efficiency. Large waves may also mean a ship has to experience unstable surf riding along the waves. These factors contribute to the increase of power consumption, and all of them are strongly related to the increase of sea states Hs that directly determine the added resistances due to waves (RAW). Therefore, in this study, a wave height based correction factor \( {C}_{H_s}=\sqrt[3.5]{H_s} \) was proposed to RAW to consider their contribution to the increase of power consumption. Then Rtotal is estimated by:

$$ {R}_{\mathrm{total}}={R}_{\mathrm{calm}}+{R}_{AA}+{R}_{AW}\times {C}_{H_s} $$
(20)

where Rcalm and the propulsive efficiency ηD can be quite accurately estimated by model test results in this study, and RAA is estimated by the well-established method in ISO (2015). The preliminary correction factor is found and tuned by analyzing the difference between conventional prediction and full-scale measurements used in this study. For a general application of this correction factor, comprehensive investigation should be conducted to establish such a flexible formula/factor, based on more extensive experimental tests and full-scale measurements. Whereas, different components in the proposed model for RAW are further verified and validated in the following analysis.

3 Verification of R aw by Model Tests in Regular Waves

A number of available ship experimental measurements were collected to validate the proposed model to predict added wave resistance, i.e., S175 container (Fujii and Takahashi 1975; Takahashi 1988), DTC container (Moctar et al. 2012), HSVA cruise (Valanto and Hong 2015), S.A. Van Der Stel (Journée 2001), and a bulk carrier (Kadomatsu 1988). All the required main particulars of those ships for the semi-empirical model are listed in Table 2. The added resistance due to waves Raw(ω| V, β) estimated by the proposed model are presented in Fig. 2 to Fig. 6, in comparison with the model test results. The nondimensional reflection–induced resistance Rawr and nondimensional ship motion–induced resistance Rawm are also illustrated in those figures.

Table 2 Main particulars of the studied ships
Full size table
Fig. 2
figure 2

Added resistance of S175 container in the regular waves with arbitrary angles at Fr = 0.250

Full size image

The S175 container and S.A Van Der Stel have smaller block coefficients (CB) and longitudinal radius of gyrations (kyy). The experiment tests using the S175 container were conducted at Froude number Fr = 0.250 with wave heading angles from 30° to 180°. As compared in Fig. 2, the proposed semi-empirical model gives really good prediction results compared to the test results for 30° and 60°. For the other heading angles, although there exist some fluctuations, it can still catch up with the trend of the test results, where the peak values of Raw decrease and move to lower wave length (λ/Lpp) region as the wave heading angle increases. For the S.A Van Der Stel, the model test was limited in the following sea, with four different Froude number Fr = 0.150, Fr = 0.200, Fr = 0.250, and Fr = 0.300. Unfortunately, almost all available measurement data points are between 0.5 < λ/Lpp < 2, thus only the latter half of the experimental results can be shown. As Fig. 3 presents, the proposed formula has accurately shifted the resonance region to the lower λ/Lpp area, and the λ/Lpp > 0.5 part has a good agreement in all small and linear values.

Fig. 3
figure 3

Added resistance of S.A Van Der Stel in the regular following wave

Full size image

For ships with a large longitudinal radius of gyration kyy, the model tests of the DTC container ship and the HSVA cruise ship were performed at Fr = 0.052 and Fr = 0.232, respectively. As Fig. 4 presents for the DTC container, the proposed model gives a good prediction of peak values of Raw when β < 120°. It can also track the recorded values for relative large heading angles 120 ° ≤ β ≤ 180°. It should be noted that the Raw becomes negative, as in Fig. 4d, e. For the HSVA cruise ship in Fig. 5, the agreement between estimation by the proposed model and the test results is very good at both tails and peak value areas when encountering wave angle between 30° and 120°. For the bulk carrier, it has a relatively large CB with a full hull shape. The model test was executed at the Froude number Fr = 0.100 for the quartering sea, beam sea, and the following sea. Figure 6 also shows consistent results between the estimations and model tests for both peak values and tails of Raw.

Fig. 4
figure 4

Added resistance of DTC container in the regular waves with arbitrary angles at Fr = 0.052

Full size image
Fig. 5
figure 5

Added resistance of HSVA cruise in the regular waves with arbitrary angles at Fr = 0.232

Full size image
Fig. 6
figure 6

Added resistance of studied bulk carrier in the regular waves with arbitrary angles at Fr = 0.100

Full size image

The proposed semi-empirical formulas have shown an excellent capability to estimate added resistance in arbitrary heading angles compared with the model test results. The fluctuation and gap are probably found in most of the semi-empirical models. It is a combination of insufficient model accuracy and measurement uncertainties. In setting up an experimental test for added resistance, the uncertainties exist in different measuring approaches, hardware and experimental configurations. Also, the viscosity effects play an increased role. Thus, in the derivation and validation of the proposed formula, the whole trend of the shift of resonance location, the peak amplitude, and the tail increase or decrease in the short wavelength area is the most important. For the estimation of RAW in irregular waves, the difference can be greatly reduced during the integration along the entire wave spectrum.

4 Validation by Full-Scale Measurements at Actual Sea Conditions

The full-scale measurements recorded by a PCTC, a container ship, and a chemical tanker, are used to validate the proposed model for predicting speed loss in actual sailing wave conditions. The main particulars of these ships are shown in Table 3 as inputs for the following speed loss prediction. The three ships were instrumented with various sensors to collect a large amount of ship navigation and performance-related data, up to a gigabyte per day. The parameters of the full-scale measurement data from all three ships are similar. In the full-scale measurements, the shaft torque, RPM, and propulsive power were recorded by sensors installed in marine engines. The ship’s sailing locations (longitude, latitude), speed over ground, ship draft, and ship heading were also recorded. The measurements were collected with a frequency of 1 Hz, while the mean values are statistically evaluated every 15 min. The typical routes in the full-scale measurements are illustrated in Fig. 7. The sea environment along the measured routes is extracted from the hindcast database.

Table 3 Main characteristics of the studied PCTC, container ship, and chemical tanker for full-scale measurements
Full size table
Fig. 7
figure 7

Typical routes of the three studied ships during the measurement campaign. The PCTC and chemical tanker were sailing worldwide, while the container ship was sailing in the North Atlantic.

Full size image

To predict a ship’s speed loss, the power setting should be first identified. In this study, all the sailing waypoints (associated with certain sea states) with the engine power close to 9000 kW (64% MCR) for the PCTC, 17,000 kW (80% MCR) for the container ship, and 6000 kW (70% MCR) for the chemical tanker, are selected for the following analysis. There are enough waypoints in the full-scale measurement that can fulfill the power setting requirement. For the resistance estimation, the ship baselines (speed-power curve in calm water conditions) obtained from model tests and sea trials are provided by the shipowners in this study. The coefficient of wind resistance for the PCTC is obtained from wind tunnel tests, while for the chemical tanker and the container ship, the wind resistance RAA is calculated according to the semi-empirical models in ISO (2015). The total propulsive efficiency ηD was extracted from the open water tests.

4.1 Sources of Metocean Data

For the speed loss prediction at a specific engine power, it is essential to get an accurate sea environment (metocean data) encountered along the sailing routes. For the three case study ships, the encountered metocean data, such as the mean wave direction (Dwave), mean wave period (Tz), Hs, and wind speed Uwind and Vwind are extracted from the reanalysis dataset ERA5 (Copernicus 2019). The current velocity Ucurrent and Vcurrent are obtained from the Copernicus Marine Server (CMEMS 2019). The extracted metocean data from the hindcast datasets are assumed to be the actually encountered conditions.

All the waypoints from the specific engine power for each case study ship are divided into various groups based on the Beaufort numbers (BNs), i.e., BN-3, BN-4, BN-5, BN-6, and BN-7, based on the encountered Hs. The probable interval of Hs is determined from the ISO suggestion (ISO 2015) listed in Table 4.

Table 4 The probable Hs span for Beaufort scales considered in the validation dataset separation
Full size table

4.2 Kwon’s Method for Comparison

A widely used empirical model was proposed by Kwon (2008) to estimate a ship’s speed loss for the development of ship operation-related measures. It is chosen here for the comparison of speed loss prediction and the impact study of voyage optimization systems. The speed loss is written as:

$$ \frac{V_{\mathrm{calm}}-{V}_{\mathrm{real}}}{V_{\mathrm{calm}}}={C}_f{C}_{\alpha }{C}_{\beta } $$
(21)

where Cf denotes speed loss caused by wind and wave, and ship types and displacements ∇ primarily decide it, Cα is a function in terms of a ship’s CB, Fr in different loading condition, and Cβ depends on β and BN as in Table 5 (the detailed formulas for Cf and Cα can be referred to Kwon (2008)).

Table 5 Weather direction reduction factor Cβ
Full size table

4.3 Comparison and Validation of the Model by a Blunt Chemical Tanker

For all the chosen waypoints from the chemical tanker, the wave β around 0°, 30°, 60°, 90°, 120°, 150°, and 180° for each Beaufort scale subset are selected to estimate the ship’s speed loss by both Kwon’s method and the proposed method here, which are compared with the measured speeds as illustrated in Fig. 8.

Fig. 8
figure 8

The speed loss estimation by both the Kwon’s method and the proposed model in comparison with the measurements for the case study chemical tanker

Full size image

It should be noted that the proposed model uses sea parameters Hs, Tz, Uwind, Vwind, etc. to estimate the speed loss, while Kwon’s method uses Beaufort numbers to categorize these parameters into several groups. Therefore, the estimated speeds by the proposed model are averaged in each group to be compared with the Kwon’s method. In order to decrease the uncertainty, the relative encountered wave angle between 0 ° and 10° and 170 ° and 180° is considered the head sea and following sea. From the full-scale measurements, the waypoints with β contain all heading angles within the interval β ± 5°, for instance, β located between 85 ° and 95° is associated with the heading angle of 90°.

In Fig. 8, the radius of the polar plot expresses the ship’s sailing speed in knots, and the polar angle describes the wave heading angle in degrees. The green dash-dotted line represents the “imaginary” baseline Vcalm for still water conditions, while the black dash-dotted line is obtained by full-scale measurement from the averaging measured speeds along with various heading angles. It is clearly shown that speeds predicted by the Kwon’s method always fluctuate around the baselines for all BNs. Obviously, for this blunt ship, Kwon’s method fails to predict the speed loss at sea. The proposed model can well predict the speed losses (actual speeds shown as the circle markers) from the full-scale measurements.

Figure 9 presents the details to obtain the measured sailing speed in the polar plots, as in Fig. 8. The measured speeds and wave heading angles are used to generate heatmaps, which can help to visualize how the Vreal changes as β increases from the head sea to the following sea. The darker areas in the heatmap contain more full-scale data (Vreal versus β). The full-scale–measured Vreal is significantly scattered along the averaged lines in the heatmaps. Both figures show that the most considerable speed reduction occurs in head wave operations and the effect becomes weaker when the β increase. The speed loss increases significantly as the Beaufort number rises, i.e., at harsher sea condition, and the most significant reduction is about 3 knots for the case study chemical tanker under BN-6 condition, i.e., 21.4% of the Vcalm under calm water conditions. In addition to the head waves, quartering waves, beam waves, the speed reduction is also noticed for the following sea and could not be ignored at severe wave conditions. Under the BN-6 condition, the speed loss is up to 0.4 kn (2%) for the chemical tanker at the following sea.

Fig. 9
figure 9

The heatmap and averaged measured speed Vreal in terms of the wave heading angle β for the studied chemical tanker

Full size image

4.4 Comparison and Validation for Slender Ships (a Container Ship and a PCTC)

A PCTC and a container ship are chosen to study the capability of the proposed model to predict speed loss for slender ships. Similar estimations as the chemical tanker are conducted, and the results of the comparison are illustrated in Figs. 10 and 11.

Fig. 10
figure 10

The speed loss estimation by both the Kwon’s method and the proposed model in comparison with the measurements for the case study PCTC

Full size image
Fig. 11
figure 11

The speed loss estimation by both the Kwon’s method and the proposed model in comparison with the measurements for the case study container ship

Full size image

Since each Beaufort scale represents quite a wide range of sea conditions as in Table 4, the measured ship speed Vreal for the same BN and β can differ significantly (more than several knots) especially for high BNs. The Kwon’s method predicts a reasonable trend of speed loss in terms of Beaufort scales and wave heading angles for the slender ships. The prediction errors of the mean speed loss within sea conditions of the same BN start to increase as sea conditions become severer. Moreover, Kwon’s method can not predict the speed loss for a sea state with specific metocean parameters, such as Hs, Tz, etc.

The proposed model cannot only predict better averaging measured speed Vreal (red circle markers coincide to the measurement averaged curve) even for the relative harsher wave condition, but also give more accurate speed loss estimation for upper and lower bound for wave conditions within each Beaufort scale (as the grey circle markers), which is estimated using limits of Hs within each Beaufort scale as in Table 4. In Fig. 10 and Fig. 11, the grey dotted lines represented speeds evaluated using the measurement data close to the considered Beaufort scale piecewise boundary, such as 2.5 m and 4.0 m for BN-6 condition for Fig. 10d, c. The largest margins between the upper and lower bound for each Beaufort scale are observed from the head sea to the quartering sea. For the harsh wave condition, the margin between the grey dotted line is more evident, and Kwon’s method has relatively poor prediction results. Sometimes, the estimated speed even lies out of the speed margin. The capability of predicting a ship’s speed loss at specific sea conditions rather than the approximate Beaufort scales is essential to develop measures to guide a ship’s operations, since the 1-m difference in Hs within the same Beaufort scale can lead to a significant error of speed loss prediction. In the following, the impact of such a prediction error on a ship’s voyage optimization is investigated.

5 Sensitivity of Voyage Optimizations to Speed Prediction Models

The shipping industry is facing great challenges to increase energy efficiency and reduce air emissions. One of the most efficient measures for such purposes is the so-called voyage optimization systems (DNV GL 2015), which can assist captains for voyage planning to avoid harsh weather conditions, to reduce fuel consumption, enhance the ship/cargo safety, and increase a ship’s arrival punctuality. The accuracy of the model used to predict a ship’s speed loss in a voyage optimization system is essential to the reliability of such a system. The intention of the following study is to demonstrate how sensitive the voyage optimization results to the accuracy of speed loss prediction models. Therefore, a generic model should be calibrated to accurately reflect the performance of an individual ship.

In this study, the voyage optimization is conducted by a three-dimensional Dijkstra’s algorithm proposed by Wang et al. (2019) to allow a more flexible speed adjustment and voyage planning. In such a system, the waypoint grid system is generated firstly for the potential sailing area composed of both time and space. A brief introduction of the workflow and its interaction with the speed loss (performance model) of the optimization method is presented in Fig. 12. To investigate the importance of implementing an accurate speed loss prediction model in a voyage optimization system, the container ship sailing in the North Atlantic is chosen, to demonstrate the difference of voyage optimization results caused by two different speed loss prediction models, i.e., the proposed model and the widely used Kwon’s method. Four winter voyages, named as 2009-01-18 and 2009-12-26 for eastbound and 2009-02-18 and 2010-01-13 for westbound, are used to demonstrate the impact. The actual routes (locations and time of a series of waypoints) and the measured fuel consumption are adopted to a quantity analysis.

Fig. 12
figure 12

The flowchart presents the interaction between the fuel consumption model and the optimization algorithm, for a voyage optimization process

Full size image

First, the optimized trajectories for those selected voyages are compared with the actual sailing in Fig. 13 when the proposed model, the Kwon’s method are used for voyage optimization, respectively. It shows that the speed loss prediction models have an essential impact on the voyage optimization results, i.e., two models lead to significantly different trajectories for the same voyage planning. Table 6 lists the details of voyage optimization results in comparison with actual sailing, such as the sailing distance, ETA, fuel consumption, and the mean values of encountered significant wave height Hs. The distances along different optimized routes vary from several kilometers to more than 100 km due to different speed loss models being used. For a fair impact study, the fuel consumption along all the three routes (actual sailing, optimized using the proposed speed loss model, and optimized using the Kwon’s model) is computed by the proposed model in this study. In the brackets, the actual fuel consumption and that estimated by the Kwon’s model are given as well. It shows that the voyage optimization based on the proposed speed loss model has achieved the best fuel saving, since the planned voyages are navigated in areas with the lowest Hs. Except the voyage 2009-01-18, the voyage optimization using the proposed model chooses a short distance route and lower speed leading to less fuel.

Fig. 13
figure 13

Optimum trajectories for the selected case study

Full size image
Table 6 Results of voyage optimization using the proposed model and Kwon’s method in comparison with the actual routes
Full size table

It should be noted that for the voyage optimization using Kwon’s method, the fuel consumption estimated by itself and the proposed model shows great discrepancy (from 15% to more than 40%). The contradictory results are caused by the different speed loss prediction models. For example, even though the voyage optimization by the proposed speed loss model recommends routes with moderate sea conditions (lower E[Hs]), the fuel consumption for those voyages is much higher than that using Kwon’s method. This is due to the incapability of the Kwon’s method for the speed loss prediction of the case study ship. Nevertheless, Kwon’s model has a relatively better speed loss prediction for this slender container ship. If the chemical tanker would be chosen for the demonstration, a huge difference in voyage optimization results will be expected.

Finally, the encountered significant wave height Hs and ship speed (V) along the optimized routes and the actual routes are presented in Fig. 14 for two typical voyages, i.e., the eastbound voyage 2009-01-18 and the westbound voyage 2010-01-13. The maximum difference of the encountered Hs for the voyage 2009-01-18 is almost 2 m. The voyage optimization using the proposed model recommends sailing speed 2 knots faster than that using Kwon’s method in the sailing area between 35 and 20 ° W to avoid encountering harsh sea environments. When the ship encountered large Hs above 6 m, the voyage optimization using the proposed model recommends to slow down significantly compared to the actual route to decrease the added resistance due to waves. A similar difference can be also observed for the voyage 2010-01-03. The optimized route using Kwon’s method encountered harsher wave conditions, while the route optimized by the proposed model can adjust the speed to sail in the calmest wave condition. The variation of sailing distance, therefore, can be also explained as different speed loss prediction models are used in the voyage optimization. Those different models may lead to completely different sailing patterns, even though the same optimization algorithm is used. For example, the Kwon’s method based voyage optimization may recommend a route encountering high sea states (Hs) with lower sailing speed. In contrast, the proposed model-based voyage optimization may recommend sailing faster to avoid severe sea environments. All these results indicate the importance of having an accurate speed loss prediction model in a ship’s voyage optimization system.

Fig. 14
figure 14

Encountered significant wave height Hs and ship speed V along the optimized and actual ship routes for the two case study voyages

Full size image

6 Conclusion

This study develops a semi-empirical model to predict a ship’s speed loss with arbitrary wave heading angles when sailing at actual sea environments (irregular waves). The model extends semi-empirical formulas of added resistance in head waves to consider all wave attacking angles. It requires limited input parameters of ship characteristics. Furthermore, a nonlinear correction factor in terms of significant wave height is added in the added resistance model to consider the nonlinear increase of fuel consumption when a ship is sailing in harsh sea environments. The proposed semi-empirical model has been validated by experimental tests in regular waves from 5 different types of ships with good agreements. The full-scale measurements from three case study ships, i.e., a merchant chemical tanker (blunt ship) and a PCTC (slender ship) sailing worldwide, as well as a container ship (slender ship) sailing in North Atlantic, are employed to validate the proposed model for the speed loss prediction when ships are sailing in a seaway (sea states of irregular waves). For the speed loss prediction under the actual sailing environments, significant speed losses are observed for the three case study ships under the BN-6 condition (the PCTC and the chemical tanker) and the BN-7 condition (the container ship). For head sea operations, the speed reduction is on average 17.6% for the PCTC, 21.4% for the tanker, and 14.1% for the container ship. The speed loss reduces as the wave heading angle moves to beam and following sea conditions, although there still exist a 5% speed loss in the following sea. The proposed model gives much more accurate speed loss predictions than the Kwon’s method, especially for blunt ships, as well as for severe sea conditions in head wave operations.

Both the proposed model and the Kwon’s model are implemented in a voyage optimization algorithm to study sensitivity of voyage optimization in terms of the accuracy of speed loss models. A huge impact on voyage optimization results due to different speed models is observed in terms of sailing distance, trajectories, sailing speed, encountered sea environments, etc. In this study, the proposed model shows a good agreement with the aforementioned ship type for both blunt or slender ships in the worldwide navigational area.