1 Introduction

A ship hull girder is a thin-walled structure formed by plates and stiffeners, which is mainly influenced by vertical bending as a result of the action of various forces, including the ship’s own weight, cargo weight, buoyancy, and wave loads. Typically, the strength of a ship structure is evaluated and controlled in three levels, namely, longitudinal strength, transverse strength, and local strength. Assessment of the longitudinal strength, or in other words, the strength of the main hull girder, is the most important part of strength calculations for ship structures to ensure their structural adequacy. When the applied longitudinal (vertical) bending moment on the ship hull girder reaches or exceeds its ultimate bending capacity, the ship is likely to collapse in two halves following the occurrence of buckling or yielding in its deck or bottom regions.

Different simplified methods have been developed to estimate the ultimate strength of a ship hull girder. The first attempt was made by Caldwell (1965). He first replaced any stiffened panel within the cross section of the ship hull girder with a plate panel that has an equivalent thickness and then calculated the fully plastic bending moment of the cross section, taking the buckling effects into account. For the buckling part, the yielding stress was multiplied by a factor demonstrating strength reduction, a quantity that was not fully known at that time. The so-called simplified Caldwell’s approach was thereafter improved by other researchers such as Nishihara (1983), Mansour et al. (1995), and Paik and Mansour (1995).

Smith (1977) presented a progressive collapse analysis procedure to recognize buckling effects more precisely. In Smith’s method, a ship’s cross section is divided into smaller elements, including unstiffened and stiffened plates. Initially, the average stress–average strain relationship is to be determined for any element within the ship’s cross section under the in-plane load, with the effects of yielding and buckling taken into consideration. Then, a progressive collapse analysis is conducted, assuming that the cross-sectional plane remains plane during bending and each element behaves according to its average stress–average strain relationship. Progressive collapse analysis using conventional finite element methods with the nonlinear effects for both material and geometry taken into account is possible. However, to achieve reliable results, high computational and human efforts are needed. After Smith, many researchers have attempted to derive new methods to constitute the average stress–average strain relationship for unstiffened/stiffened plate elements. Yao (1995, 2003) performed a thorough review of research studies on the ultimate strength assessment of ship hull girders, leading to some future research directions.

The subject of strength capacity analysis of aged ships has attracted the attention of researchers. Gordo et al. (1996) investigated the effects of four levels of corrosion on the ultimate strength of the hull girder on the basis of simplified method. Each level of corrosion reduced the thickness of flange and plating by 0.5 mm and web thickness by 1.0 mm. They found a 14% reduction in the ultimate bending moment of a ship section with the corrosion level of 4.

Guedes Soares and Garbatov (1996) presented a time-variant formulation to model the degrading effect of corrosion on the reliability of ship hulls. The effect of corrosion was represented as a time-dependent decrease in plate thickness that affects the midship section modulus. One repair policy was considered, and the example results showed the effect of plate replacement when its thickness reached 75% of the original thickness. The example results also illustrated how the limit value of the thickness in the repair criteria influences the reliability and the decision on repair actions.

Wirsching et al. (1977) assessed there liability of a ship hull girder considering the effects of corrosion on the ultimate strength of the vessel for 20 years of service life. In their work, the section modulus of the vessel was treated as a random process with a monotonically decreasing mean value. Also, a linear relation between the ultimate strength bending moment and yielding bending moment was assumed. For an example tanker, a maximum probability factor of failure 0.012 was obtained for a mean corrosion rate of 0.2 mm/year and 0.0053 for a mean corrosion rate of 0.1 mm/year.

Paik et al. (2003) used a set of time-dependent corrosion wastage models for 23 different member locations/categories of bulk carriers. They suggested the nominal design corrosion values for the primary members on the basis of the annualized corrosion rates. They also studied the effect of time-variant corrosion wastage on the ultimate hull girder strength and the section modulus. The criteria for repair and maintenance of heavily corroded structural members to keep the ultimate longitudinal strength at an acceptable level were discussed.

Vu Van and Yang (2017) studied the effect of corrosion on a VLCC (very large crude oil carrier) hull in the sagging bending with two levels of corrosion wastage and three coating lives by using the incremental–iterative method (Smith’s method). On the basis of their calculations, about 33% reduction in the ultimate strength of the vessel in the case of severe corrosion and age of 30 years was observed.

A formulation was presented by Guedes Soares and Garbatov (1999) for the assessment of the reliability of a ship hull with respect to the failure of the longitudinal members as a result of fatigue and corrosion. Their model allowed for the existence of multiple cracks and accounted for the crack growth process. The midship section modulus was described by a stochastic process. A new model was presented for the effect of corrosion in the framework of a time-dependent process with two stages. In the first one, no corrosion occurred due to the existence of coating protection. Upon failure of the protection system, the general corrosion was assumed to decrease plate thickness and affect the midship section modulus. The inspection was modeled as a random process. One repair policy was also considered in the example, which consisted of plate replacement when its thickness reached 75% of the original thickness. The time-dependent degrading effect of corrosion and crack growth was also modeled as a random process. The reliability was predicted by a time-variant formulation.

Hu et al. (2004) proposed a methodology to assess the time-variant ultimate strength of a ship hull girder under the degradations of corrosion and fatigue. First, an empirical formula based on finite element analysis was provided to estimate the ultimate strength of unstiffened and stiffened plates. Then, a nonlinear corrosion damage based on Weibull distribution was considered with an average rate of 0.061 mm/year. Finally, with the use of the simplified method, the ultimate strength of a ship hull section was determined. According to their results, the ultimate strength bending moment reduced by 30% and 37.5 due to crack and corrosion in the no-repair case for age of 25 years for hogging and sagging bending modes, respectively.

The objective of this study is to investigate the effects of different types of corrosion models on the ultimate strength and collapse behavior of a floating production, storage, and offloading (FPSO) vessel hull girder in both hogging and sagging conditions. To perform the current investigation, the computer code HULLST, which was originally developed and validated by Nikolov and Yao 1991, Nikolov and Yao 1992) based on Smith’s method, is employed. The HULLST computer code was extended by Yao et al. (2003) so that it could be applied when assessing the ultimate strength of ship hull girders considering local pressure loads.

The procedure implemented into the HULLST computer code for progressive collapse analysis of a hull girder can be summarized as follows:

  1. 1)

    The cross section is subdivided into small elements composed of plates and stiffened plates.

  2. 2)

    Their average stress–average strain relationships are derived by the analytical method.

  3. 3)

    The curvature of the cross section in the vertical direction is given incrementally, assuming that the plane cross section remains plane and that bending takes place with respect to the instantaneous neutral axes.

  4. 4)

    At a certain incremental step, the in-plane rigidity of the elements is obtained using the slope of average stress–average strain curve at each specified strain.

  5. 5)

    With the use of the in-plane rigidities of individual elements, locations of the instantaneous neutral axes are determined, and the flexural rigidities of the cross section are calculated.

  6. 6)

    Increments of bending moment corresponding to the applied increments of curvature are then obtained. At the same time, the increments of strains and stresses in individual elements are calculated.

  7. 7)

    At the end of each step, increments of curvatures and bending moments are summed, as well as those of strains and stresses to provide their cumulative values.

  8. 8)

    The same procedure is repeated from step (3).

With the use of the results of Khedmati et al. (2011) and Nouri et al. (2012), the HULLST computer code is further enabled to consider the effects of various types of corrosion (uniform, random, pitting, and tanker pattern) when investigating the ultimate strength of ship hull girders. The procedure to obtain analytically the average stress–average strain relationships for uncorroded/corroded steel plates under uniaxial compression is fully demonstrated by Khedmati and Nouri (2015).

2 Ship Chosen for the Case Study

2.1 Main Dimensions and Structural Scantlings

A double-hull FPSO vessel is selected to investigate the effects of corrosion on the ultimate strength of the ship hull girder. The FPSO vessel under consideration has an approximate length of 300 m, a breadth of 58.5 m, and a height of 32 m. The design draught is 23.5 m, the ballast draught is 8 m, and the distance between the main frames is 5 m. The full specifications of the midship section, including structural scantlings of the plates and stiffeners, together with the type/grade of materials can be observed in Figure 1.

Figure 1
figure 1

Scantling of the midship section of the FPSO vessel

Full size image

The plates and stiffeners of the deck and bottom regions are made of high-tensile-strength steel of grade AH with the yield strength of 315 MPa. Fracture-sensitive regions such as the bilge keel corners are made of high-tensile-strength steel of grade DH with the yield strength of 315 MPa. Also, the plates and stiffeners of the side shells and the longitudinal bulkheads, other than the deck and bottom corners, are made of ordinary-strength steel of grade B with the yield strength of 235 MPa. In the places where the side shells are connected to the deck and the bottom, high-tensile-strength steel of grade AH is used.

Geometrical dimensions and steel grades of the longitudinal stiffeners in the midship section of the FPSO vessel are summarized in Table 1.

Table 1 Geometrical dimensions and steel grades of the longitudinal stiffeners in the midship section of the FPSO vessel (unit: mm)
Full size table

2.2 Discretization of the Midship Section

To employ the HULLST computer code, the midship section (or any other section under consideration) needs to be discretized into individual elements, which mostly consist of unstiffened/stiffened plate elements. In the case of the FPSO vessel adopted for the analyses herein, a total of 203 elements are recognized as depicted in Figure 2.

Figure 2
figure 2

Element numbers of the midship section of the FPSO vessel

Full size image

Unstiffened/stiffened plate elements are accompanied with different components of initial geometrical deflections, as shown in Figure 3; this is while the effects of residual stresses are ignored in this study.

Figure 3
figure 3

Different components of initial geometrical imperfections. (a) Initial deflection of the plate, (b) initial deflection of the stiffener and (c) initial angular distortion of the stiffener

Full size image

The initial deflection of the plate part in Figure 3a is in a so-called idealized thin-horse mode (Yao et al. 1992) as described by Eq. (1)

$$ {w}_0=\sum \limits_{m=1}^{11}{A}_{0m1}\sin \frac{m\uppi x}{a}\sin \frac{\uppi y}{b} $$
(1)

where a is the length of the plate, b the breadth of the plate, and m is the number of longitudinal half-waves in the plate.

The coefficients of this mode (A0m1) are given in Table 2 (Yao et al. 1992) as functions of the plate aspect ratio and its slenderness. The coefficients are scaled that the maximum magnitude of initial deflection, w0 max, is

$$ {w}_{0\max }=0.05{\beta}^2t $$
(2)

where t is the uncorroded thickness of the plate.

Table 2 Coefficients of thin-horse mode initial deflection as a function of plate aspect ratio (Yao et al. 1992)
Full size table

The slenderness parameter is defined as

$$ \beta =\frac{b}{t}\sqrt{\frac{\sigma_Y}{E}} $$
(3)

The initial deflection for the stiffener is expressed by Eq. (4) and represented by Figure 3b

$$ {w}_{s0}=\left(0.0025\times a\right)\sin\ \left(\frac{\uppi \mathrm{x}}{\mathrm{a}}\right) $$
(4)

The initial angular distortion of the stiffener is taken as (Figure 3c)

$$ {\varphi}_0{h}_w=\left(0.0025\times a\right)\sin\ \left(\frac{\uppi \mathrm{x}}{\mathrm{a}}\right) $$
(5)

where hw is the height of the stiffener web.

3 Corrosion Conditions Considered for the Progressive Collapse Analyses

The effects of different types of corrosion covering uniform corrosion, random corrosion, pitting corrosion, and tanker pattern (random) corrosion with a lifetime of 5, 10, 15, 20, and 25 years on the ultimate strength of the studied ship were investigated using expanded HULLST software in both hogging and sagging conditions. The procedure for calculating the equivalent corrosion depth considering no repair is described in the following for each of the corrosion conditions.

3.1 First Condition: Uniform Corrosion

In this condition, the equivalent corrosion depth is calculated using the corrosion relationship proposed by Melchers et al. (2010) for the studied midship section considering the ages 5, 10, 15, 20, and 25 years. The corrosion equation developed by Melchers et al. is as follows:

$$ \left\{\begin{array}{c}\mu =0.20{t}_i\kern4em \mathrm{for}\ {t}_i\le 1.3\ \left[\mathrm{year}\right]\ \\ {}\mu =0.13+0.10{t}_i\kern1.5em \mathrm{for}\ {t}_i>1.3\ \left[\mathrm{year}\right]\ \end{array}\right. $$
(6)

μ where and ti are the average depth of corrosion and age in a year, respectively.

3.2 Second Condition: Random Corrosion

Khedmati et al. (2011) performed a series of nonlinear elastic–plastic finite element analyses on the plates in different conditions of uncorroded, uniformly corroded, and randomly corroded. The plates were subjected to in-plane compression load. Full-range average stress–average strain relationships of the plates were derived considering the changes in plate aspect ratio, plate slenderness or thickness, mean corrosion depth, and standard deviation of random thickness variation. The aspect ratio, thickness, and random corrosion parameters have different effects on the strength characteristics of the corroded plate. Random corrosion has weakening effects on the buckling and ultimate strengths of the plate, while uniform corrosion leads to an intermediate condition for the plate with different probable random thickness variations.

To investigate the strength characteristics of the randomly corroded plate under longitudinal in-plane compression, without any modeling of the random thickness variations, the following simple equation was derived to reach an equivalent thickness assuming a standard deviation of 0.2 mm:

$$ {\mu}_{\mathrm{Random}}=\mu +S $$
(7)

where S is the standard deviation.

The equivalent corrosion depth for the second condition, or the so-called random corrosion, is determined using a combination of Eqs. (6) and (7) for the midship section under study at different ages of 5, 10, 15, 20, and 25 years

$$ \left\{\begin{array}{l}\mu =0.20{t}_i+\mathrm{S}\kern4.5em \mathrm{for}\ {t}_i\le 1.3\ \left[\mathrm{year}\right]\ \\ {}\mu =0.13+0.10{t}_i+\mathrm{S}\kern1.5em \mathrm{for}\ {t}_i>1.3\ \left[\mathrm{year}\right]\ \end{array}\right. $$
(8)

3.3 Third Condition: Pitting Corrosion

A series of validated nonlinear elastic–plastic finite element analyses on the plates in different uncorroded and pitted conditions, subjected to in-plane compression load, was later conducted by Nouri et al. (2012). Full-range average stress–average strain relationships of the plates were derived considering the changes in plate aspect ratio, plate slenderness or thickness, density of cone-type pitting, pit diameter, and ratio of pit diameter to the depth of the pits.

To assess the strength characteristics of the one-side pitted plate under longitudinal in-plane compression without any modeling of the pitting, they developed a practical proposal to calculate the effective thickness of the plate. This was achieved through replacement of the pitted plates with their equivalent uncorroded plates, considering two conditions to be fulfilled. The first condition was that the ultimate strength of the pitted plate equals that of the uncorroded plate. The second condition was that the final residual strength of the pitted plate equals that of the uncorroded plate.

The equivalent thickness formulation proposed by Nouri et al. (2012) in the case of one-side pitting corrosion has the following form:

$$ {\mu}_{\mathrm{Pitting}}=1.51\mu +1.68 $$
(9)

The equivalent corrosion depth for the third condition in this study, or the so-called pitting corrosion, is determined using a combination of Eqs. (6) and (9) for the midship section under study at different ages of 5, 10, 15, 20, and 25 years

$$ \left\{\begin{array}{c}\mu =1.51\times \left(0.20{t}_{\mathrm{i}}\right)+1.68\kern4em \mathrm{for}\ {t}_{\mathrm{i}}\le 1.3\ \left[\mathrm{year}\right]\ \\ {}\mu =1.51\times \left(0.13+0.10{t}_{\mathrm{i}}\right)+1.68\kern1.5em \mathrm{for}\ {t}_{\mathrm{i}}>1.3\ \left[\mathrm{year}\right]\ \end{array}\right. $$
(10)

3.4 Fourth Condition: Tanker Pattern (Random) Corrosion

Corrosion in a ship hull structure is related to a variety of factors, including temperature, travel direction, and loading condition. On the basis of the study by Zayed et al. (2018), the tanker structure can be divided into different regions according to their differences in loading conditions (Figure 4). Region A in both fully loaded and ballast conditions is under the influence of air from both sides. Region B is in the ballast condition under the influence of air from both sides and is submerged from both sides in the fully loaded condition. Region C in the fully loaded condition from both sides is submerged, but its internal surface is in contact with the air and the external surface is in contact with sea water in the ballast condition. Region D is considered submerged from both sides in both fully loaded and ballast conditions.

Figure 4
figure 4

Division of FPSO vessel structure on the basis of corrosion behavior (Zayed et al. 2018)

Full size image

Zayed et al. (2018) and Guedes Soares et al. (2008) investigated the corrosion behavior of steel tankers on the basis of a new nonlinear standardized corrosion model considering the effects of various environmental factors, which is described in the form of

$$ {d}_{\mathrm{n}}\left({t}_{\mathrm{i}}\right)=\left\{\begin{array}{c}{d}_{\infty}\left[1\hbox{-} \exp \left(\hbox{-} \left({t}_{\mathrm{i}}-{\tau}_{\mathrm{c}}\right)/{\tau}_{\mathrm{t}}\right)\right]\kern1.75em \mathrm{for}\ {t}_{\mathrm{i}}>{\tau}_{\mathrm{c}}\ \\ {}0\kern10.75em \mathrm{for}\ {t}_{\mathrm{i}}\le {\tau}_{\mathrm{c}}\ \end{array}\right. $$
(11)

where dn is the depth of corrosion (function of time), d∞ is the long-term depth of corrosion, τc is the coating life in a year, and τt is the transition time in a year.

The methodology behind the above-described model is that the corroded thickness of each particular region is seen in the short term in an effective time interval, and finally, a long-term corrosion model is obtained with the accumulation of their corroded thicknesses.

Figure 5 demonstrates the corrosion behavior in different regions of the FPSO vessel under consideration on the basis of the so-called tanker pattern corrosion model (Zayed et al. 2018; Guedes Soares et al. 2008). The coating life in this case is taken as 4 years.

Figure 5
figure 5

Corrosion behavior in different regions of the FPSO vessel on the basis of the tanker pattern corrosion model

Full size image

In summary, in the fourth condition corresponding to the case of tanker pattern (random) corrosion, the results of studies of Zayed et al. (2018) and Guedes Soares et al. (2008) are combined with Eq. (7) proposed by Khedmati et al. (2011). Accordingly, the corrosion depth is calculated for the ages of 5, 10, 15, 20, and 25 years of the ship under assessment, assuming a so-called tanker pattern (random) corrosion behavior.

4 Results and Discussions

4.1 Case of Intact FPSO Vessel

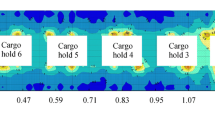
Progressive collapse analysis is conducted on the intact FPSO vessel hull girder in both hogging and sagging conditions using the modified version of HULLST computer code. Changes in the vertical bending moment and the height of the neutral axis as functions of vertical curvature are shown in Figure 6. Figure 7 presents the stress distributions at different stages of progressive collapse analysis. Notably, the triangle (∆) and circle (○) symbols placed on some elements within the stress plots in Figure 7 indicate the onset of yielding and occurrence of buckling, respectively, in that element. The results of progressive collapse analysis of the intact FPSO vessel hull girder are summarized in Table 3.

Figure 6
figure 6

Changes in vertical bending moment and height of neutral axis as functions of vertical curvature (intact FPSO vessel hull girder)

Full size image
Figure 7
figure 7

Stress distributions at different stages of progressive collapse analysis (intact FPSO vessel hull girder)

Full size image
Table 3 Results of progressive collapse analysis of intact FPSO vessel hull girder
Full size table

In Figure 6, e is the height of the neutral axis, D is the height of the ship, MY is the resultant bending moment acting on the cross section, and MiY is the initial yielding bending moment of the intact cross section

Points C and H on the curves of vertical bending moment–vertical curvature (or simply speaking, the moment–curvature curves) shown in Figure 6 correspond to the ultimate strength levels at hogging and sagging conditions, respectively. On the one hand, the moment–curvature curves generally have an ascending trend until the ultimate strength level, while they follow a descending trend in the post-ultimate-strength regions. On the other hand, after the ship attains its ultimate strength, the height of the neutral axis (measured from the ship bottom) increases in case of the hogging condition and decreases in case of the sagging condition (Figure 6).

A decrease in the bending capacity of the ship cross section and a change in the height of its neutral axis should be interpreted in conjunction with the stress distributions extracted and shown in Figure 7. Smith’s method adopted in the HULLST computer code is inherently a curvature-controlled procedure.

An incremental growth of the curvature of FPSO vessel hull girder in the hogging/sagging conditions leads to the increase in the tensile stress for deck/bottom elements and the compressive stress for bottom/deck elements, respectively. In turn, excessive tensile/compressive stresses in the hogging/sagging conditions may finally result in yielding of the deck/bottom members and buckling of the bottom/deck members, respectively. With the progressive buckling of the bottom/deck members in the hogging/sagging conditions and the reduction of their in-plane stiffness (reflected in the form of negative slopes of the member’s average stress–average strain curve), the neutral axis of the ship cross section moves upwards/downwards, respectively.

Figure 7 shows that for the hogging mode, in step A, no (buckling/yielding) failure is observed in the cross-sectional members. Instep B, some of the deck members that have the biggest distance to the neutral axis fail. In step C, which corresponds to the ultimate strength level, the failure pattern of cross-sectional members does not change considerably. However, according to the behavioral curves of the contributing members, the maximum bending capacity is attained. In steps D and E, following the ultimate strength level, all the deck members and some of the members in both side shells and longitudinal bulkheads fail under tension. Furthermore, buckling failure is propagated in a number of members in the bottom, side shells, and longitudinal bulkheads. A cumulative consequence of extensive buckling/yielding failures in the ship cross section appears in the form of a sharp drop in its bending capacity in the post-ultimate-strength region of the moment–curvature curve indicated in Figure 6.

Different steps of progressive collapse analysis of the ship cross section for the sagging mode are also depicted in Figure 7. As can be confirmed, in step F, no failure takes place. In step G, the first trace of the failures appears in the form of buckling in a number of inner side shell members located near the deck owing to the relatively lower grade of the material. The ship cross section reaches its maximum strength in step H when the deck members are fully buckled. In steps I and J, failures further develop, thereby expanding the buckling in some members of the side shells and longitudinal bulkheads. In addition, yielding in the remaining members of bottom, side shells, and longitudinal bulkheads is observed. As a result, the strength of the ship cross section is significantly reduced according to the trends revealed in the moment–curvature curves shown in Figure 6.

Table 3 categorizes the values of bending moments and curvatures of the ship cross section corresponding to different steps shown in Figure 6. Values of the initial yielding bending moment (MiY) related to the state of initial yielding of the ship cross-sectional members, which were determined based on the simple beam theory, and their corresponding curvature (κiY) are presented in Table 3. As can be understood, the ultimate bending strength of the intact FPSO vessel hull girder in the hogging condition is greater than that in the sagging condition. The normalized ultimate bending moment is 1.00 in the hogging condition and 0.91 in the sagging condition.

4.2 Case of Corroded FPSO Vessel

The summary of the outcomes related to the progressive collapse analysis of the FPSO vessel hull girder with the assumption of different corrosion conditions for the lifetimes of 5, 10, 15, 20, and 25 years is presented in this section.

Moment–curvature curves are summarized in Figure 8 for the corroded FPSO vessel hull girder in different corrosion conditions. The ultimate strength of the FPSO vessel hull girder is reduced with the increase in age. The reduction is relatively slight for both uniform corrosion and random corrosion (with a standard deviation of 0.2 mm) conditions, while it is significant in cases of pitting corrosion and tanker pattern (random) corrosion.

Figure 8
figure 8

Changes in vertical bending moment as a function of vertical curvature at different ages (corroded FPSO vessel hull girder)

Full size image

Figures 9, 10, 11, and 12 show a collection of the cross-sectional stress distributions at the ultimate strength level for different ages of the FPSO vessel hull girder suffering from the presumed corrosion conditions. In general, the ultimate strength amounts are close to each other in two cases of uniform corrosion and random corrosion due to the low difference in the corrosion depths. The composition of failure of the members in the ultimate strength step is completely changed because of earlier buckling of the members in the pitting corrosion condition. The situation for the failure of the members is even worse than in the other conditions, such as in the tanker pattern corrosion condition, because of the high rate of corrosion in the bottom members considering the environmental factors.

Figure 9
figure 9

Stress distributions at the ultimate strength level for the FPSO vessel with different ages (uniform corrosion)

Full size image
Figure 10
figure 10

Stress distributions at the ultimate strength level for the FPSO vessel with different ages (random corrosion)

Full size image
Figure 11
figure 11

Stress distributions at the ultimate strength level for the FPSO vessel with different ages (pitting corrosion)

Full size image
Figure 12
figure 12

Stress distributions at the ultimate strength level for the FPSO vessel with different ages (tanker pattern [random] corrosion)

Full size image

According to Figure 9, for the case of uniform corrosion in the hogging condition, the ultimate strength level failure pattern of the cross section at the age of 10 years is more expanded than that at the age of 5 years, while the ultimate strength level failure patterns of the cross section are similar at the ages of 10, 15, 20, and 25 years. When the FPSO vessel hull girder bends in a sagging way, for all the analyzed ages (e.g., 5, 10, 15, 20, and 25 years), the cross-sectional members fail at the ultimate strength level with almost the same pattern. At the ultimate strength step of the hogging mode, the members of the deck yielded and the members of the bottom buckled, but in the ultimate strength step of the sagging mode, only the members of the deck buckled and no yielding happened in the bottom. This condition could reflect the inappropriate design of the deck members and the reason for the lower ultimate bending strength of the sagging condition in comparison with that of the hogging condition.

The results in Figure 10 for the random corrosion condition reveal that the failure pattern of the cross-sectional members at the ultimate strength step for various ages of 5, 10, 15, 20, and 25 years is almost unchanged for both hogging and sagging modes of bending. However, in the sagging condition, only buckling damage of the deck members is observed.

As shown in Figure 11 for the pitting corrosion condition, the failure pattern of the cross-sectional members at the ultimate strength level is not constant in the hogging mode; thus, the number of yielded deck members decreased at ages 10, 15, 20, and 25 years in comparison with that at 5 years of age. Moreover, the combination of buckling failure for the members of the bottom does not change considerably. In the sagging mode, similar to the conditions of uniform corrosion and random corrosion, only buckling occurs for the deck members in a way that the number of buckled members is partially reduced at the older ages.

Stress distributions that correspond to the tanker pattern corrosion condition at the ultimate strength step are shown in Figure 12. In the case of hogging, the number of failed deck members decreases with increase in the age of the vessel, so that yielding is not seen any more at the age of 25 years. Buckling is observed at all ages for the members of the bottom and some members of side shells and longitudinal bulkheads. In the sagging mode, similar to the conditions of uniform, random, and pitting corrosion, only buckling of deck members takes place and no significant change occurs in the pattern of failure of the members at older ages.

The results of the progressive collapse analysis for the corroded FPSO vessel hull girder are summarized in Tables 4, 5, 6, and 7. The value of residual strength factor (RF) is calculated in those tables using the following equation:

$$ RF=\frac{M_{\mathrm{ultimate}}}{M_{\mathrm{design}}} $$
(12)

where Multimate is the ultimate bending moment of the section (also called Mmax) and Mdesign is the design bending moment.

Table 4 Summary of results of progressive collapse analysis of FPSO vessel hull girder and values of residual strength factor in case of uniform corrosion
Full size table
Table 5 Summary of results of progressive collapse analysis of FPSO vessel hull girder and values of residual strength factor in case of random corrosion
Full size table
Table 6 Summary of results of progressive collapse analysis of FPSO vessel hull girder and values of residual strength factor in case of pitting corrosion
Full size table
Table 7 Summary of results of progressive collapse analysis of FPSO vessel hull girder and values of residual strength factor in case of tanker pattern (random) corrosion
Full size table

On the basis of the RU-SHIP standard (DNVGL 2011) and also Sun and Bai (2000), the following calculations are made:

  • The still-water bending moment is

$$ {M}_{\mathrm{sw}}=\left\{\begin{array}{c}-0.065{C}_{\mathrm{w}}{L}^2B\left({C}_{\mathrm{B}}+0.7\right)\kern1.25em \mathrm{for}\ \mathrm{sagging}\ \\ {}{C}_{\mathrm{w}}{L}^2B\left(-0.15{C}_{\mathrm{B}}+0.1225\right)\kern0.5em \mathrm{for}\ \mathrm{hogging}\ \end{array}\right. $$
(13)

  • The wave bending moment is

$$ {M}_{\mathrm{w}}=\left\{\begin{array}{c}-0.11{C}_{\mathrm{w}}{L}^2B\left({C}_{\mathrm{B}}+0.7\right)\kern1.25em \mathrm{for}\ \mathrm{sagging}\ \\ {}0.19{C}_{\mathrm{w}}{L}^2B\left({C}_{\mathrm{B}}\right)\kern4em \mathrm{for}\ \mathrm{hogging}\ \end{array}\right. $$
(14)

where L is the length of the ship, B is the breadth of the ship, CB is the block coefficient of the ship, and

$$ {C}_{\mathrm{w}}=\left\{\begin{array}{c}10.75-{\left(\left(300-L\right)/100\right)}^{3/2}\kern0.5em \mathrm{for}\ 100<L\le 300\\ {}10.75\kern8.5em \mathrm{for}\ 300<L\le 350\\ {}10.75-{\left(\left(L-350\right)/150\right)}^{3/2}\kern0.5em \mathrm{for}\ 350<L\kern2.25em \end{array}\right. $$
(15)

  • The design bending moment is finally obtained as

$$ {M}_{\mathrm{design}}={M}_{\mathrm{sw}}+{M}_{\mathrm{w}} $$
(16)

The values of the design bending moments for the studied FPSO vessel are determined as follows:

$$ {M}_{\mathrm{design}}=\left\{\begin{array}{c}-15326\ \mathrm{MN}\kern0.75em \mathrm{for}\ \mathrm{sagging}\ \\ {}+15329\ \mathrm{MN}\kern1em \mathrm{for}\ \mathrm{hogging}\ \end{array}\right. $$
(17)

According to the summarized results of the uniform corrosion condition (Table 4), compared with the intact condition, the ultimate strength at the age of 25 years is reduced by 16.2% and 14.96% for the hogging mode and the sagging mode, respectively. The minimum value of RF in the hogging mode is 1.90 for 25 years of age; for the intact case, this factor is 2.27 at that age. The corresponding values of this factor are 1.75 and 2.06, respectively, for the sagging mode.

Table 5 summarizes the results for the second condition of corrosion. In the random corrosion condition with a standard deviation of 0.2 mm, a slight difference in ultimate strength values is observed from those in the uniform corrosion condition. At the age of 25 years, the ultimate strength reduction was about 1.54% compared with the uniform corrosion condition and 17.49% compared with the intact condition. Those in the sagging mode are 1.64% and 16.35%, respectively. The minimum values of RF are 1.87 and 1.73 for the hogging mode and the sagging mode, respectively, both at the age of 25 years.

Table 6 lists the results for the third case of corrosion. In the pitting corrosion condition, the ultimate strength reduction rate is much more severe than that in the uniform corrosion condition, so that for a 25-year-old ship, an ultimate strength reduction of about 20% is observed relative to the uniform corrosion condition and about 32% relative to the intact condition in both hogging and sagging modes. The minimum acquired RF is 1.54 for the hogging mode and 1.40 for the sagging mode.

A summary of the results obtained for corrosion in the fourth condition (random corrosion with tanker pattern) is presented in Table 7. At the age of 25 years, the reduction in ultimate strength in the case of hogging is about 25% compared with the uniform corrosion condition and 37% compared with the intact condition. These values are 19% and 31%, respectively, for the sagging case. The minimum RF in both cases of hogging and sagging is 1.43.

Figures 13 and 14 present the values of the ultimate strength obtained from 52 progressive collapse analyses for different corrosion conditions, including uniform corrosion, random corrosion, pitting corrosion, and tanker pattern corrosion. These figures show that the values of ultimate strength in two cases of uniform corrosion and random corrosion (with a standard deviation of 0.2 mm) are similar to each other, and their differences in hogging and sagging modes are almost constant. The behaviors are different in the pitting corrosion and tanker pattern corrosion conditions. The reduction of the ultimate strength bending moment is more pronounced in both hogging and sagging modes for the pitting corrosion and tanker pattern corrosion conditions. In the hogging ode, for the age of less than 10 years, the ultimate strength of the pitting corrosion condition is lower than that of the tanker pattern corrosion. After 10 years to 25 years of life, the tanker pattern corrosion produces a lower ultimate strength than the pitting corrosion condition. This phenomenon occurred due to the high rate of corrosion in the ship bottom in the tanker pattern corrosion. In the sagging mode, for less than 15 years of life, the pitting corrosion condition gives a lower ultimate strength than the tanker pattern corrosion. After 15 years of life up to 25 years, the two corrosion conditions have an almost similar ultimate strength.

Figure 13
figure 13

Changes in ultimate strength as a function of age (hogging condition)

Full size image
Figure 14
figure 14

Changes in ultimate strength as a function of age (sagging condition)

Full size image

Figures 15 and 16 present the changes in RF versus age for the conditions of uniform corrosion, random corrosion, pitting corrosion, and tanker pattern corrosion in both hogging and sagging modes of bending. The vessels are normally designed for 25 years of life, and values of RF less than 1.50 are not allowed (Amdahl and Skallerud 2002; Paik and Thayamballi 2003). The tanker pattern corrosion condition and, with some degree of caution, the pitting corrosion lead to RFs less than the permissible level when the age of the vessel is 20 years and above.

Figure 15
figure 15

Changes in residual strength factor as a function of age (hogging condition)

Full size image
Figure 16
figure 16

Changes in residual strength factor as a function of age (sagging condition)

Full size image

Nouri (2011) provides thorough insights into the analyses performed and reported herein.

5 Conclusions

Some simplified approximations developed by the authors in their previous research outputs were implemented into the computer program HULLST, an in-home computer code written to perform progressive collapse analysis of ship hull girders. The code is now further enabled to assess the analyses under longitudinal bending considering different types of corrosion in ship cross-sectional structural members. The average stress–average strain relationships for unstiffened/stiffened plate elements subjected to in-plane tensile/compressive loads are derived in an analytical manner by employing the authors’ simplified approximations.

The modified HULLST code is applied to the progressive collapse analysis of an FPSO vessel hull girder. Forty-two analyses were performed on the FPSO vessel hull girder considering different corrosion scenarios, including uniform corrosion, random corrosion, pitting corrosion, and tanker pattern corrosion. The analyses were conducted on the bending of the ship hull girder in both hogging and sagging conditions. The following outcomes can be drawn:

  • The responses in vertical bending are almost the same for the cases of uniform corrosion and random corrosion (with a standard deviation of 0.2 mm) in either hogging or sagging conditions. A monotonic decrease in the ultimate strength of the ship hull girder is observed as the age of the ship increases.

  • Both uniform corrosion and random corrosion models have close outcomes. The value of relative reduction in the ultimate strength of the ship hull girder (compared with the intact condition) ranges roughly from 6% for the age of 5 years to 17% for the age of 25 years in the hogging mode. The relative reduction in the ultimate strength ranges from 4% to 16% in the sagging mode.

  • The pitting corrosion and tanker pattern (random) corrosion models lead to higher relative reductions in ultimate strength. The pitting corrosion model leads to a 16%–32% relative reduction in the ultimate strength for ship ages of 5–25 years in either hogging or sagging mode. The relative reduction of the ultimate strength ranges within 6%–37% in the hogging mode and 3%–31% in the sagging mode when the tanker pattern (random) corrosion model is employed at ship ages of 5 to 25 years.

  • The tanker pattern random (corrosion) condition (or model), which divides the tanker structure into different regions according to their differences in loading conditions, is believed to reflect the most realistic condition for the corrosion in similar ship structures to the FPSO vessels.

  • At ship ages below 5 years, simpler uniform corrosion and random corrosion models lead to ultimate strength values that are similar to those obtained for the tanker pattern random corrosion model.

  • The ultimate strength values for the pitting corrosion model approach those obtained for the tanker pattern random corrosion model for ship ages above 10 years.

  • When the ship ages are between 5 and 10 years, the tanker pattern random corrosion model has a unique effect on the ultimate strength value, where it cannot be exactly simulated by the other three corrosion models.

  • Further research is proposed to study the corrosion phenomena and their influences on the ultimate strength behavior of vessels, especially those aged above 20 years, considering planned repairs.