1 Introduction

The majority of renewable energy sources, such as wind and solar energies, have a fluctuating character, which alters the quality of the power injected into the electrical grid (Kumar et al. 2016; Anvari et al. 2016). In fact, the integration of these renewable sources into the electrical grid can lead to the major need for the adjustment of voltage and frequency to overcome eventual electrical disturbances (e.g., voltage droops and short circuits) (Antonova et al. 2012). By contrast, marine current energy is more stable than wind and solar energies and represents a promising solution to deal with the aforementioned issues (Melikoglu 2018; Chen et al. 2018). Indeed, marine current energy mainly originates from the tides, which are a direct result of the combination of the Earth’s rotation and the gravitational forces exerted on a water body by the Moon and Sun (Hodur 1997). Thus, predicting the particular location of the main component of these currents for long time periods is possible (Hodur 1997; Rourke et al. 2010).

In addition, according to Thiébaut and Sentchev (2015), marine current resources are abundant in such a scale that their use for energy production can satisfy the world’s energy demand. Marine current turbines (MCTs) are evolving rapidly because more reliable oceanographic data are available and all of the advanced techniques developed, tested, and applied for wind turbines can be adapted to MCTs even if the dynamics of tides are totally different from those of wind (Fox et al. 2018).

In recent years, numerous studies of the hydrodynamic aspects (Mycek et al. 2014; Frost et al. 2015; Blackmore et al. 2016) and the design of specific generators for the marine environment (Benelghali et al. 2012; Seck et al. 2018; Chen et al. 2019) have been conducted. Meanwhile, other studies focus on the electronic part of power (Pham et al. 2017; Einrí et al. 2019; Omkar et al. 2019; Qian et al. 2019).

To improve the energy conversion performance of MCTs and ensure that tidal energy resources are cost-effective, rotor speed regulation, which can be classified into two types, i.e., fixed and variable speeds, is investigated in this study. Jena and Rajendran (2015) and Kettache (Khettache 2019) conducted a comparative study between fixed-speed and variable-speed wind generators. The variable-speed wind turbine is more advantageous than the fixed-speed wind turbine because it increases the energy efficiency, improves the quality of the kinetic energy produced, and stabilizes the fluctuations of the voltage and power of the electrical grid.

In the context of wind turbine technologies, many command algorithms have been designed and developed in the past decades to optimize the operation of turbines to maximize the energy efficiency. These controllers can be classified into four categories, namely, optimal control, nonlinear control, predictive control, and fuzzy logic.

Liu et al. (2016) proposed a fuzzy logic controller for the wind turbine system to achieve the objective of maximum power extraction based on a two-mass model. Bassi et al. (Bassi and Mobarak 2017) examined the variable-speed wind turbine in full and partial load segments through predictive control. This approach considers the maximum power point, with the goal of maximizing the power generated by the wind turbine.

In the litrature, many controllers based on nonlinear control have been used to model wind turbines. Boukhezzar and Siguerdidjane (2010, 2011) used a nonlinear controller to deal with the wind power capture optimization problem while restricting transient loads on the drivetrain components. Prasad et al. (2019) developed a new control approach for the generations and loads in the integrated wind power system. This control approach is based on nonlinear control.

Finally, optimal control has been widely used to model and design the variable-speed wind turbine. Optimal control can be applied in two quadratic linear forms, namely, linear quadratic regulator (LQR) and linear quadratic Gaussian (LQG).

Barrera-Cardenas and Molinas (2012) applied the LQG control to model wind turbines. The proposed LQG control has shown useful properties, good performance, and robustness in controller design which has been applied to wind energy converter systems. Kumar and Stol (2010) proposed and tested the use of Simulink to simulate the LQR controller for wind turbines to achieve better rotor speed regulation. To maximize the energy generated from wind, Fakharzadeh et al. 2013) presented a linear control law using the LQR approach. Bayat and Bahmani (2017) addressed both the problems of power regulation and wind turbine control using the LQR approach feedback. Mahmoud and Oyedeji (2016) proposed a new voltage control scheme based on the LQR control design for a grid-connected wind farm. The proposed solution can be conveniently utilized for multi-input multi-output systems.

Although the control design is widely used in wind turbine technology, to the best of our knowledge, only a few studies considered the control of MCTs. Zhou et al. (2013) proposed two control strategies (i.e., speed control and torque control) for the power limitation of the MCT when the speed of the marine current exceeds the nominal value. The torque control strategy limits the generator power to a certain value during the dynamic process. However, the proposed control strategy limits only the power for the high-speed marine current. It does not deal with the entire range of variations of the marine current speed. Toumi et al. (2017) reported on speed control using only the classical proportional–integral correctors. The design of this type of control is robust in the case where the MCT is coupled with the permanent magnet synchronous generator. Nevertheless, this type of control cannot maximize the energy efficiency of the MCT. To cope with these drawbacks, in this study, we propose an efficient LQR design for maximizing the power efficiency and energy capture of the MCT. Our decision to use this controller is motivated by the results obtained in the context of wind turbine technology.

The main contributions of this study are summarized as follows:

  • We have used a profile of the daily variation of marine current speed in the northern coasts of Morocco;

  • We have developed a hydrodynamic model based on the experimental results of Mason-Jones et al.;

  • We have modeled flexible transmission using the two-mass model;

  • We have applied a linearization technique to regulate the system around a specific operating point;

  • We have developed a new optimal control based on the LQR approach that achieves the optimization of the operation of the turbine;

  • We have obtained the simulation results of the assembled system using MATLAB Simulink.

The remainder of this paper is organized as follows: in Section 2, we describe the MCT system and the aerodynamic and two-mass models. In Section 3, we present the linearization model for the determination of a state space. In Section 4, we develop a new optimal control based on the LQR approach to find a compromise between the optimization of the energy generated by the turbine and the reduction of the load at the level of two-mass mechanical shaft. In Section 5, we provide an overview of the system control objective implementation of the MCT system in the low-speed and high-speed areas of the marine current. In Section 6, we validate our optimal control performance using MATLAB Simulink. Finally, in Section 7, we conclude this paper and indicate the direction of future work.

2 Marine Current Turbine System Modeling

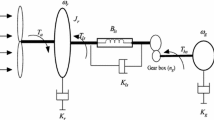
The marine current energy conversion chain, which is a combination of three subsystems, is modeled in Figure 1:

  1. 1)

    The aerodynamic subsystem (Figure 1(a)) consists of several blades (mostly three blades) and a hub. The blades of the MCT extract the kinetic energy from the marine current and convert it into mechanical energy.

  2. 2)

    The mechanical subsystem (Figure 1(b)) is composed of the gearbox (also called the drivetrain). This subsystem transforms the rotation rate of the shaft from low rotational speed at the rotor side into high rotational speed at the generator side.

  3. 3)

    The electromechanical subsystem (Figure 1(c)) is composed of the generator and a power electronics module, which converts the mechanical energy at the turbine into electrical energy. This subsystem will not be modeled in this work. In fact, the dynamics of electrical machines and power electronics systems are faster than that of the other parts of the MCT. Consequently, the system will be considered a mechanical structure. Therefore, the dynamics of the generator can be disregarded. The Tem value of the generator is considered equal to the reference value Tem-ref. Pe is equal to the product of Tem and Ωg:

Figure 1
figure 1

MCT model. (a) Aerodynamic system. (b) Drive train. (c) Generator

Full size image
$$ {P}_{\mathrm{e}}={\varOmega}_{\mathrm{g}}\cdotp {T}_{\mathrm{e}\mathrm{m}} $$
(1)

We describe the model of each subsystem in the following subsections:

2.1 Model of the Marine Current and Aerodynamic Subsystem

2.1.1 Model of the Resource

Before installing the MCT, it is necessary to model the resources of the considered site. For this, the speed of the marine current can be predicted using two methods (Gaamouche et al. 2018):

  1. 1)

    Direct measurement: This method can be performed using conventional devices (e.g., helical current meters and acoustic doppler current profilers), a model proposed by the SHOM (French Naval Hydrographic and Oceanographic Service), or marine ships.

  2. 2)

    Modelization: Several techniques, such as harmonic analysis method, double cosine method, TideSim, and Tide 2D, can be used to model marine currents.

The lack of data of marine current speed in Morocco leads to difficulties in utilizing this resource. Figure 2 presents the variation of marine current speed for a certain day in April 2018 in the northern coasts of the Moroccan kingdom near Spanish borders. The data measured by the European Marine Observation and Data Network were utilized in this study. This figure shows that we can launch such project in this region.

Figure 2
figure 2

Marine current speed profile

Full size image

2.1.2 Aerodynamic Modeling

The aerodynamic power recovered by the rotor of the MCT can be expressed as follows:

$$ P=\frac{1}{2}\rho S{V}_m^3 $$
(2)

where S=π·R2 is the surface of turbine rotation and ρ is approximately equal to 1024 kg/m3 for seawater.

Despite the tremendous technological advances, a tidal turbine can extract only a fraction of this power, as shown in the following equation:

$$ {P}_t=P\cdotp {C}_p=\frac{1}{2}\rho S{C}_p{V}_m^3 $$
(3)

In this study, we considered that the MCT is not pitched. Moreover, Cp can be approximated by an equation depending only on λ, which is defined as the ratio between Ωt and Vm:

$$ \lambda =\frac{\Omega_t\cdotp {R}_t}{V_m} $$
(4)

Mason-Jones et al. (2012) provided a relevant set of experimental data to validate the theoretical and numerical methods for MCT. In this study, we focused on the Cp curve according to λ, which is obtained from these experimental data when the turbine rotates at a uniform speed of 3.08 m/s over a diameter of 20 m. We notice that the data presented in Table 1 are extracted from this curve. On the basis of this table, we proposed the interpolation function of Cp to model the turbine. This function can be expressed as follows:

$$ {C}_p={a}_0+{a}_1\cos \left(\lambda \times 0.174\right)+{b}_1\sin \left(\lambda \times 0.174\right)+{a}_2\cos \left(2\times \lambda \times 0.174\right)+{b}_2\sin \left(2\lambda \times 0.174\right)+{a}_3\cos \left(3\times \lambda \times 0.174\right)+{b}_3\sin \left(3\times \lambda \times 0.174\right)+{a}_4\cos \left(4\times \lambda \times 0.174\right)+{b}_4\sin \left(4\times \lambda \times 0.174\right) $$
(5)
Table 1 Experimental data of Cp and λ
Full size table

Cp can be considered a strong nonlinear function of λ.

Afterward, we implemented our interpolation function for modeling the turbine using the MATLAB Simulink environment. To validate our proposed model, in this work, we selected the turbine “Guinard Energies P66 3.5 kW.” The obtained curve of Cp is shown in Figure 3. We notice that the maximum Cp value is 0.39, which corresponds to a tip speed ratio of 3.67 to a marine current speed of 3 m/s. This value is considered the optimal tip speed ratio (λopt) to achieve maximum power point tracking under rated marine current speeds.

Figure 3
figure 3

Cp curve of the MCT

Full size image

2.2 Model of the Mechanical Subsystem

The mechanical subsystem (Figure 1(b)) is composed of the gearbox (drivetrain). The gearbox adjusts the speed of the turbine to that of the generator through two shafts, namely, the slow shaft on the turbine side and the fast shaft on the generator side. In the literature, the two types of mechanical transmission models are rigid transmission and flexible transmission. The flexible transmission model attracted our attention because the mechanical coupling between the turbine and the electric machine is modeled using the two-mass model, as shown in Figure 1(b). The two masses are connected to a flexible shaft characterized by the elasticity coefficient of the drive shaft of the blades k and the coefficient of friction of the shaft relative to the gearbox d. For wind turbines, this two-mass model is sufficient to properly represent the dynamic behavior of the turbine (Fakharzadeh et al. 2013). For this purpose, the MCT drive system will be modeled using the two-mass model. Then, we write the following equations for the low-speed drivetrain:

$$ \left\{\begin{array}{c}{J}_{\mathrm{t}}\frac{\mathrm{d}{\Omega}_{\mathrm{t}}}{\mathrm{d}\mathrm{t}}={T}_{\mathrm{aer}}-{T}_{\mathrm{mec}}\\ {}{J}_{\mathrm{G}}\frac{\mathrm{d}{\Omega}_{\mathrm{G}}}{\mathrm{d}\mathrm{t}}={T}_{\mathrm{mec}}-{G}_{\mathrm{g}}\cdotp {T}_{\mathrm{em}}\\ {}\frac{\mathrm{d}{T}_{\mathrm{mec}}}{\mathrm{d}\mathrm{t}}=k\left({\Omega}_{\mathrm{t}}-{\Omega}_{\mathrm{g}}\right)+\mathrm{d}\left(\frac{\mathrm{d}{\Omega}_{\mathrm{t}}}{\mathrm{d}\mathrm{t}}-\frac{\mathrm{d}{\Omega}_{\mathrm{G}}}{\mathrm{d}\mathrm{t}}\right)\end{array}\right. $$
(6)

where Jt and Ωt are the inertia and rotational speed of the turbine, respectively; Gg is the gain of gearbox; and Ωg and Jg are the rotational speed and inertia of the generator brought back to the low-speed shaft, respectively, which are defined as follows:

$$ \left\{\begin{array}{c}{\Omega}_{\mathrm{G}}=\frac{\Omega_{\mathrm{g}}}{G_{\mathrm{g}}}\\ {}{J}_{\mathrm{G}}={G}_{\mathrm{g}}^2\cdotp {J}_{\mathrm{g}}\end{array}\right. $$
(7)

Taer is the aerodynamic torque extracted by the turbine, which is expressed as follows:

$$ {T}_{\mathrm{aer}}=k\times {\Omega}_{\mathrm{t}}^2 $$
(8)

where K is derived as follows:

$$ K=\frac{{\uprho \uppi \mathrm{R}}_t^5{C}_p}{2{\lambda}^3} $$
(9)

Then, the nonlinear system (Eq. (6)) of the MCT can be expressed as follows:

$$ \left\{\begin{array}{c}{J}_t\frac{\mathrm{d}{\varOmega}_t}{\mathrm{d}\mathrm{t}}=K\cdotp {\varOmega}_t^2-{T}_{\mathrm{mec}}\\ {}{J}_G\frac{\mathrm{d}{\varOmega}_G}{\mathrm{d}\mathrm{t}}={T}_{\mathrm{mec}}-{G}_g\cdotp {T}_{\mathrm{em}}\\ {}\frac{\mathrm{d}{T}_{\mathrm{mec}}}{\mathrm{d}\mathrm{t}}=k\left({\varOmega}_t-{\varOmega}_g\right)+\mathrm{d}\left(\frac{k{\varOmega}_t^2-{T}_{\mathrm{mec}}}{J_t}-\frac{T_{\mathrm{mec}}+{G}_g{T}_{\mathrm{em}}}{J_G}\right)\end{array}\right. $$
(10)

3 Linearized and State Representation of the MCT System

Given that determining the optimal control for nonlinear systems is difficult, deriving a solution for an equivalent linear control system is necessary. For the MCT system, nonlinearity is detected in the aerodynamic torque Taer. For this, we need to adopt a linearization approach for Taer (Eq. (8)) according to Ωt.

The operating point corresponding to the marine current speed Vm is variable. Consequently, linearizing the MCT system around different operating points corresponding to the marine current speed Vm is possible. Thus, we can obtain the derivative of the system from an operating point given the marine current speed Vm:

$$ {\left.\Delta {C}_{\mathrm{aer}}=\frac{{\delta C}_{\mathrm{aer}}}{\delta {\varOmega}_t}\right|}_{\mathrm{op}}\varDelta {\varOmega}_t={\beta}_0{\varDelta \varOmega}_t $$
(11)

where

$$ {\beta}_0=\frac{{\rho \uppi R}_{\mathrm{t}}^3{V}_{\mathrm{m}}^2}{2{\Omega}_{t0}}\left[\frac{{\delta C}_{\mathrm{p}}\left(\lambda \right)}{\delta \lambda}-\frac{C_{\mathrm{p}0}}{\lambda_0}\right] $$
(12)

The symbol ∆ designates the variation according to the chosen operating point (OP). New state variables corresponding to the variations around the operating point are defined as follows:

$$ \Delta {\varOmega}_{\mathrm{t}}={\varOmega}_{\mathrm{t}}-{\varOmega}_{\mathrm{t}0} $$
$$ \Delta {\varOmega}_{\mathrm{G}}={\varOmega}_{\mathrm{G}}-{\varOmega}_{\mathrm{G}0} $$
$$ \Delta {T}_{\mathrm{mec}}={T}_{\mathrm{mec}}-{T}_{\mathrm{mec}0} $$

On the basis of the preceding expressions, the linearization of the flexible model (Eq. (8)) around an operating point leads to the following equations:

$$ \left\{\begin{array}{c}{J}_t{\Delta \Omega}_t={\beta}_0{\Delta \Omega}_t-{\Delta T}_{\mathrm{mec}}\\ {}\kern2.75em {J}_G{\Delta \Omega}_G={\Delta T}_{\mathrm{mec}}-{G}_g{\Delta T}_{\mathrm{em}}\kern3em \\ {}{\Delta T}_{\mathrm{mec}}=\left(K+\frac{{d\beta}_0}{J_t}\right){\Delta \Omega}_t-{K\Delta \Omega}_G-d\left(\frac{1}{J_t}+\frac{1}{J_G}\right){\Delta T}_{\mathrm{mec}}\end{array}\right. $$
(13)

The linearization of the nonlinear system around an operating point, expressed in Eq. (11), enabled us to express the state space model as follows:

$$ \left[\begin{array}{c}{\Delta \Omega}_t\\ {}{\Delta \Omega}_G\\ {}{\Delta C}_{\mathrm{mec}}\end{array}\right]=\left[\begin{array}{ccc}\frac{\beta_{0i}}{J_t}& 0& \frac{1}{J_t}\\ {}0& 0& \frac{1}{J_g- BV}\\ {}k+\frac{{d\beta}_0}{J_t}& -k& -d\left(\frac{1}{J_t}+\frac{1}{J_G}\right)\end{array}\right]\left[\begin{array}{c}{\Delta \Omega}_t\\ {}{\Delta \Omega}_G\\ {}{\Delta C}_{\mathrm{mec}}\end{array}\right]+\left[\begin{array}{c}0\\ {}\frac{G_g}{J_G}\\ {}\frac{{d G}_g}{J_G}\end{array}\right]{\Delta C}_{\mathrm{em}} $$
(14)

In a more compact form, the system expressed in Eq. (14) can be rewritten as follows:

$$ \boldsymbol{x}=\boldsymbol{Ax}+\boldsymbol{Bu} $$
(15)

where

$$ \boldsymbol{x}=\left[\begin{array}{c}{\Delta \Omega}_{\mathrm{t}}\\ {}{\Delta \Omega}_{\mathrm{G}}\\ {}{\Delta C}_{\mathrm{mec}}\end{array}\right],\boldsymbol{A}=\left[\begin{array}{ccc}\frac{\beta_{0i}}{J_{\mathrm{t}}}& 0& \frac{1}{J_{\mathrm{t}}}\\ {}0& 0& \frac{1}{J_{\mathrm{g}}- BV}\\ {}k+\frac{{d\beta}_0}{J_{\mathrm{t}}}& -k& -d\left(\frac{1}{J_{\mathrm{t}}}+\frac{1}{J_{\mathrm{G}}}\right)\end{array}\right], $$
$$ \boldsymbol{B}=\left[\begin{array}{c}0\\ {}\frac{G_{\mathrm{g}}}{J_{\mathrm{G}}}\\ {}\frac{dG_{\mathrm{g}}}{J_{\mathrm{G}}}\end{array}\right],\mathrm{and}\ \boldsymbol{u}={\Delta C}_{\mathrm{em}} $$

In Figure 4, we can distinguish four operating areas of a variable-speed MCT, in which the index a1 of the matrix Ai,j depends on the variation of the marine current:

  1. 1)

    Zones 1 and 4: The MCT does not provide any power because the marine current speed is lower than the start speed and higher than the rated speed. Thus, the MCT will be stopped.

  2. 2)

    Zone 2: For the low marine current speed (Vm≤VΩt−r):

    $$ {A}_{11}=\frac{-\uprho \uppi {R}_{\mathrm{t}}^4{V}_{\mathrm{m}}{C}_{\mathrm{pmax}}}{2{\lambda}_0^2{J}_t} $$
  3. 3)

    Zone 3: When the marine current speed is between VΩt−r≤Vm≤Vm−r:

    $$ {A}_{11}=\frac{\uprho \uppi {R}_{\mathrm{t}}^3{V}_{\mathrm{m}}^2{C}_{\mathrm{p}\mathrm{max}}}{2{J}_{\mathrm{t}}\ {\Omega}_{\mathrm{t}-\mathrm{r}}}\ \left[\frac{\partial {C}_{\mathrm{P}}}{\partial \lambda }-\frac{C_{\mathrm{p}}}{\lambda}\right] $$
    Figure 4
    figure 4

    Control regions for a turbine controller

    Full size image

4 LQR Optimal Control

The objective of optimal control has two main orientations. The first orientation aims to minimize energy, whereas the second orientation seeks to reduce the convergence time of the system. The general objective is to find the optimal control that minimizes the criterion that varies according to the orientation adopted. A large variety of optimal control techniques have been applied to the MCT in a permanent attempt to improve its function and benefit as much as possible from the energy that it can produce. Optimal control is the state feedback of a nonlinear time-invariant system with LQR that has evolved significantly in recent years. The principle of the LQR command is shown in Figure 5 (Khargonekar et al. 1990; Anderson et al. 2007; Athans and Falb 2013; Levine 2018).

Figure 5
figure 5

Principle of the LQR command

Full size image

In general, the system model can be expressed as the following state space equation:

$$ \left\{\begin{array}{c}\boldsymbol{x}=\boldsymbol{Ax}(t)+\boldsymbol{Bu}(t)\\ {}\boldsymbol{y}=\boldsymbol{Cx}(t)\end{array}\right. $$
(16)

where x(t) € ℝn denotes the state vector, u(t) € ℝn denotes the control vector, y(t) € ℝq denotes the output vector, A is the matrix of evolution or state, B is the control or input matrix, and C is the output matrix or measured value. Moreover, the pair (A, B) is assumed to denote that the system is controllable. The process of the feedback regulator needs to follow the state space equation. The simplified problem of the LQR is to find the matrix of the corrector K, which minimizes the function of the cost (or the criterion of performance), as follows:

$$ J=\frac{1}{2}{\int}_0^{\infty}\left({\boldsymbol{x}}^{\mathrm{T}}\boldsymbol{Qx}+{\boldsymbol{u}}^{\mathrm{T}}\boldsymbol{Ru}\right)\mathrm{d}t $$
(17)

where the weighting matrices Q and R satisfy the following expression:

$$ \boldsymbol{Q}={\boldsymbol{Q}}^{\mathrm{T}}\ge 0,\boldsymbol{R}={\boldsymbol{R}}^{\mathrm{T}}>0 $$
(18)

The Hamiltonian system is written as follows:

$$ H\left(\boldsymbol{x},\boldsymbol{u},\boldsymbol{p},t\right)={\boldsymbol{p}}^{\mathrm{T}}\boldsymbol{A}(t)\boldsymbol{x}+{\boldsymbol{p}}^{\mathrm{T}}\boldsymbol{B}(t)\boldsymbol{u}+\frac{1}{2}\left({\boldsymbol{x}}^{\mathrm{T}}\boldsymbol{Q}(t)\boldsymbol{x}+{\boldsymbol{u}}^{\mathrm{T}}\boldsymbol{R}(t)\boldsymbol{u}\right) $$
(19)

The Hamiltonian system must satisfy the following conditions:

  • The state equation:

$$ p=-\frac{\partial H}{\partial x}=-{\boldsymbol{A}}^{\mathrm{T}}(t)\boldsymbol{p}-\boldsymbol{Q}(t)\boldsymbol{x} $$
(20)

  • The absence of a constraint on the command:

$$ \frac{\partial H}{\partial u}=-{\boldsymbol{B}}^{\mathrm{T}}(t)\boldsymbol{p}-\boldsymbol{R}(t)\boldsymbol{u}=0 $$
(21)

From Eq. (21), we deduce the following expression:

$$ {u}_{\mathrm{opt}}=-{\boldsymbol{R}}^{-1}(t){\boldsymbol{B}}^{\mathrm{T}}p(t) $$
(22)

Then, the dynamic equation of the closed-loop system can be written as follows:

$$ \dot{x}={\boldsymbol{A}}^{\mathrm{T}}(t)\boldsymbol{x}(t)-\boldsymbol{B}(t){\boldsymbol{R}}^{-1}(t){\boldsymbol{B}}^{\mathrm{T}}(t)\boldsymbol{p}(t) $$
(23)

Equations (20) and (21) can be written in the form of a matrix system, which is also called the Hamiltonian system:

$$ \frac{\mathrm{d}}{\mathrm{d}t}\left(\begin{array}{c}\boldsymbol{x}(t)\\ {}\boldsymbol{p}(t)\end{array}\right)=\left(\begin{array}{cc}\boldsymbol{A}(t)& -\boldsymbol{B}(t){\boldsymbol{R}}^{-1}(t){\boldsymbol{B}}^{\mathrm{T}}\\ {}-\boldsymbol{Q}(t)& -{\boldsymbol{A}}^{\mathrm{T}}(t)\end{array}\right)\left(\begin{array}{c}\boldsymbol{x}(t)\\ {}\boldsymbol{p}(t)\end{array}\right) $$
(24)

With p(t)=P(t)x(t), Eq. (20) can be rewritten as follows:

$$ \dot{p}=-\left({\boldsymbol{A}}^{\mathrm{T}}(t)P(t)+\boldsymbol{Q}(t)\right)\boldsymbol{x}(t)=\dot{P}\boldsymbol{x}(t)+\dot{P}(t)\boldsymbol{x}(t) $$
(25)

Equation (23) can be rewritten as follows:

$$ \left(\dot{P}+P\boldsymbol{A}+{\boldsymbol{A}}^{\mathrm{T}}P-P\boldsymbol{B}{\boldsymbol{R}}^{-1}{\boldsymbol{B}}^{\mathrm{T}}P+\boldsymbol{Q}\right)X=0 $$
(26)

P is the positive solution (symmetric) to the algebraic Riccati equation (Eq. (26)):

$$ P+P\boldsymbol{A}+{\boldsymbol{A}}^{\mathrm{T}}P-P\boldsymbol{B}{\boldsymbol{R}}^{-1}{\boldsymbol{B}}^{\mathrm{T}}P+\boldsymbol{Q}=0 $$
(27)

Then, we derive the minimum criterion of the initial state (x0 at t0):

$$ {J}_{\mathrm{min}}=\frac{1}{2}{x}_0^{\mathrm{T}}P\left({t}_0\right){x}_0 $$
(28)

Notably, the optimal control obtained can be written as state feedback u=−K(t) x, where:

$$ \boldsymbol{K}=-{\boldsymbol{R}}^{-1}{\boldsymbol{B}}^{\mathrm{T}}P $$
(29)

5 Control Objectives

In this part, we developed the control laws that can be applied to zones 2 and 3 (Figure 4) on the basis of the marine current speed:

  • When \( {V}_{\mathrm{m}}\le {V}_{\Omega_{\mathrm{t}-\mathrm{r}}} \), the main control objectives are as follows: The MCT starts to generate energy at a certain marine current speed. As result, the operation of the MCT is related to the low marine current speed. In this area, the control objective is to operate the turbine at maximum efficiency. To ensure that the power coefficient is maintained at the optimal value Cpmax=Cp(λ0), λ must reach its optimum value λ0 (Figure 3). This means that the control in this area acts on the electromagnetic torque of the generator, which in turn acts on the rotational speed and reduces its variations from the reference value Ωt−ref, as expressed in Eq. (30).

    The controller must minimize the fluctuations of the mechanical torque Tmec, which affects the quality of the electrical power generated (although this effect is less important in this area than in other areas). The reference equation for maximizing energy conversion is expressed as follows:

    $$ \left\{\begin{array}{cc}{\Omega}_{T- ref}=\frac{\lambda_0{V}_m}{R_t};& for\ {V}_m\le {V}_{\Omega_{t-r}}\\ {}{T}_{aero- ref}=\frac{1}{2}\rho \pi {R}_t^5{\Omega}_{T- ref}^2\frac{C_{pmax}}{\lambda_0};& for\kern0.5em {V}_m\le {V}_{\Omega_{t-r}}\end{array}\right. $$
    (30)

  • When \( {V}_{\Omega_{\mathrm{t}-\mathrm{r}}} \) ≤ Vm ≤ Vm−r, the main control objectives are as follows: When the marine current reaches the value of \( {V}_{\varOmega_{\mathrm{t}-\mathrm{r}}} \), the MCT corresponds to the intermediate marine current speeds. In this area, the rotational speed of the turbine reaches its nominal value. The main control objective is to reduce the variations of Ωt from the nominal value Ωt−r while acting on the electromagnetic torque. The reference equation for this area is expressed as follows:

    $$ \left\{\begin{array}{cc}{\Omega}_{T- ref}={\Omega}_{t-r};& {V}_{\Omega_{t-r}}\le {V}_m\le {V}_{m-r}\\ {}{C}_{aero- ref}=\frac{1}{2}\rho \pi {R}_t^5{\Omega}_{T- ref}^2\frac{C_{p-I}}{\lambda_0};& {V}_{\Omega_{t-r}}\le {V}_m\le {V}_{m-r}\end{array}\right. $$
    (31)

    with:

    $$ \left\{\begin{array}{c}{\lambda}_0=\frac{\Omega_{t-r}{R}_t}{V_m};\\ {}{C}_{\mathrm{pmax}}={C}_p\left({\lambda}_0\right);\end{array}\right.{\displaystyle \begin{array}{c}{V}_{\Omega_{t-r}}\le {V}_m\le {V}_{m-r}\\ {}{V}_{\Omega_{t-r}}\le {V}_m\le {V}_{m-r}\end{array}} $$
    (32)

    The reference values for the electromagnetic and mechanical torques in zones 1 and 2 are derived as follows:

    $$ \left\{\begin{array}{c}{T}_{\mathrm{em}-\mathrm{ref}}=\frac{T_{\mathrm{aero}-\mathrm{ref}}}{G_g}\\ {}{T}_{\mathrm{mec}-\mathrm{ref}}={T}_{\mathrm{em}-\mathrm{ref}}\ \end{array}\right. $$
    (33)

    The linearization of the aerodynamic torque, as presented in Section 3, makes it possible to rewrite Eq. (14) in the following form:

    $$ \left\{\begin{array}{c}\boldsymbol{x}=\boldsymbol{Ax}+\boldsymbol{B}\Delta {T}_{\mathrm{em}}\\ {}\boldsymbol{y}=\boldsymbol{x}\end{array}\right. $$
    (34)

    The proposed control strategy aims to minimize the LQR:

    $$ J=\frac{1}{2}{\int}_0^{\infty}\left({\boldsymbol{x}}^{\mathrm{T}}\boldsymbol{Qx}+\Delta {T}_{\mathrm{em}}^{\mathrm{T}}\boldsymbol{R}\Delta {T}_{\mathrm{em}}\right)\mathrm{d}t $$
    (35)

Figure 6 presents the block diagram of the system controlled during operation.

Figure 6
figure 6

Block diagram of the system controlled during operation

Full size image

6 Simulation Results

To validate our proposed control strategy based on the LQR approach, we conducted simulations using the MATLAB Simulink software. The simulation results of the MCT are depicted in Figure 7.

Figure 7
figure 7

Simulation of the MCT system with LQR regulator using MATLAB Simulink

Full size image

The considered system is a variable-speed, fixed-pitch MCT with a nominal power rating of 3.5 kW. Table 2 lists the values of the parameters used in the simulation.

Table 2 Simulation parameters
Full size table

The aim of the proposed control law is to minimize the quadratic criterion previously expressed in Eq. (35). The weight coefficients used in the quadratic criterion J are derived as follows:

$$ \left\{\begin{array}{c}\boldsymbol{Q}=\left[\begin{array}{ccc}1& 0& 0\\ {}1& 1000& 0\\ {}1& 0& 1\end{array}\right]\\ {}R=\left[100\right]\end{array}\right. $$
(36)

The resolution of Riccatti’s equation (i.e., Eq. (34)) for the investigated system defines the control gain K, which is previously expressed in Eq. (29). The result is the optimal state feedback, which is expressed in Eq. (37) or (38) in the following form:

$$ \Delta \boldsymbol{u}=-\boldsymbol{K}(t)\Delta \boldsymbol{x} $$
(37)

or

$$ \left\{\begin{array}{c}\mathbf{\Delta }\boldsymbol{u}=\boldsymbol{u}-{u}_{\mathrm{ref}};\boldsymbol{u}={T}_{\mathrm{em}}\\ {}\mathbf{\Delta }\boldsymbol{x}=\boldsymbol{x}-{x}_{\mathrm{ref}};\boldsymbol{x}=\left[\begin{array}{c}{\Omega}_t\\ {}{\Omega}_G\\ {}{T}_{\mathrm{mec}}\end{array}\right]\end{array}\right. $$
(38)

From this equation, we able to derive the following expression:

$$ {T}_{\mathrm{em}}=-\boldsymbol{K}\times \boldsymbol{\Delta x}+{T}_{\mathrm{em}-\mathrm{ref}} $$
(39)

To illustrate the effectiveness of our proposed control system for a variable-speed MCT, we conducted two simulations of zones 2 and 3. The results are presented in Figure 4.

6.1 Partial Load Operation (Zone 2)

In this simulation, we considered the low-speed MCT that corresponds to \( {V}_{\mathrm{m}}\le {V}_{\Omega_{\mathrm{t}-\mathrm{r}}} \). Figure 8 shows the different parameters that we have optimized to maximize the energy collected by the turbine. Figure 8 (a) presents the variation of the marine current velocity profile used to determine in which region control will be applied. Moreover, Figure 8 (d) shows that the proposed LQR control follows the reference values nearly perfectly, with a static error of 0. Moreover, the gain provided by this control is equal to K=[0.2079−02896−0.0353] when Vm = 1 m/s.

Fig. 8
figure 8

MCT speed variation and state and output variables in the partial load regime (zone 2)

Full size image

Figure 8 (b), (c), and (e) present the variations of three parameters, namely, rotor speed, generator speed, and mechanical torque, respectively. The LQR controller ensures that the system maintains the power coefficient at the optimal value Cpmax. As a result, the parametres can be optimized in zone 2. Figure 8 (f) shows the variation of the electrical power according to generator speed and electromagnetic torque. Figure 8 (f) clearly shows that LQR maximizes the electrical power.

6.2 Partial Load Operation (Zone 3)

In this simulation, the rotational speed of the MCT reaches its rated value that corresponds to \( {V}_{\varOmega_{\mathrm{t}-\mathrm{r}}} \) ≤ Vm ≤ Vm−r. Figure 9 shows the different parameters that we have optimized to maintain the turbine at its optimum speed. In addition, these parameters enable the generator to turn at a speed that does not fluctuate rapidly (minimize the transient load). Figure 9 (a) presents the variation of the marine current velocity profile used to determine in which region control will be applied. In this case, a marine current profile with the average value of Vm = 3 m/s was imposed.

Figure 9
figure 9

MCT speed variation and state and output variables in the partial load regime (zone 3)

Full size image

Figure 9 (d) shows that our proposed LQR control can be applied to zone 3, with a good performance in terms of electromagnetic torque. Furthermore, from this figure, we notice that the static error is always equal to 0 and the gain provided by this control is equal to K=[0.1851−0.2899−0.0337] at Vm = 3 m/s.

Figure 9 (b), (c), and (e) show the variations of three parameters, namely, rotor speed, generator speed, and mechanical torque, respectively. We notice that the LQR controller can ensure that the system maintains the rotational speed at the nominal value. Consequently, the simulation results indicate that these three parameters have been optimized with the use of LQR control. In addition, Figure 9 (f) presents the variation of the output power of the MCT. We notice that the value of this parameter decreases from the nominal value to 3.5 kW because we used the LQR control.

On the basis of the simulation results obtained for zones 2 and 3, we confirm that our proposed LQR control can be set and used to act only on the electromagnetic torque to automatically regulate the different parameters of the MCT system, such as rotor speed, generator speed, and mechanical torque.

7 Conclusions

In this study, we proposed the LQR optimal controller approach coupled with the reference model of the outputs for the variable-speed MCT. Our solution maximizes power capture where the tidal speed is greater or less than the nominal speed.

In the first step, we introduced the differential equations for modeling the state space representation, which connects the outputs and controls to ensure better precision, and the reference model of the outputs whose main role is to impose the desired dynamic on the response of the system’s outputs, including the power produced, whose response should be rapid.

In the second step, the LQR command, which involves minimizing the quadratic criterion that takes into consideration all of the variables of the system, was presented. Furthermore, the LQR command can ensure the best compromise between the desired performance and the feedback of the command. This principle of criterion minimization leads us to determine the optimal control structure of the state feedback for the linearized MCT system around different operating points.

The obtained simulation results enabled us to conclude that our linear control can provide a satisfactory performance in terms of following the reference values for any marine current speed nearly perfectly. In future work, we will focus on the application of more sophisticated control strategies to deal with the influence of any marine current speed by considering the entire system.