Dynamic Oppositional Symmetries for Color, Jungian and Kantian Categories

Abstract

This paper investigates some classical oppositional categories, like synthetic versus analytic, posterior versus prior, imagination versus grammar, metaphor versus hermeneutics, metaphysics versus observation, innovation versus routine, and image versus sound, and the role they play in epistemology and philosophy of science. The epistemological framework of objective cognitive constructivism is of special interest in these investigations. Oppositional relations are formally represented using algebraic lattice structures like the cube and the hexagon of opposition, with applications in the contexts of modern color theory, Kantian philosophy, Jungian psychology, and linguistics.

1 A Short Story of Shifting (At)Tentions

Cornell university campus security has a bad reputation for giving tickets for any, even the most frivolous, traffic violations, see [44, II, ch. 10, prob. 13] However, back in 1987, at a road intersection, a good cop spared me from one after a fast stop—that I characterized by null velocity or zero derivative, that is, dx/dt=0. Furthermore, after asking why such an instantaneous stop was not good enough, I got (essentially) the following explanation: The Stop sign requires a complete or slow stop, characterized by the ceasing of all movement, including the (damped) oscillation of the chassis after the wheels stop. Hence, the car only comes to a slow stop after the energy in the suspension system is dissipated, implying zero integral displacements over a finite time interval, $\delta$, that is, Int[t, t+$\delta$] dx = 0. At the moment, I politely thanked the cop for giving me only a warning but was annoyed by what I felt as nitpicking.

A few months later, while driving on snow for the first time in my life, I tried to do a fast stop only to see it transmute into a slow skidding movement, and barely avoided a serious accident. At the moment, I blamed the (soon after replaced) tires on my car, but saw nothing wrong with my driving skills. Nevertheless, that night I had a dream about the incident and, waking up, realized the wisdom of the formerly received advice and how to avoid similar occurrences when driving on snow. Moreover, I realized the importance of having adequate concepts to think about my experiences and the benefits of having corresponding words to express them in language.

Figure 1 illustrates how important it is to make the distinctions under scrutiny living in Ithaca, NY, where winter is cold and snowy, in contrast to my native country, Brazil, where it never snows. The tree diagram in Figure¹ 1 l, from [151], depicts the distinctions I initially had in mind at the beginning of this short story. Figure 1b illustrates my perplexity when facing new situations requiring more refined concepts and a richer lexical palette. However, this traffic sign seems like a riddle conceived by the sphinx, stating veiled treats and giving obscure advice. In contrast, the sign in Fig. 1c has clear warning and educational purposes, for it succinctly explains relevant distinctions, considers implied choices and their consequences, and even introduces pertinent lexical expressions.

This short story also illustrates important attention shifts, structured around classical oppositional structures. As already mentioned, at the beginning of this story I was fully aware of the move versus stop opposition (due to parking tickets), and the slow versus fast movement opposition (due to speeding tickets). Later on, I was made aware of the (for me, new) opposition category of fast versus slow stops (and corresponding tickets), and had to integrate all these oppositions into a coherent structure that was more complex that the one I initially had in mind. For further analyses related to this case, see [14, 15, p. 183], [70, 69, p. 621], [151] In the next sections, I will analyze in detail similar oppositional structures related to color, Kantian and Jungian categories.

Fig. 1

Hierarchical conceptual splitting and lexical disambiguation

In the aforementioned dream, I “felt” how difficult it is to dissipate the car’s kinetic energy on a slippery road, and understood why snow-stops require slow-stops (pun intended).² On the one hand, having finer distinctions concerning concepts of fast, slow, move, and stop, and a richer structure for organizing them, allowed me to better analyze my predicaments. On the other hand, the same concepts afforded me a better synthetic vision, allowing me to see pertinent connections between similar situations that lead to effective behavioral adjustments. Initially, I had to be mindful of these adjustments but, after a while, the new behavioral patterns became fully automatic, and driving on snow became a natural and pleasant thing to do. This short story is intended to highlight some analytic, synthetic, logical, and metaphorical powers and properties of language and ontologies – topics to be investigated in the sequel using, as a paradigmatic model, modern color theory.

2 Modern Color Theory

This section gives a brief review of basic notions of modern color theory needed for our considerations in the following sections. In 1704, Isaac Newton publishes the book Opticks, where he develops a series of experiments and explanations for the behavior of light. First, Newton showed that a glass prism can decompose a white light ray into a spectrum of colors we see in the rainbow, where colors are arranged in a linear segment, progressing, from left to right in Fig. 2l, in the following order: Red, Yellow, Green, Cyan, Blue and Violet. Colors change gradually along the spectral line, where the aforementioned color names only mark a few standard location points. Hence, someone could use additional location points, like orange between Red and Yellow, or lime between Yellow and Green, or else dispense with a proper name for Cyan between Green and Blue. However, the aforementioned colors written with capital initials have a special role to play in the sequel.

Fig. 2

Newton (1704) spectra and Ouroboros

Using prisms and mirrors, one can mix light of two single colors, that is, superpose light taken from narrow bands in the spectrum. Most of the time, these mixtures only generate a color impression already present in between them in the linear spectrum. However, by mixing different proportions of Red and Blue, additional colors are obtained, like shades of Purple (more red than blue), Magenta, and Violet (more blue than red). Newton used a color wheel, similar to the one depicted in Fig. 2c, to give a graphical representation of mixed spectral colors. Today, the range of non-spectral colors (going from shades of purple, to magenta, to shades of violet) is called the paradoxical region of the (expanded) color wheel, as highlighted in Fig. 2c. Carl Gustav Jung compared the color wheel to the alchemical symbol of the Ouroboros, a snake that bites its own tail, see Fig. 2r, where the snake’s body spans the linear spectrum while the snake’s head and tail span the paradoxical region.

2.1 Maxwell’s Theory of Color Composition

More than a century after Newton’s work, in 1860, James Clerk Maxwell demonstrated that all colors perceived by the human eye can be obtained by mixing, in different proportions, three specific primary colors, namely, Red, Green, and Blue (RGB). The device used by Maxwell in his experiments is remarkably simple, using three discs, one for each primary color, made of paper and having a radial slit, see Fig. 3l and [116]. The paper discs are then mounted on a supporting metal disc, exposing angular color sections of adjustable sizes. Spinning the discs, a viewer has the visual perception of a color mixture in the same proportion of the exposed color sections.

Fig. 3

Maxwell (1860) compositional color structure

Maxwell’s triangle, depicted in Fig. 3r, gives a mathematical representation of his experiment. The compositional or barycentric coordinates, $\left<r,g,b\right>$ , specify the position of a point P inside an equilateral triangle of unitary height by its distances to each of the triangle’s sides. By Viviani’s theorem, these coordinates must be non-negative and add up to one, that is, $r,g,b \in [0,1]$ and $r+g+b=1$. Physically, P will be at the center of mass or equilibrium point of the triangle if we place at its vertices, $\{R,G,B\}$, corresponding non-negative masses adding up to unity. The following coordinates for some already familiar colors may help the reader get used to this coordinate system: $Y=\left<\nicefrac {1}{2},\nicefrac {1}{2},0\right>$ , $C=\left<0,\nicefrac {1}{2},\nicefrac {1}{2}\right>$ , $M=\left<\nicefrac {1}{2},0,\nicefrac {1}{2}\right>$ , $P=\left<\nicefrac {3}{4},0,\nicefrac {1}{4}\right>$ , $V=\left<\nicefrac {1}{4},0,\nicefrac {3}{4}\right>$ ; finally, the coordinates $\left<\nicefrac {1}{3},\nicefrac {1}{3},\nicefrac {1}{3}\right>$ give the gray point at the center of the triangle.

Notice that the barycentric coordinate system only specifies colors by relative weights. If in Maxwell’s experiment, we use distinct sets of paper discs with brighter or more obscure colors, we will get lighter or darker shades of gray at the center point of the triangle. Maxwell’s device includes a smaller set of blacK and White paper discs close to the spinning center (since the letter B is already used for blue, we use K for black). Regulating the size of exposed segments of RGB and KW discs allows us to match shades of gray obtained at the larger and smaller spinning rings and, in so doing, evaluate the relative brightness of color papers or combinations thereof.

Fig. 4

RGB coordinates and cube projection. Wundt (1892) - Smith (1978) hexcone encoding: Brightness value or Luminosity, [0,100$\%$]; Saturation, [0,100$\%$]; & Hue, [0,360$^\circ$]

Figure 4tl depicts the RGB rectangular coordinate system. In contrast to the barycentric system, the rectangular coordinates are independent. For convenience, they are normalized in the [0, 1] interval, but they are no longer subject to the constraint of adding up to unity. This is a natural coordinate system to use when we can independently regulate the intensity of RGB light sources, like three lamps of these colors illuminating a white wall, or three color LEDs (light-emitting diodes) in a single pixel of a TV screen.

In many applications, it is convenient to use separate coordinates for absolute brightness and other distinctive aspects of color sensation. Painters have for centuries tried to accurately describe such essential characteristics. Figure 4b depicts the HSL and HSB variants of the hexcone coordinate system, developed to handle independently three separate characteristics of color sensation, namely, brightness or luminosity value, hue, and saturation. This system has the form of a hexagonal prism or pyramid, see [191] and [156]. The vertical coordinate, ranging from zero to 1 or 100%, conveys brightness or luminosity. Hue relates to a position in the color wheel, and is given by a continuous angular coordinate that starts at 0$^\circ$, for Red, and reaches, at 60$^\circ$ increments, Y, G, C, B, and M. Saturation is the radial coordinate ranging from zero, for a pale or undifferentiated gray at the center, to 1 or 100%, for a pure color at the border. The hexcone system was developed in the mid-XX century for color-TV broadcasting and computer graphics, and is now an ubiquitous form of color encoding embedded in technological applications.

Figure 4tr depicts the color hexagon, a helpful diagram depicting geometric relations between distinct coordinate systems. The color hexagon can be seen as a projection of the RGB cube, depicted in Fig. 4tl, along its KW axis, which is perpendicular to the hexagon. A small gray hexagon can be seen at the center of the cube; hidden below it, lays the black corner at the bottom of the cube. The white corner, which should be at the top of the cube, has been removed, together with its entire quadrant, in order to expose some inner layers and make the construction of the cube easier to understand.

2.2 Hering’s Theory of Color Opposition

Besides the several alternatives examined in the last section, other coordinate systems are useful in varied applications. For example, instead of the angular and radial polar coordinates used in the hexcone system, one can use orthogonal [0, 1] coordinates along perpendicular axes in the hexagon in order to specify the balance between opposing reference colors. For example, Fig. 5t uses a vertical coordinate along the YB axis and a horizontal coordinate along the RG axis. Analogously, Fig. 5b uses the MG and RB axes of “opposing” colors. Due to their geometrical shape, as depicted in the hexagon, the preceding systems are known, respectively, as the Yellow-headed kite and the Magenta-headed kite, see [69] Some of the reasons for using such oppositional systems are explained in the sequel. The meaning of the arrows and additional lines drawn inside the hexagon will be explained in Sect. 2.3.

Fig. 5

Orthogonal axes for Yellow and Magenta -headed kites

Shortly after Maxwell, in 1860, postulated his tripolar compositional theory of color, Ewald Hering, in 1878, postulated a rival quadripolar oppositional theory, according to which, color vision is based on two antagonistic contrast signals for color proper, namely, R/G and Y/B, plus a third contrast signal for brightness, K/W. Figure 6r depicts orthogonal axes corresponding to these three signals, that coincide with those in Fig. 5tc. The circle of oppositional colors shown in Fig. 6c is taken directly from Hering work.

Fig. 6

Hering (1878) oppositional color structure

Hering used experiments concerning color constancy of objects displayed against varying backgrounds, visual perception of color contrasts, and color perception by individuals with color vision deficiencies as empirical evidence to support his theory. Only in the XX century could neural physiology reveal the mechanisms behind these phenomena. At the eye’s retina, there are three distinct types of color receptors, just as predicted by Maxwell’s tripolar compositional theory. However, a neural network at the optic nerve (connecting eye to brain) recombines the retinal color signals into antagonistic contrast signals with the same structure predicted by Hering’s theory, as shown in Fig. 6l. From this neural network architecture, we can understand why the Yellow-headed kite coordinate system shown in Fig. 5t is useful when studying the human perception of color contrast and related phenomena.

2.3 Logical Representation of Color (De)Composition

This section provides a logical view of the mereological relations, that is, of the compositional and decompositional properties of colors studied in this section. It does so by presenting abstract diagrammatic representations of these relations that can capture them in compact visual forms that are easy to grasp and understand. In the sequel, these diagrammatic representations are used in the analyses of other categories exhibiting similar logical structures.

Maxwell’s experiments demonstrate how primary colors can be added. Mixing light of two primary colors generates one of the secondary colors, as shown in the Hasse diagram shown at figure Fig. 7l, namely, R + B = M, R + G = Y, and B + G = C. This diagram represents an algebraic lattice, that also includes a blacK element at its bottom and a White element at its top, corresponding to the absence or the presence of all three primary colors. As shown by Maxwell, primary colors constitute a additive basis, meaning that other color perception can be generated by mixing the three primary colors in the right proportion. In the same way, secondary colors constitute a subtractive basis, meaning that other color perception can be generated by filtering, from a white light source, the three secondary colors in the right proportion. A set of stained glass filters can be used for direct empirical demonstration of this property, which is implied by the algebraic lattice structure. The bit-string color representations that appear in Fig. 7 are Boolean or $\{0,1\}$ versions of the continuous coordinate systems used to specify color mixtures examined in previous subsections. These bit-strings can capture and concisely display the essential logical properties of this compositional system.

Fig. 7

Left: Hasse diagram for (transitive) mereological relations of entailment or inferiority ($\longrightarrow$). Right: Aristotelian diagram of opposition for additive (RGB) and subtractive (CMY) colors with corresponding mereological or bit-string relations of complementarity ($=\!=$), contrariety ($-\,-$), sub-contrariety ($\cdots$), and entailment ($\longrightarrow$)

The Aristotelian diagram shown in Fig. 7r, gives an alternative representation of these logical or mereological relations (i.e., compositional and decompositional properties). It clearly and succinctly displays the following logical relations: Implication or entailment relations (as in the Hasse diagram) are represented by arrows, ($\longrightarrow$). Contrariety relations are represented by dashed lines ($-\,-$); contrary conditions cannot both be valid or true, although they might both be invalid or false. Sub-contrariety relations are represented by dotted lines ($\cdots$); sub-contrary conditions cannot both be false, although they might both be true. Contradiction relations are represented by parallel lines ($=\!=$); contradictory conditions must have opposite validity status or truth-false values.

3 Praxis, Lexicalization, and Archetypes

This section examines the ideas of archetype and lexicalization, preparing discussions about the role they play in the evolution of language, either in the context of color perception or in alternative contexts of human activity.

In Judo and other martial arts, an athlete trains by executing, over and over again, some basic techniques. Repetition commits these techniques to “muscle memory”, allowing the required movements to be executed without hesitation in a fully automatic way. In so doing, the athlete builds “new instincts” for her or himself, being able to retrieve and execute such procedures or behavioral patterns in a (quasi) reflexive manner. Afterward, in combat, laborious conscious thinking about what to do and how to do it may be bypassed, resulting in decisiveness and agility that often lead straight to victory. Judo practitioners also want to talk about the things they do, so they create specific names for the basic techniques they use, known in Japanese as Waza, or . In time, some of these names become standard words used in language that, later on, are enthroned as headwords in the pertinent dictionary or, using the jargon of computer science, become elements of the pertinent ontology, see [166, 167, 170] and references therein. Ontologies serve many purposes, for example, the rules of a Judo tournament use the waza ontology to determine how and which techniques can be used. The historical process in which words are created and standardized in the language used by a human community is called lexicalization, a main topic discussed in this section.

Judo waza require hard work to be properly introjected. In contrast to these “artificial instincts”, human babies display a set of involuntary reflexes that are inherited and inborn. They allow a baby to perform some simple tasks essential to survival, like blinking, sucking, grasping, stepping, etc. These inherited reflexes offer starting points for development processes aiming to build up more complex skills and behaviors. For example, the stepping reflex is a starting point for the development of walking—something that any human being strives for and will eventually do in his own style. Finally, some human behaviors or functions, like breathing or heart beating, can develop and operate in a fully autonomous way, requiring no conscious attention whatsoever. After all, breathing must start, and never stop, from the moment of birth, while heart beating must begin much earlier.

Ernst Haeckel’s biogenic law states that, in the embryonic development of an individual’s body, ontogeny (i.e., the individual’s development) recapitulates (i.e., follows in the steps of) phylogeny (i.e., its species’ evolution), see [33, 56, 101, 159, 167] and references therein. Similarly, in the Jungian framework, one speaks of an individuation process that reenacts in the ontogeny of each individual certain archetypes of instinctual behavior or prototypical conduct. Also, it is assumed that (basic patterns for) such archetypes are phylogenetically transmitted and genetically inherited by any member of its species. Moreover, it is assumed that archetypes are adaptive, that is, that they have been selected in the evolution of a species for enabling (re)actions that contribute to an individual’s survival. Therefore, archetypes are considered teleological, that is, we regard them as capable of manifesting themselves in a purposeful manner, see [77, 131, 171, 192] and references therein.

Furthermore, in the Jungian framework, archetypes may be unconscious, that is, they may operate partially or totally outside the individual’s conscious attention. Finally, even if normally operating in an unconscious background, it is assumed that an archetype is capable of manifesting itself psychically (i.e., mentally or psychologically) in the form of archetypal images. In so doing, it may bring to an individual’s conscious attention something akin to mental representations of Platonic ideal forms or ideas, known as $\epsilon \iota \delta \eta$ or $\epsilon \iota \delta \omega \lambda \alpha$ (eidæ, eidola); see [24, 172] and references therein.

3.1 Color Archetypes and Neotypes

Let us now return to the topic of human perception and understanding of colors. Section 2 presented a summary of modern compositional and oppositional color theory, and how they were developed from the XVIII until the XX century. Let us then consider the following questions:

Could we, humans, somehow have had prior knowledge of essential facts of modern color theory? Could mankind have developed, long ago, a similar Weltanschauung? Could some basic knowledge about the structural organization of color vision have been perceived, presented, and recorded in language a priori (i.e., before) the development of modern means and methods of scientific investigation? Furthermore, if the answer to the former questions is in the affirmative, could this pre-scientific knowledge have been kept unconscious, that is, could it always have been kept alive but hidden in plain sight? In the sequel, I present some arguments supporting the preceding conjectures.

The World Color Survey (WCS) and several related projects across the fields of linguistics, anthropology, and neurophysiology of color perception were conducted during the XX century, see [80, 81], yielding important conclusions pertinent to the topics under discussion, namely:

• (1) All traditional human languages have a small set of words that jointly partition the psychological color space;

• (2) Languages evolve by expanding this set along a path that proceeds near a “characteristic encoding order” or “standard lexicalization sequence”. Moreover, this sequence follows the hierarchical branching process given next:

  • (a) Separation between light (White) versus darkness (blacK);

  • (b) Separation between warm (Red, Yellow) versus cold (Green, Blue) colors;

  • (c) Splitting of warm colors between Red and Yellow (Red usually retaining its primitive lexical form and hence becoming the oldest fundamental color);

  • (d) Splitting of cold colors between Green and Blue.

The aforementioned hierarchical branching process can be obtained from the output signals of the neural network displayed in Fig. 6l, by aggregating and then disaggregating them again into: One combined W/K signal; Two combined W/K and GB/RY signals; and Three separate W/K + G/R + B/Y signals. Figure 5t gives intuitive representations of the fully disaggregated color perception space. For further details on color perception and lexicalization, see [13, 40, 93, 104, 107].

In this way, the historical evolution of color words in traditional human languages seem to have been able to perceive, present, and record essential information concerning modern color theory. However, such basic lexicons had to be developed before any color theory was available, or even conceivable, for how could we possibly theorize about “things” we could not yet talk about?! (or about concepts we could not yet distinguish?!) A reasonable explanation for all these interconnected phenomena is that the ontogeny of human languages proceeds along tracks laid by the (invariant) architecture of color perception physiology that is genetically encoded and phylogenetically transmitted to each new human being.

Fig. 8

Top: Traditional color terms in English / Hebrew; Capital (vs. lower-case) letters correspond to simple lexical forms. Bottom: Hebrew terms, etymology and correlates

Figure 8tl shows, in capital letters, the vertices corresponding to the standard color lexicon of most traditional human languages, including English and German; the close correspondence with Figs. 5t and 6l should be obvious. Variations on lexicalization path do occur: For example, Japanese never made the final split between Green and Blue, using for both the same word, aoi, or , while Russian splits blue into light blue (goluboy) and dark blue (siniy). Meanwhile, Hebrew, as shown in Fig. 8tr,b, developed a richer palette of traditional color words, for reasons analyzed in the sequel.

3.2 Hebrew Colors: Revealed, Veiled, and Unveiled

Figure 8tl displays a set of four words corresponding to the four basic colors in Hering’s oppositional color theory. As previously discussed, these words constitute the traditional basic color lexicon of English, German, and many other languages (plus blacK and White words for an additional orthogonal axis, as depicted in Figs. 4 and 5). Figure 5t depicts an orthogonal coordinate system for the color space that is oriented according to the Yellow-headed kite. This system has four cardinal points that match the four capitalized color words at the vertices of Fig. 8tl. The Yellow-headed kite also agrees with the way in which the (non)capitalized letters in Fig. 8tl break the logical and geometrical symmetry of the color hexagon.

In contrast, Fig. 8tr shows the traditional basic color lexicon of the Hebrew language. Figure 8b explains these words, their meanings, etymological derivations, and some correlates of possible interest. Comparing Fig. 8tl and tr we notice the inclusion of a word for Cyan, like in Russian, and the inclusion of two more words, for Purple and Violet, near the Magenta vertex of the hexagon. Figure 5b depicts an orthogonal coordinate system oriented according to the Magenta-headed kite. This reorientation corresponds to an attention shift in the color space to the regions covered by the aforementioned lexical expansion, as suggested by Fig. 8tr. The Magenta-headed kite also agrees with the way in which the (non)capitalized letters in Fig. 8tr break the full logical and geometrical symmetry of the color hexagon.

The expansion of the basic color lexicon to seven words goes several steps beyond the previously discussed standard lexicalization sequence leading to RGBY. There are, however, strong reasons for this expansion motivated by ancient traditional practices. Since early biblical times, Jewish religion made use of colors along the RMBC arch, with specific ritual roles attributed to Purple, Cyan, and crimson, see Exodus 25:4, 26:31, 39:1–3, although this last color, designated by a compound expression (tola’at shani), never became fully lexicalized. For further details and explanations, see [4, 18] and [197].

The rituals of Jewish religion are supposed to have been instructed by the word of God. However, these instructions would make no sense if the words used in revelation could not be understood, or if the designated colors could not be obtained. Therefore it is important, in present times, to have precise and reliable information concerning ancient meanings of biblical words (as they were understood at the legendary time of revelation, or at least at pertinent historical times of religious practice) and also concerning equally old color technologies; those are highly non-trivial tasks.

Fortunately, there is ample material to support detailed studies in this area. First, the biblical text itself is one of the largest and best-preserved corpora of the ancient literature of western civilization. Second, every detail and minutia of the biblical text has been the subject of extensive secondary literature developed over millennia. The Talmud is the best-known example thereof, consisting of the Mishnah, compilations of older oral traditions from c.200CE, and the Gemara, compilations of further comments from c.350CE (Jerusalem version) and c.500CE (Babylonian version). Third, extensive archaeological studies employing, among others, methods of analytical chemistry, give us today a clear picture of the dyeing technologies developed and available in the Mediterranean and near-east regions at the pertinent periods.

Fig. 9

Hexaplex dyes and color production diagram

Ample archaeological evidence shows that the aforementioned colors were obtained from sea snails, certainly Hexaplex trunculus and possibly also Murex brandaris, see Fig. 9bcb. These colors were used by several civilizations in the Mediterranean region, where dying textiles mas a major industry, motivation for commerce, and source of wealth. Figure 9bct shows a silver coin from c.450BCE engraved with an hexaplex shell, attesting the importance of Tyrian purple for this Phoenician city. Figure 9brb displays some samples of textiles dyed in this way, exhibiting a wide range of colors in the RPMVBC arch, see [79, 144]. Modern chemistry identifies 6,6’-Dibromoindigo, see Fig. 9brt, as the key molecule of this ancient business. During the extraction and dyeing process, one or both of the Bromide atoms can be removed from the molecule by ultra-violet radiation in sun light rendering, in the last case, the Indigo dye nowadays obtained from a much cheaper vegetable source, Indigofera tinctoria. Moreover, hydrogen bonds at the Oxygen and Nitrogen atoms can be activated in different ways of binding the molecule to substrata. All these variations in using this wonder molecule account for endless color variations. The same hydrogen bonds facilitate good fixation of the dye, rendering enduring (non-fading) products.

Historical records show that Tyrian purple and similar dyes had a market value of several times their weight in gold, being among the most expensive commodities traded in the ancient world. Such exorbitant prices were explained by the social role these dyes had in many Mediterranean societies, where it was used in clothing and banners to visually identify the prestige and status of the bearer. For example, in the Roman empire, only kings and generals could wear a toga picta, a garment fully dyed in Royal blue or Tyrian purple. Meanwhile, a toga praetexta, a white garment edged with appropriate color stripes, identified the role and rank of important members of society, like the military, senators, magistrates, priests, etc., see [142].

Figure 9t depicts a production diagram for these colors, showing interdependences and reinforcement loops in functional interactions that maintain, strengthen, and perpetuate the industry and its associated culture (or the other way around). Practical know-how of dye chemistry (alchemy) allowed the fabrication of textiles with bright, stable, and well-defined colors that could, in turn, be used as social markers to visually identify users by their role and rank, hence helping the smooth operation of complex organizations. Such visual markers constituted tokens of visual communication used in social and religious contexts. Moreover, these markers were immersed in a web of inter-related meanings providing rich and multi-layered ways of expression.

Knowledge concerning dyeing technology implied commercial competitive advantages and was often guarded as industrial and trade secret, which probably explains the scarcity and obscurity of contemporary written accounts thereof. Moreover, overexploitation made raw materials scarce, and dye production unreliable. Furthermore, from the first centuries of the common era on, the Roman and Byzantine empires imposed strict controls over the production, commercialization and use of these dyes throughout the regions under their domain. The instability and decline of the Roman and Byzantine empires in late antiquity and the middle ages further hampered this industry. Finally, a variety of new products brought from the east, like Indigo, made dyes obtained from sea snails noncompetitive.

At the beginning of the modern era, production of these dyes was exceedingly rare, and the associated know-how was mostly forgotten. Jewish scholars could only lament the loss of this knowledge, and the consequent impossibility of observing and practicing some rituals requiring tekhelet—a cyan, blue, or maybe violet dye obtained from some strange marine creature. In summary, a community of practice that had lost some of its practices had also lost some associated knowledge, see [138, 188], and the following quotations. Only in the XXI century were these practices reinstated in some Jewish communities, after sufficient archaeological and chemical research, followed by theological study, debate, and (never consensual) agreements on how to reconstitute these practices.

Einen Satz verstehen, heisst, eine Sprache verstehen. Eine Sprache verstehen, heisst eine Technik beherrschen.

To understand a sentence means to understand a language. To understand a language means to have mastered a technique.

Wittgenstein, [190, pr.199], apud [28, ch.4, p.125].

A process cannot be understood by stopping it. Understanding must move with the flow of the process, must join it and flow with it.

Frank Herbert, [62, p. 21], apud [151, p. 6].

The materials studied in this section can give us some hints on how epistemological processes can be entangled in complex dichotomous relations of a priori conditions versus a posteriori possibilities, or of antecedent pre-requisites versus subsequent developments. Figure 9bl shows a crank leaver used to manually turn an old car’s engine in order to start its combustion cycle and, in this way, get the engine running by itself. It alludes to actions that must be taken, procedures that must be developed, or resources that must be available before (i.e. a priori) another process can, later on (i.e. a posteriori), be developed, start, or proceed.

In the cases at hand, human physiology of color perception seems to be a determinant precondition for the unfolding of the standard lexicalization sequence that, in turn, seems to be a prerequisite for additional lexicalization steps extending the standard color palette. Moreover, the production diagram in Fig. 9t hints at even more complex circular relations of positive reinforcement or negative feedback between such processes. For further analyzes of such complex interdependence relations and their epistemological consequences, see [49, 162] and [160, ch. 6]. Furthermore, the following sections introduce a few more dichotomous relations characterizing epistemological processes that are correlated to those previously mentioned.

4 Language, Synthesis, and Analysis

Let us now examine the Hebrew words used to denote the seven lexicalized colors appearing in Fig. 8. Most of these words point to an analogy or abstraction where a color name generalizes the color of something in particular. The ways in which these words are generated deserves close attention.

Hebrew, like all Semitic languages, is based on a system of tri-literal roots, where three consonants, from an alphabet of twenty-two, form basic units of meaning. There is also a small inventory of ancient bi-literal roots that are very old in the history of the language, but are still in full use. Each consonantal root can then be inflected by vocalization and other grammatical alterations, generating specific words in the final form in which they appear in a sentence. Some of such inflections are used to characterize the grammatical function the word has in a sentence, much like it happens in indo-european languages. Other inflections are used to generate clusters of words with closely related meanings. Finally, “small phonetic mutations” can generate new tri-literal roots, where clusters related by paronomasia, i.e. that sound alike, are likewise related by meaning; see [89, 143, 170, 172] and references therein.

The words in Fig. 8 give a few examples of such generative or (possible, plausible) correlative relations: (1a) Red, adom, is generated by extending by a single letter the bi-literal root meaning blood, dam. (1b) Yellow, tzahov, is generated from the word for gold, zahav, by a mutation that replaces the first consonant in the root by a similar sounding one. The following pairs of words share the same consonantal root, only using a different vocalization pattern: (1c) Green, yaroq, and vegetation, yaraq; (1d) Blue, kachol, and antimony, kachal; (2a) Violet, sagol, and grape cluster, segula. Finally, (2b) Purple is generated from the same root of the word for textile; and (3) Crimson is just a descriptive compound expression. This paragraph enumeration distinguishes a 1st set in the standard lexicalization sequence, a 2nd set of additional lexicalizations, and a 3rd set of non-lexicalized expressions.

The words in Fig. 8 constitute a specialized vocabulary for colors. In computer science, such a vocabulary, organized in a dictionary explaining the semantic functions of these words, i.e. their meanings, how to use them, and their interrelations, is known as an ontology, see [166, 167] and references therein. On the one hand, these words “divide” the continuous color spectrum into a discrete and small set of color regions. The use of this ontology affords simple reference and efficient handling of color in practical life. On the other hand, each one of these words allows us to, in a “unified” way, speak of, refer to, or represent a color property common to many particular things, namely, that of (nearly, in spectral order) sharing the same color. In this article, I will refer to these “dividing” versus “unifying” powers of such an ontology as its analytic versus synthetic aspects,³

In the philosophical literature, the two poles of the synthetic versus analytic dichotomy have been interpreted or characterized in many different ways; see [73, 74] for pertinent comparisons in the works of Kant, Bolzano, and Frege. I make this dichotomy in a way that serves the specific purposes of this article in hope this simple instance can serve as a useful proxy for examining far more sophisticated cases, as discussed in the following sections.

The synthetic aspect and the etymological or grammatical derivation of each of the Hebrew color words previously examined makes them implicit metaphors. For the purposes of this article, it will be useful to look at a metaphor ($\mu \epsilon \tau \alpha$, meta = across, after; $\varphi \epsilon \rho \omega$, phero = to bear, to carry) from two orthogonal perspectives or axes, namely, an axis of similarities and compatibilities versus an axis of differences and disparities between two distinct sites, situations, or (sets of) objects. The axis of similarities and compatibilities between the two sites allows or motivates the transport of pertinent ideas, useful knowledge, or relevant meanings across the barrier imposed by the axis of differences and disparities, just like a ferryboat carrying valuable goods between two sides of a river, see Figs. 10tl, 14tl, tr.

The term metaphorical model refers to a metaphor explained along both its orthogonal axes, like the preceding comparison between a metaphor and a ferryboat. The term analogy refers to a model succinctly stated, for example: “A metaphor is, in some aspects, like a ferryboat crossing a river”; or “These yellow flowers look, in color, like gold”; or “The sequence of arithmetic operations implied by an algebraic formula can be represented by the structure of a tree diagram”, see Fig. 10tc. The term simile refers to an analogy described only along its similarity axis, for example: “A metaphor is like a ferryboat”. In its most succinct form, a metaphor is reduced to an identity, for example: “A metaphor is a ferryboat”; see [100, p. 136] for further details.

As seen in the previous section, traditional color ontologies are not arbitrary: The standard lexicalization sequence corresponds to invariant and preset structures of human physiology for color perception, while additional lexicalizations reflect salient features of the technology and civilization a language serves. This concerns an essential analytic characteristic of good ontologies that is captured by Socrates’ quotation opening this article.

Fig. 10

Top: Cable ferry, exact law or rule—a parsing “tree” with its root at the top and leaves at the bottom, and wire-walk.Bottom: Analyzing an ox, bridge, or protein at Its precise joints

Figure 10bl shows two distinct ways, traditional in Argentina and Brazil, to “carve an ox at its joints”. Nevertheless, although distinct, both ways follow the same basic principles: First, a good carver knows how to run the knife precisely through cartilage connections at narrow gaps between hard bones of the animal and, in so doing, easily separate major anatomical parts. Second, a good carver knows how to run the knife precisely through fine layers or thin sheets of soft tissue separating major muscle groups. Figure 10bl displays the resulting major cuts and their names in each of the aforementioned ontologies, see also [26, Sec.1.1] and [120]. Finally, the carver knows how to prepare small meat portions with specific culinary qualities. It is important to remark that the intrinsically precise nature of the aforementioned cutting operations, especially in the first and second steps, afford great consistency and stability for the entire process, resulting in final products exhibiting some regular (approximately invariant) characteristics. These regular characteristics are what a consumer implicitly demands when he or she asks for a meat cut by its proper (ontological) name.

The analytic, synthetic, and metaphoric aspects are intrinsic and unavoidable aspects of language, and scientific languages are no exception. In Newtonian physics, the gravitational force applied to a body is supposed to act “like a rope” pulling it, only without the rope! The last statement is an oxymoron—an obvious self-contradiction, an embarrassing situation known in the specialized literature as “action at a distance”, see [35, 68]. We ought to recognize that the concept of Newtonian force is essentially metaphorical and, as previously stated, metaphors must always be regarded from two orthogonal perspectives, namely, that of similarities and that of disparities. The next quotation addresses this point:

Scientific metaphors define more abstract, general, or complex concepts in terms of distinct and more concrete, specific, or simpler concepts. Hence, it is unavoidable to have some degree of inconsistency in the underlying properties and functions of the objects involved in these definitions. Lakoff and Johnson, [95].

Nevertheless, the concept of Newtonian force is a good metaphor, for it is able to successfully carry valuable goods (meanings, means, and methods) across the differences separating distinct situations. More specifically, from a similarity perspective, these forces can be regarded as “working in the same way”, for example: (a) The mathematical rule used to compute the resulting force when multiple ropes are pulling an object, namely, the parallelogram law, is exactly the same rule used in the case of Newtonian forces. This law allows us to analyze complex force systems and, via decomposition and recomposition operations, calculate the system’s single resultant, see [167]. (b) Important measurable effects, like resulting static deformations or dynamic accelerations, are exactly the same for either direct contact or action at a distant forces. These similarities make the metaphor worthwhile, this is why it makes sense to use, in both situations, the same word – force.

As a last metaphor to be analyzed in this section, “a protein is like the DNA strand from which it was translated”. However, Fig. 10br shows how different those two things are. Nevertheless, this is a good metaphor—under appropriate conditions, it works! In fact, this metaphor and its associated language make life as we know it possible. At the molecular level, it reduces the production of a complex protein (an object with 3-d geometry) to a well-defined step-by-step assembly (a linearly ordered discrete process) of amino acids according to DNA encoded sequences.

At the cellular level, the genetic language (mediated by the proteic apparati it encodes) is used to represent stresses posed by the environment and to teleologically react (by controlling the expression of a discrete set of word-like genes) to these stresses in order to preserve the cell and its resources or, if necessary, to fix what is broken and regenerate the cell’s integrity.

This recurring effort of self-preservation, or autopoiesis, creates stable conditions, or homeostasis, in which the system’s processes can proceed in order to constantly repair and regenerate the machinery that actually performs its operations. In short, homeostasis and autopoiesis constantly and cyclically (re)generate the stable conditions and the invariant structures that characterize the cell as a living organism. For further considerations on autopoiesis, see [37, 38, 92, 115, 183, 184, 195, 196]. Finally, it is interesting to consider how this approach takes the linguistic view developed in this article all the way down to the rock-bottom foundations of life itself.

5 Equality, $=$, the Hallmark of Exact Sciences

In this section we examine the role of (generalized) equality relations in exact sciences and, accordingly, introduce the wire-walk metaphor for precise laws in science and their representation as sharp hypotheses in statistics. The wire-walk metaphor and its interpretations will be used in the following sections to examine and overcome a variety of percieved problems or dilemmas engendered by oppositional categories studied throughout this article.

Equality is represented in mathematics by the sign $=$ . Several variants of this concept may, depending on the context, be distinguished by variations of the basic equality sign, for example: similarity, $\sim$ ; approximation, $\approx$ ; asymptotic approximation, $\simeq$ ; proportionality, $\propto$ ; value attribution, $:=$ ; value comparison, $=\,=$ ; value-and-type comparison, $=\,=\,=$ ; equivalence, $\equiv$ ; definition, $=\hspace{-8pt}\Delta \hspace{-8pt}=$ ; etc. Other closely related concepts may be distinguished by the scope of a statement, for example, the functional identity $\cos ^2= 1-\sin ^2$, indicates a point equality, $\cos ^2(x)= 1-\sin ^2(x)$, valid over the range $x\in [0, 2\pi ]$.

Who are the heroes of a book in exact sciences? The answer can be found in the general index of the book, next to the words equation, law, rule, formula, algorithm, definition, etc., usually in reference to keystone statements formulated around the equality sign or some of its variants. This section discusses the nature and importance of such equational statements, also studied in the philosophy of science and foundations of statistics under the titles of exact laws and sharp or precise hypotheses; see also [45, 132, 177].

Figure 11tl displays the normal vibration modes of a string of length $L=1$ that is fixed at both extremes, like the strings of a guitar. The n-th normal mode, depicted at the corresponding row of the figure, is also known as the string’s n-th harmonic or, for n=1, as its fundamental mode. The n-th normal mode has $n+1$ nodes or stationary points: The two points at the extremes, 0 and L, plus $n-1$ points dividing the string in n segments of equal size. The figure also highlights the first node (away from 0) at each normal vibration mode, that are located by the L-scaled harmonic series:

$$\begin{aligned} \lambda _1= L, \ \ \lambda _2= L/2, \ \ \lambda _3= L/3, \ \ldots \end{aligned}$$

Pythagoras of Samos (c.570-495 BC) and his school already understood that the harmonic series characterizes the relative pitch of musical notes produced by string instruments, providing a mathematical basis for musical theory; see [11, 75, 163] and references therein.

Let us now return to Socrates’ metaphor of dividing things where the natural joints are. Stretching our imagination, we can think of each segment of a normal mode as a “bone”, in the sense of being an element of the vibrating string, and think of each node as a joint or articulation point between them. The pythagorean musical theory uses these basic elements to analyze the sound produced by musical instruments and the harmony of musical chords and melodies and, in so doing, this theory carves (music’s) nature at its joints.

A (static) string can be conceived as a 1-dimensional object, for a position in the string is specified by 1 measurement, namely, a distance along its length. The harmonic series gives exact or precise locations to the nodes of a normal vibration mode. In practice, these stationary points can only be located within a confidence interval $[\lambda -\delta , \lambda +\delta ]$, a.k.a. $\lambda \pm \delta$ or $\lambda$ plus-or-minus $\delta$, were $\delta$ is a tolerance margin. The better the technology and craftsmanship of a musical instrument, the tighter its tolerance margins, the more precise the musical notes produced by the instrument, and the more beautiful the resulting harmonies. In the idealized case of absolute precision, the tolerance interval has zero length, $\delta =0$, corresponding to a single point, that is a 0-dimensional object.

Fig. 11

Zero measure (length, area, volume) locus of some exact laws: Pythagorean vibrating strings; Kepler’s parabolic mirror; and Equations defining elliptical orbits

5.1 Kepler’s Exact Laws and Metaphorical Wire-Walks

Arthur Koestler [90] places Johannes Kepler (1571–1630) at the watershed marking the beginning of modern science. We use Kepler’s work to illustrate some ideas under discussion and, in so doing, corroborate his position at the watershed in the capacity of a metaphorical wire-walker, see Fig. 10tr.

Figure 11tc depicts possible orbits of a planet in Keplerian astronomy that range, according to their eccentricity, from circular ($e=0$), to elliptic ($e<1$), parabolic ($e=1$), and hyperbolic ($e>1$). Figure 11b and the following equations give two alternative ways of defining the locus of an ellipse in the plane, namely, relating Cartesian coordinates scaled by the size of the semi-axes, and specifying the radial in terms of the angular polar coordinate.

$$\begin{aligned} \frac{x^2}{a^2} +\frac{y^2}{b^2} =1 \ \ \text{ or } \ \ r(\theta ) = \frac{a(1-e^2)}{1 \pm e \cos (\theta )} \, \ \text{ where } \ \ e = \sqrt{1 -\frac{b^2}{a^2}} = \frac{c}{a} \, \ \ c = a-d_1 . \end{aligned}$$

There are some aspects of Kepler’s law prescribing an elliptical orbit that deserve further attention, see [46]. First, it is a good example of what is known in the philosophy of science as an exact law, corresponding in statistical test theory to the notion of precise or sharp hypothesis. Each of these equations states a constraint that takes away one degree of freedom from a point in the specified locus or place of movement of the system. Since a free point in the plane has 2 degrees of freedom, that is, its position is specified by two independent coordinates, a free point at the ellipse has 1 degree of freedom left, making it (the ellipse) a 1-dimensional object.

The standard size measure of a geometrical object in a plane is its area, and the area of any 1-dimensional object is zero. In this sense, we say that a physical or astronomical law stating an elliptical orbit is precise or exact. In the same way, the standard measure of a geometrical object in a line is its length, and the length of a (0-dimensional) point is zero, as in the previously examined example of the vibrating string. A free point in the 3-dimensional Euclidean space has three degrees of freedom, corresponding, for example, to the three independent Cartesian coordinates, [x, y, z]. If we set the ecliptic plane, where all planetary orbits rest, at $z=0$, a Keplerian planet moves in space over a locus specified by two equations, each of them taking away 1 degree of freedom. Under these conditions, a Keplerian orbit is conceived as a (3–2=1)-dimensional object in 3-d space. The standard size measure of a geometrical objects in 3-d space is its volume, and the volume of any object of dimension smaller than 3 is zero. So (or even more so), we say that a law stating a 1-d orbit in 3-d space is precise or exact.

Figure 11tr depict the surface of a parabolic mirror. Kepler’s studies in optics showed how lenses and mirrors with quadratic surfaces could be used to concentrate parallel light rays into a single point, namely, the focus, see [171] and references therein. A quadratic surface (conceived as a deformed plane) is a 2-d object immersed in the 3-d Euclidean space. Moreover, the volume of any 2-dimensional object in 3-d space is zero. Therefore, following arguments similar to those in the last paragraph, we say that Kepler’s recipes for building optical devices are another good example of exact or precise laws.

Back to our carving metaphor, the first step consisted of separating major anatomical parts of the ox by cutting through bone joints, while the second step consisted of separating major muscle groups by cutting along thin sheets of soft tissue between them. The surface of a lens or the face of a mirror is an interface between two distinct optical media, for example, the air through which light propagates outside and the glass or metal from which a lens or mirror is made. Hence, stretching our imagination, we can understand the analogy between the mirror’s (inter)face and the thin sheets of soft tissue guiding the carver’s knife.

As in anything done by human hands, absolute precision is unattainable. However, modern astronomical mirrors are manufactured with astonishing precision. For example, NASA’s James Webb space telescope has a 6.5 ms primary mirror whose surface is polished to an average roughness of only 20 nanometers, a relative precision of about 3 parts in a billion! Stern [171] and the references therein describe in detail fundamental techniques developed much earlier in the history of astronomical instrumentation and explain their relevance in the context of the present discussion. Similar to the case of musical instruments, the better the precision of astronomical telescopes, the sharper the resulting images, and the clearer our view of the universe.

Back to the carving metaphor, as technologies improve, the more precise the corresponding cutting operations, the better our abilities to discriminate and analyze objects in our environment, the greater our powers for working with them, and, usually, the clearer our understanding of the science involved. In fact, the other way around, the operational precision of a given technology is arguably one of the most important metrics of its degree of development and also of the development of the scientific theories on which it is based.

The emphasis of this subsection on scientific exactness or precision motivates its title for, stretching our imagination, and also looking at Fig. 10tr and bc, one can see that a wire-walk offers a very narrow bridge (in the limit, a 1-d line connection), in contrast to a normal bridge that offers a wide (2-d surface) pathway for the user to walk upon.

Finally, sharp or precise hypotheses are, on the one hand, statements indicating a locus of null volume (zero Lebesgue measure) and, on the other hand, statements that, if empirically worthy and using appropriate statistical methods, should be able to receive strong (statistical, and hence probability based) evidential support. This potential contradiction is known in foundations of statistics as the zero probability paradox. Thankfully, statistical and logical inference methods rendering good theoretical and pragmatical solutions to this paradox do exist, as discussed in [165, 173], and Section 7.

5.2 Kepler’s Data Analyses and Theoretical Syntheses

At the time Kepler started his work, all known astronomical models conceived planetary orbits by a superposition of circular motions. A typical planetary orbit was described by a small epicycle carried along a larger deferent, with all these circular planetary motions carefully synchronized and placed on a common ecliptic plane. In Greek astronomy, deferent and epicycle models were also used to build simulation machines capable of describing past movements of the planets and of predicting their future positions in the sky with great accuracy. The Antikythera mechanism, from c.200BC and found in a shipwreck in 1900, was studied by Derek de Solla Price in 1974, who was able to reverse engineer this complex mechanism composed by more then 30 high precision gears, see [157, 172] and the references therein. Nevertheless, after the fall of the Hellenic civilization, knowledge concerning this technology was lost and forgotten, consequently limiting the practical motivations for such astronomical models, and also impairing their theoretical understanding.

Kepler struggled for many years trying to find a good explanation for the extremely precise measurements of the astronomical positions of the planet Mars he received from the Danish astronomer Tycho Brahe (1546–1601). At first, he tried to fit Brahe’s data using various cycle and epicycle models, but this traditional method (and ontology) proved inadequate for the task at hand. Finally, and quite reluctantly, Kepler developed a new theory, presented in his masterpiece—Astronomia Nova, the New Astronomy, Celestial Physics and the Movements of Planet Mars, a book published in Prague, in 1609. This book includes Kepler’s 1st law, stating that a planet follows an elliptical orbit around the sun—fixed at one of its foci, see Fig. 11br. Kepler’a 2nd law states that the focus-to-planet radial vector sweeps equal areas in equal times, and his 3rd law states that the square of the orbital period is proportional to the orbit’s major axis’ length.

At the time Kepler published his astronomical laws, he already had substantial experience with the mathematics of elliptic and other quadratic curves. Five years before, Kepler wrote Astronomiae pars Optica—on the Optical part of Astronomy, a book published in Frankfurt in 1604. Section 4 of Chapter IV of this book, De Coni sectionibus, is dedicated to the study of conic sections, the curves defined by the intersection of a cone with a plane, see Fig. 12l. Kepler investigates the transformation of conic sections as the conic projection angle gradually increases, showing that, while the form of the intersection curve continuously changes, some important properties of the curve remain identical, due to the existence of some invariant mathematical relationships, see Fig. 12cl. Kepler describes his investigation method as a manner of—speaking analogically rather than geometrically, analogice magis quam geometrice loquendo.

Kepler explicitly declares how much he likes this analogical method, considering these metaphors as the best way of teaching the secrets of the universe. Furthermore, he considers this metaphorical way of teaching, in itself, as wordy and wonderful as the specific results it renders; Kepler respects his teachers as much as he is grateful for the lesson they teach:

Plurimum namque amo analogias, fidelissimos meos magistros, omnium natures arcanorum conscios.

Above all, I love analogies, my most reliable teachers, knowledgeable of all secrets of nature.

Johannes Kepler, Astronomiae pars Optica, [83, ch.IV, sec.4].

Quippe mihi non multo minus admirandae videntur occasiones, quibus homines in cognitionem rerum coelestium deveniunt; quam ipsa natura rerum coelestium.

The roads by which men arrive at their insights in celestial matters seem to me almost as worthy of wonder as these matters in themselves.

Johannes Kepler, Astronomia Nova, [84, summary of ch.45].

As an application of his analogical method, Kepler studies the reflective properties of the ellipse, showing that the light emitted by a lamp placed at one focus is reflected by the ellipse so to converge to the second focus, see Fig. 12c. Due to this property, and having in mind mechanical applications, Kepler calls these previously unnamed geometrical points by the name of focus: Nos lucis causa, et oculis in Mechanicam intentis ea puncta Focos appellabimus, using the Latin word for oven, fire-place, or burning-point.

Moreover, Kepler uses his analogical method to explain that the circle and the parabola are extreme cases of the ellipse, the circle having the two foci coinciding at the center, and the parabola having one focus taken to an infinite distance. In this way, he characterizes—the parabola and the circle as the most acute and most obtuse of all the possible ellipses, Etenim omnium Ellipsium, acutissima est parabole, obtusissima circulus. Apollonius had already used the word focus to describe the same geometrical point in the parabola, but Kepler boldly expands the scope of this concept and generalizes the meaning of this word. After all, Kepler’s 1st law made this most distinguished point the place of the sun, at the center of the universe.

As a second application of his analogical method, Kepler shows how to extend the famous string procedure for drawing a parabola: For drawing an ellipse, one can use a string of length equal to the major axis (2a) keeping the endpoints of the string fixed at the foci, see Fig. 12c. In the case of the parabola, an analogous construction replaces the focus at the infinite by a directrix line perpendicular to the symmetry axis, see Fig. 12r, where the respective endpoint of the string can slide. Using these construction methods, it is easy to demonstrate the aforementioned reflection properties.

Fig. 12

Kepler’s continuous transformations and analogies

Kepler also uses and develops his analogical method in later works, like Nova Stereometria, published in Linz at 1615. The application of Kepler’s analogical method to geometry was further developed in later times by, among others, Gottfried Wilhelm Leibniz (1646–1716) under the name of lex continui, and by Jean-Victor Poncelet (1788–1867) under the name of continuity-principle or principle of permanence of mathematical relationships, see [141, pp. xii-i-xiv], [182,183,184, 180,181,182, p. 19], and [176].

Kepler’s method of analogy can be regarded as an early precursor of modern differential and integral calculus, using ideas related to gradual or continuous transformations and, for that purpose, introducing a terminology to denote concepts like: Infinite displacements, infinito intervallo distant; Convergence of a curve to its asymptotic lines, hoc magis rectae seu asymptoto suae fit similis; and Existence of a necessary limit case, sic itaque in terminis; etc; where all these concepts are - Needed to complete an analogy, tantum ad analogiam complendam; see [83, 85, 87, 88].

Differential and Integral Calculus together with analytic and vector geometry are, arguably, the fundamental (or foundational) languages of modern exact sciences. Arguments of calculus constitute keystones of Isaac Newton’s masterpiece, Principia Mathematica, published in 1687, although his first systematic treatment of calculus was published only in 1704, as an appendix to his book Opticks: A Treatise of the Reflexions, Refractions, Inflexions and Colours of Light—Also two treatises of the species and magnitude of curvilinear figures, see [128].

The evolution of astronomy and physics from Kepler to Newton, and the parallel development of the ideas and language of calculus is a fascinating story; for pertinent historical comments, see [5, 10, 22, 32, 35, 36, 91, 103, 113, 114, 158, 189]. I will only highlight a remarkable coincidence concerning the development of these parallel languages and theories by Kepler and Newton that (at least in logical, if not in chronological order of publication) are first developed in a work on optics, to be later used in a masterpiece on physics or astronomy, see [83, 84, 86, 127, 128]. It reminds me of an observation made by Einstein in the following quotation:

“The task of physics is simply to provide a formal description of the connection between observations.” This is the programme of Mach and the positivists that succeeded him. What, however, are ‘observations’? In 1926 Einstein said to young Heisenberg: “Only theory can determine what is able to be observed.”(Die Teil und das Ganze, p.92). What does that mean? “One can only see that which one knows” was the archaeologist Ludwig Curtius’ last statement to one of his pupils. Weizsäcker [186, p. 418].

The following quotations, by the great mathematician Gian-Carlo Rota, acknowledge the importance of analogical thinking in mathematical discovery, and also the paradoxical but persistently ungrateful attitude of being ashamed and trying to hide the helpful hand of our graceful teachers:

Mathematics is the study of analogies between analogies. All science is. Scientists want to show that things that don’t look alike are really the same. That is one of their innermost Freudian motivations. In fact, that is what we mean by understanding. Gian-Carlo Rota, [149, p. 214].

The enrapturing discoveries of our field systematically conceal, like footprints erased in the sand, the analogical train of thought that is the authentic life of mathematics. Gian-Carlo Rota, [149, Preface].

What can explain this paradoxical attitude of trying to hide or conceal the footprints of analogy in the way we practice, teach and philosophize about science? In my opinion, this is just a side effect of the double nature of metaphorical thinking, as restated in the following quotation:

The greatest thing by far is to be a master of metaphor. It is the one thing that cannot be learnt from others; and it is also a sign of genius, since a good metaphor implies an intuitive perception of the similarity in dissimilars. Aristotle, [6, 1459a, 5-8].

The dissimilarity perspective accompanying any metaphor may bring a sensation of vertigo that comes when glimpsing into the abyss of the unknown. The following comments by Jung attest to some psychological needs and consequences of metaphorical paradoxes, see also [71, 72].

This is one of those paradoxes that are the rule: a statement about something metaphysical can only be antinomial. Jung, [77, IX ii, pr.390].

Any content that transcends consciousness, and for which the apperceptive apparatus does not exist, can call forth the same kind of paradoxical or antinomial symbolism. Jung, [77, XI, pr.277].

Moreover, the equational metaphors used in exact sciences may further exacerbate this vertigo, for wire-walkers are constantly reminded of their precarious equilibrium act over the abyss, see Fig. 10tr. This vertigo is therefore the presumed origin of the hostility towards metaphorical thinking, producing the side effects of trying to conceal precious insights and intuitions, and risking to throw away our best ladders of ascension. Nevertheless, following Kepler, I see the metaphorical wire-walking of exact sciences as their greatest strength, for it generously opens new ways for symbolic exploration, scientific progress, and evolution of knowledge. For several views of metaphorical and analogical thinking in science and mathematics, see [1, 20, 23, 24, 43, 48, 50, 53, 65, 121, 130, 141, 146, 196].

6 Tongs Made with Tongs and Entangled Pairs of Pairs: Synthetic $\times$ Analytic, Posterior $\times$ Prior, Imagination $\times$ Grammar, Metaphor $\times$ Hermeneutics, Latent $\times$ Observed, Image $\times$ Sound

Pairs of tongs are complicated things to make or even to speak about. A pair is either singular or plural or both simultaneously. In a pair of tongs, it denotes two equals that, opposing each other, can not be the same. In order to make a tong, to manipulate it in the fire of the forge, a blacksmith needs to hold it using a pair of tongs. But who then made the first pair of tongs? In the following quotation, the Hebrew root   tsebat, can mean, as a noun, pliers, tongs, tweezers and, as a verb, tied, twisted, entangled. Jewish mysticism states that the first pair of tongs, later given to Tubal-Cain, the first blacksmith, were created at twilight, a mystical time between the end of creation and the beginning of the existing universe.

Things made at twilight time: ... and also tongs, made with tongs. Pirkei Avot, [7, 5:6]

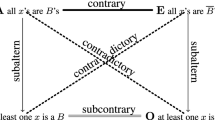
Figure 13 depicts logical diagrams conceived to help us to visualize and understand the theoretical intricacies of interacting tongs related to the synthetic versus analytic and posterior versus prior pairs of oppositional concepts. From a logical point of view, the Aristotelian diagram at Figs. 7r and 13r have exactly the same structure, known as the hexagon of opposition. Meanwhile, the Hasse diagrams in Figs. 7l and 13l have very similar structures and interpretations. These diagrams depict the entailment (implication) and oppositional (contrariety, sub-contrariety, and contradiction) relations underlying, respectively, the mereological or compositional relations of color theory, and the relations between the basic logical combinations of two (dependent) categories, A and B, and their negations.

Some sub-diagrams of the hexagon of opposition, or the corresponding algebraic sub-latices depicted in the Hasse diagrams, including the well-known square of opposition, were exhaustively studied in medieval logic, see [172] and references therein. Astonishingly, the logically complete hexagon of opposition only appeared, after a long delay, independently and almost simultaneously, in the fields of color theory and philosophical logic, in the XX century. This kind of surprising coincidence—like the simultaneous occurrence of two events not connected by direct causal relations that are, nevertheless connected by important relations of meaning, significance or interpretation—is called, in Jungian psychology, synchronicity. In the last statements, it is important to remark that astonishment, surprise, and meaningfulness, as psychological phenomena they are, always lie in the eye of the beholder(s).

In [172] I made some remarks about the synchronic emergence of the hexagon of opposition in the aforementioned time and fields, but my reference for the first appearance of the logical hexagon was the work of Robert Blanché in 1953, [18, 19]. Nevertheless, at the lecture given by Andrew Aberdein at the 7th Square of Opposition conference, in Leuven, 2022, I had the opportunity to learn about the work of Leonard Nelson (1882–1927), who presented his version of the hexagon of opposition in 1921. The Hasse diagram in Fig. 13l is depicted in [125, p. 80], [126, p. 99]. The corresponding Aristotelian diagram in Fig. 13r, although not depicted in graphical form, is described and analyzed in detail in Nelson’s text, see also the comments by Aberdein in [2, 3]. Nelson used these diagrams to study Kantian categories of prior versus posterior and synthetic versus analytic and their interrelations, see Fig. 13.

Fig. 13

Tongs of Tubal-Cain, made at the twilight of the world’s creation. Nelson (1921) Hasse / Aristotelian diagrams for categories of A = analytic, B = a posteriori, $not\,A$ = synthetic, $not\,B$ = a priori; and logical relations of entailment ($\longrightarrow$), contradiction ($=\!=$), contrariety ($-\,-$), and sub-contrariety ($\cdots$)

After presenting my paper at the 7th Square of Opposition, I had immediate feedback and subsequent discussions concerning the nature and interrelation of several pairs of oppositional concepts in this section’s title, either referring to [172], or regarding Jungian theory, see [78], or in relation to Nelson’s work. This section discusses the relations between these pairs of oppositional concepts in the contexts they were presented in previous sections of this article. These contexts are far more mundane, concrete, simple, and accessible than the technical and abstract context of Kantian philosophy or that of subsequent related works by Bolzano and Frege discussed in [74]. Nevertheless, I hope, these more accessible contexts are still pertinent for carrying on the discussion at hand yielding valuable conclusions. Moreover, the relatively simple instances used to discuss these categories makes it easier to (a) extend the discussion over multiple and diverse linguistic and theoretical scopes, and (b) show how intricately entangled these tongs can become.

6.1 Cable-Ferries versus Wire-Walks: Reification, Stratification, etc.

Every time an Argentinian and a Brazilian meet at a barbecue, hot ontological debates are likely to arise. Each one is attached to hers or his barbecue (asado, churrasco) practices and corresponding vocabulary, see Fig. 10bl and [129]. The fellow diner’s attention is focused according to fixed ontological commitments, even if the meat steak on hers or his plate was cut and prepared in a different way. Likewise, the traditional use of different color ontologies may require careful translations and practical adaptations, as in the case of the aoi or blueish-green color used in traffic lights in Japan, see [29].

Metaphors once alive at their inception, die and become fossils fixed in stone; they become reified. That is, they become our routine and automatized theoria and praxis,⁴, our standard way to look at things and to do things, they point to the beaten path as the (only) way to go, see [94, 96]. Moreover, it is often the case that an ontology and its associated theories and practices are most effective if jointly adopted by an entire community, a situation that greatly amplifies convergence and stability effects. The DNA language considered in Sect. 4 offers an extreme example or reification, for alternative coding systems could have been (and probably were) developed and used in the evolution of life. Nevertheless, only one genetic coding system (with minor DNA and RNA variations) survived and is currently in use on earth.

A wire-walker calls the attention of everyone; In contrast, a bucolic cable ferry can go unnoticed, see Fig. 10tl and tr. In this respect, wire-walking seems to be a metaphor better suited to describe statements made in a young theory, using novelty concepts, with users still struggling to distinguish the orthogonal axes of similarities and disparities, or maybe in a theory that is still in dispute with older ones. Meanwhile, the cable ferry seems to provide a metaphor better suited to describe statements made in a theory that already became well accepted and understood, or even the established paradigm.

Reified metaphors are often taken for granted, they become part of the scenery, and are (mis)taken as self-evident, strictly literal, or free of analogical comparisons. Statements formulated using mathematical language are particularly prone to this kind of mistake, as analyzed in [164, 165].

Finally, let us consider innovation and evolution, as they push life forward, opposing and counteracting the inertia of reification. In biology, evolution makes use of a variety of mechanisms like genetic mutation, horizontal gene transfers, vertical inheritance, sexual recombination, exceptional genetic fusion events, symbiogenesis and symbiosis at multiple ecological levels, etc. These mechanisms further entangle evolutionary branches in the tree of life into multiple splits and fusions, as explored at length by Lynn Margulis and her coauthors; see [110,111,112]. The following metaphorical explanation gives a very succinct but understandable summary of the core idea:

The branches of animal evolution trees do not just branch but fuse... Animal evolution resembles the evolution of machines, where typewriters and television-like screens integrate into laptops, and internal combustion engines and carriages merge to form automobiles. The principle stays the same: Well-honored parts integrate into startling new wholes. Margulis  and  Sagan,  [110, p. 172].

Computational genetic programming allows for controlled experiments in genetic evolution, including important aspects of the genetic coding as a language, like the spontaneous emergents of semantic features in this language and the way in which these features are used in the community of evolving organisms; see [66] and references therein. These experiments allow us to study how these random evolution mechanisms offer efficient and effective pathways to innovation, always creating and testing new molecular metaphors, trying to further expand already working ontologies, and selecting and preserving those innovations that improve the fitness and further empower the organisms using them.

Finally, a comment on the so called yoyo problem. Computer scientists developed clever methods, known as object-oriented programming and class inheritance, that allow them to easily reuse computer code for alternative purposes, see [25, 178]. However, the undisciplined use of such methods results in yoyo effects, namely, difficult-to-trace dependencies and side effects that interlink processes operating at distinct hierarchical levels or sharing inherited features in confusing ways. Furthermore, the most undisciplined programmer I know is biology doing its genetic programming in the evolution of life, a behavior that generates massive yoyo entanglements.

6.2 Entangled Pairs of Pairs of Tongs

Aristotle introduces a distinction between two types of thinking, namely thinking as considering images ($\phi \alpha \nu \tau \alpha \sigma \mu \alpha \tau \alpha$, phantasmata) versus thinking as considering characters ($\gamma \rho \alpha \mu \mu \alpha \tau \alpha$, grammata) And whereas the former focuses on the visual “form” ($\epsilon \iota \delta o \varsigma$, eidos), the latter is rather oriented towards discerning the “formula” or plan ($\lambda o \gamma o \varsigma$, logos) that is realized in the actual organism. ... Carl Gustav Jung likewise distinguished these two types of thinking. While imaginative thinking builds on mental images (Aristotle’s $\phi \alpha \nu \tau \alpha \sigma \upsilon \alpha \tau \alpha$), rational thinking is directed by concepts and arguments: by logic. And whereas imaginative thinking is associative and free-floating, rational thinking operates on the basis of linguistic, logical, and mathematical principles (and is therefore more demanding and exhausting, mentally speaking). Finally, whereas imaginative thinking is the oldest form of thinking (more attuned to the spontaneous functioning of the human mind), rational thinking is a more recent acquisition, historically speaking. Zwart,  [198, p. 4].

Zwart’s quotation aligns several pairs of tongs that appear in this section’s title. This alignment may be fine for the perspective taken by Zwart in his specific context of interest. However, the case studies in this paper show several counterexamples for Zwart’s suggested couplings; for example, in the case of Hebrew color ontology: (a) The grammatical (letter) and vocalization (sound) mutations used to build color analogies are aligned to their synthetic or imaginative character; and (b) The prior versus posterior or older versus more recent qualifications (lexical, biological, technological) in a color ontology are stratified in multiple levels. Furthermore, the ontologies consolidated in older substrata are used, in their full synthetic and analytic powers and capabilities, to support later ontological developments. This complex stratification does not conform to Zwart’s simple scheme.

In modern science, it is easy to find similar counterexamples to Zwart’s suggested alignments, like grammatical imagination or diagrammatic reasoning. In fact, I believe arguments of this kind to be extremely relevant in mathematics and exact sciences, see for example the case studies presented in [172], and also [54, 59, 102, 124, 152, 153]. Nevertheless, for this article, I have chosen the Hebrew colors example exactly because it can be presented involving no mathematics whatsoever. Like in the color-headed kites studied in Sect. 2, different jobs or different steps in a job, may benefit or require the use of working tongs in distinct roles, functions, and alignments, with consequent attention shifts and conceptual reorientations.

In statistics, the statement $\Pr (x\in X \,\vert \,\alpha \in A, \beta \in B, \gamma \in \Gamma ,\ldots )= p$ asserts that p is the probability that the stochastic variable x assumes a value in set X, given the parameters, under the conditions or assuming the hypotheses concerning stochastic variables $\alpha , \beta , \gamma ,$ etc. listed to the right of the conditional symbol, $\,\vert \,\,$. In a statistical model, variables in the sample space, conventionally written in Latin letters, are conceived as observed or observable quantities, while variables in the parameter space, conventionally written with Greek letters, are conceived as latent or metaphysical—in the sense of referring to non-observable entities or of having a causal explanatory function, see [34, 52]. Moreover, statistical hypothesis tests, build over conditional probability statements of this kind, are the standard tools of the trade used in the practice of science for accepting, verifying, and validating (or not) scientific hypotheses. For further details, see Sect. 7.

The facts in the last paragraph imply that, in a statistical model, even if available data can be directly linked to single “observed facts”, the surrounding conditions, hypotheses, or modeling parameters, must be described in metaphysical terms (in the sense of non-observable references or of explanatory functions). However, any reference to metaphysical concepts is intrinsically metaphorical. This unavoidable entanglement of hard data and abstract concepts is poetically described in the following quotation from Johann Wolfgang von Goethe’s 1833 Maxims and Reflections:

Everything that exists is analogous to all that exists; therefore existence seems to us at the same time isolated and interconnected. If one follows the analogy too far, everything falls together as identical, and if one avoids it completely, everything is scattered into the infinite. In both cases, contemplation stagnates, in one case, as overly alive or, in the other case, as brought to death.⁵ Goethe,  [185, n.554, p.112].

The statistician Bruno de Finetti (1906–1985) used to add a double conditional symbol, $\,\vert \,\!\,\vert \,$, at the top right corner of the first page of any document he wrote, meaning that any statement within was conditional on all necessary hypotheses, either explicitly stated, or implicitly assumed, possibly including some that he had forgotten, or was not conscious or unaware of. From the considerations in this subsection, I believe “$\,\vert \,\!\,\vert \,\,!\,$” is a caveat emptor that should be posted at the entrance of any mirror-house or at the prolegomena to any future relational theory of tongs (and there are plenty of them going around without this safety warning).

6.3 Positivist Illusions, and Solipsist or Consensualist Disillusions

Epistemology and philosophy of statistics in the XIX and early XX century were dominated by the schools of Positivism, Logical empiricism, and their aftermaths.

These schools assumed to be possible, desirable, or necessary to make science under very strict conditions, like the following (or variations thereof):

• (a) Use of regimented languages referring exclusively to observable facts, and free of any metaphorical figures or metaphysical entities;

• (b) Make a clear-cut and complete separation of analytic and synthetic statements;

• (c) Make available complete and exhaustive listings of assumed hypotheses or prior conditions to any proposition;

• (d) Assume the existence of secure and stable alignments (like synthetic and a posteriori to empirical observation) of key categories qualifying scientific statements used for testing, verifying, or validating scientific theories. From the arguments made so far in this article, it should be abundantly clear that I believe such conditions are not only untenable but also essentially misconceived.

Several alternative schools of thought came to denounce the positivist illusions, arriving, however, at very different conclusions—including a pair of alternative “disillusions” (disappointment, discouragement, disenchantment) named solipsism and consensualism—a.k.a. (inter)subjectivism. They are all-or-nothing, extreme, or radical reactions to the fall of positivism.

Solipsism, skepticism, extreme sujectivism, and their variations negate any form of objective knowledge. Any truth is only in the eye of the beholder, any certainty, even if quantitatively graduated and reasonably conditioned by its assumed hypotheses, is just a hopeless mirage. Solipsism, in the words of I.J. Good [55, p. 93], apud [167], is an inexpugnable castle. We can only hope that, sooner or later, their reclusive inhabitants will miss the sunlight and the fresh air, and come outside to have a more significant engagement with science that, in turn, can then play a more meaningful role in their lives.

Consensualism, on the other hand, allows for any form of wishful thinking—as long as it is sanctioned by a qualified endorsing community. Consensualism has the extra advantage of consensual self-validation: If all members of this community agree consensualist epistemology is valid, and that they are a qualified community, then their conclusions must be valid by this (self)validating consensual agreement! I do not deny the role consensualism plays in some forms of social organization, including religious sects and Internet bubbles. However, most people agree science needs, deserves, and can have more reliable demarcation and validation criteria.

7 Final Remarks, Conclusions, and Future Research

In this article we have examined some tongs made of oppositional categories, like Synthetic versus Analytic, Posterior versus Prior, Imagination versus Grammar, Metaphor versus Hermeneutics, Metaphysical versus Observational, Innovation versus Routine, Image versus Sound, etc. We examined the utility of these conceptual grasping tools for working at the forges of science and epistemology, and how they can be used to focus our attention and deal with important aspects of entities being manipulated at the forge. Moreover, narrowly defined conditions in a specific context of application may be able to decouple or fix existing correlations between certain aspects each of these tongs is designed to hold. Nevertheless, even small variations in context, scope, or conditions of application may require attention shifts, lead to distinct perspectives, and imply different correlations or engender new logical entanglements.

The last conclusions are incompatible with projects in mainstream XIX and XX-century philosophy of science developed by the schools of positivism and logical empiricism. These schools, in turn, served as the epistemological basis for (virtually) all of the philosophy of statistics developed in the XIX and XX century, including either the frequentist school developed by Karl Pearson, Ronald Fisher, etc., or the Bayesian revival school developed by Bruno de Finetti, Leonard Savage, etc., see [169]. Moreover, statistical hypotheses testing provides much needed and accepted validation standards used in the practice of science. In this manner, positivist ideas and ideals had a persistent influence (even if indirectly, via concepts embedded in the language of XX century statistics) over our ways of thinking about science.

Negative reactions to the aforementioned situation include the resurgence of contemporary forms of solipsism or consensualism, or a tendency to take a blasé approach to these issues that deemphasizes foundational studies and critical thinking, focusing instead on pragmatic technicalities. Notwithstanding this state of affairs, we claim that the epistemological framework of Objective cognitive constructivism offers a viable alternative to properly qualify objective scientific knowledge that, at the same time, gives a proper place to ontology and metaphysics, as discussed in the next subsections.

7.1 Objective Knowledge, Wire-Walks, and Wonder-Networks

Richard Dawkins, in his foreword for [17], makes a comparison between digital versus analogical audio or video recording, production, and distribution. The decay or degradation characteristic of analogical media (like vinyl records and magnetic tapes) impose strong limits on the quality and number of production or reproduction steps. In contrast, digital technologies (almost) do not have intrinsic degradation problems and, consequently, do not impose corresponding restrictions in their processing steps or ways of distribution.

It is possible to extend this contrast analysis to other forms of high versus low quality processing networks. For example, one could contrast high versus low-quality roads or pipelines for the transportation of material goods. High-quality networks may impose tolls and taxes but (almost) never damage transported goods (like on bumpy roads), they may require energy to overcome friction and other resistances but (almost) never cause decay or degradation (like in leaky pipelines). We consider wonder-networks as limit cases of very high fidelity information networks or very high-quality transportation networks. Such technological wonder-networks are regarded in this article as analogs to conceptual wire-walk networks whose links are made of equational relations, as those examined in Sect. 5. Figure 14 and [146, pp. 116–119, 388–391] display increasingly more abstract or schematic views of real (hence imperfect, but still wonderful) transportation networks.

Fig. 14

London subway network geographical map and Henry Beck’s electrical-schematic interconnection diagram

The Objective Cognitive Constructivism epistemological framework, or OCogCon for short, offers a way out of the entrapments posed by, on the one hand, the positivist illusions and, on the other hand, by the solipsist or consensualist disillusions. It fully recognizes and denounces the naive or untenable nature of the positivist assumptions examined in the last subsection. Moreover, it provides a proper and effective way to approach ontology and metaphysics in the scope of natural science. In this way, OCogCon overcomes their obvious inadequacy for the epistemological needs of a working scientist.

Objective cognitive constructivism relies on the possibility of making science using empirical woder-networks corresponding to conceptual networks of equational relations, or vice-versa. OCogCon is an epistemological framework based on the science and technology attested abilities for wire-walking, and for composing multiple wire-walks into complex, far-reaching, and reliable networks. Accordingly, the OCogCon framework must include statistical tools used to measure how much or how well statistical hypotheses corresponding to these wonder-networks are supported by empirical data.

Several measures of support for statistical hypothesis were developed in the XIX and XX centuries, and are generically known as measures of statistical significance, confidence level, or goodness of fit. Nevertheless, such traditional measures of support often present technical difficulties when handling sharp or precise hypotheses—the specific kind that is needed for modeling conceptual networks of equational relations, that, in turn, are used to build theoretical representations of scientific or technological wonder-networks.

$\,\text{ ev }\,(H\,\vert \,X)$—the epistemic value of hypothesis H given the observed data X, a.k.a. the e-value of H given X; and the FBST—the Full Bayesian Significance Test; are statistical methods and logical inference tools specifically designed to solve the aforementioned conundrum. The e-value and the FBST are cornerstones of a comprehensive and coherent logic and statistical theory tailor-made for evaluating and testing either a single sharp statistical hypothesis, or a composition of several sharp hypotheses (representing several interconnected links in a wonder-network). The e-value and the FBST have intrinsic theoretical characteristics of mathematical simplicity, logical coherence, and statistical consistency (asymptotic convergence). Moreover these methods have excellent operational characteristics, being usually easier to implement, statistically more efficient, and exhibiting better computational performance than traditional alternatives. For technical details, many application examples, mathematical and logical characterizations, and discussion of their philosophical and epistemological consequences, see [21, 41, 42, 49, 66, 67, 98, 99, 108, 133, 135, 155, 160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175].

7.2 The Right Science and Mathematics for Philosophy of Science

This article payed great attention to equational statements, also known in the philosophy of science as exact laws and in foundations of statistics as sharp or precise hypotheses, considering the role these statements play in epistemology. Such a study needs to be contextualized, including the discussion of concrete examples. There I unexpectedly found myself in the middle of an ongoing war, risking to take some crossfire. Some people want such epistemological discussions to be based on simple prototypical statements like – “The sky is blue” or “All swans are white”, while others want to jump straight away to examples in General Relativity or Quantum Mechanics. I have avoided some of the perils (and also renounced some of the rewards) that can be found at these extremes, choosing instead to follow through a middle ground, according to a celebrated aphorism attributed to Einstein:

Make everything as simple as possible, but not simpler.

The examples used in this article aim to be illustrative of real science but also accessible with a good high-school background, see [12, 51, 60, 62, 137, 187]. Our discussion of these examples assumes honors high-school or first year college mathematics, including basic Euclidean and analytic geometry, vector and matrix algebra, notions of calculus, and simple applications thereof, see [8, 9, 30, 47, 48, 57, 82, 97, 109, 123, 136, 181].

7.3 Future Research: Limited Complexity, Responsibility, etc.

In future research, we intend to investigate additional topics relating logical or algebraic oppositional structures, Jungian psychology and philosophy of science. Recent research in oppositional logic enables the construction of algebraic lattices of arbitrary dimension. However, most of the applications seen in practice use structures of relatively small dimension. Jung had pointed to the human mind’s preference for low dimensional representations, relating this fact to the possibility of finding radical solutions for polynomial equations of degree up to four, see [16, ch.XV, sec.8] and next quotation.

It is a property of the number four that equations of the fourth degree can be solved, whereas equations of the fifth degree cannot. Jung, [76, p. 310].

Several lines of research in modern psychology attest to the human mind’s preference or necessity of using representation spaces of low dimension. Cowan [31] makes the case for psychological representation models using up to four factors, while Miller [122] advocates for a practical limit between five and nine. We believe that the relation between the structure and number of explaining factors of a scientific model and its human ineligibility deserves further attention, quantitative modeling and research.

Moreover, Jung believed that ideas giving us powerful insights, intuitions or interpretations can always be traced back to archetypes; see next quotation. I believe that the art and science of building intuitive models and their didactic presentation deserves further attention and that, moreover, it can benefit from the desirable quantitative and qualitative characteristics suggested by Jung. Furthermore, this perspective relates to Mirroring hypothesis or Conway’s law, a general principle of system’s theory stating that—The structure of a system reflects the structure of the organization that built it, see [105, 193]. Exploring these connections can further enrich this proposed path for further research.

All the most powerful ideas in history go back to archetypes... the central concepts of science, philosophy, and ethics are no exception to this rule Jung, [77, VIII, pr.342].

Finally, we plan to investigate how solipsist or consensualist epistemological attitudes can foster extreme forms of science denial or hostility, as manifested, for example, in climate change negation and anti-vaccine movements. We believe that epistemological frameworks providing better support and stronger forms of validation to objective scientific knowledge can have a positive social impact, including increased awareness and more responsible attitudes concerning science, technology, and their role in daily life. For alternative views of this subject, see [118, 154] and references therein.

Figures: Position locators: t=top, b=bottom, l=left, c=center, r=right. Images I generated using LaTeX and TikZ or pb-diagram: 1 l; 2lb; 3r; 4tr; 5(all); 6r; 7(all); 8(all); 9t; 13 l,r. Images in Public Domain or under Creative Commons license (commercial use allowed): 4tr; 9,bct,brt; 10bc,br; 11(all); 12 l,cr,r; 13c. Images prepared for this paper by graphic artists Alex Freitas and Ian Freitas: 1c; 1r; 2lt; 3 l; 4b; 6 l; 10tc. Images from books in public domain, more than 70 years past after dates of publication and author’s death: 2r, from [27]; 6c, from [64]; 9bl, from [61]; 10 l, from [148]; 12cl, from [83]. Images used with the kind permission given by the author or responsible for copyright: 1c, by Bruce MacEvoy, from [106]; 9bcb, by Daniel Ledon, from http://www.stromboidea.de; 9brb, by Ioannis Karapanagiotis, from [145]; 10tr, by Tom McPherson, from [119]; 10bl, by olaargentina.com, from [129]; 14 l,r, by London transport museum.