Abstract
Val Plumwood and Richard Sylvan argued from their joint paper The Semantics of First Degree Entailment (Routley and Routley in Noûs 6(4):335–359, 1972, https://doi.org/10.2307/2214309) and onward that the variable sharing property is but a mere consequence of a good entailment relation, indeed they viewed it as a mere negative test of adequacy of such a relation, the property itself being a rather philosophically barren concept. Such a relation is rather to be analyzed as a sufficiency relation free of any form of premise suppression. Suppression of premises, therefore, gained center stage. Despite this, however, no serious attempt was ever made at analyzing the concept. This paper shows that their suggestions for how to understand it, either as the Anti-Suppression Principle or as the Joint Force Principle, turn out to yield properties strictly weaker than that of variable sharing. A suggestion for how to understand some of their use of the notion of suppression which clearly is not in line with these two mentioned principles is given, and their arguments to the effect that the Anderson and Belnap logics T, E and R are suppressive are shown to be both technically and philosophically wanting. Suppression-freedom, it is argued, cannot do the job Plumwood and Sylvan intended it to do.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Analytic Introduction
The plan for the paper is as follows: The minimal logic considered in this paper, unless otherwise stated, is the logic BB. The consequence relations will throughout the paper be Hilbertian. The definition of a Hilbert proof, as well as how to piece together the relevant logics referred to in this paper, is given in Sect. 2. Section 3 gives a historical account of the notion of suppression, rooting it in Anderson and Belnap’s paper on enthymemes, and explains the work Richard Sylvan—with various collaborators—intended the concept to do. Section 4 defines the first notion of suppression—extensional suppression—and shows that that property is in fact properly weaker than that of variable sharing, in fact, properly weaker than the weak variable sharing property and, furthermore, contra the claims of Sylvan and Plumwood, too weak to rule out even all the implicational paradoxes even of the first degree. Section 5 is a short digression on the Ackermann property in which it is shown that that property is not entailed by variable sharing, and does not entail the property of extensional suppression freedom. That property is also dealt with in Sect. 6 which first shows that the proof of the claim made in Routley et al.’s Relevant Logics and Their Rivals
[27] that there are logics stronger than E and R which are obviously suppressive despite having the variable sharing property, is incorrect. I give an analysis of a new notion of suppression appealed to by Routley et al. and show that although it does rule out one principle argued to be suppressive, namely the E-axiom \(((A \rightarrow A) \rightarrow B) \rightarrow B\), it also rules the Reductio axiom  suppressive—an axiom at least Routley was favorable towards—while not ruling the other E-axioms which differentiate E from DK—one of Routley’s favorite logics—suppressive. I then go through the arguments adduced by Routley et al. to the effect that these principles are suppressive, finding all of them rather wanting before Sect. 7 gives a brief summary.
suppressive—an axiom at least Routley was favorable towards—while not ruling the other E-axioms which differentiate E from DK—one of Routley’s favorite logics—suppressive. I then go through the arguments adduced by Routley et al. to the effect that these principles are suppressive, finding all of them rather wanting before Sect. 7 gives a brief summary.
2 The Hilbert Consequence Relation and Various Relevant Logics Defined
Definition 1
A proof of a formula A from a set of formulas \(\Gamma \) in the logic L is defined to be a finite list \(A_1, \ldots ,A_n\) such that \(A_n = A\) and every \(A_{i\le n}\) is either a member of \(\Gamma \), a logical axiom of L, or there is a set \(\Delta \subseteq \{A_j \mathrel {|} j<i\}\) such that \(\Delta \vdash A_i\) is an instance of a rule of L. The existential claim that there is such a proof is written \(\Gamma \vdash _{{\mathbf {L}}} A\).
Table 1 shows how the most familiar relevant logics are pieced together. To improve readability, I have followed the standard convention of dropping parenthesis to the effect that  is to be parsed as
is to be parsed as  . This is also the convention adhered to in all quotes to be found in this paper. In addition, however, Sylvan and his collaborators made use of Church’s dot notation. I have, however, taken the liberty of rendering all quotes in non-dot notation. Note, furthermore, that Sylvan used ‘&’ to denote extensional conjunction, whereas I use ‘\(\wedge \)’. ‘\(\leftrightarrow \)’ is rarely used, but when it is it is defined thus: \(A \leftrightarrow B =_{df} (A \rightarrow B) \wedge (B \rightarrow A)\).
. This is also the convention adhered to in all quotes to be found in this paper. In addition, however, Sylvan and his collaborators made use of Church’s dot notation. I have, however, taken the liberty of rendering all quotes in non-dot notation. Note, furthermore, that Sylvan used ‘&’ to denote extensional conjunction, whereas I use ‘\(\wedge \)’. ‘\(\leftrightarrow \)’ is rarely used, but when it is it is defined thus: \(A \leftrightarrow B =_{df} (A \rightarrow B) \wedge (B \rightarrow A)\).

3 Enthymemes: On the Origin of Suppression
Arguments such as

are often used when introducing the notion of entailment—what it means for a sentence to logically follow from a collection of sentences taken as assumptions—as examples of intuitively valid, but in fact invalid arguments; the explanation being that although the argument does in fact preserve truth, it does not do so in virtue of its form. Even simpler than the explanation for why the argument is and ought to be invalid, however, or so the usual introductory story goes, is the fix which restores the validity to the argument: by adding as an extra assumption the true claim that all yellow things are colored things—a semantical postulate which simply reports a fact about use of the predicates ‘yellow’ and ‘colored’—the argument becomes an instance of the old-time syllogism called Barbara.
This is, in fact, the classical so-called missing premise account of an enthymeme—an intuitively valid argument which is invalid because it lacks a premise which happens to in fact be true and readily available in the context the argument is given in. The latter point is reflected even in the word enthymeme which comes from Greek and means in mind. Thus, normally, it would be quite OK to simply drop the premise relying on the conversational context to supply it.Footnote 1
Now an argument with two premises and a single conclusion can be represented in argument form as

but it can also be represented in conditional form, where the conditional, in some way or another, represents the relation of entailment. The school of relevant logic started out in the late 1950s as an alternative to the already existing modal school of analyzing the relationship between entailment and the relation expressed by the material conditional. The stricter-claim, going back to both Hugh MacCall and Clarence Irving Lewis,Footnote 2 was that the material conditional is not a good candidate for expressing entailment because of the paradoxes of material implication. The three most commonly acknowledged such paradoxes stems from Russell, who writes that
the assertion that q is true or p false turns out to be strictly equivalent to “p implies q”; [...]. It follows from the above equivalence that of any two propositions there must be one which implies the other, that false propositions imply all propositions, and true propositions are implied by all propositions. [29, § 16]
An implicational paradox is intuitively, then, an implicational sentence with in some sense unrelated antecedent and consequent; the truth of the implication has nothing to do with the relation of content of its constituent parts, but is solely due to the impoverished logical space considered. A remedy for the paradoxes might therefore be found in a more opulent logical space.
The material implicational paradoxes were regarded by both MacCall and Lewis to conclusively show that the material conditional does not express entailment, and introduced the strict conditional as a better candidate for this. This is the starting point for the school of relevant logics, initiated in the 1950s by Ackermann, but carried out to a whole research program by Anderson and Belnap. Although the logical space afforded by the strict conditional undoubtedly is more opulent than that of the material conditional, it as well, according to Anderson and Belnap, is infested with implicational paradoxes. For instance, any logical truth is strictly entailed by every proposition, and every logical falsehood entails every proposition. As a combined example of such an implicational paradox is the Kleene axiom which holds true in classical, inuitionistic, as well as in the modal logics S1–S5, where \(\twoheadrightarrow \) is, respectively, the material, intuitionistic, and strict conditional. The Kleene axiom will figure prominently throughout this paper.
which holds true in classical, inuitionistic, as well as in the modal logics S1–S5, where \(\twoheadrightarrow \) is, respectively, the material, intuitionistic, and strict conditional. The Kleene axiom will figure prominently throughout this paper.
To overcome such paradoxes, Anderson and Belnap set forth the variable sharing property as a necessary property for \(A \rightarrow B\) to be logically true. Although the main thrust behind the latter two’s onslaught on classical as well as intuitionistic and modal logic, was that such logics violate principles of relevance, they also gave an analysis of enthymemes which they thought to lend support to their choice of the logic E as the logic of entailment. They argue in [4] that because the classical theory of enthymemes—the missing premise theory—is correct, neither the material, nor the intuitionistic, nor the strict conditional can express entailment. Here is a rather lengthy quote expressing their view:
The present argument is simply this: both views make hash of the distinction between logically valid arguments and enthymemes. For on both theories we have as a “theorem of logic” a principle according to which true premises aren’t really there at all (“true premises may be suppressed”):
Suppose now that an argument is valid if and only if the corresponding material or intuitionistic “implication” statement is true. Then, since the argument from M and m to C is valid, \( M \mathrel { \& } m \supset C\) is true; and since m is true as well and, hence, suppressible, \(M \supset C\) is true; hence the argument from M to C is valid, and in precisely the same sense as is the argument from M and m to C. But to say that the argument from M to C is thus valid is in direct contradiction to the doctrine that enthymematic arguments suppress required premises. [4, pp. 714f]Footnote 3
What Anderson and Belnap find wrong with the material, the intuitionistic and the strict conditional is that all these allow one to suppress premises: simply true ones in the first case, provably true in the second, and necessarily true in the third case. Anderson and Belnap conclude that if entailment proper, and not simply enthymematical implication, is to be expressible using a conditional, then one needs a conditional and a logic which does not sanction wholesale suppression. They contend that their favorite relevant logic E is the best candidate for this job. The paper ends with the following (which they claim to be an obvious truth):
If we are very careful, and always put down all the premises we need (i.e., if we argue logically), then we arrive precisely at the formal system E of logical implication [...] or entailment. [4, p. 722]
Although the motivational story of enthymemes and suppression lived on within the school of relevant logics, I think it is fair to say that it rarely was treated as anything beyond this. On the proof-theoretic side, Anderson and Belnap’s notion of a relevant deduction—that the premises must somehow be used in obtaining the conclusion—took center stage, whereas the variable sharing property—that for the conditional \(A \rightarrow B\), where \(\rightarrow \) is the conditional expressing entailment, to be logically true, A and B need to share a propositional variable—took care of the semantical intuition that there need to be some commonality of meaning between A and B if the first is to entail the latter. The first property was regarded by Anderson and Belnap as a necessary and sufficient property for preserving relevance in an argument, whereas the variable sharing property was regarded as necessary in this regard.
There is another school—the Routley school—within relevant logic, however, going back to [28], which did not focus on Anderson and Belnap’s use-criterion—precisified as the so-called Entailment Theorem—to the same extent. That tradition had a bent towards logics weaker than Anderson and Belnap’s E. It is still claimed that the variable sharing property is a necessary one, but the Entailment Theorem—Anderson and Belnap’s claim that relevance-preserving arguments involve premise use in an essential way—is rejected as a relevant criterion of entailment.Footnote 4 Routley et al. [27, p. 232] further deny that variable sharing can be strengthened “with other minor qualifications” so as to yield a sufficiency-criterion for relevance-preserving entailment. Their main charge against the Anderson-Belnap tradition seems to be that this tradition is claimed to hold a maximizing principle of logic choice: in the case of R: choose the strongest paradox-free logic possible, and in the case of E: choose the strongest paradox-free logic free of modal fallacies, where a modal fallacy is any theorem \(A \rightarrow B\), where A expresses a contingent proposition, whereas B expresses an entailment, and therefore a necessary proposition. It was already noted by Urquhart in [32] that this is a gross misrepresentation of Anderson and Belnap’s position. The interesting contribution, however, is their insistence that the implicational paradoxes and variable sharing violation are a mere symptom of the more fundamental feature of suppression. To quote Priest’s approval of their dictum: “the Routleys argue cogently that the failure of relevance, in the technical sense, is but a symptom of suppression, which is the fundamental malaise.” [19, p. 90]. Entailment is, according to the Routley tradition, to be analyzed as a sufficiency relation, and so can’t be suppressive; neither the material, nor the intuitionistic, nor the strict conditional express such a sufficient relation, but at best an enthymematical, and therefore suppressed, version of one such.
It was shown in [18] that even classical logic satisfies Anderson and Belnap’s Entailment Theorem, and so the Routley tradition’s claim in this regard was correct. Thus, since the variable sharing property fails for classical logic, satisfying the Entailment Theorem can’t be upheld as a sufficient criterion for relevancy if, as all within the relevant school seem in agreement it ought be, the variable sharing property is upheld as necessary. Both properties, then, can at best be regarded as necessary. The question rises, therefore, as to the nature of relevance: Could suppression-freedom be spelled out in such a way as to yield a sufficiency property for relevance?
The main aim of this paper is to analyze the Routley school’s treatment of suppression. We will see that despite letting the notion of suppression gain such an important role, the Routley tradition seems content with using the notion without properly defining it. They do claim that a logic can have the variable sharing property, yet have evidently suppressive principles. I will show, however, that the proof given to this effect is glaringly fallacious. Furthermore, we will see that two ways of making the notion of suppression precise—as what is called the Anti-Suppression Principle and as the Joint Force Principle—yield properties which, although they do rule out some, but not all, of the paradoxes, are in fact much weaker than the variable sharing property. I will then show that that principle is, like the variable sharing property, independent of the so-called Ackermann Property—that \(A \rightarrow (B \rightarrow C)\) is not a theorem for formulas A in which \(\rightarrow \) does not occur.
Suppression precisified in such a way cannot therefore yield a notion of suppression more fundamental, at least not entailment-wise, than the variable sharing property, and so using it as a sufficient property for relevance will not do. I will also look at another notion of suppression which Routley et al. appealed to in arguing that even the three favorite logics of Anderson and Belnap, namely R, E and T, are suppressive. I will argue, however, that that notion of suppression is tailor-fit to rule out only one logical principle, namely the E-axiom \(((A \rightarrow A) \rightarrow B) \rightarrow B\) which
[27] tendentiously calls Suppression; indeed, one of the other principles clearly ruled out by that notion of suppression, the reductio axiom  , was not regarded as clearly suppressive, whereas the other principle which were so regarded are clearly not. To obtain the strongest of Routley’s favorite logics, DL, from E, one needs to chasten not only the suppression axiom, but also
, was not regarded as clearly suppressive, whereas the other principle which were so regarded are clearly not. To obtain the strongest of Routley’s favorite logics, DL, from E, one needs to chasten not only the suppression axiom, but also
The claim made is not necessarily that all these axioms are suppressive, only that R, E and T harbor suppressive logical principles. In their discussion it is especially the contraction axioms, discussed in [27, § 3.9], in both the form \((A \rightarrow (A \rightarrow B)) \rightarrow (A \rightarrow B)\) as well as the weaker variant \(A \wedge (A \rightarrow B) \rightarrow B\), an axiom which is interderivable in all relevant logics with the contraction rule, i.e. \(A \rightarrow (A \rightarrow B) \vdash A \rightarrow B\), which is not argued to be suppressive, but rather incorrect on other accounts than being suppressive. The suppressive features of R, E and T must then be due to the first three axioms. I will evaluate the arguments adduced to this effect finding them rather wanting. The conclusion this paper draws, then, is that making freedom from suppression the core notion of relevant entailment is, given the best available analysis of what suppression is supposed to be, a dead end. However, analyzing entailment as a sufficiency relation, need not be.
4 Guilty of Logical Suppression in the First Degree
The enthymeme-tradition was taken up by Richard Sylvan (né Richard Routley) and Val Plumwood (née Val Routley) in their joint paper The Semantics of First Degree Entailment [28]. That paper is best known for having first introduced the now well-known Routley-star operator which is used to give an intensional semantics for negation. It is also, to my knowlegde, the first work by either of these authors on enthymemes and logical suppression, and spawned off a new school of relevant logics with a focus towards weaker logics than Anderson and Belnap’s two favorite logics E and R. In it they claim that a semantics for an implicational connective which forces no kind of suppression will have to allow for the maximum variation principle:
for every proposition B which is not a consequence of A there is some set-up which A is in to which B does not belong. Any violation of this maximum variation principle will allow suppression somewhere. [28, p. 341]
In fact, they take maximum variation, sufficiency of the antecedent to the consequent and suppression-freedom to be logically equivalent notions [28, p. 341]. They note, however, that a definition of logical consequence based upon either of the latter two concepts would be circular, but nevertheless hold that the latter two afford “a useful guide as to whether a suppression-permitting implication has been confused with entailment.” [28, fn. 3]. Their take on entailment, or logical consequence, is that it is to be analyzed as a sufficiency relation; it is this which is conceptually basic whereas the notions of maximum variation and suppression-freedom are the concepts used by the Routleys to explicate the notion of a sufficiency relation.
[28] only deals with the semantics of the first-degree fragment of Anderson and Belnap’s logic E. Thus the semantics only deals with formulas generated from propositional variables and the connectives  as well as formulas \(A \rightarrow B\) where A and B are themselves generated solely from the three mentioned connectives. What is interesting, however, is that they managed to prove the variable sharing property from the fact that their model allows for maximum variation with respect to the given provability relation. Since suppression-freedom is supposed to be equivalent to maximum variation, one might think that this lends credence to the thought that suppression-freedom is the more fundamental property. This is precisely what the Routleys claim:
as well as formulas \(A \rightarrow B\) where A and B are themselves generated solely from the three mentioned connectives. What is interesting, however, is that they managed to prove the variable sharing property from the fact that their model allows for maximum variation with respect to the given provability relation. Since suppression-freedom is supposed to be equivalent to maximum variation, one might think that this lends credence to the thought that suppression-freedom is the more fundamental property. This is precisely what the Routleys claim:
Though elimination of suppression eliminates the paradoxes, elimination of the paradoxes and of relevance violations does not guarantee absence of suppression, because certain limited kinds of suppression do not lead to relevance violations. Therefore the satisfaction of relevance requirements is not itself sufficient to guarantee suitability of an implication for interpretations which require suppression freedom. [28, p. 359]
[28] undoubtedly made heavy use of the maximum variation principle in spelling out the ideas of both suppression-freedom and entailment as a sufficiency-relation. 10 years after the publication of that article, the notion of suppression and its importance for relevance is taken up again in Relevant Logics and Their Rivals [27]. That book deals primarily with logics without degree-restrictions on \(\rightarrow \)-formulas. However, the main material dealing with suppression in that book is to be found in § 2.10 which is by and large a slight modification of the account of suppression found in [28] and like it only pertains to the first-degree fragment.Footnote 5 They do claim that “most of our general remarks about the damaging nature of suppression and the reasons for avoiding it apply equally to the higher degree forms.” [27, p. 142]. Regrettably, however, it is never cleared up what does not apply.
The claim that suppression is of central importance and variable sharing is not is also echoed throughout [27]. The following quote from the introduction is representative:Footnote 6\(^{,}\)Footnote 7
Though weak relevance is not a fundamental matter for entailment [...] but a derivative feature of a good sufficiency relation, it provides an extremely important formal test of adequacy. [27, p. 3]
Although the possibly different account of higher order suppression remains a bit unclear, it is not any longer the model-theoretic maximum variation principle which does the heaviest lifting in explicating the notion of a sufficiency relation. Instead a principle of first degree suppression—both positive and negative—is put forth and given a “syntactical characterization” as follows:
A is positively suppressed in \(B \rightarrow C\) when \( B \mathrel { \& }A \rightarrow C\) but not \(B \rightarrow C\). Thus a statement is suppressed in an implication when, although not stated as part of the antecedent and not a consequence of the antecedent, it is presupposed in obtaining the consequent from the antecedent. Positive suppression, which corresponds to the traditional notion of an enthymeme, can easily be rectified by conjoining the suppressed statement to the insufficient antecedent, rendering it sufficient. A is negatively suppressed [...] where \(B \rightarrow A \vee C\) but not \(B \rightarrow C\). [27, p. 142]
Since  and \(B \rightarrow A \vee C\) can be inferred from each other in all the relevant logics under scrutiny, negative suppression of A in \(B \rightarrow C\), reduces to positive suppression of
and \(B \rightarrow A \vee C\) can be inferred from each other in all the relevant logics under scrutiny, negative suppression of A in \(B \rightarrow C\), reduces to positive suppression of  in
in  . I will in the following therefore not differentiate between positive and negative suppression. Let’s call this kind of suppression extensional since it concerns extensional conjuncts of antecedents of \(\rightarrow \)-statements. The notion of suppression here is still less than clear, however; what does it mean to claim that A is suppressed in \(B \rightarrow C\)? One could explain this as Bis sufficient forC suppresses A when \(B \wedge A\) is in fact sufficient for C, but B on its own isn’t. This, however, is still shy of a workable definition which can be translated into a property of logics which then can be compared to that of the variable sharing property. This, however, is rectified by the syntactical principle called the Anti-Suppression Principle:
. I will in the following therefore not differentiate between positive and negative suppression. Let’s call this kind of suppression extensional since it concerns extensional conjuncts of antecedents of \(\rightarrow \)-statements. The notion of suppression here is still less than clear, however; what does it mean to claim that A is suppressed in \(B \rightarrow C\)? One could explain this as Bis sufficient forC suppresses A when \(B \wedge A\) is in fact sufficient for C, but B on its own isn’t. This, however, is still shy of a workable definition which can be translated into a property of logics which then can be compared to that of the variable sharing property. This, however, is rectified by the syntactical principle called the Anti-Suppression Principle:
for every statement p there is some statement q such that the consequences of q are a proper subset of the joint consequences of p and q. There is no privileged class of statements which are generally suppressible. [27, p. 146]
My suggestion for how to interpret their claim is that they claim that at least a necessary requirement for a logic to be suppression-free is that it satisfies the following property:Footnote 8
Definition 2
A logic L satisfies the Anti-Suppressive Principle (ASP) just in case for every formula A, there exist formulas B and C such that \(\vdash _{{\mathbf {L}}} A \wedge B \rightarrow C\), but \(\nvdash _{{\mathbf {L}}} B \rightarrow C\).
Lemma 1
ASP rules out both of the following implicational paradoxes:

Proof
I’ll show that the latter is ruled out; the proof of the first is similar only with added negation steps.
Assume that  is a theorem of a logic which satisfies ASP. It follows that there are sentences B and C such that
is a theorem of a logic which satisfies ASP. It follows that there are sentences B and C such that  is a logical theorem, while \(B \rightarrow C\) is not. However, since
is a logical theorem, while \(B \rightarrow C\) is not. However, since  ,
,  and so transitivity yields that \(\vdash B \rightarrow C\). \(\square \)
and so transitivity yields that \(\vdash B \rightarrow C\). \(\square \)
Note, again, that the above principle is formulated in [27] in the context of the first degree fragment. However, a principle akin to ASP does appear later in the book when the degree-restriction is lifted, under the name The Joint Force Principle:
For every proposition p there is some other q such that p and q are jointly sufficient for r but neither p nor q on its own is sufficient for r. Formally, the Joint Force Principle says:
.Footnote 9 It tells us that the joint consequences of propositions may be more than the sum of the consequences of each. [27, p. 369]
This seems, intuitively at least, stronger than the Anti-Suppression Principle. So as not to cause any confusion, let’s have this principle properly defined as well:Footnote 10
Definition 3
A logic L satisfies the Joint Force Principle (JFP) just in case for every formula A, there exist formulas B and C such that \(\vdash _{{\mathbf {L}}} A \wedge B \rightarrow C\), but \(\nvdash _{{\mathbf {L}}} A \rightarrow C\) and \(\nvdash _{{\mathbf {L}}} B \rightarrow C\).
Since JFP is obviously at least as strong as ASP, it seems clear that if suppression-freedom is not reducible to JFP, then at least they are committed to the necessity of the principle in any analysis of entailment as a sufficiency relation, and if JFP is not to be regarded as a sufficient property in and of itself, then at least as a necessary ingredient of a sufficient set of clauses determining what a sufficiency relation is.Footnote 11
It is, then, possible to ask the following questions:
Question 1
Is the variable sharing property a derived feature of any sufficiency relation for which JFP holds?
Question 2
Does JFP rule out the implicational paradoxes?
Question 3
Does JFP rule out the implicational paradoxes of the first degree?
Even though ASP and JFP do rule out some of the more common implicational paradoxes, the correct answer to all of the above questions is no. In fact, JFP turns out to be properly weaker than the so-called Weak Variable Sharing Property and therefore fails to rule out implicational paradoxes such as the Kleene axiom as well as Dummett’s axiom\((A \rightarrow B) \vee (B \rightarrow A)\), both of which apply to the first-degree fragment.
as well as Dummett’s axiom\((A \rightarrow B) \vee (B \rightarrow A)\), both of which apply to the first-degree fragment.
This, then, will show that the three concepts of maximum variation, sufficiency of the antecedent to the consequent and suppression-freedom are in fact not equivalent notions—not even in the first degree fragment—as claimed by Plumwood and Sylvan in [28, p. 341] and reiterated in [27, p. 144]. Thus extensional suppression-freedom cannot function as a means of explicating the conceptually fundamental notion, namely entailment understood as a sufficiency relation, which is the stated goal within the Routley tradition. The explanation, then, for why the variable sharing property is provable for the first degree fragment is because of the semantic theory, that is, because of maximum variation, and not because of freedom from suppression.
I will now provide the proofs which show that no is indeed the correct answer to all of the above questions. Before we begin, we need to properly define the two variable sharing properties:
Definition 4
A logic L has the Variable Sharing Property (VSP) just in case for every formula A and B, \(\vdash _{{\mathbf {L}}} A \rightarrow B\) only if A and B share a propositional parameter.
VSP was formulated in [6] where it was shown that E had VSP. Later it was remarked that Belnap’s eight-element algebraic model which he used to prove his theorem, in fact also validates the assertion axiom
and therefore validates all of R, and hence that also R has VSP.
The logic RM is obtained from R by adding the mingle axiom
Dunn and Meyer began investigating this logic in the late 1960’s. To their surprise, however, they found that RM does not have VSP as  as well as the Kleene axiom turned out to be logical theorems of RM
[14]. Meyer, then, showed that RM has the following weaker property:Footnote 12
as well as the Kleene axiom turned out to be logical theorems of RM
[14]. Meyer, then, showed that RM has the following weaker property:Footnote 12
Definition 5
A logic L has the Weak Variable Sharing Property (WVSP) just in case for every formula A and B, \(\vdash _{{\mathbf {L}}} A \rightarrow B\) only if either A and B share a propositional parameter, or both  and \(\vdash _{{\mathbf {L}}} B\).
and \(\vdash _{{\mathbf {L}}} B\).
One of the implicational paradoxes was that ‘of any two propositions there must be one which implies the other’ [29, § 16]. One of the logical theorems of RM expresses precisely this, namely Dummett’s axiom
Under the heading Why we don’t like mingle, Anderson and Belnap quote The Divine Comedy’s “All hope abandon, ye who enter in!”, their view being that if \(\rightarrow \) is to express “if ..., then __”, then Dummett’s axiom can’t be a logical theorem. Dummett’s axiom was in fact introduced by Skolem in 1913 [33, p. 154], notably as equivalent, given intuitionistic logic, to Skolem’s axiom:Footnote 13
[27, p. 269, fn. 1] denounced this principle as a principle which “for every proposition denies the Joint Force Principle.” This, however, is a poor rendering of their principle, the denial of which is that there exists a formula A such that for all B’s and C’s, if \(A \wedge B \rightarrow C\) is a logical theorem, then so is either \(A \rightarrow C\) or \(B \rightarrow C\); Skolem’s axiom on its own does not suffice for deriving either \(A \rightarrow C\) or \(B \rightarrow C\) as logical theorems under the proviso that \(A \wedge B \rightarrow C\) is a logical theorem. Nor is Skolem’s axiom, as we shall see, in any way incompatible with upholding JFP.
Theorem 1
WVSP entails JFP
Proof
Assume that L has WVSP, but not JFP. Then there is some A such that for every B and C, if \(\vdash A \wedge B \rightarrow C\), then either \(\vdash A \rightarrow C\) or \(\vdash B \rightarrow C\). Let C be \(A \wedge B\) and let B be a propositional variable which does not occur in A. Then since \(\vdash A \wedge B \rightarrow A \wedge B\), either \(\vdash A \rightarrow A \wedge B\) or \(\vdash B \rightarrow A \wedge B\). It follows that either \(\vdash A \rightarrow B\) or \(\vdash B \rightarrow A\). However, since A and B do not share any propositional variables, it follows from WVSP that \(\vdash B\) if \(\vdash A \rightarrow B\) and  if \(\vdash B \rightarrow A\). Neither alternative can be true since B was assumed to be a propositional variable. \(\square \)
if \(\vdash B \rightarrow A\). Neither alternative can be true since B was assumed to be a propositional variable. \(\square \)
Theorem 2
JFP does not entail WVSP.
Proof
Let SIE (Suppressive Irrelevant E) be the logic E with the axiom of intensional Paradox, Kleene’s axiom, Skolem’s axiom, disjunctive syllogism, as well as the Anti Joint-Force rule added:

SIE does not have WVSP since  is not one of its logical theorems although (iP) is. However, it does satisfy JFP: Consider the model in Fig. 1.Footnote 14 Let A be any formula and assign every propositional variable in it to either 1 or 2. It is easy to check that \(\{1, 2\}\) is a subalgebra so that \(\llbracket A\rrbracket \in \{1, 2\}\) as well. Let B be a propositional variable and assign 0 to it, and further let C be \(A \wedge B\). Then \(\vdash A \wedge B \rightarrow C\), but \(\llbracket A \rightarrow C\rrbracket = 0\). By simply reassigning B to 3 one then gets that \(\llbracket B \rightarrow C\rrbracket = 0\). Since the algebraic models are sound with regards to SIE it follows that \(\nvdash A \rightarrow C\) and \(\nvdash B \rightarrow C\) which therefore ends the proof that SIE satisfies JFP.\(\square \)
is not one of its logical theorems although (iP) is. However, it does satisfy JFP: Consider the model in Fig. 1.Footnote 14 Let A be any formula and assign every propositional variable in it to either 1 or 2. It is easy to check that \(\{1, 2\}\) is a subalgebra so that \(\llbracket A\rrbracket \in \{1, 2\}\) as well. Let B be a propositional variable and assign 0 to it, and further let C be \(A \wedge B\). Then \(\vdash A \wedge B \rightarrow C\), but \(\llbracket A \rightarrow C\rrbracket = 0\). By simply reassigning B to 3 one then gets that \(\llbracket B \rightarrow C\rrbracket = 0\). Since the algebraic models are sound with regards to SIE it follows that \(\nvdash A \rightarrow C\) and \(\nvdash B \rightarrow C\) which therefore ends the proof that SIE satisfies JFP.\(\square \)
Corollary 1
JFP does not rule out all first-degree implicational paradoxes.
Proof
SIE validates both the Kleene axiom and Dummett’s axiom, and so its first-degree fragment validates these as well despite it having JFP. \(\square \)
This section has shown that the notion of extensional suppression does not suffice for ruling out the implicational paradoxes. The short next section will show that this is also the case when strengthening the requirement to also encompass the Ackermann Property.
5 The Ackermann Property: A Digression
There is another property which is sometimes held forth as an important property for entailment-logics to have, namely the Ackermann Property:
Definition 6
A logic L satisfies the Ackermann Property (AP) just in case L has no logical theorems on the form \(A \rightarrow (B \rightarrow C)\) where A is a \(\rightarrow \)-free formula.
The property was designed to guard against so-called fallacies of modality, and not against fallacies of relevance. Failures of the Ackermann Property are, according to
[5, p. 44], fallacies of modality because they express that “entailments follow from, or are entailed by, contingent propositions.” Anderson and Belnap defined the modal operators using \(\rightarrow \): \(\Box A =_{df} (A \rightarrow A) \rightarrow A\), and  . In order to get suitable modal principles to hold, the logic has to be quite strong; stronger than what the Routley tradition thought acceptable. Still, the Routley tradition did insist on the validity of the Ackermann Property in the case where \(\rightarrow \) is to express entailment
[27, p. 223]. I will not discuss this further; the main purpose of the following is only to make the connections, or lack thereof, between the Ackermann Property and extensional suppression. Later I will demonstrate a similar result pertaining to intensional suppression.
. In order to get suitable modal principles to hold, the logic has to be quite strong; stronger than what the Routley tradition thought acceptable. Still, the Routley tradition did insist on the validity of the Ackermann Property in the case where \(\rightarrow \) is to express entailment
[27, p. 223]. I will not discuss this further; the main purpose of the following is only to make the connections, or lack thereof, between the Ackermann Property and extensional suppression. Later I will demonstrate a similar result pertaining to intensional suppression.
Theorem 3
VSP does not entail AP.
Proof
This is a well-known result. The logic R has the variable sharing property, although not the Ackermann Property since it validates the assertion axiom \(A \rightarrow ((A \rightarrow B) \rightarrow B)\). \(\square \)
The question, then, is whether the Ackermann Property entails ASP or JFP. The answer is ‘no’, as the following theorem shows:
Theorem 4
AP does not entail ASP.
Proof
Let \(\mathbf {\Pi '^\star }\) be the logic \(\Pi '\) with the Kleene axiom added as well as Intensional Strong Excluded Middle axiom:

Because of the (iSEM)-axiom, \(\mathbf {\Pi '^\star }\) does not satisfy ASP. However, it does have the Ackermann Property. This is seen by noting that the model in Fig. 2 is a model for \(\mathbf {\Pi '^\star }\).Footnote 15 Let A be any formula built from propositional variables using  . Assign 4 to every such variable. A will then be assigned to either 1 or 4. For such an evaluation of A, however, the model falsifies \(A \rightarrow (B \rightarrow C)\) for every formula B and C, which therefore ends the proof that \(\mathbf {\Pi '^\star }\) has the Ackermann Property. \(\square \)
. Assign 4 to every such variable. A will then be assigned to either 1 or 4. For such an evaluation of A, however, the model falsifies \(A \rightarrow (B \rightarrow C)\) for every formula B and C, which therefore ends the proof that \(\mathbf {\Pi '^\star }\) has the Ackermann Property. \(\square \)
Corollary 2
JFP together with AP do not rule out all first-degree implicational paradoxes.
Proof
Let L be the intersection of \(\mathbf {\Pi '^\star }\) and SIE. It follows from the proofs of Theorem 2 and Theorem 4 that L satisfies both JFP and AP despite having  as a logical theorem. \(\square \)
as a logical theorem. \(\square \)
We have in this short section seen that the Ackermann Property is independent of the Joint Force Principle. We saw, however that their combination can’t be the final analysis of suppression if this is to be, as Routley et al. argue, the “fundamental matter for entailment”, from which the variable sharing property is “but a derivative feature” [27, p. 3]. Note, then, that some of their claims with regards to suppression is clearly not captured by the extensional notion of suppression. The next section therefore looks at another notion of suppression which is appealed to in order to rule that even Anderson and Belnap’s three favorite logics, T, E and R, harbor suppressive principles.
6 Speak of the Devil and He Doth Appear: The Rhetorics of Suppression
We saw in the previous sections that both attempts at making the notion of suppression-freedom precise yielded a principle properly weaker than that of variable sharing. The Routley tradition never, as far as I know, made any attempts at comparing the different notions of relevance, settling rather for arguing against what can at best be seen as an imprecise notion of suppression. Furthermore, although they often claim that variable sharing is a mere byproduct of a good sufficiency relation, the proper analysis of which is via suppression-freedom, hardly any evidence is conjured up to support this view.
They do make two substantial claims with regards to the relationship between suppression and the VSP:
-
1.
There are logics stronger than Anderson and Belnap’s favorite logics T, E and R which are clearly suppressive despite satisfying VSP.
-
2.
T, E and R are themselves suppressive.
The notion of suppression here can’t be that of extensional suppression if that is cashed out as either ASP or JFP since we saw in the last section that both these are even properly weaker than WVSP. Routley et al., however, seem to suggest that there are suppression principles which are not captured by these two principles. This section tries to hone in on what this new notion of suppression can be taken to be, and whether it, or it together with some extensional notion, yields a notion of suppression which truly classifies T, E and R as suppressive. Although we will see that the intensional variants of ASP and JFP do this, I will argue that even when taken in conjunction, the extensional and intensional notions of suppression do not do the job intended by Routley et al., namely to provide an analysis of what a good sufficiency relation is. Furthermore, the intensional notions of suppression do not rule out all the principles deemed suppressive by Routley et al., and the reason for adopting them seem less than clear.
Before we get to intensional suppression, however, let’s look at the evidence given by Routley et al. for the claim that there are logics stronger than T, E and R which are obviously suppressive despite having the variable sharing property, namely the second part of Theorem 3.15 ( [27, p. 231]):
FalseClaim
Both E and R extended by either of the rules
where \({\mathbf {t}}\) represents the conjunction of theorems of E or R, has the Variable Sharing Property.
The alleged proof of this claim is that the resultant logics still have Belnap’s eight-element model of relevance as one of its models. As we shall see, however, that is plainly false. Since \({\mathbf {t}}\rightarrow (D \rightarrow D)\) holds in all relevant logics (all which are endowed with the Ackermann truth constant \({\mathbf {t}}\), that is), \(A \rightarrow (B \wedge (D \rightarrow D) \rightarrow C)\) suffices for deriving \(A \rightarrow (B \wedge {\mathbf {t}}\rightarrow C)\). Adding the first rule, therefore, yields the weaker logic, and so I will only consider this. The following theorem shows that (I) is in fact incompatible with not only VSP, but also ASP:
Theorem 5
No logic extending BB satisfies ASP if augmented by (I).
Proof
Assume that L extends BB augmented by (I), but that L has ASP.
Let A be the formula \((B \wedge (C \rightarrow C)) \rightarrow (C \rightarrow C)\). From Ax1 we then have that \(\vdash _{{\mathbf {L}}} A \rightarrow (B \wedge (C \rightarrow C) \rightarrow (C \rightarrow C))\), and so (I) yields \(\vdash _{{\mathbf {L}}} A \rightarrow (B \rightarrow (C \rightarrow C))\). Since A itself is a logical theorem, modus ponens yields that \(\vdash _{{\mathbf {L}}} B \rightarrow (C \rightarrow C)\).
Since we have assumed that L has ASP, we also know that there are formulas D and E such that \(\vdash _{{\mathbf {L}}} D \wedge (C \rightarrow C) \rightarrow E\), but \(\nvdash _{{\mathbf {L}}} D \rightarrow E\). However, we have just seen that \(D \rightarrow (C \rightarrow C)\) is a logical theorem of L, and so using the BB-rule R6, we then get that \(D \rightarrow D \wedge (C \rightarrow C)\) is a logical theorem. Using the transitivity of \(\rightarrow \), we then get that \(\vdash _{{\mathbf {L}}} D \rightarrow E\) which then ends the proof. \(\square \)
Note here that we do not need all of BB[I] for this proof to go through. Negation does not figure in the proof, and so the positive fragment suffices. The transitivity rules R3 & R4 can furthermore be replaced by a mere transitivity rule, and that it suffices that the rules are admissible so as to be theorem-preserving.
What is notable about (I) and (II) is that neither of them seem to be instances of either positive or negative suppression. What might seem as instances of extensional suppression are the commuted variants of (I) and (II), namely
It seems, however, that branding any instances of these rules suppressive too easily allows one to eliminate logics; for instance, both TM and RM validate the rule \((B \wedge (B \rightarrow B)) \rightarrow (B \rightarrow B) \vdash B \rightarrow (B \rightarrow B)\), but even if one agrees with Anderson and Belnap’s judgment over mingle axiom, it seems wrong to shun it because the noted rule holds.Footnote 16 After all, even \(B \vdash A \rightarrow (A \rightarrow A)\) holds in these logics. This, however, is none-the-less what Routley et al. claim: “\(A \rightarrow (A \rightarrow A)\) comes from \( A \mathrel { \& } (A \rightarrow A) \rightarrow (A \rightarrow A)\) by suppression of \(A \rightarrow A\)” [27, p. 241]. This, then, is the trouble with the intuitive notion of suppression which Routley et al. use to marshal against, in their point of view, adverse logical principles: any rule of the general form \(B \wedge A \rightarrow C \vdash B \rightarrow C\), or even any convoluted variant such as \(D \rightarrow (B \wedge A \rightarrow C) \vdash D \rightarrow (B \rightarrow C)\) or \(E \rightarrow (D \rightarrow (B \wedge A \rightarrow C)) \vdash E \rightarrow (D \rightarrow (B \rightarrow C))\), etc., can, just as long as A satisfies some desiderata such as being true, necessary true, provably true, or provably true entailment, be regarded as a suppressive rule. However, all the logics considered by Routley et al. allow one to suppress any Asuitably\(\rightarrow \)-entailed by B, so that any of the “suppressive” inference schemes above are pieces of valid inference just as long as \(B \rightarrow A\) is a theorem of the logic in question. On the other side, \(B \wedge A \rightarrow B \vdash B \rightarrow B\) holds in all logics even though A need not in any way be related to B, nor be true, provable or the like. The sober judgment, then, seems rather to be that this loose sense of suppression can’t really be used to either determine or in any way circumscribe the extension of the consequence relation.
It seems, then, that to get a workable notion of suppression stronger than JFP, which would not only entail the variable sharing property, but also rule the Anderson-Belnap logics T, E and R as suppressive, one would need to go beyond the extensional notion of suppression. Relevant logics are sometimes equipped with not just an extensional conjunction, but also an intensional one; the binary \(\circ \) connective called fusion defined by the residuation rules \(A \rightarrow (B \rightarrow C) \vdash A \circ B \rightarrow C\) and \(A \circ B \rightarrow C \vdash A \rightarrow (B \rightarrow C)\). Now amongst the four authors of [27], at least Brady and Routley wanted to adopt a logic which could handle the naïve theories of truth, classes and sets non-trivially. Both adopted logics containing the axiom \((A \rightarrow B) \wedge (B \rightarrow C) \rightarrow (A \rightarrow C)\). However, [27, pp. 366f] showed that any such logic which also has the fusion connective will trivialize all of the mentioned naïve theories.Footnote 17 Fusion was therefore not adopted as a logical connective. One may, however, still try to work out a notion of suppression which restricts not only rules on the form \(B \wedge A \rightarrow C \vdash B \rightarrow C\), but also \(B \rightarrow (A \rightarrow C) \vdash B \rightarrow C\). Finding a criterion for which such rules to deem suppressive, will then, just as in the extensional case, be the hard task.
Such a notion of suppression is precisely what is appealed to in [27, §§ 3.8–3.9]. It is this notion of suppression which is appealed to when ruling out most of the principles which differentiates the Anderson-Belnap logics from Routley’s two favorite logics DK and DL:
A more detailed examination of the characteristics and principles of systems E and R confirms this presumption. Both systems contain many incorrect and defective principles and qualified suppression principles. [27, p. 263]
Their judgement is even reflected in the name they give to one of the defining axioms of E: the axiom \(((A \rightarrow A) \rightarrow B) \rightarrow B\) is named Suppression. In what follows I will go through their reasons for thinking that the following five axioms of E, the latter three also belonging to T, are suppressive:

The reason \(((A \rightarrow A) \rightarrow B) \rightarrow B\) is called Suppression to begin with is that, according Routley et al., it suppresses \(A \rightarrow A\) in \(((A \rightarrow A) \rightarrow B) \rightarrow ((A \rightarrow A) \rightarrow B)\). The intuition behind this is give as follows:
A leading feature of the Peripatetic theory of implication [...], which aimed at giving an account of what may be called progressive reasoning, was rejection of the decidedly non-progressive principle of Identity, \(A \rightarrow A\). Thus it is true that
(1) If \(A \rightarrow A\) then (as a matter of logic) the Peripatetic theory of implicationFootnote 18 is wrong: i.e. \((A \rightarrow A) \rightarrow B\) for the wff B given.
But (1) does not imply that the Peripatetic theory is wrong, i.e. \((1) \rightarrow B\) is false. (As the counterexample plainly shows the law of Identity is illegitimately suppressedFootnote 19.) Identity has been taken not merely as true, but as unchallengeable, as not open to rejection. [...] No proposition, not even the law of Identity, should be so protected from questioning and doubt. Of course this sort of protection is just the shielding suppression affords. [27, p. 267]
I find it hard to connect the idea that no proposition is beyond doubt and the claim that \(((A \rightarrow A) \rightarrow B) \rightarrow B\) expresses that this is in fact not so, namely that \(A \rightarrow A\) is beyond doubt: if \((A \rightarrow A) \rightarrow B\) is indeed true, then it seems that B is true as well, since, after all, \(A \rightarrow A\)is true. Furthermore, if the parenthesized “as a matter of logic” means that \((A \rightarrow A) \rightarrow B\) is logically true, it would, presumably at least, make B logically true as well, since \(A \rightarrow A\) is logically true. Of course, that is not to say that either B or \(A \rightarrow A\) are beyond doubt, only that one ought to revise ones commitment to the latter if one comes to think the Peripatetic theory of implication is indeed true. One ought, if one so does while at the same time retains ones commitment to modus ponens, to revise ones belief in the E-axiom as well, seeing as \(A \rightarrow A\) is in fact derivable using this axiom:
However, unless one already has reasons for thinking that the Peripatetic theory is indeed true, I don’t see why one ought to revise the belief in a principle antithetical to that theory. I therefore find the argument here less than persuasive.
Since the target of the Routley et al.’s argument, \(((A \rightarrow A) \rightarrow B) \rightarrow B\), is even called Suppression, it seems that one might miss something vital regarding their notion of suppression if the argument is tossed aside so abruptly, however. I suggest, therefore, that we simply bracket off the reasons given for thinking that the E-axiom is suppressive in order to better understand Routley et al.’s notion of suppression. It is evidently not suppressive in the extensional sense brought out by the Anti-Suppession and Joint Force Principles. I therefore suggest that the E-axiom is best viewed as an archetypal instance of an altogether different notion of suppression, which I will designate intensional suppression. We have seen that the notion of extensional suppression turned out to be properly weaker than variable sharing, and so that notion of suppression can’t be used to rule E and R suppressive, but this intensional sense of suppression might.
Now \(((A \rightarrow A) \rightarrow B) \rightarrow B\) is obtained, or so the story goes, from \(((A \rightarrow A) \rightarrow B) \rightarrow ((A \rightarrow A) \rightarrow B)\) by suppressing \(A \rightarrow A\). The relevant form of this intensional sense of suppression, therefore, seems to be that even though \(B \rightarrow (A \rightarrow C)\) is a theorem, where A is a theorem as well, \(B \rightarrow C\) need not be. Maybe this notion, or maybe it together with the extensional notion of suppression, might turn out strong enough to indeed rule the Anderson-Belnap logics to be suppressive and yield the variable sharing property as a derivable feature. Let’s therefore define the intensional variant of both the Anti-Suppression and the Joint Force Principles:
Definition 7
A logic L satisfies the Intensional Anti-Suppression Principle (IASP) just in case for every formula A, there exist formulas B and C such that \(\vdash _{{\mathbf {L}}} B \rightarrow (A \rightarrow C)\), but \(\nvdash _{{\mathbf {L}}} B \rightarrow C\).
Definition 8
A logic L satisfies the Intensional Joint Force Principle (IJFP) just in case for every formula A, there exist formulas B and C such that \(\vdash _{{\mathbf {L}}} B \rightarrow (A \rightarrow C)\), but \(\nvdash _{{\mathbf {L}}} B \rightarrow C\) and \(\nvdash _{{\mathbf {L}}} A \rightarrow C\).
Now the E-axiom can obviously not be a logical theorem of any logic with any of these two properties. Thus both properties rule both E and R to be suppressive. The question, then, is whether any of the principles do the job of also branding the other mentioned E-axioms as suppressive. Apart from Reductio, which I will get back to, this is not the case, as the following theorem shows:
Theorem 6
L satisfies IJFP, where L is identified TW plus

Proof
Consider the model for L depicted in Fig. 3. \({\mathcal {S}} = \{2, 3\}\) is here a subalgebra and therefore closed under all propositional functions. But then if A is any formula and all its propositional variables are assigned to elements in \({\mathcal {S}}\), A will be evaluated to some element in the subalgebra as well. Let B be a propositional variable. Then the model falsifies \(A \rightarrow B\) by assigning B to 0, since \(2 \rightarrow 0 = 3 \rightarrow 0 = 0\). Furthermore, if one assigns B to 4, then since \((2 \rightarrow 4) \rightarrow 4 = (3 \rightarrow 4) \rightarrow 4 = 0\), the model with such an evaluation of B also falsifies \((A \rightarrow B) \rightarrow B\). Thus for propositional variables B and any formula A, even though L has \((A \rightarrow B) \rightarrow (A \rightarrow B)\) as a theorem, neither \(A \rightarrow B\) nor \((A \rightarrow B) \rightarrow B\) are logical theorems which then ends the proof that L satisfies IJFP.\(\square \)
A model for L of Theorem 6
Theorem 7
The combination of IJFP, JFP and AP does not suffice for ruling out the implicational paradoxes, not even the first degree ones, nor do they suffices for yielding WVSP.
Proof
Let L be the logic TW plus the following principles:

L is a sublogic of SIE of Theorem 2 which satisfied JFP. It is also a sublogic of \(\mathbf {\Pi '^\star }\) of Theorem 4 which satisfied AP. Thus L has both these properties.
That it also satisfied IJFP can be seen by considering the model for L in Fig. 4. Let A be any formula and assign to every propositional variable in it either 1 or 2. It is easy to check that \(\{1, 2\}\) is closed under every propositional function, and so A will be assigned to either 1 or 2. Let B be a propositional variable and assign it to 0. Then both \(A \rightarrow B\) and \((A \rightarrow B) \rightarrow B\) will be assigned to 1 which is not a designated value. Since \((A \rightarrow B) \rightarrow (A \rightarrow B)\), it follows that L has IJFP.
Thus L has all three properties, yet validates the Kleene axiom. Thus the combination of the three properties does not suffice for ruling out the implicational paradoxes even of the first degree. Furthermore, since L has (iP) as an axiom it can’t have WVSP since  is not one of its theorems.\(\square \)
is not one of its theorems.\(\square \)
A model for L of Theorem 7
The above theorem shows, then, that strengthening the notion of suppression so as to include both the extensional and intensional versions of the Joint Force Principle as well as the Ackermann Property, is still not enough to rule out the implicational paradoxes—even the first degree such. Furthermore, that even though IJFP, unlike JFP, yields a relevance criterion not implied by the already available ones as it does classify the E-axiom as suppressive, the combination of anti-suppressive principles considered so far fails to do one of the jobs Routley et al. intended suppression to do, namely to rule out all of the following as suppressive:
I will get back to the reasons given for thinking that the three latter axioms are suppressive. Before that, however, we should consider whether there are principles which are intuitively not suppressive, but which are classified as such by IJFP.
One of Routley’s favorite logic was DK. If augmented by the counter-example rule  (equivalently
(equivalently  ), one obtains the logic DR introduced in
[8] which is the strongest logic Brady considers which has the Depth Variable Sharing Property.Footnote 20 These two logics satisfy all the relevance- and anti-suppression properties discussed in this paper:
), one obtains the logic DR introduced in
[8] which is the strongest logic Brady considers which has the Depth Variable Sharing Property.Footnote 20 These two logics satisfy all the relevance- and anti-suppression properties discussed in this paper:
Corollary 3
DK and DR satisfy the following properties: IJFP, JFP, AP, as well as VSP.
Proof
Since these two logics are sublogic of E they satisfy JFP, AP, as well as VSP. Furthermore, since they are sublogics of the logic in Theorem 6, it follows that they also satisfy IJFP. \(\square \)
Not only does the logic in Theorem 6 validate all of DR, it also validates all of Anderson and Belnap’s E, shy of the axioms \(((A \rightarrow A) \rightarrow B) \rightarrow B\) and  . The first of these is obviously intensionally suppressive in the sense that any logic with this principle will fail to satisfy IJFP. What about the latter principle, Reductio? DR only validates Reductio as a two-way rule, that is
. The first of these is obviously intensionally suppressive in the sense that any logic with this principle will fail to satisfy IJFP. What about the latter principle, Reductio? DR only validates Reductio as a two-way rule, that is  , holds in DR—the rule is equivalent to excluded middle—as well as the contraposed version
, holds in DR—the rule is equivalent to excluded middle—as well as the contraposed version  . DR does not, however, validate the Reductio axiom, and so the question remains whether DL—Routley’s other favorite logic got from DK by replacing excluded middle by Reductio—satisfies IJFP. Routley et al. did express some reservations towards this axiom, although I must confess that I fint it hard to get a clear idea of their reasons why. It is discussed in the the same section as contraction, so let’s first see why they thought contraction not to hold.
. DR does not, however, validate the Reductio axiom, and so the question remains whether DL—Routley’s other favorite logic got from DK by replacing excluded middle by Reductio—satisfies IJFP. Routley et al. did express some reservations towards this axiom, although I must confess that I fint it hard to get a clear idea of their reasons why. It is discussed in the the same section as contraction, so let’s first see why they thought contraction not to hold.
One might have thought that the contraction axiom involves some kind of suppression; that \((A \rightarrow (A \rightarrow B)) \rightarrow (A \rightarrow B)\) is got from \((A \rightarrow (A \rightarrow B)) \rightarrow (A \rightarrow (A \rightarrow B))\) by suppressing an A. However, we saw in Theorem 6 that the contraction axiom can be an axiom of quite strong logics which satisfy IJFP. Routley et al. do not charge contraction, nor the weaker rule version or its equivalent axiom form \(A \wedge (A \rightarrow B) \rightarrow B\) (called Ass by Routley et al.), of suppression. Their main argument against contraction is rather that it limits the logical space to non-paradoxical situations, and therefore trivialize self-referential theories such as naïve truth, property and set theory
[27, § 3.9].Footnote 21 Since “Reductio,  , does not exclude situations in the same way or to the same extent as Ass [...].”, Routley et al. state that “in systemic investigations we shall generally carry Reduction as an optional extra.”
[27, p. 282].Footnote 22
, does not exclude situations in the same way or to the same extent as Ass [...].”, Routley et al. state that “in systemic investigations we shall generally carry Reduction as an optional extra.”
[27, p. 282].Footnote 22
One might have thought that since they state that Reductio is equivalent to the axiom  (
[27, p. 229]), and furthermore that in logics such as DK only
(
[27, p. 229]), and furthermore that in logics such as DK only  holds, that they suspected Reductio to involve some form of suppression. What they say, however, is that
holds, that they suspected Reductio to involve some form of suppression. What they say, however, is that
without a Commutation Rule, such as \(\delta \)Footnote 23, there is no way of suppressing
in its internally nested position and arriving, as in system E, at
. [27, p. 282]
One way of deriving  provided both
provided both  and
and  are theorems, would be to use \(\delta \). It is false, however, that some form of commutation is needed: one can also use Reductio together with Conjunctive Syllogism (Ax12), neither of which are classified as commutative principles. Furthermore, Routley at al. argue Ax12 to be the correct form of transitivity and therefore non-suppressive, and so if
are theorems, would be to use \(\delta \). It is false, however, that some form of commutation is needed: one can also use Reductio together with Conjunctive Syllogism (Ax12), neither of which are classified as commutative principles. Furthermore, Routley at al. argue Ax12 to be the correct form of transitivity and therefore non-suppressive, and so if  is suppressed in
is suppressed in  , it would seem that it is Reductio which has to be the culprit. The easiest way to see that Reductio, at least in the presence of Ax12, does involves intensional suppression modeled after the E-axiom, is by realizing that
, it would seem that it is Reductio which has to be the culprit. The easiest way to see that Reductio, at least in the presence of Ax12, does involves intensional suppression modeled after the E-axiom, is by realizing that  is a theorem of DL. Both \(A \rightarrow A\) and
is a theorem of DL. Both \(A \rightarrow A\) and  were regarded as logical theorems by Routley et al., and so it seems that Reductio allows one to suppress
were regarded as logical theorems by Routley et al., and so it seems that Reductio allows one to suppress  from
from  to obtain
to obtain  in the same way that the E-axiom allows one to suppress \(A \rightarrow A\) from \(((A \rightarrow A) \rightarrow B) \rightarrow ((A \rightarrow A) \rightarrow B)\). I think this shows clearly that Routley et al. ought to have judged Reductio suppressive since they so emphatically judged the E-axiom to be suppressive. The following theorem and corollary simply shows that IASP in fact fails under the conditions mentioned.
in the same way that the E-axiom allows one to suppress \(A \rightarrow A\) from \(((A \rightarrow A) \rightarrow B) \rightarrow ((A \rightarrow A) \rightarrow B)\). I think this shows clearly that Routley et al. ought to have judged Reductio suppressive since they so emphatically judged the E-axiom to be suppressive. The following theorem and corollary simply shows that IASP in fact fails under the conditions mentioned.
Theorem 8
No extension of BB plus the three axioms

satisfies IASP.
Proof
This follows simply by noting that  is a theorem of any such logic.Footnote 24 Thus for any B and C, if
is a theorem of any such logic.Footnote 24 Thus for any B and C, if  , then also \(\vdash B \rightarrow C\). \(\square \)
, then also \(\vdash B \rightarrow C\). \(\square \)
As an immediate corollary to the above theorem we get the following:
Corollary 4
DL does not satisfy IASP.
We have earlier seen that the extensional notions of suppression are eclipsed by even weak variable sharing (Theorems 1 and 2), and that the Ackermann Property is independent from ASP (Theorems 3 and 4). The following theorem shows that IJFP is in fact independent from both VSP and AP:
Corollary 5
IJFP, VSP and AP are all independent.
Proof
-
The logic of Theorem 6 satisfies IJFP, but since it has the Mingle axiom it fails to satisfy both AP and since it validates the Kleene axiom it fails to satisfy VSP.
-
TM, T with \(A \rightarrow (A \rightarrow A)\) added, satisfies VSP ( [16, Cor. 4.6]). Because of Mingle, however, it does not satisfy AP and because of Reductio it does not satisfy IJFP (Theorem 8).
-
Since E satisfies AP, that property does not entail IJFP since \(((A \rightarrow A) \rightarrow B) \rightarrow B\) is a theorem of E. Nor does it entail VSP (Theorem 4)
\(\square \)
We have so far seen that the anti-suppression properties fail to rule out the implicational paradoxes—even the first degree such. Furthermore, they classify principles claimed not to be clearly suppressive—Reductio—as suppressive, yet fail to capture what is claimed to be suppressive principles of E, namely the \(\Box \!\wedge \)-axiom and the pre- and suffixing axioms. We have already looked at the reasons given for thinking that the E-axiom and Reductio are suppressive. What, then, are the reasons given for thinking that the three other mentioned E-axioms involve suppression? I will now show that the reasons given are also in this case rather wanting.
The \(\Box \!\wedge \)-axiom is said to yield to “similar counterexamples” as the E-axiom ( [27, p. 268]), although none are given. The story with the E-axiom is that it suppresses the theorem \(A \rightarrow A\) in the antecedent of the consequent of \(((A \rightarrow A) \rightarrow B) \rightarrow ((A \rightarrow A) \rightarrow B)\). Thus if the \(\Box \!\wedge \)-axiom is to be similar, it ought to be the case that for some theorem C, \(\Box A \wedge \Box B \rightarrow (C \rightarrow \Box (A \wedge B))\) is a theorem, but that \(\Box A \wedge \Box B \rightarrow \Box (A \wedge B)\) fails to be a logical theorem without it being forcibly added as a primitive axiom. This story, however, is hard to substantiate as logics with the variable sharing property tend not to have theorems on the form \(\Box A \wedge \Box B \rightarrow (C \rightarrow \Box (A \wedge B))\) since the weakening axiom \(A \rightarrow (C \rightarrow A)\) can’t be a theorem of such logics. We can strengthen this observation as follows:
Theorem 9
If \(\Box A \wedge \Box B \rightarrow (C \rightarrow \Box (A \wedge B))\) is a theorem of any sublogic of R, then C shares propositional variables with both A and B. \(\square \)
Proof
Assume that \(\Box A \wedge \Box B \rightarrow (C \rightarrow \Box (A \wedge B))\) is a theorem and for contradiction that C does not share propositional variables with, say, B. Consider the Crystal lattice displayed in Fig. 6. That model is a known model of R and will therefore evaluate \(\Box A \wedge \Box B \rightarrow (C \rightarrow \Box (A \wedge B))\) to some value different from 0. Assign every propositional variable in A to 2 and every variable in B to 3. Since both \(\{2\}\) and \(\{3\}\) are subalgebra it follows that both A and \(\Box A\) will be evaluated to 2, that both B and \(\Box B\) will be evaluated to 3, and that both \(\Box A \wedge \Box B\) and \(\Box (A \wedge B)\) will be evaluated to 1. Since C does not share propositional variables with B we can also assign to every remaining propositional variable in C the value 2 so that C will be evaluated to 2 as well. We now get a contradiction since \(1 \rightarrow (2 \rightarrow 1) = 0\). \(\square \)
Thus if the \(\Box \!\wedge \)-axiom is suppressive, it only suppresses certain specific theorems. Maybe there are such cases, but I haven’t been able to find any. I therefore conclude that if indeed the \(\Box \!\wedge \)-axiom is a suppressive principle, it is so in a sense not adequately specified by Routley et al.
Let’s move on to the transitivity axioms. \((A \rightarrow B) \rightarrow ((C \rightarrow A) \rightarrow (C \rightarrow B))\) and \((A \rightarrow B) \rightarrow ((B \rightarrow C) \rightarrow (A \rightarrow C))\) are collectively called ESyll, short for Exported Syllogism, by Routley et al., and are both deemed to be suppressive. It is called exported in reference to the axiom they call Exportation, namely \((A \wedge B \rightarrow C) \rightarrow (A \rightarrow (B \rightarrow C))\), their view being that ESyll is an exported version of Conjunctive Syllogism (CSyll), \((A \rightarrow B) \wedge (B \rightarrow C) \rightarrow (A \rightarrow C)\). Now Exportation yields irrelevance since \(A \wedge B \rightarrow B\) is a logical axiom and so Exportation therefore yields \(A \rightarrow (B \rightarrow B)\), and since they view irrelevance as an form of suppression, Exportation is regarded as a suppressive principle. Routley et al. know of course that ESyll does not result in irrelevance, but argue that the fact that it “is an exported form of CSyll should, if anything, increase our suspicions of it.” [27, p. 269]. Their main argument against ESyll, however, is as follows:
The contribution ESyll makes over and above CSyll would appear to be that of allowing the suppression of certain true implications in certain positions. This is a very limited form of suppression and it is not one which produces spectacular effects, like more wholesale suppression, in the form of irrelevance. But if we are attempting to explicate the concept of sufficiency, it must be rejected for just the same reasons as the more obvious and general suppression principles and resulting irrelevant forms. ESyll principles provide good examples of those sorts of principles we alluded to earlier, namely those that allow a certain degree of suppression but not so much as to produce irrelevance. Remember that relevance is only a necessary condition for an adequate system; so the fact that ESyll can be added to certain systems without inducing irrelevance provides on its own no justification for ESyll. [27, p. 271]
The thought here seems to be that the fact that \(A \rightarrow B\) is true does not suffice for allowing it to be dropped from the logically true claim \((A \rightarrow B) \wedge (B \rightarrow C) \rightarrow (A \rightarrow C)\). This, however, according to Routley et al., is what in effect is afforded by ESyll, which therefore is regarded as a suppressive principle.
Now Routley et al. would object to suppression of merely true formulas as well the suppression of theorems. Note, however, that in order for ESyll to be suppressive in the way specified in the above quote, Routley et al. need to use the concept of a rule in two different senses: for what is wrong with \((A \rightarrow B) \rightarrow ((C \rightarrow A) \rightarrow (C \rightarrow B))\), they say, is that it forces the consequent upon us when the antecedent is merely true. However, the rule \(A \rightarrow B \vdash (C \rightarrow A) \rightarrow (C \rightarrow B)\) is a rule of most relevant logics—indeed all such logics considered in this paper and therefore Routley’s two favorite logics DK and DL as well. They do state that rules are to be interpreted as theorem preservingFootnote 25, but if that is the case, then the consequent of \((A \rightarrow B) \rightarrow ((C \rightarrow A) \rightarrow (C \rightarrow B))\) need not be forced upon us just because the antecedent is true. Furthermore, if one looks at how rules are in fact used, the claim that rules are to be interpreted as only theorem-preserving seems not to be adhered to by Routley et al. For instance, the already mentioned triviality proof for naïve set theory in [27, p. 367] happily uses the primitive rule \(A \rightarrow (B \rightarrow C) \vdash A \circ B \rightarrow C\), where \(\circ \) is the intensional conjunction called fusion to get \(w \in w \circ w \in w \rightarrow p\) from \(w \in w \rightarrow (w \in w \rightarrow p)\), where the latter formula is deduced from the formula \(\exists w \forall x (x \in w \leftrightarrow (w \in w \circ w \in w \rightarrow p))\). Thus they use rules as applying to formulas deducible from assumptions which are not logical theorems, and so use the rules as truth-preserving, not merely as theorem-preserving. But then if ESyll detaches upon having a mere true antecedent, that is because modus ponens is regarded as truth-preserving, not only as theorem-preserving. It is, of course, possible to restrict the pre- and suffixing rules, R3 & R4—jointly refered to by Routley et al. as the affixing rules—of DK/DL to be only theorem-preserving without also restricting the other two rules—modus ponens and adjunction. That would then beget different logics than DK/DL as defined both here as well as all other presentations of DK/DL by the authors of [27]. Generally, however, it seems that it is more plausible to interpret rules stated in the same syntactical way as the same type of rules: either all rules are to be interpreted as theorem preserving, or all rules are to be interpreted as truth preserving. But then if R3 & R4 are regarded as suppressive when taken as truth-preserving rules, why think that beefing up the premise from merely true to logically true would make for an unsuppressive rule? Why is it permissible to suppress \(A \rightarrow B\) in \((A \rightarrow B) \wedge (B \rightarrow C) \rightarrow (A \rightarrow C)\) when \(A \rightarrow B\) is a theorem, but not when it is merely true?
The only sensible answer, it seems, would be to conclude that it is not only ESyll which is suppressive—in a way not covered by any principle discussed by Routley et al. I should note—but also that the affixing rules are suppressive. Routley et al. did worry that these rules could be suppressive as well.Footnote 26 In order to shed light on this matter, Routley et al. [27, § 4.2] reaxiomatized the logic B so as to include Substitutivity of Coimplicants, \(A \leftrightarrow B \vdash D(A) \rightarrow D(B)\), as a primitive rule, where D(B) is obtained from D(A) by replacing one or more instance of A by B. In addition they added the axioms \((C \rightarrow A \wedge B) \rightarrow (C \rightarrow B)\) and \((A \vee B \rightarrow C) \rightarrow (A \rightarrow C)\). These are easily verified to be deductively equivalent axiomatizations. The possible suppressiveness of the affixing rules is then formulated with CSyll as well as this reaxiomatization of B as a backdrop:
These reaxiomatisations of B and its extensions focus the issue as to the correctness of the affixing rules on some special cases concerning & and \(\vee \). Thus if
$$ \begin{aligned} (C \rightarrow A\mathrel { \& }B) \rightarrow (C \rightarrow A) \end{aligned}$$is a correct principle for sufficiency or conditionality then Prefixing is admissible. If, however, this principle really has \( A \mathrel { \& } B \rightarrow A\) as a further premiss and is obtained by suppression of this premiss from the correct
$$ \begin{aligned} (C\rightarrow A \mathrel { \& } B) \mathrel { \& } (A \mathrel { \& } B \rightarrow A) \rightarrow (C \rightarrow A), \end{aligned}$$then the principle is not a genuine sufficiency one and should be rejected as an entailment principle. [27, p. 293]
Thus Routley et al. regard it as an open issue whether not only ESyll, but also the affixing rules are suppressive. They seem to model this on the same idea as the rules (\(\hbox {I}^c\))&(\(\hbox {II}^c\)) above. As with these rules, however, the sober judgement here is surely that there simply is no available evidence which points to either ESyll or the affixing rules being suppressive.
Routley et al. did not discuss the suppressiveness of the affixing principles further in volume one of Relevant Logics and their Rivals, and when, after the untimely passing of Sylvan, the second volume, [7], eventually came out 21 years later, Brady, the editor of the second volume, wrote in the preface that the focus on the issue of suppression would not be continued in that volume. The reason given, however, was that Brady thought that the suppression exhibited by ESyll was benign and so focusing on suppression alone would not suffice for reaching the so-called depth-relevant logics—DR and beneath [7, p. 4]. Since no further account of suppression was ever given, the idea of the suppressiveness of the affixing principles in particular, but also suppression in general, was left in a rather unsettled state. I conclude, rather, that the suppressiveness of the affixing principles seems simply to be ill argued for and badly motivated; there just seems to be no clear case made for the suppressiveness of these principles.
I have in this section tried to make sense of some of Routley et al.’s use of the notion of suppression which does not fit into the extensional notion precisified by ASP and JFP. It was suggested that this could be viewed as a slightly different intensional variant of suppression and the principles IASP and IJFP were suggested for capturing it. It was shown, however, that neither this notion, not even in combination with extensional suppression, sufficed for ruling out the implicational paradoxes. Such paradoxes are not, according to Routley et al., features of a good sufficiency relation, and thus it seems that analyzing such a relation in terms of the principles ASP, JFP, IASP and IJFP will not be satisfactory. Furthermore, we have seen that although intensional suppression did rule out the E-axiom \(((A \rightarrow A) \rightarrow B) \rightarrow B\), it also ruled out Reductio which Routley et al. did not judge to be suppressive. It furthermore did not rule the other principles differentiating DK and E as suppressive, contra what was in fact claimed. The arguments for why such principles are suppressive and therefore unacceptable for entailment taken as a sufficiency relation were shown to be, to put it lightly, less than persuasive. I have, of course, not demonstrated that there is no notion of suppression which will do the job Routley et al. wanted suppression to do. However, the burden of proof is now on the suppressivist to specify the rules of the game; if one is to uphold the verdict that T, E and R are suppressive, then one needs to specify what suppression here is and why such suppressive features can’t be features of entailment taken as a sufficiency relation.
7 Summary
This essay has looked closer at Val Plumwood and Richard Sylvan’s, with collaborators, notion of suppression. Plumwood and Sylvan developed it from that of an enthymeme, a notion which had already been used to argue for the supremacy of the relevant logic E over classical, intuitionistic and modal logics by Anderson and Belnap. Plumwood and Sylvan, however, argued that it was freedom from suppression which was the fundamental feature of entailment. Entailment, they claimed, is a sufficiency relation, and so does not admit any form of premise suppression. Anderson and Belnap’s idea of analysing relevance as variable sharing and premise use, they claimed, did not guarantee freedom from suppression; although variable sharing was regarded as an important property, it was viewed as no more than a mere negative test of adequacy and eclipsed by the richer notion of suppression.
I have shown in this paper that the extensional so-called Anti-Suppression Principle and the Joint Force Principle are both weaker than the Variable Sharing Property, in fact properly weaker than even the Weak Variable Sharing Property. As such, the principles do not suffice for ruling out the implicational paradoxes, not even the ones of the first degree, contra what is claimed in both
[27] and
[28]. A notion of intensional suppression was specified to give content to the claim that the E-axiom \(((A \rightarrow A) \rightarrow B) \rightarrow B\)—an axiom even named Suppression in
[27]—is suppressive. It was shown, however, that neither this notion of suppression is strong enough, even when augmented with the extensional notion of suppression, to rule out the implicational paradoxes. We saw that the argument given for rejecting the archetypal intensional suppressive principle, i.e. the E-axiom, was less than clear, and even though the intensional notion of suppression did rule two of the axioms of E and R to be suppressive, only one of these axioms, the E-axiom, was regarded as clearly suppressive by Routley et al., whereas the other one,  , was in fact taken as an axiom of one of Sylvan’s favorite logics, DL. We also saw that the other principles which differentiate DL from the Anderson-Belnap logics T and E were in fact neither extensionally nor intensionally suppressive. Thus neither this notion of suppression could do the job intended for it, namely to provide reasons for thinking that the Anderson-Belnap logics T, E, and R cannot be viewed as capturing notions of entailment viewed as sufficiency relations. Their arguments against the alleged suppressive principles of these logics were shown to be rather wanting, and their proof that there are logics which satisfies the variable sharing property, yet are obviously suppressive, was shown to be rather obviously fallacious.
, was in fact taken as an axiom of one of Sylvan’s favorite logics, DL. We also saw that the other principles which differentiate DL from the Anderson-Belnap logics T and E were in fact neither extensionally nor intensionally suppressive. Thus neither this notion of suppression could do the job intended for it, namely to provide reasons for thinking that the Anderson-Belnap logics T, E, and R cannot be viewed as capturing notions of entailment viewed as sufficiency relations. Their arguments against the alleged suppressive principles of these logics were shown to be rather wanting, and their proof that there are logics which satisfies the variable sharing property, yet are obviously suppressive, was shown to be rather obviously fallacious.
Their failure to make any serious effort at specifying what suppression is in such a way as to make it clear that the logical principles charged of being suppressive can indeed be recognized as such, as well as their failure to compare the notion of suppression to the notions of relevance already available—specifically to variable sharing, since they claim this to be a test and a derivative feature of a good sufficiency relation—seems in hindsight rather peculiar. To think of entailment as a sufficiency relation may yield some philosophical insight. If this is to be analyzed as freedom from suppression, however, honest toil in making the notion precise has to be made. Doubting that such toil will bear any fruit, I bid suppression-freedom farewell!
Notes
One prominent example of this account of an enthymeme can be found in Book 1, Chapter 4 of Buridan’s Treatise on Consequences [10]. The missing premise account of enthymemes has been the standard theory of Aristotelian enthymemes. Rapp, however, argues convincingly in [21] that an enthymeme for Aristotle can, but need not, be valid. It should, however, be a clear demonstration, given the audience at hand, that the conclusion follows from the premises. Aristotelian enthymemes pertain to rhetorics and as such have prudential features such as, relative to the audience at hand, not being too long or too complicated, nor have premises not accepted by the audience, and so on.
The same passage is also to be found in [3, p. 47]
Under the heading for § 3.7 called Other—sometimes questionable or vacuous—criteria for the choice of system Routley et al. argue in [27] against taking the Entailment Theorem, or what they call Deduction Equivalence (DE), as a sufficient analysis of the notion of coherence, that the logical theorems should cohere with the rules of the logic:
DE holds for a very large class of relevant, and also irrelevant, logics. In short, the requirement offers little discriminatory power, indeed none that has not already been independently motivated. [27, p. 258]
[27] is authored by Richard Routley as its main author, and with Val Plumwood, Robert K. Meyer and Ross T. Brady as co-authors. The origin of the ideas regarding suppression is to due to Plumwood, however: [27, p. 140, fn. 2] credits the material on first-degree suppression as originating with Plumwood’s unpublished conference paper Some false laws of logic, and subsequently modified by Plumwood and Sylvan. Neither of the other two co-authors have, to my knowledge, endorsed Plumwood and Sylvan’s suppression-freedom analysis of entailment in their own writings. Plumwood’s paper was read in 1967 at both the Australian Association of Philosophy Conferences and at St. Andrews University [27, p. 104, fn. 2]. I have, I’m sad to say, not been able to obtain a copy of Plumwood’s paper, nor the paper presented in February 1969 at the Portsea Conference of the Melbourne De Morgan Society a shortened version of which was eventually published as [28].
By ‘weak relevance’ is here simply meant the variable sharing property.
The claim that the variable sharing property is a mere negative test of relevancy is reiterated in [20, p. 172].
The Anti-Suppression Principle turns out to be equivalent to the principle used by Ackermann to explicate the sense of his rigorous implication when he writes that “the concept of implication—understood as a logical connection between two statements—does not encompass statements which imply or is implied by every other.” [1, p. 113] (my own translation). Expanding further on this, however, will have to wait for another occasion.
(Pq) is the existential propositional quantifier, whereas (p) is the universal one. There is an obvious typo here as the first quantifier should have been the universal quantifier.
Note that it is also possible to interpret the latter principle as the stronger claim that for every A there exist formulas B and C such that \(\vdash _{{\mathbf {L}}} A \wedge B \rightarrow C\), and
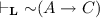 and
and 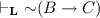 . This, however, seems to be too strong: firstly, since both of Routley’s two favorite logics DK and DL have the classical two-valued Boolean algebra as one of their models where \(\rightarrow \) is simply interpreted as \(\supset \), neither of these two logics can satisfy this principle. If, however, these logics are augmented with an explicit propositional contradiction, which is in fact how DK is presented in
[24] and DL in
[26], this argument doesn’t apply. It is still quite doubtful that such a logic satisfies the principle. Regardless of this, however, it seems that the principle is too strong: the logic DJ is a proper sublogic of both of Routley’s favorite logics DK and DL, and it would be natural to suppose that if DK and DL are suppression-free in that they satisfy the Joint Force Principle, then so will any sublogic of these logics, and therefore also DJ. However, DJ does not satisfy this stronger property simply because it has no theorems of the form
. This, however, seems to be too strong: firstly, since both of Routley’s two favorite logics DK and DL have the classical two-valued Boolean algebra as one of their models where \(\rightarrow \) is simply interpreted as \(\supset \), neither of these two logics can satisfy this principle. If, however, these logics are augmented with an explicit propositional contradiction, which is in fact how DK is presented in
[24] and DL in
[26], this argument doesn’t apply. It is still quite doubtful that such a logic satisfies the principle. Regardless of this, however, it seems that the principle is too strong: the logic DJ is a proper sublogic of both of Routley’s favorite logics DK and DL, and it would be natural to suppose that if DK and DL are suppression-free in that they satisfy the Joint Force Principle, then so will any sublogic of these logics, and therefore also DJ. However, DJ does not satisfy this stronger property simply because it has no theorems of the form 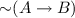 [9, p. 159]. I will therefore set this interpretation aside.
[9, p. 159]. I will therefore set this interpretation aside.I haven’t been able to decide the question whether JFP is properly stronger than ASP and so leave this as an open question.
The proof of this is to be found in [2, p. 417].
Since it is too late to rename Dummett’s axiom, I suggest that this axiom, which is not, according to [33, p. 155], mentioned by Dummett, should be called Skolem’s axiom. Skolem’s axiom obviously entails Dummett’s axiom even in the weak relevant logic BB (hint for getting the derivation rolling: let C be \(A \wedge B\)). However, Dummett’s axiom does not entail Skolem’s axiom even in DW. I leave the verification of this also as a MaGICal exercise. Note, however, that Dummett’s and Skolem’s axioms are equivalent in BB augmented so as to validate reasoning by cases, that \(A \vee B \vdash C\) if both \(A \vdash C\) and \(B \vdash C\) (which in fact is the rule that Skolem [30, p. 62] used in showing that Skolem’s axiom is derivable from Dummett’s axiom). I leave the proof to the reader.
Note also that VSP does not on its own rule out Dummett’s axiom: it was shown in [23, prop. 6.19] that if one weakens the logic B by replacing the contraposition rule
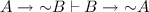 by modus tollens, i.e. the rule
by modus tollens, i.e. the rule 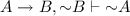 , then the resultant logic has the VSP even when Dummett’s axiom is added (they only state that the suffixing rule holds in their model \(\hbox {M}_{\text{ DF68 }}\), but is easy to verify that also the independent prefixing rule (R4) does, and so their model validates all of B, except for the contraposition rule).
, then the resultant logic has the VSP even when Dummett’s axiom is added (they only state that the suffixing rule holds in their model \(\hbox {M}_{\text{ DF68 }}\), but is easy to verify that also the independent prefixing rule (R4) does, and so their model validates all of B, except for the contraposition rule).All models displayed in this paper have been found with the aid of MaGIC—an acronym for Matrix Generator for Implication Connectives—which is an open source computer program created by John K. Slaney [31]. All models will be displayed as Fig. 1 with a set of designated elements \({\mathcal {T}}\), a displayed ordering and the matrices for at least \(\rightarrow \) and
 . \(\wedge \) and \(\vee \) are to be interpreted as greatest lower bound and least upper bound relative to the displayed ordering.
. \(\wedge \) and \(\vee \) are to be interpreted as greatest lower bound and least upper bound relative to the displayed ordering.It is in fact Ackermann’s model from [1, § 6] which he used to show that \(\Pi '\) has the Ackermann Property.
Note that even though RM does not satisfy VSP, TM does (see [16, Cor. 4.6] for a proof).
For more relevant triviality proofs using fusion, see [17, §§ 6 & 9].
The salient feature of that theory is the claim that \(A \rightarrow A\) fails to be true for allA’s. See [7, § 8.2] for some discussion of it.
Roughly, if \(\vdash A \rightarrow B\), then A and B share a propositional variable at the same \(\rightarrow \)-depth. Note that this property in fact rules out all these four axioms above, as well as Reductio. The property was first introduced in [8]—published in 1984, but initially received by the journal in 1980, and so two year prior to the publication of [27]. However, depth relevance is, as far as I have found, only mentioned twice in [27]: once in the tentative table of content for the planned second volume of Relevant Logics and their Rivals—§ 15.6: “Further conditions for adequacy on choice of logics of inference and deducibility: depth relevance” [27, p. ix]—and once on its last page of the main text (p. 406) where it is advertised that the “leading D systems” will be shown to have “the important feature of depth relevance” in the planned § 15.6. Note, however, that Routley et al. do mention so-called Deep logics, or Deeper logics. These are identified as logics without the ESyll axioms ( [27, p. 226]) and supposedly “treat all statements [...] as non-suppressible” [27, p. 141]. DK and DL are mentioned as examples of such deep logics, but beyond this, however, the term was never precisified. Brady does identify deep relevant logics and depth relevant logics in [7, p. 195], but it seems better to view the latter as a successor-concept since DL is not depth relevant. I find it doubtful that depth relevance would fit as an analysis of the topic of this paper, namely Routley et al.’s notion of suppression, and since they so emphatically reject that the variable sharing property, even with “minor qualifications”, should be viewed as a central feature of entailment [27, p. 232], I will not discuss depth relevance further.
The other reasons adduced against contraction are that such principles require extra modelling conditions which there are no compelling reason to accept; have complex and “remote” modelling conditions; yield undecidability. These reasons do not relate to suppression, and so I will not discuss them further.
They do mention the link between Contraction and Reductio, namely that Reductio is an instance of the contraction axiom in minimal logic. This, however, is not the case in E in which the reductio and contraction axioms are independent ( [2, § 26.2]). Furthermore, in order to obtain Reductio from Contraction one needs not only the instance
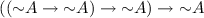 of the E-axiom, but also the instance
of the E-axiom, but also the instance 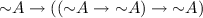 of R’s assertion axiom (Ax11) which is not a theorem of E. Negation in logics where both these hold is implicational, in that every
of R’s assertion axiom (Ax11) which is not a theorem of E. Negation in logics where both these hold is implicational, in that every  -formula is equivalent to a \(\rightarrow \)-formula. This is not the case in E, and therefore not the case in weaker logics than E either. This has probably been noted before, but as I haven’t been able to find a proof of it (a partial discussion is found in
[2, § 14.3]), let me note that this follows from the fact that the model for E in Fig. 5 is such that
-formula is equivalent to a \(\rightarrow \)-formula. This is not the case in E, and therefore not the case in weaker logics than E either. This has probably been noted before, but as I haven’t been able to find a proof of it (a partial discussion is found in
[2, § 14.3]), let me note that this follows from the fact that the model for E in Fig. 5 is such that 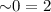 , but 2 is not to be found in the matrix for \(\rightarrow \). For a more philosophical discussion of negation as implicational in the context of relevant logics, see
[15].
, but 2 is not to be found in the matrix for \(\rightarrow \). For a more philosophical discussion of negation as implicational in the context of relevant logics, see
[15].The rule \(A \rightarrow (B \rightarrow C), B \vdash A \rightarrow C\).
Conjunctive syllogism (Ax12) gives one
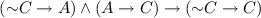 from which Reductio, some simple double negation fiddling, and the transitivity of \(\rightarrow \) yields
from which Reductio, some simple double negation fiddling, and the transitivity of \(\rightarrow \) yields 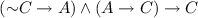 . From this the contraposition axiom and some more double negation fiddling suffices for
. From this the contraposition axiom and some more double negation fiddling suffices for 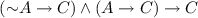 , from which the rules of BB suffices for yielding
, from which the rules of BB suffices for yielding 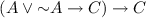 .
.The following is a clear example of this:
For example, the rule of Modus Ponens, symbolised:
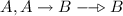 , is read: where A and \(A \rightarrow B\) are theorems so is B. Generally the rules are not, in what follows, intended to reflect entailment relations, or inferential connections such as that expressed by ‘As ...; therefore... ’; they are simply schemes for generating theorems from theorems.
[27, p. 287]
, is read: where A and \(A \rightarrow B\) are theorems so is B. Generally the rules are not, in what follows, intended to reflect entailment relations, or inferential connections such as that expressed by ‘As ...; therefore... ’; they are simply schemes for generating theorems from theorems.
[27, p. 287]Their basic logic is in fact the logic A being simply Routley’s logic DK minus the affixing rules [27, pp. 221f]. This, then, sets them apart from the view of Lewis who, just like Routley et al., included Conjunctive Syllogism as an axiom of his logics S2 and S3, but renounced S3 in favor of S2 when it turned out that S3 had the suffixing axiom as a theorem. His reaction was also that “it gives the inference
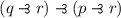 whenever
whenever 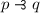 is a premise. Except as an elliptical statement for ‘
is a premise. Except as an elliptical statement for ‘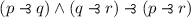 and
and 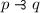 is true,’ this inference seems dubious.”
[12, p. 496]. Despite this, Lewis seems to have been untroubled by Parry’s proof that the suffixing rule holds for S2 (cf.
[12, p. 507]).
is true,’ this inference seems dubious.”
[12, p. 496]. Despite this, Lewis seems to have been untroubled by Parry’s proof that the suffixing rule holds for S2 (cf.
[12, p. 507]).
References
Ackermann, W.: Begründung einer strengen Implikation. J. Symb. Log. 21(2), 113–128 (1956). https://doi.org/10.2307/2268750
Anderson, A.R., Belnap, N.D.: Entailment: The Logic of Relevance and Necessity, vol. 1. Princeton University Press, Princeton (1975)
Anderson, A.R., Belnap, N.D., Dunn, M.J.: Entailment: The Logic of Relevance and Necessity, vol. 2. Princeton University Press, Princeton (1992)
Anderson, A.R., Belnap Jr., N.D.: Enthymemes. J. Philos. 58(23), 713–723 (1961). https://doi.org/10.2307/2023169
Anderson, A.R., Belnap Jr., N.D.: The pure calculus of entailment. J. Symb. Log. 27(1), 19–52 (1962). https://doi.org/10.2307/2963676
Belnap, N.D.: Entailment and relevance. J. Symb. Log. 25(2), 144–146 (1960). https://doi.org/10.2307/2964210
Brady, R. (ed.): Relevant Logics and their Rivals, vol. 2. Ashgate Publishing Co., Portland (2003)
Brady, R.T.: Depth relevance of some paraconsistent logics. Stud. Log. 43(1–2), 63–73 (1984). https://doi.org/10.1007/BF00935740
Brady, R.T.: Universal Logic. CSLI Publication, Stanford (2006)
Buridan, J.: Treatise on Consequences. Fordham University Press, New York (2015). Translated, with an introduction by Stephen Read
Lewis, C.I.: Implication and the algebra of logic. Mind XXI(84), 522–531 (1912). https://doi.org/10.1093/mind/XXI.84.522
Langford, C.H., Lewis, C.I.: Symbolic Logic, 2nd edn. Dover Publications, New York (1959)
MacColl, H.: ‘If’ and ‘imply’. Mind XVII(3), 453–455 (1908). https://doi.org/10.1093/mind/XVII.3.453
Meyer, R.K.: R-mingle and relevant disjunction. J. Symb. Log. 36(2), 366 (1971). https://doi.org/10.2307/2270323
Meyer, R.K., Martin, E.P.: Logic on the Australian plan. J. Philos. Log. 15(3), 305–332 (1986). https://doi.org/10.1007/BF00248574
Méndez, J.M., Robles, G., Salto, F.: Ticket entailment plus the mingle axiom has the variable-sharing property. Log. J. IGPL 20(1), 355–364 (2011). https://doi.org/10.1093/jigpal/jzr046
Øgaard, T.F.: Paths to triviality. J. Philos. Log. 45(3), 237–276 (2016). https://doi.org/10.1007/s10992-015-9374-6
Øgaard, T.F.: Non-Boolean classical relevant logics I. Synthese (2019). https://doi.org/10.1007/s11229-019-02507-z
Priest, G.: In Contradiction. Oxford University Press, Oxford, 2nd edition (2006). https://doi.org/10.1093/acprof:oso/9780199263301.001.0001
Priest, G., Routley, R.: Systems of paraconsistent logic. In: Priest, G., Sylvan, R., Norman, J. (eds.) Paraconsistent Logic: Essays on the Inconsistent, pp. 151–186. Philosophia Verlag, München (1989)
Rapp, C.: Aristotle’s rhetoric. In: Zalta, E.N., (ed), The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University, spring 2010 edition (2010). https://plato.stanford.edu/archives/spr2010/entries/aristotle-rhetoric/
Read, S.: Hugh MacColl and the algebra of strict implication. Nord. J. Philos. Log. 3(1), 59–83 (1999)
Robles, G., Méndez, J.M.: A general characterization of the variable-sharing property by means of logical matrices. Notre Dame J. Formal Log. 53(2), 223–244 (2012). https://doi.org/10.1215/00294527-1715707
Routley, R.: Dialectical logic, semantics and metamathematics. Erkenntnis 14(3), 301–331 (1979). https://doi.org/10.1007/BF00174897
Routley, R.: Review of Entailment: The Logic of Relevance and Necessity, Vol. 1, by Alan R. Anderson and Nuel D. Belnap. Australasian J. Philos. 58(4), 405–408 (1980). https://doi.org/10.1080/00048408012341401
Routley, R., Meyer, R.K.: Dialectical logic, classical logic, and the consistency of the world. Stud. Sov. Thought 16(1), 1–25 (1976). https://doi.org/10.1007/BF00832085
Routley, R., Meyer, R.K., Plumwood, V., Brady, R.T.: Relevant Logics and Their Rivals, vol. 1. Ridgeview, Atascadero (1982)
Routley, R., Routley, V.: The semantics of first degree entailment. Noûs 6(4), 335–359 (1972). https://doi.org/10.2307/2214309
Russell, B.: Principles of Mathematics. Cambridge University Press, Cambridge (1903)
Skolem, T.: On the structure of groups in the identity calculus. In: Fenstad, J.E. (ed) Selected Works in Logic: By Th. Skolem, pp. 252–263. Universitetsforlaget, Oslo (1970)
Slaney, J.K.: MaGIC, Matrix Generator for Implication Connectives: Release 2.1 notes and guide. Technical report (1995). http://ftp.rsise.anu.edu.au/techreports/1995/TR-ARP-11-95.dvi.gz
Urquhart, A.: Review of Relevant Logics and Their Rivals, Vol. 1 by Richard Routley, Robert K. Meyer, Val Plumwood and Ross T. Brady. Studia Logica, 47(2):169–171 (1988). https://doi.org/10.1007/BF00370291
von Plato, J.: Skolem’s discovery of Gödel-Dummett logic. Stud. Log. 73(1), 153–157 (2003). https://doi.org/10.1023/A:1022997524909
Acknowledgements
Open Access funding provided by University of Bergen.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
I am grateful to colleagues at the University of Bergen for comments on a draft of this paper. I would also like to thank Shawn Standefer, as well as the anonymous referees, for comments and suggestions which helped improve this paper considerably.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Øgaard, T.F. Farewell to Suppression-Freedom. Log. Univers. 14, 297–330 (2020). https://doi.org/10.1007/s11787-020-00255-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11787-020-00255-0






 .
.




 in its internally nested position and arriving, as in system E, at
in its internally nested position and arriving, as in system E, at  .
[
.
[
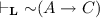 and
and 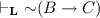 . This, however, seems to be too strong: firstly, since both of Routley’s two favorite logics DK and DL have the classical two-valued Boolean algebra as one of their models where
. This, however, seems to be too strong: firstly, since both of Routley’s two favorite logics DK and DL have the classical two-valued Boolean algebra as one of their models where 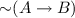 [
[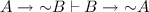 by modus tollens, i.e. the rule
by modus tollens, i.e. the rule 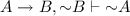 , then the resultant logic has the VSP even when Dummett’s axiom is added (they only state that the suffixing rule holds in their model
, then the resultant logic has the VSP even when Dummett’s axiom is added (they only state that the suffixing rule holds in their model  .
. 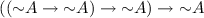 of the E-axiom, but also the instance
of the E-axiom, but also the instance 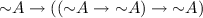 of R’s assertion axiom (Ax11) which is not a theorem of E. Negation in logics where both these hold is implicational, in that every
of R’s assertion axiom (Ax11) which is not a theorem of E. Negation in logics where both these hold is implicational, in that every  -formula is equivalent to a
-formula is equivalent to a 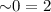 , but 2 is not to be found in the matrix for
, but 2 is not to be found in the matrix for 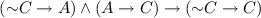 from which Reductio, some simple double negation fiddling, and the transitivity of
from which Reductio, some simple double negation fiddling, and the transitivity of 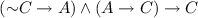 . From this the contraposition axiom and some more double negation fiddling suffices for
. From this the contraposition axiom and some more double negation fiddling suffices for 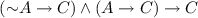 , from which the rules of BB suffices for yielding
, from which the rules of BB suffices for yielding 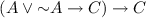 .
.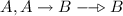 , is read: where A and
, is read: where A and 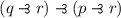 whenever
whenever 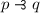 is a premise. Except as an elliptical statement for ‘
is a premise. Except as an elliptical statement for ‘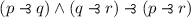 and
and 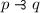 is true,’ this inference seems dubious.”
[
is true,’ this inference seems dubious.”
[