1 Introduction

Solving partial differential equations is challenging due to the nonlinear, high-dimensional, and often non-analytical nature of the equations involved. Various numerical and analytical methods have been developed to address these challenges in recent years. Among those is the spectral Tau method that produces, from a truncated series expansion in a complete set of orthogonal functions, an approximate polynomial solution for differential problems. Although powerful it is not widely used due to the lack of automatic mechanisms to wrap the analytical problem in a numerical treatable form.

Previous numerical implementations are usually dedicated to the solution of a particular problem, and there is no mathematical library that solves differential problems in a general and automatic way. There are, however, a few mathematical libraries implementing the spectral Galerkin method, such as Shenfun  [1] and particularly the Chebfun project [2, 3], but not the spectral Tau method. Contrary to the most common spectral Galerkin method, where the expansion functions must satisfy the boundary conditions, in the Tau method, the coefficients of the series are computed by forcing the differential problem to be exact in its spectral representation as far as possible. Additional conditions are set such that the initial/boundary conditions are exactly satisfied.

The spectral Tau method to approximate the solution of partial differential problems is implemented as part of the Tau Toolbox—a numerical library for the solution of integro-differential problems. This mathematical software provides a general framework for the solution of such problems, ensuring accurate and fast approximate solutions. It enables a symbolic syntax to be applied to objects to manipulate and solve differential problems with ease, high accuracy, and efficiency.

In this paper we discuss the implementation of such a numerical solution for partial differential equations, presenting the construction of the problem’s algebraic representation, specifying different procedure possibilities to tackle the linear systems involved, and exploring solution mechanisms with different orthogonal polynomial bases.

The paper is organized as follows. After the preliminary introduction, in Sect. 3 we present an implementation of the spectral Tau method, following the operational traditional approach [4], to solve partial differential problems and use examples to illustrate its efficiency. A tuned direct method is devised to ensure the solution is well adapted to the original Lanczos’ idea, following [5]. It can be used on problems set on n-dimensional spaces but it can be both resource and time-consuming. In Sect. 4, we incorporate low-rank techniques [6, 7] within the existing operational spectral Tau approach and devise an implementation that produces an approximate solution fast and with good accuracy for smooth functions [8, 9]. This approach is only possible, for now, for bi-dimensional problems. An example of applying this low-rank implementation to numerically solve partial differential problems is given in the following section. We summarize our results in Sect. 5.

2 Preliminaries

Let \(\Omega \subset \mathbb {R}^n\) be a compact domain, \(\mathbb {F}(\Omega )\) and \(\mathbb {G}(\Omega )\) spaces of functions defined on \(\Omega \), and \(u(x_1, \dots , x_n) \in \mathbb {F}(\Omega )\) an unknown function, with independent variables \((x_1, \dots , x_n) \in \Omega \). The problem can be formulated as

$$\begin{aligned} \text {find }u \in \mathbb {F}(\Omega ) \text { such that} {\left\{ \begin{array}{ll} \mathcal {D}u = f \\ \mathcal {C}_iu = s_i,\ i=1,\dots , \nu \end{array}\right. }, \end{aligned}$$
(1)

where \(\mathcal {D}\), \(\mathcal {C}_i\), \(i=1, \dots ,\nu \), are given differential operators defined on \(\mathbb {F}(\Omega ) \rightarrow \mathbb {G}(\Omega )\), and f and \(s_i\) are given functions belonging to \(\mathbb {G}(\Omega )\).

Considering the inner products in the polynomial space \(\mathbb {P}(\Omega )\), \(\langle .,. \rangle _i : \mathbb {P}_i^2([a_i, b_i])\rightarrow \mathbb {R}\), the following sets of orthogonal polynomials

$$\begin{aligned} \mathcal {P}_i=[P_0^{(i)}, P_1^{(i)},\dots ]^T :\quad \langle P_j^{(i)}, P_k^{(i)}\rangle = \Vert P_j^{(i)}\Vert ^2\delta _{jk},\quad i=1,\dots n. \end{aligned}$$

can be built.

Polynomial basis for \(\mathbb {P}(\Omega )\) are then constructed, \(\mathcal {P} = \mathcal {P}_1\otimes \mathcal {P}_2\dots \otimes \mathcal {P}_n =[P_0, P_1,\dots ]^T\), where \(\otimes \) is the Kronecker product. The sought solution u can be expressed as a polynomial in this basis as

$$\begin{aligned} u =\sum _{j=0}^\infty a_j P_j, \quad j=(j_1, \dots , j_n) \in \mathbb {N}^n_0, \end{aligned}$$

where \(\mathbb {N}_0\) is the set of nonnegative integers.

3 Traditional Tau Approach

3.1 Tau Method

The Tau method consists in the truncation of u in the multi-order \(k=(k_1,\dots , k_n) \in \mathbb {N}^n_0\), giving rise to

$$\begin{aligned} u_k =\sum _{j=0}^k a_{k,j}P_j, \end{aligned}$$

solution of the perturbed problem with the form

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathcal {D}u_k = f + \tau _k, \quad \tau _k =\sum _{j\in \mathbb {J}} \tau _{k,j}P_j\\ \mathcal {C}_i u_k = s_i,\quad i=1,\dots ,\nu \end{array}\right. } \end{aligned}$$

with \(\mathbb {J} \in \mathbb {N}^n_0\).

The differential operator, being linear and of the form

$$\begin{aligned} \mathcal {D} = \sum _{j=0}^{\nu }f_j \frac{\partial ^{|j|}}{\partial x^j},\quad \text {where}\; {\left\{ \begin{array}{ll} j=(j_1,\ldots ,j_n) &{} \in \mathbb {N}^n_0 \\ \nu =(\nu _1,\ldots ,\nu _n) &{} \in \mathbb {N}^n_0\\ |j|=\sum _{i=1}^n j_i \end{array}\right. }, \end{aligned}$$

with coefficients \( f_j\approx \sum _{\ell =0}^{d_j} f_{j,\ell }x^{\ell }, \; x\in \Omega ,\; \ell ,d_j\in \mathbb {N}^n_0\), can be cast in matrix form \(\textsf{D}\) by

$$\begin{aligned} \textsf{D} = \sum _{j=0}^{\nu }\sum _{k=0}^{d_j} f_{j,k}\textsf{M}_1^{k_1}\textsf{N}_1^{j_1}\otimes \textsf{M}_2^{k_2}\textsf{N}_2^{j_2}\otimes \cdots \otimes \textsf{M}_n^{k_n}\textsf{N}_n^{j_n} \end{aligned}$$

with

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \textsf{M}_i=[\mu _{j,k}^{(i)}], &{} \mu _{j,k}^{(i)}=\frac{1}{|| P_{j}^{(i)} ||^2}<\!P_{j}^{(i)}, x_i P_{k}^{(i)}\!>_i \\ \textsf{N}_i= [\eta _{j,k}^{(i)}], &{} \eta _{j,k}^{(i)}=\frac{1}{|| P_{j}^{(i)} ||^2} <\!P_{j}^{(i)}, \frac{d}{dx_i} P_{k}^{(i)}\!>_i \end{array}\right. },\ i=1,\ldots ,n. \end{aligned}$$

Likewise, the boundary conditions

$$\begin{aligned} \mathcal {C}_i=\sum _{j=0}^{n}\sum _{k=0}^{\nu -1} g_{i,j}\left. \dfrac{\partial ^{|k|}}{\partial x^{k}}\right| _{x_j=x_i},\ i=1,\ldots ,\nu \end{aligned}$$

are translated in terms of the coefficients of \(u_k\) by \(\textsf{C}=\left[ \textsf{C}_i \right] _{i=1}^{\nu }\):

$$\begin{aligned} \textsf{C}_i = \sum _{j=0}^n \sum _{k=0}^{\nu -1} g_{i,j} \textsf{N}_1^{k_1}\otimes \cdots \otimes \textsf{N}_{j-1}^{k_{j-1}} \otimes \textsf{N}_j^{k_j} \mathcal {P}_j(x_i) \otimes \textsf{N}_{j+1}^{k_{j+1}}\otimes \cdots \otimes \textsf{N}_n^{k_n}\end{aligned}$$

Finally, the Tau coefficient matrix is built

$$\begin{aligned} \textsf{T} = \begin{bmatrix} \textsf{C} \\ \textsf{D} \end{bmatrix}_{nr\times nc}, \end{aligned}$$

where the number of boundary rows is \(nbr=\sum _{j=1}^{\nu }\prod _{j\ne i=1}^{n} (k_i+1)\), the number of rows is \(nr = nbr+\prod _{i=1}^{n} (k_i+h_i+1)\) and the number of columns is \(nc=\prod _{i=1}^{n} (k_i+1)\), \(nr>nc\). Note that \(h_i =\max \{h_{ij}\}\), \(h_{i0}\) the height of D and \(h_{ij}\) the height of \(\mathcal {C}_i\), in \(x_j\), \(j=1,...,n\).

Given f and \(s_i,\ i=1,\ldots \nu \), the problem’s right-hand side, we define the coefficients vectors in the polynomial approximations

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \textsf{s}_i=[s_{i,j}]_{j=0}^k, &{} s_i\approx \sum _{j=0}^{k}s_{i,j}P_j,\; i=1,\ldots \nu \\ \textsf{f}=[f_{j}]_{j=0}^k, &{} f\approx \sum _{j=0}^{k}f_{j}P_j \end{array}\right. }, \end{aligned}$$

from which the Tau right-hand side vector

$$\begin{aligned} \textsf{b} = \begin{bmatrix} \textsf{s} \\ \textsf{f} \end{bmatrix}_{nr\times 1},\quad \text {with } \textsf{s}=\left[ \textsf{s}_i \right] _{i=1}^{\nu } \end{aligned}$$

can be constructed.

The system \(\textsf{T}\textsf{a}=\textsf{b}\) is overdetermined and large dimensional. Different solvers may produce the usual Tau solution or a kind of weak form of it (e.g. linear least squares approach).

We provide an algorithm to solve the problem \(\textsf{T}\textsf{a}=\textsf{b}\) with a direct method ensuring a solution that fully satisfies the initial/boundary conditions and minimizes the error on the operator terms – Tau solution. This approach, drawn in Algorithm 1, is based on an adaptation of the LU factorization: a two-level approach. The pivoting process prioritizes two types of rows: (i) those that define boundary conditions, which impose a threshold on the growth factor, and (ii) those that specify terms of the operator with a lower degree.

Algorithm 1
figure a

solve \(\textsf{T}\textsf{a}=\textsf{b}\) with LU2 special decomposition

Full size image

3.2 Numerical Illustration

To illustrate the use of this approach, we solve Saint-Venant’s torsion problem for a prismatic bar with a square section

$$\begin{aligned} {\left\{ \begin{array}{ll}\displaystyle \frac{\partial ^2 u}{\partial x^2} + \frac{\partial ^2 u}{\partial y^2} = -2\\ u(\pm 1,y)=u(x,\pm 1)=0 \end{array}\right. }. \end{aligned}$$
(2)

The analytic solution can be developed as

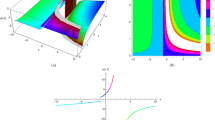
$$\begin{aligned} u(x,y)=\frac{32}{\pi ^3}\sum _{n\ge 0}\frac{(-1)^n}{(2n+1)^3}\left[ 1-\frac{\cosh ((n+1/2)\pi \, y)}{\cosh ((n+1/2)\pi )}\right] \cos ((n+1/2)\pi \, x), \end{aligned}$$

and we use a truncation of the series to evaluate the quality of the Tau approximate solution provided by Tau Toolbox using the traditional approach. Figure 1 shows, for problem (2), the difference surface between the truncated solution, using 99 terms, and the Tau approximation, for small polynomial degrees.

Fig. 1
figure 1

Difference surface (between the serie’s solution with 99 terms and the Tau approximation \(u_{m,n}\), \(m,n=4\), and \(m,n=8\))

Full size image

The results clearly evidence the quality of the approximation, bearing in mind the low polynomial degrees involved. Furthermore, they show a remarkable equioscillatory behavior [4].

On the other hand, the elapsed time to compute the approximation and memory resources are high whenever a moderate/high polynomial approximation is required. In Fig. 2 we depict the elapsed time required to compute a Tau approximate solution for the Saint-Venant’s problem using Algorithm 1 and a linear least squares approach. We report also on the time required to unpack the problem and build the linear system. Clearly, time increases exponentially with the polynomial degree.

Fig. 2
figure 2

Computation time in seconds for the Tau approximation (logarithmic scale)

Full size image

To overcome this limitation, a Gegenbauer-Tau implementation together low-rank approximation techniques are used, as explained in the next section.

4 A Gegenbauer-Tau Approach with Low-Rank Approximation

4.1 Gegenbauer-Tau Approach

Following the ideas in [9], formulating the Tau method in terms of Gegenbauer polynomials and their associated sparse matrices, can bring additional benefits in terms of computational efficiency and numerical stability.

First recall that Gegenbauer, also known as ultraspherical, polynomials \(C_j^{(\alpha )}\), \(j\ge 0\) are orthogonal polynomials, belonging to the more general class of Jacobi polynomials, orthogonal on \([-1,1]\) with respect to the weight function \((1-x^2)^{\alpha -\frac{1}{2}}\). Although they can be used with any real parameter \(\alpha > -\frac{1}{2}\), three particular cases appear with special emphasis in applications: Legendre polynomials \(P_j(x)=C_j^{(\frac{1}{2})}(x)\); Chebyshev of second kind \(U_j(x)=C_j^{(1)}(x)\) and Chebyshev of first kind, the limit case, \(T_j(x)=\lim _{\alpha \mapsto 0^+} \frac{1}{2\alpha }C_{j}^{(\alpha )}(x)\).

Of great relevance is that a Gegenbauer polynomial \(C_j^{(\alpha )}\) satisfies the property of derivatives [10]

$$\begin{aligned} \dfrac{d}{dx}C_j^{(\alpha )}(x) = {\left\{ \begin{array}{ll} 2\alpha C_{j-1}^{(\alpha +1)}(x), &{} \alpha \ne 0\\ jU_{j-1}(x), &{} \alpha =0 \end{array}\right. },\ j\ge 1. \end{aligned}$$

And, applying \(\ell \) times the last relation, one gets

$$\begin{aligned} \begin{aligned} \dfrac{d^\ell }{dx^\ell }C_j^{(\alpha )}(x) = {\left\{ \begin{array}{ll} {\left\{ \begin{array}{ll} 2^\ell (\alpha )_\ell C_{j-\ell }^{(\alpha +\ell )}(x), &{}{} \alpha \ne 0\\ 2^{\ell -1}(\ell -1)! j C_{j-\ell }^{(\ell )}(x), &{}{} \alpha = 0 \end{array}\right. } &{}{} j\ge \ell \\ 0 &{}{} j<\ell \end{array}\right. } \end{aligned}\end{aligned}$$

where \((\alpha )_\ell =\alpha (\alpha +1)\cdots (\alpha +\ell -1)\) is the raising factorial (or Pochhammer symbol).

Let, for \(\alpha >-\frac{1}{2}\), \(\mathcal {C}^{(\alpha )}=[C_0^{(\alpha )}, C_1^{(\alpha )}, \ldots ]^T\) be a Gegenbauer polynomial basis, and

$$\begin{aligned} u=\sum _{j=0}^{\infty } u_j C_j^{(\alpha )}=\textsf{u}\mathcal {C}^{(\alpha )} \end{aligned}$$
(3)

be a formal series represented by the coefficients vector \(\textsf{u}=[u_0,u_1,\ldots ]\), then the \(\ell \)th derivative

$$\begin{aligned} \dfrac{d^\ell }{dx^\ell } u = \textsf{N}_\ell \textsf{u}\mathcal {C}^{(\ell +\alpha )} \end{aligned}$$

is represented by a sparse matrix operator

$$\begin{aligned} \textsf{N}_\ell ={\left\{ \begin{array}{ll} 2^\ell (\alpha )_\ell \Lambda ^\ell , &{} \alpha \ne 0 \\ 2^{\ell -1}(\ell -1)!\times \mathop {\textrm{diag}}(\ell ,\ell +1,\ldots )\Lambda ^\ell , &{} \alpha =0 \end{array}\right. }, \end{aligned}$$

where

$$\begin{aligned} \Lambda =\begin{bmatrix} 0 &{} 1 &{} &{} &{} \\ &{} &{} 1 &{} &{} \\ &{} &{} &{} 1 &{} \\ &{} &{} &{} \ddots \\ \end{bmatrix} \end{aligned}$$

is the shift operator.

However, since \(\textsf{N}_\ell \) takes coefficients in \(\mathcal {C}^{(\alpha )}\) into coefficients in \(\mathcal {C}^{(\ell +\alpha )}\), all terms on the differential problem must be also translated into coefficients in \(\mathcal {C}^{(\ell +\alpha )}\). This can be accomplished using the relation [10]

$$\begin{aligned} C_j^{(\alpha )}(x)={\left\{ \begin{array}{ll} \displaystyle \frac{\alpha }{j+\alpha }(C_j^{(\alpha +1)}(x)-C_{j-2}^{(\alpha +1)}(x)), &{} \alpha \ne 0\\ \displaystyle \frac{1}{2}(U_j(x)-U_{j-2}(x)), &{} \alpha = 0 \end{array}\right. }, \end{aligned}$$

which can be applied via the following operator matrices

$$\begin{aligned} \textsf{S}_{\alpha }=\begin{bmatrix} 1 &{} &{} -\frac{\alpha }{\alpha +2} &{} &{} \\ &{} \frac{\alpha }{\alpha +1} &{} &{} -\frac{\alpha }{\alpha +3} &{} \\ &{} &{} \frac{\alpha }{\alpha +2} &{} &{} -\frac{\alpha }{\alpha +4} \\ &{} &{} &{} \frac{\alpha }{\alpha +3} &{} \ddots \\ \end{bmatrix}\ \text {if}\ \alpha \ne 0\ \text {and}\ \textsf{S}_{0}=\begin{bmatrix} 1 &{} &{} -\frac{1}{2} &{} &{} \\ &{} \frac{1}{2} &{} &{} -\frac{1}{2} &{} \\ &{} &{} \frac{1}{2} &{} &{} -\frac{1}{2} \\ &{} &{} &{} &{} \ddots \\ \end{bmatrix}. \end{aligned}$$

This is important to explore since spectral methods usually represent differential operators by dense matrices, even if there is some cost associated with the change in polynomial basis.

Finally, to have an operational formulation of the Tau method in terms of Gegenbauer polynomials, we have to represent the multiplication operation by an algebraic operator. This can be done from the three-term characteristic recurrence relation [10]

$$\begin{aligned} xC_{j}^{(\alpha )}(x) = {\left\{ \begin{array}{ll} \displaystyle \frac{j+1}{2(j+\alpha )}C_{j+1}^{(\alpha )}(x)+\frac{j+2\alpha -1}{2(j+\alpha )}C_{j-1}^{(\alpha )}(x), &{} \alpha \ne 0\\ \displaystyle \frac{1}{2-\delta _{j,0}}[T_{j+1}(x)+T_{j-1}(x)], &{} \alpha = 0 \end{array}\right. },\ j\ge 0, \end{aligned}$$

with \(C_{-1}^{(\alpha )}=0\) and \(C_{0}^{(\alpha )}=1\). This can be written in matrix form using matrices

$$\begin{aligned} \textsf{M}_{\alpha }=\begin{bmatrix} &{} \frac{\alpha }{\alpha +1} &{} &{} &{} \\ \frac{1}{2\alpha } &{} &{} \frac{2\alpha +1}{2(\alpha +2)} &{} &{} &{} \\ &{} \frac{1}{\alpha +1} &{} &{} \frac{\alpha +1}{\alpha +3} \\ &{} &{} \frac{3}{2(\alpha +2)} &{} \ddots \\ \end{bmatrix}\ \text {if}\ \alpha \ne 0\ \text {and}\ \textsf{M}_{0}=\begin{bmatrix} &{} \frac{1}{2} &{} \\ 1 &{} &{} \frac{1}{2} &{} &{} \\ &{} \frac{1}{2} &{} &{} \frac{1}{2} &{} \\ &{} &{} \frac{1}{2} &{} \ddots \\ \end{bmatrix}. \end{aligned}$$

So, if \(u=\textsf{u}\mathcal {C}^{(\alpha )}\) (3) and \(D=\sum _{\ell =0}^{\nu } f_\ell \dfrac{d^\ell }{dx^\ell }\) is a differential operator with coefficients \(f_\ell =\sum _{i=0}^{n_\ell } f_{\ell ,i} x^i\), then

$$\begin{aligned} D u = \textsf{D}\textsf{u}\mathcal {C}^{(\alpha +\nu )} \end{aligned}$$

with

$$\begin{aligned} \textsf{D}= f_{\nu }(\textsf{M}_{\alpha +\nu })\textsf{N}_{\nu } +\sum _{\ell =0}^{\nu -1} S_{\alpha +\nu -1}\cdots S_{\alpha +\ell } f_\ell (\textsf{M}_{\alpha +\ell })\textsf{N}_\ell , \end{aligned}$$

and

$$\begin{aligned} f_\ell (\textsf{M}) = \sum _{i=0}^{n_\ell } f_{\ell ,i} \textsf{M}^i. \end{aligned}$$

The resulting linear system, \(\textsf{T}\textsf{a}=\textsf{b}\) has the usual trapezoidal shape and can be solved by LU factorization, where

$$\begin{aligned} \textsf{T} = \begin{bmatrix} \textsf{C} \\ \textsf{D} \end{bmatrix}_{nr\times nc}. \end{aligned}$$

Using Gegenbauer polynomials, matrix \(\textsf{T}\) is well-conditioned [11].

Another possibility is to use QR factorization, following Algorithm 2, which works on a triangular matrix similar to \(\textsf{T}\).

Algorithm 2
figure b

solve \(\textsf{T}\textsf{a}=\textsf{b}\) with QR special decomposition

Full size image

4.2 Low-Rank Implementation

In this subsection, we succinctly summarize the inclusion of low rank approximations in the resolution of partial differential problems. Indeed, partial differentiation can be adapted to the use of low-rank approximations since it can be represented by a tensor product of univariate differentiation. For the moment, only the bidimensional case is treated.

Let us consider the two-dimensional partial differential problem from (1)

$$\begin{aligned} \text {find }u \in \mathbb {F}(\Omega ) \text { such that} {\left\{ \begin{array}{ll} \mathcal {D}u = f \\ \mathcal {C}_x u = (s_{x1},\ldots ,s_{x\nu _1})^T \\ \mathcal {C}_y u = (s_{y1},\ldots ,s_{y\nu _2})^T \end{array}\right. }, \end{aligned}$$
(4)

for \(\Omega \subset \mathbb {R}^2\), \(u(x, y) \in \mathbb {F}(\Omega )\), and

$$\begin{aligned} \mathcal {D} = \sum _{i=0}^{\nu _2}\sum _{j=0}^{\nu _1} p_{i,j}(x,y) \frac{\partial ^{i+j}}{\partial y^i \partial x^j}, \end{aligned}$$

a linear operator, where \(\nu _1\) is the differential order of \(\mathcal {D}\) in the x variable and \(\nu _2\) in the y variable, and \(p_{i,j}(x,y)\) are functions defined on \(\Omega \). A low-rank approximation for a bivariate function \(p_{i,j}\) (tau.Polynomial2) can be expressed by a sum of outer products of univariate polynomials (tau.Polynomial1):

$$\begin{aligned} p_{i,j}(x,y)=\sum _{\ell =1}^{k_{ij}}c_\ell ^{ij}(y)r_\ell ^{ij}(x), \end{aligned}$$

with \(0\le i \le \nu _2\) and \(0 \le j \le \nu _1\). As a consequence, the partial differential operator \(\mathcal {D}\) can be expressed by a low-rank representation of rank k as

$$\begin{aligned}\mathcal {D}u=(\mathcal {D}^y\otimes \mathcal {D}^x)u=\sum _{j=1}^k(\mathcal {D}^yc_j)(\mathcal {D}^xr_j), \; u(x,y)=\sum _{j=1}^\infty d_jc_j(y)r_j(x),\end{aligned}$$

where \(c_j(y)\) and \(r_j(x)\) belong to the tau.Polynomial1 class.

Thus, a sum of tensor products of linear ordinary differential operators is built from a separable representation of a partial differential operator. Then the ordinary differential operator is tackled with the Gegenbauer-Tau spectral approach, and finally a \(\nu _2 \times \nu _1\) discretized generalized Sylvester matrix equation is solved to provide an approximate solution to the problem. A detailed explanation on these steps can be found in [9, 11]. This set of actions brings benefits in terms of computational efficiency and numerical stability.

4.3 Numerical Illustration

We begin by illustrating the Saint-Venant problem using the Tau Toolbox:

figure c

The writing of the code is intuitive and self-explanatory. The problem is set in the library by calling |tau.Problem2|. By default, \([-1,1]\) is the domain, and ChebyshevT is the basis for all variables. The result is a Tau object |u| computed via the |solve| functionality of Tau Toolbox:

figure d

The computations were carried out using a low-approximation factorization of rank 33, even if the discretization involved a \(257\times 257\) matrix. The approximate solution and the error are depicted in Fig. 3.

Fig. 3
figure 3

Approximate solution and difference surface (between an approximate solution f(x, y) sum of the first 99 terms and the Gegenbauer-Tau approximation \(u_{256,256}\))

Full size image

In Fig. 4 we show the performance achieved in the computation of the low-rank approximate solution with Gegenbauer-Tau approach. For very large polynomial degree approximation, there is no gain to achieve since the rank of the problem stays unchanged. As expected, the computation time increases with the degree of the approximation but is much less than the traditional approach.

Fig. 4
figure 4

Performance of the Gegenbauer-Tau approach with low-rank approximations

Full size image

Another example is the partial differential problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \dfrac{\partial ^2 u}{dx^2}+\dfrac{\partial ^2u}{dt^2}-(t^2+x^2 -2) u= -2(t+x)\sin (t+x)e^{tx}\\ u(-1, t)=e^{-t}\cos (t-1) \\ u(2, t) =e^{2t}\cos (t+2) \\ u(x, -\frac{1}{2})=e^{-\frac{x}{2}}\cos (x-\frac{1}{2}) \\ u(x, \frac{1}{2}) =e^{\frac{x}{2}}\cos (x+\frac{1}{2}) \end{array}\right. }. \end{aligned}$$
(5)

with exact solution given by \(u(x,t)=e^{tx} \cos (x + t)\). The excerpt of the code to solve the problem follows:

figure e
Fig. 5
figure 5

Approximate solution and difference surface (between the exact solution f(x, t) and the approximation \(u_{33,33}\)) provided by Tau Toolbox

Full size image

The solution of problem (5) is computed to almost machine precision (see Fig. 5), working on matrix structures with rank 12 to approximate the operators:

figure f

5 Conclusion

In this work we have introduced the Tau Toolbox—a MATLAB/Python toolbox for the solution of integro-differential problems, presented implementation details on how to solve bidimensional PDEs making use of low-rank approximations and Gegenbauer polynomials, and illustrated the simplicity of use of Tau Toolbox in the solution of PDEs as well as the efficiency of the implemented approach.