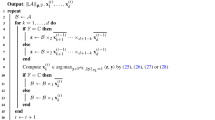Common Factors in Fraction-Free Matrix Decompositions

Abstract

We consider LU and QR matrix decompositions using exact computations. We show that fraction-free Gauß–Bareiss reduction leads to triangular matrices having a non-trivial number of common row factors. We identify two types of common factors: systematic and statistical. Systematic factors depend on the reduction process, independent of the data, while statistical factors depend on the specific data. We relate the existence of row factors in the LU decomposition to factors appearing in the Smith–Jacobson normal form of the matrix. For statistical factors, we identify some of the mechanisms that create them and give estimates of the frequency of their occurrence. Similar observations apply to the common factors in a fraction-free QR decomposition. Our conclusions are tested experimentally.

Introduction

Although known earlier to Dodgson [8] and Jordan¹ (see Durand [9]), the fraction-free method for exact matrix computations became well known because of its application by Bareiss [1] to the solution of a linear system over $\mathbb {Z}$, and later over an integral domain [2]. He implemented fraction-free Gaussian elimination of the augmented matrix $[A\ B]$, and kept all computations in $\mathbb {Z}$ until a final division step. Since, in linear algebra, equation solving is related to the matrix factorizations LU and QR, it is natural that fraction-free methods would be extended later to those factorizations. The forms of the factorizations, however, had to be modified from their floating-point counterparts in order to retain purely integral data. The first proposed modifications were based on inflating the initial data until all divisions were guaranteed to be exact, see for example Lee and Saunders [17], Nakos et al. [21] and Corless and Jeffrey [7]. This strategy, however, led to the entries in the L and U matrices becoming very large, and an alternative form was presented in Zhou and Jeffrey [26], and is described below. Similarly, fraction-free Gram–Schmidt orthogonalization and QR factorization were studied in Erlingsson et al. [10] and Zhou and Jeffrey [26]. Further extensions have addressed fraction-free full-rank factoring of non-invertible matrices and fraction-free computation of the Moore–Penrose inverse [15]. More generally, applications exist in areas such as the Euclidean algorithm, and the Berlekamp–Massey algorithm [16].

More general domains are possible, and here we consider matrices over a principal ideal domain $\mathbb {D}$. For the purpose of giving illustrative examples and conducting computational experiments, matrices over $\mathbb {Z}$ and $\mathbb {Q}[x]$ are used, because these domains are well established and familiar to readers. We emphasize, however, that the methods here apply for all principal ideal domains, as opposed to methods that target specific domains, such as Giesbrecht and Storjohann [12] and Pauderis and Storjohann [24].

The shift from equation solving to matrix factorization has the effect of making visible the intermediate results, which are not displayed in the original Bareiss implementation. Because of this, it becomes apparent that the columns and rows of the L and U matrices frequently contain common factors, which otherwise pass unnoticed. We consider here how these factors arise, and what consequences there are for the computations.

Our starting point is a fraction-free form for LU decomposition [15]: given a matrix A over $\mathbb {D}$,

$$\begin{aligned} A = P_r LD^{-1} U P_c, \end{aligned}$$

where L and U are lower and upper triangular matrices, respectively, D is a diagonal matrix, and the entries of L, D, and U are from $\mathbb {D}$. The permutation matrices $P_r$ and $P_c$ ensure that the decomposition is always a full-rank decomposition, even if A is rectangular or rank deficient; see Sect. 2. The decomposition is computed by a variant of Bareiss’s algorithm [2]. In Sect. 6, the $L D^{-1} U$ decomposition also is the basis of a fraction-free QR decomposition.

The key feature of Bareiss’s algorithm is that it creates factors which are common to every element in a row, but which can then be removed by exact divisions. We refer to such factors, which appear predictably owing to the decomposition algorithm, as “systematic factors”. There are, however, other common factors which occur with computable probability, but which depend upon the particular data present in the input matrix. We call such factors “statistical factors”. In this paper we discuss the origins of both kinds of common factors and show that we can predict a nontrivial proportion of them from simple considerations.

Once the existence of common factors is recognized, it is natural to consider what consequences, if any, there are for the computation, or application, of the factorizations. Some consequences we shall consider include a lack of uniqueness in the definition of the LU factorization, and whether the common factors add significantly to the sizes of the elements in the constituent factors. This in turn leads to questions regarding the benefits of removing common factors, and what computational cost is associated with such benefits.

A synopsis of the paper is as follows. After recalling Bareiss’s algorithm, the $L D^{-1} U$ decomposition, and the algorithm from Jeffrey [15] in Sect. 2, we establish, in Sect. 3, a relation between the systematic common row factors of U and the entries in the Smith–Jacobson normal form of the same input matrix A. In Sect. 4 we propose an efficient way of identifying some of the systematic common row factors introduced by Bareiss’s algorithm; these factors can then be easily removed by exact division. In Sect. 5 we present a detailed analysis concerning the expected number of statistical common factors in the special case $\mathbb {D}=\mathbb {Z}$, and we find perfect agreement with our experimental results. We conclude that the factors make a measurable contribution to the element size, but they do not impose a serious burden on calculations.

In Sect. 6 we investigate the QR factorization. In this context, the orthonormal Q matrix used in floating point calculations is replaced by a $\Theta$ matrix, which is left-orthogonal, i.e. $\Theta ^t\Theta$ is diagonal, but $\Theta \Theta ^t$ is not. We show that, for a square matrix A, the last column of $\Theta$, as calculated by existing algorithms, is subject to an exact division by the determinant of A, with a possibly significant reduction in size.

Throughout the paper, we employ the following notation. We assume, unless otherwise stated, that the ring $\mathbb {D}$ is an arbitrary principal ideal domain. We denote the set of all m-by-n matrices over $\mathbb {D}$ by $\mathbb {D}^{m\times n}$. We write ${\mathbf {1}}_{n}$ for the n-by-n identity matrix and $\mathbf {0}_{m\times n}$ for the m-by-n zero matrix. We shall usually omit the subscripts if no confusion is possible. For $A \in \mathbb {D}^{m\times n}$ and $1 \le i \le m$, ${A}_{i,*}$ is the ith row of A. Similarly, ${A}_{*,j}$ is the jth column of A for $1 \le j \le n$. If $1 \le i_1 < i_2 \le m$ and $1 \le j_1 < j_2 \le n$, we use ${A}_{{i_{1}\ldots i_{2}},{j_{1}\ldots j_{2}}}$ to refer to the submatrix of A made up from the entries of the rows $i_1$ to $i_2$ and the columns $j_1$ to $j_2$. Given elements $a_1,\ldots ,a_n \in \mathbb {D}$, with ${{\,\mathrm{diag}\,}}(a_1,\ldots ,a_n)$ we refer to the diagonal matrix that has $a_j$ as the entry at position (j, j) for $1 \le j \le n$. We will use the same notation for block diagonal matrices.

We denote the set of all column vectors of length m with entries in $\mathbb {D}$ by $\mathbb {D}^{m}$ and that of all row vectors of length n by $\mathbb {D}^{1\times n}$. If $\mathbb {D}$ is a unique factorization domain and $v = (v_1,\ldots ,v_n) \in \mathbb {D}^{1\times n}$, then we set $\gcd (v) = \gcd (v_1,\ldots ,v_n)$. Moreover, with $d \in \mathbb {D}$ we write $d \mid v$ if $d \mid v_1 \wedge \cdots \wedge d \mid v_n$ (or, equivalently, if $d \mid \gcd (v)$). We also use the same notation for column vectors.

We will sometimes write column vectors $w \in \mathbb {D}^{m}$ with an underline $\underline{w}$ and row vectors $v \in \mathbb {D}^{1\times n}$ with an overline $\overline{v}$ if we want to emphasize the specific type of vector.

Bareiss’s Algorithm and the $L D^{-1} U$ Decomposition

For the convenience of the reader, we start by recalling Bareiss’s algorithm [2]. Let $\mathbb {D}$ be an integral domain², and let $A \in \mathbb {D}^{n\times n}$ be a matrix and $b \in \mathbb {D}^{n}$ be a vector. Bareiss modified the usual Gaussian elimination with the aim of keeping all calculations in $\mathbb {D}$ until the final step. If this is done naïvely then the entries increase in size exponentially. Bareiss used results from Sylvester and Jordan to reduce this to linear growth. Bareiss defined the notation³

$$\begin{aligned} A^{(k)}_{ij} = \det \begin{bmatrix} A_{1,1} &{}\quad \cdots &{}\quad A_{1,k} &{}\quad A_{1,j} \\ \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ A_{k,1} &{}\quad \cdots &{}\quad A_{k,k} &{}\quad A_{k,j} \\ A_{i,1} &{}\quad \cdots &{}\quad A_{i,k} &{}\quad A_{i,j} \end{bmatrix}\ , \end{aligned}$$

(2.1)

for $i>k$ and $j>k$, and with special cases $A_{i,j}^{(0)}=A_{ij}$ and $A_{0,0}^{(-1)}=1$.

We start with division-free Gaussian elimination, which is a simple cross-multiplication scheme, and denote the result after k steps by $A^{[k]}_{ij}$. We assume that any pivoting permutations have been completed and need not be considered further. The result of one step is

$$\begin{aligned} A^{[1]}_{i,j}= A_{1,1}A_{i,j}-A_{i,1}A_{1,j} =\det \begin{bmatrix} A_{1,1} &{}\quad A_{1,j} \\ A_{i,1} &{}\quad A_{i,j} \end{bmatrix} = A^{(1)}_{i,j}\ , \end{aligned}$$

(2.2)

and the two quantities $A^{[1]}_{i,j}$ and $A^{(1)}_{i,j}$ are equal. A second step, however, leads to

$$\begin{aligned} A^{[2]}_{i,j}= A^{[1]}_{2,2}A^{[1]}_{i,j}-A^{[1]}_{i,2}A^{[1]}_{2,j} = A_{1,1}\det \begin{bmatrix} A_{1,1} &{}\quad A_{1,2} &{}\quad A_{1,j} \\ A_{2,1} &{}\quad A_{2,2} &{}\quad A_{2,j} \\ A_{i,1} &{}\quad A_{i,2} &{}\quad A_{i,j} \end{bmatrix} = A_{1,1} A^{(2)}_{i,j}\ . \end{aligned}$$

(2.3)

Thus, as stated in Sect. 1, simple cross-multiplication introduces a systematic common factor in all entries $i,j>2$. This effect continues for general k (see [2]), and leads to exponential growth in the size of the terms. Since the systematic factor is known, it can be removed by an exact division, and then the terms grow linearly in size. Thus Bareiss’s algorithm is

$$\begin{aligned} A^{(k+1)}_{i,j} =\frac{1}{A^{(k-1)}_{k,k}}\left( A^{(k)}_{k+1,k+1} A^{(k)}_{i,j}-A^{(k)}_{i,k+1}A^{(k)}_{k+1,j} \right) \ , \end{aligned}$$

(2.4)

and the division is exact. The elements of the reduced matrix are thus minors of A. The main interest for Bareiss was to advocate a ‘two-step’ method, wherein one proceeds from step k to step $k+2$ directly, rather than by repeated Gaussian steps. The two-step method claims improved efficiency, but the results obtained are the same, and we shall not consider it here.

In Jeffrey [15], Bareiss’s algorithm was used to obtain a fraction-free variant of the LU factorization of A. We quote the main result from that paper here as Theorem 1. The idea behind the factorization is that schemes which inflate the initial matrix A, such as Lee and Saunders [17] and Nakos et al. [21] and Corless and Jeffrey [7] do not avoid the quotient field, but merely move the divisors to the other side of the defining equation, at the cost of significant inflation. In any subsequent application, the divisors will have to move back, and the inflation will have to be reversed. In contrast, the present factorization isolates the divisors in an explicit inverse matrix. The matrices $P_r, L, D, U, P_c$ appearing in the decomposition below contain only elements from $\mathbb {D}$, but the inverse of D,if it were evaluated, would have to contain elements from the quotient field. By expressing the factorization in a form containing $D^{-1}$ unevaluated, all calculations can stay within $\mathbb {D}$.

Theorem 1

(Jeffrey [15, Thm. 2]). A rectangular matrix A with elements from an integral domain $\mathbb {D}$, having dimensions $m\times n$ and rank r, may be factored into matrices containing only elements from $\mathbb {D}$ in the form

$$\begin{aligned} A = P_r L D^{-1} U P_c = P_r \begin{pmatrix} \mathcal {L} \\ \mathcal {M} \end{pmatrix} D^{-1} \begin{pmatrix} \mathcal {U}&\quad \mathcal {V} \end{pmatrix} P_c \end{aligned}$$

where the permutation matrix $P_r$ is $m\times m$; the permutation matrix $P_c$ is $n\times n$; $\mathcal {L}$ is $r\times r$, lower triangular and has full rank:

$$\begin{aligned} \mathcal {L} = \begin{bmatrix} A^{(0)}_{1,1} \\ A^{(0)}_{2,1} &{}{}\quad A^{(1)}_{2,2} \\ \vdots &{}{}\quad \vdots &{}{}\quad \ddots \\ A^{(0)}_{r,1} &{}{}\quad A^{(1)}_{r,2} &{}{}\quad \cdots &{}{}\quad A^{(r-1)}_{r,r} \\ \end{bmatrix}\ ; \end{aligned}$$

(2.5)

$\mathcal {M}$ is $(m-r)\times r$ and could be null; $\mathcal {U}$ is $r\times r$ and upper triangular, while $\mathcal {V}$ is $r\times (n-r)$ and could be null:

$$\begin{aligned} \mathcal {U} = \begin{bmatrix} A^{(0)}_{1,1} &{}{}\quad A^{(0)}_{1,2} &{}{}\quad \cdots &{}{}\quad A^{(0)}_{1,r} \\ &{}{}\quad A^{(1)}_{2,2} &{}{}\quad \cdots &{}{}\quad A^{(1)}_{2,r} \\ &{}{}\quad &{}{}\quad \ddots &{}{}\quad \vdots \\ &{}{}\quad &{}{}\quad &{}{}\quad A^{(r-1)}_{r,r} \\ \end{bmatrix}\ . \end{aligned}$$

(2.6)

Finally, the D matrix is

$$\begin{aligned} D^{-1} = \begin{bmatrix} A^{(-1)}_{0,0} A^{(0)}_{1,1} &{}\quad \\ &{}\quad A^{(0)}_{1,1} A^{(1)}_{2,2} &{} \\ &{}\quad &{}\quad \ddots \\ &{}\quad &{}\quad &{}\quad A^{(n-2)}_{n-1,n-1}A^{(n-1)}_{n,n} \\ \end{bmatrix}^{-1}\ . \end{aligned}$$

(2.7)

Remark 2

It is convenient to call the diagonal elements $A^{(k-1)}_{k,k}$ pivots. They drive the pivoting strategy, which determines $P_r$, and they are used for the exact-division step (2.4) in Bareiss’s algorithm.

Remark 3

As in numerical linear algebra, the $LD^{-1}U$ decomposition can be stored in a single matrix, since the diagonal (pivot) elements need only be stored once.

The proof of Theorem 1 given in Jeffrey [15] outlines an algorithm for the computation of the $L D^{-1} U$ decomposition. The algorithm is a variant of Bareiss’s algorithm [1], and yields the same U. The difference is that Jeffrey [15] also explains how to obtain L and D in a fraction-free way.

Algorithm 4

($LD^{-1}U$ decomposition)

Input::

A matrix $A \in \mathbb {D}^{m\times n}$.

Output::

The $LD^{-1}U$ decomposition of A as in Theorem 1.

• 1. Initialize $p_0 = 1$, $P_r = {\mathbf {1}}_{m}$, $L = \mathbf {0}_{m\times m}$, $U = A$ and $P_c = {\mathbf {1}}_{n}$.

• 2. For each $k = 1,\ldots ,\min \{m,n\}$:

  • (a) Find a non-zero pivot $p_k$ in ${U}_{{k\ldots m}{k\ldots n}}$ and bring it to position (k, k) recording the row and column swaps in $P_r$ and $P_c$. Also apply the row swaps to L accordingly. If no pivot is found, then set $r = k$ and exit the loop.

  • (b) Set $L_{k,k} = p_k$ and $L_{i,k} = U_{i,k}$ for $i=k+1,\ldots ,m$. Eliminate the entries in the kth column and below the kth row in U by cross-multiplication; that is, for $i > k$ set ${U}_{i,*}$ to $p_k {U}_{i,*} - U_{ik} {U}_{k,*}$.

  • (c) Perform division by $p_{k-1}$ on the rows beneath the kth in U; that is, for $i > k$ set ${U}_{i,*}$ to ${U}_{i,*} / p_{k-1}$. Note that the divisions will be exact.

• 3. If r is not set yet, set $r = \min \{m,n\}$.

• 4. If $r < m$, then trim the last $m-r$ columns from L as well as the last $m-r$ rows from U.

• 5. Set $D = {{\,\mathrm{diag}\,}}(p_1, p_1 p_2, \ldots , p_{r-1} p_r)$.

• 6. Return $P_r$, L, D, U, and $P_c$.

The algorithm does not specify the choice of pivot in step 2a. Conventional wisdom (see, for example, Geddes et al. [11]) is that in exact algorithms choosing the smallest possible pivot (measured in a way suitable for $\mathbb {D}$) will lead to the smallest output sizes. We have been able to confirm this experimentally in Middeke and Jeffrey [18] for $\mathbb {D}= \mathbb {Z}$ where size was measured as the absolute value. In step 2c the divisions are guaranteed to be exact. Thus, an implementation can use more efficient procedures for this step if available (for example, for big integers using mpz_divexact in the gmp library which is based on Jebelean [14] instead of regular division).

One of the goals of the present paper is to discuss improvements to the decomposition explained above. Throughout this paper we shall use the term $L D^{-1} U$ decomposition to mean exactly the decomposition from Theorem 1 as computed by Algorithm 4. For the variations of this decomposition we introduce the following term:

Definition 5

(Fraction-Free LU Decomposition). For a matrix $A \in \mathbb {D}^{m\times n}$ of rank r we say that $A = P_r L D^{-1} U P_c$ is a fraction-free LU decomposition if $P_r \in \mathbb {D}^{m\times m}$ and $P_c \in \mathbb {D}^{n\times n}$ are permutation matrices, $L \in \mathbb {D}^{m\times r}$ has $L_{ij} = 0$ for $j > i$ and $L_{ii} \ne 0$ for all i, $U \in \mathbb {D}^{r\times n}$ has $U_{ij} = 0$ for $i > j$ and $U_{ii} \ne 0$ for all i, and $D \in \mathbb {D}^{r\times r}$ is a diagonal matrix (with full rank).

We will usually refer to matrices $L \in \mathbb {D}^{m\times r}$ with $L_{ij} = 0$ for $j > i$ and $L_{ii} \ne 0$ for all i as lower triangular and to matrices $U \in \mathbb {D}^{r\times n}$ with $U_{ij} = 0$ for $i > j$ and $U_{ii} \ne 0$ for all i as upper triangular even if they are not square.

As mentioned in the introduction, Algorithm 4 does result in common factors in the rows of the output U and the columns of L. In the following sections, we will explore methods to explain and predict those factors. The next result asserts that we can cancel all common factors which we find from the final output. This yields a fraction-free LU decomposition of A where the size of the entries of U (and L) are smaller than in the $L D^{-1} U$ decomposition.

Corollary 6

Given a matrix $A \in \mathbb {D}^{m\times n}$ with rank r and its standard $L D^{-1} U$ decomposition $A = P_c L D^{-1} U P_c$, if $D_U = {{\,\mathrm{diag}\,}}(d_1,\ldots ,d_r)$ is a diagonal matrix with $d_k \mid U_{k,*}$ for $k = 1, \ldots , n$, then setting $\hat{U} = D_U^{-1} U$ and $\hat{D} = D D_U^{-1}$ where both matrices are fraction-free we have the decomposition $A = P_c L \hat{D}^{-1} \hat{U} P_c$.

Proof

By Theorem 1, the diagonal entries of U are the pivots chosen during the decomposition and they also divide the diagonal entries of D. Thus, any common divisor of $U_{k,*}$ will also divide $D_{kk}$ and therefore both $\hat{U}$ and $\hat{D}$ are fraction-free. We can easily check that $A = P_c L D^{-1} D_U D_U^{-1} U = P_c L \hat{D}^{-1} \hat{U} P_c$. $\square$

Remark 7

If we predict common column factors of L we can cancel them in the same way. However, if we have already canceled factors from U, then there is no guarantee that $d \mid L_{*,k}$ implies $d \mid \hat{D}_{kk}$. Thus, in general we can only cancel $\gcd (d, \hat{D}_{kk})$ from $L_{*,k}$ (if $\mathbb {D}$ allows greatest common divisors). The same holds mutatis mutandis if we cancel the factors from L first.

It will be an interesting discussion for future research whether it is better to cancel as many factors as possible from U or to cancel them from L.

LU and the Smith–Jacobson Normal Form

This section explains a connection between “systematic factors” (that is, common factors which appear in the decomposition due to the algorithm being used) and the Smith–Jacobson normal form. For Smith’s normal form, see [5, 20], and for Jacobson’s generalization, see [22]. Given a matrix A over a principal ideal domain $\mathbb {D}$, we study the decomposition $A=P_rLD^{-1}UP_c$. For simplicity, from now on we consider the decomposition in the form $P_r^{-1} A P_c^{-1} = L D^{-1} U.$ The following theorem connecting the $LD^{-1}U$ decomposition with the Smith–Jacobson normal form can essentially be found in [2].

Theorem 8

Let the matrix $A \in \mathbb {D}^{n\times n}$ have the Smith–Jacobson normal form $S = {{\,\mathrm{diag}\,}}(d_1,\ldots ,d_n)$ where $d_1,\ldots ,d_n \in \mathbb {D}$. Moreover, let $A = L D^{-1} U$ be an $L D^{-1} U$ decomposition of A without permutations. Then for $k=1,\ldots ,n$

$$\begin{aligned} d_k^* = \prod _{j=1}^k d_j \mid U_{k,*} \quad \text {and}\quad d_k^* \mid L_{*,k}. \end{aligned}$$

Remark 9

The values $d_1^*, \ldots , d_n^*$ are known in the literature as the determinantal divisors of A.

Proof

The diagonal entries of the Smith–Jacobson normal form are quotients of the determinantal divisors [20, II.15], i. e., $d_1^* = d_1$ and $d_k = d^*_k/d^*_{k-1}$ for $k=2,\ldots ,n$. Moreover, $d_k^*$ is the greatest common divisor of all $k\times k$ minors of A for each $k=1,\ldots ,n$. The entries of U and L, however, are k-by-k minors of A, as displayed in (2.5) and (2.6). $\square$

From Theorem 8, we obtain the following result.

Corollary 10

The kth determinantal divisor $d_k^*$ can be removed from the kth row of U (since it divides $D_{k,k}$ by Theorem 6) and also $d_{k-1}^*$ can be removed from the kth column of L because $d_{k-1}^* \mid d_k^*$ and $d_j^*$ divides the jth pivot for $j = k-1,k$. Thus, $d_{k-1}^* d_k^* \mid D_{k,k}$.

We illustrate this with an example using the polynomials over the finite field with three elements as our domain $\mathbb {Z}_3[t]$. Let $A \in \mathbb {Z}_3[t]^{4\times 4}$ be the matrix

$$\begin{aligned} A = \begin{pmatrix} 2 t^{2} + t + 1 &{}\quad 0 &{}\quad t^{2} + 2 t &{}\quad 2 t^{3} + 2 t^{2} + 2 t + 2 \\ t^{3} + t^{2} + 2 t + 1 &{}\quad t^{2} &{}\quad 0 &{}\quad 2 t^{3} + t^{2} + 2 \\ t^{4} + t^{3} + t + 2 &{}\quad t^{3} + 2 t^{2} + t &{}\quad 2 t^{3} + t^{2} + t &{}\quad 2 t^{2} + t + 1 \\ 2 t &{}\quad t &{}\quad 2 t &{}\quad t^{2} + 2 t \end{pmatrix}. \end{aligned}$$

Computing the regular (that is, not fraction-free) LU decomposition yields $A = L_0 U_0$ where

$$\begin{aligned} L_0 = \begin{pmatrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ \frac{- t^{3} - t^{2} + t - 1}{t^{2} - t - 1} &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ \frac{- t^{4} - t^{3} - t + 1}{t^{2} - t - 1} &{}\quad \frac{t^{2} - t + 1}{t} &{}\quad 1 &{}\quad 0 \\ \frac{t}{t^{2} - t - 1} &{}\quad \frac{1}{t} &{}\quad \frac{t^{4} - t^{3} - t^{2} + t - 1}{t^{4} - t^{3} - t^{2} - 1} &{}\quad 1 \end{pmatrix} \end{aligned}$$

and

$$\begin{aligned} U_0 = \begin{pmatrix} - t^{2} + t + 1 &{}\quad 0 &{}\quad t^{2} - t &{}\quad -t^{3} - t^{2} - t - 1 \\ 0 &{}\quad t^{2} &{}\quad \frac{t^{5} + t^{3} - t^{2} - t}{t^{2} - t - 1} &{}\quad \frac{- t^{6} + t^{4} + t^{3} + t}{t^{2} - t - 1} \\ 0 &{}\quad 0 &{}\quad \frac{- t^{4} + t^{3} + t^{2} + 1}{t^{2} - t - 1} &{}\quad \frac{t^{5} - t^{4} + t^{3} - t^{2} - t - 1}{t^{2} - t - 1} \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \frac{t^{2} - t}{t^{4} - t^{3} - t^{2} - 1} \end{pmatrix}. \end{aligned}$$

On the other hand, the $L D^{-1} U$ decomposition for A is $A = L D^{-1} U$ where

$$\begin{aligned} L = \begin{pmatrix} - (t^2 - t - 1) &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ t^3 + t^2 - t + 1 &{}\quad - t^2 (t^2 - t - 1) &{}\quad 0 &{}\quad 0 \\ (t^2 + 1) (t^2 + t - 1) &{}\quad - t (t + 1)^2 (t^2 - t - 1) &{}\quad (t + 1) t^2 (t^3 + t^2 + t - 1) &{}\quad 0 \\ - t &{}\quad - t (t^2 - t - 1) &{}\quad t^2 (t^4 - t^3 - t^2 + t - 1) &{}\quad (t - 1) t^3 \end{pmatrix}, \end{aligned}$$

$$\begin{aligned} D= & {} {{\,\mathrm{diag}\,}}\bigl (- (t^2 - t - 1),\; t^2 (t^2 - t - 1)^2,\\&\quad - (t + 1) t^4 (t^2 - t - 1) (t^3 + t^2 + t - 1),\;(t + 1) (t - 1) t^5 (t^3 + t^2 + t - 1)\bigr ) \end{aligned}$$

and

$$\begin{aligned} U = \begin{pmatrix} - (t^2 - t - 1) &{}\quad 0 &{}\quad t (t - 1) &{}\quad - (t + 1) (t^2 + 1) \\ 0 &{}\quad - t^2 (t^2 - t - 1) &{}\quad - t (t - 1) (t^3 + t^2 - t + 1) &{}\quad t (t^5 - t^3 - t^2 - 1) \\ 0 &{}\quad 0 &{}\quad (t + 1) t^2 (t^3 + t^2 + t - 1) &{}\quad - t^2 (t^5 - t^4 + t^3 - t^2 - t - 1) \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad (t - 1) t^3 \end{pmatrix} \end{aligned}$$

(showing the entries completely factorised). The Smith–Jacobson normal form of A is

$$\begin{aligned} {{\,\mathrm{diag}\,}}\bigl (1, t, t, t (t-1)\bigr ); \end{aligned}$$

and thus the determinantal divisors are $d_1^* = 1$, $d_2^* = t$, $d_3^* = t^2$, and $d_4^* = t^3 (t-1)$. As we can see, $d_j^*$ does indeed divide the jth row of U and the jth column of L for $j=1,2,3,4$. Moreover, $d_1^* d_2^* = t$ divides $D_{2,2}$, $d_2^* d_3^* = t^3$ divides $D_{3,3}$, and $d_1^* d_2^* = t^5 (t-1)$ divides $D_{4,4}$.

Efficient Detection of Factors

When considering the output of Algorithm 4, we find an interesting relation between the entries of L and U which can be exploited in order to find “systematic” common factors in the $L D^{-1} U$ decomposition. Theorem 11 below predicts a divisor of the common factor in the kth row of U, by looking at just three entries of L. Likewise, we obtain a divisor of the common factor of the kth column of L from three entries of U. As in the previous section, let $\mathbb {D}$ be a principal ideal domain. We remark that for general principal ideal domains the theorem below is more of a theoretical result. Depending on the specific domain $\mathbb {D}$, actually computing the greatest common divisors might not be easy (or even possible). The theorem becomes algorithmic, if we restrict $\mathbb {D}$ to be (computable) Euclidean domain. For other domains, the statement is still valid; but it is left to the reader to check whether algorithms for computing greatest common divisors exist.

Theorem 11

Let $A\in \mathbb {D}^{m\times n}$ and let $P_r L D^{-1} U P_c$ be the $L D^{-1} U$ decomposition of A. Then

$$\begin{aligned} \Bigl . \frac{ \gcd (L_{k-1,k-1}, L_{k,k-1}) }{ \gcd (L_{k-1,k-1}, L_{k,k-1}, L_{k-2,k-2}) } \;\Bigm |\; {U}_{k,*} \Bigr . \end{aligned}$$

and

$$\begin{aligned} \Bigl . \frac{ \gcd (U_{k-1,k-1}, U_{k-1,k}) }{ \gcd (U_{k-1,k-1}, U_{k-1,k}, U_{k-2,k-2}) } \;\Bigm |\; {L}_{*,k} \Bigr . \end{aligned}$$

for $k=2,\ldots ,m-1$ (where we use $L_{0,0} = U_{0,0} = 1$ for $k = 2$).

Proof

Suppose that during Bareiss’s algorithm after $k-1$ iterations we have reached the following state

$$\begin{aligned} A^{(k-1)} = \begin{pmatrix} T &{}\quad \underline{*} &{}\quad \underline{*} &{}\quad {\varvec{*}}\\ \overline{0} &{}\quad p &{}\quad * &{}\quad \overline{*} \\ \overline{0} &{}\quad 0 &{}\quad a &{}\quad \overline{v} \\ \overline{0} &{}\quad 0 &{}\quad b &{}\quad \overline{w} \\ \mathbf {0} &{}\quad \underline{0} &{}\quad \underline{*} &{}\quad {\varvec{*}}\end{pmatrix}\ , \end{aligned}$$

where T is an upper triangular matrix, $p,a,b \in \mathbb {D}$, $\overline{v}, \overline{w} \in \mathbb {D}^{1\times n-k-1}$ and the other overlined quantities are row vectors and the underlined quantities are column vectors. Assume that $a \ne 0$ and that we choose it as a pivot. Continuing the computations we now eliminate b (and the entries below) by cross-multiplication

$$\begin{aligned} A^{(k-1)} \leadsto \begin{pmatrix} T &{}{}\quad \underline{*} &{}{}\quad \underline{*} &{}{}\quad {\varvec{*}}\\ \overline{0} &{}{}\quad p &{}{}\quad * &{}{}\quad \overline{*} \\ \overline{0} &{}{}\quad 0 &{}{}\quad a &{}{}\quad \overline{v} \\ \overline{0} &{}{}\quad 0 &{}{}\quad 0 &{}{}\quad a\overline{w} - b\overline{v} \\ \mathbf {0} &{}{}\quad \underline{0} &{}{}\quad \underline{0} &{}{}\quad {\varvec{*}}\end{pmatrix}. \end{aligned}$$

Here, we can see that any common factor of a and b will be a factor of every entry in that row, i. e., $\gcd (a,b) \mid a\overline{w} - b\overline{v}$. However, we still have to carry out the exact division step. This leads to

$$\begin{aligned} A^{(k-1)} \leadsto \begin{pmatrix} T &{}\quad \underline{*} &{}\quad \underline{*} &{}\quad {\varvec{*}}\\ \overline{0} &{}\quad p &{}\quad * &{}\quad \overline{*} \\ \overline{0} &{}\quad 0 &{}\quad a &{}\quad \overline{v} \\ \overline{0} &{}\quad 0 &{}\quad 0 &{}\quad \frac{1}{p}(a\overline{w} - b\overline{v}) \\ \mathbf {0} &{}\quad \underline{0} &{}\quad \underline{0} &{}\quad {\varvec{*}}\end{pmatrix} = A^{(k)}. \end{aligned}$$

The division by p is exact. Some of the factors in p might be factors of a or b while others are hidden in $\overline{v}$ or $\overline{w}$. However, every common factor of a and b which is not also a factor of p will still be a common factor of the resulting row. In other words,

$$\begin{aligned} \Bigl . \frac{\gcd (a,b)}{\gcd (a,b,p)} \;\Bigm |\; \frac{1}{p}(a\overline{w} - b\overline{v}) \Bigr .. \end{aligned}$$

In fact, the factors do not need to be tracked during the $L D^{-1} U$ reduction but can be computed afterwards: All the necessary entries a, b and p of $A^{(k-1)}$ will end up as entries of L. More precisely, we shall have $p = L_{k-2,k-2}$, $a = L_{k-1,k-1}$ and $b = L_{k,k-1}$.

Similar reasoning can be used to predict common factors in the columns of L. Here, we have to take into account that the columns of L are made up from entries in U during each iteration of the computation. $\square$

As a typical example consider the matrix

$$\begin{aligned} A = \begin{pmatrix} 8 &{}\quad 49 &{}\quad 45 &{}\quad -77 &{}\quad 66 \\ -10 &{}\quad -77 &{}\quad -19 &{}\quad -52 &{}\quad 48 \\ 51 &{}\quad 18 &{}\quad -81 &{}\quad 31 &{}\quad 69 \\ -97 &{}\quad -58 &{}\quad 37 &{}\quad 41 &{}\quad 22 \\ -60 &{}\quad 0 &{}\quad -25 &{}\quad -18 &{}\quad -92 \end{pmatrix}. \end{aligned}$$

This matrix has a $L D^{-1} U$ decomposition with

$$\begin{aligned} L = \begin{pmatrix} 8 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ -10 &{}\quad -126 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 51 &{}\quad -2355 &{}\quad 134076 &{}\quad 0 &{}\quad 0 \\ -97 &{}\quad 4289 &{}\quad -233176 &{}\quad -28490930 &{}\quad 0 \\ -60 &{}\quad 2940 &{}\quad -148890 &{}\quad -53377713 &{}\quad 11988124645 \end{pmatrix} \end{aligned}$$

and with

$$\begin{aligned} U = \begin{pmatrix} 8 &{}\quad 49 &{}\quad 45 &{}\quad -77 &{}\quad 66 \\ 0 &{}\quad -126 &{}\quad 298 &{}\quad -1186 &{}\quad 1044 \\ 0 &{}\quad 0 &{}\quad 134076 &{}\quad -414885 &{}\quad 351648 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad -28490930 &{}\quad 55072620 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 11988124645 \end{pmatrix}. \end{aligned}$$

Note that in this example pivoting is not needed, i.e., we have $P_r = P_c = {\mathbf {1}}$. The method outlined in Theorem 11 correctly predicts the common factor 2 in the second row of U, the factor 3 in the third row and the factor 2 in the fourth row. However, it does not detect the additional factor 5 in the fourth row of U.

The example also provides an illustration of the proof of Theorem 8: The entry $-414885$ of U at position (3, 4) is given by the determinant of the submatrix

$$\begin{aligned} \begin{pmatrix} 8 &{}\quad 49 &{}\quad -77 \\ -10 &{}\quad -77 &{}\quad -52 \\ 51 &{}\quad 18 &{}\quad 31 \\ \end{pmatrix} \end{aligned}$$

consisting of the first three rows and columns 1, 2 and 4 of A. In this particular example, however, the Smith–Jacobson normal form of the matrix A is ${{\,\mathrm{diag}\,}}(1,1,1,1,11988124645)$ which does not yield any information about the common factors.

Given Theorem 11, one can ask how good this prediction actually is. Concentrating on the case of integer matrices, the following Theorem 12 shows that with this prediction we do find a common factor in roughly a quarter of all rows. Experimental data suggest a similar behavior for matrices containing polynomials in $\mathbb {F}_p[x]$ where p is prime. Moreover, these experiments also showed that the prediction was able to account for $40.17\%$ of all the common prime factors (counted with multiplicity) in the rows of U.⁴

Theorem 12

For random integers $a,b,p \in \mathbb {Z}$ the probability that the formula in Theorem 11 predicts a non-trivial common factor is

$$\begin{aligned} \mathrm {P}\Bigl (\frac{\gcd (a,b)}{\gcd (p,a,b)} \ne 1\Bigr ) = 6 \frac{\zeta (3)}{\pi ^2} \approx 26.92\%. \end{aligned}$$

Proof

The following calculation is due to Hare [13] and Winterhof [25]: First note that the probability that $\gcd (a,b) = n$ is $1/n^2$ times the probability that $\gcd (a,b) = 1$. Summing up all of these probabilities gives

$$\begin{aligned} \sum _{n=1}^\infty \mathrm {P}\bigl (\gcd (a,b) = n\bigr ) = \sum _{n=1}^\infty \frac{1}{n^2} \mathrm {P}\bigl (\gcd (a,b) = 1\bigr ) = \mathrm {P}\bigl (\gcd (a,b) = 1\bigr ) \frac{\pi ^2}{6}. \end{aligned}$$

As this sum must be 1, this gives that the $\mathrm {P}\bigl (\gcd (a,b) = 1\bigr ) = 6/\pi ^2$, and the $\mathrm {P}\bigl (\gcd (a,b) = n\bigr ) = 6/(\pi ^2 n^2)$. Given that $\gcd (a,b) = n$, the probability that $n \mid c$ is 1/n. So the probability that $\gcd (a,b) = n$ and that $\gcd (p,a,b) = n$ is $6/(\pi ^2 n^3)$. So $\mathrm {P}\bigl (\gcd (a,b)/\gcd (p,a,b) = 1\bigr )$ is

$$\begin{aligned} \sum _{n=1}^\infty \mathrm {P}\bigl (\gcd (a,b) = n \text { and } \gcd (p,a,b) = n\bigr ) = \sum _{n=1}^\infty \frac{6}{\pi ^2 n^3} = 6 \frac{\zeta (3)}{\pi ^2}. \end{aligned}$$

$\square$

There is another way in which common factors in integer matrices can arise. Let d be any number. Then for random a, b the probability that $d \mid a+b$ is 1/d. That means that if $v,w \in \mathbb {Z}^{1\times n}$ are vectors, then $d \mid v + w$ with a probability of $1/d^n$. This effect is noticeable in particular for small numbers like $d = 2,3$ and in the last iterations of the $L D^{-1} U$ decomposition when the number of non-zero entries in the rows has shrunk. For instance, in the second last iterations we only have three rows with at most three non-zero entries each. Moreover, we know that the first non-zero entries of the rows cancel during cross-multiplication. Thus, a factor of 2 appears with a probability of $25\%$ in one of those rows, a factor of 3 with a probability of $11.11\%$. In the example above, the probability for the factor 5 to appear in the fourth row was $4\%$.

Expected Number of Factors

In this section, we provide a detailed analysis of the expected number of common “statistical” factors in the rows of U, in the case when the input matrix A has integer entries, that is, $\mathbb {D}=\mathbb {Z}$. We base our considerations on a “uniform” distribution on $\mathbb {Z}$, e.g., by imposing a uniform distribution on $\{-n,\dots ,n\}$ for very large n. However, the only relevant property that we use is the assumption that the probability that a randomly chosen integer is divisible by p is 1/p.

We consider a matrix $A=(A_{i,j})_{1\le i,j\le n}\in \mathbb {Z}^{n\times n}$ of full rank. The assumption that A be square is made for the sake of simplicity; the results shown below immediately generalize to rectangular matrices. As before, let U be the upper triangular matrix from the $LD^{-1}U$ decomposition of A:

$$\begin{aligned} U = \begin{pmatrix} U_{1,1} &{}\quad U_{1,2} &{}\quad \dots &{}\quad U_{1,n} \\ 0 &{}\quad U_{2,2} &{}\quad \dots &{}\quad U_{2,n} \\ \vdots &{}\quad &{}\quad \ddots &{}\quad \vdots \\ 0 &{}\quad \dots &{}\quad &{}\quad U_{n,n} \end{pmatrix}. \end{aligned}$$

Define

$$\begin{aligned} g_k := \gcd (U_{k,k},U_{k,k+1},\dots ,U_{k,n}) \end{aligned}$$

to be the greatest common divisor of all entries in the kth row of U. Counting (with multiplicities) all the prime factors of $g_1,\dots ,g_{n-1}$, one gets the plot that is shown in Fig. 1; $g_n$ is omitted as it contains only the single nonzero entry $U_{n,n}=\det (A)$. Our goal is to give a probabilistic explanation for the occurrence of these common factors, whose number seems to grow linearly with the dimension of the matrix.

As we have seen in the proof of Theorem 8, the entries $U_{k,\ell }$ can be expressed as minors of the original matrix A:

$$\begin{aligned} U_{k,\ell } = \det \begin{pmatrix} A_{1,1} &{}\quad A_{1,2} &{}\quad \dots &{}\quad A_{1,k-1} &{}\quad A_{1,\ell } \\ A_{2,1} &{}\quad A_{2,2} &{}\quad \dots &{}\quad A_{2,k-1} &{}\quad A_{2,\ell } \\ \vdots &{}\quad \vdots &{}\quad &{}\quad \vdots &{}\quad \vdots \\ A_{k,1} &{}\quad A_{k,2} &{}\quad \dots &{}\quad A_{k,k-1} &{}\quad A_{k,\ell } \end{pmatrix}. \end{aligned}$$

Observe that the entries $U_{k,\ell }$ in the kth row of U are all given as determinants of the same matrix, where only the last column varies. For any integer $q\ge 2$ we have that $q\mid g_k$ if q divides all these determinants. A sufficient condition for the latter to happen is that the determinant

$$\begin{aligned} h_k := \det \begin{pmatrix} A_{1,1} &{}\quad \dots &{}\quad A_{1,k-1} &{}\quad 1 \\ A_{2,1} &{}\quad \dots &{}\quad A_{2,k-1} &{}\quad x \\ \vdots &{}\quad \vdots &{}\quad &{}\quad \vdots \\ A_{k,1} &{}\quad \dots &{}\quad A_{k,k-1} &{}\quad x^{k-1} \end{pmatrix} \end{aligned}$$

is divisible by q as a polynomial in $\mathbb {Z}[x]$, i.e., if q divides the content of the polynomial $h_k$. We now aim at computing how likely it is that $q\mid h_k$ when q is fixed and when the matrix entries $A_{1,1},\dots ,A_{k,k-1}$ are chosen randomly. Since q is now fixed, we can equivalently study this problem over the finite ring $\mathbb {Z}_q$, which means that the matrix entries are picked randomly and uniformly from the finite set $\{0,\dots ,q-1\}$. Moreover, it turns out that it suffices to answer this question for prime powers $q=p^j$.

The probability that all $k\times k$-minors of a randomly chosen $k\times (k+1)$-matrix are divisible by $p^j$, where p is a prime number and $j\ge 1$ is an integer, is given by

$$\begin{aligned} P_{p,j,k} := 1-\Bigl (1+p^{1-j-k}\,\frac{p^k-1}{p-1}\Bigr )\prod _{i=0}^{k-1}\bigl (1-p^{-j-i}\bigr ), \end{aligned}$$

which is a special case of Brent and McKay [3, Thm. 2.1]. Note that this is exactly the probability that $h_{k+1}$ is divisible by $p^j$. Recalling the definition of the q-Pochhammer symbol

$$\begin{aligned} (a;q)_k := \prod _{i=0}^{k-1} (1-aq^i),\quad (a;q)_0 := 1, \end{aligned}$$

the above formula can be written more succinctly as

$$\begin{aligned} P_{p,j,k} := 1-\Bigl (1+p^{1-j-k}\,\frac{p^k-1}{p-1}\Bigr )\Bigl (\frac{1}{p^j};\frac{1}{p}\Bigr )_k. \end{aligned}$$

Now, an interesting observation is that this probability does not, as one could expect, tend to zero as k goes to infinity. Instead, it approaches a nonzero constant that depends on p and j (see Table 1):

$$\begin{aligned} P_{p,j,\infty } := \lim _{k\rightarrow \infty } P_{p,j,k} = 1-\Bigl (1+\frac{p^{1-j}}{p-1}\Bigr )\Bigl (\frac{1}{p^j};\frac{1}{p}\Bigr )_\infty \end{aligned}$$

Table 1 Behavior of the sequence $\bigl (P_{p,j,k}\bigr ){}_{k\in \mathbb {N}}$ for some small values of $p^j$

Using the probability $P_{p,j,k}$, one can write down the expected number of factors in the determinant $h_{k+1}$, i.e., the number of prime factors in the content of the polynomial $h_{k+1}$, counted with multiplicities:

$$\begin{aligned} \sum _{p\in \mathbb {P} }\sum _{j=1}^\infty P_{p,j,k}, \end{aligned}$$

where $\mathbb {P} =\{2,3,5,\dots \}$ denotes the set of prime numbers. The inner sum can be simplified as follows, yielding the expected multiplicity $M_{p,k}$ of a prime factor p in $h_{k+1}$:

$$\begin{aligned} M_{p,k} := \sum _{j=1}^\infty P_{p,j,k}= & {} \sum _{j=1}^\infty \biggl (1-\Bigl (1+p^{1-j-k}\,\frac{p^k-1}{p-1}\Bigr )\Bigl (\frac{1}{p^j};\frac{1}{p}\Bigr )_{\!k}\biggr ) \\= & {} -\sum _{j=1}^\infty \biggl (\Bigl (\frac{1}{p^j};\frac{1}{p}\Bigr )_{\!k}-1\biggr )-p^{1-k}\frac{p^k-1}{p-1}\sum _{j=1}^\infty \frac{1}{p^j}\Bigl (\frac{1}{p^j};\frac{1}{p}\Bigr )_{\!k} \\= & {} -\sum _{j=1}^\infty \sum _{i=1}^k (-1)^i p^{-ij-i(i-1)/2} \left[ \begin{array}{l} {k} \\ {i} \end{array} \right] _{1/p}\! -p^{1-k}\,\frac{p^k-1}{p-1} \frac{p^k}{p^{k+1}-1} \\= & {} \sum _{i=1}^k \frac{(-1)^{i-1}}{p^{i(i-1)/2}(p^i-1)} \left[ \begin{array}{l} {k} \\ {i} \end{array} \right] _{1/p} \! + \frac{1}{p^{k+1}-1} - \frac{1}{p-1} \end{aligned}$$

In this derivation we have used the expansion formula of the q-Pochhammer symbol in terms of the q-binomial coefficient

$$\begin{aligned} \left[ \begin{array}{l} {n}\\ {k} \end{array} \right] _{q} := \frac{\bigl (1-q^n\bigr )\bigl (1-q^{n-1}\bigr )\cdots \bigl (1-q^{n-k+1}\bigr )}{\bigl (1-q^k\bigr )\bigl (1-q^{k-1}\bigr )\cdots \bigl (1-q\bigr )}, \end{aligned}$$

evaluated at $q=1/p$. Moreover, the identity that is used in the third step,

$$\begin{aligned} \sum _{j=1}^\infty \frac{1}{p^j}\Bigl (\frac{1}{p^j};\frac{1}{p}\Bigr )_{\!k} = \frac{p^k}{p^{k+1}-1}, \end{aligned}$$

is certified by rewriting the summand as

$$\begin{aligned} \frac{1}{p^j}\Bigl (\frac{1}{p^j};\frac{1}{p}\Bigr )_{\!k} = t_{j+1} - t_j \quad \text {with}\quad t_j = \frac{p^k(p^{1-j}-1)}{p^{k+1}-1}\Bigl (\frac{1}{p^j};\frac{1}{p}\Bigr )_{\!k} \end{aligned}$$

and by applying a telescoping argument.

Hence, when we let k go to infinity, we obtain

$$\begin{aligned} M_{p,\infty } = \lim _{k\rightarrow \infty } \sum _{j=1}^\infty P_{p,j,k} = \sum _{i=1}^\infty \frac{(-1)^{i-1}}{p^{i(i-1)/2}(p^i-1)} \frac{\bigl (p^{-i-1};p^{-1}\bigr )_\infty }{\bigl (p^{-1};p^{-1}\bigr )_\infty } - \frac{1}{p-1}. \end{aligned}$$

Note that the sum converges quickly, so that one can use the above formula to compute an approximation for the expected number of factors in $h_{k+1}$ when k tends to infinity

$$\begin{aligned} \sum _{p\in \mathbb {P} } M_{p,\infty } \approx 0.89764, \end{aligned}$$

which gives the asymptotic slope of the function plotted in Figure 1.

As discussed before, the divisibility of $h_k$ by some number $q\ge 2$ implies that the greatest common divisor $g_k$ of the kth row is divisible by q, but this is not a necessary condition. It may happen that $h_k$ is not divisible by q, but nevertheless q divides each $U_{k,\ell }$ for $k\le \ell \le n$. The probability for this to happen is the same as the probability that the greatest common divisor of $n-k+1$ randomly chosen integers is divisible by q. The latter obviously is $q^{-(n-k+1)}$. Thus, in addition to the factors coming from $h_k$, one can expect

$$\begin{aligned} \sum _{p\in \mathbb {P} }\sum _{j=1}^\infty \frac{1}{p^{j(n-k+1)}} = \sum _{p\in \mathbb {P}}\frac{1}{p^{n-k+1}-1} \end{aligned}$$

many prime factors in $g_k$.

Fig. 1

Number of factors depending on the size n of the matrix. The curve shows the function F(n), while the dots represent experimental data: for each dimension n, 1000 matrices were generated with random integer entries between 0 and $10^9$

Summarizing, the expected number of prime factors in the rows of the matrix U is

$$\begin{aligned} F(n)= & {} {} \sum _{k=2}^{n-1} \sum _{p\in \mathbb {P} } M_{p,k-1} + \sum _{k=1}^{n-1} \sum _{p\in \mathbb {P} } \frac{1}{p^{n-k+1}-1} \\ {}= & {} {} \sum _{p\in \mathbb {P} } \biggl (\sum _{k=0}^{n-2}M_{p,k} + \sum _{k=0}^{n-2} \frac{1}{p^{k+2}-1} \biggr ) \\ {}= & {} {} \sum _{p\in \mathbb {P} } \sum _{k=0}^{n-2} \biggl (\sum _{i=1}^k \frac{(-1)^{i-1}}{p^{i(i-1)/2}(p^i-1)} \left[ \begin{array}{l} {k} \\ {i} \end{array} \right] _{1/p}\!+ \frac{1}{p^{k+2}-1} + \frac{1}{p^{k+1}-1} - \frac{1}{p-1}\biggr ). \end{aligned}$$

From the discussion above, it follows that for large n this expected number can be approximated by a linear function as follows:

$$\begin{aligned} F(n) \approx 0.89764\,n - 1.53206. \end{aligned}$$

QR Decomposition

The QR decomposition of a matrix A is defined by $A=QR$, where Q is an orthonormal matrix and R is an upper triangular matrix. In its standard form, this decomposition requires algebraic extensions to the domain of A, but a fraction-free form is possible. The modified form given in [26] is $QD^{-1}R$, and is proved below in Theorem 15. In [10], an exact-division algorithm for a fraction-free Gram-Schmidt orthogonal basis for the columns of a matrix A was given, but a complete fraction-free decomposition was not considered. We now show that the algorithms in [10] and in [26] both lead to a systematic common factor in their results. We begin by considering a fraction-free form of the Cholesky decomposition of a symmetric matrix. See [23, Eqn (3.70)] for a description of the standard form, which requires algebraic extensions to allow for square roots, but which are avoided here.

This section assumes that $\mathbb {D}$ has characteristic 0; this assumption is needed in order to ensure that $A^t A$ has full rank.

Lemma 13

Let $A \in \mathbb {D}^{n\times n}$ be a symmetric matrix such that its $L D^{-1} U$ decomposition can be computed without permutations; then we have $U = L^t$, that is,

$$\begin{aligned} A = L D^{-1} L^t. \end{aligned}$$

Proof

Compute the decomposition $A = L D^{-1} U$ as in Theorem 1. If we do not execute item 4 of Algorithm 4, we obtain the decomposition

$$\begin{aligned} A = \tilde{L} \tilde{D}^{-1} \tilde{U} = \begin{pmatrix} \mathcal {L} &{}\quad {\mathbf {0}} \\ \mathcal {M} &{}\quad {\mathbf {1}} \end{pmatrix} \begin{pmatrix} D &{}\quad {\mathbf {0}} \\ {\mathbf {0}} &{}\quad {\mathbf {1}} \end{pmatrix}^{-1} \begin{pmatrix} \mathcal {U} &{}\quad \mathcal {V} \\ {\mathbf {0}} &{}\quad {\mathbf {0}} \end{pmatrix}. \end{aligned}$$

Then because A is symmetric, we obtain

$$\begin{aligned} \tilde{L} \tilde{D}^{-1} \tilde{U} = A = A^t = \tilde{U}^t \tilde{D}^{-1} \tilde{L}^t \end{aligned}$$

The matrices $\tilde{L}$ and $\tilde{D}$ have full rank which implies

$$\begin{aligned} \tilde{U} (\tilde{L}^t)^{-1} \tilde{D} = \tilde{D} \tilde{L}^{-1} \tilde{U}^t. \end{aligned}$$

Examination of the matrices on the left hand side reveals that they are all upper triangular. Therefore also their product is an upper triangular matrix. Similarly, the right hand side is a lower triangular matrix and the equality of the two implies that they must both be diagonal. Cancelling $\tilde{D}$ and rearranging the equation yields $\tilde{U} = (\tilde{L}^{-1} \tilde{U}^t) \tilde{L}^t$ where $\tilde{L}^{-1} \tilde{U}^t$ is diagonal. This shows that the rows of $\tilde{U}$ are just multiples of the rows of $\tilde{L}^t$. However, we know that the first r diagonal entries of $\tilde{U}$ and $\tilde{L}$ are the same, where r is the rank of $\tilde{U}$. This yields

$$\begin{aligned} \tilde{L}^{-1} \tilde{U}^t = \begin{pmatrix} {\mathbf {1}}_{r} &{}\quad {\mathbf {0}} \\ {\mathbf {0}} &{}\quad {\mathbf {0}} \end{pmatrix}, \end{aligned}$$

and hence, when we remove the unnecessary last $n-r$ rows of $\tilde{U}$ and the last $n-r$ columns of $\tilde{L}$ (as suggested in Jeffrey [15]), we remain with $U = L^t$. $\square$

As another preliminary to the main theorem, we need to delve briefly into matrices over ordered rings. Following, for example, the definition in [6, Sect. 8.6] an ordered ring is a (commutative) ring $\mathbb {D}$ with a strict total order > such that $x > x'$ together with $y > y'$ implies $x + y > x' + y'$ and also $x > 0$ together with $y > 0$ implies $x y > 0$ for all $x, x', y, y' \in \mathbb {D}$. As Cohn [6, Prop. 8.6.1] shows, such a ring must always be a domain, and squares of non-zero elements are always positive. Thus, the inner product of two vectors $a, b \in \mathbb {D}^{m}$ defined by $(a,b) \mapsto a^t \,b$ must be positive definite. This implies that given a matrix $A \in \mathbb {D}^{m\times n}$ the Gram matrix $A^t A$ is positive semi-definite. If we additionally require the columns of A to be linearly independent, then $A^t A$ becomes positive definite.

Lemma 14

Let $\mathbb {D}$ be an ordered domain and let $A \in \mathbb {D}^{n\times n}$ be a symmetric and positive definite matrix. Then the $L D^{-1} U$ decomposition of A can be computed without using permutations.

Proof

By Sylvester’s criterion (see Theorem 22 in the “Appendix”) a symmetric matrix is positive definite if and only if its leading principal minors are positive. However, by Remark 2 and Equation 2.1, these are precisely the pivots that are used during Bareiss’s algorithm. Hence, permutations are not necessary. $\square$

If we consider domains which are not ordered, then the $L D^{-1} U$ decomposition of $A^t A$ will usually require permutations: Consider, for example, the Gaussian integers $\mathbb {D}= \mathbb {Z}[i]$ and the matrix

$$\begin{aligned} A = \begin{pmatrix} 1 &{}\quad i \\ i &{}\quad 0 \end{pmatrix}. \end{aligned}$$

Then

$$\begin{aligned} A^t A = \begin{pmatrix} 0 &{}\quad i \\ i &{}\quad -1 \end{pmatrix}; \end{aligned}$$

and Bareiss’s algorithm must begin with a row or column permutation⁵.

We are now ready to discuss the fraction-free QR decomposition. The theorem below makes two major changes to Zhou and Jeffrey [26, Thm. 8]: first, we add that $\Theta ^t \Theta$ is not just any diagonal matrix but actually equal to D. Secondly, the original theorem did not require the domain $\mathbb {D}$ to be ordered, which means that the proof cannot work.

Theorem 15

Let $A \in \mathbb {D}^{m\times n}$ with $n\le m$ and with full column rank where $\mathbb {D}$ is an ordered domain. Then the partitioned matrix $(A^t A \mid A^t)$ has $LD^{-1}U$ decomposition

$$\begin{aligned} (A^t A \mid A^t) = R^t D^{-1} (R \mid \Theta ^t), \end{aligned}$$

where $\Theta ^t \Theta = D$ and $A = \Theta D^{-1} R$.

Proof

By Lemma 14, we can compute an $L D^{-1} U$ decomposition of $A^t A$ without using permutations; and by Theorem 13, the decomposition must have the shape

$$\begin{aligned} A^t A = R^t D^{-1} R. \end{aligned}$$

Applying the same row transformations to $A^t$ yields a matrix $\Theta ^t$, that is, we obtain $(A^t A \mid A^t) = R^t D^{-1} (R \mid \Theta ^t).$ As in the proof of Zhou and Jeffrey [26, Thm. 8], we easily compute that $A = \Theta D^{-1} R$ and that $\Theta ^t \Theta = D^t (R^{-1})^t A^t A R^{-1} D = D^t (R^{-1})^t R^t D^{-1} R R^{-1} D = D.$ $\square$

For example, let $A\in \mathbb {Z}[x]^{3\times 3}$ be the matrix

$$\begin{aligned} A=\begin{pmatrix} x &{}\quad 1 &{}\quad 2 \\ 2 &{}\quad 0 &{}\quad -x \\ x &{}\quad 1 &{}\quad x + 1 \end{pmatrix}. \end{aligned}$$

Then the $LD^{-1}U$ decomposition of $A^tA=R^tD^{-1}R$ is given by

$$\begin{aligned} R= & {} \begin{pmatrix} 2 (x^2+2) &{}\quad 2 x &{}\quad x (x+1) \\ 0 &{}\quad 8 &{}\quad 4 (x^2+x+3) \\ 0 &{}\quad 0 &{}\quad 4 (x-1)^2 \end{pmatrix},\\ D= & {} \begin{pmatrix} 2 (x^2+2) &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 16 (x^2+2) &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 32 (x-1)^2 \end{pmatrix}, \end{aligned}$$

and we obtain for the QR decomposition $A = \Theta D^{-1} R$:

$$\begin{aligned} \Theta = \begin{pmatrix} x &{}\quad 4 &{}\quad -4 (x-1) \\ 2 &{}\quad -4 x &{}\quad 0 \\ x &{}\quad 4 &{}\quad 4 (x-1) \end{pmatrix}. \end{aligned}$$

We see that the $\Theta D^{-1} R$ decomposition has some common factor in the last column of $\Theta$. This observation is explained by the following theorem.

Theorem 16

With full-rank $A \in \mathbb {D}^{n\times n}$ and $\Theta$ as in Theorem 15, we have for all $i=1,\ldots ,n$ that

$$\begin{aligned} \Theta _{in} = (-1)^{n+i} \det \limits _{i,n} A \cdot \det A \end{aligned}$$

where $\det _{i,n}A$ is the (i, n) minor of A.

Proof

We use the notation from the proof of Theorem 15. From $\Theta D^{-1} R = A$ and $\Theta ^t \Theta =D$ we obtain

$$\begin{aligned} \Theta ^t A = \Theta ^t \Theta D^{-1} R = R. \end{aligned}$$

Thus, since A has full rank, $\Theta ^t = R A^{-1}$ or, equivalently,

$$\begin{aligned} \Theta = (R A^{-1})^t = (A^{-1})^t R^t = (\det A)^{-1} ({\text {adj}} A)^t R^t \end{aligned}$$

where ${\text {adj}} A$ is the adjoint matrix of A. Since $R^t$ is a lower triangular matrix with $\det A^t A = (\det A)^2$ at position (n, n), the claim follows. $\square$

For the other columns of $\Theta$ we can state the following.

Theorem 17

The kth determinantal divisor $d_k^*$ of A divides the kth column of $\Theta$ and the kth row of R. Moreover, $d_{k-1}^* d_k^*$ divides $D_{k,k}$ for $k \ge 2$.

Proof

We first show that the kth determinantal divisor $\delta _k^*$ of $(A^t A \mid A^t)$ is the same as $d_k^*$. Obviously, $\delta _k^* \mid d_k^*$ since all minors of A are also minors of the right block $A^t$ of $(A^t A \mid A^t)$. Consider now the left block $A^t A$. We have by the Cauchy–Binet theorem [4, § 4.6]

$$\begin{aligned} \det \limits _{I,J} (A^t A) = \sum _{\genfrac{}{}{0.0pt}{}{K \subseteq \{1,\ldots ,n\}}{|K| = q}} (\det \limits _{K,I} A) (\det \limits _{K,J} A) \end{aligned}$$

where $I, J \subseteq \{1,\ldots ,n\}$ with $|I| = |J| = q \ge 1$ are two index sets and $\det _{I,J} M$ denotes the minor for these index sets of a matrix M. Thus, $(d_k^*)^2$ divides any minor of $A^t A$ since it divides every summand on the right hand side; and we see that $d_k^* \mid \delta _k^*$.

Now, we use Theorems 15 and 8 to conclude that $d_k^*$ divides the kth row of $(R \mid \Theta ^t)$ and hence the kth row of R and the kth column of $\Theta$. Moreover, $D_{k,k} = R_{k-1,k-1} R_{k,k}$ for $k \ge 2$ by Theorem 1 which implies $d_{k-1}^* d_k^* \mid D_{k,k}$. $\square$

Knowing that there is always a common factor, we can cancel it, which leads to a fraction-free QR decomposition of smaller size.

Theorem 18

For a square matrix A, a reduced fraction-free QR decomposition is $A=\hat{\Theta }\hat{D}^{-1}\hat{R}$, where $S={\text {diag}}(1,1,\ldots ,\det A)$ and $\hat{\Theta }= \Theta S^{-1}$, and $\hat{R}=S^{-1}R$. In addition, $\hat{D}=S^{-1}DS^{-1}=\hat{\Theta }^t \hat{\Theta }$.

Proof

By Theorem 16, $\Theta S^{-1}$ is an exact division. The statement of the theorem then follows from $A=\Theta S^{-1} S D^{-1} S S^{-1} R$. $\square$

If we apply Theorem 18 to our previous example, we obtain the simpler QR decomposition, where the factor $\det A=-2(x-1)$ has been removed.

$$\begin{aligned} \begin{pmatrix} x &{}\quad 4 &{}\quad 2 \\ 2 &{}\quad -4 x &{} 0 \\ x &{}\quad 4 &{}\quad -2 \end{pmatrix}\; \begin{pmatrix} 2 (x^2+2) &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 16 (x^2+2) &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 8 \end{pmatrix}^{\!-1} \begin{pmatrix} 2 (x^2+2) &{}\quad 2 x &{}\quad x (x+1) \\ 0 &{}\quad 8 &{}\quad 4 (x^2+x+3) \\ 0 &{}\quad 0 &{}\quad -2 (x-1) \end{pmatrix}. \end{aligned}$$

The properties of the QR-decomposition are strong enough to guarantee a certain uniqueness of the output.

Theorem 19

Let $A \in \mathbb {D}^{n\times n}$ have full rank. Let $A = \Theta D^{-1} R$ the decomposition from Theorem 15; and let $A = \tilde{\Theta } \tilde{D}^{-1} \tilde{R}$ be another decomposition where $\tilde{\Theta }, \tilde{D}, \tilde{R} \in \mathbb {D}^{n\times n}$ are such that $\tilde{D}$ is a diagonal matrix, $\tilde{R}$ is an upper triangular matrix and $\Delta = \tilde{\Theta }^t \tilde{\Theta }$ is a diagonal matrix. Then $\Theta ^t \tilde{\Theta }$ is also a diagonal matrix and $\tilde{R} = (\Theta ^t \tilde{\Theta })^{-1} \tilde{D} R$.

Proof

We have

$$\begin{aligned} \tilde{\Theta } \tilde{D}^{-1} \tilde{R} = \Theta D^{-1} R \qquad \text {and thus}\qquad \Theta ^t \tilde{\Theta } \tilde{D}^{-1} \tilde{R} = \Theta ^t \Theta D^{-1} R = R. \end{aligned}$$

Since R and $\tilde{R}$ have full rank, this is equivalent to

$$\begin{aligned} \Theta ^t \tilde{\Theta } = R \tilde{R}^{-1} \tilde{D}. \end{aligned}$$

Note that all the matrices on the right hand side are upper triangular. Similarly, we can compute that

$$\begin{aligned} \tilde{\Theta }^t \Theta D^{-1} R = \tilde{\Theta }^t \tilde{\Theta } \tilde{D}^{-1} \tilde{R} = \Delta \tilde{D}^{-1} \tilde{R} \end{aligned}$$

which implies $\tilde{\Theta }^t \Theta = \Delta \tilde{D}^{-1} \tilde{R} R^{-1} D.$ Hence, also $\tilde{\Theta }^t \Theta = (\Theta ^t \tilde{\Theta })^t$ is upper triangular and consequently $\tilde{\Theta }^t \Theta = T$ for some diagonal matrix T with entries from $\mathbb {D}$. We obtain $R = T \tilde{D}^{-1} \tilde{R}$ and thus $\tilde{R} = T^{-1} \tilde{D} R$. $\square$

Appendix: Sylvester’s Criterion

We include a version of Sylvester’s Criterion for ordered domains $\mathbb {D}$. The proof is by Morrow [19]; but we repeat it for the convenience of the reader. We note that by Cohn [6, Thm. 8.6.2], the ordering of $\mathbb {D}$ can be extended to an ordering of the field of fractions $\mathbb {F}$ of $\mathbb {D}$ in just one way. Thus, we are able to use $\mathbb {F}$ in the proof. Of course, if we can show that the result holds over $\mathbb {F}$, then it will in particular also hold over $\mathbb {D}$.

We preface the proof of Sylvester’s criterion with two easy lemmata.

Lemma 20

Let $A \in \mathbb {F}^{n\times n}$ and $Q \in {\text {GL}}_{n}(\mathbb {F})$. Then A is positive definite if and only if $Q A Q^t$ is positive definite.

Proof

For any vector $v \in \mathbb {F}^{n}$ we have $v \ne 0$ if and only if $Q^t v \ne 0$. Thus, $v^t A v > 0$ for all $v \in \mathbb {F}^{n} \setminus \{0\}$ if and only if $v^t (Q A Q^t) v > 0$ for all $v \in \mathbb {F}^{n} \setminus \{0\}$. $\square$

Lemma 21

Let $A \in \mathbb {F}^{n\times n}$ be any matrix, and let $Q \in {\text {GL}}_{n}(\mathbb {F})$ be a lower triangular matrix with only 1’s on the main diagonal. Then the leading principal minors of A and $Q A Q^t$ are the same.

Proof

For arbitrary $1 \le k \le n$, partition

$$\begin{aligned} A = \begin{pmatrix} A_{11} &{}\quad A_{12} \\ A_{21} &{}\quad A_{22} \end{pmatrix} \qquad \text {and}\qquad Q = \begin{pmatrix} Q_{11} &{}\quad {\mathbf {0}} \\ Q_{21} &{}\quad Q_{22} \end{pmatrix} \end{aligned}$$

such that $A_{11}, Q_{11} \in \mathbb {F}^{k\times k}$ and the other submatrices are of the according dimensions. Note that $\det Q_{11} = 1$ since Q is lower triangular with only 1’s on the main diagonal. Then

$$\begin{aligned} Q A Q^t = \begin{pmatrix} Q_{11} &{} \quad {\mathbf {0}} \\ Q_{21} &{}\quad Q_{22} \end{pmatrix} \begin{pmatrix} A_{11} &{}\quad A_{12} \\ A_{21} &{}\quad A_{22} \end{pmatrix} \begin{pmatrix} Q_{11}^t &{} \quad Q_{21}^t \\ {\mathbf {0}} &{}\quad Q_{22}^t \end{pmatrix} = \begin{pmatrix} Q_{11} A_{11} Q_{11}^t &{}\quad * \\ * &{}\quad * \end{pmatrix}; \end{aligned}$$

and the kth principal minor of $Q A Q^t$ is $\det (Q_{11} A_{11} Q_{11}^t) = \det A_{11}$ and thus the same as the kth principal minor of A. $\square$

Now we can give the version of Sylvester’s criterion for ordered rings.

Theorem 22

(Sylvester’s Criterion) Let $\mathbb {D}$ be an ordered domain, and let $A \in \mathbb {D}^{n\times n}$ be a symmetric matrix. Then A is positive definite if and only if the principal minors of A are positive.

Proof

Let $\mathbb {F}$ be the field of fractions over $\mathbb {D}$. We are going to show Sylvester’s criterion for $\mathbb {F}$. This implies that it holds over $\mathbb {D}$ as well.

Write $A = (a_{ij})_{ij}$. If A is positive definite, we must have $a_{11} = e_1^t A e_1 > 0$ where $e_1 = (1,0,\ldots ,0)^t$ is the first unit vector. Thus, we can use Gaussian elimination with $a_{11}$ as a pivot in order to eliminate all other entries in the first column. We collect these elementary transformations into the matrix $E \in {\text {GL}}_{n}(\mathbb {F})$. Since A is symmetric, $A E^t = (E A)^t$ and thus multiplication by $E^t$ on the right will eliminate the entries from the first row of A except for $a_{11}$. The matrix

$$\begin{aligned} E A E^t = \begin{pmatrix} a_{11} &{}\quad 0 \\ 0 &{}\quad \tilde{A} \end{pmatrix} \end{aligned}$$

is still positive definite by Lemma 20 and has the same principal minors as A. Since also in particular $\tilde{A}$ must be semi-definite, we can inductively apply similar transformations to bring A into a diagonal shape. We can collect all these elementary transformations into a matrix $Q \in {\text {GL}}_{n}(\mathbb {F})$ which will be lower triangular and with only 1’s on the main diagonal. We have $Q A Q^t = {{\,\mathrm{diag}\,}}(b_1, \ldots , b_n) = B$ with $b_1, \ldots , b_n \in \mathbb {F}$. Now, Lemma 20 means that B is positive definite and Lemma 21 implies that the principal minors of A and B are the same. For any $1 \le k \le n$, we have thus $e_k^t B e_k = b_k > 0$ where $e_k$ is the kth unit vector. Hence, the kth principal minor $b_1 \cdots b_k$ of B is positive; and so is the kth principal minor of A.

For the other direction, assume now that the principal minors of A are positive. Then in particular the first principal minor $a_{11}$ is non-zero and as before we may transform A into

$$\begin{aligned} E A E^t = \begin{pmatrix} a_{11} &{}\quad 0 \\ 0 &{}\quad \tilde{A} \end{pmatrix} \end{aligned}$$

with $E \in {\text {GL}}_{n}(\mathbb {F})$ as before. Since this preserves the principal minors, we can conclude that the kth principal minor of A is the $(k-1)$th minor of $\tilde{A}$ times $a_{11}$ for all $k=2,\ldots ,n$. In particular, we see that the principal minors of $\tilde{A}$ must be positive (since $a_{11}^{-1}$ is positive); which allows us once more to apply the same elimination process inductively to $\tilde{A}$. As before, we end up with a matrix $Q \in {\text {GL}}_{n}(\mathbb {F})$ such that $Q A Q^t = {{\,\mathrm{diag}\,}}(b_1, \ldots , b_n) = B$ and $b_1, \ldots , b_n \in \mathbb {F}$ are positive since the principal minors of A are positive. Let $v \in \mathbb {F}^{n} \setminus \{0\}$. Then $u = (Q^t)^{-1} v \ne 0$ and

$$\begin{aligned} v A v^t = u^t Q A Q^t u = u^t {{\,\mathrm{diag}\,}}(b_1, \ldots , b_n) u = \sum _{k=0}^n b_k u_k^2 > 0 \end{aligned}$$

since $u_1^2, \ldots , u_n^2 \ge 0$ and $u_k^2 > 0$ for at least one $k = 1, \ldots , n$ (by Cohn [6, Prop. 8.6.1]). Hence, A is positive definite. $\square$