1 Introduction

Let \(\mathcal {H}_0({\mathbb {D}})\) be the set of analytic functions on the open unit disk \({\mathbb {D}}= \{z \in {\mathbb {C}}: |z| <1\}\) that fix zero, and let \(\mathcal {S} \subseteq \mathcal {H}_0({\mathbb {D}})\) be the set of univalent functions with the added normalization that the derivative at 0 is 1. A harmonic function \(f: {\mathbb {D}}\rightarrow {\mathbb {C}}\) with \(f(0)=0\) can be uniquely represented as \(f = h + \overline{g}\) with \(h,g \in \mathcal {H}_0({\mathbb {D}})\). We call \(\omega = g^{\prime }/h^{\prime }\) the dilatation of f. Furthermore, if we write \(f(z) = f(x+i y) = u(x,y)+ iv(x,y)\), then f is sense-preserving if the Jacobian, \(J_f\), of the mapping \((x, y) \mapsto (u, v)\) is positive. The function f is locally univalent if \(J_f\) never vanishes on \({\mathbb {D}}\), and \(f=h+\overline{g}\) is locally univalent and sense-preserving if and only if \(|g^{\prime }(z)| < |h^{\prime }(z)|\) for all \(z \in {\mathbb {D}}\) [10]. In this case, we simply say f is locally univalent. In addition, we call f univalent if f is one-to-one and sense-preserving on \({\mathbb {D}}\). Let \(\mathcal {S}_H\) be the family of harmonic univalent functions on \({\mathbb {D}}\) of the form \(f=h+\overline{g}\) normalized by \(h(0)=g(0)=0\) and \(h^{\prime }(0)=1\). Clearly, \(\mathcal {S} \subsetneq \mathcal {S}_H\).

A domain \(D \subseteq {\mathbb {C}}\) is convex in the direction of \(\gamma \), \(\gamma \in [0, \pi )\), if every line parallel to the line through 0 and \(e^{i \gamma }\) has a connected intersection with D. If \(\gamma = 0\), we use the phrase convex in the direction of the real axis. A domain D that is convex in every direction is convex, and \(\mathcal {K}\) and \(\mathcal {K}_H\) denote the respective subclasses of \(\mathcal {S}\) and \(\mathcal {S}_H\) for which \(f({\mathbb {D}})\) is convex.

If \(f = h+\overline{g} \in \mathcal {S}_H\) has the added normalization that \(g^{\prime }(0)=0\), then we write \(f \in \mathcal {S}_H^0\), and we will attach similar superscript notation to the subfamilies of \(\mathcal {S}_H\) above with this additional normalization.

If \(f(z) = \sum _{n=1}^\infty a_n z^n\) and \(g(z)=\sum _{n=1}^\infty b_n z^n\) are analytic on \({\mathbb {D}}\), the function \((f*g)(z) = \sum _{n=1}^\infty a_n b_n z^n\) is called the Hadamard product or convolution of f and g. In a similar manner, if \(f=h+\overline{g}\) and \(F=H+\overline{G}\) are harmonic on \({\mathbb {D}}\), we also call the function \(f * F = h*H+ \overline{g*G}\) the Hadamard product or convolution of f and F.

Beginning with [3], many geometric results on the convolution of two suitably normalized harmonic mappings from certain families of mappings, such as those mapping into a half-plane or a strip, are based on theorems that show when the convolution is locally univalent, it is in fact univalent and convex in one direction. Further, many harmonic convolution results (see for example [5, 12, 15]) take one of the suitably normalized mappings to be the harmonic analogue to the analytic half-plane mapping \(I(z)=z/(1-z)\). This mapping is called the standard harmonic right half-plane mapping and is given by

$$\begin{aligned} \ell _0(z) = \frac{I(z) + zI^{\prime }(z)}{2} + \overline{\frac{I(z)-zI^{\prime }(z)}{2}}. \end{aligned}$$

Additionally, recent attention has been given to a generalized right half-plane mapping \(F_c: {\mathbb {D}}\rightarrow \{w \in {\mathbb {C}}: {{\,\textrm{Re }\,}}w > -1/(1+c)\}\), \(c>0\), introduced in [18] and given by

$$\begin{aligned} F_c(z) = \frac{I(z) + czI^{\prime }(z)}{1+c} + \frac{\overline{I(z)-czI^{\prime }(z)}}{1+c} = H_c(z) + \overline{G_c(z)} \end{aligned}$$
(1.1)

Indeed, through a simple substitution of \(a=(1-c)/(1+c)\) (and sometimes adding a missing normalizing factor) one sees that other right half-plane mappings oft labeled \(F_a\) or \(f_a\) (see for example [9, 13, 15, 16]) mapping \({\mathbb {D}}\) onto \(\{w \in {\mathbb {C}}: {{\,\textrm{Re }\,}}w > -(1+a)/2\}\) are in fact the mappings above in (1.1). Notice of course too that \(F_1 = \ell _0\). Further, if \(\omega _c\) is the dilatation of \(F_c\), observe

$$\begin{aligned} \omega _c(z) = \frac{(1-c)/(1+c)-z}{1-(1-c)/(1+c)z} \end{aligned}$$
(1.2)

and \(H_c(z)+G_c(z) = (1+\omega _c(0))z/(1-z).\) Building upon this generalized half-plane mapping, we define a two-parameter family of slanted generalized right half-plane mappings.

Definition 1.1

For a \(c>0\) and \(\alpha \in [0,2\pi )\), we define \(F_{c,\alpha }: {\mathbb {D}}\rightarrow {\mathbb {C}}\) to be the slanted generalized right half-plane mapping given by

$$\begin{aligned} F_{c,\alpha }(z) = e^{-i\alpha }H_c(e^{i\alpha }z) + \overline{e^{i\alpha }G_c(e^{i\alpha }z)} \end{aligned}$$
(1.3)

where \(H_c\) and \(G_c\) are as in (1.1).

Again using the simple substitution noted above of \(a = (1-c)/(1+c)\), one can see numerous convolution results in the context of this slanted generalized right half-plane mapping \(F_{c,\alpha }\). For example, Theorem 5 in [16] can be refashioned through this substitution to state that \(F_{c,\alpha } * F_{d,0}\) is univalent and convex in the direction of \(-\alpha \) provided \(0<d<2/c\). Likewise, Corollary 2.6 in [9] could read as \(F_{c,0} * F_{c,0}\) is univalent and convex in the direction of the real axis for \(c \in (0,\sqrt{2}]\). In a similar way, Theorem 2.1 from [13], Theorems 1.1 and 2.1 from [15], and Theorems 4 and 6 from [16] can be recognized as results for a slanted generalized right half-plane mapping \(F_{c,\alpha }\) convolved with another mapping into a half-plane or into an asymmetric slanted strip. We also note that many of the convolution results referenced above prescribe a monomial or a disk automorphism for the dilatation of the mapping into a half-plane or into an asymmetric slanted strip.

In this paper, we begin with additional background including a new generalization for harmonic convolutions that involve mappings into a slanted half-plane or slanted asymmetric strip wherein local univalence of the convolution results in the convolution being univalent and convex in one direction. Following this, the significant component of this paper is the development of properties of the dilatation of the convolution of a slanted generalized right half-plane mapping \(F_{c,\alpha }\) as in Definition 1.1 with a mapping into a slanted half-plane or slanted asymmetric strip having a finite Blaschke product dilatation, thus generalizing the structure for this dilatation beyond specific monomials or disk automorphisms. Moreover, the properties of the dilatations that we develop allow for the direct application of some polynomial zero distribution techniques to assess local univalence of the convolution in a much broader setting than has been utilized in recent particular settings. For some examples of particular settings and the use of zero distribution techniques, see [9, 11, 13,14,15]. Finally, we conclude by using one of the generalized results on the local univalence of a convolution along with one of our main theorems on the convolution dilatation properties to prove a family of convolutions involving a mapping into a half-plane with two-factor Blaschke product dilatation and a slanted generalized right half-plane mapping \(F_{c,\alpha }\) is univalent and convex in one direction.

2 Additional Background and Initial Results

The shear construction which is based on the following theorem of Clunie and Sheil-Small [2] has been the basis for various foundational theorems [3, 4] regarding geometric properties of the convolution of two planar harmonic mappings on \({\mathbb {D}}\).

Theorem A

[2] A function \(f=h+\overline{g}\) locally univalent on \({\mathbb {D}}\) is a univalent mapping of \({\mathbb {D}}\) onto a domain convex in the direction of \(\gamma \), \(\gamma \in [0,\pi )\), if and only if the analytic function

$$h(z)-e^{2i\gamma }g(z), \quad \gamma \in [0,\pi )$$

is a conformal univalent mapping of \({\mathbb {D}}\) onto a domain convex in the direction of \(\gamma \).

For a given \(\gamma \in [0,2\pi )\), analytic \(\omega : {\mathbb {D}}\rightarrow {\mathbb {D}}\), and \(\varphi \in \mathcal {S}\), consider the function \(f= h+\overline{g} \in \mathcal {S}_H\) with dilatation of the form \(\omega _\gamma (z) = e^{2i\gamma }\omega (z)\) and satisfying

$$\begin{aligned} h(z) + e^{-2i\gamma }g(z) = (1+\omega (0))e^{-i\gamma }\varphi (e^{i\gamma }z), \quad z \in {\mathbb {D}}. \end{aligned}$$
(2.1)

We will call \(\varphi \) in (2.1) the shearing function.

Remark 2.1

For a good resource on mapping properties of an f generated by \(\varphi ,\) \(\omega \), and \(\gamma \) through a shearing construction as described above see [6].

A function \(f \in \mathcal {S}_H\) mapping \({\mathbb {D}}\) onto \(H_\gamma = \{w: {{\,\textrm{Re }\,}}(e^{i \gamma }w)>-1/2\}\) is said to be a slanted half-plane mapping and it is known that such a mapping must satisfy (2.1) with shearing function \(\varphi (z) = z/(1-z)\) [5]. Moreover, a function \(f \in \mathcal {S}_H\) satisfying (2.1) with \(\varphi (z) = z/(1-z)\) is known to map \(\mathbb {D}\) onto convex subdomains of the slanted half-plane \(H_\gamma \) [1, 5].

Remark 2.2

Note that the slanted generalized right half-plane mapping \(F_{c,\alpha }\) given by Definition 1.1 can be realized through a shear construction as well. For details of the development of these maps from that perspective see [16].

Let \(\beta \in [\pi /2, \pi )\). A function \(f \in \mathcal {S}_H\) mapping \({\mathbb {D}}\) onto

$$\Omega _\gamma = \left\{ w : \frac{\beta -\pi }{2 \sin \beta }< {{\,\textrm{Re }\,}}(e^{i \gamma }w)< \frac{\beta }{2 \sin \beta }\right\} $$

is said to be a slanted asymmetric strip mapping and it is known that such a mapping must satisfy (2.1) with shearing function

$$\varphi (z) = \frac{1}{2i \sin \beta } \log \frac{1+ze^{i\beta }}{1+ze^{-i\beta }}.$$

Similarly, a function \(f \in \mathcal {S}_H\) satisfying (2.1) with this \(\varphi \) known to map \({\mathbb D}\) onto convex subdomains of the slanted asymmetric strip \(\Omega _\gamma \) [4, 8].

The following two theorems rely on the shear construction and motivate the study of convolutions between harmonic mappings into slanted half-planes or between a harmonic mapping into a slanted half-plane and a harmonic mapping into a slanted asymmetric strip. The first is a slight reformulation of Theorem 2.2 in [17] which will facilitate some details in later results.

Theorem B

[17] For \(k=1,2\), let \(\gamma _k \in [0,2\pi )\) and \(\omega _{\gamma _k} = e^{2i\gamma _k}\omega _k\) for some analytic \(\omega _k: {\mathbb {D}}\rightarrow {\mathbb {D}}\). Consider \(f_k = h_k + \overline{g}_k \in \mathcal {S}_H\), \(k=1,2\), with dilatation of the form \(\omega _{\gamma _k}\) satisfying

$$\begin{aligned} h_k(z) + e^{-2i\gamma _k}g_k(z) = (1+\omega _k(0))\frac{z}{1-ze^{i\gamma _k}}, \quad z \in {\mathbb {D}}. \end{aligned}$$
(2.2)

If \((1+\omega _{1}(0))(1+\omega _{2}(0))>0\) and \(f_1 * f_2\) is locally univalent, then \(f_1 * f_2\) is in \(\mathcal {S}_H\) and is convex in the direction of \(-(\gamma _1+\gamma _2)\).

The theorem below generalizes Theorem 2.1 in [17] to mappings into a slanted asymmetric strip \(\Omega _\gamma \). The proof follows along the lines of that of Theorem 7 in [3] and so is omitted.

Theorem 2.3

For \(k=1,2\), let \(\gamma _k \in [0,2\pi )\) and \(\omega _{\gamma _k} = e^{2i\gamma _k}\omega _k\) for some analytic \(\omega _k: {\mathbb {D}}\rightarrow {\mathbb {D}}.\) Consider \(f_{k} = h_{k}+\overline{g}_{k} \in \mathcal {S}_H\), \(k=1,2,\) with dilatation of the form \(\omega _{\gamma _k}\) satisfying for \(z \in {\mathbb {D}}\)

$$\begin{aligned} \left( h_1 + e^{-2i\gamma _1}g_1\right) (z) = (1+\omega _{1}(0))\frac{z}{1-ze^{i\gamma _1}}, \end{aligned}$$

and

$$\begin{aligned} \left( h_2+e^{-2i\gamma _2}g_2\right) (z) = \frac{(1+\omega _{2}(0))e^{-i\gamma _2}}{2i\sin \beta } \log \frac{1+ze^{i(\beta +\gamma _2)}}{1+z e^{-i(\beta -\gamma _2)}}, \quad \beta \in [\pi /2,\pi ). \end{aligned}$$

If \((1+\omega _{1}(0))(1+\omega _{2}(0))>0\) and \(f_1 * f_2\) is locally univalent, then \(f_1 * f_2\) is in \(\mathcal {S}_H\) and is convex in the direction of \(-(\gamma _1+\gamma _2)\).

In our main results (Theorems 3.4, 3.5), we will prove some useful properties for the dilatation of the convolution of a slanted generalized right half-plane mapping \(F_{c,\alpha }\) as in Definition 1.1 with an \(f \in \mathcal {S}_H\) as in (2.1) that maps into a slanted half-plane or a slanted asymmetric strip such that f has a finite Blaschke product dilatation. That is, we will take the dilatation of f to be of the form

$$\sigma \prod _{k=1}^n \frac{z+ a_k}{1+\overline{a}_kz}, \quad a_k \in {\mathbb {D}},\quad k=1,\ldots , n,\quad |\sigma |=1.$$

Specifically, we will show the dilatation of \(F_{c,\alpha } * f\) is a rational function of the form

$$\begin{aligned} \lambda \prod _{k=1}^m \frac{z+b_k}{1+\overline{b}_kz}, \quad b_k \in {\mathbb {C}},\quad k=1, \ldots , m,\quad |\lambda |=1 \end{aligned}$$
(2.3)

expressed in terms of c, \(\alpha \), and the dilatation of f, the mapping into a slanted half-plane or slanted asymmetric strip.

A few quick observations show the advantage of the main theorems. If in (2.3), \(|b_k|=1, k=1, \ldots , m\), then the dilatation of the convolution \(F_{c,\alpha } * f\) is in fact a constant of modulus 1 and hence, \(F_{c,\alpha }*f\) is not locally univalent in this case. Thus, we see that, without loss of generality, proving \(b_1 \in {\mathbb {D}}\) and \(b_k \in \overline{{\mathbb {D}}}\) for \(k=2,\ldots , m\) shows the dilatation of the convolution \(F_{c,\alpha } * f\) is itself a finite Blaschke product and hence, proves the convolution is locally univalent. Thus, provided additional hypotheses on the normalizing factors given Theorem B or Theorem 2.3 are satisfied, this in turn shows \(F_{c,\alpha } * f\) is univalent and convex in one direction. This is to say, for f with a finite Blaschke product dilatation, the main results provide a direct path to analyzing the distribution of zeros in the numerator of the dilatation of the convolution \(F_{c,\alpha } * f\) to demonstrate local univalence in a more general setting than has been done in particular cases thus far. Examples of this approach for specific cases, and also mentioned in the Introduction, that use techniques such as Cohn’s rule or the Shur–Cohn algorithm include [9, 11, 13, 15] in which the prescribed dilatations are typically monomials or a disk automorphism.

3 Main Results

In order to state and prove our two main theorems (Theorems 3.4, 3.5), we first need to establish notation and identities for some polynomials as well as prove a number of lemmas.

To that end, for \(n \in {\mathbb {N}}\), let \(\mathcal {P}_n\) be the space of complex polynomials of degree at most n, and define \(\Phi _n: \mathcal {P}_n \rightarrow \mathcal {P}_n\) as

$$\begin{aligned} \Phi _n[P](z) = z^n\overline{P(1/\overline{z})}. \end{aligned}$$
(3.1)

In other words, if \(P(z) = \sum _{k=0}^n a_k z^k\), \(a_k \in {\mathbb {C}}, k = 0, \ldots , n\),

$$\begin{aligned} \Phi _n[P](z) = \sum _{k=0}^n \overline{a}_{n-k}z^k. \end{aligned}$$
(3.2)

If the degree of the polynomials P and Q are less than or equal to j and k respectively, it is evident that \(\Phi _{j+k}[{ PQ}] = \Phi _j[P] \Phi _k[Q]\).

When P is a polynomial of degree \(n \in {\mathbb {N}}\), denote the polynomial \(\Phi _n[P]\) as \(P^*\). This polynomial \(P^*\) is often called the conjugate polynomial or the conjugate reciprocal of P (see for example [19, p. 153]). In addition to expressing \(P^*\) as a sum like that in Eq. (3.2), writing the degree n polynomial P as

$$P(z) = \lambda \prod _{k=1}^n (z+b_k), \quad b_k \in {\mathbb {C}},\quad k=1,\ldots , n,\quad \lambda \in {\mathbb {C}}\setminus \{0\}$$

gives

$$P^*(z) = \Phi _n[P](z) = \overline{\lambda } \prod _{k=1}^n \left( 1 + \overline{b}_kz\right) ,$$

and notice if \(P(0)=0\), \(P^*\) has degree \(j<n\). Thusly, in such a case, \((P^*)^* = \Phi _j[\Phi _n[P]] \not = P^*\). However, for any \(P \in \mathcal {P}_n\), \(\Phi _n[\Phi _n[P]] = P\).

Further, it is well understood (see [7] for example) a rational function is a finite Blaschke product if and only if it can be written as \(\sigma P/P^*\) for some \(|\sigma |=1\) and a monic polynomial P with all its zeros in \({\mathbb {D}}\).

The next lemmas provide useful identities that are needed for the proof of our main theorems.

Lemma 3.1

Let \(\Phi _n\) be as defined in (3.1). The following identities hold for any polynomial P of degree \(n \in {\mathbb {N}}\):

$$\begin{aligned} nP(z) - zP^{\prime }(z) = \Phi _{n-1}[(P^*)^{\prime }](z) \end{aligned}$$

and

$$\begin{aligned} nP^*(z) - z(P^*)^{\prime }(z) = \Phi _{n-1}[P^{\prime }](z) \end{aligned}$$

This lemma is easily verified through the form of \(\Phi _n\) in (3.2).

Lemma 3.2

Let \(\Phi _n\) be as defined in (3.1), P be a polynomial of degree n, and \(Q: {\mathbb {C}}\rightarrow {\mathbb {C}}\) be defined as \(Q = P^*P^{\prime }-P(P^*)^{\prime }\). Then \(\Phi _{2n-1}[Q](z) = z Q(z).\)

Proof

Using the identities from Lemma 3.1, we have

$$\begin{aligned} \Phi _{2n-1}[Q](z)&= \Phi _n[\Phi _n[P]](z) \Phi _{n-1}[P^{\prime }](z) - \Phi _n[P](z) \Phi _{n-1}[(P^*)^{\prime }](z) \\&= P(z) (n P^*(z) - z (P^*)^{\prime }(z)) - P^*(z)(nP(z)-zP^{\prime }(z)) \\&= z Q(z). \end{aligned}$$

\(\square \)

Before we state and prove the two main theorems, we have one final lemma that provides a general form for the dilatation of the convolution of a slanted generalized right half-plane \(F_{c,\alpha }\) defined in Definition 1.1 with another harmonic mapping expressed entirely in terms of this latter mapping’s shearing function and dilatation and a slanting parameter, thus allowing us to easily substitute various shearing functions and dilatations for later results.

Lemma 3.3

Let \(\varphi \in \mathcal {S}\), \(\omega : {\mathbb {D}}\rightarrow {\mathbb {D}}\) be analytic, and \(\gamma \in [0,2\pi )\). Consider \(f = h+\overline{g} \in \mathcal {S}_H\) with dilatation of the form \(\omega _\gamma (z) = e^{2i\gamma }\omega (z)\) and satisfying

$$\begin{aligned} h(z) + e^{-2i\gamma }g(z) = (1+\omega (0))e^{-i\gamma }\varphi (e^{i\gamma }z), \quad z \in {\mathbb {D}}. \end{aligned}$$
(3.3)

Taking \(F_{c, \alpha }\) to be a slanted generalized right half-plane mapping as in Definition 1.1 and writing \(\omega _{c,\alpha ,\gamma }\) as the dilatation of the convolution \(F_{c,\alpha } * f\), for \(\zeta = e^{i \alpha } z\), \(z \in {\mathbb {D}}\),

(3.4)

Proof

Let \(H_{c,\alpha }(z) = e^{-i\alpha }H_c(e^{i\alpha }z)\) and \(G_{c,\alpha }(z) = e^{i\alpha }G_c(e^{i\alpha }z)\) where \(H_c\) and \(G_c\) are as defined in (1.1). Then

$$\begin{aligned} (H_{c,\alpha } * h)(z)&= \frac{1}{1+c} \left( \frac{z}{1-e^{i\alpha }z} + \frac{cz}{(1-e^{i\alpha }z)^2}\right) * h(z) \\&= \frac{e^{-i\alpha }}{1+c} \left( h(e^{i \alpha } z) +c e^{i\alpha }zh'(e^{i\alpha }z)\right) \end{aligned}$$

and

$$\begin{aligned} (G_{c,\alpha } * g)(z)&= \frac{e^{i\alpha }}{1+c} \left( \frac{e^{i\alpha }z}{1-e^{i\alpha }z} + \frac{ce^{i\alpha }z}{(1-e^{i\alpha }z)^2}\right) * g(z) \\&= \frac{e^{i\alpha }}{1+c} \left( g(e^{i \alpha } z) -c e^{i\alpha }zg'(e^{i\alpha }z)\right) . \end{aligned}$$

Using \(g^{\prime } =\omega _\gamma h^{\prime }\) and (3.3),

$$h^{\prime }(z) = (1+\omega (0))\frac{\varphi ^{\prime }(e^{i\gamma }z)}{1+\omega (z)}.$$

Therefore,

where \(\zeta = e^{i \alpha } z.\) After some algebra on this last line, the result is evident. \(\square \)

Our first main theorem provides properties of the dilatation of the convolution of the slanted generalized right half-plane mapping \(F_{c,\alpha }\) in Definition 1.1 and a mapping onto the slanted half-plane \(H_\gamma \) or a convex subdomain of \(H_\gamma \) (see discussion following Remark 2.1).

Theorem 3.4

Let \(F_{c,\alpha }\) be a slanted generalized right half-plane mapping as in Definition 1.1. Let \(\omega : {\mathbb {D}}\rightarrow {\mathbb {D}}\) be a finite Blaschke product written as \(\sigma P/P^*, |\sigma |=1\), for P a monic polynomial of degree \(n \in {\mathbb {N}}\) with all its zeros in \({\mathbb {D}}\). Finally, let f be as defined in Lemma 3.3 with \(\varphi (z) = z/(1-z)\) and dilatation \(\omega _\gamma \).

Then the dilatation \(\omega _{c,\alpha ,\gamma }\) of \(F_{c,\alpha } * f\) is the rational function

$$\omega _{c,\alpha ,\gamma }(z) = \lambda \frac{N(e^{i\alpha }z)}{N^*(e^{i \alpha }z)}, \quad z \in {\mathbb {D}},\quad |\lambda |=1$$

where

$$\begin{aligned} N(z)&= P(z)(P^*(z)+\sigma P(z))(1-c-(1+c)e^{i\gamma }z) \nonumber \\&\quad -{}c z(1-e^{i\gamma }z)\left[ P^*(z)P^{\prime }(z)-P(z)(P^*)^{\prime }(z)\right] . \end{aligned}$$
(3.5)

Proof

Using \(\varphi (z) = z/(1-z)\) in Lemma 3.3, we have for \(\zeta = e^{i\alpha } z\), \(z \in {\mathbb {D}}\),

$$\omega _{c,\alpha ,\gamma }(z) = e^{2i(\alpha +\gamma )} \displaystyle \frac{\omega (\zeta )(1+\omega (\zeta ))(1-c -(1+c)e^{i\gamma }\zeta )-c \zeta \omega ^{\prime }(\zeta )(1-e^{i\gamma }\zeta )}{(1+\omega (\zeta ))(1+c - (1-c) e^{i \gamma }\zeta )-c \zeta \omega ^{\prime }(\zeta )(1-e^{i\gamma }\zeta )}.$$

Let \(Q = P^*P^{\prime }-P(P^*)^{\prime }\). Now, replacing \(\omega \) in terms of P and \(P^*\) in \(\omega _{c,\alpha ,\gamma }\) above leads to

(3.6)

where N and D are the numerator and denominator, respectively, in (3.6). Clearly, N aligns with (3.5) for \(\zeta = e^{i\alpha }z\).

We may write \(P(z) = \prod _{k=1}^n (z+a_k), a_k \in {\mathbb {D}}, k=1,\ldots , n\). Since \(|\prod _{k=1}^n a_k| < 1\) and \(|\sigma |=1\), the degree of \(P^*+\sigma P\) is n. Further, because the degree of P is n, a straightforward calculation using (3.2) shows the degree of Q is at most \(2n-2\). Hence, the degree of N is \(2n+1\). Thus, by Lemma 3.2,

$$\begin{aligned} N^*(z)&= \Phi _{2n+1}[N](z) \\&= \Phi _{n}[P](z)\Phi _{n}[P^*+\sigma P](z)((1-c)z -(1+c)e^{-i\gamma }) \\&\quad -{}c(z-e^{-i\gamma })\Phi _{2n-1}[Q](z) \\&= -e^{-i\gamma }\Big (P^*(z)(P(z)+\overline{\sigma }P^*(z))(1+c-(1-c)e^{i\gamma }z) \\&\quad -{}cz(1-e^{i\gamma }z)Q(z)\Big ) \\&= -e^{-i\gamma }D(z). \end{aligned}$$

From this, we see

$$\omega _{c,\alpha ,\gamma }(z) = e^{2i(\alpha +\gamma )}\frac{N(\zeta )}{D(\zeta )} = -e^{i(2\alpha +\gamma )} \frac{N(\zeta )}{N^*(\zeta )}, \quad \zeta = e^{i\alpha }z,\quad z \in {\mathbb {D}}$$

which completes the proof. \(\square \)

Our next theorem provides properties of the dilatation of the convolution of the slanted generalized right half-plane mapping \(F_{c,\alpha }\) as in Definition 1.1 and a mapping onto the slanted asymmetric strip \(\Omega _\gamma \) or a convex subdomain of this strip (see discussion following Remark 2.2).

Theorem 3.5

Let \(F_{c,\alpha }\) be a slanted generalized right half-plane mapping as in Definition 1.1. Let \(\omega : {\mathbb {D}}\rightarrow {\mathbb {D}}\) be a finite Blaschke product written as \(\sigma P/P^*, |\sigma |=1\), for P a monic polynomial of degree \(n \in {\mathbb {N}}\) with all its zeros in \({\mathbb {D}}\). Finally, let f be as defined in Lemma 3.3 with

$$\begin{aligned} \varphi (z) = \frac{1}{2i\sin \beta } \log \frac{1+ze^{i\beta }}{1+z e^{-i\beta }}, \quad \beta \in [\pi /2,\pi ). \end{aligned}$$
(3.7)

and dilatation \(\omega _\gamma \).

Then the dilatation \(\omega _{c,\alpha ,\gamma }\) of \(F_{c,\alpha } * f\) is the rational function

$$\omega _{c,\alpha ,\gamma }(z) = \lambda \frac{N(e^{i\alpha }z)}{N^*(e^{i \alpha }z)}, \quad z \in {\mathbb {D}},\quad |\lambda |=1$$

where \(N:{\mathbb {D}}\rightarrow {\mathbb {C}}\) is

$$\begin{aligned} N(z)&= P(z)(P^*(z)+\sigma P(z)) (1-c+2 (\cos \beta ) e^{i\gamma }z+(1+c)e^{2i\gamma }z^2) \nonumber \\&\quad -{}cz\left( 1+2 (\cos \beta ) e^{i\gamma }z+e^{2i\gamma }z^2\right) (P^*(z)P^{\prime }(z)-P(z)(P^*)^{\prime }(z)). \end{aligned}$$
(3.8)

Proof

Using \(\varphi \) given in (3.7), from Lemma 3.3, for a given \(\beta \in [\pi /2,\pi )\), we have for \(\zeta = e^{i\alpha } z, z \in {\mathbb {D}}\),

Following as in the proof of Theorem 3.4, we may write \(P(z) = \prod _{k=1}^n (z+a_k), a_k \in {\mathbb {D}}, k=1,\ldots , n\). Let \(Q = P^*P^{\prime }-P(P^*)^{\prime }\), \(p_1(z) = 1-c + 2 (\cos \beta ) z+ (1+c)z^2\), and \(p_2(z) = 1+2(\cos \beta ) z +z^2\). Observe \(p_1^*(z) = 1+c + 2 (\cos \beta ) z +(1-c)z^2\) and \(p_2^*(z) = p_2(z)\). Now, replacing \(\omega \) in terms of P and \(P^*\) in the equation for \(\omega _{c,\alpha ,\gamma }\) above leads to

$$\begin{aligned} \omega _{c,\alpha ,\gamma } (z)&= e^{2i(\alpha +\gamma )} \nonumber \\&\quad \times \frac{\sigma P(\zeta )(P^*(\zeta )+\sigma P(\zeta )) p_1(e^{i\gamma } \zeta )-c \sigma \zeta Q(\zeta ) p_2(e^{i\gamma }\zeta )}{P^*(\zeta )(P^*(\zeta )+\sigma P(\zeta ))p_1^*(e^{i\gamma }\zeta )-c \sigma \zeta Q(\zeta )p_2(e^{i\gamma }\zeta )}\nonumber \\&= e^{2i(\alpha +\gamma )} \nonumber \\&\quad \times \frac{P(\zeta )\left( P^*(\zeta )+\sigma P(\zeta )\right) p_1(e^{i\gamma } \zeta )-c \zeta Q(\zeta ) p_2(e^{i\gamma }\zeta )}{P^*(\zeta )\left( \overline{\sigma } P^*(\zeta )+P(\zeta )\right) p_1^*(e^{i\gamma }\zeta )-c \zeta Q(\zeta )p_2(e^{i\gamma }\zeta )} \\&= e^{2i(\alpha +\gamma )} \frac{N(\zeta )}{D(\zeta )}\nonumber \end{aligned}$$
(3.9)

where N and D are the numerator and denominator, respectively, in (3.9). Clearly, N aligns with (3.8) with \(\zeta = e^{i\alpha }z\).

Using the same argument as in the proof of Theorem 3.4, here the degree of N is \(2n+2\). Thus, using Lemma 3.2, we have

$$\begin{aligned} N^*(z)&= \Phi _{2n+2}[N](z) \\&= \Phi _{n}[P](z) (\Phi _{n}[P^* +\sigma P](z)) ((1-c)z^2+2(\cos \beta )e^{-i\gamma }z\\&\quad +(1+c)e^{-2i\gamma }) -{}c \Phi _2[p_2](e^{i\gamma }z) \Phi _{2n-1}[Q](z) \\&= e^{-2i\gamma }\Big (P^*(z) (P(z)+\overline{\sigma }P^*(z))p_1^*(e^{i\gamma }z)-c z p_2(e^{i\gamma }z)Q(z)\Big ) \\&=e^{-2i\gamma }D(z). \end{aligned}$$

From this, we see

$$\omega _{c,\alpha ,\gamma }(z) = e^{2i\alpha } \frac{N(\zeta )}{N^*(\zeta )}, \quad \zeta = e^{i\alpha }z,\quad z \in {\mathbb {D}}$$

which completes the proof. \(\square \)

4 Two-Factor Blaschke Product Dilatation Case

Our final result is an application of one of our main theorems, Theorem 3.4, and the generalized result in Theorem B. Specifically, we provide a family of univalent convolutions convex in one direction between the slanted right half-plane mapping \(F_{1,\alpha }\) and a half-plane mapping f. As noted in the introduction, convolution results have typically involved a particular mapping into a half-plane or asymmetric strip convolved with another mapping f into a half-plane or strip whose dilatation is a monomial or disk automorphism. In this final result, we take the dilatation of the half-plane mapping f to be a two-factor Blaschke product dilatation expanding the scope of such convolution results.

Theorem 4.1

Let \(F_{1,\alpha }\) be a slanted right half-plane mapping as in Definition 1.1. Let \(P(z) = (z+a_1)(z+a_2)\), \(a_1 \in [-1,1/3]\) and \(a_2=a_1/(2a_1-1)\) and let \(\omega : {\mathbb {D}}\rightarrow {\mathbb {D}}\) be defined as \(\omega = P/P^*\). Finally, let f be as defined in Lemma 3.3 with \(\gamma =0\), \(\varphi (z) = z/(1-z)\), and dilatation \(\omega _0 = \omega \). Then \(F_{1,\alpha } * f\) is in \(\mathcal {S}_H\) and is convex in the direction of \(-\alpha \).

In order to prove this theorem, we need the following lemma which follows directly from Theorem 3.4.

Lemma 4.2

Let \(P(z) = (z+a_1)(z+a_2), a_1, a_2 \in {\mathbb {R}}\). With \(c=\sigma =1\) and \(\gamma =0\) in (3.5), we have \(N(z) = -2z(b_4z^4+b_3z^3+b_2z^2+b_1z+b_0)\) where

$$\begin{aligned} b_4&= 1+a_1a_2,\\ b_3&= \frac{1}{2}(a_1+a_2)(5+3a_1a_2),\\ b_2&= 2a_1a_2(1+a_1a_2)+(a_1+a_2)\left( 2(a_1+a_2)+\frac{1}{2}(1-a_1a_2)\right) ,\\ b_1&= 3a_1^2a_2+3a_1a_2^2+(1+a_1a_2)\left( \frac{1}{2}(a_1+a_2)+1 -a_1a_2\right) , \end{aligned}$$

and

$$\begin{aligned} b_0 = a_1a_2(1+a_1a_2)+\frac{1}{2}(a_1+a_2)(1-a_1a_2). \end{aligned}$$

Proof of Theorem 4.1

Let \(N_1(z) = b_4z^4+b_3z^3+b_2z^2+b_1z+b_0\) where \(b_k\), \(k=0, 1, 2, 3, 4\) are as in Lemma 4.2. In light of Theorem 3.4, to prove \(F_{1,\alpha }*f\) is locally univalent for \(a_1 \in [-1, 1/3]\) and \(a_2=a_1/(2a_1-1)\), it suffices to show the zeros of \(N_1\) are in \(\overline{{\mathbb {D}}}\). Substituting \(a_2=a_1/(2a_1-1)\) into \(b_k\), \(k=0, 1, 2, 3, 4\) in Lemma 4.2 gives

$$\begin{aligned} b_4&= \frac{a_1^2+2a_1-1}{2a_1-1}\\ b_3&= \frac{a_1^2(3a_1^2+10a_1-5)}{(2a_1-1)^2},\\ b_2&= \frac{3a_1^2(3a_1-1)(a_1+1)}{(2a_1-1)^2},\\ b_1&= \frac{6a_1^4+2a_1^3+3a_1^2-4a_1+1}{(2a_1-1)^2}, \end{aligned}$$

and

$$b_0 = \frac{2a_1^2}{2a_1-1}$$

which leads to

$$\begin{aligned} (2a_1-1)^2N_1(z)&= (2a_1-1)\left( a_1^2+2a_1-1\right) z^4 + a_1^2\left( 3a_1^2+10a_1-5\right) z^3 \nonumber \\&\quad + 3a_1^2(3a_1-1)(a_1+1)z^2+\left( 6a_1^4+2a_1^3+3a_1^2-4a_1+1\right) z \nonumber \\&\quad +2a_1^2(2a_1-1) \nonumber \\&= (z+1)\left( (a_1^2+2a_1-1)z+2a_1^2\right) \nonumber \\&\quad \times \left( (2a_1-1)z^2+\left( 3a_1^2-2a_1+1\right) z+2a_1-1\right) \end{aligned}$$
(4.1)

Let \(p_1(z) = (a_1^2+2a_1-1)z+2a_1^2\) and \(p_2(z)= (2a_1-1)z^2+(3a_1^2-2a_1+1)z+2a_1-1\). For \(a_1 \in [-1,1/3]\), the zero of \(p_1\) is in \(\overline{{\mathbb {D}}}\) because for \(f(x) = -2x^2/(x^2+2x-1)\), it is easy to see through elementary calculus that \(0 \le f(x) \le 1\) for \(x \in [-1,1/3]\). Further, for \(a_1 \in [-1,1/3]\), the zeros of \(p_2\) are given by

$$\frac{-(3a_1^2-2a_1+1) \pm i (a_1-1)\sqrt{3(a_1+1)(1-3a_1)}}{2(2a_1-1)}.$$

It is simple to show

$$\left( 3a_1^2-2a_1+1\right) ^2 +3(a_1-1)^2(a_1+1)(1-3a_1) = 4(2a_1-1)^2$$

and thus, the zeros of \(p_2\) are in \(\partial {\mathbb {D}}\). Therefore, \(F_{1,\alpha }*f\) is locally univalent for \(a_1 \in [-1,1/3]\) and \(a_2=a_1/(2a_1-1)\). Since the dilatation of \(F_{1,\alpha }\) fixes 0 [see (1.2)] and \(1+\omega (0)=1+a_1^2/(2a_1-1) > 0\) for \(a_1 \in [-1,1/3]\), by Theorem B, \(F_{1,\alpha } * f\) is in \(\mathcal {S}_H\) and is convex in the direction of \(-\alpha \). \(\square \)

Note in the above theorem, in order for Theorem B to be satisfied, \(a_1\) must be real and \(a_1 \in {\mathbb {R}}\) cannot be extended beyond \([-1,1/3]\) else f fails to be univalent. Further, observe from proof we have shown that the dilatation \(\omega _{1,\alpha ,0}\) of \(F_{1,\alpha } * f\) for \(a_1 \in [-1,1/3]\) is

$$\omega _{1,\alpha ,0}(z) = - z e^{2i\alpha } \frac{\left( a_1^2+2a_1-1\right) ze^{i\alpha }+2a_1^2}{2a_1^2 z e^{i\alpha }+ a_1^2+2a_1-1}.$$

It is worth casting the result from this section in light of other particular prior results to see how this is a generalization. For example, observe for \(a_1=0\), the dilatation of f is \(\omega _0(z) = z^2\) and so in this case, the result of Theorem 4.1 coincides with Theorem 4 in [16] by taking \(\theta =0\) and \(a=0\) (which is equivalent to \(c=1\) above). Additionally, taking \(a_1\) to be \(-1\) or 1/3, the dilatation of f is \(\omega _0(z) = - (z+1/3)/(1+z/3)\). One can see this as a special case of Theorem 2.5 in [9] for \(a=0\) and \(b=1/3\), albeit, a correction to the formula for \(f_a\) found in this paper is needed to satisfy the additional normalizing multiplier of the shearing function hypothesis in Theorem B.

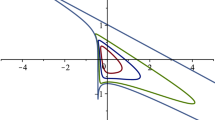
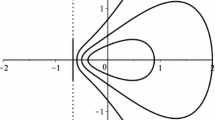
See Fig. 1 for images of some examples of convolutions from Theorem 4.1 that are convex in the direction of the real axis since \(\alpha =0\). Note there are three boundary discontinuities in each case and there is boundary collapsing between these discontinuities that occur in the image. See [6] for more details on this type of mapping behavior.

Fig. 1
figure 1

Images of \((F_{1,0}*f)(z) = (\ell _0 * f)(z)\) with \(|z|=r, r=0.2, 0.4, 0.6, 0.8, 0.99\) (solid) and \(z=r e^{i t}, |r|\le 0.99, t=0, \pi /6, \pi /4, \pi /2, \pi /3, 2\pi /3, 3 \pi /4, 5\pi /6\) (dashed) for f as in Theorem 4.1

Full size image

In closing, Theorems 3.4 and 3.5 allow quick access to the structure of the dilatation of the convolution of a slanted generalized right half-plane mapping \(F_{c,\alpha }\) as defined in Definition 1.1 with either another mapping into a slanted half-plane or a slanted asymmetric strip, and indeed these theorems encompasses a number of previous results that instead began with specific functions and dilatations of the other mapping into a slanted half-plane or a slanted asymmetric strip. See again for example [9, 11, 13,14,15]. With the dilatation structures of Theorems 3.4 and 3.5 in hand, one can now move towards establishing broader results, including considering other zero distribution techniques that may take advantage of the form of the dilatation to obtain more univalence and direction-convexity results of these convolutions through use of Theorems B and 2.3.