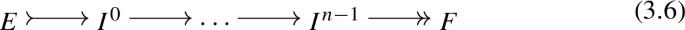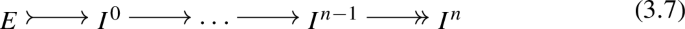Schanuel’s Lemma for Exact Categories

Abstract

We prove an injective version of Schanuel’s lemma from homological algebra in the setting of exact categories.

1 Introduction

Schanuel’s lemma is a useful tool in homological algebra and category theory. It appears to have come about as a response to a question by Kaplansky, see [4, p. 166], and simplifies the definition of the projective (or, injective) homological dimension in module categories, hence in abelian categories. The typical categories that arise in functional analysis are not abelian but lately, the use of exact structures on additive categories of Banach modules and related ones has been suggested and indeed been exploited successfully.

In [3], Bühler develops homological algebra for bounded cohomology in the setting of Quillen’s exact categories. In [1], exact categories of sheaves of operator modules over C*-ringed spaces are studied. Relative cohomology and cohomological dimension for (not necessarily self-adjoint) operator algebras is the topic of [6], see also [8]. In view of this, it seems beneficial to establish an injective version of Schanuel’s lemma for exact categories and show how it yields the injective dimension theorem.

When we equip an additive category $\mathscr {A}$ with an exact structure we fix a pair $(\mathscr {M},\mathscr {P})$ consisting of a class of monomorphisms $\mathscr {M}$ and a class of epimorphisms $\mathscr {P}$ such that each $\mu \in \mathscr {M}$ and $\pi \in \mathscr {P}$ form a kernel-cokernel pair which we write as

where E, F and G are objects in $\mathscr {A}$. We require that $\mathscr {M}$ and $\mathscr {P}$ contain all identity morphisms and are closed under composition, and term their elements as admissible monomorphisms and admissible epimorphisms, respectively. Furthermore, the push-out of an admissible monomorphism along an arbitrary morphism exists and yields an admissible monomorphism, and, likewise, the pull-back of an admissible epimorphism along an arbitrary morphism exists and yields an admissible epimorphism. If these conditions are fulfilled and $(\mathscr {M},\mathscr {P})$ is invariant under isomorphisms, $(\mathscr {M},\mathscr {P})$ is called an exact structure on $\mathscr {A}$ and will typically be denoted by ${\mathscr {E}\!x}$. The pair $(\mathscr {A},{\mathscr {E}\!x})$ is said to be an exact category.

Unlike in abelian categories not every morphism in an exact category has a canonical factorisation into an epimorphism followed by a monomorphism. One therefore has to restrict to admissible morphisms which are those that arise as $\mu \circ \pi$ for some $\mu \in \mathscr {M}$ and $\pi \in \mathscr {P}$. (It is easy to check that, once such factorisation exists, it is unique up to unique isomorphism.)

The kernel-cokernel pairs replace the usual short exact sequences in abelian categories while long exact sequences are built from admissible morphisms. A very readable introduction into exact categories is given in [2].

In this note, we provide the details of how Schanuel’s lemma works in general exact categories and establish the Injective Dimension Theorem (Theorem 3.5).

2 Preliminaries

We include here the necessary terminology and initial results, for a fixed exact category $(\mathscr {A},{\mathscr {E}\!x})$, where ${\mathscr {E}\!x}=(\mathscr {M},\mathscr {P})$.

Definition 2.1

An object I in an exact category $(\mathscr {A},{\mathscr {E}\!x})$ is $\mathscr {M}$-injective if, when given and a morphism $f\in Mor _{\mathscr {A}}{({E},{I})}$, for objects $E,F\in \mathscr {A}$, there exists a morphism ${g}\in Mor _{\mathscr {A}}{({F},{I})}$ making the following diagram commutative

The exact category has enough $\mathscr {M}$-injectives if, for every $E\in \mathscr {A}$, there exist an $\mathscr {M}$-injective object I and an admissible monomorphism .

We will also make use of the following characterisations of $\mathscr {M}$-injective objects.

Proposition 2.2

Let E be an object in an exact category $(\mathscr {A},{\mathscr {E}\!x})$. The following are equivalent.

• (i) E is $\mathscr {M}$-injective;

• (ii) Every admissible monomorphism , for $F\in \mathscr {A}$, has a left inverse;

• (iii) There exist an $\mathscr {M}$-injective object $I\in \mathscr {A}$ and a morphism $E\longrightarrow {I}$ with a left inverse (i.e., E is a retract of an $\mathscr {M}$-injective object).

The arguments are standard.

As exact categories are additive, we can form the product of any two objects (and thus, of any finite number of objects).

Proposition 2.3

Let E, F, G be objects in an additive category $\mathscr {A}$. The following are equivalent:

• (i) F is a product of E and G;

• (ii) F is a coproduct of E and G;

• (iii) There exist a kernel-cokernel pair in $\mathscr {A}$,

  

  (2.1)

  and morphisms $\widetilde{\mu }\in Mor _{\mathscr {A}}{({F},{E})}$ and $\widetilde{\pi }\in Mor _{\mathscr {A}}{({G},{F})}$ such that $\widetilde{\mu }\circ \mu =id _{E}$ and $\pi \circ \widetilde{\pi }=id _{G}$, and $\mu \circ \widetilde{\mu }+\widetilde{\pi }\circ \pi =id _{F}$;

• (vi) There exist a kernel-cokernel pair in $\mathscr {A}$,

  

  (2.2)

  and a morphism $\widetilde{\mu }\in Mor _{\mathscr {A}}{({F},{E})}$ such that $\widetilde{\mu }\circ \mu =id _{E}$, the identity morphism on E.

Moreover, if these equivalent conditions are met, the kernel-cokernel pair in Diagram (2.2) will belong to every exact structure that can be placed on $\mathscr {A}$.

Proof

Finite products, coproducts and biproducts coincide in an additive category (see, e.g., [7, Proposition 7.1–Corollary 7.3.]), and condition (iii) is just the definition of F being a biproduct of E and G. That condition (iii) is equivalent to condition (iv) can be proven in the exact same way as the ‘Splitting Lemma’ in module theory (see, e.g., [5, Proposition 4.3.]). The final statement of this proposition is a direct consequence of the conditions required for monomorphisms and epimorphisms to be admissible; see [2, Lemma 2.7.] for details.

Kernel-cokernel pairs satisfying condition (iii) of Proposition 2.3 are said to be split. For objects E and F in $\mathscr {A}$ we will denote their (co)product by $E\oplus {F}$.

Proposition 2.4

Suppose is a kernel-cokernel pair in ${\mathscr {E}\!x}$.

• (i) For any $A\in \mathscr {A}$, there is a kernel-cokernel pair in ${\mathscr {E}\!x}$,

  

• (ii) If $F\cong E\oplus {G}$, then F is $\mathscr {M}$-injective if and only if both E and G are $\mathscr {M}$-injective.

Proof

We first prove (i). For $A\in \mathscr {A}$, there exist split kernel-cokernel pairs

and $\pi \circ \tau \in Mor _{\mathscr {A}}{({F\oplus {A}},{G})}$ is an admissible epimorphism, as a compostion of morphisms in $\mathscr {P}$. Define $\varphi \in Mor _{\mathscr {A}}{({E\oplus {A}},{F\oplus {A}})}$ by

$$\begin{aligned} \varphi =\widetilde{\tau }\circ {\mu }\circ \widetilde{\iota } +\theta \circ \rho \end{aligned}$$

using the same notation as in Proposition 2.3. Then $(\varphi , \pi \circ \tau )$ is the desired kernel-cokernel pair.

To show this, it is enough to demonstrate that $\varphi$ is a kernel of $\pi \circ \tau$. First note the composition

$$\begin{aligned} (\pi \circ \tau )\circ \varphi = id _{F}\circ (\pi \circ {\mu })\circ \widetilde{\iota } + \pi \circ (\tau \circ \theta )\circ \rho = 0. \end{aligned}$$

Now suppose there exist $B\in \mathscr {A}$ and a morphism $f\in Mor _{\mathscr {A}}{({B},{F\oplus {A}})}$ such that $(\pi \circ \tau )\circ {f}=0$. As $\mu$ is a kernel for $\pi ,$ there exists a unique morphism $g'\in Mor _{\mathscr {A}}{({B},{E})}$ such that $\mu \circ {g'}=\tau \circ {f}$. Define $g\in Mor _{\mathscr {A}}{({B},{E\oplus {A}})}$ by

$$\begin{aligned} g=\iota \circ {g'}+\widetilde{\rho }\circ \widetilde{\theta }\circ {f}. \end{aligned}$$

Then $\varphi \circ {g}=(\widetilde{\tau }\circ \tau )\circ {f} + (\theta \circ \widetilde{\theta })\circ {f}= id _{F\oplus {A}}\circ {f}=f$.

To finish the proof of (i), we show that there is no other morphism $h\in Mor _{\mathscr {A}}{({B},{E\oplus {A}})}$ such that $\varphi \circ {h}=f$. Suppose we have such a morphism h. Then, $\widetilde{\theta }\circ {f} = \widetilde{\theta }\circ \varphi \circ {h} = \rho \circ {h}$, and $\mu \circ {g'} = \tau \circ f = \tau \circ \varphi \circ h = \mu \circ \widetilde{\iota }\circ h,$ and therefore $g'=\widetilde{\iota }\circ h$. Combining these facts gives:

$$\begin{aligned} h = id _{E \oplus A}\circ h = (\iota \circ \widetilde{\iota } + \widetilde{\rho } \circ \rho ) =\iota \circ g' + \widetilde{\rho }\circ \widetilde{\theta }\circ {f} =g, \end{aligned}$$

as required.

For assertion (ii) suppose $F\cong E\oplus G$. Then there exist morphisms $\widetilde{\mu }\in Mor _{\mathscr {A}}{({F},{E})}$ and $\widetilde{\pi }\in Mor _{\mathscr {A}}{({G},{F})}$ such that $\widetilde{\mu }\circ \mu =id _{E}$ and $\pi \circ \widetilde{\pi }=id _{G}$, and $\mu \circ \widetilde{\mu }+\widetilde{\pi }\circ \pi =id _{F}$. In particular, E and G are retracts of F. By Proposition 2.2, if F is $\mathscr {M}$-injective so are E and G. Finally, suppose E and G are $\mathscr {M}$-injective and there is an admissible monomorphism

where $B\in \mathscr {A}$. Because E and G are $\mathscr {M}$-injective, there exist $g_E\in Mor _{\mathscr {A}}{({B},{E})}$ such that $\widetilde{\mu }=g_E \circ f$ and $g_G\in Mor _{\mathscr {A}}{({B},{G})}$ such that and $\pi = g_F \circ f$. Let $g= \mu \circ g_E + \widetilde{\pi }\circ g_G$, then g is a left inverse of f, indeed:

$$\begin{aligned} g \circ f= \mu \circ (g_E \circ f) + \widetilde{\pi }\circ (g_G \circ f) = \mu \circ \widetilde{\mu }+\widetilde{\pi }\circ \pi =id _{F}. \end{aligned}$$

Hence, by Proposition 2.2, F is $\mathscr {M}$-injective. $\square$

3 Schanuel’s Lemma

Fix an exact category $(\mathscr {A},{\mathscr {E}\!x})$. The following is the injective version of Schanuel’s lemma for exact categories.

Proposition 3.1

Suppose and are kernel-cokernel pairs in ${\mathscr {E}\!x}$, and that $I, I'$ are $\mathscr {M}$-injective objects. Then $I\oplus {F'}\cong I'\oplus {F}$ in $\mathscr {A}$.

Proof

First, by the axioms of an exact structure, we can form the following push-out,

where every morphism is an admissible monomorphism. Extending this diagram to include the given cokernels, and adding in some zero morphisms, we get the following commutative diagram:

By the universal property of push-outs, there are a unique morphism $p\in Mor {({C},{F})}$ such that $ph'=0$ and $ph=\pi$, and a unique morphism $p'\in Mor {({C},{F'})}$ such that $p'h=0$ and $p'h'=\pi '$. Hence, we have the following commutative diagram:

The result will follow if the middle row and middle column are both split kernel-cokernel pairs. As $h, h'\in \mathscr {M}$ and $I,I'$ are $\mathscr {M}$-injective, this will be the case if both $(h',p)$ and $(h,p')$ are kernel-cokernel pairs. We deal with $(h',p)$, the other pair is done in the exact same way.

To show that $(h',p)$ is a kernel-cokernel pair, it is enough to verify that p is a cokernel of $h'$. Suppose there exist an object $G\in \mathscr {A}$ and a morphism $q\in Mor {({C},{G})}$ such that $qh'=0$. We are done if we find a unique morphism $\psi \in Mor {({F},{G})}$ such that the following diagram is commutative:

We have $(qh)\mu =q(h\mu )=q(h'\mu ')=0$ and, because $(\mu ,\pi )$ is a kernel-cokernel pair, there exists a unique morphism $t\in Mor {({F},{G})}$ such that $t\pi =qh$. Therefore, the following diagram is commutative:

By the universal property of push-outs, q is the unique morphism $C\rightarrow {G}$ that makes Diagram (3.5) commutative. However, $(tp)h=t(ph)=t\pi$ and $(tp)h'=t(ph')=0$. So, $q=tp$ and setting $\psi =t$ makes Diagram (3.4) commutative. Finally, suppose there also exists $t'\in Mor {({F},{G})}$ such that $q=t'p$. Recalling from Diagram (3.3) that $\pi =ph$, we have

$$\begin{aligned} t'\pi = t'(ph)=(t'p)h=(tp)h=t(ph)=t\pi , \end{aligned}$$

and, because $\pi$ is an epimorphism, $t'=t$. Thus, uniqueness has been verified.

Corollary 3.2

Suppose there is a diagram of morphisms in an exact category $(\mathscr {A},{\mathscr {E}\!x})$ of the form

such that I and $I'$ are $\mathscr {M}$-injective, the horizontal lines are in ${\mathscr {E}\!x}$ and the vertical arrow is an isomorphism. Then $I\oplus {F'}\cong I'\oplus {F}$ in $\mathscr {A}$.

We extend Schanuel’s lemma to injective resolutions in Proposition 3.4 below. Recall that a morphism is admissible if it is the composition $\mu \circ \pi$ for some $\mu \in \mathscr {M}$ and $\pi \in \mathscr {P}$. Such factorisation is unique up to unique isomorphism ([2, Lemma 8.4]).

Definition 3.3

For an object $E\in \mathscr {A}$, an $\mathscr {M}$-injective resolution of E is a sequence of admissible morphisms of the form:

such that, for each $n\ge 0,$ the object $I^n$ is $\mathscr {M}$-injective, and

forms a kernel-cokernel pair in ${\mathscr {E}\!x}$ (this is the exactness condition at $I^n$).

If $\mathscr {A}$ has enough $\mathscr {M}$-injectives, we can build an injective resolution for every object in $\mathscr {A}$.

Proposition 3.4

Suppose we have the following $\mathscr {M}$-injective resolutions of E, with the factorisation of each admissible morphism included:

and

Then, for each $n\ge {1}$, we have isomorphisms

$$\begin{aligned} I^0{\oplus }J^1{\oplus }I^2{\oplus }\cdots {\oplus }J^{2n-1}{\oplus }G^{2n} \,{}\cong {}\, J^0{\oplus }I^1{\oplus }J^2{\oplus }\cdots {\oplus }I^{2n-1}{\oplus }H^{2n} \end{aligned}$$

and

$$\begin{aligned} I^0{\oplus }J^1{\oplus }I^2{\oplus }\cdots {\oplus }J^{2n-1}{\oplus }I^{2n}{\oplus }H^{2n+1} \,{}\cong {}\, J^0{\oplus }I^1{\oplus }J^2{\oplus }\cdots {\oplus }I^{2n-1}{\oplus }J^{2n}{\oplus }G^{2n+1}. \end{aligned}$$

Proof

We prove this by induction. For $n=1$, first note that Corollary 3.2, applied to the diagram

gives $I^0{\oplus }H^1 \cong J^0{\oplus }G^1$. By Proposition 2.4, there is a diagram of the form

and Corollary 3.2 gives $I^0{\oplus }J^1{\oplus }G^2 \cong J^0{\oplus }I^1{\oplus }{H^2}$. To finish the proof for $n=1$, we again apply Proposition 2.4 followed by Corollary 3.2, to get a diagram

and an isomorphism $I^0{\oplus }J^1{\oplus }I^2{\oplus }{H^3} \cong J^0{\oplus }I^1{\oplus }{J^2}{\oplus }{G^3}.$

Assume the result holds some $n\ge 1$. By Proposition 2.4, there is a diagram of the form

and Corollary 3.2 gives

One final application of Proposition 2.4 yields the following diagram:

By Corollary 3.2,

$$\begin{aligned} \begin{aligned}&I^0{\oplus }J^1{\oplus }I^2{\oplus }\cdots {\oplus }J^{2(n+1)-1}{\oplus }I^{2(n+1)}{\oplus }H^{2(n+1)+1}\\&\quad \cong \, J^0{\oplus }I^1{\oplus }J^2{\oplus }\cdots {\oplus }I^{2(n+1)-1}{\oplus }J^{2(n+1)}{\oplus }G^{2(n+1)+1} \end{aligned} \end{aligned}$$

as required. $\square$

We can now prove the Injective Dimension Theorem.

Theorem 3.5

Let $\mathscr {M}$ be the class of admissible monomorphisms in an exact category $(\mathscr {A},{\mathscr {E}\!x})$. Suppose $\mathscr {A}$ has enough $\mathscr {M}$-injectives. The following are equivalent for $n\ge {1}$ and every $E\in \mathscr {A}$.

• (i) If there is an exact sequence of admissible morphisms

  

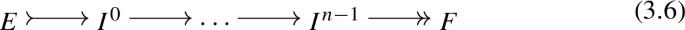
  with each $I^{m}$, $0\le m\le n-1$ injective, then F must be injective;

• (ii) There is an exact sequence of admissible morphisms

  

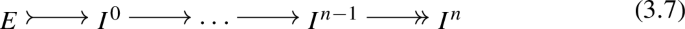
  with each $I^{m}$, $0\le m\le n$ injective.

Proof

Let $E\in \mathscr {A}$. First we show (i) implies (ii). As $\mathscr {A}$ has enough $\mathscr {M}$-injectives, we can build an $\mathscr {M}$-injective resolution of E:

Relabel $J^k$ as $I^k$ for all $0\le k \le n-1$ and $G^n$ as $I^n$, this gives an exact sequence as in Diagram (3.7), and $I^n$ must be $\mathscr {M}$-injective, by condition (i).

Now suppose that condition (ii) holds. There must exist an injective resolution of E of the form

and for any exact sequence as in Diagram (3.6), with each $I^n$ injective, there exists an injective resolution

with $G^n=F$. By Proposition 3.4, there exists a kernel-cokernel pair

and a morphism $\widetilde{\mu }\in Mor _{\mathscr {A}}{({I},{F})}$ such that $\widetilde{\mu }\circ \mu =id _{F}$, and I is a finite product of $\mathscr {M}$-injective objects. Then by Proposition 2.4, I is injective and $\widetilde{\mu }$ is a left inverse for $\mu$, hence, by Proposition 2.2, F is $\mathscr {M}$-injective.

Definition 3.6

Let $\mathscr {M}$ be the class of admissible monomorphisms in an exact category $(\mathscr {A},{\mathscr {E}\!x})$. We say $E\in \mathscr {A}$ has finite $\mathscr {M}$-injective dimension if there exists an exact sequence of admissible morphisms as in Diagram (3.7) with all $I^m$ $\mathscr {M}$-injective. If E is of finite $\mathscr {M}$-injective dimension we write $Inj _{\mathscr {M}}-dim \,{(E)}=0$ if E is $\mathscr {M}$-injective and $Inj _{\mathscr {M}}-dim \,{(E)}=n$ if E is not $\mathscr {M}$-injective and n is the smallest natural number such that there exists an exact sequence of admissible morphisms as in Diagram (3.7) where every $I^m$ is $\mathscr {M}$-injective. If E is not of finite $\mathscr {M}$-injective dimension, we write $Inj _{\mathscr {M}}-dim \,{(E)}=\infty$.

The global dimension of the exact category $(\mathscr {A},{\mathscr {E}\!x})$ is

$$\begin{aligned} \sup \left\{ {Inj _{\mathscr {M}}-dim \,{(E)}}\,|\,{E\in \mathscr {A}} \right\} \in {\mathbb {N}}_0\cup \{\infty \}. \end{aligned}$$

Remark 3.7

The $\mathscr {M}$-injective dimension of an object E in an exact category $(\mathscr {A},{\mathscr {E}\!x})$ can be obtained by examining any of its $\mathscr {M}$-injective resolutions. Indeed, suppose the following is an $\mathscr {M}$-injective resolution of E (with the factorisation of each admissible morphism included):

Then, by Theorem 3.5, $Inj _{\mathscr {M}}-dim \,{(E)}\le n$ if and only if $G^n$ is $\mathscr {M}$-injective.

The original version of Schanuel’s lemma is formulated for projective resolutions, see, e.g., [4, Lemma 5.1] or [9, Theorem 3.41]. An analogous version using the epimorphisms in the class $\mathscr {P}$ can be obtained in any exact category with exact structure $(\mathscr {M},\mathscr {P})$.