1 Introduction

For a pair of entire functions \((u, \psi )\) on the complex plane \(\mathbb {C}\), the induced weighted composition operator \(W_{(u,\psi )}\) maps f to \(u f(\psi ).\) If \(u=1\), then \(W_{(u,\psi )}\) is just the composition map \(C_\psi : f\mapsto f(\psi )\). On the other hand, if \(\psi \) is the identity map, then \(W_{(u,\psi )}\) reduces to the multiplication operator \(M_u: f\mapsto uf\). Thus, \(W_{(u,\psi )}\) generalizes the two operators and can be written as a product \( W_{(u,\psi )}= M_u C_\psi \). The theory of weighted composition operators traces back to the sixties in the work of Forelli [6] where it was shown that the isometries on the Hardy spaces \( H^p\) whenever \(1< p <\infty \) and \( p \ne 2 \) are weighted composition operators. De Leeuw [9] later showed that the same conclusion holds on the space \(H^1\) as well. Since then, the operator has become a natural object of study and its investigation has rapidly evolved in function related operator theory. A number of researchers have studied the operator in various settings expressing its spectral and topological properties in terms of the function theoretic properties of the inducing pairs of symbols \((u,\psi )\); see for example [2, 5, 11, 12, 16, 17] and the references therein.

In this note, we study the dynamical properties of the operators and their adjoints on the Fock space \({\mathcal {F}}_2\). We recall that \({\mathcal {F}}_2\) consists of square integrable analytic functions on the complex plane \(\mathbb {C}\) with respect to the Gaussian measure \(d\mu (z)= \frac{1}{\pi }e^{-|z|^2} dA(z)\) where dA is the Lebesgue area measure in \(\mathbb {C}\). It is a reproducing kernel Hilbert space endowed with the inner product

$$\begin{aligned} \langle f, g\rangle = \int _{\mathbb {C}} f(z)\overline{g(z)}d\mu (z), \end{aligned}$$

norm \(\Vert f\Vert _2:=\sqrt{ \langle f, f\rangle } \), kernel function \(K_w(z)= e^{{\overline{w}} z}\) and normalized kernel \(k_w= \frac{K_w}{\Vert K_w\Vert _2}\).

A great deal of the studies on weighted composition operators have been devoted to characterizing boundedness and compactness spectral properties over various function spaces. On Fock spaces, these properties have been well understood and described for example in [11, 12, 17] and expressed in different conditions among which following the work in [11], \(W_{(u,\psi )}\) is bounded on \({\mathcal {F}}_2\) if and only if u belongs to the space and

$$\begin{aligned} \sup _{z\in \mathbb {C}} |u(z)|e^{\frac{1}{2}(|\psi (z)|^2-|z|^2)} <\infty . \end{aligned}$$
(1.1)

Furthermore, it was proved that condition (1.1) implies \( \psi (z)= az+b, |a|\le 1\) and whenever \(|a|=1\), the multiplier function has the special form

$$\begin{aligned} u=u(0)K_{-{\overline{a}}b}. \end{aligned}$$
(1.2)

Recently, Carroll and Gilmore [2], used the idea of the order of an entire function and proved the following analogous result when u is non-vanishing and \(|a|<1\).

Lemma 1.1

Let \(\psi (z)= az+b, \ |a|<1\) and u be a non-vanishing entire function on \(\mathbb {C}\). Then \(W_{(u,\psi )}\) is

  1. (i)

    compact on \({\mathcal {F}}_2\) if and only if u has the form

    $$\begin{aligned} u(z)= e^{a_0+a_1z+ a_2z^2} \end{aligned}$$
    (1.3)

    for some constants \(a_0, a_1, a_2\) such that \(|a_2|<\frac{1-|a|^2}{2}\).

  2. (ii)

    bounded but not compact on \({\mathcal {F}}_2\) if and only if u has the form in (1.3) with \(|a_2|=\frac{1-|a|^2}{2}\) and either \(a_1+a{\overline{b}}=0\) or \(a_1+a{\overline{b}}\ne 0\) and

    $$\begin{aligned} a_2= - \frac{(1-|a|^2)(a_1+a{\overline{b}})^2}{2|a_1+a{\overline{b}}|^2}. \end{aligned}$$

The representations in (1.2) and (1.3) will play important roles in the rest of our consideration. An important feature following these representations is that there exists an interesting interplay between u and \(\psi \) such that \(W_{(u,\psi )}= M_u C_\psi \) is bounded (compact) on \({\mathcal {F}}_2\) while both \(C_{\psi }\) and u fail to be. For example one can set \(u_0(z)= e^{-z}\), \(\psi _0(z)= z+1\), and observe that \(W_{(u_0,\psi _0)}\) is bounded while both the factors remain unbounded. The purpose of this note is to study the effect of this interplay on the dynamical structures of \(W_{(u,\psi )}\) and its adjoint on \({\mathcal {F}}_2\).

Recall that a bounded linear operator T on a separable Banach space \({\mathcal {H}}\) is said to be cyclic if there exists a vector f in \({\mathcal {H}}\) for which the span of the orbit

$$\begin{aligned} \text {Orb}(T,f)=\big \{ f,\ Tf,\ T^2f,\ T^3 f, \ ...\big \} \end{aligned}$$

is dense in \({\mathcal {H}}\). Such an f is called a cyclic vector for T. The operator is hypercyclic if the orbit itself is dense, and T is supercyclic with vector f if the projective orbit

$$\begin{aligned} \mathbb {C}.\text { Orb}(T,f)= \big \{ \lambda T^nf, \ \ \lambda \in \mathbb {C}, \ n= 0, 1, 2, ...\big \} \end{aligned}$$

is dense. These dynamical properties of T depend on the behaviour of its iterates \(T^n= T \circ T\circ T \circ ...\circ T-n \ \text {times}\). For detailed background, one may consult the monograph [1].

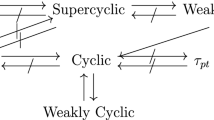
It is worth noting that identifying cyclic and hypercyclic operators has been a subject of great interest partly because they play central role in the study of other operators. More specifically, it is known that every bounded linear operator on an infinite dimensional complex separable Hilbert space is the sum of two cyclic operators [18]. Interestingly, this result holds true with the summands being hypercyclic operators [1, p.50]. In [13], we reported that there exists no supercyclic (and hence hypercyclic) composition operator on Fock spaces. On the other hand, the orbit of any vector f under \(W_{(u,\psi )}\) has elements of the form

$$\begin{aligned} W_{(u,\psi )}^n f= f(\psi ^n) \prod _{j=0}^{n-1} u(\psi ^j) \end{aligned}$$
(1.4)

for all nonnegative integers n and \(\psi ^0\) is the identity map. This shows that the product of weighted composition operators is another weighted composition operator with symbol \((u_n, \psi ^n)\) where

$$\begin{aligned} u_n= \prod _{j=0}^{n-1} u(\psi ^j). \end{aligned}$$
(1.5)

The formula in (1.4) further displays a kind of interplay between the functions \(\psi \) and u and generates interest to ask whether the interplay results in hypercyclic, supercyclic or cyclic weighted composition operators and their adjoints on the Fock space as it did for example on the boundedness and compactness structures. The result in [13] was extended later in [14] for the weighted composition operators asserting that the interplay between the additional multiplier function u and \(\psi \) has failed to make any projective orbit dense enough in \({\mathcal {F}}_2\). This result was also obtained in [2]. The first question is then what happens to this structure for the adjoint of the operators. Note that the adjoint \(W_{(u,\psi )}^*\) of a bounded weighted composition operator \(W_{(u,\psi )}\) on \({\mathcal {F}}_2\) satisfies

$$\begin{aligned} \langle W_{(u,\psi )} f, g\rangle = \langle f, W_{(u,\psi )}^*g\rangle \end{aligned}$$

for all \(f, g \in {\mathcal {F}}_2\). We recall that the adjoint of a weighted composition operator on \( {\mathcal {F}}_2\) is not necessarily a weighted composition operator. Indeed, L. Zhao and C. Pang [19] proved that for pairs of entire functions \(u_1, \psi _1\) and \(u_2, \psi _2\) from \({\mathcal {F}}_2\), the relation \(W_{(u_1, \psi _1)}^*= W_{(u_2, \psi _2)}\) holds if and only if

$$\begin{aligned} \psi _1(z)= az+b, u_1(z)= dK_c(z), \psi _2(z)= {\overline{a}}z+c, \text {and} \ \ u_2(z)= {\overline{d}}K_c(z) \end{aligned}$$

where a, b, c and d are constants such that \(d\ne 0\) and either \(|a|<1\) or \(|a|=1\) and \(c+{\overline{a}}b=0\). Thus, an operator and its adjoint can have quite different dynamical structures. An example is the multiplication operator on Hardy spaces which the operator fails to be hypercyclic while the structures are different for its adjoint as can be seen [1, p.26]. Let us now show that the space \({\mathcal {F}}_2\) fails to support supercyclic adjoint weighted composition operators either.

Theorem 1.2

Let u and \(\psi \) be analytic maps on \(\mathbb {C}\) such that \(W_{(u,\psi )}^*\) is bounded on \({\mathcal {F}}_2\). Then \(W_{(u,\psi )}^*\) cannot be supercyclic on \({\mathcal {F}}_2\).

The proof of the result is presented in Sect. 2.1. Given the absence of supercyclic \(W_{(u,\psi )}\) and \(W_{(u,\psi )}^*\) on the space \({\mathcal {F}}_2\), the next natural question is what happens to the weaker cyclicity properties for the two classes of operators. Clearly, supercyclicity is a much stronger property than cyclicity. We now state the main result of our article which effectively answers the above question. The proof will be presented in several statements in the next section.

Theorem 1.3

Let u and \(\psi (z)=az+b, \ |a|\le 1\) be analytic maps on \(\mathbb {C}\) such that \(W_{(u,\psi )}\) is bounded on \({\mathcal {F}}_2\). Then the following statements are equivalent.

  1. (i)

    \(W_{(u,\psi )}\) is cyclic on \({\mathcal {F}}_2\);

  2. (ii)

    u is non-vanishing and \(a^k\ne a\) for all positive integers \( k\ge 2\);

  3. (iii)

    \(W_{(u,\psi )}^*\) is cyclic on \({\mathcal {F}}_2\).

The equivalency of statements (i) and (ii) is proved in Theorem 2.4 while that of (ii) and (iii) is proved in Theorem 2.5. The theorem asserts that a weight function cannot have zeros if the corresponding induced weighted composition operator or its adjoint admits a cyclic vector. Furthermore, the cyclicity of \(W_{(u,\psi )}\) or its adjoint requires that the iterates of the derivative of the symbol \(\psi (z)= az+b\) to be pairwise distinct. This is indeed the condition required for the cyclicity of the composition operator [13]. It means that every nonzero multiplier function makes it possible for the weighted operator to inherent the same cyclic structure as the unweighted case. We note also that the cyclicity condition clearly restricts \(\psi \) to be a nonconstant function.

2 Proof of the Main Results

The fixed point behaviour of the map \(\psi (z)= az+b\) plays an important role in determining the cyclic structure of a bounded weighted composition operator and its adjoint. Thus, in the rest of the manuscript we denote by \(z_0\) such a fixed point where \(z_0= b/(1-a)\) for \(a\ne 1\), and \(z_0=0\) for \(a=1\) and \(b=0.\)

Let us now identify eigenvectors of the weighted composition operators which will be used to prove our main results apart from being interest of its own.

Lemma 2.1

Let u and \( \psi \) be analytic functions on \(\mathbb {C}\), and \(W_{(u,\psi )}\) be bounded on \({\mathcal {F}}_2\) and hence \(\psi (z)= az+b\) with \(|a|\le 1\). Let u be non-vanishing on \(\mathbb {C}\). Then for all \(m\ge 0\), the sequence

$$\begin{aligned} f_m(z)= {\left\{ \begin{array}{ll}(z-z_0)^m e^{\frac{a{\overline{b}}}{a-1}z}\ \ \ |a|=1, \ a\ne 1\\ (z-z_0)^m e^{h(z)}, \ \ 0<|a|<1 \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} h(z)= \frac{a_1}{1-a}(z-z_0)+ \frac{2a_2z_0}{1-a}(z-z_0)+ \frac{a_2}{1-a^2}(z-z_0)^2 \end{aligned}$$
(2.1)

\(a_1, a_2\) as in Lemma 1.1 constitutes a sequence of eigenvectors for \(W_{(u,\psi )}\). In this case

$$\begin{aligned} \{ u(z_0) a^m, m\in \mathbb {N}_0\}\subset \sigma _p(W_{(u,\psi )}) \end{aligned}$$

where \(\sigma _p(W_{(u,\psi )})\) refers to the point spectrum of \(W_{(u,\psi )}\).

Proof

For \(|a|=1\) and \(a\ne 1\), we apply the representation of the weight function in (1.2) and compute

$$\begin{aligned} W_{(u,\psi )} f_m(z)&= \,\, u(0) K_{-{\overline{a}}b}(z) f_m(az+b)= u(0)a^m (z-z_0)^m e^{\frac{a{\overline{b}}}{a-1}(az+b)}\\&=\,\, u(0)a^m e^{\frac{a|b|^2}{a-1}} f_m(z)= u(z_0)a^mf_m(z) \end{aligned}$$

which also implies that \(u(z_0)a^m\) represents a sequence of eigenvalues in this case.

When \(0<|a|<1\), observe that because of the condition in Lemma 1.1, the sequence of functions \(f_m\) belong to the space \( {\mathcal {F}}_2\). Then applying the same lemma, we may rewrite the weight function as

$$\begin{aligned} u(z)&=\,\, e^{a_0+a_1z+ a_2z^2}= u(z_0) e^{-(a_0+a_1z_0+a_2z_0^2)+ a_0+a_1z+ a_2z^2} \\&=\,\,u(z_0)e^{a_1(z-z_0)+ 2a_2z_0(z-z_0)+a_2(z-z_0)^2}. \end{aligned}$$

Next, for \(m\ge 0\),

$$\begin{aligned} W_{(u,\psi )} f_m(z)= u(z) f_m(az+b)= u(z_0) a^m (z-z_0)^m e^{g(z)+h(az+b)} \end{aligned}$$

where \(g(z)= a_1(z-z_0)+ 2a_2z_0(z-z_0)+a_2(z-z_0)^2\).

Now, a simple computation shows that

$$\begin{aligned} g(z)+h(az+b)= h(z). \end{aligned}$$

Therefore

$$\begin{aligned} W_{(u,\psi )} f_m= u(z_0) a^m f_m. \end{aligned}$$
(2.2)

The relation in (2.2) implies \(u(z_0) a^m\) is a sequence of eigenvalues in this case as well and completes the proof. \(\square \)

2.1 Proof of Theorem 1.2

First we mention that if \(W_{(u,\psi )}^*\) is supercyclic, then u cannot vanish in the complex plane. The same conclusion holds with the weaker cyclicity property. A proof for this will be given once later in Theorem 2.5. Thus, we can assume that u is non-vanishing in this proof and apply Lemma 2.1 as needed.

Since \(W_{(u,\psi )}\) is bounded, we set \(\psi (z) =az+b, \ |a|\le 1\) and consider two different cases.

Case 1: Let \(|a|<1\). Then by Lemma 2.1, it follows that the set

$$\begin{aligned} \big \{u(z_0) a^m, \ \ m\in \mathbb {N}_0\big \} \end{aligned}$$
(2.3)

is contained in the point spectrum of the adjoint of \( W_{(u,\psi )}^*, \sigma _p(W_{(u,\psi )}).\) On the other hand, by [1, Proposition 1.26] the point spectrum of the adjoint of a supercyclic operator is either empty or

$$\begin{aligned} \sigma _p(W_{(u,\psi )})= \{\lambda \} \end{aligned}$$
(2.4)

for a single number \(\lambda \ne 0\). By (2.3), the point spectrum is nonempty. Thus, it suffices to show that the point spectrum contains at least two elements. First observe that if \(u(z_0) = 0,\) then zero belongs to the point spectrum and contradicts (2.4) and hence the operator is not supercyclic.

Assume that \(a= 0\) and hence \(\psi (z)= b\). Then the relation in (1.4) implies

$$\begin{aligned} (W_{(u,\psi )})^n f(z)= f(b)u(b)^n. \end{aligned}$$

A simple calculation shows that any non zero function g in the space such that \(g(b)=0\) is orthogonal to the projective orbit of f under \( W_{(u,\psi )}^*\). Thus, \( W_{(u,\psi )}^*\) cannot be supercyclic in this case either. On the other hand, if \(a\ne 0 \), then the set in (2.3) contains infinitely many elements and contradicts (2.4) and hence \(W^*_{(u,\psi )}\) is not supercyclic.

Case 2 It remains to show the case for \(|a|=1\). This is rather immediate as \(u= u(0) K_{-{\overline{a}}b} \), by Theorem 3.2 of [11], \(W_{(u,\psi )}\) is a constant multiple of a unitary operator and hence normal. Since the adjoint of a normal operator is normal, \(W^*_{(u,\psi )}\) is also normal. Then, our conclusion follows from a result of Hilden and Wallen [8] and completes the proof.

2.2 Cyclic \(W_{u,\psi }\) and \(W_{(u,\psi )}^*\)

Having proved that no supercyclic \(W_{u,\psi }^*\) is supported on the Fock space, we now study the weaker cyclicity property. We may first recall that even if an operator is cyclic on Hilbert space, its adjoint does not necessarily have to be cyclic. If both an operator and its adjoint are cyclic, they do not necessarily have to share the same cyclic vector. But for special types of operators, normal operators, the following interesting result holds.

Lemma 2.2

Let T be a normal operator on a Hilbert space \({\mathcal {H}}\). Then \(f\in {\mathcal {H}}\) is a cyclic vector for T if and only if it is a cyclic vector for its adjoint \(T^*\).

The proof of the lemma is contained in [10, p.74] which was also referred to as a solution to problem 164 in Halmos’ problem book [7].

Lemma 2.3

Let u and \(\psi (z)=az+b, \ |a|= 1\) be analytic maps on \(\mathbb {C}\) such that \(W_{(u,\psi )}\) is bounded on \({\mathcal {F}}_2\). If \(a^m = a\) for some \( m\ge 2\) and \(u(z_0)\ne 0 \), then both \(W_{(u,\psi )}\) and \(W_{(u,\psi )}^*\) are not cyclic on \({\mathcal {F}}_2\).

Proof

Let us first show that \(W_{(u,\psi )}\) is not cyclic and consider three different cases.

Case 1: \(a\ne 1\). In this case, we may first set \(\psi _{z_0}(z) = z-z_0\) and claim that the weighted composition operator induced by \((k_{z_0}, \psi _{z_0})\) is an isometric bijective map on \({\mathcal {F}}_2\) with inverse \(W_{(k_{-z_0},\psi _{z_0}^{-1})}\). To this claim, for every \(f\in {\mathcal {F}}_{2}\)

$$\begin{aligned} \Vert W_{(k_{z_0},\psi _{z_0})}f\Vert _2^2&= \frac{1}{\pi } \int _{\mathbb {C}} |k_{z_0}(z)|^2 |f(z-z_0)|^2 e^{-|z|^2}dA(z) \quad \quad \quad \quad \\&=\frac{1}{\pi } \int _{\mathbb {C}} |f(z-z_0)|^2 e^{-|z-z_0|^2} \bigg ( |k_{z_0}(z)|^2 e^{|z-z_0|^2-|z|^2}\bigg ) dA(z)\\&= \frac{1}{\pi } \int _{\mathbb {C}} |f(z-z_0)|^2 e^{-|z-z_0|^2} dA(z)=\Vert f\Vert _2^2. \end{aligned}$$

This shows that the operator is a linear isometry and hence satisfies the injectivity condition \( W_{(k_{z_0},\psi _{z_0})}^{-1} W_{(k_{z_0},\psi _{z_0})}= I.\) See also [20, Proposition 2.38] for this isometry. On the other hand, for each \(f\in {\mathcal {F}}_{2}\)

$$\begin{aligned} W_{(k_{z_0},\psi _{z_0})} W_{(k_{-z_0},\psi _{z_0}^{-1})} f(z)= k_{z_0}(z) k_{-z_0}(z-z_{0}) f(z)= f(z) \end{aligned}$$

which also shows that \(W_{(k_{z_0},\psi _{z_0})}W_{(k_{z_0},\psi _{z_0})}^{-1}= I\), and hence the claim.

Next, using \(z_0= b/(1-a)\) and (1.2) for every \(f\in {\mathcal {F}}_{2}\) we compute

$$\begin{aligned}&W_{(k_{-z_0},\psi _{z_0}^{-1})} W_{(u,\psi )} W_{(k_{z_0},\psi _{z_0})} f(z)\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \\&\quad = k_{-z_0}(z)u(\psi _{z_0}^{-1}(z)))k_{z_0}(\psi (\psi _{z_0}^{-1}(z)) f( \psi _{z_0}(\psi (\psi _{z_0}^{-1}(z))))\\&\quad = k_{-z_0}(z)u(0) K_{-{\overline{a}}b}(z+z_0) k_{z_0}(az+b+az_0) f(az)= u(z_0) C_{\Psi _0} f(z) \end{aligned}$$

where \(C_{\Psi _0}\) the composition operator induced by the symbol \(\Psi _0(z)= az\). This shows that \( W_{(u,\psi )} \) is similar to the composition operator \(C_{\Psi _0}\) up to a scalar multiple. Since \(u(z_0)=u(0)e^{\frac{a|b|^2}{a-1}}\ne 0\), the constant multiplier above is non-zero. Moreover, since cyclicity is similarity invariant, it suffices to show that \(C_{\Psi _0}\) is not cyclic whenever \(a^m= a\) for some \(m\ge 2\). But this follows immediately from [13, Theorem 2.5]. Thus, \(W_{(u,\psi )}\) is not cyclic. On the other hand, since the operator \(W_{(u,\psi )}\) is normal in this case [11], its adjoint is also normal and hence the conclusion for \(W_{(u,\psi )}^*\) follows from Lemma 2.2.

Case 2: \(a=1\) and \(b= 0\). Then a simple computation shows that for any \(f\in {\mathcal {F}}_2\),

$$\begin{aligned} W_{(u,\psi )}^m f= f u(0)^m \end{aligned}$$

asserting that all the elements in the orbit are scalar multiplies of the vector f. Any vector g in \( {\mathcal {F}}_2\) orthogonal to f is also orthogonal to the closed linear span of its orbit under \(W_{(u,\psi )}\). Thus, it suffices to show that there exists such a non-zero g. To this end, since \(S=\overline{\text {span}\{f\}}\) is a closed subspace of \({\mathcal {F}}_2\), the projection operator \(P: {\mathcal {F}}_2\rightarrow S\) is continuous. Then for \(f_1\in {\mathcal {F}}_2\backslash S\), the function

$$\begin{aligned} g= f_1-Pf_1\in S^\perp \end{aligned}$$

and orthogonal to the linear span of the orbit.

Case 3 \(a=1\) and \(b\ne 0\). Then, by a result of [11], the operator \(W_{(u,\psi )}\) is normal and hence not cyclic. If it were cyclic, then a classical result of Von Neumann [15] implies that the operator has simple spectrum. On the contrary, by [16, Theorem 3.1], the spectrum of \(W_{(u,\psi )}\) is the set

$$\begin{aligned} \big \{ z\in \mathbb {C}: |z| = |u(0)| e^{\frac{|b|^{2}}{2}} \big \} \end{aligned}$$

which is not simple. By Lemma 2.2, the adjoint operator is not cyclic either, and completes the proof. \(\square \)

Theorem 2.4

Let u and \(\psi (z)=az+b, \ |a|\le 1\) be analytic maps on \(\mathbb {C}\) such that \(W_{(u,\psi )}\) is bounded on \({\mathcal {F}}_2\). Then \(W_{(u,\psi )}\) is cyclic on \({\mathcal {F}}_2\) if and only if u is non-vanishing and \(a^k\ne a\) for all positive integers \( k\ge 2\).

Proof

We may first proof the necessity of the condition. If the operator is cyclic and \(u(w)= 0\) for some \(w\in \mathbb {C}\), then using (1.5),

$$\begin{aligned} u_n(w)= u(w)\prod _{j=1}^{n-1} u(\psi ^j(w))= 0 \end{aligned}$$

for all \(n\in \mathbb {N}_0\). This shows that the orbit of any function \(f\in {\mathcal {F}}_2\) under \(W_{(u,\psi )}\) contains only functions that vanish at w which obviously extends to the closed linear span of the orbit. This is a contradiction.

For \(|a|=1\), the necessity of the condition \(a^k\ne a\) for all positive integers \( k\ge 2\) readily follows from Lemma 2.3.

To prove the sufficiency, we argue as follows. Observe that since the polynomials are dense in \({\mathcal {F}}_2\), the closed linear span of \( g_m(z)= (z-z_0)^m\) is dense. Then by an interesting result of [?], the closed linear span of \((g_m g)\) is also dense for every non-vanishing function \( g\in {\mathcal {F}}_2\). Thus, setting in particular

$$\begin{aligned} g(z)= {\left\{ \begin{array}{ll} e^{\frac{a{\overline{b}}}{a-1}z}\ \ \ |a|=1, \ a\ne 1\\ e^{h(z)}, \ \ 0<|a|<1 \end{array}\right. } \end{aligned}$$

where h is as in (2.1), it follows from the above and Lemma 2.1 that the operator \(W_{(u,\psi )}\) has eigenvectors \((f_m= g g_m)\) with pairwise distinct eigenvalues \(u(z_0)a^m\). Furthermore, the linear span of the vectors \(f_m\) is dense in \( {\mathcal {F}}_2\). Then, by a result of K. Clancey and D. Rogers [4, Lemma 4 and Theorem 3], the operator is cyclic and indeed has a dense set of cyclic vectors. \(\square \)

Theorem 2.5

Let u and \(\psi (z)=az+b, \ |a|\le 1\) be analytic maps on \(\mathbb {C}\) such that \(W_{(u,\psi )}^*\) is bounded on \({\mathcal {F}}_2\). Then \(W_{(u,\psi )}^*\) is cyclic on \({\mathcal {F}}_2\) if and only if \(a^k\ne a\) for all positive integers \( k\ge 2\) and u is non-vanishing.

Proof

Necessity The necessity of the condition \(a^k\ne a\) for all positive integers \( k\ge 2\) follows from Lemma 2.3.

Let us show that u is non-vanishing. If \(|a|=1\), then by (1.2), u vanishes at a point if and only if u is the zero function which obviously implies that the operator is not cyclic. On the other hand, \(\psi \) can not be a constant since \(a^k\ne a\). Thus, we may assume \(0<|a|<1\) and \(W^*_{(u,\psi )}\) is cyclic with a cyclic vector f. Aiming to argue in the contrary, suppose that u vanishes at w. Then since the reproducing kernels are dense in the space, there exists a sequence \( s^m_f= \sum _{j=1}^m a_jK_{z_j} \rightarrow f \) as \(m\rightarrow \infty \) where one of the \(z_j's\) can be chosen in such a way that

$$\begin{aligned} \psi ^i(z_j) = a^iz_j+\frac{b(1-a^i)}{1-a}= w \end{aligned}$$

for some \(i\ge 1\). A computation with the adjoint property gives

$$\begin{aligned} W_{(u,\psi )}^* K_{z}= \overline{u({z})} K_{\psi ({z})} \end{aligned}$$

which implies

$$\begin{aligned} W_{(u,\psi )}^{*n}s^m_f=\sum _{j=1}^m a_j \overline{u(z_j)}\prod _{i=1}^{n-1} \overline{u({\psi ^i(z_j)})} K_{\psi ^n(z_j)} \rightarrow W_{(u,\psi )}^{*n} f \end{aligned}$$

as \(m\rightarrow \infty \). This implies that the orbit of f under \(W^*_{(u,\psi )}\) contains only a finite number of elements and its linear span can not be the whole space \({\mathcal {F}}_2\).

Sufficiency If \(|a|=1\), then the result follows from Lemma 2.2 and Theorem 2.4 since both \(W_{(u,\psi )}\) and \(W_{(u,\psi )}^*\) are normal operators. Thus, we proceed to verify the sufficiency for the case when \(0<|a|<1\). We may first assume that \(b=0\) and exhibit that \(K_z, \ z\ne 0\) is a cyclic vector for \(W_{(u,\psi )}^*\). Now, fix a vector \(f\in {\mathcal {F}}_2\) that is orthogonal to the orbit of \(K_z\) under \(W_{(u,\psi )}^*\). We claim that f should be the zero function. To see this, note that for every m

$$\begin{aligned} 0&= \langle f, \ W_{(u,\psi )}^{*m} K_z \rangle = \langle W_{(u,\psi )}^{m} f, \ K_z \rangle \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \nonumber \\&= W_{(u,\psi )}^{m} f(z)= f(a^mz) \prod _{j=0}^{m-1} u(a^jz). \end{aligned}$$
(2.5)

By assumption, u is non-vanishing on \(\mathbb {C}\) and hence (2.5) holds only if for all m

$$\begin{aligned} f(a^m z)=0. \end{aligned}$$
(2.6)

Now, since \(|a|<1 \), the sequence \({\overline{a}}^m z \rightarrow 0\) as \(m\rightarrow \infty \) for every \(z\in \mathbb {C}\). Therefore, the relation in (2.6) holds only if f vanishes on the null sequence \(a^m z\). It follows that f is the zero function as asserted.

It remains to consider the case when \(b\ne 0\) and hence \( z_0\ne 0.\) In this case we may set \(\psi _1(z)= az\),

$$\begin{aligned} u_1(z)= \frac{u(z+z_0)}{\Vert K_{-z_0}\Vert _2^{2} } e^{-\overline{z_0}z+ \overline{z_0}(az+az_0+b)} \end{aligned}$$

and observe that \(\psi _1(0)= 0\) and \(u_1(0)= u(z_0)\). A straightforward calculation shows that

$$\begin{aligned} W_{(u_2,\psi _2)} W_{(u, \psi )} W_{(u_2,\psi _2)}^{-1}= W_{(u_1, \psi _1)} \end{aligned}$$
(2.7)

and \( W_{(u_2,\psi _2)}^{-1}= W_{(u_3, \psi _3)}\) where \(u_2(z)= k_{-z_0}(z)\), \(\psi _2(z)= z+z_0\), \(u_3=k_{z_0}\), and \(\psi _3(z)=z-z_0\). It follows that the weighted composition operators \(W_{(u_1, \psi _1)}\) and \(W_{(u, \psi )}\) are similar and so does their adjoints. Thus, our conclusion follows from the first case and completes the proof of the sufficiency. \(\square \)

2.3 The Composition Operator and its Adjoint

The adjoint of a bounded composition operator on the Fock space is not necessarily a composition operator. As proved in [3, Lemma 2], for \(\psi = az+b\), the adjoint of \(C_\psi \) is rather a weighted composition operator where the weight function is a reproducing kernel, namely that \(C_\psi ^*= W_{(K_b,\phi )}\) where \(\phi (z)= {\overline{a}}z\). It follows from this, Theorem 1.2 and [14, Theorem 2.1]( see also [2, Theorem 5.1]) neither the composition nor its adjoint can be supercyclic on \({\mathcal {F}}_2\).

The cyclicity property of \(C_\psi ^*\) is described below by an exact the same condition as that of the composition operator itself.

Corollary 2.6

Let \(C_\psi \) be bounded on \({\mathcal {F}}_2\), that is \(\psi (z)= az+b, |a|\le 1\) and \(b= 0\) whenever \( |a|= 1.\) Then the following statements are equivalent.

  1. (i)

    \(C_\psi \) is cyclic on \({\mathcal {F}}_2\);

  2. (ii)

    \(a^k\ne a\) for each positive integer \(k\ge 2\);

  3. (iii)

    \(C_\psi ^*\) is cyclic on \({\mathcal {F}}_2\).

Note that since \(C_\psi ^*= W_{(K_b,\phi )}\) and \(K_b\) is non-vanishing, the equivalency of statement (ii) and (iii) follows from Theorem 2.4. As a special case of Lemma 2.1, we observe that the sequence \(g_m(z)= (z-z_0)^m, m\in \mathbb {N}_0\) represents eigenvectors for \(C_\psi \) with corresponding eigenvalues \(a^m\). It follows from the assumption \(a^m\ne a\) that \(C_\psi \) has set of eigenvectors with corresponding distinct eigenvalues \(a^m\). Furthermore, the linear span of such vectors is dense in \({\mathcal {F}}_2\). Then, by a result of K. Clancey and D. Rogers [4, Lemma 4 and Theorem 3] the operator has a dense set of cyclic vectors.

We close this section with a remark on the dynamics of the multiplication operator on the Fock space. Unlike the composition operator, a bounded multiplication operator on \({\mathcal {F}}_2\) cannot be cyclic. It is known that the multiplication operator \(M_zf=zf\) is cyclic on the disc algebra since

$$\begin{aligned} \text {span}\{Orb(M_z,1)\}= \text {span}\{1,z,z^2,...\} \end{aligned}$$

is dense in the algebra \(A(\mathbb {D})\). But the operator \(M_z\) is not even defined on the Fock space \({\mathcal {F}}_2\). In fact only constant multipliers are admissible on Fock spaces.