Radon Transforms in Hyperbolic Spaces and Their Discrete Counterparts

Abstract

In the hyperbolic disc (or more generally in real hyperbolic spaces) we consider the horospherical Radon transform R and the geodesic Radon transform X. Composition with their respective dual operators yields two convolution operators on the disc (with respect to the hyperbolic measure). We describe their convolution kernels in comparison with those of the corresponding operators on a homogeneous tree T, separately studied as acting on functions on the vertices or on the edges. This leads to a new theory of spherical functions and Radon inversion on the edges of a tree.

1 Introduction

The aim of this article is to compare various types of Radon transforms on hyperbolic spaces and on homogeneous trees, a subject on which the authors collaborated with Carlos Berenstein, coauthoring with him a preliminary survey. Our goal is to present these ideas in a renewed version with the addition of several original results on Radon transforms on homogeneous trees: in particular, a theory of spherical functions, the Plancherel measure and the Radon inversion on the edges.

The Radon transform was introduced in [33] as the operator on continuous compactly supported functions in the plane defined by integrating over lines. This operator and its inversion formula, studied later in [28], have become of wide interest in applied mathematics because of Computerized Axial Tomography (C.A.T.) and its need of fast hardware implementations of the inversion formula. Many different variants of the Radon transform have been investigated since then, in a long list of articles in pure and in applied mathematics. Despite its long history, the Radon transform is still in the focus of current research, both in continuous and discrete settings: see, for instance, [2, 10, 16, 34] and their references lists.

For instance, it is of interest to consider Radon transforms on the hyperbolic disc. One motivation for these extensions, introduced and deeply investigated in a series of papers by S. Helgason (see [25] for references), is due to the fact that there are two natural analogs of lines in hyperbolic geometry, and consequently two extensions of the Radon transform. The first is to geodesics in the hyperbolic metric: that is, arcs of Euclidean circles in the Poincaré disc which cross the boundary orthogonally. The second extension is to horospheres, that are circles in the disc tangent to the boundary. Following Helgason, we shall call Radon transform the latter, and X-ray transform the former, and denote them by R and X, respectively.

The typical approach to the inversion of the Radon transform in the flat plane is based upon some type of radial average. In order to reconstruct the value of f at a point x, one considers the average of Rf over all lines through x. This amounts to applying to Rf the dual Radon transform $R^*$. Unfortunately $R^*Rf$ does not coincide with f; however, the operator $R^*R$ commutes with translations, therefore it is a convolution operator on functions on the plane (it also commutes with rotations, hence the convolution kernel is radial). Thus, in order to invert R, it is enough to invert this convolution operator on an appropriate function space, a task which is made easier by spectral theory (i.e., Fourier analysis).

The same approach works in the hyperbolic disc. The set of horospheres through a point x can be identified with the boundary $\Omega$ of the disc, and the set of geodesics through x with the set of unordered pairs $(\Omega \times \Omega {\setminus }\text {diagonal})/\{\pm 1\}$. Hence these spaces inherit natural Borel structures and Borel measures which are covariant under the group of automorphisms of the disc. Here the dual transforms $R^*$ and $X^*$ are defined in terms of these measures (and of the hyperbolic measure on the disc). The operators $R^*R$ and $X^*X$ are convolution operators on the disc (with respect to the hyperbolic measure). By inverting these convolvers we obtain inversion formulas for R and X. A similar approach works for the geodesic transform and the horospherical transform in n-dimensional hyperbolic space.

Explicit inversion formulas can be found in [5, 23] for X, and in [25] for R. We shall explore the intriguing similarity, observed in [1, 6, 7, 14, 15], between Radon transforms on the disc and analogous operators defined on homogeneous trees. This led to regard homogeneous trees as discrete counterparts for the hyperbolic disc and semisimple rank-one symmetric spaces in the study of representation theory, harmonic functions, Hardy spaces, and integral geometry. In some cases, this resemblance has been extended to general trees; for a detailed bibliography, see [11, 20, 29] and references therein. In particular, the horospherical Radon transform on trees has been studied in [7, 12, 15, 20] and the X-ray transform in [1, 6]. Homogeneous trees do not provide a discrete model for n-dimensional hyperbolic space except when $n=2$ (that is, for the disc); discrete models for higher dimensional hyperbolic spaces should be obtained from higher-rank Bruhat-Tits buildings, see [3, 4].

From the point of view of Radon transforms, the analogy between the hyperbolic disc and homogeneous trees is best seen by comparing the continuous and the discrete convolution kernels of $R^*R$ and $X^*X$. We start this comparison in Sect. 2 by deriving the explicit expression of the radial convolution kernels $J_R$ of $R^*R$ and $J_X$ of $X^*X$ on the hyperbolic disc (the general expression in n-dimensional hyperbolic space will also be stated). The corresponding kernels on the vertices of a homogeneous tree T are obtained in Sect. 3. We shall see, both for the disc and for T, that the value $J_X(d)$ of the kernel $J_X$ at pairs of points at distance d is inversely proportional to the ‘length’ of the circle of radius d, whereas $J_R(d)$ is inversely proportional to the length of the circle of radius d/2.

The computation of the convolution kernel $J_R$ on the set V of vertices of T leads to a direct computation of the inverse convolution operator (Corollary 3.4), hence to the inversion of R. On the other hand, no such direct computation seems feasible on the set E of edges of T. Because of this, we prove many preliminary results in analysis for functions on E.

Analysis on functions on V is well-known, and makes extensive use of spherical functions, the spectrum of the Laplace operator and its Plancherel measure, and the spherical Fourier transform. Here we need to study similar problems and techniques for functions on E. Spherical functions and the spherical Fourier transform on E have been indirectly computed in [27], where E is regarded as a graph, that is not a tree but the dual graph of T; hence those results may be transported to functions on E. On the other hand, the Plancherel measure and the Radon transform on E have not yet appeared in the literature. The geodesic and the horospherical Radon transforms on V are dealt with in Sects. 3.2,3.3, respectively. The geodesic Radon transform on E is studied in Sect. 4, where a simple inversion formula is found. The Poisson kernel for edges of T, the edge-spherical functions and the spectrum of the Laplacian on E are studied in the first part of Sect. 5. The Plancherel measure on E is computed in Sect. 5.4, and the horospherical Radon transform on E is introduced in Sect. 5.5. Finally, the Radon back-projection on E is studied in Sect. 6.1 and shown to give rise to a convolution operator acting on a Schwartz class on E to a space of distributions, whose inversion is obtained in Sect. 6.2.

Unlike the hyperbolic disk and rank-one symmetric spaces, trees appear in several different setups. Indeed, trees may be non-homogeneous, hence discrete analogs of Riemannian spaces that are not group-invariant. There is an intermediate case: semi-homogeneous trees, that are trees with two different alternating degrees of homogeneity. The isometry groups of these trees are not transitive but have index 2. The homogeneous tree whose degree is a prime number p has a transitive group of isometries isomorphic to the p-adic semisimple group $PGL(2,\mathbf {Q}_p)$ and is the typical lowest-rank Bruhat-Tits building. A combinatorial generalization (Tits buildings) includes all homogeneous trees. Semi-homogeneous trees give all the other examples of combinatorial Tits buildings of the same rank. Therefore these trees can be appropriately included in the environment of discrete structures where Radon transforms bear strong analogies to continuous symmetric spaces. This paper describes also the kernels of $R^*R$ and $X^*X$ on vertices of semi-homogeneous trees, in comparison to the continuous environment. A more extensive account of integral geometry on trees will appear in [16].

2 Radon Transforms in the Hyperbolic Disc

2.1 The X-Ray Transform

The results of this subsection are adapted from [5, 25]. As a model for the real hyperbolic space $\mathbf {H}^2$ we shall take the open unit disc $U=\{z\in \mathbf {C}:\big |{z}\big |<1\}$ of $\mathbf {C}$ endowed with the Poincaré metric

$$\begin{aligned} ds ^2 =\frac{ 4 \big |{dz}\big |^2}{\bigl (1-\big |{z}\big | ^2\bigr )^2}, \end{aligned}$$

which is conformal to the Euclidean metric $\big |{dz}\big |^2$ and has constant curvature $-1$. The relation between the hyperbolic and the Euclidean distance d(z, 0) of z from the origin is

$$\begin{aligned} \big |{z}\big | =\tanh \frac{d(z,0)}{2}, \quad \text {i.e.,}\quad d(z,0) =\log \frac{1+\big |{z}\big |}{1-\big |{z}\big |}. \end{aligned}$$

The elements of the group ${{\,\mathrm{Aut}\,}}^+ U$ of orientation-preserving isometries of U are the Möbius transformations

$$\begin{aligned} U\ni z\mapsto \tau _{\theta , w}(z) = e^{i\theta }\frac{z+ w }{1+\overline{w} z} \end{aligned}$$

parametrized by $w\in U$ and $\theta \in \mathbf {R}/2\pi \mathbf {Z}$. Observing that $\tau _{0,w}=\tau _{0,-w}^{-1}$ maps 0 to w, one easily computes the hyperbolic distance between arbitrary z, w as

$$\begin{aligned} d(z,w) =\log \frac{\big |{1-z\overline{w}}\big |+\big |{z-w}\big |}{\big |{1-z\overline{w}}\big |-\big |{z-w}\big |}. \end{aligned}$$

The geodesics of U are arcs of (Euclidean) circles which intersect the unit circle $\partial U$ of $\mathbf {C}$ perpendicularly. Taking geodesic polar coordinates centered at 0 on U, we write $z=e^{i\theta }\tanh (r/2)$, where $r=d(0,z)$ and $\theta \in \mathbf {R}$. The Poincaré metric is then expressed by

$$\begin{aligned} d s ^2 = d r ^2+\sinh ^2 r \,d\theta ^2. \end{aligned}$$

(1)

Therefore a geodesic circle of radius r (the set of points at hyperbolic distance r from a fixed center) has hyperbolic length

$$\begin{aligned} A(r) =2\pi \sinh r. \end{aligned}$$

${{\,\mathrm{Aut}\,}}^+ U$ acts transitively on the set of geodesics $\Gamma$ in U, hence $\Gamma$ has a non-zero invariant measure. The X-ray transform X is defined on functions on U having sufficiently fast decay at $\partial U$ as

$$\begin{aligned} Xf(\gamma ) =\int _\gamma f(z)\,ds(z) \quad \text {for every } \gamma \in \Gamma . \end{aligned}$$

For simplicity we shall assume f to be in $\mathcal {S}(U)$, the space of smooth functions rapidly decreasing with all their derivatives. To define the dual $X^*$ of X, let $\gamma _\theta$ be the geodesic through 0 and $e^{i\theta }$, and set

$$\begin{aligned} X^*\phi (0) =\frac{1}{2\pi } \int _0^{2\pi } \phi (\gamma _\theta ) \,d\theta \end{aligned}$$

for all, e.g., essentially bounded functions on $\Gamma$. For arbitrary $z\in U$ set $X^*\phi (z)=X^*(\phi \circ \tau _{0,z})(0)$.

We now compute $X^*X$ and show that it is the convolution operator (with respect to the convolution product induced by ${{\,\mathrm{Aut}\,}}^+ U$) with the radial kernel $J_X(r)=2/A(r)=1/\pi \sinh r$. The convolution product on a metric space induced by a transitive group of automorphisms is explained at the beginning of the “Appendix”, where for simplicity we shall restrict attention to the setup of homogeneous trees. Here we briefly explain the setup of the disk U. Denote by $d\mu$ the Haar measure on the unimodular group $G={{\,\mathrm{Aut}\,}}^+ U$ and by dv the quotient measure on $G/G_0$, that is, the volume element on U, namely

$$\begin{aligned} dv = \sinh r \,d\theta \,dr \end{aligned}$$

(2)

Let $G_0$ be the isotropy subgroup at 0 and $g\mapsto \widetilde{g}=gG_0$ the canonical projection onto $G/G_0$. Via this projection, a function f on $U=G/G_0$ can be bijectively lifted to a right-$G_0$-invariant function on G; the function f is radial around 0 if and only if the lifted function is bi-$G_0$-invariant. If f, k are functions on U with k radial, then the convolution $k*f$ becomes

$$\begin{aligned} k*f\bigl ( \widetilde{g} \bigr ) =\int _{G/G_0} k\bigl (\widetilde{h^{-1}g}\bigr ) f\bigl ( \widetilde{h} \bigr )\,dv(\widetilde{h}) \end{aligned}$$

(see more details in the “Appendix”). If $z=e^{i\theta }\tanh (r/2)$, $z'= e^{i\theta '}\tanh (r'/2)\in U$, and $g_z\in G$ verifies $g_z(0)=z$, then

$$\begin{aligned} k*f ( z ) = k*f ( g_z (0) ) =\int _{G/G_0}k \bigl (\widetilde{h^{-1}g_z}(0)\bigr ) f\bigl ( \widetilde{h} (0)\bigr )\,dv(\widetilde{h}). \end{aligned}$$

Since G is unimodular,

$$\begin{aligned} k*f ( z ) =\int _{G/G_0}k \bigl ( \widetilde{h} (z)\bigr ) f\bigl (\widetilde{h ^{-1}}(0)\bigr )\,dv(\widetilde{h} ) =\int _ U k ( h_{z'} (z) ) f ( {h_{z'}^{-1}}(0) )\,dv( z'). \end{aligned}$$

In particular, since $h_{z'}^{-1}=h_{-\theta ',r'}$ and k is radial,

$$\begin{aligned} \begin{aligned} k*f(0)&= \int _U k(z') f({h_{z'}^{-1}}(0))\,dv(z')\\&= \int _0^{2\pi } \int _0^\infty k\biggl ( \tanh \frac{r'}{2}\biggr ) f\biggl (e^{-i\theta '}\tanh \frac{r'}{2}\biggr )\sinh r' \,d\theta ' \,dr'. \end{aligned} \end{aligned}$$

(3)

Theorem 2.1

We have

$$\begin{aligned} X^*Xf =J_X*f, \quad \text {where }J_X(r)=\frac{1}{\pi \sinh r}. \end{aligned}$$

Proof

Both $X^*X$ and the operator of convolution with $J_X$ commute with the action of ${{\,\mathrm{Aut}\,}}^+ U$ on $\mathcal {S}(U)$, therefore it is enough to prove that they take the same value at 0 when applied to $f\in \mathcal {S}(U)$. Indeed, by (1) ds coincides with dr on a geodesic through the origin. Then, by (3),

$$\begin{aligned} \begin{aligned} X^*Xf(0)&=\frac{1}{2\pi } \int _0^{2\pi } d\theta \int _ {\gamma _\theta }f(z)\,ds(z) =\frac{1}{\pi }\int _0^{2\pi } \int _0^\infty f\biggl (e^{i\theta } \tanh \frac{r}{2}\biggr )\,dr \,d\theta \\&= \int _U f\biggl (e^{i\theta } \tanh \frac{r}{2}\biggr ) \frac{1}{ \pi \sinh r } \,dv =J_X*f(0). \square \end{aligned} \end{aligned}$$

$J_X$ is the symbol of the operator $L^{-1/2}$, where L is the Laplace–Beltrami operator. This computation was used with Carlos Berenstein [5, Theorem 4.3] to obtain an inversion formula for X that factors through $X^*X$. The inverse is obtained by the left action on $X^*X$ of a convolution operator followed by the Laplace–Beltrami operator L. The convolution operator is given by the radial function $(1 -\coth r)/4\pi$ on U. In higher dimensional hyperbolic spaces the behavior of $X^*X$ is similar. In fact in $\mathbf {H}^n$ we have $X^*Xf=J_X*f$, where $J_X(r)=\pi ^{-n/2}\sinh ^{1-n}r$, except for $n=3$ (where $J_X(r)=\cosh r \sinh ^{-3} r/2\pi ^3$ and the Laplace–Beltrami operator is replaced by $L +1)$. See also [25, Chapter II, Table II-1] with an outline of other inversion formulas that do not factor through $X^*X$.

2.2 The Horospherical Radon Transform

In $\mathbf {R}^2$ with the Euclidean metric, a straight line can be regarded either as a distance-minimizing curve, i.e., a geodesic, or else as a ‘circle of infinite radius’, that is, the limit of a circle constrained to contain a fixed point and whose center moves to infinity along a half-geodesic originating at that point; i.e., as a horosphere. (In a symmetric Riemannian space M, horospheres—also called horocycles—are the orbits of maximal nilpotent subgroups of the connected component of the identity in the group of isometries of M.) Therefore, as pointed out in the introduction, there are two counterparts of straight lines in the setting of the hyperbolic disc U (a realization of $\mathbf {H}^2$): geodesics, discussed in the previous subsection, and horospheres, i.e., Euclidean circles tangent to $\partial U$ internally. A horosphere is orthogonal to all geodesics which touch its point of tangency with $\partial U$. Denote with $\mathcal {H}$ the set of all horospheres of U. ${{\,\mathrm{Aut}\,}}^+ U$ acts transitively on $\mathcal {H}$, hence $\mathcal {H}$ is equipped with an invariant measure.

As done for the geodesic case, the (horospherical) Radon transform R is given on (say) rapidly decreasing functions on U as

$$\begin{aligned} Rf (h) =\int _h f(z) \,ds(z) \quad \text {for every }h\in \mathcal {H}. \end{aligned}$$

The dual Radon transform $R^*$ is defined as follows. If $h_\theta$ is the horosphere through 0 and $e^{i\theta }$, set

$$\begin{aligned} R^* \phi (0) =\frac{1}{2\pi } \int _0^{2\pi } \phi (h_\theta ) \,d\theta \end{aligned}$$

for all, e.g., essentially bounded functions on $\mathcal {H}$; then, for general $z\in U$, set $R^*\phi (z)=R^*(\phi \circ \tau _{0,z})(0)$.

Theorem

On $\mathbf {H}^2$, $R^*R$ is the convolution operator with the radial kernel 1/A(r/2), that is,

$$\begin{aligned} R^*R f =J_R*f, \quad \text {where }J_R(r)=\frac{1}{2\pi \sinh (r/2)}. \end{aligned}$$

Fig. 1

Computation of the length element of a horosphere in the hyperbolic disc.

Proof

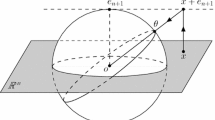
As in the proof of Theorem 2.1, without loss of generality we can restrict our attention to 0. The length element ds on a horosphere $h_\theta$ through 0 equals $dr/\!\cos \psi$ at $z\ne 0$, where $d(0,z)=r$, and $\psi$ is the angle between $h_\theta$ and the geodesic $\gamma _{\arg z}$ through 0 and z (see Fig. 1).

It is easy to show that

$$\begin{aligned} \cos \psi =\sqrt{1-\tanh ^2(r/2)} =\frac{2 \sinh (r/2)}{ \sinh r }, \end{aligned}$$

so that, taking into account that each horosphere through 0 has two ‘branches’ stemming from 0, we see from (1),(2) that

$$\begin{aligned} \begin{aligned} R^*Rf(0)&=\frac{1}{2\pi } \int _0^{2\pi } d\theta \int _ {h_\theta }f(z)\,ds(z) =\frac{1}{\pi }\int _0^{2\pi } \int _0^\infty f\bigl (e^{i\theta } \tanh (r/2)\bigr )\frac{dr}{\cos \psi } \,d\theta \\&= \int _U f\bigl (e^{i\theta } \tanh (r/2)\bigr ) \frac{1}{2\pi \sinh (r/2)}\,d v =J_R*f(0). \square \end{aligned} \end{aligned}$$

Horospheres (or horocycles) in $\mathbf {H}^n$ are (Euclidean) spheres tangent to the boundary internally. In a fashion very similar to the above, one proves that $R^*R$ is the convolution operator with the radial kernel

$$\begin{aligned} J_R(r) =\frac{ \Gamma ( n /2 ) }{2\sqrt{\pi }\Gamma \bigl ((n-1)/2\bigr )\sinh (r/2)}. \end{aligned}$$

As in the case of the X-ray transform, this leads to an inversion formula for R that factors through $R^*R$, and holds for every n; see a comparative outline in [25, Chapter III, Theorem 3.1], and full details in [24, Chapter I, §4, in particular Theorem 4.5]. The inverse operator is always given by the left action on $R^*R$ of Q(L) for a suitable polynomial Q. For $\mathbf {H}^2$, up to suitable normalization, the polynomial is the identity. In $\mathbf {H}^n$ for larger n, again up to normalization, one has

Again as in the case of the X-ray transform, there are also direct inversion formulas that do not factor through $R^*R$, generalizations of the original inversion formulas on Euclidean spaces [33].

3 Radon Transforms on the Vertices of a Homogeneous Tree

3.1 Vertices of Homogeneous Trees

Let T be a homogeneous tree in which each vertex belongs to $q+1$ edges, with $q\ge 2$. Since T has no loops, it is the Cayley graph of the free product $\mathcal {G}$ of $q+1$ copies of the two-element group $\mathbf {Z}_2$. In particular, $\mathcal {G}$ acts simply transitively on T and induces a convolution product on functions on the set V of vertices and on the set E of edges of T. $\mathcal {G}$ is not the only subgroup of ${{\,\mathrm{Aut}\,}}T$ acting simply transitively. The properties of the convolution, however, do not depend on the choice of this subgroup, but only on the geometry of the tree. We give more details in the “Appendix” on how to define the convolution on certain algebras of functions on T independently of the choice of $\mathcal {G}$.

The set V is equipped with the discrete topology. Two distinct vertices are adjacent, or neighbors, if they belong to the same edge: we shall write $v\sim v'$. In general, the chain of edges from v to $v'$ is the minimal finite sequence $v=v_0,v_1,\dotsc ,v_n=v'$ in V such that $v_{j-1}\sim v_j$ for every $j=1,\dotsc ,n$. The distance $d(v,v')$ is the non-negative integer n. We choose once and for all a reference vertex $v_0$ and write $\big |{v}\big |=d(v,v_0)$, the length of v. For $v, v'\in V$ we denote by $S(v,v')$ the set of all vertices $v''$ such that the path from v to $v''$ contains $v'$. We write $S(v)=S(v_0,v)$, and call sectors the sets of this type.

A ray is a sequence $[w_0,w_1,w_2,\dotsc ]$ of distinct vertices such that $w_i\sim w_{i+1}$ for every i. A geodesic in V is the union of two rays that share only the initial vertex. This coincides with the notion of geodesic induced by the distance d. Denote by $\Gamma$ the set of geodesics of V, and by $\Omega$ the set of rays starting at $v_0$. It does not matter which starting vertex is chosen, since we can regard rays as equivalent if they coincide except for a finite number of vertices. In each equivalence class there is a unique representative starting at $v_0$.

Both $\Gamma$ and $\Omega$ are equipped with a Hausdorff topology as follows. Let $\Omega _{w,v}$ be the set of rays which start at w and pass through v. A sub-base for the topology of $\Omega$ consists of all arcs $\Omega _v=\Omega _{v_0,v}$ for v ranging in V. In particular, $\Omega _{v_0}=\Omega$. With this topology, $\Omega$ is a compact space, usually called the boundary of T. On the other hand, we have $\Gamma =(\Omega \times \Omega \setminus \text {diagonal})/\{\pm 1\}$, because each geodesic is obtained by an unordered pair of distinct rays sharing a chain starting at $v_0$ (only the last vertex of the chain belongs to the geodesic). Therefore the topology of $\Omega$ induces a (non-compact) topology on $\Gamma$. By the same token, one lifts Borel measures from $\Omega$ to $\Gamma$. In particular, for every $v\in V$ there exists a unique probability measure $\nu _v$ on $\Omega$ which is invariant under the isotropy subgroup $({{\,\mathrm{Aut}\,}}T)_v$ of ${{\,\mathrm{Aut}\,}}T$ at v; denote by $\rho _v$ the induced probability measure on $\Gamma$.

Denote by $\Gamma _{w,v}$ the set of geodesics which contain w, $v\in V$, and by $\Gamma _w=\Gamma _{w,w}$ the set of geodesics through w. If j is a nonnegative integer, the number $N_j$ of vertices at distance j from a given vertex is given by

$$\begin{aligned} N_j= {\left\{ \begin{array}{ll} 1 &{}\text {if }j = 0,\\ (q+1)q^{j-1} &{}\text {if }j\ge 1. \end{array}\right. } \end{aligned}$$

Then the measure $\nu _w$ is described by

$$\begin{aligned} \nu _w(\Omega _{w,v}) =\frac{1}{N_{d(w,v)}} \quad \text {for every }v\in V. \end{aligned}$$

Proposition 3.1

Proof

If $v=w$, decompose

$$\begin{aligned} \Gamma _w =\biggl (\bigcup _{\begin{array}{c} u, t\sim w\\ u\ne t \end{array}}\Omega _{w,u} \times \Omega _{w,t}\biggr )\bigg /\{\pm 1\}. \end{aligned}$$

Since there are $(q+1)q$ different choices of u, t as distinct neighbors of w, and $\nu _w(\Omega _{w,u})=\nu _w(\Omega _{w,t})=1/(q+1)$, we get $\rho _w(\Gamma _w)=q/(q+1)$.

For $v\ne w$, let $n=d(v,w)$ and let s be the neighbor of w in V which lies on the path from w to v. Then $\rho _w(\Gamma _{w,v})=2\nu _w(\Omega _{w,v})(1-\nu _w(\Omega _{w,s}))$ (the factor 2 comes from counting geodesics twice according to whether their beginning endpoint is chosen on the side of w or of v), $\nu _w(\Omega _{w,v})=1/N_n$, and $1-\nu _w(\Omega _{w,s})=q/(q+1)$. $\square$

3.2 The X-Ray Transform on Vertices

The results of this subsection are taken from [6, §3]; see also [1]. The X-ray transform is the operator $X:\ell ^1(V)\rightarrow \ell ^\infty (\Gamma )$ given by

$$\begin{aligned} Xf (\gamma ) =\sum _{v\in \gamma }f(v) \quad \text {for each }f\in \ell ^1(V)\text { and }\gamma \in \Gamma . \end{aligned}$$

The dual transform is the operator $X^*:\ell ^\infty (\Gamma )\rightarrow \ell ^\infty (V)$ defined as

$$\begin{aligned} X^*\phi (v) =\frac{1}{\rho _v(\Gamma _v)} \int _{\Gamma _v } \phi (\gamma ) \,d\rho _v(\gamma )\quad \text {for all } \phi \in \ell ^\infty (\Gamma ). \end{aligned}$$

Let $\chi _j$ be the sum operator at distance j, defined by

$$\begin{aligned} \chi _j f(v) =\sum _{w:d(v,w)=j} f(w) \qquad \text {for }v\in V, \end{aligned}$$

i.e., $\chi _j f(v)$ is the sum of f on the circle of radius j centered at v (in particular, $\chi _0$ is the identity operator); $\chi _j$ is a radial convolution operator (with respect to the convolution product induced by ${{\,\mathrm{Aut}\,}}T$). By abuse of notation, we shall denote its convolution kernel again by $\chi _j$: it is given by

$$\begin{aligned} \chi _j(v,w)= {\left\{ \begin{array}{ll} 1 &{}\text {if }d(v,w) = j,\\ 0 &{}\text {if }d(v,w)\ne j. \end{array}\right. } \end{aligned}$$

Theorem 3.2

$X^*X$ acts on functions on V as the convolution operator with the radial kernel $J_X=\chi _0+2\sum _{j=1}^\infty (1/N_j)\chi _j$. That is,

$$\begin{aligned} X^*X =\chi _0+2\sum _{j=1}^\infty \frac{1}{(q+1)q^{j-1}}\chi _j \quad \text {on }\ell ^1(V). \end{aligned}$$

Proof

Set $\phi = Xf$. If f vanishes outside $\{v\}$, then $X^*\phi (v)=f(v)=\chi _0 f(v)$, while $\chi _j f(v)=0$ for $j\ge 1$. On the other hand, if f vanishes outside $\{u\}$, with $u\ne v$, and $n=d(u,v)$, then

$$\begin{aligned} X^*\phi (v) =\frac{\rho _v(\Gamma _{v,u})}{\rho _v(\Gamma _ v )} f(u) =\frac{2}{N_n}\chi _n f(v) \end{aligned}$$

by Proposition 3.1, while $\chi _j f(u)=0$ for $j\ne n$. The case of arbitrary f follows by linearity and the density of finitely supported functions in $\ell ^1(V)$. $\square$

The series in the above statement is absolutely convergent in the convolution operator norm on $\ell ^2(V)$. This follows from Haagerup’s convolution theorem [22, Lemma 1.4]; also [20, Proposition VIII.1.5], [8, Theorem 5.1], [6, proof of Proposition 3.2]. An explicit inversion formula for the X-ray transform can be derived from this fact, see [1, 6]. Inversion of $X^*X$ is achieved by showing that the Laplace operator $\Delta _V=\mu _1 -\delta _0$, with $\mu _1=\chi _1/(q+1)$, is a multiple of a left inverse of $X^*X$. The left inverse operator turns out to be

$$\begin{aligned} \Phi _X =\frac{2(q+1)^3}{q(q-1)^2} \biggl (\chi _0 +\frac{2q}{q+1} \sum _{n=1}^\infty (-1)^n q^{-n} \chi _n\biggr ). \end{aligned}$$

If T is not homogeneous, let $q_v+1$ be the number of neighbors of the vertex v. No group acts on T in general, so the words ‘convolution’ and ‘radiality’ lose their meaning. Also, one must choose a transient transition operator P on V. It is natural to choose the nearest-neighbor isotropic transition operator at each vertex. Then $X^*$ can be defined as in the homogeneous case with respect to an appropriate choice of the family of boundary probability measures $\{\rho _v:v\in V\}$; a natural choice was made in [6, Proposition 2.3] as the measure induced on $\Gamma$ by $\nu _v \times \nu _v$ on $\Omega \times \Omega$, where $\nu _v$ is the hitting distribution of the Markov process generated by P starting at v. Then $X^*X$ can be written as the operator of summation $X^*Xf=\sum _{v\in V}J_X(\,\cdot \,,v)f(v)$. If $\rho _v$ is chosen as above, the kernel is

where $[u{=}v_0,v_1,\dotsc ,v_n{=}v]$ is the path from u to v. The proof is similar to the homogeneous case and is left to the reader. We just mention that on a semi-homogeneous tree, if we write $q_+$ for $q_u$ and denote by $q_-$ the opposite homogeneity degree, the kernel $J_X(u,v)$, becomes

where $\mathbf {q}=\sqrt{q_+ q_-}$ is the average growth of the semi-homogeneous tree.

3.3 The Horospherical Radon Transform on Vertices

The results of this subsection are taken from [7, 9, 15]. We start by introducing the notion of horosphere of vertices in a tree. As we only need to deal with homogeneous trees, it is natural, although somewhat less elegant, to give a definition which apparently depends on the choice of the reference vertex $v_0$. For a reference-free presentation see [12].

Let $v\in V$ and $\omega \in \Omega$, regarded as a ray that starts at $v_0$. The horospherical index $h_\omega (v)$ is defined as $d(v_0,u)-d(v,u)$, where u is the branching vertex between the ray $\omega$ and the finite path from $v_0$ to v. In other words, u is the vertex of $\omega$ which is closest to v, and d(v, u) equals $d(v,\omega )$, the distance between v and the ray $\omega$. Therefore $h_\omega (v)=d(v,v_0)-2d(v,\omega )$. For every $k\in \mathbf {Z}$, the horosphere $h(k,\omega )$ is the set $\{v\in V:h_\omega (v)=k\}$. Every two vertices in the same horosphere are at even distance. The horospheres through $v_0$ have index 0.

We equip the space $\mathcal {H}$ of horospheres with the product topology of $\mathbf {Z}\times \Omega$. This parametrization depends on the choice of $v_0$, whereas the induced topology on $\mathcal {H}$ does not, as can be easily seen. Denote by $\mathcal {H}_{v,v'}$ the set of horospheres that contain v and $v'$, an open and closed subset of $\mathcal {H}$ that is empty if $d(v,v')$ is odd (as remarked earlier). For simplicity, set $\mathcal {H}_v=\mathcal {H}_{v,v}$. We equip $\mathcal {H}$ with the $({{\,\mathrm{Aut}\,}}T)$-invariant measure $\sigma =m\times \nu _{v_0}$, where m is the measure on $\mathbf {Z}$ given by $m(\{n\})=q^n$, see [16]. While $\sigma (\mathcal {H})=\infty$, nevertheless $\sigma$ is a probability measure on $\mathcal {H}_{v_0}=\{0\}\times \Omega$ (the set of horospheres through $v_0$) as well as on $\mathcal {H}_v$ for every v.

The (horospherical) Radon transform $R:\ell ^1(V)\rightarrow L^\infty (\mathcal {H})$, in analogy with the geodesic case, is given by

$$\begin{aligned} Rf(h) =\sum _{v\in h}f(v) \quad \text {for every }f\in \ell ^1(V)\text { and } h\in \mathcal {H}. \end{aligned}$$

The dual Radon transform $R^*:L^\infty (\mathcal {H})\rightarrow \ell ^\infty (V)$ is defined as follows. Set

$$\begin{aligned} R^*\phi (v) =\int _{\mathcal {H}_v}\phi (h) \,d\sigma (h) \quad \text {for every } \phi \in L^\infty (\mathcal {H}). \end{aligned}$$

The operator $R^*R$ therefore maps $\ell ^1(V)$ to $\ell ^\infty (V)$, and commutes with the action of ${{\,\mathrm{Aut}\,}}T$ on $\ell ^1(V)$.

Theorem 3.3

The horospherical Radon transform on V satisfies

$$\begin{aligned} R^*R =\chi _{v_0}+(1-1/q)\sum _{j=1}^\infty \frac{1}{N_j}\chi _{2j} \quad \text {on }\ell ^1(V). \end{aligned}$$

Proof

It is enough to compute $R^*R$ on every Dirac delta $\delta _v$ for $v\in V$ and evaluate at $v_0$. We have $R^*R\delta _v(v_0)=\sigma (\mathcal {H}_{v_0,v})$. This vanishes if $v_0$ and v are an odd distance apart. If the distance is nonzero and even, let $[v_0,v_1,\dotsc ,v_{2n}{=}v]$ be the finite path from $v_0$ to v, and the end $\omega$ corresponding to each horosphere h in $\mathcal {H}_v$ must belong to $\Omega _{v_n}\setminus \Omega _{v_{n+1}}$; indeed, $v_n$ must be the closest vertex to v of the ray $\omega$, in order for the index $h_\omega (v)$ to vanish. Since $\Omega _{v_{n+1}}\subset \Omega _{v_n}$,

$$\begin{aligned} \sigma (\mathcal {H}_{v_0,v_{2n}}) =\nu _{v_0}(\Omega _{v_ n }) -\nu _{v_0}(\Omega _{v_{n+1}}) = \frac{1}{N_ n } - \frac{1}{N_{n+1}} = \frac{ q-1 }{(q+1)q^n}. \end{aligned}$$

Since $\sigma (\mathcal {H}_{v_0})=1$, as remarked before, $R^*R$ acts as the convolution operator with the radial kernel $J_R=\chi _{v_0}+(1-1/q)\sum _{j=1}^\infty (1/N_j)\chi _{2j}$. $\square$

The inverse operator can be computed by solving a second-order difference equation for the values of the radial kernel $J_R$, with the result hereunder, appeared in [15, §5] following an outline of [7] that makes use of the resolvent of the normalized nearest-neighbor transition operator on T and the Carleman formula.

Corollary 3.4

The inverse of $R^*R$ on V is the convolution operator with kernel

We shall give a similar argument in Sect. 5.5, in the set-up of functions on edges instead of vertices, not studied before.

The kernel representation of Theorem 3.3 has an extension to semi-homogeneous trees with homogeneity degrees $q_+$ at w and $q_-$ at vertices of the other parity. The following expression for the kernel can be derived from [15, Proposition 4.3]:

4 Functions on Tree Edges and the X-Ray Transform

4.1 The Graph of Tree Edges and Convolution Operators

When a tree is regarded as a simplicial complex there are two types of simplices: vertices and edges. So far we have given a survey of Radon transforms on functions defined on vertices. We shall henceforth look at the other set-up, where all the results are new.

Two edges $e,e'$ are adjacent if they share exactly one vertex. So, every edge has 2q neighbors. The concepts of chain, distance, ray, geodesic, boundary and automorphisms are defined for edges as done for vertices in Sect. 3.1. Indeed, these concepts are intrinsic to T, not to V and E. We shall fix a reference edge $e_0$ and set $\big |{e}\big |=d(e,e_0)$.

Let us study the graph associated to E under the natural notion of adjacency. Every $e\in E$ becomes a vertex of this graph, that by abuse of notation we still denote by E. Two edges e, $e'$ are adjacent in T if and only if they are adjacent regarded as vertices of this graph. In other words, E is the dual graph of T. The group $\mathcal {G}=\mathbf {Z}_{q+1}*\mathbf {Z}_{q+1}$ acts as a simply transitive group of isometries of E (see the “Appendix”). The distance on E lifts to a distance on $\mathcal {G}$, called block distance. The graph E has the same group of isometries of T, hence $\mathcal {G}$ is a subgroup of ${{\,\mathrm{Aut}\,}}T={{\,\mathrm{Aut}\,}}E={{\,\mathrm{Aut}\,}}V$, simply transitive on edges but with two orbits on V and non-trivial isotropy subgroups. The convolution product on $\ell ^2(\mathcal {G})$ corresponds to a convolution product on $\ell ^2(E)$, with the same operator norm.

An estimate for the norm of convolution operators on $\mathcal {G}$ was given in [26] in analogy to Haagerup’s well-known convolution estimate [22], hence it also holds for convolution operators on $\ell ^2(E)$. The statement is more general than we need here. The part relevant to the rest of this article is the following:

Lemma

(Haagerup’s inequality [22, 26]) If $f:\mathcal {G}\rightarrow \mathbf {C}$ is supported on the circle of words of block distance $n>0$ from the identity, then

$$\begin{aligned} {\big \Vert {f*g}\big \Vert }_2 \le (q-1)(n+1){\big \Vert {f }\big \Vert }_2 {\big \Vert { g}\big \Vert }_2 \quad \text {for every }g\in \ell ^2(\mathcal {G}). \end{aligned}$$

(4)

Here the constant is larger than the one originally claimed in [26, Theorem 1.(ii)], although asymptotically equivalent; that argument actually leads to the constant written here.

Spherical functions on a polygonal graph were studied in [27] whence the properties of spherical functions on the edges of a homogeneous tree can be derived. We give some of the statements in the rest of this Section.

4.2 The Algebra of Radial Functions on Edges

By abuse of notation, a convolution operator with a radial convolution kernel f will be denoted again by f, by setting $f(e,e')=f(d(e,e'))$. If $C_n=\{e\in E:\big |{e}\big |=n\}$, then

$$\begin{aligned} \big |{C_n}\big | =2q ^n \quad \text {for }n>0. \end{aligned}$$

(5)

Remark 4.1

Every edge except $e_0$ has q forward neighbors (farther from $e_0$), one backward neighbor (closer to $e_0$) and $q-1$ neighbors at the same distance from $e_0$ as e. (Instead, on V the neighbors have constant parity: this yields a slightly different relation for vertex convolution, see [20] and its references).

Lemma 4.2

Let $\chi _n$ be the characteristic function of the set of edges at distance n from $e_0$. Then $\{\chi _n\}$ satisfies the convolution product rule

$$\begin{aligned} \chi _1 *\chi _n= {\left\{ \begin{array}{ll} \chi _ 1 &{}\text {if }n=0;\\ 2q\chi _ 0 +(q-1)\chi _1 +\chi _ 2 &{}\text {if }n=1;\\ q\chi _{n-1} +(q-1)\chi _n +\chi _{n+1} &{}\text {if }n>1. \end{array}\right. } \end{aligned}$$

Proof

The case $n=0$ is trivial. Since $\chi _1=\sum _{e'\sim e_0} \delta _{e'}$,

$$\begin{aligned} \chi _1 *\chi _1 =\sum _{e''\sim e' } \sum _{e' \sim e_0} \delta _{e''}. \end{aligned}$$

Each edge $e''$ in this double sum has length 0, 1, or 2:

• $e''=e_0$ appears in the sum as many times as there are neighbors of $e_0$ (namely 2q times);

• each $e''\sim e_0$ appears as many times as there are edges $e'\sim e_0$ on the same side of $e''$ with respect to $e_0$, except $e''$ itself (namely $q-1$ times);

• each $e''$ of length 2 appears only once.

Therefore the statement is proved for $n=1$.

For $n>1$

$$\begin{aligned} \chi _1 *\chi _n =\sum _{e''\sim e'} \sum _{ \big |{e'}\big |=n} \delta _{e''}. \end{aligned}$$

The right-hand side vanishes unless $\big |{e''}\big |=n-1, n$ or $n+1$. If $\big |{e''}\big |=n-1$, then $e''\sim e'$ gives a non-zero contribution to the sum if and only if $\big |{e'}\big |=n$ and $e''$ belongs to the path from $e_0$ to $e'$; for each $e''$ there are exactly q such edges $e'$. If $\big |{e''}\big |=n$, then $e''$ appears in the sum as many times as there are neighbors $e'$ of $e''$ with $\big |{e'}\big |=n$, namely the $q-1$ edges $e'\ne e''$ that share with $e''$ the vertex closer to $e_0$. If $\big |{e''}\big |=n+1$, every such edge appears as many times as there are edges $e'$ with $\big |{e'}\big |=n$ in the path from $e_0$ to $e''$, namely once. $\square$

Corollary 4.3

Normalize $\chi _n$ by $\eta _n=\chi _n/\big |{C_n}\big |$. Then

$$\begin{aligned} \eta _ 1 *\eta _ n =\frac{1}{2q} \eta _{n-1} +\frac{q-1}{2q} \eta _{n } +\frac{1}{2} \eta _{n+1} \qquad \text {for every }n\ge 1. \end{aligned}$$

In particular the convolution algebra $\mathcal {R}_\#$ of radial finitely supported functions on E (with identity) is generated by $\eta _1$, hence it is commutative.

The radialization operator $\mathcal {E}$ around $e_0$ acts on a function g on E by

$$\begin{aligned} \mathcal {E}g(e ) =\sum _{e':\big |{e'}\big | =\big |{e}\big |} \frac{g(e')}{\big |{C_{\big |{e}\big |}}\big |}. \end{aligned}$$

If f, g are functions on E, set ${\big \langle {f,g}\big \rangle }=\sum _e f(e)g(e)$ whenever the series is absolutely convergent; $({f,g})_2={\big \langle {f,\overline{g}}\big \rangle }$ is the $\ell ^2$-inner product. An obvious, yet useful property satisfied by the radialization operator is the following: if f, g are functions on E with f radial such that fg is summable, then

$$\begin{aligned} {\big \langle {f, g}\big \rangle } ={\big \langle {f,\mathcal {E}g}\big \rangle }. \end{aligned}$$

(6)

4.3 The X-Ray Transform on Edges

Geodesics and rays of edges are defined in the same way as for vertices, and naturally identified with geodesics, respectively rays, of vertices, so they give rise to a boundary canonically identifiable with the boundary for V. Each pair of edges $e\ne e'$ induces an arc $\Omega _{e,e'}\subset \Omega$ that consists of the equivalence classes of all rays starting at e and containing $e'$; it is clear that the arcs induced by E are the same as those induced by V. We shall write $\Omega _e=\Omega _{e_0,e}$.

We denote by $\nu _e$ the probability measure on $\Omega$ that is invariant under the isotropy subgroup $({{\,\mathrm{Aut}\,}}T)_e$ of ${{\,\mathrm{Aut}\,}}T$ at e. Then we have, in the same way as in Proposition 3.1, a measure $\rho _e$ on the space of geodesics of edges containing e, equivariant under $({{\,\mathrm{Aut}\,}}T)_e$. For $e, e'\in E$ let $\Gamma _{e,e'}$ be the set of geodesics of edges that contain both e and $e'$.

Proposition 4.4

$$\begin{aligned} \rho _e(\Gamma _ {e,e'}) =\frac{1}{2} q^{-d(e,e')}. \end{aligned}$$

Proof

Each edge $e=[v,w]$ splits $\Omega$ into the disjoint union of the subsets $\Omega _{v,w}$ and $\Omega _{w,v}$, that have the same $\nu _e$-measure because they are interchanged by any element of $({{\,\mathrm{Aut}\,}}T)_e$ that interchanges the endpoints of e.

Fix a boundary point $\omega$ and consider the subset $\Omega _{\omega ,e}$ of $\Omega$ given by all $\omega '$ such that the geodesic with endpoints $\omega ,\omega '$ contains e. Then $\Omega _{\omega ,e}$ is one of the two subsets of the splitting of $\Omega$ induced by e, hence it has $\nu _e$-measure 1/2.

For each geodesic that contains distinct $e,e'$ consider its boundary point $\omega$ closest to e. The set of these boundary points is $\Omega _{e',e}$, of $\nu _e$-measure 1/2. The other boundary point of these geodesics varies in $\Omega _{e,e'}$, a set of $\nu _e$-measure $q^{-d(e',e)}/2$ by (5). Therefore the set of geodesics with these ordered endpoints has measure $q^{-d(e',e)}/4$. Counting also the geodesics with reversed endpoints we obtain the expression in the statement. $\square$

The X-ray transform on E is the operator $X:\ell ^1(E)\rightarrow \ell ^\infty (\Gamma )$ given by

$$\begin{aligned} Xf (\gamma ) =\sum _{e\in \gamma }f(e) \quad \text {for each }f\in \ell ^1(E)\text { and }\gamma \in \Gamma . \end{aligned}$$

Its dual is the operator $X^*:\ell ^\infty (\Gamma )\rightarrow \ell ^\infty (E)$ defined as

$$\begin{aligned} X^*\phi (e) =\frac{1}{\rho _e(\Gamma _e)} \int _ {\Gamma _e}\phi (\gamma ) \,d\rho _e(\gamma ). \end{aligned}$$

It is clear that, for every $e,e'\in E$, the convolution operator with kernel $\chi _j$ satisfies

$$\begin{aligned} \chi _j \delta _e (e')= {\left\{ \begin{array}{ll} 1 &{}\quad \text {if }d(e,e') = j,\\ 0 &{}\quad \text {if }d(e,e')\ne j. \end{array}\right. } \end{aligned}$$

This fact, via the same argument as for Theorem 3.2, using Proposition 4.4 instead of 3.1 yields:

Theorem

For the X-ray transform X on E, the expression of the operator $X^*X$ in terms of the radial kernels $\chi _j$ is:

$$\begin{aligned} X^*X =\sum _{j=0}^\infty q^{-j}\chi _j \quad \text {on }\ell ^1(E). \end{aligned}$$

The series converges absolutely in the operator norm on $\ell ^2(E)$, by Haagerup’s inequality (4): therefore it converges to a bounded operator on $\ell ^2$.

Corollary

Let $\Delta _E=\eta _1 -\eta _0$ be the Laplace operator on E. Then $\bigl (q/(1-q)\bigr )\Delta _E$ is a left inverse of $X^*X$, hence $\bigl (q/(1-q)\bigr )\Delta _E X^*$ is a left inverse of the edge X-ray transform X.

Proof

Since $\chi _0=\eta _0=\mathbf {I}$, the identity, and by (5) $\chi _j=2q^j \eta _j$ for $j>0$, we have

$$\begin{aligned} X^*X= \eta _0 +2\sum _{j=1}^\infty \eta _j. \end{aligned}$$

By Corollary 4.3,

$$\begin{aligned} (\eta _0 -\eta _1)X^*X =\eta _0 -\eta _1 + 2 \sum _{j\ge 1} \eta _j -\frac{1}{q} \sum _{j\ge 1} \bigl (\eta _{j-1} +(q-1)\eta _j +q\eta _{j+1} \bigr ) = \frac{q-1}{q} \eta _ 0. \end{aligned}$$

$\square$

5 Spherical Functions on Edges and the Spectrum of the Laplacian

5.1 The Tree Boundary and the Poisson Kernel

The Poisson kernel on V, when T is equipped with the nearest-neighbor isotropic stochastic transition operator $\mu _1$, has been extensively studied in [11, 13, 20, 21] and their bibliographic lists. Here we introduce and study it on edges. The harmonic functions on E are the eigenfunctions with eigenvalue 1 of $\eta _1$. Since T has exponential growth, it is trivial to construct non-constant harmonic functions, including positive ones; equivalently, the random walk induced by $\eta _1$ is transient. $\Omega$ is the Poisson boundary of $\eta _1$ regarded as the generator of a random walk. It is well known that the probability measure $\nu _e$ introduced in Sect. 4.3 is the reproducing measure at e of harmonic functions, in the sense that, for every harmonic function h on E that extends continuously to $E\cup \Omega$, one has $h(e)=\int _\Omega h(\omega )\,d\nu _e(\omega )$. If $\nu =\nu _{e_0}$, then $\nu (\Omega _{e_1})=\nu (\Omega _{e_2})$ if $\big |{e_1}\big |=\big |{e_2}\big |$. Then, by (5),

$$\begin{aligned} \nu (\Omega _e) =\frac{1}{2} q^{-\big |{e}\big |} \quad \text {for }\big |{e}\big |>0. \end{aligned}$$

(7)

Since all $\Sigma _n$ are finite $\sigma$-algebras, $\nu _e$ is transformed by each $\lambda \in {{\,\mathrm{Aut}\,}}T$ to the measure $\nu _{\lambda e}$ which is absolutely continuous with respect to $\nu _e$. It is easy to compute the Radon-Nikodym derivative $d\nu _{e_1}/d\nu _{e_2}(\omega )$. It is enough to compute $d\nu _e /d\nu (\omega )$. We call Poisson kernel the limit

$$\begin{aligned} K (e , \omega ) =\lim _{e'\rightarrow \omega } \frac{\nu _e(\Omega _{e'})}{\nu (\Omega _{e'})}. \end{aligned}$$

The rays starting at the edges $e_0,e$, respectively, and belonging to the same equivalence class $\omega \in \Omega$ merge after a finite number of steps: call $e_\omega$ the first common edge. Define the horospherical index as

$$\begin{aligned} h(e,\omega ) =d(e_\omega ,e_0) -d(e_\omega ,e ). \end{aligned}$$

The horosphere $\mathbf {h}(\omega ,n)$ tangent at $\omega$ with index $n\in \mathbf {Z}$ with respect to $e_0$ is the set of all edges e where $h(e,\omega )=n$, namely those that are reached from $e_0$ moving a certain number $m_+$ of steps towards $\omega$ and then $m_-$ steps away from $\omega$, with $m_+ -m_-=n$. We have $h(\lambda e,\lambda \omega )=h(e,\omega )$ if $\lambda \in ({{\,\mathrm{Aut}\,}}T)_{e_0}$.

The space $\mathcal {H}$ of horospheres is identified with $\Omega \times \mathbf {Z}$ via the global coordinates defined by $e_0$. In this identification, $\mathcal {H}$ is equipped with the product topology induced by $\Omega \times \mathbf {Z}$, that is easily seen to be independent of the choice of $e_0$.

Proposition

For every e, $\omega$,

$$\begin{aligned} K(e,\omega ) =q^{h(e,\omega )}. \end{aligned}$$

5.2 Spherical Functions on Edges

The properties of spherical functions on E are proved as in the general theory of spherical functions for a Gel’fand pair, see for instance [20, Ch. III]). We shall skip most of the proofs. Similar arguments for spherical functions on polygonal graphs are in [27].

A function $\phi$ on E is spherical if it is radial, $\phi *u=c_\phi u$ for every u in the $\ell ^1$-completion $\ell ^1_\#$ of $\mathcal {R}_\#$ with some constant $c_\phi$ independent of u, and $\phi (e_0)=1$.

Proposition 5.1

A radial function $\phi$ is spherical if and only if $h\mapsto {\big \langle {\phi ,h}\big \rangle }$ is a multiplicative functional on the convolution algebra $\mathcal {R}_\#$. Thus, the set of bounded spherical functions is the Gel’fand spectrum of the Banach algebra $\ell ^1_\#$.

Every spherical function is uniquely determined by its value $\lambda (\phi )=\phi _{(1)}$ attained at distance 1 from $e_0$.

Corollary

Let h be a radial function. If $\eta _1*h=ch$ with $c\ne 0$, then h is a multiple of the spherical function $\phi$ such that $\lambda (\phi )=c$. If $\eta _1*h=0$ then $h=0$.

Proof

If $e\sim e_0$, then by radiality $h(e)={\big \langle {h,\eta _1}\big \rangle }=h*\eta _1(e_0)=ch(e_0)$. Hence, if $h(e_0)=0$, then $h\equiv 0$ by Lemma 4.2, otherwise $h/h(e_0)$ is a normalized radial eigenfunction of $\eta _1$, hence of $\mathcal {R}_{\#}$, and therefore it is a spherical function. $\square$

Proposition 5.2

For $z\in \mathbf {C}$, the functions

$$\begin{aligned} \phi _z(e ) =\int _\Omega K^z(e,\omega ) \,d\nu ( \omega ) \end{aligned}$$

are spherical functions and

$$\begin{aligned}&\eta _1 *\phi _z =\gamma (z)\phi _z,&\end{aligned}$$

(8)

$$\begin{aligned}&\text {with}\quad \gamma (z) =\frac{q^z +q-1+q^{1-z}}{2q} =\frac{\cosh \bigl ((z-1/2)\log {q}\bigr )}{\sqrt{q}}+\frac{q-1}{2q}. \end{aligned}$$

(9)

Conversely, every spherical function arises in this way. Finally, we have the majorization principle

$$\begin{aligned} \big |{\phi _ z}\big | \le \phi _{\mathfrak {R}z}. \end{aligned}$$

Corollary

The map $\gamma$ is periodic of period $2\pi i/\log {q}$ and we have $\gamma (1/2+it)=\gamma (1/2-it)$. Therefore

$$\begin{aligned} \gamma (1/2+i\mathbf {R}) =\bigl \{\gamma (1/2+i t):0\le t\le \pi /\log {q}\bigr \}. \end{aligned}$$

The properties of spherical functions on E follow immediately from multiplicativity on $\mathcal {R}_\#$ and the recurrence relation of Lemma 4.2 and are similar to those proved for V in [20].

Proposition

The following are equivalent for a function $\phi$ on E:

• $\phi =\phi _z$;

• $\phi$ is radial and, if $\phi _{(n)}=\phi (e)$ whenever $\big |{e}\big |=n$, then $\phi _0=1$, $\phi _1=\gamma (z)$ and

  $$\begin{aligned} \phi _{(1)} \phi _{(n)} =\frac{1}{2q} \phi _{(n-1)} +\frac{q-1}{2q} \phi _{(n )} +\frac{1}{2} \phi _{(n+1)} \qquad \text {for every } n>0. \end{aligned}$$

  (10)

• $\phi (e_0)=1$ and $\eta _1 *\phi =\gamma (z)\phi$.

As a consequence we obtain a nice expansion of edge-spherical functions as linear combinations of exponentials.

Corollary 5.3

Set

$$\begin{aligned} c(z) =\frac{q-1+q^{1-z}-q^z }{2 (q^{1-z}-q^z)}, \end{aligned}$$

for which $\overline{c(z)}=c(\overline{z})$, therefore

$$\begin{aligned} \overline{c(1/2+it)} = c(1/2-it) \qquad \text {for every }t\in \mathbf {R}. \end{aligned}$$

(11)

If $\Pi =\{z:q^{2z-1}=1\}=\{1/2+ik\pi /\log {q}:k\in \mathbf {Z}\}$ and $y_z(e)=q^{-z\big |{e}\big |}$ for $e\in E$:

Furthermore

Finally, the $\ell ^1$ spectrum of $\eta _1$, that is the Gel’fand spectrum of $\ell ^1_\#$, is the ellipse

$$\begin{aligned} \{\gamma (z):0\le \mathfrak {R}z\le 1\} =\biggl \{\biggl (\frac{2q\mathfrak {R}\gamma (z)-(q-1)}{q+1}\biggr )^2 +\biggl (\frac{2q\mathfrak {I}\gamma (z) }{q-1}\biggr )^2 \le 1\biggr \}. \end{aligned}$$

Definition 5.4

It follows from Lemma 4.2 that there are polynomials $Q_n$ of degree n such that $\eta _n=Q_n(\eta _1)$. On the other hand, the functionals $g\mapsto {\big \langle {\phi _z,g}\big \rangle }$ are multiplicative on the radial algebra (Proposition 5.1), hence

$$\begin{aligned} \phi _z (n) = {\big \langle {\phi _z,\eta _n}\big \rangle } = {\big \langle {\phi _z,Q_n(\eta _1)}\big \rangle } =Q_n\bigl ({\big \langle {\phi _z,\eta _1}\big \rangle }\bigr ) =Q_n\bigl ( \gamma (z) \bigr ). \end{aligned}$$

(12)

The functions $Q_n$ are called spherical polynomials. By abuse of terminology, sometimes also the functions $\widetilde{Q}_n(z)=Q_n(\gamma (z))$ are called spherical polynomials (although they are not polynomials in the variable z).

Corollary 5.5

For every $z\in \mathbf {C}$, $\big |{\widetilde{Q}_n(z)}\big |\le \big |{\widetilde{Q}_n(\mathfrak {R}z)}\big |$.

Proof

It follows from the majorization principle of Proposition 5.2: $\big |{\widetilde{Q}_n(z)}\big |=\big |{\phi _z(n)}\big |\le \big |{\phi _{\mathfrak {R}z}(n)}\big |=\big |{\widetilde{Q}_n(\mathfrak {R}z)}\big |$. $\square$

5.3 Spectrum of the Laplace Operator on Edges

The following results link spherical functions with the $\ell ^2$-spectral theory of the Laplace operator on edges $\eta _1$.

Theorem 5.6

The spectrum of $\eta _1$ on $\ell ^2(E)$ is the real segment

$$\begin{aligned} S= & {} \bigl \{\gamma (z):\mathfrak {R}z=1/2\bigr \} =\bigl [\gamma (1/2+i\pi /\log {q}), \gamma (1/2 ) \bigr ]\\= & {} \biggl [\frac{q-1}{2q}-\frac{1}{\sqrt{q}}, \frac{q-1}{2q}+\frac{1}{\sqrt{q}}\biggr ], \end{aligned}$$

its spectral radius $\rho (\eta _1)$ is $(q-1)/2q+1/\sqrt{q}$, and its resolvent $\xi _{\gamma (z)}$ at the eigenvalue $\gamma (z)$ is the convolution operator on $\ell ^2$ given by the function

$$\begin{aligned} r_z(e) =\frac{2q}{ q^{1-z}-q^ z -(q-1)} q^{-z\big |{e}\big |} =\frac{1}{c(1-z)(q^{ -z}-q^{z-1} )} q^{-z\big |{e}\big |} \end{aligned}$$

(13)

with $\mathfrak {R}z>1/2$. In other words, $r_z$ satisfies the resolvent equation

$$\begin{aligned} \eta _1 r_z -\gamma (z)r_z =\delta _{e_0}. \end{aligned}$$

(14)

For $\mathfrak {R}z<1/2$, $r_z(e)$ grows with $\big |{e}\big |$, hence it does not act as a convolution operator on $\ell ^2$.

Proof

By identifying E with the free product $\mathcal {G}=\mathbf {Z}_{q+1}*\mathbf {Z}_{q+1}$ introduced in Sect. 4.1 we give a meaning to expressions such as $e^{-1}$ where e is an edge. If a spherical function $\phi _z$ is positive definite, then $\gamma (z) \in S$. Indeed, for every $e\in E$, the edges e and $e^{-1}$ clearly have the same length, by construction of $\mathcal {G}$. So, since $\phi _z$ is radial, $\phi _z(e^{-1})=\phi _z(e)$, but if it is positive definite, $\phi _z(e^{-1})=\overline{\phi _z(e)}$. Hence such $\phi _z$ is real valued. Being positive definite, it is also bounded by $\phi (e_0)$; but $\phi _z$ is bounded if and only if $0\le \mathfrak {R}(z)\le 1$, by Corollary 5.3, and it is real only if $\gamma (z)\in \mathbf {R}$, by the recurrence relation (10) (because $\gamma (z)=\phi _z(e)$ for $\big |{e}\big |=1$).

Now we show the opposite implication: if $\gamma (z)\in \mathbf {R}$ and $0\le \mathfrak {R}z \le 1$ then $\phi _z$ is positive definite, that is, it induces a functional $f\mapsto {\big \langle {f,\phi _z}\big \rangle }$ that takes positive values on the positive elements f of the involutive algebra $\ell ^1$. These positive elements form the positive cone generated by functions of the type $f=h^* *h$, where $h^*(e)=\overline{h(e^{-1})}$, and are positive definite functions. The radialization maps positive definite functions (that is, positive elements of the involutive algebra $\ell ^1$), to radial positive definite functions (that is, positive elements of the involutive algebra $\ell _\#^1$). Thus $\mathcal {E}f$ is a linear combination with positive coefficients of functions of the type $g^* *g$ for some radial g. Without loss of generality, we can restrict attention to a positive element f such that $\mathcal {E}f=g^* *g$. Then

$$\begin{aligned} {\big \langle { f,\phi _z}\big \rangle } = {\big \langle {\mathcal {E}f,\phi _z}\big \rangle } = {\big \langle {g^* *g,\phi _z}\big \rangle } =\overline{{\big \langle { g,\phi _z}\big \rangle }} {\big \langle { g,\phi _z}\big \rangle } \ge 0 \end{aligned}$$

by (6), Proposition 5.1 and the fact that $\phi _z$ is real valued for $\mathfrak {R}z =1/2$. So we have shown that $\phi _z$ is positive definite if $z=z_t=1/2+it$ with $t\in \mathbf {R}$ or if $z=\sigma$ or $\sigma +i\pi /\log {q}$ with $1/2\le \sigma \le 1$. We need to determine which of these positive definite functions are multiplicative linear functionals continuous on the $C^*$-algebra $C^*_\lambda$ of convolution operators on $\ell ^2$. For the relevant background, the reader is referred to [18].

By Corollary 5.3 we have $\phi _{1/2+it}\in \ell ^{2+\epsilon }$, and, by the asymptotic rate of decay of spherical functions, the product $\phi _\sigma \phi _{1/2+it}$ is positive definite and belongs to $\ell ^2$, hence to the Fourier algebra $A(\mathcal {G})=\ell ^2(\mathcal {G})*\ell ^2(\mathcal {G})$. In particular, $\phi _\sigma \phi _{1/2+it}$ has norm 1 in the Banach algebra $B(\mathcal {G})$ of positive definite functions. On the other hand, $\phi _\sigma$ converges pointwise to 1 as $\sigma \rightarrow 1$ because $\phi _1$ is the constant function 1. Therefore $\phi _{1/2+it}$ is the pointwise limit of functions $\phi _\sigma \phi _{1/2+it}$ of norm 1 in $B(\mathcal {G})$, hence it defines a multiplicative linear functional continuous on $C^*_\lambda$. This shows that $\gamma (1/2+it/\log {q})$ belongs to the spectrum of $\eta _1$ in $C^*_\lambda$. The extreme points of the spectrum of $\eta _1$ are $\rho =\gamma (1/2)=1/\sqrt{q}+(q-1)/2q$, $\rho '=\gamma (1/2+it/\log {q})=-1/\sqrt{q}+(q-1)/2q$ and $\{\gamma (z):\mathfrak {R}z=1/2\}=[\rho ',\rho ]$.

Suppose that $\gamma (z)\notin [-\rho ,\rho ]$. Then $\mathfrak {R}z\ne 1/2$: since $\gamma (z)=\gamma (1-z)$ we may assume $\mathfrak {R}z>1/2$. As before, write $y_z(e)=q^{-z\big |{e}\big |}$. We know from (8) that $\eta _1 y_z(e)=\gamma (z)y_z(e)$ for every $e\ne e_0$. Instead, $\eta _1 y_z(e_0)$ is the value of $y_z$ on edges of length 1, that is $q^{-z}$; moreover, $y_z(e_0)=1$. Hence

$$\begin{aligned} (\eta _1-\gamma (z)\mathbf {I})y_z(e_0) =q^{-z}-\gamma (z) =\frac{q^{1-z}-q^z-(q-1)}{2q}. \end{aligned}$$

Therefore

$$\begin{aligned} (\eta _1-\gamma (z)\mathbf {I})y_z =\frac{q^{1-z}-q^z-(q-1)}{2q} \delta _{e_0}. \end{aligned}$$

Thus, for $\mathfrak {R}z>1/2$, the function $r_z(e)=2qy_z^{-z\big |{e}\big |} /\bigl (q^{1-z} -q^z -(q-1)\bigr )$ is the resolvent of $\eta _1$ provided that it is a bounded convolution operator on $\ell ^2$. This follows from Haagerup’s inequality for edges (4), $\Vert {r_z}\Vert _{C^*_\lambda } \le (q-1)\sum _{n\ge 0} (n+1){\big \Vert {\chi _n r_z}\big \Vert }_2$. So it is enough to prove that the series converges. If $\big |{e}\big |=n$, then $r_z(e)\sim q^{-nz}$, and so, by (5),

$$\begin{aligned} \sum _{n\ge 0} (n+1) {\big \Vert {\chi _n r_z}\big \Vert }_2 \sim \sum _{n\ge 0} (n+1)\big |{q^{-nz}}\big |{\big \Vert {\chi _n }\big \Vert }_2 = \sum _{n\ge 0} (n+1) q^{(1/2 -\mathfrak {R}z)n} <\infty . \end{aligned}$$

(15)

The last identity in (13) follows from the definition of c(z). $\square$

It was shown in [20] that the spectrum of $\mu _1$ as a convolution operator on $\ell ^2(V)$ is the real segment

$$\begin{aligned} S_V =\bigl \{\gamma (z) :\mathfrak {R}z=1/2 \bigr \} =\bigl [\gamma (1/2+i\pi /\log {q}), \gamma (1/2 )\bigr ] =\biggl [-\frac{2\sqrt{q}}{q+1}, \frac{2\sqrt{q}}{q+1} \biggr ]. \end{aligned}$$

Therefore the spectral radius of $\mu _1$ on $\ell ^2(V)$ is $\rho (\mu _1)=2\sqrt{q}/(q+1)$, and its resolvent at the eigenvalue $\gamma (z)$ is the convolution operator by the function

$$\begin{aligned} s_z(v) =\frac{q+1}{ q^{-z}-q^ z }q^{-z\big |{v}\big |} =\frac{1}{c(1-z)(q^{-z}-q^{z-1})}q^{-z\big |{v}\big |} \end{aligned}$$

with $\mathfrak {R}z>1/2$, i.e., $\mu _1 s_z -\gamma (z)s_z=\delta _{v_0}$, and the c-function is

$$\begin{aligned} c(z) =\frac{q^{1-z}-q^{z-1}}{(q+1)(q^{ -z}-q^{z-1})}. \end{aligned}$$

In particular, the spectrum of $\mu _1$ on $\ell ^2(V)$ is symmetric with respect to the origin. This confirms the well known property [32] of symmetry of the spectrum of the adjacency operator on a bipartite graph (i.e., a graph whose set of vertices is the union of two disjoint sets and each edge is represented by a pair of vertices in the two different sets). On the other hand, the spectrum of $\eta _1$ on $\ell ^2$ is not symmetric, as seen in Theorem 5.6, and the edges can be regarded as “vertices” in the graph described in the “Appendix”, that is not bipartite except in the trivial case of the tree given by the integers. Indeed, for larger numbers of neighbors there are at least three edges in E connecting at a vertex in V, hence each of them touches the other two and so the “vertices” of the graph form triangles.

Remark 5.7

The alternating function $\epsilon (v)=(-1)^{\big |{v}\big |}$, i.e., the parity of vertices, is an eigenfunction of $\mu _1$ with eigenvalue $-1$, and multiplication by $\epsilon (v)$ maps eigenfunctions of $\mu _1$ to other eigenfunctions of $\mu _1$, since $\epsilon (u)=-\epsilon (v)$ for all neighbors u of each vertex v. Indeed, if h is an eigenfunction with eigenvalue $\gamma _V$, then $\epsilon h$ has eigenvalue $-\gamma _V$, and the spectrum of $\mu _1$ is invariant under reflection around the origin, as already observed. We have $-\gamma _V (z)=\gamma _V (z+i\pi /\log {q})$, and so the resolvent at the eigenvalue $-\gamma _V (z)$ is $\epsilon s_z = s_{z+i\pi /\log {q}}$. Moreover, $\epsilon$ does not change if we move the reference vertex $v_0$ to another vertex at even distance, and becomes $-\epsilon$ if we move the reference vertex by an odd distance.

The same is not true for edges. Unless $e=e_0$, there are edges $e'\sim e$ such that $\big |{e'}\big |=\big |{e}\big |$. If we set $\epsilon (e)=(-1)^{\big |{e}\big |}$, $\epsilon$ depends on the reference edge in a non-trivial way, and in the environment of edges $\gamma (z+i\pi /\log {q})\ne -\gamma (z)$. We show that $\epsilon r_z=r_{\widetilde{z}}$ for some $\widetilde{z}\in \mathbf {C}$. Indeed, we claim that $\epsilon r_z$ is a multiple of the resolvent at an eigenvalue $\gamma (\widetilde{z})=\sigma (\gamma (z))$, where $\sigma$ is the central reflection of $\mathbf {C}$ around the midpoint $(q-1)/2q$ of the $\ell ^2$ spectrum S, i.e., $\sigma (w)=(q-1)/q -w$. That is,

$$\begin{aligned} \gamma (\widetilde{z}) =\frac{q-1}{q} -\gamma ( z ). \end{aligned}$$

(16)

So $\widetilde{z}\in S$ if (and only if) $z\in S$. Indeed, by Remark 4.1, for every $e\ne e_0$,

$$\begin{aligned} \eta _1(\epsilon r_z)(e) = \frac{-q^{1-z}-q^z+(q-1)}{2q} \epsilon r_z (e) =\biggl (\frac{q-1}{q} -\gamma (z)\biggr )\epsilon r_z (e), \end{aligned}$$

which proves the claim: $\epsilon r_z$ satisfies the resolvent equation (14) at the eigenvalue $(q-1)/q-\gamma (z)$. Moreover, since $\big |{\epsilon r_z}\big |=\big |{r_z}\big |$, by (15) $\epsilon r_z$ satisfies Haagerup’s estimate (4), hence it is the $\ell ^2$-resolvent of $\eta _1$ at this eigenvalue.

By the expression 9 of $\gamma$, (16) reduces to $q^{\widetilde{z}}+q^{1-\widetilde{z}}=-(q^z +q^{1-z})$. Equivalently, by writing z, $\widetilde{z}\in S$ as $z=1/2+it$, $\widetilde{z}=1/2+is$ with $t,s\in [0,\pi /\log {q})$, one has $\cos (t\log {q})=-\cos (s\log {q})$. The solutions are $t\log {q}=\pi \pm s\log {q}$, that is, restricting to $[0,\pi /\log {q}]$,

$$\begin{aligned} \widetilde{z}= z +ik\pi /\log {q}\qquad \text {or}\qquad \widetilde{z}=\overline{z}+ik\pi /\log {q}\qquad \text {with }k=0,1. \end{aligned}$$

(17)

5.4 Spherical Fourier Transform on Edges and the Plancherel Formula

The spherical Fourier transform $\widehat{h}(z)$ of a function $h\in \ell ^1(E)$ at $z\in \mathbf {C}$ is defined as

$$\begin{aligned} \widehat{h} (z) = {\big \langle {h,\phi _z}\big \rangle } =\sum _{e\in E} h(e)\phi _z(e). \end{aligned}$$

Corollary

We have

$$\begin{aligned} \widehat{\eta _1}(z) = \gamma (z). \end{aligned}$$

(18)

For every $h\in \ell ^1_\#$ and $\phi _z\in \ell ^\infty$ one has

$$\begin{aligned} \phi _z * h = h *\phi _z =\widehat{h}(z) \phi _z \end{aligned}$$

If $\phi _z$ is bounded and real (that is, if $\gamma (z)\in \mathbf {R}$, or, equivalently, if $\mathfrak {R}z=1/2$ or if $\mathfrak {I}z=in\pi /\log {q}$, $n\in \mathbf {Z}$ and $0\le \mathfrak {R}z\le 1$), then, for every $h\in \ell ^1_\#$, the $\ell ^2$ inner product $({\phi _z*h,h})_2={\big \langle {\phi _z*h,\overline{h}}\big \rangle }$ is equal to $\big |{\widehat{h}(z)}\big |^2$.

Proof

Identity (18) follows from Proposition 5.2. By (8), $\phi _z *\eta _1=\eta _1 *\phi _z=\gamma (z)\phi _z$, hence, by (12), all functions h in $\mathcal {R}_\#$ satisfy the second identity, and the same holds for the $\ell ^1$-completion. In particular, if h is radial, ${\big \langle {\phi _z,h}\big \rangle }=\phi _z*h(e_0)=\widehat{h}(z)$. Then, if $\phi _z$ is real, ${\big \langle {\phi _z,\overline{h}}\big \rangle }=\overline{\widehat{h}(z)}$ and ${\big \langle {\phi _z *h,\overline{h}}\big \rangle }=\widehat{h}(z){\big \langle {\phi _z,\overline{h}}\big \rangle }=\widehat{h}(z)\overline{\widehat{h}(z)}$. $\square$

A celebrated Harish-Chandra theorem expresses the Plancherel measure for the spherical Fourier transform on semi-simple Lie groups in terms of the c-function appearing in the asymptotic expansion of spherical functions as sum of exponentials. An analog for free groups acting on vertices of T has been proved in [20, Chapter 3, §4] via a direct calculation. Although a direct proof of the analogous statement for edges is possible, we opt for a more elegant approach based on the Carleman formula [17, p. 192]: for any $h\in \ell ^2_\#$ and any continuous compactly supported u on $\mathbf {R}$, the spectral resolution $E(d\lambda )$ of the operator $\eta _1$ on $\ell ^2$ is expressed as

$$\begin{aligned} \int _{-\infty } ^\infty u(\lambda )({E(d\lambda ) h,h})_2 = -\frac{1}{2i}\lim _{\epsilon \rightarrow 0^+} \int _{-\infty } ^\infty u(\lambda )({(\xi _{\lambda +i\epsilon } -\xi _{\lambda -i\epsilon })*h,h})_2\,d\lambda , \end{aligned}$$

(19)

where the resolvent function $\xi _\lambda$ of $\eta _1$ on $\ell ^2$ at the eigenvalue $\lambda$ (cf. Theorem 5.6) is holomorphic outside the spectrum S, hence the limit vanishes outside S and the integration can be limited to this interval.

Our argument in the next theorem is inspired by the approach of [19] for polygonal graphs (see also [30]), although our proof is more precise and accurate.

Theorem

For every $h\in \ell ^2_\#$, the following Plancherel formula holds:

$$\begin{aligned} {\big \Vert {h}\big \Vert }_2^2 = \frac{\log {q}}{4} \int _0^{\pi /\log {q}} \big |{\widehat{h}(1/2+it)}\big |^2 \big |{ c (1/2+it)}\big |^{-2}dt, \end{aligned}$$

Proof

If $z=1/2+it$, from (9) we have $\gamma (z)=(q-1)/2q+\sqrt{q}\cos (t\log {q})/q$ and

$$\begin{aligned} \begin{aligned} \gamma (z + \delta )&=\gamma (z)+\frac{( q^ \delta -1)q^ z +(q^{-\delta }-1)q^{1-z}}{2q} \\&=\gamma (z)+\frac{(\cosh (\delta \log {q})-1) \cos ( t \log {q}) +i \sinh (\delta \log {q}) \sin ( t \log {q})}{\sqrt{q}}. \end{aligned} \end{aligned}$$

Setting $\epsilon =i\bigl (\gamma (z)-\gamma (z+\delta )\bigr )$, from the relation

$$\begin{aligned} \gamma (z)+i\epsilon =\gamma (z+ \delta ) \end{aligned}$$

(20)

we obtain

$$\begin{aligned} \begin{aligned} \epsilon&=\frac{ \sinh (\delta \log {q}) \sin (t \log {q})}{\sqrt{q}}-i\frac{(\cosh (\delta \log {q})-1) \cos (t \log {q})}{\sqrt{q}}\\&=\frac{ \sin (t \log {q})}{\sqrt{q}}\delta \log {q}+ O(\delta ^2), \end{aligned} \end{aligned}$$

(21)

and $\delta (\epsilon )=\epsilon \sqrt{q}/(\log {q})\sin (t\log {q})+O(\epsilon ^2)$. Therefore $\delta$ is asymptotically proportional to $\epsilon$ for $\epsilon \rightarrow 0$, with a non-negative constant of proportionality. Hence, as $\mathbf {R}\ni \epsilon \rightarrow 0^+$, $\delta (\epsilon )$ tends to 0 and is asymptotically tangent to the real axis, unless the coefficient of proportionality vanishes. The coefficient vanishes only if $\sin (t\log {q})=0$, that is at the extreme points of the spectrum S, and this does not affect the spectral measure in the interior of the spectral interval (it might only produce atoms at the endpoints). Note that $\gamma (1/2+w)=\gamma (1/2-w)$. By (21),

$$\begin{aligned} \gamma (1/2+it)-i\epsilon =\gamma \bigl (1/2+it - \delta +O(\delta ^2)\bigr ) =\gamma \bigl (1/2-it + \delta +O(\delta ^2)\bigr ). \end{aligned}$$

Therefore we can rewrite the right-hand side of Carleman’s formula (19) as

$$\begin{aligned}&-\frac{1}{2i} \lim _{\epsilon \rightarrow 0^+} \int _{S} u(\gamma ) ({(\xi _{\gamma +i\epsilon } -\xi _{\gamma -i\epsilon })*h,h})_2 \,d\gamma \\&\quad \begin{aligned} =-\frac{1}{2i} \lim _{\delta \rightarrow 0^+}&\int _0^{\pi /\log {q}} u(1/2+it) ({(\xi _{\gamma (1/2+it+\delta )} -\xi _{\gamma (1/2+it-\delta +O(\delta ^2))})*h,h})_2\\&\qquad \cdot \gamma '(1/2+it)\,dt. \end{aligned} \end{aligned}$$

It follows from the expression (13) of $r_z$ that, for $z=1/2+it$,

$$\begin{aligned} \xi _{\gamma (z+\delta )} = r_ {z+\delta } =\frac{q^{-(1/2+it+\delta )\big |{e}\big |}}{c(1/2-it-\delta ) (q^{- 1/2-it-\delta } -q^{- 1/2+it+\delta })}. \end{aligned}$$

By Corollary 5.3, the denominator in the last identity has a non-zero limit as $\delta \rightarrow 0$, hence $\lim _{\delta \rightarrow 0} r_{1/2+it\pm \delta }=\lim _{\epsilon \rightarrow 0} \xi _{\gamma (1/2+it)\pm i\epsilon }$ exists and is non-zero.

Because of the rate of decay of $\xi _{\gamma (z)}$, in the equality $\xi _{\gamma (z+\delta )}=r_{z+\delta }$, if $\delta \in \mathbf {R}$ we must limit attention to $\delta >0$ because the $\ell ^2$-resolvent $r_{z+\delta }$ must belong to $\ell ^2$ (and in general we should limit attention to $\mathfrak {R}\delta >0$). This means that, when approaching $\gamma (1/2+it)\in S$ with

$$\begin{aligned} \gamma (1/2 + it)\pm i\epsilon =\gamma \bigl (1/2 + it \pm \delta +O(\delta ^2)\bigr ) =\gamma \bigl (1/2\pm it + \delta +O(\delta ^2)\bigr ), \end{aligned}$$

we are approaching the point $z=1/2\pm it$ in the z-plane always from the right-hand half-space. In terms of the variable $\gamma (z)$, although $\delta >0$ implies that $\epsilon \rightarrow 0^+$, the subscript $\gamma (1/2+it+\delta )$ in the integrand, for $0<t<\pi /\log {q}$, approaches $\gamma (1/2+it)$ from above, and the subscript $\gamma \bigl (1/2+it-\delta +O(\delta ^2)\bigr )$ approaches the same eigenvalue, regarded as $\gamma (1/2+i(-t))$, from below as requested.

Note also that, by (9),

$$\begin{aligned} d\gamma (z) =\frac{ (q^ z -q^{1-z}) \log {q}}{2q} \,dz =\frac{\log {q}}{2} (q^ {z-1}-q^{ -z})\,dz. \end{aligned}$$

Therefore, for $0<t<\pi /\log {q}$,

$$\begin{aligned}&\lim _{\epsilon \rightarrow 0^+} (\xi _{\gamma (1/2+it)+i\epsilon } -\xi _{\gamma (1/2+it)-i\epsilon })\,d\gamma \\&\quad \begin{aligned}&= \frac{\log {q}}{2} \biggl (\frac{q^{ -(1/2+it)\big |{e}\big |}}{c (1/2-it) (q^{ -1/2-it} -q^{ -1/2+it})} -\frac{q^{ -(1/2-it)\big |{e}\big |}}{c (1/2+it) (q^{ -1/2+it} -q^{ -1/2-it})}\biggr )\\&\qquad \cdot i(q^{ -1/2+it} -q^{ -1/2-it})\,dt\\&=-i\frac{\log {q}}{2} \biggl (\frac{ q^{-(1/2+it)\big |{e}\big |}}{c(1/2-it)} +\frac{ q^{-(1/2-it)\big |{e}\big |}}{c(1/2+it)}\biggr )\,dt =-i (\log {q}) \frac{\phi _{1/2+it}(e)}{2\big |{c(1/2+it)}\big |^2}\,dt; \end{aligned} \end{aligned}$$

the last identity follows from the expansion of the spherical function in Corollary 5.3 and from identity (11). Then, again by the same Corollary,

$$\begin{aligned} \begin{aligned} \lim _{\epsilon \rightarrow 0^+} ({(\xi _{\gamma (1/2+it)+i\epsilon } -\xi _{\gamma (1/2+it)-i\epsilon })*h,h})_2\,d\gamma&=-i(\log {q})\frac{({\phi _{1/2+it} *h,h})_2}{2\big |{c(1/2+it)}\big | ^2} \,dt\\&=-i(\log {q})\frac{ \big |{\widehat{h}(1/2+it) }\big |^2}{2\big |{c(1/2+it) }\big |^2} \,dt. \end{aligned} \end{aligned}$$

Since $\gamma '$ vanishes at the endpoints of the spectrum, and $\lim _{\epsilon \rightarrow 0} \xi _{\gamma (1/2+it)\pm i\epsilon }$ is finite for every $t\in \mathbf {R}$, the integrand in Carleman’s formula is bounded, and the dominated convergence theorem allows us to take the limit for $\delta \rightarrow 0$ inside the integral. This yields the Plancherel formula of the statement, because, as u is a continuous function on $\mathbf {R}$ that is constantly 1 on S, by definition of spectral measure,

$$\begin{aligned} \int _{-\infty } ^\infty u(\gamma )({E(d\gamma )h,h})_2 =\int _ S ({E(d\gamma )h,h})_2 ={\big \Vert {h}\big \Vert }_2^2. \end{aligned}$$

In particular, the Plancherel measure has no poles at the endpoints of the interval $[1/2,1/2+i\pi /\log {q}]$. Let us give a direct proof of this fact. By (20), (21), $\gamma (1/2+\delta )-\gamma (1/2)=i\epsilon =\bigl (\cosh (\delta \log {q})-1\bigr )/\sqrt{q}$ so, if $\delta >0$, then $\delta \mapsto \gamma (1/2+\delta )$ approaches $\gamma (1/2)$ from the right-hand, that is from the positive real semi-axis. Instead, again for $\delta >0$, $\gamma (1/2+i\pi /\log {q}+\delta )-\gamma (1/2+i\pi /\log {q})=-\bigl (\cosh (\delta \log {q})-1\bigr )/\sqrt{q}$, and the other endpoint $\gamma (1/2+i\pi /\log {q})$ is approached from the negative real semi-axis. Since we need $\epsilon \in \mathbf {R}$, we cannot require any longer that $\delta >0$, although, as mentioned above, we need at least $\mathfrak {R}\delta >0$. We have shown that the expressions $\gamma (1/2+\delta )-\gamma (1/2)$ and $\gamma (1/2+i\pi /\log {q}+\delta )-\gamma (1/2+i\pi /\log {q})$ are asymptotically proportional to $\delta ^2$. Therefore the displacements $\gamma (1/2)\pm i\epsilon$ with $\epsilon >0$ are obtained by the two curves in the z-plane $\epsilon \mapsto 1/2+\delta (\pm i\epsilon )\approx 1/2+C\sqrt{\pm i\epsilon }$, with $C=(\log {q})^2 /2\sqrt{q}$ (here $\delta (\epsilon )$ is as after (21), and the determination of the complex square root is $\sqrt{\pm i\epsilon }=e^{\pm i\pi /4} \sqrt{\epsilon }$ so that $\mathfrak {R}\delta =C\mathfrak {R}\sqrt{\pm i\epsilon }>0$). These curves are asymptotically tangent to the half-lines at slope $\pm 1$ respectively given by $s\mapsto 1/2+(1\pm i)s$ with $s>0$. Similarly, $\gamma (1/2+i\pi /\log {q})$ is approached by the curves $\epsilon \mapsto 1/2+i\pi /\log {q}+\delta (\pm i\epsilon )=1/2+i\pi /\log {q}-C\sqrt{\pm i\epsilon }$, asymptotically tangent to the half-lines with slopes $\pm 1$ given by $s\mapsto 1/2+i\pi /\log {q}+(1\pm i)s$ with $s<0$. Here the determination of the square root is the same as before. Now it is easy to see from the expression of $r_z$ that, along these curves, the difference $(r_{1/2+(1+i)\delta }-r_{1/2+(1-i)\delta })(e)$ tends to zero as $\delta \rightarrow 0$. The same fact happens at $z=1/2+i\pi /\log {q}$. Hence there are no poles even at the extreme points, and so no atoms for the Plancherel measure. $\square$

Corollary 5.8

For every $h\in \ell ^1$ and for every $e\in E$,

$$\begin{aligned} h (e) = \frac{\log {q}}{4} \int _0^{\pi /\log {q}} \widehat{h} (1/2+it) \phi _{1/2+it}(e) \big |{c(1/2+it)}\big |^{-2}\,dt. \end{aligned}$$

Proof

We first deduce this inversion formula at $e=e_0$ from the Plancherel formula. By (6), $\widehat{h}=\widehat{\mathcal {E}h}$, hence in order to compute $h(e_0)$ we can limit attention to the radialization of h. It is enough to prove the formula for positive elements $h=g^* *g\in \ell ^1_\#$ as in the proof of Theorem 5.6. For these elements, by radialization, the inversion formula at $e_0$ follows immediately from the Plancherel formula since ${\big \Vert {g}\big \Vert }_2^2=h(e_0)$ and $\big |{\widehat{g}^2}\big |=\widehat{g^* *g}=\widehat{h}$. For $e\ne e_0$, as in Proposition 5.1 let $\lambda _e$ be the element of the subgroup $\mathcal {G}\subset {{\,\mathrm{Aut}\,}}T$ that maps $e_0$ to e. Then the statement follows by applying the inversion formula at the reference edge to $h\circ \lambda _e$ and making use of the multiplicative rule of Proposition 5.1. $\square$

5.5 The Schwartz Class on Edges and the Paley–Wiener Theorem

For any function f on E and any $r\in \mathbf {R}$, consider the seminorms

$$\begin{aligned} \big |{f}\big |_ {r} =\sup _{e\in E} (1+\big |{ e }\big |)^r \big |{f(e)}\big | q^{\big |{ e }\big |/2}. \end{aligned}$$

The Schwartz class $\mathcal {S}$ consists of all complex functions f such that $\big |{f}\big |_ {r}<\infty$ for every r. Since $\big |{f}\big |_ {r}\le \big |{f}\big |_ {s}$ for $r\le s$, $\mathcal {S}$ is equipped with a topology induced by a countable family of seminorms, hence it is a Fréchet space. The factor $q^{\big |{e}\big |/2}$ in the definition of the Schwartz class is an $\ell ^2$ norm compensation for the growth of circles, see (5).

Corollary

The dual space of $\mathcal {S}$ is the space of distributions $\mathcal {S}'$ consisting of all functions g on E such that $\big |{g}\big |_ {r}<\infty$ for some r (the supremum of these exponents r is the order of g). Whenever $p<2<s$ we have $\ell ^p\subset \mathcal {S}\subset \ell ^2\subset \mathcal {S}'\subset \ell ^s$.

Proof

If $f\in \mathcal {S}$, then

$$\begin{aligned} \big |{f(e)}\big | \le \big |{f}\big |_ {s}(1+\big |{e}\big |)^{-s} q^{-\big |{e}\big |/2} \qquad \text {for every }s. \end{aligned}$$

(22)

On the other hand, $g\in \mathcal {S}'$ satisfies the same inequality for some r. Hence

$$\begin{aligned} \big |{{\big \langle {f,g}\big \rangle }}\big | \le \big |{f}\big |_ {s} \big |{g}\big |_ {r}\sum _{e\in E} q^{-\big |{e}\big |} (1+\big |{e}\big |)^{-(r+s)} \qquad \text {for every }s \end{aligned}$$

and the right-hand side is finite for $r+s>1$. Therefore we have $\big |{{\big \langle {f,g}\big \rangle }}\big |\le \big |{f}\big |_ {s}\big |{g}\big |_ {r}\sum _{e\in E} q^{-\big |{e}\big |/2} (1+\big |{e}\big |)^{-(r+s)}$, so $g\mapsto {\big \langle {f,g}\big \rangle }$ is a continuous functional on $\mathcal {S}$. The claim on inclusions follows immediately from (22). $\square$

The following is an analog of a result outlined in [7, Theorem 3.2]. We give a complete and detailed proof.

Proposition 5.9

Denote by $\mathcal {S}_\#$, $\mathcal {S}'_\#$ the subspaces of $\mathcal {S}$, respectively $\mathcal {S}'$, consisting of radial functions (with respect to the fixed reference element). Then

$$\begin{aligned} \mathcal {S}_\# * \mathcal {S}&\subset \mathcal {S},\\ \mathcal {S}_\# * \mathcal {S}'&\subset \mathcal {S}',\\ \mathcal {S}'_\# * \mathcal {S}&\subset \mathcal {S}', \end{aligned}$$

and the left convolution operators defined by $\mathcal {S}_\#$ and $\mathcal {S}'_\#$ are continuous.

Proof

By Corollary 5.3, we know that $q^{-\big |{e}\big |/2}=\phi _{1/2} (e)/\bigl (1+(q-1)\big |{e}\big |/2q\bigr )\approx \big |{e}\big |q^{-\big |{e}\big |/2}$. To keep the notation simpler, in this proof we write $\phi =\phi _{1/2}$, hence $q^{-d(e,e')/2}=\delta _e*\phi (e')/\bigl (1+(q-1)d(e,e')/2q\bigr )$. Then, by the same Corollary, for every function h on E all seminorms $\big |{h}\big |_ {s}$ are finite if and only if so are the seminorms

$$\begin{aligned} \big |{h}\big |_ {s}' =\sup _{e\in E} (1+\big |{e}\big |)^s \frac{\big |{h(e)}\big |}{\phi (e)}. \end{aligned}$$

Then, by (30),(22), in order to prove the first inclusion it is enough to show that, for all $f\in \mathcal {S}$, $g\in \mathcal {S}_\#$, $\big |{g*f}\big |_ {t}'<\infty$ for all $t\in \mathbf {R}$. Since the seminorm $\big |{\,\cdot \,}\big |_ {t}'$ is monotonically increasing with t, it is enough to restrict attention to $t>0$. Since g is radial, we have $g*f(e)=\sum _{e'\in E} g\bigl (d(e,e')\bigr )f(e')$ and

$$\begin{aligned} \big |{g*f(e)}\big | \le \big |{f}\big |_ {r}' \big |{g}\big |_ {s}'\sum _{e'\in E} \bigl (1+ d(e,e')\bigr )^{-s} \bigl (1+\big |{e'}\big |\bigr )^{-r}\phi ( e' ) \phi \bigl (d(e,e')\bigr ). \end{aligned}$$

We have $\big |{g}\big |_ {s}'<\infty$ for every s because $g\in \mathcal {S}$. As $\big |{e}\big |=d(e,e_0)$, it follows from the triangle inequality that $1+\big |{e}\big |\le \bigl (1+d(e,e')\bigr )\bigl (1+\big |{e'}\big |\bigr )$. Then, if we choose $s=t>0$,

$$\begin{aligned} \bigl (1+ d(e,e')\bigr )^{-s} \le \bigl (1+\big |{e'}\big |\bigr )^{ s} \bigl (1+\big |{e }\big |\bigr )^{-s}, \end{aligned}$$

and the previous inequality gives

$$\begin{aligned} \begin{aligned} \big |{g*f(e)}\big |&\le \big |{f}\big |_ {r}' \big |{g}\big |_ {s}'\bigl (1+\big |{e }\big |\bigr )^{-s } \sum _{e'\in E} \bigl (1+\big |{e'}\big |\bigr )^{ s-r} \phi ( e' ) \phi \bigl (d(e,e')\bigr )\\&= \big |{f}\big |_ {r}' \big |{g}\big |_ {s}'\bigl (1+\big |{e }\big |\bigr )^{-s } \sum _{n\ge 0} (1+ n )^{ s-r} \phi ( n ) \sum _ {\big |{e'}\big |=n} \phi \bigl (d(e,e')\bigr ). \end{aligned} \end{aligned}$$

By the multiplicative property of Proposition 5.1,

$$\begin{aligned} \sum _{\big |{e'}\big |=n} \phi (d( e, e')) =\sum _{\big |{e'}\big |=n} (\delta _e*\phi )(e') =\big |{C(e_0,n)}\big | \phi (n ) \phi (e ). \end{aligned}$$

(23)

By (5)

$$\begin{aligned} \begin{aligned} \big |{g*f(e)}\big |&\le C \big |{f}\big |_ {r}' \big |{g}\big |_ {s}'\bigl (1+\big |{e}\big |\bigr )^{-s} \phi (e) \sum _{n\ge 0} (1+n)^{s-r} \phi (n)^2 q^n\\&< C'\big |{f}\big |_ {r}' \big |{g}\big |_ {s}'\bigl (1+\big |{e}\big |\bigr )^{-s} \phi (e) \sum _{n\ge 0} (1+n)^{s-r} n ^2 \end{aligned} \end{aligned}$$

again by the asymptotics of spherical functions in Corollary 5.3. For $s<r-3$ the series converges. Hence, for $0<s=t<r-3$, $\big |{g*f(e)}\big |<C\big |{f}\big |_ {r}'\big |{g}\big |_ {s}'\bigl (1+\big |{e}\big |\bigr )^{-s} \phi (e)$. We have just proved that, if $\big |{f}\big |_ {r}',\big |{g}\big |_ {s}'<\infty$ and $s>0$, then $\big |{g*f}\big |_ {s}'<\infty$ for $r>s+3$. The first inclusion follows because r is arbitrary.

In the second inclusion, $\big |{f}\big |_ {r}',\big |{g}\big |_ {s}'<\infty$ for some r and all s. Choose $s>0$ and use the triangle inequality in the form $1+\big |{e'}\big |\le \bigl (1+d(e,e')\bigr )\bigl (1+\big |{e}\big |\bigr )$, hence $\bigl (1+d(e,e')\bigr )^{-s} \le \bigl (1+\big |{e}\big |\bigr )^s \bigl (1+\big |{e'}\big |\bigr )^{-s}$. We make use again of (23) and get $\big |{g*f(e)}\big |\le C''\big |{f}\big |_ {r}'\big |{g}\big |_ {s}'\bigl (1+\big |{e}\big |\bigr )^s \phi (e)\sum _{n\ge 0} n^2 (1+n)^{-(s+r)}$. The series converges for $s>3-r$. Since s is arbitrary, this inequality is satisfied for suitable $s>0$. This proves the second inclusion.

For the third inclusion, $\big |{f}\big |_ {r}',\big |{g}\big |_ {s}'<\infty$ for all r and some s. Choose $r>0$, and use the triangle inequality in the form $1+d(e,e')\le \bigl (1+\big |{e}\big |\bigr )\bigl (1+\big |{e'}\big |\bigr )$. Since $r>0$, $\bigl (1+\big |{e'}\big |\bigr )^{-r} \le \bigl (1+d(e,e')\bigr )^{-r} \bigl (1+\big |{e}\big |\bigr )^r$. The same steps lead to $\big |{g*f(e)}\big |\le C\big |{f}\big |_ {r}'\big |{g}\big |_ {s}'\bigl (1+\big |{e}\big |\bigr )^r \phi (e)\sum _{n\ge 0} n^2 (1+n)^{-(s+r)}$, and the series converges for $r>3-s$. Since s is fixed and r is arbitrary, this inequality is satisfied for suitable $r>0$. $\square$

By Theorem 5.6, the spectrum of $\eta _1$ as a convolution operator on $\ell ^2$ is $S=\gamma (1/2+i\mathbf {R}) =[a_-,a_+]$ with $a_\pm =(q-1)/2q\pm 1/\sqrt{q}$; moreover, $\gamma (1/2)= a_+$. We need to estimate the spherical polynomials $\widetilde{Q}_n$ on S.

Lemma

For every $k\in \mathbf {N}$,

$$\begin{aligned} \big |{D^k\widetilde{Q}_n(x)}\big | \le q^{-(n-k)/2} \biggl (1+n\frac{q-1}{2\sqrt{q}}\biggr )\prod _{j=n-k+1}^n j^2 \quad \text {for }x\in S. \end{aligned}$$

Proof

From Definition 5.4 and Corollary 5.5, one has that $\big |{\widetilde{Q}_n \bigl (\gamma (1/2+it)\bigr )}\big |=\big |{\phi _{1/2+it}(n)}\big |\le \phi _{1/2}(n)$, that is, $\big |{\widetilde{Q}_n(x)}\big |\le \phi _{1/2}(n)=M_n$ for all $x\in S$, with $M_n=\bigl (1+n(q-1)/2\sqrt{q}\bigr )q^{-n/2}$. It follows from [31, p. 40] that, if a polynomial p of degree n satisfies the inequality $\big |{p}\big |\le M$ on $[a_-,a_+]$, then its derivative satisfies $\big |{Dp}\big |\le 2Mn^2 /(a_+-a_-)$ in $[a_-,a_+]$. Here $a_+-a_-=2/\sqrt{q}$. Hence $\big |{D\widetilde{Q}_n}\big |\le M_n n^2 \sqrt{q}=n^2 \bigl (1+n(q-1)/2\sqrt{q}\bigr )q^{-(n-1)/2}$ on S. The polynomial $D\widetilde{Q}_n$ has degree $n-1$, so the same argument shows that $D^2 \widetilde{Q}_n$ is bounded by $qn^2 (n-1)^2 M_n=q^{-(n-2)/2} n^2 (n-1)^2 \bigl (1+n(q-1)/2\sqrt{q}\bigr )$. We conclude by iteration. $\square$

Theorem 5.10

The spherical Fourier transform is an isomorphism of $\mathcal {S}_\#$ onto $C^\infty (S)$, and of $\mathcal {S}'_\#$ onto the space of distributions with support in S.

Proof

It is enough to show the first part of the statement, as the second follows by duality. By (5), the spherical Fourier transform of $h\in \mathcal {S}_\#$ is $\widehat{h}(z)=2\sum _{n\ge 0} q^n h(n) Q_n(z)$. If $x=\gamma (z)$, it is enough to prove the convergence of the series $\sum _{n\ge 0} q^n h(n) \widetilde{Q}_n(x)$ in $C^\infty (S)$, that is, that for each $k\ge 0$ the series $D^k \widehat{h}(x)=\sum _{n\ge 0} q^n h(n)D^k \widetilde{Q}_n(x)$ converges uniformly. The assumption $h\in \mathcal {S}_\#$ implies that $\big |{h(n)}\big | \le c_{r} (1+n)^{-r} q^{-n/2}$ for every r. If $r=2k+3$, by the previous lemma the summands decay as $n^{-2}$ and uniform convergence follows.

To prove the converse, take any $g\in C^\infty (S)$. By the inversion formula of Corollary 5.8 we must show that the radial function

$$\begin{aligned} h(n) =\frac{\log {q}}{4} \int _0^{\pi /\log {q}} \phi _{1/2+it}(n) g\bigl (\gamma (1/2+it)\bigr ) \big |{c(1/2+it)}\big |^{-2}dt \end{aligned}$$

belongs to $\mathcal {S}_\#$. By the expansion in Corollary 5.3,

$$\begin{aligned} \begin{aligned} h(n)&=\frac{\log {q}}{4} q^{-n/2} \int _0^{\pi /\log {q}}g\bigl (\gamma (1/2+it)\bigr ) \biggl (\frac{q^{ int}}{c(1/2+it)} +\frac{q^{-int}}{c(1/2-it)}\biggr )\,dt\\&=\frac{\log {q}}{2} q^{-n/2} \int _0^{\pi /\log {q}} q^{ int} \frac{g\bigl (\gamma (1/2+it)\bigr )}{c(1/2+it)}\,dt, \end{aligned} \end{aligned}$$

where the last identity follows from the fact that the first integral is the sum of two terms, and these terms are interchanged by the reflection $t\mapsto -t$, that leaves the integral invariant because of the periodicity and symmetry properties of the functions $\gamma$ and c. Therefore the two terms are equal.

Since $c(1/2+it)\ne 0$ for $0<t<\pi /\log {q}$ and c has simple poles at $t=0$ and $t=\pi /\log {q}$, the sequence $h(n)q^{n/2}$ is the n-th Fourier coefficient of a function in $C^\infty [0,\pi /\log {q}]$, and so it is rapidly decreasing. This means that $h\in \mathcal {S}_\#$. $\square$

6 The Horospherical Radon Transform on Edges

6.1 The Radon Transform on Edges and Its Dual

The Radon transform R maps any function f on E to a function Rf on the space $\mathcal {H}$ of horospheres by

$$\begin{aligned} Rf(\omega ,n) =\sum _{e\in \mathbf {h}(\omega ,n)} f(e). \end{aligned}$$

We look at the volumes of the intersections of circles and horospheres: for $n\in \mathbf {Z}$ and $m\in \mathbf {N}$, let $k(n,m)=\big |{\mathbf {h}(\omega ,n)\cap C_m}\big |$ (because of radial symmetry, k(n, m) does not depend on the tangency point $\omega$). The numbers k(n, m) can be easily computed as in [16]; here we need only their asymptotics. We state the result.

Lemma 6.1

$$\begin{aligned} k(n,m)= {\left\{ \begin{array}{ll} 1 &{}\text {if }n=m,\\ (q-1)q^{(m-n-1)/2} &{}\text {if }\big |{n}\big |<m\text { and }n+m\text { is odd,}\\ q^ m &{}\text {if }n=-m,\\ 0 &{}\text {otherwise.} \end{array}\right. } \end{aligned}$$

Therefore k(n, m) vanishes if $m<\big |{n}\big |$ and is $O(q^{(m-n)/2})$ if n is fixed and $m\rightarrow \infty$.

If $\big |{e}\big |=n$, the set of tangency points of horospheres in $\mathcal {H}$ through e of index n is the boundary arc $\Omega _e$, with measure proportional to $q^{-n}$. As we did for $\mathcal {S}$, we can normalize with the square root of this factor and define the Schwartz class $\mathcal {S}(\mathcal {H})$ as the space of all continuous functions F on $\mathcal {H}$ such that, for all $r\in \mathbf {R}$,

$$\begin{aligned} \big |{F}\big |_ {r} =\sup _{\begin{array}{c} \omega \in \Omega \\ n \in \mathbf {Z} \end{array}} (1+\big |{n}\big |)^r q^{n/2} \big |{F(\omega ,n)}\big | <\infty . \end{aligned}$$

(24)

The left-hand side is a seminorm on the space $\mathcal {S}(\mathcal {H})$. Equipped with these seminorms, $\mathcal {S}(\mathcal {H})$ is a Fréchet space.

Theorem 6.2

The Radon transform is a continuous linear operator from $\mathcal {S}$ to $\mathcal {S}(\mathcal {H})$.

Proof

By (22), if $f\in \mathcal {S}$, $r\in \mathbf {R}$ and $\mathbf {h}=\mathbf {h}(\omega ,n)\in \mathcal {H}$,

$$\begin{aligned} \big |{Rf(\mathbf {h})}\big | \le \big |{f}\big |_ {r}\sum _{e\in \mathbf {h}} (1+\big |{e}\big |)^{-r} q^{-\big |{e}\big |/2} = \big |{f}\big |_ {r}Rw_r(\mathbf {h}), \end{aligned}$$

where $w_r(e)=(1+\big |{e}\big |)^{-r}q^{-\big |{e}\big |/2}$. Therefore it is enough to show that $\big |{Rw_r}\big |_ {r-1}$ is finite. One has

$$\begin{aligned} Rw_r (\omega ,n) =\sum _{e\in \mathbf {h}(\omega ,n)} (1+\big |{e}\big |)^{-r}q^{-\big |{e}\big |/2} =\sum _{m=\big |{n}\big |}^\infty k(n,m) (1+ m )^{-r}q^{- m /2}. \end{aligned}$$

The series on the right-hand side does not depend on $\omega$, and by Lemma 6.1 its terms are bounded by $C(1+m)^{-r} q^{-n/2}$ for some $C>0$. Hence, for each $r>1$, one has $\sum _{m\ge 0} (1+\big |{n}\big |+m)^{-r}<C(1+\big |{n}\big |)^{1-r}$. Therefore $\big |{Rw_r (\omega ,n)}\big |<Cq^{-n/2} (1+\big |{n}\big |)^{1-r}$ and so $\big |{Rw_r}\big |_ {r-1}$ is finite for $r>1$. $\square$

With notation as before (7), the space $\mathcal {H}$ is equipped with the (${{\,\mathrm{Aut}\,}}T$)-invariant measure $\sigma =m\times \nu _{e_0}$, where m is the measure on $\mathbf {Z}$ given by $m(\{n\})=q^n$ (see [16]). For any $e\in E$, let $\mathcal {H}_e$ be the set of horospheres containing e. If F is a bounded measurable function on $\mathcal {H}$, its dual Radon transform is defined as

$$\begin{aligned} R^* F( e) =\int _{\mathcal {H}_e} F(\mathbf {h}) \,d\sigma (\mathbf {h}). \end{aligned}$$

Set $B({e,n})=\{\omega :e\in \mathbf {h}(\omega ,n)\}$. Then the last expression becomes

$$\begin{aligned} R^* F(e) =\sum _{n=-\infty } ^\infty \int _{B(e,n)} F(\omega , n) \,d\nu _e(\omega ) =\sum _{n=-\infty } ^\infty q^n \int _{B(e,n)} F(\omega , n) \,d\nu (\omega ), \end{aligned}$$

(25)

because, by (7), the factor $q^n$ is the value of $d\nu _e/d\nu (S_e)$.

Theorem 6.3

The dual Radon transform is a continuous linear operator from $\mathcal {S}(\mathcal {H})$ to $\mathcal {S}'$.

Proof

Let $F\in \mathcal {S}(\mathcal {H})$. For every $r\in \mathbf {R}$, by (24), (25),

$$\begin{aligned} \big |{R^* F(e)}\big | \le \sum _{n=-\infty } ^\infty q^ n \int _{B(e,n)} \big |{F(\omega ,n)}\big |\,d\nu (\omega ) \le \big |{F}\big |_ {r}\sum _{n=-\infty } ^\infty q^{n/2} (1+\big |{n}\big |)^{-r} \nu (B(e,n)). \end{aligned}$$

For each e of fixed length, $\nu (B(e,n))$ is independent of e, by rotational invariance. Therefore $\nu (B(e,n))$ is proportional to the intersection cardinality $k(n,\big |{e}\big |)$, i.e., $\nu (B(e,n)) =k(n,\big |{e}\big |)/\big |{C_{\big |{e}\big |}}\big |$. Since $\big |{C_{\big |{e}\big |}}\big |\approx q^{\big |{e}\big |}$, by Lemma 6.1 we have $\nu (B(e,n))\approx q^{-(n+\big |{e}\big |)/2}$ if $\big |{n}\big |\le \big |{e}\big |$, and 0 otherwise. Therefore

$$\begin{aligned} \big |{R^* F(e)}\big | \le C\big |{F}\big |_ {r}q^{-\big |{e}\big |/2} \sum _{n=-\big |{e}\big |} ^{ \big |{e}\big |} (1+\big |{n}\big |)^{-r} . \end{aligned}$$

If $r\ge 0$, the terms of the sum with positive indices are non-increasing, hence $\sum _{n=1}^{k} (1+\big |{n}\big |)^{-r}\approx \int _0^k (1+x)^{-r}\,dx=1-(1+k)^{1-r}$. The right-hand side is bounded for each $r\ge 1$. Hence, for all $r\ge 1$ and some $C>0$, $\big |{R^* F(e)}\big |\le C\big |{F}\big |_ {r}q^{-\big |{e}\big |/2}$. Thus $\big |{R^* F}\big |_ {0}<C\big |{F}\big |_ {r}$ if $r>1$. $\square$

6.2 Radon Transform Inversion on Edges

By their covariant definition, the Radon transform and its dual transform commute with the action of ${{\,\mathrm{Aut}\,}}T$. Therefore the same is true for $R^*R$, bounded from $\mathcal {S}$ to $\mathcal {S}'$ by Theorems 6.2 and 6.3:

Corollary 6.4

$R^*R$ is a bounded convolution operator from $\mathcal {S}$ to $\mathcal {S}'$.

Its convolution kernel $\Psi =R^* R\delta _{e_0}$ is in $\mathcal {S}'$. Being invariant under $({{\,\mathrm{Aut}\,}}T)_{e_0}$, it is a radial function. Our goal is to find a continuous left convolution inverse, that is, a function $\Phi$, necessarily radial, such that $\Phi *\Psi =\delta _{e_0}$ and that the convolution operator with kernel $\Phi$ maps the image $R^*R\mathcal {S}$ to $\mathcal {S}$ and is continuous in the topology of $\mathcal {S}'(E)$.

For $\big |{e}\big |=n$, it is easy although tedious to verify, as in [16], that the value $\psi _n$ of $\Psi (e)=R^* R\delta _{e_0} (e)= R^* \chi _{\mathcal {H}_{e_0}}=\sigma (\mathcal {H}_e \cap \mathcal {H}_{e_0})$ is

(26)

We know that $\Psi \in \mathcal {S}'_\#$, and, by Corollary 5.3, all the spherical functions $\phi _z$ belong to $\mathcal {S}_\#'$ but not to $\mathcal {S}_\#$. Therefore $\widehat{\Psi }(z)={\big \langle {\Psi ,\phi _z}\big \rangle }$ does not converge in the ordinary sense: we shall compute it by functional analysis and the resolvents.

Lemma

For $e\in E$, let $y_z(e)=q^{-z\big |{e}\big |}$, $\widetilde{y}_z(e)=(-1)^{\big |{e}\big |}y_z(e)= y_{\widetilde{z}}(e)$ (notation as in Remark 5.7) and $M_z=(y_z-\widetilde{y}_z)/2$. Then, if $r_z$ is as in Theorem 5.6, one has

$$\begin{aligned} M_z(e) =\frac{q^{1-z}-q^z-(q-1)}{2q} r_z(e) = q^{ -z \big |{e}\big |} \end{aligned}$$

if $\big |{e}\big |$ is odd, and zero otherwise. In particular,

$$\begin{aligned} \Psi =\delta _{e_0}+\frac{q-1}{2\sqrt{q}} M_{1/2}. \end{aligned}$$

(27)

Moreover,

$$\begin{aligned} \widehat{M_z}(w) =\frac{(q^{1-z}-q^z)\bigl (\gamma (w) -(q-1)/2q\bigr ) -(q -1 )\bigl ( \gamma (z)-(q-1)/2q\bigr )}{2q \bigl (\gamma (w)+\gamma (z)-(q-1)/ q\bigr ) \bigl (\gamma (w)-\gamma (z) \bigr )}. \end{aligned}$$

(28)

Proof

$M_z(e)=q^{-(2k+1)z}$ if $\big |{e}\big |=2k+1$ and $M_z(e)=0$ if $\big |{e}\big |=2k$. Then, by (26), $M_{1/2}(e)=2\Psi (e)\sqrt{q}/(q-1)$ for $e\ne e_0$ and $M_{1/2}(e_0)=0$. This proves (27).

Since $\widehat{\eta }_1(w)=\sum _{e\in E} \eta _1(e)\phi _w(e)=\gamma (w)$, it follows from (18) and the resolvent equation (14) that $\widehat{r}_z(w)=1/(\gamma (w)-\gamma (z))$. Hence, by (13),

$$\begin{aligned} \widehat{y}_z (w) =\frac{q^{1-z}-q^z-(q-1)}{2q\bigl (\gamma (w) -\gamma (z)\bigr )}. \end{aligned}$$

On the other hand, by (16),(17),

$$\begin{aligned} \widehat{\widetilde{y}}_z(w) =\widehat{y}_{z+i\pi /\log {q}}(w) =\frac{q^z-q^{1-z}-(q-1)}{2q}\frac{1}{\gamma (w) +\bigl (\gamma (z)-(q-1)/q\bigr )}. \end{aligned}$$

Now $\widehat{M_z}=(\widehat{y}_z-\widehat{\widetilde{y}}_z)/2$ yields (28). $\square$

By Theorem 5.6, $\gamma (1/2)=\rho (\eta _1)=(q-1)/2q+1/\sqrt{q}$. Hence the expression $\gamma (1/2)-(q-1)/2q$ in the numerator of (28) of $\widehat{M_{1/2}}$ equals $1/\sqrt{q}$, and, by (27),

$$\begin{aligned} \begin{aligned} \widehat{\Psi }(w)&=1-\frac{(q-1)^2}{4q^2\bigl (\gamma (w)-(q-1)/2q+1/\sqrt{q}\bigr ) \bigl (\gamma (w)-(q-1)/2q-1/\sqrt{q}\bigr )}\\&=1-\frac{(q-1)^2}{4q^2\bigl (\gamma (w)-(q-1)/2q \bigr )^2 -4q} . \end{aligned} \end{aligned}$$

(29)

By Corollary 6.4 and the Paley-Wiener theorem 5.10, the multiplication operator by $\widehat{\Psi }$ is bounded on $\mathcal {S}'(S)$. Since $\widehat{\Psi }$ is smooth in the interior of S and has simple poles at the endpoints, this multiplication maps $C^\infty (S)$ to the space C of smooth functions with simple poles at the endpoints (therefore to the distribution space $\mathcal {S}'(S)$). Hence C is the spherical Fourier transform of the image of $R^*R$ acting on $\mathcal {S}(E)$.

If there exists an inverse convolution operator $\Phi$, then its symbol must be $\widehat{\Phi }=1/\widehat{\Psi }$, and multiplication by this function should give rise to a bounded operator from $\mathcal {S}'(S)$ to $C^\infty (S)$, that of course is impossible. However, we claim that multiplication by $1/\widehat{\Psi }$ is a continuous operator on $\mathcal {S}'(S)$. Indeed, we first show that $1/\widehat{\Psi } \in C^\infty (S)$. Since $\gamma$ is holomorphic, by (29) it is enough to show that $\widehat{\Psi }$ never vanishes in S. This amounts to

$$\begin{aligned} 4q ^2{\biggl (\gamma (w)-\frac{q-1}{2q}\biggr )^2-4q} \ne (q-1)^2 \end{aligned}$$

for $w=1/2+it$, where we can restrict attention to $0\le t\le \pi /\log {q}$. As $\gamma (1/2+it)=\cos (t\log {q})/\sqrt{q}+(q-1)/2q$ by (9), the non-vanishing condition becomes

$$\begin{aligned} 4q \cos ^2 (t\log {q}) \ne 4q+(q-1)^2. \end{aligned}$$

This is true for every t when $q\ne 1$, that is, on non-trivial trees.

A similar argument shows that $1/\widehat{\Psi }\ne 0$ in the interior of S and has a zero of order one at the endpoints $\pm \rho$. So the multiplication by $1/\widehat{\Psi }$ maps $C^\infty (S)$ to the proper subspace of $C^\infty (S)$ of functions vanishing at the endpoints with zeros of order one, and maps the functions that are smooth in the interior of S and have simple poles at the endpoints, that is the image C of $(R^* R)\widehat{~}$, surjectively onto $C^\infty (S)$. So we have proved the following statement, thereby achieving our goal:

Theorem

$1/\widehat{\Psi }$ is the symbol of a left inverse of $R^*R:\mathcal {S}(E)\rightarrow \mathcal {S}'(E)$, a continuous operator in the topology of $\mathcal {S}'(E)$.

An easy computation shows that

$$\begin{aligned} \widehat{\Psi }(1/2+it) =1 +\frac{(q-1)^2}{4q\sin ^2 (t\log {q})} =\biggl (\frac{4q \sin ^2 (t\log {q})}{(q-1)^2 +4 \sin ^2 (t\log {q})}\biggr )^{-1} \end{aligned}$$

as well as

$$\begin{aligned} c(1/2+it)&= \frac{1}{2} \biggl (1 +i\frac{q-1}{2\sqrt{q}\sin (t\log {q})}\biggr ),\\ \big |{c(1/2+it)}\big |^{-2}&= \frac{16 q\sin ^2 (t\log {q})}{4 q\sin ^2 (t\log {q})+(q-1)^ 2} \end{aligned}$$

and, for $t\ne ki/\log {q}$,

$$\begin{aligned} \phi _{1/2+it}(e) =q^{-\big |{e}\big |/2}\biggl (\cos (t\big |{e}\big |\log {q}) +\frac{q-1}{2\sqrt{q}\sin (t \log {q})} \sin (t\big |{e}\big |\log {q})\biggr ). \end{aligned}$$

Therefore, by the inversion formula (5.8) applied to $1/\widehat{\Psi }$,

$$\begin{aligned} \begin{aligned} \Phi (e) = q ^{-\big |{e}\big |/2} ( \log {q})&\int _0^{\pi /\log {q}} \frac{ 4q \sin ^2 (t \log {q})}{ 4 \sin ^2 (t \log {q})+(q-1)^2} \frac{16q \sin ^2 (t \log {q})}{ 4q \sin ^2 (t \log {q})+(q-1)^2}\\&\qquad \cdot \biggl (\cos (t\big |{e}\big |\log {q}) +\frac{ q-1}{2\sqrt{q}\sin (t \log {q})} \sin (t\big |{e}\big |\log {q})\biggr ) \,dt. \end{aligned} \end{aligned}$$

The denominators in the first two factors of the integrand never vanish and are bounded away from 0, so these factors are positive and bounded (moreover, each tends to zero quadratically at the endpoints of the interval). The third factor is bounded in absolute value by $1+(q-1)\big |{e}\big |/2\sqrt{q}$, attained when t tends to 0 or to $\pi /\log {q}$, and therefore $\big |{\Phi (e)}\big |<Cq^{-\big |{e}\big |/2}$ for some constant C. So the seminorm of order 0 of $\phi$ is finite, hence $\phi$ belongs to $\mathcal {S}'_\#$ and to $\ell ^p$ for $p>2$. If this were the exact rate of decay, then Hölder’s inequality would not imply that the series that defines $\Phi *\Psi$ is absolutely convergent, because, by (26), $\Psi \in \ell ^r$ only for $r>2$.

The actual decay of $\Phi$ is faster, thanks to the third factor in the integral. Indeed, its first summand, $\cos (t\big |{e}\big |\log {q})$, multiplied by the product of the first two factors, yields its cosine Fourier coefficient of order $\big |{e}\big |$ of this product, that is a $C^\infty$ periodic function; hence this term of the integral vanishes faster than polynomially as $\big |{e}\big |\rightarrow \infty$. The second summand of the last factor yields a sine Fourier coefficient that behaves in the same way, because the sine function in its denominator is canceled by the numerators of the other factors. Therefore $\Phi (e)=\zeta (\big |{e}\big |)q^{-\big |{e}\big |/2}$ with $\zeta$ vanishing at infinity faster than polynomially, hence $\Phi \in \mathcal {S}_\#$ and the series that defines $\Phi *\Psi$ is convergent because $\Psi \in \mathcal {S}'_\#$. By Proposition 5.9, not only does $\Phi$ define a bounded operator $\mathcal {S}'(E)\rightarrow \mathcal {S}'(E)$ (mapping in particular $\Psi$ to $\Phi *\Psi \in \mathcal {S}'_\#$), but it gives also a bounded convolution operator on $\mathcal {S}(E)$. Note, however, that $\Phi \notin \ell ^2$ and does not define a bounded convolution operator on $\ell ^2$ to $\ell ^\infty$, and the convolution with $\ell ^2$ functions, and even with distributions, as for instance $\Psi$, is convergent although it may be not absolutely convergent.

Appendix: Automorphisms of Trees and Convolution Products

The isotropy subgroup $K_v$ of $G={{\,\mathrm{Aut}\,}}T$ at $v\in V$ is compact, and $G/K_v$ is discrete. Since T is homogeneous, G acts transitively upon V, and $G/K_v$ is in bijection with V. Moreover, $K_v$ acts transitively upon the circle $C_n$ of vertices at any distance n from v, or equivalently, the action of G is doubly transitive.

By this bijection, summable functions on the discrete space V lift to summable functions on G (with respect to its Haar measure). Hence, the convolution product on G gives rise to a convolution product on $L^1$, and in particular on finitely supported functions therein; we shall often restrict attention to this space. The liftings from $G/K_{v_0}$ to G identify right-$K_{v_0}$-invariant functions on G with functions on V. Write $K=K_{v_0}$: then the bi-K-invariant functions on G are radial functions on V, in the sense that they depend only on the distance from $v_0$. We denote the corresponding $L^1$ spaces by $L^1_\#$. We shall show that (G, K) is a Gel’fand pair, that is, $L^1_\#$ is an abelian convolution algebra. All this also works word by word for vertices.

Let $\mu$ denote the Haar measure on G normalized on K. The usual definition of convolution for functions on G is $u_1*u_2(\tau )= \int _G u_1(\lambda ^{-1}\tau )u_2(\lambda )\,d\mu (\lambda )$, since G is unimodular. Let $\lambda \mapsto \widetilde{\lambda }$ be the canonical projection of G to G/K, $\widetilde{\mu }$ the quotient measure of $\mu$ (that is, the counting measure) on G/K. If $u_2$ is right-K-invariant and $u_1$ bi-K-invariant, we have

$$\begin{aligned} \begin{aligned} u_1*u_2(\widetilde{\tau })&=\int _{G/K} \int _ K u_1( \kappa ^{-1} \lambda ^{-1}\tau ) u_2( \lambda \kappa ) \,d \mu ( \kappa ) \,d\widetilde{\mu }(\widetilde{\lambda })\\&=\int _{G/K} u_1( \lambda ^{-1}\tau ) u_2( \lambda ) \,d\widetilde{\mu }(\widetilde{\lambda }) =\int _{G/K} u_1( \widetilde{\lambda ^{-1}\tau } ) u_2( \widetilde{\lambda }) \,d\widetilde{\mu }(\widetilde{\lambda }). \end{aligned} \end{aligned}$$

Convolution can be handled in a simpler way if we produce a suitable cross-section in G/K, and precisely a subgroup $\mathcal {G}$ of G such that the quotient map $\mathcal {G}\rightarrow G/K$ is one-to-one and onto. We would like to choose such subgroup $\mathcal {G}$ based on the geometry of the tree. The way to do so has been known for a long time. Label every edge that touches a reference vertex $v_0\in V$ with a letter $a_0,\dotsc ,a_q$. Then label with the same set of letters all edges stemming from a neighbor $v_1$ of $v_0$: to the edge $[v_0, v_1]$ we assign the same letter that was assigned at the first step, and so on. Label each edge-path $\{v_0,v_1,v_2\}$ of length 2 by the word $a_{j_1}a_{j_2}$, where $a_{j_1}$ is the letter associated to $[v_0,v_1]$ and $a_{j_2}$ is associated to $[v_1,v_2]$. Iterate this procedure to label all finite paths of edges starting at $v_0$ (that is, all vertices) with words in the letters $a_0,\dotsc ,a_q$: the labeling is well defined because the tree has no loops.

The semigroup of all words in the letters $a_0,\dotsc ,a_q$ with the juxtaposition product is made into a group by setting $a_j^{-1}=a_j$; the empty word, its identity element, is associated to $v_0$. Limiting attention to reduced words, that is, canceling every occurrence of two consecutive identical letters, we see that V is in bijective correspondence with this group, isomorphic to the direct product $\mathcal {G}=*_{j=0}^q\mathbf {Z}_2$ because T has no loops. Each reduced word $w=a_{j_1}\cdots a_{j_n}$ can be regarded as a finite chain in V starting at $v_0$: each element $w_j\ne v_0$ of this chain is obtained multiplying its predecessor $w_{j-1}$ by $a_{k_j}$ on the right. The left regular action of $\mathcal {G}$ onto itself becomes an action on this set of words, isometric in the metric of V (the natural distance in T), that is, preserving adjacency. Thus $\mathcal {G}\subset {{\,\mathrm{Aut}\,}}T$ and $\mathcal {G}\cap K_{v_0}$ is the identity element, that is the empty word. $\mathcal {G}$ is transitive, and clearly T is the Cayley graph of $\mathcal {G}$ with generators $a_0,\dotsc ,a_q$. If the homogeneity degree q is odd, i.e., there is an even number $q+1=2r$ of neighbors, then, by a similar argument, another simply transitive subgroup of ${{\,\mathrm{Aut}\,}}T$ is isomorphic to the free group $\mathbf {F}_r=*_{j=1}^r \mathbf {Z}$ [13, 20].

We can build a similar labeling for edges, although there is a difference. We can regard E as the set of vertices of some graph E, whose edges correspond to pairs of adjacent edges in E. Then E has loops, and this leads to a simply transitive group of isometries that is not a free product of $q+1$ copies of $\mathbf {Z}_2$ or a free group, but the free product $\mathbf {Z}_{q+1}*\mathbf {Z}_{q+1}$, where $\mathbf {Z}_{q+1}$ is the cyclic group with $q+1$ elements.

Indeed, the Cayley graph of this group (with respect to the generators of its factors) has E as its set of vertices. More precisely, E can be regarded as a graph via the dual graph construction, that identifies each edge with a vertex of the associated graph. Two vertices of this graph are contiguous if the corresponding edges in E join at a vertex $v\in V$. Then the graph E is the symmetric graph of complete polygons of $q+1$ sides, defined in [26]. The vertices of each polygon in this graph correspond to the $q+1$ edges in E that share a given endpoint; each vertex in the graph belongs to exactly two polygons, namely those corresponding to the two endpoints in V of the edge in E associated to that vertex of the graph. For each pair of vertices in the graph, the shortest path connecting them lies in only one chain of consecutively adjacent polygons. This “tree of polygons” is the Cayley graph of $\mathbf {Z}_{q+1}*\mathbf {Z}_{q+1}$ if we choose all the 2q non-zero elements of each factor $\mathbf {Z}_{q+1}$ as generators. Clearly, this graph is hyperbolic in the sense of Gromov. The block distance between two vertices of the graph is the number of “polygons” visited by the shortest path joining them plus 1: two vertices belonging to the same polygon have distance 1, two vertices in adjoining polygons have distance 2 and so on.

Nevertheless, every group $\mathcal {G}$ of automorphisms acting simply transitively on either V or E induces a convolution product on functions that depends on the choice of $\mathcal {G}$. On the other hand, the full automorphism group G does not act simply transitively. To show in which sense G defines a convolution product we shall consider its action on E; the statements for V are exactly the same. Take f bi-K-invariant, g right-K-invariant functions on G. Both can be regarded as functions on E, with f radial around $e_0$. Their convolution on E becomes

$$\begin{aligned} f*g(e)=\sum _{e'\in E} f\bigl (d(e,e')\bigr )g(e'). \end{aligned}$$

(30)

If f and g are both bi-K-invariant, this is

$$\begin{aligned} f*g ( e ) = f*g\bigl (d(e ,e_0)\bigr ) =\sum _{y\in E} f\bigl (d(e ,e' )\bigr ) g\bigl (d(e',e_0)\bigr ). \end{aligned}$$

The convolution of bi-K-invariant functions is bi-K-invariant, hence $L^1_\#$ is a convolution algebra, the closure in the $L^1$ norm of the algebra $\mathcal {R}_\#$ of radial finitely supported functions. Radial functions on E are bi-K-invariant functions on G and are constant on the circles in E with center $e_0$. For every functions f, g on E with f radial, $\tau (f*g)=f*\tau g$, where $\tau g$ is defined by $\tau g(e)=g(\tau ^{-1} e)$. Indeed,

$$\begin{aligned} \begin{aligned} \tau (f*g)(e)&=\sum _{e' } g( e' ) f\bigl (d(\tau ^{-1}e ,e' )\bigr ) =\sum _{e''} g ( \tau ^{-1}e'' ) f\bigl (d(\tau ^{-1}e , \tau ^{-1}e'' )\bigr )\\&=\sum _{e''} g( \tau ^{-1}e'' ) f\bigl (d( e ,e'')\bigr ) =f *\tau g(e). \end{aligned} \end{aligned}$$