The relationship between projective geometric and rational quadratic b-spline curves

Abstract

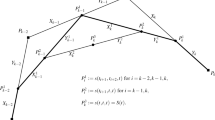
For two rational quadratic B-spline curves with same control vertexes, the cross ratio of four collinear points are represented: which are any one of the vertexes, and the two points that the ray initialing from the vertex intersects with the corresponding segments of the two curves, and the point the ray intersecting with the connecting line between the two neighboring vertexes. Different from rational quadratic Bézier curves, the value is generally related with the location of the ray, and the necessary and sufficient condition of the ratio being independent of the ray’s location is showed. Also another cross ratio of the following four collinear points are suggested, i. e. one vertex, the points that the ray from the initial vertex intersects respectively with the curve segment, the line connecting the segments end points, and the line connecting the two neighboring vertexes. This cross ratio is concerned only with the ray’s location, but not with the weights of the curve. Furthermore, the cross ratio is projective invariant under the projective transformation between the two segments.