The constrained equal losses family of rules for claims problems

Abstract

In this study, we introduce a family of rules for claims problems called the CEL-family. The family is defined by means of a parameter $\theta \in [0,1]$ as a notion of solidarity and contribution. It contains the constrained equal losses and the constrained equal awards rules. We perform an axiomatic analysis considering the main properties in the literature, for the sake of comparison. We apply the family to the distribution of the European Regional Development Funds to study how the rules in the family treat regions with relatively smaller claims compared to regions with relatively larger claims.

1 Introduction

If a firm goes bankrupt, how should its liquidation be divided among stakeholders? How can fixed taxes be assigned to individuals with different incomes? These kinds of situations can be addressed in the so-called claims problems. In general, a claims problem is defined as a situation in which an infinitely dividable endowment is allocated to a group of agents, while the agents’ aggregate claim exceeds the endowment (to deepen their understandings, readers are referred to (O’Neill 1982; Aumann and Maschler 1985); and a comprehensive survey conducted by (Thomson 2019).

To address these challenges, a collection of allocation methods known as “rules" are employed. Within the current literature, numerous rules are referenced, including but not limited to equal division (Aumann and Maschler 1985), claim-proportional division, the constrained equal awards, and the constrained equal losses rules (Maimonides 2000). In an axiomatic analysis, these rules undergo evaluation through the application of a set of principles referred to as “axioms". These axioms aim to harmonize fairness principles with concepts of equity, solidarity, effort, and rights.

One of the rules we discussed is constrained equal losses, which distributes losses (i.e., the difference between aggregate claims and the endowment) equally among all claimants. The distinctive characteristic of this rule lies in its handling of “residual claims", those relatively small claims which, even after eliminating them from the problem, would still result in a claims surplus (where the total claims exceed the endowment). The constrained equal losses completely overlooks these claims. This particular attribute makes constrained equal losses a more suitable choice for situations like tax allocation, where individuals with lower incomes are exempt from paying taxes. However, when the goal is to distribute awards, this rule has the drawback of leaving residual claims without any portion of the award.

While the claims problems literature may suggest that rules like constrained equal awards are typically favored for award allocation, there are circumstances in which constrained equal losses might be a more effective approach for distributing awards. One such scenario is the study conducted by Solís-Baltodano et al. (2022) that examines the allocation of the European Regional Development Fund (ERDF)—a financial aid program designed to support less developed regions—among European Union member states and it proposes that constrained equal losses is the most suitable approach for distributing the ERDF. According to Solís-Baltodano et al. (2022), to provide greater support to the less developed regions, the majority of the fund should be allocated to them. Consequently, a fair and equitable allocation rule is not appropriate for distributing the fund. The study identifies the claim of each region, through which the less developed regions assert a greater claim on funds compared to the more developed ones. Subsequently, Solís-Baltodano et al. (2022) demonstrate that by taking these claims into account, constrained equal losses is the most effective method for allocating the fund, as it prioritizes larger claimants (less developed regions).

However, what is notable in Solís-Baltodano et al. (2022) is that the constrained equal losses rule may allocate nothing to some regions with substantially smaller claims. These regions, as defined by the study, are the most developed ones. Nevertheless, it is not a valid justification to say that these regions do not require any share of the funds. Consequently, an alternative method should be suggested that not only supports the larger claimants but also protects the smaller claimants.

To tackle this challenge and address similar scenarios where resource allocation aims to prioritize larger claims while safeguarding the interests of smaller ones, we suggest a revision of the constrained equal losses. Our proposal involves introducing a minimum allocation before implementing the rule, to guarantee that each agent has access to a minimum level of resources.¹

To determine the minimal amount, we propose to consider the smallest claim ($c_{1}$) and ensure a positive amount for it. By doing so, we can guarantee a positive minimum allocation for all claims across the board.

We suggest expanding upon the concept mentioned earlier by introducing a novel set of rules encompassing various combinations of the minimal allocation concept and the constrained equal losses rule. We refer to this new family of rules as the “CEL-family". Within the CEL-family framework, we examine and analyze all potential combinations of egalitarian resource division and the application of the constrained equal losses rule.

The significance of studying the CEL-family as a method for award sharing, when the goal is to support larger claimants, becomes more apparent when we consider the lack of any other alternatives in the existing literature for such situations. One alternative method that can be considered is the sequential priority rule. However, it should be noted that this rule may result in a higher number of agents receiving zero allocation.

After defining the family of rules, we provide an axiomatic analysis of the main properties for the sake of comparison between the main rules. In doing so, we consider basic properties, besides some solidarity and invariance principles. Finally, we apply the CEL-family to the ERDF problem, studying the combination of the convergence and solidarity principles.

The rest of the paper is organized as follows. Section 2 provides the definition of the claims problems and the rules. Sections 3 and 4 define the CEL-family and introduce the axiomatic analysis, respectively. Section 5 applies this family to the distribution of the ERDF, and Sect. 6 provides some final remarks.

2 Preliminary definitions

Consider a set of agents $N=\left\{ 1,2,...,n\right\}$ and an amount $E \in \mathbb {R}_{+}$ of an infinitely divisible resource, the endowment, that has to be allocated among them. Each agent has a claim, $c_{i}\in \mathbb {R}_{+}$ on it. Let $c\equiv (c_i)_{i\in N}$ be the claims vector. A claims problem (O’Neill 1982) is a pair (E, c) with $C=\sum _{i \in N}{c_{i}} \ge E>0$ and $\mathcal {B}$ is the set of all claims problems. Without loss of generality, we assume that agents are ordered according to their claims so that .

A rule is a single-valued function $\varphi : \mathcal {B} \rightarrow \mathbb {R}_{+}^{n}$ such that, $0 \le \varphi _{i} (E,c) \le c_{i}$ for all $i \in N$ (non-negativity and claims-boundedness) and ${\sum _{i \in N} }\varphi _{i}(E,c)$ $=E$ (efficiency).

We provide the definitions of rules which are mentioned throughout the paper: the proportional, the constrained equal awards, the constrained equal losses, and the $\alpha _{min}$-Egalitarian.

The proportional (P) rule divides the endowment proportionally according to the agents’ claims. For each $(E,c)\in \mathcal {B}$ and each $i \in N$, $P_{i}(E,c)=\lambda c_{i},$ where $\lambda =\dfrac{E}{\underset{i\in N}{\sum }\ c_{i}}.$

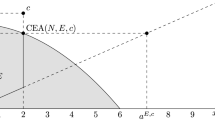
The constrained equal awards (CEA) (Maimonides 2000) rule assigns the endowment equally such that no agent receives more than her claim. For each $(E,c)\in \mathcal {B}$ and each $i \in N$, $CEA_{i}(E,c) \equiv \min \left\{ c_{i},\mu \right\} ,$ where $\mu$ is chosen so that $\underset{i\in N}{\sum }\min \left\{ c_{i},\mu \right\} =E.$

Note that the CEA rule derives from the equal awards division (EA). In this method, the endowment is distributed equally among all members, i.e., for each $(E,c)\in \mathcal {B}$ and each $i \in N$, $EA_{i}(E,c)= \frac{E}{n}.$ Nevertheless, it becomes apparent that in certain scenarios where equal distribution is applied, an agent might receive a share exceeding their claim, thus contravening the claim-bound criterion of a claim rule.

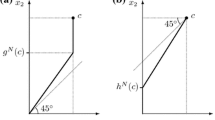
The constrained equal losses (CEL) (Maimonides 2000) rule allocates the difference between aggregate claims and the endowment (i.e., losses) equally to each agent, such that no agent receives a negative amount. For each (E, c) $\in \mathcal {B}$ and each $i\in N,$ $CEL_{i}(E,c)\equiv \max \left\{ 0,c_{i}-\mu \right\} ,$ where $\mu$ is such that $\underset{i\in N}{\sum }\max \left\{ 0,c_{i}-\mu \right\} =E.$

The $\mathbf {\alpha _{\min }}$-Egalitarian ($\alpha _{\min }$) (Giménez-Gómez and Peris 2014) rule is a compromise of the EA and P rules. If the endowment is sufficient, the rule guarantees a minimal amount equal to the smallest claim to all agents and distributes the remaining endowment proportionally to the agents’ revised claims. If the endowment is not enough, then it is divided equally among the agents. For each (E, c) $\in \mathcal {B}$ and each $i\in N,$ if $c_{1}\ge \frac{E}{n}$, then $\alpha _{min_{i}}(E,c)= \frac{E}{n}$ and if $c_{1}< \frac{E}{n}$ then $\alpha _{min_{i}}(E,c)= c_{1} + P_i(E-nc_{1}, c-c^1)$, where .

The next example shows how the previous rules work.

Example 1

Let $(E,c)= (600,(100,200,300,400))$.

$P(E,c)=(60,120,180,240)$, here the endowment is divided proportionally to each agent’s claim.

$CEA(E,c)=(100, \frac{500}{3}, \frac{500}{3}, \frac{500}{3})$, here the first agent is fully compensated and the remaining endowment is divided equally among the rest of the agents.

$CEL(E,c)= (0,100,200,300)$, divides the losses ($L=1000-600$) equally among the agents such that each agent receives the subtraction of her claim and the equal portion of the losses.

$\alpha _{\min }(E,c)=(100,100+\frac{100}{3}, 100+\frac{200}{3},200)$, allocates a minimal amount to all agents equal to $c_{1}=100$, then the claims are revised down by the minimal right and the Proportional rule is applied to allocate the remaining endowment.

3 The CEL-family rules

We introduce the CEL-family, a collection of rules that extend the CEL rule by ensuring a guaranteed minimal allocation. Each rule within the CEL-family is differentiated by the minimal amount guaranteed to claimants. This minimal allocation is derived through a comparison between $c_{1}$ and $\frac{\theta E}{n}$. For any value of $\theta \in [0,1]$, if $\frac{\theta E}{n}$ is less than or equal to $c_{1}$, the agents are allocated at least $\frac{\theta E}{n}$ and, if $\frac{\theta E}{n}$ is greater than $c_{1}$, no agent receives less than $c_{1}$.

By adjusting the parameter $\theta$ toward zero, we observe an increase in the inequality of outcomes produced by the rules within the CEL-family. Specifically, setting $\theta$ to zero results in the application of the CEL rule, which is recognized as the most inequitable approach to reward allocation within the claims problem context.

Formally, the following holds.

Definition 1

The CEL-family ($CEL^\theta$) is defined as all rules such that for some $\theta \in [0, 1]$, for all $(E,c) \in \mathcal {B}$,

$$\begin{aligned} CEL^\theta (E,c)=\left\{ \begin{array}{cc} \left( \frac{\theta E}{n}\right) ^1 + CEL\left( E-\theta E, c-\left( \frac{\theta E}{n}\right) ^1\right) &{} \text {if} \;\; \frac{\theta E}{n} \le c_{1}\\ {c}^1+CEL\left( E-nc_{1}, c-c^1\right) &{} \text {otherwise,}\\ \end{array}\right. \end{aligned}$$

where $\left( \frac{\theta E}{n}\right) ^1=\left( \frac{\theta E}{n},\dots ,\frac{\theta E}{n}\right) _{1\times n}$ and $c^1=(c_1,\dots ,c_1)_{1\times n}$.

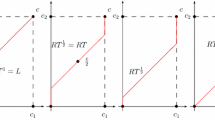
Equivalently we can say, $CEL^\theta (E,c)= min^1(E,c) + CEL (E-MIN(E,c), c- min^1(E,c))$, where $min(E,c) \equiv \min \{\frac{\theta E}{n}, c_1\}$, $min^1(E,c)=(min(E,c),\dots ,min(E,c))_{1\times n}$, and $MIN(E,c) \equiv n \cdot min(E,c)$.²

The $CEL^\theta$ rule initially assigns a minimal right ($\frac{\theta E}{n}$) to all agents. Then, after revising down the endowment and the claims by the minimal rights, it applies an equal division of their losses to the revised claims. As previously mentioned, when $\theta =0$, the $CEL^\theta$ rule corresponds to the CEL rule. Furthermore, setting $\theta =1$ results in the CEA rule.

Example 2

For the sake of comprehension, let us use Example 1 and $\theta =0.25$. First, the CEL-family assigns a minimal right equal to $\min \{ \frac{\theta E}{n}, c_{1}\}= 37.5$. Then, the endowment and the claims are revised down by the minimal right. After that, the revised endowment is divided by applying CEL to the revised claims. Therefore, the final allocation is $CEL^\theta (E,c)= (37.5,87.5,$ 187.5, 287.5).

4 Axiomatic analysis of the CEL-family

Within this section, we delve into the examination of numerous axioms frequently employed in claims problems research. Our objective is to determine whether the rules within the CEL-family adhere to these properties. To facilitate comparisons with existing literature, we have structured our analysis according to the framework established by Moreno-Ternero and Villar (2006).

Therefore, we analyze some basic properties like homogeneity, equal treatment of equals, anonymity, and order preservation which are satisfied by all the rules in the family, and consistency, which is only satisfied by the CEL rule. We also study some more specific properties (claim monotonicity, endowment monotonicity, and composition down) that are satisfied by all the rules in the family. We show that population monotonicity, composition up, composition from minimal rights, claims truncation invariance, independence of residual claims, exclusion, and sustainability are only satisfied by the extreme members of the family.

4.1 Basic properties

Homogeneity states that if the claims and the endowment are multiplied by the same positive number, then so should all awards. For each $(E,c) \in \mathcal {B}$ and each $\lambda >0$, $\varphi (\lambda E, \lambda c)= \lambda \varphi (E,c).$

Equal treatment of equals requires that agents with identical claims must be allocated an equivalent share. For each $(E,c)\in \mathcal {B}$, and each $i,j\in N$, such that $c_{i}= c_{j}$, then $\varphi _{i}(E,c)= \varphi _{j}(E,c)$.

Anonymity implies that the allocation process should disregard the identification of individual agents and solely consider their claims as the basis for distribution. For each $(E,c)\in \mathcal {B}$, such that $\pi \in \Pi ^N$, and each $i\in N$, then $\varphi _{\pi (i)}(E,c')=\varphi _{i}(E,c),$ where $c'\equiv ( c_{\pi (j)})_{j\in N}$.

Order preservation (Aumann and Maschler 1985) states that the order of the claims must be respected. If agent i’s claim is at least as large as agent j’s claim, the awards and losses allocated to agent i must be at least as much as the ones allocated to agent j. For each $(E,c)\in \mathcal {B}$, and each $i,j\in N$, such that $c_{i}\ge c_{j}$, then $\varphi _{i}(E,c)\ge \varphi _{j}(E,c),$ and $c_{i}-\varphi _{i}(E,c)\ge c_{j}-\varphi _{j}(E,c).$

Consistency (Aumann and Maschler 1985) states that if some agents leave the problem, the remaining agents should not be affected. For each $(E,c)\in \mathcal {B}$, and each $N'\subseteq N$, if $x=\varphi (E,c)$, then $x_{N'}=\varphi (\sum _{N'}x_i,c_{N'})$.

Proposition 1

All the rules within the CEL-family satisfy homogeneity, equal treatment of equals, anonymity, and order preservation.

Proof

Let $(E,c) \in \mathcal {B}$ and $\lambda >0$.

Since CEL satisfies homogeneity, we have

$$\begin{aligned} \begin{aligned} CEL^{\theta }(\lambda E, \lambda c)&= \lambda min^1(E,c)+CEL(\lambda E-\lambda MIN(E,c), \lambda c-\lambda min^1(E,c))\\&=\lambda min^1(E,c)+\lambda CEL(E-MIN(E,c),c-min^1(E,c))\\ {}&= \lambda CEL^{\theta }(E,c).\\ \end{aligned} \end{aligned}$$

Next, we prove equal treatment of equals. Let $i,j\in N$ such that $c_i=c_j$,

$$\begin{aligned} CEL^{\theta } (E,c)= min^1(E,c)+ CEL (E-MIN(E,c), c-min^1(E,c)). \end{aligned}$$

Therefore for i, j we have,

$$\begin{aligned} CEL^{\theta }_{i} (E,c)= min(E,c)+ CEL_{i} (E- MIN(E,c), c-min^1(E,c)) \end{aligned}$$

and

$$\begin{aligned} CEL^{\theta }_{j} (E,c)= min(E,c)+ CEL_{j} (E- MIN(E,c), c-min^1(E,c)). \end{aligned}$$

Since CEL satisfies equal treatment of equals, it is proved that

$$\begin{aligned} CEL^{\theta }_{i} (E,c)=CEL^{\theta }_{j} (E,c). \end{aligned}$$

To prove anonymity, let $\pi \in \Pi ^N$, and $c'\equiv ( c_{\pi (j)})_{j\in N}$.

$$\begin{aligned} CEL^\theta (E,c)= min^1(E,c)+ CEL (E-MIN(E,c),c-min^1(E,c)) \end{aligned}$$

and

$$\begin{aligned} CEL^{\theta }_{\pi (i)}(E,c')= min^1(E,c')+ CEL_{\pi (i)}(E-MIN(E,c'),c'-min^1(E,c')). \end{aligned}$$

By anonymity of CEL, we have that for all $j\in N$,

$$\begin{aligned} CEL^{\theta }_{\pi (j)}(E,c')=CEL^{\theta }_{j}(E,c). \end{aligned}$$

Therefore, since $min(E,c)=min(E,c')$, we have $CEL^{\theta }_{\pi (j)}(E,c')=CEL^\theta _j (E,c)$ for all $j\in N$.

Finally, we prove order preservation. Let $i,j\in N$ such that $c_i\le c_j$.

Since CEL satisfies order preservation, we have,

$$\begin{aligned} \begin{aligned} CEL^{\theta }_i (E,c)&= min(E,c)+ CEL_i (E-MIN(E,c), c-min^1(E,c)) \\&\le min(E,c)+ CEL _j(E-MIN(E,c), c-min^1(E,c))\\ {}&= CEL^{\theta }_j (E,c). \end{aligned} \end{aligned}$$

Again by order preservation satisfied by CEL,

$$\begin{aligned} \begin{aligned} c_i-CEL^{\theta }_i (E,c)&= c_i - min(E,c) - CEL_i (E-MIN(E,c), c-min^1(E,c)) \\&\le c_j -min(E,c) - CEL _j(E-MIN(E,c), c-min^1(E,c)) \\ {}&= c_j- CEL^{\theta }_j (E,c). \end{aligned} \end{aligned}$$

$\square$

Proposition 2

None of the rules within the CEL-family (except CEA and CEL) satisfy consistency.

Proof

Note that for any $\theta \in (0,1]$ whenever $c_{n}-c_{n-1} \ge E- MIN(E,c)$, consistency does not hold. Indeed, the only rules in the CEL-family that satisfy consistency are CEA and CEL (Thomson 2003). $\square$

4.2 Solidarity properties

In this section, we study monotonicity properties that have been considered as solidarity axioms in the literature (Moreno-Ternero and Roemer 2006).

Claim monotonicity(Thomson 2003) states that if an agents’ claim increases, they should receive at least as much as they did initially. For each $(E,c) \in \mathcal {B}$, each $i \in N$, and each $c'_{i} > c_{i}$, $\varphi _i (E, (c'_{i}, c_{-i})) \ge \varphi _i(E,c).$

Endowment monotonicity (Curiel et al. 1987; Young 1987) requires that if the endowment increases, the agents are allocated at least the amounts they received initially. For each $(E,c)\in \mathcal {B}$ and each $E^*\in \mathbb {R}_{+}$ such that $C>E^*>E,$ then $\varphi _{i}(E^*,c)\ge \varphi _{i}(E,c),$ for each $i\in N.$

Population monotonicity (Thomson 1983) indicates that as the number of agents increases while keeping the endowment constant, each agent’s allocation should not exceed the initial amount. For each $N \in \mathcal {N}$,³ each $(E,c)\in \mathcal {B}$, and each $N'\subset N$, if $\sum _{N'}c_i\ge E$, then $\varphi (E, c_{N'})\ge \varphi _{N'}(E,c).$

Proposition 3

All the rules within the CEL-family satisfy claim monotonicity and endowment monotonicity. None of the rules within the CEL-family (except CEA and CEL) satisfy population monotonicity.

Proof

• (i) We prove claim monotonicity.

  $$\begin{aligned} CEL^\theta (E,c)= min^1(E,c)+ CEL \bigl (E-MIN(E,c), c-min^1(E,c) \bigr ). \end{aligned}$$

If we increase the claim of claimant $i\in N$ from $c_i$ to $c'_i$, $c'_i>c_i$. Let $c'=(c'_{i},c_{-i})$ the vector of claims where only i’s claim changes, the rest remaining equal.

$CEL^\theta (E, (c'_i, c_{-i}))= min^1(E,c')+ CEL \bigl (E-MIN(E,c'), (c'_i,c_{-i})-$ $min^1(E,c')\bigr ).$

If $i\ne 1$. Notice that in this case, $min(E,c)=min(E,c')$, then $MIN(E,c)=$ $MIN(E,c')$. Therefore, as the CEL rule satisfies claim monotonicity, we have,

$$\begin{aligned} \begin{aligned} CEL_i^\theta (E,c)&=min(E,c)+ CEL_i \bigl (E-MIN(E,c), c-min^1(E,c)\bigr ) \\&\le min(E,c')+ CEL_i \bigl (E-MIN(E,c'), c'-min^1(E,c')\bigr ) \\&= CEL_i^\theta (E, (c').\\ \end{aligned} \end{aligned}$$

If $i=1$ we have $min(E,c)\equiv \min \{c_1,\frac{\theta E}{n}\}\le \min \{c'_1,\frac{\theta E}{n}\}\equiv min(E,c')$, . Then by claim monotonicity of the CEL rule, we have

$$\begin{aligned} \begin{aligned} CEL_1^\theta (E,c)&=min (E,c)+ CEL_1 \bigl (E-MIN (E,c), c-min^1(E,c)\bigr ) \\&\le min(E,c') + CEL_1 \bigl (E-MIN(E,c'), c'-min^1(E,c')\bigr ) \\&=CEL_1^\theta (E, c').\\ \end{aligned} \end{aligned}$$

• (ii) Next, we prove endowment monotonicity. Let $C \ge E^*>E$. Let denote by $min(E^*,c)\equiv \min \{c_1,\frac{\theta E^*}{n}\}$ which satisfies $min(E,c)\le min(E^*,c)$, and $MIN(E^*,c)\equiv n \cdot min(E^*,c)$, and $\min (E^*,c))_{1\times n}$. Since CEL satisfies endowment monotonicity we have,

  $$\begin{aligned} \begin{aligned} CEL^{\theta }(E,c)&= min^1(E,c)+ CEL(E-MIN(E,c), c-min^1(E,c))\\&\le min^{1}(E^*,c)+ CEL(E-MIN(E,c), c-min^1(E,c))\\&\le min^{1}(E^*,c)+ CEL(E^{*}-MIN(E^*,c),c-min^1(E,c)) \\&= min^{1}(E^*,c)+ CEL(E^{*}-MIN(E^*,c),c-min^{1}(E^*,c))\\&=CEL^{\theta }(E^*,c).\\ \end{aligned} \end{aligned}$$

• (iii) The rules in the CEL-family do not satisfy population monotonicity. For any $\theta \in (0,1)$ whenever $c_{1} \le \frac{\theta E}{n}$, and for any $i\ne 1\in N$, $c_{i} \ge \frac{\theta \underset{i=2}{\overset{n}{\sum }} CEL_{i}^{\theta }(E,c)}{n-1}$, population monotonicity does not hold. For instance, consider $(E,c)=(30,(5,20,30))$, $CEL^{1}(E,c)=(5,7.5,17.5)$. By considering, $N'=\{2,3\}$, $CEL^{1}(E,c)=(15,15)$, since $c_{2} \le (CEL_{2}^{1}(E,c)+CEL_{3}^{1}(E,c))/2$.

Finally, note that only for the CEL rule, and, when $\theta =1$ and $c_1\ge \frac{E}{n}$, i.e., $CEL^{1}= CEA$, Population monotonicity holds (Thomson 2003). $\square$

4.3 Composition properties

Within this subsection, we explore scenarios where, after applying a rule to allocate the initial endowment, the total endowment undergoes a change. The following two properties outline distinct approaches to address this circumstance.

Composition down (Moulin 2000) examines a scenario where we initially allocate the endowment using a specific rule, but upon reassessment, the endowment’s value is found to be lower than initially assessed. In response to this situation, two alternative actions emerge. First, we can nullify the initial distribution and reallocate the adjusted endowment using the same division rule. Alternatively, we may treat the initial allocation as the agents’ claims and apportion the revised endowment among these newly defined claims. The principle of composition down stipulates that the outcomes of both options must be equivalent. For each $(E,c)\in \mathcal {B},$ and each $E^* < E$, $\varphi (E^*,c)=\varphi (E^*,\varphi (E,c)).$

Composition up (Young 1988) presents a contrasting scenario to composition down. It pertains to situations where, following the division of the endowment according to the division rule, a re-evaluation reveals that the endowment is worth more than its initial assessment. In response to this situation, two actions can be considered. First, one may nullify the initial allocation and reallocate the revised endowment. The second option involves providing agents with their initial allocation, subsequently adjusting their claims down from these initial allocations, and distributing the additional amount of the endowment among agents based on their revised claims. In this case, agents receive a combined sum of their initial allocation and the supplementary allocation. Composition up asserts that the allocation from both options must be identical. For each $(E,c)\in \mathcal {B}$, and each $E'> E,$ $\varphi (E^{\prime },c)=\varphi (E,c)+\varphi (E^{\prime }-E,c-\varphi (E,c)).$

Proposition 4

The rules within the CEL-family fulfill composition down. None of the rules (except CEA and CEL) satisfy composition up.

Proof

• (i) Let $E^*<E$, therefore $min(E,c)\ge min(E^*,c)$. Then, since CEL satisfies composition down and $E^*-MIN(E^*,c)\le E-MIN(E,c)$, we have:

$$\begin{aligned} \begin{aligned} CEL^{\theta }(E^*,CEL^{\theta }(E,c))&=CEL^{\theta }(E^*,(min^1(E,c) +CEL(E-MIN(E,c),c\\&\quad - min^1(E,c))))\\&=min^{1}(E^*,c)+CEL(E^*-MIN(E^*,c), min^1(E,c)\\&\quad +CEL(E-MIN(E,c),c-min^1(E,c))-min^{1}(E^*,c))\\&=min^{1}(E^*,c)\\&\quad + CEL(E^*-MIN(E^*,c),c\\&\quad -min^1(E,c)+ min^1(E,c)-min^{1}(E^*,c)) \\&=min^{1}(E^*,c) + CEL(E^*-MIN(E^*,c),c-min^{1}(E^*,c))\\&= CEL^{\theta }(E^*,c).\\ \end{aligned} \end{aligned}$$

• (ii) Note that for any $\theta \in (0,1)$ whenever $CEL_{n-1} (E- MIN(E,c),$ $c- min^1(E,c) ) \ne 0$, then, $c_{n}-CEL_{n} (E- MIN(E,c),c- min^1(E,c) )$ $=c_{n-1}-CEL_{n-1} (E- MIN(E,c),$ $c- min^1(E,c) )$. So, $E^*-E$ is equally distributed between these two claimants. It is straightforwardly obtained that this allocation does not coincide with the direct distribution of $E^*$, where the distance between $c_n$ and $c_{n-1}$ remains.

Finally, note that the two rules in the CEL-family satisfying composition up are CEL and the particular case when $c_1\ge \frac{\theta E}{n}$, and $\theta =1$, i.e., $CEL^{1}$= CEA (Moulin 2000). $\square$

4.4 Lower-bound and upper-bound properties and self-duality

In this section, we study some properties related to the structure of the claims problems, considering changes in the claims or in the endowment.

Composition from minimal rights (Dagan and Volij 1993) states that every agent is guaranteed a minimum allocation of resources. This minimum allocation represents the residual portion of the endowment after all other claims have been satisfied, as long as this allocation remains non-negative. For each $(E,c)\in B$, $\varphi (E,c)= m(E,c)+\varphi (E-M(E,c), c-m(E,c))$, where $m(E,c)= (m_i(E,c))_{i\in N} =(\max \{0, E-\sum _{j\in N-\{i\}}c_j \})_{i\in N}$ and $M(E,c)=\sum _{i\in N} m_i(E,c).$

Claims truncation invariance (Curiel et al. 1987; Dagan and Volij 1993) indicates that agents cannot demand more than the available endowment. When an agent’s claim surpasses the endowment, the portion of the claim exceeding the endowment is disregarded. For each $(E,c)\in B$, $\varphi (E,c)= \varphi (E, (\min \{c_{i},E\})_{i\in N}).$

Self-duality (Aumann and Maschler 1985) examines the issue from two contrasting angles: one from the perspective of the awards received and the other from the portion of the claim that remains unfulfilled. Consequently, it suggests that the challenge of dividing either “what is available" or “what is missing" should yield identical awards. for each $(E,c)\in \mathcal {B}$ and each $i\in N$, $\varphi _{i}(E,c)=c_{i} - \varphi _{i}(C-E,c)$.

Proposition 5

None of the rules within the CEL-family satisfy composition from minimal rights (except CEL), claims truncation invariance (except CEA), and self-duality.

Note that this statement is straightforwardly obtained from the definitions of the rules. On the one hand, from Thomson (2003), it is clear enough that within the CEL-family, only the particular case when $c_1\ge \frac{\theta E}{n}$, and $\theta =1$, i.e., $CEL^{1}$= CEA, and CEL satisfy claims truncation invariance and composition from minimal rights, respectively. Moreover, none of them satisfies self-duality (Aumann and Maschler 1985).

On the other hand, note that if $\theta \in (0,1)$, then each claimant will receive a strictly positive allocation of the endowment, violating minimal rights that may be zero when either the resources are too small or the are claims are large enough. Furthermore, by definition, the CEL rule recommendation depends on the distance between claimants. Then, if this distance varies, the recommendation also varies, so the CEL-family does not satisfy claims truncation invariance either. Finally, by definition of the CEL-family, a part of the endowment is distributed by CEL, so it does not satisfy self-duality.

4.5 Protective properties

In this section, we explore properties that demonstrate reverse behaviors when confronted with extremely small claims. These properties were studied in the literature by Herrero and Villar (2001), Herrero and Villar (2002), and Yeh (2006). The properties are sustainability, independence of residual claims, and exclusion.

Sustainability states that claims identified as “sustainable" must be fully honored. Sustainable claims are characterized by their minimal magnitude to such an extent that if the claims of other agents are replaced with that of the sustainable claim, the cumulative claims would not surpass the endowment, thereby the claims problems issue is resolved. For all $(E,c)\in B$, and each $i\in N$, if $\sum _{j\in N} \min \{c_i,c_j\}\le E$ then $\varphi _i(E,c)= c_i$.

Independence of residual claims disregards the so-called “residual" claims. The residual claims are of such minimal magnitude that, even upon their subtraction from the claims of other claimants, the aggregate claims continue to exceed the available endowment. For all $(E,c)\in B$, if $E\le \sum _{j\in N} \max \{ 0,c_j-c_i \}$ then $\varphi _i(E,c)= 0$.

Exclusion (Herrero and Villar 2001) is interpreted as a subset of the “Independence of residual claims" property. It states that all claims smaller than the per capita loss ($(C-E)/n$) should be excluded from the allocation process. For two-claimant cases, independence of residual claims and exclusion are equivalent. For all $(E,c)\in B$, and each $i\in N$, if $c_i\le \frac{C-E}{n}$ then $\varphi _i(E,c)= 0$.

Proposition 6

None of the rules within the CEL-family satisfy sustainability (except CEA), independence of residual claims (except CEL), and exclusion (except CEL).

Proof

• (i) By Herrero and Villar (2001), CEA satisfies sustainability, i.e., if $c_{1} \ge \frac{\theta E}{n}$ and $\theta =1$, then $CEL^{\theta }$ also does. If $\theta \ne 1$ it is straightforward to see that it does not. Consider the following example, $(E,c)=(30,(5,10,50))$, $CEL_{2}^{\theta }(E,c)<c_{2}$, violating sustainability.

• (ii) By Herrero and Villar (2001), CEL satisfies independence of residual claims and exclusion, i.e., if $\theta =0$, then $CEL^{\theta }$ also does. If $\theta \ne 0$, it is straightforward to see that it does not, since $CEL_{i}^{\theta }(E,c)>0$, for any $(E,c) \in \mathcal {B}$.

$\square$

4.6 Summary of properties and families

To conclude the axiomatic analysis of the CEL-family, we study its relationship with two prominent families of rules: the parametric rules (Young 1987) and the ICI rules (Thomson 2003).

As defined by Young (1987), a rule is parametric if the ith agent’s award is a function that depends only on $c_i$ and a parameter $\lambda$, which is related to the size of the amount to be divided.

Young (1987) shows that a rule is parametric if and only if it satisfies equal treatment of equals, continuity, and consistency. Therefore, the proportional rule, the constrained equal awards, the constrained equal losses, and the Talmud (Aumann and Maschler 1985) rules are parametric rules. However, as a consequence of Proposition 2, the CEL-family of rules are not parametric rules.

The ICI-family (Thomson 2003) contains the constrained equal awards, the constrained equal losses, the Talmud, and the minimal overlap (O’Neill 1982) rules.

ICI rules exhibit the evolution of each claimant’s award as a function of the endowment: it is increasing first, constant next, and finally increasing again.

Thomson (2008) shows that a rule belongs to the ICI-family if and only if it is consistent, among other properties. Therefore, as a consequence of Proposition 2, the CEL-family of rules are not ICI-family rules.

In the following table, we summarize all the results from the previous sections. Here, we have the main properties and which are the rules in the CEL-family that satisfy each one of them.

Table 1 Summary of the examined properties for all the rules in the CEL-family, the CEA, and the CEL

5 ERDF allocation

The European Regional Development Fund (ERDF) is an aid program established by the European Union (EU) to support its member states. The fund’s primary objective is to reduce the economic development gap between regions within the EU. In other words, it aims to address the backwardness of less developed countries and push them toward improving their development level.

To distribute this fund, member states are categorized into three groups of regions based on their gross domestic product (GDP) per capita. The less developed regions (R3) have a GDP per capita less than 75% of the average GDP per capita of EU-27, transition regions (R2) have a GDP per capita between 75% and 100% of the average GDP per capita of EU-27, and more developed regions (R1) have a GDP per capita above 100% of the average GDP per capita of EU-27. This classification results in the definition of 47 regions within the EU.

Solís-Baltodano et al. (2022) studied the allocation of the ERDF and proposed that this allocation can be viewed as a claims problem situation. Their research focused on the 2014–2020 period when the budget was around 182.150 million euros. They defined the claims of the regions in a way that reflects the amount of money each region needs. As a result, it can be deduced that less developed regions demand more money and have larger claims.

The EU pursues the objective of achieving equalization in economic development across its territory. This implies providing greater support to less developed regions, thereby allocating more funding from the ERDF to enhance their development. The implementation of different claims problem rules in the research by Solís-Baltodano et al. (2022) concluded that CEL can serve equalization in the EU. The CEL is a rule that deprives smaller claimants (i.e., more developed regions) and allocates the main part of the endowment to larger claimants (i.e., less developed regions). Although their proposal seems logical, their results show that CEL allocates nothing to some of the regions with smallest claims. Therefore, the application of CEL in the real world cannot be deemed to be practical.

The rules of the CEL-family present preferable options. This is because they ensure a minimum entitlement to all agents, adjustable through parameter $\theta$. Decreasing $\theta$ brings the CEL-family rule closer to CEL, thereby resulting in a more unequal allocation of endowments favoring larger claimants. This adjustment aligns with the objective of ERDF allocation, which prioritizes greater support for larger claimants, namely less developed regions.

Table 2 shows the results of distributing the ERDF using various rules, including P, CEA, CEL, and $\alpha _{\min }$, in combination with the CEL-family. The parameter $\theta$ in CEL-family is set to two extreme values of 0 (which corresponds to CEL) and 1, as well as a value close to 0. This table facilitates a comparison of the results obtained from these different rules in conjunction with the CEL-family.

The ERDF data reveal that when the $\theta$ is greater than or equal to 0.08, the minimal right allocated to regions equals $c_{1}$. However, an issue arises here as $c_{1}$ represents the claims of the richest region. Consequently, allocating a minimal right of $c_{1}$ completely satisfies the needs of this affluent region, potentially conflicting with the primary objective of the ERDF, which is to support less developed regions. To address this concern, we can adjust the value of $\theta$ to be smaller than 0.08, leading to a partial satisfaction of the richest region. As $\theta$ decreases, the allocation to the richest region also decreases. For instance, we can select $\theta$ equal to 0.001 as an illustrative example. Determining the optimal value of $\theta$ and achieving an effective allocation that promotes the development of disadvantaged regions requires careful consideration of multiple economic aspects.

When comparing the allocation of CEL with the CEL-family, we observe that CEL-family effectively addresses the issue of zero allocation to smaller claims by ensuring they receive a minimal positive amount. Notably, when $\theta$ is set to 1, even the smallest claim is fully honored. However, as previously noted, we have the flexibility to adjust this behavior by reducing the value of $\theta$.

Table 2 The existing distribution of ERDF funds alongside the proposed allocations according to various rules, per capita (numbers are in million euros)

6 Final remarks

The paper presents a family of rules called CEL-family which encompasses all the possible combinations of the egalitarian division of the endowment and the Constrained equal losses rule. The rules within this family serve the concept of unequal allocation, and allow us to select either the egalitarian division of resources or of losses, depending on the context. So, if $\theta =0$, it would correspond to the constrained equal losses, and if $\theta =1$, in a particular case (i.e., when $\frac{\theta E}{n}$ is smaller than $c_{1}$ ), it would correspond to the constrained equal awards rule. Customizing $\theta$ allows the CEL-family to be tailored to specific contexts and fairness criteria. By adjusting $\theta$, we can make the allocation more equitable or more efficient, depending on the goals of the resource allocation. This flexibility is a significant advantage over other allocation rules, which may not be as easily adapted to different scenarios. The CEL-family maintains a balance between equity and efficiency, two common competing criteria in resource allocations. By allowing $\theta$ to be adjusted, the CEL-family can navigate the compromise between these two criteria, leading toward more equity or more efficiency as needed. This balance is crucial for achieving fair outcomes that also consider the overall efficiency of resource allocation.

The application of the CEL-family to the allocation of the European Regional Development Fund (ERDF) demonstrates its effectiveness in reducing the allocation to more developed regions and concurrently increasing the share of less developed regions at any level of $\theta$. As the value of $\theta$ decreases, the allocation to less developed regions further increases, aligning with the ERDF’s objective of reducing backwardness in underdeveloped regions.

Finally, it must be noted that future research could explore the identification of essential factors to consider when determining the optimal value of $\theta$, thus enhancing the practicality of the CEL-family in various real-world scenarios.

Additionally, it is noteworthy that one could try to find an axiomatic characterization of the CEL-family that, to the best of our knowledge, is still an open problem.