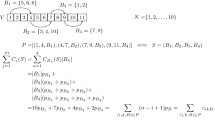1 Introduction

In the batch scheduling problem, jobs are processed on each machine grouped in batches. The batch scheduling can be parallel or serial, depending on the processing rule of the jobs within the batch: if the jobs in the batch are processed simultaneously, this is the case of a parallel batch; otherwise, if the jobs within the batch are processed one after another, the batch is serial. Typical examples of parallel batches are furnaces and ovens that can be used, for instance, in mould manufacturing and semiconductor industries (Liu et al. 2016; Ozturk et al. 2012); instead, serial batches are usually exploited when a setup is needed before processing a new batch. In this paper, we address the parallel batch scheduling problem. Jobs in each batch are processed in parallel, so the processing time of the whole batch is equal to the maximum processing time amongst the jobs that compose it. The objective is to compose the batches and to sequence them, to optimize a performance measure. Usually, batches have a maximum size, depending on the technological characteristics of the process (Potts and Kovalyov 2000); for instance, the batch might have a maximum weight, or a maximum volume. Thus, to form the batches, the size constraint must be taken into account.

The batch scheduling problem is typical of semiconductor industries, mold manufacturing (Liu et al. 2016), medical device sterilization (Ozturk et al. 2012), heat-treating ovens (Mönch and Unbehaun 2007), chemical processes in tanks or kilns (Takamatsu et al. 1979), semiconductor and wafer fabrication industries (Mönch et al. 2013), and testing of electrical circuits (Hulett et al. 2017). Also additive manufacturing (AM) often requires batch production to optimize the chamber space (Zhang et al. 2020). However, here the processing times depend on different factors than those of conventional production, and the resulting scheduling problem could be different.

Sometimes, batch production needs to address multiple sizes in composing the batches. For instance, in AM, chambers can produce various parts simultaneously, either by placing products in the 2-dimensional space or by stacking products and hence using the 3-dimensional space of the chamber. Thus, when creating the batches, constraints on several dimensions must be considered; for instance, if the AM technology in use is able to stack parts in the chamber, then there is a maximum vertical span (height) and a maximum horizontal area that cannot be exceeded. These dimensions (e.g. height, horizontal area) will be called sizes in the paper. Similarly, other industries could have the same batch requirements. Moreover, for technological reasons, in shop floors where various product families are produced, batches must be composed of jobs of the same family. This is the case for families that need different manufacturing operations.

Due to the current industrial challenges, this paper addresses the single machine batch scheduling problem with multiple sizes and incompatible job families. The aim is to find the batch schedule that minimizes the total completion time; thus, with the Graham’s three-field standard notation (Graham et al. 1979), the addressed problem is defined as \(1 \vert p\textit{-}batch, s_{ij} \le b_i,incomp \vert \sum C_j\) (where \(p\textit{-}batch\) defines the parallel batching, \(s_{ij}\le b_i\) the multiple sizes, and incomp the incompatible job families).

The remainder of the paper is structured as follows. The relevant literature on the batch scheduling problem is reviewed in Sect. 2. The problem is formalized in Sect. 3, and the solution approaches are presented in Sect. 4. The numerical results are discussed in Sect. 5, while Sect. 6 concludes the paper.

2 Literature review

The batch scheduling problem has been addressed for a few years by many researchers (Ikura and Gimple 1986) because of its many fields of application. From the complexity point of view, Uzsoy (1994) first proved the NP-hardness for the \(1 \vert p\textit{-}batch, \; s_j \le b \vert \sum C_j\) problem, where jobs have different sizes, equal processing times and must be batched on a single machine. Since batching has raised the interest of many researchers in the scheduling field, there are many applications and problem variants that have been addressed in the literature. A complete overview of batching problems is given by Potts and Kovalyov (2000), who reviewed both parallel and serial batching problems and discussed major results and algorithms on the subject.

In the following, a brief review of the literature on single machine parallel batch scheduling problems with total completion time as performance measure, incompatible job families, and/or multiple sizes is discussed. Some examples of recent papers that address the parallel batch scheduling with other objective functions are: Muter (2020), Emde et al. (2020), Tan et al. (2018), Shahidi-Zadeh et al. (2017).

First, some variations of the single size batch scheduling problem have been studied. For instance, Azizoglu and Webster (2000) generalized the model of Uzsoy (1994) to the weighted case \(1 \vert p\textit{-}batch,s_j\le b \vert \sum w_j C_j\) with arbitrary job sizes and weights. They extended the existing branch and bound procedure to this case and exploited some dominance properties. Rafiee Parsa et al. (2016) addressed the \(1 \vert p\textit{-}batch,s_j\le b \vert \sum C_j\) problem by proposing an ant colony optimization metaheuristic. Alfieri et al. (2021) recently formulated a new MIP for the same problem based on a graph model, where the nodes of the graph represent job positions and arcs represent batches. The proposed model is solved by means of a column generation technique (Desrosiers and Lübbecke 2005) and allows to compute effective lower bounds. The model is also extended to the parallel machines environment. A column generation approach was also developed by Ozturk (2020), who considered identical parallel machines. The problem is here decomposed into two stages: first, a column generation is used to generate batches, and second these batches are scheduled on machines using an integer linear model.

With respect to incompatible job families, the batch scheduling problem was addressed by Azizoglu and Webster (2001), who adapted the solution procedure used in Azizoglu and Webster (2000) for the single family case to the incompatible job family case \(1\vert p\textit{-}batch, s_j \le b, incomp \vert \sum w_j C_j\), where the jobs in the same family have equal processing times. The same problem was also solved through several heuristic approaches by Dobson and Nambimadom (2001), who addressed a version of the \(1 \vert p\textit{-}batch,s_j \le b, incomp \vert \sum w_j C_j\) problem, where the jobs of a family share the same processing time and the objective function is the mean weighted flow time.

To the authors’ knowledge, this is the first attempt to address the batch scheduling problem with total completion time minimization, and jobs with multiple sizes and incompatible families. As the problem is NP-hard, a flow formulation is exploited to solve it through two column generation-based heuristics. The column generation finds a continuous-relaxed solution, then two different heuristics from the literature are used to move from the continuous to the integer solution of the problem: the first is based on the so-called price-and-branch heuristic (Desrosiers and Lübbecke 2005), the other on a variable rounding procedure (Druetto and Grosso 2022). An extensive experimental campaign was run to compare the two heuristics, which both prove to be very effective for this scheduling problem. As the results will show, variable rounding is the most effective both in terms of computation time and quality of solution. Other useful insights for practical applications will be derived from the results.

3 Problem definition

The single machine batching problem is considered, in which a set \(N=\{1,\dots ,n\}\) of jobs must be grouped in batches, and the batches must be scheduled on the machine. Setup times between batches are assumed to be negligible and are not considered.

The machine processes jobs in batches, and batches must respect physical constraints, such as maximum height, volume, weight, and so on. Let m be the number of different sizes to be addressed (e.g. \(m=3\) if the physical constraints imply maximum height, volume and weight), and \(b_i\) be the batch capacity associated to the size i (with \(i=1,\dots ,m\)). Each job j has a processing time \(p_j\), and m size values \(s_{ij}\), with \(i=1,\dots ,m\). For instance, if batches must respect a maximum volume (\(b_1\)) and a maximum height (\(b_2\)), then each job j will be characterized by its own volume \(s_{1j}\) and its own height \(s_{2j}\).

In the machine, jobs must be clustered in batches, such that the sum of job sizes \(s_{ij}\) of all jobs in a batch does not exceed the batch dimension \(b_i, \, i=1,\dots ,m\).

In addition, jobs are grouped into families that represent different process requirements. Hence, jobs from different families must be processed in different batches. There are \(n_f\) families, and each job j belongs to a family f, \(f=1,\dots ,n_f\).

A solution to the problem is made by a batch schedule, i.e., a sequence of feasible batches \(S={B_1,\dots ,B_{n_B}}\). The total number of batches \(n_B\) is not known a priori, but it depends on how jobs are clustered in each solution. However, the number of batches \(n_B\) must be in the range between \(n_f\) and n, as there should exist at least one batch for each family, and there are at maximum n batches each composed of one single job.

All jobs in a batch B are assumed to be processed simultaneously and the processing time \(p_B\) of batch B equals the longest processing time of jobs contained in it i.e., \(p_B = \{\max p_j \ \forall j \in B\}\). Also, a job is completed when all other jobs in the same batch are completed, i.e., the completion time \(C_j\) of each job equals the completion time of the batch it belongs to. The aim is to find the sequence \(S={B_1,\dots ,B_{n_B}}\) that minimizes the total completion time.

In the paper, the three combinations of constraints will be considered i.e., the problem \(1\vert p\textit{-}batch,s_{ij}\le b_i, incomp \vert \sum C_j\), the multi-size problem without families (\(1 \vert p\textit{-}batch,s_{ij}\le b_i\vert \sum C_j\)), and the family problem with single size-jobs (\(1 \vert p\textit{-}batch,s_j\le b,incomp \vert \sum C_j\)).

4 Two column generation-based heuristics

The flow model used by Alfieri et al. (2021) is exploited and adapted to the problem at hand to develop two heuristic algorithms. The flow model considers the feasible batches as binary variables and associates a cost to each of them, whose sum is to be minimized in the objective function. Usual flow constraints guarantee the flow preservation from a source node to the last and a second set of constraints guarantee that each job is scheduled exactly once (for the details on the flow formulation, the reader is referred to Alfieri et al. (2021)). Both heuristics rely on an initial column generation algorithm, which solves the continuous relaxation of the flow model. Then, the heuristics use different techniques to move from the continuous solution found by the column generation to the final integer solution of the problem, as will be explained in the following.

4.1 The CG-LB column generation algorithm

The column generation starts from a restricted formulation of the relaxed continuous flow model and iteratively selects promising variables (i.e., promising batches) through a so-called pricing procedure. The column generation finds as an output the optimal solution of the continuous relaxation of the flow model. This solution is then used as a starting point to find the integer solution of the initial problem in the heuristics. The details of the column generation are explained in the following.

First, an initialization phase is needed. Jobs are first sorted according to the Shortest Processing Time (SPT) rule, which is optimal for the scheduling of all jobs on a serial machine with the \(\sum C_j\) objective function (Chandru et al. 1993). Then, some feasible batches are generated by clustering together the sorted jobs until one of the maximum batch dimensions is reached, or until a job belonging to a different family is selected. When the batch is closed, it is placed on all possible schedule positions, and then, a new batch is developed with the same rule. The final output of the initialization is the set H, which contains a set of feasible batches.

The set H is set as the initial column set in the column generation, which is used to solve the continuous relaxation of the flow model. The algorithm iterates between solving the Restricted Master Problem (RMP, i.e., the problem with only a subset of variables) and the pricing problem (the problem of selecting new columns to be added to the RMP) until the continuous optimum is found.

In the pricing procedure, the dual multipliers associated with the RMP are computed to find the most promising variables, i.e., those with the most negative reduced cost, to be included in the next iteration of the RMP.

The pricing problem searches for the minimum reduced cost \(\bar{c}_{ikB^*}\) associated to arc \((i,k,B^*)\), among all arcs (i, k, B) that correspond to feasible batches. Let \(v_j\) be the dual multiplier corresponding to the constraints that guarantee that all jobs are included in the final schedule, and let \(u_i,u_k\) be the dual multipliers corresponding to the flow maintenance constraints. Recall that each job j belongs to a family \(f_j\) and has m different sizes \(s_{hj}\) (\(h \in \{1,\dots ,m\}\)), corresponding to the m batch capacities \(b_h\); furthermore, the batch cardinality \(\vert B \vert\) must be equal to \((k-i)\). Then, the problem can be formulated as follows.

$$\begin{aligned} \bar{c}_{ikB^*} = \min _B \left\{ \begin{array}{l} c_{ikB} - \sum _{j \in B} v_j:\\ \qquad \sum _{j \in B} s_{hj} \le b_h \quad \forall h \in \{1,\dots ,m\},\\ \qquad f_j = f_{j'} \quad \forall j, j' \in B,\\ \qquad \vert B \vert =(k-i) \end{array}\right\} - (u_i - u_k) \end{aligned}$$
(1)

For each new possible feasible batch B, the evaluation of the corresponding reduced cost depends on the position in the sequence, on the processing time and on the jobs included in the batch. By isolating the parts depending on the position in an external loop that considers every i, k with \(k>i\), the problem at hand is reduced to the computation of the feasible batch containing \(k-i\) jobs with maximum value. This problem can be formulated as a cardinality-constrained multi-weight knapsack, which has to be solved for every starting and ending position. Indeed, jobs are the items, their dual multipliers are profits, and their sizes are the weights.

The solution space of the multi-weight knapsack problem with cardinality constraint is explored via a dynamic programming algorithm. Specifically, for every pair of i, k with \(k>i\), and for each job \(r=1,\dots ,n\), let \(g_r(\tau _1, \dots , \tau _m, l)\) be the optimal knapsack with capacities \(\tau _h\) for all \(h \in \{1,\dots ,m\}\), cardinality \(l=k-i\), and that considers only jobs \(r,r+1,\dots ,n\). The binary variable \(y_j \in \{0, 1\}\) equals 1 if job j is selected for the knapsack, 0 otherwise. Then, the algorithm searches for the following values.

$$\begin{aligned} g_r(\tau _1, \dots , \tau _m, l) =&\max \Bigg \{\sum _{j=r}^n v_j y_j : \sum _{j=r}^n s_{1j} y_j \le \tau _1, \, \dots , \, \sum _{j=r}^n s_{mj} y_j \le \tau _m, \nonumber \\&\quad \sum _{j=r}^n y_j = l, \, f_j = f_r, \, y_j \in \{0, 1\}\Bigg \} \end{aligned}$$
(2)

This can be computed with the following recursion as in Kellerer et al. (2004):

$$\begin{aligned} g_r(\tau _1, \dots ,& \tau _m, l) = \max {\left\{ \begin{array}{ll} g_{r'}(\tau _1-s_{1r}, \dots , \tau _m-s_{mr}, l-1) + v_r & (y_r = 1)\\ g_{r'}(\tau _1, \dots , \tau _m, l) & (y_r = 0) \end{array}\right. } \end{aligned}$$
(3)

where \(r'\) is the next job in the Longest Processing Time (LPT) ordering that belongs to the same family of the job that started the recursion. In this way, family incompatibilities are addressed. The boundary conditions are as follows:

$$\begin{aligned} g_r(\tau _1, \dots ,&\tau _m, 1) = {\left\{ \begin{array}{ll} v_r &{} \text {if }s_{hr} \le \tau _h \, (y_r = 1)\\ 0 &{} \text {otherwise }\, (y_r = 0) \end{array}\right. }&r=1, \dots , n, \, \tau _h = 0, \dots , b_h \end{aligned}$$
(4)
$$\begin{aligned} g_r(\tau _1, \dots ,&\tau _m, 0) = 0&r = 1, \dots , n, \, \tau _h = 0, \dots , b_h \end{aligned}$$
(5)
$$\begin{aligned} g_r(\tau _1, \dots ,&\tau _m, l) = -\infty&\text {if }l > n - r + 1\text { or }\tau _h < 0 \end{aligned}$$
(6)

Equations (4)–(6) hold for all \(h \in \{1, \dots , m\}\) since all sizes must be considered. It is worth noting that the dynamic programming state space increases of one dimension for every size of the jobs.

The variables with negative reduced cost found through this pricing procedure are added to the RMP, and the procedure is repeated until no negative reduced costs are found. The final solution of the column generation is the optimum (CG-UB) for the continuous problem, and a lower bound for the integer problem. This algorithm, called Column Generation Lower Bound, will be referred to as CG-LB in the following.

4.2 The CG-UB and VR-UB heuristic procedures

Two heuristics are proposed to find an integer solution for the problem, and both starts from the lower bound given by the column generation CG-LB.

The first heuristic is called Column Generation Upper Bound (CG-UB), and it is the same used by Alfieri et al. (2021). Once the continuous optimum CG-LB is found, the variable domain of the problem is changed from continuous to binary, and the MIP is solved to get a heuristic integer solution, namely CG-UB. This evaluation can be quite slow, especially when the number of jobs increases. Solving such a MIP to the optimum is NP-hard, indeed. Some strategies to speed up the evaluation could include stopping the evaluation after a fixed number of open nodes (but that amount should increase with the number of considered jobs), or after a certain time limit has been reached (but it can lead to large CG-UB/CG-LB gaps), or after a certain gap is reached (but the timing to reach such a gap could be too slow again). A time limit will be set for the numerical results of Section 5.

The second heuristic is the Variable Rounding Upper Bound, namely VR-UB, and consists in the variable rounding procedure proposed in Druetto and Grosso (2022). Differently from CG-UB, this approach generates good upper bounds within shorter computation times. Promising variables are sequentially fixed to 1 i.e., a batch is forced to be included in the solution. Then, the leftover part of the RMP is re-optimized with continuous variables, up to the point when the entire sequence is established. Between each rounding and re-optimization step, the feasibility is restored through a modified version of the initialization algorithm. This modified version is run only on the not-fixed part of the sequence and considers only jobs not included in the fixed batches yet.

figure a

The detailed variable rounding procedure is summarized in Algorithm 1, and it works as follows. First, CG-LB is computed and the RMP is populated. Then, among all columns that start from \(i=1\) i.e., all batches in the first position of the sequence, the one whose flow value is the closest to 1 is selected and enforced to be part of the solution. Also, no other columns can start from the same position. The procedure is repeated on the remaining part of the problem, by keeping all the already generated columns. Then, again, a new selection is made among all columns that start from \(i=k\), where k was the ending position of the column fixed in the previous step.

The column generation and variable rounding procedures are iterated until the value \(i=\vert N \vert + 1\) is reached, i.e., when there exist a sequence of batches from 1 to \(\vert N \vert + 1\), where all non-zero flow variables are equal to 1; this is the heuristic solution VR-UB for the original problem.

As shown in Algorithm 1, during the variable rounding procedure, another optimization of the algorithm is made (lines 8-11 of Algorithm 1). If the selected column already has a flow with value 1 i.e., it is already integer in the continuous optimum, there is no need to re-optimize the model, since the value obtained would be the same as before and no new columns would be generated.

5 Numerical results

Random instances are generated to test the proposed algorithm. The generation approach used in Alfieri et al. (2021), Rafiee Parsa et al. (2016), Uzsoy (1994) is here replicated.

In the experiment, some factors are varied to test the proposed approach in various scenarios. Specifically, the number of jobs n has been varied in \(n=\{20,40,60,80,100,200\}\), as the larger is n, the more complex is the problem to be solved. Jobs have various sizes, and each size can be sampled from two different uniform distributions: \(\sigma _{10}=U(1,10)\) and \(\sigma _{5}=U(1,5)\); the results should confirm that smaller intervals make the problem more complex, as more feasible batches can be created. The evaluated numbers of sizes per job are \(m = \{1,2,3\}\), to test the efficiency of the approach in the multi-size cases. For each size, a distribution must be chosen between \(\sigma _{10}\) and \(\sigma _{5}\) and, for each value of m, all possible combinations of \(\sigma _{10}\) and \(\sigma _5\) are evaluated. Last, the tested numbers of families are \(n_f=\{1,3,5,7,10\}\), to address the case of incompatible job families. All in all, 174 combinations of factors are tested. For each combination, 10 instances are solved, thus leading to 1740 experiments. For conciseness purposes, only results for \(n=\{20,60,100,200\}\) are shown below; the trend highlighted by this subset of experiments is confirmed by the experiments on the other sizes.

Some system characteristics have been fixed as parameters in all the instances. Specifically, for each job, the processing time is sampled from a uniform distribution U(1, 100). If more than one family is considered, the family is randomly assigned to every job with equal probability. Also, for each size, the batch capacity \(b_i\) is fixed to 10, as commonly used in the literature (Azizoglu and Webster 2000; Rafiee Parsa et al. 2016; Alfieri et al. 2021).

Beside the instances generated as mentioned above, additional tests are run with \(b_i = 50\) and with size distribution \(\sigma _{50} = U(1,50)\). The aim is to test the algorithm performance in the case where jobs have sizes with higher granularity. The results are presented separately in Appendix A.

Two heuristic algorithms are compared: the column generation combined with the MIP solver (CG-UB), and the column generation with the variable rounding procedure (VR-UB). Both are described in Sect. 4.

The proposed methods are developed in C++, and the optimization procedure is done by calling the CPLEX solver, version 12.9. Tests are run on a computer having a 3.70 GHz Intel i7 processor with 32 GB RAM.

In the following, the results are shown separately for the following cases: multi-size with no families (Table 1); incompatible families with one size (Tables 2 and 3); multi-size and incompatible families (Table 4, which shows only the cases of 3 and 7 families for reasons of conciseness). Results of single-size single-family instances are not reported in the paper for reasons of conciseness.

In all the tables, each row reports various statistics for a single combination of factors (grouping together the 10 instances) on the performance of the CPLEX’s integer solution (CG-UB) and of the variable rounding procedure (VR-UB). Specifically, each row is characterized by:

  • the number of jobs n;

  • the distributions for each size (columns \(s_1\), \(s_2\), \(s_3\) contain respectively the distribution of size 1, 2 or 3, if jobs have one, else −);

  • the number of incompatible families \(n_f\);

  • the number of reached optima \(\alpha\) (where the optimum is reached in the case \(LB=UB\)), knowing that the optimum is reached when the continuous CG-LB is characterized by all integer variables;

  • the average (Avg t) and maximum (Max t) computation time over the 10 instances, expressed in seconds;

  • the average (Avg \(\%\) g) and maximum (Max \(\%\) g) percentage gap computed on the single instance as:

    $$\begin{aligned} {\textbf {gap}}_{\texttt {{\textbf {CG-UB}}}} = \frac{\texttt {{\textbf {CG-UB}}}-\texttt {{\textbf {CG-LB}}}}{\texttt {{\textbf {CG-UB}}}} \times 100, \qquad {\textbf {gap}}_{\texttt {{\textbf {VR-UB}}}} = \frac{\texttt {{\textbf {VR-UB}}}-\texttt {{\textbf {CG-LB}}}}{\texttt {{\textbf {VR-UB}}}} \times 100. \end{aligned}$$

The column generation procedure that generates promising batches and builds a fractional solution works very fast. Finding the optimal integer solution using those batches is instead a time consuming issue for large instances. For this reason, a time limit of 100 CPU s has been set.

Table 1 Algorithm performance on the multi-size case
Full size table
Table 2 Algorithm performance on the family case for \(\sigma _{10}\)
Full size table
Table 3 Algorithm performance on the family case for \(\sigma _{5}\)
Full size table
Table 4 Algorithm performance on the multi-size family case
Full size table

First, both the CG-UB and \(\texttt {VR-UB}\) approaches are very fast. Indeed, for instances up to 60 jobs, the overall computation time is of the order of one second. Across all instances, the largest computation time for \(\texttt {VR-UB}\) is 96.2 s, while CG-UB sometimes reaches the 100 second time limit.

The instances with sizes distributed following \(\sigma _{5}\) are more difficult than those following \(\sigma _{10}\). Indeed, if comparing the instances in Tables 2 and 3 with 200 jobs, the average computation time of CG-UB moves from the order of 20 s for \(\sigma _{10}\) cases to times larger than 100 s for \(\sigma _{5}\). The same is true for \(\texttt {VR-UB}\), although computation times are lower for both cases. As \(\sigma _{5}\) reduces the maximum size a job can have, there are more possible combinations of jobs in a single batch, thus both computation times and gaps increase. However, if more than one size constraint is considered (Tables 1 and 4), even with \(\sigma _{5}\) the number of combinations decreases, and the dynamic programming that searches for feasible batches is able to cut uninteresting combinations. Thus, the greater the number of job sizes, the faster the algorithm works.

The number of jobs negatively impacts the computation time and the gaps, both for CG-UB and \(\texttt {VR-UB}\). Specifically, CG-UB often needs more than 100 s to solve instances with 200 jobs, especially in the cases of \(\sigma _{5}\) size distributions. Instead, \(\texttt {VR-UB}\) is able to handle these instances in most cases, but its computation time largely increases with respect to the instances with a small number of jobs. Moreover, with smaller numbers of jobs, both algorithms are more likely able to find optimal solutions; indeed, the number of optimal solutions \(\alpha\) is larger with smaller instances.

When incompatible families are addressed, a noticeable difference in computation times can be seen when the number of families increases. This is shown both in Tables 2 and 3 and in Table 4. In the former tables, the average computation time decreases with the increase of the number of families. For instance, with \(n=100\) and \(s_1 = \sigma _{10}\), the average computation time goes from 2.51 with 3 families to 0.97 with 10 families for the CG-UB, and from 1.24 to 0.74 for the \(\texttt {VR-UB}\). When multi-size is involved, the same decrease in computation time is shown in Table 4; interestingly, if \(\sigma _{5}\) distribution is given to the sizes, the difference in computation time with different families is even larger. As an example, if comparing the cases with \(n=100; \; m=3; \; s_i = \sigma _{10} \, \forall i\) and \(n=100; \; m=3; \; s_i = \sigma _{5} \, \forall i\), the difference in the average computation times from 3 to 7 families for the CG-UB moves from the order of 0.68 s to the order of 39.41 s. In the same instances, for the \(\texttt {VR-UB}\) approach, there is no difference between computation times of 3 and 7 families for the \(\sigma _{10}\) instances, and there is a difference of the order of 1.52 s for the \(\sigma _{5}\) instances. As explained in Section 4, the search in the state space from job r that belongs to family f can be restricted to the subset of jobs belonging to the same family. This modification of the search procedure does not impact on the structure of the state space, and leads to a decrease in computation time proportional to the number of families.

Lastly, comparing the results of CG-UB and \(\texttt {VR-UB}\) across all results, the proposed variable rounding tends to be faster than CG-UB, and obtains comparable or better performance. Specifically, for the single-size multi-family cases \(\texttt {VR-UB}\) is always faster than CG-UB. Indeed, Tables 2 and 3 show that both average and maximum computation times are smaller for \(\texttt {VR-UB}\) in all the cases. When the single-family multi-size cases are considered (Table 1), CG-UB and \(\texttt {VR-UB}\) have comparable performance in the instances with a small number of jobs and \(\sigma _{10}\) distribution. However, \(\texttt {VR-UB}\) achieves remarkable improvements in gaps for the cases with large numbers of jobs and sizes with \(\sigma _{5}\) distributions. For instance, in the experiments with \(n=200; s_i = \sigma _5 \, \forall i\), the average gap moves from 56.80 % (two sizes) and 22.85 % (three sizes) for CG-UB to 1.37 % (two sizes) and 1.14 % for \(\texttt {VR-UB}\), respectively. It is worth noting that the large CG-UB gap for larger instances is due to the enforced time limit. In terms of computation times, \(\texttt {VR-UB}\) results to be faster than CG-UB in almost all the cases. Also, CG-UB often reaches the time limit when 200 jobs are considered. Further experiments have been conducted for the cases where CG-UB reaches the time limit, and the results show that the computation times are consistently larger than \(\texttt {VR-UB}\). For the multi-size family case, the same considerations hold, proving the outperforming of \(\texttt {VR-UB}\) with respect to CG-UB.

Although some gaps are slightly better for \(\texttt {CG-UB}\) (except for the cases where the time limit is exceeded), the relative difference is not worth the extra time required in comparison to the faster \(\texttt {VR-UB}\). For instance, consider the single-size multi-family case with \(n = 200; \; s_1 = \sigma _{10}\) and \(n_f = 7\) in Table 2. The algorithm \(\texttt {CG-UB}\) finds the optimum value (without reaching the time limit) in an average time of 16.94s, with a mean gap equal to \(0.83 \%\); on the same instances \(\texttt {VR-UB}\) takes only 8.00s in the worst case (less than the half of \(\texttt {CG-UB}\) average case), with an average gap equal to \(1.39 \%\), i.e., only half a point worse than \(\texttt {CG-UB}\).

As the additional tests of Appendix A show, the efficiency of the algorithms is not affected for instances with larger job sizes and batch capacity. The average gaps are competitive for both algorithms; however, they suffer from the computation point of view since the pricing procedure becomes more difficult in these cases.

6 Conclusions

The parallel batch scheduling problem has become more and more addressed by the scientific and industrial communities because of its applications in many industrial fields.

This paper addresses the \(1 \vert p\textit{-}batch,s_{ij} \le b_i,incomp \vert \sum C_j\) problem. To the authors’ knowledge, this paper is the first attempt in the literature to consider multiple sizes and family incompatibility constraints together. Also, no assumptions are made on the distribution and/or the value of the processing times.

The solution approach is based on the flow formulation of the problem by Alfieri et al. (2021); this formulation is exploited to develop two column-generation based heuristics: one is based on the price-and-branch heuristic (\(\texttt {CG-UB}\)) of Alfieri et al. (2021), the other on the variable rounding procedure (\(\texttt {VR-UB}\)) proposed in Druetto and Grosso (2022). The column generation finds a continuous-relaxed solution, then the two heuristics are used to move from the continuous to the integer solution of the problem. An extensive experimental campaign compared the two heuristics, which both proved to be very effective for this scheduling problem. Indeed, the proposed approaches can handle instances up to 200 jobs, and both find very good optimality gaps in all the addressed instances. Moreover, with a small number of jobs, the proposed algorithms are able to find optimal solutions in most of the cases.

Numerical results show that the smaller the job sizes, the more difficult the batch scheduling problem becomes. Having more than one size constraint simplifies the problem from the computation standpoint. Also, having more families simplifies the problem, as the number of feasible combinations of jobs is reduced.

Also, comparing the two heuristics, interesting results emerged. In simple instances (i.e., with a small number of jobs, large job sizes and a small number of families) the difference between the two approaches is not appreciable. The real gain can be perceived in difficult instances, where both computation times and gaps largely decrease. Specifically, instances with 200 jobs can not be solved by the \(\texttt {CG-UB}\) approach in 100 second time limit, however the variable rounding \(\texttt {VR-UB}\) is able to achieve good gaps in less than the time limit. In general, almost all instances are solved within a minute and the gap rarely overcomes \(5\%\). The variable rounding procedure is therefore shown to be a valid alternative to the \(\texttt {CG-UB}\).

At its current state, the proposed approach is able to solve single-machine batch scheduling problems. Further research will be devoted to adapting the approach to parallel machines and to weighted completion times (\(\sum w_j C_j\)).