Abstract
Disruption management is an approach to the rescheduling of operations following an unanticipated event occurring that has been applied in a wide range of applications, including airline scheduling and project management. This review focusses on the use of disruption management in vehicle routing and scheduling applied to road freight distribution. The paper discusses the key features of disruption management and examines the relevant objectives and types of disruption that may occur in this context. Different formulations and solution methods are described. A set of relevant papers are summarised and classified according to the type of disruption addressed, the relevant objectives and the solution approach.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
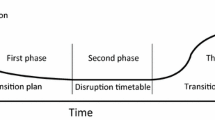
Disruption Management refers to dynamically revising an operational plan in real time, once a disruption occurs. It is very important in situations where the operational plan has been published in advance, and especially when its execution is subject to major disruptions. When the published operational plan is revised, some costs will occur that are associated with the transition from the original to the modified plan. The deviation cost might be a financial cost, caused, for example, by paying overtime to employees, or might be something not so easy to quantify, such as the dissatisfaction or loss of customers. It is essential to take those deviation costs into account when generating a new plan. A key feature of disruption management is the ability to deal with a disruption without knowing in advance that it is going happen and to provide good solutions in time for them to be implemented.
A formal definition of disruption management can be found in Yu and Qi (2004): “At the beginning of a business cycle, an optimal or near-optimal operational plan is obtained by using certain optimization models and solution schemes. When such an operational plan is executed, disruptions may occur from time to time caused by internal and external uncertain factors. As a result, the original operational plan may not remain optimal, or even feasible. Consequently, we need to dynamically revise the original plan and obtain a new one that reflects the constraints and objectives of the evolved environment while minimising the negative impact of the disruption. This process is referred to as disruption management.”
Disruptions may occur in many settings and in their book Yu and Qi (2004) go on to provide examples including production scheduling, supply chain management and transport planning.
Clausen et al. (2010) provide a thorough review of models and methods used in disruption management in the airline industry, including aircraft, crew, passenger and integrated recovery. They also provide an overview of model formulations of the aircraft and crew scheduling problems, as well as an overview of research within schedule robustness in airline scheduling. In this article, a disruption is defined as “a state during the execution of the current operation, where the deviation from plan is sufficiently large that the plan has to be changed substantially”. Disruption management then refers to the replanning after a disruption has occurred.
The key factors that are involved in disruption management are as follows:
-
(i)
The time for replanning may be limited. This will normally be the case and so limits the computation time available for any algorithm used to produce a revised plan for recovery. The time needed to receive information concerning the disruption and to communicate the revised plan to those who implement it must also be taken into consideration.
-
(ii)
The original undisrupted plan may be a useful starting point for the new plan. When constructing the revised plan, there is no need to determine a complete plan from scratch. In disruption management, there will always be an original plan to consult.
-
(iii)
It may be appropriate to include new costs relating to deviations from the original plan. Whereas the original plan may have been created with a single objective of minimising relevant costs, the disruption management model may need to include other considerations, particularly the costs of deviating from the original plan. The disruption management model is, therefore, often a multi-objective model and the relevant objectives will be discussed later.
-
(iv)
There may be constraints in the new plan that were not in the original. These constraints may be as a result of the disruption that has occurred, such as a blocked road due to an accident or the unavailability of a failed vehicle. Sometimes there will be additional constraints due to commitments that have been agreed after the original plan was published.
Visentini et al. (2013) provide a review concerning the methods used for real-time vehicle schedule recovery in transportation services. They do not use the term “disruption management” in their title or abstract, preferring to refer to “real-time vehicle schedule recovery methods”, but their review clearly covers disruption management methods as used in transportation services. They classify Real-Time Vehicle Schedule Recovery Problems (RTVSRP) into 3 categories: vehicle rescheduling for road-based services, train-based rescheduling and airline schedule recovery problems. They classify the models of each category according to the problem formulation and the solution strategy.
In this review, we have decided to focus on disruption management in vehicle routing and scheduling for road freight transport. This means that the models used are closely related to the models that are used to address the Vehicle Routing Problem and its related variants.
The Vehicle Routing Problem (VRP) is the problem of determining the optimal set of routes to be traversed by a fleet of vehicles, in order to serve a given set of customers. The problem was introduced in Dantzig and Ramser (1959). Since then, numerous papers and books have been published describing different models and algorithms for the optimal or approximate solution of the many different variants of the VRP. Toth and Vigo (2014) discuss and review formulations and algorithms used for the VRP and related problems. The models and algorithms proposed for the solution of the VRP and its variants are used for the solution of different real-world applications arising in transportation systems. Typical applications include the delivery or collection of goods, school bus routing, dial-a-ride systems, routing of salespeople, routing of maintenance units etc. The VRP and its variants are known to be NP-hard.
The basic version of the VRP is the Capacitated Vehicle Routing Problem (CVRP), which involves the determination of the optimal set of routes to be traversed by a fleet of vehicles based at a single central depot, in order to distribute goods to a set of geographically dispersed customers, while minimising the total travel cost. Capacity constraints are imposed. All vehicles are identical, with a fixed capacity and must start and finish at the depot. All the customers require deliveries and the customer demands are fixed, known in advance and cannot be split. All customers have to be served.
The Vehicle Routing Problem with Time Windows (VRPTW) is an extension of the CVRP in which the service of each customer must start within an associated time interval, called a time window, and the vehicle must stop at the customer location for the duration of the service time of that customer. This may be particularly relevant to disruption management as the original plan may have created customer expectations about the time when service will be delivered.
There is also a significant literature on dynamic or real-time vehicle routing and scheduling. These articles particularly deal with situations where customer demand may arise, or be cancelled, during the operation and so plans must be constantly updated to react to the changing demand patterns. Other sources of dynamism may arise from changing travel times and vehicle availability. Some of the modelling and algorithmic approaches used to address a dynamic vehicle routing problem may provide useful insights for disruption management in vehicle routing and scheduling.
Pillac et al. (2013) present a review of the Dynamic Vehicle Routing Problems (DVRPs) with more than 150 references. That study classifies routing problems from the perspective of information quality (deterministic versus stochastic input) and evolution of information (whether or not the information available to the planner may change during the execution of the routes).
Psaraftis et al. (2016) also present a survey paper on Dynamic Vehicle Routing Problems and provide a taxonomy of DVRP papers according to 11 criteria: type of problem, logistical context, transportation mode, objective function, fleet size, time constraints, vehicle capacity constraints, the ability to reject customers, the nature of the dynamic element, the nature of the stochasticity (if any) and the solution method.
In Chapter 11 of the recent book edited by Toth and Vigo (2014), Bektaş et al. (2014) also present a survey of DVRPs. In this chapter, apart from providing an overview of the relevant literature, the authors present the state of the art in frameworks and strategies, providing a detailed analysis of the DVRP.
1.1 Relevant objectives
When determining the original plan for vehicle routing and scheduling in the context of road freight transport, it is usual to focus on an objective of minimising the relevant costs subject to constraints on the operation. Sometimes fixed costs of using vehicles and their drivers are included in the objective to be minimised, while in other cases, the number of available vehicles may be regarded as a constraint and the objective to be minimised depends only on distance-related costs.
After a disruption has occurred, there will still normally be a focus on minimising the costs of the revised plan that deals with the disruption, but the following additional objectives may also need to be taken into consideration that may not have been included in the original plans:
(i) The deviation from the original plan for customers. Customers may have made arrangements to receive deliveries at particular times according to the original schedule. For some sorts of deliveries, customers may be quite flexible about the timing of deliveries, but in other cases where members of staff need to be available to receive goods or when deliveries have been scheduled to avoid overlaps with other delivery operations, then the customer will experience a degree of dissatisfaction with a significant change in delivery time. The change may lead to increased costs for the customer, such as when additional overtime payments are incurred for members of staff who are waiting to help unload the delivery. Some estimate of this cost can be incorporated as an additional objective to be minimised in the disruption management model. An operator may also wish to give a higher priority to more important customers in terms of the size of the deviation from the original plan and this too may be incorporated in this objective. There may also be trade-offs to be considered in terms of the number of customers who will have a late delivery against the total deviation from the planned delivery schedule.
(ii) The deviation from the original plan for drivers. There may be direct extra costs involved for drivers if the revised plan involves the use of overtime or special payments. Additionally, there may be problems in requiring a driver to deliver to an unfamiliar customer. This could increase the service time if the driver assigned is unfamiliar with access arrangements at the customer. Also the customer may prefer to deal with a familiar driver. These are all factors which may be important in assessing the revised plan.
When the objectives for a particular application have been decided, it may be possible to convert them all to monetary values and so have a disruption management problem with a single objective of minimising the sum of these relevant costs. Where there are more subjective issues to consider, then it may be preferable to adopt a multi-objective approach with a disruption management model that will present a set of Pareto optimal alternative solutions to the decision maker. However this approach generally requires more time to compute and select the revised plan and so may be more difficult to achieve in the limited time available before the revised plan is needed.
2 Formulation and solution approaches
There are various ways to formulate a disruption management problem, which depend on the details of the application and the amount of flexibility that is to be allowed in revising the original plan.
One important consideration is the type of commodity which is being distributed to customers and whether the goods loaded into vehicles at the start of each trip are only for the specific customers to be visited by that vehicle or whether the commodity is a general one where any customer can be served by any vehicle. In the case of delivering packages or parcels addressed to specific recipients, then the goods loaded must be regarded as customer-specific. If a commodity such as gas canisters or bottled water is to be distributed, then any customer can receive a delivery from any vehicle and the commodity can be regarded as non customer-specific. This distinction is important in terms of the feasibility of the revised plans. For example, following a vehicle breakdown, if the vehicle is carrying customer-specific commodities, then it must be visited by other vehicles to pick up the remaining goods it was carrying before taking them to other customers. But if the failed vehicle was carrying non customer-specific commodities, then there is no need for it to be visited by any of the other vehicles delivering to the remaining customers on its route.
Another issue is the degree of flexibility that is to be allowed in the revised plan. For example, some formulations assume that following a vehicle breakdown, the remaining customers on its route will be served by one of the other vehicles in the same order after completing one of their original trips. This simplifies the formulation of the disruption management problem. Such a formulation can be easily modified for situations involving non customer-specific and customer-specific commodities. However there are cases where less costly revised plans can be built if the remaining customers that were to have been visited by the failed vehicle are allowed to be served by two or more different vehicles.
For example, suppose that there are two customers remaining to be served on a trip affected by a vehicle breakdown and non customer-specific commodities are being distributed. If two of the other vehicles have enough capacity to add a delivery to one of those remaining customers, but not both, then revising the routes of these two vehicles to serve one of the remaining customers each is likely to be cheaper than a revised plan where a vehicle needs to reload at the depot, or another vehicle needs to be employed,in order to serve both the remaining customers on the affected trip.
A further detail of the formulation that should be specified is when vehicles can be re-routed after starting a trip in the original plan. Some formulations require that an existing trip must be completed by a vehicle before it can be used to respond to the disruption. In other cases, the formulation may allow a vehicle to divert from its original route during a trip. The change in route might only be allowed after the vehicle has finished serving the next customer on its route, which could aid implementation if the driver can only receive new instructions from the transport manager while at a customer location. If there are good communication facilities between the transport manager and the drivers, then it may be feasible to divert a vehicle during its journey between customers, but in this case, it is particularly important to allow for the time needed between the disruption being reported and the production of the revised plan when implementing the changes.
Particularly in the case of vehicle breakdown, an important consideration is whether another vehicle and driver are available at the depot or not. If one is available or can be hired, then any additional costs incurred should be taken into account in the formulation.
There are also differences in disruption management formulations regarding the service to customers included for service in the original plan. Some formulations assume that all original customers must receive their service, even if it is at a different time to the original plan, while other formulations allow for the possibility of cancelling some customer orders. In this case, the loss in profit or a customer dissatisfaction cost is normally included in the objective.
The disruption management problem is normally some sort of optimisation problem, subject to constraints. It may be expressed as an integer linear programme. If this is done, there is then the question of whether to solve it exactly or whether it is more appropriate to devise a heuristic algorithm to obtain a good answer quickly. This will depend on how the problem has been formulated, the size of the problem instances and the computational time that is available to produce and communicate the revised plan. The vehicle routing problem itself is well known to be NP-Hard and so it might be expected that an associated disruption management problem may also be NP-Hard. This may not necessarily be the case, though some papers contain proofs that their formulation of the disruption management problem is NP-Hard. Even if the disruption management problem is NP-Hard, it may still be viable to make use of an exact approach in practice and an example is provided by Li et al. (2008).
As has already been mentioned, in disruption management there are potentially several objectives that are relevant. It is therefore important to consider whether one of these objectives (e.g. the operational costs) is so important that only this objective needs to be taken into consideration in a single objective formulation. Alternatively, some form of multiple-objective approach could be employed. This could be a simple weighting system where a single objective to be optimised is formed by summing the values of the relevant objectives weighted by parameters that reflect their importance. A lexicographic approach could be employed where the relevant objectives are ordered in terms of importance and the revised disruption plan is made taking these priorities into account. As in other multi-criteria problems, methods are available to determine a set of non-dominated solutions forming a Pareto front from which the decision maker can select a preferred solution. However there may not be enough time available before the revised plan needs to be implemented for all these potential solutions to be calculated and one selected.
2.1 Multi-objective optimisation for vehicle routing and scheduling
The book by Branke et al. (2008) constitutes a comprehensive guide to multi-objective optimisation. Since Pareto optimal solutions cannot be ordered completely, in order to be able to select the most preferred solution for a problem involving multiple conflicting objectives, the decision maker needs to provide additional preference information. Multi-objective optimisation methods are often classified into the four following classes, according to the role of the decision maker in the solution process: (i) no-preference methods, where there is no preference information available from the decision maker, (ii) a priori methods, where the decision maker first provides preference information and aspirations and then the solution process tries to find a Pareto optimal solution satisfying those as well as possible, (iii) a posteriori methods, where a representation of the set of Pareto optimal solutions is generated first, and then the decision maker is asked to select the most preferred one among them, and (iv) interactive methods, where an iterative solution algorithm is formed and repeated several times, and after each iteration, some information is given to the decision maker and he/she is asked to specify preference information. Some of the basic methods of non-interactive multi-objective optimisation are: weighting method, \(\epsilon \)-constraint method, method of global criterion, neutral compromise solution, method of weighted metrics, achievement scalarizing function approach, value function method, lexicographic ordering, and goal programming.
Marler and Arora (2004) present a survey of continuous non-linear multi-objective optimisation (MMO) concepts and methods.
Alves and Climaco (2007) provide a review of interactive methods devoted to multi-objective integer and mixed-integer (MOIP/MOMIP) programming problems.
Rancourt and Paquette (2014) introduce and solve the US MOVRTDSP, a multi-objective vehicle routing and truck driver scheduling problem which satisfies the legislative requirements on work and rest hours in the US. They present a Tabu Search algorithm which solves the problem and provides a heuristic non-dominated solution set, from which trade-offs between operating costs and driver inconvenience are evaluated. Trade-offs between the number of vehicles used and the operating costs are also investigated.
Ombuki et al. (2006) represent the VRPTW as a multi-objective problem with two objectives to be minimised, namely the number of vehicles used and the total cost, and present a genetic algorithm solution using the Pareto ranking technique.
Jozefowiez et al. (2008) provide a survey of multi-objective optimisation in routing problems. They examine routing problems in terms of their definitions, their objectives and the multi-objective algorithms proposed for solving them. They report that the two main strategies most widely used for solving multi-objective routing problems are weighted aggregation and multi-objective evolutionary algorithms.
Lust and Teghem (2010) present a survey on the multi-objective travelling salesman problem, along with a new approach for the problem, which they call two-phase Pareto local search.
3 Discussion of papers
In this section, a set of papers have been selected describing an approach to disruption management in the context of vehicle routing and scheduling for freight distribution. Some of the papers employ a methodology that can be applied more widely, but the focus in this review is on the freight distribution scenario.
The papers are listed according to the year of publication. Table 1 provides a summary of the papers covered. The first column references the paper. The second column indicates the main type or types of disruptions addressed in the paper where V denotes vehicle breakdown, L denotes a disrupted link in the road network, S denotes a disruption in the supply of goods and C denotes a disruption in customer demand. The third column lists the main objectives considered in the paper and the final column indicates the solution approach.
Li et al. (2007a) introduce the Vehicle Rescheduling Problem (VRSP) which seeks to serve the passengers/cargo on the affected trip and complete all remaining trips, while minimising the operation and delay costs. They present a prototype decision support system which recommends solutions for the single-depot vehicle rescheduling problem (SDVRSP) and for the single-depot vehicle scheduling problem (SDVSP). They use a quasi-assignment formulation and a combined forward-backward auction algorithm, developed by Freling et al. (2001) to solve both the SDVSP and the SDVRSP, where the latter is treated as a sequence of SDVSP problems. The rescheduling decision support system is used in a real world problem involving the operational planning of solid waste collection for a city in Brazil.
Li et al. (2007b) also study the single-depot VRSP with focus on its modelling, algorithmic and computation aspects. A model formulation and several fast algorithms are presented, including parallel synchronous auction algorithms. They introduce the concept of the common feasible network (CFN). Among the algorithms they consider, parallel CFN-based auction algorithms have the best performance.
Ernst et al. (2007) describe a case study where software has been developed to assist a recreational vehicle rental company based in New Zealand in its operations. The dynamic version of the software is referred to as the Dynamic Vehicle Assignment and Scheduling System (D-VASS). It is used to respond to availability queries from reservation staff, but can also be used to modify the schedule when there are disruptions such as vehicle breakdowns or delays in returning vehicles. The heuristic developed aims to minimise the sum of costs due to foregone profit if potential rentals are not included, relocation costs, substitution costs and costs due to delayed starts beyond requested commencement times, subject to a set of constraints. The heuristic is based on the successive shortest path method for solving the assignment problem.
Zhang and Tang (2007) present a rescheduling model for a Vehicle Routing Problem with Time Windows. The paper concentrates on vehicle disruptions, where a vehicle becomes unavailable due to a breakdown or a traffic incident. The objective is to find a new schedule that minimises total distance and deviations from the original plan. A hybrid algorithm which combines ant colony optimization (ACO) with scatter search is proposed to solve the disruption problem. Computational results are reported to show the effectiveness of the hybrid algorithm.
Li et al. (2008) provide a further investigation of the case study involving waste collection in Porto Alegre, Brazil that was included in Li et al. (2007a). This study concentrates on the rescheduling problem where a trip that has been scheduled is cut due to the breakdown of one of the vehicles. The objective is taken to be minimising the sum of the operational and delay costs. The formulation is presented as a non-linear programme which is converted using a standard technique into an integer linear programme. Additional constraints had to be taken into consideration, such as the need to obtain approximately balanced assignments of truck loads to different recycling facilities. Computational results are reported based on real-world data. The instances used were relatively small, consisting of 23 vehicles and 31 trips, which meant that the integer linear programmes could be solved optimally using CPLEX in a short CPU time. The results showed reductions in the distances travelled and the time delays compared to the manual strategy that was employed.
Wang and Cao (2008) address the case where, during the execution of a solution plan for a vehicle routing problem with backhaul and time windows, a disruption occurs in the form of a change in demand concerning the demand for backhaul services. A recovery model is proposed considering the disruption to customers from deviations to planned service times and the operating costs to the logistics service provider. Two strategies and a local search algorithm are designed to find an optimal or near-optimal solution in real time.
Li et al. (2009a) introduce and study Real-Time Vehicle Rerouting Problems with Time Windows, applied in the case of a disruption to delivery and/or pickup services due to vehicle breakdowns. They define the Real-Time Vehicle Rerouting Problem with Time Windows as follows: “ Given a depot, a number of vehicles with the limited capacities, and a set of customer services having demands with time windows, given the travel time between all pairs of locations, given the vehicle routes originally planned, and given a breakdown vehicle with the breakdown time and position, find feasible route reassignments with the minimum weighted sum of operating, fixed vehicle, service cancellation and route disruption costs, in which (i) each vehicle performs a feasible sequence of services, satisfying constraints related to the service time windows and vehicle capacities; and (ii) a service is either satisfied, or cancelled with a large service cancellation cost when some constraints cannot be satisfied. ” The authors present a path-based formulation of the problem and a heuristic incorporating Lagrangian relaxation and an insertion based primal heuristic. They also use a dynamic programming based heuristic to solve the Lagrangian relaxation problem quickly, but not necessarily to optimality. Computational experiments are performed on benchmark problems taken from Solomon (1987) to show the effectiveness of the proposed algorithm. Additionally, the authors show that the Real-Time Vehicle Rerouting Problems with Time Windows, both in the case of a pickup and in the case of a delivery service, are NP-hard by association with the VRPTW and the TSPTW, respectively.
Li et al. (2009b) addresses a similar disruption management problem to the one studied in Li et al. (2009a). The approach is characterised by a formulation that seeks to minimise the total weighted sum of costs relating to operating costs, disruption costs and trip cancellation costs. In this paper, computational experiments are carried out using a range of randomly generated problems. The results are compared with a simple intuitive approach and it is found that the proposed algorithm is more beneficial compared to the intuitive approach when there is no back-up vehicle available at the depot or when breakdowns occur later rather than earlier in a trip.
Wang et al. (2009a) present a disruption management model to solve the vehicle routing problem with vehicle breakdown. The problem under study and the proposed model are similar to the ones presented in Wang et al. (2010), which is discussed in more detail later. This paper uses a genetic algorithm for its solution approach.
In Wang et al. (2009b)the emphasis is on applying a disruption management approach when there are changes to the customers and their demand requests. A model is constructed which is compatible with the Vehicle Routing Problem with Time Windows (VRPTW). The solution approach is based on a genetic algorithm and computational results are presented to illustrate the method used.
Wang and Shi (2009) address the case of a travel time delay of a route in a single-depot VRPTW. The delay could be caused by traffic congestion due to an accident or another unexpected event during a vehicle’s route. The model and solution method are similar to those discussed in Wang et al. (2009a). Experimental results are provided for a small set of problems.
Wang et al. (2010) study the “Urgency Vehicle Routing Disruption Management Problem” where a disruption caused by a vehicle breakdown occurs in a logistics distribution system. They propose a mathematical model which is based on the theory of disruption management. A Lagrangian relaxation is used to simplify the model, decomposing it into two parts. An insertion algorithm is then used to obtain a feasible solution for the primal problem. When a disruption occurs, the authors assume that there are extra vehicles available at the depot. They also allow the cancellation of servicing of some customers. In order to quantify the magnitude of the disruption, the authors focus on three aspects of a solution: the service time of customers, the routes of service vehicles and the costs of the logistics provider.
The model involves three objective functions. The first objective is the sum of the differences of the service time between the new plan and the original plan, for each customer. This is the total time deviation for the whole set of customers, which seeks to be minimised, and reflects the need that the service times in the new plan should be as close to the ones in the original plan as possible. The second objective seeks to minimise the deviation of routes between the original plan and the recovery plan. The third objective seeks to minimise other costs incurred by the deviation from the original plan, including the costs from deviation of routes, the cost of sending additional vehicles and the cost of cancelling some customers. The Lexicographic approach is used to deal with the multiple objectives.
Mu et al. (2011) study the disrupted VRP with vehicle breakdown during the execution of a vehicle routing plan. It is assumed that vehicles deliver a single commodity, which is transferable between customers (such as oil or gas), so that any customer can be served by any vehicle, as long as the vehicle carries enough quantity to serve him/her. The case of an extra vehicle being available at the depot is considered. All customers must be served and there is no upper bound on the total length or duration of the routes. The paper shows the link between the formulation adopted for the disruption management problem and an Open Vehicle Routing Problem where the end points of each trip are fixed. Two Tabu Search heuristic algorithms are developed and tested over a set of test problems generated for the purpose. The computational results of the heuristics are then compared to an exact algorithm based on the method proposed by Letchford et al. (2007) for the Open Vehicle Routing Problem.
Hu and Sun (2012) present a knowledge-based modelling approach for disruption management in urban distribution. The knowledge of experienced schedulers is combined with operations research models and algorithms to revise the distribution plan. Policies, algorithms and models are represented by appropriate knowledge representation schemes, in order to support automated or semi-automated modelling by computers. The integration of the two kinds of knowledge combines the advantages of both and the approach is developed in Hu et al. (2013) which is described later.
Minis et al. (2012) also study the case where, during the execution of the original VRP plan, a vehicle breakdown occurs. The problem is modelled as a variation of the Team Orienteering Problem (TOP), with a fixed upper bound on the length in time or distance of each route, and fixed vehicle capacity. A heuristic is proposed, which compares favourably to a computationally more expensive Genetic Algorithm. Specifically, for a computational time of 10 minutes, the heuristic results are only 3 % away from those of the GA for the most complex problem set used (98 clients). The GA was used to set benchmark solutions for the heuristic, which is justified by the fact that the GA was used to solve TOP benchmark problems and gave results very close to the best published results. The authors assume that the orders are customer-specific, so each vehicle can only serve its own customers and the customers of the failed vehicle. There is no extra vehicle available at the depot. The problem is modelled as a profit maximization problem, in which a set of vehicles are routed to maximize the total reward accumulated by serving clients, within a predefined time horizon, where some of the customers might not be served. Priority is given to the most important customers, where the importance is considered equivalent to the reward of the TOP. In order to serve clients of the failed vehicle, an active vehicle must first visit the location of the failed vehicle and load the relevant orders from the failed vehicle to the active one. An active vehicle is allowed to visit the failed vehicle more than once. The proposed heuristic has been incorporated in a real-time fleet management system of a food company operating in the region of Attica, Greece, and tested in practical breakdown cases with success.
Ngai et al. (2012) is an example of a paper where the emphasis is on the design of a complete decision support system that can help to reschedule a distribution plan following an accident or other incident which disrupts the original plan. The system includes a model management subsystem which aims to minimise the total operating costs of the rescheduled plan. A prototype system was built and evaluated for a case study concerning a supplier of portable toilets based in Hong Kong.
Wang et al. (2012) propose a recovery model for disruptions for the VRPTW, capable of handling a combination of disruptions. They try to follow closely the principles of Disruption Management and aim to reduce any deviations from the original plan. The authors report that, according to interviews with delivery drivers, drivers usually prefer routings they are familiar with, because they know the customers, the exact locations and the delivery processes. Customers also prefer familiar delivery staff.
Therefore, they propose a mathematical model with the following three objectives. The first objective, which is a measurement of the disruption on customers, seeks to minimise the deviation of the time of start of service of customers between the original plan and the recovery plan. The second objective, which is a measurement of the disruption on drivers, seeks to minimise the deviation of routes between the original plan and the recovery plan. Apart from penalizing the change in travel distance, this objective penalizes any change which involves moving a customer from one route to another, or exchanging customers between routes. The third objective, which is a measurement of the disruption on providers, seeks to minimise the deviation of the total delivery costs between the original plan and the recovery plan (which is equivalent to minimising the total delivery costs of the recovery plan, since the costs of the original plan are fixed). They define the delivery costs as a linear combination of the total travel distance and the number of vehicles used.
In their study they consider the following types of disruption: vehicle breakdown, blocked vehicle, damaged cargo (fully or partially), change of customer’s time windows, change of customer’s delivery address, change of customer’s demand amount, removal of customers. They also consider combinations of those disruptions occurring successively or simultaneously. They apply the Nested Partitions Method (NPM) to solve the problem. The authors conclude by acknowledging the need for a more effective and efficient multi-objective optimisation algorithm, which would aid in the development of a decision support system for different disruption events that occur during logistics deliveries.
Dhahri et al. (2013) present a rescheduling model based on Variable Neighbourhood Search (VNS), for the VRPTW when one or more vehicles require maintenance activities after the supply of a set of customers. In this paper only one type of disruption is considered, namely vehicle breakdown.
Mamasis et al. (2013) also address the case where, during the distribution of a single product to a set of customers by a fleet of vehicles, a single vehicle is immobilized (vehicle breakdown). Some active vehicles are then rerouted to serve selected clients of the immobilized vehicle. This re-planning problem is modelled as a variation of the Team Orienteering Problem. All vehicle routes are constrained to an upper time or distance limit. A vehicle capacity constraint is also present. There are no extra or back-up vehicles available at the depot. Active vehicles are allowed to visit the depot and/or the immobilized vehicle (more than once, if needed), for replenishment purposes. Clients are served based on their importance, which is a rating assigned a priori to each client. Some clients may remain unserved. Reallocation of clients among vehicles is feasible, given that the respective vehicles carry enough quantity of the product to satisfy clients’ demand, since the product to be delivered is common to all clients. The rerouting decisions in the modified plan are based on client importance, routing costs (times) and capacity restrictions.
A heuristic is proposed which can provide solutions in almost real-time. The effectiveness of the heuristic is tested by comparing its solutions with those obtained by an appropriate Genetic Algorithm, which yields high quality results but is computationally expensive.
Some applications of the problem mentioned in this paper include: Distribution systems dealing with critical commodities, such as vital supplies in relief logistics, cash in money transfer operations, transfer of staff or ammunition from incapacitated military vehicles (in battlefield operations), or in general distribution of any single product (e.g. bottled water).
Mu and Eglese (2013) study the situation when the supply of the commodity does not arrive at the depot on time, so that not enough of the commodity is available to be loaded on all vehicles at the start of the delivery period. The Disrupted Capacitated VRP with Order Release Delay (DCVRP-ORD) is introduced, which involves multiple trips and allows some vehicles to wait at the depot. Two Tabu Search heuristic algorithms are proposed. The authors assume that vehicles deliver a single commodity, which is transferable between customers (such as oil or gas), so that any customer can be served by any vehicle, as long as it carries enough quantity to serve him/her.
Jiang et al. (2013) study two variants of the disrupted VRP: A single-vehicle delivery disruption management recovery model with service priority, and a more generalized multi-vehicle version of it. The customers are divided into high-priority and low-priority customers. When a delay happens, priority is given to serving all the key customers in their original time windows; this is imposed as a hard constraint. A genetic algorithm is proposed to solve the problems.
Hu et al. (2013) develop a knowledge-based modelling approach, referred to as PAM (disruption-handling Policies, local search Algorithms and object-oriented Modelling), which can dynamically handle disruptions in Real-time Vehicle Routing Problems. Their study is similar to the one presented in Hu and Sun (2012). This approach combines the scheduling knowledge of experienced schedulers with the optimisation knowledge concerning OR models and algorithms, to obtain an effective solution in real time. Types of disruptions examined in this paper include: postponed delivery time, advanced delivery time, repairable vehicle breakdown, road construction, demand increasing, order cancelling, disabled road, disabled vehicle. The first four types of disruption are handled using the same ‘time violation’ policy, whereas a separate policy is used for each of the remaining four types of disruption.
Spliet et al. (2014) study the Vehicle Rescheduling Problem (VRSP). In the classical CVRP the demand is deterministic and known before planning. This paper considers the situation where the demand becomes known at a late moment. For example, in the retail industry a common situation occurs when individual stores place their orders a few days, or sometimes just one day, before delivery. In such a case, it is beneficial for operational processes to prepare the delivery plan before the orders are placed. A common practice in this case is to have a long term schedule or master schedule prepared, serving as a guiding plan over a certain period of time during which multiple deliveries are made. For example, a master schedule could describe the weekly or daily deliveries for the next 6 months. Such a master plan is usually created by solving deterministic CVRP instances based on the average customer demands and demand predictions for the upcoming period. Since the master schedule is prepared before demand realizations become apparent, when the demand becomes known, this schedule may no longer be optimal, or even feasible. In these cases, which occur frequently in practice, the master schedule has to be revisited. A new schedule has to be constructed, once demand realizations become known, which will typically deviate from the master plan. Given the master schedule and a demand realization, the VRSP seeks to find a new schedule which minimises the total travel cost and the cost of deviating from the master plan, while respecting the capacity constraints. The authors present a MIP formulation for the rescheduling problem, based on a CVRP formulation by Baldacci et al. (2004), along with a two-phase heuristic solution method.
4 Conclusions
This brief focused survey has shown that there is a rich variety of approaches and solution methods used for disruption management in vehicle routing and scheduling.
The area is ripe for future research to improve on existing methods and to provide even better decision support for those managing distribution operations using road vehicles. Technical developments that should be taken into account in devising new approaches include the following aspects:
-
(i)
Quicker and better communications between drivers and management are now available to obtain timely and reliable information about the current status of the vehicle and to inform drivers of revised plans. This may allow additional time to build a revised plan.
-
(ii)
Faster and more powerful computers will allow exact approaches to be considered for some applications where heuristics were formerly the only viable option.
-
(iii)
Advances in methods for both exact optimisation and heuristic methods will allow larger problem instances to be solved more quickly. For example, disruption management may benefit from the use of approaches to automatically design heuristics that have been used successfully in production scheduling applications as presented in Branke et al. (2016).
There may also be better ways to take advantage of the structure of the disruption management problem that has been formulated and to exploit information obtained when the original distribution plan was developed.
However it is clear that the effectiveness of any revised plan to cope with disruption depends on how the problem has been formulated. The flexibility that is allowed in revising the plan, such as whether customers yet to be served on the trip affected by a vehicle breakdown must be served by a single alternative vehicle in the same order, can have a significant effect on the outcome. Similarly, revised plans can be significantly influenced by whether existing customer requests for service can be cancelled or not. The trade-offs between different objectives could be very different in different applications. The multi-objective nature of disruption management provides a particular challenge in producing general solution methods that can be used successfully for a wide range of distribution operations.
References
Alves MJ, Climaco J (2007) A review of interactive methods for multiobjective integer and mixed-integer programming. Eur. J. Oper. Res. 180(1):99–115
Baldacci R, Hadjiconstantinou E, Mingozzi A (2004) An exact algorithm for the capacitated vehicle routing problem based on a two-commodity network flow formulation. Oper. Res. 52(5):723–738
Bektaş T, Repoussis PP, Tarantilis CD (2014) Dynamic vehicle routing problems. In: Toth P, Vigo D (eds) The Vehicle Routing Problem. SIAM, Philadelphia
Branke J, Deb K, Miettinen K, Slowinski R (eds) (2008) Multiobjective Optimization: Interactive and Evolutionary Approaches. Springer, Berlin
Branke J, Nguyen S, Pickardt C, Zhang M (2016) Automated design of production scheduling heuristics: a review. IEEE Trans. Evol. Comput. 20(1):110–124
Clausen J, Larsen A, Larsen J, Rezanova NJ (2010) Disruption management in the airline industry-concepts, models and methods. Comput. Oper. Res. 37(5):809–821
Dantzig GB, Ramser JH (1959) The truck dispatching problem. Manag. Sci. 6:80–91
Dhahri, A., Zidi, K., Ghedira, K.: Vehicle routing problem with time windows under availability constraints. In: 2013 International Conference on Advanced Logistics and Transport, pp. 308–314 (2013)
Ernst AT, Horn M, Krisnamoorthy M, Kilby P, Degenhardt P, Moran M (2007) Static and dynamic order scheduling for recreational rental vehicles at tourism holdings limited. Interfaces 37(4):334–341
Freling R, Wagelmans A, Paixao J (2001) Models and algorithms for single-depot vehicle scheduling. Trans. Sci. 35:165–180
Hu X, Sun L (2012) Knowledge-based modeling for disruption management in urban distribution. Expert Syst. Appl. 39:906–916
Hu X, Sun L, Liu L (2013) A PAM approach to handling disruptions in real-time vehicle routing problems. Decis. Support Syst. 54(3):1380–1393
Jiang L, Wang H, Ding B (2013) Disruption management recovery model of distribution delay with service priority. Asian Soc. Sci. 9(2):170–179
Jozefowiez N, Semet F, Talbi E (2008) Multi-objective vehicle routing problems. Eur. J. Oper. Res. 189:293–309
Letchford AN, Lysgaard J, Eglese RW (2007) A branch-and-cut algorithm for the capacitated open vehicle routing problem. J. Oper. Res. Soc. 58(12):1642–1651
Li JQ, Borenstein D, Mirchandani PB (2007a) A decision support system for single-depot vehicle rescheduling problem. Comput. Oper. Res. 34(4):1008–1032
Li JQ, Mirchandani PB, Borenstein D (2007b) Vehicle rescheduling problem: model and algorithms. Networks 50(3):211–229
Li JQ, Borenstein D, Mirchandani PB (2008) Truck schedule recovery for solid waste collection in Porto Alegre, Brazil. Int. Trans. Oper. Res. 15:565–582
Li JQ, Borenstein D, Mirchandani PB (2009a) Real-time vehicle rerouting problems with time windows. Eur. J. Oper. Res. 194:711–727
Li JQ, Borenstein D, Mirchandani PB (2009b) A vehicle rescheduling problem with real-time vehicle reassignments and trip cancellations. Trans. Res. Part E 45:419–433
Lust T, Teghem J (2010) The multiobjective traveling salesman problem: a survey and a new approach. In: Coello C, Dhaenens C, Jourdan L (eds) Advances in Multi-objective Nature Inspired Computing, Studies in Computational Intelligence, vol 272. Springer, Berlin, pp 119–141
Mamasis K, Minis I, Dikas G (2013) Managing vehicle breakdown incidents during urban distribution of a common product. J. Oper. Res. Soc. 64:925–937
Marler R, Arora J (2004) Survey of multi-objective optimization methods for engineering. Struct. Multidiscip. Optim. 26(6):369–395
Minis I, Mamasis K, Zeimpekis V (2012) Real-time management of vehicle breakdowns in urban freight distribution. J. Heuristics 18(3):375–400
Mu Q, Eglese R (2013) Disrupted capacitated vehicle routing problem with order release delay. Ann. Oper. Res. 207:201–216
Mu Q, Fu Z, Lysgaard J, Eglese R (2011) Disruption management of the vehicle routing problem with vehicle breakdown. J. Oper. Res. Soc. 62:742–749
Ngai EWT, Leung TKP, Wong YH, Lee MCM, Chai PYF, Choi YS (2012) Design and development of a context-aware decision support system for real-time accident handling in logistics. Decis. Support Syst. 52:816–827
Ombuki B, Ross J Band, Hanshar F (2006) Multi-objective genetic algorithms for vehicle routing problem with time windows. Appl. Intell. 24:17–30
Pillac V, Gendreau M, Gueret C, Medaglia AL (2013) A review of dynamic vehicle routing problems. Eur. J. Oper. Res. 225(1):1–11
Psaraftis HN, Wen M, Kontovas CA (2016) Dynamic vehicle routing problems: three decades and counting. Networks 67(1):3–31
Rancourt ME, Paquette J (2014) Multicriteria optimization of a long-haul routing and scheduling problem. J. Multi-Criteria Decis. Anal. 21(5–6):239–255
Solomon MM (1987) Algorithms for the vehicle-routing and scheduling problems with time window constraints. Oper. Res. 35(2):254–265
Spliet R, Gabor AF, Dekker R (2014) The vehicle rescheduling problem. Comput. Oper. Res. 43:129–136
Toth P, Vigo D (eds) (2014) Vehicle Routing: Problems, Methods, and Applications, 2nd edn. SIAM, Philadelphia
Visentini MS, Borenstein D, Li JQ, Mirchandani PB (2013) Review of real-time vehicle schedule recovery methods in transportation services. J. Sched. 17:541–567
Wang, X., Cao, H.: A dynamic vehicle routing problem with backhaul and time window. In: Proceedings of the 2008 IEEE International Conference on Service Operations and Logistics, and Informatics, pp. 1256–1261 (2008)
Wang, X., Wang, Z., Wu, X., Hu, X.: A model and an improved genetic algorithm for the vehicle routing problem with break-down vehicles. In: Fourth International Conference on Innovative Computing, Information and Control (ICICIC), pp. 696–699 (2009a)
Wang X, Xu C, Yang D (2009b) Disruption management for vehicle routing problem with the request changes of customers. Int. J. Innov. Comput. Inform. Control 5(8):2427–2438
Wang X, Ruan J, Shi Y (2012) A recovery model for combinational disruptions in logistics delivery: considering the real-world participators. Int. J. Product. Econ. 140(1):508–520
Wang XP, Wu X, Hu XP (2010) A study of urgency vehicle routing disruption management problem. J. Netw. 5(12):1426–1433
Wang, Z., Shi, J.: A model for urban distribution system under disruptions of vehicle travel time delay. In: Second International Conference on Intelligent Computation Technology and Automation, pp. 433–436 (2009)
Yu G, Qi X (2004) Disruption Management: Framework, Models and Applications. World Scientific Publishing Co. Pte Ltd, Singapore
Zhang, X., Tang, L.: Disruption management for the vehicle routing problem with time windows. In: Huang, D., Heutte, L., Loog, M. (eds.) Advanced Intelligent Computing Theories and Applications with Aspects of Contemporary Intelligent Computing Techniques, Proceedings of the Third International Conference on Intelligent Computing, ICIC 2007, Qingdao, vol. 2, pp. 225–234 (2007)
Author information
Authors and Affiliations
Corresponding author
Additional information
This invited paper is discussed in the comments available at https://doi.org/10.1007/s11750-018-0466-7, https://doi.org/10.1007/s11750-018-0467-6, and https://doi.org/10.1007/s11750-018-0468-5.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Eglese, R., Zambirinis, S. Disruption management in vehicle routing and scheduling for road freight transport: a review. TOP 26, 1–17 (2018). https://doi.org/10.1007/s11750-018-0469-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11750-018-0469-4