Estimation of stability index for symmetric $\alpha$-stable distribution using quantile conditional variance ratios

Abstract

The class of $\alpha$-stable distributions is widely used in various applications, especially for modeling heavy-tailed data. Although the $\alpha$-stable distributions have been used in practice for many years, new methods for identification, testing, and estimation are still being refined and new approaches are being proposed. The constant development of new statistical methods is related to the low efficiency of existing algorithms, especially when the underlying sample is small or the distribution is close to Gaussian. In this paper, we propose a new estimation algorithm for the stability index, for samples from the symmetric $\alpha$-stable distribution. The proposed approach is based on a quantile conditional variance ratio. We study the statistical properties of the proposed estimation procedure and show empirically that our methodology often outperforms other commonly used estimation algorithms. Moreover, we show that our statistic extracts unique sample characteristics that can be combined with other methods to refine existing methodologies via ensemble methods. Although our focus is set on the symmetric $\alpha$-stable case, we demonstrate that the considered statistic is insensitive to the skewness parameter change, so our method could be also used in a more generic framework. For completeness, we also show how to apply our method to real data linked to financial market and plasma physics.

1 Introduction

The $\alpha$-stable distributions are an important modeling tool as they constitute a domain of attraction for sums of independent random variables. That is, if the sum of independent and identically distributed (i.i.d.) random variables converges in distribution, then the limiting distribution belongs to the $\alpha$-stable family by the generalized Central Limit Theorem, see (Lévy 1924; Khinchine and Lévy 1936; Shao and Nikias 1993), and Samorodnitsky and Taqqu (1994) for classical references. The family of $\alpha$-stable probability distribution is often used to describe the generalized white noise, without any assumptions imposed on the underlying moments; note that the sums of i.i.d. $\alpha$-stable random variables retain the shape of the original distribution, which is known as the stability property, see (Feller 1971) and Jakubowski and Kobus (1989).

The first applications of the $\alpha$-stable distributions were related to generic financial data description and telephone line noise modeling, see (Mandelbrot 1960) and Chambers et al. (1976). Since the 1990 s, the $\alpha$-stable distributions have found numerous other applications linked e.g. to financial markets, telecommunications, condition monitoring, physics, biology, medicine, and climate dynamics, see (Rachev and Mittnik 2000; Bidarkota et al. 2009; Yu et al. 2013; Żak et al. 2017, 2016; Majka and Góra 2015; Kosko and Mitaim 2004; Barthelemy et al. 2008; Sokolov et al. 1997; Lomholt et al. 2005), and references therein. See also (Nikias and Shao 1995; Janicki and Weron 1994; Wegman et al. 1989; Nolan 2020; Durrett et al. 2011; Lan and Toda 2013; Peng et al. 1993; Ditlevsen 1999) for classical positions on $\alpha$-stable distributed processes.

In general, the $\alpha$-stable distributions are characterized by four parameters corresponding to location, scale, tail structure, and symmetry. In this paper, we consider symmetric $\alpha$-stable distributions and focus on the modeling of the tail index $\alpha \in (0,2]$, also called the stability index, responsible for the tail power-law behavior of the $\alpha$-stable distribution, see (Nolan 2020). For $\alpha <2$, the $\alpha$-stable distribution belongs to the wide class of the heavy-tailed distributions and in this case the corresponding random variable has infinite variance; the smaller the value of $\alpha$, the heavier the tail. On the other hand, for $\alpha =2$, the $\alpha$-stable distribution reduces to the Gaussian distribution. Also, it should be noted that in general the probability density function (PDF) of the $\alpha$-stable distribution is not given in an explicit form, and the distribution structure is typically expressed via its characteristic function.

In this paper, we consider the problem of statistical estimation of the stability index for the symmetric $\alpha$-stable distribution. The estimation problem has been studied by many authors for more than 50 years and one can find various approaches in the literature. The most recognized methods are linked to quantiles, see e.g. (Fama and Roll 1971; McCulloch 1986; Dominicy and Veredas 2013; Huixia et al. 2012; Leitch and Paulson 1975), characteristic functions, see e.g. (Press 1972; Cizek et al. 2005; Koutrouvelis 1980; Kogon and Williams 1998; Mohammadreza et al. 2017; Arad 1980; Paulson et al. 1975), maximum likelihood, see e.g. (DuMouchel 1973; Nolan 2001; Mittnik et al. 1999; Muneya and Akimichi 2006; Brorsen and Yang 1990), Hill’s estimators, see e.g. (Pictet et al. 1998; Pickands 1975; de Haan and Resnick 1980; Dekkers et al. 1990; Resnick 1997), fractional lower order moments or log-moments, see e.g. (Zolotarev 1981; Ma and Nikias 1995; Kuruoglu 2001; Kateregga et al. 2017), and other techniques tailored for the $\alpha$-stable distributions, see e.g. (Lombardi and Godsill 2006; Escobar-Bach et al. 2017; Teimouri et al. 2018; Garcia et al. 2011; Tsihrintzis and Nikias 1996; Sathe and Upadhye 2020; de Haan and Themido Pereira 1999; Matsui and Takemura 2008). Also, we refer to Akgiray and Lamoureux (1989) for a comparative study of the estimation algorithms for the $\alpha$-stable distribution.

While most of the considered estimators have nice theoretical properties and their asymptotic behavior is well studied, they are not very effective when applied to practical data. This is mainly due to the fact that, for $\alpha$-stable distributed data, most estimation algorithms require a large sample size and substantial computational power to be effective. This is especially visible when the stability index is close to 2, i.e. when the $\alpha$-stable distribution tends to the Gaussian distribution. The related problem of discriminating the $\alpha$-stable distribution from the Gaussian one was discussed in the literature e.g. in Burnecki et al. (2012, 2015); Pitera et al. (2022); Wyłomańska et al. (2020).

To overcome the problem of small sample size, the lack of the explicit form of PDF, and the infinite variance of the underlying sample, the approach proposed in this paper is based on the quantile conditional variance (QCV) class of statistics. The QCV-based methods have been recently used mainly in the context of goodness-of-fit testing or to explain empirical phenomena such as the 20/60/20 rule, see (Jelito and Pitera 2021; Jaworski and Pitera 2016). Also, this methodology has been recently applied for local damage detection based on the signals with heavy-tailed background noise or studies on the asymptotic behavior of empirical processes; see (Hebda-Sobkowicz et al. 2020, Hebda-Sobkowicz et al. 2020, Ghoudi 2018).

Although the theoretical variance for the $\alpha$-stable distribution with $\alpha <2$ is infinite, the QCV always exists and can be used to characterize the $\alpha$-stable distribution up to the location, see (Jaworski and Pitera 2020). Here, we extend the $\alpha$-stable distribution goodness-of-fit methodology proposed in Pitera et al. (2022) and show that it can be effectively used for $\alpha$-stable tail index estimation in the symmetric case. While our approach can be generally classified as the quantile method, we show that it is more effective in terms of the root mean square error when compared to the commonly used algorithms proposed in McCulloch (1986). This is mainly due to the fact that QCV gathers information about multiple quantiles at the same time and better reflects the tail structure. Moreover, the empirical QCV-based ratio statistics proposed in this paper are easy to implement as they are based on sample QCV. This makes our approach effective for small samples and computationally effective. In addition, our data study shows that the QCV approach could be successfully applied to estimate the tail index in the near-Gaussian environment, i.e. when the true stability index is close to 2. As already mentioned, in this paper we focus on the tail index estimation for the symmetric $\alpha$-stable distributions when the location and scale are unknown. However, we also demonstrate that the proposed approach is in fact insensitive to the skewness parameter changes and could be easily extended to a general setting. Finally, it is worth mentioning that the QCV approach extracts sample characteristics different to the ones extracted by other estimation procedures such as the regression methods. Consequently, the QCV approach could also be used to refine the existing frameworks, e.g. via ensemble learning, see (Polikar 2006) and references therein.

The rest of the paper is organized as follows. In Sect. 2, we recall the definition of the symmetric $\alpha$-stable distribution as well as the main facts related to the corresponding tail behavior. Moreover, we discuss the characterization of the $\alpha$-stable distribution via the conditional variance. Next, in Sect. 3 we analyze the sample QCV for the $\alpha$-stable distribution and introduce the estimation technique based on the QCV approach. In Sect. 4 we present the simulation study where for Monte Carlo simulated samples we demonstrate the efficiency of the methodology proposed. In this section, we compare the results with the benchmark methods. By simulation study, we also demonstrate the robustness of the methodology in question for the skewness parameters change. Then, for empirical illustration, in Sect. 5 we perform $\alpha$-parameter fitting for two empirical datasets from financial market and plasma physics. Finally, we provide concluding remarks in Sect. 6.

2 The symmetric $\alpha$-stable distribution

There are many ways to define the family of $\alpha$-stable distributions. In this paper we use the 0-parametrization and follow the characteristic function approach, see Section 1.3 in Nolan (2020) in which other parametrizations are stated. Namely, we say that the random variable X follows the $\alpha$-stable distribution with parameters $\alpha \in (0,2]$, $\beta \in [-1,1]$, $c > 0$, $\mu \in {\mathbb {R}}$ and write $X \sim S(\alpha , \beta ,c,\mu )$ if its characteristic function is given by

$$\begin{aligned} \phi (u)= & {} {\mathbb {E}}( \exp (iuX)) \nonumber \\= & {} {\left\{ \begin{array}{ll} \exp \left( -c^\alpha |u|^\alpha \left( 1 + i\beta {{\,\textrm{sgn}\,}}(u) \tan \frac{\pi \alpha }{2}\left( |cu|^{1-\alpha } - 1 \right) \right) + i \mu u \right) &{} \text {if } \alpha \ne 1,\\ \exp \left( -c|u| \left( 1 + i\beta \frac{2}{\pi }{{\,\textrm{sgn}\,}}(u) \log \left( c|u|\right) \right) + i\mu u\right) &{} \text {if } \alpha = 1. \end{array}\right. } \nonumber \\ \end{aligned}$$

(1)

The parameter $\alpha \in (0,2]$ is linked to the stability index, i.e. it determines the rate at which the tails of the distribution diminish; see Theorem 1.2 in Nolan (2020) for details. Note that for $\alpha = 2$, the $\alpha$-stable distribution simplifies to the Gaussian distribution with the expectation equals $\mu$ and the variance equals $2c^2$. The parameter $\beta \in [-1,1]$ is used to quantify the skewness of the heavy-tailed distribution. However, note that the classical Pearson’s skewness coefficient is undefined for $\alpha <2$. In particular, for $\beta >0$ ($\beta <0$, respectively) the $\alpha$-stable distribution is skewed to the right (left, respectively) and if $\beta = 0$, then the $\alpha$-stable distribution is symmetric around the location parameter $\mu \in {\mathbb {R}}$. The coefficient $c>0$ is the scale parameter, see (Samorodnitsky and Taqqu 1994; Janicki and Weron 1994).

In the following, we focus on the normalized and symmetric $\alpha$-stable distributions, i.e. we assume that $X\sim S(\alpha ,0,1,0)$ with $\alpha \in (0,2]$. Note that the location-scale normalization is made only to streamline the narrative of this paper which is focused on the tail-index estimation. In fact, the conditional variance ratio-based fitting statistic ${{\hat{N}}}$ that will be introduced in Sect. 3 will be location-scale invariant, so that our framework could be used in the general symmetric setting. In the following, for brevity, we write $X\sim S\alpha S$ and say that X follows the symmetric $\alpha$-stable distribution. For any $\alpha \in (0,2]$, we use $F_{\alpha }(\cdot )$, $f_{\alpha }(\cdot )$, and $Q_{\alpha }(\cdot )$, to denote the cumulative distribution function (CDF), the probability density function (PDF), and the quantile function (inverse CDF) of the symmetric $\alpha$-stable distribution, respectively. Note that the explicit formula for PDF of $S\alpha S$ is known only for the Gaussian distribution ($\alpha =2$) and the Cauchy distribution ($\alpha =1$). However, it is possible to provide an integral representation of $f_{\alpha }(\cdot )$. Namely, from Theorem 3.2 in Nolan (2020), for $\alpha \in (0,2)$, we have

$$\begin{aligned} f_\alpha (x) = \frac{1}{\pi } \int _0^\infty \cos (xt) \exp (-t^\alpha )dt, \quad x\in {\mathbb {R}}. \end{aligned}$$

(2)

2.1 Tails of the symmetric $\alpha$-stable distribution

Let us now focus on the asymptotic behavior of the symmetric $\alpha$-stable distribution with $\alpha \in (0,2)$. As stated in Theorem 1.2 in Nolan (2020), the tails of $S\alpha S$ distribution with $\alpha \in (0,2)$ could be characterized using power law dynamics with an additional exponent factor linked to the parameter $\alpha$. For transparency, we recall this result in Theorem 1. Note that here we use a simplified notation $f(x)\overset{x\rightarrow x_0}{\sim }\ g(x)$ whenever $\lim _{x\rightarrow x_0}\frac{f(x)}{g(x)}=1$ and $\Gamma (\cdot )$ to denote the Gamma function. Also, note that a similar characterization of the normal distribution tails could be found in Lemma 2 in Chapter VII of Feller (1968).

Theorem 1

For any $\alpha \in (0,2)$, $X\sim S\alpha S$, and $c_\alpha := \sin (\frac{\pi \alpha }{2}) \Gamma (\alpha )/\pi$, we get

$$\begin{aligned} {\mathbb {P}}[X > x] \overset{x\rightarrow \infty }{\sim }\ c_\alpha x^{-\alpha }\quad \text {and} \quad f_{\alpha }(x) \overset{x\rightarrow \infty }{\sim }\ \alpha x^{-(\alpha +1)}. \end{aligned}$$

(3)

Next, in Proposition 2, we state the asymptotic behavior of the quantile function of the symmetric $\alpha$-stable distribution for $\alpha \in (0,2)$. This could be seen as a complementary result to Theorem 1. Note that a similar asymptotic characterization for the normal quantile function could be found in Example 8.13 in DasGupta (2008). The proof of Proposition 2 is deferred to Appendix B.

Proposition 2

For any $\alpha \in (0,2)$ and ${\bar{c}}_{\alpha }:=\left( \frac{\Gamma (\alpha )\sin (\pi \alpha /2)}{\pi } \right) ^{1/\alpha }$, we get

$$\begin{aligned} Q_{\alpha }(p) \overset{p\rightarrow 1^-}{\sim } {\bar{c}}_{\alpha }(1-p)^{-1/\alpha }. \end{aligned}$$

Using Proposition 2 we can show that, for quantile levels p high enough, the quantiles curves $(p,Q_{\alpha }(p))$ are monotone with respect to the parameter $\alpha$; see Proposition 3 for details and Fig. 1 for a numerical illustration. This shows that the observation stated in Theorem 1.2 in Nolan (2020), which links the parameter $\alpha$ to the tail thickness, could be expressed in terms of the quantile functions. Also, note that this result could be associated with the concept of the first order tail stochastic dominance, see (Zieliński 2001; Ortobelli et al. 2016; Bednorz et al. 2021) for some other results on the stochastic ordering in reference to $\alpha$-stable distributions. The proof of Proposition 3 is deferred to Appendix B.

Fig. 1

Plots of the quantile functions $Q_{\alpha }(\cdot )$ for $\alpha \in \{0.1,0.5,1,1.5,2\}$. The left panel shows the full domain $p\in (0,1)$, while the right panel shows the sub-domain $p\in [0.6,0.9]$. The dashed vertical line corresponds to the quantile level $p_0=0.75$. Note that, for $p\ge 0.75$, we can see that the quantile curves $(p,Q_{\alpha }(p))$ do not cross each other which indicates that quantile values are monotone with respect to the tail index $\alpha$, as stated in Proposition 3

Proposition 3

For any $\alpha _1,\alpha _2\in (0,2]$ satisfying $\alpha _1<\alpha _2$ there exists $p_0\in (1/2,1)$ such that for any $p\in [p_0,1)$ we get

$$\begin{aligned} Q_{\alpha _1}(p)>Q_{\alpha _2}(p). \end{aligned}$$

(4)

Remark 4

From simulations, we see that the constant $p_0\in (1/2,1)$ from Proposition 3 can be chosen independently of $\alpha _1$ and $\alpha _2$, and it satisfies the inequality $p_0\le 0.75$; see Fig. 1. The difficulty of analytical calculation of $p_0$ could be linked to the fact that the proof of Proposition 3 is based on the tail approximation of the quantile function; cf. Theorem 1.2 in Nolan (2020) and Proposition 2 in this paper. Since we were not able to find $p_0$ analytically, we deduced it from the numerical studies. We refer to Theorem 1.2 in Nolan (2020) and the following remarks for more information on technical calculation difficulties for $\alpha$-stable distribution tails; see also the discussion after Equation 3.2 in Fama and Roll (1971).

Remark 5

From Proposition 3 and Remark 4 we see that the quantile function values are monotone with respect to the tail index for sufficiently large quantile levels. This result should be compared with Zieliński (2001), where the full-domain dispersive ordering result for the stable distributions is shown. However, this result is stated in the 2-parametrization while in this paper we follow the 0-parametrization. In fact, as seen in Fig. 1, the full-domain ordering does not hold for the 0-parametrization, so the result from Zieliński (2001) cannot be extended to our setting. We refer to Proposition 3.7 in Nolan (2020) as well as to the following discussion for more details about various parametrizations of the $\alpha$-stable distribution family.

2.2 Quantile conditional variance for $\alpha$-stable distributed random variables

In this section, we discuss the conditional variance characterization of the symmetric $\alpha$-stable distributions. Let us consider a generic $X\sim S\alpha S$ with some $\alpha \in (0,2]$. For any $0<a<b<1$, we define the quantile conditioning set $M_{\alpha }(a,b):=\{X\in ( Q_{\alpha }(a),Q_{\alpha }(b))\}$. The quantile conditional mean (QCM) and the quantile conditional variance (QCV) of X on $M_{\alpha }(a,b)$ are given by

$$\begin{aligned} \mu _\alpha (a,b)&:= {\mathbb {E}}[X| M_\alpha (a,b) ], \end{aligned}$$

(5)

$$\begin{aligned} \sigma _\alpha ^2(a,b)&:={\mathbb {E}}[X^2| M_\alpha (a,b)]-({\mathbb {E}}[X| M_\alpha (a,b)])^2, \end{aligned}$$

(6)

Note that $\sigma ^2_{\alpha }(a,b)$ is simply the quantile trimmed variance of X, i.e. the conditional variance on the quantile interval $( Q_{\alpha }(a),Q_{\alpha }(b)]$. Also, note that for any $\alpha \in (0,2]$ and $0<a<b<1$, the quantile conditional mean $\mu _\alpha (a,b)$ and the quantile conditional variance $\sigma ^2_{\alpha }(a,b)$ are well-defined and finite. The family $(\sigma ^2_{\alpha }(a,b))_{a,b}$ characterizes the $\alpha$-stable distribution up to an additive shift, see (Pitera et al. 2022) for details.

To compute the value of QCV one may use the representation based on the probability density or quantile functions. More specifically, recalling that X is absolutely continuous with the density $f_\alpha (\cdot )$ and using (6) with $p=Q_{\alpha }(x)$, we get

$$\begin{aligned} \sigma ^2_{\alpha }(a,b)&=\frac{1}{b-a}\int _{Q_{\alpha }(a)}^{Q_{\alpha }(b)} x^2 f_{\alpha }(x)dx-\left( \frac{1}{b-a}\int _{Q_{\alpha }(a)}^{Q_{\alpha }(b)} x f_{\alpha }(x)dx\right) ^2 \nonumber \\&=\frac{1}{b-a}\int _{a}^{b} (Q_{\alpha }(p))^2 dp-\left( \frac{1}{b-a}\int _{a}^{b} Q_{\alpha }(p)dp\right) ^2. \end{aligned}$$

(7)

As expected, the explicit formula for $\sigma ^2_{\alpha }(a,b)$ could be derived only for the Gaussian ($\alpha =2$) and the Cauchy ($\alpha =1$) distributions, see (Pitera et al. 2022). Namely, for the Gaussian case, i.e. $X\sim S\alpha S$ with $\alpha =2$, we get

$$\begin{aligned} \sigma ^2_2(a,b)= & {} 2 \left( \frac{\Phi ^{-1}(a) \phi (\Phi ^{-1}(a)) - \Phi ^{-1}(b)\phi (\Phi ^{-1}(b))}{b-a}\right. \nonumber \\{} & {} \left. - \frac{\left( \phi \left( \Phi ^{-1}(a) \right) - \phi \left( \Phi ^{-1}(b) \right) \right) ^2}{(b-a)^2} \right) , \end{aligned}$$

(8)

where $\phi (\cdot )$ and $\Phi (\cdot )$ are standard Gaussian PDF and CDF, respectively, while for the Cauchy case, i.e. $X\sim S\alpha S$ with $\alpha =1$, we get

$$\begin{aligned} \sigma ^2_1(a,b)= & {} \frac{1}{b-a}\left( \frac{F_1^{-1}(b) - F_1^{-1}(a)}{D(a,b)} - 1\right) \nonumber \\{} & {} - \frac{1}{4D^2(a,b)(b-a)^2} \log ^2 \left( \frac{1+F_1^{-1}(b)^2}{1+F_1^{-1}(a)^2} \right) , \end{aligned}$$

(9)

where $D(a,b):= \tan ^{-1} \left( F_1^{-1}(b)\right) - \tan ^{-1} \left( F_1^{-1}(a)\right)$.

Recalling that the smaller the tail index $\alpha$, the heavier the tails, we expect that the quantile conditional variance on an appropriately chosen tail set should be monotone with respect to $\alpha$. Consequently, QCV could be used to measure the heaviness of the tail of the symmetric $\alpha$-stable distributions. This intuition is formalized in Theorem 6; see also Fig. 2 for a numerical illustration.

Fig. 2

Plots of the conditional variances $\sigma ^2_{\alpha }(a,b)$ as functions of $\alpha$ with various a and b. The curves are based on the Monte Carlo simulations with 1 000 000 replications each. As seen on the left panel, if a and b satisfy $0.65\le a< b<1$, then we get that the map $\alpha \rightarrow \sigma ^2_{\alpha }(a,b)$ is decreasing. However, as seen on the right panel, if $a<0.65$, this property may not hold

Theorem 6

Let $\alpha _1,\alpha _2\in (0,2]$ be such that $\alpha _1<\alpha _2$. Then, there exists $p_1\in (1/2,1)$ such that, for any $a,b\in [p_1,1)$ satisfying $a<b$, we get

$$\begin{aligned} \sigma ^2_{\alpha _1}(a,b)>\sigma ^2_{\alpha _2}(a,b). \end{aligned}$$

Proof

Let us fix $\alpha _1,\alpha _2\in (0,2]$ satisfying $\alpha _1<\alpha _2$. Note that, recalling (7), for any $a,b\in [1/2,1)$ satisfying $a<b$, we get

$$\begin{aligned}&\sigma ^2_{\alpha _1}(a,b)-\sigma ^2_{\alpha _2}(a,b)\nonumber \\&=\frac{1}{b-a}\int _{a}^{b} (Q_{\alpha _1}(p)-Q_{\alpha _2}(p))(Q_{\alpha _1}(p)+Q_{\alpha _2}(p)) dp\nonumber \\&\qquad -\left( \frac{1}{b-a}\int _{a}^{b} (Q_{\alpha _1}(p)-Q_{\alpha _2}(p)) dp\right) \nonumber \\&\qquad \left( \frac{1}{b-a}\int _{a}^{b} (Q_{\alpha _1}(p)+Q_{\alpha _2}(p))dp\right) . \end{aligned}$$

(10)

Let us define $g(\cdot ):=Q_{\alpha _1}(\cdot )-Q_{\alpha _2}(\cdot )$ and $h(\cdot ):=Q_{\alpha _1}(\cdot )+Q_{\alpha _2}(\cdot )$, and note that (10) could be expressed as

$$\begin{aligned} \sigma ^2_{\alpha _1}(a,b)-\sigma ^2_{\alpha _2}(a,b)= & {} \frac{1}{b-a}\int _{a}^{b} g(p) h(p) d p\\{} & {} - \left( \frac{1}{b-a} \int _{a}^{b} g(p) d p \right) \left( \frac{1}{b-a} \int _{a}^{b} h(p) d p \right) . \end{aligned}$$

Then, it is enough to show that $g(\cdot )$ and $h(\cdot )$ are (strictly) increasing. Indeed, using the classic Chebyshev integral inequality (see e.g. Theorem 8 in Section 2.5 of Mitrinović (1970)), from the monotonicity of $g(\cdot )$ and $h(\cdot )$, we get $\frac{1}{b-a} \int _{a}^{b} g(x) h(x) d x > \left( \frac{1}{b-a} \int _{a}^{b} g(x) d x \right) \left( \frac{1}{b-a} \int _{a}^{b} h(x) d x \right)$, which shows $\sigma ^2_{\alpha _1}(a,b)-\sigma ^2_{\alpha _2}(a,b)>0$. Note that $h(\cdot )$ is increasing as the sum of the increasing functions $Q_{\alpha _1}(\cdot )$ and $Q_{\alpha _2}(\cdot )$. Thus, to conclude the proof it is enough to show that $g(\cdot )$ is increasing. Recalling that $Q_{\alpha }(\cdot )$ is the inverse of $F_{\alpha }(\cdot )$, we get

$$\begin{aligned} \frac{d g}{dp}(p)=\frac{1}{f_{\alpha _1}(Q_{\alpha _1}(p))}-\frac{1}{f_{\alpha _2}(Q_{\alpha _2}(p))}, \quad p\in (1/2,1). \end{aligned}$$

Thus, for any $p\in (1/2,1)$, we get $\frac{d g}{dp}(p)>0$ if and only if $f_{\alpha _1}(Q_{\alpha _1}(p))<f_{\alpha _2}(Q_{\alpha _2}(p))$. Consequently, it is enough to show that

$$\begin{aligned} \lim _{p\rightarrow 1^-} \frac{f_{\alpha _2}(Q_{\alpha _2}(p))}{f_{\alpha _1}(Q_{\alpha _1}(p))}=\infty . \end{aligned}$$

(11)

Indeed, the identity (11) implies that, starting from some $p_1\in (1/2,1)$, we get $\frac{dg}{dp}(p)>0$, and consequently the map $p\mapsto g(p)$ is (strictly) increasing on $[p_1,1)$.

Now, let us show (11). For completeness, separate arguments for $\alpha _2<2$ and $\alpha _2=2$ are provided. For $\alpha _2 < 2$, using Theorem 1 and Proposition 2, we get

$$\begin{aligned}&\lim _{p\rightarrow 1^-} \frac{f_{\alpha _2}(Q_{\alpha _2}(p))}{f_{\alpha _1}(Q_{\alpha _1}(p))}\nonumber \\&= \lim _{p\rightarrow 1^-} \frac{f_{\alpha _2}(Q_{\alpha _2}(p))}{\alpha _2 {c}_{\alpha _2}(Q_{\alpha _2}(p))^{-(\alpha _2 +1)}} \cdot \frac{\alpha _1 {c}_{\alpha _1}(Q_{\alpha _1}(p))^{-(\alpha _1 +1)}}{f_{\alpha _1}(Q_{\alpha _1}(p))}\cdot \frac{\alpha _2 {c}_{\alpha _2}(Q_{\alpha _2}(p))^{-(\alpha _2 +1)}}{\alpha _1 {c}_{\alpha _1}(Q_{\alpha _1}(p))^{-(\alpha _1 +1)}} \nonumber \\&=\frac{\alpha _2{c}_{\alpha _2}}{\alpha _1 {c}_{\alpha _1}}\lim _{p\rightarrow 1^-} \frac{(Q_{\alpha _2}(p))^{-(\alpha _2 +1)}}{(Q_{\alpha _1}(p))^{-(\alpha _1 +1)}} \nonumber \\&=\frac{\alpha _2{c}_{\alpha _2}}{\alpha _1 {c}_{\alpha _1}}\lim _{p\rightarrow 1^-} \left( \frac{Q_{\alpha _2}(p)}{{\bar{c}}_{\alpha _2}(1-p)^{-1/\alpha _2}}\right) ^{-(\alpha _2 +1)}\cdot \left( \frac{{\bar{c}}_{\alpha _1}(1-p)^{-1/\alpha _1}}{Q_{\alpha _1}(p)}\right) ^{-(\alpha _1 +1)}\nonumber \\&\qquad \cdot \frac{\left( {\bar{c}}_{\alpha _2}(1-p)^{-1/\alpha _2}\right) ^{-(\alpha _2+1)}}{\left( {\bar{c}}_{\alpha _1}(1-p)^{-1/\alpha _1}\right) ^{-(\alpha _1+1)}} \nonumber \\&=\frac{\alpha _2{c}_{\alpha _2}({\bar{c}}_{\alpha _1})^{\alpha _1+1}}{\alpha _1 {c}_{\alpha _2}({\bar{c}}_{\alpha _2})^{\alpha _2+1}} \lim _{p\rightarrow 1^-} (1-p)^{1/\alpha _2-1/\alpha _1}. \end{aligned}$$

(12)

Recalling that $\alpha _1<\alpha _2$, we get $\lim _{p\rightarrow 1^-} (1-p)^{1/\alpha _2-1/\alpha _1} = \infty$, which concludes the proof in this case.

Next, assume $\alpha _2 = 2$. Noting that the map $[0,\infty )\ni x\mapsto f_2(x)$ is decreasing and using Proposition 3, as in (12), we obtain

$$\begin{aligned}&\lim _{p\rightarrow 1^-} \frac{f_{2}(Q_{2}(p))}{f_{\alpha _1}(Q_{\alpha _1}(p))} \ge \lim _{p\rightarrow 1^-} \frac{f_{2}(Q_{\alpha _1}(p))}{f_{\alpha _1}(Q_{\alpha _1}(p))} \\&= \lim _{p\rightarrow 1^-} \frac{e^{-\frac{1}{4}(Q_{\alpha _1}(p))^2}}{f_{\alpha _1}(Q_{\alpha _1}(p))} = \frac{({\bar{c}}_{\alpha _1})^{\alpha _1+1}}{\alpha _1} \lim _{p\rightarrow 1^-} \frac{e^{-\frac{1}{4}((Q_{\alpha _1}(p))^2}}{(1-p)^{1+1/\alpha _1}}. \end{aligned}$$

Consequently, by considering the logarithm of the last ratio, we get that to prove $\frac{f_{2}(Q_{\alpha _1}(p))}{f_{\alpha _1}(Q_{\alpha _1}(p))}=\infty$, it is enough to show $\lim _{p\rightarrow 1^-} \left( \!-\frac{1}{4} (Q_{\alpha _1}(p))^2 - \ln \left( (1-p)^{1+\frac{1}{\alpha _1}}\!\right) \!\right) = \infty$ or equivalently

$$\begin{aligned} \lim _{p\rightarrow 1^-} \left( (Q_{\alpha _1}(p))^2 +4 \ln \left( (1-p)^{1+\frac{1}{\alpha _1}}\right) \right) = -\infty . \end{aligned}$$

(13)

Recalling that $Q_{\alpha _1}(p)\sim {\bar{c}}_{\alpha _1} (1-p)^{-1/\alpha _1 }$ due to Proposition 3, it is enough to prove

$$\begin{aligned} \lim _{p\rightarrow 1^-}\left( ({\bar{c}}_{\alpha _1} (1-p)^{-1/\alpha _1 })^2 + 4\left( \! 1 + \frac{1}{\alpha _1}\!\right) \ln (1-p)\!\right) = -\infty . \end{aligned}$$

(14)

Using substitution $x:=1-p$, we get

$$\begin{aligned}{} & {} \lim _{p\rightarrow 1^-}\left( ({\bar{c}}_{\alpha _1} (1-p)^{-1/\alpha _1 })^2 + 4\left( 1 + \frac{1}{\alpha _1}\right) \ln (1-p)\right) \\{} & {} \quad = \lim _{x\rightarrow 0^+}\left( ({\bar{c}}_{\alpha _1})^2 x^{-2/\alpha _1 } + 4\left( 1 + \frac{1}{\alpha _1}\right) \ln x\right) \ \\{} & {} \quad = \lim _{x\rightarrow 0^+}\frac{1+({\bar{c}}_{\alpha _1})^{-2} x^{2/\alpha _1 } 4\left( 1 + \frac{1}{\alpha _1}\right) \ln x}{({\bar{c}}_{\alpha _1})^{-2} x^{2/\alpha _1 } }. \end{aligned}$$

Then, applying L’Hôpital’s rule, we obtain

$$\begin{aligned}{} & {} \lim _{x\rightarrow 0^+}\frac{1+({\bar{c}}_{\alpha _1})^{-2} x^{2/\alpha _1 } 4\left( 1 + \frac{1}{\alpha _1}\right) \ln x}{({\bar{c}}_{\alpha _1})^{-2} x^{2/\alpha _1 } } \\{} & {} \quad = 4\left( 1 + \frac{1}{\alpha _1}\right) \lim _{x\rightarrow 0^+}\frac{ \frac{2}{\alpha _1} x^{\frac{2}{\alpha _1} - 1} \ln x + x^{\frac{2}{\alpha _1} - 1}}{\frac{2}{\alpha _1}x^{\frac{2}{\alpha _1} -1}} \\{} & {} \quad = 4\left( 1 + \frac{1}{\alpha _1}\right) \lim _{x\rightarrow 0^+}\left( \frac{2}{\alpha _1} \ln x+1\right) =-\infty , \end{aligned}$$

which shows (14) and concludes the proof. $\square$

Remark 7

From simulations, we get that the constant $p_1\in (1/2,1)$ from Theorem 6 can be chosen independently of $\alpha _1$ and $\alpha _2$, and it satisfies the inequality $p_1\le 0.65$. On the other hand, if the quantile level is smaller than 0.65, then the monotonicity condition from Theorem 6 may be violated. Indeed, a numerical check shows that $\sigma ^2_{0.5}(0.25,0.75)\approx 0.28$ and $\sigma ^2_{1}(0.25,0.75)\approx 0.275$, while $\sigma ^2_{1.5}(0.25,0.75)\approx 0.285$. For transparency, these observations are illustrated in Fig. 2. The left panel shows exemplary choices of $0.65\le a<b<1$ for which we can see that the map $\alpha \mapsto \sigma ^2_{\alpha }(a,b)$ is decreasing while the right panel shows several other cases in which this property is violated.

2.3 Extracting the tail index using a quantile conditional variance ratio

From Theorem 6 combined with Remark 7 we learn that for $X\sim S\alpha S$ and adequately chosen tail quantile split values $0<a<b<1$, the function $G_1(\alpha ):=\sigma ^2_\alpha (a,b)$ should be monotone. Moreover, one would expect that for a central quantile split $(d,1-d)$, where $0<d<0.5$ is relatively close to 0.5, the rate of change of the function $G_2(\alpha ):=\sigma ^2_\alpha (d,1-d)$ is smaller when compared to $G_1$ in a sense that for any $\alpha \in (0,2]$ we get

$$\begin{aligned} \left| \frac{\partial }{\partial \alpha }G_1(\alpha )\right| > \left| \frac{\partial }{\partial \alpha }G_2(\alpha )\right| . \end{aligned}$$

(15)

Thus, given the split (a, b, d), we can define the variance ratio function $N:(0,2]\rightarrow {\mathbb {R}}_{+}$,

$$\begin{aligned} N(\alpha ):= & {} 2\frac{G_1(\alpha )}{G_2(\alpha )} =2\frac{\sigma ^2_\alpha (a,b)}{\sigma ^2_\alpha (d,1-d)}\nonumber \\= & {} \frac{\sigma ^2_\alpha (a,b)+\sigma ^2_\alpha (1-b,1-a)}{\sigma ^2_\alpha (d,1-d)}; \end{aligned}$$

(16)

note that the last equality follows from the fact that for the symmetric $\alpha$-stable distribution we always get $\sigma ^2_\alpha (a,b)=\sigma ^2_\alpha (1-b,1-a)$. The function N defined in (16) is expected to be strictly monotone with respect to $\alpha$. While the direct proof of the monotonicity of (16) is challenging due to the theoretical difficulties stated in Remark 4 and Remark 7, one could numerically verify its monotonicity for a given set of (a, b, d) e.g. by approximating the related integrals. This is illustrated in Fig. 3. Assuming the strict monotonicity, we can easily recover the value of $\alpha$ given the value of $N(\alpha )$ by using the inverse transform $N^{-1}(\cdot )$. This intuition will be used to construct a fitting statistic in Sect. 3.

Also, noting that $N(\cdot )$ is invariant with respect to the affine transformations of the underlying random variable X, one could use values of $N(\cdot )$ to extract the value of the tail index $\alpha$ within the general class of symmetric $\alpha$-stable random variables $X\sim S(\alpha ,0,c,\mu )$. In other words, while the value $N(\alpha )$ depends strongly on tail index $\alpha \in (0,2]$, it is invariant with respect to scale $c >0$ and location $\mu \in {\mathbb {R}}$, so that this fitting statistic could by used for tail-index extraction.

Fig. 3

Dynamics of $G_1(\alpha )=\sigma ^2_\alpha (a,b)$, $G_2(\alpha )=\sigma ^2_\alpha (d,1-d)$, and $N(\alpha )=2G_1(\alpha )/G_2(\alpha )$ for various choices of (a, b, d). The left panel presents the values of the function $G_1(\cdot )$ for $(a,b)\in \{(0.01,0.25),(0.01,0.15),(0.05,0.35)\}$. The middle panel presents the value of $G_2(\cdot )$ for $d\in \{0.1,0.25,0.30\}$. The right panel presents the ratio values of $N(\cdot )$ for $(a,b,d)\in \{(0.01,0.25,0.25),(0.01,0.15,0.1)\}$. As one can observe, the function $N(\cdot )$ seems to be monotone with respect to $\alpha$ for adequately chosen values of (a, b, d), which is expected due to (15). In particular, the variability of $G_1$ is much bigger than the variability of $G_2$ for the chosen parameters in the sense that the monotonicity of $G_1$ induces monotonicity of N; note y-axis scale difference in the plots

3 Conditional variance as fitting statistics

In this section, we show how to use the variance ratio function $N(\cdot )$ introduced in (16) for tail index parameter fitting. First, let us introduce the statistical framework and recall the basic properties of the sample QCV estimator. Given $n\in {\mathbb {N}}$, i.i.d sample $(X_1,...X_n)$, and quantile split $0< a< b < 1$, the sample QCV estimator is given by

$$\begin{aligned} {\hat{\sigma }}^2_X(a,b) := \frac{1}{[nb] - [na]} \sum _{i=[na]+1}^{[nb]} (X_{(i)} - {\hat{\mu }}_X(a,b))^2, \end{aligned}$$

(17)

where $X_{(i)}$ corresponds to the ith order statistic of the sample, ${\hat{\mu }}_X(a,b):=\frac{1}{[nb] - [na]} \sum _{i=[na]+1}^{[nb]} X_{(i)}$ denotes the conditional sample mean, and $[x]:= \max \{k \in {\mathbb {Z}}: k \le x \}$ is the integer part of $x\in {\mathbb {R}}$. It should be noted that (17) can be easily calculated as the sample variance of a sub-sample in which the conditioning is based on order statistics. Moreover, from Jelito and Pitera (2021) and Pitera et al. (2022) we know that estimator ${\hat{\sigma }}^2_X(a,b)$ is consistent and $\sqrt{n}\cdot {\hat{\sigma }}^2_X(a,b)$ tends to the Gaussian distribution as $n\rightarrow \infty$.

Second, we introduce and discuss the properties of the variance ratio estimator. Given the split (a, b, d) for $0<a<b<1$ and $0<d<0.5$, we introduce a sample version of (16) by setting

$$\begin{aligned} {{\hat{N}}} := \frac{{{\hat{\sigma }}}^2_X (a,b) + {{\hat{\sigma }}}^2_X (1-b,1-a)}{{{\hat{\sigma }}}^2_X (d,1 - d)}. \end{aligned}$$

(18)

The consistency and asymptotic normality of the statistic given in (17) imply consistency and asymptotic normality of (18), see Theorem 1 in Jelito and Pitera (2021) for the idea of the proof. Moreover, since statistic (17) is location invariant and scale proportional, we get that statistic given in (18) is both location and scale invariant. Consequently, it can be used for direct tail index estimation as its value does not depend on other (unknown) parameters, i.e. scale $c>0$ and location $\mu \in {\mathbb {R}}$. In general, the statistic (18) may be interpreted as the ratio between the tail and central dispersion.

Finally, from Sect. 2.3 we know that for appropriate choices of (a, b, d), the function $\alpha \rightarrow N(\alpha )$ defined in (16) is a bijection. Thus, using the consistency of ${{\hat{N}}}$, we can take $N^{-1}(\cdot )$ to fit the tail index parameter given the value of ${{\hat{N}}}$. Namely, using the standard statistical plug-in procedure, we set

$$\begin{aligned} {\hat{\alpha }}:= N^{-1}({\hat{N}}). \end{aligned}$$

(19)

Note that the consistency and asymptotic normality of ${\hat{N}}$ transfers to the consistency and asymptotic normality of ${\hat{\alpha }}$. Also, it is worth highlighting that we decided to put an upper bound on estimates resulting from (19) to the value 2 as this is the biggest value of the $\alpha$ parameter for stable distributions; the similar procedure is applied to the other methods considered in this paper due to the fact that the parameter space is constrained.

In the following, we propose two specific choices of the splits (a, b, d) that guarantee the bijection property. Namely, we consider the splits $(a_1,b_1,d_1):=(0.015,0.25,0.25)$ and $(a_2,b_2,d_2):=(0.01,0.17,0.1)$ that correspond to variance ratios $N_1(\alpha ):= 2\sigma _\alpha ^2(0.015,0.25) / \sigma _\alpha ^2(0.25,0.75)$ and $N_2(\alpha )$ $:= 2\sigma _\alpha ^2(0.01,0.17) / \sigma _\alpha ^2(0.1,0.9)$, with sample estimators

$$\begin{aligned} {{\hat{N}}}_1:= & {} \frac{{\hat{\sigma }}^2_X (0.015,0.25) + {\hat{\sigma }}^2_X (0.75,0.985)}{\hat{\sigma }}^2_X (0.25,0.75)\quad \text {and}\nonumber \\ {{\hat{N}}}_2:= & {} \frac{{{\hat{\sigma }}}^2_X (0.01,0.17) + {{\hat{\sigma }}}^2_X (0.83,0.99)}{{\hat{\sigma }}}^2_X (0.1,0.9), \end{aligned}$$

(20)

and output estimators of the tail-index $\alpha$ are given by

$$\begin{aligned} {{\hat{\alpha }}}_1:=N_1^{-1}({{\hat{N}}}_1)\quad \text {and}\quad {{\hat{\alpha }}}_2:=N_2^{-1}({{\hat{N}}}_2). \end{aligned}$$

(21)

For brevity, we often refer to ${\hat{\alpha }}_1$ and ${\hat{\alpha }}_2$ as QCV tail index $N_1$ estimator and QCV tail index $N_2$ estimator, respectively, or simply as $N_1$ estimator and $N_2$ estimator, respectively. The first estimator is introduced to provide a generic fit for any $\alpha \in [1,2]$ which covers the most practical application of the $\alpha$-stable distribution, while the second one is tailored for near-Gaussian cases, where $\alpha$ is relatively close to 2.0. The choice of the split values in both cases was based on numerical experiments. Namely, we decided to choose the parameters which minimize the average RMSE between true and estimated values of $\alpha$ for various sets of the true parameters $\alpha$. For $N_1$, the average was taken on the tail index grid based on the interval [1, 2] while for $N_2$, we used the narrowed interval [1.85, 2].

Let us now provide a more extensive comment on the estimation procedure. First, note that the specific values of $N_1(\alpha )$ and $N_2(\alpha )$ are not available in the closed form. In fact, these quantities are defined as the ratios of the appropriate QCVs, which can be computed explicitly only in specific cases; see the discussion following (7). However, the values of $N_1(\alpha )$ and $N_2(\alpha )$ can be approximated using a numerical integration procedure. In this paper, we use the standard trapezoidal rule approximation applied to the $\alpha$-stable distribution PDF. For completeness, in Fig. 4 we compare the approximated values of $N_1$ and $N_2$ with sample-based values of ${{\hat{N}}}_1$ and ${{\hat{N}}}_2$, for $n=1000$. While the obtained numerical results are in agreement with the conjecture of the monotonic behavior of the fitting statistics ${{\hat{N}}}_1(\alpha )$ and ${{\hat{N}}}_2(\alpha )$, some errors are expected due to uncertainty encoded in the underlying samples. In particular, note that for $\alpha$ close to 1 the values of ${{\hat{N}}}_1(\alpha )$ tend to be bigger, increasing the distance between theoretical and empirical estimates, while for $\alpha$ close to 2 the the values of $N_1(\alpha )$ and ${{\hat{N}}}_1(\alpha )$ are closer to each other. That said, our target is to estimate $\alpha$ by applying inverse $N_1^{-1}$ and $N_2^{-1}$ transforms, which could reduce the error in the final estimator.

Fig. 4

Conditional variance ratios $N_1(\alpha )$ and $N_2(\alpha )$ compared with their estimates, i.e. values of ${{\hat{N}}}_1(\alpha )$ and ${{\hat{N}}}_2(\alpha )$ obtained for various values of $\alpha$. The left panel shows $N_1(\alpha )$ for $\alpha \in [1,2]$ while the right panel shows $N_2(\alpha )$ for $\alpha \in [1.7,2]$. The results are based on 400 strong Monte Carlo samples for $\alpha$ dispersed uniformly on the underlying interval and for $n=1000$. The curves $\alpha \rightarrow N_1(\alpha )$ and $\alpha \rightarrow N_2(\alpha )$ are based on the trapezoidal integration procedure applied to (7)

Consequently, to assess the target adequacy of our estimation procedure, in Fig. 5, we compare true values of $\alpha$ with the estimates ${\hat{\alpha }}_1$ and ${\hat{\alpha }}_2$ obtained via (21) for multiple Monte Carlo simulations for samples size $n=1000$. This serves as a first sanity check indicating that the procedures proposed correctly estimate the underlying parameter. Also, the right panel in Fig. 5 suggests that, for $\alpha$ close to 2, the estimator ${\hat{\alpha }}_2$ outperforms ${\hat{\alpha }}_1$ as the estimates exhibit smaller dispersion. This is consistent with the rationale behind the construction of ${\hat{\alpha }}_2$, i.e. the fact that this estimator was intended to capture the near-Gaussian cases of the $\alpha$-stable distributions. Let us also note that multiple estimated values of $\alpha$ are equal to 2 when true value of $\alpha$ falls in the range [1.85, 2). This is due to the fact that the parameter space is constrained, i.e. our estimation technique assumes that if the estimated value exceeds 2 (which is a natural limit for the stability parameter in the $\alpha$-stable distributions), then we set the estimated value as the limit value. The same procedure is used for other estimation techniques discussed in this paper. Since the trimming may impact the estimation error assessment, special attention should be paid to extreme values of $\alpha$, see Fig. 6 for illustration.

Fig. 5

Tail index $\alpha$ compared with estimators ${{\hat{\alpha }_1}}$ and ${{\hat{\alpha }_2}}$, for various values of true $\alpha$ and sample size $n=1000$. The left panel shows the full domain $\alpha \in [1,2]$, while the right panel shows the sub-domain $\alpha \in [1.8,2]$. The results are based on 400 Monte Carlo samples for $\alpha$ dispersed uniformly on the underlying interval, each of size $n=1000$. Note that the estimates ${\hat{\alpha }}_1$ and ${{\hat{\alpha }_2}}$ are obtained using the inverse of $N_1$ and $N_2$, see (21) and Fig. 4 for details. Note that when true $\alpha$ is close to 2, multiple estimated values of $\alpha$ are equal to 2 due to constrained parameter space

Fig. 6

Empirical box-plots of ${\hat{\alpha }}_1$ for sample size $n\in \{250,500,1000,2000,4000\}$ and tail-index $\alpha \in \{1.1,1.5,1.9\}$. Each box-plot is based on 10 000 Monte Carlo samples of size n drawn from the corresponding $S\alpha S$ distribution. Note that for $\alpha =1.9$ and relatively small sample sizes many estimated values are equal 2 results from the upper bound set on the estimated value due to the constrained parameter space. As expected, the box plot is more symmetric for bigger sample sizes due to the estimator’s consistency

Fig. 7

Empirical distribution of ${\hat{\alpha }}_1$ for $\alpha \in \{1.1,1.5,1.9\}$ and the sample sizes $n \in \{250,500,1000\}$. Each plot is based on 10 000 Monte Carlo samples. Vertical lines confront the true value of $\alpha$ with the average of ${\hat{\alpha }}_1$. Please note that the peak for the value 2 results from the upper bound set on the estimated value due to the constrained parameter space, i.e. right-tail error values are accumulated in 2. As expected, the bigger the sample size, the smaller the accumulation

To assess the consistency of the proposed estimators, in Fig. 6 we show Monte Carlo-based box-plots for ${\hat{\alpha }}_1$ estimator for various pre-fixed values of $\alpha$ and different sample sizes. As expected, the estimated value tends to the true value with decreasing error rate. The statistical properties of the proposed estimators are further investigated in Fig. 7 in which we present the full Monte Carlo distribution of ${\hat{\alpha }}_1$. As expected, the plot shows that the average value of the estimate is close to the true value of $\alpha$ and the variance of the estimator decreases as the sample size increases. Also, the distribution of ${\hat{\alpha }}_1$ for moderate values of $\alpha$ is close to the Gaussian distribution. However, since the tail index cannot exceed 2, the distribution of ${\hat{\alpha }}_1$ for $\alpha$ close to 2 is naturally asymmetric. This is caused by the upper bound (equal to 2) imposed on the estimated value linked to the constrained interval. In consequence, the right-tail error is accumulated on the interval edge. However, the asymmetry disappears in the limit, for any $\alpha <2$, when the sample size tends to infinity.

To better understand this phenomenon, we decided to illustrate the relation between estimator error and sample size for $\alpha$ close to 2. Namely, in Fig. 8 we present lower and upper 10% estimates quantiles for $\alpha \in \{1.8,1.9,2.0\}$. From the plot, one can see that the bigger the sample size, the smaller the estimation error, and that the error size nearby the parameter space bound (equal to 2) is relatively stable. We want to emphasize that even for Gaussian data some small error in estimated value is expected but one would often obtain the interval endpoint value equal to 2 due to the constrained estimation interval and consequent accumulation of the right-tail estimation error. It is also worth noting that while in this article we focus on parameter fitting rather than discrimination between Gaussian and non-Gaussian cases, from Fig. 8 we see that our methodology could be in fact used to propose a proper goodness-of-fit test which aim is to discriminate between those two cases. This aspect is left for future research. We refer to Pitera et al. (2022), where a goodness-of-fit framework based on conditional moments has been developed for $\alpha$-stable data; such analysis might be used prior to the usage of parameter-fitting algorithm. The results for ${\hat{\alpha }}_2$ are similar and are omitted for brevity.

Fig. 8

Empirical upper and lower 10% quantiles of ${\hat{\alpha }}_1$ for sample size $n\in [250,4000]$ and tail-index $\alpha \in \{1.8,1.9,2.0\}$. Each point is based on 10 000 Monte Carlo samples of size n drawn from the corresponding $S\alpha S$ distribution. The plot could be used to identify a sample size that is required to achieve a certain level of estimation accuracy for $\alpha$ close to 2. Note that we set the upper bound on the estimated value equal to 2 due to the constrained parameter space. In particular, note that we did not plot the upper 10% quantile for $\alpha =2$ as it is fully aligned with the horizontal line corresponding to the true parameter. As expected, the results for $\alpha <2$ and bigger sample sizes are centered around the true value due to the estimator’s consistency

To sum up, we conclude that the estimators proposed in (21) behave as expected and enjoy multiple useful properties, such as Gaussian-like limiting distribution and small bias. In the next section, we confront the proposed estimators with other benchmark procedures to illustrate that the framework introduced in this paper is competitive and, in many instances, outperforms some commonly used estimation methods.

4 Simulation study and performance evaluation

In this section, we study the performance of the estimators ${\hat{\alpha }}_1$ and ${\hat{\alpha }}_2$ defined in (21) and confront it with the performance of various benchmark alternatives. The evaluation process is Monte Carlo based, where the estimated values for different tail indices $\alpha \in [1,2]$ and different sample sizes $n\in \{250,500,1000\}$ are confronted with each other. In each case, we set Monte Carlo size to $k = 100\, 000$. Given a reference tail-index $\alpha$, a reference sample size n, and a reference estimation technique, we use a performance metric given by the root mean squared error (RMSE) defined as

$$\begin{aligned} \textrm{RMSE} := \sqrt{\frac{1}{k} \sum _{i=1}^{k} (\alpha - {\hat{\alpha }}^i)^2}, \end{aligned}$$

(22)

where $\alpha$ is the true value of the parameter and ${\hat{\alpha }}^i$ is the value estimated on the ith sample of size n, for $i=1, \ldots , k$.

The remaining part of this section is organized as follows. In Sect. 4.1, we briefly describe several benchmark estimation procedures discussed in the literature and, in Sect. 4.2, we compare them with the estimators defined in (21). Next, in Sect. 4.3, we show that the estimators presented in (21) are in fact robust with respect to asymmetry, so that our estimation technique could also be effectively applied for $\beta \ne 0$, which indicates asymmetry in data.

4.1 Benchmark estimation procedures

In the literature, one can find various approaches used for the estimation of the stability index for the $\alpha$-stable distribution. They can be classified into three main categories, i.e. quantile methods, characteristic function-based algorithms, moment-related procedures, and maximum likelihood techniques. In this section, we present the five most common approaches that can be considered as representatives of these classes. We focus on the estimation of the stability parameter $\alpha$ as this corresponds to the main topic of this paper. However, note that some of the discussed methods could also be used for an estimation of the other parameters of generic stable distributions.

The quantile-based approach for the estimation of $\alpha$ parameter in the symmetric case was first proposed in Fama and Roll (1971), where authors applied a simple idea based on the observation that the quantiles of an appropriate large level (e.g. $95\%$) of the symmetric $\alpha$-stable distribution decrease monotonically for $\alpha \in [1,2]$. This idea was then extended by McCulloch (1986) for the general (non-symmetric) case. In a nutshell, to estimate $\alpha$, McCulloch proposes to compute the following statistic

$$\begin{aligned} \nu (\alpha ):=\frac{Q_{\alpha }^{-1}(0.95)-Q_{\alpha }^{-1}(0.05)}{Q_{\alpha }^{-1}(0.75)-Q_{\alpha }^{-1}(0.25)}, \end{aligned}$$

(23)

where $Q_{\alpha }$ is the quantile function of the symmetric $\alpha$-stable distribution. Then, denoting by ${{\hat{\nu }}}$ the sample estimator of (23), we look for the parameter $\alpha$ which gives the same sample and theoretical values, i.e. we define the McCulloch Estimator (MCH) as

$$\begin{aligned} {\hat{\alpha }_{MCH}}:=\nu ^{-1}({{\hat{\nu }}}). \end{aligned}$$

(24)

It should be noted that the value of ${\hat{\alpha }}_{MCH}$ cannot be determined analytically as the theoretical quantiles of the symmetric $\alpha$-stable distribution are not given in an explicit form. Thus, it was proposed to apply the Monte Carlo simulations and was provided the tabulated values of $\nu (\alpha )$. In McCulloch (1986) it was proven that if the sample size is large enough, then the method gives reliable estimates of the underlying parameters, see also Chapter 4 in Nolan (2020) for further discussion. For other generalizations of the quantile-based approach see e.g.. (Dominicy and Veredas 2013; Huixia et al. 2012; Maymon et al. 2000).

The second technique is the so-called regression method based on the characteristic function. This approach is a natural choice for the estimation of $\alpha$-stable distribution parameters. The idea of this approach was first introduced by Press (1972). In a nutshell, using (1) with $(\beta ,c,\mu )=(0,1,0)$, we get

$$\begin{aligned} \log (-\log \phi (u))=\alpha \log |u|, \quad u\in {\mathbb {R}}. \end{aligned}$$

Thus, the parameter $\alpha$ can be recovered as the regression coefficient in the regression of $\log (-\log \phi (u))$ against $\log |u|$ for u from some predetermined set $\{u_1,\ldots , u_k\}$. In practice, given a sample $\{X_1,X_2,\ldots ,X_n\}$, the characteristic function $\phi (u)$ is estimated by its sample version ${\hat{\phi }}(u):=\frac{1}{n}\sum _{j=1}^{n}\exp \left( iuX_j\right)$, $u\in {\mathbb {R}},$ and the Regression Estimator (REG) is given as a solution to the least squares problem, i.e.

$$\begin{aligned} {\hat{\alpha }_{REG}}:= \mathop {\textrm{argmin}}\limits _{\alpha } \left( \sum _{i=1}^k\left( \log (-\log {{\hat{\phi }}}(u_i))-\alpha \log |u_i|\right) ^2\right) ; \end{aligned}$$

(25)

see e.g. (Cizek et al. 2005) for details. Usually, the convergence of Press’s method to the population values depends on the choice of estimation points, whose selection is problematic. Thus, Koutrouvelis (1980) proposed a much more accurate method which starts with an initial estimate of the parameters and proceeds iteratively until some prespecified convergence criterion is satisfied. This technique is now considered as the classical regression-type approach for the estimation of the $\alpha$-stable distribution’s parameters. In the literature one can find various extensions and improved versions of this approach; see e.g. (Kogon and Williams 1998; Mohammadreza et al. 2017; Arad 1980; Paulson et al. 1975) for details.

The next group of estimation procedures is associated with moments of suitably transformed random variables. This transformation should assure that the associated moment exists and can be reliably estimated. In this group, we focus on the fractional lower order moment (FLOM) method and the log-moments estimator (LOG).

The rationale behind the fractional lower order moment method is associated with the fact that for $\alpha \in (0,2)$, $X\sim S\alpha S$, and $p\in (-1,\alpha )$, the pth absolute moment of X exists and satisfies ${\mathbb {E}}|X|^{p}=c(\alpha ,p)$, where $c(\alpha ,p):=\Gamma (1-p / \alpha ) /(\Gamma (1-p) \cos (\pi p / 2))$. Moreover, for any fixed $p\in (0,\min (1,\alpha ))$, the quantity ${\mathbb {E}}|X|^{p}{\mathbb {E}}|X|^{-p}=c(\alpha ,p)c(\alpha ,-p)$ is monotonically decreasing with respect to $\alpha$. Thus, denoting by $m_p$ and $m_{-p}$ the sample estimates of ${\mathbb {E}}|X|^{p}$ and ${\mathbb {E}}|X|^{-p}$, respectively, and setting $L_p(\alpha ):={\mathbb {E}}|X|^{p}{\mathbb {E}}|X|^{-p}-m_pm_{-p}$, we may define the FLOM estimator as a result of the moment-matching procedure

$$\begin{aligned} {\hat{\alpha }_{FLOM}}:=L_p^{-1}(0). \end{aligned}$$

(26)

In practice, one needs to choose the right value of p to ensure the proper convergence. In particular, the chosen p needs to be less than the unknown parameter $\alpha$; see Section II.A in Ma and Nikias (1995) and Section 4.6 in Nolan (2020) for more details. We refer also to Żuławiński et al. (2022) for the proposition of selecting the optimal value of p when the fractional order moments are used for the estimation procedures.

The next procedure is related to the variance of the logarithmic transformation of the $\alpha$-stable distribution and was originally proposed by Zolotarev (1981). More specifically, letting $X\sim S\alpha S$ and $Z:=\ln X$, we get that the variance of Z satisfies ${\mathcal {D}}^2(Z)=\frac{\pi ^2(1+2/\alpha ^2)}{12}$. Then, for a sample ${\textbf{X}}:=\{X_1,X_2,\ldots ,X_n\}$, we set ${\textbf{Z}}:=\{\ln X_1,\ln X_2,\ldots ,\ln X_n\}$ and define the corresponding estimator of the $\alpha$ parameter as

$$\begin{aligned} {\hat{\alpha }_{LOG}}:= \left( \frac{6{\hat{\sigma ^2}}_Z}{\pi ^2}-\frac{1}{2}\right) ^{-1/2}, \end{aligned}$$

(27)

where $\sigma ^2_Z$ is the sample variance of ${\textbf{Z}}$. We refer to Section II.B in Ma and Nikias (1995) and Section 4.8.1 in Nolan (2020) for more detailed discussion.

Table 1 RMSE for $N_1$, $N_2$, MCH, and REG estimators based on 100 000 Monte Carlo samples for $n \in \{250, 500,$$1000\}$ and $\alpha \in \{1, 1.1, \ldots , 2\}$. The best performance is marked in bold. Note that while RMSE values for all estimators decrease when the sample size is increased, the relative RMSE ordering is stable

The last benchmark method presented in this paper is based on the maximum likelihood approach. For a sample ${\textbf{X}}:=\{X_1,X_2,\ldots ,X_n\}$, we calculate the log-likelihood function

$$\begin{aligned} L({\textbf{X}};\alpha )=\sum _{j=1}^n\log \left( f_{\alpha }(X_j)\right) , \end{aligned}$$

(28)

where $f_{\alpha }(\cdot )$ is the PDF of the symmetric $\alpha$-stable distribution. Then, the Maximum Likelihood Estimator (MLE) is given as the maximizer of $L({\textbf{X}};\alpha )$, i.e.

$$\begin{aligned} {\hat{\alpha }_{MLE}}:=\mathop {\textrm{argmax}}\limits _{\alpha } L({\textbf{X}};\alpha ). \end{aligned}$$

(29)

It is worth highlighting that, usually, the $\alpha$-stable PDF is not available in the explicit form and it needs to be approximated numerically. Thus, the maximum-likelihood-based approaches discussed in the literature differ in the choice of the approximating algorithm, see e.g. (DuMouchel 1973; Nolan 2001; Mittnik et al. 1999; Muneya and Akimichi 2006; Brorsen and Yang 1990).

Let us conclude this section with a comment on the practical use of the estimation methods. While the true stability parameter $\alpha$ may not exceed the value 2, usually there is no guarantee that the direct application of the techniques described in this section gives the estimate in the admissible interval (in particular, this applies to LOG estimator given by (27)). Thus, to ensure the non-degeneracy of the estimates, all values are trimmed at the level 2.

4.2 QCV estimators performance assessment

In this section we evaluate the performance of $N_1$ and $N_2$ estimators using the RMSE metric and confront the obtained results with other methods introduced in the previous section. The preliminary analysis indicated that $N_1$, $N_2$, and all other benchmark methods outperform FLOM and log-moments estimators, so we decided not to present the corresponding results in the main body of this paper and defer them to Appendix A. Note that this observation is consistent with the results presented in Nolan (2020), where the performance of the considered benchmark methodologies is also studied. Moreover, the MLE approach requires big amount of time-consuming calculations and our preliminary check indicates that this method is outperformed by other procedures in almost all instances. Still, for completeness, in Appendix A we include this technique and present the comparison of all benchmark methods for the reduced number of Monte Carlo simulations, i.e. for $k_1:=1000$; see Table 6 therein for the summary of the results. To sum up, in this section, we focus on performance evaluation for $N_1$, $N_2$, MCH, and REG estimators defined in (21), (24), and (25).

Fig. 9

REG and $N_1$ estimated values for exemplary values of $\alpha \in \{1.1,1.5,1.9\}$ and $n=250$. For each $\alpha$, we present the results for 1 000 Monte Carlo simulations

All computations are performed in R 4.0.4 and library stabledist is used for simulations. The results for the benchmark estimators are based on our own implementation of the classical algorithms adjusted to the stable symmetric case.

The RMSE results for all considered estimators computed for 100 000 Monte Carlo runs with various values of $\alpha$ and $n\in \{250,500,1000\}$ are presented in Table 1.

We can see that for any choice of $\alpha$ and n, the estimator based on $N_1$ outperforms the McCulloch method. Also, for $\alpha$ in small to medium range, the $N_1$ method shows the best results among all compared procedures. For $\alpha$ close to 2, the regression and $N_2$ methods provide the best results; the closer we are to the Gaussian case, the better the regression method performs. This shows that while $N_1$ is a good overall fit statistic, $N_2$ is good for the tail-index estimation when $\alpha$ is close to 2.

Next, we want to check whether the QCV method meaningfully complements the existing benchmark methods and brings some new statistical information. If this is the case, one might refine the existing methodology e.g. by using ensemble learning with the QCV estimator, see e.g. (Polikar 2006) and references therein. We decided to focus on the comparison between the QCV estimator and the REG estimator since they exhibited the best performance in Table 1.

First, we decided to confront the estimated REG and $N_1$ values. Because $N_1$ is based on different characteristics than the regression method, one would expect a certain level of uncorrelation between the estimated values (errors) even though both approaches estimate the same parameter on the same sets. This is indeed the case as shown in Fig. 9, in which the results for sample size $n=250$ and $\alpha \in \{1.1,1.5,1.9\}$ are presented. Similar conclusions are true for other sample sizes, and for $N_2$ statistics.

Table 2 RMSE for REG, $M_1$, and $M_2$ estimators based on 100 000 Monte Carlo samples for $n \in \{250, 500, 1000\}$ and $\alpha \in \{1, 1.1, \ldots , 2\}$. The best performance is marked in bold. Note that while RMSE values for all estimators decrease when the sample size is increased, the relative RMSE ordering is stable

Second, we want to sanity check whether we can refine the estimation procedure by combining the information encoded in the REG and QCV estimators. Given a sample, and estimated values ${\hat{\alpha }}_1$, ${\hat{\alpha }}_2$ and ${\hat{\alpha _{\text {REG}}}}$, the simplest way to check this is to consider the averaged estimators

$$\begin{aligned} {\hat{\alpha }}_{M_1}:=\frac{{\hat{\alpha }}_{1}+{\hat{\alpha }}_{\text {REG}}}{2}\quad \text {and}\quad {\hat{\alpha }}_{M_2}:=\frac{{\hat{\alpha }}_{2}+{\hat{\alpha }}_{\text {REG}}}{2}, \end{aligned}$$

(30)

which we refer to simply as $M_1$ estimator and $M_2$ estimator. In particular, we can confront the performance of REG, $M_1$, and $M_2$ method using RMSE metric in a similar way it was done in Table 1. The results of this test are presented in Table 2.

One can note that in almost all instances the averaged estimators $M_1$ and $M_2$ outperforms the REG estimator. It confirms that the QCV estimator contains information that is not encoded in the REG estimator and could be used to refine existing approaches using e.g. ensemble learning. In fact, the simple averaging scheme already leads to a substantial reduction of RMSE.

To provide a summary, in Fig. 10 we present box-plots of estimated values for all considered estimators, for $\alpha \in \{1.1,1.5,1.9\}$ and $n = 500$. It can be seen that, in each case, the median of estimates for $N_1$, MCH, and REG are close to the true value of $\alpha$. Next, the dispersion of the results for $N_1$ is smaller than for MCH and comparable with REG. Still, for $\alpha =1.1$ and $\alpha =1.5$, the $N_1$ estimator outperforms the REG estimator in terms of RMSE as already shown in Table 1. Also, the right panel in Fig. 10 confirms that the $N_2$ method is particularly effective for $\alpha$ close to 2. Finally, looking at $M_1$ and $M_2$, we see that the best results are obtained by combining REG and QCV approaches.

4.3 Asymmetry robustness

While the proposed methodology is created for the symmetric $\alpha$-stable distribution family, in this section we demonstrate that it can also be applied for generic $\alpha$-stable distributions, especially when the stability index is relatively close to 2; recall that for $\alpha =2$, the $\alpha$-stable distribution is reduced to the Gaussian distribution which is independent of $\beta$ parameter. To demonstrate the robustness to the parameter change, in Table 3 we present the averages of the estimated $\alpha$ parameters based on $10\,000$ Monte Carlo simulations for sample size $n=1000$ and various combinations of theoretical $\alpha$ and $\beta$ parameters from sets $\{1.1,1.2,\ldots , 2\}$ and $\{0,0.1,\ldots ,1\}$, respectively. The negative values of $\beta$ were not taken into account, as changing the sign of $\beta$ corresponds to the reflection of the random variable value across the Y axis. The results in Table 3 show that, irregardless of $\beta$, the average estimates of $\alpha$ are relatively close to the theoretical values. This suggests that both $N_1$ and $N_2$ estimators can be considered as robust in reference to $\beta$.

Fig. 10

Boxplots of 100 000 estimates for the considered methods with $n = 500$ and $\alpha \in \{1.1, 1.5, 1.9\}$. The horizontal line represents the true value of $\alpha$

Table 3 Averages of the estimated $\alpha$ parameter for $10\,000$ Monte Carlo simulations of $\alpha$-stable distributed samples with $n=1000$ elements. In the simulations we considered all combinations of the $\alpha$ and $\beta$ parameters from the sets $\{1.1,1.2,\ldots , 2\}$ and $\{0,0.1,\ldots ,1\}$, respectively

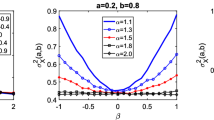
In Fig. 11, we demonstrate the RMSE value of the estimated stability index for various combinations of $\alpha \in \{1.1,1.2,\ldots ,2\}$ and $\beta \in \{0, 0.1,\ldots ,1\}$; as before, the number of Monte Carlo simulations is equal to $10\,000$ and sample size equals $n=1000$. The results presented in the level plots indicate relatively small error changes when the methodology is applied to non-symmetric data, that is, for $\beta \ne 0$. This effect is visible especially for the parameter $\alpha$ close to 2. The vertical stripes on the level plots for the $\alpha$ parameter close to 2 have almost the same colours, which confirms that for this case the $N_1$ and $N_2$ estimators are robust for the $\beta$ parameter. Namely, we observe the same degree of error in Fig. 11 but from Table 3 we learn that the mean estimated value does not depend on $\beta$ which indicates robustness when combined together.

To further confirm the resistance of the proposed estimation methods to $\beta$ induced skewness, in Fig. 12 we show the absolute differences between the averaged estimated values for fixed $\alpha$ and $\beta$, when confronted with symmetric alternative ($\beta =0$). More specifically, for each $\alpha \in \{1.1, 1.2, \ldots , 2\}$ and $\beta \in \{0, 0.1,\ldots ,1\}$, we calculate

$$\begin{aligned} \textstyle \left| \frac{1}{k}\sum _{i=1}^k {{\hat{\alpha }}}({\textbf{X}}_i^{(\alpha ,\beta )})-\frac{1}{k}\sum _{i=1}^k {{\hat{\alpha }}}({\textbf{X}}_i^{(\alpha ,0)})\right| , \end{aligned}$$

(31)

where $k=10\,000$ is the number of Monte Carlo samples, ${{\hat{\alpha }}}({\textbf{X}})$ is the estimate based on a sample ${\textbf{X}}$, and ${\textbf{X}}_i^{(\alpha ,\beta )}$, $i=1, \ldots , M$, are i.i.d. $n=1000$-element samples from $S(\alpha , \beta , 1,0)$ distribution. The left panel shows the results for the estimator based on $N_1$, while the right panel shows the results for $N_2$. The results presented in Fig. 12 demonstrate how $|\beta | \rightarrow 1$ affects the quality of the estimators. We observe that the estimated values of the stability index for the asymmetric data are relatively close to those obtained for the symmetric samples (i.e. when $\beta =0$), with a maximal (average) difference equal to 0.05 for sample size $n=1000$. This confirms that both $N_1$ and $N_2$ estimators are robust in reference to $\beta$ specification.

Fig. 11

RMSE of the estimated stability index for various combinations of $\alpha \in \{1.1,1.2,\ldots ,2\}$ and $\beta \in \{0.0, 0.1,\ldots ,1\}$; the number of Monte Carlo simulations is $10\, 000$ and the sample size is $n=1000$. The left panel shows the results for $N_1$, while the right panel shows the results for $N_2$

Fig. 12

Absolute differences between the averaged estimates of the stability parameter $\alpha$ in the symmetric and asymmetric case, see (31). The results for various combinations of $\alpha \in \{1.1,1.2,\ldots ,2\}$ and $\beta \in \{0, 0.1,\ldots ,1\}$ are presented. The number of Monte Carlo simulations is $10\, 000$ and the sample size is $n=1000$. The left panel shows the results for $N_1$, while the right panel shows the results for $N_2$

5 Real data analysis

In this section, we show how to apply our estimation methodology to real data. To demonstrate the universality of the proposed approach, we analyze data from two areas, financial market and plasma physics. For simplicity, since our focus is set on the estimation of the stability parameter $\alpha \in (0,2]$, we assume that the analyzed data constitute samples of independent observations coming from (the same) $\alpha$-stable distribution. In particular, note that while the real data is often heteroscedastic and short-term dependence might be visible, such simplification is often made to assess the overall distributional fit. To simplify the narrative, we have decided to pick data that was already considered as coming from the (close to symmetric) $\alpha$-stable distribution in the pre-existing literature and focus mainly on stability index parameter fitting. That said, for completeness, some top-level data descriptions and analyses are provided. In the following subsections we refer the readers to the appropriate bibliography positions.

Fig. 13

Plot of the residuals of GARCH(1,1) model fitted to the logarithmic returns of IMB stock prices (left panel) with the histogram (middle panel). The right panel presents QQ-plot with $95\%$ confidence interval (blue field) which confirms non-Gaussian distribution of the data (color figure online)

5.1 Financial data example

In this section, we follow the financial market example introduced in Nolan (2004). Namely, we consider the daily logarithmic returns for IBM stock for 10 years period from 01/01/2003 to 31/12/2012. Since the returns exhibit strong non-stationary heteroscedastic behavior, a proper noise extraction filter should be used. To be consistent with Nolan (2004), we apply the GARCH(1,1) filter to the logarithmic returns and consider GARCH model residuals instead of logarithmic returns. In the end, we obtain the residual sample of size $n=2516$. We refer to Fig. 13 for data illustration, see (Nolan 2004) for more details about data processing.

The non-Gaussian distribution of the analyzed residuals could be confirmed by the classical Gaussian goodness-of-fit tests. For example, the p-values from the Shapiro-Wilk test and Jarque-Bera test are less than $2.2\times 10^{-16}$. The heavy-tailed behavior is in fact visible directly in the QQ-plot presented in Fig. 13. On the other hand, the results for $\alpha$-stable goodness-of-fit tests do not reject $\alpha$-stable distribution hypothesis. The p-values for Kolmogorov-Smirnov test, Kuiper test, Watson test, Cramer-von Mises test, and Anderson-Darling test are equal to 0.287, 0.182, 0.076, 0.058, and 0.085, respectively; the p-values of the tests for $\alpha -$stable distribution were calculated based on 1000 Monte Carlo simulations from a pre-fitted parameter, see (Cizek et al. 2005) for details. In view of the above analysis as well as the discussion presented in Nolan (2004), we apply the methodology proposed in the current article and estimate the tail index from residual data.

In Table 4, we present the estimation results for $N_1$ and $N_2$ statistics.

Table 4 Estimates of $\alpha$ parameter with $95\%$ confidence intervals (CI) based on $10\,000$ bootstrap samples for the financial dataset. For comparison, we demonstrate the results for benchmark methods dedicated for symmetric (MCH, REG) and general (MCH2, REG2) $\alpha$-stable distribution

Moreover, for completeness, we present estimated values of $\alpha$ for the McCulloch and regression methods analyzed in Sect. 4. As before, we denote the methods by MCH and REG, respectively. It is worth recalling that these estimation techniques are dedicated to the symmetric $\alpha$-stable distributions, i.e. when $\beta =0$. Thus, for comparison, in Table 4 we also demonstrate the results of modified MCH and REG estimators that simultaneously estimate $\alpha$ and $\beta$ parameters. For transparency, we denote them as MCH2 and REG2, respectively. For all estimators in scope we construct the $95\%$ bootstrap confidence intervals based on $10\,000$ bootstrap samples. While, as in Sect. 4, we decided not to analyze the MLE-based results, we estimate the values for completeness. The value of the parameter for the symmetric and non-symmetric maximum likelihood method is equal to 1.8271 and 1.6807, respectively. We can see that the results for $N_1$ and $N_2$ statistic are in-between the results obtained by MCH and REG methods. We note, the estimated values of $\alpha$ demonstrated in Nolan (2004) indicate that the stability index for analyzed residuals (obtained using MLE method) is between 1.77 and 1.87. Algorithms based on $N_1$ and $N_2$ statistics return slightly smaller values. However, $N_2$-based method gives more similar values to those presented by Nolan (2004); this method seems more adequate for cases when $\alpha$ is closer to 2.

Fig. 14

Plasma data for torus radial position $r=9.5$ cm (Dataset 1 and Dataset 2). Dataset 1 (top row) describes the fluctuations before the L-H transition point while Dataset 2 (bottom row) represents the fluctuation after the L-H transition point. The left panels present the raw data, the middle panels present histograms, and the right panels present QQ-plots with $95\%$ confidence intervals (blue fields). The graphical analysis confirms the non-Gaussian distribution of Dataset 1 and Gaussian distribution (or close to Gaussian) for Dataset 2 (color figure online)

Table 5 Estimation of $\alpha$ parameter with $95\%$ confidence intervals (CI) based on $10\,000$ bootstrap samples. For comparison, we demonstrate the results for benchmark methods dedicated to symmetric (MCH, REG) and general (MCH2, REG2) $\alpha$-stable distribution

5.2 Physics data example

In this part we investigate the data obtained in experiments on the controlled thermonuclear fusion from the device “Kharkiv Institute of Physics and Technology”, Kharkiv, Ukraine. The same datasets are examined in Burnecki et al. (2012, 2015) and Pitera et al. (2022), where a detailed description of the time series in reference to $\alpha$-stable distribution family is provided. Let us only mention that the data describe the floating potential fluctuations (in volts) of plasma turbulence that are characterized by high levels of fluctuations of the electric field and particle density. In the fluctuations, the phenomenon called L-H transition has been observed. The L-H transition is a sudden transition from the low confinement mode (L mode) to a high confinement mode (H mode). During the transition, a regime shift could be observed, which might be associated with the change of the tail index. Namely, we examine two datasets, denoted by Dataset 1 and Dataset 2, that describe the floating potential fluctuations for torus radial position $r = 9.5$ cm. Dataset 1 is related to the fluctuations before the transition point, Dataset 2 describes the fluctuation after the transition; see (Beletskii et al. 2009) for the detailed description of the experimental set-up, the measurement procedure, etc. Each dataset contains $n=2000$ normalized observations, see Fig. 14 for data illustration.

Analysing only the histograms of the considered datasets, one may conjecture that they follow Gaussian distribution, i.e. the shapes of the histograms resemble Gaussian PDF. However, the analyses provided in Burnecki et al. (2012, 2015) and Pitera et al. (2022) indicate that this conclusion is not true for both time series. For example, in Burnecki et al. (2015), a visual test for discriminating between light- and heavy-tailed distributed data was proposed, which pointed out differences between the prior transition point and the posterior transition point. It was demonstrated that Dataset 1 can be described by the $\alpha$-stable distribution with $\alpha <2$ (yet close to 2) while Dataset 2 is closer to the Gaussian distribution. The results presented in Burnecki et al. (2015) were confirmed by Pitera et al. (2022), where a goodness-of-fit test for the $\alpha$-stable distribution based on the conditional variance methodology was proposed. The non-Gaussian distribution of Dataset 1 is also confirmed by the Shapiro-Wilk test and Jarque-Bera test. For Dataset 1, the p-values of the Shapiro-Wilk and the Jarque-Bera tests are equal to $1.417 \times 10^{-6}$ and $3.33 \times 10^{-10}$, respectively. For Datasets 2, the hypothesis of the Gaussian distribution is not rejected and the corresponding p-values are equal to 0.077 and 0.149. See Fig. 14 for QQ-plot illustration for both datasets. Also, as in the previous example, the goodness-of-fit tests for $\alpha -$stable distribution mentioned in Sect. 5.1 do not reject the null hypothesis. For Dataset 1, the corresponding p-values are equal to 0.92, 0.87, 0.86, 0.83, and 0.46, respectively. To summarize, the preliminary analyses of the datasets and discussion provided in our previous papers allow us to apply the methodology proposed in this paper, i.e. using the $\alpha$-stable framework for modeling the considered data.

We have applied the proposed estimation methodology to the datasets from plasma physics following the same framework as in Sect. 5.1. The results are presented in Table 5. The MLE and MLE2 parameter fits for Dataset 1 are equal to 1.998 and 1.930, while for Dataset 2 they are equal to 2.000 and 1.996.

The results obtained based on QCV approach confirm and complement previous results. The results based on $N_1$ and $N_2$ statistics for Dataset 1 clearly indicate the stability index between 1.8 and 1.96. Let us recall that if the parameter $\alpha$ is close to 2, then $N_2$ should be more adequate; thus, the upper limit of the CI for the $N_1$ method might be considered as non-sharp. The benchmark techniques dedicated to the symmetric $\alpha$-stable distribution (i.e. MCH and REG) for Dataset 1 fail, as they indicate the Gaussian distribution. The methods that simultaneously estimate both $\alpha$ and $\beta$ parameters (i.e. MCH2 and REG2) seem to overestimate the stability index. For Dataset 2, all estimated values are close to 2, as expected.

6 Summary and conclusions

In this paper, we show that the QCV approach can be used to construct an effective fitting statistics for the symmetric $\alpha$-stable distributions. The proposed estimators show good performance both on the simulated and real data, and often outperform other benchmark frameworks. The methods proposed in this paper are build on the results obtained recently in Pitera et al. (2022), where goodness-of-fit testing framework based on QCV has been studied. In fact, in this paper we show that the statistical QCV-based procedures can be effectively used for parameter estimation. It is worth noting that while the standard method of moments estimators cannot be directly applied in the $\alpha$-stable case due to the infinite variance, out method is based on quantile conditional variances which always exist and consequently can be directly used for the fitting. Also, we want to highlight some form of similarity between our method and the classical McCulloch method, see (23). In a nutshell, in the McCulloch framework the fitting statistic is based on the appropriate function of tail quantiles while the procedures proposed in this paper use the quantile tail variances, see (20). As expected, the quantile conditional variances are more informative than quantiles which results in better performance of the proposed method, see Sect. 4.2 for details. Next, it is worth mentioning that while we focus on the symmetric case, the QCV ratio-based statistic is in fact almost insensitive to changes in the skewness parameter and our method could be applied to a more generic framework. Finally, we have shown that the proposed approach extracts sample characteristics different to the ones extracted by the other benchmark frameworks, so that our idea could be used to refine existing methodologies e.g. via fitting methods ensembling.

Appendices

Appendix A. Additional tables

In this section, we present additional tables with numerical results. This complements the analysis in Sects. 4.2 and 4.3. First, in Table 6 we present the RMSE metrics for $N_1$, $N_2$, MCH, REG, MLE, FLOM, and LOG methods; see Sect. 4.1 for details. Note that for FLOM we use the generic parameter $p:=0.9$ for all $\alpha \in [1,2]$; we did not want to adjust this parameter for a particular $\alpha$ value as this would effectively result in an ensemble method. Also, note that to obtain the results, we used a reduced number of Monte Carlo simulations $k_1:=1000$ as this speeds up the computations (in particular, for MLE). The results in Table 6 complement the outcomes presented in Table 1 by adding the metrics for the maximum likelihood method as well as fractional and log-moments estimators. As seen in Table 6, the MLE, FLOM and LOG methods exhibits relatively poor performance, particularly for $\alpha$ in moderate to high range. Taking into account this observation and the fact that the results for MLE require a high number of time-consuming calculations, we decided not to include the outcomes for MLE, FLOM and LOG in Sect. 4.2.

Table 6 RMSE for 1000 Monte Carlo samples with sizes $n \in \{250, 500, 1000\}$ and the stability parameter $\alpha \in \{1, 1.1, \ldots , 2\}$. The symbols $N_1$ and $N_2$ refer to the estimators defined by (21). The symbols MCH, REG, MLE, FLOM, and LOG represent the McCulloch, the regression, the maximum likelihood, fractional lower order moments, and the log-moments methods, respectively. The best performance is marked in bold

Second, in Table 7 we present the RMSE metrics of the estimated stability index for various combinations of $\alpha$ and $\beta$. These results are used to produce Fig. 11.

Table 7 RMSE of the estimated stability index for various combinations of $\alpha \in \{1.1,1.2,\ldots ,2\}$ and $\beta \in \{0, 0.1,\ldots ,1\}$; the number of Monte Carlo simulations is $10\, 000$ and the sample size is $n=1000$

Appendix B. Deferred proofs

In this section we present technical proofs that were deferred to the appendix.

Proof of Proposition 2

Let us fix $\alpha \in (0,2)$. Let $X\sim S\alpha S$, let ${\bar{F}}_{\alpha }(\cdot ):=1-F_{\alpha }(\cdot )$ be the survival function of X, and let ${\bar{Q}}_{\alpha }(\cdot )$ be the inverse of ${\bar{F}}_{\alpha }(\cdot )$. Using Theorem 1, we get $\lim _{x\rightarrow \infty } \frac{{\bar{F}}_{\alpha }(x)}{c_{\alpha }x^{-\alpha }}=1$. Thus, setting $x={\bar{Q}}_{\alpha }(p)$ for $p\in (0,1)$, we get $\lim _{p\rightarrow 0^+} \frac{{\bar{F}}_{\alpha }({\bar{Q}}_{\alpha }(p))}{c_{\alpha }\left( {\bar{Q}}_{\alpha }(p)\right) ^{-\alpha }}=1.$ Now, recalling that ${\bar{F}}_{\alpha } \left( {\bar{Q}}_{\alpha }(p)\right) =p$, we know this is equivalent to $\lim _{p\rightarrow 0^+} \frac{p}{c_{\alpha }\left( {\bar{Q}}_{\alpha }(p)\right) ^{-\alpha }}=1$. By considering the $\alpha$-root of the inverted limit, we know that $\lim _{p\rightarrow 0^+} \frac{{\bar{Q}}_{\alpha }(p)}{{\bar{c}}_{\alpha }p^{-1/\alpha }}=1.$ Finally, noting that ${\bar{Q}}_{\alpha }(p)={Q}_{\alpha }(1-p)$ for $p\in (0,1)$, we get

$$\begin{aligned} \lim _{p\rightarrow 1^-} \frac{Q_{\alpha }(p)}{{\bar{c}}_{\alpha }(1-p)^{-1/\alpha }}=1, \end{aligned}$$

which concludes the proof. $\square$

Proof of Proposition 3

Let $\alpha _1,\alpha _2\in (0,2]$ be such that $\alpha _1<\alpha _2$. In order to prove (4), it is enough to show that

$$\begin{aligned} \lim _{p\rightarrow 1^-} \frac{Q_{\alpha _1}(p)}{Q_{\alpha _2}(p)}=\infty . \end{aligned}$$

(32)

Indeed, from (32) it follows that there exists some $p_0\in (1/2,1)$ such that for any $p\ge p_0$ we have $\frac{Q_{\alpha _1}(p)}{Q_{\alpha _2}(p)}>1$, which shows (4).

Let us now prove (32). For transparency, we provide separate arguments for $\alpha _2<2$ and for $\alpha _2=2$. First, we assume that $\alpha _2<2$. Then, using Proposition 2, we get

$$\begin{aligned}{} & {} \lim _{p\rightarrow 1^-} \frac{Q_{\alpha _1}(p)}{Q_{\alpha _2}(p)} \nonumber \\{} & {} = \lim _{p\rightarrow 1^-} \left[ \frac{Q_{\alpha _1}(p)}{{\bar{c}}_{\alpha _1}(1-p)^{-1/\alpha _1}}\cdot \frac{{\bar{c}}_{\alpha _2}(1-p)^{-1/\alpha _2}}{Q_{\alpha _2}(p)}\cdot \frac{{\bar{c}}_{\alpha _1}(1-p)^{-1/\alpha _1}}{{\bar{c}}_{\alpha _2}(1-p)^{-1/\alpha _2}}\right] \nonumber \\{} & {} =\frac{{\bar{c}}_{\alpha _1}}{{\bar{c}}_{\alpha _2}}\lim _{p\rightarrow 1^-} (1-p)^{1/\alpha _2-1/\alpha _1}. \end{aligned}$$

(33)

Recalling that $\alpha _1<\alpha _2$ we get $1/\alpha _2-1/\alpha _1<0$ and consequently $\lim _{p\rightarrow 1^-} (1-p)^{1/\alpha _2-1/\alpha _1}=\infty$. Noting that $\frac{{\bar{c}}_{\alpha _1}}{{\bar{c}}_{\alpha _2}}>0$, we conclude this part of the proof.

Second, we assume $\alpha _2 = 2$. Then, using Example 8.13 from DasGupta (2008), we get $Q_{2}(p) \overset{p\rightarrow 1^-}{\sim } \sqrt{2 \ln (\frac{1}{1-p})}$. Consequently, as in (33), we get

$$\begin{aligned}{} & {} \lim _{p\rightarrow 1^-} \frac{Q_{\alpha _1}(p)}{Q_{2}(p)} \\{} & {} = \lim _{p\rightarrow 1^-} \left[ \frac{Q_{\alpha _1}(p)}{{\bar{c}}_{\alpha _1}(1-p)^{-1/\alpha _1}}\cdot \frac{\sqrt{2 \ln (\frac{1}{1-p})}}{Q_{2}(p)}\cdot \frac{{\bar{c}}_{\alpha _1}(1-p)^{-1/\alpha _1}}{\sqrt{2\ln (\frac{1}{1-p})}}\right] \\{} & {} =\frac{{\bar{c}}_{\alpha _1}}{\sqrt{2}}\lim _{p\rightarrow 1^-} \frac{1}{(1-p)^{1/\alpha _1}(\ln (1-p))^{1/2}}. \end{aligned}$$

Note that it is enough to show that the denominator goes to 0. Since $\alpha _1 < 2$ and $(1-p) \rightarrow 0^+$ as $p\rightarrow 1^-$, we get

$$\begin{aligned} \lim _{p\rightarrow 1^-} (1-p)^{1/\alpha _1}(\ln (1-p))^{1/2}\le & {} \lim _{p\rightarrow 1^-} (1-p)^{1/2}\left( \ln (1-p)\right) ^{1/2}\\= & {} \lim _{p\rightarrow 1^-}\left( (1-p)\ln (1-p)\right) ^{1/2} \\= & {} 0, \end{aligned}$$

which concludes the proof. $\square$