1 Introduction

The subject of bump hunting (BH) refers to the set estimation task (Baíllo et al. 2000) of discovering meaningful data regions, called bumps, in a sample space (Good and Gaskins 1980). The most representative example is the study of modal regions in a probability density function (pdf), which are literally bumps in its graph. Even though the concept has a broader scope, BH remains relatively unexplored.

Consider the problem of identifying made shots on a basketball court. Coaches, scouts and other personnel might be interested in extracting shooting patterns for adopting specific pre-game strategies, assessing talent or working on player development. Figure 1 illustrates four different ways of constructing bumps with basketball shot data. Figure 1a, b corresponds to Hyndman’s classical highest density region (HDR) configurations, while Fig. 1c, d follows our novel curvature-based characterizations. Each of them presents a distinctive perspective on the underlying shooting tendencies. Figure 1a, c points at fine-grained locations, whereas Fig. 1b, d covers entire influence areas. Smaller regions suggest spots to prioritize in an offensive or defensive scheme. The larger ones connect the dots, revealing general trends. Both views complement each other to offer a complete picture.

Fig. 1
figure 1

Four ways of constructing bumps for basketball converted shot data. The exact 804 made shot locations are scattered across each sub-figure. The top left and right bumps correspond to HDRs comprising 35% and 95% of all observations. The bottom left bumps highlight regions where the pdf subgraph is locally concave. The bottom right bumps comprise points where the Laplacian of the underlying pdf takes negative values

Full size image

1.1 Goals

We propose a new BH curvature-based methodology addressing some blind spots of classical methods. Figure 1a, b either misses or masks relevant information. The finer-grained 35%-HDR does not include the perimeter concave bumps in Fig. 1c. Meanwhile, the 95%-HDR fails to keep the short, mid- and long ranges well separated, as opposed to the Laplacian bumps in Fig. 1d.

Contributions. The main contributions of this paper are:

:

Presenting a general set estimation framework for curvature-based BH.

:

Extending concave bumps to the multivariate setting.

:

Introducing mean curvature and Laplacian bumps.

:

Deriving consistency convergence rates for curvature bump boundaries.

:

Building valid and consistent confidence regions for curvature bumps.

:

Showcasing the numerous applications of curvature-based BH.

1.2 Related work

One of the first BH references was due to Good and Gaskins (1980). They offered a premier definition of a bump as the concave region delimited between two inflection points. Moreover, they suggested an extension to the multivariate case. Figure 1c corresponds to our implementation of multivariate concave bumps.

In 1996, Hyndman introduced the concept of HDR, which he conceives as level sets of the pdf \(f\) that enclose a certain probability mass (Hyndman 1996). More formally, the \((1 - \alpha )\)-level HDR is defined as \(R(f_{\alpha })= \{\textrm{x}: f(\textrm{x}) \ge f_{\alpha }\}\), where \(f_{\alpha }\) is the largest value such that \(\mathbb {P}\left( \textrm{X}\in R(f_{\alpha }) \right) \ge 1 - \alpha \), and the random variable (rv) \(\textrm{X}\) is such that \(\textrm{X}\sim f\). HDRs satisfy the nice property of being the smallest sets with a given probability mass.

Chaudhuri and Marron (1999) presented SIgnificant ZERo crossings of derivatives (SiZer), envisioning bumps as places where the first derivative becomes zero. Chaudhuri and Marron (2002) showcased the role of second derivatives in an unpublished manuscript. Also Godtliebsen et al. (2002) explored curvature features from a pointwise perspective by assessing Hessian eigenvalue sign combinations in the bivariate case. A multivariate extension to Godtliebsen et al. (2002) was formulated by Duong et al. (2008), targeting the pointwise significance of non-zero Hessian determinants. Lastly, Marron and Dryden (2021) elaborate on second derivatives in their book Object Oriented Data Analysis.

1.3 Outline

The new methodology is presented in Sect. 2. The supplementary material (SM) (Chacón and Fernández Serrano 2023) provides the necessary differential geometry foundations. In turn, Sect. 3 is entirely dedicated to asymptotic consistency and inference results. A sports analytics application is explored in Sect. 4. The SM (Chacón and Fernández Serrano 2023) includes all the proofs and computational details. We reflect on the proposed methodology in Sect. 5.

2 Methods

Our methodology finds alternative ways of analysing sample spaces by exploiting pdfs’ curvature properties, adhering to Chaudhuri and Marron’s defence of pdf derivatives. Considering Hyndman’s approach a well-established tool, we believe there are still some blind spots to address with curvature.

Hyndman’s HDRs have the advantage of always including global modes. However, they may generally miss local modes if small enough; lowering the threshold \(\alpha \) might not capture them without obfuscating the HDR. On the other hand, when varying \(\alpha \) works, questions remain on the specific value it should take. Moreover, sometimes it is necessary to explore the whole range of \(\alpha \in (0, 1)\) to recover all the relevant pdf features (Stuetzle 2003).

Consider a \(d\)-variate pdf \(f: \mathbb {R}^{d} \rightarrow [0, \infty )\). We define bumps as subsets of \(\mathbb {R}^{d}\) of the form

$$\begin{aligned} \mathcal {B}^{\phi }= \{ \textrm{x}\in \mathbb {R}^{d} : (-1)^{s}\phi [f](\textrm{x}) \ge 0 \} , \end{aligned}$$
(1)

for some functional \(\phi \) measuring the curvature of \(f\) at any point, and some sign selector \(s\in \{0, 1\}\) that will usually be kept implicit. If the gradient \(\nabla \phi [f]\) does not vanish near the zero level set of \(\phi [f]\), the bump boundary \(\partial \mathcal {B}^{\phi }\) is retrieved by substituting the inequality with an equality sign in (1) (Qiao 2020, Remark 3.1); see Theorem 2 ahead for a formal condition (Chen et al. 2017, Assumption G) (Chen 2022). Contrary to HDRs, the idea behind (1) is that \(\phi \) carries an implicit threshold, say zero, to determine if a point belongs to the bump, solving the arbitrariness of the choice of \(\alpha \) in HDRs.

Once some curvature functional is chosen, we propose to employ a kernel plug-in estimator of \(\mathcal {B}^{\phi }\), replacing \(f\) with its kernel density estimator (KDE) in (1). Thus, given a sample \(\textrm{X}_1, \dots , \textrm{X}_{n}\) of independent and identically distributed (i.i.d.) random variables with pdf \(f\) and a bandwidth \(h> 0\), we consider the KDE of \(f\) as

$$\begin{aligned} \hat{f}_{n, h}(\textrm{x})= \frac{1}{n}\sum _{i= 1}^{n}K_{h}(\textrm{x}- \textrm{X}_{i}) = \frac{1}{nh^{d}} \sum _{i= 1}^{n}K\left( \frac{\textrm{x}- \textrm{X}_{i}}{h} \right) , \end{aligned}$$
(2)

for some kernel function \(K\), typically a \(d\)-variate pdf. Using (2), we then define the plug-in estimator of (1) as

$$\begin{aligned} \tilde{\mathcal {B}}_{n, h}^{\phi }= \{ \textrm{x}\in \mathbb {R}^{d} : (-1)^{s}\phi [\hat{f}_{n, h}](\textrm{x}) \ge 0 \} . \end{aligned}$$
(3)

To a first approximation, a scalar bandwidth is chosen for simplicity. Chacón and Duong demonstrated that, for \(d> 1\), unconstrained bandwidth matrices produce significant performance gains, especially in kernel density derivative estimation (KDDE) (Chacón and Duong 2018, Section 5.2). Preliminary experiments seem to support their recommendation also for curvature-based BH. Nonetheless, all the theoretical developments and, consequently, all the exhibition figures in this paper obey this simplification. On the other hand, the kernel \(K\) has a lower impact on the results. Most of the statements in Sect. 3 do not impose a particular choice. However, all of them are compatible with the Gaussian kernel (see Arias-Castro et al. 2016; Chen et al. 2015, 2016), which is almost universally preferred in a multivariate setting (Chacón and Duong 2018, p. 15).

For \(d= 1\), Chaudhuri and Marron studied the functional \(\phi [f] = f''\), which leads to concave bumps, if \(s= 1\), or convex dips, if \(s= 0\). Different alternatives arise in the multivariate case. The geometrical concepts in the SM (Chacón and Fernández Serrano 2023) lay the grounds for characterizing bumps in alternative ways to HDRs. Considering pdfs as hypersurfaces, notions like the mean and Gaussian curvatures find new usages in statistics. Figure 2 illustrates the two main kinds of curvature bumps in this paper. Even though \(\phi \) may a priori depend on partial derivatives of \(f\) of arbitrary order r, the theory of hypersurfaces in the SM (Chacón and Fernández Serrano 2023) suggests that our quest for curvature features is essentially fulfilled with up to second derivatives of the pdf \(f\).

Given the connection of curvature with second derivatives, we propose targeting \(r= 2\) in one of the standard bandwidth selectors (Chacón and Duong 2013). The same heuristic worked well for KDE-based applications such as mean shift clustering or feature significance testing (Chacón and Duong 2018, Chapter 6).

Fig. 2
figure 2

Curvature bumps for a bivariate Gaussian mixture encompassing two equally weighted components with means \(\varvec{\mu }_1 = [-3/2, 0]\), \(\varvec{\mu }_2 = [3/2, 0]\) and covariance matrices \(\Sigma _1 = [1, -0.7; -0.7, 1]\), \(\Sigma _2 = [1, 0.7; 0.7, 1]\). The top two sub-figures show the same graph of the pdf \(f\). The area colours refer to the values taken by a specific curvature functional \(\phi [f]\) at each point. For the left-hand picture, this function is the \(\lambda _{1}[f]\) that defines concave bumps (5); on the right, it is the mean curvature \(\text {div}(\bar{\nabla }f)\) in (7). The magenta halos represent the zero level sets of those functionals and, thus, the corresponding bump boundaries. Concave and mean curvature bump boundaries are shown in blue and cyan in the bottom sub-figure, along with a 1000-observation random sample from the mixture, where each point is coloured according to the value of \(f\)

Full size image

2.1 Concavity and convexity

Given a sufficiently smooth pdf \(f\), let us define \(\lambda _{i}[f]\), for \(i\in \{1, 2, \dots , d\}\), as the function mapping \(\textrm{x}\in \mathbb {R}^{d}\) to the \(i\)-th largest possibly repeated eigenvalue of \(\textrm{D}^{2}f(\textrm{x})\), the Hessian matrix of \(f\) at \(\textrm{x}\), i.e.

$$\begin{aligned} \lambda _{1}[f](\textrm{x}) \ge \lambda _{2}[f](\textrm{x}) \ge \dots \ge \lambda _{d}[f](\textrm{x}) , \end{aligned}$$
(4)

for all \(\textrm{x}\in \mathbb {R}^{d}\). As mentioned in the SM (Chacón and Fernández Serrano 2023), the eigenvalues of the Hessian (or the shape operator, equivalently) determine local concavity and convexity. Let us assume that \((-1)^{s}\lambda _{i}[f] > 0\), for all \(i\) on some subset \(\mathcal {U}\subset \mathbb {R}^{d}\). If \(s= 0\), \(f\) will be locally convex, whereas if \(s= 1\), it will be locally concave on \(\mathcal {U}\). Considering the ordering of functions (4), we can express the former concave and convex bumps in terms of a single functional, aligned with a specific sign \(s\), as, respectively,

$$\begin{aligned} \mathcal {B}^{\lambda _1}= & {} \{ \textrm{x}\in \mathbb {R}^{d} : \lambda _{1}[f](\textrm{x}) \le 0 \} , \end{aligned}$$
(5)
$$\begin{aligned} \mathcal {B}^{\lambda _{d}}= & {} \{ \textrm{x}\in \mathbb {R}^{d} : \lambda _{d}[f](\textrm{x}) \ge 0 \} . \end{aligned}$$
(6)

The concave region (5) yields the most recognizable flavour of bumps in the literature, this time in a multivariate setting. It is the method depicted in Fig. 1c. As for (6), they are actually not bumps but dips. Assuming non-degenerate Hessians, concave bumps typically delineate areas near local pdf modes, while convex dips do with local minima. Consequently, the former and the latter are known as peaks and holes (Godtliebsen et al. 2002, Table 1).

When concave bumps contain local modes, they make the most natural definition of a \(d\)-dimensional neighbourhood. Although straightforward, considering modal regions as \(\varepsilon \)-fattenings or enlargements (see Sect. 3.1.1) poses challenges regarding the choice of \(\varepsilon > 0\), as similarly argued for \(\alpha \) in HDRs. Besides, employing a single radius \(\varepsilon \) limits the overall expressiveness of the bump. On the other hand, if we saw modal regions as basins of attraction instead (Chacón 2015), despite \(\varepsilon \) disappearing and attaining more flexibility, we would not be pursuing a solution to a BH problem any more but a clustering one, giving up on the cohesive sense of bumps. In this respect, concave bumps provide us with an elegant compromise answer.

Moreover, this modal vicinity notion seamlessly incorporates the missing mode scenario. Concave bumps point out incipient modal regions as the central mouth in Fig. 2a, c, which does not contain a mode. Such weak modal regions are well-known in the context of univariate mode hunting as shoulders, representing complicated cases (Cheng and Hall 1999). As for BH, \(d\)-dimensional shoulders deserve attention as evidence of hidden structure. See the NFL application in the SM (Chacón and Fernández Serrano 2023) for an interpretable dynamic shoulder. In turn, the mouth in Fig. 2 is characteristic of mixtures whose components influence each other significantly. All in all, concave bumps subsume the modal regions, having a slightly broader reach.

2.2 Gradient divergence

Concave bumps may be too restrictive in some use cases. Imagine the pdf graph as a landscape, with mountains being local high-density regions. Concave bumps originate near mountain peaks, missing most of the hillside. Mean curvature allows the discovery of entire mountain chains.

The shape operator is a linear map of the tangent space that measures how a manifold bends in different directions [see the SM (Chacón and Fernández Serrano 2023) for a formal definition]. Let us consider its eigenvalues: the principal curvatures. Concavity requires all principal curvatures to be negative. By contrast, the mean curvature adds them all so that only the net sign matters. Computing curvature in this way fills the gaps between concave peaks in a long ridge (Godtliebsen et al. 2002, Table 1), as depicted in Fig. 2b, c in the form of a boomerang.

The SM (Chacón and Fernández Serrano 2023) shows the connection between the mean curvature and divergence of the normalized version of the gradient \(\bar{\nabla }f = \nabla f / \sqrt{1 + \Vert \nabla f \Vert ^2}\). The divergence operator takes positive values when the argument field diverges from a point, whereas the sign is negative when it converges. Therefore, we define the mean curvature bump as

$$\begin{aligned} \mathcal {B}^{\bar{\nabla }}= \{ \textrm{x}\in \mathbb {R}^{d} : \text {div}(\bar{\nabla }f)(\textrm{x}) \le 0 \} . \end{aligned}$$
(7)

When the gradient is slight, as is usually the case for pdfs (one can even tweak the scale of the random variables to make \(\Vert \nabla f \Vert \) small), the Laplacian \(\Delta f = \text {div}(\nabla f) = \sum _{i= 1}^{d}\partial ^2 f/ \partial x_{i}^2\) roughly approximates the mean curvature (see Folland 2002, Equation 5.28). Hence, we define the Laplacian bump as

$$\begin{aligned} \mathcal {B}^{\Delta }= \{ \textrm{x}\in \mathbb {R}^{d} : \Delta f(\textrm{x}) \le 0 \} . \end{aligned}$$
(8)

Note that \(\mathcal {B}^{\lambda _1}\subset \mathcal {B}^{\Delta }\). Even though (8) may be less intrinsic than (7), it has a more straightforward form, for \(\Delta \) is a second-order linear differential operator on \(f\). A discretized version of the Laplacian operator has been used for contour detection in image processing through the Laplacian-of-Gaussian algorithm (Haralick and Shapiro 1992). We have already seen an example of a Laplacian bump in Fig. 1d. The results would have been almost indistinguishable if the mean curvature had been employed.

The term ridge was used above to convey a mountain range covering several peaks following Godtliebsen et al. (2002). Ridges also refer in the statistical literature to a specific definition of higher-dimensional pdf modes (Chen et al. 2015). This concept of ridge shares with Laplacian and mean curvature bumps the ability to unveil filament-like structures. However, ridges are intrinsically one-dimensional in their most typical form. For them to extend to \(\mathbb {R}^{d}\), one would need to take an \(\varepsilon \)-enlargement, introducing some arbitrariness and rigidity with \(\varepsilon \) that gradient divergence bumps do not have. In our context, we will stick to the informal meaning of ridge in the following sections.

2.3 Intrinsic curvature

The Gaussian curvature is an intrinsic measure derived from the shape operator [see the SM (Chacón and Fernández Serrano 2023) for a precise definition]. This and the Hessian determinant provide alternative ways to detect warps. The analysis of these two notions is more subtle than in the previous sections: from the definition of Gaussian curvature in the SM (Chacón and Fernández Serrano 2023), many sign combinations among the multiplied principal curvatures produce the same net sign.

The Gaussian curvature and the Hessian determinant differ by a positive factor; thus, if we set the bump detection threshold at zero, we can restrict our analysis to the latter. In the bivariate case, the bump

$$\begin{aligned} \mathcal {B}^{\det }= \{ \textrm{x}\in \mathbb {R}^2 : \det ({\textrm{D}^{2}f})(\textrm{x}) \ge 0 \} \end{aligned}$$
(9)

coincides with the union of (5) and (6). Therefore, (9) is helpful for detecting both concave bumps and convex dips simultaneously. We will refer to (9) as a Gaussian bump.

3 Asymptotics

This section will demonstrate the soundness of plug-in estimators in the asymptotic regime for curvature bumps.

3.1 Consistency

We rely on a recent result by Chen to prove consistency (Chen 2022). Let

$$\begin{aligned} \mathcal {M}= & {} \{ \textrm{x}\in \mathbb {R}^{d}: \Psi (\textrm{x}) = 0 \} , \end{aligned}$$
(10)
$$\begin{aligned} \tilde{\mathcal {M}}= & {} \{ \textrm{x}\in \mathbb {R}^{d}: \tilde{\Psi }(\textrm{x}) = 0 \} \end{aligned}$$
(11)

be two solution manifolds defined by their criterion functions \(\Psi , \tilde{\Psi }: \mathbb {R}^{d} \rightarrow \mathbb {R}\), respectively. Chen’s stability theorem shows that \(\mathcal {M}\) and \(\tilde{\mathcal {M}}\) are near whenever the criterion functions and their derivatives are close. In our context, \(\Psi \) will represent a curvature measure and \(\tilde{\Psi }\) the corresponding kernel plug-in estimator so that \(\mathcal {M}\) and \(\tilde{\mathcal {M}}\) are the boundaries of the associated curvature bumps.

3.1.1 Notational preliminaries

The theory of convergence in the uniform norm for KDDE allows applying Chen’s stability theorem to the curvature BH problem.

Vectors of nonnegative integers \(\varvec{\beta }= (\beta _1, \dots , \beta _{d}) \in \mathbb {Z}_{+}^{d}\) shall represent partial derivatives through \(\partial ^{\varvec{\beta }}f= \partial ^{\left| \varvec{\beta } \right| }f/ \partial x_{1}^{\beta _{1}} \cdots \partial x_{d}^{\beta _{d}}\), where \(\left| \varvec{\beta } \right| = \sum _{i= 1}^{d}\beta _{i}\). Let us call \(\mathbb {Z}_{+}^{d}[k] = \{\varvec{\beta }\in \mathbb {Z}_{+}^{d}: \left| \varvec{\beta } \right| \le k\}\). We also include the case \(\varvec{\beta }= \varvec{0}\), which represents the identity. Let us also define, for any derivative index vectors \(\varvec{\beta }_{1}, \dots , \varvec{\beta }_{m} \in \mathbb {Z}_{+}^{d}\), the function \(\partial ^{\varvec{\beta }_{1}, \dots , \varvec{\beta }_{m}}f: \mathbb {R}^{d} \rightarrow \mathbb {R}^{m}\) as \(\partial ^{\varvec{\beta }_{1}, \dots , \varvec{\beta }_{m}}f(\textrm{x}) = (\partial ^{\varvec{\beta }_{1}} f(\textrm{x}), \dots , \partial ^{\varvec{\beta }_{m}} f(\textrm{x}))\).

We will denote \(\mathcal {C}^{\ell }(A)\) the class of functions \(\varphi : A\subset \mathbb {R}^{d} \rightarrow \mathbb {R}\) with continuous partial derivatives up to \(\ell \)-th order. Likewise, we will say that a function \(\varphi : \mathbb {R}^{d} \rightarrow \mathbb {R}\) is Hölder continuous with exponent \(\alpha \in (0, 1]\) if there exists \(C\in (0, \infty )\) such that \(\left| \varphi (\textrm{x}) - \varphi (\textrm{y}) \right| \le C\Vert \textrm{x}- \textrm{y} \Vert ^{\alpha }\), for all \(\textrm{x}, \textrm{y}\in \mathbb {R}^{d}\) (Jiang 2017). By convention, we include the case \(\alpha = 0\) when Hölder continuity does not hold for any positive exponent.

For any \(\varphi : \mathbb {R}^{d} \rightarrow \mathbb {R}\) and some \(A\subset \mathbb {R}^{d}\), we denote \(\Vert \varphi \Vert _{\infty } = \sup _{\textrm{x}\in A}{\vert \varphi (\textrm{x}) \vert }\), and we will indicate that the supremum is over \(A\) by explicitly stating that \(\Vert \varphi \Vert _{\infty }\) satisfies some property on \(A\). Also, write \(\Vert \varphi \Vert _{\infty , k} = \max \left\{ \Vert \partial ^{\varvec{\beta }}\varphi \Vert _{\infty }: \varvec{\beta }\in \mathbb {Z}_{+}^{d}, \left| \varvec{\beta } \right| = k\right\} \). All these norms will formalize how close the criterion functions and their respective derivatives are.

On the other hand, the stability theorem invokes some other concepts related to sets. Let us define the distance from a point \(x \in \mathbb {R}^{d}\) to some subset \(A\subset \mathbb {R}^{d}\) as \(d(\textrm{x}, A) = \inf _{\textrm{y}\in A} \Vert \textrm{x}- \textrm{y} \Vert \), and the \(\varepsilon \)-fattening of a set \(A\subset \mathbb {R}^{d}\), where \(\varepsilon > 0\), as \(A \oplus \varepsilon = \{ \textrm{x}\in \mathbb {R}^{d}: d(\textrm{x}, A) \le \varepsilon \}\). Finally, the Hausdorff distance between two subsets \(A, B\subset \mathbb {R}^{d}\) is \(\textrm{Haus}(A, B) = \max \left\{ \sup _{\textrm{x}\in B} d(\textrm{x}, A), \sup _{\textrm{x}\in A} d(\textrm{x}, B) \right\} \).

The problem of uniformly bounding the KDDE error refers to finding an infinitesimal bound for \(\sup _{\textrm{x}\in \mathbb {R}^{d}}\vert \partial ^{\varvec{\beta }}\hat{f}_{n, h}(\textrm{x})- \partial ^{\varvec{\beta }}f(\textrm{x}) \vert \). Note that the latter is bounded by the bias \(\sup _{\textrm{x}\in \mathbb {R}^{d}}\vert \mathbb {E}[\partial ^{\varvec{\beta }}\hat{f}_{n, h}(\textrm{x})] - \partial ^{\varvec{\beta }}f(\textrm{x}) \vert \) plus the stochastic error \(\sup _{\textrm{x}\in \mathbb {R}^{d}}\vert \partial ^{\varvec{\beta }}\hat{f}_{n, h}(\textrm{x})- \mathbb {E}[\partial ^{\varvec{\beta }}\hat{f}_{n, h}(\textrm{x})] \vert \). We will analyse both terms separately.

3.1.2 Bias analysis

Lemma 1 is an extended version of (Arias-Castro et al. 2016, Lemma 2) with alternative hypotheses to ensure consistency under less stringent differentiability assumptions. Namely, we resort to Hölder and uniform continuity, following the example of Jiang (2017) and (Nadaraya 1989, Theorem 1.1, p. 42).

Lemma 1

Let \(\varvec{\beta }\in \mathbb {Z}_{+}^{d}\) be a partial derivative index vector. Let \(f\) be a pdf in \(\mathcal {C}^{\left| \varvec{\beta } \right| + r}(\mathbb {R}^{d})\), for some \(r\in \mathbb {Z}_{+}\cup \{\infty \}\), with all partial derivatives bounded up to \((\left| \varvec{\beta } \right| + r)\)-th order. Assume that \(\partial ^{\varvec{\beta }}f\) is Hölder continuous on \(\mathbb {R}^{d}\) with exponent \(\alpha \in [0, 1]\). If the exponent is \(\alpha = 0\), then ultimately assume that \(\partial ^{\varvec{\beta }}f\) is uniformly continuous. Finally, let \(\hat{f}_{n, h}\) be the KDE of \(f\) based on a true pdf kernel \(K\) vanishing at infinity and satisfying the moment constraints

$$\begin{aligned} \int _{\mathbb {R}^{d}}\textrm{x}\ K(\textrm{x}) \ d{\textrm{x}}= & {} \varvec{0}, \\ \int _{\mathbb {R}^{d}}\left| \textrm{x}_{i} \textrm{x}_{j} \right| \ K(\textrm{x}) \ d{\textrm{x}}< & {} \infty , \end{aligned}$$

for all \(i, j\in \{1, \dots , d\}\). Then,

$$\begin{aligned} \sup _{\textrm{x}\in \mathbb {R}^{d}}\vert \mathbb {E}[\partial ^{\varvec{\beta }}\hat{f}_{n, h}(\textrm{x})] - \partial ^{\varvec{\beta }}f(\textrm{x}) \vert = {\left\{ \begin{array}{ll} O(h^{s}), &{} \textrm{if} \ \max \{r, \alpha \} > 0 \\ o(1)\ \textrm{as} \ h\rightarrow 0, &{} \textrm{otherwise} \end{array}\right. } , \end{aligned}$$

where \(s= \max \{\alpha , \min \{r, 2\}\}\).

3.1.3 Stochastic error analysis

Lemma 2 appears as an auxiliary result in Arias-Castro et al. (2016) in the case \(\ell = 3\), but the proof works for an arbitrary \(\ell \).

Lemma 2

(Arias-Castro et al. 2016). Let \(f\) be a bounded pdf in \(\mathbb {R}^{d}\) and let \(\hat{f}_{n, h}\) be the KDE of \(f\). Fix a nonnegative integer \(\ell \) as the maximum partial derivative order. Assume that \(K\) is a product kernel of the form \(K(x_1, \dots , x_{d}) = \prod _{i= 1}^{d} \upkappa _{i}(x_{i})\), where each \(\upkappa _{i}\) is a univariate PDF of class \(\mathcal {C}^{\ell }(\mathbb {R})\). Further, assume that all the partial derivatives up to \(\ell \)-th order of \(K\) are of bounded variation and integrable on \(\mathbb {R}^{d}\). Then, there exists \(b\in (0, 1)\) such that, if \(h\equiv h_{n}\) is a sequence satisfying \(\log n\le nh^{d} \le bn\), then

$$\begin{aligned} \sup _{\textrm{x}\in \mathbb {R}^{d}}\vert \partial ^{\varvec{\beta }}\hat{f}_{n, h}(\textrm{x})- \mathbb {E}[\partial ^{\varvec{\beta }}\hat{f}_{n, h}(\textrm{x})] \vert = O\left( \sqrt{\frac{\log n}{nh^{d+ 2\left| \varvec{\beta } \right| }}}\right) , \end{aligned}$$

almost surely (a.s.) for all \(\varvec{\beta }\in \mathbb {Z}_{+}^{d}[\ell ]\).

Finally, note that Lemma 2 also holds for a sufficiently small but constant \(h\).

3.1.4 Total error analysis

Combining Lemmas 1 and 2, we obtain a general consistency result in the supremum norm for KDDE. We will focus on the Gaussian kernel for simplicity, but any other satisfying the conditions in both Lemmas 1 and 2 would do.

Theorem 1

Let \(\varvec{\beta }\in \mathbb {Z}_{+}^{d}\) be a partial derivative index vector. Let \(f\) be a pdf in \(\mathcal {C}^{\left| \varvec{\beta } \right| + r}(\mathbb {R}^{d})\), for some \(r\in \mathbb {Z}_{+}\cup \{\infty \}\), with all partial derivatives bounded up to \((\left| \varvec{\beta } \right| + r)\)-th order. Assume that \(\partial ^{\varvec{\beta }}f\) is Hölder continuous on \(\mathbb {R}^{d}\) with exponent \(\alpha \in [0, 1]\). If the exponent is \(\alpha = 0\), then ultimately assume that \(\partial ^{\varvec{\beta }}f\) is uniformly continuous. Let \(\hat{f}_{n, h}\) be the KDE of \(f\) based on the Gaussian kernel. Finally, let \(h\equiv h_{n}\) be a sequence converging to zero as \(n\rightarrow \infty \) and satisfying \(nh^{d} \ge \log n\). Then,

$$\begin{aligned} \sup _{\textrm{x}\in \mathbb {R}^{d}}\vert \partial ^{\varvec{\beta }}\hat{f}_{n, h}(\textrm{x})- \partial ^{\varvec{\beta }}f(\textrm{x}) \vert = {\left\{ \begin{array}{ll} O\left( h^{s} + \sqrt{\frac{\log n}{nh^{d+ 2\left| \varvec{\beta } \right| }}}\right) , \ {} &{} \textrm{if} \ \max \{r, \alpha \} > 0 \\ o(1)+ O\left( \sqrt{\frac{\log n}{nh^{d+ 2\left| \varvec{\beta } \right| }}}\right) , \ {} &{} \textrm{otherwise} \end{array}\right. } , \end{aligned}$$

a.s. as \(n\rightarrow \infty \), where \(s= \max \{\alpha , \min \{r, 2\}\}\). In particular,

$$\begin{aligned} \sup _{\textrm{x}\in \mathbb {R}^{d}}\vert \partial ^{\varvec{\beta }}\hat{f}_{n, h}(\textrm{x})- \partial ^{\varvec{\beta }}f(\textrm{x}) \vert \xrightarrow [n\rightarrow \infty ]{{a.s.}}0 \, \ \textrm{if} \ \frac{\log n}{nh^{d+ 2\left| \varvec{\beta } \right| }}\xrightarrow [n\rightarrow \infty ]{}0 . \end{aligned}$$

3.1.5 Manifold stability

Theorem 2 gathers the essential elements of Chen’s stability theorem needed in our context.

Theorem 2

(Chen 2022). Let \(\Psi , \tilde{\Psi }: \mathbb {R}^{d} \rightarrow \mathbb {R}\) and let \(\mathcal {M}\) and \(\tilde{\mathcal {M}}\) be as defined in (10) and (11), respectively. Assume that:

  1. A1.

    There exists \(\delta > 0\) such that \(\Psi \) has bounded first-order derivatives on \(\mathcal {M} \oplus \delta \).

  2. A2.

    There exists \(\lambda > 0\) such that \(\Vert \nabla \Psi (\textrm{x}) \Vert > \lambda \), for all \(\textrm{x}\in \mathcal {M} \oplus \delta \).

  3. A3.

    \(\Vert \tilde{\Psi }- \Psi \Vert _{\infty }\) is sufficiently small on \(\mathbb {R}^{d}\).

Moreover, suppose that:

  1. B1.

    \(\tilde{\Psi }\) has bounded first-order derivatives on \(\mathcal {M} \oplus \delta \).

  2. B2.

    \(\Vert \tilde{\Psi }- \Psi \Vert _{\infty , 1}\) is sufficiently small on \(\mathcal {M} \oplus \delta \).

Then, \(\textrm{Haus}(\tilde{\mathcal {M}}, \mathcal {M}) = O(\Vert \tilde{\Psi }- \Psi \Vert _{\infty })\).

We have introduced in Theorem 2 a slight relaxation on the differentiability constraint for \(\tilde{\Psi }\). Chen supposes differentiability and bounds on \(\mathbb {R}^{d}\), whereas we allow for a narrower domain \(\mathcal {M} \oplus \delta \). This deviation is justified since hypotheses \((\textrm{A})\) imply \(\tilde{\mathcal {M}}\subset \mathcal {M} \oplus \varepsilon \subset \mathcal {M} \oplus \delta \), where \(\varepsilon < \delta \). Since pdfs typically vanish at infinity, it might be unfeasible to ask \(\tilde{\Psi }= \phi [\hat{f}_{n, h}]\) to be differentiable everywhere. This is the case for the eigenvalues (4) in Proposition 1, where condition (12) would not hold if the infimum were taken over \(\mathbb {R}^{d}\).

Finally, putting all the pieces together, we get the following main result.

Theorem 3

Assume the following:

\(\tiny {\blacklozenge }\):

Let \(\phi \) be a curvature functional defined over \(d\)-variate pdfs depending on their partial derivatives up to \(\ell \)-th order. More formally, given a pdf \(p\), we have \(\phi [p] = \varphi \circ \partial ^{\varvec{\beta }_{1}, \dots , \varvec{\beta }_{m}}p\), for some \(\varphi : \mathbb {R}^{m} \rightarrow \mathbb {R}\) and derivative index vectors \(\varvec{\beta }_{1}, \dots , \varvec{\beta }_{m} \in \mathbb {Z}_{+}^{d}[\ell ]\).

\(\tiny {\blacklozenge }\):

Let \(f\) be a pdf in \(\mathcal {C}^{\ell + r}(\mathbb {R}^{d})\), for some \(r\in \{1, 2, \dots , \infty \}\), with all partial derivatives bounded up to \((\ell + r)\)-th order. If \(r= 1\), further assume that the \((\ell + 1)\)-th partial derivatives of \(f\) are either Hölder continuous with exponent \(\alpha \in (0, 1]\) or uniformly continuous.

\(\tiny {\blacklozenge }\):

Let \(\hat{f}_{n, h}\) be the KDE of \(f\) based on the Gaussian kernel.

\(\tiny {\blacklozenge }\):

Let \(h\equiv h_{n}\) converge to zero and satisfy \(\lim _{n\rightarrow \infty }n^{-1} h^{-(d+ 2\ell + 2)} \log n = 0\).

Let the curvature bump boundary and its plug-in estimator, respectively, be

$$\begin{aligned} \partial \mathcal {B}^{\phi }= & {} \{ \textrm{x}\in \mathbb {R}^{d} : \phi [f](\textrm{x}) = 0 \} , \\ \partial \tilde{\mathcal {B}}_{n, h}^{\phi }= & {} \{ \textrm{x}\in \mathbb {R}^{d} : \phi [\hat{f}_{n, h}](\textrm{x}) = 0 \} . \end{aligned}$$

Further, suppose that:

\(\tiny {\blacklozenge }\):

There exists \(\delta > 0\) such that \(\varphi \in \mathcal {C}^{1}(\mathcal {U})\), for some open set \(\mathcal {U}\subset \mathbb {R}^{m}\) containing the images of \(\partial \mathcal {B}^{\phi } \oplus \delta \) under both \(\partial ^{\varvec{\beta }_{1}, \dots , \varvec{\beta }_{m}}f\) and \(\partial ^{\varvec{\beta }_{1}, \dots , \varvec{\beta }_{m}}\hat{f}_{n, h}\) a.s.

\(\tiny {\blacklozenge }\):

There exists \(\lambda > 0\) such that \(\Vert \nabla \phi [f](\textrm{x}) \Vert > \lambda \), for all \(\textrm{x}\in \partial \mathcal {B}^{\phi } \oplus \delta \).

Then,

$$\begin{aligned} \textrm{Haus}(\partial \tilde{\mathcal {B}}_{n, h}^{\phi }, \partial \mathcal {B}^{\phi })= O\left( h^{\min \{r, 2\}} + \sqrt{\frac{\log n}{nh^{d+ 2\ell }}} \right) \xrightarrow [n\rightarrow \infty ]{{a.s.}}0 . \end{aligned}$$

The optimal bound is \(\textrm{Haus}(\partial \tilde{\mathcal {B}}_{n, h}^{\phi }, \partial \mathcal {B}^{\phi })= O([ n^{-1} \log n]^{2 / (d+ 2\ell + 4)})\), achieved with \(h\asymp [ n^{-1} \log n]^{1 / (d+ 2\ell + 4)}\) (\(r\ge 2\)). The former coincides up to a logarithmic term with the optimum in KDDE for \(\ell \)-th order partial derivatives according to the root mean integrated square error criterion, which is \(O(n^{-2 / (d+ 2\ell + 4)})\) (Chacón et al. 2011).

Theorem 3 straightforwardly leads to bump boundary convergence results for the determinants and traces of the shape operator and the Hessian matrix.

Example 1

Consider the Laplacian and Gaussian bumps (8) and (9) for a bivariate pdf \(f: \mathbb {R}^2 \rightarrow [0, \infty )\), with \(\phi [f]\) equal to, respectively,

$$\begin{aligned} \textrm{tr}(\textrm{D}^{2}f)\equiv & {} \Delta f = \frac{\partial ^2 f}{\partial x_{1}^2} + \frac{\partial ^2 f}{\partial x_{2}^2} , \\ \det ({\textrm{D}^{2}f})= & {} \frac{\partial ^2 f}{\partial x_{1}^2} \frac{\partial ^2 f}{\partial x_{2}^2} - \left( \frac{\partial ^2 f}{\partial x_{1}\partial x_{2}} \right) ^2 . \end{aligned}$$

For the trace, the underlying derivative functional is \(\varphi (a_1, a_2) = a_1 + a_2\), considering \(\varvec{\beta }_{1} = (2, 0)\) and \(\varvec{\beta }_{2} = (0, 2)\). In turn, the functional is \(\varphi (a_1, a_2, a_3) = a_1 a_2 - a_3^2\) for the determinant, taking \(\varvec{\beta }_{1}\) and \(\varvec{\beta }_{2}\) as before plus \(\varvec{\beta }_{3} = (1, 1)\). In both cases, \(\varphi \) is an infinitely smooth function over \(\mathcal {U}= \mathbb {R}^{m}\), making every \(\delta > 0\) satisfy the requirement in Theorem 3 without imposing additional hypotheses on the original pdf and its KDE.

The case for the Hessian eigenvalues is more involved. The functions \(\lambda _{i}[f]\) in (4) are not generally \(\mathbb {R}^{d}\)-differentiable. To solve this differentiability issue, we will follow the standard assumption in Kato’s book that, for every \(\textrm{x}\in \mathbb {R}^{d}\), all the eigenvalues of \(\textrm{D}^{2}f(\textrm{x})\) have multiplicity one (Kato 1995, Theorem 5.16, p. 119). We will ask for an even stronger hypothesis to ensure that all plug-in estimators \(\lambda _{i}[\hat{f}_{n, h}]\) are eventually distinct everywhere for large \(n\) a.s.

Proposition 1

Let \(f\) be a pdf and let \(\hat{f}_{n, h}\) be its KDE. Let us assume that \(f\) and \(\hat{f}_{n, h}\) satisfy all the conditions in Theorem 1 so that the second-order partial derivatives of \(f\) are consistently approximated with plug-in estimators. Let us call \(\partial \mathcal {B}^{\phi }\) the bump boundary for the criterion function \(\phi \equiv \lambda _{j}[f]\), for some \(j\in \{1, \dots , d\}\). If there exists \(\delta > 0\) such that

$$\begin{aligned} \inf _{\textrm{x}\in \partial \mathcal {B}^{\phi } \oplus \delta } \{\lambda _{i}[f](\textrm{x}) - \lambda _{i + 1}[f](\textrm{x})\} > 0 , \end{aligned}$$
(12)

for all \(i\in \{1, \dots , d- 1\}\), then (12) also holds a.s. for \(n\) sufficiently large if we replace \(f\) by \(\hat{f}_{n, h}\). In particular, both \(\lambda _{j}[f]\) and \(\lambda _{j}[\hat{f}_{n, h}]\) are infinitely differentiable functions of the second-order partial derivatives of \(f\) and \(\hat{f}_{n, h}\), respectively, on some neighbourhood \(\partial \mathcal {B}^{\phi } \oplus \delta \) a.s. for \(n\) sufficiently large.

3.2 Inference

In this section, we derive bootstrap inference for curvature bumps, following similar steps as in the scheme developed by Chen et al. for pdf level sets (Chen et al. 2017). To accommodate the required techniques, we will exclusively focus on curvature functionals \(\phi \) deriving from the pdf Hessian \(\textrm{D}^{2}f\).

3.2.1 Inference scheme

We will simplify the inference problem by targeting \(f_{h}: \mathbb {R}^{d} \rightarrow [0, \infty )\), given by \(f_{h}(\textrm{x}) = \mathbb {E}[\hat{f}_{n, h}(\textrm{x})]\), instead of \(f\), considering the bias negligible for a small \(h\). There are compelling arguments favouring \(f_{h}\) against \(f\) for inference purposes (see Chen et al. 2017, Section 2.2 for a thorough discussion).

Let us call \(\mathcal {B}_{h}^{\phi }\) the smoothed version of (1) derived by replacing \(f\) with \(f_{h}\). We will assume that \(\mathcal {B}_{h}^{\phi }\subset \Theta \), for some \(\Theta \subset \mathbb {R}^{d}\), or at least that the inferential procedure focuses on \(\mathcal {B}_{h}^{\phi }\cap \Theta \). Ideally, \(\Theta \) should be as small as possible (hopefully \(\Theta \ne \mathbb {R}^{d}\)) so that the resulting confidence regions are efficient.

Given \(\alpha \in (0, 1)\), a path for narrowing down a (\(1 - \alpha \))-level confidence region for \(\mathcal {B}_{h}^{\phi }\) is constructing two sets

(13)

for some margin \(\zeta _{n, h}^{\alpha }\in [0, \infty )\). Note that , thus (13) are set bounds for the \(\tilde{\mathcal {B}}_{n, h}^{\phi }\) in (3) approximating \(\mathcal {B}_{h}^{\phi }\). This vertical scheme is similar to Chen et al.’s second method for pdf level set inference (Chen et al. 2017) and a particular case of Mammen and Polonik’s universal approach (Mammen and Polonik 2013).

Our inference results will establish conditions to ensure the previous set inequality eventually holds too with probability \(1 - \alpha \) when replacing \(\tilde{\mathcal {B}}_{n, h}^{\phi }\) with \(\mathcal {B}_{h}^{\phi }\) while the set bounds (13) draw nearer \(\mathcal {B}_{h}^{\phi }\), namely

(14)

as \(n\rightarrow \infty \), for some sequence \(\{ \tilde{\zeta }_{n, h}^{\alpha }\}_{n= 1}^{\infty }\). The inference scheme (14) can be proven for all curvature bumps using Theorem 4. From Sect. 3.1, it is an exercise to realize that, under the conditions in which (14) will hold, and with a few mild additional assumptions, the boundaries of the set bounds (13) converge in the Hausdorff distance to \(\partial \mathcal {B}_{h}^{\phi }\).

In what follows, we will equivalently denote \(\mathcal {Q}_{p} \{ X \} \equiv \mathcal {Q}_{X}(p)\) the \(p\)-th quantile, \(p\in (0, 1)\), of the rv \(X\) (van der Vaart 1998, p. 304).

Theorem 4

In the context described above, assume the following:

  1. I

    There exists a sequence of random variables \(\{Z_{n, h}\}_{n= 1}^{\infty }\) such that, for sufficiently large \(n\in \mathbb {N}\), \(\mathcal {S}_{n, h}[\phi ] \equiv \sup _{\textrm{x}\in \Theta }\vert \phi [\hat{f}_{n, h}](\textrm{x}) - \phi [f_{h}](\textrm{x}) \vert \le Z_{n, h}\) a.s. Let us further assume that \(\sqrt{n}Z_{n, h}\) converges weakly (van der Vaart and Wellner 1996) to some rv \(\mathcal {Z}\) as \(n\rightarrow \infty \), denoted by \(\sqrt{n}Z_{n, h} \leadsto \mathcal {Z}\). Suppose that \(\mathcal {Z}\) has a continuous and strictly increasing cumulative distribution function (cdf ).

  2. II

    For each \(\alpha \in (0, 1)\), there is \(\{ \zeta _{n, h}^{\alpha }\}_{n= 1}^{\infty }\) satisfying \(\zeta _{n, h}^{\alpha }\ge \mathcal {Q}_{1 - \alpha } \{ Z_{n, h} \}\), for all \(n\in \mathbb {N}\), and \(\lim _{n\rightarrow \infty }\zeta _{n, h}^{\alpha }= 0\).

  3. III

    For each \(\alpha \in (0, 1)\), there is \(\{ \tilde{\zeta }_{n, h}^{\alpha }\}_{n= 1}^{\infty }\) satisfying \(\vert \tilde{\zeta }_{n, h}^{\alpha }- \zeta _{n, h}^{\alpha } \vert = o(n^{-1/2})\) as \(n\rightarrow \infty \).

Then, for all \(\alpha \in (0, 1)\), the asymptotic validity of the inference scheme (14) holds.

The following sections will introduce theoretical results leading to bootstrap estimates \(\tilde{\zeta }_{n, h}^{\alpha }\) that can be feasibly computed in practice.

Mammen and Polonik’s approach (Mammen and Polonik 2013) achieves a sharp asymptotic coverage probability \(1 - \alpha \) in (14). A key difference separating their proposal from Chen, Genovese, and Wasserman’s and ours is that they manage to bootstrap from an rv that is a supremum over a neighbourhood of the level set, unlike \(\mathcal {S}_{n, h}[\phi ]\) in Theorem 4, which considers the whole \(\Theta \). See Qiao and Polonik (2019) for an overview of similar local strategies for level sets. Based on that, Mammen and Polonik’s method will generally be less conservative.

3.2.2 Bootstrap outline

The main point to fill the Theorem 4 template is approximating the stochastic errors for second-order linear differential operators \(\mathcal {D}\)

$$\begin{aligned} \mathcal {E}_{n, h}[\mathcal {D}] = \sup _{\textrm{x}\in \Theta }\vert \mathcal {D}\hat{f}_{n, h}(\textrm{x}) - \mathcal {D}f_{h}(\textrm{x}) \vert , \end{aligned}$$
(15)

using bootstrap estimates

$$\begin{aligned} \mathcal {E}_{n, h}^{*}[\mathcal {D} | \mathfrak {X}_{n}] = \sup _{\textrm{x}\in \Theta }\vert \mathcal {D}\hat{f}_{n, h}^{*}(\textrm{x} | \mathfrak {X}_{n}) - \mathcal {D}\hat{f}_{n, h}(\textrm{x} | \mathfrak {X}_{n}) \vert , \end{aligned}$$
(16)

where \(\hat{f}_{n, h}^{*}(\cdot | \mathfrak {X}_{n})\) denotes the KDE based on \(n\) i.i.d. random variables \(\textrm{X}^{*}_1, \dots , \textrm{X}^{*}_{n} \sim \mathbb {P}^{*}_{n}\{\mathfrak {X}_{n}\}\) of the empirical bootstrap probability measure \(\mathbb {P}^{*}_{n}\{\mathfrak {X}_{n}\}\) assigning equal masses \(1/n\) to each component \(\textrm{x}_{i} \in \mathbb {R}^{d}\) of a particular \(n\)-size i.i.d. realization \(\mathfrak {X}_{n}= \{\textrm{x}_1, \dots , \textrm{x}_{n}\}\) from \(f\), and \(\hat{f}_{n, h}(\cdot | \mathfrak {X}_{n})\) is the realization of the KDE based on \(\mathfrak {X}_{n}\), i.e.

$$\begin{aligned} \hat{f}_{n, h}^{*}(\textrm{x} | \mathfrak {X}_{n})= & {} \frac{1}{n}\sum _{i= 1}^{n}K_{h}(\textrm{x}- \textrm{X}^{*}_{i}) , \\ \hat{f}_{n, h}(\textrm{x} | \mathfrak {X}_{n})= & {} \frac{1}{n}\sum _{i= 1}^{n}K_{h}(\textrm{x}- \textrm{x}_{i}) . \end{aligned}$$

Assume that both (15) and (16) use the same kernel \(K\) everywhere. Estimating confidence regions for curvature bumps will go through, directly or indirectly, approximating the cdf of (15) with that of (16).

3.2.3 Gaussian process approximation

Lemma 3 allows a Gaussian process (GP) approximation between the suprema (15) and (16). See (van der Vaart and Wellner 1996) for further knowledge about GPs. The empirical process (van der Vaart and Wellner 1996) on a sample \(\textrm{X}_1, \dots , \textrm{X}_{n}\) of i.i.d. \(d\)-dimensional random variables indexed by a class \(\mathcal {F}\) of measurable functions \(\varphi : \mathbb {R}^{d} \rightarrow \mathbb {R}\) is defined as the functional \(\mathbb {G}_{n}\) mapping a function \(\varphi \in \mathcal {F}\) to the rv

$$\begin{aligned} \mathbb {G}_{n}(\varphi ) = \frac{1}{\sqrt{n}} \sum _{i= 1}^{n}\left( \varphi (\textrm{X}_{i}) - \mathbb {E}\left[ \varphi (\textrm{X}_{i}) \right] \right) . \end{aligned}$$

Lemma 3 invokes the pointwise measurable (PM) and Vapnik-Chervonenkis (VC)-type classes of functions. We refer the reader to van der Vaart and Wellner (1996) for the former and briefly define the latter, including the auxiliary Definition 1.

Definition 1

. Let \((\mathcal {V}, \Vert \cdot \Vert )\) be a vector space with a seminorm and let \(\mathcal {F}\subset \mathcal {V}\). We define the \(\epsilon \)-covering number of \(\mathcal {F}\), denoted by \(\mathcal {N}(\mathcal {F}, \mathcal {V}, \epsilon )\), as the minimum number of \(\epsilon \)-balls of the form \(\{ \textrm{x}\in \mathcal {V}: \Vert \textrm{x}- \textrm{y} \Vert < \epsilon \}\), where \(\textrm{y}\in \mathcal {V}\), needed to cover \(\mathcal {F}\).

Definition 2

. Let \(\mathcal {F}\) be a class of measurable functions \(\varphi : \mathbb {R}^{d} \rightarrow \mathbb {R}\). Let \(\Psi \) be an envelope function for \(\mathcal {F}\), i.e. \(\Psi : \mathbb {R}^{d} \rightarrow \mathbb {R}\) measurable such that \(\sup _{\varphi \in \mathcal {F}} \left| \varphi (\textrm{x}) \right| \le \Psi (\textrm{x})\) for all \(\textrm{x}\in \mathbb {R}^{d}\). An \(\mathcal {F}\) class equipped with an envelope \(\Psi \) is called a VC-type class if there exist \(A, \nu \in (0, \infty )\) such that, for all \(\epsilon \in (0, 1)\),

$$\begin{aligned} \sup _{\mathbb {Q}} \mathcal {N}(\mathcal {F}, \mathcal {L}^{2}(\mathbb {R}^{d}; \mathbb {Q}), \epsilon \Vert \Psi \Vert _{2, \mathbb {Q}}) \le \left( \frac{A}{\epsilon } \right) ^{\nu } , \end{aligned}$$

where the supremum is taken over all finitely discrete probability measures \(\mathbb {Q}\) defined on \(\mathbb {R}^{d}\) and \(\Vert \Psi \Vert _{2, \mathbb {Q}} = ( \int _{\mathbb {R}^{d}}\left| \Psi \right| ^2 d\mathbb {Q})^{1/2}\) is the seminorm of \(\mathcal {L}^{2}(\mathbb {R}^{d}; \mathbb {Q})\).

We will denote the Kolmogorov distance as \(\uprho _{\mathrm {{cdf}}} \left( X, Y \right) = \sup _{t\in \mathbb {R}} \left| F_{X}(t) - F_{Y}(t) \right| \), where \(F_{X}\) is the cdf of the rv \(X\). Likewise, \(X{\mathop {=}\limits ^{d}}Y\) will denote equality in distribution between the random variables.

Lemma 3

(Chernozhukov et al. 2014; Chen et al. 2015, 2016). Consider a sample \(\textrm{X}_1, \dots , \textrm{X}_{n}\) of i.i.d. random variables. Let \(\mathcal {F}\) be a PM and VC-type class of functions with constant envelope \(b\in (0, \infty )\). Let \(\sigma \in (0, \infty )\) be such that \(\sup _{\varphi \in \mathcal {F}}{\mathbb {E}\left[ \varphi (\textrm{X}_1)^2 \right] } \le \sigma ^2 \le b^2\). Let \(\mathbb {B}\) be a centred tight GP with sample paths on the space of bounded functions \(\ell ^{\infty }(\mathcal {F})\), and with covariance function

$$\begin{aligned} \textrm{Cov}(\mathbb {B}(\varphi _1), \mathbb {B}(\varphi _2)) = \mathbb {E}\left[ \varphi _1(\textrm{X}_1) \varphi _2(\textrm{X}_1) \right] - \mathbb {E}\left[ \varphi _1(\textrm{X}_1) \right] \mathbb {E}\left[ \varphi _2(\textrm{X}_1) \right] , \end{aligned}$$
(17)

for \(\varphi _1, \varphi _2 \in \mathcal {F}\). Then, there exists an rv \({\textbf {B}} {\mathop {=}\limits ^{d}}\sup _{\varphi \in \mathcal {F}}\vert \mathbb {B}(\varphi ) \vert \) such that, for all \(\gamma \in (0, 1)\) and \(n\) sufficiently large,

$$\begin{aligned} \mathbb {P}\left( \left| \sup _{\varphi \in \mathcal {F}}\vert \mathbb {G}_{n}(\varphi ) \vert - {\textbf {B}} \right| > A_1\frac{b^{1/3} \sigma ^{2/3} \log ^{2/3} n}{\gamma ^{1/3} n^{1/6}} \right) \le A_2\gamma , \end{aligned}$$

where \(\mathbb {G}_{n}\) is based on \(\textrm{X}_1, \dots , \textrm{X}_{n}\), and \(A_1, A_2\) are universal constants.

If we apply Lemma 3 to (15), we get the following result.

Theorem 5

Let \(\mathcal {D}\) denote any linear \(\ell \)-th order differential operator. Let \(K\in \mathcal {C}^{\ell }(\mathbb {R}^{d})\) be a kernel with bounded \(\ell \)-th derivatives. Further, suppose that the class

$$\begin{aligned} \mathcal {K}= \left\{ \textrm{y}\in \mathbb {R}^{d} \mapsto \partial ^{\varvec{\beta }}K\left( \frac{\textrm{x}- \textrm{y}}{h} \right) : \textrm{x}\in \Theta , h> 0, \varvec{\beta }\in \mathbb {Z}_{+}^{d}, \left| \varvec{\beta } \right| = \ell \right\} \end{aligned}$$
(18)

is VC-type. Let \(h\equiv h_{n}\) be a sequence with \(h\in (0, 1)\) and \(h^{-(d+ \ell )} = O(\log n)\). Moreover, let \(\mathbb {B}\) be a GP with the same properties as in Lemma 3 and indexed by

$$\begin{aligned} \mathcal {F}_{h}= \left\{ \textrm{y}\in \mathbb {R}^{d} \mapsto \frac{1}{\sqrt{h^{d+ \ell }}} \mathcal {D}K\left( \frac{\textrm{x}- \textrm{y}}{h} \right) : \textrm{x}\in \Theta \right\} . \end{aligned}$$
(19)

Then, there exists \({\textbf {B}} _{h}{\mathop {=}\limits ^{d}}\sup _{\varphi \in \mathcal {F}_{h}}\vert \mathbb {B}(\varphi ) \vert \) such that, for \(n\) sufficiently large,

$$\begin{aligned} \uprho _{\mathrm {{cdf}}} \left( \sqrt{nh^{d+ \ell }}\mathcal {E}_{n, h}[\mathcal {D}], {\textbf {B}} _{h} \right) = O\left( \left[ \frac{\log ^7 n}{nh^{d+ \ell }} \right] ^{1/8}\right) \xrightarrow [n\rightarrow \infty ]{}0 . \end{aligned}$$

Moreover, if we fix \(h\in (0, 1)\) and define \(\bar{{\textbf {B}} }_{h}= {\textbf {B}} _{h}/ \sqrt{h^{d+ \ell }}\), then \(\sqrt{n}\ \mathcal {E}_{n, h}[\mathcal {D}]\) converges in probability to \(\bar{{\textbf {B}} }_{h}\), denoted \(\sqrt{n}\ \mathcal {E}_{n, h}[\mathcal {D}] \xrightarrow {\mathbb {P}} \bar{{\textbf {B}} }_{h}\), as \(n\rightarrow \infty \).

A similar result establishes the asymptotic distribution for (16).

Theorem 6

Let \(\mathcal {D}\) denote any linear \(\ell \)-th order differential operator. Let \(K\in \mathcal {C}^{\ell }(\mathbb {R}^{d})\) be a kernel with bounded \(\ell \)-th derivatives. Further, suppose that the class \(\mathcal {K}\) in (18) is VC-type. Moreover, let \(\mathbb {B}_{\mathfrak {X}_{n}}\) be a GP with the same properties as in Lemma 3, indexed by \(\mathcal {F}_{h}\) as in (19), and with covariance

$$\begin{aligned} \textrm{Cov}(\mathbb {B}_{\mathfrak {X}_{n}}(\varphi _1), \mathbb {B}_{\mathfrak {X}_{n}}(\varphi _2)) = \frac{1}{n}\sum _{i= 1}^{n}\varphi _1(\textrm{x}_{i}) \varphi _2(\textrm{x}_{i}) - \frac{1}{n^2} \prod _{j= 1}^{2} \left( \sum _{i= 1}^{n}\varphi _{j}(\textrm{x}_{i}) \right) , \end{aligned}$$

where \(\textrm{x}_{i}\) is the \(i\)-th observation in \(\mathfrak {X}_{n}\). If \(h\equiv h_{n}\) is a sequence with \(h\in (0, 1)\) and \(h^{-(d+ \ell )} = O(\log n)\), then there exists \({\textbf {B}} _{n, h}\{\mathfrak {X}_{n}\}{\mathop {=}\limits ^{d}}\sup _{\varphi \in \mathcal {F}_{h}}\vert \mathbb {B}_{\mathfrak {X}_{n}}(\varphi ) \vert \) such that, for \(n\) sufficiently large,

$$\begin{aligned} \uprho _{\mathrm {{cdf}}} \left( \sqrt{nh^{d+ \ell }}\mathcal {E}_{n, h}^{*}[\mathcal {D} | \mathfrak {X}_{n}], {\textbf {B}} _{n, h}\{\mathfrak {X}_{n}\} \right) = O\left( \left[ \frac{\log ^7 n}{nh^{d+ \ell }} \right] ^{1/8}\right) \xrightarrow [n\rightarrow \infty ]{}0 . \end{aligned}$$

Theorem 6 holds for any observations \(\mathfrak {X}_{n}\). The applicability of this theorem relies on the assumption that \({\textbf {B}} _{n, h}\{\mathfrak {X}_{n}\} \leadsto {\textbf {B}} _{h}\) a.s. This connection crystallises in the following result, which can be straightly derived from Theorems 5 and 6.

Theorem 7

Let \(\mathcal {D}\) denote any linear \(\ell \)-th order differential operator. Let \(K\in \mathcal {C}^{\ell }(\mathbb {R}^{d})\) be a kernel with bounded \(\ell \)-th derivatives. Further, suppose that the class \(\mathcal {K}\) in (18) is VC-type. Let \(h\equiv h_{n}\) be a sequence with \(h\in (0, 1)\) and \(h^{-(d+ \ell )} = O(\log n)\). Moreover, let us write \(\Omega _{n, h}(\mathfrak {X}_{n})\equiv \uprho _{\mathrm {{cdf}}} \left( {\textbf {B}} _{n, h}\{\mathfrak {X}_{n}\}, {\textbf {B}} _{h} \right) \), where \({\textbf {B}} _{h}\) and \({\textbf {B}} _{n, h}\{\mathfrak {X}_{n}\}\) are as in Theorems 5 and 6, respectively. Let us allow \(\mathfrak {X}_{n}\) to vary as a random sample from the pdf \(f\) underlying the covariance structure (17) of  \({\textbf {B}} _{h}\). Further, suppose that \(\Omega _{n, h}(\mathfrak {X}_{n})= o(1)\) a.s. under the previous hypotheses on \(h\). Then, for \(n\) sufficiently large,

$$\begin{aligned} \uprho _{\mathrm {{cdf}}} \left( \sqrt{nh^{d+ \ell }}\mathcal {E}_{n, h}^{*}[\mathcal {D} | \mathfrak {X}_{n}], {\textbf {B}} _{h} \right) = O\left( \Omega _{n, h}(\mathfrak {X}_{n})+ \left[ \frac{\log ^7 n}{nh^{d+ \ell }} \right] ^{1/8}\right) \xrightarrow [n\rightarrow \infty ]{{a.s.}}0 . \end{aligned}$$

We can state sufficient conditions under which \(\Omega _{n, h}(\mathfrak {X}_{n})\) would converge to zero a.s. Corollary 1 gathers all the previous findings in an easy, ready-to-use form.

Corollary 1

In the hypotheses of Theorem 7, if we further take a constant \(h\) and define \(\bar{{\textbf {B}} }_{h}= {\textbf {B}} _{h}/ \sqrt{h^{d+ \ell }}\), then

$$\begin{aligned} \begin{aligned} \uprho _{\mathrm {{cdf}}} \left( \sqrt{n}\ \mathcal {E}_{n, h}[\mathcal {D}], \bar{{\textbf {B}} }_{h} \right)&\xrightarrow [n\rightarrow \infty ]{}0 \\ \uprho _{\mathrm {{cdf}}} \left( \sqrt{n}\ \mathcal {E}_{n, h}^{*}[\mathcal {D} | \mathfrak {X}_{n}], \bar{{\textbf {B}} }_{h} \right)&\xrightarrow [n\rightarrow \infty ]{{a.s.}}0 \end{aligned} . \end{aligned}$$

In particular, \(\sqrt{n}\ \mathcal {E}_{n, h}^{*}[\mathcal {D} | \mathfrak {X}_{n}] \leadsto \bar{{\textbf {B}} }_{h}\) a.s. Moreover, \(\sqrt{n}\ \mathcal {E}_{n, h}[\mathcal {D}] \xrightarrow {\mathbb {P}} \bar{{\textbf {B}} }_{h}\). Finally, \(\bar{{\textbf {B}} }_{h}\) has a continuous and strictly increasing cdf.

3.2.4 Inference for curvature bumps

The results from the previous section hold the key to ensuring (14) for curvature bumps.

Laplacian bumps. Theorem 8 straightly follows from Corollary 1 and Theorem 4.

Theorem 8

Let us fix \(h\in (0, 1)\). Let \(\mathcal {E}_{n, h}^{*}[\cdot | \mathfrak {X}_{n}]\) be as defined in (16) with KDE based on a kernel \(K\in \mathcal {C}^{2}(\mathbb {R}^{d})\) with bounded second derivatives. Taking \(\ell = 2\), suppose that the class \(\mathcal {K}\) in (18) is VC-type. For any \(\alpha \in (0, 1)\), define the margin \(\tilde{\zeta }_{n, h}^{\alpha }= \mathcal {Q}_{1 - \alpha } \{ \mathcal {E}_{n, h}^{*}[\Delta | \mathfrak {X}_{n}] \}\). Then, for all \(\alpha \in (0, 1)\), the asymptotic validity of the inference scheme (14) holds a.s. for the smoothed version of the Laplacian bump (8).

Concave bumps and convex dips. Concave bumps and convex dips are more involved. To obtain a parallel result to Theorem 8, we will borrow the Tail Value at Risk (TVaR) concept from financial risk management (Dhaene et al. 2006). The TVaR at level \(p\in (0, 1)\) of an rv \(X\) is defined as

$$\begin{aligned} \mathrm {{TVaR}}_{p} \left\{ X \right\} = \frac{1}{1 - p} \int _{p}^1 \mathcal {Q}_{X}(q) \ dq. \end{aligned}$$

The TVaR is utilized to aggregate risks governed by an unknown dependence structure, for it satisfies \(\mathrm {{TVaR}}_{p} \left\{ X \right\} \ge \mathcal {Q}_{p} \{ X \}\) and is sub-additive (Dhaene et al. 2006). Contrary to quantiles, weak convergence does not guarantee TVaR convergence. Lemma 4 requires the random variables to be asymptotically uniformly integrable (a.u.i.) (van der Vaart 1998, p. 17).

Lemma 4

Let \(\{X_{n}\}_{n= 1}^{\infty }\) be an a.u.i. sequence of random variables satisfying \(X_{n} \leadsto X\) for some rv \(X\) with a strictly increasing cdf. Then, \(\lim _{n\rightarrow \infty }\mathrm {{TVaR}}_{p} \left\{ X_{n} \right\} = \mathrm {{TVaR}}_{p} \left\{ X \right\} \) for all \(p\in (0, 1)\), being the limit finite.

Then, Lemma 4 allows proving the main result.

Theorem 9

Let us fix \(h\in (0, 1)\). Let \(\mathcal {E}_{n, h}[\cdot ]\) and \(\mathcal {E}_{n, h}^{*}[\cdot | \mathfrak {X}_{n}]\) be as defined in (15) and (16) with KDE based on the same kernel \(K\in \mathcal {C}^{2}(\mathbb {R}^{d})\) with bounded second derivatives. Taking \(\ell = 2\), suppose that the class \(\mathcal {K}\) in (18) is VC type. For any \(\alpha \in (0, 1)\), define the margin

$$\begin{aligned} \tilde{\zeta }_{n, h}^{\alpha }= \sum _{i= 1}^{d}\sum _{j= 1}^{d} \mathrm {{TVaR}}_{1 - \alpha } \left\{ \mathcal {E}_{n, h}^{*}[\textrm{D}_{ij} | \mathfrak {X}_{n}] \right\} , \end{aligned}$$

where \(\textrm{D}_{ij}\) denotes second-order partial differentiation in the \(i\) and \(j\) variables. Moreover, let us assume the following:

(1):

Letting \(\bar{{\textbf {B}} }_{h}[\textrm{D}_{ij}]\) be the rv such that \(\sqrt{n}\ \mathcal {E}_{n, h}[\textrm{D}_{ij}] \xrightarrow {\mathbb {P}} \bar{{\textbf {B}} }_{h}[\textrm{D}_{ij}]\), the sum rv \(\mathcal {Z}= \sum _{i= 1}^{d} \sum _{j= 1}^{d} \bar{{\textbf {B}} }_{h}[\textrm{D}_{ij}]\) has a continuous and strictly increasing cdf.

(2):

For each pair \((i, j)\), we have:

:

\(\{ \sqrt{n}\ \mathcal {E}_{n, h}[\textrm{D}_{ij}]\}_{n= 1}^{\infty }\) is a.u.i.

:

\(\{ \sqrt{n}\ \mathcal {E}_{n, h}^{*}[\textrm{D}_{ij} | \mathfrak {X}_{n}]\}_{n= 1}^{\infty }\) is a.u.i. a.s.

Then, for all \(\alpha \in (0, 1)\), the asymptotic validity of the inference scheme (14) holds a.s. for the smoothed version of the concave bump (5) and the convex dip (6).

The assumptions (1) and (2) seem natural. Hypothesis (1) asks a sum of nonnegative random variables with continuous and strictly increasing cdfs to have a continuous and strictly increasing cdf too, which should be valid except in pathological cases. Similarly, knowing both sequences in hypothesis (2) converge weakly, being a.u.i. amounts to the convergence of their expectations (van der Vaart 1998, Theorem 2.20).

Gaussian bumps. A similar result to Theorem 9 holds for Gaussian bumps (9).

Theorem 10

Consider the same hypotheses in Theorem 9 in the case \(d= 2\). Assume a Gaussian kernel \(K\). Further, assume that the true pdf \(f\) is bounded. Let \(C\) be a constant such that \(C> (\pi h^4)^{-1}\). For any \(\alpha \in (0, 1)\), define the margin

$$\begin{aligned} \tilde{\zeta }_{n, h}^{\alpha }= C\ \sum _{i= 1}^{2} \sum _{j= 1}^{2} \mathrm {{TVaR}}_{1 - \alpha } \left\{ \mathcal {E}_{n, h}^{*}[\textrm{D}_{ij} | \mathfrak {X}_{n}] \right\} . \end{aligned}$$

Then, for all \(\alpha \in (0, 1)\), the asymptotic validity of the inference scheme (14) holds a.s. for the smoothed version of the Gaussian bump (9).

4 Application

We will explore a sports analytics application for \(d= 2\) in the National Basketball Association (NBA). See the SM (Chacón and Fernández Serrano 2023) for additional applications with \(d\in \{1, 3\}\) in two American leagues: the National Football League (NFL) and the Major League Baseball (MLB). Each player and team has its own style, a form of DNA. Following the biological analogy, if a single gene activates a trait in natural DNA, even minor bumps in data may reveal essential features.

All three sports applications are representative of the use of kernel methods for exploratory data analysis (EDA). Moreover, our proposal has a marked visual intent, thus excelling in low dimensions. In this context, the curse of dimensionality that harms kernel methods, demanding larger sample sizes to retain precision, becomes less relevant (Chacón and Duong 2018, Section 2.8).

Bivariate made shots in the NBA Most people are familiar with basketball’s three-point line (3PL), behind which a made shot earns not two but three points. Sports analytics have demonstrated that attempting more of these shots is well worth the risk, given the increased efficiency of three-point shooters. This trend has recently changed the basketball landscape, especially in the NBA.

Chacón exemplified univariate multimodality with shooting distances to the basket in the NBA (Chacón 2020). We could see that the highest mode in a pdf model of all shots for the 2014–2015 season peaked beyond the 3PL. Looking at shots from a bivariate perspective will reveal the 3PL not as two separate modes but as a ridge (Chacón and Duong 2018).

We will examine bumps from shot data by the three best scorers in the 2015-2016 NBA season: Stephen Curry, James Harden and Kevin Durant. Figures 3 and 4 present different perspectives on concave and Laplacian bumps. Setting the near-the-rim shots aside, the three players have different shooting DNAs. Stephen Curry (Fig. 4a) operates beyond the 3PL, covering the entire ridge. He also demonstrates good range with even some half-court shots. However, he barely uses the mid-range area. His shooting patterns are mostly symmetrical. James Harden (Fig. 4b) has similar trends to Curry’s. He almost covers the 3PL while leaning towards some mid-range areas without half-court shots. Some notable asymmetries are present. Kevin Durant (Fig. 4c) has a more balanced game between mid and long shots. He shoots facing the basket mainly, with lower usage of lateral shots.

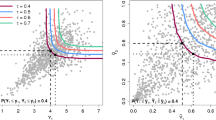
Figure 5 complements the previous figures with confidence sets. As refers to concave bumps, a wholly or partially ring-shaped area around the basket can be excluded with confidence for the three players. Apart from the shots near the rim, we cannot find other spots likely contained in the concave bumps. Regarding Laplacian bumps, the lower-bound confidence sets become more relevant, even far apart from the rim. For Curry, up to four high-confidence spots appear beyond the 3PL, including the left-field corner; for Harden, the number of outside high-confidence spots decreases to two, while for Durant, there is only one.

Fig. 3
figure 3

Concave and Laplacian bumps for Stephen Curry, James Harden and Kevin Durant. The three sub-figures have the same structure. On the left are concave bumps (5); on the right are Laplacian bumps (8). On either side, the two-dimensional surface is the fitted KDE pdf. The area colour refers to the curvature functional value at each point. The bump boundaries appear as lines on a flat basketball court at the top

Full size image
Fig. 4
figure 4

Shot scatter data with concave and Laplacian bumps for Stephen Curry, James Harden and Kevin Durant. The three sub-figures have the same structure. Each point corresponds to a made shot location. The number of observations is 804, 710 and 698 for Stephen Curry, James Harden and Kevin Durant. The lines represent bump boundaries: magenta for concave bumps (5); blue, Laplacian bumps (8). The colour of the dots in the scatter plot conveys the value of the KDE pdf at each point

Full size image
Fig. 5
figure 5

Confidence sets for Stephen Curry, James Harden and Kevin Durant’s bumps. The three sub-figures have the same structure. On the left, 90%-confidence sets for concave bumps (5); on the right, 90%-confidence sets for Laplacian bumps (8). The confidence margins are based on 200 bootstrap samples, each with the same resample size as the original one. On either side, the area colours convey the same meaning. The non-blue sandy areas fall outside the confidence set bounds; the blue-coloured areas lie inside the confidence region. The darkest blue corresponds to the lower-bound confidence set: a set that is likely contained in the bump. The remaining blue areas cover the upper-bound confidence set: a set that likely contains the bump. Finally, the mid-light blue colour points out the estimated bump

Full size image

5 Discussion

Our curvature BH methodology represents the next step in density BH techniques, a path opened by Good and Gaskins (1980) and consolidated with Hyndman (1996) and Chaudhuri and Marron (1999). Rather than sticking to a purely probabilistic view on pdfs, our proposal thrives on sound geometry principles that have produced good results in applied areas like image processing (Haralick and Shapiro 1992).

Our work strongly relies on KDDE, continuing the exploration of applications for higher-order partial derivatives of the pdf (Chacón and Duong 2013). On the other hand, we bring to curvature BH some cutting-edge techniques for level set estimation and inference that extend the pointwise-oriented initial works by Godtliebsen et al. (2002) and Duong et al. (2008).

The presented curvature framework shows great applicability from a theoretical standpoint. Under mild assumptions, the mean curvature, Laplacian and Gaussian bumps are consistent with affordable convergence rates. The confidence regions for Laplacian bumps are also asymptotically valid and consistent. The cases for Gaussian bumps (inference), concave bumps and convex dips (consistency and inference) are slightly more technical. Notwithstanding, pathological cases should not often appear in practice.

The NBA application shows promise for EDA and clustering. Figure 4a presents a most pleasing result, identifying the 3PL area and the most relevant shooting spots. Both bumps are valuable and combine to produce insightful visualizations. Comparing the pictures in Fig. 4, we see that curvature bumps capture the players’ rich shooting DNAs. Despite the ultimately unavoidable threat of the curse of dimensionality in KDE settings (Chacón and Duong 2018), the relatively small sample sizes did not detract from the accuracy of the results.

Our methodology’s apparent least impressive achievement is confidence regions despite asymptotic guarantees. In Fig. 5, the upper-bound confidence sets tend to be conservative. This was not wholly unexpected, as Chen, Genovese, and Wasserman warned (Chen et al. 2017). The margin is especially coarse for the concave bumps. In practice, we can mitigate this effect by splitting the bump and calculating the margin over smaller domains, employing a pilot estimation for guidance. Nonetheless, further research following Mammen and Polonik’s universal approach (Mammen and Polonik 2013) should yield even better results.