Abstract
Linear mixed effects models (LMMs) are a popular and powerful tool for analysing grouped or repeated observations for numeric outcomes. LMMs consist of a fixed and a random component, which are specified in the model through their respective design matrices. Verifying the correct specification of the two design matrices is important since mis-specifying them can affect the validity and efficiency of the analysis. We show how to use empirical stochastic processes constructed from appropriately ordered and standardized residuals from the model to test whether the design matrices of the fitted LMM are correctly specified. We define two different processes: one can be used to test whether both design matrices are correctly specified, and the other can be used only to test whether the fixed effects design matrix is correctly specified. The proposed empirical stochastic processes are smoothed versions of cumulative sum processes, which have a nice graphical representation in which model mis-specification can easily be observed. The amount of smoothing can be adjusted, which facilitates visual inspection and can potentially increase the power of the tests. We propose a computationally efficient procedure for estimating p-values in which refitting of the LMM is not necessary. Its validity is shown by using theoretical results and a large Monte Carlo simulation study. The proposed methodology could be used with LMMs with multilevel or crossed random effects.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We consider a (single-level) linear mixed effects model (LMM) (Laird and Ware 1982) with n groups (clusters) each having \(n_i\) entries, which can be described by the following equation:
The random vector \(\varvec{y}_i\) is a vector of dependent variables with elements \(y_{ij}\), \(j=1,\ldots ,n_i\), which are assumed to be independent across groups but correlated within a group. The matrix \(\varvec{X}_i\) is a given \(n_i \times m\) matrix of fixed effects, and \(\varvec{\beta }\) is an \(m\times 1\) vector of corresponding fixed effects coefficients. \(\varvec{Z}_i\) is a given \(n_i\times k\) matrix of random effects, and \(\varvec{b}_i\) is a \(k\times 1\) random vector of random coefficients. The random vectors \(\varvec{b}_i\) and \(\varvec{\epsilon }_i\) are assumed to be independent, with mean zero and covariance matrices \(\varvec{D}\) and \(\sigma ^2 \varvec{I}\), respectively, where \(\varvec{b}_i\) and \(\varvec{\epsilon }_i\) are independent of \(\varvec{X}_i\) and \(\varvec{Z}_i\).
We will assume that the matrices \(\varvec{X}_i, \varvec{Z}_i\), as well as the numbers of their rows \(n_i\), are generated randomly. More precisely, we will assume that they are determined by the independent and identically distributed (i.i.d.) random elements \(\left\{ D_i\right\} _{i \in {\mathbb {N}}}\), where \(D_i\) is defined as \(D_i = (\varvec{\nu }_i, \varvec{X}_i^{\#}, \varvec{Z}_i^{\#})\) . The random vector \(\varvec{\nu }_i \in \left\{ 0, 1\right\} ^{n_{\max } \times 1}\) determines the \(n_i\) as \(n_i = \nu _{i1}+\cdots +\nu _{in_{\max }}\) and determines which \(n_i\) out of the \(n_{\max }\) rows from the random matrices \(\varvec{X}_i^{\#} \in {\mathbb {R}}^{n_{\max } \times m}, \varvec{Z}_i^{\#}\in {\mathbb {R}}^{n_{\max } \times k}\), are included in the matrices \(\varvec{X}_i\) and \(\varvec{Z}_i\). Here, \(n_{\max }\in {\mathbb {N}}\) is a constant. Defining \(\varvec{\nu }_i\) allows us to apply our theory to data with groups of varying sizes and at the same time use a more accessible theory based on i.i.d. observations.
The approach proposed in this paper relies on testing two null hypotheses. The first null hypothesis is that the conditional mean of \(\varvec{y}_i\) is equal to
and thus, under \(H_0^F\), the matrices of fixed effects \(\varvec{X}_1,\ldots , \varvec{X}_n\) are correctly specified.
The second null hypothesis states that the conditional mean and the conditional variance of the random vector \(\varvec{y}_i\) are correctly specified, that is
Therefore, under the null hypothesis \(H_0^O\), the matrices of fixed and random effects \(\varvec{X}_1,\ldots ,\varvec{X}_n\), \(\varvec{Z}_1,\ldots , \varvec{Z}_n\) are correctly specified.
Checking whether the assumed LMM is correctly specified is important since model mis-specification affects the validity and efficiency of regression analysis. The most commonly used techniques for assessing the goodness-of-fit of LMMs are graphical tools such as residual plots (Pinheiro and Bates 2000; Wu 2009). These procedures are highly subjective and often completely uninformative. Loy et al. (2017) derived an approach based on the concept of visual p-values (Majumder et al. 2013) to make such plots less subjective. Having to rely on human experts observing the plots is, however, impractical.
While there are numerous formal tests for checking the distributional assumptions of model (1.1) (Jiang 2001; Ritz 2004; Claeskens and Hart 2009; Efendi et al. 2017), only a few tests are available for checking its choice of design matrices. Tang et al. (2014) derived a test statistic for the validity of a fixed effects design matrix. The test involves partitioning the fixed effects design matrix. The performance of the test depends on the choice of the partition and can be poor if the partition is not selected appropriately. Lee and Braun (2012) used a permutation approach for inferences regarding the inclusion or exclusion of the random effects in LMMs. Pan and Lin (2005) and Sánchez et al. (2009) proposed evaluating the choice of the design matrix for generalized LMMs (GLMMs) by considering the cumulative sum (cusum) of the ordered residuals. For LMMs, this approach has no power against alternatives in which the fixed effects design matrix is correctly specified but the random effects design matrix is not. That is, it cannot detect a mis-specification of the random effects design matrix. However, it has some appealing features, and we based our methodology on it. For example, it provides, in addition to a formal hypothesis test, an informative visual presentation that gives hints about how to improve the fit of the model (Lin et al. 2002).
González-Manteiga et al. (2016) proposed a test based on the distance between two empirical error distribution functions, extending the ideas of Van Keilegom et al. (2008) for cross-sectional independent data. This approach can be used to evaluate the choice of the fixed effects design matrix (also semiparametric and generalized linear models can be considered), and it has been shown to be more powerful than the approach of Pan and Lin (2005). However, there is currently a shortage of implementations of it. Likewise, methods utilizing the link between random effects and penalized regressions have been applied to test whether the fixed effects are linear, quadratic, etc. (Greven et al. 2008; Wood 2013, 2012; Huet and Kuhn 2014). To the best of our knowledge, there is no test available for checking the correct specification of both design matrices.
Note that we are not interested in the distributional assumptions of model (1.1) but only in the correct specification of the design matrices for the fixed and random effects. Extending the approach presented in Pan and Lin (2005), we construct two empirical stochastic processes that inspect \(H_0^O\), the entire model, and \(H_0^F\), only the fixed part of the model. We formally prove that when the fixed effects design matrix is correctly specified, the process for checking only the fixed effects design matrix will be robust against the mis-specification of the random effects design matrix. Intuitively, this should hold since the estimator of \(\varvec{\beta }\) is consistent given only the correct specification of the fixed effects design matrix (Zeger et al. 1988). Since the parameter sets of the fixed and random effects parts of the LMM are chosen separately, i.e., independently, a mis-specification of the random effects part of the model is implied when the null hypothesis that both design matrices from the model are correctly specified (\(H_0^O\)) is rejected and the null hypothesis that the fixed effects part of the model is correctly specified (\(H_0^F\)) is not rejected.
The above observation allows one to construct a procedure with which to address the mis-specifications of both LMM design matrices one at a time. The procedure combines two tests based on empirical stochastic processes, where the process for testing the entire model is novel. The asymptotic theory for these two tests is derived based on the strong fundamental stochastic process theory presented by van der Vaart and Wellner (1996). Finally, these empirical stochastic processes may be nicely visualized, and the deviations from the null hypothesis for each process can easily be judged from the figures. We also introduce a smoothing parameter, which facilitates visual inspection and can improve the power of the tests and show how the amount of smoothing can be determined from the data.
The challenging part for all applications of the (empirical) stochastic processes in this context is obtaining their null distribution. Given the complexity of the problem introduced by the dependence among the residuals, the asymptotic distribution for even the most trivial test statistic is analytically intractable. In application to linear models (LMs), the null distribution is obtained by using bootstrapping (Stute et al. 1998a) or simulations (Su and Wei 1991; Lin et al. 2002). The simulation approach has also been used for marginal models (MMs) (Lin et al. 2002) and single-level GLMMs (Pan and Lin 2005). We propose a computationally efficient bootstrap approach for correctly approximating the null distribution of the proposed processes, in which refitting of the LMM is not necessary. This approach creates new residuals, which will be called modified residuals, constructs stochastic processes based on them and evaluates the test statistic. We will show that several distributions could potentially be used when creating the modified residuals, as long as some mild assumptions about their moments are satisfied, and we will investigate the finite sample performance for some obvious candidate distributions.
In Sect. 2, we outline the approach, and in Sect. 3, we introduce some additional notation. Next, in Sect. 4, we present the definitions of the proposed empirical stochastic processes and define modified residuals. A short subsection regarding the algorithmic data-driven choice of the smoothing parameter concludes the section. The assumptions under which we establish the empirical stochastic processes’ weak convergence are provided in Sect. 5. We show the asymptotic validity of the proposed methodology under the null (in Sect. 6) and alternative hypotheses (in Sect. 7). In Sect. 8, we showcase the finite sample performance for a selection of Monte Carlo simulation results. An application to a real data example is given in Sect. 9. The paper concludes with a summary of the most significant findings and possibilities for future research. For brevity, we only consider single-level LMMs in detail; a possible extension to LMMs with more complex random effects structures is discussed in the supplementary material. Proofs and additional simulation results are shown in the supplementary material.
2 Overview of the proposed approach
Our approach is based on the repeated application of Algorithm 1. In each application of the algorithm, we use residuals and fitted values from a fitted LMM with assumed design matrices \(\varvec{X}_i\) and \(\varvec{Z}_i\), but we define the residuals and the fitted values in two different ways depending on which hypothesis, \(H_0^F\) or \(H_0^O\), is being tested. (The details will be discussed later.) Constructing a smoothed empirical process based on ordering the appropriately standardized residuals by the fitted values, we first test \(H_0^F\), and if it is rejected, the fixed effects design matrix is corrected, the new model is fitted, and the execution of the algorithm to test \(H_0^F\) is repeated until there is no more evidence against \(H_0^F\). When correcting the fixed effects design matrix, graphical examples of representative processes from Lin et al. (2002) can be used to obtain hints about the form of mis-specification. At this point, the hypothesis \(H_0^O\) is tested. If it is rejected, this implies a mis-specification of the random effects design matrix. Analogous to the case for fixed effects, the random effects design matrix is then corrected, the new model is fitted, and the algorithm testing \(H_0^O\) is repeated until there is no more evidence against \(H_0^O\).

The theoretical setting under which we prove the validity of our approach assumes that there is some stochastic mechanism that is generating the groups of data \(\varvec{y}_i\). This mechanism is also assumed to be generating the matrices \(\varvec{X}_i, \varvec{Z}_i\) and is assumed to be generating groups of data that may have different sizes. The parameters \(\varvec{\beta }, \varvec{D}\) and \(\sigma ^2\) are assumed to be fixed. All our asymptotic results assume that the number of groups n grows to infinity.
The advantage of this theoretical setting is that under some assumptions given later, the proposed approach can be shown to be valid on the type of data to which linear mixed models are very often applied. Another advantage of this theoretical approach is that we do not have to deal with independent nonidentically distributed data such as in the theoretical approach considered in Hagemann (2017), which introduces various technical problems regarding measurability, making the theory less accessible.
3 Notation and general definitions
We use \({{\,\mathrm{span}\,}}\mathopen {}\left( \varvec{M}\right) \mathclose {}, \varvec{M} \in {\mathbb {R}}^{m_1 \times m_2}\) to denote the column span or the image of matrix \(\varvec{M}\). Given a vector subspace \(V \subset {\mathbb {R}}^n\), we denote its orthogonal complement by \(V^{\perp }\). As usual, a hat over a symbol will be used to denote an estimate of this quantity. For example, the estimator \(\hat{\varvec{V}}_i\) of the matrix \(\varvec{V}_i\), defined as
is equal to \(\hat{\varvec{V}_i} = {\hat{\sigma }}^2 \varvec{I} + \varvec{Z}_i \hat{\varvec{D}} \varvec{Z}_i{^\top }\).
We define the following quantities:
The random vectors \(\tilde{\varvec{b}}_i\) are known as BLUPs. The motivation for their use can be found in Demidenko (2005).
Furthermore, we define
Here, \(\left( \varvec{Z}_i{^\top }\varvec{Z}_i\right) ^+\) denotes the Moore–Penrose inverse of the matrix \(\left( \varvec{Z}_i{^\top }\varvec{Z}_i\right) \). The matrix \(\varvec{V}_i^{- 1/2}\) denotes the square root of the positive definite matrix \(\varvec{V}_i^{-1}\). Note that the random vectors \(\varvec{e}^O_i\) and \(\varvec{e}^F_i\) are defined so that their conditional variances are equal to
Therefore, it also holds that \(\text{ var }\mathopen {}\left( \varvec{e}^F_i\right) \mathclose {} = \varvec{I}\). The conditional covariance matrix of \(\varvec{e}^O_i\) is an orthogonal projection matrix. Hence, the absolute values of the conditional covariances of the elements of \(\varvec{e}^O_i\) are bounded by 1. These results slightly simplify the theoretical results.
When dealing with empirical stochastic processes, we mostly use the same notation as van der Vaart and Wellner (1996). We denote the probability space as \(({\mathcal {X}}, {\mathcal {A}}, {{\,\mathrm{P }\,}})\). The random elements \(X_i \in {\mathcal {X}}\) are defined as \(X_i = (\varvec{\nu }_i, \varvec{X}_i^{\#}, \varvec{Z}_i^{\#}, \varvec{e}_i^{\#})\). Recall that the random vector \(\varvec{\nu }_i\) and random matrices \(\varvec{X}_i^{\#}, \varvec{Z}_i^{\#}\) determine the random element \(D_i\). The random vector \(\varvec{e}_i^{\#} \in {\mathbb {R}}^{n_{\max } \times 1}\) is defined so that its rows, determined by \(\varvec{\nu }_i\), determine the random vector \(\varvec{e}_i\). The random element \(X_i\) therefore completely determines every known quantity in (1.1).
When discussing the independence of random vectors and of matrices and vectors that are implicitly or explicitly determined by the random elements \(\left\{ X_i\right\} _{i \in {\mathbb {N}}}\), we will always refer to the independence conditional on \(\varvec{\nu }_i\). We do not require any additional conditions regarding the independence of the rows of matrices \(\varvec{X}_i\) and \(\varvec{Z}_i\) within a group.
Let \(\delta _{X_i}\) denote the Dirac measure on the space \(({\mathcal {X}}, {\mathcal {A}})\). Let \(X_1,\ldots , X_n \) be n random elements in \(({\mathcal {X}}, {\mathcal {A}})\). Define the empirical measure \({{\,\mathrm{P }\,}}_n\) as \({{\,\mathrm{P }\,}}_n =(\delta _{X_1}+\cdots +\delta _{X_n})/n\). Define the empirical stochastic process based on n observations as:
As in van der Vaart and Wellner (1996), we will index (empirical) stochastic processes by functions. For example,
where \({{\,\mathrm{P }\,}}f = \int _{{\mathcal {X}}} f d {{\,\mathrm{P }\,}}\).
Let \( {\varvec{m}}: {\mathcal {X}}\rightarrow {\mathbb {R}}^m\) be some function that is linear in \(\varvec{e}_i\), i.e.,
where \(\varvec{\Psi }_i\) is a matrix that is not dependent on \(\varvec{e}_i\) and has elements with finite variance. For example, when using MLE or REML, \(\varvec{\Psi }_i\) is equal to (Demidenko 2005)
The symbol \(\leadsto \) denotes convergence in distribution, and \(\overset{*}{\leadsto }\) denotes convergence in distribution conditional on the data, that is, conditional on \(X_1, X_2, \ldots \) To establish \(\overset{*}{\leadsto }\), we will use the theory from Chapter 2.9 of van der Vaart and Wellner (1996) denoting multipliers as \(\xi _i\).
4 Definition of the empirical stochastic processes
Let \(\lambda \in (0, \infty )\) be a constant. Define a function \(\sigma _\lambda : {\mathbb {R}}\rightarrow [0, 1]\), which is a continuous approximation of the indicator function that we will use in constructing the empirical stochastic processes. More precisely, let \(p : [0, 1] \rightarrow [0, 1]\) be a twice-differentiable monotonous function with \(p(0) = 1\) and \(p(1) = 0\). Then, we define the function \(\sigma _{\lambda }\) as:
Define the function p so that as \(\lambda \) increases, the function \(\sigma _{\lambda }\) becomes a better approximation for the indicator function. Define \(\sigma _{\infty } : {\mathbb {R}}\rightarrow [0, 1]\) to be equal to
where \({\mathbf {1}}_{A}\) denotes the indicator function of the set A. When the function \(\sigma _{\lambda }\) is applied to each component of a vector \(\varvec{x} \in {\mathbb {R}}^d\), we write it as \(\varvec{\sigma }_{\lambda }\mathopen {}\left( \varvec{x}\right) \mathclose {}\). For a random vector \(\varvec{x} \in {\mathbb {R}}^d\) and a scalar \(t \in {\mathbb {R}}\), let \(\varvec{\sigma }_{\lambda }\mathopen {}\left( \varvec{x}, t\right) \mathclose {}\) denote \(\varvec{\sigma }_{\lambda }\mathopen {}\left( \varvec{x}, t\right) \mathclose {} = \varvec{\sigma }_{\lambda }\mathopen {}\left( \varvec{x} - t \varvec{1}\right) \mathclose {}\).
We base the test for \(H_0^O\) on the process \(\hat{W}_n^O\), while the test for \(H_0^F\) is based on the process \(\hat{W}_n^F\). The processes \(\hat{W}_n^O\) and \(\hat{W}_n^F\) are empirical versions of the processes \(W_n^O\) and \(W_n^F\), defined as:
and they are obtained by replacing the unknown quantities in (4.1) by their respective consistent estimators. We will show later that when mis-specifying the fixed effects design matrix, the mean function for the process \(\hat{W}_n^F\) is nonzero for some t, while it is zero for all t when the fixed effects design matrix is correctly specified, regardless of the (in)correct specification of the random effects design matrix. Moreover, we will show that the mean function for the process \(\hat{W}_n^O\) is nonzero for some t if the fixed and/or random effects design matrix is mis-specified. These deviations from a zero-mean stochastic process can then also easily be observed visually by plotting the process against t. In addition to the processes \(\hat{W}_n^O\) and \(\hat{W}_n^F\), we define the process
where \(X_{ij,l}\) is the lth column and jth row, \(j=1,\ldots ,n_i\), of the design matrix for the fixed effects \(\varvec{X}_i\), \(i=1,\ldots ,n\), and the sum extends only over some subset of the columns of the fixed effects design matrix. Using \(\hat{W}_n^{F^S}(t)\) allows one to test a possible lack of fit due to the specified subset of the fixed effects covariates. By inspecting \(\hat{W}_n^{F^S}(t)\), it is also possible to detect the omission of an important interaction effect of two or more variables. For example, if the p-value based on \(W_n^{F^S}(t)\), defined as a subset of two variables, is significant at some level \(\alpha \) and the two p-values based on \(\hat{W}_n^{F^S}(t)\), defined as a subset of only one variable, are both insignificant at level \(\alpha \), this implies that an important interaction effect between the two variables was omitted. Since the process \(\hat{W}_n^{F^S}\) is very similar to the process \(\hat{W}_n^F\), it will not be thoroughly examined separately.
We calculate p-values using either the Kolmogorov–Smirnov (KS) or Cramér–von Mises (CvM) type statistic, i.e.,
and
where \(\hat{W}_n\) is \(\hat{W}_n^{O}\), \(\hat{W}_n^{F}\) or \(\hat{W}_n^{F^S}\). Instead of obtaining the theoretical probabilities for a value of a test statistic, we rely on the repeated evaluation of these test statistics on the processes defined using modified residuals, which are defined as:
where the random elements \(X_i^*\) are equal to \(X_i^* = (\varvec{\nu }_i, \varvec{X}_i^{\#}, \varvec{Z}_i^{\#}, \xi _i \varvec{e}_i^{\#})\). \(\varvec{\nu }_i, \varvec{X}_i^{\#}, \varvec{Z}_i^{\#}\) and \(\varvec{e}_i^{\#}\) are the components of the random element \(X_i\). We will show that the choice of the distribution of the multipliers, \(\xi _i\), does not matter asymptotically, as long as they are independent, zero-mean, unit-variance variables with some additional restrictions on the existence of higher-order moments, which will be presented in the next section. In small samples, the choice of the distribution can make a difference, as will be illustrated in the simulation study.
The processes \(\hat{W}_n^{O*}(t)\) and \(\hat{W}_n^{F*}(t)\), empirical versions of \(W_n^{O*}\) and \(W_n^{F*}\), which are defined as:
are then obtained by replacing the unknown quantities with their respective consistent estimators. Note that the underlying data do not change, but the data from the modified residuals do. Therefore, we will later prove the convergence of these empirical stochastic processes conditionally on the data, which is in line with the bootstrap approach presented in Chapter 3.6 of van der Vaart and Wellner (1996).
For a very large \(\lambda \), the proposed processes behave similarly to commonly used processes constructed as cumulative sum(s) of the model’s residuals for LMs (Christensen and Lin 2015; Lin et al. 2002; Stute et al. 1998a; Diebolt and Zuber 1999; Su and Wei 1991; Fan and Huang 2001; Stute et al. 1998b), MMs (Lin et al. 2002) and single-level GLMMs (Pan and Lin 2005). A similar process to the \(W_n^F(t)\) process of (4.1) was considered by Pan and Lin (2005), but they used different residuals when constructing the process and only considered the situation in which \(\lambda =\infty \). Using the function \(\sigma _\lambda \) facilitates the visual inspection of the processes by smoothing them. At the same time, the choice of \(\lambda <\infty \) can potentially increase the power.
4.1 Data-driven choice of the smoothing parameter \(\lambda \)
One potential data-driven choice of the smoothing parameter \(\lambda \) is to define a grid of different \(\lambda \)s, selecting the one that gives the largest value of the test statistic. To obtain the correct size and to avoid the need for multiplicity correction, this is also done for the processes using the modified residuals. Since \(\lambda \) affects the scale of the process, and hence the scale of the test statistic, the test statistics need to be standardized to account for the difference in scaling. For this purpose, we suggest using the estimated standard error of the test statistic, which can be obtained from the processes using the modified residuals. The entire procedure is presented in Algorithm 2.

5 Assumptions under \(H_0\)
It is reasonable to assume that when the choice of the design matrices of a certain model is assessed, this model has already been fitted to the data. Our assumptions, therefore, while seeming strict at first glance, mainly require that the model has been fitted using parameter estimators that satisfy certain conditions. The assumptions required to establish the convergence of the proposed empirical stochastic processes are listed below. A brief discussion of the assumptions is given at the end of this section.
-
(A1)
The data \(\left\{ X_i\right\} _{i \in {\mathbb {N}}} \) are a sequence of i.i.d. random elements. \(n_i, i \in {\mathbb {N}}\) is assumed to be at most \(n_{\max }\), where \(n_{\max }\) is some constant that is at least \(k + 1\). That is, \(\varvec{X}_i \in {\mathbb {R}}^{n_{i} \times m}, \varvec{Z}_i \in {\mathbb {R}}^{n_{i} \times k}\) and \(\varvec{e}_i \in {\mathbb {R}}^{n_{i}\times 1}\). Matrices \(\varvec{X}_i \in {\mathbb {R}}^{n_i \times m}\) and \(\varvec{Z}_i \in {\mathbb {R}}^{n_i \times k}\) have full rank almost surely, and their elements have bounded second moments.
-
(A2)
We assume that we have consistent estimators \(\hat{\varvec{\beta }}, \hat{\varvec{D}}\) and \({\hat{\sigma }}\) of the unknown parameters \(\varvec{\beta } \in {\mathbb {R}}^m, \varvec{D} \in {\mathbb {R}}^{k \times k}\) and \(\sigma > 0\), respectively. The matrix \(\varvec{D}\) is positive definite. The estimator \(\hat{\varvec{\beta }}\) is asymptotically independent of the estimators \(\hat{\varvec{D}}\) and \({\hat{\sigma }}\). Furthermore,
$$\begin{aligned} \sqrt{n} (\varvec{\beta } - \hat{\varvec{\beta }}) = \frac{1}{\sqrt{n}} \sum _{i=1}^n {\varvec{m}}(X_i) + o _P\mathopen {}\left( 1\right) \mathclose {} . \end{aligned}$$We assume that \({{\,\mathrm{P }\,}} {\varvec{m}}= \varvec{0}\) and that every element of \({{\,\mathrm{P }\,}} {\varvec{m}} {\varvec{m}}{^\top }\) is smaller than \(\infty \).
-
(A3)
The components of the functions \(t \mapsto \text{ E }[\varvec{X}_i{^\top }\varvec{P}_i \sigma _{\lambda }(\varvec{y}^O_i, t)]\) and \(t \mapsto \text{ E }[\varvec{X}_i{^\top } \varvec{V}_i^{- 1/2} \sigma _{\lambda }(\varvec{y}^F_i, t)]\) are continuous almost everywhere.
-
(A4)
The i.i.d. random variables \(\xi _i\) have mean zero and variance 1, and there exists some \(r > 2\) such that \(\text{ E }\mathopen {}\left( \xi ^r\right) \mathclose {} < \infty \).
-
(A5)
The i.i.d. random variables \(\varvec{\epsilon }_i\) are multivariate normal variables with zero mean and variance \(\sigma ^2 \varvec{I}\).
Assumption (A1) ensures that, by Theorem 11 in Chapter 3 of Demidenko (2005), the model is identifiable. Hence, we could ease the requirements in assumption (A1), but we would then need to assume additional conditions regarding the estimation process.
Note that the assumption (A2) holds when the errors are distributed normally and we use MLE, REML or the Fisher–Scoring algorithm to estimate the parameters of the LMM. More information on this can be found in Chapters 2 and 3 in Demidenko (2005). Without the normality assumption, (A2) holds when using the estimator proposed by Peng and Lu (2012) under some additional regularity conditions (see Peng and Lu (2012) for more details).
Assumption (A3) helps us establish that the stochastic processes are equicontinuous. The most apparent use of this assumption is in the proof of Theorem 2, when \(\lambda = \infty \).
The last condition in (A4) implies that \(\left\Vert \xi _i\right\Vert _{2,1} = \int _0^{\infty } \sqrt{{{\,\mathrm{P }\,}}(\left| \xi _i\right| > t)} d t < \infty \), by exercise 2.9.1 in van der Vaart and Wellner (1996). This condition is a required assumption in the multiplier central limit theorem that we use in the proof of Theorem 3. This condition is satisfied, for example, in the case in which \(\xi _i\) are Rademacher or standard normal random variables.
The assumption (A5) will be needed to show that under \(H_0\), \(W_n^O\) is a zero-mean process. Without this assumption, this result would still hold if we assumed that \(\varvec{Z}_i=(1,\ldots ,1){^\top }\) holds for \(i=1,\ldots ,n\). The reason why this result could otherwise not be established is presented in more detail in the supplementary information, where a counterexample is constructed.
Note that the dimensions m and k are assumed to be fixed. With some additional assumptions, such as those found in Jiang (1996), or by showing that certain estimators of \(\varvec{\beta }, \varvec{D}\) and \(\sigma \) satisfy the conditions in He and Shao (2000), we could extend our setting to settings with increasing m and k. In this case, we would use the same ideas, with some additional references to Sect. 2.11.3 of van der Vaart and Wellner (1996).
6 Asymptotic behaviour under \(H_0\)
In this section, we present a part of the theoretical justification for our method when the model is correctly specified. More precisely, we prove that the stochastic processes on which our approach is based, under the assumptions from the previous section, converge in distribution as the number of groups of data n grows to infinity. We also prove that the stochastic processes based on the modified residuals converge weakly conditionally on the data and that their limits are equal to the limits of the processes based on the original residuals. Here we only summarize the main ideas of the proofs of the presented theorems. Detailed proofs can be found in the supplementary material.
First, we justify the use of the function \(\varvec{\sigma }_{\lambda }\). Let \({\mathcal {V}}({\mathcal {F}})\) denote the Vapnik–Chervonenkis index (VC index) of a class of functions \({\mathcal {F}}\), as defined in van der Vaart and Wellner (1996, pp.141).
Define the classes of functions \({\mathcal {F}}^O\) and \({\mathcal {F}}^F\) as:
Note that \({{\,\mathrm{P }\,}}f^F_t = 0\) for every \(t \in {\mathbb {R}}\). This follows from the fact that the random vector \(\varvec{e}^F_i\) has zero mean and is independent of \(\varvec{y}^F_i\), since it is defined so that it does not depend on the random matrix \(\varvec{X}_i\).
To show that \( {{\,\mathrm{P }\,}}f^O_t = 0\) for every \(t \in {\mathbb {R}}\), we additionally assume that (A5) holds. Note the equality \(\varvec{e}^O_i=\varvec{P}_i \varvec{e}_i = \varvec{P}_i \varvec{\epsilon }_i\). \(\varvec{P}_i\) is the orthogonal projection such that \(\varvec{Z}_i \varvec{v} = \varvec{Z}_i (\varvec{I} - \varvec{P}_i) \varvec{v}\) for any vector \(\varvec{v}\); therefore, it can be seen that \(\text{ cov }(\varvec{e}^O_i,\varvec{y}^O_i|D_i)=0\). Then, since \(\text{ E }(\varvec{e}^O_i|D_i)=0\), we also have that \(\text{ cov }(\varvec{e}^O_i,\varvec{y}^O_i)=0\). The desired result then follows after noting that under Assumption (A5), \(\varvec{e}^O_i\) and \(\varvec{y}^O_i\) are jointly multivariate normal.
Therefore, the empirical stochastic processes \(W_n^O\) and \(W_n^F\) at t can be written as:
The next theorem ensures that under some assumptions, the processes \(W_n^O\) and \(W_n^F\) converge.
Theorem 1
Under the assumption (A1), the families of functions \({\mathcal {F}}^F\) defined as in (6.1) are \({{\,\mathrm{P }\,}}\)-Donsker. Under the assumptions (A1) and (A5), the families of functions \({\mathcal {F}}^O\) defined as in (6.1) are \({{\,\mathrm{P }\,}}\)-Donsker.
Short proof of Theorem 1
The assumption (A5) ensures that \({{\,\mathrm{P }\,}}f_t^O = 0\) for \(t \in {\mathbb {R}}\). Furthermore, the classes of functions \({\mathcal {F}}^O\) and \({\mathcal {F}}^F\) are both VC classes, with VC indices equal to 2. The reason for this is that the functions \(f_t^O\), for \(t \in {\mathbb {R}}\), are constructed so that the subgraph of \(f_s^O\) is contained in \(f_t^O\) for every \(s \le t\). The same holds for the functions \(f_t^F, t \in {\mathbb {R}}\).
We can therefore use Theorem 2.6.7 from van der Vaart and Wellner (1996), which implies that the uniform entropy condition in Theorem 2.5.2 from van der Vaart and Wellner (1996) is satisfied. We proceed by constructing two square measurable envelopes to satisfy all of the requirements in Theorem 2.5.2, which proves this theorem. We can do this because of assumption (A1). \(\square \)
Now, we define the following two families of functions:
We define the limit empirical stochastic process \({{\,\mathrm{{\mathbb {G}} }\,}}\) similar to \({{\,\mathrm{{\mathbb {G}} }\,}}_n\) for \(f \in {\mathcal {F}}^O \cup {\mathcal {F}}^F\) as
Note the equality \([ {\varvec{m}}(X_1)+\cdots + {\varvec{m}}(X_n)]/\sqrt{n} = {{\,\mathrm{{\mathbb {G}} }\,}}_n {\varvec{m}}\). The next result establishes the convergence of \(\hat{W}_n^O\) and \(\hat{W}_n^F\).
Theorem 2
Assume that (A1) and (A2) hold. For \(\hat{W}_n^O\), additionally assume that (A5) holds. Then, if either \(\lambda < \infty \) or \(\lambda = \infty \) and assumption (A3) holds, the processes \(\hat{W}_n^O\) and \(\hat{W}_n^F\) converge in distribution to
Short proof of Theorem 2
We can use the assumption (A2) to show that the processes \(\hat{W}_n ^O\) and \(\hat{W}_n^F\) can be written as sums of either \(W_n^O\) or \(W_n^F\), and in the case of \(\hat{W}_n^O\),
From this, we can use the continuity of the function \(t \mapsto \varvec{\sigma }_{\lambda }\mathopen {}\left( \cdot , t\right) \mathclose {}\) for \(\lambda < \infty \) or the Assumption (A3) when \(\lambda = \infty \), in combination with Lemma 2.12 from van der Vaart (1998), to show that the second summand in the above process is equicontinuous. Then, we apply the same reasoning as in the proof of Theorem 19.23 from van der Vaart (1998) to show that the process \( \hat{W}_n^O\) converges weakly.
The proof of the weak convergence of \(\hat{W}_n^F\) is very similar.
\(\square \)
Theorem 3 shows that the processes based on the modified residuals, conditionally on the data, converge weakly and that their limits are equal to the limits of the processes based on the original residuals.
Theorem 3
Assume that the Assumptions (A1), (A2) and (A4) hold. For \(\hat{W}_n^{O*}\), additionally assume that (A5) holds. Then, if either \(\lambda < \infty \) or \(\lambda = \infty \) and Assumption (A3) holds, the processes \(\hat{W}_n^{O*}\) and \(\hat{W}_n^{F*}\) converge in distribution conditionally on the data to
Short proof of Theorem 3
Since the i.i.d. random variables \(\xi _i\) have zero mean and variance 1, the distributions of finite collections of marginals of \(\hat{W}_n^O\) and \(\hat{W}_n^{O*}\) are the same, and the distributions of finite collections of marginals of \(\hat{W}_n^F\) and \(\hat{W}_n^{F*}\) are the same.
Furthermore, assumption (A4) allows us to use the central multiplier theorem 2.9.6 from van der Vaart and Wellner (1996). This, together with the same kind of argument as that given at the end of the previous theorem, completes the proof. \(\square \)
7 Asymptotic behaviour under some alternative hypotheses
In this section, we prove that our method rejects the null hypothesis under one of the three alternative hypotheses stated below.
We assume that we have access only to the random vectors \(\varvec{y}_i\) from the original data, but instead of the true matrices  and
and  , which determine the outcome vector \(\varvec{y}_i, i = 1, \ldots , n\), by
, which determine the outcome vector \(\varvec{y}_i, i = 1, \ldots , n\), by

(where  and
and  are independent sequences of i.i.d. random vectors, which are independent of
are independent sequences of i.i.d. random vectors, which are independent of  ,
,  and \(D_{i}\) and have mean zero and variances
and \(D_{i}\) and have mean zero and variances  and
and  , where
, where  is some positive definite matrix and
is some positive definite matrix and  ), we have access to some possibly different matrices \(\varvec{X}_i\) and \(\varvec{Z}_i\). The numbers of columns in matrices \(\varvec{X}_i\) and \(\varvec{Z}_i\) may be different than the numbers of columns in
), we have access to some possibly different matrices \(\varvec{X}_i\) and \(\varvec{Z}_i\). The numbers of columns in matrices \(\varvec{X}_i\) and \(\varvec{Z}_i\) may be different than the numbers of columns in  and
and  . The i.i.d. sequences of random elements to which we have access will be denoted by \(\left\{ X_i\right\} _ {i \in {\mathbb {N}}}\) and \(\left\{ D_i\right\} _ {i \in {\mathbb {N}}}\), and the i.i.d. sequence of random elements that generated the random vectors \(\varvec{y}_i\) will be denoted by
. The i.i.d. sequences of random elements to which we have access will be denoted by \(\left\{ X_i\right\} _ {i \in {\mathbb {N}}}\) and \(\left\{ D_i\right\} _ {i \in {\mathbb {N}}}\), and the i.i.d. sequence of random elements that generated the random vectors \(\varvec{y}_i\) will be denoted by  , where
, where  . Note that the processes will be based on \(\left\{ X_i\right\} _{i \in {\mathbb {N}}}\).
. Note that the processes will be based on \(\left\{ X_i\right\} _{i \in {\mathbb {N}}}\).
We will use the following two statements:
-
(S1)
We say that a sequence of random matrices \(\varvec{X}_i, i \in {\mathbb {N}}\) is correctly specified when the equation
 (7.1)
(7.1)does not hold for at most finitely many i.
-
(S2)
We say that a sequence of random matrices \(\varvec{Z}_i, i \in {\mathbb {N}}\) is specified correctly when, conditionally on
 and \(D_i\), the equation
and \(D_i\), the equation  (7.2)
(7.2)does not hold for at most a finite number of i.
Note that the negation of the two statements (S1) and (S2) is that the equations (7.1) and (7.2), respectively, do not hold for an infinite number of i but not necessarily all \(i \in {\mathbb {N}}\).
The three alternative hypotheses are then given as follows:
-
(\(H_1\)) The random matrices \(\varvec{X}_i, i \in {\mathbb {N}}\) are not specified correctly, and the matrices \(\varvec{Z}_i, i \in {\mathbb {N}}\) are specified correctly.
-
(\(H_2\)) The random matrices \(\varvec{X}_i, i \in {\mathbb {N}}\) are specified correctly, and the matrices \(\varvec{Z}_i, i \in {\mathbb {N}}\) are not specified correctly.
-
(\(H_3\)) The random matrices \(\varvec{X}_i, i \in {\mathbb {N}}\) are not specified correctly, and the matrices \(\varvec{Z}_i, i \in {\mathbb {N}}\) are not specified correctly.
In all three alternative hypotheses, we also assume the following:
-
(B1)
The random elements \(X_i\) are i.i.d., and their elements have bounded second moments.
-
(B2)
The estimators \(\hat{\varvec{\beta }}, \hat{\varvec{D}}\) and \(\hat{\sigma }\) are obtained in the same way as the estimators based on the original data in (A2). We assume that they converge to the limits \(\varvec{\beta }, \varvec{D}\) and \(\sigma \). We can therefore write
$$\begin{aligned} \sqrt{n} \left( \varvec{\beta }- \hat{\varvec{\beta }}\right) = \frac{1}{ \sqrt{n}} \sum _{i=1}^n {\varvec{m}}(X_i) + o _P\mathopen {}\left( 1\right) \mathclose {} . \end{aligned}$$We also assume that the estimator \(\hat{\varvec{D}}\) and its limit \(\varvec{D}\) are positive definite.
Note that if the assumption (B2) is not satisfied—more specifically, if one of the estimators \(\hat{\varvec{\beta }}, \hat{\varvec{D}}\) or \({\hat{\sigma }} \) does not converge—then the process of fitting the LMM may fail.
A probable cause of the violation of (S1) is that the column span of \({\varvec{X}^{(n)}}\),
does not contain a part of the column span of  ,
,

for every n. This happens, for example, when the matrix \(\varvec{X}^{(n)}\) does not contain a certain column of  .
.
More concretely, assume that we use either the MLE or REML method of estimating the parameters and that the matrix  , which has full rank almost surely, is generated as in Sect. 8, i.e., that its entries are i.i.d. with the possible presence of a column of ones. Furthermore, assume that there is at least one column of
, which has full rank almost surely, is generated as in Sect. 8, i.e., that its entries are i.i.d. with the possible presence of a column of ones. Furthermore, assume that there is at least one column of  that is not present in the matrix \({\varvec{X}}^{(n)}\). If the intercept is not present in the matrices \(\varvec{X}^{(n)}\) and
that is not present in the matrix \({\varvec{X}}^{(n)}\). If the intercept is not present in the matrices \(\varvec{X}^{(n)}\) and  , then (S1) does not hold.
, then (S1) does not hold.
However, if the intercept is present in both matrices \(\varvec{X}^{(n)}\) and  , then (S1) still holds, because the intercept causes the residuals to be centred around 0. But when the missing columns are a function of the columns that are present in both matrices \(\varvec{X}^{(n)}\) and
, then (S1) still holds, because the intercept causes the residuals to be centred around 0. But when the missing columns are a function of the columns that are present in both matrices \(\varvec{X}^{(n)}\) and  , (S1) does not hold.
, (S1) does not hold.
Observe that since the matrix \(\varvec{P}_i, i \in {\mathbb {N}}\) is defined so that it maps any vector from \({{\,\mathrm{span}\,}}\mathopen {}\left( \varvec{Z}_i\right) \mathclose {}\) to zero, in the case when (7.2) does not hold,  . Therefore, the random vectors \(\varvec{e}^O_i\) and \(\varvec{y}^O_i\) are correlated conditionally on
. Therefore, the random vectors \(\varvec{e}^O_i\) and \(\varvec{y}^O_i\) are correlated conditionally on  and \(D_i\), and
and \(D_i\), and

for every t in some open interval I. Additionally, because the random elements \(X_i\) and  are assumed to be i.i.d., this interval I is the same for every i. An example of this arises when the matrices \(\varvec{Z}_i\) do not contain a column of
are assumed to be i.i.d., this interval I is the same for every i. An example of this arises when the matrices \(\varvec{Z}_i\) do not contain a column of  that is not a linear combination of other columns of
that is not a linear combination of other columns of  , for \(i \in {\mathbb {N}}\).
, for \(i \in {\mathbb {N}}\).
In the next theorem and proofs, we use the same quantities—random vectors, random matrices and stochastic processes—as in the previous section. In this case, however, they will not be based on random elements  but will be based on the available data \(\left\{ X_i\right\} _{i \in {\mathbb {N}}}\).
but will be based on the available data \(\left\{ X_i\right\} _{i \in {\mathbb {N}}}\).
Theorem 4
Assume that (B1) and (B2) hold. Then,
-
1.
If hypothesis (\(H_1\)) holds,
$$\begin{aligned} \sup _{t \in {\mathbb {R}}} \left| \frac{1}{\sqrt{n}} \hat{W}_n^O(t) \right| \overset{P}{\rightarrow }c_O \ne 0,&\;\;\;\; \sup _{t \in {\mathbb {R}}} \left| \frac{1}{\sqrt{n}} \hat{W}_n^{O*}(t)\right| \overset{P}{\rightarrow }0 , \\ \sup _{t \in {\mathbb {R}}} \left| \frac{1}{\sqrt{n}} \hat{W}_n^F(t) \right| \overset{P}{\rightarrow }c_F \ne 0,&\;\;\;\; \sup _{t \in {\mathbb {R}}} \left| \frac{1}{\sqrt{n}} \hat{W}_n^{F*}(t)\right| \overset{P}{\rightarrow }0 . \end{aligned}$$ -
2.
If hypothesis (\(H_2\)) holds,
$$\begin{aligned} \sup _{t \in {\mathbb {R}}} \left| \frac{1}{\sqrt{n}} \hat{W}_n^O(t) \right| \overset{P}{\rightarrow }c_O \ne 0,&\;\;\;\; \sup _{t \in {\mathbb {R}}} \left| \frac{1}{\sqrt{n}} \hat{W}_n^{O*}(t)\right| \overset{P}{\rightarrow }0 , \end{aligned}$$and the processes \(\hat{W}_n^F\) and \(\hat{W}_n^{F*}\) converge weakly to the same limit.
-
3.
If hypothesis (\(H_3\)) holds,
$$\begin{aligned} \sup _{t \in {\mathbb {R}}} \left| \frac{1}{\sqrt{n}} \hat{W}_n^O(t) \right| \overset{P}{\rightarrow }c_O \ne 0,&\;\;\;\; \sup _{t \in {\mathbb {R}}} \left| \frac{1}{\sqrt{n}} \hat{W}_n^{O*}(t)\right| \overset{P}{\rightarrow }0 , \\ \sup _{t \in {\mathbb {R}}} \left| \frac{1}{\sqrt{n}} \hat{W}_n^F(t) \right| \overset{P}{\rightarrow }c_F \ne 0,&\;\;\;\; \sup _{t \in {\mathbb {R}}} \left| \frac{1}{\sqrt{n}} \hat{W}_n^{F*}(t)\right| \overset{P}{\rightarrow }0 . \end{aligned}$$
Short proof of Theorem 4
Note that \((\xi _1+\cdots +\xi _n){{\,\mathrm{P }\,}}f^{O}_t / \sqrt{n} \) and \((\xi _1+\cdots +\xi _n){{\,\mathrm{P }\,}}f^{F}_t / \sqrt{n} \) are zero mean. We can then use the same arguments as in Theorems 2 and 3 to prove that the processes \(\hat{W}_n^{O*}\) and \(\hat{W}_n^{F*}\) converge weakly conditionally on the data \(\left\{ X_i\right\} _{i = {\mathbb {N}}}\). On the other hand, \( {\sqrt{n}} {{\,\mathrm{P }\,}}f^{O}_t\) and \( {\sqrt{n}} {{\,\mathrm{P }\,}}f^{F}_t\) do not converge under any of (\(H_1\)), (\(H_2\)) and (\(H_3\)), except in the case of (\(H_2\)) and \( {\sqrt{n}} {{\,\mathrm{P }\,}}f^{F}_t\).
\(\square \)
Theorem 4 (cases 1 and 3) implies that when the matrices \(\varvec{X}_i\) are not correctly specified, the mean functions of the processes \(\hat{W}_n^O(t)\) and \(\hat{W}_n^F(t)\) will be nonzero for some t, while the mean functions of the respective bootstrapped processes, \(\hat{W}_n^{O*}(t)\) and \(\hat{W}_n^{F*}(t)\), will be zero for all t, regardless of the (in)correct specification of the matrices \(\varvec{Z}_i\). In contrast, when \(\varvec{X}_i\) are correctly specified but \(\varvec{Z}_i\) are not, this only holds for the process \(\hat{W}_n^O(t)\), whereas the mean functions of \(\hat{W}_n^{O*}(t)\), \(\hat{W}_n^F(t)\) and \(\hat{W}_n^{F*}(t)\) will be zero for all t.
8 Simulation results
In the simulation study below, we report the results for \(\hat{W}_n^F(t)\), the F-process, and for \(\hat{W}_n^{O}(t)\), the O-process.
The analysis was performed in R (R version 3.4.3) using the R package gofLMM (available on GitHub, https://github.com/rokblagus/gofLMM). The LMMs were fitted by using the function lme from the nlme package (Pinheiro and Bates 2000). The variance parameters were estimated by REML. The p-values were estimated by using \(M=500\) random realizations of null approximations simulating \(\xi _i\), \(i=1,\ldots ,n\), from a standard normal distribution (Pan and Lin 2005) (normal), a Rademacher distribution (i.e., the sign-flipping approach (Winkler et al. 2014), SF) that attaches a mass of 0.5 to the points \(-1\) and 1 and a Mammen two-point distribution (Stute et al. 1998a) (Mammen) that attaches masses \((\sqrt{5}+1)/2\sqrt{5}\) and \((\sqrt{5}-1)/2\sqrt{5}\) to the points \(-(\sqrt{5}-1)/2\) and \((\sqrt{5}+1)/2\); these distributions have been shown to work well in regression settings (Hagemann 2017). Note that all distributions satisfy \(\text{ E }(\xi )=0\) and \(\text{ E }(\xi ^2)=1\), while \(\text{ E }(\xi ^3)=0\) in the case of the standard normal and Rademacher distributions and \(\text{ E }(\xi ^3)=1\) for the Mammen distribution, thus satisfying the conditions in Assumption (A4) in our theoretical investigation. In the definition of \(\sigma _{\lambda }\), two different options for specifying the function p were considered,
and
considering different values of \(\lambda =\{0.5,1,2,4,6,8,10,\infty \)} (note that for \(\lambda =\infty \), the function \(\sigma _{\lambda }\) is the indicator function irrespective of the definition of p); these values of \(\lambda \) were also specified in the grid when using the data-driven approach for choosing \(\lambda \) presented in Sect. 4.1. The differences between the two functions p are not substantial, and hence, only the results for the function defined in (8.1) are shown here (see the supplementary material for the results obtained with the other definition of p for some values of \(\lambda \)). For computational reasons, \(\sigma _{\lambda }\) is only evaluated at distinct fitted values.
The p-values were simulated 5000 times; the simulation margin of errors is thus \(\pm 0.003\), \(\pm 0.006\) and \(\pm 0.008\) for \(\alpha =0.01\), 0.05 and 0.1, respectively. For the F-process, we compare the performance of our proposed tests with the approach proposed by Pan and Lin (2005) (equivalent to using the standard normal distribution when simulating \(\xi _i\) and setting \(\lambda =\infty \)) and the restricted likelihood ratio test (RLRT) of Greven et al. (2008). The RLRT was performed using the function exactRLRT from the R package RLRsim (Scheipl et al. 2008).
We omit the KS test statistics from the results, since they are less powerful than those of CvM. Throughout, the results were similar in terms of size for different choices of \(\lambda \), and hence, only the results for the data-driven choice of \(\lambda \) are shown when considering the performance of the tests under \(H_0\). The results for various values of \(\alpha \) when considering the power of the tests were as expected, with larger power obtained with larger values of \(\alpha \); hence, only the results for \(\alpha =0.05\) are shown in illustrating the performance of the tests when mis-specifying the model.
The outcome was simulated from a linear mixed model with random intercepts and slopes
where \(j=1,\ldots ,n_i\) and \(i=1,\ldots ,n\). The number of observations for all n groups was the same. All quantities on the right side of (8.2) were simulated independently from each other: the covariates \(X_{ij,1}\sim {\mathcal {U}}(0,1)\) and \(X_{ij,2}\sim {\mathcal {U}}(0,1)\), random effects \(b_{i,0}\sim {\mathcal {N}}(0,0.25)\) and \(b_{i,1}\sim {\mathcal {N}}(0,\sigma _{b,1}^2)\), error term \(\epsilon _{ij}\sim {\mathcal {N}}(0,0.5)\), \(\beta _3\), and \(\sigma _{b,1}^2\) were set according to the scenarios in the next subsections.
8.1 Example I: Size under normal errors and normal random effects
The outcome was simulated from (8.2), specifying the variance of the random effect \(b_{i,1}\) as \(\sigma _{b,1}^2 = 0.25\) and \(\beta _3=0\). The fitted model was the same as the simulated model. The simulations were performed for \(n=50,75\) and \(n_i=5,10,20\).
Size under normal errors and normal random effects for different \(\alpha \) (columns) and processes (rows) using the CvM test statistics; \(\lambda \) was chosen using the data-driven approach presented in Sect. 4.1. Each figure shows the difference between the empirical rejection rate and the nominal level (y axis) for different number of observations inside groups (x axis) and different numbers of groups (left, \(n=50\); right, \(n=75\)). The colours specify different distributions used in the proposed bootstrap approach. The shaded areas are the simulation margins of error. RLRT—restricted likelihood ratio test of Greven et al. (2008) (colour figure online)
The empirical sizes of the tests were close to nominal levels for both processes and all distributions (Fig. 1). The exceptions were the situations with a smaller sample size, where the tests for the O-process based on the Mammen and standard normal distributions were slightly too conservative; the difference between the empirical rejection rate and the nominal level was, however, not substantial, and it diminished with increasing sample size. Importantly, this was not a consequence of our data-driven approach for choosing \(\lambda \), since similar results were also obtained when considering fixed values of \(\lambda \) that formed the grid (data not shown). The RLRT was too conservative, rarely rejecting the null hypothesis regardless of the sample size. Very similar results were obtained when relaxing the normality assumption in the error and random effect terms, showing the robustness of our approach against non-normality (see the supplementary material).
8.2 Example II: Mis-specified random effects design matrix
The outcome was simulated from (8.2), \(\beta _3=0\), varying the dispersion of \(b_{i,1}\) by \(\sigma _{b,1}^2=0.5,1,1.5\) and considering \(n=50,75\) and \(n_i=10\). The fixed effects part of the fitted model was correctly specified, but the random effects part included only a random intercept.
Power under a mis-specified random effects design matrix for different \(\lambda \) (columns) and processes (rows) using the CvM test statistics; \(\alpha =0.05\). Each figure shows the empirical rejection rate (y axis) for a different variability of the missed random effect \(b_{i,1}\) (x axis) and a different number of groups (left, \(n=50\); right, \(n=75\)). The colours specify different proposed distributions used in the proposed bootstrap approach. The shaded areas are the simulation margins of error under the null hypothesis. RLRT—restricted likelihood ratio test of Greven et al. (2008). For a normal distribution and \(\lambda =\infty \) (\(\sigma _{\lambda }\) is the indicator function), the results for the F-process are equivalent to using the approach of Pan and Lin (2005); opt—the \(\lambda \) chosen using the data-driven approach presented in Sect. 4.1 (colour figure online)
As suggested by our theoretical results, the empirical sizes of the tests for the fixed effects part of the model were close to the nominal level for all values of \(\lambda \), demonstrating robustness against a mis-specification of the random effects design matrix (Fig. 2). As in the previous examples, the RLRT did not perform well. The tests for the O-process rejected the null hypothesis more often than the nominal level. The rejection rates were larger with smaller \(\lambda \) and larger n and/or \(\sigma _{b,1}^2\), with the SF approach being the most powerful. (This was more evident with large values of \(\lambda \).) The data-driven approach for choosing \(\lambda \) performed well, with a power that was only slightly smaller than that obtained with the \(\lambda \) that yielded the largest power amongst all the values considered in the grid.
8.3 Example III: Mis-specified fixed effects design matrix
The outcome was simulated from (8.2) with \(b_{i,1}\) variance \(\sigma _{b,1}^2=0.25\) and varying \(\beta _3 = 0.5,1,1.5\), considering \(n=50,75\) and \(n_i=10\). The random effects part of the fitted model was correctly specified, but the fixed effects part included only the linear effects of the covariates.
Power under a mis-specified fixed effects design matrix for different \(\lambda \) (columns) and processes (rows) using the CvM test statistics; \(\alpha =0.05\). Each figure shows the empirical rejection rate (y axis) for different fixed effects \(\beta _3\) (x axis) and different numbers of groups (left, \(n=50\); right, \(n=75\)). The colours specify different proposed distributions used in the proposed bootstrap approach. The shaded areas are the simulation margins of error under the null hypothesis. RLRT—restricted likelihood ratio test of Greven et al. (2008). For the normal distribution and \(\lambda =\infty \) (\(\sigma _{\lambda }\) is the indicator function), the results for the F-process are equivalent to using the approach of Pan and Lin (2005); opt—the \(\lambda \) chosen using the data-driven approach presented in Sect. 4.1 (colour figure online)
The empirical rejection rates of all tests were larger than the nominal level, showing that the tests are powerful against this alternative (Fig. 3). The rejection rates when using the F-process were larger than those when using the O-process. The test based on the SF approach was the most powerful (this was more obvious for the O-process and large values of \(\lambda \)). The power increased with larger n and \(\beta _3\). The power with the O-process increased with smaller \(\lambda \). In contrast, for the F-process, the power was generally smaller for smaller values of \(\lambda \). The data-driven approach for choosing \(\lambda \) performed well for both processes, yielding power comparable to what could be obtained by using the value of \(\lambda \) that obtained the largest power. For the F-process, our approach was more powerful than the RLRT.
8.4 Example IV: Mis-specified fixed and random effects design matrices
The outcome was simulated from (8.2) with \(\beta _3=1\) and a varying dispersion of \(b_{i,1}\) with \(\sigma _{b,1}^2=0.25,0.5,1,1.5\), considering \(n=50,75\) and \(n_i=10\). The fixed effects part of the fitted model included only the linear effects of the covariates, and the random effects part included only a random intercept.
Power under mis-specified fixed and random effects design matrices for different \(\lambda \) (columns) and processes (rows) using the CvM test statistics; \(\alpha =0.05\). Each figure shows the empirical rejection rate (y axis) for a different variability of the missed random effect \(b_{i,1}\) (x axis) and a different number of groups (left, \(n=50\); right, \(n=75\)). The colours specify different proposed distributions used in the proposed bootstrap approach. The shaded areas are the simulation margins of error under the null hypothesis. RLRT—restricted likelihood ratio test of Greven et al. (2008). For the normal distribution and \(\lambda =\infty \) (\(\sigma _{\lambda }\) is the indicator function), the results for the F-process are equivalent to those when using the approach of Pan and Lin (2005); opt—the \(\lambda \) chosen using the data-driven approach presented in Sect. 4.1 (colour figure online)
The empirical rejection rates of all tests were larger than the nominal level, showing that the tests are powerful against this alternative (Fig. 4). The rejection rates when using the O-process were larger than those when using the F-process. As expected, the power of the F-process decreased with increasing \(\sigma _{b,1}^2\). Similar to the other examples, the SF approach was the most powerful, but the differences between the approaches were small in this particular example. The power of the O-process increased with smaller values of \(\lambda \). In contrast, the power of the F-process was the smallest with \(\lambda =0.1\) and was comparable with the other values of \(\lambda \). The proposed data-driven approach again performed well, exhibiting good power. For the F-process, our approach was more powerful than the RLRT.
9 Application
We apply the proposed methodology to cross-sectional data from the 2004 American National Election Study (ANES 2022) (see the supplementary material for an application to longitudinal data). The ANES is a series of surveys on voters’ opinions before and after elections in the USA. The 2004 ANES data, with the outcome variable feeling thermometer reading for George W. Bush (a variable with values from 0 to 100, with higher values indicating a more positive feeling towards Bush) and a large set of possible predictor variables, were used as a real data example in Peng and Lu (2012).
Since variable effects tend to be mediated by social and cultural context at the state level, the natural way to handle this data was to fit a linear mixed effects model in which individuals are sampled from states. Peng and Lu (2012) used the data as an illustration for their proposed model selection procedure that uses iterative penalized regression to extract important variables to be included in the fixed and random effects design matrices. On the ANES data set, it yielded a final model with 11 variables for the fixed effects design matrix and two variables for the random effects design matrix, omitting the intercept in the random effects design matrix. We applied our methodology to their final model, which is a good starting point for the fine-tuning that can be done with our proposed methodology.
We prepared the 2004 ANES data in the same way as in Peng and Lu (2012) (the 1212 respondents were decreased to 1156 individuals from 24 states, the number of subjects in each state ranged from 19 to 136, five states were excluded, and the included variables were recoded in the same fashion). The regression coefficients of the nlme fit for the model (9.1),
differ only slightly from the ones published in Peng and Lu (2012) due to different data set versions (see the supplementary material for more details). The only numerical variable in the model is age, and all the others are dichotomous. The codes 0 and 1 are used to represent not having and having a characteristic, respectively (see the supplementary material for the exact meaning of each variable).
In the first row of Fig. 5, we show our proposed empirical stochastic processes (black) for the final Peng–Lu fit of the model. The \(M=500\) generated null F- and O-processes obtained by using the SF approach are shown in grey. The fit is not good (there is a low p-value for the F-process), with a sequence of (mainly) negative ordered residuals in the middle of the plot following a sequence of (mainly) positive residuals.
The addition of six two-way interactions between dichotomous variables (defence-Iraq, liberal-Iraq, democrat-Iraq, indep-Iraq, democrat-black and christian-black) to the fixed effects design matrix yields a reasonable fit for the fixed effects (see the left plot in the second row of Fig. 5 for the F-process; see the longitudinal example presented in the supplementary material for an illustration of how subset F-processes can be used to detect important omitted interaction effects). However, the p-value for the O-process is still significant at the 5% level, implying that the random effects design matrix is mis-specified. The final improvement of fit comes with the inclusion of black, Iraq, and two-way interactions for christian-black and christian-Iraq in the random effects design matrix, which also cause the p-value of the O-process to become insignificant at the 5% level (Fig. 5, right plot in the third row).
By fine-tuning the model obtained by Peng and Lu (2012) (with the addition of interactions to the fixed and random effects design matrices), the interpretation of the final model yields additional insight. It can be observed, for example, that democrats’ expected feeling thermometer towards Bush is very low, but this changes significantly if the person supports the war in Iraq.
Processes \(\hat{W}_n^F(t)\) (left) and \(\hat{W}_n^{O}(t)\) (right) for the three different models (a Rademacher distribution was used to obtain the 500 simulated null processes, shown as grey lines). Row 1 corresponds to model (9.1), row 2 to the same model enhanced with 6 two-way interactions and row 3 to the final model for the 2014 ANES data set. The p-values above each graph correspond to the CvM test statistic with \(\lambda =1200\) chosen from the grid \(\{5,10,50,200,500,1000,1200\}\) using the proposed data-driven procedure
10 Discussion and conclusions
We proposed a novel procedure for testing the assumed specification of the design matrices of fitted LMMs, for which an asymptotic theory based on the strong fundamental stochastic process theory presented by van der Vaart and Wellner (1996) was derived; its validity in terms of size was demonstrated, and its power against several alternatives was showcased. The approach is based on inspecting different empirical stochastic processes that are constructed as smoothed cumulative sums of appropriately standardized and ordered model residuals: the O-process, the F-process, and the subset F-process. Investigating the O-process allows us to test the correct specification of both design matrices. In contrast, investigating the F-process (or the subset F-process) allows us to investigate the assumed fixed effects design matrix (or some subset thereof).
We showed that the O-process is expected to fluctuate around zero when the fixed and random effects design matrices are correctly specified, while it is not when either (or both) of the fixed and random effects design matrices are mis-specified. In contrast, it was shown that the F-process and subset F-process fluctuate around zero when the fixed effects design matrix is correctly specified, regardless of the (in)correct specification of the random effects design matrix. While we did not construct a process that would target only the random component, a mis-specification of the random effects design matrix can still be detected. That is, we showed that when there is no evidence that the fixed effects design matrix is mis-specified but enough evidence to deduce that the entire LMM is mis-specified, this implies a mis-specification of the random effects design matrix.
Any observed fluctuations or deviations from zero can be evaluated visually and by means of p-values by using the proposed computationally efficient approach, which does not require re-estimating the LMM. Several different multiplier distributions could be used when estimating the p-values. Asymptotically, the choice of the multiplier distribution is not important as long as Assumption (A4) holds. However, it could make a difference in finite samples. In our simulation study, we considered three options: a standard normal distribution, a Rademacher distribution (i.e., a sign-flipping approach) and a Mammen two point distribution. While the three distributions performed similarly in terms of size, attaining the nominal level, the approach based on the Rademacher distribution yielded better results in terms of power. Therefore, even though the differences between the three distributions in terms of power were not substantial, we would recommend using the Rademacher distribution, especially with a smaller sample size.
The indicator function is usually used in the context of goodness-of-fit testing (equivalently to using a cumulative sum of ordered residuals). We proposed replacing the indicator function with a continuous function of \(\lambda \) (and the model’s fitted values), which for large values of \(\lambda \) is a close approximation of the indicator function. The constant \(\lambda \) can be seen as a smoothing parameter of the cusum process, facilitating the visual inspection of the plots and making it easier to identify potential improvements in the model’s fit. In our simulations, smoothing improved the power of the O-process. For the F-process, the differences in power for most considered values of the smoothing parameter were small in our examples. The exceptions were very small values of the smoothing parameter (i.e., a very large amount of smoothing), where the power was reduced due to (excessive) smoothing. However, we have also identified examples, where smoothing can improve the power for the F-process (one example is shown in the supplementary material). We proposed a straightforward data-driven approach for choosing the amount of smoothing. This approach performed well in our simulations, obtaining power comparable to what could potentially be obtained by specifying a single value of \(\lambda \) that yielded the largest power amongst all the values forming the grid. There might still be room to further improve the power, e.g., by not relying on a pre-specified grid, which we think represents an interesting subject for future research. By using a different multiplier distribution (and smoothing) we were able to improve the power of the approach proposed by Pan and Lin (2005) for checking the correct specification of the fixed effects design matrix. González-Manteiga et al. (2016) proposed an approach which has greater power than the Pan and Lin (2005) approach and it would be interesting to compare it to our method; however, readily available code makes this difficult.
While we only considered single-level LMMs in detail, the proposed methodology could be adapted to multiple nested levels of random effects, but at a cost of notational inconvenience (see the supplementary information). In principle, the methodology presented here could be extended to GLMMs. However, further extensions to nonlinear link GLMMs could be problematic when trying to distinguish between the reasons for a (possible) lack of fit due to fixed or random effects design matrices since the parameter sets of fixed and random effects cannot be chosen separately, i.e., independently.
References
ANES (2022) 2004 American National Election studies data. https://electionstudies.org/data-center/2004-time-series-study/. Accessed 2 Oct 2022
Christensen R, Lin Y (2015) Lack-of-fit tests based on partial sums of residuals. Commun Stat Theory Methods 44(13):2862–2880. https://doi.org/10.1080/03610926.2013.844256
Claeskens G, Hart JD (2009) Goodness-of-fit tests in mixed models. TEST 18(2):213–239. https://doi.org/10.1007/s11749-009-0148-8
Demidenko E (2005) Mixed models: theory and applications. Wiley Series in Probability and Statistics. Wiley. https://books.google.si/books?id=Z2FZlSDEAPoC
Diebolt J, Zuber J (1999) Goodness-of-fit tests for nonlinear heteroscedastic regression models. Stat Probab Lett 42(1):53–60. https://doi.org/10.1016/S0167-7152(98)00189-8
Efendi A, Drikvandi R, Verbeke G, Molenberghs G (2017) A goodness-of-fit test for the random-effects distribution in mixed models. Stat Methods Med Res 26(2):970–983. https://doi.org/10.1177/0962280214564721
Fan J, Huang LS (2001) Goodness-of-fit tests for parametric regression models. J Am Stat Assoc 96(454):640–652. https://doi.org/10.1198/016214501753168316
González-Manteiga W, Martínez-Miranda MD, Van Keilegom I (2016) Goodness-of-fit test in parametric mixed effects models based on estimation of the error distribution. Biometrika 103(1):133–146. https://doi.org/10.1093/biomet/asv061
Greven S, Crainiceanu CM, Küchenhoff H, Peters A (2008) Restricted likelihood ratio testing for zero variance components in linear mixed models. J Comput Graph Stat 17(4):870–891
Hagemann A (2017) Cluster-robust bootstrap inference in quantile regression models. J Am Stat Assoc 112(517):446–456. https://doi.org/10.1080/01621459.2016.1148610
He X, Shao QM (2000) On parameters of increasing dimensions. J Multivar Anal 73(1):120–135. https://doi.org/10.1006/jmva.1999.1873 (https://www.sciencedirect.com/science/article/pii/S0047259X99918730)
Huet S, Kuhn E (2014) Goodness-of-fit test for gaussian regression with block correlated errors. Statistics 49:1–28. https://doi.org/10.1080/02331888.2014.913047
Jiang J (1996) REML estimation: asymptotic behavior and related topics. Ann Stat 24(1):255–286. https://doi.org/10.1214/aos/1033066209
Jiang J (2001) Goodness-of-fit tests for mixed model diagnostics. Ann Stat 29(4):1137–1164. https://doi.org/10.1214/aos/1013699997
Laird NM, Ware JH (1982) Random-effects models for longitudinal data. Biometrics 38(4):963–974
Lee OE, Braun TM (2012) Permutation tests for random effects in linear mixed models. Biometrics 68(2):486–493. https://doi.org/10.1111/j.1541-0420.2011.01675.x
Lin DY, Wei LJ, Ying Z (2002) Model-checking techniques based on cumulative residuals. Biometrics 58(1):1–12. https://doi.org/10.1111/j.0006-341X.2002.00001.x
Loy A, Hofmann H, Cook D (2017) Model choice and diagnostics for linear mixed-effects models using statistics on street corners. J Comput Graph Stat 26(3):478–492. https://doi.org/10.1080/10618600.2017.1330207
Majumder M, Hofmann H, Cook D (2013) Validation of visual statistical inference, applied to linear models. J Am Stat Assoc 108(503):942–956. https://doi.org/10.1080/01621459.2013.808157
Pan Z, Lin DY (2005) Goodness-of-fit methods for generalized linear mixed models. Biometrics 61(4):1000–1009. https://doi.org/10.1111/j.1541-0420.2005.00365.x
Peng H, Lu Y (2012) Model selection in linear mixed effect models. J Multivar Anal 109:109–129. https://doi.org/10.1016/j.jmva.2012.02.005 (https://www.sciencedirect.com/science/article/pii/S0047259X12000395)
Pinheiro JC, Bates DM (2000) Mixed-effects models in S and S-PLUS. Springer, New York, NY [u.a.]
Ritz C (2004) Goodness-of-fit tests for mixed models. Scand J Stat 31(3):443–458. https://doi.org/10.1111/j.1467-9469.2004.02_101.x
Sánchez BN, Houseman EA, Ryan LM (2009) Residual-based diagnostics for structural equation models. Biometrics 65(1):104–115
Scheipl F, Greven S, Küchenhoff H (2008) Size and power of tests for a zero random effect variance or polynomial regression in additive and linear mixed models. Comput Stat Data Anal 52(7):3283–3299. https://doi.org/10.1016/j.csda.2007.10.022 (https://www.sciencedirect.com/science/article/pii/S0167947307004306)
Stute W, González-Manteiga W, Presedo Quindimil M (1998) Bootstrap approximations in model checks for regression. J Am Stat Assoc 93(441):141–149
Stute W, Thies S, Zhu LX (1998) Model checks for regression: an innovation process approach. Ann Stat 26(5):1916–1934. https://doi.org/10.1214/aos/1024691363
Su JQ, Wei LJ (1991) A lack-of-fit test for the mean function in a generalized linear model. J Am Stat Assoc 86(414):420–426
Tang M, Slud EV, Pfeiffer RM (2014) Goodness of fit tests for linear mixed models. J Multivar Anal 130:176–193. https://doi.org/10.1016/j.jmva.2014.03.012 (http://www.sciencedirect.com/science/article/pii/S0047259X14000682)
van der Vaart AW (1998) Asymptotic statistics. Cambridge University Press. https://doi.org/10.1017/cbo9780511802256
van der Vaart AW, Wellner JA (1996) Weak convergence and empirical processes. Springer, New York. https://doi.org/10.1007/978-1-4757-2545-2
Van Keilegom I, González-Manteiga W, Sánchez Sellero C (2008) Goodness-of-fit tests in parametric regression based on the estimation of the error distribution. TEST 17(2):401–415. https://doi.org/10.1007/s11749-007-0044-z
Winkler AM, Ridgway GR, Webster MA, Smith SM, Nichols TE (2014) Permutation inference for the general linear model. Neuroimage 92:381–397. https://doi.org/10.1016/j.neuroimage.2014.01.060 (http://www.sciencedirect.com/science/article/pii/S1053811914000913)
Wood SN (2012) On \(p\)-values for smooth components of an extended generalized additive model. Biometrika 100(1):221–228. https://doi.org/10.1093/biomet/ass048
Wood SN (2013) A simple test for random effects in regression models. Biometrika 100(4):1005–1010. https://doi.org/10.1093/biomet/ast038
Wu L (2009) Mixed effects models for complex data. CRC Press, Chapman & Hall/CRC Monographs on Statistics & Applied Probability
Zeger SL, Liang KY, Albert PS (1988) Models for longitudinal data: a generalized estimating equation approach. Biometrics 44(4):1049–1060
Acknowledgements
Jakob Peterlin is a young researcher funded by the Slovene Research Agency (ARRS). The authors acknowledge the financial support by ARRS (Methodology for data analysis in medical sciences, P3-0154, and projects J3-1761 and N1-0035). The constructive comments of two Reviewers and the Associate Editor are gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Peterlin, J., Kejžar, N. & Blagus, R. Correct specification of design matrices in linear mixed effects models: tests with graphical representation. TEST 32, 184–210 (2023). https://doi.org/10.1007/s11749-022-00830-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11749-022-00830-1
Keywords
- Asymptotic convergence
- Correlated data
- Empirical stochastic processes
- Monte Carlo simulations
- Sign-flipping
- Wild bootstrap




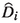 and
and 




