A new inferential approach for response-adaptive clinical trials: the variance-stabilized bootstrap

Abstract

This paper discusses disadvantages and limitations of the available inferential approaches in sequential clinical trials for treatment comparisons managed via response-adaptive randomization. Then, we propose an inferential methodology for response-adaptive designs which, by exploiting a variance stabilizing transformation into a bootstrap framework, is able to overcome the above-mentioned drawbacks, regardless of the chosen allocation procedure as well as the desired target. We derive the theoretical properties of the suggested proposal, showing its superiority with respect to likelihood, randomization and design-based inferential approaches. Several illustrative examples and simulation studies are provided in order to confirm the relevance of our results.

1 Introduction

While randomized clinical trials are essential for scientific progress and for promoting the public health at large, there is an uncomfortable ethical dilemma, because in most clinical trials half the patients will be randomized to a potentially ineffective or harmful treatment. This dilemma becomes more acute in the context of grave or emerging novel infectious diseases. Motivated by the ethical demand of individual care, in the last two decades there has been an increasing attention in the literature on response-adaptive (RA) designs.

By using the information provided by earlier responses and past assignments, RA procedures are sequential rules in which the treatment allocation probabilities change in order to favour at each step the treatment that appears to be superior and, asymptotically, to reach a desired treatment allocation proportion—the so-called target—representing a valid trade-off between ethics and inference (see, e.g., Rosenberger et al. (2001) and Baldi Antognini and Giovagnoli (2010)). Indeed, since the ethical goal of maximizing the subjects’ care often conflicts with the statistical one of drawing correct inferential conclusions about the identification of the better treatment and its relative superiority, the targets generally depend on the unknown treatment effects: although a priori unknown, they can be approached by RA procedures that estimate sequentially the parameters to progressively converge to the chosen target [see for a review Atkinson and Biswas (2014), Baldi Antognini and Giovagnoli (2015) and Rosenberger and Lachin (2015)]. Some examples are the Sequential Maximum Likelihood design (Melfi and Page 2000), the Doubly-adaptive Biased Coin design (Eisele 1994) and the Efficient Randomized Adaptive DEsign (ERADE) introduced by Hu et al. (2009) in order to improve the convergence to the chosen target.

Although the adaptation process induces a complex dependence structure between the outcomes, several authors provided the conditions under which the classical asymptotic likelihood-based inference is still valid for RA procedures [see, e.g., Durham et al. (1997) and Melfi and Page (2000)]. In particular, let us assume that the observations relative to either treatment—say A and B—are iid belonging to the exponential family parameterized in such a way that $\theta _j\in \varTheta \subseteq {\mathbb {R}}$ denotes the mean effect of treatment j, while $v_j= v(\theta _j)>0$ is the corresponding variance $(j=A,B)$. Special cases of practical relevance in the clinical context for modeling the primary endpoint, that in what follows will be referred to as statistical models, are binary (with $\theta _j\in (0;1)$, $v(\theta _j)=\theta _j(1-\theta _j)$) and Poisson ($\theta _j\in {\mathbb {R}}^+$, $v(\theta _j)=\theta _j$) distributions for dichotomous and count data, respectively, while the normal model (with $\theta _j\in {\mathbb {R}}$ and $v(\theta _j)=v_j$ independent from $\theta _j$) is also encompassed for continuous responses as well as the exponential one ($\theta _j\in {\mathbb {R}}^+$, $v(\theta _j)=\theta ^2_j$) for survival outcomes.

The inferential goal usually consists in estimating/testing the superiority of A wrt B and, therefore, interest lies in the treatment contrast $\vartheta =\theta _A-\theta _B$, while $\theta _B$ is usually regarded as a nuisance parameter, so from now on we take into account the model re-parameterization $(\theta _A,\theta _B) \rightarrow (\vartheta ,\theta _B)$. Let $\pi _n$ be the allocation proportion to A (respectively, $1-\pi _n$ to B) after n steps, if the RA design is chosen such that

$$\begin{aligned} \lim _{n \rightarrow \infty }\pi _n = \rho (\vartheta ,\theta _B)\in (0;1)\quad a.s. \quad \text {with } \rho (\cdot )\ \text {continuous, } \end{aligned}$$

(1)

then the applicability of standard asymptotic inference is ensured. Generally satisfied by RA rules proposed in the literature, this crucial condition prescribes that the target $\rho$ must be a non-random quantity different from 0 and 1, to avoid possible degeneracy of likelihood methods. Moreover, by assuming (without loss of generality) that high responses are preferable for patients’ care, an additional common assumption is:

$$\begin{aligned} \rho \ \text {is monotonically increasing in } \vartheta \ \ \text {with }\ \rho (0,\theta _B)=1/2. \end{aligned}$$

(2)

For example, adopting the Play-the-Winner rule proposed by Zelen (1969) for binary trials, the allocation proportion of A converges to $\rho _{PW}(\vartheta ,\theta _B)=(1-\theta _B)/[2(1-\theta _B)-\vartheta ]$. Whereas, other targets proposed in the literature depend only on the treatment difference: for instance, in the case of normal homoscedastic trials, Bandyopadhyay and Biswas (2001) and Atkinson and Biswas (2005) suggest $\rho _N(\vartheta ) = \varPhi \left( \vartheta /T\right)$, while Baldi Antognini et al. (2018a) discuss $\rho _L(\vartheta ) = \{ e^{-\vartheta /T}+1\}^{-1}$, where $\varPhi$ is the cumulative distribution function of the standard normal and $T > 0$ a tuning parameter.

For moderate-large samples, namely the most representative framework in the context of phase-III clinical trials, several authors showed (both theoretically and via simulations) that the likelihood-based approach could present anomalies in terms of coverage probabilities of confidence intervals, as well as inflated type-I errors or inconsistency of Wald’s test, especially when the chosen targets exhibit a strong ethical component (Rosenberger and Hu 1999; Yi and Wang 2011; Atkinson and Biswas 2014; Baldi Antognini et al. 2018a; Novelli and Zagoraiou 2019). To avoid these drawbacks, Wei (1988) and Rosenberger (1993) suggested to conduct randomization-based inference for RA trials. Under this framework, the null hypothesis of equality of the two arms corresponds to an allocation in which the treatment assignments are unrelated to the responses, so the randomization test is carried out by computing the distribution of the allocations conditionally on the observed outcomes (that are treated as deterministic). Since the distribution of the test depends on the adopted RA procedure, exact results are quite few and, generally, p-values are computed via Monte Carlo methods. Following a design-based approach, Baldi Antognini et al. (2018b) recently introduced a test based on the treatment allocation proportion induced by a suitably chosen RA rule showing that, in some circumstances, this test could be uniformly more powerful than the Wald test.

After discussing drawbacks and limitations of the available inferential approaches, the aim of this paper is to provide a new inferential methodology for RA clinical trials by combining a variance stabilizing transformation with a bootstrap method. We derive the theoretical properties of the suggested proposal, showing that it is more accurate than the other approaches, regardless of the adopted RA rule as well as the chosen target. Several illustrative examples are provided for normal, binary, Poisson and exponential data. Starting from a discussion in Sect. 2 about the existing approaches, highlighting their inadequacy for RA clinical trials, Sect. 3 deals with the new variance-stabilized bootstrap procedure and its theoretical properties. An extensive simulation study is carried out in Sect. 4 to confirm the relevance of our results, also comparing the performances of the newly introduced approach to those of other inferential methods. Finally, Sect. 5 deals with some concluding remarks.

2 Available inferential approaches

2.1 Likelihood-based inference

Although for RA designs the MLEs $\hat{\varvec{\theta }}_n=({\hat{\theta }}_{An},{\hat{\theta }}_{Bn})^t$ of $\varvec{\theta }=(\theta _A,\theta _B)$ remain the same as those of the non-sequential setting (i.e., the sample means), this is not true for their distribution due to the complex dependence structure generated by the adaptation process. However, the standard asymptotic inference is allowed for RA designs satisfying (1). Indeed, let ${\mathbf {M}}_n=\text {diag} (\pi _n/ v_A; [ 1-\pi _n]/ v_B )$ be the normalized Fisher information and ${\hat{\vartheta }}_n = {\hat{\theta }}_{An} - {\hat{\theta }}_{Bn}$, then $\sqrt{n} ({\hat{\vartheta }}_n - \vartheta ) \hookrightarrow {\mathcal {N}} \left( 0,\sigma ^2\right)$, where $\sigma ^2=v_A/\rho (\vartheta ,\theta _B)+v_B/[1-\rho (\vartheta ,\theta _B)]$ and, due to the continuity of the target,

$$\begin{aligned}&\lim _{n \rightarrow \infty }\rho ({\hat{\vartheta }}_n,{\hat{\theta }}_{Bn})=\rho (\vartheta ,\theta _B)\; \; a.s.\quad \text {and} \\&\lim _{n \rightarrow \infty } {\mathbf {M}}_n={\mathbf {M}}=\text {diag}(\rho (\vartheta ,\theta _B)/v_A;[ 1-\rho (\vartheta ,\theta _B)]/v_B)\;\; a.s. \end{aligned}$$

So, letting ${\hat{v}}_{jn}$s be consistent estimators of the treatment variances, then ${\hat{\sigma }}^2_n={\hat{v}}_{An}/\rho ({\hat{\vartheta }}_n,{\hat{\theta }}_{Bn}) +{\hat{v}}_{Bn}/[1-\rho ({\hat{\vartheta }}_n,{\hat{\theta }}_{Bn})]$ and the $(1-\alpha )\%$ asymptotic confidence interval is $CI(\vartheta )_{1-\alpha }=({\hat{\vartheta }}_n \pm n^{-1/2}z_{1-\alpha /2}{\hat{\sigma }}_n)$, where $z_{\alpha }$ is the $\alpha$-percentile of $\varPhi$. Moreover, to test $H_0 : \vartheta = 0$ against $H_1 : \vartheta > 0$ (or $H_1 : \vartheta \ne 0$), Wald statistic $W_n=\sqrt{n}{\hat{\vartheta }}_n {\hat{\sigma }}_n^{-1}$ is usually employed. Under $H_0$, $W_n$ converges to the standard normal distribution and, due to the consistency of ${\hat{\sigma }}^2_n$, the power can be approximated by

$$\begin{aligned} \varPhi \left( \sqrt{n}\vartheta \sigma ^{-1} - z_{1 - \alpha } \right) , \quad \vartheta > 0. \end{aligned}$$

(3)

Even if condition (1) theoretically guarantees the applicability of likelihood inference, this approach may present critical drawbacks, in particular for targets characterized by a high ethical component. Indeed, as shown in Baldi Antognini et al. (2018a) and Novelli and Zagoraiou (2019), if $\rho$ tends either to 0 or 1, the asymptotic variance of ${\hat{\vartheta }}_n$ tends to diverge. Therefore, the quality of the CLT approximation is compromised, leading to unreliable confidence intervals and inflated type-I errors. Furthermore, some targets (like, e.g., $\rho _N$ and $\rho _L$) could induce a consistent loss of inferential precision, since the Wald test becomes inconsistent and it displays a non-monotonic power.

2.2 Randomization-based inference

Randomization—also known as re-randomization—tests are a class of nonparametric procedures obtained by recomputing a test statistic $D_n$ (as ${\hat{\vartheta }}_n$ or other discrepancy measures between the two arms, like those based on ranks) over permutations of the data (Rosenberger and Lachin 2015). Taking into account the null hypothesis (under which the allocations are unrelated to the patients’ outcomes), the procedure is carried out by considering the set of responses as fixed and deterministic values, and computing all the possible ways in which the subjects could have been assigned to the treatments. However, since the computation of all the treatment assignment permutations and their probabilities is not feasible, even for small or moderate sample sizes, in practice randomization tests are computed using Monte Carlo methods. In particular, the allocation sequence is generated L times and, for each sequence, the statistic of interest $d_n^l$ is computed, obtaining $\{d_n^{l}, l=1,\ldots ,L\}$. Then, a consistent estimator of the p-value is obtained by calculating the proportion of the generated sequences that yields a value of the test equal or more extreme than the value $d_n$ of the test statistic evaluated on the observed data. Then, the p-value can be approximated by the proportion of sequences where $|d_n^l| \ge |d_n|$, namely ${\hat{P}}_{rand}=L^{-1}\sum _{l=1}^{L}\mathbb {I}(|d_n^l|\ge |d_n|)$, where $\mathbb {I}(\cdot )$ is the indicator function, so that the test of level $\alpha$ rejects $H_0$ if ${\hat{P}}_{rand}$ is lower than the significance level. Analogously, the power of the randomization test can be approximated via Monte Carlo methods by repeating H times the above-mentioned procedure and computing the proportion of rejections (Beran 1986).

One of the main strengths of randomization tests consists in avoiding any parametric assumption on the population model; this makes them a valid alternative to the standard likelihood methods, especially when the conventional model assumptions may not hold or be verified (Rosenberger et al. 2019). However, the behavior of randomization tests strictly depends on the particular RA procedure that has been adopted and their applicability may be severely limited by the quite restricted specification of the null hypothesis being tested. For instance, if the chosen RA design depends only on the treatment effects, then the null hypothesis of randomization test actually corresponds to testing the equality of the effects, with an alternative that is naturally two-sided (i.e., the allocations depend on the treatment outcomes). Although these procedures have been also applied for the one-sided alternative $H_1: \vartheta >0$, they are not suitable for a general hypothesis testing problem. For instance, assuming $\rho _{PW}$ for binary trials or $\rho _N$ for normal outcomes discussed above, a commonly used alternative $H_1: \vartheta >\delta$ for a prefixed minimum significant difference $\delta$ cannot be tested via re-randomization. Moreover, such an approach does not directly allow the construction of confidence intervals.

2.3 Design-based inference

Taking into account targets depending only on the treatment difference, namely $\rho =\rho (\vartheta )$, satisfying (1)–(2) with $\rho (\vartheta )=1-\rho (-\vartheta )$ to treat the two arms symmetrically, Baldi Antognini et al. (2018b) have recently introduced a design strategy for normally response trials that overcomes some drawbacks of the Wald test. In particular, under condition (1), both $\rho ({\hat{\vartheta }}_n)$ and the treatment allocation proportion $\pi _n$ are consistent estimators of $\rho (\vartheta )$. Thus, if we further assume

$$\begin{aligned} \rho \ \text {is twice continuously differentiable with bounded derivatives,} \end{aligned}$$

(4)

adopting ERADE [or an asymptotically best RA procedure as defined by Zhang and Rosenberger (2006)], then $\sqrt{n}(\pi _n -\rho (\vartheta ))\hookrightarrow {\mathcal {N}}(0,\lambda ^2)$, where $\lambda ^2 = [\rho '(\vartheta )]^2 \left\{ v_A/ \rho (\vartheta )+v_B/[1-\rho (\vartheta )]\right\}$ is the so-called Rao–Cramer lower bound and $\rho '$ is the derivative of $\rho$ (the asymptotic normality follows from the Delta-method, provided that $\rho '(\vartheta )\ne 0$). Thus, let ${\hat{\lambda }}^2_n = [\rho '({\hat{\vartheta }}_n)]^2\left[ {\hat{v}}_{An}/\pi _n+ {\hat{v}}_{Bn}/(1-\pi _n)\right]$ be a consistent estimator of $\lambda ^2$, then $CI(\rho (\vartheta ))_{1-\alpha }=(\pi _n \pm z_{1-\alpha /2}{\hat{\lambda }}_n/ \sqrt{n})$ and, due to the monotonicity of $\rho$, the asymptotic confidence interval for $\vartheta$ could be derived by applying the inverse mapping $\rho ^{-1}$ to the endpoints of $CI(\rho (\vartheta ))_{1-\alpha }$. Analogously, testing the equality of the treatment effects is equivalent to testing $H_0:\rho (\vartheta )=1/2$ (against $H_1 : \rho (\vartheta )>1/2$ or $H_1 : \rho (\vartheta )\ne 1/2$, corresponding to $H_1 : \vartheta > 0$ or $H_1 : \vartheta \ne 0$, respectively). Under $H_0$, the test statistic $Z_n = \sqrt{n}\left( \pi _n - 1/2\right) {\hat{\lambda }}_n^{-1}$ converges to the standard normal distribution, while given $H_1 : \rho (\vartheta )>1/2$, the power of the $\alpha$-level test $Z_n$ can be approximated by

$$\begin{aligned} \varPhi \left( \frac{\sqrt{n}\left[ \rho (\vartheta ) - \frac{1}{2}\right] }{{\rho }'(\vartheta ) \sqrt{\frac{v_A}{\rho (\vartheta )}+\frac{v_B}{1-\rho (\vartheta )}}} - z_{1 - \alpha } \right) , \quad \vartheta > 0. \end{aligned}$$

(5)

Test $Z_n$ is consistent provided that $\lim _{\vartheta \rightarrow {\overline{\vartheta }}}[1-\rho (\vartheta )][\rho '(\vartheta )]^{-2}>0$, where ${\overline{\vartheta }}=\sup _{\theta _A \in \varTheta } \vartheta$. Moreover, under some additional conditions on $\rho$, power (5) is monotonically increasing in $\vartheta$ and $Z_n$ tends to be more powerful than the Wald test. However, the major drawback of this approach is its strong dependence on the chosen target, which could significantly affect $\lambda ^2$ through its ethical skew, leading to possibly inflated type-I errors. Indeed, by combining (1), (2), (4) and the symmetric structure of the target,

• (i) $\rho '(\vartheta )=\rho '(-\vartheta ) \ge 0$ for every $\vartheta$, with $\rho '(0)\ne 0$ to guarantee the applicability of the Delta-method;

• (ii) $\rho ''(\vartheta )=-\rho ''(-\vartheta )$ for every $\vartheta$, which implies that $\rho ''(0)=0$;

• (iii) $0<\rho '(0)<\infty$, which clearly limits the choice of the target as well as the values of the tuning parameter T, if present ($\lambda ^2$ is strongly affected by $\rho '$, which represents the ethical improvement of the chosen target, especially when $\rho '(0)$ tends to grow quickly).

These are the main reasons why the design-based test could present inflated type-I errors for several targets and some values of T. For instance, taking into account normal response trials, although $\rho _N$ and $\rho _L$ are twice differentiable with $\rho ''_N(0)=\rho ''_L(0)=0$, these targets tend to be highly sensitive to small variations in the treatment difference $\vartheta$ around 0 (i.e., under $H_0$), especially for small values of T; whereas the target

$$\begin{aligned} \rho _{S}(\vartheta )=\frac{1}{2}+ \frac{\vartheta }{2(|\vartheta |+T)} \end{aligned}$$

(6)

is not twice differentiable at 0; moreover, $\rho '_S(0)$ vanishes as T grows and tends to be unbounded as $T\rightarrow 0$, so damaging the CLT approximation (as we will point out in Table 1).

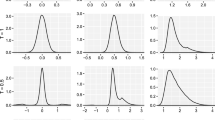
Example 1

Figure 1 shows the simulated distributions of the allocation proportion $\pi _n$ under $H_0:\vartheta = 0$, adopting $\rho _S$ and $\rho _L$ with $T \in \{0.5, 1, 2\}$, obtained by simulating 100000 homoscedastic normally distributed trials with $n=250$ using ERADE (with randomization parameter $\gamma = 0.5$). Adopting $\rho _L$, for $T = 0.5$ the resulting distribution tends to be concentrated on the extremes, presenting peaks on 0 and 1, while for $T\ge 1$ the asymptotic normality is preserved. Under $\rho _S$ instead, small values of T tend to both increase the variability of the distribution of $\pi _n$ and to accentuate the departure from normality; this effect is greatly mitigated for $T>1$.

Fig. 1

Simulated distribution of $\pi _n$ under $H_0$ adopting $\rho _S$ and $\rho _L$ as T varies

Test $Z_n$ could be naturally extended to a target $\rho (\vartheta , \theta _B)$ depending on the nuisance parameter $\theta _B$ by letting $\lambda ^2=\nabla \rho ^t {\mathbf {M}}^{-1}\nabla \rho$ and to other models belonging to the exponential family, as we will discuss in Sect. 4 for binary, Poisson and exponential outcomes.

3 The variance-stabilized bootstrap-t approach

In order to avoid the aforementioned drawbacks of both likelihood-based and design-based inference, also overcoming the limitations of randomization-based tests, we now propose a new inferential approach for RA procedures developed through a variance-stabilized bootstrap-t method (Tibshirani 1988; Efron and Tibshirani 1994). By mapping the statistic of interest via a variance stabilizing transformation and computing its bootstrap-t distribution, this proposal allows us to avoid the problems related to the instability of the asymptotic variance as well as the quality of the CLT approximation.

The main idea behind the variance stabilization is the following: let X be a random variable with expected value $\mu$ and variance $\nu =\nu (\mu )$, letting $g(\cdot )$ a regular transformation such that $g'(\mu )=\nu (\mu )^{-1/2}$, then the variance of g(X) tends to be first-order constant, namely it is at least approximately independent on $\mu$ in a first-order Taylor expansion. Therefore, given a chosen target $\rho$, by applying such a variance stabilizing transformation to the estimated treatment difference ${\hat{\vartheta }}_n$, we are able to get over the possible degeneracy of its asymptotic variance $\sigma ^2_{\rho }$. In particular, for every fixed $\theta _B \in \varTheta$ (and $v\in {\mathbb {R}}^+$ for normal homoscedastic outcomes), by letting $\sigma ^2_{\rho } = \sigma ^2_{\rho }(\vartheta )$ and $g(x)=\int ^x \sigma _{\rho }^{-1}(t)\mathrm{d}t$, then $\sqrt{n}[({\hat{\vartheta }}_n) - g(\vartheta )]\hookrightarrow {\mathcal {N}} \left( 0,1\right)$ from the Delta-method. Therefore, by letting

$$\begin{aligned} {\mathcal {T}}_n =\sqrt{n}[g({\hat{\vartheta }}_n)-g(0)], \end{aligned}$$

(7)

the $\alpha$-level right-sided test consists in rejecting the null hypothesis $H_0:\vartheta =0$ when ${\mathcal {T}}_n>z_{1-\alpha }$. Hence, the power is $\Pr (\sqrt{n}[g({\hat{\vartheta }}_n) - g(\vartheta )]> z_{1-\alpha } -\sqrt{n}[g(\vartheta )-g(0)])$, which can be approximated by $\varPhi \left( \sqrt{n}[g(\vartheta )-g(0)] - z_{1 - \alpha } \right)$, for $\vartheta > 0$.

Notice that the transformation $g(\cdot )$ depends on the chosen target as well as on the statistical model through the variance function, and thus it could also depend on $\theta _B$ and v; therefore, the estimation of the nuisance parameters is requested for computing the statistical test and from now on we let ${\hat{v}}_n$ be a consistent estimator of v. The following Corollary presents the transformation $g(\cdot )$ and the corresponding test ${\mathcal {T}}_n$ for the most common statistical models and for some selected targets. In particular, a widely used one is

$$\begin{aligned} \rho _R(\vartheta , \theta _B) = \frac{\vartheta +\theta _B}{\vartheta +2 \theta _B}, \end{aligned}$$

(8)

which corresponds to the Neyman allocation for exponential outcomes and to the E-optimal design for Poisson responses (also considered by Zhang and Rosenberger (2006) for normal trials with non-negative means and by Baldi Antognini and Giovagnoli (2010) for binary outcomes).

Corollary 1

Let us consider the target $\rho _R$ in (8):

• (i) for binary outcomes, $\theta _B \in (0;1)$, $-\theta _B< \vartheta <1-\theta _B$ and $\sigma _{\rho _R}^2=1-(1-\vartheta -2 \theta _B)^2$;thus, $g(\vartheta )=-\arcsin (1-\vartheta -2 \theta _B)$ and ${\mathcal {T}}_n=\sqrt{n}\{\arcsin (1-2{\hat{\theta }}_{Bn})-\arcsin (1-{\hat{\vartheta }}_n-2{\hat{\theta }}_{Bn})\}$;

• (ii) for exponential trials, $\theta _B>0$ and $\vartheta >-\theta _B$, $g(\vartheta )=\ln (\vartheta +2 \theta _B)$ and ${\mathcal {T}}_n=\sqrt{n}\ln (1+{\hat{\vartheta }}_n/2{\hat{\theta }}_{Bn})$;

• (iii) for normal homoscedastic data with $\theta _B>0$ and $\vartheta >-\theta _B$, so $g(\vartheta )=2\theta _B v^{-1/2}[\sqrt{1+\vartheta /\theta _B}-\arctan (\sqrt{1+\vartheta /\theta _B})]$ and therefore

  $$\begin{aligned} {\mathcal {T}}_n =2{\hat{\theta }}_{Bn}\sqrt{\frac{n}{{\hat{v}}_n}}\left\{ \sqrt{1+\frac{{\hat{\vartheta }}_n}{{\hat{\theta }}_{Bn}}} -\arctan \left( \sqrt{1+\frac{{\hat{\vartheta }}_n}{{\hat{\theta }}_{Bn}}}\right) -1+\frac{\pi }{4}\right\} ; \end{aligned}$$

• (iv) for Poisson data $\theta _B>0$ and $\vartheta > -\theta _B$, $g(\vartheta )=\sqrt{2(\vartheta +2 \theta _B)}$ and ${\mathcal {T}}_n =\sqrt{n}\{(2{\hat{\vartheta }}_n+4{\hat{\theta }}_{Bn})^{1/2} - 2{\hat{\theta }}_{Bn}^{1/2} \}$.

Whereas, for Poisson responses the Neyman allocation reads

$$\begin{aligned} \rho _{Z}(\vartheta , \theta _B) = \frac{\sqrt{\vartheta +\theta _B}}{\sqrt{\vartheta +\theta _B} + \sqrt{\theta }_B}, \end{aligned}$$

(9)

hence $g(\vartheta ) = 2 \left\{ \sqrt{\vartheta + \theta _B} - \sqrt{\theta _B}\ln \left( \sqrt{\theta _B} + \sqrt{\vartheta + \theta _B} \right) \right\}$ and then

$$\begin{aligned} {\mathcal {T}}_n=2 \sqrt{n}\left\{ \sqrt{{\hat{\vartheta }}_n + {\hat{\theta }}_{Bn}} - \sqrt{{\hat{\theta }}_{Bn}}\ln \left( \frac{1}{2} + \frac{\sqrt{{\hat{\vartheta }}_n + {\hat{\theta }}_{Bn}}}{ 2\sqrt{{\hat{\theta }}_{Bn}}} \right) \right\} . \end{aligned}$$

Adopting $\rho _L$, for normal homoscedastic outcomes $\vartheta \in {\mathbb {R}}$ and $g(\vartheta )=2Tv^{-1/2}\arctan (e^{\vartheta /2T})$, hence

$$\begin{aligned} {\mathcal {T}}_n =2T\sqrt{\frac{n}{{\hat{v}}_n}}\left\{ \arctan \left( e^{{\hat{\vartheta }}_n/2T} \right) -\frac{\pi }{4} \right\} , \end{aligned}$$

which does not depend on $\theta _B$.

Notice that for some targets, e.g., $\rho _{PW}$, the transformation function $g(\cdot )$ is not available in closed form and it should be evaluated numerically using standard integration routines (like, e.g., integrate in R).

Assuming that the outcomes belong to the exponential family discussed in Sect. 1, the following results hold.

Theorem 1

The variance-stabilized test ${\mathcal {T}}_n$ is consistent, and its power function is monotonically increasing in $\vartheta$, regardless of the chosen target.

Proof

Due to its definition, the variance stabilizing transformation $g(\cdot )$ is a continuous and monotonically increasing function and, therefore, the power of ${\mathcal {T}}_n$ is increasing too. Furthermore, by noticing that $\lim _{\vartheta \rightarrow {\overline{\vartheta }}}g(\vartheta )=g({\overline{\vartheta }})>g(0)$, test ${\mathcal {T}}_n$ is always consistent. $\square$

Theorem 2

If the target $\rho$ is chosen such that

$$\begin{aligned} \int _0^x \sigma _{\rho }^{-1}(t)\mathrm{d}t\ge x\sigma _{\rho }^{-1}(x), \quad \forall x> 0, \end{aligned}$$

(10)

the variance-stabilized test ${\mathcal {T}}_n$ is uniformly more powerful than Wald’s test. Furthermore, condition (10) holds if $\sigma _{\rho }^2(\vartheta )$ is increasing for $\vartheta >0$.

Proof

Condition (10) can be easily derived from the power function of test ${\mathcal {T}}_n$ combined with (3). Moreover, the last statement follows from the mean value theorem; indeed, due to the continuity of $\sigma _{\rho }(\cdot )$, there exists a given $c\in [0;x]$ such that $\int _0^x \sigma _{\rho }^{-1}(t)\mathrm{d}t=x\sigma _{\rho }^{-1}(c)$ and therefore, if $\sigma _{\rho }^2(x)$ is increasing in x, then $\sigma _{\rho }^{-1}(c)\ge \sigma _{\rho }^{-1}(x)$ since $c\le x$. $\square$

As an example, let us consider $\rho _L$ for normal homoscedastic data. Condition (10) simplifies to

$$\begin{aligned} 2T\arctan ( e^{x/2T})- \frac{x e^{x/2T } }{e^{x/T }+1} \ge 0, \end{aligned}$$

which can be verified by noticing that the left hand side is an increasing function for every $x>0$ and it is equal to 0 for $x=0$. As we will show in the following Corollary, for normal homoscedastic outcomes test ${\mathcal {T}}_n$ is uniformly more powerful than Wald’s test, regardless of the chosen target (see also Table 1). In general, however, the superiority of ${\mathcal {T}}_n$ depends on the adopted target and the given statistical model.

Corollary 2

For normal homoscedastic outcomes, test ${\mathcal {T}}_n$ is uniformly more powerful than $W_n$ regardless of the chosen target. Adopting $\rho _R$ for exponential data, as well as under $\rho _{Z}$ for Poisson trials, test ${\mathcal {T}}_n$ is uniformly more powerful than $W_n$.

Proof

In the case of normal homoscedastic outcomes, for every $\rho$ satisfying (2), $\sigma _{\rho }^2(\vartheta )$ is increasing in $\vartheta$ for every $\vartheta >0$. Indeed,

$$\begin{aligned} \sigma _{\rho }^2(\vartheta )=\frac{v}{\rho (\vartheta ,\theta _B)[1-\rho (\vartheta , \theta _B)]}, \end{aligned}$$

where from (2), for every $\theta _B\in {\mathbb {R}}$, the target is increasing in $\vartheta$ with $\rho (\vartheta ,\theta _B) \ge 1/2$ for $\vartheta >0$. Therefore, for every pair $(\vartheta _1,\vartheta _2)$ with $0<\vartheta _1<\vartheta _2$, then $1/2\le \rho (\vartheta _1,\theta _B)\le \rho (\vartheta _2,\theta _B)$ and thus $\sigma _{\rho }^2(\vartheta _1)\le \sigma _{\rho }^2(\vartheta _2)$, since $\rho (\vartheta _1,\theta _B)+ \rho (\vartheta _2,\theta _B)\ge 1$.

As regards $\rho _R$ for exponential data, condition (10) simplifies to $\ln \left( 1+ \vartheta /2\theta _B\right) \ge (1+2\theta _B/\vartheta )^{-1}$, which is trivially verified for any $\vartheta > 0$ and $\theta _B>0$. Analogously, adopting $\rho _{Z}$ for Poisson trials, $\sigma _{\rho _Z}^2(\vartheta )=(\sqrt{\vartheta +\theta _B} + \sqrt{\theta }_B)^2$, that is increasing in $\vartheta$ for every $\vartheta > 0$ and $\theta _B>0$. $\square$

In order to overcome possible problems related to the quality of the CLT approximation, we apply such a variance stabilizing transformation into a bootstrap framework. Since standard re-sampling techniques (like the nonparametric bootstrap) may not be suitable for non-exchangeable/dependent data, we suggest a parametric bootstrap that makes use of the estimated parameters and generates replicates of both the allocation sequence derived by the chosen RA rule and the corresponding outcomes, without re-sampling the observed data. Following the same arguments of Rosenberger and Hu (1999), who have derived bootstrap confidence intervals for adaptive designs, if the RA procedure satisfies condition (1), then the bootstrap method is still first-order consistent. Indeed, in this case the MLEs are consistent and asymptotically normal, so the first-order consistency of the bootstrap estimators follows directly [see the Appendix of Rosenberger and Hu (1999)]. Moreover, such a variance-stabilized bootstrap-t method has been proven to be transformation-respecting, second-order correct and accurate, providing also good performances in fairly general settings (DiCiccio and Efron 1996; Hall 2013).

More specifically, given a RA design fulfilling conditions (1)–(2), the proposed strategy is the following:

• 1. at the end of the trial with n subjects derive $\varvec{{\hat{\theta }}}_n$;

• 2. generate $B_1$ replicates of the RA trial with size n using $\varvec{{\hat{\theta }}}_n$ as underlying parameters, obtaining $\varvec{{\hat{\theta }}}_n^{*i}$ and then ${\hat{\vartheta }}_n^{*i}$, for $i=1,\ldots ,B_1$;

• 3. for each i, generate $B_2$ replications of the trial using $\varvec{{\hat{\theta }}}_n^{*i}$ as underlying parameters and compute the bootstrap estimate ${\hat{\nu }}_n^{*i}$ of the variance of $\sqrt{n}{\hat{\vartheta }}_n^{*i}$ over the $B_2$ replicates, deriving ${\hat{\nu }}_n^{*i}$ ($i=1,\ldots ,B_1$);

• 4. fit a curve to the points $\left\{ (\sqrt{n}{\hat{\vartheta }}_n^{*i},{\hat{\nu }}_n^{*i})\right\} _{i=1,\ldots ,B_1}$ using a nonlinear regression technique—such as lowess running smoother (Cleveland 1979)—to estimate $\nu (\cdot )$ and compute the variance stabilizing transformation $g(x) = \int ^{x} \nu (s)^{-1/2}\mathrm{d}s$ by using a numerical integration technique;

• 5. generate $B_3$ new replicates of the trial using $\varvec{{\hat{\theta }}}_n$ to obtain ${\hat{\vartheta }}_n^{*j}$ ($j=1,\ldots ,B_3$) and then compute the $(1-\alpha )$-percentile $t_{1-\alpha }^*$ of the studentized distribution $\sqrt{n}\{g({\hat{\vartheta }}_n^*)-g({\hat{\vartheta }}_n)\}$.

Let ${\mathcal {T}}_n^*$ be the bootstrap version of (7), given $H_1 : \vartheta > 0$, the $\alpha$-level test rejects $H_0$ when ${\mathcal {T}}_n^*>t_{1-\alpha }^*$ (the two-tailed alternative can be derived accordingly). Then, denoting by $t_n^{*j}$ the test statistic calculated for the jth bootstrap replicate ($j=1,\ldots ,B_3$), the p-value can be approximated by ${\hat{P}}_{boot} = B_3^{-1}\sum _{j=1}^{B_3} \mathbb {I}(t_n^{*j} \ge t_n^* )$, where $t_n^*$ is the value of ${\mathcal {T}}_n^*$ evaluated on the observed data. Finally, the power of test ${\mathcal {T}}_n^*$ can be approximated via Monte Carlo methods by repeating H times steps $1{-}5$ and computing the percentage of rejections (Beran 1986). As regards the construction of confidence intervals, by the inverse mapping $g^{(-1)}$,

$$\begin{aligned} CI(\vartheta )_{1-\alpha }=\left( g^{(-1)}\{g({\hat{\vartheta }}_n) -n^{-1/2} t_{1-\alpha /2}^* \} ; g^{(-1)}\{g({\hat{\vartheta }}_n) - n^{-1/2}t_{\alpha /2}^* \}\right) . \end{aligned}$$

Remark 1

The use of different sets of bootstrap replicates for the estimation of (i) the variance transformation $g(\cdot )$ (steps 2–3) and (ii) the percentile $t_{1-\alpha }^*$ (step 5) is intended to limit the burden of computation required, reducing considerably the calculation wrt to the usual untransformed bootstrap-t method. Indeed, as shown by Tibshirani (1988), $B_1 = 100$ and $B_2 = 25$ are sufficient to reliably estimate $g(\cdot )$, while at least $B_3 = 1000$ is needed to derive $t_{1-\alpha }^*$. It is worth stressing that the implementation of our proposal is not time consuming: with a regular laptop, it takes about 1 second to perform a hypothesis test as well as to build a confidence interval.

4 A comparative simulation study

In this section, we compare the performances of the newly introduced test ${\mathcal {T}}_n^*$ with the ones of Wald’s statistic $W_n$, the design-based test $Z_n$ and the randomization test $D_n$ (using ${\hat{\vartheta }}_n$ as discrepancy measure). In order to do so, we have performed a simulation study employing ERADE ($\gamma = 0.5$) with $n = 250$ and a starting sample of $n_0 = 2$ for each treatment. In the first scenario, the responses are assumed to be homoscedastic normally distributed with unknown common variance $v = 1$. Table 1 summarizes the results adopting targets $\rho _L$ and $\rho _{S}$ (with $T = 0.5$, 1 and 2), obtained with 100000 Monte Carlo replications of the trial for $W_n$, $Z_n$ and $D_n$, while we set $B_1 = 300$, $B_2 = 100$ and $B_3 = 10000$ for ${\mathcal {T}}_n^*$.

Table 1 Simulated power of tests ${\mathcal {T}}_n^*$, $Z_n$, $W_n$ and $D_n$, for normal homoscedastic responses, under $\rho _L$ and $\rho _{S}$ as T and $\vartheta$ vary

Because of its strong ethical skew, target $\rho _L$ induces an anomalous behavior of the power of $W_n$, which tends to the significance level as $\vartheta$ grows (especially as the ethical skew increases, namely for $T \le 1$, when the power function rapidly vanishes); note that all the remaining tests are consistent. Whereas, adopting $\rho _{S}$, the consistency of the Wald test is preserved, while $Z_n$ exhibits inflated type-I errors. In general, the new test ${\mathcal {T}}_n^*$ preserves the nominal type-I error and provides an improvement in inferential precision wrt to all the competitors. This is particularly true with $\rho _S$: indeed for $T=0.5$ the gain of power of ${\mathcal {T}}_n^*$ wrt to $W_n$ and $D_n$ is about $4\%$ and $7\%$, respectively.

The second scenario deals with binary trials: Table 2 describes the performance of the four tests adopting $\rho _{PW}$ and $\rho _{R}$ as $\theta _B$ varies. While preserving the nominal type-I error, ${\mathcal {T}}_n^*$ shows the highest power in all the scenarios, with an improvement of about $8\%$ wrt to $D_n$ and up to $4\%-5\%$ wrt $Z_n$ and $W_n$, respectively. Test $Z_n$ shows a slight inflation of type-I error for $\rho _{PW}$ and $\theta _B = 0.7$. It is worth stressing that ${\mathcal {T}}_n^*$, $Z_n$ and $D_n$ confirm their consistency with all the adopted targets, while this is not true for Wald’s test under $\rho _{PW}$.

Table 2 Simulated power of tests ${\mathcal {T}}_n^*$, $Z_n$, $W_n$ and $D_n$, for binary trials adopting $\rho _{PW}$ and $\rho _{R}$, with $\theta _B = 0.1, 0.4$ and 0.7

Table 3 describes the simulation results obtained with exponential and Poisson data adopting $\rho _{R}$ and $\rho _{Z}$, respectively. Under these scenarios, ${\mathcal {T}}_n^*$ confirms the good results in terms of power, with a gain up to $4\%$ wrt $D_n$ and up to $2{-}3\%$ wrt $Z_n$ and $W_n$, respectively. Tests $Z_n$ and $W_n$ tend to perform quite similarly, while the randomization test $D_n$ exhibits the lowest inferential precision.

Table 3 Simulated power of tests ${\mathcal {T}}_n^*$, $Z_n$, $W_n$ and $D_n$, for exponential and Poisson outcomes, adopting $\rho _{R}$ and $\rho _{Z}$, with $\theta _B = 1, 5$ and 10

Taking now into account CIs, Table 4 compares the simulated $CI(\vartheta )_{0.95}$ obtained in the case of normal homoscedastic trials (with $v=1$) adopting $\rho _{L}$ and $\rho _{S}$ with ERADE $(\gamma = 0.5)$ and $n=250$, as $\vartheta$ and T vary. Here, Lower (L) and Upper (U) bounds are obtained by averaging the endpoints of the simulated trials. Under $\rho _L$, for $T = 2$, all the considered approaches perform quite similarly, with an empirical coverage that increases as the empirical evidence increases. Although for $\vartheta \le 1.5$ the endpoints obtained through the bootstrap procedure are close to the asymptotic likelihood-based ones, as $\vartheta$ grows the likelihood-based CIs tend to degenerate, while the bootstrap ones maintain their reliability with only a slight increase in their widths. Note that, due to the inverse-mapping, the applicability of the design-based CIs is severely limited: when the chosen target approaches 1 (i.e., for small values of T or when $\vartheta$ grows), the CIs for $\rho$ often contain values outside (0; 1) and therefore the inverse-mapping cannot be properly applied (for this reason, we use the symbol − in Tables 4 and 5). This is particularly evident for $T < 1$ or $\vartheta > 1.5$. Adopting $\rho _S$ instead, design-based CIs do not diverge but strongly undercover when $\vartheta = 0$. Likelihood-based and bootstrap-based CIs perform fairly well, with the latter displaying slightly asymmetric right endpoints.

Table 4 Simulated $CI(\vartheta )_{0.95}$ for normal homoscedastic responses adopting $\rho _{L}$ and $\rho _S$ as T and $\vartheta$ vary

Following the same setting of the previous tables, Table 5 summarizes the simulated $CI(\vartheta )_{0.95}$ obtained for binary trials with $\rho _{PW}$ and $\rho _{R}$ as $\vartheta$ and $\theta _B$ vary. Bootstrap-based and likelihood-based CIs confirm their good performances with quite similar empirical coverage; bootstrap intervals are on average slightly less wider and right shifted. As previously discussed, the design-based CIs show an extremely unstable behavior, in particular when the targets approach 1 (i.e., as $\theta _B$ grows for $\rho _{PW}$ or as $\theta _B$ tends to 0 for $\rho _R$), also due to their dependence on the nuisance parameter. While the EC for the CIs of $\rho$ is always close to its nominal value, the inverse-mapping transformation can cause either an undercoverage for $\rho _{PW}$ or an overcoverage for $\rho _R$ for the CIs of $\vartheta$.

Table 5 Simulated $CI(\vartheta )_{0.95}$ for binary trials adopting $\rho _{PW}$ and $\rho _R$ as $\theta _B$ and $\vartheta$ vary

Table 6 displays the simulated $CI(\vartheta )_{0.95}$ obtained for exponential and Poisson outcomes adopting $\rho _{R}$ and $\rho _{Z}$ as $\vartheta$ and $\theta _B$ vary. Bootstrap-based and likelihood-based CIs perform fairly well, while the design-based CIs are, on average, slightly wider.

Table 6 Simulated $CI(\vartheta )_{0.95}$ for exponential and Poisson outcomes adopting $\rho _{R}$ and $\rho _Z$, respectively, as $\theta _B$ and $\vartheta$ vary

Finally, it is worth highlighting that our proposal exhibits good inferential performances also for small/medium sample sizes. In the same setting of the previous tables, Tables 7 and 8 summarize the results about the simulated power and $CI(\vartheta )_{0.95}$ for $n = 100$, adopting $\rho _{R}$. We set $\theta _B = 0.1$ for binary data, while for homoscedastic normal, exponential and Poisson responses $\theta _B = 1$. Note that now the sample size is reduced to the $40\%$ of that of the previous tables, this clearly translates into lower power and wider confidence intervals. Nevertheless, ${\mathcal {T}}_n^*$ confirms its consistency, also preserving at the same time the type-I error, for all the considered models; moreover, the bootstrap-based CIs maintain their reliability in terms of both empirical coverage and interval width.

Table 7 Simulated power of test ${\mathcal {T}}_n^*$ adopting $\rho _{R}$ for binary (with $\theta _B = 0.1$), homoscedastic normal, exponential and Poisson (with $\theta _B = 1$) data, for $n = 100$

Table 8 $CI(\vartheta )_{0.95}$ for binary (with $\theta _B = 0.1$), homoscedastic normal, exponential and Poisson (with $\theta _B = 1$) data, for $n = 100$

5 Discussion

In this paper, we propose a new inferential strategy for response-adaptive clinical trials based on the variance-stabilized bootstrap-t method. This is motivated by the fact that the available inferential approaches present several drawbacks, such as (i) inconsistency of Wald’s test, local decreasing power and unreliable CIs for likelihood inference, (ii) reduction in the empirical coverage of CIs and inflated type-I errors for the design-based approach, (iii) unsuitability of randomized-based inference for general hypothesis testing problems.

We derive the theoretical properties of the suggested methodology, showing that the degeneracy of the Fisher information is avoided, guaranteeing at the same time the consistency of the test as well as a monotonically increasing power function. In general, this proposal preserves the nominal type-I error, attenuates the dependence on the nuisance parameters and is more efficient than the other methods, regardless of the chosen RA rule as well as the adopted target and its ethical skew. By means of an extensive simulation study, we show that the new inferential strategy has very good performances in terms of power compared to the above-mentioned inferential approaches. In addition, the suggested bootstrap approach turns out to provide reliable confidence intervals in terms of both empirical coverage and interval width, avoiding then the possible degeneracies and instability of the likelihood-based and the design-based approach, respectively. Moreover, our proposal exhibits good performances in terms of inferential accuracy even for small/medium sample sizes.

Although in actual practice, the large majority of phase-III trials are planned for comparing $K=2$ treatments, the case of $K>2$ could be also of interest and now we briefly discuss a possible extension of the proposed methodology. Even if for two treatments the variance stabilizing transformation g is guaranteed (whose closed-form expression could or could not be available on the basis of the variance function and the chosen target), for several treatments this transformation does not exist in general. Let $\varvec{\theta }=(\theta _1,\ldots ,\theta _K)^t$ and ${\varvec{v}}=(v_1,\ldots ,v_K)^t$ be the vectors of treatment effects and variances, respectively, while $\varvec{\rho }(\varvec{\theta })=(\rho _1(\varvec{\theta }),\ldots ,\rho _K(\varvec{\theta }))^t$ now denotes the target, namely $\rho _k(\varvec{\theta })$ is the target allocation of the kth treatment group $(k=1,\ldots ,K)$ with ${\mathbf {1}}_{K}^t\varvec{\rho }(\varvec{\theta })=1$ (where ${\mathbf {1}}_{K}$ is the $K-$dim vector of ones). In this setting, the inferential focus is on the contrasts $\varvec{\vartheta }={\mathbf {A}}^t\varvec{\theta }$ where, considering without loss of generality the first treatment as the reference one, ${\mathbf {A}}^t=[{\mathbf {1}}_{K-1} \vert -{\mathbf {I}}_{K-1}]$ (here ${\mathbf {I}}_{K-1}$ is the $(K-1)-$dim identity matrix). After n steps, letting ${\hat{\varvec{\theta }}}_n=({\hat{\theta }}_{n1},\dots , {\hat{\theta }}_{nK})^t$ be the MLE of $\varvec{\theta }$, if condition (1) holds for every treatment group, then ${\hat{\varvec{\theta }}}_n$ is strongly consistent and asymptotically normal with $\sqrt{n}({\hat{\varvec{\theta }}}_n-\varvec{\theta })\overset{d}{\longrightarrow } \text {N}({\varvec{0}}_K, {\mathbf {M}}^{-1})$, where ${\varvec{0}}_{K}$ is the K-dim vector of zeros and ${\mathbf {M}}=\text {{diag}}\left( \rho _{k}(\varvec{\theta })/v_{k} \right) _{k=1,\dots , K}$. Therefore, the MLE $\varvec{{\hat{\vartheta }}}_n={\mathbf {A}}^t\varvec{{\hat{\theta }}}_n$ is strongly consistent and asymptotically normal with $\sqrt{n}(\varvec{{\hat{\vartheta }}}_n -\varvec{\vartheta })\overset{d}{\longrightarrow } \text {N}({\varvec{0}}_{K-1}, {\mathbf {A}}^t{\mathbf {M}}^{-1}{\mathbf {A}})$. From the multi-dimensional Delta-method, the problem now consists in finding a proper covariance stabilizing transformation, namely a function $G:\mathbb {R}^{K-1}\rightarrow \mathbb {R}^{K-1}$ stabilizing ${\mathbf {A}}^t{\mathbf {M}}^{-1}{\mathbf {A}}$, i.e., such that $\sqrt{n}(G(\varvec{{\hat{\vartheta }}}_n) -G(\varvec{\vartheta }))\overset{d}{\longrightarrow } \text {N}({\varvec{0}}_{K-1}, {\mathbf {I}}_{K-1})$. By letting ${\mathbf {J}}=(\partial G /\partial {\varvec{x}})\Vert _{{\varvec{x}}=\varvec{\vartheta }}$ be the Jacobian matrix of the partial derivatives of G evaluated at $\varvec{\vartheta }$, then G is a covariance stabilizing transformation if and only if ${\mathbf {J}}^t{\mathbf {J}}=({\mathbf {A}}^t{\mathbf {M}}^{-1}{\mathbf {A}})^{-1}$. Essentially, this corresponds to ${\mathbf {J}}=({\mathbf {A}}^t{\mathbf {M}}^{-1}{\mathbf {A}})^{-1/2}$, namely a mapping G whose Jacobian is equal to a square root of the symmetric and positive definite matrix $({\mathbf {A}}^t{\mathbf {M}}^{-1}{\mathbf {A}})^{-1}$ should be identified. Unfortunately, this transformation may not exist and it should be checked for any chosen model and target by applying standard matrix differential equations; however, the computational complexity grows extremely fast as K increases, leading to a very complicated programming except for $K=3$, as discussed in Holland (1973).