Abstract
This paper treats functional marked point processes (FMPPs), which are defined as marked point processes where the marks are random elements in some (Polish) function space. Such marks may represent, for example, spatial paths or functions of time. To be able to consider, for example, multivariate FMPPs, we also attach an additional, Euclidean, mark to each point. We indicate how the FMPP framework quite naturally connects the point process framework with both the functional data analysis framework and the geostatistical framework. We further show that various existing stochastic models fit well into the FMPP framework. To be able to carry out nonparametric statistical analyses for FMPPs, we study characteristics such as product densities and Palm distributions, which are the building blocks for many summary statistics. We proceed to defining a new family of summary statistics, so-called weighted marked reduced moment measures, together with their nonparametric estimators, in order to study features of the functional marks. We further show how other summary statistics may be obtained as special cases of these summary statistics. We finally apply these tools to analyse population structures, such as demographic evolution and sex ratio over time, in Spanish provinces.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Many types of functional data, such as financial time series, animal movements, growth functions for trees in a forest stand, the spatial extensions of outbreaks of a disease over time with respect to the outbreak centres, population growth functions of towns/cities in a country, and different functions describing spatial dependence (e.g. LISA functions; see Section 11 in Supplementary Materials and the references therein), are represented as collections \(\{f_1(t),\ldots ,f_n(t)\}\), \(t\in {{\mathcal {T}}}\subset [0,\infty )\), \(n\ge 1\), of functions/paths in some k-dimensional Euclidean space \({{\mathbb {R}}}^k\), \(k\ge 1\); note that the argument t need not represent time, it could, for example, represent spatial distance. The common approach to deal with such data within the field of functional data analysis (FDA) (Ramsay and Silverman 2005) is to assume that the functions \(f_i\), \(i=1,\ldots ,n\), belong to some suitable family of functions (usually an \(L_2\)-space) and are realisations/sample paths of some collection of independent and identically distributed (iid) random functions/stochastic processes \(\{F_1(t),\ldots ,F_n(t)\}\), \(t\in {{\mathcal {T}}}\), with sample paths belonging to the family of functions in question.
For many applications, however, the following two adequate questions may quite naturally arise:
-
1.
Does it make sense to assume that the random elements \(F_1,\ldots ,F_n\), which have generated the functional data set \(\{f_1,\ldots ,f_n\}\), are in fact iid?
-
2.
Is the study designed in such a way that the sample size n is known a priori, or is n in fact unknown before the data set is realised?
The first question can be framed within the context of multivariate (Gaussian) random fields/processes, and it has been addressed quite extensively in the literature; see, e.g. Banerjee et al. (2014), Gelfand and Banerjee (2010), Genton and Kleiber (2015). The second question, however, in particular in combination with the first question, has not really been explored to any degree, and it would be beneficial to have a foundation with a proper structure for such analyses.
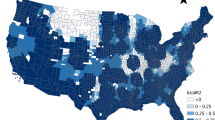
Top panels: Spanish province data. Log-scale demographic evolution (top left) and sex ratio (top right) in 47 provinces of Spain, for the years 1998–2017. Bottom panel: Movement tracks. The movement tracks of two Mongolian wolves (bottom left). Movement tracks of 15 Ya Ha Tinda elks in Banff National Park, Canada (bottom right); the red squares are the starting points of the tracks
Functional data sets (believed to be) generated in accordance with the above remarks will be referred to as functional marked point patterns, and Fig. 1 provides illustrative examples of such data sets. The top panels show two functional marked point patterns based on the centres of the provinces on the Spanish mainland. To each point, which corresponds to a centre, we have associated the demographic evolution of the population on logarithmic scale (left) and the sex ratio (right), over the years 1998–2017. In the top right panel, for each of the 47 functions/provinces, the horizontal red dashed line corresponds to \(y=1\), which illustrates the case where we have the same size of genders in the province in question. The bottom panels show animal movement tracks. The lower left panel shows the movement tracks of two Mongolian wolves, starting from random initial monitoring locations (red squares); the data are taken from the Movebank website. The lower right panel shows the movement tracks of 15 Ya Ha Tinda elk (Hebblewhite and Merrill 2008), starting from some random initial monitoring locations.
Another setting where these questions also naturally arise is found in spatio-temporal geostatistics (Montero et al. 2015). Assume that each of the data-generating stochastic processes \(F_i(t)=Z(x_i,t)\), \(t\in {{\mathcal {T}}}\), \(i=1,\ldots ,n\), is associated with a spatial location \(x_i\in W\subset {{\mathbb {R}}}^d\) and that Z(x, t), \((x,t)\in W\times {{\mathcal {T}}}\), is a (Gaussian) spatio-temporal random field. Here, the functions \(F_1,\ldots ,F_n\) are clearly not independent (ignoring pathological cases) and one may further ask whether it would not in fact make sense to assume that the sampling/monitoring locations \(x_1,\ldots ,x_n\) are actually randomly generated. In addition, does it make sense to assume that the total number of such locations was fixed a priori, or did these locations, for example, appear over times (in relation to each other), thus allowing us to treat them as a randomly evolving entity with a random total number of components \(N\ge 1\)? For instance, all the weather stations monitoring precipitation in a given country/region have (most likely) arrived over time, in relation to each other, rather than being placed at their individual locations at the same time. For example, we do not know a priori how many stations will have appeared during the period 2010–2040 and where they will be located.
Taking these remarks into account, we argue that for many functional data sets \(\{f_1(t),\ldots ,f_n(t)\}\), \(t\in {{\mathcal {T}}}\subset [0,\infty )\), \(n\ge 1\), it would make sense to assume i) that \(n\ge 1\) is the realisation of some discrete non-negative random variable N and ii) that (conditional on \(N=n\)) the random functions \(F_1,\ldots ,F_n\) are possibly dependent. A natural way to tackle the statistical analysis under such non-standard assumptions is to assume that the functional data set is generated by a point process in some space \({{\mathcal {F}}}\) of functions \(f:{{\mathcal {T}}}\rightarrow {{\mathbb {R}}}^k\). This would mean that we would model the functional data set (a functional marked point pattern) as the realisation of a set of random functions \(\{F_1(t),\ldots ,F_N(t)\}\), \(t\in {{\mathcal {T}}}\), of random size N. Note that by construction, all components \(F_i\) have the same marginal distributions. Under such a setup, a so-called binomial point process (Møller and Waagepetersen 2004; van Lieshout 2000) would yield the classical FDA setup mentioned above. Note that the idea of analysing point patterns (collections of points) with attached functions has already been noted in the literature (Comas 2009; Delicado et al. 2010).
It is often the case that these functions have some sort of spatial dependence. For example, two functions \(f_i\) and \(f_j\), with starting points \(f_i(0)\) and \(f_j(0)\) which are spatially close to each other in \({{\mathbb {R}}}^k\), either gain or lose from each other’s vicinity. Accordingly, it seems natural to generate \(F_1,\ldots ,F_N\) conditionally on some collection of random spatial locations \(X_i\) and some further set of random variables \(L_i\) associated with the random functions \(F_i\); conditionally on the spatial locations, the \(L_i\)’s would influence the random functions \(F_i\) in a non-spatial sense. We argue that the natural setting to do this is through functional marked point processes (FMPPs). More precisely, we define a FMPP \(\varPsi =\{(X_i,(L_i,F_i))\}_{i=1}^N\) as a spatial point process \(\varPsi _G=\{X_i\}_{i=1}^N\) in \({{\mathbb {R}}}^d\) to which we assign marks \(\{(L_i,F_i)\}_{i=1}^N\); note that by forcing all \(L_i\) to take the same value, we may reduce the FMPP to the collection \(\{(X_i,F_i)\}_{i=1}^N\).
We here take a full grip and provide a proper framework for FMPPs, where we in particular take into account that for the standard point process machinery to go through (in particular the use of regular conditional probability distributions), one has to assume that the mark space, and thereby the function space \({{\mathcal {F}}}\), is a Polish space (Daley and Vere-Jones 2008). In particular, one may then provide a reference stochastic process \(X^{{{\mathcal {F}}}}\), with sample paths in \({{\mathcal {F}}}\), whose distribution \(\nu _{{{\mathcal {F}}}}\) on \({{\mathcal {F}}}\) acts as a reference measure which one integrates with respect to (in a Radon–Nikodym sense). We further provide a plethora of examples from the literature which fit into the FMPP framework and discuss these in some detail. Examples include geostatistics (Cressie and Kornak 2003) with random sampling locations, point processes marked with ‘spatio-temporal random closed sets’, e.g. spatio-temporal Boolean models (Sebastian et al. 2006), constructed functional marks, e.g. so-called LISA functions (Mateu et al. 2007), and the Renshaw-Särkkä growth-interaction model (Cronie and Särkkä 2011; Cronie et al. 2013; Renshaw and Särkkä 2001; Särkkä and Renshaw 2006). To be able to carry out statistical analyses in the context of FMPPs, various moment characteristics, such as product densities, are required and we here cover such characteristics. A key observation here is that we, in contrast to previous works, completely move away from the (arguably unrealistic) assumption of stationarity. We then proceed to discussing various general marking structures, such as the marks having a common marginal distribution and the marks being (conditionally) independent. To study interactions between functional marks, we further define new types of summary statistics (of arbitrary order), which we refer to as weighted marked reduced moment measures and mark correlation functionals. These summary statistics are essentially mark-test function-weighted summary statistics which have been restricted to pre-specified mark groupings. We study them in different contexts and show how they under different assumptions reduce to different existing summary statistics. In addition, we provide nonparametric estimators for all the summary statistics and show their unbiasedness. We also show how these summary statistic estimators can be employed to carry out functional data analysis when the functional data-generating elements are spatially dependent (according to a FMPP). We finally apply our summary statistic estimators to the data illustrated in the first two panels of Fig. 1, in order to analyse population structures such as demographic evolution and sex ratio of human population over time in Spanish provinces.
2 Functional marked point processes
Throughout, let \({{\mathcal {X}}}\) be a subset of d-dimensional Euclidean space \({{\mathbb {R}}}^d\), \(d\ge 1\), which is either compact or given by all of \({{\mathbb {R}}}^d\). Denote by \(\Vert \cdot \Vert =\Vert \cdot \Vert _d\) the d-dimensional Euclidean norm, by \({{\mathcal {B}}}({{\mathcal {X}}})\) the Borel sets of \({{\mathcal {X}}}\subset {{\mathbb {R}}}^d\) and by \(|\cdot |=|\cdot |_d\) the Lebesgue measure on \({{\mathcal {X}}}\); \(\int {\mathrm {d}}x\) denotes integration w.r.t. \(|\cdot |\). It will be clear from the context whether \(|\cdot |\) is used for the Lebesgue measure or the absolute value. We denote by \({{\mathcal {B}}}(\cdot )^n\) the n-fold product of an arbitrary Borel \(\sigma \)-algebra \({{\mathcal {B}}}(\cdot )\) with itself. Moreover, we denote by \(\mu _1\otimes \mu _2\) the product measure generated by measures \(\mu _1\) and \(\mu _2\) and by \(\mu _1^n\) the n-fold product of \(\mu _1\) with itself. Recall further that a topological space is called Polish if there is a metric/distance which generates the underlying topology and turns the space into a complete and separable metric space. A closed ball of radius \(r\ge 0\), centred in \(x\in S\), where the space \({\mathcal {S}}\) is equipped with a metric \(d_{{\mathcal {S}}}(\cdot ,\cdot )\), will be denoted by \(B_{{\mathcal {S}}}[x,r]=\{y\in S:d_{{\mathcal {S}}}(x,y)\le r\}\).
Consider a point process \(\varPsi _G=\{X_i\}_{i=1}^N\), \(N\in {{\mathbb {N}}}_0=\{0,1,2,\ldots ,\infty \}\), on \({{\mathcal {X}}}\) (Illian et al. 2008; Chiu et al. 2013). Throughout the paper, we refer to \(\varPsi _G\) as a ground/unmarked point process. To each point of \(\varPsi _G\), we may attach a further random element, a so-called mark, in order to construct a marked point process \(\varPsi \). In this paper, a mark is given by a k-dimensional random function/stochastic process \(F_i(t)=(F_{i1}(t),\ldots ,F_{ik}(t))\), \(t\in {{\mathcal {T}}}\subset [0,\infty )\), a functional mark, possibly together with some further random variable \(L_i\), which we refer to as an auxiliary/latent mark. The resulting marked point process \(\varPsi =\{(X_i,(L_i,F_i))\}_{i=1}^N\), \(N\in {{\mathbb {N}}}_0\), will be referred to as a functional marked point process (FMPP). The main purpose of including auxiliary marks is to control the supports of the functional marks, on the one hand, and on the other hand, they may serve as indicators/labels for different types of points of the point process, in a classical multi-type point process sense.
2.1 Construction of functional marked point processes
To formally define a FMPP, we first need to specify the underlying mark space \({{\mathcal {M}}}\). The general theory for marked point processes (Daley and Vere-Jones 2003, 2008; van Lieshout 2000) allows us to consider any Polish space \({{\mathcal {M}}}\) as mark space. Here, we let the mark space be the Polish product space \({{\mathcal {M}}}={{\mathcal {A}}}\times {{\mathcal {F}}}\) given by the product of
-
a Borel subset \({{\mathcal {A}}}\ni L_i\) of some Euclidean space \({{\mathbb {R}}}^{k_{{{\mathcal {A}}}}}\), \(k_{{{\mathcal {A}}}}\ge 1\), referred to as the auxiliary/latent mark space,
-
a Polish function space \({{\mathcal {F}}}={{\mathcal {U}}}^k\ni F_i\), \(k\ge 1\); each element \(f=(f_1,\ldots ,f_k)\in {{\mathcal {F}}}={{\mathcal {U}}}^k\) has components \(f_j:{{\mathcal {T}}}\rightarrow {{\mathbb {R}}}\), \(j=1,\ldots ,k\).
Note that due to the Polish structures of these spaces, the Borel sets of \({{\mathcal {M}}}\) are given by the product \(\sigma \)-algebra \({{\mathcal {B}}}({{\mathcal {M}}})={{\mathcal {B}}}({{\mathcal {A}}}\times {{\mathcal {F}}})={{\mathcal {B}}}({{\mathcal {A}}})\otimes {{\mathcal {B}}}({{\mathcal {F}}})={{\mathcal {B}}}({{\mathbb {R}}}^{k_{{{\mathcal {A}}}}})\otimes {{\mathcal {B}}}({{\mathcal {U}}}^k)={{\mathcal {B}}}({{\mathbb {R}}})^{k_{{{\mathcal {A}}}}}\otimes {{\mathcal {B}}}({{\mathcal {U}}})^k\). Explicit examples of auxiliary and functional mark spaces are given in Supplementary Materials, Section 13.
Let \({{\mathcal {Y}}}={{\mathcal {X}}}\times {{\mathcal {M}}}\) and let \( N_{lf}\) be the collection of all point patterns, i.e. locally finite subsets \(\psi =\{(x_1,l_1,f_1),\ldots ,(x_n,l_n,f_n)\}\subset {{\mathcal {Y}}}\), \(n\ge 0\); \(n=0\) corresponds to \(\psi =\emptyset \). Note that local finiteness means that the cardinality \(\psi (A)=|\psi \cap A|\) is finite for any bounded Borel set \(A\in {{\mathcal {B}}}({{\mathcal {Y}}})\). Denote the corresponding counting measure \(\sigma \)-algebra on \( N_{lf}\) by \({{\mathcal {N}}}_{lf}\) (see Daley and Vere-Jones (2008, Chapter 9)); \({{\mathcal {N}}}_{lf}\) is the \(\sigma \)-algebra generated by the mappings \(\psi \mapsto \psi (A)\in {{\mathbb {N}}}_0\), \(\psi \in N_{lf}\), \(A\in {{\mathcal {B}}}({{\mathcal {Y}}})\). By construction, since point patterns here are defined as subsets, all \(\psi \in N_{lf}\) are simple, i.e. \(\psi (\{(x,l,f)\})\le \psi _{G}(\{x\})\in \{0,1\}\) for any \((x,l,m)\in {{\mathcal {X}}}\times {{\mathcal {A}}}\times {{\mathcal {F}}}\).
Definition 1
Given some probability space \((\varOmega ,\varSigma ,{{\mathbb {P}}})\), a point process \(\varPsi =\{(X_i,L_i,F_i)\}_{i=1}^N\), \(N\in {{\mathbb {N}}}_0\), on \({{\mathcal {Y}}}={{\mathcal {X}}}\times {{\mathcal {M}}}={{\mathcal {X}}}\times {{\mathcal {A}}}\times {{\mathcal {F}}}\) is a measurable mapping from \((\varOmega ,\varSigma ,{{\mathbb {P}}})\) to the space \((N_{lf},{{\mathcal {N}}}_{lf})\).
If a point process \(\varPsi \) on \({{\mathcal {Y}}}\) is such that the ground/unmarked point process \(\varPsi _G=\{x:(x,l,f)\in \varPsi \}\) is a well-defined point process in \({{\mathcal {X}}}\), we call \(\varPsi \) a (simple) functional marked point process (FMPP) and when \({{\mathcal {X}}}\subset {{\mathbb {R}}}^{d-1}\times {{\mathbb {R}}}\), \(d\ge 2\), and \(\varPsi _G\) is a spatio-temporal point process in \({{\mathcal {X}}}\), we call \(\varPsi \) a spatio-temporal FMPP.
Note that \(\varPsi \) may be treated either as a locally finite random subset \(\varPsi =\{(X_i,L_i,F_i)\}_{i=1}^N\subset {{\mathcal {Y}}}\), or as a random counting measure \( \varPsi (\cdot ) = \sum _{(x,l,f)\in \varPsi }\delta _{(x,l,f)}(\cdot ) = \sum _{i=1}^N\delta _{(X_i,L_i,F_i)}(\cdot ) \) on \(({{\mathcal {Y}}},{{\mathcal {B}}}({{\mathcal {Y}}}))\) with ground measure/process \( \varPsi _{G}(\cdot ) =\sum _{x\in \varPsi _G}\delta _x(\cdot ) =\sum _{(x,l,f)\in \varPsi }\delta _{(x,l,f)}(\cdot \times {{\mathcal {A}}}\times {{\mathcal {F}}}) = \sum _{i=1}^N\delta _{X_i}(\cdot ) \) on \(({{\mathcal {X}}},{{\mathcal {B}}}({{\mathcal {X}}}))\). In the spatio-temporal case, it may be convenient to write \(\varPsi _G=\{(X_i,T_i)\}_{i=1}^N\) to emphasise that each ground process point has a spatial component, \(X_i\in {{\mathbb {R}}}^{d-1}\), as well as a temporal component \(T_i\in {{\mathbb {R}}}\).
Remark 1
Since all of the underlying spaces are Polish, we may choose a metric \(d(\cdot ,\cdot )\) on \({{\mathcal {Y}}}\) which turns \({{\mathcal {Y}}}\) into a complete and separable metric space, with metric topology given by the underlying Polish topology. For example, we may consider \( d((x_1,l_1,f_1),(x_2,l_2,f_2)) = \max \{d_{{{\mathcal {X}}}}(x_1,x_2),d_{{{\mathcal {A}}}}(l_1,l_2),d_{{{\mathcal {F}}}}(f_1,f_2)\}, \) where \(d_{{{\mathcal {X}}}}(x_1,x_2)=\Vert x_1-x_2\Vert _d\) and the metrics \(d_{{{\mathcal {A}}}}(\cdot ,\cdot )\) and \(d_{{{\mathcal {F}}}}(\cdot ,\cdot )\) make \({{\mathcal {A}}}\) and \({{\mathcal {F}}}\) complete and separable metrics spaces (van Lieshout 2000); when \({{\mathcal {A}}}={{\mathbb {R}}}^{k_{{{\mathcal {A}}}}}\) or \({{\mathcal {A}}}\) is a compact subset of \({{\mathbb {R}}}^{k_{{{\mathcal {A}}}}}\), we may use \(d_{{{\mathcal {A}}}}(l_1,l_2)=\Vert l_1-l_2\Vert _{k_{{{\mathcal {A}}}}}\). In the spatio-temporal case, it may be natural to consider \(d_{{{\mathcal {X}}}}((x_1,t_1),(x_2,t_2))=\max \{\Vert x_1-x_2\Vert _{d-1},|t_1-t_2|\}\), \((x_1,t_1),(x_2,t_2)\in {{\mathcal {X}}}\subset {{\mathbb {R}}}^{d-1}\times {{\mathbb {R}}}={{\mathbb {R}}}^{d}\) (Cronie and van Lieshout 2015), which is topologically equivalent to \(d_{{{\mathcal {X}}}}((x_1,t_1),(x_2,t_2))=\Vert (x_1,t_1)-(x_2,t_2)\Vert _d\).
We will write \(P(R) = P_{\varPsi }(R) = {{\mathbb {P}}}(\{\omega \in \varOmega :\varPsi (\omega )\in R\})\), \(R\in {{\mathcal {N}}}_{lf}\), for the distribution of \(\varPsi \), i.e. the probability measure that \(\varPsi \) induces on \(( N_{lf}, {{\mathcal {N}}}_{lf})\). When \({{\mathcal {X}}}={{\mathbb {R}}}^d\), for any \(\psi \in N_{lf}\) and any \(z\in {{\mathbb {R}}}^d\), we will write \(\psi + z\) to denote \(\sum _{(x,l,f)\in \psi }\delta _{(x+z,l,f)}\) (or \(\{(x+z,l,m):(x,l,m)\in \psi \}\)), i.e. a shift of \(\psi \) in the ground space by the vector z. If \(\varPsi + z {\mathop {=}\limits ^{d}} \varPsi \), i.e. \(P_{\varPsi }(\cdot )=P_{\varPsi +z}(\cdot )\), for any z, we say that \(\varPsi \) is stationary. Moreover, \(\varPsi \) is isotropic if \(\varPsi \) is rotation invariant in the ground space, i.e. the rotated FMPP \(r\varPsi =\{(rX_i, L_i, F_i)\}_{i=1}^N\) has the same distribution as \(\varPsi \) for any rotation r.
2.2 Components of FMPPs
We emphasise that any collection of elements \(\{(X_1,L_1,F_1),\ldots ,(X_n,L_n,F_n)\}\subset \varPsi \), \(n\ge 1\), consists of the combination of:
-
a collection of random spatial locations \(X_1,\ldots ,X_n\in {{\mathcal {X}}}\),
-
a collection \(L_1,\ldots ,L_n\) of random variables taking values in \({{\mathcal {A}}}\),
-
an n-dimensional random function/stochastic process \(\{F_1(t),\ldots ,F_n(t)\}_{t\in {{\mathcal {T}}}}\in ({{\mathbb {R}}}^k)^n\), with realisations in \({{\mathcal {F}}}^n\); formally, this is an unordered collection of n stochastic processes in \({{\mathbb {R}}}^k\) with sample paths in \({{\mathcal {F}}}={{\mathcal {U}}}^k\subset \{f|f:{{\mathcal {T}}}\rightarrow {{\mathbb {R}}}\}^k\).
In particular, \(\varPsi _{{{\mathcal {X}}}\times {{\mathcal {A}}}}=\{(X_i,L_i)\}_{i=1}^N\) is a marked point process of the usual kind, with locations in \({{\mathbb {R}}}^d\) and marks in \({{\mathcal {A}}}\subset {{\mathbb {R}}}^{k_{{{\mathcal {A}}}}}\), i.e. each auxiliary mark \(L_i=(L_{1i},\ldots ,L_{k_{{{\mathcal {A}}}}i})\) is given by a \(k_{{{\mathcal {A}}}}\)-dimensional random vector. Depending on how \({{\mathcal {A}}}\) and the distributions of the \(L_i\)’s are specified, we are able to consider an array of different settings. For example, if \({{\mathcal {A}}}=\{1,\ldots ,k_d\}\), \(k_d\ge 2\), each random variable \(L_i\) has a discrete distribution on \({{\mathcal {A}}}\). Since \(\varPsi _{{{\mathcal {X}}}\times {{\mathcal {A}}}}\) hereby becomes a multi-type/multivariate point process in \({{\mathbb {R}}}^d\), one may call such FMPPs multi-type/multivariate (Daley and Vere-Jones 2003; van Lieshout 2000; Gelfand et al. 2010). In Supplementary Materials, Section 13, we look closer at specific choices for \({{\mathcal {A}}}\). It is often convenient to write \({{\mathcal {A}}}={{\mathcal {A}}}_d\) to emphasise when we have a discrete auxiliary mark space, such as \({{\mathcal {A}}}_d=\{1,\ldots ,k_d\}\), and \({{\mathcal {A}}}={{\mathcal {A}}}_c\) to emphasise when have a continuous space ((closure) of an open set), such as \({{\mathcal {A}}}_c={{\mathbb {R}}}^{k_{{{\mathcal {A}}}}}\).
Within the current definition of FMPPs, we may also consider the scenario where the auxiliary marks play no role and thereby may be ignored. This may be obtained by, for example, setting \({{\mathcal {A}}}=\{c\}\) for some constant \(c\in {{\mathbb {R}}}\), so that all auxiliary marks attain the value c, or equivalently, setting \(L_i=c\) a.s. for any \(i=1,\ldots ,N\), assuming that \(c\in {{\mathcal {A}}}\). It is worth remarking that the inclusion of the auxiliary marks allows us to impose an order on the points in the sense that we would consider a functional marked sequential point process; van Lieshout (2006b) connects sequential point processes with marked spatio-temporal point processes with mark space (0, 1).
Note that when we want to consider functional marks with realisations given by functions \(f(t)=(f_1(t),\ldots ,f_k(t))\in {{\mathbb {R}}}^k\), \(t\in {{\mathcal {T}}}\), which describe spatial paths, we let \(k\ge 2\). Often the spatial locations \(X_i\) describe the initial location of such a path, and it is then natural to assume that \(d=k\ge 2\) and \(f(t)\in {{\mathcal {X}}}\) a.s. for any \(t\in {{\mathcal {T}}}\). An application here would be that the marks describe movements of animals, living within some spatial domain \({{\mathcal {X}}}\); recall Fig. 1.
Recall that each functional mark \(F_i(t)=(F_{i1}(t),\ldots ,F_{ik}(t))\in {{\mathbb {R}}}^k\), \(t\in {{\mathcal {T}}}\subset [0,\infty )\), \(i=1,\ldots ,N\), is realised in the measurable space \(({{\mathcal {F}}},{{\mathcal {B}}}({{\mathcal {F}}}))\), where \({{\mathcal {F}}}={{\mathcal {U}}}^k\), \(k\ge 1\), and \({{\mathcal {U}}}\) are Polish function spaces (products of Polish spaces are Polish). By conditioning \(\varPsi \) on \(\varPsi _{{{\mathcal {X}}}\times {{\mathcal {A}}}}\), which includes conditioning on N, we obtain the random functional
which may be regarded as a stochastic process with dimension N and with the same marginal distributions for all of its components. Due to the inherent temporally evolving nature of the functional marks, one may further consider some filtration \(\varSigma _{{{\mathcal {T}}}}\), and thus obtain a filtered probability space \((\varOmega ,\varSigma ,\varSigma _{{{\mathcal {T}}}},{{\mathbb {P}}})\), such that all \(F_i=\{F_i(t)\}_{t\in {{\mathcal {T}}}}\), \(i=1,\ldots ,N\), are adapted to \(\varSigma _{{{\mathcal {T}}}}\) (see Supplementary Materials, Section 13.2, for more details).
Remark 2
Formally, \(\varPsi |\varPsi _{{{\mathcal {X}}}\times {{\mathcal {A}}}}\) may be obtained as the point process generated by the family of regular conditional probabilities obtained by disintegrating \(P_{\varPsi }\) with respect to the distribution of \(\varPsi _{{{\mathcal {X}}}\times {{\mathcal {A}}}}\) on its point pattern space (Daley and Vere-Jones 2003, Appendix A1.5.).
We impose the Polish assumption on \({{\mathcal {U}}}\) in order to carry out the usual marked point process analysis (Daley and Vere-Jones 2003, 2008); note that \({{\mathcal {U}}}\) being Polish implies that \({{\mathcal {F}}}\) is Polish and \({{\mathcal {B}}}({{\mathcal {F}}})={{\mathcal {B}}}({{\mathcal {U}}}^k)={{\mathcal {B}}}({{\mathcal {U}}})^k\). However, choosing a Polish function space \({{\mathcal {U}}}\) is a delicate matter; note that Comas et al. (2011) did not address this issue. In Supplementary Materials, Section 13.2, we consider functional mark spaces in more detail and there we cover the two most natural choices for \({{\mathcal {U}}}\), namely Skorohod spaces and \(L_p\)-spaces (Billingsley 1999; Ethier and Kurtz 1986; Jacod and Shiryaev 1987; Silvestrov 2004). Note that these two classes of functions are not mutually exclusive.
Noting that, in general, the support \({{\,\mathrm{supp}\,}}(f)=\{t\in {{\mathcal {T}}}:f(t)\ne 0\}\subset {{\mathcal {T}}}\) of a function \(f\in {{\mathcal {F}}}\) need not be given by all of \({{\mathcal {T}}}\), in some contexts it may be natural to let \(\varPsi _{{{\mathcal {X}}}\times {{\mathcal {A}}}}\) govern the supports \({{\,\mathrm{supp}\,}}(F_i)=\{t\in {{\mathcal {T}}}:F_i(t)\ne 0\in {{\mathbb {R}}}^k\}\), \(i=1,\ldots ,N\). To illustrate this idea, consider the case where \(d=1\) and \({{\mathcal {X}}}={{\mathcal {T}}}=[0,\infty )\), so that \(\varPsi _G=\{T_i\}_{i=1}^N\subset [0,\infty )\) is a temporal point process. In addition, assume that \(k_{{{\mathcal {A}}}}=1\) and that each auxiliary mark \(L_i\) is some non-negative random variable, such as an exponentially distributed one, which does not depend on \(\varPsi _G\). Let us think of \(T_i\) and \(L_i\) as a point’s birth time and lifetime, respectively. Defining the corresponding death time as \(D_i=T_i+L_i\), we may then, for example, let
for all \(t\notin [T_i,D_i)\) a.s., where 0 is the k-dimensional vector of 0s. Note further that there in addition to this may exist \(t\in [T_i,D_i)\) such that \(F_i(t)|\varPsi _{{{\mathcal {X}}}\times {{\mathcal {A}}}}=0\) in some way (e.g. absorption), which is something governed by the distribution of \(\{F_i(t)|\varPsi _{{{\mathcal {X}}}\times {{\mathcal {A}}}}\}_{t\in {{\mathcal {T}}}}\) on \({{\mathcal {F}}}\). An explicit construction to obtain this when \(k=1\) would, for example, be \(F_i(t)={{\mathbf {1}}}_{[T_i,D_i)}(t)Y_i((t-T_i)\wedge 0)\), \(t\in {{\mathcal {T}}}\), for some stochastic process Y(t), \(t\in [0,\infty )\), which starts in 0.
2.3 Reference measures and reference stochastic processes
For the purpose of integration, among other things, we need a reference measure on \(({{\mathcal {Y}}},{{\mathcal {B}}}({{\mathcal {Y}}}))\). We let it be given by the product measure
where \(C\times D\times E\in {{\mathcal {B}}}({{\mathcal {Y}}})={{\mathcal {B}}}({{\mathcal {X}}})\otimes {{\mathcal {B}}}({{\mathcal {A}}})\otimes {{\mathcal {B}}}({{\mathcal {F}}})\), and we note that as usual, the reference measure on the ground space \({{\mathcal {X}}}\) is given by the Lebesgue measure \(|\cdot |=|\cdot |_d\) on \({{\mathcal {X}}}\subset {{\mathbb {R}}}^d\), \(d\ge 1\). Moreover, we need \(\nu _{{{\mathcal {M}}}}=\nu _{{{\mathcal {A}}}}\otimes \nu _{{{\mathcal {F}}}}\) to be a finite measure so both \(\nu _{{{\mathcal {A}}}}\) and \(\nu _{{{\mathcal {F}}}}\) need to be finite measures on \(({{\mathcal {A}}},{{\mathcal {B}}}({{\mathcal {A}}}))\) and \(({{\mathcal {F}}},{{\mathcal {B}}}({{\mathcal {F}}}))\), respectively.
Regarding the reference measure on the auxiliary mark space, in the Supplementary Materials, Section 13, we provide a few examples based on different choices for \({{\mathcal {A}}}\). Most noteworthy here is that if \({{\mathcal {A}}}={{\mathcal {A}}}_d\) is a discrete space, then \(\nu _{{{\mathcal {A}}}}=\nu _{{{\mathcal {A}}}_d}\) is a discrete measure \(\nu _{{{\mathcal {A}}}_d}(\cdot )=\sum _{i\in {{\mathcal {A}}}_d}\varDelta _i\delta _i(\cdot )\), \(\varDelta _i\ge 0\) (e.g. the counting measure, given by \(\varDelta _i\equiv 1\)), if \({{\mathcal {A}}}={{\mathcal {A}}}_c\) is a continuous space, then we may choose \(\nu _{{{\mathcal {A}}}}=\nu _{{{\mathcal {A}}}_c}\) to be the \(k_{{{\mathcal {A}}}}\)-dimensional Lebesgue measure on \({{\mathcal {A}}}\), and if \({{\mathcal {A}}}\) is unbounded, e.g. \({{\mathcal {A}}}={{\mathbb {R}}}^{k_{{{\mathcal {A}}}}}\), then we may choose \(\nu _{{{\mathcal {A}}}}\) to be some probability measure. If \({{\mathcal {A}}}={{\mathcal {A}}}_d\times {{\mathcal {A}}}_c\) is given by a product of a discrete and a continuous space, then \(\nu _{{{\mathcal {A}}}}\) can be taken to be a product measure \(\nu _{{{\mathcal {A}}}_d}\otimes \nu _{{{\mathcal {A}}}_c}\).
Turning to the functional mark space \(({{\mathcal {F}}},{{\mathcal {B}}}({{\mathcal {F}}}))\), consider some suitable reference random function/stochastic process
where each \(X^{{{\mathcal {F}}}}(\omega )\in {{\mathcal {U}}}^k={{\mathcal {F}}}\) is commonly referred to as a sample path/realisation of \(X^{{{\mathcal {F}}}}\). This random element induces a probability measure
on \({{\mathcal {F}}}\), which we will employ as our reference measure on \({{\mathcal {F}}}\). Note that the joint distribution on \(({{\mathcal {F}}}^n,{{\mathcal {B}}}({{\mathcal {F}}}^n))\) of n independent copies of \(X^{{{\mathcal {F}}}}\) is given by \(\nu _{{{\mathcal {F}}}}^n\), the n-fold product measure of \(\nu _{{{\mathcal {F}}}}\) with itself. Moreover, if there is a suitable measure \(\nu _{{{\mathcal {U}}}}\) on \({{\mathcal {U}}}\), we let \(\nu _{{{\mathcal {F}}}}=\nu _{{{\mathcal {U}}}}^k\). Specifically, \(\nu _{{{\mathcal {F}}}}\), or \(X^{{{\mathcal {F}}}}\), should be chosen such that suitable absolute continuity results can be applied. More specifically, the distribution \(P_Y\) on \(({{\mathcal {F}}}^n,{{\mathcal {B}}}({{\mathcal {F}}}^n))\), \(n\ge 1\), of some stochastic process \(Y=\{Y(t)\}_{t\in {{\mathcal {T}}}}\in {{\mathcal {F}}}^n=({{\mathcal {U}}}^k)^n\) of interest should have some (functional) density/Radon–Nikodym derivative \(f_Y\) with respect to \(\nu _{{{\mathcal {F}}}}^n\), i.e. \(P_Y(E)=\int _{E}f_Y(f)\nu _{{{\mathcal {F}}}}^n(df)={{\mathbb {E}}}_{\nu _{{{\mathcal {F}}}}^n}[{{\mathbf {1}}}_E f_Y]\), \(E\in {{\mathcal {B}}}({{\mathcal {F}}}^n)\). Note that Kolmogorov’s consistency theorem allows us to specify the (abstract) distribution \(P_Y\) of Y through its finite-dimensional distributions (on \(({{\mathbb {R}}}^k)^n\)).
In many situations, a natural choice for \(\nu _{{{\mathcal {F}}}}\) is a Gaussian measure on \({{\mathcal {B}}}({{\mathcal {F}}})\), i.e. one corresponding to some Gaussian process \(X^{{{\mathcal {F}}}}\), or the distribution corresponding to a Markov process \(X^{{{\mathcal {F}}}}:(\varOmega ,\varSigma ,{{\mathbb {P}}})\rightarrow ({{\mathcal {F}}},{{\mathcal {B}}}({{\mathcal {F}}}))\). An often natural choice, which satisfies both of these properties, is the k-dimensional standard Brownian motion/Wiener process
which is generated by the corresponding Wiener measure \({\mathcal {W}}_{{{\mathcal {F}}}}\) on \({{\mathcal {B}}}({{\mathcal {F}}})\). In certain cases, one speaks of an abstract Wiener space or Cameron–Martin space. Here, issues related to absolute continuity have been extensively studied, and explicit constructions of Radon–Nikodym derivatives involve, for example, the Cameron–Martin–Girsanov (change of measure) theorem. For discussions, overviews, and detailed accounts, see, e.g. Kallenberg (2006), Rajput (1972), Maniglia and Rhandi (2004), Skorohod (1967) and the references therein.
Note that integration of a measurable function h with respect to \(\nu \) satisfies
whenever the auxiliary marks are (partially) discrete, the integral over \({{\mathcal {A}}}\) is (partially) replaced by a sum.
3 FMPP examples
The class of FMPPs provides a framework to give structure to a series of existing models, and it allows for the construction of new important models and modelling frameworks, which have uses in different applications. In Supplementary Materials, Section 11, we provide an array of different models which fit into the FMPP structure. More specifically, we look closer at the following examples:
-
By letting the functional marks be random constant functions, we obtain (equivalents of) point processes with real valued marks.
-
Deterministic functional marks, obtained by letting \(\varPsi |\varPsi _{{{\mathcal {X}}}\times {{\mathcal {A}}}}=\{f_1,\ldots ,f_N\}\) for deterministic functions \(f_1,\ldots ,f_N\in {{\mathcal {F}}}\). A particular instance of this, which we also look at extensions for, is the growth interaction process of Renshaw and Särkkä (2001), which has been extensively employed for dynamical modelling of forest stands; here, the functional marks are governed by a set of differential equations.
-
For a (spatio-temporal) FMPP \(\varPsi \), where the spatial locations \(X_i\) are located in some subset of \({{\mathbb {R}}}^2\) and \(k=1\), i.e. \({{\mathcal {F}}}={{\mathcal {U}}}\), so that \(F_i(t)=F_{i1}(t)\in {{\mathbb {R}}}\), \(t\in {{\mathcal {T}}}\), we look closer at the temporally evolving random closed set \(\varXi (t) = \bigcup _{i=1}^{N} B_{{{\mathcal {X}}}}[X_i,F_i(t)]\subset {{\mathbb {R}}}^2\), \(t\in {{\mathcal {T}}}\). This provides a natural geometric interpretation for many FMPP settings (see Fig. 4 in Supplementary Materials, Section 16).
-
Given a spatio-temporal k-dimensional random field \(Z_{x}(t)\in {{\mathbb {R}}}^k\), \((x,t)\in {{\mathcal {X}}}\times {{\mathcal {T}}}\), \(k\ge 1\), we define spatio-temporal geostatistical marking/sampling of a random field at random locations by letting \(F_i = \{Z_{X_i}(t)\}_{t\in {{\mathcal {T}}}}\in {{\mathcal {F}}}={{\mathcal {U}}}^k\), \(i=1,\ldots ,N\), conditionally on \(\varPsi _{{{\mathcal {X}}}\times {{\mathcal {A}}}}\). Here, we, for example, look closer at spatio-temporal geostatistics under such a random monitoring location setting.
-
Constructed functional marks are constructed to reflect geometries of point configurations in neighbourhoods of individual points. A typical example is given by so-called LISA functions (local estimators), which we here formally define as \(S(h,X_i;\varPsi _G{\setminus }\{X_i\})=F_{i}(h)\), \(h\in {{\mathcal {T}}}=[0,\infty )\), for some function S.
-
We discuss spatio-temporal intensity-dependent marking which we define to occur if, conditionally on \(\varPsi _G\) and the auxiliary marks, the functional marks \(F_i(t)\), \(t\in {{\mathcal {T}}}\), \(i=1,\ldots ,N\), are given as functions \(t\mapsto h(\rho _G(X_i,t))\), \(t\in {{\mathcal {T}}}\), \(i=1,\ldots ,N\), for some (random) function \(h:{{\mathbb {R}}}\rightarrow {{\mathbb {R}}}\). For instance, we may have \(F_i(t)|\varPsi _{{{\mathcal {X}}}\times {{\mathcal {A}}}}=a+b\rho _G(X_i,t)+\varepsilon (X_i,t)\), \(a,b\in {{\mathbb {R}}}\), where \(\varepsilon (x,t)\) is a spatio-temporal zero mean Gaussian noise process.
In Supplementary Materials, Section 12, we additionally provide a few (further) examples of applications, and in Supplementary Materials, Section 16, we provide examples of classical point process models which are functional marked.
4 Moment characteristics for FMPPs
Besides illustrating the connections above, the aim of this paper is to consider different statistical approaches which allow us to analyse point pattern data with functional marks. For a wide range of summary statistics, the core elements are intensity functions and higher-order product density functions. We next consider product densities and intensity reweighted product densities for FMPPs. In Supplementary Materials, Section 13, we look closer at what these entities look like under various auxiliary and functional mark space choices.
4.1 Product densities and intensity functionals
Let \(\varPsi \) be a FMPP with ground process \(\varPsi _G\). Given some \(n\ge 1\) and some measurable functional \(h:{{\mathcal {Y}}}^n={{\mathcal {X}}}^n\times {{\mathcal {A}}}^n\times {{\mathcal {F}}}^n\rightarrow [0,\infty )\), consider
Here, \(\sum ^{\ne }\) denotes summation over distinct n-tuples. We first note that the nth-order factorial moment measure \(\alpha ^{(n)}(A_1\times \cdots \times A_n)\) of \(\varPsi \) is retrieved by letting h be the indicator function for the set \(A_1\times \cdots \times A_n = (C_1\times D_1\times E_1)\times \cdots \times (C_n\times D_n\times E_n)\in {{\mathcal {B}}}({{\mathcal {Y}}}^n) = {{\mathcal {B}}}({{\mathcal {X}}}\times {{\mathcal {M}}})^n={{\mathcal {B}}}({{\mathcal {X}}}\times {{\mathcal {A}}}\times {{\mathcal {F}}})^n\). Note further that \(\alpha ^{(n)}\) coincides with the nth-order moment measure \( \mu ^{(n)}(A_1\times \cdots \times A_n) = {{\mathbb {E}}}[\varPsi (A_1)\cdots \varPsi (A_n)] \) when \(A_1,\ldots ,A_n\in {{\mathcal {B}}}({{\mathcal {Y}}})\) are disjoint.
Assume next that the nth-order (functional) product density \(\rho ^{(n)}\), i.e. the Radon–Nikodym derivative of \(\alpha ^{(n)}\) with respect to the n-fold product of the reference measure \(\nu \) in (1) with itself, exists. We have that \(\alpha ^{(n)}\) and \(\rho ^{(n)}\) satisfy the following Campbell formula (Chiu et al. 2013):
Heuristically, \(\rho ^{(n)}((x_1,l_1,f_1),\ldots ,(x_n,l_n,f_n)) \prod _{i=1}^{n} \nu (d(x_i,l_i,f_i))\) is interpreted as the probability of having ground process points in the infinitesimal neighbourhoods \(dx_1,\ldots ,dx_n\subset {{\mathcal {X}}}\) of \(x_1,\ldots ,x_n\), with associated marks belonging to the infinitesimal neighbourhoods \(d(l_1,f_1),\ldots ,d(l_n,f_n)\subset {{\mathcal {A}}}\times {{\mathcal {F}}}\) of the mark locations \((l_1,f_1),\ldots ,(l_n,f_n)\).
Turning to the ground process \(\varPsi _{G}\), through \(\alpha ^{(n)}\) we may define the nth-order ground factorial moment measure \(\alpha _{G}^{(n)}(\cdot )=\alpha ^{(n)}(\cdot \times {{\mathcal {A}}}\times {{\mathcal {F}}})\) and its Radon–Nikodym derivative \(\rho _{G}^{(n)}\) with respect to the n-fold product \(|\cdot |^n\) of the Lebesgue measure \(|\cdot |\) with itself, which is called the nth-order ground product density. Note that by letting the function h in (5) be a function on \({{\mathcal {X}}}\) only, we obtain a Campbell formula for the ground process \(\varPsi _G\). Moreover, by the existence of \(\rho _{G}^{(n)}\) and \(\rho ^{(n)}\), it follows that (Heinrich 2013)
where
are densities of the families
\((D_1\times E_1),\ldots ,(D_n\times E_n)\in {{\mathcal {B}}}({{\mathcal {M}}})={{\mathcal {B}}}({{\mathcal {A}}}\times {{\mathcal {F}}})\), of (regular) conditional probability distributions. We interpret \(Q_{x_1,\ldots ,x_n}^{{{\mathcal {A}}}}(\cdot )\) as the density of the conditional joint probability distribution of n auxiliary marks in \({{\mathcal {A}}}\), given that \(\varPsi \) indeed has n points at the locations \(x_1,\ldots ,x_n\in {{\mathcal {X}}}\). Similarly, \(Q_{(x_1,l_1),\ldots ,(x_n,l_n)}^{{{\mathcal {F}}}}(\cdot )\) is interpreted as the density of the conditional joint probability distribution of n functional marks in \({{\mathcal {F}}}\), given that \(\varPsi _G\) has points at the n locations \(x_1,\ldots ,x_n\in {{\mathcal {X}}}\) with attached auxiliary marks \(l_1,\ldots ,l_n\in {{\mathcal {A}}}\). Recalling Sects. 2.2 and 2.3, we see that \(P_{(x_1,l_1),\ldots ,(x_n,l_n)}^{{{\mathcal {F}}}}(\cdot )\) represents the probability distribution on \(({{\mathcal {F}}}^n,{{\mathcal {B}}}({{\mathcal {F}}}^n))\) of n components of \(\varPsi |\varPsi _{{{\mathcal {X}}}\times {{\mathcal {A}}}}=\{F_1|\varPsi _{{{\mathcal {X}}}\times {{\mathcal {A}}}},\ldots ,F_N|\varPsi _{{{\mathcal {X}}}\times {{\mathcal {A}}}}\}\), which may be seen as an n-dimensional random function/stochastic process \(\{F_1(t)|\varPsi _{{{\mathcal {X}}}\times {{\mathcal {A}}}},\ldots ,F_n(t)|\varPsi _{{{\mathcal {X}}}\times {{\mathcal {A}}}}\}_{t\in {{\mathcal {T}}}}\subset {{\mathcal {F}}}\). This distribution is absolutely continuous with respect to the reference measure \(\nu _{{{\mathcal {F}}}}^n\), i.e. the distribution of an n-dimensional version of the reference process \(X^{{{\mathcal {F}}}}\), with density given by (8). Note that \(\rho ^{(n)}\) is (partly) a functional since one of its component, \(Q_{(x_1,l_1),\ldots ,(x_n,l_n)}^{{{\mathcal {F}}}}(\cdot )\), is a functional; here, we use the term ‘functional’ for any mapping which takes a function as one of its arguments. The two regular probability distribution families (9) and (10) constitute the so-called n-point mark distributions (Chiu et al. 2013):
The intensity measure is given by \(\mu (A) = \mu ^{(1)}(A) = \alpha ^{(1)}(A) = {{\mathbb {E}}}[\varPsi (A)]\), \(A=C\times D\times E\in {{\mathcal {B}}}({{\mathcal {Y}}})\), and since \(\rho ^{(1)}\) exists,
and we refer to \( \rho (x,l,f) = \rho ^{(1)}(x,l,f) = Q_{(x,l)}^{{{\mathcal {F}}}}(f) Q_{x}^{{{\mathcal {A}}}}(l) \rho _G(x) \) as the intensity functional of the FMPP \(\varPsi \). Here, \(\rho _{G}(\cdot )=\rho _{G}^{(1)}(\cdot )\) is the intensity of the ground process, \(\varPsi _G\).
4.2 Correlation functionals
Pair correlation functions, which are not in fact correlations in the usual sense, are valuable tools for studying second-order dependence properties of point processes. These may be generalised to arbitrary orders \(n\ge 2\) to characterise n-point interactions between the points of a point process, and here in the FMPP context, we will refer to them as correlation functionals. Assuming that \(\rho \) and \(\rho ^{(n)}\), \(n\ge 1\), exist, the nth-order correlation functional is defined as
where
and
is the nth-order correlation function of the ground process, \(\varPsi _G\). Note that \(\gamma _{(x_1,l_1),\ldots ,(x_n,l_n)}^{{{\mathcal {F}}}}(\cdot )\) represents the conditional joint density of n functional marks, given their associated locations and auxiliary marks, divided by the conditional marginal densities of these functional marks, given their corresponding associated locations and auxiliary marks. An analogous interpretation holds for the second term, but then regarding the auxiliary marks instead and conditioned only on the locations. The particular case \(n=2\), i.e. \( g_{\varPsi }^{(2)}((x_1,l_1,f_1),(x_2,l_2,f_2)) = \gamma _{x_1,x_2}^{{{\mathcal {M}}}} ((l_1,f_1),(l_2,f_2)) g_{G}^{(2)}(x_1,x_2) , \) is referred to as the pair correlation functional (pcf) and we note that \(g_G^{(2)}(x_1,x_2)=\rho _G^{(2)}(x_1,x_2)/(\rho _G(x_1)\rho _G(x_2))\) is the pair correlation function of the ground process (Baddeley et al. 2000; Chiu et al. 2013). When \(n=2\), the first term on the right-hand side in (12) may be expressed as \(\gamma _{x_1,x_2}^{{{\mathcal {A}}}} (l_1,l_2)Q_{(x_1,l_1),(x_2,l_2)}^{{{\mathcal {F}}}}(f_1|f_2)/Q_{(x_1,l_1)}^{{{\mathcal {F}}}}(f_1)\), where \(Q_{(x_1,l_1),(x_2,l_2)}^{{{\mathcal {F}}}}(f_1|f_2)\) represents a conditional density on \({{\mathcal {F}}}\) of one functional mark, \(F_1\), given another functional mark, \(F_2\), as well as the associated locations and auxiliary marks.
5 FMPP model structures
We next look closer at a few structural distributional assumptions and model structures for FMPPs. In the context of the auxiliary marks, we have already highlighted some effects of imposing different independence assumptions on the marks. Here, we mainly focus on two assumptions which will play a role in the statistical analysis: common marginal mark distributions and (location-dependent) independent marking. In Supplementary Materials, Section 16, we further provide a few different functional marked classical point process models.
5.1 Common mark distributions
An assumption which may be realistic in a variety of different contexts is that the marks are not necessarily independent but they have the same marginal distributions. We next look closer at this setting and we note that the statements below should be understood in an almost everywhere (a.e.) setting.
Definition 2
Let \(\varPsi \) be a FMPP with ground process \(\varPsi _G\) and consider the following scenarios, defined conditionally on \(\varPsi _G\).
-
\(\varPsi \) has a common (marginal) mark distribution: The marginal one-dimensional distributions of all marks \((L_i,F_i)\), \(i=1,\ldots ,N\), are the same, i.e. they do not depend on the spatial locations. Here, the 1-point mark distributions \(P_{x}^{{{\mathcal {M}}}}(D\times E) = \int _{D} P_{(x,l)}^{{{\mathcal {F}}}}(E) P_{x}^{{{\mathcal {A}}}}(dl)\), \(x\in {{\mathcal {X}}}\), \(D\times E\in {{\mathcal {A}}}\times {{\mathcal {F}}}\), satisfy \(P_{x}^{{{\mathcal {M}}}}(D\times E) \equiv P^{{{\mathcal {M}}}}(D\times E)\),
$$\begin{aligned} P^{{{\mathcal {M}}}}(D\times E)= & {} \int _{D\times E} Q^{{{\mathcal {M}}}}(l,f) \nu _{{{\mathcal {M}}}}(d(l,f)) \\= & {} \int _{D\times E} Q_{l}^{{{\mathcal {F}}}}(f) Q^{{{\mathcal {A}}}}(l) \nu _{{{\mathcal {A}}}}(dl)\nu _{{{\mathcal {F}}}}(df), \end{aligned}$$for some probability measure \(P^{{{\mathcal {M}}}}(\cdot )\), with density \(Q^{{{\mathcal {M}}}}(l,f)=Q_{l}^{{{\mathcal {F}}}}(f) Q^{{{\mathcal {A}}}}(l)\) with respect to \(\nu _{{{\mathcal {M}}}}=\nu _{{{\mathcal {A}}}}\otimes \nu _{{{\mathcal {F}}}}\). This is, for example, the case when \(\varPsi \) is stationary (Schneider and Weil 2008, Thm 3.5.1.); \(P^{{{\mathcal {M}}}}(\cdot )\) is then commonly referred to as the mark distribution.
-
\(\varPsi \) has a common (marginal) functional mark distribution: each \(F_i|\varPsi _{{{\mathcal {X}}}\times {{\mathcal {A}}}}\in \varPsi |\varPsi _{{{\mathcal {X}}}\times {{\mathcal {A}}}}\), \(i=1,\ldots ,N\), has the same marginal distribution on \(({{\mathcal {F}}},{{\mathcal {B}}}({{\mathcal {F}}}))\), which neither depends on its spatial location nor its auxiliary mark. Here, \(P_{(x,l)}^{{{\mathcal {F}}}}\equiv P^{{{\mathcal {F}}}}\) and \(Q_{(x,l)}^{{{\mathcal {F}}}}\equiv Q^{{{\mathcal {F}}}}\), \((x,l)\in {{\mathcal {X}}}\times {{\mathcal {A}}}\).
Under the assumption of a common mark distribution, it may further be the case that the common mark distribution \(P^{{{\mathcal {M}}}}\) coincides with the reference measure \(\nu _{{{\mathcal {M}}}}=\nu _{{{\mathcal {A}}}}\otimes \nu _{{{\mathcal {F}}}}\) (so \(\nu _{{{\mathcal {A}}}}\) and \(\nu _{{{\mathcal {F}}}}\) must be probability measures), which implies that \(Q^{{{\mathcal {M}}}}(l,f) = Q_{l}^{{{\mathcal {F}}}}(f) Q^{{{\mathcal {A}}}}(l)\equiv 1\) and the correlation functionals satisfy
For example, \(\nu _{{{\mathcal {A}}}}\) may be a Bernoulli distribution with parameter \(p\in [0,1]\) and \({{\mathcal {A}}}={{\mathcal {A}}}_d=\{0,1\}\), and \(\nu _{{{\mathcal {F}}}}\) a Wiener measure \({\mathcal {W}}_{{{\mathcal {F}}}}\), whereby (marginally) \(L_i\) is a Bernoulli random variable and \(F_i\) is a Brownian motion, which are independent of each other.
Under the weaker assumption that \(\varPsi \) has a common functional mark distribution, recalling the reference process \(X^{{{\mathcal {F}}}}\) in (2), which has \(\nu _{{{\mathcal {F}}}}\) as distribution, when additionally \(P^{{{\mathcal {F}}}}=\nu _{{{\mathcal {F}}}}\) we here obtain that, marginally, each component \(F_i|\varPsi _{{{\mathcal {X}}}\times {{\mathcal {A}}}}\), \(i=1,\ldots ,N\), has the same distribution as \(X^{{{\mathcal {F}}}}\). To provide an example for this setting, note, for example, that for the (stochastic) growth-interaction model, conditionally on \(N=1\), i.e. \(\varPsi =\{(X_1,L_1,F_1)\}\), we have that the distribution of \(F_1|\varPsi _{{{\mathcal {X}}}\times {{\mathcal {A}}}}=\{F_1(t)|(X_1,L_1)\}_{t\in {{\mathcal {T}}}}\) does not change with \((X_1,L_1)\).
Remark 3
Note that when \(\varPsi \) has a common functional mark distribution, we do not necessarily assume that there is a common (marginal) auxiliary mark distribution, i.e. that \(\varPsi _{{{\mathcal {X}}}\times {{\mathcal {A}}}}\) has a common mark distribution. Under such an assumption, all \(L_i|\varPsi _G\), \(i=1,\ldots ,N\), have the same marginal distributions, which do not depend on the spatial locations, whereby \(P_{x}^{{{\mathcal {A}}}}\equiv P^{{{\mathcal {A}}}}\) and \(Q_{x}^{{{\mathcal {A}}}}\equiv Q^{{{\mathcal {A}}}}\), \(x\in {{\mathcal {X}}}\). Hence, if there is a common auxiliary mark distribution as well as a common functional mark distribution, it follows that \(P_{x}^{{{\mathcal {M}}}}(D\times E) \equiv P^{{{\mathcal {M}}}}(D\times E)=P^{{{\mathcal {F}}}}(E)P^{{{\mathcal {A}}}}(D)\), \(D\times E\in {{\mathcal {A}}}\times {{\mathcal {F}}}\), \(x\in {{\mathcal {X}}}\), i.e. \(L_i\) and \(F_i\) are conditionally independent for any \(i=1,\ldots ,N\). This is a stronger assumption than the assumption of a common mark distribution and it holds, for example, when \(P^{{{\mathcal {M}}}}=\nu _{{{\mathcal {M}}}}=\nu _{{{\mathcal {A}}}}\otimes \nu _{{{\mathcal {F}}}}\).
5.2 Location-dependent independent marking and random labelling
We next turn to two common notions of mark independence: location-dependent independent marking and random labelling.
Definition 3
We say that a FMPP \(\varPsi \) is (location-dependent) independently marked if, conditional on its ground process \(\varPsi _G\), all marks \((L_i, F_i)\), \(i=1,\ldots ,N\), are independent but not necessarily identically distributed (Daley and Vere-Jones 2003, Definition 6.4.III).
By further adding the assumption of a common marginal mark distribution to independent marking, so that the marks become independent and identically distributed as well as independent of the ground process \(\varPsi _G\), we obtain the definition of random labelling.
Hereinafter, we will use the shorter term ‘independent marking’, thus leaving out the part ‘location-dependent’, in keeping with Daley and Vere-Jones (2003). Under independent marking, each mark \((L_i, F_i)\) may depend on its associated spatial location and it follows that
for any \(D_i\times E_i\in {{\mathcal {B}}}({{\mathcal {A}}}\times {{\mathcal {F}}})\), \(i=1,\ldots ,n\), and any \(n\ge 1\). Furthermore, under random labelling, expression (15) reduces to
which further reduces to \(\prod _{i=1}^n\nu _{{{\mathcal {A}}}}(D_i)\nu _{{{\mathcal {F}}}}(E_i)\) if the common mark distribution coincides with the reference measure \(\nu _{{{\mathcal {M}}}}=\nu _{{{\mathcal {A}}}}\otimes \nu _{{{\mathcal {F}}}}\); this additionally implies that the auxiliary and functional marks are (conditionally) independent of each other. Under independent marking it clearly follows that the correlation functionals satisfy
Hence, if, for example, the pair correlation functional coincides with the pair correlation function of the ground process, then the auxiliary and functional marks are pairwise conditionally independent.
It is not always the case that one wants to have both the auxiliary and the functional marks being independent. We next turn to the case where the functional marks are independent.
Definition 4
If all the components of \(\varPsi |\varPsi _{{{\mathcal {X}}}\times {{\mathcal {A}}}}=\{F_1|\varPsi _{{{\mathcal {X}}}\times {{\mathcal {A}}}},\ldots ,F_N|\varPsi _{{{\mathcal {X}}}\times {{\mathcal {A}}}}\}\) are independent, we say that \(\varPsi \) has (location- and auxiliary mark-dependent) independent functional marks.
When \(\varPsi \) has both independent functional marks and a common marginal functional mark distribution, we say that \(\varPsi \) has randomly labelled functional marks.
Here, it follows that (recall (13))
for \(E_1,\ldots ,E_n\in {{\mathcal {B}}}({{\mathcal {F}}})\) and \(n\ge 1\). Moreover, if \(\varPsi \) has randomly labelled functional marks then \(P^{{{\mathcal {F}}}}_{(x,l)}=P^{{{\mathcal {F}}}}\) and, if additionally \(P^{{{\mathcal {F}}}}\) coincides with \(\nu _{{{\mathcal {F}}}}\), then \( P_{(x_1,l_1),\ldots ,(x_n,l_n)}^{{{\mathcal {F}}}}(E_1\times \cdots \times E_n) = \prod _{i=1}^{n} \nu _{{{\mathcal {F}}}}(E_i) \) and the functional marks \(F_1,\ldots ,F_N\) are independent copies of the reference stochastic process \(X^{{{\mathcal {F}}}}\) in (2).
Further, given that \(\varPsi \) has independent functional marks, if we additionally assume that the auxiliary marks are conditionally independent, so that \( P_{x_1,\ldots ,x_n}^{{{\mathcal {A}}}}(D_1\times \cdots \times D_n) = \prod _{i=1}^{n} P_{x_i}^{{{\mathcal {A}}}}(D_i) = \prod _{i=1}^n \int _{D_i} Q_{x_i}^{{{\mathcal {A}}}}(l_i) \nu _{{{\mathcal {A}}}}(dl_i) , \) \(D_1,\ldots ,D_n\in {{\mathcal {B}}}({{\mathcal {A}}})\), for any \(n\ge 1\), we retrieve the classical definition of independent marking for real valued marks (Daley and Vere-Jones 2003, Definition 6.4.III), and consequently that of random labelling by assuming that they are also identically distributed.
Remark 4
A weaker form of location- and auxiliary mark-dependent independent functional marking, conditional independent functional marking, may be obtained by assuming that
for any \(n\ge 1\) and some family \(\{P_{(x_1,l_1),\ldots ,(x_n,l_n)}^{{{\mathcal {F}}}}(E):(x_1,l_1),\ldots ,(x_n,l_n)\in {{\mathcal {X}}}\times {{\mathcal {A}}}, E\in {{\mathcal {B}}}({{\mathcal {F}}})\}\) of regular probability distributions. Note that here the distribution of a functional mark may depend on all the spatial locations and auxiliary marks.
5.3 Poisson processes
Poisson processes (Daley and Vere-Jones 2003; Chiu et al. 2013), the most well-known point process models, are the benchmark/reference models for representing lack of spatial interaction and constructing other, more sophisticated models. Given a positive locally finite measure \(\mu \) on \({{\mathcal {B}}}({{\mathcal {Y}}})={{\mathcal {B}}}({{\mathcal {X}}}\times {{\mathcal {A}}}\times {{\mathcal {F}}})\), a functional marked Poisson process \(\varPsi \), with intensity measure \(\mu \), is simply a Poisson process on \({{\mathcal {Y}}}\) with the additional assumption that \(\varPsi _G\) is well-defined. When \(\varPsi \) has a well-defined intensity functional \(\rho (\cdot )\), i.e. when the intensity measure in (11) satisfies \(\mu (A)=\int _{A}\rho (x,l,f)\nu (d(x,l,f))\), it follows that \(\rho ^{(n)}((x_1,l_1,f_1),\ldots ,(x_n,l_n,f_n))=\prod _{i=1}^{n}\rho (x_i,l_i,f_i)\), whereby we have \(g_{\varPsi }^{(n)}((x_1,l_1,f_1),\ldots ,(x_n,l_n,f_n)) \equiv 1\) for any \(n\ge 1\). Note that, formally, not every (functional marked) Poisson process is actually a marked point process; we may not necessarily have that \(\varPsi _G\) is a well-defined point process in \({{\mathcal {X}}}\) (van Lieshout 2000, p. 8). That being said, we here clearly have an example of independent marking. When there is a common functional mark distribution, all of the functional marks are given by independent copies of the reference process \(X^{{{\mathcal {F}}}}\) in (2). In particular, if the reference measure \(\nu _{{{\mathcal {F}}}}\) is given by a Wiener measure \({\mathcal {W}}_{{{\mathcal {F}}}}\) on \({{\mathcal {F}}}\), then the functional marks are iid Brownian motions. Moreover, when \(\varPsi \) has a common mark distribution, it becomes randomly labelled and \( \rho ^{(n)}((x_1,l_1,f_1),\ldots ,(x_n,l_n,f_n)) = \rho _G^n>0\) if the common mark distribution coincides with \(\nu _{{{\mathcal {M}}}}\).
When we condition on \(N=n\), we obtain a Binomial point process, which is simply a random (iid) sample \(\{(X_i,L_i,F_i)\}_{i=1}^n\) of size n, with density \(f(x,l,f)=\rho (x,l,f)/n\).
6 Reference measure averaged reduced Palm distributions
In the statistical analysis, we will need to consider Palm conditioning with respect to a given mark set \((D\times E)\in {{\mathcal {B}}}({{\mathcal {A}}}\times {{\mathcal {F}}})\); we interpret this as conditioning on the null event that there is a point of \(\varPsi _G\) at a given location, under the assumption that the mark associated with this point belongs to \((D\times E)\). To be able to do so, we follow van Lieshout (2006a), Cronie and van Lieshout (2016) and define the \(\nu _{{{\mathcal {M}}}}\)-averaged reduced Palm distribution with respect to \((D\times E)\in {{\mathcal {B}}}({{\mathcal {A}}}\times {{\mathcal {F}}})\).
Definition 5
Given a FMPP \(\varPsi \), its family \({{\mathbb {P}}}_{D\times E}^{!x}(\varPsi \in \cdot ) = P_{D\times E}^{!x}(\cdot )\), \(x\in {{\mathcal {X}}}\), of \(\nu _{{{\mathcal {M}}}}\)-averaged reduced Palm distributions with respect to \((D\times E)\in {{\mathcal {B}}}({{\mathcal {A}}}\times {{\mathcal {F}}})\), are defined as the probability measures \(P_{D\times E}^{!x}(R)\), \(R\in {{\mathcal {N}}}_{lf}\),
where \({{\mathbb {P}}}^{!(x,l,f)}(\varPsi \in \cdot )=P^{!(x,l,f)}(\cdot )\) denotes the reduced Palm distribution of \(\varPsi \) at \((x,l,f)\in {{\mathcal {X}}}\times {{\mathcal {A}}}\times {{\mathcal {F}}}\).
Recall that \(P^{!(x,l,f)}(R)\), \(R\in {{\mathcal {N}}}_{lf}\), may be defined through the reduced Campbell–Mecke formula (Daley and Vere-Jones 2008, Section 13.1): For any measurable functional \(h:{{\mathcal {X}}}\times {{\mathcal {A}}}\times {{\mathcal {F}}}\times N_{lf}\rightarrow [0,\infty )\),
Since \(P^{!(x,l,f)}(\cdot )\) is the distribution of the reduced Palm process \(\varPsi ^{!(x,l,f)}\), heuristically, \(P^{!(x,l,f)}(\cdot )\) is the conditional distribution of \(\varPsi \), given that \(\varPsi \) has a point at (x, l, f) which we neglect. Moreover, the probability measure \({{\mathbb {P}}}_{D\times E}^{!x}(\cdot )\) has expectation
by Fubini’s theorem.
In particular, for a Poisson process on \({{\mathcal {X}}}\times {{\mathcal {A}}}\times {{\mathcal {F}}}\), by Slivnyak’s theorem (Chiu et al. 2013),
the (unconditional) distribution of \(\varPsi \). Moreover, for a multivariate FMPP with \({{\mathcal {A}}}=\{1,\ldots ,k_d\}\), we obtain
i.e. the \(\nu _{{{\mathcal {F}}}}\)-averaged reduced Palm distribution of \(\varPsi _i=\{(x,f):(x,l,f)\in \varPsi \cap {{\mathcal {X}}}\times \{i\}\times {{\mathcal {F}}}\}\) with respect to \(E\in {{\mathcal {B}}}({{\mathcal {F}}})\), which is independent of the choice of auxiliary reference measure \(\nu _{{{\mathcal {A}}}}\). When \(\varPsi \) has a common mark distribution which coincides with the reference measure, i.e. \(P_{x}^{{{\mathcal {M}}}}(D\times E) \equiv P^{{{\mathcal {M}}}}(D\times E)=\nu _{{{\mathcal {M}}}}(D\times E)=\nu _{{{\mathcal {A}}}}(D)\nu _{{{\mathcal {F}}}}(E)\), \(x\in {{\mathcal {X}}}\), we obtain a non-stationary and reduced version of the Palm distribution of \(\varPsi \) with respect to the mark set \(D\times E\) found in Chiu et al. (2013, p. 135):
This may now be interpreted as the conditional distribution of \(\varPsi \), given that it has a point with location x with a mark belonging to \(D\times E\). Note further that under stationarity we have that \(P^{!(x,l,f)}(\cdot )\equiv P^{!(0,l,f)}(\cdot )\) for any \(x\in {{\mathcal {X}}}={{\mathbb {R}}}^d\) so the reduced Palm distributions with respect to \(D\times E\) all satisfy \(P_{D\times E}^{!x}(\cdot )\equiv P_{D\times E}^{!0}(\cdot )\). In Supplementary Materials, Section 14, we mention n-point versions of the above.
To connect the above distributions to the reduced Palm distributions \(P_G^{!x}(\cdot )\), \(x\in {{\mathcal {X}}}\), of the ground process, let h in the reduced Campbell–Mecke formula (16) depend only on the ground location and the FMPP:
where \({\bar{P}}^{!x}(d\psi ) = \int _{{{\mathcal {A}}}\times {{\mathcal {F}}}} Q_x^{{{\mathcal {M}}}}(l,f) P^{!(x,l,f)}(d\psi ) \nu _{{{\mathcal {A}}}}(dl)\nu _{{{\mathcal {F}}}}(df)\) and \({\bar{P}}^{!x}(\cdot )\) may be interpreted as an average Palm distribution of \(\varPsi \), given that it has a point at x with unspecified mark (Daley and Vere-Jones 2008, (13.1.13)). The measure \({\bar{P}}^{!x}(\cdot )\) is a distribution on the space \((N_{lf},{{\mathcal {N}}}_{lf})\) of marked point patterns, but by projecting it onto the corresponding measurable space of unmarked point patterns, we obtain the reduced Palm distribution \(P_G^{!x}(\cdot )\) of \(\varPsi _G\) at \(x\in {{\mathcal {X}}}\) (Daley and Vere-Jones 2008, p. 279). For any non-negative and measurable function h on the product of the ground space and the space of all unmarked point patterns,
where \({{\mathbb {E}}}_G^{!x}[\cdot ]\) denotes expectation under \(P_G^{!x}(\cdot )\). Moreover, when \(\varPsi \) has a common mark distribution which coincides with the reference measure, we obtain that \(P_{{{\mathcal {A}}}\times {{\mathcal {F}}}}^{!x}(\cdot )={\bar{P}}^{!x}(\cdot )\). Hence, under this assumption, the projection of \(P_{{{\mathcal {A}}}\times {{\mathcal {F}}}}^{!x}(\cdot )\) onto the space of unmarked point patterns is simply \(P_G^{!x}(\cdot )\).
7 Marked intensity reweighted moment stationarity
To be able to treat the summary statistics considered in this paper, we first have to introduce the notion of kth-order marked intensity reweighted stationarity (k-MIRS) (cf. Cronie and van Lieshout 2016; Iftimi et al. 2019).
Definition 6
A FMPP \(\varPsi \) with \(\varPsi _G\subset {{\mathcal {X}}}={{\mathbb {R}}}^d\) is called kth-order marked intensity reweighted stationary (k-MIRS), \(k\in \{1,2,\ldots \}\), if \(\inf _{(x,l,f)\in {{\mathcal {X}}}\times {{\mathcal {A}}}\times {{\mathcal {F}}}}\rho (x,l,f)>0\) and the nth-order correlation functionals (recall expression (12)), \(n=1,\ldots ,k\), satisfy
for any \(x\in {{\mathbb {R}}}^d\) (recall that \(g_{\varPsi }^{(1)}(\cdot )\equiv 1\)). In particular, the case \(k=2\) is referred to as \(\varPsi \) being second-order marked intensity reweighted stationary (SOMIRS) (Cronie and van Lieshout 2016; Iftimi et al. 2019).
Note that, loosely speaking, this definition essentially states that after having scaled away the effects of the varying intensity, the dependence structure, which is reflected by the product densities, only depends on the distance between the points. Note further that we have implicitly assumed that the product densities up to order k exist. Further details about and examples of k-MIRS processes are mentioned in Supplementary Materials, Section 15.
8 Summary statistics
Having provided various moment characteristics (Sect. 4) and notions of intensity reweighted moment stationarity (Sect. 7) for FMPPs, we may now look closer at how these can be exploited to study dependence structures in FMPPs. Characterising dependence in marked point processes can, in general, be done in various different ways. There are, however, essentially two main approaches which are studied:
-
1.
Spatial interaction between groups of points of \(\varPsi _G\), based on different classifications of the marks.
-
2.
Dependence between the marks, conditionally on the ground process.
The former approach may be carried out by means of marked second-order reduced moment measures/K-functions, marked inhomogeneous nearest neighbour distance distribution functions, marked inhomogeneous empty space functions and marked inhomogeneous J-functions, which are defined in Iftimi et al. (2019), Cronie and van Lieshout (2016), and van Lieshout (2006a). The last three of these are full-distribution summary statistics and require that the point process is k-MIRS for any order \(k\ge 1\), whereas the first two are second-order statistics which require SOMIRS. We here study the second approach, and to this end, we define some new summary statistics and, as we shall see, they generalise most existing finite-order (marked) inhomogeneous summary statistics.
Drawing inspiration from Cronie and van Lieshout (2016), Iftimi et al. (2019), and Penttinen and Stoyan (1989), we have the following definition.
Definition 7
Assuming that \(2\le n\le k\), let \(\varPsi \) be k-MIRS and consider some test function \(t=t_n\), by which we mean a measurable mapping \(t:{{\mathcal {M}}}^n=({{\mathcal {A}}}\times {{\mathcal {F}}})^n\rightarrow [0,\infty )\).
Given some \(W\in {{\mathcal {B}}}({{\mathbb {R}}}^d)\) with \(|W|>0\) and \(D\times E\in {{\mathcal {B}}}({{\mathcal {M}}})={{\mathcal {B}}}({{\mathcal {A}}}\times {{\mathcal {F}}})\) with \(\nu _{{{\mathcal {M}}}}(D\times E)=\nu _{{{\mathcal {A}}}}(D)\nu _{{{\mathcal {F}}}}(E)>0\), the corresponding t-weighted marked nth-order reduced moment measure is defined as

for \(C_i\times (D_i\times E_i)\in {{\mathcal {B}}}({{\mathbb {R}}}^d)\times {{\mathcal {B}}}({{\mathcal {M}}})={{\mathcal {B}}}({{\mathbb {R}}}^d\times {{\mathcal {A}}}\times {{\mathcal {F}}})\), \(\nu _{{{\mathcal {M}}}}(D_i\times E_i)=\nu _{{{\mathcal {A}}}}(D_i)\nu _{{{\mathcal {F}}}}(E_i)>0\), \(i=1,\ldots ,n-1\). We further refer to

\(r_1,\ldots ,r_{n-1}\ge 0\), as the t-weighted nth-order marked inhomogeneous K-function; when \(r_1=\cdots =r_{n-1}=r\ge 0\), write
 .
.
The interpretation of (18) is essentially provided by Lemma 1. Having scaled away the individual intensity contributions of the points of \(\varPsi \), conditionally on \(\varPsi \) having a point at an arbitrary location \(z\in {{\mathbb {R}}}^d\) with associated mark \((L(z),F(z))\in D\times E\), which is neglected, (18) provides the mean of the random variable \(t((L(z),F(z)),(L_1,F_1),\ldots ,(L_{n-1},F_{n-1}))\prod _{i=1}^{n-1}{{\mathbf {1}}}\{(L_i,F_i)\in D_i\times E_i\}\), where the locations \(X_1,\ldots ,X_{n-1}\) of the points associated to \(n-1\) other marks \((L_1,F_1),\ldots ,(L_{n-1},F_{n-1})\) belong to the respective sets \(z+C_i\), \(i=1,\ldots ,n-1\).
Remark 5
We could just as well have chosen to absorb the indicator function \(\prod _{i=1}^n{{\mathbf {1}}}\{(l_i,f_i)\in D_i\times E_i\}\) into the test function t in (18). The current choice has been made to emphasise the connection with the summary statistics in Cronie and van Lieshout (2016) and Iftimi et al. (2019).
In order to give a feeling for how the mark sets in (18) may be specified here in the FMPP context, consider a bivariate FMPP, i.e. \({{\mathcal {A}}}=\{1,2\}\), where \(k=1\), so that \(F_i:{{\mathcal {T}}}\rightarrow {{\mathbb {R}}}\). Next, let \(n=2\) and let \(D=\{1\}\), \(D_1=\{2\}\), \(E=\{f\in {{\mathcal {F}}}={{\mathcal {U}}}:\sup _{t\in {{\mathcal {T}}}}|f(t)| > c\}\) and \(E_1=\{f\in {{\mathcal {F}}}={{\mathcal {U}}}:\sup _{t\in {{\mathcal {T}}}}|f(t)|\le c\}\), for some positive constant c. Here, we would thus restrict the t-weighted correlation provided by (18) to only be between points of different types and, moreover, to be between the two classes of functional marks which either exceed the threshold c or not (see Sect. 8.1 for examples of test functions). For instance, in the forestry context \({{\mathcal {A}}}\) would represent the two species under consideration while c would be the threshold diameter at breast height of the trees; if we would instead set \(D=D_1={{\mathcal {A}}}\), we would ignore the species and simply study the interaction between large and small trees, irrespective of the trees’ species. Hence, we are able to study how large trees affect the survival of small trees, which is something of interest in ecology (Platt et al. 1988; Møller et al. 2016). We emphasise that it should be checked that the chosen sets \(E_i\), \(i=1,\ldots ,n-1\), are indeed measurable, given the chosen function space \(({{\mathcal {F}}},{{\mathcal {B}}}({{\mathcal {F}}}))\).
We will see that (18) is closely related to the nth-order reduced moment measure of the ground process (cf. Møller and Waagepetersen (2004, Section 4.1.2)),
the last two equalities follow from the Campbell formula, the imposed nth-order intensity reweighted stationarity of \(\varPsi _G\) (which follows from \(\varPsi \) being k-MIRS) and the Campbell-Mecke formula. An n-point generalisation of the inhomogeneous K-function \(K_{\mathrm{inhom}}(r)=K_{\mathrm{inhom}}^{(2)}(r)\) of Baddeley et al. (2000) to the nth-order intensity reweighted stationary setting is obtained by considering \(K_{\mathrm{inhom}}^{(n)}(r) = {\mathcal {K}}_G(B_{{{\mathbb {R}}}^d}[0,r]^{n-1})\), where \(B_{{{\mathbb {R}}}^d}[0,r]\) denotes the closed origin-centred ball with radius \(r\ge 0\). Note further that stationarity implies that \(\alpha _G^{(n)}(C_1\times \cdots \times C_{n-1}) = \rho _G^{n-1}{\mathcal {K}}_G(C_1\times \cdots \times C_{n-1})\) and
where, clearly, in this case \(K_{\mathrm{inhom}}^{(n)}(r)\), \(r\ge 0\), yields an n-point generalisation of the K-function of Ripley (1976). In addition, we will see in Lemma 1 that (18) is also related to the following kernel (recall (13)).
Definition 8
The (nth-order) intensity reweighted t-correlation measure (at \(x_1,\ldots ,x_n\in {{\mathbb {R}}}^d\)) is defined as

for \(x_i\in {{\mathbb {R}}}^d\) and \(D_i\times E_i\in {{\mathcal {B}}}({{\mathcal {A}}}\times {{\mathcal {F}}})\), \(i=1,\ldots ,n\), where the measure \(\nu _t(M)\), \(M\in {{\mathcal {B}}}(({{\mathcal {A}}}\times {{\mathcal {F}}})^n)\), is given by
In other words, \(\kappa _t^{\cdot }\) is a spatially dependent weighting of \(\nu _t(\cdot )\) and we interpret it as the expectation of the random variable \(t((L_1, F_1),\ldots ,(L_n,F_n))\prod _{i=1}^{n}1\{(L_i, F_i)\in D_i\times E_i\}\), conditionally on \(X_i=x_i\), \(i=1,\ldots ,n\), having scaled away the individual mark density contributions. Note that since \(\varPsi \) is simple, (19) vanishes whenever \(x_i=x_j\) for any \(i\ne j\) and, moreover, by the imposed nth-order marked intensity reweighted stationarity, we further have that \(\kappa _t^{(D_i\times E_i)_{i=1}^{n}} (x_1,\ldots ,x_n) = \kappa _t^{(D_i\times E_i)_{i=1}^{n}} (x+x_1,\ldots ,x+x_n)\) for a.e. \(x\in {{\mathbb {R}}}^d\). To highlight the connections with Penttinen and Stoyan (1989), we refer to

i.e. (19) with all mark sets set to \({{\mathcal {A}}}\times {{\mathcal {F}}}\), as the (nth-order) intensity reweighted t-correlation functional; note that it is interpreted as the expectation of the random variable \(t((L_1, F_1),\ldots ,(L_n,F_n))\), conditionally on \(X_i=x_i\), \(i=1,\ldots ,n\), having scaled away the individual mark density contributions.
Lemma 1, to which the proof is found in Supplementary Materials, Section 19, gives reduced Palm and \(\nu _{{{\mathcal {M}}}}\)-averaged reduced Palm distribution representations of (18). It also expresses (18) through (19) and \({\mathcal {K}}_G\), and it tells us that (18) is independent of the choice \(W\in {{\mathcal {B}}}({{\mathbb {R}}}^d)\). From a statistical point of view, the main importance of Lemma 1 is related to nonparametric estimation—instead of repeated sampling to estimate (18), we can simply estimate (18) by sampling over each point of the point pattern, which is an effect of the imposed k-MIRS.
Lemma 1
The t-weighted marked nth-order reduced moment measure in (18) satisfies

for almost every \(z\in {{\mathbb {R}}}^d\), where (L(z), F(z)) denotes the mark associated with the reduced Palm conditioning under \({{\mathbb {P}}}_{D\times E}^{!z}(\cdot )\)
Hence, (18) may be expressed as a spatial dependence scaling (reflected by \({\mathcal {K}}_G\)) of the spatially dependent mark-dependence function (19).
Looking closer at Lemma 1, we see that normalising (18) by \({\mathcal {K}}_G\) can reveal features of the marking structure, conditionally on the locations.
Definition 9
The normalised t-weighted marked nth-order reduced moment measure is defined as

where the normalisation of \({\mathcal {K}}_G\) in the last term is a probability measure on \(C_1\times \cdots \times C_{n-1}\).
In Supplementary Materials, Section 17, we look closer at how our summary statistics change when we assume the existence of a common mark distribution.
When \(\varPsi \) is independently marked, then \(\kappa _t^{\cdot }(x_1,\ldots ,x_n)\) coincides with \(\nu _t(\cdot )\) for any \(x_1,\ldots ,x_n\in {{\mathbb {R}}}^d\), whereby

i.e. it does not depend on \(C_1,\ldots ,C_{n-1}\), and if \(\varPsi \) has independent functional marks only then

If the ground process is a Poisson process, we say that a FMPP \(\varPsi \) is a FM ground Poisson process and by (6) it then follows that
This reduces to \(\gamma _{x_1,\ldots ,x_n}^{{{\mathcal {A}}}} (l_1,\ldots ,l_n)\) when \(\varPsi \) has independent functional marks and we obtain the usual Poisson case when \(\varPsi \) has independent marks. When \(\varPsi \) is a FM ground Poisson process, \({\mathcal {K}}_G(C_1\times \cdots \times C_{n-1})=\prod _{i=1}^{n-1}|C_i|\), whereby

and by additionally assuming independent marking,  is given by (22) and
is given by (22) and  is given by (22) multiplied by \(\prod _{i=1}^{n-1}|C_i|\).
is given by (22) multiplied by \(\prod _{i=1}^{n-1}|C_i|\).
Note that these observations may be used to statistically test independent (functional) marking and Poisson assumptions.
8.1 Choosing test functions: analysing dependent functional data
By choosing different test functions \(t(\cdot )\), we may extract different features from the marks. In practice, in a statistical context, it is most likely that one will focus only on the case \(n=2\); note the connections with Comas et al. (2011). Note in particular that when \(n=2\), if we ignore the functional marks and set \(t((l_1, f_1),(l_2,f_2))= l_1 l_2\), (18) yields an intensity reweighted version of the classical mark correlation function for the auxiliary marks. If, instead, \(t((l_1, f_1),(l_2,f_2))= (l_1-l_2)^2/2\), we obtain the classical mark variogram for the auxiliary marks (Illian et al. 2008). The question that remains is how we should choose sensible tests functions \(t(\cdot )\) which include also the functional marks.
Starting with the simple case \(t(\cdot )\equiv 1\), we obtain \(\nu _t=\nu _{{{\mathcal {M}}}}^n\) and

By additionally letting \(n=2\) in (18), we retrieve the marked second-order reduced moment measure \({\mathcal {K}}^{(D\times E)(D_1\times E_1)}(C)\) of Iftimi et al. (2019), which measures intensity reweighted interactions between points with marks in \(D\times E\) and points with marks in \(D_1\times E_1\), when their separation vectors belong to \(C\in {{\mathcal {B}}}({{\mathbb {R}}}^d)\). We stress that this measure, and thereby also (18), is non-symmetric in the mark sets, i.e. \({\mathcal {K}}^{(D\times E)(D_1\times E_1)}(\cdot )\ne {\mathcal {K}}^{(D_1\times E_1)(D\times E)}(\cdot )\) in general (Iftimi et al. 2019). In particular, choosing \(C_1\) to be the closed origin-centred ball \(B_{{{\mathbb {R}}}^d}[0,r]\) of radius \(r\ge 0\), we obtain the marked inhomogeneous K-function \(K_{\mathrm{inhom}}^{(D\times E)(D_1\times E_1)}(r)\) of Cronie and van Lieshout (2016), which measures pairwise intensity reweighted spatial dependence within distance r between points with marks in \(D\times E\) and points with marks in \(D_1\times E_1\). Moreover, setting \(C_1=\{a(\cos v, \sin v) : a\in [0,r], v\in [\phi ,\psi ] \text { or } v\in [\pi +\phi ,\pi +\psi ]\}\) for \(\phi \in [-\pi /2,\pi /2)\) and \(\psi \in (\phi ,\phi +\pi ]\), we obtain a marked inhomogeneous directional version which may be used to study departures from isotropy, and setting \(C_1=\{(x,s):\Vert x\Vert \le r\text { and }|s|\le t\}\) when \(\varPsi \) is a spatio-temporal FMPP, we obtain a spatio-temporal version \(K_{\mathrm{inhom}}^{(D\times E)(D_1\times E_1)}(r,t)\), \(r,t\ge 0\), of \(K_{\mathrm{inhom}}^{(D\times E)(D_1\times E_1)}(r)\) (Iftimi et al. 2019).
Hence, for an arbitrary n, setting \(t(\cdot )\equiv 1\) in (18) we would obtain a definition of a marked nth-order reduced moment measure,  , which has an analogous interpretation; it measures intensity reweighted spatial interaction between an arbitrary point with mark in \(D\times E\) and distinct \((n-1)\)-tuples of other points where, respectively, the separation vectors between these points and the \(D\times E\)-marked point belong to \(C_i\), \(i=1,\ldots ,n-1\), and these points have marks belonging to \(D_i\times E_i\), \(i=1,\ldots ,n-1\). Moreover, it may be of particular interest to choose all \(C_i\), \(i=1,\ldots ,n-1\), to be the same set \(C_1\). For example, \(C_i=B_{{{\mathbb {R}}}^d}[0,r]\), \(i=1,\ldots ,n-1\), \(r\ge 0\), would yield an n-point version,
, which has an analogous interpretation; it measures intensity reweighted spatial interaction between an arbitrary point with mark in \(D\times E\) and distinct \((n-1)\)-tuples of other points where, respectively, the separation vectors between these points and the \(D\times E\)-marked point belong to \(C_i\), \(i=1,\ldots ,n-1\), and these points have marks belonging to \(D_i\times E_i\), \(i=1,\ldots ,n-1\). Moreover, it may be of particular interest to choose all \(C_i\), \(i=1,\ldots ,n-1\), to be the same set \(C_1\). For example, \(C_i=B_{{{\mathbb {R}}}^d}[0,r]\), \(i=1,\ldots ,n-1\), \(r\ge 0\), would yield an n-point version,  , of the marked inhomogeneous K-function of Cronie and van Lieshout (2016), which may be used to analyse intensity reweighted interactions between a point with mark in \(D\times E\) and \(n-1\) of its r-close neighbours, which have marks belonging to the respective sets \(D_i\times E_i\), \(i=1,\ldots ,n-1\).
, of the marked inhomogeneous K-function of Cronie and van Lieshout (2016), which may be used to analyse intensity reweighted interactions between a point with mark in \(D\times E\) and \(n-1\) of its r-close neighbours, which have marks belonging to the respective sets \(D_i\times E_i\), \(i=1,\ldots ,n-1\).
It should be mentioned that when \(t(\cdot )\equiv 1\) under independent marking, \(\bar{{\mathcal {K}}}_t^{(D\times E)(D_i\times E_i)_{i=1}^{n-1}}(\cdot )\equiv 1\), which may be used to statistically test for independent marking.
We next turn to test functions which include the functional marks and we here only consider the case \(n=2\). A natural starting point, we argue, is to consider metrics (distances) between the (functional) marks. There are various choices to be considered (see e.g. Deza and Deza (2009) and the references therein) and each may reflect different features of the functional marks’ properties; although it may be natural to use the metric having generated the assumed Polish topology of the function space \({{\mathcal {F}}}\), we may naturally consider different choices here. We here choose to consider the following metrics as test functions: \(L_p\)-metrics as defined in (28) in Supplementary Materials, i.e. \(t(f_1,f_2)=d_{L_p}(f_1,f_2)=(\int _{{{\mathcal {T}}}}|f_1(t)-f_2(t)|^p{\mathrm {d}}t)^{1/p}\), \(1\le p<\infty \), the uniform metric (or \(L_{\infty }\)-metric) \(t(f_1,f_2)=d_{\infty }(f_1,f_2)=\sup _{t\in {{\mathcal {T}}}}|f_1(t)-f_2(t)|\) (see also Section 13.2), and the symmetrised Kullback–Leibler (KL) divergence,
the rationale behind using the symmetrised KL divergence (as opposed to the usual KL divergence) is that the test function \(t(\cdot ,\cdot )\) is permutation invariant/symmetrical. A further choice is to consider angles, or rather inner products; \(t(f_1,f_2)=\langle f_1,f_2\rangle =\int _{{{\mathcal {T}}}}f_1(t)f_2(t){\mathrm {d}}t\). In the literature on functional clustering, a common measure of proximity between two functions is Ferraty and Vieu (2006)
where \(k\ge 1\), provided that the kth derivatives \(df_i(t)/dt\), \(t\in {{\mathcal {T}}}\), \(i=1,2\), exist. When, conditionally on \(\varPsi _{{{\mathcal {X}}}\times {{\mathcal {A}}}}\), all the functional marks have the same mean \({\bar{F}}(t)={{\mathbb {E}}}[F_i(t)|\varPsi _{{{\mathcal {X}}}\times {{\mathcal {A}}}}]\), \(t\in {{\mathcal {T}}}\), which, for example, is the case when there is a common functional mark distribution, we may consider a functional mark counterpart of the test function for the classical variogram,
where in practice, \({\bar{F}}(t)\) may be estimated by means of \((1/n)\sum _{i=1}^nf_i(t)\), i.e. the average functional mark at time t for the observed functional part of the point pattern. Note that for each of the above choices we may reduce the interval \({{\mathcal {T}}}\) to some smaller interval \([a,b]\subset {{\mathcal {T}}}\). Moreover, we may consider combinations of them by summing them up.
When we want to consider test functions which include both functional and auxiliary marks, we may exploit metric preserving properties of certain operations (van Lieshout 2000, p. 8), such as summation and maximum, and apply these to the above mentioned test functions (metrics) for the functional marks and the metrics provided by Illian et al. (2008, p. 343) for auxiliary marks in order to define a test function for general purposes. When \(n=2\), one may, for example, consider the following two test functions:
where \(d_{{{\mathcal {F}}}}(\cdot ,\cdot )\) is a metric on function space \({{\mathcal {F}}}\) as mentioned above. For general n, we will follow the same procedure.
Moving away from the classical stationary setting to the current (intensity reweighted) inhomogeneous setting makes the interpretation of the summary statistics less straightforward. This added complexity is motivated by a number of factors. Firstly, in practice it is often natural to assume that the (spatial) sampling does not occur homogeneously. Further, one may be interested in dealing with modelling, for example, spatially varying correlations among the marks, but in the stationary case this is not possible since the (higher-order) mark distributions need to be translation invariant. Whether we consider the general inhomogeneous case or the special case of stationarity, our summary statistics provide statistical insight into the link between two different dependence structures, one with respect to the mark space and one with respect to the ground space. When we use functional metrics as test functions, we obtain a rather natural interpretation of (18). If we condition on the ground process, then what we are left with is a quantity which only depends on the functional marks. Moreover, if we consider a Poisson process on \({{\mathcal {Y}}}\) (recall (22)) then we essentially obtain a mean distance between the random functions; note that we here have a random number of iid random functions. Recalling the above discussion about marked K-functions as special cases of (18), we see that in the general (non-Poisson) case we essentially weight this mean distance by the marked K-function, i.e. we penalise it based on the marked spatial interaction of \(\varPsi \). As an effect, when the interaction in the underlying point process is weak, the outcome of the summary statistic is mainly governed by the marking structure. It may further be noted that by letting the test function be the projection \(t(f_1,f_2)=f_1(s)f_2(u)\) for some fixed \(u,s\in {{\mathcal {T}}}\), we would instead get a version of the mark correlation function and, consequently, we obtain weighted second moment-like arguments for the functional marks (negative values of the test function are handled by splitting quantities into positive and negative parts). Moreover, in principle, we could construct a test function such that our summary statistic is the expectation of a covariance function estimator. In conclusion, various notions of dependence/closeness of the functional marks can be obtained by considering different test functions.
8.2 Nonparametric statistical inference
We next turn to the nonparametric estimation of our summary statistics. Specifically, we here assume that we observe a FMPP \(\varPsi \) within a bounded spatial domain \(W\in {{\mathcal {B}}}({{\mathbb {R}}}^d)\), \(|W|>0\), i.e. we sample \(\varPsi \cap W\times {{\mathcal {M}}}= \varPsi \cap W\times {{\mathcal {A}}}\times {{\mathcal {F}}}\).
Theorem 1 provides a nonparametric estimator of the t-weighted marked nth-order reduced moment measure, and it provides a condition for edge corrections to render it unbiased. Its proof is found in Supplementary Materials, Section 19.
Theorem 1
Consider a k-MIRS FMPP \(\varPsi \) and a test function \(t=t_n:{{\mathcal {M}}}^n=({{\mathcal {A}}}\times {{\mathcal {F}}})^n\rightarrow [0,\infty )\), \(2\le n\le k\). Moreover, let \(D\times E\in {{\mathcal {B}}}({{\mathcal {M}}})={{\mathcal {B}}}({{\mathcal {A}}}\times {{\mathcal {F}}})\), \(\nu _{{{\mathcal {M}}}}(D\times E)>0\), and \(D_i\times E_i\in {{\mathcal {B}}}({{\mathcal {M}}})={{\mathcal {B}}}({{\mathcal {A}}}\times {{\mathcal {F}}})\), \(\nu _{{{\mathcal {M}}}}(D_i\times E_i)>0\), \(i=1,\ldots ,n-1\). The estimator

is an unbiased estimator of  , \(C_1\times \cdots \times C_{n-1}\in {{\mathcal {B}}}({{\mathbb {R}}}^d)^{n-1}\), provided that the intensity function \(\rho (\cdot )\) is known and that the edge correction function \(w(\cdot )\) satisfies
, \(C_1\times \cdots \times C_{n-1}\in {{\mathcal {B}}}({{\mathbb {R}}}^d)^{n-1}\), provided that the intensity function \(\rho (\cdot )\) is known and that the edge correction function \(w(\cdot )\) satisfies
for almost any \(x_i\in C_i\), \(i=1,\ldots ,n-1\). Note that \(\prod _{i=1}^{n-1}{{\mathbf {1}}}\{(x_i+x)\in W\}={{\mathbf {1}}}\{\bigcap _{i=1}^{n-1}\{(x_i+x)\in W\}\}={{\mathbf {1}}}\{x\in \bigcap _{i=1}^{n-1}(W-x_i)\}\).
Here, three relevant questions immediately arise: Which edge correction methods satisfy the condition in Theorem 1, and are there other (biased) edge correction methods which still work well in practice? How do we deal with the rather abstract reference measure \(\nu _{{{\mathcal {M}}}}=\nu _{{{\mathcal {A}}}}\otimes \nu _{{{\mathcal {F}}}}\) in (24)? How should we deal with the unknown true intensity \(\rho (\cdot )\) in (24)?
Regarding the edge correction function \(w(\cdot )\), letting \(t(\cdot )\equiv 1\) as well as assuming that \(\varPsi \) has a common mark distribution which coincides with the reference measure, we obtain the estimator
of \({\mathcal {K}}_G(C_1\times \cdots \times C_{n-1})\), based on \(\varPsi _G\cap W\), and by looking closer at the case \(n=2\) in the literature [see, e.g. Cronie and van Lieshout (2016), Gabriel (2014, Appendix 1) and Baddeley (1998)], we get guidance in identifying suitable edge corrections. We obtain that the following choices satisfy the condition of Theorem 1; the proof of Corollary 1 is given in Supplementary Materials, Section 19.
Corollary 1
The minus sampling edge correction
where \(\ominus \) denotes Minkowski subtraction, and the translational edge correction
both yield that the estimator in Theorem 1 is unbiased. Moreover, when the ground space is given by \({{\mathbb {R}}}^d\), \(d=2,3\), and \(n=2\), also the isotropic or rotational edge correction
yields an unbiased estimator (24); here \(\ell \) denotes length in \({{\mathbb {R}}}^2\) or surface area in \({{\mathbb {R}}}^3\) and \(\partial \) is used to denote the boundary of a set.
There are clearly other edge correction methods such as rigid motion correction which do not satisfy the condition in Theorem 1 but still work well in practice.
Turning to the second question, in analogy with Baddeley et al. (2000), Cronie and van Lieshout (2016), Iftimi et al. (2019), Zhao and Wang (2010), define the random measures \( \varXi _G(C;\rho _G)= \sum _{x\in \varPsi _G\cap C} 1/\rho _G(x) \) and \(\varXi (C\times D\times E;\rho ) = \sum _{(x,l,f)\in \varPsi \cap C\times D\times E} 1/\rho (x,l,f)\), \(C\times D\times E\in {{\mathcal {B}}}({{\mathbb {R}}}^d\times {{\mathcal {A}}}\times {{\mathcal {F}}})\), and note that \( {{\mathbb {E}}}\left[ \varXi (W\times D\times E;\rho ) \right] / {{\mathbb {E}}}\left[ \varXi _G(W;\rho _G) \right] = |W|\nu _{{{\mathcal {M}}}}(D\times E)/|W| = \nu _{{{\mathcal {M}}}}(D\times E) \) by the Campbell formula. Hence, \(\varXi _G(C;\rho _G)\) is an unbiased estimator of |W| and \( \widehat{\nu _{{{\mathcal {M}}}}}(D\times E;\rho ,\rho _G) =\varXi (W\times D\times E;\rho )/\varXi _G(W;\rho _G) \) is a ratio-unbiased estimator of \(\nu _{{{\mathcal {M}}}}(D\times E)\), \(D\times {{\mathbb {E}}}\in {{\mathcal {B}}}({{\mathcal {A}}}\times {{\mathcal {F}}})\). Following a suggestion by Stoyan and Stoyan (2000), in (24) it is advised to replace \(\nu _{{{\mathcal {M}}}}(D\times E)\prod _{i=1}^{n-1}\nu _{{{\mathcal {M}}}}(D_i\times E_i)\) by the corresponding estimator to obtain a ratio-unbiased estimator which yields better estimates in practice. This approach is referred to as the Hamilton principle. Moreover, in the case of the minus sampling edge correction, the arguments above should be applied to \(|W\ominus \bigcap _{i=1}^{n-1}C_i|\) instead of |W|. Assuming k-MIRS for any order \(k\ge 1\) (see Supplementary Materials, Section 15, for details) as well as some notion of ergodicity, by following the steps of the proof of Iftimi et al. (2019, Theorem 2), one could also show that (24) is strongly consistent, i.e. that it a.s. converges to (18) when we apply an increasing domain asymptotic regime. This regime is obtained by replacing the window W in (24) by a convex averaging sequence \(W_n\), \(|W_n|\rightarrow \infty \) (Daley and Vere-Jones 2008, Definition 12.2.I). The question of asymptotic normality of (24) is a more delicate matter, however, and one would likely need to consider some notion of mixing for the FMPP in question (cf. Biscio et al. 2018; Biscio and Waagepetersen 2019).
These observations directly connect to the third question, which is how we deal with the fact that the true intensity function is unknown in practice. The most common and natural approach is to replace \(\rho (\cdot )\) in Theorem 1 by a plug-in estimator \({{\widehat{\rho }}}(x,l,f)\), \((x,l,f)\in W\times {{\mathcal {A}}}\times {{\mathcal {F}}}\). This, however, connects back to the problem of specifying \(\nu _{{{\mathcal {M}}}}\) because to estimate \(\rho (\cdot )\) we need to know \(\nu _{{{\mathcal {M}}}}\)—the intensity function is a Radon–Nikodym derivative with respect to the reference measure. A pragmatic and (we argue) not so restrictive approach is to assume that there is a common functional mark distribution which coincides with the functional mark reference measure \(\nu _{{{\mathcal {F}}}}\). By doing so, any intensity estimator is of the form \({{\widehat{\rho }}}(x,l,f)={{\widehat{\rho }}}_{W\times {{\mathcal {A}}}}(x,l)={\widehat{Q}}_{x}^{{{\mathcal {A}}}}(l) {{\widehat{\rho }}}_G(x)\), \((x,l,f)\in W\times {{\mathcal {A}}}\times {{\mathcal {F}}}\), i.e. it does not depend on the functional mark values. In other words, we are in the land of estimating intensity functions for point processes with real valued marks or/and multivariate point processes. Hence, we may consider the estimator

of \({\mathcal {K}}_t^{(D\times E)(D_i\times E_i)_{i=1}^{n-1}}(C_1\times \cdots \times C_{n-1})\). Moreover, taking the Hamilton principle into account, we would here replace the reference measure related parts in (25) by the estimators \(\widehat{|W|}=\varXi (W;{{\widehat{\rho }}}_G)\), \(\widehat{\nu _{{{\mathcal {M}}}}}(D\times E;{{\widehat{\rho }}}_{W\times {{\mathcal {A}}}},{{\widehat{\rho }}}_G)\) and \(\widehat{\nu _{{{\mathcal {M}}}}}(D_i\times E_i;{{\widehat{\rho }}}_{W\times {{\mathcal {A}}}},{{\widehat{\rho }}}_G)\), \(i=1,\ldots ,n-1\). This is indeed quite remarkable—we may estimate a statistic based on something as abstract as a measure on a Polish function space, as well as a Radon–Nikodym derivative with respect to it, without ever having to know or consider any of these entities. Now, it should be noted that the Hamilton principle reference measure estimators may be ignored for certain intensity estimators since these estimators already satisfy \(\widehat{|W|}=\varXi (W;{{\widehat{\rho }}}_G)=|W|\) and \(\widehat{\nu _{{{\mathcal {M}}}}}(D\times E;{{\widehat{\rho }}}_{W\times {{\mathcal {A}}}},{{\widehat{\rho }}}_G)=\nu _{{{\mathcal {M}}}}(D\times E)\) (Cronie and van Lieshout 2018; Moradi et al. 2019). Note finally that if we impose the stronger assumption that there is a common mark distribution \(P^{{{\mathcal {M}}}}\) (auxiliary and functional marks) which coincides with \(\nu _{{{\mathcal {M}}}}\), or if we do not consider any auxiliary marks, we simply replace \({{\widehat{\rho }}}_{W\times {{\mathcal {A}}}}(\cdot )\) above by \({{\widehat{\rho }}}_G(\cdot )\).
In Supplementary Materials, Section 18, we briefly indicate how one could exploit the nonparametric estimators above to carry out minimum contrast-based parametric inference.
8.3 Simulation study
We next conduct a brief simulation experiment to illustrate how our summary statistics, i.e. the t-weighted marked nth-order reduced moment measures in (18), can be used to analyse FMPP data. The main idea is to show that the t-weighted nth-order marked inhomogeneous K-function can be used to test for random labelling, i.e. independence between functional marks and their associated spatial locations. To generate a point pattern with a random curve associated with each spatial location, we consider a spatio-temporal Gaussian random field which we sample spatially at the spatial coordinates generated by a spatial point process in \(W=[0,1]^2\); in practice, we have to sample the spatially referenced curves over a fine temporal grid \(t_1<\cdots <t_k\). The procedure is as follows: first we generate spatial coordinates \(\psi _G=\{x_i\}_{i=1}^n\) according to the following two distinct scenarios: an inhomogeneous Poisson with intensity \(\rho _G(x)=50(x_1^2+x_2)\), \(x=(x_1,x_2)\in W\), and a Thomas process with offspring dispersion parameter 0.075, parent intensity 25 and expected number of offspring for each parent being 4. The obtained point patterns are generated using the functions rpoispp() and rThomas() in the R package spatstat (Baddeley et al. 2016). To each spatial location \(x_i\) of the generated point pattern \(\psi _G\), we assign a function \(f_i(t)=z(x_i,t)\), \(t\in {{\mathcal {T}}}=[0,10]\), which is obtained by sampling a realisation z(x, t), \((x,t)\in W\times {{\mathcal {T}}}\), of a stationary spatio-temporal Gaussian random field Z at the spatial point pattern location \(x_i\), using either a double exponential or Gneiting covariance function for Z; the simulation is carried out using the RFsim() function of the R package CompRandFld (Padoan and Bevilacqua 2015). The double exponential covariance function is a separable model given by
where \(\theta =(\tau ^2,\alpha _s,\alpha _t)\), \(\tau ^2\) is the variance of the spatio-temporal process, and \(\alpha _s\) and \(\alpha _t\) are positive spatial and temporal scale parameters, respectively. For this model, we set the parameters to \(\tau ^2=1\), \(\alpha _s=0.4\) and \(\alpha _t=0.5\) in our simulations.
Separable models such as double exponential models are often chosen for convenience rather than for their ability to fit the data well and these models are rather limited, because of their lack of flexibility in modelling space–time dependencies. For such reasons, we would also like to consider a non-separable covariance model and we here choose a model from the Gneiting class of covariance functions (Gneiting 2002), which is given by
where \(\tau ^2\), \(\alpha _t\) and \(\alpha _s\) are as in the double exponential model, and \(\alpha \) and \(\gamma \) are the smoothness parameters which take values in (0, 2]. The non-separability parameter \(\beta \) takes values in [0, 1] and the model is separable if \(\beta =0\). In our simulation study, we set \(\tau ^2=1\), \(\alpha _t=1\), \(\alpha _s=0.4\), \(\alpha =1\), \(\gamma =1\) and \(\beta =0.5\).
For each scenario, we use the test function (23) in the estimator in expression (25); note that we here assume that there is a common mark distribution and that there are no auxiliary marks present. Since we in practice have to sample each functional mark discretely in time (over a fine temporal grid), each observed function \(f_i\) is represented by a collection \(f_i(t_1),\ldots ,f_i(t_{k})\), \(i=1,\ldots ,n\). As a result, the distance mapping (23) for any two observed functions \(f_1\) and \(f_2\) is approximated by
where \(a=0\), \(b=10\) and \({\bar{f}}(t)=\frac{1}{n}\sum _{i=1}^n f_i(t)\). In all our examples, we set \(n=50\); note that we here assume an equidistant sampling scheme. We thus focus on pairwise interactions and we let \(C_1\) be given by the balls \(B_{{{\mathbb {R}}}^2}[0,r]\), \(r\ge 0\), whereby we obtain a weighted K-function, where we use Ripley’s isotropic edge correction (recall Corollary 1) to correct for edge effects. Moreover, we estimate the intensity function of the ground process nonparametrically and with local edge correction utilising the density.ppp() function of the R package spatstat (Baddeley et al. 2016). To select the bandwidth, we use the criterion of Cronie and van Lieshout (2018), i.e. the spatstat function bw.CvL().
In order to study whether there is random labelling, we create a large number of new realisations (here 499), each obtained by randomly assigning the functional marks to the spatial points \(x_i\in \psi _G\), which are kept fixed. We then compute our summary statistic for each of these new realisations and generate pointwise 0.05 level envelopes based on them. If the summary statistic of the unpermuted/actual data goes outside the envelopes we proceed with the assumption that the functional marks are indeed not randomly labelled (cf. Diggle 2013; Iftimi et al. 2019; Illian et al. 2008).
Top panel: \({\widehat{K}}_t(r)\) for the simulated data using a double exponential covariance function for the spatio-temporal Gaussian random field (solid line), average and simulated 95% envelopes from 499 random relabellings of the functional marks (dashed lines). Left: for the inhomogeneous Poisson process. Right: for the Thomas process. Bottom panel: as top panel but using the Gneiting covariance function instead
Figure 2 shows \({\widehat{K}}_t(r)\) for the data and pointwise 0.05 level envelopes based on 499 permutations of the generated functional marks from a spatio-temporal Gaussian random field with a double exponential covariance function with spatial coordinates generated from the inhomogeneous Poisson process (top left) and the Thomas process (top right). The bottom panels are as in the top panels, but the Gneiting covariance function has been used instead. As one would expect, the functions go outside the envelopes and thus suggest that we are not dealing with a randomly labelled process. Hence, the subsequent analyses of the data should proceed accordingly, i.e. not assuming that the functional data in question have been generated according to an iid procedure. Looking closer at the deviations from the envelopes in Fig. 2, it becomes visibly clear that the behaviour of our summary statistics is influenced by both the spatial dependence structure of the ground process and the structure of the functional marking mechanism.
9 Data analysis: Spatial variation of population characteristics in Spain
Here, we numerically illustrate how our proposed setting and methods may be applied to real data. In particular, we will focus on the summary statistics and show their potential usefulness for extracting features in Spanish province population growth; see the discussion in Fig. 1. The boundary and centre coordinate data of the provinces of Spain are extracted as shapefiles from the R package raster (Hijmans 2019) and the statistical information about the population is taken from the web page of the Spanish Institute of Statistics (www.ine.es).
To better understand the structure and dynamics of populations, two key points are having information about i) the spatial distribution of and the magnitude variation in the demography and ii) the population growth rate. In anthropology and demography, demographical evolution and sex ratio are two important population characteristics which can change over time because of, for example, birth and death rates, economical situations or migration. However, it is natural to expect that these indices are much more similar in neighbouring regions/provinces than in distant regions/provinces. As highlighted in Sect. 1, one of the most important aspects of the analysis is to deduce whether the functional marks, i.e. the demographic evolution and sex ratio, are spatially dependent. Note that the emergence of the regions and their centres is something that occurred a long time ago, i.e. not in connection to the time frame of the functional marks considered. However, we believe that this does not reduce the interest in analysing the functional mark structures in the data.
Similar to the simulation study, for both the demographic evolution and sex ratio curves, we use the test function (23) in the estimator in expression (25); note that we here also assume that there is a common mark distribution and that there are no auxiliary marks present. In both cases, we observed the functions for 20 distinct years, starting from 1998. Hence, each such observed function \(f_i\) can be represented as the collection \(f_i(t_1),\ldots ,f_i(t_{20})\), \(i=1,\ldots ,n\). As a result, for any two observed functions \(f_1\) and \(f_2\), we approximate the distance function (23) by (26), with \(k=20\), \(a=1998\) and \(b=2017\). Hence, as simulation study we focus on pairwise interactions and we let \(C_1\) be given by the balls \(B_{{{\mathbb {R}}}^2}[0,r]\), \(r\ge 0\), whereby we obtain a weighted K-function, where we use the same procedure as in the simulation study for edge correction and estimation of the intensity of the ground process.
Spatial point pattern of the centres of 47 provinces on the Spanish mainland (top left panel). \(({\hat{K}}_t(r))^{1/3}\) for the demographic evolution in 47 provinces of Spain (solid line), average and simulated pointwise 95% envelopes under the homogeneous Poisson process for \(({\hat{K}}_t(r))^{1/3}\) (dashed lines) (top right panel). Bottom left: as top right panel but average and simulated 95% envelopes from 39 random relabellings of the demographic evolution data (dashed lines). Bottom right: as left but for the sex ratio data. In the bottom panels the curves are shown only for \(r \ge 48.27\) km since for the smaller distances the estimated functional mark K-function vanishes
The analysis is illustrated in Fig. 3. The top left panel shows the spatial point pattern of the centres of 47 Spanish provinces. The other three panels show the resulting functional marked K-functions for the Spanish provinces functional marked point pattern (Fig. 1). The transformed \({\hat{K}}_t(r)\) for the data together with simulated pointwise 95% envelopes generated from 39 simulations of a homogeneous Poisson process, obtained by keeping the functional marks fixed, is shown in the top right panel; the obtained intensity estimate was quite flat, so we proceeded by assuming homogeneity. Such envelopes are obtained for each value of r by calculating the smallest and largest simulated values of \(({\hat{K}}_t(r))^{1/3}\); see (Diggle 2013). This suggests that the functional marked Poisson process model does not fit the functional marked data set in the first panel of Fig. 1 well. Recalling the theoretical form of our summary statistics under Poisson assumptions, we see that the current Poisson assumption puts particular emphasis on the functional mark structures. However, some regular model intuitively makes the most sense in terms of describing the location data and as a follow-up one could fit a regular model, e.g. a Strauss model, to the ground point pattern and repeat the analysis above. Note that the transformation \(({\hat{K}}_t(r))^{1/3}\) is just for visualisation purposes and plays no actual role—the reason for employing a cubic root transformation instead of the common square root for the spatial point processes is the potentiality of having negative values for \({\hat{K}}_t(r)\). The bottom panels show the transformed version of \({\hat{K}}_t(r)\) for the data and the pointwise 0.05 level envelopes based on 39 permutations of the demographic evolution on logarithmic scale (left) and sex ratio (right), holding the corresponding locations fixed. For \(r<48.27\) km, \({\hat{K}}_t(r)=0\) and is thus not depicted in the last two panels. These functions suggest that there is no spatial dependence between the functional marks, which points to that the way the population size and the sex ratio have evolved from 1998 to now in different provinces are spatially independent. Hence, the subsequent analyses of the data may proceed by assuming that the functional data here have been generated according to an iid procedure. Consequently, we may proceed with a classical FDA approach for the functions and a separate spatial point pattern analysis for the centres.
10 Discussion
In principle, the current definition of FMPPs may also accommodate situations where we want to consider locations \(X_i\in {\mathcal {S}}\) and functional marks \(F_i(t)\in {\mathcal {S}}\), \(t\in {{\mathcal {T}}}\subset [0,\infty )\), which live on some (Polish) space \({\mathcal {S}}\) other than some Euclidean space; for example, \({\mathcal {S}}\) could be a linear network (Baddeley et al. 2016; Dejby 2017) or a sphere (Møller and Rubak 2016). For instance, in the linear network case, each functional mark would describe the movement along \({\mathcal {S}}\) of the ith point/event/individual, whereby we would have a setup for modelling, for example, cars driving on a road network during a given time period.
One could also extend the current setting to having \({{\mathcal {T}}}\) be an arbitrary (connected) subset of \({{\mathbb {R}}}^d\), for some arbitrary \(d\ge 1\), so that when \(d\ge 2\) the variable t in each \(F_i(t)\) represents a ‘spatial’ location and \(F_i:{{\mathcal {T}}}\rightarrow {{\mathbb {R}}}^k\) is a k-variate random field/process. Moreover, this would allow us to let \({{\mathcal {T}}}\) be any suitable interval in \({{\mathbb {R}}}\), not necessarily a subset of \([0,\infty )\), e.g. \({{\mathcal {T}}}={{\mathbb {R}}}\).
We have proposed a general framework to analyse dependent functional data, with an emphasis on the mathematical and statistical aspects of this framework. A wealth of particular cases and models can be treated using our approach, and thus, a plethora of real problems can be analysed using this new context. Although only one specific data analytic example have been illustrated here, we believe that we have clearly indicated that many different types of data can be analysed using our framework.
References
Baddeley A (1998) Spatial sampling and censoring. In: Kendall W, van Lieshout M (eds) Barndorff-Nielsen O. Stochastic Geometry, Likelihood and Computation, Chapman and Hall, pp 37–78
Baddeley A, Møller J, Waagepetersen R (2000) Non- and semi-parametric estimation of interaction in inhomogeneous point patterns. Statistica Neerlandica 54:329–350
Baddeley A, Rubak E, Turner R (2016) Spatial point patterns: methodology and applications with R. CRC
Banerjee S, Carlin B, Gelfand A (2014) Hierarchical modeling and analysis for spatial data. CRC Press, Boca Raton
Billingsley P (1999) Convergence of probability measures, 2nd edn. Wiley, New York
Biscio C, Waagepetersen R (2019) A general central limit theorem and a subsampling variance estimator for \(\alpha \)-mixing point processes. Scand J Stat 46:1168–1190
Biscio C, Poinas A, Waagepetersen R (2018) A note on gaps in proofs of central limit theorems. Stat Probab Lett 135:7–10
Chiu S, Stoyan D, Kendall W, Mecke J (2013) Stochastic geometry and its applications. Wiley, New York
Comas C (2009) Modelling forest regeneration strategies through the development of a spatio-temporal growth interaction model. Stoch Environ Res Risk Assess 23:1089–1102
Comas C, Delicado P, Mateu J (2011) A second order approach to analyse spatial point patterns with functional marks. Test 20:503–523
Cressie N, Kornak J (2003) Spatial statistics in the presence of location error with an application to remote sensing of the environment. Stat Sci 18:436–456
Cronie O, van Lieshout M (2015) A \(J\)-function for inhomogeneous spatio-temporal point processes. Scand J Stat 42:562–579
Cronie O, van Lieshout M (2016) Summary statistics for inhomogeneous marked point processes. Ann Inst Stat Math 68:905–928
Cronie O, van Lieshout M (2018) A non-model-based approach to bandwidth selection for kernel estimators of spatial intensity functions. Biometrika 105:455–462
Cronie O, Särkkä A (2011) Some edge correction methods for marked spatio-temporal point process models. Comput Stat Data Anal 55:2209–2220
Cronie O, Nyström K, Yu J (2013) Spatiotemporal modeling of Swedish scots pine stands. For Sci 59:505–516
Daley D, Vere-Jones D (2003) An introduction to the theory of point processes: volume i: elementary theory and methods, 2nd edn. Springer Series in Statistics
Daley D, Vere-Jones D (2008) An introduction to the theory of point processes: general theory and structure, 2nd edn. Springer, New York
Dejby J (2017) Capturing continuous human movement on a linear network with mobile phone towers. Master’s thesis, Umeå University, Sweden
Delicado P, Giraldo R, Comas C, Mateu J (2010) Statistics for spatial functional data: some recent contributions. Environmetrics 21:224–239
Deza M, Deza E (2009) Encyclopedia of distances. Springer, Berlin
Diggle P (2013) Statistical analysis of spatial and spatio-temporal point patterns, 3rd edn. Chapman & Hall/CRC, Boca Raton
Ethier S, Kurtz T (1986) Markov processes: characterization and convergence. Wiley-Interscience
Ferraty F, Vieu P (2006) Nonparametric functional data analysis: theory and practice. Springer, Berlin
Gabriel E (2014) Estimating second-order characteristics of inhomogeneous spatio-temporal point processes. Method Comput Appl Probab 16:411–431
Gelfand A, Banerjee S (2010) Multivariate spatial process models. In: Gelfand A, Diggle P, Fuentes M, Guttorp P (eds) Handbook of spatial statistics, CRC Press, Boca Raton, FL, chap 28, pp 495–515
Gelfand A, Diggle P, Guttorp P, Fuentes M (2010) Handbook of spatial statistics. CRC Press, Boca Raton
Genton M, Kleiber W (2015) Cross-covariance functions for multivariate geostatistics. Stat Sci 30:147–163
Gneiting T (2002) Nonseparable, stationary covariance functions for space-time data. J Am Stat Assoc 97:590–600
Hebblewhite M, Merrill E (2008) Modelling wildlife-human relationships for social species with mixed-effects resource selection models. J Appl Ecol 45:834–844
Heinrich L (2013) Asymptotic methods in statistics of random point processes. In: Spodarev E (ed) Stochastic geometry, spatial statistics and random fields: asymptotic methods. Springer, Berlin, pp 115–150
Hijmans R (2019) raster: Geographic data analysis and modeling. R package version 28-19 https://cran.r-project.org/web/packages/raster/raster.pdf
Iftimi A, Cronie O, Montes F (2019) Second-order analysis of marked inhomogeneous spatio-temporal point processes: Applications to earthquake data. Scand J Stat 46:661–685
Illian J, Penttinen A, Stoyan H, Stoyan D (2008) Statistical analysis and modelling of spatial point patterns. Wiley, New York
Jacod J, Shiryaev A (1987) Limit theorems for stochastic processes. Springer, Berlin
Kallenberg O (2006) Foundations of modern probability. Springer, New York
Maniglia S, Rhandi A (2004) Gaussian measures on separable hilbert spaces and applications. Quaderni di Matematica 2004
Mateu J, Lorenzo G, Porcu E (2007) Detecting features in spatial point processes with clutter via local indicators of spatial association. J Comput Graph Stat 16:968–990
Møller J, Rubak E (2016) Functional summary statistics for point processes on the sphere with an application to determinantal point processes. Spat Stat 18:4–23
Møller J, Waagepetersen R (2004) Statistical inference and simulation for spatial point processes. Chapman & Hall/CRC Press, Boca Raton
Møller J, Ghorbani M, Rubak E (2016) Mechanistic spatio-temporal point process models for marked point processes, with a view to forest stand data. Biometrics 72:687–696
Montero J, Fernández-Avilés G, Mateu J (2015) Spatial and spatio-temporal geostatistical modeling and kriging. Wiley, New York
Moradi M, Cronie O, Rubak E, Lachieze-Rey R, Mateu J, Baddeley A (2019) Resample-smoothing of Voronoi intensity estimators. Stat Comput 29:995–1010
Padoan SA, Bevilacqua M (2015) Analysis of random fields using comprandfld. J Stat Softw 63:1–27
Penttinen A, Stoyan D (1989) Statistical analysis for a class of line segment processes. Scand J Stat 16:153–168
Platt W, Evans G, Rathbun S (1988) The population dynamics of a long-lived conifer (pinus palustris). Am Nat 131:491–525
Rajput B (1972) Gaussian measures on \(L_p\) spaces, \(1\le p<\infty \). J Multivar Anal 2:382–403
Ramsay J, Silverman B (2005) Functional data analysis, 2nd edn. Springer, New York
Renshaw E, Särkkä A (2001) Gibbs point processes for studying the development of spatial-temporal stochastic processes. Comput Stat Data Anal 36:85–105
Ripley B (1976) The second-order analysis of stationary point processes. J Appl Probab 13:255–266
Särkkä A, Renshaw E (2006) The analysis of marked point patterns evolving through space and time. Comput Stat Data Anal 51:1698–1718
Schneider R, Weil W (2008) Stochastic and integral geometry. Springer, New York
Sebastian R, Díaz E, Díaz M, Ayala G, Toomre D (2006) Studying endocytosis in space and time by means of temporal boolean models. Patt Recogn 39:2175–2185
Silvestrov S (2004) Limit theorems for randomly stopped stochastic processes. Springer, New York
Skorohod A (1967) On the densities of probability measures in functional spaces. Proc Fifth Berkeley Symp Math Stat Probab 2:163–182
Stoyan D, Stoyan H (2000) Improving ratio estimators of second order point process characteristics. Scand J Stat 27:641–656
van Lieshout M (2000) Markov point processes and their applications. Imperial College Press, London
van Lieshout M (2006a) A \(J\)-function for marked point patterns. Ann Inst Stat Math 58:235–259
van Lieshout M (2006b) Campbell and moment measures for finite sequential spatial processes. In: Hušková M, Janžur M (eds) Proceedings Prague stochastics. Matfyzpress, Prague, pp 215–224
Zhao J, Wang J (2010) Asymptotic properties of an empirical K-function for inhomogeneous spatial point processes. Statistics 44:261–267
Acknowledgements
The authors are grateful to an anonymous referee and an associate editor for constructive feedback and suggestions. The authors are also truly grateful to N.M.M. van Lieshout (CWI, The Netherlands) for feedback on an earlier version of the paper. The authors are also grateful to Aila Särkkä (Chalmers University of Technology, Sweden) and Eric Renshaw (University of Strathclyde, UK) for ideas and discussions and for introducing us to many of the concepts underlying FMPPs. We further thank Mark Hebblewhite (University of Montana, USA) for providing us with the Ya Ha Tinda Elks movements data set. This research was supported by the Kempe foundations (SMK-1750).
Funding
Open access funding provided by University of Gothenburg.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ghorbani, M., Cronie, O., Mateu, J. et al. Functional marked point processes: a natural structure to unify spatio-temporal frameworks and to analyse dependent functional data. TEST 30, 529–568 (2021). https://doi.org/10.1007/s11749-020-00730-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11749-020-00730-2
Keywords
- Correlation functional
- Functional data analysis
- Intensity functional
- Nonparametric estimation
- Spatio-temporal geostatistical marking
- Weighted marked reduced moment measure