Second-order and local characteristics of network intensity functions

Abstract

The last decade has witnessed an increase of interest in the spatial analysis of structured point patterns over networks whose analysis is challenging because of geometrical complexities and unique methodological problems. In this context, it is essential to incorporate the network specificity into the analysis as the locations of events are restricted to areas covered by line segments. Relying on concepts originating from graph theory, we extend the notions of first-order network intensity functions to second-order and local network intensity functions. We consider two types of local indicators of network association functions which can be understood as adaptations of the primary ideas of local analysis on the plane. We develop the nodewise and cross-hierarchical type of local functions. A real data set on urban disturbances is also presented.

Introduction

The statistical analysis of spatial point patterns and processes is a highly attractive field of applied research across many disciplines studying the spatial arrangement of coordinates of events in planar spaces, in the sphere or over networks. Apart from point patterns in planar spaces or the sphere, the last decade witnessed an enormous increase of interest in the spatial analysis of structured point patterns and event-driven data over network domains. Various extensions of classical spatial domain statistics to the network space have been proposed, which in turn rely on mathematical graph theory. For example, Okabe et al. (1995) extended the Clark–Evans statistics to point patterns over planar networks, Okabe and Yamada (2001) introduced a generalization of Ripley’s K-function (Ripley 1976) to the network domain, Okabe et al. (2008) and She et al. (2015) proposed generalized Voronoi diagrams for network data, and Shiode and Shiode (2011) discussed the applicability of network-based and ordinary kriging techniques for street-level interpolation. Most recently, Anderes et al. (2017) covered parametric classes of covariance functions and Baddeley et al. (2017) discussed the concept of second-order pseudostationary of spatial point patterns over networks. In point patterns over networks, the positions of events are pre-configured by a set of line segments (e.g., roads) connecting pairs of fixed planar locations. In other words, treating the line segments as edges and the planar locations as nodes of an arbitrarily shaped graph, this implies that the positions of events are governed by a geometric structure such that the point pattern can only be observed upon the edges contained in the network.

To date, a huge range of methodological and also applied papers covering global characteristics of spatial point patterns over networks exist. Among these papers, various extensions of kernel density smoothers and second-order moment measures and functions have been proposed, including the work of Borruso (2005, 2008), Okabe and Satoh (2009), Okabe and Sugihara (2012), Yu et al. (2015), Ni et al. (2016), McSwiggan et al. (2017) and Moradi et al. (2018). Spooner et al. (2004), Ang (2010), Ang et al. (2012) and Baddeley et al. (2014) focussed on generalizations of Okabe’s and Yamada’s network K-function (Okabe and Yamada 2001) controlling for the geometry of the network. A thorough discussion of the impact of different network structures on network-based extensions of Ripley’s K-function is given in Lamb et al. (2016). Similar to the analysis of classical spatial point patterns, most of these contributions focused on the exploration and description of interrelations among events over the network and the underlying characteristics of the observed spatial point pattern.

Although less frequently, several authors also considered autocorrelation between lagged edges or nodes by means of network distances. Similar to spatial autocorrelation statistics, network autocorrelation statistics express associations among measurements attributed to nodes over a network. Early adaptations of spatial autocorrelation statistics to networks have been presented by Erbring and Young (1979) and Doreian et al. (1984) with respect to social networks, and also Black (1992), who applied Moran’s I statistic to model autocorrelations of flow data over planar networks. Further contributions that cover autocorrelation functions for planar networks are the papers by Chun (2008) and Chun (2013). An in-depth treatment of network autocorrelation is given in Peeters and Thomas (2009).

Lastly, several authors dealt with the analysis of local characteristics and covered clustering and hot-spot detection over planar networks. Early contributions to the local analysis of point patterns over spatial networks are Rogerson (1999) who discussed a local cluster detection based on a $\chi ^2$ test, and Shiode and Okabe (2004) who proposed a network cell count method. Further contributions to clustering and hot-spot detection over planar networks include the L-function analysis (Li et al. 2015), the analysis of multiscale clusters (Shiode and Shiode 2009) as well as cluster detection over road traffic (Young and Park 2014) or flow data (Tao and Thill 2016). Adaptations of local indicators of spatial association (LISA) functions to the network domain and local K-functions have been discussed by Yamada and Thill (2007) and Yamada and Thill (2010). These LISA, resp. local K, functions have been coined local indicators of network-constrained clusters (LINCS), resp. KLINCS, by the authors. Similar approaches have been covered by Berglund and Karlström (1999) and Flahaut et al. (2003) who proposed a local G statistic, and Steenberghen et al. (2004) who discussed a local I statistic. Wang et al. (2017) applied a hierarchical Bayesian model framework for the analysis of local spatial patterns, whereas Schweitzer (2006) implemented a kernel density smoother for hot-spot analysis which yields to local intensity estimates.

When dealing with spatial point data collected over networks, it is essential to incorporate the network specificity into the calculus as the locations of events are restricted to areas covered by line segments. Predominantly, as for traditional spatial point patterns statistics, techniques for analyzing point patterns over spatial networks are defined with respect to pairwise metric distances between the locations of events. In the most general case, this results in computations of point characteristics which only consider events within a disc of radius r centered around the origin. However, when dealing with real-world planar networks consisting of a wide variety of differently sized and differently shaped edges, circular definitions appear to be less suitable to incorporate the characteristics and specificity of the graph.

An alternative formalism, which in turn relies on concepts originating from graph theory, has recently been introduced by Eckardt and Mateu (2017) where the distance boundaries used for calculation are determined exclusively by the inherent network elements independently of the length of the edges, for example all edge intervals contained in the neighborhood. In detail, Eckardt and Mateu (2017) defined a class of network intensity functions and various intensity-based statistics for differently shaped graphs and various levels of aggregation covering undirected, directed and also partially directed networks. Although this approach provides additional information for point patterns over spatial networks, second-order or local characteristics of network intensity functions have not been presented so far. To address these limitations, we propose extensions of the network intensity formalism with respect to second-order characteristics and discuss adaptations of LISA functions to network intensity functions. To provide a clearer classification in context, we denote these new LISA functions as local indicators of network association (LISNA). We note that the second-order analysis of point patterns over spatial networks has recently also been addressed by Rakshit et al. (2017) who considered different metric distances. However, the approach presented in this paper differs from this reference in many important aspects. Essentially, it covers the second-order analysis of different entities contained in the network, namely edges, subsets of vertices such as neighborhoods and paths, and omits any statements in terms of radii. In addition, the present paper establishes a link to spatial autoregression statistics and LISA functions.

The remainder of this paper is organized as follows: A motivation and introduction to second-order characteristics for spatial networks are given in Sect. 2, whereas a discussion of weighting matrices and local characteristics for spatial networks follows in Sect. 3. Applications of local Moran I and local G statistics to urban disturbance-related spatial network data are given in Sect. 4. Finally, the concluding Sect. 5 comments on the major results and impacts on future research.

First- and second-order characteristics of network intensity functions

Before discussing second-order characteristics of network intensity functions in detail, some notation and terminology are introduced. For an in-depth treatment of graph theory, we refer the interested reader to the monographs of Bondy and Murty (2008) and also Diestel (2010).

Notation and terminology

We consider a graph ${\mathcal {G}}$ as a pair of two finite sets: vertices ${\mathcal {V}}$ and edges ${\mathcal {E}}$. The terms network and graph are used interchangeably. The shape of ${\mathcal {G}}$ could be undirected, directed or partially directed such that pairs of vertices in ${\mathcal {V}}$ are linked by at most one edge, namely a line or an arc. In general, elements of ${\mathcal {V}}$ and ${\mathcal {E}}$ will be expressed in lower cases.

For a given network, certain sets are of interest and are intensively used in the remainder of this paper. Any pair of distinct vertices which is linked by an edge is called adjacent. In this case, the vertices are termed the endpoints of an edge and the edge is incident to its endpoints. The set of all vertices which are joined by an undirected edge to node $v_i$ is the neighborhood ${{\,\mathrm{ne}\,}}(v_i)$. The degree of $v_i$ (${{\,\mathrm{deg}\,}}(v_i))$ is the number of distinct vertices in ${{\,\mathrm{ne}\,}}(v_i)$. Similarly, for any directed graph, we define the parents ${{\,\mathrm{pa}\,}}(v_i)$, resp. children ${{\,\mathrm{ch}\,}}(v_i)$ of $v_i$, as the set of nodes pointing to $v_i$, resp. with root $v_i$. Taking the union over both sets results in the family ${{\,\mathrm{fam}\,}}(v_i)$. Analogously to ${{\,\mathrm{deg}\,}}(v_i)$, we express the number of distinct parents of $v_i$ by ${{\,\mathrm{deg}\,}}^-(v_i)$ and the number of distinct children of $v_i$ by ${{\,\mathrm{deg}\,}}^+(v_i)$.

A path is any sequence of distinct nodes and edges, and any nodes $v_i$ and $v_j$ which are joined by a path $\pi _{ij}$ are called connected. If all edges along a path are directed, the path is called directed path where we assume that the path is direction preserving. That is, we do not consider sequences of directed edges in which a head-to-head or tail-to-tail configuration exists. A directed path from $v_i$ to $v_j$ will be indicated by $\vec {\pi }_{ij}$. In addition, we call any vertex $v_i$ pointing to $v_j$ an ancestor of $v_j$ and write ${{\,\mathrm{an}\,}}(v_j)=\lbrace v_i\in \vec {\pi }_{ij-1}\rbrace$ to denote the set of ancestors of $v_j$. Similarly, we say that $v_j$ is a descendant of $\lbrace v_i\rbrace$ if ${{\,\mathrm{an}\,}}(v_j)=\lbrace v_i\rbrace$. The set of descendants of $v_i$ is indicated by ${{\,\mathrm{de}\,}}(v_i)$.

Motivation

For motivation, we consider an arbitrarily shaped spatial network with vertices $v_1$ to $v_{11}$ and a set of edges joining some, but not all pairs of vertices, as depicted in Fig. 1. For simplicity, assume Fig. 1 displays a traffic network such that edges correspond to roads and vertices correspond to segmenting entities such as crossings or ends, whence each road has at least two ends which need not necessarily be interconnected to any alternative segment in the network. However, to obtain further parsimony, auxiliary vertices might be included into the network structure. We also note that a real-world road is a continuous one-dimensional structure, and our network-based construction is a good (perhaps not perfect) approximation of the road itself. Typically, certain roads are unidirectional by nature such that traffic can only flow in one direction, while other roads remain bidirected. That is, our spatial network contains directed as well as undirected edges and movements along the network appearing as a sequence of either directed or undirected edges. However, alternative sequences might also be present in real-world spatial networks and corresponding sequences could easily be defined. Despite such heterogeneity, some roads might also be affected by speed limits such that movements along such network sections are decelerated.

Given a collection of random point locations (a spatial point pattern) over a traffic network where the locations themselves are assumed to be governed by an underlying stochastic mechanism (a spatial point process), one could be interested in the description of egdewise, nodewise or pathwise characteristics such as the number of events that felt onto a specific road segment or took place within a certain neighborhood structure or along a path. Such characteristics have been addressed by Eckardt and Mateu (2017) by means of edgewise, nodewise and pathwise counting measures, first-order intensity functions as well as various K-functions for directed, undirected and mixed networks. Unlike alternative adaptations of Ripley’s K-function to the network domain, these K-functions are related to the expected number of events that fall into a certain distance d subject to an integer-valued threshold $\xi$ which, in turn, is computed as the number of vertices from i to j such that $d(i,j)\le \xi$ holds (see Eckardt and Mateu (2017) for a detailed treatment and specification of alternative second-order point process characteristics).

Fig. 1

Examples of possible pairs of paths in an artificial network indicated by using dashed lines: a two undirected paths, b two diametrically directed paths and c a mixed pair of paths consisting of one undirected and one directed path

We note that different from the linear network formalism presented in Ang et al. (2012), Baddeley et al. (2014), and Baddeley et al. (2017) among others, where the point pattern over the network is initially given independent on the structure network itself, and both configurations are only joint a posteriori, the above specification of the traffic network in the form of a graph through interconnected edges and sets of vertices is the base used to compute a wide range of different point process characteristics. Note that in our context, the specification of the particular subgraph structures determines the calculation of, for example, the nodewise first-order intensity function. That is, unlike the linear network formalism, the computation of network intensity functions is initially linked to the structural specificity of the network and thus explicitly controls for the structural constraints of the network on the point locations. In consequence, the specification and thus the characteristics of the graph strongly determine the characteristics of the point pattern such that different specifications of one particular network might lead to slightly varying locally computed point pattern characteristics, for example edgewise intensity functions. At the same time, the global information on the point pattern over the complete graph will yield similar results, which also holds for more globally computed characteristics such as pathwise intensity function.

Despite first-order characteristics, one might also be interested in the variation or association between pairs of edges, neighborhood structures or paths. However, considering two disjoint edges, neighborhood structures or paths, multiple second-order characteristics can be defined addressing either similar or diverse shapes. That is, the second-order edgewise intensity function could either refer to pairs of directed edges, pairs of undirected edges or, alternatively, consider pairs of one directed and of one undirected edge. In addition, pairs of directed edges might also have a diametrical orientation in the network. Similarly, for second-order neighborhood characteristics, one could be interested in the characterization of events that fell into two neighborhoods in case of undirected or mixed networks, or consider either two sets of parents, two sets of children or only one set of parents and one set of children. In addition, for higher-order neighborhood structures, one could also consider pairs of ancestors or descendants.

An illustration of three different pairs of paths is shown in Fig. 1. Figure 1a highlights two undirected paths joining $v_3$ to $v_6$ and $v_4$ to $v_{11}$. In contrast, two diametrically shifted paths are shown in Fig. 1b. Finally, Fig. 1c contains one undirected path ($v_9$ to $v_5$) and one directed path ($v_6$ to $v_3$). For any of these paired paths, one might be interested in the expected number of points, the variation in number of points or the correlation between the number of points that felt onto both paths. In addition, as for classical spatial point patterns, one could also be interested in the probability of an event in path a given an event in path b.

Recapitulating first-order network intensity functions

Before we discuss the second-order statistics for spatial networks, we briefly present the basic ideas of counting measures and statistics with respect to points contained in ${\mathcal {S}}_{E(G)}$ for different types of networks and recapitulate different first-order network intensity functions. Here, we first treat undirected graphs and discuss directed and partially directed graphs consecutively. Extension to higher-order characteristics is straightforward and follows naturally as generalizations of well-known point pattern characteristics. In general, three different types of network intensity functions can be addressed referring to different levels of network resolutions. These are the edgewise, the nodewise and the pathwise intensity functions.

Following the ideas and notation of Eckardt and Mateu (2017), we address the set of nodes at fixed locations ${\mathbf {s}}_{v}=({\mathbf {x}}_{v},{\mathbf {y}}_{v})$ contained in a spatial network ${\mathcal {G}}$ by ${\mathcal {V}}_s({\mathcal {G}})$ and refer to the set of edge intervals connecting pairs of fixed locations in ${\mathcal {G}}$ by ${\mathcal {S}}_{E_s({\mathcal {G}})}=\lbrace s_{e_1},\ldots ,s_{e_k}\rbrace$. In addition, we express the locations of a point process $X({\tilde{\mathbf {s}}})$ over ${\mathcal {S}}_{E_s({\mathcal {G}})}$ by $\tilde{{\mathbf {s}}}=(\tilde{{\mathbf {x}}}, \tilde{{\mathbf {y}}})$. The location of node $v_i$ is $s_{v_i}=(x_{v_i},y_{v_i})$. Clearly, under this definition, point patterns are only allowed to occur within a given edge interval contained in ${\mathcal {G}}$. That is, the locations $\tilde{{\mathbf {s}}}$ are said to occur randomly within edge intervals spanned between any two fixed locations $s_{v_i}$ and $s_{v_j}$ of ${\mathbf {s}}_{v}$, for example on road segments. By this, we understand a path as a sequence of consecutive edge intervals and the distance $d_{\mathcal {G}}(v_i,v_j)$ between any two nodes in ${\mathcal {V}}_s({\mathcal {G}})$ is the number of consecutive edges joining $v_i$ and $v_j$, that is, the length of a path. Hence, the shortest path distance is the minimum number of consecutive edges needed to move from $v_i$ to $v_j$ along a network.

We explicitly note that these definitions lead to fundamentally different concepts of length as considered in Ang et al. (2012), Baddeley et al. (2014) and Baddeley et al. (2017) who defined the length of a path as the sum over Euclidean distances between consecutive nodes contained in a path, and in Rakshit et al. (2017) who also considered alternative metric distances. By this, the shortest path distance is the minimum of metric distance totals of all paths joining two locations and it is not defined as the minimum number of traversed edges along a path. Unlike the above metrics, the present definition related to the number of edges along a path allows for the specification of polynomial non-circular areas of the network. Also our definition allows for the formulation of alternative point pattern characteristics such as the network pair correlation or network K-function defined over the set of points along different edge intervals whose ends are reachable along the network in $\xi$ or less steps. While the linear network framework characteristics are defined through discs with their relative versions yielding circular-type relations, the proposed graph theoretic formulations related to the number of edge intervals traversed along a path do not yield necessarily circular relations, which implicitly control for the general non-unique edge–vertex distribution and specification of the network. That is, for example, the number of traffic accidents might be closely related to external factors as speed limitations due to overcrowded streets such that high numbers of accidents are more likely to happen along high-speed areas such as motorways which usually consist of less crossings compared to dense traffic areas in the city center.

First-order network intensity functions for undirected networks

Let $N(s_{e_i})$ be the number of points that fall into the undirected edge interval $s_{e_i}$ and $ds_{e_i}$ denote an infinitesimal interval containing $s_{e_i}$ such that $N(ds_{e_i})=N(s_{e_i}+ds_{e_i})-N(s_{e_i})$. Then, we have for the first-order edgewise intensity function

$$\begin{aligned} \lambda (s_{e_i})=\lim _{|ds_{e_i}|\rightarrow 0}\lbrace \mathbb {E}\left[ N(ds_{e_i})\right] /|ds_{e_i}|\rbrace \end{aligned}$$

(1)

Using this expression, we obtain the nodewise mean intensity function $\lambda (v_i)$ for any given node $v_i$ contained in ${\mathcal {G}}$ by averaging (1) over the set of adjacent nodes.

Besides, apart from any such average intensities of points per neighborhood, one can define neighborhood intensity functions using the set of incident edges. To this end, let $\flat (v_i)$ denote the set of edge intervals with endpoint $v_i$, $N(\flat (v_i))$ be the number of points in $\flat (v_i)$ and $d\flat (v_i)$ denote an infinitesimal area covering $\flat (v_i)$. By this, we define the non-averaged neighborhood intensity function $\lambda ({{\,\mathrm{ne}\,}}(v_i))$ as

$$\begin{aligned} \lambda ({{\,\mathrm{ne}\,}}(v_i))=\lim _{|d\flat (v_i)|\rightarrow 0}\lbrace \mathbb {E}\left[ N(d\flat (v_i))\right] /|d\flat (v_i)|\rbrace . \end{aligned}$$

(2)

Using the same ideas as for $\lambda (v_i)$ and $\lambda ({{\,\mathrm{ne}\,}}(v_i))$, we can define an averaged and a non-averaged version of pathwise intensity functions for a path $\pi _{ij}$ joining $v_i$ to $v_j$ (cf. Eckardt and Mateu (2017)). As for (2), writing $\wp _{ij}$ to denote the set of edge intervals traversed once along $\pi _{ij}$, we define the non-average pathwise intensity function as

$$\begin{aligned} \lambda (\pi ^*_{ij})=\lim _{|d\wp _{ij}|\rightarrow 0}\lbrace \mathbb {E}\left[ N(d\wp _{ij})\right] |d\wp _{ij}|\rbrace \end{aligned}$$

(3)

where $N(d\wp _{ij})=N(\wp _{ij}+d\wp _{ij})-N(\wp _{ij})$ and $|d\wp _{ij}|$ is the area contained in $d\wp _{ij}$.

We note that in the classical formulation of an intensity function, we only take the number of neighbors within a particular distance from an event of interest. But here, as we go deeper into the geometry of the network, we are able to provide more specific intensity function that highlights many other possible configurations of the points depending on whether they are in the same path or neighborhood.

First-order network intensity functions for directed networks

To cover directed graphs, slight modifications of the previous notations are required. To this end, let $N(s_{e_i}^\mathrm{in})$ express the number of events on an edge leading to and $N(s_{e_i}^\mathrm{out})$ be the number of events on an edge departing from a vertex of interest, and $ds_{e_i}^\mathrm{in}$ and $ds_{e_i}^\mathrm{out}$ denote infinitesimal intervals containing $s_{e_i}^\mathrm{in}$ and $s_{e_i}^\mathrm{out}$.

Substitution of $N(s_{e_i}^\mathrm{in})$ or $N(s_{e_i}^\mathrm{out})$ for $N(s_{e_i})$ in (1) yields the directed first-order edgewise intensity functions whose average, in turn, leads to the parentwise mean intensity function $\lambda ^\mathrm{in}(v_i)$ and the childrenwise mean intensity function $\lambda ^\mathrm{out}(v_i)$. As in the undirected case, one can define non-averaging versions of $\lambda ^\mathrm{in}(v_i)$ and $\lambda ^\mathrm{out}(v_i)$ with respect to the sets of incident edge intervals with head or tail $v_i$, namely incident edge intervals pointing to $v_i$ ($\lambda ({{\,\mathrm{pa}\,}}(v_i))$) and incident edge intervals departing from $v_i$ ($\lambda ({{\,\mathrm{ch}\,}}(v_i))$). Defining $\flat ^{\mathrm{in}}(v_i)$ (resp. $\flat ^{\mathrm{out}}(v_i))$ as the set of edge intervals pointing to (resp. departing from) $v_i$ and using the same terminology as before, we obtain the non-averaging parentwise (resp. childrenwise) intensity function by substituting $N(d\flat ^{\mathrm{in}}(v_i))$ (resp. $N(d\flat ^{\mathrm{out}}(v_i))$) for $N(d\flat (v_i))$ and $d\flat ^{\mathrm{in}}(v_i)$ (resp. $d\flat ^{\mathrm{out}}(v_i)$) for $d\flat (v_i)$ in (2).

Extensions of pathwise intensity functions to directed networks follow naturally as a generalization of $\lambda (\pi _{ij})$. For the directed path $\vec {\pi }_{ij}$ pointing to $v_j$, we have

$$\begin{aligned} \lambda (\vec {\pi }_{ij})=(|{\mathcal {N}}_{\vec {\pi }}|)^{-1}\sum _{v_i\in \vec {\pi }_{ij}}\lambda (s_{e_i}) \end{aligned}$$

(4)

where ${\mathcal {N}}_{\vec {\pi }}$ is the cardinality of consecutive edge intervals along $\vec {\pi }_{ij}$. We note that in general, different from nodewise calculations, (4) is defined for an ordered pair of endpoints of a directed path such that $\lambda (\vec {\pi }_{ij})$ and $\lambda (\vec {\pi }_{ji})$ refer to different sequences of edge intervals contained in ${\mathcal {G}}$. However, $\vec {\pi }_{ij}$ and $\vec {\pi }_{jk}$ are allowed to have a common endpoint, for example $v_j$. Apart from (4), we define the directed non-average pathwise intensity function $\lambda (\vec {\pi }^*_{ij})$ as

$$\begin{aligned} \lambda (\vec {\pi }^*_{ij})=\lim _{|d\vec {\wp }_{ij}|\rightarrow 0}\lbrace \mathbb {E}\left[ N(d\vec {\wp }_{ij})\right] /|d\vec {\wp }_{ij}|\rbrace \end{aligned}$$

(5)

where $\vec {\wp }_{ij}$ is the set of edges intervals traversed once along a directed path with root $v_i$ and head $v_j$, $d\vec {\wp }_{ij}$ is an infinitesimal interval contained in $\vec {\wp }_{ij}$ and $|d\vec {\wp }_{ij}|$ is the area covered by $d\vec {\wp }_{ij}$.

Apart from directed pathwise intensity functions, one could also consider the information contained in the ancestors or descendants of a distinct node. For example, writing $\wp ^{-i}_{ij}$ for the set of edge intervals contained in ${{\,\mathrm{de}\,}}(v_i)$, a modification of (5) yields to $\lambda ({{\,\mathrm{an}\,}}(v_j))=\lim _{|d\wp ^{-j}_{ij}|\rightarrow 0}\lbrace \mathbb {E}\left[ N(d\wp ^{-j}_{ij})\right] /|d\wp ^{-j}_{ij}|\rbrace .$

First-order network intensity functions for partially directed networks

As partially directed networks are defined as hybrids of directed and undirected networks, we obtain various types of network intensity function as union over the directed and the undirected intensity functions. Using the results of Sects. 2.3.1 and 2.3.2, we obtain the nodewise mean intensity function for partial networks $\lambda ^{cg}(v_i)$ by

$$\begin{aligned} \lambda ^{cg}(v_i)=(|{{\,\mathrm{deg}\,}}^{cg}(v_i))|)^{-1} \lambda ^\mathrm{out}(v_i)\cup \lambda ^\mathrm{in}(v_i)\cup \lambda (v_i). \end{aligned}$$

(6)

Alternative versions of (6) follow naturally by modification of the union sets. For example, the union ${{\,\mathrm{pa}\,}}(\cdot )\cup {{\,\mathrm{ch}\,}}(\cdot )$ would only consider directed adjacent edges, whereas the union ${{\,\mathrm{ne}\,}}(\cdot )\cup {{\,\mathrm{ch}\,}}(\cdot )$ will exclude any edge pointing to a node of interest. Using the previous results for directed and undirected networks, we can define non-average versions of (6) as unions over $\lambda ({{\,\mathrm{ne}\,}}(v_i)),\lambda ({{\,\mathrm{pa}\,}}(v_i))$ and $\lambda ({{\,\mathrm{ch}\,}}(v_i))$ such as the familywise intensity function $\lambda ^{cg}({{\,\mathrm{fam}\,}}(v_i))=\lambda ({{\,\mathrm{pa}\,}}(v_i))\cup \lambda ({{\,\mathrm{ch}\,}}(v_i))$ which expresses the expected number of counts along all directed edge intervals which are incident to node $v_i$.

Second-order intensity and covariance density functions for planar networks

Having point patterns over spatial networks under study, one could be interested in the variation of intensity functions among two different graph entities, e.g., the pairs of distinct edges, neighborhoods or paths contained in the graph. For classical point pattern statistics, such variations are usually expressed by means of second-order properties of the point pattern such as the second-order intensity or the auto- and cross-covariance density functions. This section covers extensions of both functions to pairs of distinct edge intervals, pairs of distinct nodewise sets of edge intervals or pairs of sequences of edge intervals contained in spatial networks. These functions can then be used to characterize the locations of events over the spatial network, which in turn could exhibit randomness, clustering or regularity.

Edgewise second-order intensity and covariance density functions

Consider $s_{e_i}$ and $s_{e_j}$ denote two distinct edge intervals of possibly different shape or length contained in ${\mathcal {G}}$. Then, for any distinct edge intervals contained in any such pair, we can define either directed or undirected counting measures. First, assume that ${\mathcal {G}}$ is undirected. Then, using the same notation as before, we obtain the second-order edgewise intensity function $\lambda (s_{e_i}, s_{e_j})$ as

$$\begin{aligned} \lambda (s_{e_i}, s_{e_j})=\lim _{|ds_{e_i}, ds_{e_j}|\rightarrow 0}\lbrace \mathbb {E}\left[ N(ds_{e_i})N(ds_{e_j})\right] /|ds_{e_i}\times ds_{e_j}|\rbrace \end{aligned}$$

(7)

where $s_{e_i}\ne s_{e_j}$. Less formally, $\lambda (s_{e_i}, s_{e_j})$ is the expected number of counts for pairs of distinct undirected edge intervals. However, although (7) can be used to define edgewise versions of Ripleys’ K-function (Ripley 1976), it does not provide a suitable characterization of the theoretical properties of the spatial point pattern usually expressed by the location and scale under different spatial model specifications, for example the first two moments of a particular theoretical point process distribution. The counterpart version of the K-function based on (7) would reflect the number of edgewise neighbors and provides different information from the one obtained using a linear K-function which does not consider edgewise, nodewise or pathwise structures.

An alternative second-order characteristic which better describes these theoretical properties of the spatial point pattern subject to these two distributional parameters is the edgewise covariance density function $\gamma (s_{e_i}, s_{e_j})$:

$$\begin{aligned} \gamma (s_{e_i}, s_{e_j})=\lambda (s_{e_i}, s_{e_j})-\lambda (s_{e_i})\lambda (s_{e_j}). \end{aligned}$$

As discussed in Sect. 2.3, several different second-order edgewise intensity and covariance functions can be defined. An overview of second-order edgewise intensity functions and edgewise auto-covariance functions which can be defined for directed, undirected and partially directed networks is given in Table 1.

Table 1 Edgewise second-order intensity functions

Nodewise second-order intensity and covariance density functions

Similar to the edgewise second-order intensity functions, we could also be interested in the characterization of variations among distinct subsets of edge intervals contained in a spatial network. For this, one could address either the pairwise variation with respect to distinct nodes such as the second-order or covariance density functions for pairs of neighbors, or the pairwise variation with respect to an identical vertex, for example the variation of intensities between the parents and children of a specific node.

Given two sets of distinct neighborhoods ${{\,\mathrm{ne}\,}}(v_i)$ and ${{\,\mathrm{ne}\,}}(v_j)$ where $v_i\ne v_j$, the nodewise second-order intensity function $\lambda ({{\,\mathrm{ne}\,}}(v_i),{{\,\mathrm{ne}\,}}(v_j))$ results directly from generalization of (7). Using the same arguments as for the edgewise second-order intensity function, the auto-covariance density function $\gamma ({{\,\mathrm{ne}\,}}(v_i),{{\,\mathrm{ne}\,}}(v_j))$ can also be computed from $\lambda ({{\,\mathrm{ne}\,}}(v_i))$ and $\lambda ({{\,\mathrm{ne}\,}}(v_j))$, the non-averaged nodewise intensity functions of $v_i$ and $v_j$ as defined in (2). An overview of different nodewise second-order intensity and auto-covariance functions is given in Table 2.

Table 2 Nodewise second-order intensity functions where $\flat ^{fam}(v_j)=\flat ^\mathrm{in}(v_j))\cup N(d\flat ^\mathrm{out}(v_j))$

Pathwise second-order intensity and covariance density functions

Lastly, we can also consider the variations among distinct pairs of paths contained in a network. In general, any such variation can be defined for pairs of paths with either common or different endpoints such as V-structures in the form of $\pi _{ij}$ and $\pi _{ik}$, inverse V-structures in the form of $\pi _{ij}$ and $\pi _{hj}$, elliptic O-structures in the form of $\pi ^{(1)}_{ij}$ and $\pi ^{(2)}_{ij}$ where any edge interval is only allowed to traverse once in either $\pi ^{(1)}_{ij}$ or in $\pi ^{(2)}_{ij}$, or in the form of two distinct paths $\pi _{ij}$ and $\pi _{kl}$.

In general, for $\pi ^*_{ij}$ and $\pi ^*_{kl}$ and adopting the same ideas as before, we have

$$\begin{aligned} \lambda (\pi ^*_{ij},\pi ^*_{kl})=\lim _{|d\wp _{ij},d\wp _{kl}|\rightarrow 0}\lbrace \mathbb {E}\left[ N(d\wp _{ij})N(d\wp _{kl})\right] /|d\wp _{ij}\times d\wp _{kl}|\rbrace \end{aligned}$$

and $\gamma (\pi ^*_{ij},\pi ^*_{kl})=\lambda (\pi ^*_{ij},\pi ^*_{kl})-\lambda (\pi ^*_{ij})\lambda (\pi ^*_{kl})$ where $\lambda (\pi ^*_{ij})$ and $\lambda (\pi ^*_{kl})$ are non-averaged pathwise first-order intensity functions as introduced in (3).

As for the edgewise and nodewise second-order characteristics, various types of pathwise second-order intensity and auto-covariance functions can easily be introduced, see Table 3 for a detailed list. We remark that differently from edgewise or nodewise calculations, the second-order pathwise properties either include or exclude the endpoint of a directed path such that $\lambda (\pi ^*_{ij},\pi ^*_{kj})\ne \lambda ({{\,\mathrm{de}\,}}_{ji},{{\,\mathrm{an}\,}}_{ij})$. That is, while the edge interval $s_{e_j}=(v_{j-1},v_j)$ is included by $\vec {\pi }^*_{ij}$, it is excluded by ${{\,\mathrm{an}\,}}(v_j)$ as ${{\,\mathrm{an}\,}}(v_j)$ only considers all edge interval along the path $\vec {\pi }^*_{ij-1}$.

Table 3 Pathwise second-order intensity functions

Contrasting edge-, node- and pathwise second-order intensity and covariance density functions

The above definitions have introduced three subfamilies of second-order point characteristics for spatial network point process data which in sum provide a detailed picture on the observed network pattern, each focusing on a different scale from a more locally to a more globally structural description of the observed events. In general, while edgewise intensity functions are the base underpinning both the node- and pathwise characteristics, both alternative subfamilies of network intensity functions focus on different aspects of the point distribution over the network. Being defined through sets of either undirected, directed or mixed sets of edge intervals which are connected to a particular node, the proposed nodewise intensity functions reflect the spread of points within (pairs of) polynomial (sub)areas centered at pairs of distinct fixed nodes and are whence suitable tools for either hot- or cold-spot detection; they are also useful to decide on regularity or clustering subject to the number of points over different graph theoretic subsets such as the neighborhood or the parents. In particular, for directed and partially directed graphs, these characteristics could be used to analyze the flow of events over consecutively interrelated subsets such as the parents and children.

Different from the nodewise characteristics, the subfamily of pathwise first- and second-order intensity functions provides helpful characteristics which describe the intensity of points over sets of distinct interconnected edge intervals over the complete network and, thus, allow, for example, to evaluate and compare different routes along the network from i to j.

Local indicators of spatial association for network intensity functions

This section introduces local indicators of network associations (LISNA) functions for network intensity which can be understood as adaptations of the primary ideas of local analysis to the analysis of spatial point patterns over a network. In general, we concern two different types of LISNA functions: nodewise LISNA functions (type 1) and cross-hierarchical LISNA functions (type 2). While LISNA functions of type 1 are generalizations of Anselins’ LISA functions (Anselin 1995) to nodewise intensity functions which can be applied to any global measure of spatial association, cross-hierarchical LISNA functions express the variation between individual edge intervals and different subsets of edge intervals contained in different network entities. LISNA characteristics consider the individual contributions of a global estimator as a measure of clustering. Before we discuss LISNA functions of types 1 and 2 in detail, we briefly review the concept of LISA functions and related clustering approaches for the spatial domain.

A primer on local indicator of spatial association statistics

Spatial cluster detection has stimulated an immense interest in efficient statistical analysis tools, and several authors have contributed to this field. A local version of Ripley’s K-function (Ripley 1976) has been proposed by Getis and Franklin (1987, 2010) in order to quantify clustering at different spatial scales. Another local statistic, the local G statistic, was presented by Getis and Ord (1992, 2010) which allows to assess the degree of spatial association at various levels of spatial refinement in an entire sample or in relation to a single observation. Stoyan and Stoyan (1994) introduced both local L- and local g-functions for the analysis of neighborhood relationships. A local $H_{i}$ statistic was introduced by Ord and Getis (2012) in order to measure the spatial variability while avoiding the pitfalls of using the non-spatial F test for spatial data.

We note that several authors have considered product density LISA functions for cluster detection in spatial point patterns which will not be covered here. These LISA functions originate in the papers of Cressie and Collins (2001a, 2001b) who considered bundles of product density LISA functions for the recognition of similarity groupings in spatial subpatterns by examining individual points in the point pattern in terms of how they relate to their adjacent points in space. Similarly, Mateu et al. (2010) used product density LISA functions for cluster detection in the presence of substantial clutter, and Moraga and Montes (2011) discussed the use of product density LISA functions with respect to disease clusters.

Local indicators of spatial network associations of type 1

Weighting matrices for spatial network intensity functions

To discuss spatial auto-correlation and local associations among spatial point patterns over network structures, a suitable weighting matrix ${\mathbf {W}}$ is essential and has to be defined prior to analysis. In general, for nodewise associations, a reasonable choice of ${\mathbf {W}}$ is the adjacency matrix ${\mathbf {A}}$ of the network ${\mathcal {G}}$ which represents the structure of the graph in a compact way such that the ijth entry $a_{ij}$ of ${\mathbf {A}}$ is one if ${{\,\mathrm{ne}\,}}(v_i)=v_j$ and zero otherwise. However, as we will discuss next, ${\mathbf {W}}$ is equivalently encoded by ${\mathbf {A}}$ in most but not all cases.

Most commonly, depending on the type of the network, ${\mathbf {A}}$ is either a symmetric or an asymmetric binary matrix of dimension ${\mathcal {V}}({\mathcal {G}})\times {\mathcal {V}}({\mathcal {G}})$. However, as we consider local associations among different sets of nodes, namely the sets of neighbors, parents or children, one might not only be interested in the association within and between different sets of nodes but also in the variation of associations for different orders of network linkages. That is, apart the graph-theoretic (first-order) definitions of neighbors, parents or children as introduced in Sect. 2.1, one might also be interested in the cumulative or the partial kth order subset of nodes where $k=2,3,\ldots$. While the cumulative second-order neighbors of node $v_i$ would include all nodes which are connected to either $v_i$ or ${{\,\mathrm{ne}\,}}(v_i)$ by an edge excluding $v_i$, the partial second-order neighbors would only include those vertices which are joint to ${{\,\mathrm{ne}\,}}(v_i)$ excluding both $v_i$ and ${{\,\mathrm{ne}\,}}(v_i)$. For notational simplicity, we will address the partial kth order of ${\mathbf {A}}$ by adding a superscript k to ${\mathbf {A}}$ such that ${\mathbf {A}}^{(k)}$ is the partial kth order adjacency matrix of ${\mathcal {G}}$. Similarly, ${\mathbf {W}}^{(k)}$ denotes the spatial weighting matrix of order k.

For ${\mathbf {A}}^{(1)}$, the ijth element of ${\mathbf {A}}^{(1)}$ is only nonzero if $v_i$ and $v_j$ are joined by an edge in ${\mathcal {G}}$. Thus, if ${\mathcal {G}}$ is an undirected network, $a_{ij}=1$ also implies that $a_{ji}=1$ due to the symmetry of ${\mathbf {A}}$. Despite such first-order subsets of nodes, the definition of higher-order neighborhoods, parents or children requires a careful distinction between the notions of partial and cumulative subsets of nodes. Extensions to partial higher-order adjacency matrices ${\mathbf {A}}^{(k)}$ follow naturally as generalizations of ${\mathbf {A}}^{(1)}$, such that $a^{(k)}_{ij}$ of ${\mathbf {A}}^{(k)}$ is nonzero if $v_i$ and $v_j$ are joined by $k-1$ interior nodes, that is, if $v_i$ is connected to $v_j$ by a path of length k and vice versa. Different from such partial sets of order k, cumulative sets of order k consist of all neighbors, parents or children of a distinct node up to order k. That is, a second-order cumulative neighborhood of order k of node $v_i$ can be understood as the union over the first-order and all partial second-order neighbors of $v_i$ up to order k. Obviously, these are all vertices along all paths of length k contained in the network with origin $v_i$. Consequently, while ${\mathbf {W}}^{(k)}={\mathbf {A}}^{(k)}$, this equivalence in general does not hold for cumulative subsets of order k.

Nodewise LISNA functions

We now turn to the discussion of LISNA functions of type 1. For this, let ${{\,\mathrm{\varvec{\lambda }_{\mathcal {V}}}\,}}$ denote a vector of dimension $n\times 1$ of either averaged or non-averaged nodewise intensity functions defined with respect to either the set of n neighbors, n parents, n children or n families contained in a network and $\mu _{\mathcal {V}}$ be the mean of ${{\,\mathrm{\varvec{\lambda }_{\mathcal {V}}}\,}}$ over ${\mathcal {G}}$ and $\gamma _{\mathcal {V}}^{(0)}$ the auto-covariance of ${{\,\mathrm{\varvec{\lambda }_{\mathcal {V}}}\,}}$. In general, we assume the type of network elements associated with ${{\,\mathrm{\varvec{\lambda }_{\mathcal {V}}}\,}}$ to be unique such that, for example, all elements of ${{\,\mathrm{\varvec{\lambda }_{\mathcal {V}}}\,}}$ are parentwise intensity functions.

Given the k-order weighting matrix ${\mathbf {W}}^{(k)}$ with $w^{(k)}_{ij}\ne 0$ if $v_i$ and $v_j$ are joined by a path of length $k-1$, we obtain the auto-covariance of ${{\,\mathrm{\varvec{\lambda }_{\mathcal {V}}}\,}}$ of order k as $\gamma _{\mathcal {V}}^{(k)} = \mathbf {{{\,\mathrm{\varvec{\lambda }_{\mathcal {V}}}\,}}}^{{\mathsf {T}}}{\mathbf {W}}^{(k)}\mathbf {{{\,\mathrm{\varvec{\lambda }_{\mathcal {V}}}\,}}}/\sum _{i=1}^{n}\sum _{j=1}^{n}w^{(k)}_{ij}$.

Similarly, we define the auto-correlation of ${{\,\mathrm{\varvec{\lambda }_{\mathcal {V}}}\,}}$ as $\rho =\gamma ^{(k)}/\gamma _{\mathcal {V}}^{(0)}$ which expresses the correlation along the network in terms of distance for different lags k. As for classical spatial statistics, a general approach to characterize nodewise auto-correlations is to compute auto-correlation statistics, namely Morans’ I statistic, Geary’s C statistic or Getis’ and Orb’s G statistic. Assuming that ${\mathbf {W}}={\mathbf {A}}^{(1)}$ such that $w_{ij}=1$ if and only if $v_i$ and $v_j$ are joined by an edge interval in ${\mathcal {G}}$, the Moran I statistics for spatial networks is given by

$$\begin{aligned} I = \frac{n}{\sum _{i=1}^{n}\sum _{j=1}^{n}w_{ij}} \frac{\sum _{i=1}^{n}\sum _{j=1}^{n}w_{ij}(\lambda (v_i)-\mu _{\mathcal {V}})(\lambda (v_j)-\mu _{\mathcal {V}})}{\sum _{i=1}^{n}(\lambda (v_i)- \mu _{\mathcal {V}})^2} \end{aligned}$$

(8)

and can be understood as the ratio between the product of nodewise intensity functions and its adjacent nodes, with the nodewise intensity functions, adjusted for the weights used. That is, the Moran’s I statistic provides information on the correlation between the nodewise intensity functions and the neighboring intensity function values.

Another concept of nodewise auto-correlation along spatial networks which uses the sum of squared differences between pairs of nodewise intensity functions as its measure of covariation is provided by Geary’s C statistic:

$$\begin{aligned} C = \frac{(n-1)}{2\sum _{i=1}^{n}\sum _{j=1}^{n}w_{ij}} \frac{\sum _{i=1}^{n}\sum _{j=1}^{n}w_{ij}(\lambda (v_i)-\lambda (v_j))^2}{\sum _{i=1}^{n}(\lambda (v_i) - \mu _{\mathcal {V}})^2} \end{aligned}$$

(9)

and, additionally, by Getis’ and Orb’s G statistics,

$$\begin{aligned} G = \sum _j w_{ij}\lambda (v_j)-\sum _{j}w_{ij}\mu _{\mathcal {V}}/n\sum _jw_{ij}^2-(\sum _j w_{ij})^2/(n-1)^\frac{1}{2}. \end{aligned}$$

Apart from these global statistics, we define a local counterpart of (8) as

$$\begin{aligned} I_i = \frac{(\lambda (v_i)-\mu _{\mathcal {V}})}{{\sum _{j=1}^{n}(\lambda (v_j)-\mu _{\mathcal {V}})^2}/(n-1)}{\sum _{j=1}^{n}w_{ij}(\lambda (v_j)-\mu _{\mathcal {V}})} \end{aligned}$$

and, following the ideas of Anselin (1995), a local version of (9) as

$$\begin{aligned} C_i=\frac{1}{\sum _{i=1}^n\lambda (v_i)^2/n}\frac{\sum _{i=1}^{n}\sum _{j=1}^{n}(\lambda (v_i)-\lambda (v_j))^2}{\sum _{i=1}^n\lambda (v_i)^2} \end{aligned}$$

Local indicators of spatial network associations of type 2

We now consider LISNA functions of type 2 which can be understood as a generalization of Sect. 2.4 to second-order characteristics which describe variations in second-order network intensity functions for cross-hierarchical pairs of network entities. In general, any such cross-hierarchical pair consists of one edge interval and one subset of diverse edge intervals such as neighbors, parents or paths. By this, different from the previous section, LISNA functions of type 2 are not restricted to nodewise characteristics. But, while LISNA functions of type 1 are based on averaged and non-averaged nodewise first-order intensity functions, the present LISNA functions are related to the second-order properties of point patterns of spatial networks and only allow for non-averaged intensity functions.

In general, this section only considers LISNA functions for two different second-order properties: the LISNA function with respect to (a) second-order non-average intensity functions and (b) auto-covariance functions.

For (a), a generalization of Sect. 2.4 to cross-hierarchical terms yields

$$\begin{aligned} \lambda ({{\,\mathrm{ne}\,}}(v_i),s_{e_j})=\lim _{|d\flat (v_i),ds_{e_j}|\rightarrow 0}\lbrace \mathbb {E}\left[ N(d\flat (v_i))N(ds_{e_j})\right] /|d\flat (v_i)\times ds_{e_j}|\rbrace . \end{aligned}$$

Similarly, for (b) we have $\gamma ({{\,\mathrm{ne}\,}}(v_i), s_{e_j})=\lambda ({{\,\mathrm{ne}\,}}(v_i), s_{e_j})-\lambda ({{\,\mathrm{ne}\,}}(v_i))\lambda (s_{e_j})$.

A detailed list of all possible cross-hierarchical LISNA configurations for spatial networks is given in Table 4.

Table 4 Configurations of LINSA functions of type 2 for different types of spatial networks

Application: urban disturbance-related data

This section covers an applications of LISNA type 1 functions to spatial network data on locations of phone calls on neighbor and community disturbance recorded by local police authorities in the City of Castellón (Spain).

Data and network

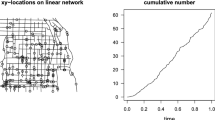
Our study is based on event data recorded along the traffic network of the City of Castellón for which we defined 1611 segmenting units. Each segmenting unit is treated as endpoint of an edge interval such that each edge interval is spanned between a pair of vertices, namely between two distinct segmenting units. By this, we obtain a spatial network with a mean number of adjacent nodes of 3.14. Next, we augmented each vertex with precise coordinates and computed the length of the edge interval as the squared geodesic distance between its geo-coded endpoints. For our analysis, we considered a geo-referenced subsample of $N= 9790$ call-in events provided by the local officials of the City of Castellón (see Fig. 2 for a visualization of the neighbor and community disturbance point pattern over the traffic network).

Fig. 2

Neighbor and community disturbance events represented as black dots recorded over the traffic network of the City of Castellón

Classification as neighbor and community disturbances has been performed prior to our analysis by police officials. The phone calls have been received at local police stations or transferred by 112 emergency services to local police call centers and geo-referenced indirectly by the provider based on precise address information. Using this geo-information, we considered an event to belong to a distinct edge interval if the coordinates fell in between the geo-coded endpoints of an edge. Adopting the network intensity function formalism to the resulting spatial network pattern, we computed edgewise mean intensity functions for all edge intervals contained in the traffic network and calculated the nodewise first-order mean intensity function for neighboring nodes. By this, we obtained average nodewise intensity values for 614 segmenting units which have been treated as input for the LISNA type 1 functions.

Global and local associations for neighbor and community disturbances

To evaluate the associations among nodewise first-order mean intensity values along the network, we first computed the Moran I and the Geary’s C statistics. For Moran’s I, we obtained a value of 0.32 and for Geary’s C a value of 0.58 which both indicate a positive auto-correlation in the distribution of nodewise mean intensity functions along the network, although it is not particularly strong. Besides the numerical characteristics, we also computed Moran’s I scatterplot (Anselin 1996) which is shown in Fig. 3. This plot compares the nodewise first-order mean intensity function of each segmenting unit with the average value of its first-order neighboring nodes. Moran I statistic is depicted as the slope in the scatterplot with the neighboring nodewise intensity value on the vertical and the nodewise intensity function on the horizontal axis. Inspecting Fig. 3, we found that almost all points in the scatterplot are placed in the upper right quadrant which confirms our findings of positive auto-correlation, where the slope of the regression lines indicates a moderate Moran I statistic.

Fig. 3

Moran’s I scatterplot for the Castellón network

To examine the order of spatial auto-correlation along the network structure, we additionally computed correlograms and Bonferroni adjusted p values for the Moran’s I and Geary’s C statistics. The results are shown in Fig. 4. Both correlograms show a consistent trend for Moran’s I and Geary’s C statistics indicating the presence of a positive auto-correlation among nodewise mean intensity functions along the network. Looking at the p values, we found a positive association among neighboring vertices up to order 6 for Geary’s C statistic and up to order 8 for Moran’s I statistic.

Fig. 4

Correlograms and Bonferroni adjusted p values for the Castellón network: a Moran’s I, b p values of Moran’s I statistics (solid line) and $\alpha$-level of 0.99 (dashed line), c Geary’s C and (d) p values of Geary’s C statistics and $\alpha$-level of 0.99 (dashed line)

To further investigate the spatial auto-correlation among the nodewise mean intensity functions, we computed different local measures of auto-correlation. For the local Moran’s I statistic, as displayed in Fig. 5, we found high–low associations among the nodewise mean intensity functions of neighboring vertices in the upper- and lower-right areas as well as the left borders of the Castellón traffic network.

Fig. 5

Local Moran’s I computed from the Castellón network

Fig. 6

Local Getis G computed from the Castellón network

At the same time, high–high associations which reflect hot spots of nodewise mean call-in intensities occurred most frequently on a vertical axis along the central area of the traffic network. These findings express a severe clustering of neighbor and community disturbance call-ins along the downtown areas of Castellón.

Apart from the local Moran I statistic (Fig. 5), we concerned the local Getis’ and Orb’s G statistic. The results of the local Getis’ and Orb’s G statistic are shown in Fig. 6.

Different from Moran’s I or Geary’s C statistics, this local statistic also differentiates between high–high and low–low correlations which are treated as positive auto-correlation by Moran’s I statistic. Inspecting this Figure, we found high values located in the center, whereas moderate low values occurred in the outlying areas of the Castellón traffic network. These findings indicate a strong spatial agglomeration of neighbor and community disturbances such that all perturbations appeared within the central areas of Castellón. One possible explanation for this local agglomeration of public disturbances can be seen in the denseness of the traffic network and the high population density in the city center.

Conclusions

This article concerns the second-order analysis of structured point patterns over networks by means of network intensity functions and proposes nodewise and cross-hierarchical types of local indicator of network association functions. We believe that the presented methodology is immediately useful in the following sense, and could stimulate a rich body of future research and new directions in the analysis of point patterns and event-driven data recorded along planar networks.

Having point data over planar line structures under study, one commonly faces heterogeneous rather than homogeneous characteristics along the network. The expected number of events is strongly associated with the specificity and geometrical complexity of the network and might be affected by the shape, the length and the characteristics of individual lines. Defining edge intervals to be the core elements, network intensity functions resolve any such methodological challenges and allow to explore the first- and higher-order characteristics of the point patterns under control of the network specificity. The proposed global and local network intensity functions provide information on interactions within and between different hierarchical levels contained in the network.

We finally note that our proposal uses graph theoretical ideas different from the more classical way of dealing with local product densities for spatial point patterns. Connections and differences between these two approaches are to be analyzed in a more focused paper.