Abstract
This paper introduces area-level compositional mixed models by applying transformations to a multivariate Fay–Herriot model. Small area estimators of the proportions of the categories of a classification variable are derived from the new model, and the corresponding mean squared errors are estimated by parametric bootstrap. Several simulation experiments designed to analyse the behaviour of the introduced estimators are carried out. An application to real data from the Spanish Labour Force Survey of Galicia (north-west of Spain), in the first quarter of 2017, is given. The target is the estimation of domain proportions of people in the four categories of the variable labour status: under 16 years, employed, unemployed and inactive.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Statistical offices are interested on the estimation of socio-economic indicators, like proportions or counts, for the whole population or for subsets called domains. Sampling designs are developed for obtaining precise estimators on their target (planned) domains. Statisticians are also asked to provide estimates for unplanned domains (small areas), where sample sizes are too small to carry out such estimations. Small Area Estimation (SAE) deals with this kind of problems by combining tools of survey sampling and statistical modelling at the unit or at the area level. The monographs of Rao (2003) and of Rao and Molina (2015) give a general description of SAE.
In Galicia (north-west of Spain), the Spanish Labour Force Survey (SLFS) provides information about labour market indicators. The territory of Galicia is hierarchically divided into counties and municipalities. As the sampling design of the SLFS is stratified with strata defined by the size of the municipalities and most municipalities are not represented in the sample, the direct estimates at the municipal or county level have a low accuracy. In this context, estimating labour force indicators is thus a SAE problem. The objective of this paper is to estimate proportions of under 16 years, employed, unemployed and inactive people in counties of Galicia crossed by sex under an area-level model-based approach.
Under the unit-level approach, Chambers et al. (2016), Hobza and Morales (2016) and Hobza et al. (2018) have derived estimators of domain proportions and counts based on M-quantile or binomial logit models for binary outcomes. Under the area-level approach, Chambers et al. (2014), Dreassi et al. (2014), Tzavidis et al. (2015) and Boubeta et al. (2016, 2017) applied binomial, negative binomial or Poisson regression models for estimating the domain counts or proportions. Esteban et al. (2012), Marhuenda et al. (2013, 2014) and Morales et al. (2015) derived estimators of proportions based on area-level linear mixed models. Concerning the Bayesian approach to small area estimation of proportions, the contributions of Farrell (2000), Larsen (2003), Chen and Lahiri (2012) and Liu and Lahiri (2017) are relevant. These approaches are based on univariate models that do not consider the possibility of jointly estimating the counts or proportions of more than two categories.
In labour force statistics, some indicators of interest are the totals or proportions of the categories of a classification variable. This is to say, they are domain compositional parameters summing up to one or to a known integer number. The seminal book of Aitchison (1986), the more recent book edited by Pawlowsky-Glahn and Buccianti (2011) and the papers Egozcue et al. (2003) and Egozcue and Pawlowsky-Glahn (2019) are basic references for an introduction to compositional data analysis.
The estimation of compositional parameters requires using multivariate models. At the unit level, Scealy and Welsh (2017) have applied a directional mixed effects model for predicting the proportions of total weekly expenditure on food and housing costs for households in a chosen set of domains. At the area level, we can find methodologies for contingency tables where the cell counts are explained by categorical auxiliary variables or by regression-based inference procedures allowing for continuous auxiliary variables. Within the first approach, Zhang and Chambers (2004) developed a class of log-linear structural models that is suited to estimation of small area cross-classified counts based on survey data. Berg and Fuller (2014) gave a SAE procedure for a two-way table of proportions with predictors based on a nonlinear mixed model. Under the regression-based setup, Ferrante and Trivisano (2010) proposed a multivariate SAE approach for count data based on the multivariate Poisson-lognormal distribution an derived hierarchical Bayes predictors. Souza and Moura (2016) and Fabrizi et al. (2016) deal with multivariate Beta regression models in SAE. Saei and Chambers (2003), Molina et al. (2007) and López-Vizcaíno et al. (2013, 2015) have applied multinomial logit mixed models to category counts for estimating domain totals of labour status categories.
This paper introduces three area-level compositional mixed models to obtain small area estimates of labour force proportions in Galicia. The first model is an additive logistic transformation of a multivariate Fay–Herriot (MFH) model with no restrictions on the covariance matrix of the vector of random effects. The second and third models are defined similarly by using centred and isometric logratio transformations, respectively. The new models give higher flexibility than the multinomial model for dealing with the covariance structure of the categories. The MFH model was suggested by Fay (1987) and studied by Datta et al. (1991, 1996), Ghosh et al. (1996), González-Manteiga et al. (2008a), Benavent and Morales (2016) and Arima et al. (2017).
We propose a trivariate Fay–Herriot (TFH) model for analyzing the SLFS data, where the vector of random effects (model errors) has an unstructured covariance matrix with unknown components and the vector of sampling errors has a known covariance matrix. As far as we know, this model is studied and applied for the first time to SAE problems. We do not implement a further parametric modelling of the last covariance matrix as Berg and Fuller (2012) do. The estimates of the TFH model parameters are obtained by using the residual maximum likelihood (REML) estimation method. The fitted model is then used to estimate the proportions of under 16 years, employed, unemployed and inactive people in Galician counties.
The estimation of the mean squared error (MSE) of a model-based predictor is an important issue that has no easy solution. Under nonlinear models, the problem is even more difficult. In this paper, we follow the resampling approach appearing in González-Manteiga et al. (2007, 2008a, 2008b) to introduce a parametric bootstrap procedure. Further research would be needed to approximate the MSEs of predictors as it is done by Slud and Maiti (2006) in transformed univariate Fay–Herriot models.
This paper introduces statistical methodology that is new in three main aspects: (1) the employment of three transformations of area-level compositional survey data, (2) the use of TFH models (as a particular case of the general multivariate case) with unstructured covariance matrix for modelling the transformed data and capturing the sample correlations and (3) the derivation of domain-level predictors of proportions and counts based on the TFH model fitted to the transformed data.
The remainder of the paper is organized as follows. Section 2 gives an introduction to the labour force data and to the SAE problem of interest. Section 3 introduces the additive, centred and isometric logratio area-level model-based approaches for estimating domain compositional parameters. Section 4 describes the considered TFH model. Section 5 develops the proposed compositional predictors and the corresponding MSE estimation procedures. Section 6 applies the proposed methodology to data from the SLFS of the first quarter of 2017 in Galicia. Section 7 gives some conclusions.
The paper contains four appendixes in a supplementary material file. Appendix A presents four simulation experiments. The target of Simulation 1 is to check the behaviour of the REML algorithm for fitting the TFH model. Simulation 2 investigates the performance of the compositional and the multinomial predictors of the category proportions. Simulation 3 analyses the parametric bootstrap estimator of the MSEs. Simulation 4 studies the behaviour of the predictors of proportions when the target data are generated by a multinomial mixed model. Appendix B reviews the competitor predictors based on multinomial mixed models. Appendix C gives the REML Fisher scoring algorithm and derives the REML score vector and Fisher information matrix. Appendix D describes the centred and the isometric logratio transformations of compositions.
2 The problem of interest
The SLFS in Galicia is a quarterly survey following a stratified two-stage random sampling design. Primary sampling units are composed by census sections, which are geographical areas with a minimum of 500 dwellings or about 3000 people. Secondary sampling units are composed by main family dwellings and permanent accommodations. Subsampling is not carried out in secondary sampling units, and data are collected on all persons who regularly live in the same dwelling. The SLFS gets information about the labour market.
Galicia is divided into four provinces. They are Coruña, Lugo, Ourense and Pontevedra, coded by the Spanish Statistical Office as 15, 27, 32 and 36, respectively. Each province is hierarchically partitioned in comarcas (counties) and municipalities. Our domains of interest are the counties crossed by sex. As there are 51 counties in the SLFS of Galicia, we have 102 domains. Our goal is to estimate domain proportions of people in the categories of the variable “labour status” by using SLFS data from the first quarter of 2017.
The SLFS is designed to obtain precise direct estimates of labour indicators at the province level. For the considered SLFS data, the minimum domain sample size is 10, the first quartile is 43 and the median is 79. Therefore, obtaining reliable estimates for target domains is a small area estimation problem and borrowing strength from auxiliary data is recommended.
In mathematical terms, Galicia is a population \(U=\cup _{d=1}^DU_d\) partitioned in D domains \(U_d\). Each domain is partitioned in subsets \(U_{dk}\), \(k=1,\ldots ,q\), defined by the classification variable “labour force status” that classifies units into a finite number of categories. The \(q=4\) categories are \(\le 15\) years (\(k=1\)), employed (\(k=2\)), unemployed (\(k=3\)) and inactive (\(k=4\)). Let N and \(N_d\) be the sizes of U and \(U_d\), respectively. Consider the study variables taking the values \(z_{dkj}=1\) if the unit j from the domain \(U_d\) is in the category k and \(z_{dkj}=0\) otherwise. The target parameters are the domain means (proportions) and the domain totals (counts), i.e.
As \(\bar{Z}_{d1}+\cdots +\bar{Z}_{dq}=1\) and \(Z_{d1}+\cdots +Z_{dq}=N_d\), with \(N_d\) known, we are interested in estimating domain compositions with \(q=4\) categories.
For any sample \(s\subset U\) extracted from the population, \(s_d\) denotes the subsample from \(U_d\) of size \(n_d\) and \(w_{dj}\) represents the SLFS sampling weight of the unit j from the subsample \(s_d\). The sample proportions and counts are as:
Direct estimators of \(\bar{Z}_{dk}\) and \(Z_{dk}\) are as:
As the SLFS sampling weights \(w_{dj}\) are derived from the inverses of the inclusion probabilities after non-response correction and calibration at the province and at the regional level, the direct estimators (2.3) are not design-based unbiased for estimating the target parameters (2.1) at the domain level. As the SLFS domain sample sizes \(n_d\) are small, the estimators (2.3) have large design-based variances. Therefore, the application of model-based approaches is advisable.
López-Vizcaíno et al. (2013) introduced a multinomial logit mixed (MLM) model for fitting \(z_{d.}=(z_{d1.},\ldots ,z_{dq-1.})\), \(d=1,\ldots ,D\), and estimating domain proportions. A related approach is fitting a MLM model to \((\hat{Z}_{d1}^{dir},\ldots ,\hat{Z}_{dq-1}^{dir})\), \(d=1,\ldots ,D\). Appendix B describes these MLM models for a response vector \(\xi _d=(\xi _{d1},\ldots ,\xi _{dq-1})\) and the corresponding predictors of the multinomial category probabilities \(p_{dk}\). In both cases, \(\xi _{dk}=z_{dk.}\) or \(\xi _{dk}=\hat{Z}_{dk}^{dir}\), the covariances, given in (2.2) of Appendix B, under MLM models are negative. Further, under the multinomial distribution, it holds that \(\text {cov}_M(\xi _{dk_1},\xi _{dk_2})=0\) if and only if \(p_{dk_1}=0\) or \(p_{dk_2}=0\), which implies that \(\text {cov}_M(\xi _{dk_1},\xi _{dk})=0\) \(\forall k\ne k_1\) or \(\text {cov}_M(\xi _{dk_2},\xi _{dk})=0\) \(\forall k\ne k_2\) . Therefore, the multinomial correlation structure is rather rigid. More concretely, if the number of categories is \(q=4\), then the six variance components (three variances and three covariances) depend only on three category parameters through the formulas (2.2) of Appendix B. In practice, the multinomial covariance structure does not necessarily fit to the true covariances \(\text {cov}(\xi _{dk_1.},\xi _{dk_2.})\), \(k_1\ne k_2\), \(k_1,k_2=1,\ldots ,q\), of sample counts or direct estimators of totals.
For the categories \(k_1, k_2=1,2,3,4\), Table 1 presents the correlations of the set of values \(\{(\hat{\bar{Z}}_{dk_1}^{dir}, \hat{\bar{Z}}_{dk_2}^{dir}): d=1,\ldots ,D\}\) (left) and \(\{(\bar{z}_{dk_1.}, \bar{z}_{dk_2.}): d=1,\ldots ,D\}\) (right). These correlations are calculated from the direct estimates (2.3) and the simple estimates (2.2) of the category proportions along the domains. As they are calculated with aggregated data at the domain level, we call them domain-level empirical correlations between categories or, in short, domain-level correlations. Table 1 shows that most, but not all, correlations are negative. Nevertheless, we find the positive correlations 0.21 (right) or 0.04 (right) and 0.07 (left) that are close to zero.
The design-based within-domain covariance \(\text {cov}_\pi (\hat{\bar{Z}}_{dk_1}^{dir}, \hat{\bar{Z}}_{dk_2}^{dir})\), \(k_1,k_2=1,\ldots ,q-1\), can be estimated by
where the case \(k_1=k_2=k\) denotes estimated variance, i.e. \(\hat{{\text {var}}}_\pi (\hat{\bar{Z}}_{dk}^{dir})=\hat{{\text {cov}}}_\pi (\hat{\bar{Z}}_{dk}^{dir},\hat{\bar{Z}}_{dk}^{dir})\). The last formulas are obtained from Särndal et al. (1992), pp. 43, 185 and 391, with the simplifications \(w_{dj}=1/\pi _{dj}\), \(\pi _{dj,dj}=\pi _{dj}\) and \(\pi _{di,dj}=\pi _{di} \pi _{dj}\), \(i\ne j\) in the second-order inclusion probabilities. By applying formula (2.4), Fig. 1 (left) plots the estimated design-based covariances \(s_{k_1k_2}=\hat{\text {cov}}_\pi (\hat{\bar{Z}}_{dk_1}^{dir}, \hat{\bar{Z}}_{dk_2}^{dir})\), \(k_1, k_2=1,2,3,4\), \(k_1\ne k_2\), for the direct estimators of all the category proportions. As these covariances are calculated from unit-level data, they are called unit-level covariances. Figure 1 shows that \(\hat{\text {cov}}_\pi (\hat{\bar{Z}}_{d1}^{dir}, \hat{\bar{Z}}_{d3}^{dir})\approx 0\), \(d=1,\ldots ,D\). Under the multinomial mixed model, this fact implies (as explained above) that the domain proportions of people in the categories “under 16 years” and “unemployed” should be close to zero, which contradicts the observed sampling proportions. Figure 1 (right) plots the corresponding unit-level correlations \(r_{k_1k_2}\). In the application to SLFS data, these unit-level covariances are used to set the error covariance matrix of the fitted TFH model.
The exploratory data analysis shows that the covariance structure of the MLM models M1 and M2, described in Appendix B, cannot take into account simultaneously both types of covariances and variances (unit level and domain level). This is to say, the multinomial mixed model does not fit well to the domain-level correlations appearing in Table 1 or to the within-domain covariances shown in Fig. 1. Further, the definition of the model itself does not allow the introduction of both types of covariances and variances as MFH models do. This is why we propose transforming the direct estimators of domain proportions and fitting the transformed data to a more flexible compositional mixed model.
3 Transformations of compositions
This section considers three transformation of q-compositions onto \(R^{q-1}\). In what follows, we use the simpler notation \(z_{dk}\triangleq \hat{\bar{Z}}_{dk}^{dir}\), \(k=1,\ldots ,q\), \({z}_d=(z_{d1},\ldots ,z_{dq-1})^\prime \) and
We assume that \(z_{dk}>0\), \(d=1,\ldots ,D\), \(k=1,\ldots ,q\), and we note that \(z_{d1}+\ldots +z_{dq}=1\). For \(d=1,\ldots ,D\), let \({y}_d=(y_{d1},\ldots ,y_{dq-1})^\prime \in R^{q-1}\) be the additive logratio transformation (alr) of \({z}_d\), i.e. \({y}_d={h}({z}_d)=(h_1({z}_d),\ldots ,h_{q-1}({z}_d))^\prime \) with
and with inverse the additive logistic (alogist) transformation
For \(i,j=1,\ldots ,q-1\), the first partial derivatives of the alogist transformation are as:
This to say, under the alogist transformation \(z_i\) is an increasing function of \(y_i\) and a decreasing transformation of \(y_j\), \(i,j =1,\ldots ,q-1\), \(j\ne i\). Alternatively, we may consider the centred or the isometric logratio (clr or ilr) transformations described in Appendix D. For ease of exposition, this paper deals mainly with the alr transformation. The mathematical developments for the clr or ilr transformations can be done similarly.
In applications to real data, we can have domain compositions \((z_{d1},\ldots ,z_{dq})\) with some zero components \(z_{dk}=0\). Since the logarithm of zero is \(-\infty \), we cannot apply alr, clr and ilr logratio transformations for analyzing compositional data. In our application to real data, we have no zeros. However, in other domain-level data we might find a low number of zeros. This can occur if a domain sample size is very small and none of the sampled units belong to a given category k. A practical solution for this problem is replacing zeros by a small numerical value \(\varepsilon >0\) and making a rounding-off adjustment process. For example, if \((z_{d1},\ldots ,z_{dq})\) has m zeros, we can apply the recommendation appearing in Section 11.5 of Aitchison (1986). This is to say, we can substitute the zeros by \(\varepsilon =(m+1)(q-m)\delta q^{-2}\) and we can subtract \(m(m+1)\delta q^{-2}\) to each positive component, where \(\delta \) is the maximum rounding-off error of the positive \(z_{dk}\)’s. We can take \(\big (\widehat{\text {var}}_\pi (z_{dk})\big )^{1/2}\) as rounding-off error of \(z_{dk}\). In any case, applied statisticians should do a sensitivity analysis of the results to the particular method employed to deal with zeros and a model diagnostic study.
The presence of structural zeros or a non-negligible amount of sample zeros is a severe issue when using alr, clr and ilr logratio transformations. We are not in favour of using the three introduced transformations in those cases. Other transformations and models for dealing with compositional data could be alternatively applied. For example, the directional mixed effects models applied by Scealy and Welsh (2017) overcome this problem.
The first derivatives of the alr transformation \(h_k\) are as:
Let \({1}_{a}\) and \({0}_a\) be the \(a\times 1\) vectors with all the components equal to one and to zero, respectively. In matrix form, we have \({H}({z}_d)=\big (H_{ij}({z}_d)\big )_{i,j=1,\ldots ,q-1}= \mathop {\hbox {diag}}\nolimits _{1\le k \le q-1}(z_{dk}^{-1})+z_{dq}^{-1}{1}_{q-1}{1}_{q-1}^\prime \).
A Taylor series expansion of \({h}({z}_d)\) around a given \({z}_0\) yields to
If we take \({z}_0=q^{-1}{1}_{q-1}\), then \(h({z}_0)={0}_{q-1}\), \(H_0=H({z}_0)=q\big ({I}_{q-1}+{1}_{q-1}{1}_{q-1}^\prime \big )\), where \({I}_{a}\) is the \(a\times a\) identity matrix. Alternatively, we can take \(z_0=\frac{1}{D}\sum _{d=1}^Dz_d\) or we can select \(z_0\) depending on d and close to \(z_d\) for a better Taylor expansion approximation. For the clr and ilr transformations, Appendix D shows that \({h}(z_0)={0}_{q-1}\) and gives \(H(z_0)\). From (3.3), we get the approximated covariance matrix:
A general area-level model for estimating \(\bar{Z}_{dk}\), \(d=1,\ldots ,D\), \(k=1,\ldots ,q\), is \({y}_d\overset{ind}{\sim }{N}_{q-1}(\mu _d,V_d)\), where \(\mu _d\) is a mean vector depending on unknown regression parameters and auxiliary variables and \(V_d\) is a covariance depending of some unknown parameters. The next section gives a flexible multivariate area-level linear mixed model for \({y}_d\), \(d=1,\ldots ,D\), which allows positive and negative covariances. Depending on the employed transformation, the resulting models for \(z_d\), \(d=1,\ldots ,D\), are called alr, clr and ilr compositional mixed models. These models arise as alternative to the MLM models, for \(z_{d.}\) or \(z_{d}\), described in Appendix B. For ease of exposition, we present the case \(q=4\) appearing in the application to real data.
4 Trivariate Fay–Herriot models
Let \(z_{d}=(z_{d1},z_{d2},z_{d3})^{\prime }\) be the vector of direct estimators (2.3) of proportions \(\bar{Z}_d=(\bar{Z}_{d1},\bar{Z}_{d2},\bar{Z}_{d3})^{\prime }\) of some classification variable with \(q=4\) categories. Let \(\widehat{\text {var}}_\pi ({z}_d)\) be the matrix of design-based covariance estimators (2.4), which can contain positive and negative covariances. Let \({y}_{d}=(y_{d1},y_{d2},y_{d3})^{\prime }\) be the alr transformation of \(z_d\). Let \(\mu _{d}=E_\pi (y_d)=(\mu _{d1},\mu _{d2},\mu _{d3})^{\prime }\) be the vector of design-based expectations of \(y_d\). The TFH model is defined in two stages. The sampling model is
where the vectors \({e}_{d}\overset{ind}{\sim } N_3\left( 0,{V}_{ed}\right) \) are independent and the \(3\times 3\) covariance matrices \({V}_{ed}=\big (\sigma _{dij}\big )_{i,j=1,2,3}\) are known. In practice, we take \({V}_{ed}=H_0\widehat{\text {var}}_\pi ({z}_d)H_0^\prime \), where \(\widehat{\text {var}}_\pi ({z}_d)\) is the covariance matrix given in (3.1) and \(H_0\) is defined in (3.4). Alternatively, \(y_d\) can be defined as the clr or ilr transformation of \(z_d\). In that case, the matrix \(H_0\) is taken from Appendix D.
Moreover, it is assumed that the \(\mu _{dk}\)’s are linearly related to \(r_k\) explanatory variables associated with the k-th category in the domain d. For \(k=1,2,3\), let \({x}_{dk}=(x_{dk1},\ldots ,x_{dkr_k})\) be a row vector containing the \(r_k\) explanatory variables for \(\mu _{dk}\) and let \({X}_{d}=\text {diag}\left( {x}_{d1},{x}_{d2},{x}_{d3}\right) _{3\times r}\) with \(r=r_1+r_2+r_3\). Let \(\beta _{k}\) be a column vector of size \(r_k\) containing the regression parameters for \(\mu _{dk}\) and let \(\beta =\left( \beta _{1}^{\prime },\beta _{2}^{\prime },\beta _{3}^{\prime }\right) ^{\prime }_{r\times 1}\). This section introduces a TFH model by assuming (4.1) and the linking model:
where the vectors \({u}_{d}\)’s are independent and independent of the vectors \({e}_{d}\)’s. Unlike the MFH models studied by Benavent and Morales (2016), the \(3\times 3\) covariance matrices \({V}_{ud}\) are unstructured and depend on six unknown parameters, \(\theta _{1}=\sigma _{u1}^2\), \(\theta _{2}=\sigma _{u2}^2\), \(\theta _{3}=\sigma _{u3}^2\), \(\theta _{4}=\rho _{12}\), \(\theta _{5}=\rho _{13}\) and \(\theta _{6}=\rho _{23}\), i.e.
The matrix \(V_{ud}\) explains the covariance structure of the alr transformations of the direct estimators \(y_d\) that is not taken into account by the sampling errors \(e_d\) or by the auxiliary variables \(X_d\). Let \({I}_n\) be the \(n\times n\) identity matrix and \(\delta _{\ell d}\) be the Kronecker delta, and define
where col and \(\hbox {col}^{\prime }\) are matrix operators stacking by columns and rows, respectively.
In matrix form, the TFH model (4.1)+(4.2) is
where \({e}, {u}_{1},\ldots ,{u}_D\) are independent with distributions
Under model (4.3), it holds that
where \({V}_{d}={V}_{ud}+{V}_{ed}\), \(d=1,\ldots ,D\). Further, the best linear unbiased estimator (BLUE) of \(\beta \) and the best linear unbiased predictors (BLUP) of u and \(\mu \) are as:
The residual maximum likelihood (REML) method maximizes the joint probability density function of a vector of \(3D-r\) independent contrasts \(\omega ={W}^\prime {y}\), where W is a \(3D\times (3D-r)\) matrix with linearly independent columns and such that \({W}^\prime {W}={I}_{3D-r}\) and \({W}^\prime {X}=0\). It holds that \(\omega \) is independent of the BLUE \(\hat{\beta }_B\) given in (4.4). The joint probability density function of \(\omega \) is the REML likelihood. The REML log-likelihood of model (4.3) is
where \(\theta =(\theta _1,\ldots ,\theta _6)\), \({P}={V}^{-1}-{V}^{-1}{X}({X}^{\prime }{V}^{-1}{X})^{-1}{X}^{\prime }{V}^{-1}\), \({P}{V}{P}={P}\) and \({P}{X}=0\). Appendix C gives the calculation of the score vector \(S(\theta )=(S_1,\ldots ,S_6)^\prime \) and the Fisher information matrix \(F(\theta )=\big (F_{a,b}\big )_{a,b=1,\ldots ,6}\), where
Appendix C also gives the REML Fisher scoring algorithm for fitting the TFH model (4.3). To initiate this algorithm, a possible set of starting values is \(\hat{\theta }_{4,0}=\hat{\theta }_{5,0}=\hat{\theta }_{6,0}=0\), \(\hat{\theta }_{k,0}=\hat{\sigma }_{uk,0}^2\), \(k=1,2,3\), where \(\hat{\sigma }_{uk,0}^2\) is the REML or the ML or the Prasad and Rao (1990) moment-based estimator of \(\sigma _{uk}^2\) in the k-th marginal Fay–Herriot model. They can be calculated with the R library sae. Another possibility is to take \(V_{ud}^{(0)}\) as the domain-level variance matrix of the alr transformations of the direct estimators of the category proportions. This is the approach described and implemented around Table 2 in the application to real data.
The output of REML Fisher scoring algorithm, \(\hat{\theta }\), is the REML estimator of \(\theta \). By plugging \(\hat{\theta }\) in \({V}_u\), we get \(\hat{V}_u={V}_u(\hat{\theta })\) and \(\hat{V}=\hat{V}_u+{V}_e\). By substituting \(\hat{V}_u\) in (4.4), we obtain the EBLUP of \(\mu ={X}\beta +{Z}{u}\), i.e.
with components
The asymptotic distributions of the REML estimators \(\hat{\theta }\) and \(\hat{\beta }\),
can be used to construct \((1-\alpha )\)-level asymptotic confidence intervals for the components \(\theta _{\ell }\) of \(\theta \) and \(\beta _i\) of \(\beta \), i.e.
where \({F}^{-1}(\hat{\theta })=(\nu _{ab})_{a,b=1,\ldots ,6}\), \(({X}^{\prime }{V}^{-1}(\hat{\theta }){X})^{-1}=(q_{ij})_{i,j=1,\ldots ,r}\) and \(z_{\alpha }\) is the \(\alpha \)-quantile of the N(0, 1) distribution. For \(\hat{\beta }_i=\beta _0\), the asymptotic p value for testing the hypothesis \(H_0:\,\beta _i=0\) is
We remark that we have changed the notation in (4.7) and (4.8), where \(\beta _i\) denotes the i-th component of the vector \(\beta \) and not the vector of regression parameters of the i-th category.
5 Compositional predictors of proportions and counts
This section denotes the expectations under the distributions of the sampling design, the Fay–Herriot model and the compositional mixed model by \(E_{\pi }\), \(E_\mathrm{FH}\) and \(E_\mathrm{C}\), respectively. Statistical offices are interested in estimating population parameters, like the domain mean \(\bar{Z}_{dk}\) defined in (2.1). However, the domain-level approach to SAE gives predictors of functions of fixed and random model effects (in short, functions of model effects—FME). For example, a Fay–Herriot (FH) model for predicting \(\bar{Z}_{dk}\),
with the standard assumptions on \(u_{\mathrm{FH},dk}\)’s and \(e_{\mathrm{FH},dk}\)’s, has \(\mu _{\mathrm{FH},dk}=E_\mathrm{FH}[z_{dk}|u_{\mathrm{FH},dk}]=x_{dk}\beta +u_{\mathrm{FH},dk}\) as the FME of interest. To connect \(\mu _{\mathrm{FH},dk}\) with \(\bar{Z}_{dk}\), it is assumed that: (1) the design-based expectation of \(z_{dk}\) is \(\bar{Z}_{dk}\), i.e. \(E_\pi [z_{dk}]=\bar{Z}_{dk}\), and (2) the design-based expectation is the realization of the model conditional expectation; in short, \(E_\mathrm{FH}[z_{dk}|u_{\mathrm{FH},dk}]=E_\pi [z_{dk}]\). Note that \(E_\mathrm{FH}[z_{dk}|u_{\mathrm{FH},dk}]\) is a function of \(u_{\mathrm{FH},dk}\). Similar assumptions are done for the MLM model described in Appendix B, i.e. (1) \(E_\pi [\bar{z}_{dk.}]=\bar{Z}_{dk}\), (2) \(E_{M}[\bar{z}_{dk.}|u_{M,dk}]=E_\pi [\bar{z}_{dk.}]\).
In practice, assumption (1) rarely holds. The direct estimator \(z_{dk}\) is not calculated with the inverse of the inclusion probabilities, but with sampling weights (expansion factors) that are not calibrated to domain totals. Therefore, \(z_{dk}\) is, in general, biased with respect to the sampling design distribution. Similarly, \(\bar{z}_{dk.}\) is also biased for estimating \(\bar{Z}_{dk}\), as it is calculated with weights equal to one. Therefore, predictors based on both models, FH and MLM, have problems to fulfil assumption (1) when dealing with real data.
Assumption (2) might be accepted if the area-level model has a “good” fit to data, which may happen if the set of auxiliary variables is highly correlated with the dependent variable. Further, by analogy to the GREG estimator, the auxiliary variables produce a calibration effect to their domain totals and a reduction of the design-based bias. In many cases, the assumptions (1) and (2) “approximately” hold and the empirical best predictor (EBP) will have some small bias, as the direct estimator has, but lower variance. So it is worthwhile to calculate EBPs based on area-level models, as they will tend to have lower design-based MSEs than direct estimators.
This paper introduces a compositional model for \(z_d\) that is introduced by assuming a TFH model on the alr transformed vector \(y_d\). In terms of \(y_d\), the compositional model does not fulfil assumption (1), because the direct estimator \(y_d\) is not design-based unbiased for the alr transformation of \(\bar{Z}_{dk}\), i.e. \(E_\pi [y_{dk}]\ne \log (\bar{Z}_{dk}/\bar{Z}_{d4})\), \(k=1,2,3\). For fulfilling the assumption (2), the FMEs to be predicted under the TFM model should be
and \(E_C[z_{d4}|u_d]=1-E_C[z_{d1}|u_d]-E_C[z_{d2}|u_d]-E_C[z_{d3}|u_d]\), \(d=1,\ldots ,D\), which are nonlinear functions of \(u_d\) based on integrals that cannot be solved analytically. Further, the EBPs of \(E_C[z_{dk}|u_d]\) are non-analytically tractable integrals of \(E_C[z_{dk}|u_d]\) with respect to the density of \(u_d\) conditioned to \(y_d\). This is why we propose predicting the alogist transformations of \(\mu _{Cdk}=E_C[y_{dk}|u_d]\) under the TFH model, i.e.
For the clr and ilr transformations, the alternative vectors are \(p_{Cd}^{clr}=\text {clr}^{-1}(\mu _{Cd})\) and \(p_{Cd}^{ilr}=\text {ilr}^{-1}(\mu _{Cd})\), respectively, where \(\mu _{Cd}=(\mu _{Cd1},\mu _{Cd2},\mu _{Cd3})\).
By predicting \({p}_{Cdk}\) instead of \(E_C[z_{dk}|u_d]\), we gain computational efficiency, but we have problems with assumption (2), as \(\bar{Z}_{dk}\) might not be considered as the realization of \({p}_{Cdk}\); in short, \({p}_{Cdk}\ne E_\pi [\bar{z}_{dk.}]\approx \bar{Z}_{dk}\). However, the disadvantage of not fulfilling the assumptions (1) and (2) can be compensated, as in practice happens with the FH and MLM models, by the use of auxiliary variables correlated with the objective variable and with the modelling of the covariance structure of the categories. So that what is lost on the one hand is recovered on the other.
In this section, two predictors of \({p}_{Cdk}\) are proposed. The compositional plug-in predictors, \(\hat{{p}}_{Cd}=(\hat{{p}}_{Cd1},\hat{{p}}_{Cd2},\hat{{p}}_{Cd3})^{\prime }\) and \(\hat{{p}}_{Cd4}\), of the proportions \({p}_{Cd}=({p}_{Cd1},{p}_{Cd2},{p}_{Cd3})^{\prime }\) and \({p}_{Cd4}\) are jointly obtained by applying the alogist transformation to \(\hat{\mu }_{Cd}=(\hat{\mu }_{Cd1},\hat{\mu }_{Cd2},\hat{\mu }_{Cd3})^{\prime }\), i.e. \(\hat{{p}}_{Cd}=\text {alogist}(\hat{\mu }_{Cd})\) or equivalently
Similarly, we may consider the plug-in predictors \(\hat{{p}}_{Cd}^{clr}=\text {clr}^{-1}(\hat{\mu }_{Cd})\) or \(\hat{{p}}_{Cd}^{ilr}=\text {ilr}^{-1}(\hat{\mu }_{Cd})\). The compositional plug-in predictors of the domain proportions \(\bar{Z}_{dk}\) are \(\hat{\bar{Z}}_{Cdk}=\hat{{p}}_{Cdk}\), and the compositional plug-in predictors of the counts \(Z_{dk}=N_{d}\bar{Z}_{dk}\) are \(\hat{Z}_{Cdk}=N_{d}\hat{\bar{Z}}_{Cdk}\), \(k=1,2,3,4\).
On the other hand, the compositional best predictors of the proportions \({p}_{Cdk}\) are \(\hat{{p}}_{Bdk}=\hat{{p}}_{Bdk}(\beta ,\theta )=E_{\beta ,\theta }[{p}_{Cdk}|\,y_d]\), \(k=1,2,3\), and \(\hat{{p}}_{Bd4}=1-\hat{{p}}_{Bd1}-\hat{{p}}_{Bd2}-\hat{{p}}_{Bd3}\). It holds that
where \({\mu }_{Cdk}=x_{dk}\beta _k+u_{dk}\), \(y_d|u_d\sim N_3(X_d\beta +u_d, V_{ed})\), \(u_d\sim N_3(0, V_{ud}(\theta ))\) and
The compositional EBP of \({p}_{Cdk}\) is \(\hat{{p}}_{Edk}=\hat{{p}}_{Bdk}(\hat{\beta },\hat{\theta })\), \(k=1,2,3,4\), and can be approximated by the following Monte Carlo algorithm:
-
1.
Calculate the TFH model parameters \(\hat{\beta }\) and \(\hat{\theta }\).
-
2.
For \(\ell =1,\ldots ,L\), \(d=1,\ldots ,D\), generate \(u_d^{(\ell )}\) i.i.d. \(N_3(0,V_{ud}(\hat{\theta }))\) and do \(u_d^{(L+\ell )}=-u_d^{(\ell )}\).
-
3.
Calculate \(\hat{{p}}_{Edk}=\hat{{p}}_{Bdk}(\hat{\beta },\hat{\theta })=\hat{A}_{dk}/\hat{B}_d\), where
$$\begin{aligned} \hat{A}_{dk}= & {} \frac{1}{2L}\sum _{\ell =1}^{2L}\frac{\exp \{\hat{\mu }_{Cdk}^{(\ell )}\}\exp \left\{ -\frac{1}{2} (y_d-X_d\hat{\beta }-u_d^{(\ell )})^\prime V_{ed}^{-1}(y_d-X_d\hat{\beta }-u_d^{(\ell )})\right\} }{1+\exp \{\hat{\mu }_{Cd1}^{(\ell )}\}+\exp \{\hat{\mu }_{Cd2}^{(\ell )}\}+\exp \{\hat{\mu }_{Cd3}^{(\ell )}\}}, \\ \hat{B}_d= & {} \frac{1}{2L}\sum _{\ell =1}^{2L}\exp \left\{ -\frac{1}{2} (y_d-X_d\hat{\beta }-u_d^{(\ell )})^\prime V_{ed}^{-1}(y_d-X_d\hat{\beta }-u_d^{(\ell )})\right\} , \end{aligned}$$where \(\hat{\mu }_{Cdk}^{(\ell )}=x_{dk}\hat{\beta }_k+u_{dk}^{(\ell )}\), \(d=1,\ldots ,D\), \(k=1,2,3\), \(\ell =1,\ldots ,2L\).
-
4.
Calculate \(\hat{{p}}_{Ed4}=1-\hat{{p}}_{Ed1}-\hat{{p}}_{Ed2}-\hat{{p}}_{Ed3}\), \(d=1,\ldots ,D\).
The compositional EBPs of the domain proportions \(\bar{Z}_{dk}\) are \(\hat{\bar{Z}}_{Edk}=\hat{{p}}_{Edk}\), \(k=1,2,3,4\). The compositional EBPs of the counts \(Z_{dk}=N_{dk}\bar{Z}_{dk}\) are \(\hat{Z}_{Edk}=N_{dk}\hat{\bar{Z}}_{Edk}\), \(k=1,2,3,4\).
For the clr and ilr transformations, the EBP of \(p_{Cdk}\) is obtained by substituting the k-th component of the alogist transformation:
by the corresponding k-th component of \(\text {clr}^{-1}\) and \(\text {ilr}^{-1}\) transformations, respectively.
The estimation of compositions, like domain proportions of categories of a classification variable, requires the selection of the last (q-th) category. The last category is not a control or reference category as it happens in some ANOVA-type statistical analyses. The introduced methodology is not invariant with respect to the selection of the category q, but provides together the predictors of the proportions of the q categories. In practice, the selection of the first \(q-1\) categories should be based on the available explanatory variables. A good approach is to select as target categories (\(k=1,\ldots ,q-1\)) those ones that can be better explained by the auxiliary variables.
For every domain d, the predictors based on multinomial or compositional models fulfil the two conditions: (1) \(0\le p_{dk}\le 1\), \(k=1,\ldots ,q\), and (2) \(\sum _{k=1}^q p_{dk}=1\). Estimating \(p_{dk}\) with predictors based on univariate area-level mixed models, like Fay–Herriot or binomial logit, is not a good option because the conditions (1) and (2) might not be fulfilled.
Concerning the estimation of the MSEs of the compositional plug-in predictors or EBPs, we follow the parametric bootstrap approach of González-Manteiga et al. (2008a). The steps of the bootstrap resampling algorithm are as follows:
-
1.
Fit the TFH model (4.3) to the data \((y_d,X_d)\), \(d=1,\ldots ,D\), and calculate \(\hat{\beta }\) and \(\hat{\theta }\).
-
2.
Generate \(u_d^{*(b)}\sim N_3\big (0,{V}_{ud}(\hat{\theta })\big )\), \(e_d^{*(b)}\sim N_3(0,V_{ed})\), \(\mu _d^{*(b)}=X_{d}\hat{\beta }+u_{d}^{*(b)}\), \(y_{d}^{*(b)}=\mu _d^{*(b)}+e_{d}^{*(b)}\), \(p_{d}^{*(b)}=\text {alogist}(\mu _d^{*(b)})\), \(d=1,\ldots ,D\).
-
3.
Calculate \(\hat{p}_{d}^{*(b)}\in \{\hat{p}_{Cd}^{*(b)},\hat{p}_{Ed}^{*(b)}\}\) based on the data \((y_{d}^{*(b)},X_d)\), \(d=1,\ldots ,D\).
-
4.
Repeat B times, \(b=1,\ldots ,B\), the steps 2–3 and calculate the bootstrap MSE estimator
$$\begin{aligned} mse_{dk}^{*}=\frac{1}{B}\sum _{b=1}^B\big (\hat{p}^{*(b)}_{dk}-p^{*(b)}_{dk}\big )^2,\,\,\, d=1,\ldots ,D,\,\,k=1,2,3. \end{aligned}$$
6 Application to Labour Force Survey data
This section gives an application of the alr compositional mixed model to the SLFS data described in Sect. 2. The TFH model is fitted to the target data and to a set of significant auxiliary aggregated variables taken from the administrative registers: PMH containing the official demographic data at municipal level, SSoc containing data from the Social Security System and SPEG containing data of employment claimants.
The considered domain-level auxiliary variables are as:
-
SS: proportion of population registered in SSoc.
-
REG: proportion of population registered as unemployed in SPEG.
-
to15, 16to24, 25to54, 55to: proportion of population aged \(\le \,15\), 16–24, 25–54 and \(\ge \,55\) registered in PMH.
The target parameters are the proportions of the four categories of the variable labour status, i.e. \(\le 15\) years, employed, unemployed and inactive people per sex in counties of Galicia. We are interested in estimating domain compositions with \(q=4\) categories. As the explanatory variables, to15, SS and REG, are highly correlated with \(\le 15\) years, employed and unemployed, respectively, for fitting compositional or multinomial mixed models to the SLFS data, we number the labour status categories from 1 to 4, so that inactive is the fourth one (q-th category).
We denote the alr transformations of the direct estimators of the category proportions by \(y_{dk}=\log (z_{dk}/z_{dq})\), \(k=1,2,3\). For the sake of brevity, we do not present the data analyses with the clr or ilr transformations. Keeping these assumptions in mind, below we present the results of the application to SLFS data.
Table 2 presents the domain-level correlations calculated for the sets \(\{(y_{dk_1}, y_{dk_2}): d=1,\ldots ,D\}\), \(k_1,k_2=1,2\). Because of the alr transformation, the domain-level correlation patterns of the y-variables are different from the corresponding ones of the z-variables given in Table 1. The correlations in Table 2 are used as seeds for the matrices \(V_{ud}\) in the Fisher scoring algorithm that calculates the REML estimators of the selected TFH model.
Table 3 presents domain-level correlations for the response variables \(y_{dk}\) of the TFH model and the auxiliary variables \(x_{dki}\). For the k-th category and the i-th auxiliary variable, the correlations are calculated for the set of values \(\{(y_{dk}, x_{dki}): d=1,\ldots ,D\}\). Reading this table by rows, it is observed that to15 is the most positively correlated variable for \(y_1\) and 25to54 and SS are the most positively correlated variables for \(y_2\). Concerning \(y_3\), the first five auxiliary variables have a similar positive correlation. As expected, 55to is negatively correlated with \(y_1\), \(y_2\) and \(y_3\).
A set of appropriate auxiliary variables is selected, and the corresponding TFH model is fitted to the data \((y_{dk}, x_{dki})\), \(d=1,\ldots ,D\), \(k=1,2,3\), \(i=1,\ldots ,r_k\). For the alr transformation, Table 4 presents the estimates of the regression parameters for the TFH model and their estimated standard deviations. It also presents the p-values, defined in (4.8), for testing the hypothesis \(H_0: \beta _{ki}=0\), \(k=1,2,3\), \(i=1,\ldots ,r_i\). Intercept parameters for \(y_1,y_2,y_3\) are denoted by \(c_1,c_2,c_3\), respectively. Appendix D presents the corresponding tables for the transformations clr and ilr. Based on those tables and on further model diagnostics, we select the alr transformation.
As all the auxiliary variables are proportions, the sign and the magnitude of the regression parameters give interesting interpretations. The alr transformation of the direct estimator of the SLFS proportion of people under 16 years, \(y_{d1}\), is solely explained with positive sign by the corresponding PMH proportion to15. For the proportion of employed people, \(y_{d2}\) tends to be greater in those domains with larger proportion of people registered in SSoc and greater proportion of working age people. The proportions of people SS and 25to54 are more relevant than 16to24 for predicting \(y_{d2}\). For the proportion of unemployed people, \(y_{d3}\) tends to be greater in those domains with larger proportion of people registered as unemployed in SPEG and greater proportion of working age people. As expected, REG is more important for predicting \(y_{d3}\) than 16to24 and 25to54. We have further fitted a second TFH model with 55to in the place of 16to24 and 25to54. The second model gives similar predictions because the auxiliary variables to15, 16to24, 25to54 and 55to sum up to one, and therefore, 55to and {16to24, 25to54} give basically the same information for predicting \(y_{d2}\) and \(y_{d3}\).
Table 5 gives the 95% confidence intervals (CIs) of the variance components, defined in (4.7), for \(\theta _1,\ldots ,\theta _6\). We observe that the variances \(\sigma _{u1}^2\), \(\sigma _{u2}^2\), \(\sigma _{u3}^2\) and the correlation \(\rho _{12}\) are significantly greater than zero.
Figure 2 plots the dispersion graphs of the target variables \(y_{d1}\) (left), \(y_{d2}\) (centre) and \(y_{d3}\) versus their auxiliary variables with larger regression parameter, i.e. to15, SS and REG, respectively. Accordingly with Table 3, we observe the linear patterns related to positive high linear correlations.
Figures 3 and 4 plot the marginal residuals and standardized marginal residuals of the fitted TFH model. The residuals are rather symmetric around zero and do not present any relevant pattern. Further, there are few standardized residuals (7 among 306) outside the interval (\(-3, 3\)).
Figure 5 plots the compositional versus the direct estimates of the proportions of people under 16 years (left), employed (centre) and unemployed (right). We observe that model-based estimators take values rather symmetrically around the direct estimates. As the direct estimators of proportions are basically design-based unbiased, Fig. 5 suggests that compositional estimators partially share this property.
In addition to the compositional plug-in predictors based on the selected compositional mixed model, we also calculate the direct estimators and the multinomial predictors. Taking into account the recommendations of López-Vizcaíno et al. (2013) and the last comment of Appendix B, the MLM model is fitted to the vectors of sample counts \(z_{d.}=(z_{d1.},z_{d2.},z_{d3.})\) with sample sizes \(n_d\), \(d=1,\ldots ,D\). For the sake of comparability, we use the same auxiliary variables as the fitted compositional model. This is to say, the auxiliary variables are listed in Table 4. Figure 6 plots the direct, multinomial and compositional plug-in estimated proportions of people under 16 years (left), employed (centre) and unemployed (right) for domains sorted by sample size. For the three categories, the compositional plug-in predictors present the smoothest behaviour across domains.
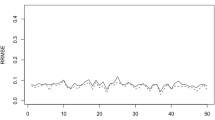
Figure 7 plots the design-based estimates of the root mean squared errors (RMSE) of the direct estimators (D) and the parametric bootstrap estimates of the RMSEs of the multinomial and the compositional plug-in predictors. For the sake of comparability, the RMSEs of the multinomial (MC) and the compositional (CC) predictors are calculated under the assumption that the distribution of the fitted TFH Fay–Herriot model is the true one. Therefore, we run the bootstrap procedure by generating data from the fitted TFH model. The RMSEs of the corresponding direct estimates are estimated by applying formula (2.4). Nevertheless, we know that in real life there are no true models, but useful models. Therefore, we also calculate parametric bootstrap estimates of the RMSEs of the multinomial predictors assuming that the multinomial model is valid. The new estimated RMSEs (MM) can be interpreted as a measure of the goodness of fit of the multinomial model to the data. Figure 7 shows that the compositional plug-in predictors have the best results in terms of RMSE.
Figures 8 and 9 map the compositional plug-in estimated county proportions of men (left) and women (right) under 16 years old and inactive, respectively. The colours are darker in areas with higher proportions. We observe that the counties with the youngest people are in the west coast, in the provinces of Coruña and Pontevedra where it is the Atlantic motorway (from Vigo to Coruña). On the contrary, it can be observed that the counties that are in the east of Galicia (in the provinces of Lugo and Ourense), in general terms, have a lot of inactive population, more than the 50% of their population. The Costa da Morte counties (in the west) are also in this situation.
Figures 10 and 11 plot the compositional plug-in estimated county proportions of men (left) and women (right) that are employed and unemployed, respectively. Concerning employment, we observe that the touristic counties around the Santiago trail have the largest proportions. On the contrary, the industrial areas around Vigo (south-west) and the agricultural areas of Ourense (south-east) present the largest proportions of unemployed people.
Figure 9 shows that the quantiles of the distribution of the proportion of inactive women are displaced to the right with respect to that of men. Therefore, the proportions of inactive women tend to be greater than those of men in the regions of Galicia. Figures 10 and 11 give the opposite conclusion for employed and unemployed people, respectively.
Tables 6, 7 and 8 present some condensed numerical results for men and women, respectively. The tables have been constructed in two steps. The domains are sorted by province. Within each province, the domains are sorted by sample size, starting by the domain with the smallest sample size. A selection of 18 domains out of 51 is done from the positions \(1,4,7,\ldots ,49\) and 51. The tables give the direct and the compositional plug-in estimates (labelled by “dir” and “mod”, respectively) and the corresponding RMSE estimates. The provinces are labelled by “prov”, with codes given in Sect. 2, and the sample sizes are denoted by n.
Tables 6 and 7 are partitioned in three vertical sections dealing with the estimation of proportion of people under 16 years, employed and unemployed people. Table 8 contains the estimated proportions of inactive men and women and the corresponding RMSE estimates. By observing the columns of RMSEs, we conclude that the compositional plug-in predictors are preferred to the direct estimators.
We recall that the compositional predictors of the four categories are derived from the fitted TFH model by applying the alogist transformation, so they are jointly calculated. The last category (inactive) is not a reference category. Their results appear in Table 8 because of the lack of space when constructing Tables 6 and 7.
7 Conclusions
This paper introduces predictors of category proportions based on an area-level compositional mixed model. A TFH model is introduced for modelling the additive logratio transformations of the direct estimators of the category proportions. The additive logistic transformations of the EBLUPs under the TFH model are the proposed compositional plug-in predictors. Similarly, the centred or the isometric logratio transformation (see Appendix D) can be employed.
In addition, the compositional empirical best predictors are also introduced and empirically investigated. The first predictor is easy to calculate, but the second one requires the approximation of integrals in \(R^3\). This numerical problem demands rather high computational time to achieve an acceptable precision. Because of this issue and the results of Simulation 2, the use of the compositional plug-in predictor is recommended.
Unlike the multinomial approach of López-Vizcaíno et al. (2013), the compositional predictors take into account the sampling design. The sampling weights are employed by means of the direct estimators of the category proportions and through the estimators of their design-based variances and covariances.
As discussed in Section 4, both models (MLM and compositional) have problems to predict the population parameter \(\bar{Z}_{dk}\). However, these problems are compensated by the use of auxiliary variables correlated with the objective variable and with the modelling of the covariance structure of the categories. It is at this point where the compositional mixed model presents its greatest advantages compared to the MLM model. The compositional approach is more flexible and can be adapted to different correlation structures, while multinomial correlation structure is rather rigid (correlations negative) and does not fit well to both types of covariances and variances (unit level and domain level). The results of four simulation experiments and the analysis of real data confirm this assertion.
The new small area estimation methodology is applied to Labour Force Survey data from Galicia, a region in north-west of Spain, in the period January–April 2017. The selected compositional mixed model has had a better fit to the data than the corresponding multinomial mixed model, and therefore, the labour status proportions per county and sex are finally estimated by using the compositional plug-in predictors with its mean squares errors calculated by parametric bootstrap.
As for the labour market results in Galicia, we can conclude that the west coast, in general terms, is the most dynamic part with a higher proportion of employed people and people under 16 years old. There is a big problem in the south-east because there are several counties with a proportion of inactive people over the 50%. This area is essentially rural. Fixing the population in rural areas, with a decent living and income levels, is one basic requirement to ensure territorial balance and environmental sustainability. Galicia is ageing and more accentuated in rural areas, due to the emigration of young people and the fall in the birth rate. This reality, with obvious economic and sociological consequences, demands answers from social and employment policies.
Although the introduced methodology is applied to the variable “labour status” with \(q=4\) categories, it can be extended to categorical variables with any number \(q\ge 2\) of categories. However, we only recommend their use for the cases \(q=2,3,4,5\). This paper presents the mathematical developments for the case \(q=4\) leading to a TFH model with six variances or covariance parameters. The cases \(q=2\) and \(q=3\) are more simpler as they require fitting univariate and bivariate Fay–Herriot models with one and three variance components, respectively. The case \(q=5\) yields to a MFH model with ten variance components, where the fitting algorithm might have convergence problems when the number of domains D is not big enough.
The application to real data can be carried out in the subpopulation of people aged 16 or more, where the number of categories is \(q=3\) (employed, unemployed and inactive). This simpler scenario requires fitting a bivariate Fay–Herriot model to the transformed survey data and obtaining the predictions of the domain proportions of the three considered categories in a similar way as it is done in the case of \(q=4\) categories. We have decided to follow the more complex TFH approach because of the strength of the available auxiliary variables and to guarantee the coherence of the estimates of the four category proportions. For the categories \(\le 15\), employed and unemployed, we have the highly correlated variables to15, SS and REG. This last fact also motivated the selection of inactive as the fourth (reference) class.
Compositional data play an important role in public statistics. In this case, we applied the introduced methodology to the SLFS, but it is useful in other topics of the official statistics, like the classification of the population by the educational level, the income level or the type of household expenditure. In all these situations, it is necessary to take into account the simplex constraints.
This work may be extended to incorporate spatial correlations between domains. In practice, it is often reasonable to assume that the effects associated with neighbouring areas are proportionally correlated with a measure of distance. Also, it is important to know the evolution of the labour market, along the quarters for the counties, in an accurate and stable form, suitable for being used in statistical offices. Therefore, extensions of the introduced methodology to models incorporating temporal correlations are also a future research task.
Change history
29 March 2021
A Correction to this paper has been published: https://doi.org/10.1007/s11749-021-00767-x
References
Aitchison J (1986) The statistical analysis of compositional data. Chapman and Hall, London
Arima S, Bell WR, Datta GS, Franco C, Liseo B (2017) Multivariate Fay–Herriot Bayesian estimation of small area means under functional measurement error. J R Stat Soc Ser A 180(4):1191–1209
Benavent R, Morales D (2016) Multivariate Fay–Herriot models for small area estimation. Comput Stat Data Anal 94:372–390
Berg E, Fuller WA (2012) Estimators of error covariance matrices for small area prediction. Comput Stat Data Anal 56:2949–2962
Berg EJ, Fuller WA (2014) Small area prediction of proportions with applications to the Canadian Labour Force Survey. J Surv Stat Methodol 2:227–256
Boubeta M, Lombardía MJ, Morales D (2016) Empirical best prediction under area-level Poisson mixed models. TEST 25:548–569
Boubeta M, Lombardía MJ, Morales D (2017) Poisson mixed models for studying the poverty in small areas. Comput Stat Data Anal 107:32–47
Chambers R, Dreassi E, Salvati N (2014) Disease mapping via negative binomial regression M-quantiles. Stat Med 33:4805–4824
Chambers R, Salvati N, Tzavidis N (2016) Semiparametric small area estimation for binary outcomes with application to unemployment estimation for Local Authorities in the UK. J R Stat Soc Ser A 179:453–479
Chen S, Lahiri P (2012) Inferences on small area proportions. J Indian Soc Agric Stat 66(1):121–124
Datta GS, Fay RE Ghosh M (1991) Hierarchical and empirical Bayes multivariate analysis in small area estimation. In: Proceedings of Bureau of the census 1991 annual research conference, U. S. Bureau of the Census, Washington, DC, pp 63–79
Datta GS, Ghosh M, Nangia N, Natarajan K (1996) Estimation of median income of four-person families: a Bayesian approach. In: Berry DA, Chaloner KM, Geweke JM (eds) Bayesian analysis in statistics and econometrics. Wiley, New York, pp 129–140
Dreassi E, Ranalli MG, Salvati N (2014) Semiparametric M-quantile regression for count data. Stat Methods Med Res 23:591–610
Egozcue JJ, Pawlowsky-Glahn V (2019) Compositional data: the sample space and its structure. TEST 28(3):599–638
Egozcue JJ, Pawlowsky-Glahn V, Mateu-Figueras G, Barceló-Vidal C (2003) Isometric logratio transformations for compositional data analysis. Math Geol 35(3):279–300
Esteban MD, Morales D, Pérez A, Santamaría L (2012) Small area estimation of poverty proportions under area-level time models. Comput Stat Data Anal 56:2840–2855
Fabrizi E, Ferrante MR, Trivisano C (2016) Hierarchical Beta regression models for the estimation of poverty and inequality parameters in small areas. In: Pratesi Monica (ed) Analysis of poverty data by small area methods. Wiley, New York
Farrell PJ (2000) Bayesian inference for small area estimation. Sankhya Ser B 62(3):402–416
Fay RE (1987) Application of multivariate regression of small domain estimation. In: Platek R, Rao JNK, Särndal CE, Singh MP (eds) Small area statistics. Wiley, New York, pp 91–102
Ferrante MR, Trivisano C (2010) Small area estimation of the number of firms’ recruits by using multivariate models for count data. Surv Methodol 36(2):171–180
Ghosh M, Nangia N, Kim D (1996) Estimation of median income of four-person families: a Bayesian time series approach. J Am Stat Assoc 91:1423–1431
González-Manteiga W, Lombardía MJ, Molina I, Morales D, Santamaría L (2007) Estimation of the mean squared error of predictors of small area linear parameters under a logistic mixed model. Comput Stat Data Anal 51:2720–33
González-Manteiga W, Lombardía MJ, Molina I, Morales D, Santamaría L (2008a) Analytic and bootstrap approximations of prediction errors under a multivariate Fay–Herriot model. Comput Stat Data Anal 52:5242–5252
González-Manteiga W, Lombardía MJ, Molina I, Morales D, Santamaría L (2008b) Bootstrap mean squared error of small-area EBLUP. J Stat Comput Simul 78:443–462
Hobza T, Morales D (2016) Empirical best prediction under unit-level logit mixed models. J Off Stat 32(3):661–669
Hobza T, Santamaría L, Morales D (2018) Small area estimation of poverty proportions under unit-level temporal binomial-logit mixed models. TEST 27(2):270–294
Larsen MD (2003) Estimation of small-area proportions using covariates and survey data. J Stat Plan Inference 112:89–98
Liu B, Lahiri P (2017) Adaptive Hierarchical Bayes estimation of small area proportions. Calcutta Stat Assoc Bull 69(2):150–164
López-Vizcaíno E, Lombardía MJ, Morales D (2013) Multinomial-based small area estimation of labour force indicators. Stat Model 13(2):153–178
López-Vizcaíno E, Lombardía MJ, Morales D (2015) Small area estimation of labour force indicators under a multinomial model with correlated time and area effects. J R Stat Soc Ser A 178(3):535–565
Marhuenda Y, Molina I, Morales D (2013) Small area estimation with spatio-temporal Fay–Herriot models. Comput Stat Data Anal 58:308–325
Marhuenda Y, Morales D, Pardo MC (2014) Information criteria for Fay–Herriot model selection. Comput Stat Data Anal 70:268–280
Molina I, Saei A, Lombardía MJ (2007) Small area estimates of labour force participation under multinomial logit mixed model. J R Stati Soc Ser A 170:975–1000
Morales D, Pagliarella MC, Salvatore R (2015) Small area estimation of poverty indicators under partitioned area-level time models. SORT Stat Oper Res Trans 39(1):19–34
Pawlowsky-Glahn V, Buccianti A (eds) (2011) Compositional data analysis. Wiley, Chichester
Rao JNK (2003) Small area estimation. Wiley, New-York
Rao JNK, Molina I (2015) Small area estimation, 2nd edn. Wiley, Hoboken
Saei A, Chambers R (2003) Small area estimation under linear an generalized linear mixed models with time and area effects. S3RI Methodology Working Paper M03/15, Southampton Statistical Sciences Research Institute
Särndal CE, Swensson B, Wretman J (1992) Model assisted survey sampling. Springer, Berlin
Scealy JL, Welsh AH (2017) A directional mixed effects model for compositional expenditure data. J Am Stat Assoc 112(517):24–36
Slud EV, Maiti T (2006) Mean-squared error estimation in transformed Fay–Herriot models. J R Stat Soc Ser B 68(2):239–257
Souza DB, Moura FAS (2016) Multivariate Beta regression with applications in small area estimation. J Off Stat 32:747–768
Tzavidis N, Ranalli MG, Salvati N, Dreassi E, Chambers R (2015) Robust small area prediction for counts. Stat Methods Med Res 24(3):373–395
Zhang L, Chambers R (2004) Small area estimates for cross-classifications. J R Stat Soc Ser B 66(2):479–496
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised due to a retrospective Open Access order.
Supported by the Instituto Galego de Estatística, by the grants PGC2018-096840-B-I00 and MTM2017-82724-R of the Spanish Ministerio de Economía y Competitividad and by the Xunta de Galicia (Grupos de Referencia Competitiva ED431C-2016-015 and Centro Singular de Investigación de Galicia ED431G/01), all of them through the ERDF.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Esteban, M.D., Lombardía, M.J., López-Vizcaíno, E. et al. Small area estimation of proportions under area-level compositional mixed models. TEST 29, 793–818 (2020). https://doi.org/10.1007/s11749-019-00688-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11749-019-00688-w