Inference with progressively censored k-out-of-n system lifetime data

Abstract

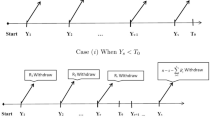
A system with n independent components which works if and only if a least k of its n components work is called a k-out-of-n system. For exponentially distributed component lifetimes, we obtain point and interval estimators for the scale parameter of the component lifetime distribution of a k-out-of-n system when the system failure time is observed only. In particular, we prove that the maximum likelihood estimator (MLE) of the scale parameter based on progressively Type-II censored system lifetimes is unique. Further, we propose a fixed-point iteration procedure to compute the MLE for k-out-of-n systems data. In addition, we illustrate that the Newton–Raphson method does not converge for any initial value. Finally, exact confidence intervals for the scale parameter are constructed based on progressively Type-II censored system lifetimes.

Appendix

Proof

(Theorem 1) We consider the limits of $\frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )$ for $\lambda \rightarrow 0$ and $\lambda \rightarrow \infty$,

$$\begin{aligned} \lim _{\lambda \rightarrow 0}\frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )&=-\,n\sum _{i=1}^vy_i+\lim _{\lambda \rightarrow 0}\bigg (\frac{v}{\lambda }+(n-k)\sum _{i=1}^vy_i(1-\exp (-y_i\lambda ))^{-1}\bigg ) \\&=\infty >0,\\ \lim _{\lambda \rightarrow \infty }\frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )&=-\,n\sum _{i=1}^vy_i+(n-k)\sum _{i=1}^vy_i-k\left( {\begin{array}{c}n\\ n-k\end{array}}\right) \sum _{i=1}^vR_iy_i\left( \left( {\begin{array}{c}n\\ n-k\end{array}}\right) \right) ^{-1} \\&=-\,k\sum _{i=1}^v(R_i+1)y_i<0. \end{aligned}$$

As a consequence the function $\frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )$ has to be zero for some $\widehat{\lambda }>0$ since it is a continuous function. Thus, $\widehat{\lambda }$ is a solution of the likelihood equation. The first derivative $\frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )$ is strictly decreasing since $\frac{\partial ^2l_{\mathbf {Y}}}{\partial \lambda ^2}({\mathbf {y}};\lambda )<0$ for $\lambda >0$, see (8). Therefore, $\widehat{\lambda }$ is the unique solution of the equation $\frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )=0$, $\lambda >0$. Then, $\widehat{\lambda }$ is the global maximum of $l_{\mathbf {Y}}$ and the MLE of $\lambda$ since $l_{\mathbf {Y}}$ is a strictly concave function on $(0, \infty )$. $\square$

Proof

(Lemma 1) First, we rewrite $\phi (x)$ for $x\in (0,\infty )$:

$$\begin{aligned} \phi (x)&=\frac{\sum _{j=-(n-k)}^0\left( {\begin{array}{c}n\\ j+n-k\end{array}}\right) \left( e^x-1\right) ^{j-1}\left( jxe^x-e^x+1\right) }{\left( \sum _{j=-(n-k)}^0\left( {\begin{array}{c}n\\ j+n-k\end{array}}\right) \left( e^x-1\right) ^{j}\right) ^2} \\&=-\frac{\sum _{j=0}^{n-k}\left( {\begin{array}{c}n\\ n-k-j\end{array}}\right) \left( e^x-1\right) ^{-j}\left( 1+\frac{jxe^x}{e^x-1}\right) }{\left( \sum _{j=0}^{n-k}\left( {\begin{array}{c}n\\ n-k-j\end{array}}\right) \left( e^x-1\right) ^{-j}\right) ^2}. \end{aligned}$$

Let $x\in (0,1]$. Then, a lower bound results from the inequalities

$$\begin{aligned} \phi (x)\ge -\frac{1+(n-k)\frac{xe^x}{e^x-1}}{\sum _{j=0}^{n-k}\left( {\begin{array}{c}n\\ n-k-j\end{array}}\right) \left( e^x-1\right) ^{-j}}\overset{(*)}{\ge }-\frac{1+(n-k)e}{\sum _{j=0}^{n-k}\left( {\begin{array}{c}n\\ n-k-j\end{array}}\right) \left( e-1\right) ^{-j}}, \end{aligned}$$

where we used the inequality $e^x-1\ge x$, $x\in [0,\infty )$, in $(*)$. For $x\in [1,\infty )$ and $j\in \mathbb {N}_0$, we obtain

$$\begin{aligned} (e^x-1)^{-1}\left( 1+\frac{jxe^x}{e^x-1}\right) =\frac{1}{e^x-1}+\frac{jxe^x}{(e^x-1)^2}\le \frac{1}{e-1}+\frac{je}{(e-1)^2}. \end{aligned}$$

In the last inequality, we used that $\frac{xe^x}{(e^x-1)^2}$ is strictly decreasing on $[1,\infty )$. As a direct consequence, we find

$$\begin{aligned} \phi (x)&\ge -\frac{\sum _{j=0}^{n-k}\left( {\begin{array}{c}n\\ n-k-j\end{array}}\right) \left( e-1\right) ^{1-j}\left( \frac{1}{e-1}+\frac{je}{(e-1)^2}\right) }{\left( \sum _{j=0}^{n-k}\left( {\begin{array}{c}n\\ n-k-j\end{array}}\right) \left( e^x-1\right) ^{-j}\right) ^2} \\&\ge -\frac{\sum _{j=0}^{n-k}\left( {\begin{array}{c}n\\ n-k-j\end{array}}\right) (e-1)^{-j}\left( 1+je(e-1)^{-1}\right) }{\left( \left( {\begin{array}{c}n\\ n-k\end{array}}\right) \right) ^2}, \quad x\in [1,\infty ). \end{aligned}$$

Hence, the function $\phi$ is bounded and continuous on $(0,\infty )$. Then, the function $\phi$ has a global minimum $\phi _{\mathrm{min}}$ on the interval $(0, \infty )$. Obviously, $\phi (x)\le 0$, $x\in (0, \infty )$. The limits for $x\rightarrow 0+$ and $x\rightarrow \infty$ are easily obtained by standard calculations.

Proof

(Theorem 2) The proof uses the Banach fixed-point theorem (cf. Papageorgiou and Kyritsi-Yiallourou 2009, p. 226) for the continuous continuation of $\xi$ on $[0, \infty )$. For the definition of the continuous continuation of $\xi$ on $[0,\infty )$, we need the following limit

$$\begin{aligned}&\lim _{\lambda \rightarrow 0}\lambda \frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )=v+(n-k)\sum _{i=1}^vy_i\times \lim _{\lambda \rightarrow 0}\frac{\lambda }{1-e^{-y_i\lambda }}\\&\quad =v+(n-k)v=(n-k+1)v, \end{aligned}$$

where we have used l’Hôspital’s rule to get $\lim _{\lambda \rightarrow 0}\frac{\lambda }{1-e^{-y_i\lambda }}=\lim _{\lambda \rightarrow 0}\frac{1}{y_ie^{-y_i\lambda }}=\frac{1}{y_i}$ for $i=1,\ldots ,v$. Then, the limit of $\xi$ for $\lambda \rightarrow 0$ is given by

$$\begin{aligned} \lim _{\lambda \rightarrow 0}\xi (\lambda )=\frac{1}{a}\frac{(n-k+1)v}{k\sum _{i=1}^v(R_i+1)y_i}>0. \end{aligned}$$

Therefore, the continuous continuation of $\xi$ on $[0,\infty )$ is defined as follows

$$\begin{aligned} \widetilde{\xi }:[0,\infty )\rightarrow [0,\infty ), \quad \lambda \mapsto {\left\{ \begin{array}{ll} \xi (\lambda ), &{}\quad \lambda \in (0,\infty ), \\ \displaystyle \lim _{\lambda \rightarrow 0}\xi (\lambda ), &{}\quad \lambda =0. \end{array}\right. } \end{aligned}$$

Since $\widetilde{\xi }(0)>0$ we conclude that $\lambda =0$ can not be a fixed-point of $\widetilde{\xi }$ on $[0,\infty )$. Hence, a fixed-point of $\widetilde{\xi }$ must be a fixed-point of $\xi$, too. Notice that we need the continuous continuation of $\widetilde{\xi }$ on $[0, \infty )$ for formal reasons in order to get a complete metric space. Now, according to the Banach fixed-point theorem, we have to show

• (I) $\widetilde{\xi }[0,\infty )\subseteq [0,\infty )$ and

• (II) $\widetilde{\xi }$ is Lipschitz continuous with Lipschitz constant $K\in [0,1)$.

Due to $\widetilde{\xi }(0)>0$, it is sufficient to show $\xi (0,\infty )\subseteq (0,\infty )$ to ensure $\widetilde{\xi }[0,\infty )\subseteq [0,\infty )$. According to Eq. (8), the first derivative of the log-likelihood function $\frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )$ is strictly decreasing and the limit for $\lambda \rightarrow \infty$ is given by $-k\sum _{i=1}^v(R_i+1)y_i$. Then, $\frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )>-k\sum _{i=1}^v(R_i+1)y_i$ for $\lambda \in (0,\infty )$. It follows $\xi (\lambda )>0$ for $\lambda \in (0,\infty )$ since $a\ge \frac{n+k}{2k}>1$. Therefore, condition (I) is satisfied.

The functions $\xi$ and $\widetilde{\xi }$ are differentiable on $(0,\infty )$ and have the same derivative. To ensure condition (II), it is sufficient to show that the derivative is bounded in the interval $[-K, K]$ with $K=\sup _\lambda |\frac{d}{\mathrm{d}\lambda }\xi (\lambda )|\in [0, 1)$ (see Arikawa and Furukawa 1999, p. 176). We define

$$\begin{aligned} A_{ij}:=\left( {\begin{array}{c}n\\ j+n-k\end{array}}\right) \left( e^{y_i\lambda }-1\right) ^{j-1}, \quad i=1,\ldots ,v \text{ and } j=-(n-k),\ldots ,0. \end{aligned}$$

Then, we get

$$\begin{aligned}&\frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )+\lambda \frac{\partial ^2 l_{\mathbf {Y}}}{\partial \lambda ^2}({\mathbf {y}};\lambda )\\&\quad =-\,n\sum _{i=1}^vy_i+(n-k)\sum _{i=1}^v\frac{y_i}{G_\lambda (y_i)}-k\left( {\begin{array}{c}n\\ n-k\end{array}}\right) \sum _{i=1}^v\frac{R_iy_i}{\sum _{j=-(n-k)}^0A_{ij}\left( e^{y_i\lambda }-1\right) } \\&\qquad -(n\!-\!k)\lambda \sum _{i=1}^vy_i^2\frac{1\!-G_\lambda (y_i)}{(G_\lambda (y_i))^2}\!+\!k\left( {\begin{array}{c}n\\ n-k\end{array}}\right) \sum _{i=1}^v R_iy_i\frac{\lambda \sum _{j=-(n-k)}^0A_{ij}je^{y_i\lambda }}{\left( \sum _{j=-(n\!-\!k)}^0A_{ij}\left( e^{y_i\lambda }-1\right) \right) ^2} \\&\quad =-\,n\sum _{i=1}^vy_i+(n-k)\sum _{i=1}^vy_i\frac{G_\lambda (y_i)-\lambda y_i(1-G_\lambda (y_i))}{(G_\lambda (y_i))^2}\\&\qquad +k\left( {\begin{array}{c}n\\ n-k\end{array}}\right) \sum _{i=1}^vR_iy_i\phi (y_i\lambda ), \quad \lambda >0. \end{aligned}$$

Using $x>1-e^{-x}$ and $e^x>x+1$ for $x>0$, we have

$$\begin{aligned} 0<&\frac{1-e^{-x}-xe^{-x}}{\left( 1-e^{-x}\right) ^2}< \frac{1-e^{-x}-\left( 1-e^{-x}\right) e^{-x}}{\left( 1-e^{-x}\right) ^2}=1, \quad x>0. \end{aligned}$$

Substituting $x=\lambda y_i>0$, we get

$$\begin{aligned} 0<\sum _{i=1}^v y_i\frac{G_\lambda (y_i)-\lambda y_i(1-G_\lambda (y_i))}{(G_\lambda (y_i))^2}<\sum _{i=1}^vy_i=v\overline{y}, \end{aligned}$$

(14)

where $\overline{y}=\frac{1}{v}\sum _{i=1}^vy_i$. Applying Lemma 1, this yields

$$\begin{aligned} \frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )+\lambda \frac{\partial ^2 l_{\mathbf {Y}}}{\partial \lambda ^2}({\mathbf {y}};\lambda )&<-n\sum _{i=1}^vy_i+(n-k)\sum _{i=1}^vy_i=-k\sum _{i=1}^vy_i \quad \text{ and } \\ \frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )+\lambda \frac{\partial ^2 l_{\mathbf {Y}}}{\partial \lambda ^2}({\mathbf {y}};\lambda )&>-n\sum _{i=1}^vy_i+k\left( {\begin{array}{c}n\\ n-k\end{array}}\right) \sum _{i=1}^vR_iy_i\phi ^*. \end{aligned}$$

Using

$$\begin{aligned} \frac{d}{\mathrm{d}\lambda }\xi (\lambda )&=\frac{1/a}{k\sum _{i=1}^v(R_i+1)y_i}\left( \frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )+\lambda \frac{\partial ^2 l_{\mathbf {Y}}}{\partial \lambda ^2}({\mathbf {y}};\lambda )\right) , \quad \lambda >0, \end{aligned}$$

we get

$$\begin{aligned} \frac{d}{\mathrm{d}\lambda }\xi (\lambda )&<-\frac{1}{a}\frac{\sum _{i=1}^vy_i}{\sum _{i=1}^v(R_i+1)y_i}<1 \quad \text {and} \\ \frac{d}{\mathrm{d}\lambda }\xi (\lambda )&>-\frac{1}{a}\frac{n\sum _{i=1}^vy_i-k\left( {\begin{array}{c}n\\ n-k\end{array}}\right) \sum _{i=1}^vR_iy_i\phi ^*}{k\sum _{i=1}^v(R_i+1)y_i}>-1. \end{aligned}$$

Thus, we know $\frac{d}{\mathrm{d}\lambda }\xi (\lambda )\in (-1,1)$ for $\lambda \in (0,\infty )$. To ensure $\sup _\lambda |\frac{d}{\mathrm{d}\lambda }\xi (\lambda )|\in [0,1)$, it is sufficient to show that $\lim _{\lambda \rightarrow 0}\frac{d}{\mathrm{d}\lambda }\xi (\lambda ),\lim _{\lambda \rightarrow \infty }\frac{d}{\mathrm{d}\lambda }\xi (\lambda )\in (-1,1)$. Using $\lim _{\lambda \rightarrow 0}G_\lambda (y_i)=0$, $\lim _{\lambda \rightarrow \infty }G_\lambda (y_i)=\infty$ for $i=1,\ldots ,v$ and l’Hôspital’s rule in $(*)$, we get

$$\begin{aligned} \lim _{\lambda \rightarrow 0}\frac{G_\lambda (y_i)-\lambda y_i\left( 1-G_\lambda (y_i)\right) }{\left( G_\lambda (y_i)\right) ^2}&{\mathop {=}\limits ^{(*)}}\lim _{\lambda \rightarrow 0}\frac{y_i\lambda }{2G_\lambda (y_i)}{\mathop {=}\limits ^{(*)}}\lim _{\lambda \rightarrow 0}\frac{1}{2e^{-y_i\lambda }}=\frac{1}{2} \quad \text{ and } \\ \lim _{\lambda \rightarrow \infty }\frac{G_\lambda (y_i)-\lambda y_i\left( 1-G_\lambda (y_i)\right) }{\left( G_\lambda (y_i)\right) ^2}&=\lim _{\lambda \rightarrow \infty }\frac{G_\lambda (y_i)-\lambda y_ie^{-y_i\lambda }}{\left( G_\lambda (y_i)\right) ^2}=1. \end{aligned}$$

Then, we arrive at

$$\begin{aligned} \lim _{\lambda \rightarrow 0}\left( \frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )+\lambda \frac{\partial ^2 l_{\mathbf {Y}}}{\partial \lambda ^2}({\mathbf {y}};\lambda )\right)&=-n\sum _{i=1}^vy_i\!+\frac{n\!-\!k}{2}\sum _{i=1}^vy_i\!=-\frac{n\!+\!k}{2}\sum _{i=1}^vy_i\,\, \text{ and } \\ \lim _{\lambda \rightarrow \infty }\left( \frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )+\lambda \frac{\partial ^2 l_{\mathbf {Y}}}{\partial \lambda ^2}({\mathbf {y}};\lambda )\right)&=-n\sum _{i=1}^vy_i+(n-k)\sum _{i=1}^vy_i-k\sum _{i=1}^vR_iy_i\\&=-k\sum _{i=1}^v(R_i+1)y_i, \end{aligned}$$

where we used the limits of $\phi$. Then, the limits of $\frac{d}{\mathrm{d}\lambda }\xi$ are given by

$$\begin{aligned} \lim _{\lambda \rightarrow 0}\frac{d}{\mathrm{d}\lambda }\xi (\lambda )&=\frac{1/a}{k\sum _{i=1}^v(R_i+1)y_i}\biggl (-\frac{n+k}{2}\sum _{i=1}^vy_i\biggr ){\mathop {>}\limits ^{(**)}} -\frac{1}{a}\cdot \frac{n+k}{2k}\ge -1 \quad \text{ and } \end{aligned}$$

(15)

$$\begin{aligned} \lim _{\lambda \rightarrow \infty }\frac{d}{\mathrm{d}\lambda }\xi (\lambda )&=\frac{1/a}{k\sum _{i=1}^v(R_i+1)y_i}\biggl (-k\sum _{i=1}^v(R_i+1)y_i\biggr )=-\frac{1}{a}\ge -\frac{2k}{n+k}>-1. \end{aligned}$$

(16)

The inequality $(**)$ is only strict for censored data, i.e., $(R_1,\ldots ,R_v)\ne (0,\ldots ,0)$. For the non-censored case, we have $a=\max \left( \frac{n+k}{2k},\frac{n}{k}\right) =\frac{n}{k}$, because $k<n$. Then, we get $\lim _{\lambda \rightarrow 0}\frac{d}{\mathrm{d}\lambda }\xi (\lambda )=-\frac{1}{a}\cdot \frac{n+k}{2k}>-1$. Hence, we have $\lim _{\lambda \rightarrow 0}\frac{d}{\mathrm{d}\lambda }\xi (\lambda ),\lim _{\lambda \rightarrow \infty }\frac{d}{\mathrm{d}\lambda }\xi (\lambda )\in (-1,0)$. Therefore, condition (II) is satisfied. Using Banach’s fixed-point theorem, we know that a fixed-point $\widehat{\lambda }$ of $\widetilde{\xi }$ exists, which is a fixed-point of $\xi$, too. Then, $\frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\widehat{\lambda })=0$ and $\widehat{\lambda }$ is the MLE of $\lambda$. Furthermore, the Banach fixed-point theorem yields that the sequence $\lambda _{h+1}=\widetilde{\xi }(\lambda _h)=\xi (\lambda _h)$ converges to $\widehat{\lambda }$ for every $\lambda _0\in (0,\infty )$. $\square$

Proof

(Lemma 2) For $i=1,\ldots ,v$, the inner part of the logarithm in (13) can be rewritten as

$$\begin{aligned}&1-\sum _{j=n-k+1}^n\left( {\begin{array}{c}n\\ j\end{array}}\right) \left( 1-\exp (-y_i\lambda )\right) ^{j}\left( \exp (-y_i\lambda )\right) ^{n-j}\\&\quad =\sum _{j=0}^{n-k}\left( {\begin{array}{c}n\\ j\end{array}}\right) \left( G_\lambda (y_i)\right) ^{j}\left( 1-G_\lambda (y_i)\right) ^{n-j}= H(y_i,\lambda ). \end{aligned}$$

According to (6), the derivative of H w.r.t. $\lambda$ is given by

$$\begin{aligned} \frac{\partial H}{\partial \lambda }(y_i,\lambda )=-k\left( {\begin{array}{c}n\\ n-k\end{array}}\right) y_i\left( G_\lambda (y_i)\right) ^{n-k}\left( 1-G_\lambda (y_i)\right) ^{k}, \end{aligned}$$

and thus negative. Hence, the inner part of the logarithm is strictly decreasing in $\lambda$ so that $\eta (\lambda )$ strictly increases in $\lambda$. The limits of $\eta (\lambda )$ for $\lambda \rightarrow 0$ and $\lambda \rightarrow \infty$ are

$$\begin{aligned} \lim _{\lambda \rightarrow 0}\eta (\lambda )&=-2\sum _{i=1}^v(R_i+1)\ln (1)=0 \quad \text{ and } \\ \lim _{\lambda \rightarrow \infty }\eta (\lambda )&=\lim _{x\rightarrow 0}-2\sum _{i=1}^v(R_i+1)\ln (x)=\infty . \end{aligned}$$

Hence, the function $\eta :(0,\infty )\rightarrow (0,\infty )$ is strictly increasing and continuous so that the equation $\eta (\lambda )=t$ has an unique solution for $t>0$. $\square$

Proof

(Theorem 3) From Lemma 2, the solutions $\eta \left[ {\mathbf {Y}},\chi _{2v}^2(\alpha /2)\right]$ and $\eta \left[ {\mathbf {Y}},\chi _{2v}^2(1-\alpha /2)\right]$ exist. Using $\eta \sim \chi _{2v}^2$, we have

$$\begin{aligned} P&\left( \eta \left[ {\mathbf {Y}},\chi _{2v}^2(\alpha /2)\right]<\lambda<\eta \left[ {\mathbf {Y}},\chi _{2v}^2(1-\alpha /2)\right] \right) \\&=P\left( \chi _{2v}^2(\alpha /2)<\eta <\chi _{2v}^2(1-\alpha /2)\right) \\&=(1-\alpha /2)-\alpha /2=1-\alpha . \end{aligned}$$

Notice that, according to Lemma 2, $\eta$ is strictly increasing in $\lambda$ so that the direction of the inequalities does not change. $\square$