A semiparametric approach for joint modeling of median and skewness

Abstract

We motivate this paper by showing through Monte Carlo simulation that ignoring the skewness of the response variable distribution in non-linear regression models may introduce biases on the parameter estimates and/or on the estimation of the associated variability measures. Then, we propose a semiparametric regression model suitable for data set analysis in which the distribution of the response is strictly positive and asymmetric. In this setup, both median and skewness of the response variable distribution are explicitly modeled, the median using a parametric non-linear function and the skewness using a semiparametric function. The proposed model allows for the description of the response using the log-symmetric distribution, which is a generalization of the log-normal distribution and is flexible enough to consider bimodal distributions in special cases as well as distributions having heavier or lighter tails than those of the log-normal one. An iterative estimation process as well as some diagnostic methods are derived. Two data sets previously analyzed under parametric models are reanalyzed using the proposed methodology.

Appendices

Appendix A. Log-symmetric distributions

The absolutely continuous and positive random variable $T$ follows log-symmetric distribution with density generator $g(\cdot )$, scale parameter $\eta$ and power parameter $\phi$ if its density function can be written as

$$\begin{aligned} f_{_T}(t;\eta ,\phi ,g(\cdot ))=\frac{1}{\sqrt{\phi }\,t}\,g\!\left( \tilde{t}\,^2\right) ,\quad t>0, \end{aligned}$$

(7)

where $\tilde{t}=\log \left[ \!\left( {t}/{\eta }\right) ^{\frac{1}{\sqrt{\phi }}}\!\right]$, $\eta > 0$, $\phi >0$, and $g(u)>0$ for $u>0$ and $\int _{0}^{\infty }\!\!\!u^{\!-\!\frac{1}{2}}\!g(u)\partial u=1$. If this condition is satisfied then it is written $T\sim {\mathcal {LS}}(\eta ,\phi ,g(\cdot ))$. For example, using $g(u)\propto \exp (-u/2)$, $g(u)\propto (1+\frac{u}{\nu })^{-\frac{\nu +1}{2}}$, $g(u)\propto \exp [-\frac{1}{2}u^{\frac{1}{1+\varrho }}]$, $g(u)\propto \exp [-\varsigma \sqrt{1+u}]$, $g(u)\propto \mathrm{IGF}\left( \iota + \frac{1}{2},\frac{u}{2}\right)$, $g(u)\propto \mathrm{cosh}({u}^{\frac{1}{2}})\exp [-\frac{2}{\alpha ^2}\,\mathrm{sinh}^2({u}^{\frac{1}{2}})]$ (for $\phi =4$) and $g(u)\propto \mathrm{cosh}({u}^{\frac{1}{2}})\times [1 + 4\,\mathrm{sinh}^2({u}^{\frac{1}{2}})/\nu \alpha ^2]^{-\frac{\nu +1}{2}}$ (for $\phi =4$) as density generator one obtains a random variable $T$ following log-normal, log-Student-$t$ (having $\nu >0$ degrees of freedom), log-power-exponential (having shape parameter $-1<\varrho <1$), log-hyperbolic (having shape parameter $\varsigma >0$), log-slash (having shape parameter $\iota >0$), Birnbaum–Saunders (having shape parameter $\alpha >0$) and Birnbaum–Saunders-$t$ (having shape parameter $\alpha >0$ and $\nu >0$ degrees of freedom) distributions, respectively, in which $\mathrm{IGF}(a,x)=\frac{1}{x^a}\int \nolimits _{0}^{x}\exp (-t)t^{a-1}\partial t$ for $a>0$ and $x\ge 0$ is the incomplete gamma function. In fact, it is possible to show that the generalized Birnbaum–Saunders distribution (Diaz-Garcia and Leiva 2005; Leiva et al. 2008) belongs to the class of log-symmetric distributions with $g(u;\alpha ,\bar{\zeta })\propto \bar{g}\left( 4\,\mathrm{sinh}^2({u}^{\frac{1}{2}})/\alpha ^2;\bar{\zeta }\right) \times \mathrm{cosh}({u}^{\frac{1}{2}})$, where $\phi =4$ and $\bar{g}(u;\bar{\zeta })$ is the kernel that characterizes the generalized Birnbaum–Saunders distribution.

1.1 Some statistical properties

If $T\sim {\mathcal {LS}}(\eta ,\phi ,g(\cdot ))$ then it is possible to verify that

• $Y=\log (T) \sim {\mathcal S}(\mu ,\phi ,g(\cdot ))$, i.e., the distribution of $Y$ belongs to the class of symmetric distributions (Fang et al. 1990) having density generator $g(\cdot )$, location parameter $\mu =\log (\eta )$ and dispersion parameter $\phi$.

• ${c}\,T \sim {\mathcal {LS}}(c\,\eta ,\phi ,g(\cdot ))$ for all constant $c>0$.

• $T^{c}\sim {\mathcal {LS}}(\eta ^c,c^2\,\phi ,g(\cdot ))$ for all constant $c\ne 0$.

• The median of $T$ is $\eta$.

• The quantile function of $T$ is given by $\vartheta (q)=\eta \,\exp (\sqrt{\phi }\,Z^{(q)})$, where $Z^{(q)}$ is the $100(q)\,\%$ quantile of $Z=({Y-\mu })/{\sqrt{\phi }}\sim \mathcal {S}(0,1,g(\cdot ))$ distribution.

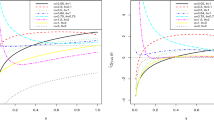
• The skewness measure proposed by Groeneveld and Meeden (1984) is given by $\varkappa ^*({q})=[{\vartheta (q)\!+\!\vartheta (1\!-\!q)\!-\!2\vartheta (1/2)}]/[{\vartheta (1\!-\!q)\!-\!\vartheta (q)}]= \mathrm{cosech}\left( \sqrt{\phi }Z^{(q)}\right) -\mathrm{cotanh}\left( \sqrt{\phi }Z^{(q)}\right)$, where $q \in (0,1/2)$ and $\mathrm{cotanh}(\cdot )$ and $\mathrm{cosech}(\cdot )$ are the hyperbolic cotangent and cosecant functions, respectively. It is possible to verify that, for every $q \in (0,1/2)$ and for fixed $\zeta$: (i) $\varkappa ^*({q})>0$, (ii) $\varkappa ^*({q})$ does not depend on $\eta$, (iii) higher is the skewness of $T$ higher is the value of $\varkappa ({q})$, and (iv) $\varkappa ^*({q})$ is a monotone increasing function of $\phi$. As a consequence, the parameter $\phi$ may be interpreted as the skewness of the $T$ distribution (for fixed $\zeta$), which is always positive.

Appendix B. ${v}(z_k)$, $d_g(\zeta )$ and $f_g(\zeta )$ expressions

For example, when it is assumed that $\xi$ follows log-normal, log-Student-$t$, log-hyperbolic, log-power-exponential and Birnbaum–Saunders distributions one obtains ${v}(z_k)=1$, ${v}(z_k)=(\nu +1)/(\nu +z^2_k)$, ${v}(z_k)=\varsigma /\sqrt{1+z^2_k}$, ${v}(z_k)=|z_k|^{-\frac{2\varrho }{\varrho +1}}/(1+\varrho )$ and ${v}(z_k)=4\, \mathrm{sinh}(z_k)\mathrm{cosh}(z_k) /\alpha ^2z_k- \mathrm{tanh}(z_k)/z_k$, respectively. Similarly, the quantity $d_g(\zeta )$ is equal to 1, $(\nu +1)/(\nu +3)$, $\{2^{1-\varrho }\Gamma [(3-\varrho )/2]\}/\{(1+\varrho )^2\Gamma [(1+\varrho )/2]\}$ and $2+\frac{4}{\alpha ^2}-\frac{\sqrt{2\pi }}{\alpha }\left\{ 1-\mathrm{erf}\left( \frac{\sqrt{2}}{\alpha }\right) \right\} \mathrm{exp}\left( \frac{2}{\alpha ^2}\right)$ when it is assumed that $\xi$ follows log-normal, log-Student-$t$, log-power-exponential and Birnbaum–Saunders distributions, respectively, where $\Gamma (\cdot )$ represents the gamma function and $\mathrm{erf}(x)=(2/\sqrt{\pi })\int _0^x e^{-t^2}dt$. Also, the quantity $f_g(\zeta )$ is equal to 3, $3(\nu +1)/(\nu +3)$ and $(\varrho +3)/(\varrho +1)$ when $\xi$ follows log-normal, log-Student-$t$ and log-power-exponential distributions, respectively.

Appendix C. Expressions of $d_k(\hat{\varvec{\mu }}|\hat{\varvec{\phi }})$ and $d_k(\hat{\varvec{\phi }}|\hat{\varvec{\mu }})$

We list in the Tables 5 and 6 the expressions of the individual contribution to the deviances for some log-symmetric distributions.

Appendix D. Observed information matrix of $\varvec{\theta }$

The observed information matrix of $\varvec{\theta }$ becomes $-\ddot{\mathbf{L}}_{_{\theta \theta }}$, where

$$\begin{aligned} \ddot{\mathbf{L}}_{_{\theta \theta }}=\frac{\partial ^2 \ell ^*({\varvec{\theta }})}{\partial \varvec{\theta }\partial \varvec{\theta }^{\top }}= \begin{bmatrix} \ddot{\mathbf{L}}_{_{\beta \beta }}&\quad \ddot{\mathbf{L}}_{_{\beta \gamma }}&\ddot{\mathbf{L}}_{_{\beta \mathrm{f}}}\\ \ddot{\mathbf{L}}_{_{\gamma \beta }}&\quad \ddot{\mathbf{L}}_{_{\gamma \gamma }}&\quad \ddot{\mathbf{L}}_{_{\gamma \mathrm{f}}}\\ \ddot{\mathbf{L}}_{_{\mathrm{f}\beta }}&\quad \ddot{\mathbf{L}}_{_{\mathrm{f} \gamma }}&\quad \ddot{\mathbf{L}}_{_{\mathrm{f}\, \mathrm{f}}} \end{bmatrix}, \end{aligned}$$

with

$$\begin{aligned} \ddot{\mathbf{L}}_{_{\beta \beta }}&= -\mathbf{D}_{_{\beta }}^{\top }\varvec{\Omega }^{-1}\mathbf{D}_{({a})}\mathbf{D}_{_{\beta }} + \sum _{k=1}^{n}\frac{z_k}{\sqrt{\phi _k}}{v}_k\mathbf{D}_{_{\beta \beta }}^{(k)},\quad \ddot{\mathbf{L}}_{_{\gamma \gamma }}=-\mathbf{W}^{\top }\mathbf{D}_{({c})}\mathbf{W},\\ \ddot{\mathbf{L}}_{_{{f}\, {f}}}&= -\mathbf{N}^{\top }\mathbf{D}_{(\mathrm{c})}\mathbf{N}-\lambda \mathbf{M}, \quad \ddot{\mathbf{L}}_{_{\gamma \beta }}^{\top }=\ddot{\mathbf{L}}_{_{\beta \gamma }}=-\mathbf{D}_{_{\beta }}^{\top }\varvec{\Omega }^{-\frac{1}{2}}\mathbf{D}_{(\mathrm{h})}\mathbf{W},\\ \ddot{\mathbf{L}}_{_{{f}\beta }}^{\top }&= \ddot{\mathbf{L}}_{_{\beta \mathrm{f}}}=-\mathbf{D}_{_{\beta }}^{\top }\varvec{\Omega }^{-\frac{1}{2}}\mathbf{D}_{({h})}\mathbf{N}\quad \text {and}\quad \ddot{\mathbf{L}}^{\top }_{_{\mathrm{f}\gamma }}=\ddot{\mathbf{L}}_{_{\gamma {f} }}=-\mathbf{W}^{\top }\mathbf{D}_{(\mathrm{c})}\mathbf{N}, \end{aligned}$$

in which $\mathbf{D}_{_{\beta \beta }}^{(k)}\!\!=\!\!\Bigl [{\partial ^2\mu _k}/{\partial \beta _i\partial \beta _j}\Bigr ]$ for $i,j=1,\ldots ,p$, $\mathbf{D}_{(a)}\!=\!\mathrm{diag}\{\mathrm{a}_1,\ldots ,{a}_n\}$, $\mathbf{D}_{(h)}\!=\!\mathrm{diag}\{\mathrm{h}_1,\ldots ,{h}_n\}$ and $\mathbf{D}_{(c)}\!=\!\mathrm{diag}\{\mathrm{c}_1,\ldots ,{c}_n\}$, being ${a}_k\!=\!{v}_k'z_k\! +\! {v}_k$ (${v}_k'$ is the first derivative of ${v}_k$ regarding $z_k$), ${h}_k\!=\! z_k({{v}_k'z_k}\!+\!{2\mathrm{v}_k})/2$ and ${c}_k=z_k {h}_k/2$.