Abstract
Marketing researchers are increasingly taking advantage of the instrumental variable (IV)-free Gaussian copula approach. They use this method to identify and correct endogeneity when estimating regression models with non-experimental data. The Gaussian copula approach’s original presentation and performance demonstration via a series of simulation studies focused primarily on regression models without intercept. However, marketing and other disciplines’ researchers mainly use regression models with intercept. This research expands our knowledge of the Gaussian copula approach to regression models with intercept and to multilevel models. The results of our simulation studies reveal a fundamental bias and concerns about statistical power at smaller sample sizes and when the approach’s primary assumptions are not fully met. This key finding opposes the method’s potential advantages and raises concerns about its appropriate use in prior studies. As a remedy, we derive boundary conditions and guidelines that contribute to the Gaussian copula approach’s proper use. Thereby, this research contributes to ensuring the validity of results and conclusions of empirical research applying the Gaussian copula approach.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Endogeneity is a key concern when using regression models in marketing studies with non-experimental data (Rutz & Watson, 2019; Sande & Ghosh, 2018). In a regression model, endogeneity occurs when one or more regressors correlate with the error term violating a fundamental causal modeling assumption of regression analysis (Wooldridge, 2020). Potential reasons for error term correlations are measurement errors, simultaneous causality, and omitted variables that correlate with one or more independent variable(s) and with the dependent variable(s) in the regression model (e.g., Papies et al., 2017; Rutz & Watson, 2019). Endogeneity problems lead to biased and inconsistent coefficients, which become causally uninterpretable.
The best approach to overcome endogeneity is to specify the model correctly according to the underlying (causal) data-generating mechanism. In practice, however, the required data is usually not available, unless researchers use experimental designs (Ebbes et al., 2016). Marketing literature has extensively discussed methods of dealing with endogeneity (e.g., Rutz & Watson, 2019; Sande & Ghosh, 2018; Zaefarian et al., 2017). Of these methods, the use of instrumental variables (IVs) is particularly well-known for addressing endogeneity problems (Wooldridge, 2010). Despite its frequent application, the IV approach has several drawbacks, as it requires identifying strong and valid instruments (i.e., they correlate strongly with the endogenous regressor but do not correlate with the error term). In applications, however, researchers often fail to revert to suitable variables whose appropriateness as instruments they can sufficiently justify theoretically (Rossi, 2014). Methodologically, only the instrument’s strength can be empirically tested and not its validity (Wooldridge, 2010). Thus, the results of the IV approach do not allow for assessing whether the endogeneity problem has improved or worsened (Papies et al., 2017).
To remedy these concerns, Park and Gupta (2012)—further referred to as P&G—introduced the Gaussian copula approach to cope with endogeneity in regression models. This IV-free method has the advantage of not requiring additional variables, because it directly models the correlation between the potentially endogenous regressor and the error term using a Gaussian copula. Thereby, the approach provides a relatively simple way of identifying and correcting endogeneity biases in regression models (Rutz & Watson, 2019).
There are two variants of the Gaussian copula approach. The original approach by P&G suggests the regression model’s estimation by using an adapted maximum likelihood function that accounts for the correlation between the regressor and the error term using the Gaussian copula (P&G, Eq. 8). The disadvantage of the maximum likelihood approach is that it can only account for one endogenous regressor in the model. In practice, almost all applications therefore use the second variant, which adds a “copula term” to the regression equation (P&G, Eq. 10)—like the control function approach for IV model estimation. The Gaussian copula control function approach can also account for multiple endogenous regressors, which require the simultaneous inclusion of multiple copula terms, one for each regressor (P&G, Eq. 12). In this variant, the copula term is a non-linear transformation of the endogenous regressor, using the inverse normal cumulative distribution function \({\Phi}^{-1}\) and the empirical cumulative distribution function H as follows (P&G, p. 572): \({P}_{t}^{*}={\Phi}^{-1}\left(H({P}_{t})\right)\) where \({P}_{t}^{*}\) is the additional copula term added to the model. This copula term’s parameter estimate is the estimated correlation between the regressor and the error term scaled by the error’s variance (P&G, Eq. 10). On the basis of bootstrapped standard errors, a statistical test of this parameter estimate allows for assessing whether this correlation is statistically significant and endogeneity problems are therefore present (Hult et al., 2018; Papies et al., 2017).
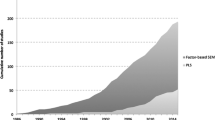
Marketing researchers seem to increasingly adopt the IV-free Gaussian copula approach to address endogeneity problems in their empirical studies. A literature search of the use of the Gaussian copula approach to address endogeneity problems in regression models, and a citation analysis of P&G’s article in literature databases, such as ABI/Informs, EBSCO, Web of Science, Scopus, and Google Scholar, reveal 69 publications by the end of 2020 (see the complete list of these publications and Fig. WA.1.1 in the Web Appendix 1). Most of the publications (62 of the 69, 89.9%) appeared in 2018, 2019, and 2020 and 58.0% (40 of 69) of these journal articles appeared in marketing journals. Besides Marketing Science, which initially published the method, premier marketing journals such as International Journal of Research in Marketing (11), Journal of the Academy of Marketing Science (7), Journal of Marketing Research (6), Journal of Retailing (6), and Journal of Marketing (5) predominantly published Gaussian copula applications. In addition, the Gaussian copula approach has been disseminated across disciplines, for example, in management with its subfields like human resources, information systems, and tourism (23 of 69 articles; 33.3%), and in economics (3 articles; 4.3%).
One of the observations from our literature review is that researchers not only use the Gaussian copula approach to improve the precision of the endogenous regressor’s parameter estimate, but also to identify whether endogeneity poses a problem for a regression model. They do so by assessing the copula term’s statistical significance to determine whether endogeneity is at a critical level in their empirical study or not (e.g., Bornemann et al., 2020; Keller et al., 2018). This approach seems plausible, as the copula term’s parameter estimate is a scaled version of the unobservable correlation between the endogenous regressor and the error term (P&G, p. 572) and can be compared to the Hausman test in a normal IV estimation (Papies et al., 2017). If this correlation is significant, the Gaussian copula approach indicates a potential endogeneity problem and the inclusion of the Gaussian copula term in the regression model should correct the endogeneity problem. Otherwise, if the correlation is not significant, researchers assume that endogeneity does not substantially affect the regression model’s results and, therefore, they often do not include the respective copula terms in their final model (e.g., Campo et al., 2021; van Ewijk et al., 2021; Wlömert & Papies, 2019).
Our literature review shows that using this procedure has a surprising result. Endogeneity only seems to be an issue in studies with larger sample sizes (Fig. 1). More specifically, 15 of the 18 studies (83.3%) with a samples size of 5,000 and larger report a significant copula term at a p-value smaller than 5%. In contrast, of the 24 studies with samples sizes of fewer than 500 observations, only eight (33.3%) identify a significant copula term. Based on these findings, some of the studies conclude that endogeneity does not seem to be an issue. This conclusion may be questionable given the overall pattern that our literature review reveals in Fig. 1. The larger the sample size, the larger the share of significant copula terms in applications. Consequently, there seems to be a sample-size-related problem with the Gaussian copula’s statistical power to identify endogeneity issues. P&G’s initial simulation results do not suggest that there are sample size restrictions. They find that the approach performs very well on sample sizes as low as 200 observations, which calls for a more detailed analysis of sample size’s role in combination with other relevant factors for estimating Gaussian copula models.
Another important observation from our literature review addresses the use of a regression intercept. Our literature review reveals that 53 of the 69 applications (76.8%) use regression models with intercept. In the remaining 16 studies, 13 (18.8%) use fully centered or standardized data, and only three studies (4.3%) do not include an intercept in an unstandardized model (Web Appendix 1, Fig. WA.1.2). This observation appears meaningful, because regression models without intercept are a restricted version of the more general model with intercept. They require strong assumptions to yield meaningful and unbiased estimates for the regression parameters. In most cases, researchers do not have sufficient support for these assumptions and therefore estimate a model with intercept (or fully center or standardize their data). However, the predominant use of regression models with intercept requires special attention, because P&G did not consider models with intercept in their initial simulation studies.
This research presents five simulation studies to substantially extend and deepen our knowledge of the Gaussian copula approach to address endogeneity issues. Study 1 replicates P&G’s original simulation with a larger sample size variation and, additionally, estimates the results of a model with intercept. The study indicates that the Gaussian copula approach for models with intercept has a considerable performance issue, and that the method requires much larger sample sizes than originally expected. In Study 2, we investigate the performance of models with intercept further by varying the true underlying intercept. Study 3 allows us to confirm these findings in respect of multilevel models with a random intercept. In Study 4, we test the Gaussian copula’s performance in a broader application with different endogeneity levels, alternative levels of explained variance, and different endogenous regressor distributions, also taking different sample sizes into account. We find that, in addition to the sample size, the endogenous regressor’s nonnormality and its assessment are another important area of concern regarding the method’s performance. Finally, in Study 5, we reevaluate the Gaussian copula approach’s robustness against misspecification of the error term distribution and the endogenous variable’s correlation structure with the error term, when estimated on models with intercept. We find that the model with intercept is much less robust against misspecification than P&G’s original model without intercept.
Overall, we find that when estimating models with intercept (or fully centered, or standardized data), which, according to our literature review, is most common in marketing applications, researchers need to be far more careful when applying the Gaussian copula approach. In models with intercept, the approach is much more sensitive to violations of its fundamental assumptions. A careless application of the Gaussian copula approach—that is, without adhering sufficiently to its identification conditions (i.e., assessing the endogenous regressor’s sufficient nonnormality, the error term distribution’s normality, and the Gaussian correlation structure)—poses a potential threat to the validity of this approach’s findings. However, our simulation results also allow us to determine boundary conditions that serve as guidelines for the Gaussian copula approach’s appropriate use and allow to obtain reliable results (e.g., with the expected error rate) when identifying and correcting endogeneity problems in regression models with intercept. While the correlation structure is inherently unobservable, researchers should ensure the following prerequisites: First, they should assess the normality of the error term by testing the regression residual’s normality. Second, researchers should confirm sufficient (and not only significant) nonnormality of the endogenous regressor. Third, they should consider far larger sample sizes than originally expected. For each of these steps, we derive clear guidelines on how researchers can verify that they have met each requirement.
The results of this research extend our knowledge of the Gaussian copula approach considerably and call for it to be far more judiciously applied by also taking additional key factors, which had been previously ignored, into account. We provide recommendations and a flowchart illustration regarding when and how the method should be appropriately applied to support decision making. Researchers could therefore take advantage of the Gaussian copula approach’s benefits to identify and correct endogeneity issues in order to ensure that their marketing studies’ results are valid, while also carefully considering its limitations.
Simulation study 1: Intercept extension of P&G’s case 1
In our first simulation study, we use the basic design of P&G’s simulations to investigate the intercepts’ influence on the Gaussian copula’s performance. This allows us to replicate and extend the originally presented simulations, allowing the results to be compared.
Design
In this study, we replicate the data generating process (DGP) in P&G’s Case 1 (i.e., their “Linear Regression Model”), but without the additional IV:
whereby Yt represents the dependent regressor, Pt the endogenous regressor, and ξt the error term in the regression model. The DGP specifies a linear model without intercept, with a uniform distribution of the endogenous regressor Pt, and a correlation of 0.50 between the endogenous regressor and the model’s error term. P&G generated 1,000 datasets for sample sizes of T = 200 and T = 400, and estimated a linear regression without intercept.
We pursue three main objectives with this simulation study. First, we estimate regression models without intercept. Our simulations thereby replicate and confirm P&G’s results. Second, our literature review indicates that most researchers (76.8%) include an intercept when estimating their models. While the DGP does not need an intercept for the reliable model estimation, because the true intercept is zero, researchers do not usually know this a-priori. They therefore usually estimate a model with intercept. Third, we consider a much wider range of sample sizes from 100 up to 60,000 observations (i.e., 100; 200; 400; 600; 800; 1,000; 2,000; 4,000; 6,000; 8,000; 10,000; 20,000; 40,000; 60,000), because our literature review indicates that the sample size might play a far more important role than initially assumed.Footnote 1
We use the DGP to obtain 1,000 datasets for every factor-level combination and estimate the two models (i.e., with and without intercept) for each dataset. We apply the Gaussian copula approach’s two different versions to each of the two models. These versions are the control function approach, which adds a copula term to the regression, and the maximum likelihood approach.
Evaluation criteria
To evaluate the Gaussian copula approach’s performance, we examine three performance criteria: mean bias, statistical power, and relative bias. For a parameter θ (e.g., a regression coefficient), the bias is defined as \(\widehat{\theta }\) – \(\theta\), which is the difference between its estimate \(\widehat{\theta }\) and its true value θ in the DGP. The bias denotes the accuracy of a parameter estimate. The closer the bias is to zero, the closer the estimate is to the true value, and the more accurate the estimate is. Positive values indicate overestimation, while negative values indicate an underestimation of the parameter. In our simulation studies, we determine the mean bias of the focal (endogenous) regressor’s parameter estimate over the 1,000 simulation datasets per factor-level combination.
In addition, we also investigate the relative bias, which depicts a parameter’s bias in the copula model divided by that in the model without copula (i.e., with untreated endogeneity problem). The relative bias allows for assessing how much of the original endogeneity bias remains after the copula approach has corrected it. This evaluation criterion is particularly useful for comparing models with different endogeneity bias in the untreated model. In Study 4, some design factors, such as the error term correlation and the error term variance, affect the original endogeneity bias and, therefore, the amount of bias that the copula approach needs to correct. A remaining bias of -0.19 might therefore be differently evaluated, depending on whether the original endogeneity bias was -0.20 or -0.90, resulting in a relative bias of 95% or 21%.
Statistical power is the probability of a hypothesis test rejecting the null hypothesis when a specific alternative hypothesis is true. In other words, it is the likelihood of obtaining a significant parameter estimate at a given α-level (i.e., type I error level), when the true parameter is different from zero. A high statistical power implies a low chance of making a type II error (i.e., failing to reject the null hypothesis when the alternative is true). In our simulations, we estimate the statistical power by the number of significant parameter estimates for the endogenous regressor or the copula term at a given α-level (e.g., p < 0.05) divided by the number of sampled datasets (i.e., 1,000 per factor-level combination).
Results
The results replicate and confirm P&G’s simulation study for models without intercept. We also find that the Gaussian copula approach accounts for the endogeneity problem and estimates the endogenous regressor’s coefficient without noticeable bias, regardless of the sample size and the estimation method used (Fig. 2 shows the results of the more popular control function approach; Web Appendix 2, Table WA.2.1, provides the outcomes of the maximum likelihood approach).
The situation changes fundamentally when we extend P&G's simulation study by estimating a regression model with intercept. The results show that, in many situations, the endogeneity problem has not been resolved. A substantial bias remains in the copula model for smaller to medium samples. The endogenous regressor’s parameter bias only reaches a negligible level for sample sizes of 4,000 and more. At sample sizes of about 40,000 observations and more, Gaussian copula models with intercept achieve a performance level comparable to those without intercept. This finding holds for both estimation methods (i.e., the control function and the maximum likelihood approach yield almost the same parameter estimates for the endogenous regressor).
To determine the copula term’s and the endogenous regressor’s statistical power, we use bootstrapping with 500 resamples (for further details see P&G; they used 50 and 100 resamples). Based on the bootstrap standard errors, we consider parameters significant if their p-value is smaller than the 5% level. As shown in our literature review, this choice of p-value is consistent with the level commonly used in studies to assess the Gaussian copula’s significance. In line with P&G’s results, the Gaussian copula models without intercept perform exceptionally well. Both the copula term and the endogenous regressor’s power levels are close to 100% across all the sample sizes (Fig. 3, Panel A and B), regardless of estimation method used. When extending the original study in terms of Gaussian copula models with intercept, the statistical power of small to medium-sized samples is less satisfactory and depends on the type of estimation method used. The results of the control function approach require more than 800 observations for the copula term’s parameter estimate to achieve power levels of 80% and higher, and more than 2,000 observations for the endogenous regressor to reach these power levels. The power of identifying a significant copula parameter is slightly higher in small sample sizes when using the maximum likelihood approach. This method needs only 600 observations for the copula term to achieve power levels of 80% and higher. The endogenous regressors’ power does not improve much, as it still requires about 2,000 observations to achieve power levels of 80%.
Mean-centering could be a naïve strategy for coping with the intercept model’s problems. A fully mean-centered (or standardized) model would not need an intercept for the reliable estimation of the regression parameters. We therefore also estimated a model without intercept, in which we mean-centered all the variables before entering the estimation, which 13 (18.8%) of the published studies also do. We find that the results of both methods are equivalent to the model with intercept (see Web Appendix 2, Tables WA.2.1 to WA.2.3).
Discussion
Our discussion addresses two important aspects of our study’s results. First, we discuss the impact of including intercepts in regression models regarding the Gaussian copula approach’s performance. Thereafter, we address potential reasons for why an intercept weakens the performance.
Consequences of intercept inclusion
Our analysis reveals two important findings. First, the Gaussian copula approach cannot always correct the endogeneity problem when estimating the regression model with intercept. Smaller sample sizes are still subject to substantial bias. Second, when estimating the model with intercept, the Gaussian copula approach has low power to identify significant error term correlations in smaller sample sizes. This finding not only holds when using the maximum likelihood approach but is also somewhat more pronounced when using the control function approach. Our literature review reveals that 64 of the 69 studies (92.8%)Footnote 2 use the latter approach when applying the copula approach empirically, which underlines the importance of these findings. While the remaining bias can be substantial, some researchers could argue that correcting some bias is still better than not correcting any. The Gaussian copula approach might therefore still be valuable although it cannot fully correct the endogeneity bias. Nevertheless, researchers should be aware that the method is less effective at reducing endogeneity bias in models with intercept when the sample sizes are small, and that they need to interpret such results more carefully.
Another important issue is the method’s ability to identify endogeneity problems. Some recommendations suggest testing for the presence of endogeneity in regression models by using the copula term’s significance (Hult et al., 2018; Papies et al., 2017). The copula approach’s low power to identify a significant parameter for the copula term in models with intercept makes this practice highly problematic if the sample sizes are not large enough. Researchers need to be far more careful when using the copula term’s significance to decide whether endogeneity poses a problem and whether or not to include the copula term. This is particularly important, since our literature review revealed that researchers currently also use this approach with relatively small sample sizes and, to some extent, probably mistakenly conclude that endogeneity is not a problematic issue in their model. There are two main reasons for the copula term’s low statistical power. First, small sample sizes lead to a substantial underestimation of the copula term’s parameter, which is a scaled version of the correlation between the endogenous regressor and the error term (Web Appendix 2, Table WA.2.2). Second, in the control function approach, the estimated parameter also comprises the error term’s variance (P&G, Eq. 10). The parameter estimate contains additional noise that inflates the standard errors and makes the estimation unreliable, especially in smaller sample sizes. Consequently, this approach has a slightly weaker power compared to the original maximum likelihood approach, which allows for estimating the parameter without the error variance’s scaling.
Overall, the simulation results show the importance of a sufficient sample size if the Gaussian copula approach is to perform well in regression models with intercept in terms of identifying and correcting endogeneity problems. This is a novel finding that has not yet been reported. While this finding imposes limitations on the method in finite samples, our simulations also show that when increasing the sample size toward infinity, the method’s bias is reduced to zero (i.e., it is a consistent estimator) and has sufficient power to identify endogeneity issues. Furthermore, we show that using mean-centered (or standardized) data is not a valid strategy for coping with this issue, which is also in line with previous research on mean-centering (Echambadi & Hess, 2007).
Potential reasons
The pronounced differences between the models estimated with and without intercept raise the question: why is there is such a big difference in their performance? Identification problems could be a potential reason for the weaker performance in models with intercept. P&G highlight two important pre-requisites for identifying the Gaussian copula model. The first is the endogenous regressor’s nonnormality: “If \({P}_{t}\) follows a normal distribution, \({P}_{t}^{*}\) is a linear transformation of \({P}_{t}\) since \({P}_{t}^{*}={\Phi}^{-1}\left(H({P}_{t})\right)\). Hence, we cannot separately identify α and \({\sigma }_{\xi }\cdot \rho\) in (10). As the true distribution of \({P}_{t}\) approaches a normal distribution, the correlation between \({P}_{t}\) and \({P}_{t}^{*}\) increases, causing a multicollinearity problem” (P&G, p. 572). The second is the error term’s normality: “We assume that the marginal distribution of the structural error term is normal” (P&G, p. 570). Both assumptions are fulfilled in our simulations’ DGPs. The error term follows a normal distribution with N(0,1), and the endogenous regressor a uniform distribution with U(0,1). However, there is still substantial correlation between the regressor \({P}_{t}\) and the copula term \({P}_{t}^{*}\) (e.g., on average we observe a correlation of 0.973 in the model with intercept). Consequently, smaller sample sizes seem to have not enough information on the difference between the nonnormal distribution of the regressor \({P}_{t}\) and the normal distribution of the copula term \({P}_{t}^{*}\) to allow a robust estimation of the parameters. If the differences are too small, it is difficult to distinguish the variation that is a result of endogenous regressor from the variation that stems from the error term. In our study, we observed that the copula term’s parameter is underestimated proportional to the parameter overestimation of the endogenous regressor. When the sample size increases, this makes more information available about the differences between the two predictors, and their bias shrinks toward zero.
But why can the model without intercept be more easily identified than the model with intercept? P&G might also provide a solution to this problem in their Appendix I, where they show that even models with endogenous regressors that are normally distributed can be identified if (1) the normal variable has a non-zero mean, and (2) the estimated model does not include an intercept. Nonnormality is therefore only required in models that are estimated with intercept. The endogenous regressor’s availability of a non-zero mean (i.e., the uniform distribution has a mean of 0.50) and the absence of an intercept can therefore compensate for smaller sample sizes’ lack of sufficient information from nonnormality. However, in models with intercept (or when mean-centering the data), this mechanism is not at play and the lack of information from sufficiently strong nonnormality makes it harder to separately identify the copula term and the regressor’s parameter, which results in the pattern of bias that we observe. Consequently, in models with intercept (or mean-centered data), the regressor’s nonnormality needs to be much stronger than in models without intercept.
Simulation study 2: Different intercept levels
In Study 1, we replicate the original simulation results by P&G and show that including a regression intercept in the estimation reduces the copula approach’s performance (both in terms of bias correction and statistical power). In this study, we extend these findings by varying the level of the intercept.
While P&G’s original DGP does not include an intercept (i.e., the intercept is zero), it is unlikely that the true intercept will be zero in practice. Estimating a regression model without intercept requires strong assumptions that are untestable a-priori. In their applications, researchers usually estimate regression models with intercept. In addition, similar to an ignored endogeneity problem, ignoring an intercept when it is necessary is also likely to induce strong bias. Consequently, it is usually not recommended to simply estimate a regression without intercept, and it is unclear whether the copula approach can compensate for this type of bias.
Design
We use the same DGP as in Study 1, but instead of using Eq. 4, which does not include an intercept, we add the intercept i to Eq. 5 constituting \({Y}_{t}\):
In this simulation study, we vary i ϵ {−10, −3, −0.50, −0.10, 0, 0.10, 0.50, 1, 3, 10}.
Results
The results show that the intercept variations do not affect the Gaussian copula approach’s bias (Fig. 4, Panel A) and power when we estimate the model with intercept. We find the same performance as in Study 1, with smaller sample sizes showing relatively high bias and low power, both of which improve with sufficiently large sample sizes.
In contrast, we find that the intercept’s variation affects the Gaussian copula approach when estimated by means of a model without intercept (Fig. 4, Panel B). When the difference between the true intercept and zero increases, the model’s bias also increases as expected. Similar to Study 1, the performance is not dependent on the sample size. However, the bias from the omitted intercept can be larger than the endogeneity bias depending on the intercept’s size. The regression model is, of course, misspecified when estimated without intercept on the basis of a DGP that includes an intercept. Constraining a parameter (in this case to zero) without sufficient prior assumptions will cause this bias in the estimation. Nevertheless, it is interesting that the Gaussian copula in a model without intercept cannot correct the bias of an omitted intercept. If researchers simply omit the intercept, they will trade one bias for another.
Discussion
If the DGP includes a non-zero intercept, estimating the model without intercept is not an option, because the results are biased, even if the model contains a Gaussian copula term. In contrast, when the estimated model includes an intercept, the Gaussian copula approach can correct the endogeneity bias if the sample size is large enough. The copula’s performance is independent of the intercept’s size, and all of Study 1’s findings apply here as well.
Simulation study 3: Multilevel model
To extend the simple linear model in Studies 1 and 2, this simulation study utilizes a multilevel model to assess the sample size’s effect in more depth. In particular, we investigate the effect of different sample sizes within-cluster (level 1) and between-clusters (level 2) on the Gaussian copula model’s performance. For this purpose, we use a two-level, random-intercept model (often referred to as a panel data model in economics). The endogeneity problem occurs at the within-cluster level as a result of a correlation between the within-cluster (level 1) predictor and the within-cluster (level 1) structural error. Although other endogeneity problems could arise in multilevel models (e.g., correlations between level 1 predictors and level 2 error terms, etc.), in our literature review, the abovementioned endogeneity problem seems to be marketers’ most common concern, as they introduce copulas to level 1 (within-cluster) predictors to avoid correlation with the level 1 structural error. Moreover, other instrument-free methods, such as the generalized method of moments approach by Kim and Frees (2007), might address the correlations between regressors and higher-level error terms.
Design
We use a similar DGP as in Study 1, but extend it to the two-level, random-intercept model. Instead of Eq. 4, which does neither include an intercept nor does it consider the clustering of level 1 (within-cluster) observations, we use the following Eq. 6:
where the outcome \({Y}_{jt}\) and regressor \({P}_{jt}\) are observed at the within-cluster level (level 1; e.g., time) with t = 1…T observations in each cluster j (level 2; e.g., brands). The random intercept \({u}_{j} \sim \mathrm{ N}\left(0, {\sigma }^{2}\right)\) denotes an error component that is specific to the cluster and captures all unobserved level 2 specific effects (e.g., all effects that are specific for a brand, but do not vary over time). Both the error component at level 2 (i.e., the random intercept \({u}_{j}\)) and the structural level 1 error component \({\xi }_{jt}\) need to be uncorrelated with the level 1 regressor \({P}_{jt}\) for efficient and consistent estimation.Footnote 3 However, similar to Study 1, we assume an error correlation between \({P}_{jt}\) and \({\xi }_{jt}\) of 0.50 in this DGP, so that Eqs. 1–3 become:
We systematically vary both the level 1 and level 2 sample sizes T and J \(\upepsilon\){5, 10, 20, 40, 60, 80, 100, 200, 400, 600, 800},Footnote 4 excluding total sample sizes lower than 100 and larger than 40,000 for reasons of efficient estimation. In addition, we set the non-random intercept \({u}_{0}\) to zero and the variance of the random intercept to one (i.e., \({\sigma }^{2}=1).\) Consequently, \({u}_{j}\) is uncorrelated with both \({P}_{jt}\) and \({\xi }_{jt}.\) We estimate the model with a random-intercept, multilevel model using maximum likelihood estimation. Moreover, we also consider a fixed-effects panel estimator. We estimate both models with and without the control function approach by adding an additional copula term.Footnote 5 Because the estimation of the copula model’s standard errors is based on non-parametric bootstrapping, we considered two different alternatives of sampling the cases in the bootstrapping. We subsequently report the results of sampling the cases at the cluster level (level 2), which is advised when estimating multilevel data models (Goldstein, 2011). However, most of the studies in our literature review do not reveal the kind of bootstrapping strategy they use. Consequently, we also use a different bootstrapping strategy in which we sample the level 1 observations directly (i.e., ignoring the hierarchical data structure) and find very similar results. Finally, we do not estimate models without intercept in this study, as the original DGP includes a random intercept and ignoring this random-intercept structure could itself induce bias and inefficiency (similar to Study 2).
Results
The results of the endogenous regressor’s bias in Fig. 5 (Panel A) show that there are basically no differences between the copula models in this study and the simple linear model in Study 1 when using the total sample size (i.e., the combination of within-cluster and between-cluster observations) as a reference. Both the random-intercept multilevel model and the fixed-effects panel model follow the same pattern as the simple linear model with copula and intercept in Study 1, with a bias that only reaches a negligible level for sample sizes of 4,000 and more. In addition, we hardly observe any variations in the bias in different combinations of level 1 (within) and level 2 (between) sample sizes, which result in the same total sample size.
The results of the copula term’s power and the endogenous regressor’s power also follow very similar patters as their counterparts in the simple linear model in Study 1. Figure 5 (Panel B) illustrates this pattern in respect of the copula term’s power in the random-intercept multilevel model and fixed-effect panel model compared to the copula term’s power in the model with intercept in Study 1. In contrast to the bias, we observe a slightly larger variation in power for different combinations of level 1 (within) and level 2 (between) sample sizes, which result in the same total sample size. More specifically, the power seems to be slightly larger if the number of level 1 observations (i.e., within cluster observations, e.g., the time series) is larger and the number of level 2 observations (i.e., the number of cross-sectional units, e.g., brands) is smaller. Table WA.3.1 (Web Appendix 3) illustrates this effect for exemplary total sample sizes ranging from 100 to 4,000 observations. However, most of the variation in the copula term’s statistical power comes from the total sample size. Overall, the general finding is the same as in Study 1: a sufficient copula term power of 80% is only reached with 800 and more total observations.
Discussion
This study shows that both the bias and the statistical power’s pattern of results are very similar to Study 1 when the total sample size is considered. Different level 1 and level 2 sample sizes resulting in the same total sample size only marginally affect the bias and statistical power. We can therefore conclude that the total sample size is the important criterion to consider when evaluating the appropriateness of the Gaussian copula approach. Further, the findings from the simple cross-sectional model are generalizable to the multilevel model’s total sample size. We therefore continue to explore this much simpler model and extend it in other important ways.
Simulation study 4: Extension by additional factors
Our previous simulation models investigated the role of the intercept when estimating the Gaussian copula approach. While these focused studies help us understand the role of the intercept and sample size, they only use a single nonnormal distribution of the endogenous regressor (i.e., the uniform distribution) and a fixed error term correlation of 0.50. In this study, we broaden our scope and investigate three additional factors that are potentially important for the performance of the Gaussian copula approach. First, the level of the error correlation with the endogenous regressor defines the endogeneity problem’s severity, potentially affecting both the bias and the power of the Gaussian copula approach (for detailed expectations regarding the different assessment criteria, see Web Appendix 4, Table WA.4.1). Second, the approach requires nonnormality of the endogenous regressor, and Study 1 has highlighted that even the uniform distribution might not be sufficiently nonnormal to identify the model in smaller sample sizes. We therefore vary the endogenous regressor’s distribution. Third, we systematically vary the ratio of explained to unexplained variance (i.e., the R2) in the regression model. This is potentially important because the endogenous regressor’s different distributions imply different variance for this variable. Combined with a fixed error term variance, this would lead to different ratio of explained to unexplained variance, potentially confounding the effect of the distribution with R2 levels. In addition, the ratio of explained to unexplained variance influences the uncertainty in the parameter estimates (i.e., the parameters’ standard errors), potentially influencing the approach’s statistical power. Since most researchers use an intercept to estimate their regression models in practice, we will only focus on the performance of models estimated with intercept in this study. Finally, we again estimate our models with the control function and the maximum likelihood approach. The simulation’s detailed design, which is very similar to that of the previous studies, can be found in Web Appendix WA.4.
Since the endogenous regressor’s nonnormality is a prerequisite to apply the Gaussian copula approach, in practice, researchers usually test whether the encountered distribution is significantly different from a normal distribution. However, it is currently unknown when the endogenous regressor’s distribution is sufficiently nonnormal to allow the application of the Gaussian copula approach. We therefore also assess different nonnormality tests and simple moment measures, like skewness and kurtosis, to identify situations which support the reliable usage of the Gaussian copula approach. Our literature review reveals that 34 of the 69 (49.3%) studies use the Shapiro–Wilk test, 4 (5.8%) the Kolmogorov–Smirnov test, 4 (5.8%) the Kolmogorov–Smirnov test with Lilliefors correction, 2 (2.9%) the Anderson–Darling test, and 2 (2.9%) Mardia’s coefficient. Moreover, only two studies (2.9%) analyze the skewness. The remaining 21 studies (30.4%) do not test or do not report how they tested nonnormality. To assess which nonnormality test best captures the degree of nonnormality needed to identify the Gaussian copula approach, we include these and additional tests (i.e., Cramer-von Mises, Shapiro-Francia, Jarque–Bera, D’Agostino, and Bonett-Seier) that the literature suggests (e.g., Mbah & Paothong, 2015; Yap & Sim, 2011) in our simulation study.
Results
The results presentation begins with the main effects of the potentially relevant factors, namely the sample size, R2, and endogeneity (error correlations), as well as their different levels, on the Gaussian copula’s performance (i.e., power and bias). Thereafter, we assess the effect of the endogenous regressor’s distribution (nonnormality) on power and bias. Next, we present the results of skewness and kurtosis as well as different nonnormality tests’ suitability to reliably identify endogeneity with Gaussian copula models. We focus our presentation on the control function approach’s results, which is the most common approach by far. Overall, the maximum likelihood approach yields similar results. The detailed results of the maximum likelihood approach are presented in the Web Appendix 4 (Table WA.4.2, Fig. WA.4.1).
Main effects of design factors
The results in Table 1 show the main effects of the sample size, R2, and endogeneity levels (error correlations) when averaged across the other simulation factors with regard to the mean and relative bias of the endogenous regressor and statistical power of the copula term and endogenous regressor (at the 5% error level).
We start the analysis by focusing on the copula term and the endogenous regressor’s statistical power. With respect to the copula term’s power, we confirm that it strongly depends on the sample size and only reaches acceptable levels beyond 2,000 observations. Moreover, the copula term’s power does not depend on the R2 level, but, as expected, depends strongly on the endogeneity level (i.e., the error correlation): the higher the error term correlation (i.e., the more severe the endogeneity problem), the higher the copula term’s power to identify endogeneity. This picture changes somewhat when we examine the endogenous regressor’s results. The endogenous regressor’s power again depends on the sample size, but also, as expected, on the R2 level: the power increases with increasing R2. It should be noted that, in this study, the endogenous regressor’s average power is higher than in the previous studies, because we consider higher R2 levels than in the original replication model (where we have an R2 of only about 10%). In contrast, the endogenous regressor’s power only depends marginally on the error term’s correlation level
With regard to the endogenous regressor’s bias, we find that it again depends strongly on the sample size. The bias decreases with increasing sample sizes. The bias is on average lower in this simulation than in the previous simulations, because we consider different endogeneity and R2 levels. However, the relative bias (i.e., the copula model’s bias divided by the endogenous model’s bias) follows the same pattern as our other simulation studies, reaching about 50% for sample sizes of 100 observations, which is similar to Studies 1 to 3 when we include the intercept in the estimation. Moreover, the endogenous regressor’s bias decreases with higher R2 levels, but the relative bias does not depend on R2 (i.e., the copula bias decreases with the same magnitude relative to the original regression’s bias). Finally, the bias also depends on the endogeneity level, with increasing bias with increasing error correlations. However, the endogeneity level again does not affect the relative bias, because the bias in the copula model increases proportionally to the bias in the original regression without copula.
We conclude and reconfirm that the Gaussian copula’s performance depends strongly on the sample size, with substantial effects on both power and bias. In contrast, the endogeneity level does not affect the copula model’s ability to correct the endogeneity bias as indicated by the relative bias, but does affect the copula term’s power. The higher the error term correlation (i.e., the more severe the endogeneity problem), the greater the power to identify endogeneity. Finally, we find that the R2 level is not relevant for the copula performance, as it neither affects the power nor relative bias. In the following analyses, we will therefore not further consider R2 variations and only focus on the interplay between the level of endogeneity, the sample size, and the distributional form.
We substantiate these findings by using a (logistic) regression with the copula and the endogenous regressor’s power, as well as the endogenous regressor’s mean and relative bias, as dependent variables and the design parameters as independent variables. The results indicate that the R2 level does not have a significant influence on the copula term’s power, or on the relative bias, while all the other simulation factors have significant effects (see the Web Appendix 4, Table WA.4.3).
Endogenous regressor’s distribution
Next, we analyze the power and relative bias of different distributional forms (i.e., different levels of nonnormality) when varying the sample sizes and the endogeneity levels. The results show that complex interactions between the distribution, sample size, and endogeneity level influence a copula term’s power (see Web Appendix 4, Fig. WA.4.2). For weak endogeneity problems, even heavily nonnormal distributions, like the log-normal or gamma distribution, show quite low power unless the sample sizes are very large. However, for larger error correlations, strongly nonnormal distributions also have sufficient power if the sample sizes are smaller.
In contrast, the endogeneity level does not affect the endogenous regressor’s relative bias. Our analysis indicates that only a combination of sample size and distributional form affects the relative bias and that larger sample sizes and the distributions’ higher nonnormality reduce the endogenous regressor’s relative bias (Fig. 6). Interestingly, we also observe a few situations in which heavily nonnormal distributions (i.e., some of the gamma, log-normal, and chi2) over-compensate the endogeneity bias in smaller sample sizes, resulting in a bias in the opposite direction of the original endogeneity bias (e.g., underestimating instead of overestimating the coefficient).
Relative bias of the endogenous regressor for different distributions with varying distribution parameters, sample sizes, and endogeneity levels. Note: Different colors represent different distribution parameters: Beta distribution (p, q): red (0.50, 0.50), green (1, 1), blue (2, 2), purple (4, 4); Chi2 distribution (df): red (2), green (8), blue (14), purple (20); Gamma distribution (α, β): red (1, 0.50), green (1, 2), blue (2, 4), purple (4, 2); Log-normal distribution (μ, σ): red (0, 1), green (0, 0.75), blue (0, 0.50), purple (0, 0.25); Student t distribution (df): red (3), green (4), blue (5), purple (6)
Nonnormality tests
Since endogeneity is not observable a-priori, researchers can only assess the distribution’s nonnormality and the sample size to decide whether the Gaussian copula approach could be applied. Accordingly, several Gaussian copula applications in our literature review test the endogenous regressor’s nonnormality by using a nonnormality test, mostly the Shapiro–Wilk test. However, common nonnormality tests’ high sensitivity to small deviations from normality is a problem. In our simulation, for example, the Shapiro–Wilk test reports a significant (at p < 0.05) finding in 96% (94% with p < 0.01) of all the cases (Table 2). Only the D’Agostino and Bonett-Seier tests have sensitivity rates below 90%. In contrast, the copula term is only significant in 67% of the cases. Consequently, nonnormality test cannot help researchers directly decide whether a distribution is sufficiently nonnormal to apply the Gaussian copula approach. Owing to our simulation study, we find that the correspondence between the copula and the nonnormality test’s significance is relatively low (between 61% and 76%), with no test clearly outperforming the other (for the correspondence analysis, see the Web Appendix 4, Table WA.4.4). This outcome is roughly equivalent to the copula term’s power (i.e., 67%).
The analyzed p-values (i.e., 0.05 and 0.01) represent arbitrary cut-off levels that may reduce the correspondence greatly. We therefore also assessed the correlation between the copula term’s bootstrap t-statistic and the nonnormality tests’ test statistic. Table 2 shows that the Anderson–Darling and Cramer-von Mises tests have the highest correlation with the copula term’s bootstrap t-statistic. In addition, the results indicate that kurtosis and skewness alone are not good predictors of the copula term’s t-statistic. Nevertheless, it is interesting that skewness seems to be more important than kurtosis. Finally, we also find that the correlation between the VIF and copula t-statistic is not very pronounced.
Discussion and boundary conditions analysis
Based on Study 4’s simulation results, we find that the amount of explained variance has no noticeable influence on the Gaussian copula’s power. In contrast, and as expected, the endogeneity level has a strong effect (i.e., it is harder to identify a small endogeneity problem). However, even for high levels of endogeneity the Gaussian copula approach still performs poorly when sample sizes are small. We also confirm the sample size’s strong effect on the Gaussian copula’s power and bias, and the importance of the endogenous regressor’s nonnormality to identify the Gaussian copula’s parameter estimates. Consequently, researchers should use the Gaussian copula approach cautiously if they suspect the endogeneity problem is not pronounced (i.e., a small error correlation), the sample size is small, or the nonnormality is insufficient.
While the sample size is observable and the nonnormality can be analyzed, the Gaussian copula approach’s objective is to determine the endogeneity level, which is unknown a-priori. However, a failure to identify a significant copula does not necessarily imply the absence of endogeneity. It could imply a relatively small endogeneity problem (which might be negligible), but it could also imply an insufficient sample size or nonnormality. A sufficient sample size and the careful assessment of nonnormality are therefore particularly important for the Gaussian copula approach’s application.
Popular nonnormality tests, such as the Shapiro–Wilk test, which, according to our literature review, is the one most often used in Gaussian copula applications, do not identify sufficient nonnormality with common p < 0.05 (or p < 0.01) thresholds. These tests are too sensitive to small deviations from nonnormality that could lead to insignificant copula terms, even for substantial endogeneity problems (i.e., large error correlations). In addition, the nonnormality should specifically stem from skewness and not (only) from kurtosis. Our results show that nonnormal distributions with high kurtosis, but small skewness, perform relatively poorly regarding identifying the copula term with small to medium sample sizes. Researchers are therefore also advised to report these more descriptive nonnormality statistics when describing their variables’ nonnormality. Finally, we find that the Cramer-von Mises tests and the Anderson–Darling test seem to be the most promising candidates for identifying sufficient nonnormality, because they correlate best with the copula term’s t-statistic. This is not surprising, as both tests build on the empirical cumulative distribution function, which also underlies the Gaussian copula approach. The Cramer-von Mises test statistic is the integral of the squared deviation of the endogenous regressor’s empirical distribution and the theoretical normal distribution. The Anderson–Darling test is an extension of the Cramer-von Mises test that adds a weighting factor to put more weight on the distribution’s tails.
Using our simulation results, we subsequently derive actionable boundary conditions for the required nonnormality and sample size, and provide recommendations that could help researchers identify situations with sufficiently high copula term power in regression models with endogeneity. In general, we find a complex relationship between the sample size, the endogenous regressor’s nonnormality, and the Gaussian copula’s power level. We reveal, for example, that the lower the number of observations, the higher the skewness levels required to obtain power levels of 80% and higher (Web Appendix, Fig. WA.4.3). Similarly, we find that smaller sample sizes require higher levels of the Anderson–Darling and Cramer-von Mises test statistics for a copula power of at least 80%. These two test statistics’ required levels decrease with a higher number of observations. In contrast, we observe no clear pattern for the kurtosis, which is in line with its low correlation with the t-statistic.
To turn these findings into more actionable recommendations, we consider all observable characteristics of our models (e.g., sample size, skewness, kurtosis, R2, and nonnormality test statistics) to derive thresholds that will ensure that the Gaussian copula approach has a high power level. Researchers can use these thresholds as an approximate point of orientation to ensure the method’s effective use in their applications. We do so by employing decision tree analysis, using the C5.0 algorithm (Kuhn et al., 2020). Based on our simulation study’s results (i.e., Study 4 of regression models with intercept), our goal is to identify situations where the Gaussian copula approach has a power of at least 80%. Figure WA.4.4 (Web Appendix) shows a decision tree result in which we consider sample size, skewness, kurtosis, and R² for predicting the copula’s power (the latter two are not relevant and therefore do not appear in the decision tree). The classification error is 6.4% with 8 false negatives and 6 false positive out of 220 simulation design conditions (i.e., 20 distributions times, 11 sample sizes). According to the results, the sample size should be larger than 1,000 observations if the skewness is larger than 0.774. If the skewness is equal to or smaller than this level, more than 2,000 observations are required to obtain an 80% power level. For smaller sample sizes in the range between 400 to 1,000 observations, a skewness level of 1.932 is required to obtain adequate power. None of our distributions achieves a sufficient power level for the copula term for sample sizes of 200 observations or smaller. Please note that these findings are derived from the outcomes of the simulation studies, which are constrained by the parameter space of the simulation design. Therefore, these thresholds are an approximate point of reference to guide decision-making. Moreover, researchers must ensure that their empirical examples meet the other necessary conditions for using the Gaussian copula approach that we investigate in this research (see Fig. 8 for a comprehensive summary).
We ran similar decision tree analyses that considered the Anderson–Darling and the Cramer-von Mises test statistics (see the Web Appendix 4, Fig. WA.4.5). For example, if the Anderson–Darling (Cramer-von Mises) test statistic has a value larger than 18.964 (3.488), the Gaussian copula’s power is 80% and higher. With a sample size of more than 1,000 observations, a somewhat lower level of the test statistic, but larger than 15.159 (2.628), can achieve this power level.Footnote 6
In summary, the endogenous variable’s nonnormality, as indicated by minimum levels of skewness, and the Anderson–Darling or the Cramer-von Mises test statistics, in combination with a sufficiently large sample size, may ensure that the Gaussian copula approach has adequate power. Our study results suggest that researchers need to ensure that there are relatively high nonnormality levels, which should stem from the endogenous variable’s skewness, and a relatively large sample size, in order to apply the Gaussian copula approach adequately in regression models with intercept.
Simulation study 5: Robustness to misspecification
Besides the nonnormality of the endogenous regressor, P&G highlight two additional important criteria to identify the Gaussian copula approach: 1) the normality of the error term, and 2) the Gaussian copula correlation structure. In their simulations, they show that the method is robust against misspecification of the error term and correlation structure. However, these simulations are also estimated without intercept. This study investigates whether including an intercept in the estimation retains this robustness or causes additional problems. To achieve this objective, we again closely replicate the simulations from P&G (for detailed design of these simulations, see Web Appendix 5). For the error term misspecification, we specify several symmetric nonnormal error distributions from the Beta and Student-t family, which are similar to those used in Study 4. We thereby extend the simulation by P&G, who only report the uniform distribution’s results (i.e., Beta[1,1]). In addition, we evaluate whether the error term’s nonnormality also manifests in nonnormality of the regression residual. If this is the case, researchers could evaluate whether their model fulfils this identification criterion. In respect of the copula structure misspecification, we use the same alternative copula models as in P&G’s article (i.e., Ali-Mikhail-Haq distribution with θ = 1, Plackett distribution with θ = 20, Farlie-Gumbel-Morgenstern distribution with θ = 1, Clayton copula with θ = 2, and Frank copula with θ = 2).
Results
In respect of the error term misspecification, we find the same overall pattern of remaining bias and low power at smaller sample sizes when the model is estimated with intercept as in our previous studies (for the detailed results, please see Web Appendix 5). However, regarding the bias, we uncover an additional problem related to the misspecification of the error term. When the error term is nonnormally distributed, the Gaussian copula approach is no longer consistent (Fig. 7). That is, the remaining bias does not shrink toward zero when the sample size increases. Instead, the bias approaches an unknown nonzero constant, depending on the error term’s level of nonnormality. In our simulation, this value is positive for negative kurtosis (e.g., beta distributions) and negative for positive kurtosis (e.g., student-t distributions).Footnote 7 In the latter case, the method overcorrects the initially positive endogeneity bias, resulting in a negative remaining bias. In all our cases, the bias does not occur when estimating the model without intercept, reconfirming P&G’s results on robustness without intercept. The power of the copula term (i.e., the test for the presence of significant error correlation) does not seem to be affected beyond the already uncovered issues in our previous simulation studies. Variations in power due to the error term distributions are relatively small and limited to smaller sample sizes.
The results show similar problems in terms of the copula misspecification when estimating the method with intercept. For some correlation structures (e.g., Frank and Farlie-Gumbel-Morgenstern), the method does not correct any bias, when estimated with intercept (while we reconfirm its robustness when estimated without intercept). Other copula models show a similar pattern as the error term’s misspecification. The bias varies by sample size, decreasing with larger sample sizes but converging to an unknown nonzero constant, which differs across the analyzed copula models.Footnote 8 For those copulas that correct the bias, the statistical power of the copula term is not affected beyond the already revealed small sample size issues. However, the statistical power of those copulas that do not correct the bias (i.e., Frank and Farlie-Gumbel-Morgenstern) is low across all sample sizes, erroneously indicating an absence of endogeneity.
Discussion
Researchers estimating models with intercept (which is the standard use case in marketing research) should not only test the endogenous regressor’s nonnormality carefully, but they should also ensure the Gaussian copula approach’s additional assumptions. While the error term’s normality can be checked by assessing the regression residual (we find promising results in this regard, which we report in Web Appendix 5), the correlation structure with the unobservable error term is inherently unobservable, and therefore solely subject to assumptions made by the researcher. If these assumptions are violated, the method may experience a strong remaining bias, not correct any bias at all, or even overcorrect the initial bias in the other direction. Hence, the copula model might not perform better than the original endogenous model.
Summary of key findings
Researchers in marketing and other disciplines are increasingly taking advantage of the IV-free Gaussian copula approach to identify and correct endogeneity problems in regression models. The method’s increasing relevance motivates a closer examination of its adequate performance on the basis of simulation studies. This research replicates and extends P&G’s initial simulation studies with several new and important simulation factors that are highly relevant in research applications. The results reveal critical issues and limitations when using the Gaussian copula approach to identify and correct regressions models with intercept. The method is not as straightforward and easy to use as previously assumed. At the same time, our simulation results allow us to provide recommendations that are essential to ensure that researchers use the Gaussian copula approach appropriately and obtain valid results on which they can base their findings and conclusions. Table 3 summarizes our findings and provides guidelines to take advantage of the IV-free Gaussian copula approach while avoiding misapplications, which may have occurred unintentionally in the past. In doing so, we contribute to the rigor of regression models’ application and to the accurate presentation and interpretation of marketing research.
In our five studies, we reveal that several factors affect the Gaussian copula approach’s performance. We focus on the interplay between the regression intercept and sample size, as P&G examined regression models without intercept and, only to a limited extent, the sample size. Our literature review reveals that these two factors play an important role when applying the Gaussian copula approach. First, almost all researchers include an intercept in their model or mean-center their data (66 of 69 studies in our literature review or 95.7%). Second, our literature review provides indications that sample size, and, therefore, the statistical power, are more important for the results than originally expected. Consequently, our simulation studies shed light on the role of the sample size and the statistical power when using the Gaussian copula approach to identify and correct endogeneity problems.
In accordance with P&G, our Studies 1 and 2 confirm the method’s high performance in regression models without intercept, even in a wider range of sample sizes. A very different picture emerges when researchers use regression models with intercept or mean-centered data, which is common in marketing studies. The Gaussian copula approach has far less power and higher remaining endogeneity bias in these regression models, especially when using the estimation method that most researchers prefer: the control function approach (i.e., adding additional copula terms as new variables to the regression model). In such models, the Gaussian copula approach’s identification and correction of endogeneity problems requires a much larger sample size. If this requirement is not met, the approach may not identify an endogeneity problem even though it is present and has substantial endogeneity bias. This finding is of central relevance, because our literature review reveals that most studies apply the Gaussian copula approach to regression models that include an intercept or mean-centered data. It is therefore very likely that studies with smaller sample sizes do not always identify significant copula terms due to their insufficient power, although endogeneity problems are present (Fig. 1). Consequently, researchers may come to the false conclusion that endogeneity problems do not affect their studies’ results and present invalid findings and conclusions.
In Study 3, we show that the findings of Studies 1 and 2 extend to multilevel models, in which the endogeneity is present at the within-cluster level (i.e., the correlation between a within-cluster predictor and the structural error) when the total sample size is taken into account. In our literature review, most studies with multilevel data have rather larger sample sizes, but a few also have total sample sizes in the range for which we identify the Gaussian copula approach’s reduced performance. Consequently, in respect of multilevel (or panel) models, the same recommendations apply regarding a sufficient sample size and nonnormality as do for the simpler, cross-sectional regression model.
Study 4 aims at helping researchers apply the Gaussian copula approach appropriately and exploit its advantages effectively. More specifically, in Study 4, we extend the simulations to include several additional factors that are relevant for regression analyses, such as the endogenous regressor’s nonnormality, the explained variance (R2 level), and the error correlation. Study 4 derives boundary conditions for these factors to guide the Gaussian copula approach’s appropriate use in studies. The findings substantiate that for sample sizes below 1,000 observations, only a few very nonnormal distributions (e.g., skewness above 2 or Anderson–Darling test statistics above 20) lead to sufficiently high power when using the copula term in regression models (i.e., larger than 80%). Nevertheless, none of our considered distributions has sufficiently large power for sample sizes equal to or less than 200 observations. In contrast, the nonnormality is still important for sample sizes above 1,000 observations, but to a lesser degree. These boundary conditions of factors of key relevance for the Gaussian copula approach’s valid use in regression models with intercept (i.e., the required sample size, the endogenous regressor’s nonnormality, and its identification with suitable nonnormality tests) allow researchers to effectively identify and correct endogeneity problems.
Using the maximum likelihood approach might be a potential solution to remedy some of these concerns, as it has slightly larger power to identify endogeneity (but has the same remaining bias). However, the control function approach has several advantages: (1) It is much faster and easier to implement in models that go beyond the simple linear regression model (e.g., panel models, binary choice models, etc.) that might make deriving the appropriate likelihood function more complex or even impossible, and (2) it allows for including more than one copula term and, therefore, for treating several endogenous regressors simultaneously. For these reasons, the maximum likelihood approach might not be a practical solution in many situations, and the gains in power are also limited.
Finally, Study 5 sheds light on the misspecification of the error term and the copula structure when regression models are estimated with intercept. This study’s results underscore concerns about the method’s estimation accuracy when an intercept is present, and contradict findings about its robustness as presented in P&G's original study. Researchers should ensure both the presence of an appropriate Gaussian copula correlation structure and a normally distributed error term. While the analysis of the regression residual allows an assessment of the error term, the correlation structure is inherently unobservable and therefore only subject to untestable theoretical considerations.
We have two recommendations for research that does not satisfy the boundary conditions identified in this research: first, researchers should carefully assess whether the data and model might be prone to empirical identification issues. They can do so by, for example, carefully checking whether the endogenous regressor has sufficient nonnormality and checking for multicollinearity issues after including the Gaussian copula, as well as testing the regressions’ residual for normality. Second, and more importantly, researchers should avoid using the Gaussian copula approach to test for endogeneity (i.e., concluding that endogeneity is not a problem due to insignificant copula terms), but should revert to traditional ways of handling endogeneity problems, such as using IVs or other means of identifying the causal mechanism.
Conclusions and future research
The Gaussian copula approach is valuable for identifying and correcting endogeneity issues in regression models when the assumptions are fulfilled. However, when the regression models contain an intercept, the method is much more constrained than initially thought. It is less robust against deviations of the error term’s normality, the Gaussian copula correlation structure between the error and the regressor, and the regressor’s nonnormality. Even if these preconditions are met, the approach requires large sample sizes to perform well in models with intercept. However, constraining the intercept to zero is usually not an option, because this would also induce substantial bias as highlighted in our Study 2. While the Gaussian copula’s simple application has gained the method the reputation of being an easy-to-use add-on in any study that has a potential endogeneity problem, our results highlight that researchers should use the Gaussian copula approach more cautiously, especially when sample sizes are small and the model includes a regression intercept (or mean-centered data). Figure 8 summarizes our studies’ findings and conclusions in a decision flowchart by illustrating the path of choices that researchers need to consider when deciding whether to apply the Gaussian copula approach. Given these new recommendations, researchers might far less often conclude that the Gaussian copula approach is a recommended method for dealing with endogeneity problems.
These recommendations represent approximate thresholds based on the results of our simulation studies that provide researchers with an indication of whether the copula can be successfully applied.Footnote 9 However, they do not replace careful theoretical consideration of the nature of endogeneity and the fulfillment of the Gaussian copula approach’s general assumptions (i.e., the nonnormality of the endogenous regressor, the normality of the error term, and the Gaussian copula correlation structure). Moreover, these recommendations are based on models with a single continuous endogenous regressor variable. It is likely that multiple endogenous regressors or discrete variables will increase the requirements for identifying the copula and, therefore, for the method’s successful application. More research is needed to extend the recommendations in respect of these areas.
Future research should therefore extend our findings by adding simulation studies that, for instance, analyze the Gaussian copula’s performance with additional endogenous regressor distributions (i.e., additional nonnormality levels) to further substantiate our thresholds. Furthermore, we are currently not aware of possibilities to test the assumption that the error term and the endogenous variable follow a Gaussian copula correlation structure. However, a misspecification potentially leads to invalid results as our simulation results show. Thus, creating a test for this assumption would greatly enhance confidence in the method’s accuracy. In addition, future studies should analyze discrete distributions further (i.e., P&G show that discrete distributions suffer even more from identification problems and that thresholds might therefore be much higher in such cases) and revert to more complex regression models with multiple endogenous regressors. Additional knowledge about these factors’ relevance will help researchers use the method adequately to derive valid inferences for marketing decision making. Moreover, future research should address the core issue that the Gaussian copula approach’s usability is limited regarding finite (small) sample sizes, but works well in the limit when sufficient information is available to identify the model. Methodological research should aim at developing a solution for this limitation.
The number of empirical applications of the Gaussian copula method is currently increasing, making it the most popular IV-free method in marketing and management research. Nevertheless, there exist a variety of other IV-free approaches such as the latent instrumental variable approach (Ebbes et al., 2005), the higher moment approach (Lewbel, 1997), and the heteroskedastic errors approach (Lewbel, 2012). These methods are based on different identification assumptions and, depending on the underlying model and data structure, they might be preferable for different models or different types of data and, therefore, in situations in which the Gaussian copula approach is not applicable. We therefore call for further research on comparing the methods under varying conditions to provide researchers with better guidelines on which method to use when. However, all IV-free approaches demand fulfillment of certain identification requirements, which are often untestable. Applying any of these methods blindly may provide no better results than merely ignoring endogeneity problems does. Consequently, it is important that researchers are aware of these approaches’ limitations, because ultimately, they always need to carefully argue that the underlying assumptions have been fulfilled.
Change history
25 February 2022
The original version of this paper was updated to add the missing compact agreement Open Access funding note.
Notes
We make the R-Code for the simulation and the results datasets available in the paper’s online repository at https://t1p.de/euqn.
Three studies do not report how they include the copula, while only two report the use of the original maximum likelihood approach.
If the within-cluster level 1 regressor \({P}_{jt}\) correlates only with the random intercept \({u}_{j}\), but not with the structural error \({\xi }_{jt}\), the fixed-effects panel model estimator is consistent, but not efficient.
Although J is usually large in typical panel data models and T small, the opposite is true of multilevel models employed in the social sciences where researchers, for example, investigate many students clustered within a few schools. In our literature review, most of the studies that use Gaussian copulas to address endogeneity in multilevel data have larger J and smaller T, although we also found studies with large T and small J. Consequently, we systematically vary both components.
To focus our analyses, we do not consider the alternative maximum likelihood method for copula estimation in this study, because it is rarely used in empirical application and complex to implement.
These thresholds become more restrictive for higher power levels. For example, to accomplish a 90% power level, the Gaussian copula approach requires more than 600 (2,000) observations at a skewness level exceeding 1.974 (0.998). Similarly, the Anderson–Darling (Cramer-von Mises) test statistic requires a value of more than 67.875 (12.246) for sample sizes equal to and smaller than 2,000 and a value of 46.832 (7.994) for sample sizes larger than 2,000 observations.
Comparing the Gaussian copula maximum likelihood approach to the control function approach, we find that the remaining biases (in both directions) are larger in the maximum likelihood approach. This suggest that the Gaussian copula control function approach is slightly more robust against error term misspecifications.
With respect to the copula model misspecification, both the approaches (i.e., maximum likelihood and control function) show indistinguishable patterns of bias. This suggests that both approaches are equally affected.
We provide sample code to illustrate how to test these assumptions in the online repository of the paper at https://t1p.de/euqn.
References
Bornemann, T., Hattula, C., & Hattula, S. (2020). Successive product generations: Financial implications of industry release rhythm alignment. Journal of the Academy of Marketing Science, 48, 1174–1191.
Campo, K., Lamey, L., Breugelmans, E., & Melis, K. (2021). Going online for groceries: Drivers of category-level share of wallet expansion. Journal of Retailing, 97, 154–172.
Ebbes, P., Wedel, M., Böckenholt, U., & Steerneman, T. (2005). Solving and testing for regressor-error (in)dependence when no instrumental variables are available: With new evidence for the effect of education on income. Quantitative Marketing and Economics, 3, 365–392.
Ebbes, P., Papies, D., & van Heerde, H. J. (2016). Dealing with endogeneity: A nontechnical guide for marketing researchers. In C. Homburg, M. Klarmann, & A. Vomberg (Eds.), Handbook of market research. Springer International Publishing.
Echambadi, R., & Hess, J. D. (2007). Mean-centering does not alleviate collinearity problems in moderated multiple regression models. Marketing Science, 26, 438–445.
Goldstein, H. (2011). Multilevel statistical models (4th ed.). Wiley.
Hult, G. T. M., Hair, J. F., Proksch, D., Sarstedt, M., Pinkwart, A., & Ringle, C. M. (2018). Addressing endogeneity in international marketing applications of partial least squares structural equation modeling. Journal of International Marketing, 26, 1–21.
Keller, W. I. Y., Deleersnyder, B., & Gedenk, K. (2018). Price promotions and popular events. Journal of Marketing, 83, 73–88.
Kim, J.-S., & Frees, E. W. (2007). Multilevel modeling with correlated effects. Psychometrika, 72, 505–533.
Kuhn, M., Weston, S., Culp, M., Coulter, N., & Quinlan, R. (2020). R package C50: C5.0 decision trees and rule-based models (version 1.3.1): https://cran.r-project.org/web/packages/C50/.
Lewbel, A. (1997). Constructing instruments for regressions with measurement error when no additional data are available, with an application to patents and R&D. Econometrica, 65, 1201–1213.
Lewbel, A. (2012). Using heteroscedasticity to identify and estimate mismeasured and endogenous regressor models. Journal of Business & Economic Statistics, 30, 67–80.
Mbah, A. K., & Paothong, A. (2015). Shapiro-Francia test compared to other normality test using expected p-value. Journal of Statistical Computation and Simulation, 85, 3002–3016.
Papies, D., Ebbes, P., & van Heerde, H. J. (2017). Addressing endogeneity in marketing models. In P. S. H. Leeflang, J. E. Wieringa, T. H. A. Bijmolt, & K. H. Pauwels (Eds.), Advanced methods in modeling markets (pp. 581–627). Springer.
Park, S., & Gupta, S. (2012). Handling endogenous regressors by joint estimation using copulas. Marketing Science, 31, 567–586.
Rossi, P. E. (2014). Even the rich can make themselves poor: A critical examination of IV methods in marketing applications. Marketing Science, 33, 655–672.
Rutz, O. J., & Watson, G. F. (2019). Endogeneity and marketing strategy research: An overview. Journal of the Academy of Marketing Science, 47, 479–498.
Sande, J. B., & Ghosh, M. (2018). Endogeneity in survey research. International Journal of Research in Marketing, 35, 185–204.
van Ewijk, B. J., Stubbe, A., Gijsbrechts, E., & Dekimpe, M. G. (2021). Online display advertising for CPG brands: (When) does it work? International Journal of Research in Marketing, 38, 271–289.
Wlömert, N., & Papies, D. (2019). International heterogeneity in the associations of new business models and broadband internet with music revenue and piracy. International Journal of Research in Marketing, 36, 400–419.
Wooldridge, J. M. (2010). Econometric analysis of cross section and panel data (2nd ed.). MIT Press.
Wooldridge, J. M. (2020). Introductory econometrics: A modern approach (7th ed.). Cengage Learning.
Yap, B. W., & Sim, C. H. (2011). Comparisons of various types of normality tests. Journal of Statistical Computation and Simulation, 81, 2141–2155.
Zaefarian, G., Kadile, V., Henneberg, S. C., & Leischnig, A. (2017). Endogeneity bias in marketing research: Problem, causes and remedies. Industrial Marketing Management, 65, 39–46.
Acknowledgements
The authors presented some of the research results depicted in this paper at the 2020 AMA Winter Academic Conference, San Diego, CA, February 14-16, 2020, but without publication in the conference proceedings. The authors thank Peter Ebbes, HEC Paris, France, and Dominik Papies, University of Tübingen, Germany, for their useful comments on our research presentation. Moreover, the authors like to thank Edward E. Rigdon, Georgia State University, United States of America, for his helpful comments to improve an earlier version of the manuscript. For their simulation studies, the authors used the high-performance computing cluster of Hamburg University of Technology, Germany.
Funding
Open Access funding enabled and organized by Projekt DEAL. This research was partly funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—VO 1555/1-1.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This manuscript was handled by Editor John Hulland.
Supplementary Information
Below is the link to the electronic supplementary material.
ESM1
(DOCX 3.85 MB)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Becker, JM., Proksch, D. & Ringle, C.M. Revisiting Gaussian copulas to handle endogenous regressors. J. of the Acad. Mark. Sci. 50, 46–66 (2022). https://doi.org/10.1007/s11747-021-00805-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11747-021-00805-y