Abstract
Single-lip deep-hole drilling (SLD) is characterized by high surface quality and compressive residual stress in the subsurface of the drill hole. These properties depend significantly on the thermomechanical conditions in the machining process. The desired subsurface properties can be adjusted in-process via process monitoring near the cutting zone with a sensor-integrated tool and closed loop control when the thermomechanical conditions are maintained in the optimum range. In this paper, a method is presented to control the thermomechanical conditions to adjust the properties in the subsurface. The process model integrated in the controller is implemented as a soft sensor and takes into account the residual stresses, the roughness, the hardness and the grain size in the surface as well as in the subsurface depending on the process control variables, such as the feed rate and cutting speed. The correlation between the process variables, the thermomechanical conditions of the cutting process and the subsurface properties are investigated both experimentally and by finite element (FE) simulations. Within a justified process parameter range, characteristic fields for the soft sensor were established for each property. In addition, the procedure of controller design and the employed hardware and interfaces are presented.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
According to the Association of German Engineers (VDI 3208), the single-lip deep hole drilling method is used for boreholes with a diameter of D = 0.5 mm to 80 mm and a depth of l = 3 D to l = 250 D. In individual cases, depths of up to 900 D can be achieved [1]. In the transitional range from D = 20 mm, the BTA method is used as an alternative [2]. Single-lip deep hole drilling (SLD) uses asymmetrical single-cutting tools applying a passive radial force to the bore wall via the incorporated guide pads. This results in interactions between the tool and the workpiece in a combination of cutting and forming [3]. The cooling lubricant required to remove the heat and the chips from the cutting area is fed at comparatively high pressures in the range of 20–250 bar inside the tool. The produced chips are transported out of the hole through the corrugation of the tool, continuously. Single-lip deep hole drilling can be applied for a wide range of materials from aluminum to super alloys and achieves a high dimensional accuracy regarding the diameter and the straightness as well as high surface qualities in the workpieces. Both the single-lip deep hole drilling process as well as the tools can be improved further with respect to maximum performance and applicability on specially designed machines. Many applications exist for single-lip deep hole drilling e.g. for diesel injection components, medical tools, plastic injection molds and many more. The drilling diameter, the drilling length and the surface quality to be produced are the most important aspects for the use of deep hole drilling processes [1].
Single-lip deep hole drilling fulfills the quality requirements very well with the achievable high surface quality and drilling tolerances of IT8 to IT9 [4]. During the process, the protruding guide pads come into contact with the bore wall and affect the subsurface of the borehole by forming. Depending on the cutting speed and the feed, which influences the thermomechanical condition in the process zone as well as the level of the normal force acting through the guide pads three different profiles can be distinguished. The so-called open profile exists at low forces and consists mainly of feed marks. The partially closed profile consists of both, marks along the complete drilling track and marks, which occur just in sections. Surface pitting occurs in the closed profile if excessive forces are applied. Grooving also occurs in all profiles, if workpiece particles stick on the the guide pads and scratch over the borehole surface [1]. Studies have shown that an increase of the feed lead to an increase of the roughness depth Rz and thus a decrease of the surface quality [5]. In addition to the roughness, the microhardness in the workpiece is also influenced by the feed. It was even found that the microhardness is increased near the drill hole and decreases with increasing distance from the surface. The highest hardness was observed with the lowest feed [5].
Experimental results are available for single-lip deep hole drilling of the stainless martensitic steel X20Cr13 in quenched and tempered condition [6]. Here, a comparison of cooling lubricant variants showed that deep hole drilling oil is more effective than emulsion for the machinability of the material. The best conditions were found for the cutting speed vc in the range of 70–90 m/min and for a feed rate f of 0.03 mm, respectively. Generally, the tool life decreased with higher feed and cutting speed values. This is caused by increasing thermal loads with higher cutting speeds and by increasing mechanical loads on the tool cutting edges with higher feed rates. Cutting speeds that were too low also lead to early tool damage due to the increased amount of hardened material.
In [7], the influence of different cutting speeds during deep hole drilling of the quenched and tempered steel 42CrMo4 + QT on the formation of thermally altered layers in the bore subsurface is discussed. Machining is carried out under minimum quantity lubrication (MQL) conditions. This shows an increase in the layer depth with increasing cutting speed and a change in the microstructure with the formation of a white etching layer (WEL). The obtained properties of the workpiece surface and the subsurface depend on the respective material modification, which can be adjusted by the applied loads during the process [8].
During machining, the subsurface of the workpiece is plastically deformed. Beside phase transformation and surface reactions, this is one of the mechanisms, which causes a refinement of the microstructure with significantly smaller grain sizes in the sub-µm range in the subsurface [9]. The severe plastic deformation increases the dislocation density in this region, contamination enters the matrix and residual stresses are introduced. Forming always introduces residual stresses in the subsurface. The change in the energy state in the material influences the diffusion on the surface. This effect can lead to an increase in the dissolution rate [10]. Depending on the alloy and the distribution of residual stresses, residual stresses can also lead to an improvement in passivity [11].
Within the framework of the subproject in the priority program SPP 2086, the focus is primarily on the analysis and the adjustment of the subsurface properties of the borehole wall during single-lip deep hole drilling depending on a wide range of different process parameter. The aim of the project is to adjust the subsurface properties such as residual compressive stresses or surface quality by means of closed loop control of the deep hole drilling process and to eliminate subsequent processes. Process-independent correlations between the thermomechanical loads in the workpiece material and the resulting changes in the material behavior are used to adjust the subsurface properties, which was proposed by [8]. The thermo-mechanical condition is monitored with a sensor-integrated tool. Temperatures at the cutting insert, acceleration of the drill head, feed force and drilling torque can be measured and transmitted from the rotating tool. In the following chapters, the sensory tool, transmission systems and methods of data acquisition and modeling of the soft sensor are described. In addition, the supporting FEM simulations of chip formation and the methodology for the formation of transfer functions and controller development is presented.
2 Sensor integrated single-lip deep hole drilling tool
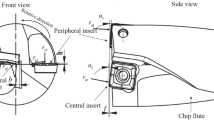
Advances in electronics, sensors and communication technologies have enabled a wide leap in mechatronic intelligent tooling systems. The integration of sensors, power sources and microcontrollers into tooling systems is predominantly used for process monitoring and control [12]. The intelligent tool systems lead to an increase in the accuracy, robustness and productivity of machining processes and enable monitoring directly at the point of action. In the holistically networked machine park of the Institute for Machine Tools (IfW) at the University of Stuttgart, self-optimizing machine concepts are developed [13], whereby not only online machine data flow into the optimization cycle, but also the data from sensor-integrated tools [14]. In addition to sensor-integrated milling tools [15], clamping devices, tool holders and spindles, a sensory single-lip deep hole drilling tool with the corresponding data transmission system has also been developed [16]. The sensor-integrated SLD was developed as part of the priority program SPP 2086 of the German Research Foundation (DFG) and enables near-acting point measurement of temperatures and accelerations. The developed SLD tool is shown in Fig. 1.
Due to the challenging process accessibility in the bore and the changing workpiece geometry in the broad application, the actual thermomechanical conditions can only be monitored externally with great effort. For this reason, there is a need for sensor-based process monitoring and control on the tool side, which enables the in-process manipulation based on measured data. The typical l/d ratios of the SLD process and the high cooling lubricant pressure also make sensor integration a challenge. The selected EB 800 from Gühring KG possesses an outer diameter of 18 mm, a length of 644 mm and is equipped with a replaceable cutting insert and four guide pads. This set up limits the installation space, which led to a very compact design in the final measuring system and was developed for operation under high mechanical and thermal loads. The following requirements must be fulfilled:
-
The electronics must be robust against cooling lubricant at pressures between 20 and 45 bar and separated from contact with the chips to be removed.
-
The tool should also be machined as little as possible to avoid significant effects on the stiffness of the tool structure and to keep the manufacturing process simple.
-
The assembly and wiring should also be done in few simple steps.
In developing the measurement system, it was assumed that measuring of both the torsional, axial and radial vibrations caused by the drilling process, as well as the resulting temperatures is feasible. The angular velocity and position of the rotating drill can be calculated in real time, which is also helpful for the process control. As the preliminary investigations for the selection of the suitable acceleration sensor have shown, the resonance frequencies of the torsional oscillations lie with the used tool at approx. 1 kHz. A fast Fourier transform (FFT) analysis of the measured drilling torque—with the KISTLER 9125A rotational dynamometer—was carried out [16].
The analog acceleration sensor ADXL377 is positioned under the front guide pad of the tool and allows measurements in three axial, radial and tangential directions, see Fig. 2 left. This setup allows the separation of the vibration components and thus identifying different process effects, such as wear, material inhomogeneities or the cause of process noise. Furthermore, this allows the calculation of the cutting speed and the position of the tool tip, which also delivers the straightness deviation [16]. The temperature is measured by three SMD 0603 AEC-Q200 PT1000 resistance temperature detectors (RTD) located directly under the cutting insert, see Fig. 2 right. The RTD are particularly well suited for this application because the change in resistance is linear over a wide temperature range, with good accuracy and response time. Both the acceleration sensor and the temperature sensors are each mounted on a specially designed circuit board.
In order to transmit the sensor data from the rotating tool, a wireless as well as a wired telemetry system were developed. The first variant is based on an Arduino microcontroller transmitting the data to a computer via Wi-Fi. Two circuits were designed, each containing a microcontroller, one for the vibration measurement and one for the temperature measurement. The two circuits and the batteries are placed in opposite to each other in a tool holder adapter. The assembled component of the wireless version is shown in Fig. 3. The adapter possesses a cooling channel and additional channels for cable feed-through.
Developed wireless data acquisition and transmission module [16]
In the wired version, an 8-channel slip ring (RX-HS020A-QS3-00008C01) from the company B-Command is used for data transmission and power supply. The schematic of the tool holder developed for this purpose can be seen in Fig. 4.
The data lines are connected directly to a commercial measuring system from National Instruments and processed with the software LabVIEW. The voltage values of the acceleration sensor and the change in resistance of the temperature sensors are acquired via the PXIe-6358 measuring card and processed in the PXIe-8840 real-time controller with the NI Linux Real-Time operating system. Power is also supplied via the PXIe-6358, but here series resistors must be used to reduce the voltage for the ADXL 377 from 5 to 3 V and to set the measuring current for the PT 1000 sensors to 300 µA. In addition to the measured data from the sensory tool, the feed force, the drilling torque as well as the pressure and flow rate of the deep hole drilling oil are recorded via the PXIe-4480 measuring card. Figure 5 shows the corresponding hardware concept for process monitoring and closed loop control.
This concept enables editing the subsurface properties via process control with the aid of the sensory tool and the corresponding soft sensor. In order to be able to integrate the control, an interface for the external control of the cutting parameters is necessary. This requires a digital control of the feed and the rotational speed of the drilling machine (deep hole drilling machine MÖ-TM-HF-16-2-S 182 of Walter Möck GmbH). As a solution, the feed override of the machine, which is designed as an encoder, was replaced by a transistor module ULN2803A. This allows switching between manual presetting of the feed or rotational speed value and digital control by means of additionally attached switches [17].
3 Soft sensor
The aim of this project is to develop an approach to adjust the subsurface properties of a bore wall by closed loop control in real time during the process. Since quantities such as residual stresses, surface roughness, microhardness or grain size in the subsurface in-process are not accessible, a soft sensor is required to predict the subsurface properties. This soft sensor concept is intended to be a simple observer by the presented implementation in LabVIEW.
3.1 Experimental investigations
The soft sensor is to be implemented as a multiple regression model, which is derived from the characteristic fields of the subsurface properties. The fields are generated by experimental investigations and FEM simulations. First, a response surface design was created in order to statistically validate the experimental results and still keep the test effort within limits compared to a full factorial test plan. The response surface design was set up with the machining parameters cutting speed vc or rotational speed n and feed rate vf as factors. For the test factors, an application-oriented range was defined and extended over the process boundaries, for the rotational speeds 1057.89–1683.11 min−1 and the feed rates 3.77–71.62 mm/min. In addition, at least three repetitions are provided, for better statistical validation. In total 39 repetitions with different process parameters are required. The parameter range is set around the cutting data recommended by the VDI, taking into account the machine performance. The cutting parameters were also taken above the minimum and maximum limits in order to push the process stability to the limits. In the test plan in Table 1 the so-called point type indicates whether the process parameters are above the limits or not: a central point is marked with a “0” (below the limit), a corner point with a “1” (at the limit) and a grid point with a “− 1” (above the limit). All experimental parameters are processed under the same conditions, for example, same machine tool, same batch of workpiece material, same tool with new inserts, etc., which is described by a “1” in the category blocks. The quenched and tempered steel 42CrMo4 + QT is used as the workpiece material. Despite its widespread use in mechanical engineering, this material is nevertheless demanding in terms of machining because its kc1.1 value is high with 2500 N/mm2. As a result, wear on the guide pads as well as cutting edge rounding occurs relatively quick, amplifying the change in thermomechanical state. Zylindrical specimens with an outer diameter of 25 mm and a length of 100 mm are used as specimens in order to minimize the effect of workpiece geometry on the heat distribution. The accelerations and temperatures are measured with the sensory tool and additionally, on the machine side, the feed force Ff and the drilling torque M are recorded. The oil flow and pressure are also measured, but remain constant.
In this project, the hypothesis is pursued that the subsurface properties are dependent on the thermomechanical state in the cutting zone and that any disturbing factors, such as cutting edge wear, can be detected via this thermomechanical state. Thus, the subsurface condition can be adjusted or kept in a constant range via the temperature on the cutting insert and via the mechanical variables such as the force, the drilling torque and the acceleration. In the first step towards the soft sensor the correlation between the thermomechanical quantities and the control variables n and vf was investigated. The mechanical quantities that characterize the deep hole drilling process are the feed force Ff and the drilling torque M. They were recorded with a KISTLER 9125A rotational dynamometer. Figure 6 shows a measured evolution of the feed force from the response surface design at medium rotational speed and feed rate. The diagram shows a typical increase in force at the start of drilling—here a drill bush was used—before the force reaches a steady state. To generate the characteristic field, the average force in the steady state was determined and collected for each machining parameter set from Table 1. Figure 7 shows the correlation of the averaged feed force with all the investigated cutting parameter sets. The surface was created by interpolating the result values using the second-order distance method. As a result, the feed force increase with increasing feed velocity is due to increasing chip thickness and metal removal rate as well as the asymmetrical tool geometry. According to Patra et al. and Biermann et al. [1, 18] a correlation exists between the increase in rotational speed and increase in radial force, which is mainly caused by the asymmetric tool geometry resulting in stronger deformation of the bore wall. With increasing rotational speed, the feed force increases, too, which is in contrast to the expected feed force decrease caused by a reduction of the chip thickness with increasing rotational speed and constant feed velocity. Supporting the presented results, Nickel et al. also found that in single-lip deep hole drilling of 42CrMo4 + QT, the feed force increases with both the increase in feed rate and the increase in cutting speed [19]. In addition, these observations were confirmed by the FE simulation results in Fig. 16.
The drilling torque evolution behaves similar to the feed force with the peak at the start of drilling and the subsequent steady state, but the load gradient and the fluctuations at the bore exit are more pronounced, see Fig. 8. This effect may be due to the non-uniform load distribution on the cutting edge due to partial and progressive exit of the tool tip. The correlation of the averaged drilling torque with the cutting parameters is shown in Fig. 9. At low rotational speed, the drilling torque initially increases with vf and then decreases again slightly. This phenomenon can also be observed at high feed rate and with increasing rotational speed.
Furthermore, the acceleration at the drill head tip in the tangential, axial, and radial directions was measured with the previously described sensory single-lip deep hole drilling tool. The acceleration signal can be used not only to detect unwanted vibrations, but also to calculate the position or the rotational speed of the cutting insert. Figure 10 shows the acceleration values at intermediate cutting data of the investigated parameter range (pass sequence = 3). As expected, the dominant component is the tangential acceleration. The measurement in three axial directions offers a great advantage, such as the identification of occurring disturbance factors. For example, it was found that the strong noise development, which is often problematic in deep drilling processes, is caused by the radial vibration. The selected measuring range of ± 200 g of the ADXL 377 is sufficient, as the measurements have shown. The sampling rate is 1 kHz.
For the soft sensor and the associated closed loop control, the information of the actual rotational speed is to be used from the acceleration signal. The rotational speed specified in the machine tool control does not correspond to the actual rotational speed at the cutting edge, which is due to the forces acting in the process and the tool elasticity at a length of 644 mm. Therefore, the actual cutting speed should be included in the regression model. The cutting speed can be calculated from both radial and tangential acceleration, with the radial acceleration method being the more accurate since no integration is required [16]. Another method of obtaining velocity information from the acceleration signal is real-time FFT analysis. Figure 11 shows an example block diagram in LabVIEW that filters the acceleration data and performs an FFT to calculate the rotational speed or cutting speed using the frequency information. Figure 12 shows the deviation between the rotational speeds specified in the machine control system and the measured maximum rotational speed amplitudes, which are the arithmetic averages of each process parameter set. With higher feed rate, the deviation from the preset becomes smaller and more independent of the rotational speed. With higher spindle rotational speed, the difference to the current rotational speed at the tool tip calculated from the frequency also increases, since this increases the drilling torque (Fig. 8) and thus also the cutting force, which can lead to a higher torsional displacement of the tool and vibrations. However, the overall difference is just in a low range between 1 and 2%. The entire control is to be implemented in LabVIEW.
The temperature measurement with the sensor-integrated tool at three positions under the cutting insert (Fig. 2) with intermediate cutting parameters (pass sequence = 3) can be seen in Fig. 13. The overall temperature level is significantly lower than the expected temperatures in the process zone. This can be explained by the positions of the sensors behind the cutting insert. An approach to obtain the actual temperature in the cutting zone from these measured values has been extensively investigated and proposed in [20]. However, for controlling the process the absolute value of the temperature is less important than the changes during the measurement. For this purpose, the uncertainty and the temporal resolution of the measured values is more important, which is sufficiently low and high, respectively. The good resolution and low measurement uncertainty can be seen from the fact that the shape of the temperature evolution curve of all three sensors agrees very well but at slightly different temperature levels, which can be attributed to the positions of the sensors. The temperature at the start of drilling rises rapidly and then remains quasi constant until the exit was reached, which is comparable to the behavior of the feed forces. At the exit, the temperature rises again. This steep increase is due to the missing cooling lubricant, which shoots out of the backside of the cylindrical sample and thus remains no longer around the cutting edge to dissipate the heat. The highest mean temperature with 53 °C is measured at position T2 (red), as this sensor is located in the outer part of the circuit board and thus closest to the cutting corner of the insert, which is in contact with the bore wall. Sensor T1 (green) measures a lower mean temperature with 47 °C, as it is located further away from the cutting zone. The lowest mean temperature was measured with 45 °C at position T3 (blue). The latter sensor is closest to the axis of rotation, which leads to a lower cutting speed in this position. To create the temperature characteristic field and making the system more robust against deviations, the average of the mean temperature in the steady state in all three positions was considered. Figure 14 shows this correlation of the mean temperature with the machining parameters. The temperature tends to increase with the feed rate and the cutting speed, although it drops again slightly at high values.
3.2 Numerical investigations
Beside the experimental investigations of the SLD process to acquire data for the soft sensor a numerical framework was set up to support the measurements by delivering additional insights into the process. Recent numerical investigations employ a coupled Eulerian–Lagrangian (CEL) approach to model the extreme deformations in the cutting processes with less mesh sensitivity and higher computational performance compared to the often applied arbitrary Lagrangian Eulerian formulation (ALE) [21]. Thus, the presented numerical investigations on SLD focuses on the CEL approach. As discussed before, the investigated process parameters were obtained from design of experiment (DoE) to parametrize regression models (see Table 1). Finally, these regression models will be included in the control concept for SLD. In addition, the experimental results were employed to validate the simulations results.
Basically, the CEL modelling approach combines the advantages of the Lagrangian formulation with the advantages of the Eulerian formulation [22]. In the Lagrangian formulation, the Lagrangian body is meshed from a discrete geometric part instance, which corresponds to the shapes of the parts being modeled. Each individual mesh node with its material point is moved and deformed as one entity in space, so the material boundary coincides with the element boundary. This conventional formulation offers geometrical accuracy, robustness and computational efficiency. However, it tends to exhibit severe mesh distortion when undergoing very large deformations. In contrast, the Eulerian formulation uses compressible Navier–Stokes equations and can be utilized to obtain a reasonable solution in situations where the material undergoes extreme deformations such as gas and fluid flow or machining problems. The Eulerian mesh is fixed in space and does not deform, whereas the material within the Eulerian domain can move and deform separately from the mesh nodes. The Eulerian elements may be partially or completely void from material, which is then represented by volume fractions within each Eulerian mesh element [23]. The solver Abaqus offers this promising simulation approach with the functionality of the typical Lagrangian FE models, such as constitutive laws or contact definitions.
Model setup
The setup of the assembled simulation model consisted of the tip of the drill head including the cutting insert and the two front guide pads as well as a penny-shaped workpiece (see Fig. 15). The geometry of the drill head was extracted from CAD data of Gühring KG and the geometry of the workpiece based on the cylindrical samples in the experiment. To reduce the computational costs a thickness of 5 mm of the workpiece was considered and just the radius of 12.5 mm was taken over from the experiment. As mentioned before, the drill head was shortened to represent the drill head tip with the prefrontal guide pads and the cutting insert. Due to the high stiffness of the insert and the guide pad in the drill head, which are based on cemented carbide, the whole drill head was considered as one rigid body part. The insert possesses an ideal sharp cutting edge radius. In order to move the driller in the correct way with respect to feeding and rotation, a reference node was defined, which is linked to all of the nodes in the drill head. Thus, on this reference node a lateral velocity along the driller axis and an angular velocity around this axis were applied. Furthermore, the degrees of freedom at the bottom surface as well as the lateral surface of the penny-shaped workpiece were restricted to avoid rigid body movement of the workpiece.
The setup of the assembled simulation model for the CEL approach [25]
As contact conditions, a general contact was defined between the drill head surface and the upper surface of the workpiece with a hard pressure overclosure correlation, which describes the interaction of the cutting insert and the workpiece in direction orthogonal to the surface. Further selected interaction properties are the Coulomb friction model with a friction coefficient of 0.32 [24].
The coupled thermomechanical simulation setup even requires heat generation due to friction assigning a factor of 0.99, which determines the distribution of heat between the interacting surfaces and an initial temperature, which was set to room temperature. In contrast to the experiments, the drilling condition within the simulations were assumed as dry.
The mesh of the Eulerian domain contains hexahedral elements with an averaged edge length of 0.25 mm. To represent the material behavior properly, thermal properties as well as mechanical properties with temperature and strain rate dependency were assigned. For machining simulations, the so-called Johnson–Cook (JC) model in combination with its damage model has proven to deliver realistic mechanical response. For the summary of the material data of the drill head as well as the workpiece and for further details of the FE model it is referred to Guski et al. [25].
Data analysis
Due to the high computational effort, a mass scaling factor of 1.0 × 105 was selected to perform the whole simulation study. In total simulations with nine different process parameter combinations, which can be found in the table of the response surface design (Table 1), were run and analyzed using this mass scaling factor. To remove the effect of the mass scaling factor on the simulation results the process parameter set with the highest feed and thus shortest calculation time was selected to perform a sensitivity analysis. The resulting quantities, such as the feed force, the drilling torque and the temperature at the cutting edge for different mass scaling factors were used to extrapolate to values without mass scaling. For this purpose, the following nonlinear regression model using the so-called Huber loss as weight function was applied [26]:
where A, B and C are the regression coefficients of the non-linear model, which have to be determined for each quantity. The determined coefficients are summarized in Table 2.
By comparing the extrapolated quantities with the quantities at a mass scaling factor of 1.0 × 105, values for the mass scaling effect were calculated. The evaluation of feed force, the drilling torque and the temperature leads to mass scaling correction factors of 0.30, 0.37 and 0.24, respectively. These values were then applied to the corresponding simulation results. This procedure has delivered more realistic results, which were used to parametrize the polynomial regression models for the soft sensor.
Simulation results
All simulation results were evaluated with respect to the feed force, the drilling torque, the temperature at the cutting edge as well as the residual stress in the bore hole wall and adjusted by the mass scaling correction factor. Each simulation delivers a value for the whole parameter space, which was defined by using the response surface design (Table 1). For evaluating the feed force and drilling torque, the reaction force and torque at the reference point in feeding direction were evaluated. For each process parameter set the simulation time was adjusted to reach the steady state regime with constant quantities. Then the arithmetic average was calculated within the steady state regime. This resulting value was plotted for each simulation with respect to the feed rate and cutting speed.
Then, a polynomial surface fit of second order with respect to the feed velocity (X) and a linear dependency according to rotational speed (Y) was applied to determine the parameters of the regression model with the form:
where bij are the estimated regression coefficients to plot a three-dimensional surface that captures the predicted value of the dependent variable (Z) at every combination of the two independent variables (X, Y).
For comparison reasons, the fitting procedure was repeated for the experimental data.
Figure 16 shows the simulation results (circle) and the experimental values (triangle) visualized by marker of the feed forces (top) and the drilling torque (bottom). In addition, the determined regression surfaces are shown. For both quantities the surfaces show a comparable shape: increasing force with increasing feed and increasing rotational speed, but a slightly higher level for the experiments. The overall behavior is correctly approximated. However, in the experiment for a high feed a decrease of the torque with increasing rotational speed and a maximum deviation of the simulation results and the experimental values for a high feed and a low rotational speed was observed. This deviation can be attributed to the influence of the absence of a lubricant and thus significantly higher workpiece temperatures, which softens the workpiece material in the simulation. As indicated by the positions of the regression surfaces to each other the simulation results underestimate the experimental results for both, the feed force and the torque. To quantify this observation a mean value for the nine different process parameters were calculated: for the feed force a mean difference of 32% and for the torque a mean difference of 26% was obtained, respectively. These mean values cover a variance from 9% (high feed velocity) to 62% (low feed velocity) of the whole process parameter space.
The procedure to identify the regression model was repeated with the temperature at the cutting edge and the temperature values of the PT1000 located directly under the cutting insert for all process parameter sets. The observed values as well as the determined regression surfaces are shown in Fig. 17 top. The deviation of the results between simulation and experiment is larger compared to the feed force or drilling torque. Due to the lubricant and measurement positions, a temperature between 40 and 60 °C in the whole parameter space was measured. In contrast, the simulations provide much higher temperatures but the same trends, an increasing temperature with increasing feed and increasing rotational speed. Whereas, the increase in temperature with increasing rotational speed is less pronounced. Overall higher temperatures are observed, which was expected due to the difference in the location of RTD underneath the insert, which is different from the evaluation point on the outer corner of the cutting insert in the simulation. On the other hand, the temperatures from the CEL simulation are underestimated compared to the temperatures in the cutting zone from the literature and from the preliminary investigations [27]. This analysis is supported by a mean difference of 66% with a maximum difference of 300% for a high feed velocity. Much smaller deviations can be found for low feed velocities.
The residual stresses in the bore hole wall were analyzed and collected for all nine process parameter sets. The analyzed values are the arithmetic average of the tangential stress in four positions around the bore hole. These values were compared with results from residual stress determination measurements with the hole drilling method. For robustness reasons the values in a depth of 50 µm were employed. Each process parameter set leads to compressive stresses in tangential direction in the subsurface region of the drill hole wall. Then, a polynomial surface fit of second order was applied to determine the parameters of the regression models according to Eq. 2. The regression surfaces and the corresponding numerical results and experimental determination of the residual stress shows Fig. 17 bottom. Overall, a good match between the numerical and experimental results were obtained. The deviations in the shape of the regression surfaces showing a concave shape for the simulation results and a convex shape for the experimental results, respectively, can be originated from an overestimation in the simulation for a small feed and small rotational speed as well as an underestimation for a high feed and a high rotational speed. In addition, the high tensile stress of 336 MPa for a high feed velocity and low rotational speed, which is close to the yield strength of the material at room temperature (410 MPa [28]) was considered as an outlier. These observations are caused by the remarkable scatter of the experimental results of the hole drilling method within the process parameter sets, which has to be taken into account for the assessment of the results. However, except of the outlier, all the determined values are in the compressive regime from − 530 to − 30 MPa.
The resulting regression coefficients and the estimated error (R2) are summarized in Table 3. Especially, the R2 is remarkable small for the feed force and the drilling torque. Since the temperature is almost constant in the entire parameter space in the experiment the agreement with the polynomial model is rather poor, as expected. The same observation holds for the residual stress but due to a large scatter in the obtained values. For this quantity, a third order polynomial model reduces the estimated error significantly.
The presented numerical investigations show, that the CEL approach is able to deliver realistic results for drilling processes. Due to simplifications of the FE models, such as a shorter workpiece, comparable large element sizes, and dry drilling condition, which are necessary due to the high computational effort, expected deviations occur in comparison to experimental results. Nevertheless, especially the mechanical quantities, such as feed force, drilling torque and residual stress, deliver a good agreement in most of the parameter space. Just in the range of high feed velocity (50–70 mm/min) and low rotational speeds (1000–1200 min−1) larger deviations were observed. Within the framework of this numerical study, the parameters of the second order polynomial regression surfaces were determined and provided to the soft sensor for online monitoring the thermomechanical status during the drilling process.
3.3 Subsurface investigations
Beside the development of the sensory tool and the determination of the characteristic fields for describing the thermomechanical conditions as a function of the process parameters the correlation between the subsurface properties and the thermomechanical conditions were investigated. Finally, this connects the process parameters with the subsurface properties, which are the target variables of the controller and soft sensor to be developed. The thermomechanical conditions, such as the feed force or the temperature are the measured variables of this closed loop controller, which are accessible during the process with the aid of the sensor-integrated tool. The process parameters are correspondingly the control variables of the controller. In order to describe the subsurface properly, the 39 specimens from the response surface design must be investigated in depth. For describing the subsurface quality, the residual stresses in the bore wall were determined and the microhardness, the roughness, the grain size and the grain morphology were examined. Afterwards, characteristic fields of the subsurface properties were generated and a multiple regression model was derived, which predicts the subsurface condition by taking into account the measured variables and the control variables.
The residual compressive stresses were measured using the hole drilling method in a distance of approx. 10 mm from the driller exit, due to better accessibility (see Fig. 18 right). First, a strain gauge rosette is adhesively bonded to the bore wall, then the specimen is cut along the axis of rotation and the released strains are measured. Subsequently, a hole is drilled in the strain gauge rosette and the strains dependent on the depth are also recorded. Finally, these strains were converted to the residual stresses in the subsurface. Figure 18 shows the resulting tangential and axial stress dependent on the depth of an example measurement at medium rotational speed and low feed rate (pass sequence = 7). As can be seen, high residual compressive stresses are generated in both directions in the single-lip deep hole drilling process, which decrease with the distance to the machined surface. The final residual compressive stress is a superposition of the stresses resulting from the cutting process as well as from the forming by the guide pads. Figure 19 shows the resulting residual stress in a depth of 50 µm for all the investigated samples as characteristic fields of the residual stresses in tangential and axial direction. The residual stress was evaluated in a depth of 50 µm due to the high uncertainty in smaller depths. On the top, the residual stresses are shown in the axial direction relative to the workpiece geometry, and on the bottom in the tangential direction. In the tangential direction, the residual compressive stresses are higher. This can be explained by the guide pads, which form the bore wall in this direction.
Furthermore, it can be clearly seen that lower rotational speeds and feed rates, or lower temperatures and feed forces tend to cause higher compressive residual stresses. Similar effects could also be observed in the turning process of aluminum alloys [29], lower cutting speed lead to compressive residual stresses. This could be explained by the temperature effect of the residual stress: higher temperatures tend to induce tensile residual stresses, while the lower the temperature is, the higher are the compressive stresses in the workpiece. This effect can be explained by the interaction of thermally and mechanically induced residual stress. For elevated temperatures, the thermal effect become more dominant and the generation of mechanical residual stresses is counteracted by a thermal component due to the frictional heat generated and the work of deformation. In this case, the residual compressive stresses are reduced in the subsurface region, as the high-temperature yield strength is exceeded during the process [30]. The comparison of the characteristic field of the temperature (Fig. 14) with the characteristic field of the residual stress in Fig. 19 shows this correlation, nicely.
For characterizing the subsurface of the bores further, microhardness measurements were performed. Thin slices were cut out in the center of the cylindrical specimen. Then the cut samples were embedded in resin for the surface preparation to carry out the hardness (HV 0.05) measurements radially outward from the bore wall. The total thickness of the bore wall is 3.5 mm. The first measuring point is located 20 µm from the bore surface; all other points are located at a distance of 100 µm from each other. The resulting hardness values are the mean values from three repetitions. As can be seen in Fig. 20 top, the scatter of the confidence interval is high, but a clear decreasing trend of the hardness with the distance from the bore surface is observed. This observation is valid for all investigated cutting parameters. By this method, the gradient can be determined and thus the degree of hardening in the subsurface. The red measuring point with a hardness of 395 HV 0.05 is located at a distance of 100 µm from the bore wall and is the mean value of 10 measurements on the circumference of the investigated slice. The standard deviation is approx. ± 6.7 HV 0.05. The mean value in this depth will be used for the soft sensor because the strain orthogonal to the indentation direction of the Picodentor HM500 Helmut Fischer close to the edge falsifies the measured values leading to an underestimation. The characteristic field in Fig. 20 bottom shows the mean values of all samples at a distance of 100 µm from the bore wall. A similar tendency as for residual stresses can be observed; with decreasing cutting speed and feed rate (i.e. at lower temperatures and feed forces) the highest hardness is achieved. However, the hardness measurements are also high at very high rotational speed and feed rate, which is a positive effect from an efficiency point of view.
In addition, the depth of grain refinement of the deep-drilled specimens was examined. For this purpose, the same slices from the center of the specimen as for the microhardness measurements were examined using the electron backscatter diffraction (EBSD) data from SEM analyses. Figure 21 shows the microstructure in the area below the surface in the sample produced with the process parameters n = 1057.89 min−1, vf = 29.09 mm/min, p = 20 bar, V̇ = 5 l/min (pass sequence = 1), exemplarily. The colors of the grains refer to a certain crystallographic orientation, which were just used to separate each grain during automatic evaluation of the microstructure.
A pearlitic microstructure with randomly orientated lamellar grains is observed for the whole area. However, a closer look on the subsurface, which shows Fig. 22 left, deliver an affected area adjacent to the surface.
The surface of the bore wall is in the upper part of the image. Close to the surface a clearl grain refinement was observed with very small equiaxed grains due to the machining up to a depth of 2 µm. Below this depth, it is also clearly seen that the grains increase and become aligned in the cutting direction. In order to quantify the depth of impact, the number of grain center in the horizontal section across the depth was evaluated. As a result, two regimes were observed: close to the surface with a high number of grains and apart from the surface with a continuously decreasing number of grains, see Fig. 22 right. The transition depth, which is assumed as the transition from the first to the second regime, was defined as the intersection of the regression lines based on a Gaussian model. In this example, a transition or impact depth (dim) of 1.82 µm was determined. This value will be used for the subsurface quantification via the regression model. With the aid of the EBSD investigations, it was found, that the drilling process affects the microstructure especially within a distance from the surface up to 5 µm depending on the process parameters. This leads to the conclusion that this subsurface area possesses a major impact on the increase in microhardness in the subsurface region, finally.
Additionally, the roughness Ra in the center of the specimen was also investigated and plotted as a characteristic field in Fig. 23. It can be seen that the surface quality improves with increasing feed velocity and rotational speed.
Four quantities have been presented that are used for as subsurface properties, the residual stresses, the microhardness, the impact depth of grain refinement and the roughness. Thus, four target variables and two control variables (n, vf) are available for the controller. This leads to a requirement of eight transfer functions, which is challenging to implement in the controller design and not robust enough because the subsurface characteristics can have opposite effects. Therefore, a promising approach is to normalize the subsurface properties and to condense them to one characteristic value, which is called SUBS for subsurface, see Eqs. 3–7. SUBS is the mean value from the normalized subsurface properties and can have a value between 0 and 100. The algebraic sign of the individual subsurface characteristic values and whether a maximum or a minimum is striven for must be taken into account. This approach enables the fitting of a multiple polynomial regression function, which describes the characteristic factor SUBSreg as a function of the control variables (n, vf) and measured variables (M, Ff, T and a respectively nist), thus condensing all the characteristic fields presented (Eq. 8). For the realization, the Minitab software is used. As a specification, terms up to second order should be used and interactions between predictors should be considered. The statistical software calculates the best fit. As can be seen, the feed velocity has a great impact on the subsurface quality. R2 is a measure of how well the model fits. An R2 of 1 indicates that the regression predictions perfectly fit the data.
3.4 Outlook on the integration of the soft sensor in the closed loop controller
In the preliminary investigations, it was found that a dynamic excitation in e.g. sinusoidal form or as chirp excitation, as it is done for highly dynamic systems to derive the transfer function, is not reasonable for a comparably slow system with a dead time of 150 ms [17]. Therefore, in the coming investigations, the transfer functions for the closed loop controller will be determined experimentally by first changing the feed velocity in steps at constant rotational speed and next changing the rotational speed at constant feed velocity. With the introduction of the characteristic value SUBS, only two transfer functions are required, for n and vf. For the experimental data the transfer function will be determined by using Matlab software with the System Identification tool. The core of the multivariable controller are two proportional–integral–derivative (PID) controllers each for vf and n and the soft sensor (SUBSreg) that predicts the subsurface quality. The PID controllers will be parameterized in Simulink using the two transfer functions. The overall design of the multivariable controller in LabVIEW can be seen in Fig. 24. The regression model is used as a function and receives real-time measurement data from the sensory tool and the measurement equipment as well as the current set values of the control variables vf and n, which guide the process and are specified by the external hardware respectively (Fig. 5). Therefore, the soft sensor possesses the function of an observer; the current process state and the control variables will be used to feed back the predicted target variable SUBS, which allows the calculation of the control deviation. In addition to the soft sensor and the PID controllers, the design includes a feedforward control, which prevents the intervention until the cutting edge is engaged. Besides, a control is implemented, which only switches on the rotational speed controller if the feed velocity has reached the upper or lower limit and the target value is not yet achieved or the control deviation is still too large. Furthermore, two function units are implemented, which convert the control values specification into a binary signal for the machine control. The next step in this work contains testing and optimizing the design.
4 Conclusion
In this study, a sensor integrated single-lip deep hole drilling tool, a soft sensor and an approach of a closed loop process control as well as the corresponding experiments for data acquisition were presented. Based on the results obtained in this study, the following conclusions can be drawn:
-
The sensor-integrated single-lip deep hole drilling tool was tested over a wide range of parameters and had proven to be robust.
-
Differences in machining parameters can be characterized clearly by the measured thermomechanical state.
-
Subsurface properties can be well modeled by the regression models based on the characteristic fields, which show the correlation with the thermomechanical process state.
-
FE models had proven to be a good tool to approximate the drilling process simulatively.
-
Although some assumptions and simplifications regarding the drill head and the drilling conditions were made in the simulations, realistic trends as well as quantities were obtained. In particular, the mechanical quantities, such as feed force, drilling torque as well as the residual stress show a good agreement with the experimental results over a wide range of process parameter, which proves the application as soft sensor data.
-
The subsurface quality can be described in good approximation via multiple regression.
-
LabVIEW offers a wide range of possibilities to determine the transfer functions experimentally in real time, to implement the multivariable controller and for the integration of the soft sensor.
References
Biermann D, Bleicher F, Heisel U, Klocke F, Möhring H-C, Shih A (2018) Deep hole drilling. CIRP Ann 67(2):673–694. https://doi.org/10.1016/j.cirp.2018.05.007
VDI 3210 (2014) Tiefbohrverfahren. Beuth Verlag, Berlin
Löbbe H (2003) Tiefbohren auf bearbeitungszentren. Vulkan, Essen
VDI 3208 (2014) Tiefbohren mit Einlippenbohrern, vol. 2014
Nickel J, Baak N, Walther F, Biermann D (2020) Influence of the feed rate in the single-lip deep hole drilling process on the surface integrity of steel components. In: Itoh S, Shukla S (eds) Lecture Notes in Mechanical Engineering, Advanced Surface Enhancement. Springer Singapore, pp 198–212.
Wittkop S (2007) Einlippentiefbohren nichtrostender Stähle. Vulkan, Essen
Eisseler R (2023) Erhöhung der Produktivität beim Einlippentiefbohren unter schwierigen Bedingungen. In: VDI Präzisions- und Tiefbohren aktuell: Technik - Tools - Trends, pp. 41–52.
Brinksmeier E, Klocke F, Lucca DA, Sölter J, Meyer D (2014) Process signatures—a new approach to solve the inverse surface integrity problem in machining processes. Proc CIRP 13:429–434. https://doi.org/10.1016/j.procir.2014.04.073
Brown M et al (2018) Destructive and non-destructive testing methods for characterization and detection of machining-induced white layer: a review paper. CIRP J Manuf Sci Technol 23:39–53. https://doi.org/10.1016/j.cirpj.2018.10.001
Ura-Bińczyk E (2021) Effect of grain refinement on the corrosion resistance of 316L stainless steel. Mater (Basel, Switzerl). https://doi.org/10.3390/ma14247517
Wang P, Ma L, Cheng X, Li X (2021) Influence of grain refinement on the corrosion behavior of metallic materials: a review. Int J Miner Metall Mater 28(7):1112–1126. https://doi.org/10.1007/s12613-021-2308-0
Vacharanukul K, Mekid S (2005) In-process dimensional inspection sensors. Measurement 38(3):204–218. https://doi.org/10.1016/j.measurement.2005.07.009
Möhring H-C, Wiederkehr P, Erkorkmaz K, Kakinuma Y (2020) Self-optimizing machining systems. CIRP Ann 69(2):740–763. https://doi.org/10.1016/j.cirp.2020.05.007
Möhring H-C, Werkle K, Maier W (2020) Process monitoring with a cyber-physical cutting tool. Proc CIRP 93:1466–1471. https://doi.org/10.1016/j.procir.2020.03.034
Möhring H-C, Werkle KT (2022) Lightweight semi-actively damped high performance milling tool. CIRP Ann 71(1):353–356. https://doi.org/10.1016/j.cirp.2022.04.051
Wegert R, Alhamede MA, Guski V, Schmauder S, Möhring H-C (2022) Sensor-integrated tool for self-optimizing single-lip deep hole drilling. IJAT 16(2):126–137. https://doi.org/10.20965/ijat.2022.p0126
Wegert R, et al. (2022) Prozessregelung beim Einlippentiefbohren/closed loop control in single-lip deep-hole drilling. wt 112(11–12):750–756. https://doi.org/10.37544/1436-4980-2022-11-12-24.
Patra K, Anand RS, Steiner M, Biermann D (2015) Experimental analysis of cutting forces in microdrilling of austenitic stainless steel (X5CrNi18-10). Mater Manuf Processes 30(2):248–255. https://doi.org/10.1080/10426914.2014.941867
Nickel J, Baak N, Volke P, Walther F, Biermann D (2021) Thermomechanical impact of the single-lip deep hole drilling on the surface integrity on the example of steel components. JMMP 5(4):120. https://doi.org/10.3390/jmmp5040120
Ramme J, Wegert R, Guski V, Schmauder S, Moehring H-C (2022) Development of a multi-sensor concept for real-time temperature measurement at the cutting insert of a single-lip deep hole drilling Tool. Appl Sci 12(14):7095. https://doi.org/10.3390/app12147095
Menze C, Wegert R, Reeber T, Erhardt F, Moehring H-C, Stegmann J (2021) Numerical methods for the simulation of segmented chips and experimental validation in machining of TI-6AL-4V. MM SJ 2021(5):5052–5060. https://doi.org/10.17973/MMSJ.2021_11_2021152
Ducobu F, Arrazola P-J, Rivière-Lorphèvre E, de Zarate GO, Madariaga A, Filippi E (2017) The CEL method as an alternative to the current modelling approaches for Ti6Al4V orthogonal cutting simulation. Proc CIRP 58:245–250. https://doi.org/10.1016/j.procir.2017.03.188
Khochtali H, BenBelgacem I, Zemzemi F, Bensalem W (2021) Comparison of coupled eulerian-lagrangian and coupled smoothed particle hydrodynamics-lagrangian in fluid-structure interaction applied to metal cutting. Arab J Sci Eng 46(12):11923–11936. https://doi.org/10.1007/s13369-021-05737-x
Pantalé O, Bacaria J-L, Dalverny O, Rakotomalala R, Caperaa S (2004) 2D and 3D numerical models of metal cutting with damage effects. Comput Methods Appl Mech Eng 193(39–41):4383–4399. https://doi.org/10.1016/j.cma.2003.12.062
Guski V, Wegert R, Schmauder S, Möhring H-C (2022) Correlation between subsurface properties, the thermo-mechanical process conditions and machining parameters using the CEL simulation method. Procedia CIRP 108:100–105. https://doi.org/10.1016/j.procir.2022.03.021
Dennis JE, Welsch RE (1978) Techniques for nonlinear least squares and robust regression. Commun Stat Simul Comput 7(4):345–359. https://doi.org/10.1080/03610917808812083
Wegert R, Guski V, Schmauder S, Möhring H-C (2020) Effects on surface and peripheral zone during single lip deep hole drilling. Procedia CIRP 87:113–118. https://doi.org/10.1016/j.procir.2020.02.025
Brnic J, Turkalj G, Canadija M, Lanc D, Brcic M (2015) Study of the effects of high temperatures on the engineering properties of Steel 42CrMo4. High Temp Mater Process. https://doi.org/10.1515/htmp-2014-0011
Junge T, Mehner T, Nestler A, Schubert A, Lampke T (2022) Surface properties in turning of aluminum alloys applying different cooling strategies. Proc CIRP 108:246–251. https://doi.org/10.1016/j.procir.2022.03.043
Habschied M, de Graaff B, Klumpp A, Schulze V (2015) Fertigung und eigenspannungen*. HTM J Heat Treat Mater 70(3):111–121. https://doi.org/10.3139/105.110261
Acknowledgements
The scientific work has been supported by the DFG within the research priority program SPP 2086. The authors thank the DFG for this funding and intensive technical support. Also, the authors acknowledge the company Gühring KG for providing technical support.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wegert, R., Guski, V., Schmauder, S. et al. In-process approach for editing the subsurface properties during single-lip deep hole drilling using a sensor-integrated tool. Prod. Eng. Res. Devel. 18, 319–337 (2024). https://doi.org/10.1007/s11740-024-01265-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11740-024-01265-3