A dynamic availability analysis of an N-component production system with interdependency effects: a fractional-order approach

Abstract

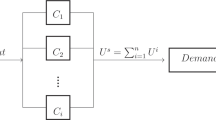
This paper presents a dynamic availability assessment of a large multi-component production system, taking into account the stochastic interdependence effect that has a negative impact on system availability. While this effect is detrimental to availability, it is necessary to consider it in maintenance modeling. The proposed model, which is based on the fractional-order model (FOM), takes into account the various states of system components, including the impacted, degraded, and failed states. We proposed an effective framework to compute a more realistic system availability, even for real systems in which the effect of interdependence occurs. The proposed model is validated using a numerical example, which provides an evaluation of the interdependence effect on various system variables. Additionally, a set of managerial insights is formulated, providing practical implications for maintenance planning and decision-making in large multi-component production systems.

Appendix A

Theorem 4

The sufficient condition for the existence and uniqueness of the solution of system (6) in the region $\Omega \times [t_0,T]$ with initial conditions $N(0)=(S(0), E(0), I(0), Q(0),H(0),R(0),S_t(0))$ and $t \in [t_0,T]$ is:

$$\begin{aligned} L& = {} d+\max (2\beta _{1}M,2(\beta _{2}M+\beta ),2(\delta +\eta +\mu ),\\{} & {} 2(\delta +\eta +\mu ),k+2\varepsilon ,2r). \end{aligned}$$

Proof

Let $X=(S,E,I,Q,H,R,S_t)^{T}$ and $X^{'}=(S',E',I',Q',H',R',S_t')^{T}$ the system (6) can be written in this form:

$$\begin{aligned} D^{\beta }X=F(X), \end{aligned}$$

(A1)

where

$$\begin{aligned} F(X)=\begin{pmatrix} m-(\beta _1+d)S+\beta _{2}E\\ \beta _1S-(\beta _2+d+\theta )E \\ \theta E-(\delta +\eta +\gamma +d)I\\ \delta I-(\Upsilon +\varepsilon +d)Q\\ \varepsilon Q+\eta I-(r+\nu +d)H\\ rH+\gamma I+\zeta S_t-dR\\ \Upsilon Q+\nu H-(\zeta +d)S_t\\ \end{pmatrix}=\begin{pmatrix} F_1(X)\\ F_2(X)\\ F_3(X)\\ F_4(X)\\ F_5(X)\\ F_6(X)\\ F_7(X) \end{pmatrix}. \end{aligned}$$

To prove the global existence and uniqueness of system (6), consider the region $\Omega \times [t_0,T]$,

where $\Omega =\left\{ (S,E,I,Q,H,R,S_t)\in \mathbb {R}^{7}_+: \max \left\{ S,E,I,Q,H,R,S_t\right\} \le M, M>0\right\}$. For any $X, X'\in \Omega$:

$$\begin{aligned}{} & {} \left\| F(X)-F(X^{'})\right\| _{1}=\sum \limits _{\underset{}{i=1}}^7|F_i(X)-F_i(X')|,\\{} & {} \quad =|-(\beta _{1}+d)(S-S')+\beta _{2}(E-E')|\\{} & {} \qquad +|\beta _{1}(S-S')-(\beta _{2}+d+\theta )(E-E')|\\{} & {} \qquad +|\theta (E-E')-(\delta +\eta +\gamma +d)(I-I')|\\{} & {} \qquad +|\delta (I-I')-(\Upsilon +d+\varepsilon )(Q-Q')|\\{} & {} \qquad +|\varepsilon (Q-Q')+\eta (I-I')-(r+d+\nu )(H-H')|\\{} & {} \qquad +|r(H-H')+\gamma (I-I')+\zeta (S_t-S_t')-d(R-R')|\\{} & {} \qquad +|\Upsilon (Q-Q')+\nu (H-H')-(\zeta +d)(S_t-S_t')|\\ \\{} & {} \quad \le L\left\| X-X'\right\| _1, \end{aligned}$$

where

$$\begin{aligned} L= & {} d+2\max (\beta _{1},(\beta _{2}+\theta ),\delta +\eta +\gamma ,\\{} & {} \varepsilon +\Upsilon ,r+\nu ,r+\nu ,\delta ), \end{aligned}$$

which proves this Lemma. $\square$

Thus, F(X) satisfies the Lipschitz’s condition [44] with respect to X.