1 Introduction

1.1 Motivation and background

Inkjet printing is a material jetting technology, in which a dispersion is deposited drop by drop onto a substrate. Due to the intentionally set overlap, the drops fuse into a continuous layer structure. Owing to its superior printing resolution [1] and excellent multi-material capability [2], inkjet printing has proven to be a promising technology for various applications. Recently, it gained attention for the fabrication of electrochemical storage devices, such as supercapacitors and batteries [3]. While intensive research efforts have been made in the field of supercapacitors, batteries are rather unexplored. The research activities concerned with materials suitable for lithium-ion batteries include dispersions based on \(\mathrm {LiFePO_{4}}\) (LFP) [4] and \(\mathrm {LiCoO_{2}}\) (LCO) [5] for the cathode side and \(\mathrm {SnO_{2}}\) [6] employed on the anode side. It allows for an accurate control of the part geometry and thus the generation of arbitrary structures [7]. This makes this technology an interminably promising approach to generate interlocked electrode architectures [8]. Such adaptation of the electrode microstructure mitigates the trade-off between the achievable energy density and the power density, enabling faster ion transport and higher mass loadings [9]. Despite the potentials, there are restrictions that impede the leveraging of the technology [7]. The process places challenging requirements on the dispersion. It is required to exhibit a high temporal stability to avoid agglomeration and sedimentation. Otherwise, the risk of nozzle clogging and bridging is increased [10]. In addition, the dispersion properties must be adjusted to the print head characteristics. This is even more challenging for electrode dispersions with typically non-Newtonian behavior, as hardly any standards exist to fully describe the rheological behavior and thus to prepare suitable formulations [11]. Accordingly, the printability of electrode dispersions has hardly been investigated prior to processing. Therefore, the cause-effect relationships underlying the drop formation and the drop deposition are reviewed and existing formulaic relationships are summarized.

Drop formation According to Wijshoff [1], a stable drop formation is referred to the printing condition in which only a single drop is generated. By contrast, the appearance of multiple drops, also referred to as satellite drops, indicates an inadequate printing regime. Jang et al. [12] stated that this phenomenon usually occurs as a consequence of pronounced filaments, which require a longer time to detach from the nozzle.

The drop formation in a print head is dominated by the interaction of the viscosity, the surface tension, and the density of the fluid. For a Newtonian fluid, the drop formation can be fully characterized by the dimensionless Ohnesorge number Oh [13], which can be expressed by the Weber number We and the Reynolds number Re [14]:

$$\begin{aligned} Oh = \frac{\sqrt{We}}{Re} = \frac{\eta }{\sqrt{\sigma \rho L}}. \end{aligned}$$
(1)

Here, \(\eta\) is the viscosity, \(\sigma\) the surface tension, and \(\rho\) the density. L represents the characteristic length, which is not subject to a standardized definition. Mostly, the nozzle diameter d [15] or the nozzle radius r [1] is used. Literature presents different conclusions pertaining to the ranges for Oh (see Table 1).

Table 1 Summary of the different approaches to the classification of Oh with the corresponding reference value for L
Full size table

Further parameters are required to describe non-Newtonian fluids [21]. Clasen et al. [11] presented an approach to assess their printability based on a set of nondimensional numbers beyond the Ohnesorge number. These numbers also incorporate the printing parameters beside the intrinsic material properties. The set consists of six numbers, which describe either fluiddynamic or material property-based attributes. According to this theory, a non-Newtonian fluid is thoroughly characterized by two fluiddynamic numbers and one material property-based number. An overview of the numbers is provided in Table 2.

Table 2 Set of nondimensional numbers to characterize non-Newtonian fluids according to Clasen et al. [11] with \(U_\textrm{eject}\): velocity of the drop, L: characteristic length, \(\lambda\): relaxation time, \(\sigma\): surface tension, \(\eta\): dynamic viscosity, and \(\rho\): density
Full size table

Furthermore, Clasen et al. [11] used the aforementioned numbers to characterize the initial filament thinning mechanism. Depending on the dominating forces, the dispensing operation can be either viscosity, inertia, or elasticity controlled. Hence, the fluids fall into two categories [11]:

Category 1: high-viscosity fluids (\(Oh~\gg ~0.2\))

High-viscosity fluids can be further categorized according to the Elasto-capillary number Ec:

  • \(Ec~\ll ~4.7\): The fluid is weakly elastic and viscosity controlled.

  • \(Ec~\gg ~4.7\): The fluid is strongly elastic and thus elasticity controlled.

Category 2: Low-viscosity or inviscid fluids (\(Oh~\ll ~0.2\))

Low-viscosity or inviscid fluids, respectively, can be further distinguished according to the Deborah number \(De_\textrm{0}\):

  • \(De_\textrm{0}~\ll ~1\): The fluid is a low-viscosity Newtonian fluid with a weakly elastic behavior. The dispensing operation is inertia controlled.

  • \(De_\textrm{0}~\gg ~1\): The fluid is inviscid, but exhibits an elastic behavior. Accordingly, the thinning regime is elasticity controlled.

Drop deposition

According to Rioboo et al. [22], the drop deposition comprises the drop impact and the substrate wetting.

A stable drop impact can be understood as the condition, in which neither splashing nor distinct spreading of the drop occurs [23]. In this context, the impact velocity was found to play the decisive role [22]. A sufficient substrate wetting can be expected when the liquid–solid contact angle between the fluid and the substrate is below 90\(^\circ\) [24].

1.2 Approach

Following the printing requirements outlined in Kolb et al. [25], this paper represents a systematic approach for an a priori evaluation of the printability of aqueous graphite dispersions designed for lithium-ion batteries. In numerous previous studies (see e.g. Kolb et al. [26]), we have already demonstrated that polyvinylpyrrolidone (PVP) represents an effective dispersant to stabilize graphite in water. In this context, we have also outlined an approach to quantify the dispersion behavior of printing dispersions [27]. Accordingly, a suitable preparation route was outlined in the presented paper that covers the synthesis of the entire anode dispersion. Graphite dispersions with varying composition were prepared and their printability was investigated by characterizing the drop formation and the drop deposition. While the drop formation was observed using in-situ process monitoring, the drop deposition was analyzed in ex-situ setups. The rheological properties were determined and used to calculate the nondimensional numbers. Conclusions were drawn with regard to the experimental results.

2 Materials and methods

2.1 Preparation of the dispersions

Electrode dispersions are complex systems with numerous components and phase boundaries. Accordingly, the preparation route has to be determined so that the sequence and the power of the devices applied meet the respective mixing purpose.

The electrosterically stabilizing additive PVP was employed as a dispersant [27], resulting in a homogeneous distribution of the particles in the medium. Carboxymethyl cellulose (CMC) and styrene-butadiene rubber (SBR) were used as binders, as this represents the state-of-the-art water-compatible system for electrode dispersions [28].

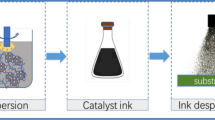
The graphite dispersions were prepared according to the procedure shown in Fig. 1. PVP (Luvitec K17, BASF, Germany) was dissolved in deionized water for 30 min using a magnetic stirrer. Concurrently, deionized water and CMC (CMC MAC200HC, Nippon Paper Industries, Japan) were merged to form a second mixture and magnetically stirred for 60 min. High-purity graphite nanoparticles (NG08BE0305, Nanografi, Turkey) of varying content were gradually added to the as-prepared PVP solution and stirred for 30 min (see Table 3). The low shear rates introduced by the magnetic stirrer allow for a wetting of the particles and an initial deagglomeration [29]. For further deagglomeration and thus a homogenization of the dispersion, the mixture was sonicated using a high-power ultrasonic homogenizer (FS-300N, Vevor, China) with a maximum power of 300 W. At a frequency of 12 kHz, mixing intervals of 20 s and intervals for cooling of 1 min were performed alternately. The total homogenization duration was 10 min. The CMC solution was added to the as-prepared graphite dispersion and stirred for another 30 min. Lastly, SBR (SBR, Zeon Corporation, Japan) was added to the mixture and stirred for 15 min. Accordingly, the binders were added to the dispersion by applying low shear rates. The ultrasonic treatment was observed to lead to a partial destruction of the polymer bonds, resulting in a decreased molecular weight [30]. This negatively affects both the rheological characteristics of the dispersion [31] and the mechanical properties of the electrode [32]. While CMC predominantly alters the inter-particle bondings and thus the cohesion, SBR affects the overall electrode flexibility and adhesion of the particle clusters to the current collector [33]. Therefore, it is indispensable that the particles are first exposed to CMC so that this polymer is the prevalent one on the total particle surface area. The as-prepared graphite dispersion was stored on a low-power roller mixer (RM 2, Edmund Bühler, Germany) until processing.

Fig. 1
figure 1

Preparation route of the graphite dispersions

Full size image
Table 3 Proportions of the components in the dispersions in relation to the respective amount of graphite
Full size table

2.2 Drop monitoring

The test setup reported by Lehmann et al. [20] was utilized for the monitoring of the drops (see Fig. 2).

The drops were generated using a piezoelectric print head (Spectra SL-128 AA, Fujifilm, Japan) with a nozzle diameter of 50 \(\upmu \hbox {m}\) in a custom test setup (VTS128, Voxeljet Technology GmbH, Germany). To record the drop formation, a high-speed camera (iSpeed, Olympus, Japan) with a Sigma objective lens with 105 mm was incorporated in the test setup.

Fig. 2
figure 2

Schematic depiction of the in-situ process monitoring setup (modified from Lehmann et al. [20])

Full size image

A high-power LED (M405LP1, Thorlabs, Inc., USA) focused behind the print head with a collimator (SM2P50-A, Thorlabs, Inc., USA) and controlled by an LED driver (LEDD1B T-Cube, Thorlabs, Inc. USA) served as the light source. Each viably printable dispersion was recorded at a frame rate of 1000 fps.

2.3 Characterization

2.3.1 Rheological properties

The rheological properties of the dispersions were determined using a rotational rheometer (Kinexus lab+, Netzsch, Germany) equipped with a passive solvent trap. A 40 mm plate-plate geometry with a sample gap of 0.1 mm was employed. Each measurement was performed at ambient temperature after an equilibration of 5 min and each measurement point resulted from three single-point measurements. As common practice for clarity, the standard deviations were not depicted. Shear rate sweeps were conducted to determine the flow behavior and the viscosity at drop ejection \(\eta _{\textrm{eject}}\). The viscosity was measured as a function of the shear rate from \(10^1\) to \(10^4\) \(\mathrm {s^{-1}}\). Amplitude tests were performed to identify the yield points and the linear viscoelastic (LVE) range of the dispersions. Therefore, the storage modulus G\(^{\prime }\) and the loss modulus G\(^{\prime \prime }\) were measured over the shear strain in a range between \(10^{-2}\) and \(10^{2}\)%. Frequency tests were carried out on the basis of the amplitude tests to determine the material behavior, which allows for an estimation of the stability. Furthermore, the relaxation times were derived. G\(^{\prime }\) and G\(^{\prime \prime }\) were determined within a frequency range between \(10^{-1}\) and \(10^{2}\) Hz.

2.3.2 Surface tension and density

The surface tension was determined according to the stalagmometric method of Traube [34]. For each sample measurement, the average weight was determined based on 10 drops. Deionized water served as calibration medium. Three measurements were performed per sample.

The density of the dispersions was determined using a density meter (DMA 5001, Anton Paar, Austria) working on the basis of oscillating U-tube principle.

2.4 Drop deposition

2.4.1 Drop impact

The in-situ drop impact was approximated by a custom test setup (see Fig. 3), which allows for an observation of the drop impact behavior on a substrate from different heights. To imitate the actual process, a copper foil attached to a glass plate served as a substrate.

The drops were generated manually using a syringe equipped with a nozzle tip with a diameter of 110 \(\upmu \hbox {m}\). This is intended to approximate the condition of a constant initial voltage at the piezoelectric element. The drop impact behavior was captured by the high-speed camera used for drop monitoring. The frame rate was set to 200 fps. The standard deviation was calculated from three samples.

Fig. 3
figure 3

Schematic depiction of the custom test setup to investigate the drop impact behavior

Full size image

2.4.2 Wetting

The contact angle \(\theta\) was determined according to the sessile drop method with a drop shape analyzer (DSA25E, Kruess Scientific, Germany). The same substrate was used as for the analysis of the drop impact. Drops with a volume of 5.5 \(\upmu \hbox {L}\) were deposited onto the substrate and observed by an integrated camera. The standard deviation resulted from three samples.

3 Results and discussion

3.1 Drop formation

3.1.1 Drop monitoring

The drop formation was observed in the dripping mode. This regime refers to the condition in which a single drop forms at the nozzle orifice and detaches due to gravity once a critical drop volume is reached [11].

The drop formation process of the viably processable graphite dispersions is depicted in Fig. 4. The captured images show the entire process from the filament ejection, thinning, and detachment to the formation of the individual drops. The black lining at the top of the images represents the cross-sections of the print head.

The dispersion with 1.0 m% graphite shows numerous satellite drops upon ejection. This effect can also be observed for the dispersion with 1.5 m% graphite, although it is less pronounced. For the dispersion with 2.0 m% graphite, the filament merges into a single drop without the formation of satellite drops. The dispersion with 2.5 m% graphite could not be processed. Accordingly, only the dispersion with 2.0 m% graphite allows for a stable drop formation.

Fig. 4
figure 4

Drop monitoring images of graphite dispersions with varying graphite content for a 1.0 m% graphite, b 1.5 m% graphite, and c 2.0 m% graphite; the voltage was set to 80 V and the frequency to 1000 Hz. The time interval between two consecutive frames was 20 \(\upmu \hbox {s}\)

Full size image

3.1.2 Characterization

Determination of the LVE region

The LVE region describes the range in which the specimen is not irreversibly destroyed by the applied shear strain [35]. In theory, the LVE region is defined as the range in which both G\(^{\prime }\) and G\(^{\prime \prime }\) show a plateau [36]. In practice, the curves are subject to high standard deviations. Here, the expression is usually more pronounced for the lower and thus less dominant component. In this case, the LVE range was approximated based on the progression of the dominant component.

The rough LVE regions determined for the various graphite dispersions are summarized in Table 5.

To ensure a non-destructive deformation in the frequency sweep, the shear-strain amplitude employed has to be within the LVE region. To maintain compatibility, a shear-strain amplitude applicable to all dispersions was pursued. Accordingly, a shear-strain amplitude of 0.1% was derived, as it lies within the respective LVE regions. This is consistent with the studies of Barnes [36], who also proposed this to be a suitable shear-strain amplitude for dispersions.

Analysis of the material behavior

Frequency sweeps allow for an analysis of the time-dependent deformation behavior [36]. The short-term behavior is simulated by applying high frequencies, whereas the long-term behavior is imitated by low frequencies [35]. The latter is applied to determine the material behavior and thus to predict the long-term stability.

Figure 5 displays the course of \(G^{\prime }\) and \(G^{\prime \prime }\) as a function of f for selected dispersion compositions.

Fig. 5
figure 5

Storage modulus G\(^{\prime }\) and loss modulus G\(^{\prime \prime }\) as a function of the frequency f at a constant shear strain of 0.1% for graphite dispersions with varying graphite content for a 1.0 m% graphite, b 2.0 m% graphite, c 5.0 m% graphite, and d 10.0 m% graphite

Full size image

Overall, it is apparent that the differences between G\(^{\prime }\) and G\(^{\prime \prime }\) become more pronounced with an increasing graphite content. For the dispersion containing 1.0 m% graphite, the data sets for G\(^{\prime }\) and G\(^{\prime \prime }\) are subject to high fluctuations. The curves show various intersections and regions, where no clear distinction can be made between G\(^{\prime }\) and G\(^{\prime \prime }\). With an increasing graphite content, G\(^{\prime }\) can successively prevail over G\(^{\prime \prime }\) and the fluctuations are significantly lower. For the dispersions with 2.0 m% and 5.0 m%, G\(^{\prime }\) and G\(^{\prime \prime }\) roughly resemble two parallel curves with a gradual gradient. For the dispersions with 10.0 m%, G\(^{\prime }\) and G\(^{\prime \prime }\) show a plateau with an approximately constant distance throughout the entire frequency range.

The material behavior of dispersions can be characterized based on the ratio of G\(^{\prime }\) and G\(^{\prime \prime }\) [36]. If G\(^{\prime }\) is higher than G\(^{\prime \prime }\), the dispersion behaves like a viscoelastic solid [36]. Conversely, if G\(^{\prime \prime }\) is higher than G\(^{\prime }\), the dispersion can be characterized as a viscoelastic liquid [36]. In terms of stability, a viscoelastic solid behavior is pursued, since agglomeration and settling effects are effectively slowed down or prevented by the solid-like dispersion network [4]. Accordingly, sufficient stability can be expected for the dispersions containing at least 2.0 m%. Furthermore, the plots indicate that the stability increases with a rising graphite content. This trend is mainly attributed to the gradually increasing binder contents. The binders effect the formation of a strong polymer-particle network, which results in an increased long-term stability [37]. This is also reflected in the decreasing gradient of the G\(^{\prime }\) and the G\(^{\prime \prime }\) curves, which indicates a strengthening crosslinking density [38].

Determination of the relaxation time \({\lambda }\)

The data obtained from the frequency sweeps allow to determine the relaxation time \(\lambda\) (see Table 5), which represents the time required to return to a more viscous state after shear stress [36]. It is defined as the inverse of the frequency f at the intersection of G′ and G\(^{\prime \prime}\).

The relaxation times of the dispersions are in the same order of magnitude. The dispersion with a graphite content of 1.0 m% shows the highest relaxation time. For the dispersion containing 10.0 m%, no relaxation time could be determined. The intersection is expected to be in a higher frequency range, resulting in a lower relaxation time. Accordingly, the dispersions with the minimum and maximum graphite content mark the extremes. In between, no clear trend can be seen. This is attributed to the inaccuracies that underlie this method. Considering the extremes, it is obvious that the relaxation time decreases with an increasing graphite content. This trend is attributable to the gradual increase in the binder contents, which are accompanied by an increase in the graphite content. Particularly the CMC contained enhances the thixotropic behavior of the dispersion system [39]. Accordingly, the tendency to a more or less rapid but complete equilibrium restoration after a shearing phase and thus shape retention is more pronounced [36].

Calculation of the shear rate at the drop ejection \({\dot{\gamma }}_\mathrm {{eject}}\)

The shear rate at which the drop is applied \({\dot{\gamma }}_\mathrm {{eject}}\) can be calculated as follows [40]:

$$\begin{aligned} {\dot{\gamma }}_\mathrm {{eject}} = \dfrac{4 Q}{\pi R_\mathrm {{eject}}^3}. \end{aligned}$$
(2)

Q represents the volume flux which is defined as follows: \(Q = v_\mathrm {{eject}} \cdot {R_\mathrm {{eject}}}^2 \pi\). Here, \(v_\mathrm {{eject}}\) is the drop velocity and \(R_\mathrm {{eject}}\) the nozzle radius.

The used print head has a nozzle diameter \(d_\mathrm {{eject}}\) of 50 \(\upmu \hbox {m}\). The maximum drop velocity \(v_\mathrm {{eject,max}}\) is specified as 8 m/s. In a previous study, we showed that the velocities achieved for particle-loaded inks are considerably lower and depend on the particle content [20]. For a Newtonian graphite dispersion with a particle content up to 10 m% suitable for binder jetting, \(v_\mathrm {{eject}}\) ranged roughly between 2.0 and 2.5 m/s. Assuming that \(v_\mathrm {{eject}}\) lies in a similar magnitude despite the different fluid behavior, \({\dot{\gamma }}_\mathrm {{eject}}\) is calculated to be in the range \(3.2 \cdot 10^{5}\)  \(\mathrm {s^{-1}}\) to \(4.0 \cdot 10^{5}\)  \(\mathrm {s^{-1}}\). For higher values of \(v_\mathrm {{eject}}\) between 2.5 and 8.0 m/s, \({\dot{\gamma }}_\mathrm {{eject}}\) lies between \(4.0 \cdot 10^{5}\) \(\mathrm {s^{-1}}\) and \(1.3 \cdot 10^{6}\) \(\mathrm {s^{-1}}\). This is in good agreement with the literature, which provides a range for \({\dot{\gamma }}_\mathrm {{eject}}\) for common print head systems between \(10^\textrm{4}\) \(\mathrm {s^{-1}}\) and \(10^\textrm{6}\) \(\mathrm {s^{-1}}\) [41].

Determination of the flow behavior

Figure 6 displays the viscosity over the shear rate.

Fig. 6
figure 6

Viscosity \(\eta\) as a function of the shear rate \({\dot{\gamma }}\) for graphite dispersions with a varying graphite content; the measured data were extrapolated by applying the Herschel–Bulkley model. The area marked in gray represents the calculated shear rate range for the test set-up used

Full size image

It is apparent that the viscosity values decrease with an increasing shear rate. The higher the graphite content is, the steeper is the gradient. Additionally, it appears that the dispersions transition more quickly to a rather linear dependence on the shear rate with an increasing graphite content, with the dispersion with 10 m% showing a nearly linear behavior over the entire measuring range. Accordingly, all dispersions exhibit a shear-thinning behavior, whereby the effect is more pronounced at higher graphite contents. This behavior is beneficial for printing, as a low viscosity is required for the dispersions to flow through the nozzle when high shear rates are applied for the drop ejection [4]. Dispersions with higher graphite contents thus offer the potential to overcome higher viscosity ranges while maintaining a high stability at rest. These observations can be accredited to the polymer-particle network that forms between the binder molecules and the graphite particles [42]. At rest condition, the particles are embedded into the polymer matrix. When a shear rate is applied, any present network structure is destroyed. This forces both the particles and the binder molecules to realign themselves in a comparably ordered structure parallel to the applied shear field [43]. The flow resistance and thus the viscosity is reduced significantly. The steeper gradient can be attributed to the higher graphite and thus also binder contents, which amplifies the aforementioned effects.

Determination of the limiting high-shear viscosity \({\eta _\textrm{eject}}\)

Depending on the particular print head specifications, the shear rate \({\dot{\gamma }}_\mathrm {{eject}}\) can exceed the measuring range of rotational rheometers. This also applies to the used test setup used. However, the viscosity curves can be extrapolated by employing a fluiddynamic model (see Fig. 6). The selection depends on the flow behavior of the respective dispersions. Considering Fig. 6, it appears that the flow behavior is predominantly influenced by the graphite and thus the binder contents. According to Abdelrahim et al. [44], the Herschel–Bulkley model is suitable for systems whose flow behavior is impacted by shear-thinning polymers, such as CMC. In addition, Kwon et al. [45] have shown the applicability of the model to electrode dispersions. Accordingly, the Herschel–Bulkley model was used for the extrapolation [46]. It obeys the following equation [35]:

$$\begin{aligned} \tau = \tau _\textrm{HB} + k \cdot {\dot{\gamma }}_\mathrm {{eject}}^\textrm{n}. \end{aligned}$$
(3)

\(\tau _\textrm{HB}\) represents the flow point, k the consistency index, and n the Herschel–Bulkley index. The parameters for the respective viscosity curves are given in Table 4. Lastly, a range for the viscosity at drop ejection \(\eta _\textrm{eject}\) was derived for the respective graphite dispersions.

Table 4 Overview of the determined Herschel–Bulkley equation parameters for the different dispersion compositions
Full size table

Determination of the surface tension \({\sigma }\)

The surface tensions determined for the dispersions are summarized in Table 5. The values appear extremely high compared to other technical printing dispersions [12]. This is attributed to the high water content and the absence of surfactants [47]. The surface tension decreases successively with an increasing graphite content. Literature shows contradictory conclusions pertaining to the influence of the particle content on the surface tension. Murshed et al. [48] and Radiom et al. [49] reported a decrease of the surface tension with a rising particle content. They attributed this observation to various effects, such as the Brownian motion [48]. In contrast, Tanvir et al. [50] and Bhuiyan et al. [51] observed an increase in the surface tension with a rising particle content. They explained this effect with the emerging interparticle forces [50]. Considering this ambiguity, Tanvir et al. [50] concluded that the contradictory statements can be ascribed to the varying particle, solvent, and additive combinations. Each dispersion will likely show its own characteristic trend depending on the dominant component.

If specified by the system, the desired surface tension range can be compared a priori with the empirically determined values.

Table 5 Values of the empirically determined dispersion values
Full size table

3.1.3 Nondimensional numbers

The nondimensional numbers for each dispersion are given in Table 6. The density values are provided in Table 5. Accordingly, the values for a stable drop formation can be derived from the dispersion with 2.0 m% graphite. Since Clasen et al. [11] did not indicate printability ranges, the values obtained cannot be compared with the literature. However, they can serve as a reference for further investigations. It is apparent that the Oh value of the dispersion with 2.0 m% is lower than the values presented in the literature for the same characteristic length.

The empirical data allow to determine the dependence of the numbers on the graphite content. It appears that a trend can be drawn for each number to a greater or lesser extent. For the viscosity-dependent numbers, however, small deviations can be recognized for the dispersions with 2.0 m% and 2.5 m%, which are attributed to the discrepancies in the extrapolation (see Fig. 6). The Oh values increase with a rising graphite content. Low Oh values cause the formation of long filaments that are susceptible to satellite drops [14]. High Oh values lead to viscous dissipation, which prevents the ejection of drops [14]. These trends are consistent with the conclusions drawn from the drop monitoring (see Fig. 4). \(De_\textrm{0}\) rises with an increasing graphite content, which indicates an increase in elasticity [52]. This trend is also reflected in the progression of Ec [11]. The increased elasticity requires longer times for the filament to detach from the nozzle (see Fig. 4). For the dispersions with a graphite content of up to 5.0 m%, Ca is lower than 1. This indicates that the drop ejected was determined by the ideal shape of the smallest surface energy [53], which is consistent with the drop monitoring images (see Fig. 4). In contrast, for the dispersion with 10.0 m%, the drop is expected to remain deformed [53]. For the We values, an increase can be observed for rising graphite contents. We characterizes the energy required for dispensing [14]. The higher We is, the more likely it is that the energy is sufficient to overcome the surface tension [54]. Wi increases with a rising graphite content. This reflects a strengthening of the viscoelasticity [55], which concurs with the results from the frequency sweeps (see Fig. 5).

Table 6 Summary of the calculated nondimensional numbers for the investigated graphite dispersions with varying graphite content with the nozzle radius r as characteristic length scale
Full size table

Furthermore, the nondimensional numbers were used to characterize the initial thinning mechanism and thus the dispensing operation (see Fig. 7). While the dispersions with a graphite content of up to 2.5 m% fall in the category of low-viscosity or inviscid fluids, the dispersions with a graphite content of 5.0 m% and 10.0 m% belong to the category of high viscosity fluids. Regardless of the category, the dominating thinning mechanism for all dispersions is the elasticity. This is attributed to the SBR contained in the dispersions, which exhibits highly elastic behavior [56].

According to Clasen et al. [11], the dispersions with up to 2.5 m% graphite are less challenging to dispense, whereas the dispersions with higher graphite contents are more likely to cause problems in the dispensing operation. This underlying trend is consistent with the observations, although the dispersion with 2.5 m% graphite could not be printed. The dispersions with a graphite content of lower than 2.0 m% could be dispensed, but did not show a stable drop formation. This indicates that the categorization presented by Clasen et al. [11] allows for a rough assessment of the dispensing behavior. It seems less suitable for a precise evaluation in terms of stable drop formation.

Table 7 Categorization of the dispersions according to Clasen et al. [11] with the fluid categories 1 (high-viscosity fluid) and 2 (low-viscosity or inviscid fluid)
Full size table

3.2 Drop deposition

3.2.1 Drop impact

The drop impact velocity as a function of the distance is shown in Fig. 7a.

Fig. 7
figure 7

Drop impact behavior as a function of the distance d between the print head and the substrate for the dispersions with varying graphite content with a drop impact velocity \(v_\textrm{impact}\) and b drop diameter ratio \(d_\textrm{drop}/d_\textrm{nozzle}\)

Full size image

The drop impact velocity rises with an increasing height due to gravity [57]. Contrary to the expectations, no clear correlation is apparent between the graphite content and the drop impact velocity. According to Tsai et al. [58], it was expected that the drop impact velocity decreases with a rising graphite content. The deviations are attributed to the inaccuracies in the dosing behavior, resulting in slightly different drop volumes.

Furthermore, the diameter of the deposited drops was examined as a function of the distance (see Fig. 7b). It appears that the dosing inaccuracies also make it difficult to identify clear trends in terms of the drop diameter. It is evident that the diameter ratio is much higher than one. This is attributed to the considerably higher nozzle diameter and also distances between the print head and the substrate compared to real process conditions. In addition, it is expected that the drop impact is also subject to scaling effects, as the volume of a drop rises with the third power of the initial diameter. Furthermore, An et al. [59] found that drops with larger diameters cause more distinct spreading on the substrate. Considering the scaling effects, it is expected that wet structures can be realized that are in the magnitude of related processes [60], provided that suitable drop overlap and process parameters are identified.

The data indicates a weakly pronounced trend that the diameter increases at higher distances. This is consistent with the studies by Rioboo et al. [22] and Scheller et al. [61], who concluded that a higher drop impact velocity (see Fig. 7a) leads to an increasing drop diameter.

Overall, no splashing was observed for the investigated graphite dispersions, regardless of the graphite content and the distance. According to Derby et al. [14], the tendency to splashing is amplified with an increasing drop impact velocity and nozzle diameter. This demonstrates that a stable drop impact behavior can also be expected under real process conditions.

Aiming at a stable drop impact behavior and a high printing resolution, the distance between the print head and the substrate should be kept to a minimum. In addition, it seems to be beneficial to keep the nozzle diameter as small as possible, while still meeting the dispersion-specific requirements regarding the particle diameter [10].

3.2.2 Wetting

Figure 8 displays the contact angle \(\theta\) between the dispersion and the copper foil over time t.

It is apparent that the average contact angle values range between approximately 68 and 84\(^\circ\). The individual contact angle values are subject to high standard deviations. These are attributed to the large inaccuracies that are common for contact angle measurements due to deviations in the positioning of the substrate, the varying roughness of the substrate [62], and the subsequent manual setting of the tangent line [63]. According to Billot et al. [64], wetting can be expected for contact angle values below 90\(^\circ\). Hence, a sufficient wetting is assumed for all examined dispersions. It can be recognized that the contact angle of all investigated dispersions decreases with an increasing duration. This is expected to be caused by the gradual evaporation of the water contained in the dispersions [21]. Lastly, no clear dependence can be recognized between the graphite content and the contact angle values. While commonly both an increasing graphite content and binder content result in higher interfacial tensions, a higher dispersant content has the opposite effect [65]. This demonstrates that a clear influence of the individual phases on the overall properties cannot be derived.

Fig. 8
figure 8

Contact angle \(\theta\) between the dispersion and the copper foil as a function of the wetting time t for the dispersions with a varying graphite content

Full size image

4 Conclusions

This paper represents a methodical approach for an a priori evaluation of the printability of an aqueous graphite dispersion for the use in inkjet printing. The dispersion was designed for the application in lithium-ion battery production. The printability was validated by characterizing the drop formation and the drop deposition behavior.

The findings of this paper can be summarized as follows:

  • The elaborated approach is suitable to systematically identify a stable and printable aqueous graphite dispersion. In addition, the conducted experiments facilitate a standardized characterization.

  • We demonstrated that the dispersion with 2.0 m% graphite shows a stable drop formation. Higher dispersion contents led to a strong increase in the elastic behavior, which impeded the ejection of drops.

  • All dispersion compositions exhibited a stable drop deposition. No splashing occurred and adequate wetting on the substrate is likely.

  • The nondimensional numbers were found to allow for a rough a priori assessment of the dispensing behavior. In contrast, they seem less appropriate for a precise analysis in terms of the drop formation stability.

  • The nondimensional numbers calculated for the stable dispersion can serve as a reference for further investigations.

Future research will be conducted to achieve the printability of dispersions with higher graphite contents. Hence, the cause-effect relationships between the binders and the overall dispersion properties will be examined. This allows for a precise reduction of the binder contents in order to improve the drop formation behavior, but not at the expense of poorer wetting and lower mechanical strength. In this regard, the application of synthetic graphite is of high interest due to the reduced total surface area. Additionally, further effort is required to reduce the surface tension, as this is expected to weaken the elastic behavior.

To link the findings with the print resolution, metrics have to be defined that quantify the drop formation behavior, the drop coalescence, and the resulting drop pattern. A profound statistical design can serve to map out parameter ranges that allow for a prediction of further printed structures.

Due to the universality of the systematic approach, it is expected to be applicable to different dispersion systems. Extensive empirical studies are needed to prove the transferability on a profound basis.