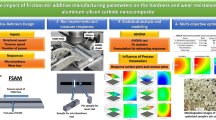
Abstract
The primary goal when manufacturing components in a blanking process is a high output to achieve good cost efficiency. Therefore, availability needs to be as high as possible. However, several process disturbances like slug pulling increase downtime and thus counteract this aim. Slug pulling is influenced by different forces that trigger the slug being pulled and those that hamper this effect. The predominating hampering force is friction between the slug and the die. Consequently, the influencing factors for this force have to be understood to reliably prevent slug pulling. In this publication, the influence of the die channel geometry on the occurring frictional forces and the part quality when blanking the non-alloy quality steel 1.0338 are investigated. Therefore, experiments with a variation of die channel geometry and punch diameter combined with force measurement are performed. Furthermore, a numeric simulation model based on the experimental results is used to investigate various die channels. The results enhance the knowledge about correlations between process parameters, slug properties, like slug deflection, and frictional forces and help to reliably prevent slug pulling.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Shear cutting is characterized by a high output quantity and low costs per unit. As a result, it has become one of the most widespread mass production processes. Two factors that have a decisive influence on the economic efficiency of shear cutting are the service life of the active elements and the occurrence of process disturbances. Generally, tool maintenance intervals are determined by the wear condition of the active elements, since wear on the cutting edges affects the height of the burr on the cutting surfaces of the parts. As soon as the burr height exceeds a certain level, the active elements have to be resharpened [1]. However, in addition to these often predictable and plannable process interruptions, unforeseen process disturbances can also occur. One of these is the phenomenon of slug pulling. Slug pulling occurs when the cut-out part does not fall downwards after material separation as planned but remains attached to the punch due to various mechanisms and is pulled upwards again [2]. In addition to damage to the part and the die, slug pulling is often accompanied by an interruption in production, which also causes costs and thus results in a reduction in profitability [3, 4].
The risk of slug pulling can be estimated based on a force equilibrium, which is established for the slug after material separation. The forces that occur can be divided into two types. While the forces causing slug removal counteract slug pulling, the forces causing slug sticking can lead to the phenomenon of slug pulling. The former include the weight of the slug, the frictional force between the slug and die, and acceleration forces. The forces causing slug sticking consist of an adhesion force caused by the lubricant, a burr clamping force between the burr on the slug and the punch cutting edge, and a vacuum force. When using punches with residual magnetism, a magnetic force between the punch and the ferromagnetic material can also occur. If the slug sticking forces exceed the slug removing forces, slug pulling can be observed. An overview of the forces acting on the slug is given in Fig. 1 [4,5,6,7].
Forces on the slug after material separation [8]
An investigation of the sticking forces was carried out by [4], where the push-off forces of the slug from the punch face were measured. However, it was often not possible to subdivide the push-off force into adhesion force and burr clamping force [4]. Kindsmueller et al. [8] investigated the slug sticking forces acting on the slug after material separation individually and independently of each other as a function of the process parameters. These included vacuum force, adhesion force, and burr clamping force. The tests were carried out in single-stroke experiments, varying the parameters of die clearance, cutting speed, cutting edge radius, punch penetration depth, and lubrication conditions. The punch diameters investigated were 10 and 20 mm. According to the results, the vacuum force during the punch return stroke is the dominant force that can cause slug pulling, especially with larger punch diameters and small die clearances. The sum of all sticking forces ranged from about 0.3 to about 6 newton, depending on the cutting parameters used. A sufficiently high frictional force in the mid-tree-digit newton range between the slug and die can thus be effective in preventing slug pulling [9].
[10] carried out an investigation of the frictional forces between the slug and die after material separation. Here, forces between almost 0 newton and more than 500 newton were measured with the copper alloy CuSn6, depending on the cutting parameters. A larger die clearance resulted in a reduced frictional force, while a larger punch edge radius significantly increased it. The lubricant also reduced the frictional force, especially for small die clearances.
The objective of this work is to investigate the influence of geometric modifications of the die channel on mechanical stresses between slug and die with a numerical approach for circular tool active elements. If those tensions are sufficiently large to counteract the slug sticking forces described in [8], this can effectively prevent the process disturbance of slug pulling. However, disproportionately too high tensions must be avoided in order to prevent excessive wear and a plastic deformation of the slug.
2 Experimental setup
2.1 Numerical simulation tool and model
All numerical results are calculated using Abaqus CAE 2020. For high accuracy combined with acceptable time usage, the model is two-dimensional with a symmetry axis through the centerline of the circular punch and a simulation grid that is refined close to the shear zone. Figure 2 a b show the stresses occurring in the blanking process. The displayed Von-Mises Stresses are the highest occurring in the whole process. These occur at geometry transitions in the die, such as the change from the conical to the straight area. The Von Mises stress values shown below are obtained by averaging the stresses of 3 times 3 mesh elements. These are shown in detail in Fig. 2a. Radial stresses are measured at the bottom dead center as the determining point for slug pulling. The radial stress values were determined by averaging the stresses of all nodes in contact with the die, weighted by element size. To determine the contact area, a script was used that considered the amount of clean cut. Elements with positive stress were subtracted. In addition, a stress threshold above which no interaction is assumed was used to further select the elements. For the DC04 shown here, this threshold is \(-163\) MPa. The value was first determined manually from several simulations. This procedure can represent the contact area with an accuracy of 8%. Furthermore, Fig. 2c illustrates slug bending (b) at the bottom dead center and the slug compression (c). The failure criterion is the Johnson–Cook equation with the first three parameters for dynamic failure, with an inverse determination of the failure parameters [11]. Thus, the simulation is not strain rate and temperature dependent [12]. A dynamic friction coefficient of 0.12 and a static friction coefficient of 0.15 were used to represent the process forces.
The numerical model is validated using the cutting surface properties from blanking experiments with the tool described below. The crack initiation and thus the fractured surface are displayed precisely, with a deviation of 3% of the sheet metal thickness. The rollover is overemphasized by 10%, and the clean cut is 7% too small. This deviation is caused by the use of the arbitrary Lagrangian–Eulerian method but does not negatively affect the quality of the results, because the relative deviation is the same for all process parameters.
Numerical calculation of stresses for a the 1 mm punch maximum Von-Mises Stress during the whole cutting process at the geometry transition and a detailed picture with the mesh, b 1 mm punch radial stress at the bottom dead center and c radial stress, slug bending and slung compression for the 5 mm punch
2.2 Investigated materials and tool geometries
In this paper, the non-alloy quality steel 1.0338 (DC04) with a hardness of 95 HV and a thickness of 1 mm served as sheet metal material. The tool active-elements consist of the cold-working steel 1.3343 (X82WMoV65) with a Young’s Modulus of 224 GPa hardened to 62 HRC. Table 1 shows the chemical compositions, determined with a spark spectrometer. During quasi-static tensile tests, the 1.0338 steel provides a Young’s Modulus of 210 GPa and a tensile strength \(R_\textrm{m}\) of 326 MPa.
In this publication, the influence of four different types of die channel geometries on the behavior of the slug, respective occurring tensions is examined. These geometries are shown in Fig. 3a. The first is a common die for industrial applications with a straight channel, that serves as the reference state (1). The second is a conical die (2). This geometry is a standard measure for slug pulling prevention due to the compression of the slug and the entailed increased stresses and frictional forces. The third and fourth variants have a straight part above, where the cutting process should not be influenced by geometry transitions and thus provide a part quality similar to the reference state; one with a short conical part (3) and one with a longer one (4). Then a conical section follows and compresses the slug to enhance the radial stress. For die (4), the last die section is a straight-shaped one again, where the slug should get stuck after the process, and the frictional forces and stresses are determined. For the straight (1) and sectioned (3) geometries the immersion depth (d) amounts to two times the sheet metal thickness (s). For the conical (2) and the sectioned (4) one (s) and (d) have the same size. Consequently, the slug compression (c) at the bottom dead center is the same for (2), (3) and (4). It is determined by the die angle \((\alpha )\) and Eq. (1). For an industrial use of the presented dies, the die channel ends right below the slug position at the bottom dead center to prevent jamming of multiple slugs.
2.3 Blanking tool
The modular experimental tool used for the validation of the numerical model, shown in Fig. 3b, enables the process parameters to be easily changed. A four-pillar structure ensures a very high level of stiffness. Two actuators with a maximum force of 31 kN on the Bihler GRM-NC servo stamping and forming machine independently move the blank holder and the blanking punch and thus decouple the influences of clamping the sheet metal and the cutting process on the frictional forces. Blanking forces and frictional forces are recorded with a piezoelectric load cell.
For all experiments, the relative die clearance is set to 10%, and the cutting edge is rounded to 50 \(\mu \)m. The punch diameter is varied between 1 and 5 mm. The slug compression for the investigated angles (c) is shown in Table 2.
2.4 Determination of cutting surface properties
Cutting surface property determination is the basis for two important tasks in this publication. First is the part quality classification, and second is the validation of the numerical results. For every parameter configuration five specimen have been blanked and for every specimen five equally distributed circular measuring points have been chosen.
There are various criteria for the part quality of blanked parts, like slug bending, edge crack sensitivity, or clean cut percentage. Common to almost all of these criteria is the dependency on time and type of crack initiation, which can directly be identified in the cutting surface properties. The fractured surface percentage for example, shows the crack initiation, while the occurrence of a secondary clean cut indicates that the cracks are not aligned. Furthermore, using the surface properties is a common way to validate numerical results. Therefore, the calculated values are compared with the ones of the real cutting process.
To quantify those properties like edge roll-over, clean cut percentage, amount of fractured surface, and burr formation, the cutting surface is scanned with the digital, confocal laser microscope Keyence VKX-100, providing a vertical accuracy of 0.7 \(\mu \)m.
3 Results
3.1 Slug bending
While the experiments with a punch diameter of 1 mm show almost no bending of the slug for all four die geometries, Fig. 4 illustrates the slug bending behavior for the 5 mm punch.
The long sectioned die (4) provokes slug bending of about 40 \(\mu \)m, similar to the reference state (1) for all angles, while the slug bending of dies (2) and (3) rises with bigger angles. The conical die (2) reaches values comparable to (1) for small angles but gets up to 145 \(\mu \)m using an angle of 5\(^{\circ }\). (3) shows the same behavior but is not that strong. It reaches a value of 112 \(\mu \)m for the largest angle.
3.2 Stresses
The Von-Mises stress has to be investigated to evaluate if the slug is subject to plastic deformation. Radial stresses between the slug and die at the bottom dead center are examined to estimate the tendency for slug pulling. All stresses in this section are measured at the bottom dead center, the lowest slug position in the shear-cutting process. The Von-Mises Stresses are illustrated in Fig. 5, and radial stresses in Fig. 6.
3.2.1 Von-Mises Stress
The shown values represent the highest locally occurring stress inside the material during the whole blanking process. For the 5 mm punch, the reference die (1) results in a maximum stress of 664 MPa. Conical dies (2) and the long sectioned ones (4) provoke stresses between 421 and 580 MPa and thus are noticeably lower than the reference stress (1). Stresses triggered by short sectioned dies (3) rise with higher angles from 384 MPa at 0.5\(^{\circ }\) to a value of 1263 MPa at 2\(^{\circ }\). For even higher angles, the stress value reaches a plateau and stays at that level.
For the smaller 1 mm punch, the Von-Mises Stress behavior is different. Stresses with the short sectioned die (3) rises from 1290 MPa (\(0.5^{\circ }\)) to 1503 MPa (\(3^{\circ }\) and \(5^{\circ }\)), the stress raises with higher angles, but stay constant when exceeding \(3^{\circ }\). The conical die (2) reaches the reference level only for \(1.5^{\circ }\) and \(5^{\circ }\) and otherwise stays lower, with a minimum of 397 MPa for \(0.5^{\circ }\). The long sectioned die (4) shows a similar behavior, but with the maxima at \(2^{\circ }\) and \(3^{\circ }\) and a minimum of 511 MPa at \(2.5^{\circ }\).
3.2.2 Radial stress
All the presented radial stresses have a negative sign, that represents pressure stress. The following given values are absolute. When using the 5 mm punch, the stresses lie within a range from 72 up to 363 MPa, while the straight reference die (1) shows 122 MPa. Each different die, except the long sectioned one (4), provides values that exceed the reference state and those that are lower. Both, the conical (2) and the long sectioned die (3) reach the maximum at an angle of 2.5\(^{\circ }\) with 363 and 149 MPa, respectively. The minima of 82 and 74 MPa can be seen at 0.5\(^{\circ }\). Radial stresses of the short sectioned die (3) exceed the reference state (1) for all investigated angles, with a maximum of 209 MPa at 1\(^{\circ }\).
The radial stress appearance differs markedly when using the 1 mm punch: The differences between the reference state (1) with 178 MPa compared to the minimum (27 MPa) and the maximum stress (446 MPa) are much more strongly pronounced than with the 5 mm punch. Furthermore, each die configuration has one angle where the maximum is higher than the reference and one with much lower radial stress. The conical die (2) has a maximum of 282 MPa (2\(^{\circ }\)) and a minimum of 27 MPa (1\(^{\circ }\)). With a stress of 326 MPa at 0.5\(^{\circ }\), the short sectioned die (3) reaches the maximum for a very low angle, while the high angles (3\(^{\circ }\) and 5\(^{\circ }\)) show low stresses of 33 and 48 MPa. At 2.5\(^{\circ }\), the contact force (radial stress multiplied by contact area) is 243 N. At \(3^{\circ }\) and \(5^{\circ }\), the forces are 15 and 42 N, respectively. At these low forces, slug pulling is very likely. The long sectioned die’s (4) behavior is the opposite. While it provides the minimum stress (57 MPa) for a low angle of \(0.5^{\circ }\), high stress values (446, 432, and 369 MPa) can be seen for high angles (\(2.5^{\circ }\), \(3^{\circ }\), and \(5^{\circ }\)).
3.3 Part quality
In this paper, the clean cut percentage serves as a parameter to evaluate the influence on part quality. Different die geometries only show a very small influence on the amount of clean cut, when blanking with a 1 mm punch. It differs between 69% for the straight die (1) and the short sectioned one (3) up to a maximum of 73% when using a conical die (2) with a high angle of \(5^{\circ }\). The behavior differs for the higher punch diameter of 5 mm, as shown in Fig. 7.
The straight die (1), as well as the two sectioned ones (3 and 4), show similar clean cut percentages between 60% and 63%. For small angles up to \(1.5^{\circ }\), the conical die (2) has the same percentage. A higher angle increases the clean cut up to 72% for an angle of \(5^{\circ }\).
4 Discussion
To prevent slug pulling during the blanking process, the radial stress between the slug and die at the bottom dead center has to be high enough to hold back the slug. Therefore the slug must have a higher outer diameter than the inner one of the die to obtain a slug oversize. This can be achieved by using dies with a constricting die channel. However, if the slug compression is too strong, the material strength can be exceeded, and thus the slug can be subject to locally plastic compression that reduces radial stresses and friction and thus enhances the probability of slug pulling. This effect becomes evident when a small increase in the die angle (\(0.5^{\circ }\)) leads to a substantial reduction of the radial stresses at the bottom dead center.
4.1 Plastic slug deformation
For the 5 mm punch, no plastic deformation can be observed because there is no sharp drop in the radial stresses with higher die angles.
In contrast, the radial stress and thus the contact force when using the 1 mm punch and the short sectioned die (3) show a sharp decrease between the die angles of \(2.5^{\circ }\) and \(3^{\circ }\). There the radial stress between the slug and die decreases by 89% from 310 to 33 MPa (see Figs. 5, 8). This drop is caused by stresses that exceed the material’s compressive strength, causing plastic deformation and material compression. In addition, the radial stress remains low even at higher die angles due to the induced reduction in slug diameter. In the experiments, this behavior was also observed. At lower angles, no slugs occurred, while at large angles, slug pulling occurred reproducibly at every stroke. This shows that the die geometry and angle must be adapted not only to the sheet material, but also to the punch diameter.
4.2 Correlation between slug bending and stresses
Slug bending is determined by the slug compression. But for the small slugs even for higher compression no bending occurs due to the high stiffness. Therefore, no correlation is determinable for the 1 mm punch.
Sheets cut with the 5 mm punch and the conical (2) or short sectioned (3) die show increasing bending with higher angles. However, the radial and Von-Mises stresses reach their maximums for medium angles between 1\(^{\circ }\) and 3\(^{\circ }\) and decrease afterward. This shows that there is an optimum slug bending at about 80 \(\mu \)m, corresponding to a compression of about 0.04 mm. Smaller values due to a low slug oversize entail low radial stress. Increasing the bending first increases radial stress but progressively changes the stress condition inside the slug from compression stress to bending stress, which finally leads to snapping. Furthermore, the slug stiffness in the radial direction declines. With decreasing compression stresses, slug stiffness, and a snapping slug, the frictional forces are too low to prevent slug pulling. In summary, the slug bending is an important factor for slug pulling prevention, especially for larger punch diameters.
4.3 Part quality
The low sensitivity of the amount of clean cut to the die geometry, when blanking with the 1 mm punch can be explained by the high initial clean cut using the straight die, caused by the high stiffness of the slug, the low bending, and thus enhanced compression stress in the shear zone. Only very high die angles can raise the clean cut percentage, but just in a small range.
The slug of the 5 mm punch shows the same amount of clean cut for all dies and angles, except the conical one. This is caused by the die channels of the sectioned dies, which are straight in the area of material separation. The following conical part does not affect the clean cut. The conical die influences clean cut because the slug provides lower stiffness and higher bending compared to the smaller die. Thus, compression stress in the shear zone is improved with higher angles and entails higher clean cut amounts.
5 Conclusion
To prevent slug pulling, the radial stress, as well as the contact area between slug and die has to be high enough to induce sufficient friction force. Earlier studies show that these start in the mid-three-digit Newton range. Additionally, the prevention measures should not influence the part quality or rather the amount of clean cut. In this paper, the dependency of the radial stress and the clean cut formation on the geometry of the die channel and the punch diameter and thus slug bending and slug oversize were investigated when blanking 1.0338. Slug bending plays a subordinate role when working with small punches (1 mm), but influences the radial stress significantly for the 5 mm punch diameter. The amount of clean cut is influenced by the stresses in the shear zone and thus the part of the die channel where the plastic deformation and the material separation happens. Consequently, the prevention measures influence the cutting process in different ways and must be adapted to the process parameters to obtain a high part quality without slug pulling.
References
Oehler G, Kaiser F (2001) Schnitt, Stanz- und Ziehwerkzeuge. Springer, Berlin (ISBN 9783540673712)
Lee TH (1988) Precautions against slug lifting in progression press working. Sheet Metal Industries, pp 581–582
Strasser F (1963) Stanzereitechnik: Wie vermeidet man das Hochkommen von Butzen und Ausschnitten? Werkstatt Betrieb 96(5):319–320
Dannenmann E, Sugondo S (1981) On the adhesion of blanks to the punch in blanking and piercing. CIRP Ann Manuf Technol 30(1):167–170
Tittel V, Bernadic L (2012) A review of methods and precautions against slug pulling. Int J Pure Appl Sci Technol 12(1):7–15
Dayton Progress Corporation (2003) High speed stamping. Available at http://www.daytonlamina.com/sites/default/files/dayton_tech-highspeed.pdf
Hedrick AJ (2006) Die basics 101: part XI. Available at https://www.thefabricator.com/article/stamping/die-basics-101-part-xi
Kindsmueller A, Schrepfer A, Stahl J, Paetzold I, Nuernberger A, Golle R, Volk W (2021) Influence of cutting parameters on mechanisms causing slug pulling. Product Eng 15(6):833–842. https://doi.org/10.1007/s11740-021-01061-3
Volk W, Kindsmueller A, Paetzold I, Stahl J (2018) Ursache und Vorhersage von hochkommenden Stanzbutzen, EFB-Forschungsbericht. ISBN: 978-3-86776-547-3
Stahl J, Paetzold I, van den Bosch L, Kindsmueller A, Golle R, Volk W (2021) The frictional force between slug and die in shear cutting after material separation. Key Eng Mater 883:285–293
Krinninger M (2019) Approaches for reducing the process-related sliver formation when cutting aluminum sheets with an open cutting line. Dissertation, Technical University of Munich
Stahl J, Troeber P, Feistle M, Golle R, Volk W (2017) An inverse approach for the geometry prediction of sheet metal parts with embossings made of high- and ultra-high strength steels. International Deep Drawing Research Group IDDRG2017, Munich
Acknowledgements
The authors would like to thank the “Arbeitsgemeinschaft industrieller Forschungsvereinigungen“Otto von Guericke” e.V.” (AiF) and the“Europaeische Forschungsgesellschaft für Blechverarbeitung e.V” (EFB) for the financial support under the grant number 21003N.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Welm, M., Kindsmüller, A., Tröber, P. et al. Stresses between die and slug in blanking and their significance for slug pulling. Prod. Eng. Res. Devel. 17, 875–882 (2023). https://doi.org/10.1007/s11740-023-01202-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11740-023-01202-w