1 Introduction

Industrial, commercial, and service facilities store and move items in warehouses. There should be an integration of warehouse design decisions and an evaluation of their impact on operation [1, 2] because efficiency results from the analysis, design, and optimization of various activities, such as [3] warehouse layout, order batching, storage assignment, and picker routing.

Large businesses may afford designed-for-purpose warehouses [4,5,6,7,8], use picking strategies suitable for large throughput [9,10,11], including combined strategies [12], and invest in automation, such as the use of autonomous mobile-rack vehicles [13], robotics [14,15,16], and automated guided vehicles to support human order pickers [17]. However, smaller businesses may need to adapt existing, irregularly-shaped, building space [18]. With few items in inventory, small businesses tend to use single order picking: each picker collects the items of one order at a time. For businesses, large or small, some conditions affect performance, such as:

  • limits on design because of available space;

  • existence of middle aisles [19] and wide aisles [20];

  • product deterioration while in storage [21];

  • accounting for product returns [22];

  • safety constraints, such as a minimum distance between the storage locations of two items;

  • convenience constraints, as when two products should be within a certain distance because it is likely that they are ordered together;

  • precedence constraints [3, 23, 24], which impose that certain products should be among the first to be picked, for being heavy, and that others should be among the last to be picked, for being light or fragile;

  • traffic constraints, with one-way aisles in parts of the warehouse;

  • order due time constraints [25, 26];

  • ergonomic considerations [27] and the risk of infections [28].

Rigorous, optimal solutions are generally beyond the capabilities of current computers and many publications use heuristic approaches (e.g., [29]) and/or empirical optimization methods inspired by physical analogies, such as simulated annealing [30], or biological analogies, such as the genetic algorithm [31,32,33], ant colony optimization [34,35,36], and particle swarm optimization [11, 37], including the development of hybrid methods [38, 39] that use artificial neural networks [40, 41] to provide quick answers. There is no guarantee that such algorithms will locate the global minimum of the objective function but computer implementations of several of them are freely available or may be readily coded.

Progress in this area has been summarized often with the focus of studies on warehouses being design and operation [1]. Storage allocation and order picking are the two topics addressed most frequently [1] because of their impact on performance. Studies addressing all the aspects of warehouse design and operation simultaneously are scarce [42], which is attributed to being a challenge too great for individual researchers [2]. A review of papers published between 1938 and 2017 [43] classifies policies to establish picking orders and to solve storage assignment problems. Out of the 32 papers (or series of papers) reviewed on order picking, 14 use heuristic algorithms and 8 use empirical optimization methods based on physical analogies. Interestingly, there is evidence that order pickers often deviate from the optimal routes assigned to them [44, 45].

Despite the impressive body of research on warehouse design and operation, there has been relatively little attention to the case of small, irregularly-shaped warehouses that operate under various simultaneous constraints. This is the focus of this work. We study storage assignment and picker routing to find the minimum amount of manpower to fulfill a typical set of orders. The formulation considers the possibility of irregularly-shaped warehouses with safety, proximity, precedence, convenience, and traffic constraints, as defined in preceding paragraphs. Our formulation includes the possibility of storing items in multiple locations [46]. For picker routing, we consider the pick-to-parts strategy [47, 48], common in small businesses.

We have used the simulated annealing method [30], in a modified form with neighbor lists and a novel class-based approach, for the optimization of storage allocation problem in an outer iterative loop. To solve the pick-to-parts problem of the inner optimization loop, we have used the Python interface of the Google OR-Tools [49] and the NetworkX [50] package for graph operations. Because of algorithms used, our work can be categorized as based on empirical optimization methods.

2 Methods

Figure 1 displays the procedure’s structure. The first step is to input the data that define a problem and an initial configuration that assigns a feasible storage position for each type of item. The subsequent step is to find the time to fulfill all the orders. After that, the procedure checks if the current storage positions lead to the shortest time so far; if they do, the time and the storage positions are kept. After evaluating the time for the last trial set of storage positions, the procedure reports its outcome, which is the set of storage positions that yield the shortest time needed to fulfill all the orders. If the last trial set of storage positions has not been reached, the procedure decides if the trial configuration becomes the current configuration based on the acceptance criterion of simulated annealing. If the trial configuration is rejected, the current configuration is retained. The subsequent step is to generate a trial configuration by modifying the current configuration by drawing new random storage positions. The following subsections provide details.

Fig. 1
figure 1

Procedure’s flowchart

Full size image

2.1 Data

The data needed to solve a problem are:

  • the (x, y, z) coordinates of each storage location;

  • the (x, y) coordinates of the points where aisles intersect;

  • the coordinates of the source \((x_s,y_s)\) and destination \((x_d,y_d)\) nodes of each one-way aisle within the warehouse. Two-way aisles are specified as a one-way aisle from the source to the destination and a one-way aisle from the destination to the source;

  • the initial storage location of each item type, with storage of the same item type in more than one location allowed;

  • the product orders. Each order consists of the number of items requested of each type;

  • proximity constraints, if existent. Each proximity constraint imposes that the Euclidean distance between two stored item types should be greater than (>), greater or equal to (\(\ge\)), less or equal to (\(\le\)) or less than (<) a specified threshold;

  • precedence constraints, if existent. Here, they are based on item masses and favor picking the heaviest items first.

The aisles are treated as the edges of a directed graph. Each edge is assumed to be a straight line of specified length either in the x-direction or y-direction. Each edge’s weight is equal to the Euclidean distance between its source and destination nodes. Because of the use of directed graphs, the edges represent one-way aisles. Two-way aisles are defined as two one-way aisles in opposite directions.

2.2 Time to fulfill orders

The goal is to determine the storage positions, picking sequence, and picking path that minimize the objective function:

$$\begin{aligned} {t_T} = \sum \limits _{i = 1}^{{n_o}} {{t_i}} \end{aligned}$$
(1)

where \({t_T}\) is the time to fulfill all the \(n_o\) orders, each of them with a fulfillment time equal to \({t_i}\). The value of \({t_i}\) is:

$$\begin{aligned} {t_i} = {t_{M,i}} + \sum \limits _{k = 1}^{{n_i}} {{t_{ki}}} \end{aligned}$$
(2)

where \({n_i}\) is the number of types of items in order i. The symbol \({t_{M,i}}\) denotes the time to move from the initial position to each of the subsequent item positions and back to the initial position, which is:

$$\begin{aligned} {t_{M,i}} = \frac{{{d_{i}}}}{{{v}}} \end{aligned}$$
(3)

where \({d_{i}}\) represents the distance traveled in the warehouse to fulfill order i and v is the picker’s speed, which is considered independent of the order. The time to pick all the items of type k of order i, \(t_{ki}\), is:

$$\begin{aligned} {t_{ki}} = {n_{ki}}{t_{k,1}}({1 + p_z|z_k - {z_{ref}}|}) \end{aligned}$$
(4)

where \({n_{ki}}\) is the number of items of type k in order i and \(t_{k,1}\) is the time to pick one item of type k from a shelf. Depending on the information available, \(t_{k,1}\) can account for the time it takes to manipulate and scan very small or very large items, among other activities. The symbol \(p_z\) represents a penalty to pick an item at a position \({z_k}\) either below or above a reference level \(z_{ref}\), which represents the fastest picking level. Other contributions may be included, such as the time to process documents and load vehicles. This is not done, to keep the focus on motion and picking inside the warehouse.

The objective function \({t_T}\) indicates the manpower needed to fulfill all the orders with a picker-to-parts strategy carried out by a single picker. For its minimization, a strategy with three iterative loops is used. In the outer loop, different trial sets of storage positions are generated. The intermediate loop aims at optimizing picking sequence for a given set of storage positions. The inner loop, for given set of storage positions and picking sequence, aims at establishing the optimal picking path.

Finding the optimal pick-up sequence to fulfill a product order for a set of storage positions is an instance of the traveling salesperson problem (TSP). For solving the TSP, it is necessary to determine the shortest path between consecutive items of the picking sequence, which is the innermost loop of the iterative procedure.

2.3 Shortest path to pick consecutive items

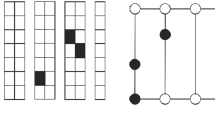
Consider Fig. 2: the red way is bidirectional, the green way is unidirectional and clockwise, and the blue way is unidirectional and counter-clockwise. In our implementation, the ways are constructed as a set of edges of a directed graph. Each edge connects neighboring graph nodes that are either end points or points of intersection in the warehouse. For example, the green way in Fig. 2 consists of three edges: from point (0,7) to point (5,7), from point (5,7) to point (5,4), and from point (5,4) to point (0,4). In bidirectional ways, each pair of nodes is connected by two edges with opposite directions. We calculated the path length as the summation of the weights of the edges traversed from the source to the destination nodes. This corresponds to the summation of the Euclidean distances between consecutive nodes. We also determined the list of traversed edges.

Fig. 2
figure 2

Irregularly-shaped storage facility: red aisles are bidirectional; green aisles are unidirectional and clockwise; blue aisles are unidirectional and counter-clockwise. Coordinates values are in meters. Black dots: storage locations on both sides of the aisles

Full size image

To complete the calculation of the shortest path to pick consecutive items, it is necessary to add the distance between each storage location and its nearest nodes, which could be an end point and/or a point of intersection in the warehouse. In Fig. 2, the storage locations are indicated by the black dots along the aisles. The coordinates of the storage locations along the central y-direction aisle, with values in meters, are (0,2.5), (0,3.5) ... (0,9.5). The coordinates of the blue-green x-direction aisle are (− 4.5,7), (− 3.5,7) ... (3.5,7), (4.5,7). The coordinates of the other storage locations follow a similar pattern.

Consider the path between items A and B in Fig. 2. The closest nodes to A are (0,7) and (− 5,7), but the latter is inaccessible in a straight line because the motion would violate the blue way’s direction. The closest nodes to B are (0,7) and (5,7), but (0,7) is inaccessible for an analogous reason. Thus, the shortest path from A to B is a horizontal straight line that passes through node (0,7). In some cases, a direct connection between the source and destination is possible as in the case of the path from point B to point C in Fig. 2.

The path from B to A is longer. Starting from point B, it passes through points (5,7), (5,4), (0,4), (0,7), (0,10), (− 5,10), (− 5,7), and then reaches point A. In some cases, when the source and destination storage locations have two feasible neighboring nodes, as when they are on bidirectional ways, it is necessary to calculate the length considering all four possible path alternatives to find the shortest one.

2.4 Configurations in simulated annealing

The simulated annealing optimization method has two main steps: (a) the random generation of trial configurations and (2) the acceptance or rejection of the trial configuration based on a probabilistic criterion, in analogy with the Monte Carlo method [51].

To generate trial configurations, each storage location occupied by an item type is considered at a time—this location will be referred to as the central location. Another storage location is drawn from the list of locations that are neighbors of the central location. A trial configuration is generated by swapping the item types stored in the central and neighboring storage locations. If the neighboring storage location is empty, the outcome of the swap is that the central location becomes empty and the neighboring location is filled with the item previously located at the central location.

A trial configuration is accepted in the simulated annealing method if its objective function, \({f_t}\), is smaller than or equal to that of the current configuration, \({f_c}\). If \({f_t}>{f_c}\), it is also accepted if:

$$\begin{aligned} r < {e^{ - \frac{{\left( {{f_t} - {f_c}} \right) }}{\theta }}} \end{aligned}$$
(5)

where r is a uniformly distributed random number between 0 and 1 and \({\theta }\) is a positive parameter that controls the acceptance ratio. If \({\theta }\) tends to infinity, the result of the right hand side of inequality (5) will tend to 1. As a consequence, the probability that inequality (5) is satisfied is high and, therefore, the probability of accepting the trial configuration is also high. On the other hand, if \({\theta }\) tends to zero, the probability of accepting the trial configuration becomes low. In the simulated annealing method, an initially high value of \({\theta }\) is decreased during the iterative process. The idea is that a broad search of the solution space occurs in the early iterations of the method, which converges to best point solution. As the method may visit a favorable configuration and replace it with a less favorable one, our implementation keeps the best configuration visited regardless of the calculation sequence.

The implementation of the simulated annealing method starts by assigning an initial value to the variable \({\theta }\), which is used in the first iteration (\({\theta _1}\)):

$$\begin{aligned} \theta _1 = \frac{{\overline{\Delta f} }}{{\ln 0.9}} \end{aligned}$$
(6)

where \({\overline{\Delta f} }\) is given by:

$$\begin{aligned} \overline{\Delta f} = \frac{{\sum \nolimits _{\ell = 1}^{{n_u}} {|{\Delta {f_\ell }} |} }}{{{n_u}}} \end{aligned}$$
(7)

In Eq. 7, \(n_u\) is the number of storage positions in use and \({\Delta {f_\ell }}\) represents the difference:

$$\begin{aligned} \Delta {f_\ell } = {f_\ell } - {f_{\ell - 1}} \end{aligned}$$
(8)

where \({f_\ell }\) and \({f_{\ell - 1}}\) are the values of the objective functions in trial storage configurations \({\ell }\) and \({(\ell - 1)}\), with the value of \({f_0}\) calculated with the user-provided initial storage positions.

An iteration of the simulated annealing method is complete after \(n_c\) trial cycles. Each trial cycle comprises several trial moves. Each trial move consists of an attempt to swap the content of two storage locations, as described previously. The value of \(\theta\) used during the second iteration is:

$$\begin{aligned} \theta _2 = 0.98 \theta _1 \end{aligned}$$
(9)

and we define:

$$\begin{aligned} \Delta {\theta _2} = {\theta _1} - {\theta _2} \end{aligned}$$
(10)

The value of \(\theta\) used during each iteration \(m \ge 3\) is calculated as follows:

$$\begin{aligned} {\theta _m} = {\theta _{m - 1}} - \Delta {\theta _m} \end{aligned}$$
(11)

where:

$$\begin{aligned} \Delta {\theta _m} = \min \left( {\frac{{{C_{V,m - 1}}}}{{{C_{V,m - 2}}}}\Delta {\theta _{m - 1}},\frac{1}{5}{\theta _{m - 1}}} \right) \end{aligned}$$
(12)

Equation 12 decreases \(\theta\), limiting its change from one iteration to the next and preventing it from becoming negative. The symbol \(C_V\) in Eq. 12 is an analogue of the heat capacity at constant volume. At the end of each iteration m, carried out with a value \(\theta _m\), the value of \(C_{V,m}\) is calculated using:

$$\begin{aligned} {C_{V,m}} = \frac{{{{\left\langle {{f^2}} \right\rangle }_m} - \left\langle f \right\rangle _m^2}}{{\theta _m^2}} \end{aligned}$$
(13)

where \({\left\langle f \right\rangle _m}\) and \({{{\left\langle {{f^2}} \right\rangle }_m}}\) are the average value of the objective function and of the squared objective function during iteration m, which occurs at \(\theta _m\). This procedure follows an adaptive cooling scheme for \(\theta\) based on heat capacities [52].

Reducing \(\theta\) decreases the probability of accepting trial configurations, as indicated by inequality (5). The criterion adopted for numerical convergence was that acceptance ratio in a given set of trial cycles was below a specified threshold (0.01, unless stated otherwise).

2.5 Constraints

Proximity constraints impose that the Euclidean distance between the storage positions of two item types should be larger or smaller than a user-specified value. If a trial set of positions violates any proximity constraint, it is rejected and a new trial set is generated.

Precedence constraints guide the picking order based on mass, fragility, or other criteria. Here, they are based on item masses: the cart loading should “ideally” be from the heaviest to the lightest item. For loading sequences different from this one, the total time to fulfill a certain order i, t\(_i\), includes an order reorganization time, \(t_{R,i}\). To calculate \(t_{R,i}\), we define a unit of time for load reorganization, \(t_r\). During the picking of order i, each time there is a displacement from a lighter item to a heavier item, \(t_{R,i}\) is increased by \(t_r\). For example, consider four item types, a, b, c, and d, with a being the heaviest item type and d being the lightest. Suppose that the following order should be fulfilled in a left-to-right sequence: \(\left[ c,a,d,b\right]\). The displacements from c to a and from d to b are from a lighter to a heavier item. With each of them receiving a penalty \(t_r\), the order reorganization time is \(t_{R,i} = 2 t_r\).

2.6 Neighbor lists

A list of neighboring storage locations is computed for each storage location. To accomplish that, the Euclidean distance between all pairs of storage sites is calculated and the fraction \(\alpha\) with the smallest distances is retained as the list of neighbors of each storage site. The fraction \(\alpha\) is a user specification and its selection represents a compromise. If \(\alpha\) is close to zero, each storage location will have few neighbors and progress towards the minimum total time may be slow because subsequent configurations will be similar. If \(\alpha\) is close to one, subsequent storage configurations may be so different that the probability of accepting them is small or constraint violations may become frequent.

2.7 Implementation details

The computer program that implements the procedure described herein was written in Python, version 3.9. It uses Python’s multiprocessing package with the evaluation of the time to fulfill each order assigned to a different processor, thus reducing the clock time to achieve the problem’s solution.

The code of the simulated annealing method was written in-house. The Google OR-Tools [49] is used in the intermediate iterative loop to solve the TSP and generate and evaluate picking sequences. Recent comparative work [53, 54] on solving the TSP ranks Google OR-Tools among the best tools available for this purpose. Graph operations are handled by the NetworkX 2.5 package [50]. NetworkX has been recently used in the analysis of the global air transport network [55], of the relationships between fictional characters [56], and in quantum mechanical calculations [57]. From NetworkX, we use functions dijkstra_path_length and dijkstra_path. The function dijkstra_path_length calculates the path length as the summation of the weights of the edges traversed from the source to the destination nodes. This corresponds to the summation of the Euclidean distances between consecutive nodes. The function dijkstra_path returns the list of traversed edges.

3 Results

This section presents the procedure’s results. Table 1 shows the values of \(v_M\), \(z_{ref}\), \(t_{k,1}\), and \(p_z\) used in all the cases.

Table 1 Specifications common to all case studies. The \(v_M\) value is from the literature [23]. The other values are assumptions adopted here
Full size table

The first example is conceptual and refers to a facility for storing few item types. It illustrates the effect of constraints on the results.

3.1 Conceptual example

Figure 2 is the basis for the formulation of this example: the red aisles are bidirectional, the green aisle is clockwise, and the blue aisle is counter-clockwise. The aisle shapes are irregular in that they do not form a rectangular grid. The storage locations are indicated by the 40 black dots along the aisles. The coordinates of the storage locations along the central y-direction aisle, with values in meters, are (0,2.5), (0,3.5) ... (0,9.5). The coordinates of the blue-green x-direction aisle are (− 4.5,7), (− 3.5,7) ... (3.5,7), (4.5,7). The coordinates of the other storage locations follow a similar pattern. All picking tours start and end at point (0,0).

3.1.1 Case study A—warehouse with some unidirectional aisles

In this case study, the items are at fixed positions and the simulated annealing method is not used to optimize their storage locations. At each storage location, there are shelves on both sides of the aisles and each shelf is 1 m above the floor level. There are 80 storage shelves available to store 71 different types of items, numbered from − 35 to 35, with 0 included. Thus, 9 shelves will remain empty. Each order contains five items, with repetition of item types allowed; for example, an order may consist of items of 4 different types, with two items of a given type. It is assumed that the probability that a given item is present in an order follows a normal distribution of average equal to 0 and standard deviation equal to 13. Based on this assumption, 100 orders were generated randomly, rounding each random real number to its nearest integer. The few random numbers generated outside the range [− 35,35] were discarded and replaced by a low probability item in such a way that each type of item is ordered at least once. Figure 3 displays the frequency of item types in the orders of the conceptual example. The jagged aspect of the curve results from the small number of items ordered, but it follows the trend of a normal distribution.

Fig. 3
figure 3

Frequency of item types in the orders of the conceptual example

Full size image

Figure 4 uses a color code to display the initial storage configuration. The positions of the 11 item types with numbers in the range [− 5,5], which would be the most commonly ordered according to a normal distribution, are represented by the red dots. The 20 item types with numbers in the ranges [− 6,15] and [6,15] are represented by the orange dots, those in the ranges [− 16,25] and [16,25] are the violet dots, and the pink dots represent item types in the ranges [− 26,35] and [26,35], which are the least frequently ordered. The black dots represent empty shelves and the start and end of all picking tours is the blue dot. The items have been placed in the warehouse according to their Manhattan distances to the blue dot, which were calculated accounting for the aisle directions.

Fig. 4
figure 4

Simplified view of the storage configuration in case study A. Red dots: item types in range [− 5,5]. Orange dots: id., [− 6,15] and [6,15]. Violet dots: id., [− 16,25] and [16,25]. Pink dots: id., [− 26,35] and [26,35]. Black dots: empty shelves. Blue dot: start and end of picking tours

Full size image

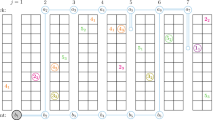
It takes \({t_T}= 3277\) s to fulfill the 100 orders. As an example, Fig. 5 shows the picking path to fulfill order 63 of the set. In this figure, the positions of the items that should be picked are shown by the orange circles, the path from one position to the next one is indicated by the black arrow, while the red, blue, and green arrows specify the direction(s) allowed in each aisle. The picking process starts by collecting one item of type 1 (Fig. 5a) and then, the picker should proceed to items − 4 (Fig. 5b) and − 15 (Fig. 5c) by traversing the bidirectional aisles depicted in red. The sequential picking of items − 35 and − 25 (Fig. 5d, e) requires following the blue and green unidirectional aisles. The final stretch takes the picker back to the initial position, first taking the green unidirectional aisle and then the central red bidirectional aisle (Fig. 5f).

Fig. 5
figure 5

Picking path to fulfill order 63 with the initial storage positions of case study A in the conceptual example. The red aisles are bidirectional; the green aisles are unidirectional and clockwise; the blue aisles are unidirectional and counter-clockwise. The shelves are 1 m above the floor level

Full size image

3.1.2 Case study B—warehouse with bidirectional aisles

With the items stored in the same positions and all aisles bidirectional, the time to fulfill all the orders is \({t_T}= 2937\) s. The corresponding picking path for order 63 is shown in Fig. 6, in which all aisles are shown as red arrows to indicate they are bidirectional. Compared to the result of Fig. 5, the difference is the motion between the items of types − 35 and − 25, shown in Figs. 5e and 6e, because there is no need to traverse the blue aisle. Thus, the path is simpler and shorter because of the fewer constraints on motion. As a result of analogous relaxations on motion constraints for other orders, the time to fulfill the orders is smaller than in the case with unidirectional aisles.

Fig. 6
figure 6

Picking path to fulfill order 63 with the initial storage positions of case study A in the conceptual example. All aisles are bidirectional. The shelves are 1 m above the floor level

Full size image

3.1.3 Case study C—warehouse with bidirectional aisles and safety constraint

With all aisles bidirectional, we impose that the Euclidean distance between the storage positions of items of types − 1 and 1, which are among those most frequently ordered, should be larger than 5.5 m. The initial storage positions are the same as in case studies A and B, with exception of the position of items of type − 1, which are placed in a shelf previously empty at position (− 4.5,7). In this way, the initial configuration is feasible because it satisfies the minimum distance constraint between the items of types − 1 and 1. With such a configuration, the time to fulfill all the orders is 3070 s. Unlike the previous examples, the simulated annealing method of the outer iterative loop is activated to relocate the items in storage. It runs with \(\alpha =0.10\), that is, the list of neighbors of each storage location contains the 10% nearest shelves. A configuration with \({t_T}= 2996\) s is found. Thus, with simulated annealing, it was possible to determine storage locations that led to a value of \({t_T}\) smaller than that of the initial configuration. Comparing the initial and final configurations, the contents of 41 shelves changed as a result of optimization. Also, \({t_T}= 2937\) s in case study B is smaller than \({t_T}= 2996\) s in case study C. In both cases, all aisles are bidirectional but the minimum distance constraint of case study C increases the \({t_T}\) value.

Figure 7 displays a summary of the obtained configuration using the same color code of Fig. 4, based on the frequency of each product in the set of orders. Despite the change in the content of 41 shelves, the color distribution in these two figures is similar. This indicates that the swaps in storage position occurred with little disruption of the general trend of the initial configuration.

Fig. 7
figure 7

Simplified view of the storage configuration in case study C. Red dots: item types in range [− 5,5]. Orange dots: id., [− 6,15] and [6,15]. Violet dots: id., [− 16,25] and [16,25]. Pink dots: id., [− 26,35] and [26,35]. Black dots: empty shelves. Blue dot: start and end of picking tours

Full size image

3.1.4 Case study D—warehouse with bidirectional aisles and precedence constraints

This case considers precedence constraints. In it, the item storage positions and the directions of the aisles replicate those of case study B, that is, all aisles are bidirectional and the items stored in the same positions as in case study A. The types most commonly ordered are specified as the lightest and the least commonly ordered are specified as the heaviest. The following equation was used to specify the mass of each item type k (\(-35 \le k \le 35\)), \(m_k\), in kg:

$$\begin{aligned} {m_k} = 1.25 + 0.25|k |\end{aligned}$$
(14)

In this way, \({m_0} = 1.25\) kg and, for example, \({m_{35}} = {m_{-35}} = 10.00\) kg.

To test an extreme situation, we specified \(t_r = 100\) s, which is larger than the time for the direct displacement between any two shelves of this case study. In this way, a large time penalty is imposed on any inversion of the heaviest-to-lightest precedence. Again using order 63 for discussion, its picking follows the type sequence − 35, − 25, − 15, − 4 , and 1, that is, the heaviest-to-lightest precedence.

Figure 8 displays the outcome of order 63 when the specification is \(t_r = 1\) s. With this value, the best picking sequence is neither that of unconstrained case (case study B, Fig. 6) nor the heaviest-to-lightest sequence obtained when \(t_r = 100\) s, because the item of type-15 is the first to be picked. The time to fulfill all the orders is \({t_T}= 3018\) s, which is larger than that of case study B (\({t_T}= 2937\) s).

Fig. 8
figure 8

Picking path to fulfill order 63 with the initial storage positions of case study A in the conceptual example. All aisles are bidirectional. Precedence constraint was applied with \(t_r=1\) s. The shelves are 1 m above the floor level

Full size image

3.1.5 Case study E—warehouse with bidirectional aisles and second storage location for commonly ordered items

The aisle directions are bidirectional as in case study B. The item storage positions are as in case studies A and B, except for the use of a second storage location for items of type-6, which appears in 12 of the 100 orders. Referring to Fig. 2, its original storage location is (− 2.5,2) and the second location is (− 1.5,7), which was empty in the previous case studies. With this storage configuration, it takes \({t_T}= 2911\) s to fulfill all the orders. This is less than \({t_T}= 2937\) s needed in case study B because the second storage location for items of type-6 creates alternative picking paths that may reduce \({t_T}\). In fact, the item of type-6 is picked from the second location in 10 of the 12 orders.

3.1.6 Conceptual example: discussion

The first remark is that the procedure proposed here can handle perpendicular aisles of any size, either unidirectional or bidirectional. It can also handle safety constraints based on the minimum distance between the locations of two item types. Further, the procedure can handle precedence constraints that favor heaviest-to-lightest picking sequences and the existence of multiple storage locations for a given item type.

Table 2 summarizes the results. As expected, the case with no constraints and all aisles bidirectional—case study B—has a small value of \({t_T}\), compared to case studies A, C, and D. With the addition of constraints, some of the paths selected in case study B become infeasible and this increases \({t_T}\). On the other hand, case study E introduces a relaxation on the problem because the existence of additional storage locations for a given item creates alternative paths that may reduce the time to fulfill all the orders.

Table 2 Effect of constraints on picking times of the conceptual example
Full size table

3.2 Example of a small industry of consumer-oriented products

This example is motivated by the drive to improve the warehouse efficiency of a small cleaning products industry in Paraguay, which had a large increase in sales during the COVID-19 pandemic in 2020–2021. For historical reasons, the shape of the warehouse is irregular: its aisles do not form a rectangular grid but are perpendicular and bidirectional. Figure 9 displays its representation, with the coordinates in meters. The black dots show the storage locations, either on one side or both sides of the aisles.

Fig. 9
figure 9

Industrial warehouse: all aisles are bidirectional. The coordinates values are in meters. The black dots show the storage locations, either on one side or both sides of the aisles

Full size image

The industry stores 191 item types, which are identified here by numbers from − 95 to 95, with 0 included. The average number of items in the orders is 30.2 with an standard deviation of 12.6. A set of 100 orders was generated randomly according to this criterion, with more than one item of each type allowed in any given order. In this set, the largest order contains 55 items and smallest contains a single item. Further, it is assumed that the probability that a given item type is present in an order follows a normal distribution with average and standard deviation equal to 0 and 32, respectively. A set of items was randomly generated according to this criterion to establish the item types and amounts present in each order. Small manipulations of the random values were done to ensure that each item type appears in at least one order. Figure 10 displays the the total frequency of the item types in all orders. A total of 244 storage positions was considered. They are at 122 combinations of x and y coordinates and at 2 different levels, which are assumed to be 1 m and 2 m above the floor level. An additional location is defined as the start/end point of all picking tours. With 191 item types and 244 storage positions, 53 of which will remain empty, there are \({{{244!} /{53!}}} \approx 3.291 \times {10^{408}}\) possible configurations.

Fig. 10
figure 10

Frequency of item types in the orders of the industrial example

Full size image

To establish the initial storage, the positions of the shelves were sorted according to their Euclidean distance (considering their x, y, and z coordinates) to the start/end point of the picking tours. The items were sorted according to their frequency in the orders. To evaluate the heuristics used to generate configurations, we start with a configuration that is inadequate, with these two sorted lists paired in such a way that the items most frequently ordered have the largest Euclidean distances to the start/end point of the picking tours. We refer to this initial arrangement as reverse match. The time to fulfill all 100 orders was \(t_T =18844.5\) s. With the items most frequently ordered at the smallest Euclidean distances to the start/end point of the picking tours, which we refer to as direct match, we obtained \(t_T = 16098.5\) s, which is 16.6% shorter than that of the reverse match configuration. This direct match is aligned with the concepts of the heuristic, conventional XYZ analysis, widely adopted in industry to classify inventory items according to demand variability.

Starting from the reverse match configuration, with each iteration comprising \(n_c=10\) trial cycles and neighbor lists with the 50% nearest storage locations to any central storage location, simulated annealing provided a solution with \(t_T =18123.5\) s. Compared to the \(t_T =18844.5\) s of the original reverse match configuration, \(t_T =18123.5\) s represents a reduction of about 3.8% but is larger than \(t_T = 16098.5\) s of the direct match configuration. This suggests that it is preferable to launch simulated annealing with a favorable configuration, such as the direct match configuration as defined above. By doing that, with \(n_c=10\) trial cycles during each iteration and neighbor lists with the 50% nearest storage locations to any central storage location, a value of \(t_T =15857.0\) s was obtained. This value is 1.5% less time than that of the initial direct match configuration configuration. This calculation was repeated for different percentages of the storage locations in the neighbor lists. Table 3 summarizes the results. With the smallest percentage tested, 1%, the result is similar to that of the original direct match configuration, suggesting that there is an inadequate sampling of the possible configurations. With the largest percentages tested, 99% and 99.5%, the results are also similar to those of the original direct match configuration. In this case, configurations that are vastly different from the original one are generated. Because the direct match configuration is a good starting point, few of the sampled configurations improve on it. Among the tested cases, the best results were obtained with 10% and 50% of the storage locations in the neighbor lists.

Table 3 Allocation of storage positions in a small industry with simulated annealing: effect of initial condition and size of the neighbor list
Full size table

Next, assuming that the initial arrangement is a good estimate, such as the direct match configuration, we consider the possibility of splitting the 244 storage positions in 10 classes. The first class contains the 25 closest storage positions to the start/end point of the picking tours, based on Euclidean distances. Euclidean distances are a convenient way of simplifying the allocation of storage positions to classes but it should be emphasized that all distances used during the iterative procedures are Manhattan distances. The second class contains the next 25 storage positions. The same criterion defines the subsequent classes, until the tenth class, which contains the 19 storage positions most distant from the start/end point of the picking tours. Then, simulated annealing was applied by class, from the first to the last class, with \(n_c=10\) trial cycles, neighbor lists with the 10% nearest storage locations to any central storage location, and stopping each application of simulated annealing when the acceptance of new configurations dropped below 10%. For example, for the first class, the algorithm attempts to swap the content of each of the 25 storage locations with the content of a randomly selected neighbor storage locations, some of which may belong to another class. Thus, the contents of storage locations that belong to other classes may change as a consequence of swaps that originate from the first class. As the neighbor lists contain 10% of the storage locations, that is, 24 locations, the typical exchanges occur between storage locations that either belong to the same class or to adjacent classes. Once the application of simulated annealing to the first class ends, the application to the second class begins from the best configuration obtained thus far and with a value of \(\theta = \theta _1\), calculated with Eq. 6 for the first class. This process is repeated until all classes have been considered. With this approach, we obtained \(t_T = 15558.0\) s, which is about 3.4% shorter than the original direct match configuration (which follows the concept of an XYZ arrangement), outperforming all our single-run applications of simulated annealing shown in Table 3.

We also evaluated the effect of a second storage position for items of type 2, which is item type most commonly ordered. To do that, we modified the original direct match configuration, placing the second storage location for items of type 2 next to the start/end point of the picking tours. Because of that, all the other item types were displaced by one storage location farther from the start/end point of the picking tours. For this configuration, prior to the application of simulated annealing, the value of \(t_T\) is equal to 15946.0 s. Using the class-based simulated annealing approach, it is obtained that \(t_T = 15309.0\) s. This time is 249.0 s (1.6%) shorter than the the value of \(t_T = 15558.0\) s found with simulated annealing for the case of a single storage location for each item type.

Figure 11 displays the best \(t_T\) value after applying simulated annealing to each storage location class, in the cases without and with a second storage location for items of type 2. The best value of \(t_T\) decreases until the end of the third class and remains unchanged afterward. This occurs because the first classes contain the locations closest to the start/end point of the picking tours: they are filled with the item types that affect \(t_T\) the most. Adding an extra storage location for the most commonly ordered item type contributes to reducing the time to fulfill the orders.

Fig. 11
figure 11

Progress of simulated annealing applied by class to the industrial example

Full size image

4 Conclusions

The procedure developed here can solve the problem of assigning products to storage locations in a warehouse so that it takes minimum time to fulfill all the orders of a set. The procedure handles constraints, including the simultaneous existence of one-way and two-way paths within the warehouse and the possible use of more than one location to store the same type of item.

An optimization approach with three nested loops was adopted. In the outer loop, simulated annealing generates different sets of storage positions. In the intermediate loop, the traveling salesperson algorithm of the Google OR-Tools package is used to find the best picking sequence for each order in a set of orders. In the inner loop, the best path between the storage locations of any two items within the warehouse is found using functions of the NetworkX package. This three-loop optimization approach was successful in decreasing the amount of time needed to fulfill all the orders of a set. The use of freely available packages, such as Google OR and NetworkX, enabled the fast implementation of the procedure.

The storage configurations that lead to the shortest times to fulfill a set of orders were obtained by initializing the calculations with the item types sorted according to their frequencies in the set of orders and placing them in storage with the most commonly ordered items next to the start/end point of the picking tours. This typically good configuration is refined using a novel class-based approach to simulated annealing optimization, which is applied for the first time in this type of problem. The storage locations are split in classes to which simulated annealing is sequentially applied. For a small cleaning products industry that operates a warehouse with an inventory of 191 products, the procedure provides an improvement of pick-up times of about 1.5% compared to the situation prior to any storage optimization. When an extra storage location was used for the most commonly ordered item type, the pick-up time was about 4.9% shorter than prior to optimization.