1 Introduction

Over the recent years, several processes have been developed that are summarized under the term “Additive manufacturing” (AM), today. Considering its benefits, the application of AM technologies to the manufacture of polymer and metal products is already established in many industries. An area in which AM has a great application potential is optics. Glass as a more frequently used material in this area has, in contrast to metals and polymers, several advantages such as thermal stability, chemical resistance, and high optical transmission for the near-ultraviolet (NUV) to the near-infrared (NIR) range. Several studies prove that additive manufacturing of glass is feasible by different approaches such as extrusion printing [1, 2], selective laser melting/sintering [3, 4], stereolithography, subsequent oven sintering [5], and wire-feed additive manufacturing [4, 6] as direct energy deposition (DED). Possible applications for the additive manufacturing of glass in the field of optics are the printing of optical networks [7], as well as the design of optics with new optical functionalities that cannot be manufactured in a conventional way. Further applications would be the printing of glass joints for structural constructions where not recyclable adhesive joints can be substituted [8]. For medical and chemical applications, the technology could be interesting for the printing of microfluidic channels for lab-on-chip designs.

Laser glass deposition (LGD) is a fiber-based process and can be categorized as DED -process. It consists of a CO2-laser with an adjustable output power that is used as an energy source along with a four-axis system to melt the glass fiber and move the depositing stage and substrate [9]. Variable process parameters are for example laser power (PL), feed rate of glass fiber (f), axis velocity (vx, vy, and ω). In this method, the defocused laser beam is perpendicular to the substrate with different laser spot diameters. Therefore, the diameter of the laser spot (LSD) can be adjusted and also considered as a process control variable. Figure 1 illustrates the working principle of the process.

Fig. 1
figure 1

Experiment setup of LGD process

Full size image

As shown, the glass fiber is conveyed at the feed rate f to the melting zone under the CO2 laser with the power of PL. In this step, the glass is melted and deposited on the substrate. By the movement of the axes, the substrate will move and carry the deposited glass out of the melting zone, while the glass cools and solidifies. Luo et al. [5] studied different types of glass for a glass-based DED type of additive manufacturing.

For the production of optical elements, quartz glass is the most widely used material due to its high transparency and temperature resistance [9]. Witzendorff et al. [9] investigated the effect of various process parameters such as the laser power, axis velocity, fiber feed rate, and feeding direction to find a process window that allows continuous printing of multiple glass fiber layers. Also, the study highlighted the importance of temperature control for process planning.

Energy input and consequently resulting temperature is a decisive factor in the LGD process. On the one hand, the changing temperature can change the material properties of the substrate and the feed material, and at the same time, it influences the additively manufactured geometry. In addition, during manufacturing and depending on the temperature change in the substrate, difficulties such as high residual stresses or thermal shock can occur. Changes in the temperature on the substrate and in the melt zone can be made by changing process parameters such as laser power, axis velocity, fiber feed rate, and laser spot diameter. Different tool path strategies can also affect the temperature. Several studies have been done to model the thermal phenomena present in laser-based additive manufacturing processes [10,11,12,13].

The temperature in the LGD process has been numerically investigated using different approaches. Luo et al. [5] have simulated the resulting temperature for different laser powers to find out the vaporization region and accordingly material loss [14]. Pohl et al. [15] modeled a moving laser at the substrate to simulate the temperature under variation of laser power, the laser spot diameter, and axis velocity during fiber-based CO2 laser welding of fused silica. The dependence and change of the lateral temperature distribution under variation of the axis velocity were investigated in a further study using a 3D model [16]. Also, the temperature distribution in the glass fiber and on the substrate was investigated in a 2D model under variation of the process parameters [17].

2 Objective

As shown, the energy input and change in temperature act as crucial factors in the LGD process. Especially in process planning, it is important to know which temperature will be achieved under the applied parameters and tool path, which can directly influence the resulting geometry. Therefore, the study of temperature changes under different conditions in the melt zone and on the substrate is an essential step in process planning. For this purpose, numerical investigation can be beneficial. Using simulation models reduces experimental cost and effort, whereby due to the limitations of temperature measurement, simulations provide a deeper process understanding. In finite element simulations, the temperature can be calculated by varying different parameters after time for different positions where the cooling or heating of the substrate can be studied.

This article aims to investigate the influence of process parameters and different tool path strategies on the temperature in the additive manufacturing of glass by laser. Also, the effect of other process boundary conditions such as substrate size and the initial temperature of the substrate is taken into account. For this purpose, a finite element numerical model is created and simulated in ANSYS. The numerical thermal analyses are performed to study the heating and the resulting temperature on the quartz glass during the LGD process. Thereby, it is investigated how the process parameters can influence the resulting temperature. Also, the influence of different tool path strategies, such as zigzag or spiral, as well as different turning angles on the temperature will be analyzed.

3 Temperature model

In this study, a mechanical transient thermal model is used to simulate the resulting temperature due to laser heating as a heat source in LGD. The movement of the laser beam with Gaussian distribution on the substrate was modeled and simulated.

As shown in Fig. 2a, the conveyed glass fiber with a diameter of 0.4 mm covers a comparatively very small area of the laser spot (with a diameter of e.g., 5 mm). Also, the glass fiber and the substrate are both composed of fused silica. Thus, the irradiated glass fiber and the area of the substrate can be assumed as a plane surface under the perpendicular laser beam irradiation. In order to simplify the model and conduct the simulations in this work, the conveyed glass fiber can be omitted in the thermal modeling of the process (Fig. 2b). Also, the measured temperature in the experiments with feeding material and the experiments without feeding material shows a maximal difference of 230 °C considering feed rate values and also different relation between feed rate and axis velocity in the experiments. Therefore, to simplify the model and simulation calculations, fiber feeding is not included in the modeling.

Fig. 2
figure 2

Schematic representation of LGD process: a detailed model, b simplified simulation model

Full size image

The thermal equilibrium equation defines the following 3D heat conduction equation for the Substrate given by

$${\uprho }_{{\text{C}}} \frac{{\delta {\text{T}}}}{{\delta {\text{t}}}} = \frac{\delta }{{\delta {\text{x}}}}\left( {{\text{k}}\frac{{\delta {\text{T}}}}{{\partial {\text{x}}}}} \right) + \frac{\delta }{{{\delta y}}}\left( {{\text{k}}\frac{{\delta {\Gamma }}}{{\delta {\text{y}}}}} \right) + \frac{\delta }{{\delta {\text{z}}}}\left( {{\text{k}}\frac{{\delta {\Gamma }}}{{\delta {\text{z}}}}} \right) + Q$$
(1)

where ρ is the material density (g/cm3); c is the specific heat capacity (J/kg-K); T is the temperature (K); t is the interaction time (s); k is thermal conductivity (W/mK); and \(Q = \left( {x,y,z,t} \right)\) is the volumetric heat generation (W/mm2), that not considered for this simulation.

The heating of a point of the surface (x,y,z) with a Gaussian laser beam can be calculated by the following equation:

$${\text{q}} = {\text{Ce}}^{{\frac{{ - \left[ {\left( {{\text{x}} - {\text{x}}_{0} } \right)^{2} + \left( {{\text{y}} - {\text{y}}_{0} } \right)^{2} + \left( {{\text{z}} - {\text{z}}_{0} } \right)^{2} } \right]}}{{r^{2} }}}}$$
(2)

where q is the heat flux of the desired surface, r is the laser beam radius, C is the source power intensity, x0, y0, z0 is the instantaneous position of the center of the heat flux which is on the path at the distance.

The initial condition of uniform temperature distribution throughout the glass substrate before laser irradiation and its moving at time \(t = 0{ }\) can be applied as:

$${\text{T}}\left( {{\text{x}},{\text{y}},{\text{z}},0} \right) = {\text{T}}_{0} \left( {{\text{x}},{\text{y}},{\text{z}}} \right)$$
(3)

where T0 is the ambient temperature.

The temperature of the glass substrate surface Tsurf at \({\text{z}} = 0\), where the z-axis is perpendicular to the laser spot, can be calculated using the following equation:

$$- {\text{k}}\left( {\frac{{\partial {\text{T}}}}{{\partial {\text{z}}}}} \right)_{{{\text{z}} = 0}} = {\text{q}} - {\text{h}}\left( {{\text{T}}_{0} - {\text{T}}_{{{\text{surf}}}} } \right)$$
(4)

where h is the heat transfer coefficient at the glass surface which is taken as temperature-dependent.

The full heat transfer equation can be solved numerically, taking into account radiative heat loss, surface heat loss due to convection, and temperature-dependent material properties (Table 1).

Table 1 Technical properties of fused silica used in the simulation
Full size table

In the applied model, the evaporation and melting of material on the substrate are not considered. The 3D model incorporates air-based convection from five sides. The 3D substrate meshed with cells of 0.4 × 0.4 × 0.4 mm3. Figure 3 illustrates the developed 3D model in ANSYS (2019 R3). The simulations are carried out with an explicit solver in time steps of 0.01 s.

Fig. 3
figure 3

Simulation model in ANSYS

Full size image

In order to evaluate the simulation model, the maximal simulated temperature of the tool path on the substrate was evaluated and compared with the measured temperature from experiments. In the experimental process, the temperature of the melting zone was measured by a pyrometer (KTRD 1550-1, Maurer GmbH), which is set for CO2 laser processing of fused silica (emission coefficient = 0.9) and measures within a temperature range of 300–2500 °C at a measuring wavelength of 5 µm. The pyrometer integrates the temperature over a spot diameter of 1.5 mm. In the analysis of the simulated temperature of the heated area, it has shown that the max. temperature and the average temperature for the circle with a diameter of 1.5 mm have a difference of less than 20 °C. Therefore, for the evaluation of the simulation, due to the evaluation effort for averaged temperature, the maximum generated temperature for each moment of the simulation was used.

As shown in Fig. 4, the quartz glass substrate will be positioned on the base plate where the quartz glass fiber will be fed.

Fig. 4
figure 4

Experimental setup

Full size image

Figure 5 shows this temperature for a straight tool path with 36 mm length in comparison with experiment result with the same process design. At the end of the path and after the laser was off, the simulation was continued for a while to investigate the cooling behavior as well.

Fig. 5
figure 5

Maximal simulated temperature over the process time

Full size image

The simulation results show a similar temperature increase at the beginning and temperature changes during the laser moving. Also, cooling behavior after the end of the laser radiation is the same as in the experiments. To validate the simulation model, the simulation results were compared with the experimental results.

As shown in Fig. 6, the simulation results show very similar temperatures as in the experiment. Besides the measurement uncertainty of the pyrometer according to the manufacturer (0.5%), it should be noted that the setting of the process parameters, such as the diameter of the laser spot or the laser power, cannot be as accurate as simulations, which can also lead to deviations in the resulting temperature of the melting zone. Also, the positioning of the pyrometer cannot be done so precisely that exactly the center of the laser spot as measured in the simulation. The simulated temperature for the experiment with the measured temperature of 2380 °C, shows a deviation higher than 220 °C. The reason for this is the evaporation of fused silica at temperatures higher than 2350 °C, which was not taken into account in the simulations. Therefore, an overheating in the simulation leads to a higher temperature.

Fig. 6
figure 6

Comparison of simulated temperatures with measured temperature from experiments without fiber feeding

Full size image

In order to validate the accuracy of the simulated results against the actual process with glass feed, simulated results were compared with the experimental results. As shown in Fig. 7, the simulation results again show approximately the same differences found experimentally between with glass feeding and without it.

Fig. 7
figure 7

Comparison of simulated temperatures with measured temperature from experiments with fiber feeding

Full size image

The results show a temperature difference between the experiments with feeding material and the simulation without feeding material between 180 and 220 °C, which depends on the set feed rate and its relation to axis velocity. As above, two simulation results show a higher temperature than measured in the 2500 °C range. This can be explained by the effect of glass evaporation, which increases the temperature in the simulation by not taking the evaporation into account.

4 Results and discussion

4.1 Influence of process parameters on the resulting temperature

In order to investigate the influence of the process parameters and process boundary conditions on the temperature, a series of simulations was carried out under variations as described in Table 2. In each simulation, a straight line of 36 mm was defined as a tool path. The laser power, spot diameter, and velocity were varied according to a full factorial design of experiments.

Table 2 Variations of process parameters and boundary conditions for temperature simulations, the values marked with an asterisk are standard values used in simulations
Full size table

To investigate the influence of each variable on the temperature, a correlation analysis according to the “Pearson” method [18] was conducted. Based on the results shown in Fig. 8, the applied compressed air, in terms of the air velocity, to remove the evaporated polymer coating from the melting zone, as well as the size of the substrate, indicated by thickness, does not have a noticeable influence on the temperature in comparison to the other process parameters. Although, the influence of cooling compressed air depends on the orientation and distance of the nozzle from the melting zone, which cannot be adjusted so precisely in the experiments.

Fig. 8
figure 8

Correlation analysis between process parameters and process conditions and maximal temperature of glass material

Full size image

The results show that the spot size and laser power have a significant effect on the resulting temperature, much more than the axis velocity. Whereas the increase of the axis velocity leads to a linear decrease of the temperature. Based on this, the laser spot diameter and laser power are more important in process planning to control the resulting temperature.

To consider the effect of the two parameters on the temperature in process planning, the intensity of the laser (IL) on the surface can be evaluated. Figure 9 shows the relationship between laser intensity and simulated temperature for different laser powers, laser spot diameters in an axis velocity of 90 mm/min.

Fig. 9
figure 9

Relation between intensity and the simulated max. temperature

Full size image

The following regression functions (5) and (6) with a coefficient of determination of 0.98 describe the relationship between the laser intensity (W/mm2) and the resulting temperature T (°C) in an axis velocity of 90 mm/min on a fused silica substrate.

$$T = 890 Ln\left( {I_{L} } \right) + 679$$
(5)

Equation 5 can be expanded for the laser power in (W) and Spot size in (mm) as follow:

$$T = 890 Ln\left( {\frac{{4P_{L} }}{{LSD^{2} \cdot \pi }}} \right) + 679$$
(6)

Using Eq. 6, different combinations of laser power and laser spot diameter were calculated (Fig. 10).

Fig. 10
figure 10

Temperature of melting zone calculated from the regression function for the \(v = 90 {\text{mm}}/\min\)

Full size image

In terms of the softening and evaporation temperature of the fused silica, the ideal values for the laser power and laser spot diameter (shaded area in Fig. 10) can be determined based on the conducted calculations. This is a helpful reference for process planning to find the optimal process window, prevent undesirable damage, and later achieve the desired geometry.

To include the effect of axis velocity in (mm/min) on temperature as well, Eq. 6 can be extended as follows.

$$T = 890 Ln\left( {\frac{{4P_{L} }}{{LSD^{2} \cdot \pi }}} \right) - v \cdot 213 + 998.5$$
(7)

As shown in Fig. 11, the calculated temperature from Eq. 7 shows very similar temperatures to simulation results. Therefore, this equation can be used as a basic rule for process planning, to calculate the maximum resulting temperature without simulation effort.

Fig. 11
figure 11

Comparison of Temperature calculated by regression model with simulated temperatures

Full size image

4.2 Influence of different tool path strategies on the resulting temperature

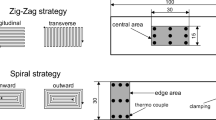
Due to the difficulty of separating the glass fibers after each material deposition in the LGD process, a continuous tool path is attempted to plan for the manufacturing of a component whenever possible. There are different ways to create a multilayer surface, among others zigzag, spiral (from outside to inside or from inside to outside), etc. Therefore, it is important to study the effect of these different path planning on the heat supplied or the resulting temperature. Thereby, the dwell time has to be investigated. Dwell time in this context shows how long it takes a tool to travel a distance to return to the same position. This allows process planning to consider the reheating or cooling process of a position for the deposited glass. Especially because the diameter of the laser spot is very larger compared to the tool path distance, the next path will have a higher initial temperature compared to the previous path. Therefore, the time needed to reach this preheated position is very important. The dwell time for the above-mentioned tool paths can be calculated by the following equations.

The dwell time \(\left( {t_{{{\text{dw}}}} } \right)\) for each position \(x\) in the zigzag tool path with \(l\) as a length of each layer and \(d\) as the distance between layers can be calculated with the following equation:

$$t_{dw} = \frac{{2\left( {l - x} \right) + d}}{v}$$
(8)

where \(x\) is the current position between the start point of each layer as \(0\) and the endpoint of it as \(l\): \(0 < x \le l\) and \(v\) is the axis velocity.

According to Eq. 8, the distance between every two layers and the axis velocity can affect the dwell time.

In order to have a closed multilayer surface with a spiral tool path, the maximum number of layers is calculated as follows:

$$n_{max} = \frac{l}{2d}$$
(9)

The dwell time between each layer in the tool path strategy spiral from out to in can be calculated as below:

$$t_{dw} = \frac{{\left( {8 \cdot \left( {n_{max} - n + 1} \right) - 1} \right) \cdot d}}{v}$$
(10)

where \(n\) is the layer number, which is \(1\) for the first outer layer.

Also, the dwell time between each layer in the tool path strategy spiral from in to out can be calculated as below:

$$t_{dw} = \frac{{\left( {8n - 1} \right) \cdot d}}{v}$$
(11)

where \(n\) is the layer number, which is \(1\) for the first inner layer.

Therefore, the dwell time in the inside-out spiral increases continuously during the process, while it decreases continuously in the spiral in the other direction.

To investigate the effect of dwell time in different tool path strategies on the generated temperature, the movement of the laser beam on the substrate with a spiral or zigzag tool path with constant axis velocity was simulated (Fig. 12). According to Eqs. 8, 10, and 11, the dwell time in the Zigzag and the spiral tool path is influenced by the distance between the layers and the speed at constant laser spot size. In the real process with glass feeding, the distance between the two paths is set to between 0.4 and 1 mm considering the size of the glass fiber and the deposited glass [19]. Therefore, it is important to know how far these different distances influence the resulting maximal temperature of the tool path. In the simulation of the zigzag path, the effect of the distance between layers on the temperature changing was simulated. Whereby the influence of different axis velocities and their directions on change of temperatures was studied in simulations of spirals.

Fig. 12
figure 12

Tool path strategies examples: Zigzag; Spiral “in to out”; Spiral “out to in”

Full size image

The simulated temperatures of these tool paths are depicted in Fig. 11.

The simulated temperature of the zigzag tool path (Fig. 13a) shows a more uniform temperature profile compared to spirals despite the temperature jumps during turning. In the spiral simulations, the path from inside to outside, where the dwell time increases as the layer number goes up, has a more uniform temperature profile than from outside to inside. Although the laser movement at 180 mm/min for a straight path line should cause less temperature (about 250 °C) than 90 mm/min, the results show that this difference becomes much less in a spiral tool path. Whereas the difference is even less with the tool path spiral from outside to inside. Also, temperature peaks lead to high residual stresses in the glass and could lead to failure.

Fig. 13
figure 13

Simulated temperatures for different tool paths

Full size image

Another aspect in the planning of tool paths is the changing of direction. The change of direction of the tool path has an impact on the temperature. The reason for this is the overlapping surfaces that are irradiated several times by laser. As shown in Fig. 14, this area can be calculated for a rotation angle between 0 and 90° as follows.

$$A_{o} = \frac{{D^{2} }}{4 \cdot sin\left( a \right)}$$
(12)
Fig. 14
figure 14

Calculation of overlapping area for different turning angles

Full size image

The change of this area depending on the turning angle is depicted more clearly in the following figure.

As shown, the smaller the derivation angle, the larger the overlapping area, which leads to an increase in the resulting temperatures. In this study, the influence of different turning angles on the change of the temperature profile was simulated for the standard situation from Table 2 with a 5 mm laser spot diameter.

According to the simulation results, the temperature change at the turning points 30° as expected, higher than 45°, and 60°, which are almost equal. In comparison to them at 90°, the changes are negligible, in which less area will be irradiated several times by laser in compare to the other corners (Fig. 15).

Fig. 15
figure 15

Simulated temperature for different turning angles

Full size image

5 Conclusion and outlook

In this paper, the influence of process parameters and tool path on the energy input and the resulting temperature in the Laser Glass Deposition process was numerically investigated. For this purpose, a 3D model was developed to simulate the temperature generated by moving a laser spot on a fused silica substrate. Using this model, the temperature in the melting zone was simulated under variation of process parameters such as laser power, laser spot diameter, axis velocity, and other process boundary conditions. After analyzing the simulation results, it was found that the laser power and laser spot diameter have a significant effect on the temperature in compare to the other parameters. Based on this, a regression function was created so that the generated temperature can be calculated by corresponding laser power, laser spot diameter, and axis velocity. This function can be well used in planning the process for applied fused silica to estimate the generated temperature. As a result, an optimal process window of laser power and laser spot diameter at 90 mm/min between softening and evaporation points of quartz glass was defined.

Moreover, different tool path strategies for the production of horizontally multilayered surfaces were thermally investigated. The results showed a more uniform temperature profile with zigzag movement than the spiral tool path. The selection of the turning point angle in the path planning and its influence on the temperature change was also investigated. It was observed that the 90° corner in contrast to the smaller angle has no significant influence on the temperature change.

In future studies, it is important to consider the effect of laser spot diameter on the temperature in the investigation of the effects of path planning. The size of the laser spot directly affects the temperature as well as the area directly irradiated by the laser. Thus, the relationship between the size of the laser spot and the distance between tool paths of layers and its influence on heating and the temperature needs to be investigated in the next works. In addition, the feeding of the fiber is to be taken into account in the process model in the future.