1 Introduction

Thermally induced workpiece distortions are a common problem in the industry during cutting machine operations [1]. Especially during grinding high thermal loads occur, which can lead to significant undesired distortions in long thin workpieces [2].

The production of steel parts consists of a complex composition of sub-processes. Each of them influences the workpiece properties and can cause undesirable characteristics [3]. These consist mainly of changes in geometry, surface structure, chemical composition, microstructure, texture and residual stresses [3]. An example of such a development is the creation of workpiece distortion. This is influenced to varying degrees depending on the machining process. In combination with a high demand for the dimensional accuracy of a workpiece, straightening processes become necessary to ensure the required quality. The grinding of linear guide rails is an example for this, generating distortions that negatively influence the geometric precision of the rails.

Currently, straightening processes are mainly done iteratively and manually by flame treatment based on experience and empirical values [4]. This process exploits the physical principle of the expansion of the metal when heated. During expansion, residual compressive stresses initially build up which, at sufficiently high temperatures, lead to plastic deformation. These are retained after subsequent cooling [5]. However, flame treatment is increasingly being replaced by an automated method. A laser can be used as a targeted heat source [6]. This is particularly challenging when part distortions are subject to high variation over the number of workpieces. As a result, the process potentially contributes to the ineffectiveness of the entire process chain. Based on this problem, the motivation for the present work arises to develop a system for distortion compensation.

The objective of the following research work is the identification of suitable process parameters for the straightening process by laser treatment, which allow a specific compensation of the distortions. A detailed analysis of mechanisms of laser bending and the effectiveness of scientifically investigated distortion strategies form the beginning of the development of a methodology for distortion compensation.

A model is created to analyze the effects of identified process parameters on distortion formation, based on current methods for finite element simulation of heat transfer and engineering mechanics problems.

2 Theoretical approach

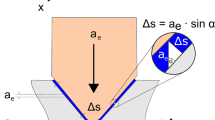
The present work deals with the compensation of the distortion of a profiled workpiece, which was induced by a grinding process within a V-groove. Results of previous research by Schieber et al. have shown that compensation can be implemented by generating compressive load stresses on the same side of the workpiece or tensile residual stresses on the opposite side (Fig. 1) [7].

Fig. 1
figure 1

The distorted workpiece after profile grinding in the V-groove with the considered thermal compensation strategy

Full size image

Thus, compared to deep rolling as a mechanical strategy for the introduction of compressive load stresses [8], a laser beam can also be used for subsequent machining [9].

The thermal residual stresses induced by this process are the basis for the compensation. A frequently used process in the industry is exemplified by laser surface hardening [10]. During this process, the workpiece is hardened locally on the treated surface and in the corresponding subsurface region. Due to the absorption of the laser energy at the surface, this exceeds the temperature over the austenitization limit [11]. The cooling rate is decisive for the type of transformation process. Since there is a high heat flux into the inner volume of the component due to the high thermal conductivity of metals, the surface cools rapidly. Depending on the initial microstructure, transformation processes and temperature differences induce both transformation and shrinkage stresses locally, which can then be combined to form a tensile and compressive residual stress profile [12].

During flame straightening, heat is introduced into a component in a temporally and locally limited manner to induce residual stresses and achieve a change in geometry. Upon cooling, the heated area shortens due to plastic deformation and phase transformation, causing the entire component to deform. The geometry change serves to compensate for deformations from previous machining processes. To avoid entering the austenite range (723 \(^\circ\)C for pure carbon steel), the flame straightening temperature must not be exceeded, which for steels is between 650 \(^\circ\)C and 700 \(^\circ\)C [13]. The temperature of the steel is determined by the temperature at which the material is straightened. Influencing variables during flame straightening include the thermal expansion coefficient and the thermal conductivity of the material [14].

A laser machining process is investigated in the scope of this work, which aims to replace the distortion compensation previously performed by flame straightening. Due to the better controllability of the heat input by a laser compared to a flame torch, a more precise distortion compensation can be accomplished. In addition, the heat treatment is much more energy-efficient [15] and contributes itself to automated use [6].

In this type of thermal distortion compensation, a laser is used as a heat source to locally increase the temperature and induce plastic deformation. During the warm-up phase, the workpiece deforms toward the side not being processed by the laser due to the local thermal expansion of the laser-facing side (Fig. 1). In the subsequent cooling phase, the part shrinks in the opposite direction. Laser bending can be used in production for sheet metals [16] as well as for profiles [17]. The forming of high-strength alloys was investigated by Rigas and Merklein [18]. A correlation between the laser beam size and the deformation behavior was found for sheets with a thickness of 1 mm. For thicker sheets, the influence of the laser beam size decreased significantly [18].

Wang et al. investigated the distortion compensation of steel by laser processing using numerical and experimental methods [19]. A Gaussian shaped heat source was modeled and validated by experimental studies. Elongated steel cuboids, like the linear guide rails considered in this work, served as sample geometry. The workpieces studied exhibited a parabolic distortion curve with a maximum distortion value in the center.

The mechanisms during laser treatment can be divided into two groups (thermal and mechanical processes). Thermal processes are present, which include the temperature gradient mechanism (TGM) and the residual stress point mechanism (RSPM). A mechanism that is not due to thermal expansion is the residual stress relaxation mechanism (RSRM) [20]. The basis of the TGM is the introduction of a temperature gradient into the component. The laser radiation is absorbed locally, resulting in the formation of a temperature gradient. Since steel has a positive coefficient of thermal expansion, an increase in temperature leads to expansion. The present temperature gradient leads to different expansions, which in turn cause compressive stresses. If the stresses do not exceed the yield point, the process is fully elastic. However, if the yield point is exceeded, plastic deformation occurs within the previous laser influence zone, which causes tensile residual stresses after cooling. These cause the sheet to bend in the direction of the laser source. The laser power and the feed rate have been identified as influential parameters for the TGM [20].

The RSRM can be described as a local annealing process. During this process, residual stresses are also relieved. If rapid and inhomogeneous cooling takes place subsequently, new residual stresses may arise under certain circumstances. If the process is conducted several times in succession, the expression of the RSRM decreases with each repetition [20].

The MEM is based on different temporal temperature profiles in the zone of influence of the laser. Locally, temperatures leading to a phase transformation can be exceeded. Within the laser influence zone, the austenitizing temperature is exceeded, resulting in the formation of austenite. Due to the lower volume of austenite compared to ferrite, the upper region shrinks, and the workpiece bends in the direction of the laser source. If rapid cooling subsequently occurs due to high thermal conductivity in the material, the previous austenitic region is at least partially transformed into martensite. Martensite occupies a larger volume than austenite and than initial ferrite. This induces expansion of the upper region of the steel workpiece and causes bending in the opposite direction of the laser irradiation [7]. The newly formed martensite is surrounded by an area of elastic ferrite in which RSRM has occurred. The MEM has an influence depending on which phase the starting material is in. Especially in the thermal deformation of metals, there is often a combination of several of the mechanisms just mentioned and described [20].

On the other hand, Hutterer et al. looked at flexible forming processes. They set up a closed loop control system for laser straightening of deformations in order to be able to specifically process complex geometries. Besides the selection of suitable irradiation strategies for laser shaping, the consideration of the field of the material, the geometry and the laser was also important. The goal was to automatically repair hail damage in the car body using heat treatment. Starting from a CAD model read in the preprocessor, a feature extraction of optical 3D measurements of the profile was performed in the course of a rough correction. From this, an irradiation strategy for distortion compensation was derived by means of a nominal and actual workpiece comparison. Subsequently, an additional fine correction was carried out if necessary [21].

Rigas et al. dealt with numerical and experimental investigations concerning distortion reducing laser heat treatments of aluminum workpieces. Local heat treatments reduce geometrical accuracy. Suitable short-term heat treatment was used to eliminate the distortion of these workpieces by simulative and experimental design. For this purpose, both the heat effect on accuracy and the temperature-dependent material changes were investigated. They found that a linear irradiation strategy compared to a spotwise irradiation strategy allows faster workpiece heating and thus higher distortion [22].

The influence of multi-pass laser treatment of AISI 4140 workpieces on distortion was analyzed by Lu et al. A continuous wave laser with a rectangular beam shape was used. Different feed rates and numbers of passes result in changed residual stress profiles. When the number of passes is increased, the compressive residual stress at the surface decreases slightly. In deeper workpiece zones, however, these residual stresses increase [23].

Based on this starting point, the thermal straightening strategy can be transferred to the typical application in the manufacture of linear guide rails. For this purpose, the distortion ranges, which occur during grinding in the V-groove, must first be defined. From previous research results by Schieber et al., these were analyzed based on a variation of the feed rate and the depth of cut of the grinding wheel [7]. The usual parameter sets, which are also used for profile grinding in industry, were investigated. The upper limit was formed by the parameters at which no grinding burn occurred. The workpiece properties were identical to those used in the present study. The maximum measured distortion value for profile grinding was 0.23 mm at a depth of cut of 0.8 mm and a feed rate of 1500 mm/min. This distortion provides a reference value for compensation by the laser in the following.

3 Details of the experiment

3.1 Material

The AISI 4140 workpiece used in this work, which approximates a linear guide rail commonly applied in industry, was circumferentially milled with dimensions 23 mm \(\times\) 38 mm \(\times\) 250 mm (h \(\times\) w \(\times\) l). The V-groove profile was added with dimensions of 8.67 mm \(\times\) 19 mm (h \(\times\) b) and a radius of 2 mm in the groove base centered over the entire length with a stock removal of 0.6 mm. For better comparability of the distortion results, the workpieces used were stress relieved (QT 200 \(^\circ\)C, 55 HRC) before laser treatment. The proportions of the alloying elements can be found in Table 1.

Table 1 The chemical composition of the workpiece
Full size table

3.2 Methods

The experiments and the corresponding numerical mapping in the finite element simulation were performed with different laser parameter combinations. For this purpose, the laser power and the laser feed rate were varied in a full-factorial manner. The laser powers P were 2.0, 2.4, 2.7, and 3.1 kW. The feed rates were set at 0.6, 0.7, 0.8, and 0.9 m/min. This resulted in a total of 16 different combinations (Table 2).

Table 2 The laser parameters
Full size table

The ranges of parameter combinations used for laser power and feed rates were defined, as in the simulations, based on findings from preliminary tests [7]. 48 samples were processed with 16 different parameter combinations. To measure the workpiece distortions after laser processing, 13 measuring points were recorded on the bottom of the workpiece, each on two rows at intervals of 20 mm, using a coordinate measuring machine (Fig. 2).

Fig. 2
figure 2

Steps of simulated laser processing at the lower surface of the workpiece. The red rings represent the defocused laser positions. The process consists of moving from position 1 to 2, 3 to 4, and cooling between 2 and 3. The lower part shows the view of the yz-plane. The origin of the coordinate measuring machine data points in the middle of the workpiece is visible as well as the shifted origin of the y-axis for the data analysis (colour figure online)

Full size image

The determination of the shape deviation was conducted in each case before and after the processing of the workpieces. In the evaluation, the results obtained from the two rows were then averaged over each of the three workpieces with the same parameter set. A TruDisk 4001 laser from Trumpf (Ditzingen, Germany), which emitted light with a wavelength of 1030 nm and a maximum power of 4 kW, was used for the laser processing. A light guide cable with a diameter of 600 \(\upmu\)m connected the laser with the optics from Precitec (Gaggenau, Germany). The optics were mounted on a robot and the sample lied, defined by several stop points but not firmly clamped, on a processing table (Fig. 3).

Fig. 3
figure 3

Experimental setup for laser processing (robot with optics, sample on processing plate)

Full size image

Before the experiments were performed, the lenses of the optics were positioned to use as uniform an annular heat source as possible. The defocused laser beam was well suited for the application described here to be able to generate a distributed heat flux across the width of the workpiece. The samples were cooled in a water tank between the two passes.

3.3 Analysis of the distortion data

During the evaluation, the average value of the displacement in the y-direction of both measuring lines was formed for each z-position. This allowed an averaged distortion curve to be determined as a function of the z-position. In the next step, the curve was shifted in the y-direction until the value for the displacement exceeded 0 for one endpoint and was 0 for the second endpoint so that there was no sign change in the distortion curve (Fig. 2).

The peak-to-valley value \(\varDelta PV\) was determined from the distortion curves defined as described above. The \(\varDelta PV\) value describes the difference between the PV value in the initial state and the PV value after machining [24]. For this purpose, the distortion values (from the workpiece measurement before and after machining) were averaged in the y-direction for the two endpoints (one is at zero) and the difference to the absolute largest value of the distortion curve was formed.

For each set of parameters (variation of laser travel path orientation and feed rate), data sets were available from three workpieces, respectively, following the procedure described above. In the last step, the mean value of the \(\varDelta PV\) value was formed in each case from the three workpieces with the same manufacturing parameters.

3.4 Investigations of microstructure and hardness behavior

For a better understanding of the process at the material level, metallographic investigations, and hardness measurements according to Vickers were carried out in the progress of this research.

The cross section preparation was based on the procedures described in the literature [25]. Specifically, the sample was taken from the center of the component, with the cut surface perpendicular to the z-direction of the workpiece. The samples were ground, polished and etched.

Microscopic examination was performed using a BX61 reflected light microscope from Olympus (Shinjuku, Japan).

The hardness curve, Vickers HV 1/5 (i.e., loading with 1 kg weight for 5 s) was determined as a function of the distance to the laser-treated surface on another ground sample prepared according to the method just described but not etched.

Fig. 4
figure 4

The geometry of the workpiece and applied boundary conditions for the finite element simulation

Full size image

3.5 Modeling

The modeling boundary conditions of the laser processing were based on the preliminary experiments already performed [7]. Since simulations are associated with significantly lower costs compared to laser experiments, they were conducted first in this work to ensure that the parameter ranges used for the laser power and the feed rates are reasonable.

Since only small distortions (less than 1% with respect to the length of the linear guide rail) are to be obtained, the plasticity model for small plastic deformations was selected in the FEM simulation. In contrast to the model with large plastic deformations, the deformation was divided additively into a plastic and an elastic component. The shape change hypothesis, which is based on von Mises’ considerations and is suitable for multidimensional stress states, was used as the yield condition. The behavior of the material after the yield point has been exceeded was described by an isotropic strain hardening model. Since large numbers of cycles were not achieved during distortion compensation by the laser, and to simplify the model numerically, modeling of the kinematic hardening was omitted in this work. Changing material properties due to temperature gradients during the laser process, i.e., the elastic modulus, the heat transfer coefficient, the thermal expansion coefficient, and the Poisson’s ratio, were considered by temperature-dependent characteristics from the literature and material databases.

To save computational capacity and reduce simulation time, symmetry in the longitudinal direction of the workpiece was used (see symmetry plane in Fig. 4). The simulations were performed with the half which has positive x-values.

To allow both a distortion of the component and a stable simulation, four floating bearings at the lower corners of the workpiece, which allow a movement on the xz-plane, and one fixed bearing on the symmetry plane were defined. The fixed bearing is necessary to perform a stable simulation. Another point of the fixed one is the better comparibility with the experimental \(\varDelta PV\) value due to a direct maximum distortion value output without shifting the workpiece along the y-axis like the data points of coordinate measuring machine in Fig. 2.

The initial and ambient temperatures were defined as 20 \(^\circ\)C. An annular, defocused, and moving laser source was defined on the opposite side of the V-groove. The heat flux to the clamping support surface is determined by the thermal conductivity of the steel. For simplification, the heat transfer coefficient was kept constant for all surfaces of the workpiece on which convection and radiation occurred.

Following investigations on the modeling of an annular laser source, the moving heat flux q was defined as follows:

$$\begin{aligned} q= & {} \frac{a\cdot P}{2\pi r_{0}^{2} \left( e^{-(\frac{R}{2r_{0}})^{2}}+\frac{R}{r_{0}}\cdot \sqrt{\frac{\pi }{2}}\cdot \left( 1+erf\left( \frac{R}{\sqrt{2}r_{0}}\right) \right) \right) } \nonumber \\&\cdot e^{\frac{x^{2}+y^{2}+R^{2}-2\cdot R \cdot \sqrt{x^{2}+y^{2}}}{2\cdot r_{0}^{2}}} \end{aligned}$$
(1)

The absorption coefficient a was set to the value 1 for simplicity. The radius R with 7.5 mm (diameter d = 15 mm) defines the geometry of the ring. \(r_0\) describes the width of the ring with 2 mm. The laser power P varied between 2.0 and 3.1 kW. For each power the heat flux profile was manually recalculated for the simulation. To avoid numerical instabilities, it is necessary to define the boundary conditions in such a way that they change as uniformly as possible. For this reason, the heat source was defined outside the component (50 mm distance) at the beginning of the simulation and only later moved over the guide rail. The component was traversed twice in total (Fig. 2). After the first line has been lasered with a process time between 23.33 and 35 s according to the feed rate, a cooling time of approximately 170 s was simulated (depending on the speed). In the next step, the line was traversed in the opposite direction with the same process time of step 1 in Fig. 2, and then cooling was simulated again for approximately 170 s. Table 3 shows the defined process times, which were read into the simulation as a defined path.

Table 3 Time points at different positions (Fig. 2) for different laser feed rates; once position no. 4 is reached, a cooling process is simulated up to time point 400 s
Full size table

3.6 Mesh

The longitudinally symmetrical property of the linear guide rail was used in this work to simulate only half of the workpiece and thus reduce the required computational effort. The meshing was realized by a free cuboid mesh on the xy-plane with four or five elements on the two longest side edges and a subsequent extrusion in the z-direction with element spacing of 2.5 mm. This resulted in a total of 2000 volume elements.

To test the meshing independence, the element spacing of the extrusion was reduced to 1 mm, resulting in a crosslinking of the component with 5000 volume elements. The results were compared for peak-valley values with maximum distortion at the center of the linear guide rail of the parameter combination with a 3.1 kW laser power and 0.6 m/min feed rate. Due to the very small change in the \(\varDelta PV\) value with further refinement, normal meshing with 2000 volume elements was considered sufficient.

4 Results and discussion

4.1 Workpiece distortion due to laser processing

In this work, laser experiments were conducted with 16 different parameter combinations. In addition to the previously described laser processing procedure, an averaging of the distortion results with the same process parameters was done. Figure 5 shows the \(\varDelta PV\) values for different process parameter combinations of laser power and feed rate. An increase in the laser power and a decrease in the feed rate result in an enlarged distortion value. The large differences in the \(\varDelta PV\) values for the parameter combinations 2.0 kW at 0.7 m/min with −0.081 mm and 2.0 kW at 0.8 m/min with −0.019 mm as well as between 2.0 kW at 0.9 m/min with −0.016 mm and 2.4 kW at 0.9 m/min with −0.132 mm are evident. The distortion values of the parameter combinations 2.4 kW at 0.9 m/min, 2.0 kW at 0.7 m/min, 2.0 kW at 0.6 m/min range between the comparatively very low value of the two combinations 2.0 kW at 0.8 m/min and 2.0 kW at 0.9 m/min and the other parameter configurations. At higher laser powers and simultaneously lower feed rates, the distortions reach values up to a maximum of −0.265 mm (0.6 m/min and 3.1 kW).

Fig. 5
figure 5

The experimental peak-to-valley distortions \(\varDelta PV\) in the y-direction for feed rates \(v_l\) between 0.6 and 0.9 m/min and laser powers P between 2.0 and 3.1 kW

Full size image

4.2 Hardness measurement and metallographic examinations

To better understand the step-like behavior of the distortion during the laser experiments, metallographic material investigations were conducted. For this purpose, a preliminary test workpiece processed with a laser power of 2.9 kW and a feed rate of 0.6 m/min was used. After further workpiece preparation, micrographs were taken at higher magnification. Two areas can be identified in Fig. 6. Starting from the surface, a narrow light area with a thickness between approximately 0.6 and 0.9 mm is visible. This is followed by a dark area. At higher magnification, roundish grain structures can be seen in the transition area in Fig. 6b.

Fig. 6
figure 6

Section of the sample along the workpiece symmetry line after a laser treatment with a feed rate of 0.6 m/min and a power of 2.9 kW

Full size image
Fig. 7
figure 7

Vickers hardness curve (HV1/5) along the symmetry line after laser treatment with a feed rate of 0.6 m/min and a power of 2.9 kW

Full size image

In addition, a hardness profile measurement was performed on the above-mentioned preliminary test workpiece, starting at the laser-machined side (Fig. 7). The change in hardness correlates with the different areas in Fig. 6. The hardness reaches a maximum value of approximately 700 HV1/5 near the surface and drops sharply.

The positions of the micrographs from Fig. 6 are shown in the hardness diagram. In the first layer (a) a splintery microstructure, presumably martensite, and in (b) a transition region from large grains, whose hardness is lower, to an acicular, bainitic region (c) can be seen. This influence of the temperature behavior on the microstructure and thus on the properties of AISI 4140 refined the numerical mapping and the simulative results by this approach.

4.3 Simulated distortion

While the laser is moving along the workpiece surface, the exposed side expands due to the higher temperature, resulting in a curvature of the guide rail in the negative y-direction. After cooling (at 400 s), the residual local plastic deformation causes distortion or curvature in the positive y-direction. Figure 8 shows the distortion results from the simulation compared with the experiments from Fig. 5. As an example, only the distortion curves with a constant laser power of 2.4 kW and variable feed rates as well as a constant feed rate of 0.7 m/min and variable laser powers are given here for a detailed comparison with the experiments.

Fig. 8
figure 8

a The peak-to-valley distortion \(\varDelta PV\) in the y-direction for different feed rates \(v_l\) and a constant laser power P of 2.4 kW; b the peak-to-valley distortion in the y-direction for different laser powers P and a constant feed rate \(v_l\) of 0.7 m/min

Full size image

For better comparability, the curves were shifted in the y-direction so that the displacement at the two ends of the workpiece (at a z-position of 0 and 250 mm) has a value of zero. Figure 8a reveals the values for a constant laser power P of 2.4 kW and the four variations of the feed rates \(v_l\) between 0.6 and 0.9 m/min.

While a distortion of −0.235 mm is shown at a feed rate of 0.6 m/min with a constant laser power of 2.4 kW, this decreases with 0.9 m/min and a value of −0.132 mm. The simulated values indicate an agreement within the error range from the averaged distortion values of the three workpieces processed with the same parameters. There is a larger jump between the values with a larger deviation between simulation and experiments at 0.7 and 0.8 mm. On the one hand, this confirms the good mapping and definition of the boundary conditions. On the other hand, it also shows the problem and limitation of the model to perfectly reproduce the changes in the microstructure when exceeding the austenitization limit.

Higher laser power has a similar effect as a lower feed rate. The energy input is increased and thus the distortion also increases. In Fig. 8b, the simulated distortion values were compared with the respective experimental distortions at a constant feed rate of 0.7 m/min and variable laser powers between 2.0 and 3.1 kW. The greater the laser power and the lower the feed rate, the greater the \(\varDelta PV\) value.

The value for the parameter combination 2.0 kW and 0.7 m/min shows the lowest distortion of the parameter series with a distortion of 0.081 mm. The simulation, however, deviates from this with a lower value due to the greater influence of the fixed bearing (Fig. 4) on the distortion curve. This only occurs for small deformations, where the simulation model and the evaluation method are used to reach their limits. The outward measuring points for the samples, which were processed with 3.1 kW laser power, differ significantly in their distortion values, at this point again due to the strong microstructural changes in the edge zone.

In summary, it can be stated that the strategy of targeted thermal straightening defined here could compensate for a deformed workpiece utilizing simulative modeling and distortion prediction. Comparing the achieved \(\varDelta PV\) values with the distortions from the literature, which were achieved by grinding in the V-groove in the opposite y-direction, it has been shown that it is possible to compensate for smaller distortions as well as the maximum values of up to 0.23 mm [7]. Here, the results between a ground and an unground lasered specimen were compared. So with the mentioned laser process, it is possible to use this approach to straighten the specimen without the heat-treatment prior to laser straightening [7].

5 Conclusion

Within the scope of this work, the laser-induced distortions of long workpieces, like those of linear guide rails, were investigated experimentally and simulatively. The procedure succeeded and could also be transferred to other component geometries for the defined introduction of compensating distortions.

For the thermal processing of the workpieces, a defocused, annular laser source was used for the distributed introduction of tensile residual stresses. The temperature behavior was coupled with the mechanical behavior via the material parameters. Temperature-dependent material data were used for plasticity modeling.

During the simulations, both the feed rate and the laser power were varied, and the maximum distortion value was determined in each case. This was followed by laser experiments with the same process parameters. The change in geometry of the samples was measured.

In both simulation and experiment, higher laser powers and slower feed rates lead to greater distortion. However, the distortion data from the laser experiments show a much more erratic behavior than the simulations.

Hardness measurements and microsection examinations of the processed samples confirmed microstructural transformation processes due to laser processing.

In future studies on distortion compensation, the models of profile grinding, and thermal straightening must now be combined to be able to analyze thermomechanical effect superpositions in the workpiece and to obtain a valid overall prediction model.