Abstract
The components of a body in white consist of many individual thin-walled sheet metal parts, which usually are manufactured in deep-drawing processes. In general, the conditions in a deep-drawing process change due to changing tribology conditions, varying degrees of spring back, or scattering material properties in the sheet blanks, which affects the resulting pre-strain. Mechanical joining processes, especially clinching, are influenced by these process-related pre-strains. The final geometric shape of a clinched joint is affected to a significant level by the prior material deformation when joining with constant process parameters. That leads to a change in the stiffness and force transmission in the clinched joint due to the different geometric dimensions, such as interlock, neck thickness and bottom thickness, which directly affect the load bearing capacity. Here, the influence of the pre-straining in the deep drawing process on the force distribution in clinch points in an automotive assembly is investigated by finite-element models numerically. In further studies, the results are implemented in an optimization tool for designing clinched components. The methodology starts with a pre-straining of metal sheets. This step is followed by 2D rotationally symmetric forming simulations of the joining process. The resulting mesh of each forming simulation is rotated and 3D models are obtained. The clinched joint solid model with pre-strains is used further to determine the joint stiffnesses. With the simulation of the same test set-up with an equivalent point-connector model, the equivalent stiffness for each pre-strain combination is determined. Simulations are performed on a clinched component to assess the influence of pre-strain and sheet thinning on the clinched joint loadings by using the equivalent stiffnesses. The investigations clearly show that for the selected component, the loadings at the clinch points are dependent on the sheet thinning and the stiffnesses due to pre-strain. The magnitude of the influence varies depending on the quantity considered. For example, the shear force is more sensitive to the joint stiffness than to the sheet thinning.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Even with the transition from internal combustion to electric cars, lightweight construction is important to meet climate targets [1]. The mass of the body-in-white is usually reduced by lightweight design using dissimilar material. Mechanical joining processes such as clinching are well suited for joining similar and dissimilar materials. In clinching, a non-detachable joint is created in a cold forming operation. [2]
The mechanical behavior of a clinched joint is strongly dependent on its geometry, especially the interlock and the neck thickness [3]. Changing the joining direction of a non-uniform sheet combination with different thicknesses leads to a different interlock and neck thickness and thus changes the failure behavior and the maximum load-bearing capacity of the clinched joint [4]. It is well known that the maximum shear force increases with a larger neck thickness. Thick to thin sheet combinations have higher shear strength due to a higher neck thickness [5]. If there is a neck failure under tension loading, then the neck thickness is decisive for the maximum tensile force. In the case of unbuttoning, the size of the interlock determines the pull-out strength. [6] The influence of the forming history, work hardening and sheet thickness reduction on clinched joints is described in [3] and [7]. The investigations show that the pre-forming of the sheets before the joining operation changes the geometry and thus the pull-out and shear strength of the clinched joint. Since geometrical characteristics, maximum forces, and stiffness correlate in general, those relationships are also valid for the axial and shear stiffness. All the above-mentioned dependencies on a clinched joint, lead to clinched joints with different mechanical properties when clinching two deep-drawn parts with the same tool and joining process parameters. This is due to the different local sheet thicknesses and pre-strain states which are common in deep-drawn parts.
Each clinched joint is a single part of the overall joining design, which is the sum of all joining elements, which are represented by their positions, their technology and their parameters [8]. Clinching is a joining technology that creates point-shaped joints, which is the reason why research on joining design consisting of point-shaped joints will be discussed in the following. The research almost completely refers to spot welds, as they are more commonly used, but the methods can be applied to clinched assemblies. It is known that changing the distribution of the joints influences their loading, which can be described by an intensity criterion [9]. Furthermore, the joining design influences the overall stiffness of a complex joined assembly, as a vehicle body. For example, the reduction of the number of spot welds due to failure significantly decreases the stiffness of a vehicle body during lifetime [10]. Since the production costs increase with a higher number of joints [11], many research contributions dealing with the optimization of the joining design. The optimization methods for a joining design aim to reduce the number of joints. At the same time, the vehicle body stiffness should be increased or at least not decreased [12]. The modeling effort for these optimizations is constantly increasing. For example, the optimization of the spotweld layout in [12] is carried out purely on a finite element model of a vehicle body using static and modal analysis as load cases. In [13] driving simulations are performed in a multibody model and operating loads are obtained. Subsequently, those loads are transferred to a finite element vehicle body model and the optimization of the joining design is done. In fatigue simulation driving simulations are also used to obtain more accurate predictions [14]. Another recent development in the simulation and dimensioning of joined assemblies is the consideration of stiffness degradation in the joints due to fatigue. In [15], the degradation of spot welds due to fatigue is considered in a vehicle body model. The method accurately predicts the changes in strain around the spot welds. The actual decrease of the body stiffness is even higher due to stiffness changes in the base material which is not considered in the simulation. [15]
A next further step in the simulation of joining designs could be the consideration of the manufacturing process. Within the scope of this research the entire process chain is represented. This enables an investigation, how the calculated loads at each clinched joint differ when the previous deep drawing operations are considered. The subject of the following investigations is the constitution of cause-effect relationships between the joint loadings and the sheet thinning in the flanges and the joint stiffnesses. In other words, the research question is, how the error caused by not considering the material history is distributed among the sheet thinning in the flanges and the different joint stiffnesses due to pre-strain? Does the neglection of the sheet thinning creates a higher error as neglecting the joint stiffness due to pre-strain? Is it vice versa? Are the errors made in the identical direction?
To answer this question, first the relationship between the pre-strain in the sheet in the joining zone and the resulting sheet thickness before joining and the relationship between the pre-strain and the resulting joint stiffnesses after the clinching process must be known. The stiffnesses must necessarily be determined very locally. If this is not achieved, the determined stiffnesses do not exclusively represent the joint stiffness due to the deformation of the sheets [16]. In the best case, the relationship between the pre-strain and the clinch joint stiffnesses can be described by continuous functions. Second, these stiffnesses must be converted into stiffnesses of equivalent clinched joint models for the simulation of assemblies. Third, the sensitivity analysis must be performed.
2 Determination of the influence of the pre-strain and pre-stress on the clinched joint stiffnesses
In this section, the influence of the pre-strain of the sheets on the clinched joint is investigated. Further, the associated stiffnesses are determined for each pre-strain combination. Therefore, the pre-straining of the sheet, the joining operation, and head tension and shear tests are simulated for various pre-strain combinations. In this section two metamodels with numerically determined local stiffnesses of the clinched joints as a function of the pre-strain are illustrated.
2.1 Method
The basic approach for determining clinched joint properties as a function of pre-strain is described in [17]. The approach is adapted to determine the local elastic stiffnesses in the axial and shear direction. It is further extended to include the determination of stiffnesses for a point-connector model, which is essential for modeling clinched joints in a component or a full vehicle model. The parametrized models and the automatic evaluation presented in this work allow the calculation of a high number of model variants. Conclusions are then drawn about the sensitivity and robustness of the process as a function of the pre-strain of the sheets. The scheme of the methodology is shown in Fig. 1.
2.2 Model sampling and model configuration
In the first stage, the model sampler defines the investigation space by specifying certain pre-stretching values for the top and base sheet. The sequence of the approach is as follows: The parameters selected in the sampler (Step 1) are directly implemented into the models (Step 2), where the FEM models are adjusted. In the sampler 50 data points of different pre-forming combinations are chosen. As can be seen in Fig. 1 A the criterion for the preforming is an absolute distance s. For the selection of the datapoints (s1/s2 pairs) a D-optimal design and a step size of 0.2 is chosen. The minimum s-value is 0 and the maximum is 2, which corresponds to a pre-strain of 0% respectively 35.5%. Furthermore, the material and the nominal thickness of the sheets are defined in this step. In this study, a clinched joint of two 1.5 mm steel sheets of HCT590x is investigated. HCT590x is cold working steel with a two-phase structure, which is widely used in the automotive industry. The mechanical properties of the investigated materials were previously investigated and adopted in this study. For the elasto-viscoplastic material description of the dual-phase steel, the Johnson–Cook constitutive model is used. The FEM simulations are calculated implicitly with the LS-Dyna-Solver version smp_d_R12. The sampling and the calculation of metamodels are done with the software LS_OPT.
2.3 Metal sheet pre-straining and clinching process
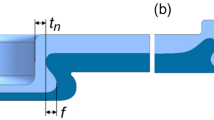
The clinching process with pre-forming of the sheets is carried out in three different FEM simulations just as the test for determining the stiffnesses. First, the process-related pre-strain in the direction of the sheet metal is simulated. The pre-strain leads to thickness reduction and increased yield stress due to strain hardening. The pre-deformation is calculated in a rotationally symmetric 2D model, which leads to a biaxial pre-strain due to the model. Anisotropic effects in the sheet plane are not considered. The procedure of pre-straining was presented in more detail in [17]. After the elastic spring is back, the subsequent clinching process simulation is performed. The geometry of the tools used in the simulation is the same as the one used in the empirical evaluation. The forming process is controlled by a displacement, which is described by a constant joining speed and a maximum joining distance of the punch. This maximum distance correlates with the residual bottom thickness. The joining process and the return stroke as elastic spring back are calculated in the same simulation model. A mesh of the geometry of the clinched joint with all internal values like stress and strain is obtained after the simulation as can be seen in Fig. 2. For quality aspects, three geometrical characteristic parameters (neck thickness, interlock and residual bottom thickness) are considered relevant for the clinched joint. Figure 2 shows the cross-section of the joint and the contour of the simulation of the joining process. The model has already been verified as valid in [17] since both the process force during joining and the geometric result contour show a good agreement between experiment and simulation. The model does not consider the accumulation of damage during the process chain and the resulting influence on the material behavior. In addition, Coulomb friction law is implemented in the contacts between the sheet metals and the contacts between the tools and the sheets.
Micrograph of HCT590x (1.5 mm)/HCT590x (1.5 mm) clinched joint and contour from process simulation [17]
2.4 3D-Modell rotation and Strain/Stress mapping
To determine the stiffnesses of the joint, a 3D model is generated from the 2D model. This is necessary because the shear stiffness cannot be calculated with a 2D-rotational model, due to the non-axisymmetric deformation. The automatic mapping is also implemented directly in the methodology. It is the first step in the joint stiffness calibration, numbered 3C in Fig. 1.
The mapping enables the initialization of a 3D Lagrangian calculation model with data from the last cycle of a previous 2D rotational symmetric joining process simulation. The 3D mesh is generated by rotating the 2D mesh. For the calculation without pre-strain, the rotation procedure is shown in Fig. 3. The mapping transfers data such as node coordinates, plastic strains, and stresses so that the stress and strain state after the joining operation is represented. The transfer of the strain leads to a consideration of the strain hardening caused by the joining process of the material. The procedure is described in more detail in [18].
2.5 Determining the local clinched joint stiffnesses
The calculation is performed in two steps. First, the clinched joint springs back while no boundary conditions are set in the model. Subsequently, constraint conditions are activated simulating the testing process. For this purpose, the translational degrees of freedom of all nodes on the circular surface of the lower circular blank are fixed. The upper circular blank is shifted laterally or upwards via a displacement condition on the nodes on the round margin surface. The simulation is performed in LS-DYNA R12 using the implicit solver with double precision. Afterward, force–displacement curves of the testing process are generated. The measured force is the sum of the nodal forces on the cylinder surface of the top sheet. The displacement is measured at a node on the upper cylinder and is equal to the given constraint condition. Stiffness is determined by linear regression using the least squares method. Figure 5 shows the result of the numerical local head tensile stiffness test. The results of the testing are shown in section (b). Here the influence of the base sheet can be seen by the colored marking of the individual simulation force–displacement curves. With increasing pre-strain of the base-sheet before joining, the force curve and thus the stiffness decreases. The force–displacement curves do not start at zero. This is due to the process-related pretension of the clinch connection. The stiffness of the curves is evaluated by a linear regression using the python scikit library. The fit meets two criteria. The coefficient of determination R2 is higher than 0.96 and as many points as possible are included where the condition is still fulfilled. This means when including the next point, the value falls below the desired value for R2. In Fig. 7a the stiffness determination of a single joint can be seen. The stiffness values determined by linear regression can be represented by a metamodel. The metamodel is a mathematical described assumption for the relationship between the pre-strain of the top and base sheet metal and the resulting stiffness of a clinched joint. In Fig. 4 metamodels obtained by common approaches are shown. The prediction accuracy is expressed by the coefficient of determination R2. The higher the value, the higher is the accuracy of the response surface. For all further investigations in this study, the metamodels are obtained using a polynomial quadratic approach. The drawback of the slightly lower accuracy compared to the accuracy of the response surface obtained by a feedforward neural network approach, is overcompensated by simplicity. The polynomial quadratic approach is much easier and a continuous function can be obtained easily. The Kriging algorithm leads to an overfitting, which is not desired.
The root mean squared error (RMS) of the response surface model, obtained by using the polynomial quadratic approach, is 0.109. This value represents the accumulated resulting average error of the approach. It is the sum of the numerical error, the error made during stiffness determination and the error induced by the mathematical approximation function of the metamodel. Figure 5c compares the value calculated and evaluated by the script with the value predicted by the metamodel. The mathematical function as well as the identified factors A–F for the metamodel description can be seen in section (d). The mathematical approach and the calculated stiffness values can be found in section (a). In the illustration, the surface that is derived from the function shown is also drawn. This color scheme of the surface was taken from [17] and is based on the geometric quality rating of the joint. The green mark means that the connection is considered feasible. This means that the three geometric parameters (neck thickness, interlock and residual bottom thickness) do not fall below any limit due to the pre-forming. In turn, this means that the red area considers clinched joints to be infeasible. The infeasible area marked in figure a is caused by the interlock falling below the minimum size of 0.1 mm. The limit for neck thickness (0.15 mm) is not exceeded in analogy to the investigations in [17] and is therefore not relevant for the selection of the feasible points.
The evaluation of the shear stiffness is equivalent to the determination of the axial stiffness as shown in Fig. 6. Again, in section (b), the force displacement curves determined in the simulation are evaluated. Here the influence of the pre-deformation of the top sheet on the force–displacement curve is shown by color-coding. In contrast to the evaluation of the head tension, the curves start at zero force. There is no relevant elastic prestressing in the direction of the shear and thus no pre-force. In this instance, a linear regression, comparable to the axial stiffness, is used to evaluate the shear stiffness. The calculated values are then approximated by a metamodel based on a quadratic polynomial approach. Section (c) of Fig. 6 evaluates the procedure. The coefficient of determination is 0.938. The RMS is 0.0622. The coefficient of determination as well as the error of both prognoses is lower for the shear stiffness evaluation than for the axial stiffness evaluation. Section (d) shows the mathematical function of the metamodel and the determining factors. The determined and evaluated metamodel is shown in section (a). The red infeasible area resulting from exceeding the interlock limit is highlighted. The influence of the pre-forming of the top and base sheet on the stiffness can also be seen here. Figure 7b shows the linear regression calculation process of the phyton script for an exemplary clinched joint model. The criteria of the fit of the shear stiffness are the same as the ones for the axial stiffness.
3 Integrating the stiffnesses into a component simulation and assessment of the influence of the pre-strain and sheet thinning on the clinched joint loadings
3.1 Determining the equivalent stiffnesses
The maximum strengths of a clinched joint, its stiffnesses and its failure behavior are usually determined experimentally by performing tests with the patented LWF-KS-2 [19] or with modified ARCAN [20] specimens. Both test setups ensure that the measurement of clinched joint properties is affected only slightly by the surrounding sheet metal. This is especially important for the determination of the pull-out strength [16]. In [21], a point-connector model is used to describe the stiffnesses of self-piercing rivets under different loading conditions with anisotropic stiffness parameters, which improves the prediction quality significantly. In this paper, a point connector is also used. In order to exclude an influence of the sheet on the determined stiffness, the stiffness is measured extremely locally.
The determined stiffnesses of the clinched joints should be transmitted into a FE model of a component, which is modelled with shells. Embedding the 3D clinched joint directly into the shell structure would be very costly in two aspects. Due to the high number of elements, the computation time of the model increases and if the pre-strain is varied, the 3D models have to be replaced, which increases the effort for model preparation. When performing a crash simulation, the computational effort increases as well, due to the dependency of the maximum time step from the smallest edge length [22]. Therefore, a point-connector model is used to represent the clinched joints. The model of [23] is a variation of the model of [24] which is also similar to the formulation of [25]. The models [23], [24] and [25] were developed to represent self-piercing rivets. In [23], no bending moment is calculated. In this research, the model of [24] is used. The shells are connected by a uniform interpolation approach. The nodes that are coupled are located around an imaginary cylinder around the center node. The model of [16] is developed for representing clinched joints. In that model the nodes in the shell planes which are coupled are also identified by using a cylindrical approach. However, the nodes are coupled by a rigid displacement condition.
Although the point-connector model provides a local representation for the clinched joint, using the local stiffnesses of the virtual test directly would not lead to a correct representation of the clinched joint behavior. To guarantee this, a small model is built, and the force–displacement curves are matched afterwards. The model is shown schematically in Fig. 8. The model consists of shells for the lower and upper sheet and the point connector for the clinched joint. Thus, this model is a simplified one of the detailed representation. The edge length of the shells is 1.0 mm, the thickness is 1.5 mm. The shells represent the mid-surface of the sheets. Over the shell thickness, each element has five integration points. The radius of the coupling zone of the point-connector model is 5.0 mm. The torsional stiffness is set to 0 N/rad and the bending stiffness to 1010. The calculation is performed in LS-DYNA R12 using the explicit solver.
A function for converting the stiffnesses determined the virtual tests to the equivalent stiffnesses is generated for each loading direction. A quadratic approximation is observed in the normal direction and a linear relationship in the shear direction which is shown in Fig. 8. The coefficient of determination R2 of both fits is higher than 0.999. The conversion function for the stiffness is given in (1) and (2). The values for the corresponding coefficients are given in Table 1.
Using the metamodels, depicted in Figs. 5 and 6, predicting the stiffnesses and the conversion functions described here, allows computing the equivalent stiffnesses for the point-connector model for any pre-strain combination, without performing any further simulation.
3.2 Setup of the component model
By transferring the clinched joints into a component, the influence of the changed joint stiffnesses due to the pre-strain and the influence of the thinning of the sheets in the flanges on the clinched joint loading will be carried out. For this purpose, a suitable component is sought on which these investigations can be carried out. The clinched joint investigated above combines a symmetrical sheet combination made of dual-phase steel. Both sheets are made from HCT590x and their thickness is 1.5 mm. A part of the left front structure including the side member of a free available car body model [26] has been chosen to have an exemplary assembly which is as realistic as possible. The connection in the flanges is realized by spot welds in the vehicle body. These points are generally suitable for substitution with clinched joints and thus are substituted in the model. Clinched joints originally connecting three sheets were split into two joints, so that two groups of shell elements can be assigned to every joint. For this the two new joints are shifted a little bit apart. The shell elements of the sheet metal parts are thickened to 1.5 mm and the same material curve of HCT590x is assigned. The structure is fixed to the A-pillar and loaded on the two beam sections. The model set-up is depicted in Fig. 9. The settings of the model are the same as in the shell model for fitting the point connector which is shown schematically in Fig. 8.
In the assembly only feasible clinched joints are used, which means that the pre-strain must be equal or less than 18% as explained earlier. The resulting ranges of the stiffnesses and thickness are listed in Table 2.
3.3 Method
A total of 121 simulations are carried out to assess the influence of sheet thinning of the flanges and changed clinched joint stiffnesses on the loading in the individual points. The simulations are divided into three groups:
-
Group A: Simulation of all flanges with nominal plate thickness of 1.5 mm and with a nominal clinched joint stiffnesses without pre-strain. Number of simulations:1
-
Group B: Simulation of all flanges with a nominal plate thickness of 1.5 mm and different clinched joint stiffnesses due to pre-strain. Number of simulations: 40
-
Group C: Simulation of all flanges with nominal clinched joint stiffness and thinned sheet thicknesses. For this purpose, the sheet thicknesses belonging to the clinched joint stiffnesses from group B are used.
-
Group D: Simulation of all flanges with clinched joint stiffnesses due to pre-strain and thinned sheet thicknesses. Number of simulations: 40
Since no forming simulation for the sheet metal parts has been performed the pre-strain in the flanges, as well as the pre-strain and sheet thinning in the rest of the components is not considered. As the load is purely elastic, the pre-straining in the sheet metal parts can be neglected. If the thinning of the components were also changed, this effect would outweigh the other two. A local influence of the flanges and the local stiffnesses would then no longer be recognizable. Figure 10 shows exemplary which areas are varied in their sheet thickness in the sheet metal parts. After the simulations, the influence of the thinning in the joining flanges and the influence of the joint stiffnesses are carried out.
3.4 Results of the component loading
The relative standard deviations are determined for the data series of group B-D and plotted in histograms which are illustrated in Fig. 11. Hence, it is assumed that the influence is only relevant if the scatter is greater than 10%. Since 95% of all values lie in a standard deviation in the interval μ + − 1.96σ, the limit value is set to 2σ for the sake of simplicity.
It can be clearly seen that both, the variation of the sheet thicknesses and the variation of the clinched joint stiffnesses change the loads in the clinched joints. If the effect is superimposed, the influence is clearly greater, which can be seen by the transparent columns with black lines. The maxima of those columns are significantly shifted further to the right.
In Table 3 the absolute and relative number of joints that scatter more than 10% when considering the interval 2σ are listed. This results in the following observations:
-
The scatter in the joint loadings is highest when the joint stiffnesses and the thickness thinning of the flanges is considered
-
The axial force, the bending moment and the loading angle in the clinched joints varies more due to the change in sheet thickness than due to the different clinched joint stiffnesses caused by the pre-strain.
-
The change in joint stiffnesses due to the local pre-strain in the joining area has a greater influence on the shear force than the sheet thinning.
In a shear force-normal force diagram of one single clinched joint the scattering of the forces can be seen. The dots when considering both effects are very close to the dots when considering sheet thinning in the flanges and different clinched joint stiffnesses due to pre-strain separately. This observation is valid for all clinched joints. As an example, such a diagram for one clinched joint is shown in Fig. 12. On the right, the component with its displacement deformation and the position of the exemplary selected clinched joint is shown.
4 Discussion and outlook
With the modeling of the entire process chain, it is possible to separately represent the influence of the changed stiffnesses of the clinched joints and the sheet thicknesses in the flanges. The results show that neglecting the stiffness reduction by pre-forming leads to a significantly higher error than neglecting the actual thinned sheet thickness in the scatter of the loading in the shear direction. In the selected load case, the joints are mainly loaded to shear, which is typical in real joined structures [27]. The load in the axial direction, the bending moment, and the loading angle are more sensitive to sheet thinning in the flanges than to stiffness change.
It is interesting that the sheet thicknesses and stiffnesses are reduced by pre-forming, but the actual load in a clinched joint scatter in both directions. The decrease in stiffness due to pre-forming can be clearly seen in the metamodels (Figs. 5a, 6a). When a clinched joint is loaded even more in one simulation than in the initial, the joints around it have been more significantly reduced in their stiffnesses. This means that load redistribution occurs, which can be seen in fatigue life calculations with degradation as well [15]. In consequence, it is essential to take the pre-forming into account when dimensioning clinched components. According to Table 3, there are cases for about 80% of the clinched joints, in which the loading angle is significantly different to the angle which is assumed by a simulation neglecting pre-forming. To consider the influence of pre-forming on the joint stiffnesses efficiently during the component loading simulation, analytical functions are needed to describe the equivalent stiffnesses in dependence of the pre-strain. For the combination presented here, such formulas are given if the equations of the metamodels are inserted into (1), respectively (2).
It should also be emphasized that when inspecting all shear force- axial force diagrams (see Fig. 12, left), it is noticeable that in most cases the blue and red points do not cover the same area. This means that the influence of sheet thinning and different stiffnesses do not influence the joint loadings in the same way. When both effects are considered, the sum of the other scatter is covered to a good approximation. In Fig. 12 this can be seen by the green dots. Neglecting either effect when determining the loadings acting in a clinched joint is not recommended. A link where the dot of the initial simulation is in the force diagram is not apparent, by looking only on the diagrams.
The fact that the normal force is influenced much more strongly than the shear force by the sheet thinning is due to a slightly bending of the sheets. In the shear direction, on the other hand, a slight decrease in sheet thickness hardly changes the sheet stiffness, which is why the shear force is less sensitive to the sheet thickness change outside the joint. Nevertheless, this result is particularly remarkable since the normal stiffness was varied more than the shear stiffness.
However, it must be noted that the effect of the different axial stiffness is underestimated due to the modeling. As can be seen in Fig. 5b, non-pre-strained sheets lead to clinch joints with an axial preload. This axial preload was not transferred into the point connector model as described in the methodology. This leads to a slight skew of the load angle.
Based on the presented results, a further step is to look at the interaction of the decrease in stiffness of a single joint with the loadings of the surrounding joints. This might help to better understand the effect of the redistribution which can be observed in the shown simulations. Furthermore, the joint distribution of the model of Fig. 9 could be optimized. To achieve this, it is proposed to perform forming simulations of the sheet metal parts first. Subsequently, the flanges can be parameterized and a Size Optimization can be performed where the stiffnesses are adjusted to the predominant strain using the metamodels. A Size Optimization without considering pre strain and sheet thinning is demonstrated in [28]. It would be also worth to look at the energy density distribution afterwards and thus assess how evenly the material in the flanges are loaded.
5 Conclusions
In this paper, a point connector is used to describe the loadings in a clinched joint depending on the pre-strain before the joining operation. Continuous functions for the determination of the stiffnesses and continuous functions for the determination of the equivalent stiffnesses for a point-connector model for a clinched joint are determined. The pre-strain of the two connected sheets are the only values included in these formulas. By simulating the entire process chain the following results are obtained:
The findings show that considering the pre-strain before the clinching process is highly recommended. The altered stiffnesses of the joints changes the load distribution in the joints by redistributing the loadings. By separating the effect of the local changed stiffnesses in the joints and the effect of global sheet thinning in the flanges, it is shown that the reduced joint stiffnesses has a much higher influence on the shear loading. The loading in the normal direction and the loading angle are more sensitive to the sheet thinning in the flanges.
The continuous equations for calculating the equivalent stiffnesses can be used directly in an optimization algorithm to adjust the stiffnesses. For example, the layout of the joints can be optimized using Size Optimization. The maximum load bearing capacity can also be determined with the presented method in a further step and can be passed directly to an optimization algorithm. Since the point-connector model is suitable for modeling dynamic loads, the methodology can be extended to crash modelling.
References
Wolfram P, Tu Q, Heeren N, Pauliuk S, Hertwich EG (2021) Material efficiency and climate change mitigation of passenger vehicles. J Indl Ecol 25(2):494–510. https://doi.org/10.1111/jiec.13067
Martinsen K, Hu SJ, Carlson BE (2015) Joining of dissimilar materials. CIRP Ann 64(2):679–699. https://doi.org/10.1016/j.cirp.2015.05.006
Jiang T, Liu ZX, Wang PC (2015) Effect of aluminum pre-straining on strength of clinched galvanized SAE1004 steel-to-AA6111-T4 aluminum. J Mater Process Technol 215:193–204. https://doi.org/10.1016/j.jmatprotec.2014.08.016
Chen C, Zhang H, Zhao S, Xiaoqiang R (2021) Effects of sheet thickness and material on the mechanical properties of flat clinched joint. Front Mech Eng 16(2):410–419. https://doi.org/10.1007/s11465-020-0618-y
Chen C, Han X, Zhao S, Xu F, Zhao X, Ishida T (2018) Influence of sheet thickness on mechanical clinch-compress joining technology. Proc Inst Mech Eng E J Process Mech Eng 232(6):662–673. https://doi.org/10.1177/0954408917735717
Varis J (2006) Ensuring the integrity in clinching process. J Mater Process Technol 174(1–3):277–285. https://doi.org/10.1016/j.jmatprotec.2006.02.001
Hahn O, Kruzok JR (1998) Umformtechnisches Fügen vorverformter Halbzeuge-Teil 1: Stahl, Berichte aus dem Laboratorium für Werkstoff- und Fügetechnik, Band 37. Shaker, Paderborn. ISBN: 978-3826543944
Eggink DHD, Groll MW, Perez-Ramirez DF, Biedert J, Knödler C, Papentin P (2019) Towards automated joining element design. Procedia Comput Sci 159:87–96. https://doi.org/10.1016/j.procs.2019.09.163
Bhatti QI, Ouisse M, Cogan S (2011) An adaptive optimization procedure for spot-welded structures. Comput Struct 89(17–18):1697–1711. https://doi.org/10.1016/j.compstruc.2011.04.009
Donders S, Brughmans M, Hermans L, Tzannetakis N (2005) The effect of spot weld failure on dynamic vehicle performance. Sound Vib 39(4):16–24
Junqueira DM, Silveira ME, Ancelotti AC (2018) Analysis of spot weld distribution in a weldment—numerical simulation and topology optimization. Int J Adv Manuf Technol 95:4071–4079. https://doi.org/10.1007/s00170-017-1555-8
Ryberg AB, Nilsson L (2016) Spot weld reduction methods for automotive structures. Struct Multidiscip Optim 53(4):923–934. https://doi.org/10.1007/s00158-015-1355-4
Saito T, Shiozaki T, Tamai Y. (2019) A study of topology optimization for spot welding locations in automotive body by using driving simulation. SAE technical paper 2019(01), p 0830.https://doi.org/10.4271/2019-01-0830
Farrahi GH, Ahmadi A, Kasyzadeh KR (2020) Simulation of vehicle body spot weld failures due to fatigue by considering road roughness and vehicle velocity. Simul Model Pract Theory 105:102168. https://doi.org/10.1016/j.simpat.2020.102168
Rösch P, Schmidt H, Bruder T (2018) A novel approach to simulate the stiffness behaviour of spot welded vehicle structures under multi axial variable amplitude loading. MATEC Web Conf 165:17005. https://doi.org/10.1051/matecconf/201816517005
Breda A, Coppieters S, Debruyne D (2017) Equivalent modelling strategy for a clinched joint using a simple calibration method. Thin Walled Struct 113:1–12. https://doi.org/10.1016/j.tws.2016.12.002
Bielak CR, Böhnke M, Beck R, Bobbert M, Meschut G (2021) Numerical analysis of the robustness of clinching process considering the pre-forming of the parts. J Adv Join Process 3:100038. https://doi.org/10.1016/j.jajp.2020.100038
Bielak CR, Böhnke M, Bobbert M, Meschut G (2021) Further development of a numerical method for analyzing the load capacity of clinched joints in versatile process chains. In: 24th international conference on material forming, Liège, Belgique PoPuPS. https://doi.org/10.25518/esaform21.4298
Hahn O, Gieske D (1994) Neue Einelementprobe zum Pruefen von Punktschweissverbindungen unter kombinierten Belastungen. Schweißen und Schneiden 46/1:9-12. ISSN: 0036-7184
Porcaro R, Hanssen AG, Aalberg A, Langseth M (2004) Joining of aluminium using self-piercing riveting: testing, modelling and analysis. Int J Crash 9(2):141–154. https://doi.org/10.1533/ijcr.2004.0279
Otroshi M, Meschut G, Bielak C, Masendorf L, Esderts A (2021) Modeling of stiffness anisotropy in simulation of self-piercing riveted components. Key Eng Mater 883:35–40. https://doi.org/10.4028/www.scientific.net/kem.883.35
Livermore Software Technology Corporation (2019) LS_DYNA theory manual (r11261), p 25-1
Bier M, Sommer S (2013) Simplified modeling of self piercing riveted joints for crash simulation with a modified version of *CONSTRAINED_INTERPOLATION_SPOTWELD. 9th LS-DYNA Conference 2013, Manchester. https://www.dynalook.com/conferences/9th-european-ls-dyna-conference/simplified-modeling-of-self-piercing-riveted-joints-for-crash-simulation-with-a-modified-version-of-constrained_interpolation_spotweld. Accessed 21 Nov 2019
Hanssen AG, Olovsson L, Porcaro R, Langseth M (2010) A large-scale finite element point connector model for self-piercing rivet connections. Eur J Mech A Solids 29(4):484–495. https://doi.org/10.1016/j.euromechsol.2010.02.010
Weyer S, Hooputra H, Zhou F (2006) Modelling of self-piercing rivets using fasteners in crash analysis. ABAQUS USERS' conference. 2006, Boston
Singh H (2012) Mass reduction for light-duty vehicles for model years 2017–2025. Report no. DOT HS 811 666, program reference: DOT contract DTNH22-11-C-00193; 2012 contract prime: Electricore, Inc., Auburn Hills: EDAG, Inc.
Martin S, Camberg A, Tröster T (2020) Probability distribution of joint point loadings in car body structures under global bending and torsion. Proc Manuf 47:419–424. https://doi.org/10.1016/j.promfg.2020.04.324
Pakalapati V, Katkar V, Babar R (2011) CAE based ‘multi objective optimization approach for spot weld connections layout’ in automotive structure. SAE technical paper 2011(01), p 0794. https://doi.org/10.4271/2011-01-0794
Funding
Open Access funding enabled and organized by Projekt DEAL. The funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)–TRR 285–Project-ID 418701707, subproject A01 and B01 is gratefully acknowledged. Thanks, are also due to the Paderborn Center for Parallel Computing (PC2) for funding this project with the computing time provided.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Martin, S., Bielak, C.R., Bobbert, M. et al. Numerical investigation of the clinched joint loadings considering the initial pre-strain in the joining area. Prod. Eng. Res. Devel. 16, 261–273 (2022). https://doi.org/10.1007/s11740-021-01103-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11740-021-01103-w